Impact of Laser Power and Scanning Speed on Single-Walled Support Structures in Powder Bed Fusion of AISI 316L
Abstract
1. Introduction
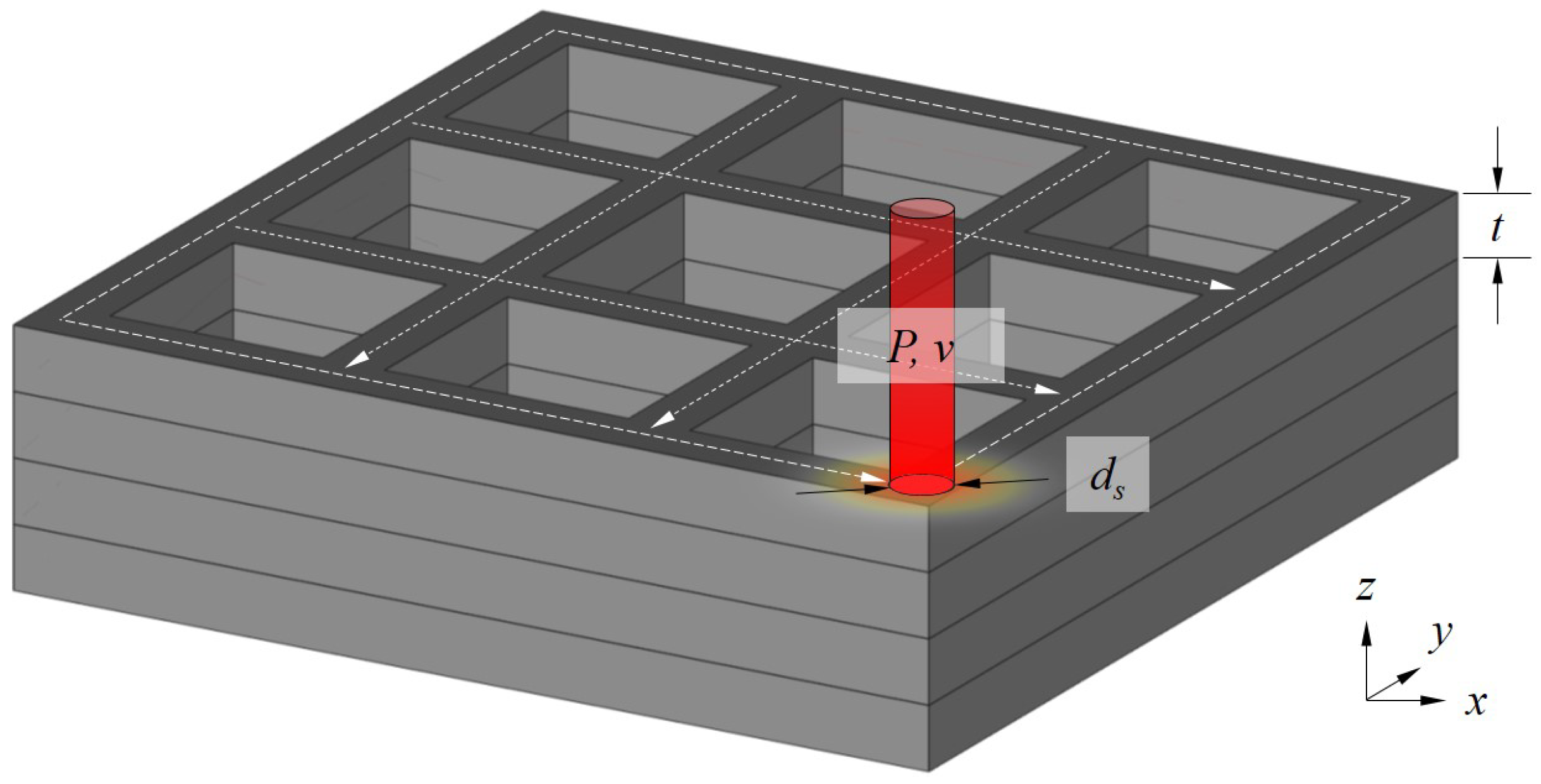
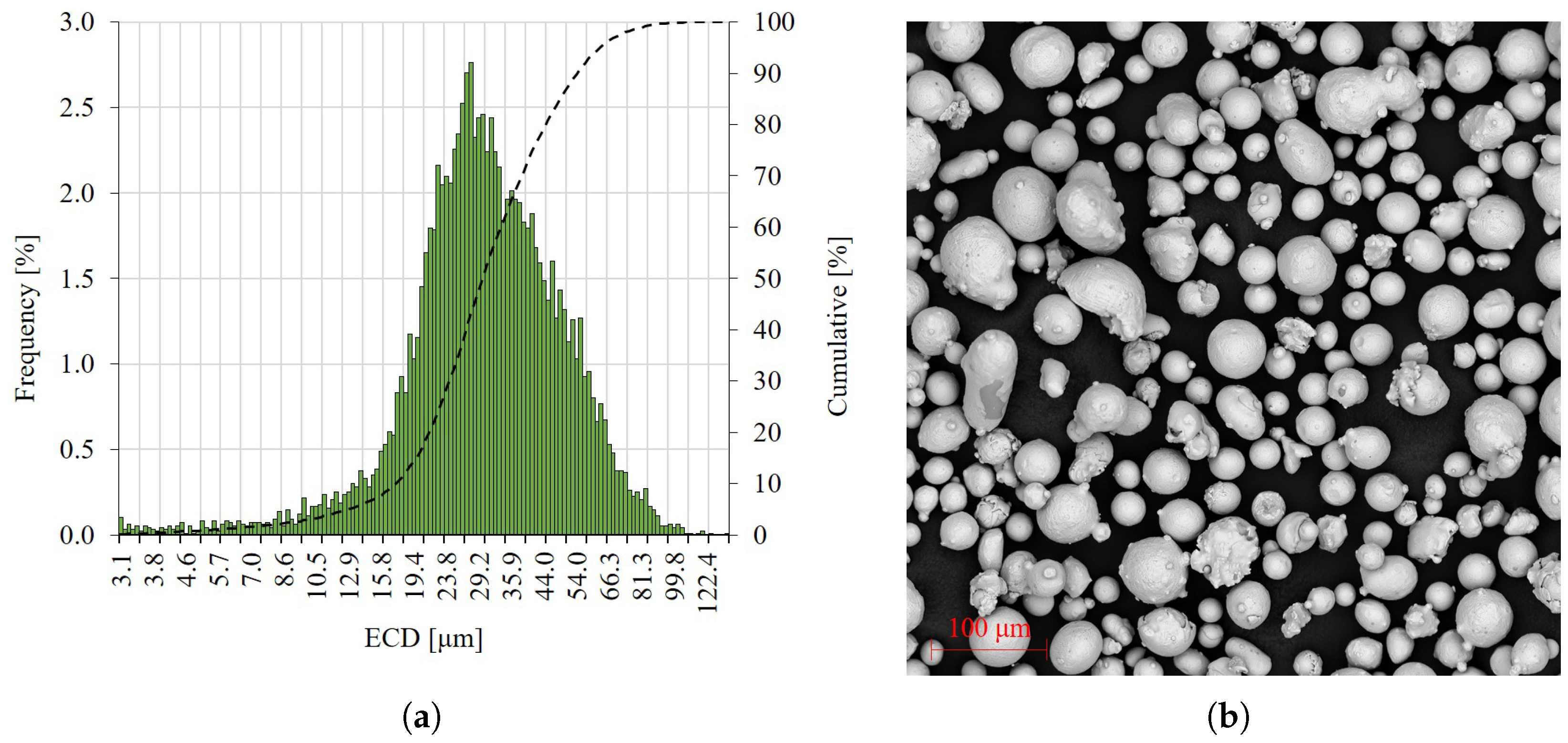
2. Materials and Methods
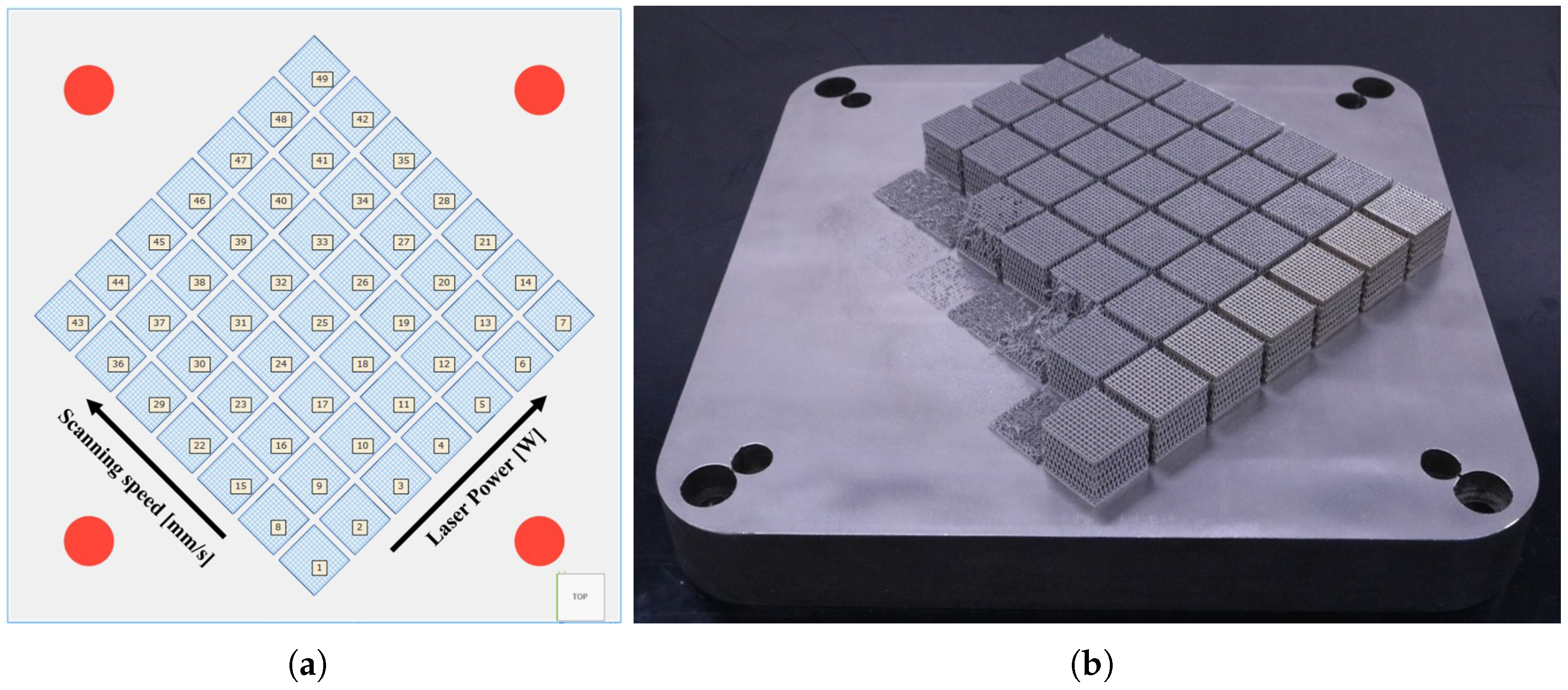
2.1. Processing Parameter Exploration
2.2. Mechanical Characterization
3. Results and Discussions
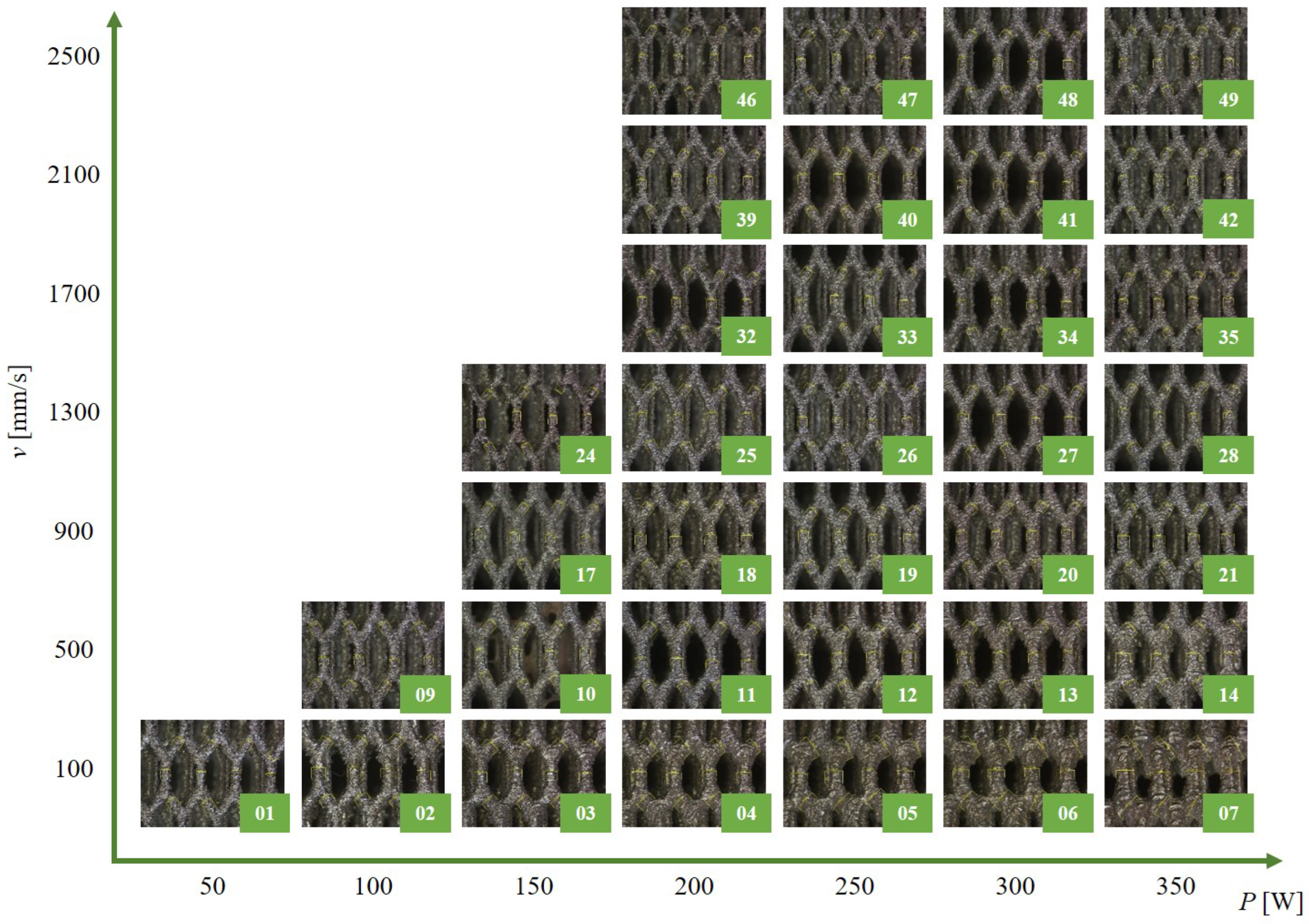
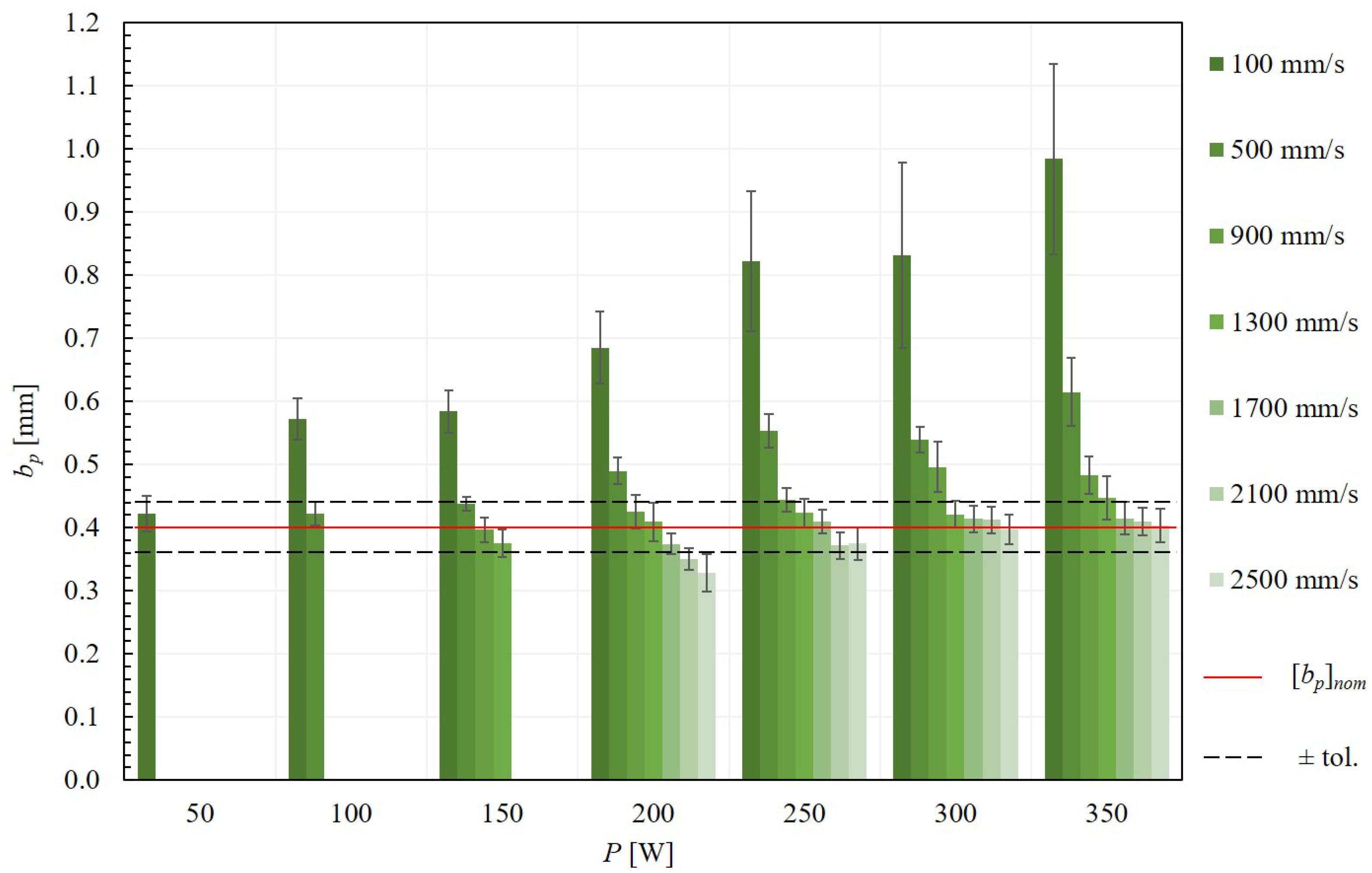
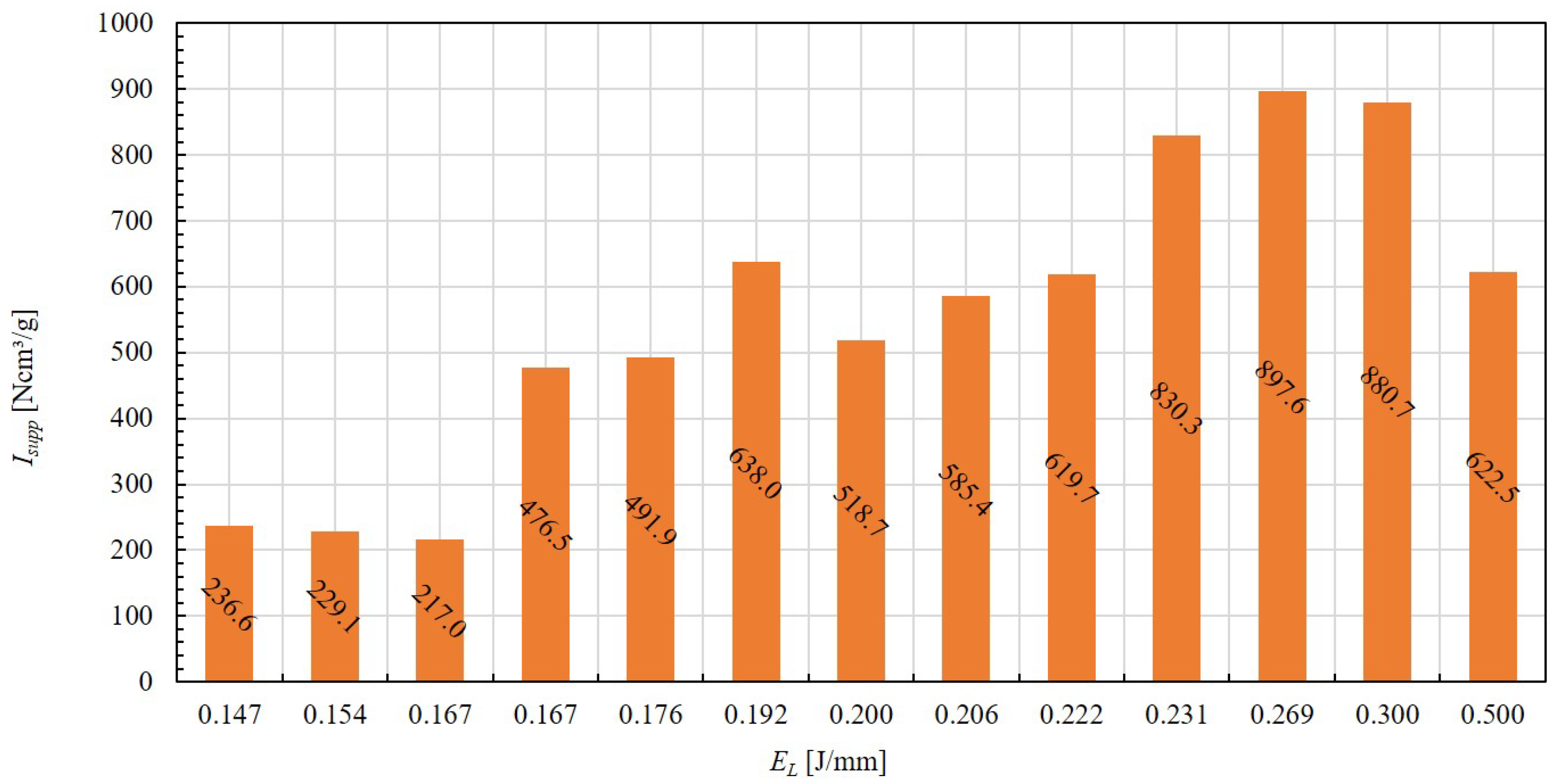
3.1. Processing Parameter Exploration
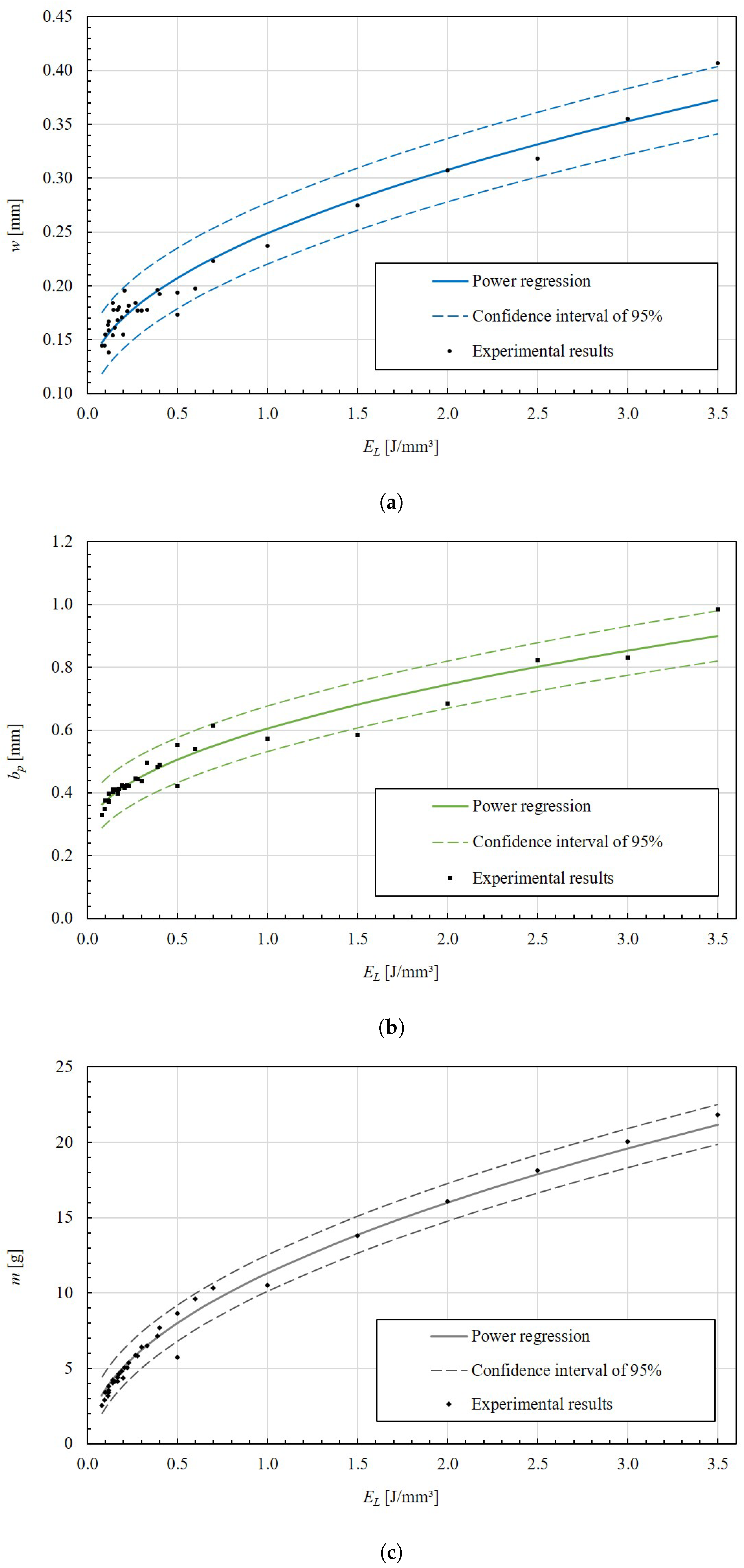
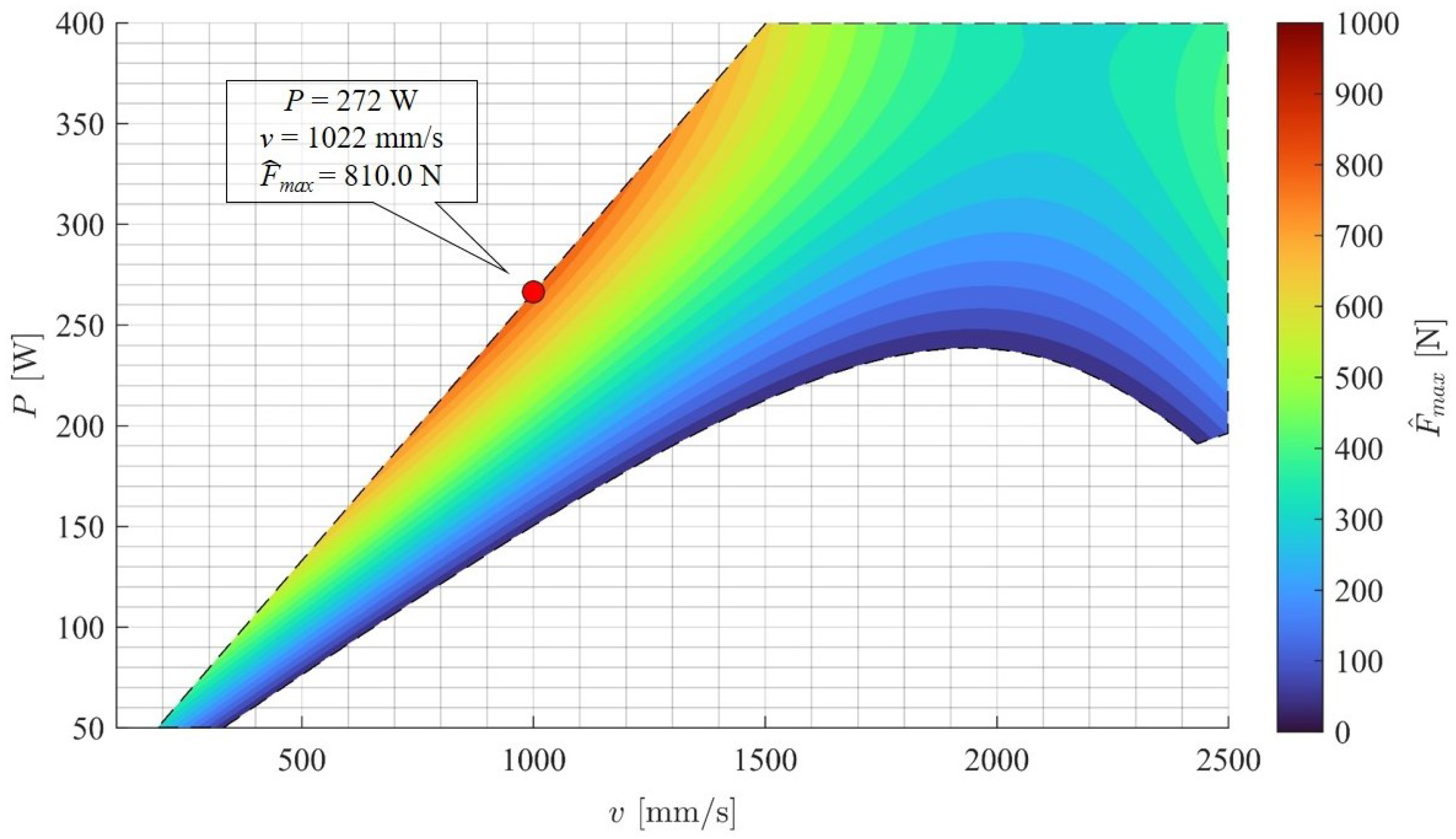
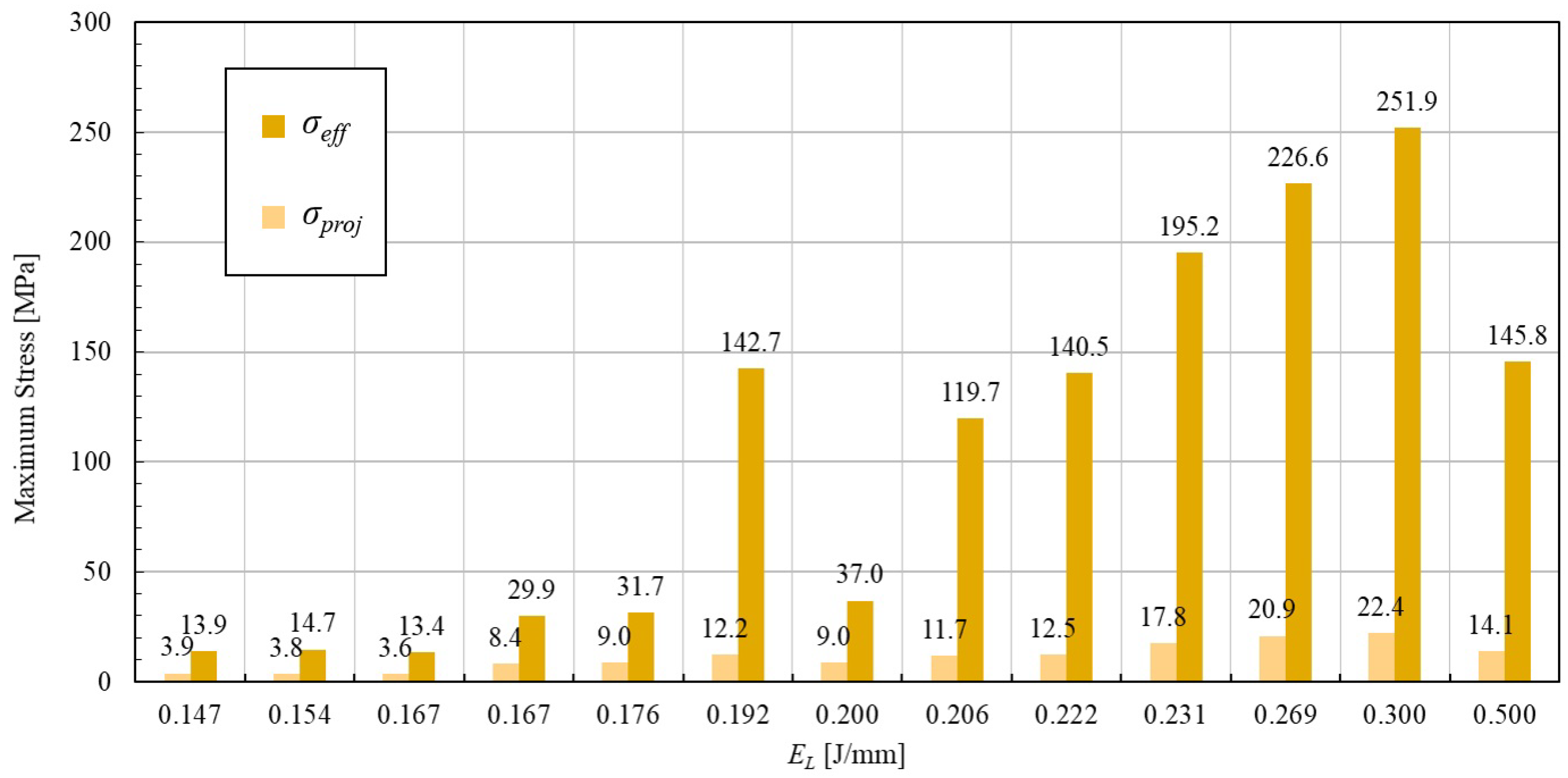
3.2. Mechanical Characterization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ISO/ASTM 52900:2021; Additive Manufacturing–General Principles–Fundamentals and Vocabulary. International Organization for Standardization: Geneva, Switzerland, 2021.
- Wohlers Associates, Inc. Wohlers Report 2023: 3D Printing and Additive Manufacturing Global State of the Industry; Wohlers Associates: Fort Collins, CO, USA, 2023. [Google Scholar]
- McConnell, S.; Tanner, D.; Kourousis, K.I. Productivity improvement opportunities for metal powder bed fusion technologies: A systematic literature review. Rapid Prototyp. J. 2024, 30, 231–246. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar]
- Elsen, M. Complexity of Selective Laser Melting: A New Optimisation Approach. Ph.D Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2007. [Google Scholar]
- Wang, D.; Yang, Y.; Yi, Z.; Su, X. Research on the fabricating quality optimization of the overhanging surface in SLM process. Int. J. Adv. Manuf. Technol. 2013, 65, 1471–1484. [Google Scholar] [CrossRef]
- Kruth, J.-P.; Deckers, J.; Yasa, E.; Wauthle, R. Assessing and comparing influencing factors of residual stresses in selective laser melting using a novel analysis method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 980–991. [Google Scholar] [CrossRef]
- Charles, A.; Elkaseer, A.; Thijs, L.; Hagenmeyer, V.; Scholz, S. Effect of process parameters on the generated surface roughness of down-Facing surfaces in selective laser melting. Appl. Sci. 2019, 9, 1256. [Google Scholar] [CrossRef]
- Zhang, K.; Fu, G.; Zhang, P.; Ma, Z.; Mao, Z.; Zhang, D.Z. Study on the Geometric Design of Supports for Overhanging Structures Fabricated by Selective Laser Melting. Materials 2019, 12, 27. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, X.; Stringer, J. Support Structures for Additive Manufacturing: A Review. J. Manuf. Mater. Process. 2018, 2, 64. [Google Scholar] [CrossRef]
- Cloots, M.; Zumofen, L.; Spierings, A.; Kirchheim, A.; Wegener, K. Approaches to minimize overhang angles of SLM parts. Rapid Prototyp. J. 2017, 23, 362–369. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J.-P. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Calignano, F.; Galati, M.; Iuliano, L. A Metal Powder Bed Fusion Process in Industry: Qualification Considerations. Machines 2019, 7, 72. [Google Scholar] [CrossRef]
- Mahmood, M.A.; Chioibasu, D.; Ur Rehman, A.; Mihai, S.; Popescu, A.C. Post-Processing Techniques to Enhance the Quality of Metallic Parts Produced by Additive Manufacturing. Metals 2022, 12, 77. [Google Scholar] [CrossRef]
- Autodesk. Netfabb Help: To Define a Part as a Support Structure. Available online: https://help.autodesk.com/view/NETF/2025/ENU/?guid=GUID-6DF4CD36-ED33-4A3F-B073-892DCA5AC864 (accessed on 7 June 2025).
- Materialise. Optimal Metal Supports for Additive Manufacturing. Available online: https://www.materialise.com/en/inspiration/articles/optimal-metal-supports (accessed on 7 June 2025).
- Oliveira, J.P.; LaLonde, A.D.; Ma, J. Processing parameters in laser powder bed fusion metal additive manufacturing. Mater. Des. 2020, 193, 108762. [Google Scholar] [CrossRef]
- Bassoli, E.; Sola, A.; Celesti, M.; Calcagnile, S.; Cavallini, C. Development of Laser-Based Powder Bed Fusion Process Parameters and Scanning Strategy for New Metal Alloy Grades: A Holistic Method Formulation. Materials 2018, 11, 2356. [Google Scholar] [CrossRef] [PubMed]
- Weber, S.; Montero, J.; Bleckmann, M.; Paetzold, K. Parameters on Support Structure Design for Metal Additive Manufacturing. In Proceedings of the Design Society: DESIGN Conference, Cavtat, Croatia, 26–29 October 2020; pp. 1145–1154. [Google Scholar] [CrossRef]
- Calignano, F. Design optimization of supports for overhanging structures in aluminum and titanium alloys by selective laser melting. Mater. Des. 2014, 64, 203–213. [Google Scholar] [CrossRef]
- Bobbio, L.D.; Qin, S.; Dunbar, A.; Michaleris, P.; Beese, A.M. Characterization of the strength of support structures used in powder bed fusion additive manufacturing of Ti-6Al-4V. Addit. Manuf. 2017, 14, 60–68. [Google Scholar] [CrossRef]
- Lindecke, P.; Blunk, H.; Wenzl, J.; Möller, M.; Emmelmann, C. Optimization of support structures for the laser additive manufacturing of TiAl6V4 parts. Procedia CIRP 2018, 74, 53–58. [Google Scholar] [CrossRef]
- Leary, M.; Maconachie, T.; Sarker, A.; Faruque, O.; Brandt, M. Mechanical and thermal characterisation of AlSi10Mg SLM block support structures. Mater. Des. 2019, 2019, 108138. [Google Scholar] [CrossRef]
- Gong, H.-J.; Teng, C.; Zeng, K.; Pal, D.; Stucker, B.E.; Dilip, J.J.S.; Beuth, J.L.; Lewandowski, J.J. Single Track of Selective Laser Melting Ti-6Al-4V Powder on Support Structure. In Proceedings of the 26th Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 8–10 August 2016; Available online: https://api.semanticscholar.org/CorpusID:55217472 (accessed on 7 June 2025).
- Morgan, D.; Agba, E.; Hill, C. Support Structure Development and Initial Results for Metal Powder Bed Fusion Additive Manufacturing. Procedia Manuf. 2017, 10, 819–830. [Google Scholar] [CrossRef]
- Schmitt, M.; Kempter, B.; Schlick, G.; Reinhart, G. Parameter Identification Approach for Support Structures in Laser Powder Bed Fusion and Analysis of Influencing Factors. Procedia CIRP 2020, 94, 260–265. [Google Scholar] [CrossRef]
- Vaglio, E.; De Monte, T.; Lanzutti, A.; Totis, G.; Sortino, M.; Fedrizzi, L. Single Tracks Data Obtained by Selective Laser Melting of Ti6Al4V with a Small Laser Spot Diameter. Data Brief 2020, 33, 106443. [Google Scholar] [CrossRef]
- Großmann, A.; Felger, J.; Frölich, T.; Gosmann, J.; Mittelstedt, C. Melt Pool Controlled Laser Powder Bed Fusion for Customised Low-Density Lattice Structures. Mater. Des. 2019, 181, 108054. [Google Scholar] [CrossRef]
- Dabwan, A.; Anwar, S.; Al-Samhan, A.M.; AlFaify, A.; Nasr, M.M. Investigations on the Effect of Layers’ Thickness and Orientations in the Machining of Additively Manufactured Stainless Steel 316L. Materials 2021, 14, 1797. [Google Scholar] [CrossRef]
- Sefene, E.M. State-of-the-Art of Selective Laser Melting Process: A Comprehensive Review. J. Manuf. Syst. 2022, 63, 250–274. [Google Scholar] [CrossRef]
- ASTM E8/E8M:2016; Standard Test Methods for Tension Testing of Metallic Materials. American Society for Testing and Materials: West Conshohocken, PA, USA, 2016.
- Gallego, D.A.; Oliveira, H.R.; Volpato, N. Tensile Strength Specimens for Non-Solid Block Support Structures Manufactured by Laser Powder Bed Fusion: A Preliminary Study. In Proceedings of the 27th International Congress of Mechanical Engineering, Florianópolos, Brazil, 25–27 September 2023. [Google Scholar] [CrossRef]
- ASME SA-240/SA-240M:2007; Standard Specification for Chromium and Chromium-Nickel Stainless Steel Plate, Sheet, and Strip for Pressure Vessels and for General Applications. American Society of Mechanical Engineers: New York, NY, USA, 2007.









| Design Parameter | Description | Value | Reference |
|---|---|---|---|
| Perforation angle | 60.0 deg | Materialise [16] | |
| Rotation angle | 45.0 deg | Materialise [16] | |
| Scan line distance | 1.50 mm | Schmitt [26] | |
| Solid height | 1.50 mm | Schmitt [26] | |
| Perf. beam thickness | 0.40 mm | Lindecke [22] | |
| Perforation height | 1.00 mm | Schmitt [26] |
| [J/mm] | v [mm/s] | |||||||
|---|---|---|---|---|---|---|---|---|
| 100 | 500 | 900 | 1300 | 1700 | 2100 | 2500 | ||
| P [W] | 50 | 0.500 | 0.100 | 0.056 | 0.038 | 0.029 | 0.024 | 0.020 |
| 100 | 1.000 | 0.200 | 0.111 | 0.077 | 0.059 | 0.048 | 0.040 | |
| 150 | 1.500 | 0.300 | 0.167 | 0.115 | 0.088 | 0.071 | 0.060 | |
| 200 | 2.000 | 0.400 | 0.222 | 0.154 | 0.118 | 0.095 | 0.080 | |
| 250 | 2.500 | 0.500 | 0.278 | 0.192 | 0.147 | 0.119 | 0.100 | |
| 300 | 3.000 | 0.600 | 0.333 | 0.231 | 0.176 | 0.143 | 0.120 | |
| 350 | 3.500 | 0.700 | 0.389 | 0.269 | 0.206 | 0.167 | 0.140 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallego, D.A.; Rodrigues Oliveira, H.; Cunha, T.; Trevizan Pacheco, J.; Kovalenko, O.; Volpato, N. Impact of Laser Power and Scanning Speed on Single-Walled Support Structures in Powder Bed Fusion of AISI 316L. J. Manuf. Mater. Process. 2025, 9, 254. https://doi.org/10.3390/jmmp9080254
Gallego DA, Rodrigues Oliveira H, Cunha T, Trevizan Pacheco J, Kovalenko O, Volpato N. Impact of Laser Power and Scanning Speed on Single-Walled Support Structures in Powder Bed Fusion of AISI 316L. Journal of Manufacturing and Materials Processing. 2025; 9(8):254. https://doi.org/10.3390/jmmp9080254
Chicago/Turabian StyleGallego, Dan Alexander, Henrique Rodrigues Oliveira, Tiago Cunha, Jeferson Trevizan Pacheco, Oksana Kovalenko, and Neri Volpato. 2025. "Impact of Laser Power and Scanning Speed on Single-Walled Support Structures in Powder Bed Fusion of AISI 316L" Journal of Manufacturing and Materials Processing 9, no. 8: 254. https://doi.org/10.3390/jmmp9080254
APA StyleGallego, D. A., Rodrigues Oliveira, H., Cunha, T., Trevizan Pacheco, J., Kovalenko, O., & Volpato, N. (2025). Impact of Laser Power and Scanning Speed on Single-Walled Support Structures in Powder Bed Fusion of AISI 316L. Journal of Manufacturing and Materials Processing, 9(8), 254. https://doi.org/10.3390/jmmp9080254






