Physics-Informed Preform Design for Flashless 3D Forging via Material Point Backtracking and Finite Element Simulations

Abstract

Accurate preform design in forging processes is critical for improving part quality, conserving material, reducing manufacturing costs, and eliminating secondary operations. This paper presents a finite element (FE) simulation-based methodology for preform design aimed at achieving flashless and near-flashless forging. The approach leverages material point backtracking within FE models to generate physics-informed preform geometries that capture complex material flow, die geometry interactions, and thermal gradients. An iterative scheme combining backtracking, surface reconstruction, and point-cloud solid modeling was developed and applied to several three-dimensional forging case studies, including a cross-joint and a three-lobe drive hub. The methodology demonstrated significant reductions in flash formation, particularly in parts that traditionally exhibit severe flash under conventional forging. Beyond supporting the development of new flashless forging sequences, the method also offers a framework for modifying preforms during production to minimize waste and for diagnosing preform defects linked to variability in frictional conditions, die temperatures, or material properties. Future integration of the proposed method with design of experiments (DOE) and surrogate modeling techniques could further enhance its applicability by optimizing preform designs within a localized design space. The findings suggest that this approach provides a practical and powerful tool for advancing both new and existing forging production lines toward higher efficiency and sustainability.

1. Introduction

In forging processes, the initial billet is deformed into the desired shape by compressive forces. Complex geometries often require intermediate forging steps, and the design of accurate preform dies and billets for these steps is essential to ensure part quality, conserve material, eliminate rehabilitative operations, and reduce costs. Material costs for forged parts are significant—up to 90% for titanium components—underscoring the value of efficient preform design. Traditionally, forging sequence planning has relied on prototyping and designer expertise, but recent advances have led to several automated and semi-automated methodologies. These can be broadly classified into three groups, as summarized in

Table 1. Classification of methods used in preform design for multi-stage forging. A brief summary of strengths and limitations is provided in this table; detailed discussions are presented in the respective sections for Groups 1, 2, and 3.

Group	Category	Typical Techniques	Stage Focus	Strengths	Limitations	Interaction with Other Groups
Group 1	Multi-stage sequence generation	Expert systems Mass-distribution-based methods AI/fuzzy logic system	More than two stages	Fast sequence generation; early-stage planning	Accuracy is limited without physics-based refinement	Provides initial multi-stage plans to Groups 2 and 3
Group 2	Two-stage preform design	Inverse FEM based methods (modern) Geometric resemblance methods Backtracking of material points Geometric mapping methods (historical) Isothermal surfaces methods	Two-stage processes. Axisymmetric and plane strain	Physics-based design; near-net-shape preforms	Challenging for complex 3D parts; needs accurate deformation data	Can operate independently or feed into Group 3 for fine-tuning
Group 3	Optimization and refinement	DOE (Design of Experiments) Surrogate models Machine learning Multi-objective optimization	Any stage (as a post-process)	Fine-tunes geometry; improves manufacturability	Requires an initial shape and can be computationally expensive	Refines designs from Groups 1 and 2 for final deployment

: (1) multi-stage sequence generation, (2) two-stage forging preform design, and (3) optimization and refinement techniques. Each group plays a critical role in addressing the spectrum of complexity in industrial forging, from conceptual sequence planning to precision geometry tuning under realistic constraints.

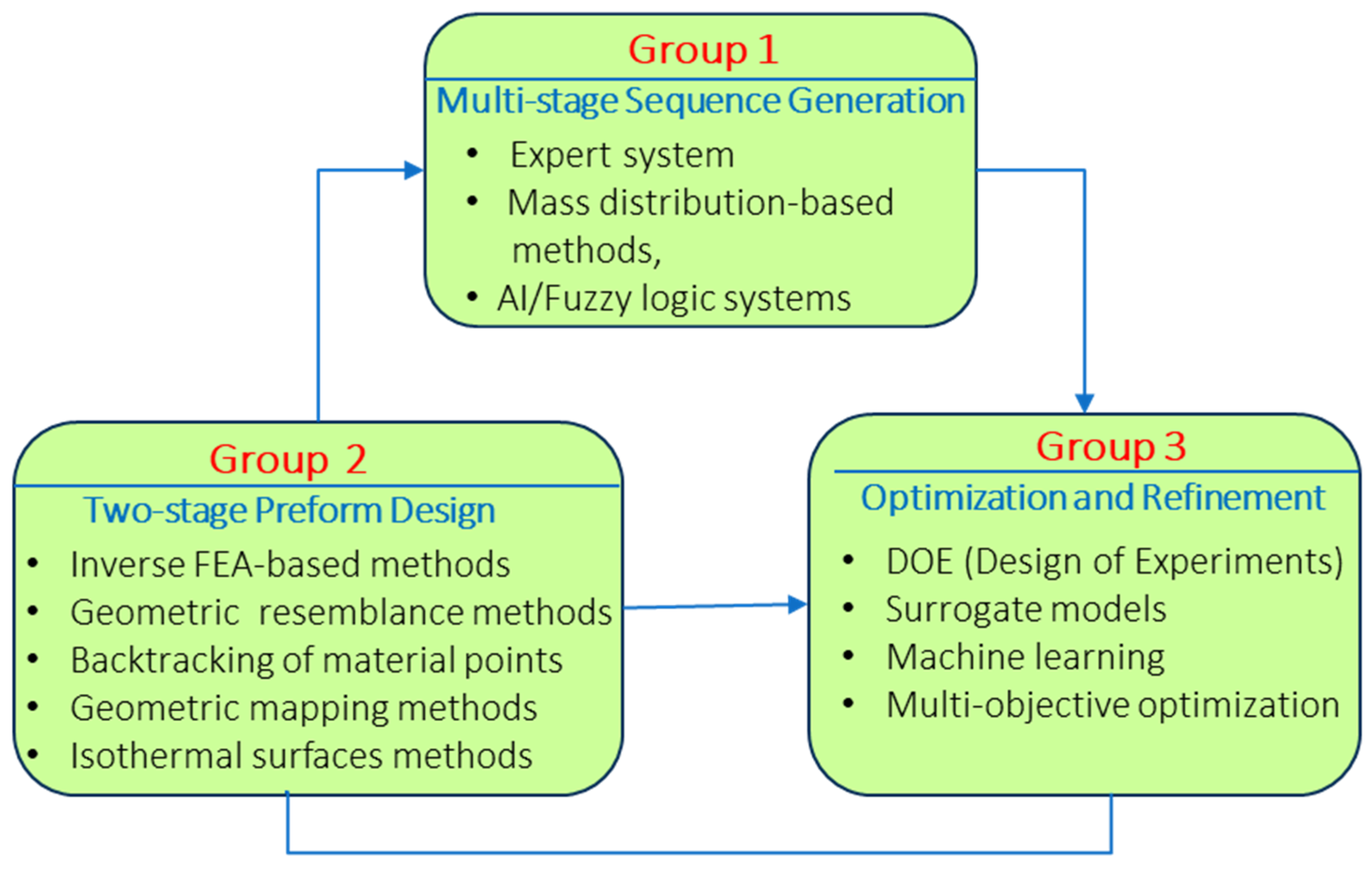
1.1. Group 1: Multi-Stage Sequence Generation

Techniques in Group 1 aim to automatically generate forging sequences for parts requiring more than two stages, particularly in complex industrial components. These methods offer the strength of rapid initial sequence generation and early-stage design guidance. However, they often require subsequent refinement through simulation or optimization to ensure accurate material flow and manufacturability. Early efforts in this direction focused on developing rule-based expert systems. Vemuri et al. [1] introduced the BID (Blocker Initial-guess Design) system, one of the first knowledge-based frameworks for blocker design. BID codified expert heuristics to generate blocker shapes for rib-web type forgings, adjusting key parameters such as rib height and web thickness. Expanding on this concept, Kim and Altan [2] developed FORMEX, a computer-aided environment that integrated rule-based reasoning with CAD tools and FEM simulation to support both product geometry modification and multi-stage forming sequence design.

Further contributions aimed to address hot forging applications. Caporalli et al. [3] presented the ADHFD (Automated Design of Hot Forging Dies) system, a semi-automated part modification, preform design, and sequence generation for flashless precision hot forging, combining rule-based modules with CAD and FEM tools. In parallel, Osakada et al. [4] advanced expert system capabilities by integrating FEM simulation data with statistical analysis and neural networks to develop a self-learning hybrid system for cold forging process planning. Formal sequence generation also evolved through knowledge modularization. Bariani and Knight [5] proposed a system based on backward design logic, geometric primitives, and structured rule groups for the cold forging of rotationally symmetric parts, balancing automation with designer flexibility. Complementing these efforts, Kim and Park [6] developed an integrated system for axisymmetric hot forging that designed billets, busters, blockers, and finishers automatically, introducing shape and volume factors to fine-tune blocker design. Kim and Im [7] developed a system integrating billet sizing, process type selection, and sequence generation for axisymmetric parts, with iterative re-design capabilities. Matsunaga et al. [8] extended these concepts to non-axisymmetric parts through GeneDie, a rule-based design tool that uses die stereotypes and forming surface functions to generate alternative die configurations. Their method allowed the mapping of final product surfaces to functionally meaningful die features, expanding applicability to parts with asymmetry and intricate features.

Similarly, Umeda et al. [9] introduced GeneSteR, a system that performs backward planning using a library of shape transformation rules to reduce a part to its billet form step by step. This approach removes reliance on historical design data, using geometric logic to infer viable preforms. Recent advancements such as the Forging Sequence Design (FSD) system by Hedicke-Claus et al. [10] take automation further by integrating STL geometry analysis, neural network-based shape classification, and fuzzy logic to estimate the number of forging stages. Their method produces intermediate geometries using point-shift algorithms informed by material flow heuristics. Together, these systems form a continuum from early rule-based expert systems to modern AI-augmented sequence generators, providing a foundation for forging process planning that reduces reliance on trial-and-error and enables the early-stage digital exploration of multi-stage forging processes.

1.2. Group 2: Two-Stage Forging Preform Design

Group 2 focuses on techniques specifically suited for two-stage operations, which remain prevalent in practical forging due to equipment and cost constraints. These methods are grounded in physical deformation history, providing near-net-shape designs based on inverse analysis or backtracking. Nonetheless, challenges arise when applying them to highly three-dimensional or bifurcated geometries where geometric reconstruction becomes complex. Early efforts laid the groundwork for modern approaches. Park et al. [11] proposed a node-detachment-based geometric mapping strategy to trace backward from final part shapes to initial billets in axisymmetric forging. Zhao et al. [12] expanded on inverse simulation concepts by developing an inverse die contact tracking method that combines forward and inverse FE analyses. Die–workpiece contact sequences from forward simulations are recorded and modified to define boundary conditions in the inverse run. This mesh-independent method facilitates smooth surface reconstruction and was validated on a four-stage plane strain forging example. Their approach achieved full die fill with minimal flash and no fold-over defects, showcasing the value of controlled contact history in inverse design.

Chang and Bramley [13] advanced inverse methods by proposing a reverse-simulation approach based on upper-bound finite element procedures. Their method progressively released die contact areas to approximate feasible preform geometries. Di Lorenzo and Micari [14] introduced a statistical inverse design method for preform optimization. Using finite element simulations and response surface methodology (RSM), they derived optimal preform parameters for minimizing flash and underfilling in cold-forged C-shaped parts, demonstrating the potential of coupling inverse analysis with statistical modeling. Park and Hwang [15] addressed preform design challenges in asymmetric rib-web type components by combining a 2D FEM analysis of critical cross-sections with iterative 3D volume redistribution to balance flow and ensure defect-free forging. Sedighi and Tokmechi [16] proposed a two-stage preform design methodology based on the finite volume method (FVM) rather than FEM, emphasizing computational efficiency and using a control criterion derived from load–stroke curves to iteratively refine preform geometry.

Yang and Ngaile [17] introduced a geometric resemblance method for preform design, using cross-sectional interpolation and iterative FEM validation to achieve manufacturable near-net shapes with minimal user input. Their method was validated using 2D axisymmetric and plane strain parts, demonstrating robust material flow consistency and minimal flash formation. A fast 3D inverse simulation approach for preform estimation in hot die forging was introduced by Santangelo et al. [18], leveraging Medial Axis Transformation (MAT) to approximate material flow paths based solely on die cavity geometry. The method estimates flow resistance using geometric metrics such as local surface curvature and orientation relative to die motion. Meyer et al. [19] proposed a simulation-driven preform strategy integrating cross-wedge rolling (CWR), lateral extrusion, and bi-directional forging to achieve flashless crankshaft production. Using Forge 3 simulations, they established optimized multi-stage process chains for symmetrical and asymmetrical crankshafts. A modified, fully enclosed bi-directional tool was designed to control material displacement with precision, and experimental trials confirmed the efficacy of this method in producing flash-free components with refined microstructures. Knust et al. [20] later tackled preform design for cross-wedge rolling, developing quasi-2D analyses and optimization strategies to improve strain distribution and material flow.

A notable branch of inverse preform design techniques involves the electric potential (or isothermal surface) method, proposed by Lee et al. [21]. These methods formulate preform generation as a potential field problem, mathematically modeled by Laplace’s equation, wherein the die cavity and billet surfaces are assigned different boundary values (e.g., temperatures or electric potentials). The resulting isopotential contours or surfaces, extracted between the initial and final shapes, are interpreted as plausible intermediate preforms. This method offers a computationally efficient and mesh-independent way of constructing flow-aligned preforms, producing smooth geometries with consistent material flow paths. Cai et al. [22] enhanced the method for axisymmetric die cavities using 3D Laplacian solutions and surface offsetting to better match volume constraints. Guan et al. [23] expanded the framework to incorporate multi-objective evolutionary optimization, combining potential-based preform construction with field-based strain energy minimization. Biba et al. [24] later implemented this method in QForm to enable the semi-automated, CAD-compatible generation of smooth and flash-reducing preform shapes for 3D forgings. While the electric potential method provides a geometrically smooth and computationally simple preform design path, the selection of isotherms is empirical, and physical variables like strain rate, flow stress, and friction are not incorporated into the isotherm generation.

Recent work reflects the integration of artificial intelligence and machine learning into inverse preform design. Kim et al. [25] developed a CNN-based approach that accounts for both forging-induced damage and post-forging heat treatment effects, significantly improving IN718 disk quality by predicting optimal preforms directly from deformation and thermal history data. Building upon this trend, Park et al. [26] introduced a 3D preform design framework combining β-Variational Autoencoders (β-VAE) and deep neural network surrogates to generatively optimize preform shapes for complex components such as EV manifolds and brake calipers. Collectively, these Group 2 methods represent a continuum from early geometric heuristics to sophisticated simulation-driven and AI-enhanced strategies. They offer computationally tractable, physics-informed pathways for preform generation, increasingly serving as essential initialization tools for the robust optimization strategies discussed in Group 3.

1.3. Group 3: Optimization and Refinement

Group 3 encompasses data-driven and simulation-based techniques that refine preform geometry derived from Groups 1 and 2. These methods excel in handling multi-objective optimization and accounting for manufacturing variability. Their main limitation lies in their reliance on good initial geometry and the potentially high computational cost associated with large-scale simulation or surrogate model training. Early work emphasized topology optimization and geometric mapping strategies. Shao et al. [27] used strain-based topology optimization to enhance material flow uniformity and reduce folding defects during forging. Torabi et al. [28] employed RSM and genetic algorithms to improve turbine blade forging, balancing load, flash, and strain using a simulation-validated surrogate model. Iterative refinement approaches have also remained strong. Saquib et al. [29] utilized Deform 3D simulations to iteratively converge on an optimal camshaft preform, balancing flash and under-fill while adjusting preform geometry through multiple simulation loops. In a broader comparative study, Shao et al. [30] evaluated different surrogate modeling techniques—RSM, Radial Basis Functions (RBF), and Kriging—identifying Kriging combined with Particle Swarm Optimization as the most robust strategy for multi-objective aerofoil preform optimization.

More recent studies increasingly integrate machine learning and reliability-based design. Lee et al. [31] trained 3D Convolutional Neural Networks (CNNs) to predict optimal preform shapes directly from forged geometries. Their deep learning model, validated through FEM simulations, successfully generated viable preforms without requiring traditional initial design guesses. Oh et al. [32] introduced a Reliability-Based Design Optimization (RBDO) framework using Kriging surrogate models to manage manufacturing dimensional tolerances, achieving over 99% reliability in final forged parts under realistic variability conditions. These works show how Group 3 techniques close the design loop by tuning geometry to meet performance, reliability, and manufacturability goals. Their application is essential to the industrial deployment of forging sequences generated by Groups 1 and 2.

1.4. Integration and Research Outlook

Figure 1 illustrates the interdependence of these three groups. Group 1 generates feasible multi-stage plans, Group 2 provides analytical or geometric designs for two-stage forming, and Group 3 refines these through robust optimization. Together, they form an integrated toolset for modern forging design. For complex components, workflows may begin with expert systems (Group 1), pass through geometry-driven approximation (Group 2), and end with DOE- or AI-guided refinement (Group 3). To serve the forging industry at scale, future research should prioritize hybrid methods that unify these strengths. For instance, CNN-based preform suggestions (Group 3) could initialize multi-stage point-shift systems (Group 1), while geometric resemblance models (Group 2) could seed surrogate-based optimizations (Group 3). Such integration promises faster, smarter, and more adaptive forging workflows.

Despite the progress summarized across Groups 1 through 3, notable gaps remain in the field of preform design, particularly for 3D forging. Many inverse and optimization-based approaches have limited applicability when it comes to complex, asymmetric parts due to challenges in surface reconstruction, non-proportional deformation, or mesh sensitivity. Additionally, few studies have demonstrated full workflows that bridge material flow prediction with manufacturable preform geometries derived directly from simulation data. Methods requiring predefined preform shapes or extensive parameter tuning remain impractical for industrial deployment. As a result, advancements and innovative preform design methods are needed. The primary aim of this research is to evaluate the effectiveness of the geometric resemblance methodology in determining preform geometries for three-dimensional parts. This study builds on the research efforts outlined in Group 2 above. The authors previously developed this method and tested it on two-dimensional problems, including axisymmetric and plane strain scenarios.

2. Methodology

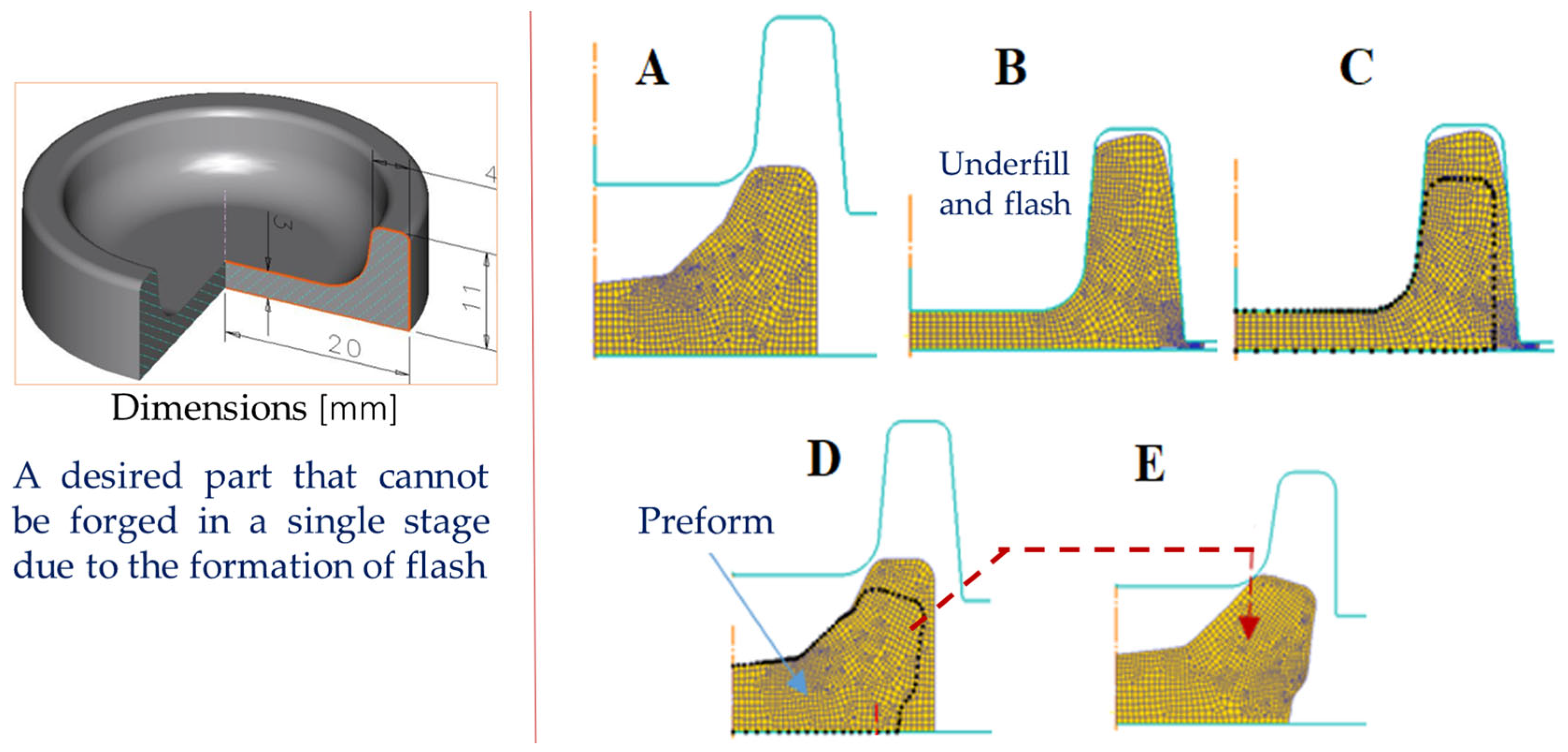
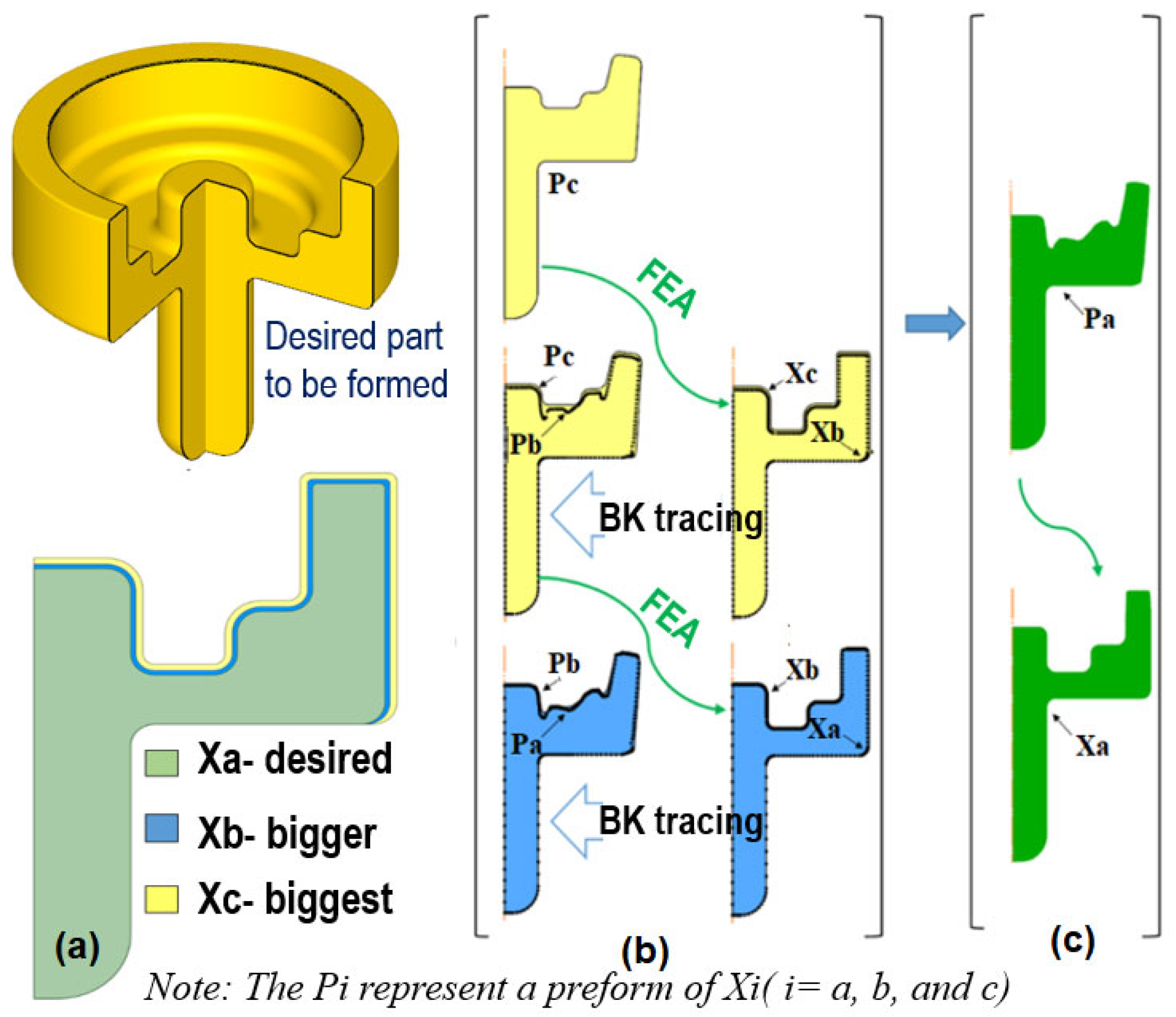
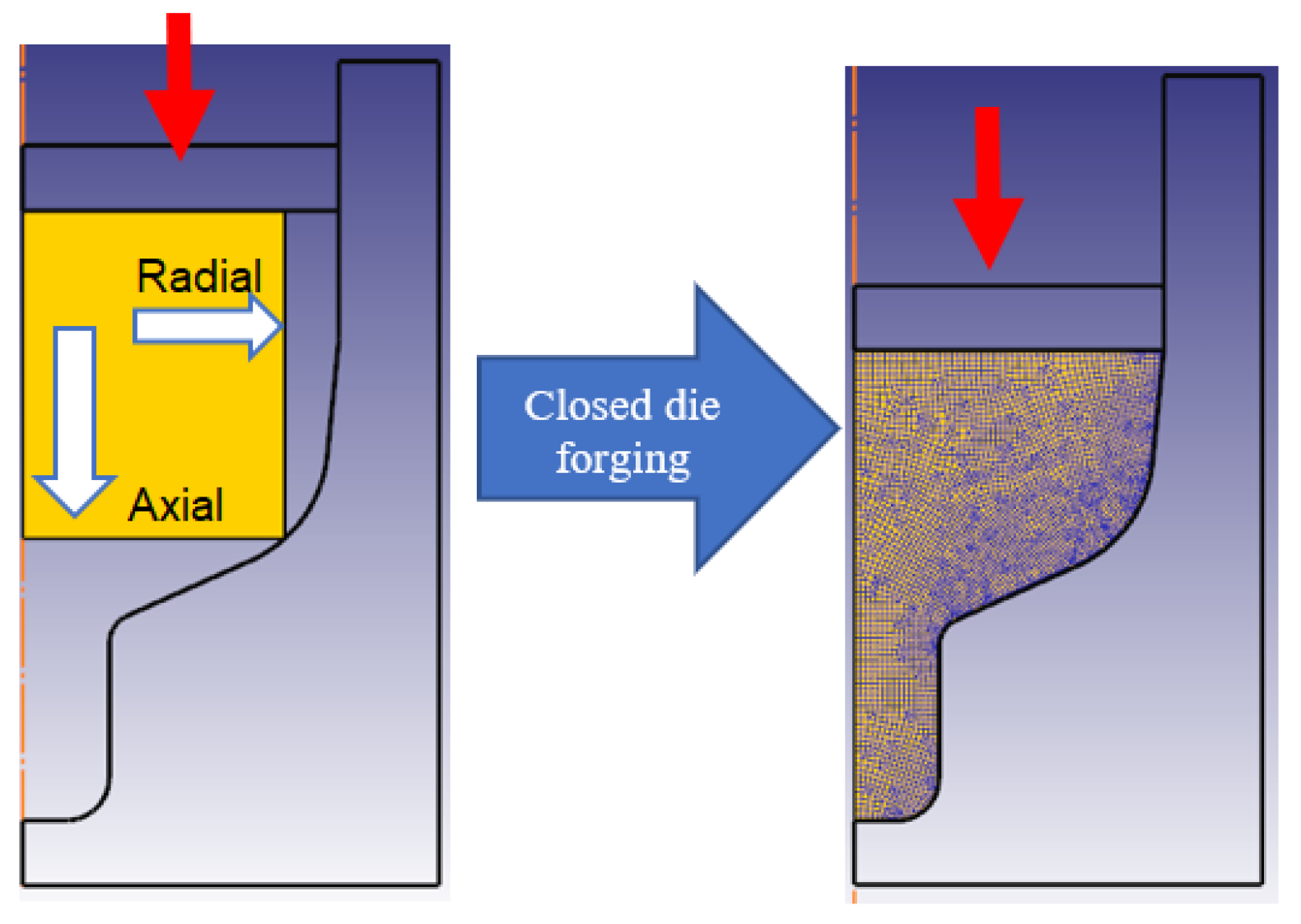
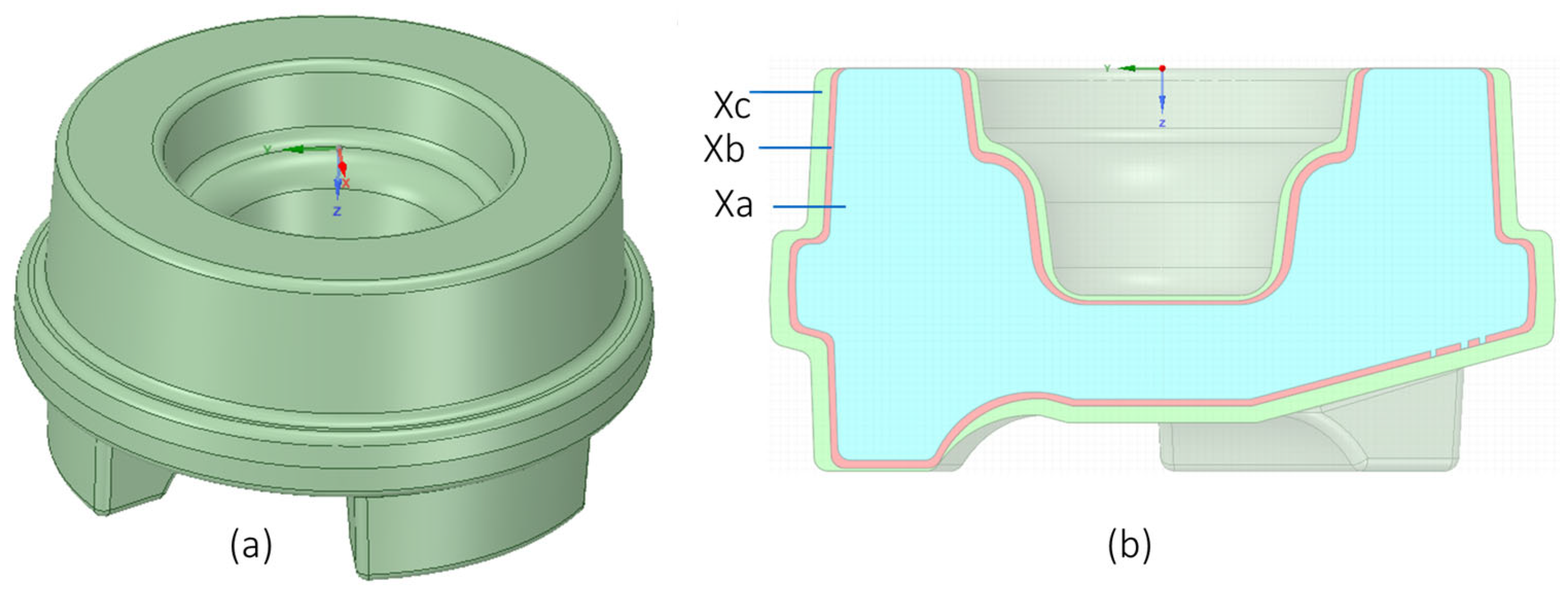
2.1. Principle of the Preform Design Using Geometrical Resemblance

The primary criterion in the preform design of a multi-stage forging process is to ensure that the final forged part is free from common defects such as die under-fill, folding, laps, or internal fractures. A properly designed preform should facilitate material flow to avoid these outcomes while minimizing flash formation. The methodology proposed here leverages the capability of finite element (FE) simulation software to track material points throughout the deformation process, allowing the designer to iteratively refine the preform geometry in a physics-informed manner. The term physics-informed in this context refers to the fact that the backtracked preform geometry reflects the deformation history and material flow field governed by the underlying physical parameters in the FEM simulation, including loading, interfacial friction, strain rate effects, and temperature distribution, rather than relying on empirical rules or purely geometric approximations. An overview of this workflow is illustrated in Figure 2.

The process begins by constructing a geometrically expanded baseline geometry, a deliberately enlarged version of the final part that serves as the input for the first FE simulation (Figure 2A). This initial shape is not a trial-and-error “guess,” but rather a systematic enlargement of the target geometry, scaled either proportionally or non-proportionally depending on the complexity of the part and the symmetry of the deformation. The enlarged shape ensures sufficient material is present to explore material flow into localized features during the simulation.

This expanded shape is then forged virtually using a forward FE simulation (Figure 2B), which captures the deformation behavior under realistic conditions, including interface friction, loading vectors, material flow stress, and thermal gradients. The simulation will produce a part that is larger and may contain defects, but it serves a critical role purpose: it provides a displacement field that reflects how material would flow under the actual process conditions. Regardless of whether defects are localized at the boundary, a backward-tracking approach is initiated by overlaying the desired final part geometry onto the simulation result (Figure 2C). It is important to emphasize that the occurrence of defects in this initial simulation step is both expected and useful; rather than being indicative of a flawed preform, these features reveal key material flow characteristics under realistic forging conditions. The resulting deformation field becomes the foundation for constructing a refined, defect-free preform through material point backtracking.

By selecting material points along the boundary of the desired geometry and tracing them backward through the deformation field, a new preform profile can be reconstructed (Figure 2D,E). This reconstructed preform geometry inherently incorporates the relevant physics of the forging process, including thermal and strain gradients, and represents a significant refinement over the initial configuration. A comparison between the expanded baseline shape (Figure 2A) and the reconstructed preform (Figure 2E) illustrates the effectiveness of the method in converging toward an optimized, flash-minimizing design.

This iterative process is repeated as needed, with each FE simulation yielding improved insight into how the material deforms. Over successive cycles, the reconstructed preform converges toward a geometry that forges cleanly into the final shape with minimal flash and no defects. In concept, this convergence is similar to a Newton–Raphson iteration; the process begins with an inclusive approximation and iteratively narrows in on the solution using physics-informed feedback. However, unlike purely mathematical solvers, this method provides intuitive, visually traceable updates that guide the designer using deformation history and boundary evolution. This approach provides a robust and practical framework for preform design in forging applications. It eliminates reliance on empirical preform assumptions by incorporating material flow physics from the start, thereby enabling the efficient discovery of flashless and defect-free forging geometries.

Figure 3 further illustrates this process using a three-stage iterative scheme to converge on the optimal preform Pa. Figure 4 provides a flow chart and clarifies the notations used in this iterative preform design approach. The key steps are outlined below:

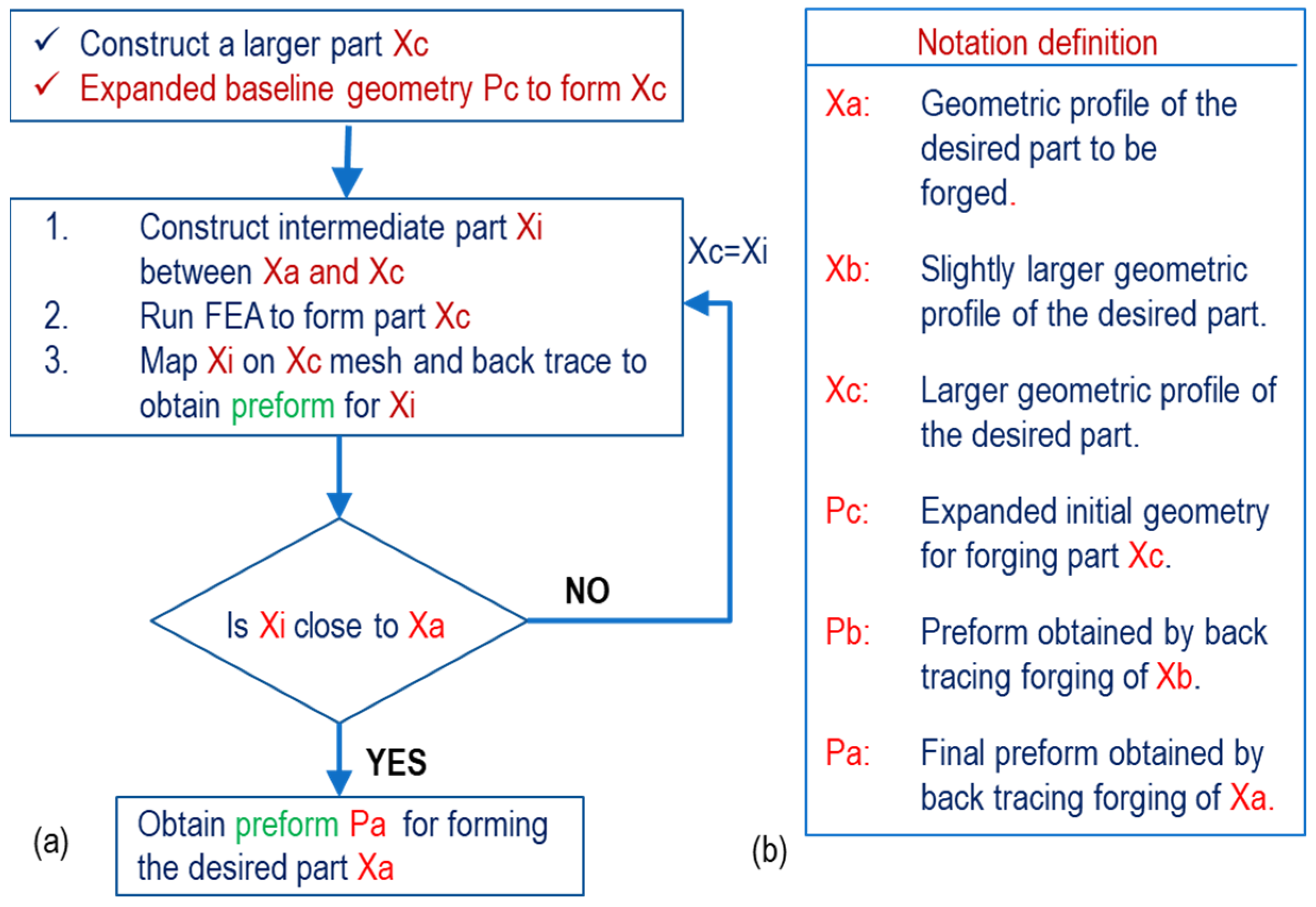
(i)

Define the desired part geometry as Xa. Construct an oversized, geometrically similar part Xc as an initial target.

(ii)

Employ an expanded baseline preform Pc to forge part Xc. While Xc may exhibit defects such as underfill or flash, it must completely enclose an intermediate part Xb.

(iii)

Identify the geometry Xb and trace its boundary points backward from Xc to preform Pc to define the intermediate preform Pb.

(iv)

Construct a new intermediate geometry Xi that closely resembles Xa. Backtrack the material points of Xi from its forging step (preform Pb) to define a new preform Pi.

(v)

Repeat step (iv) iteratively until Xi closely approximates Xa. The final preform Pa is determined by tracing material points of Xa back to the forging step associated with Pi.

This iterative scheme significantly reduces the number of trial-and-error attempts and results in a defect-free preform.

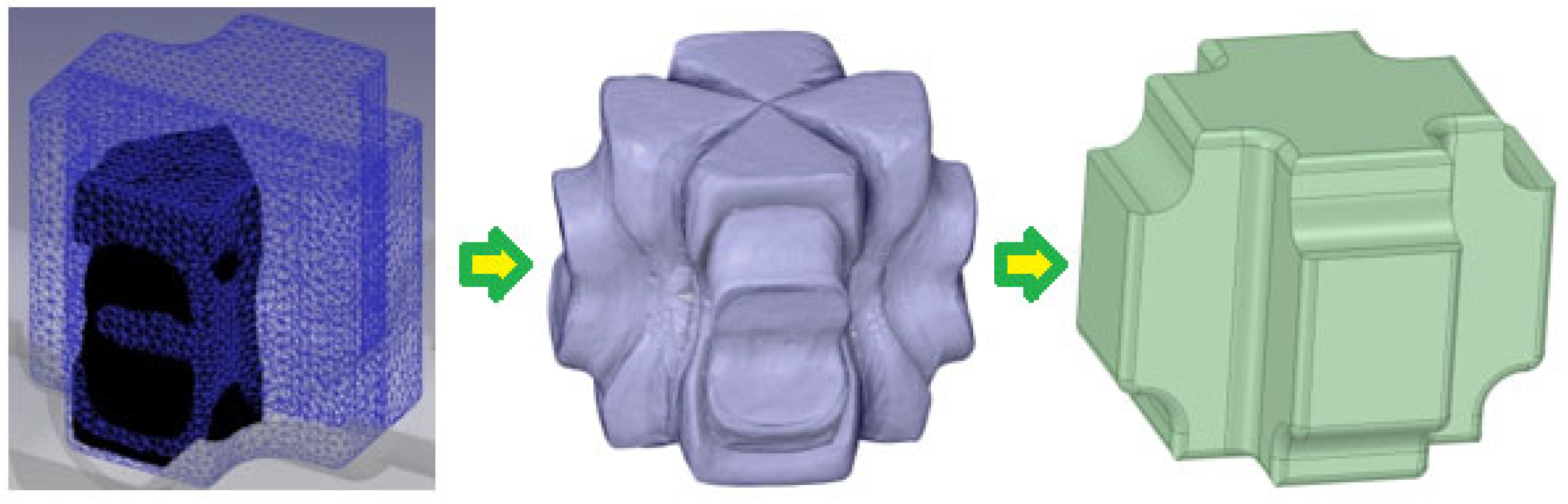
2.2. Preform Design for Three-Dimensional Parts

For 2D problems, such as axisymmetric or plane strain conditions, preform design is relatively straightforward. These problems are easier to visualize, and the geometrical construction is constrained to linear and curvilinear boundaries. However, extending this methodology to 3D geometries introduces several challenges: (a) complex reconstruction of 3D geometry from scattered point data (point cloud); (b) increased mesh refinement requirements for 3D FE models to avoid distorted preform shapes; (c) necessity for robust algorithms to manage large volumes of material data points.

Figure 5 and Figure 6 show the material flow behavior in 2D and 3D forging processes, respectively. In 2D deformation, material points tend to move along constrained paths, typically toward die boundary lines. In contrast, in 3D deformation, material points exhibit more complex trajectories as they move toward die surfaces. These points experience multiple degrees of freedom and follow paths influenced by strain gradients, frictional resistance, and die geometry.

This difference in flow behavior makes preform design for 3D forging more difficult. The material in a 3D process may follow the path of least resistance through the die cavity, leading to unpredictable or suboptimal flow if not properly accounted for. Establishing a robust preform shape based on backward-tracking methods becomes significantly more challenging in these cases due to the high variability in material movement across space and time.

Thus, although the core methodology remains the same as outlined in Figure 2, Figure 3 and Figure 4, the following subsections detail the additional steps and techniques required to design effective preforms for 3D forging operations.

2.2.1. Material Point Generation and Mapping for Backtracking

To implement the backward-tracking method in a 3D FE environment, material point tracking must begin with the accurate creation of representative surface or boundary points. The software used in this study includes DEFORM 3D version 13.1 for simulation, SpaceClaim integrated in ANSYS 2022 R2 for CAD modeling and surface repair, and Python 3.11 scripts for data formatting. The procedures are as follows:

(i)

A solid 3D part is created (Figure 7a) and meshed, and typically stored as an STL file (Figure 7b).

(ii)

The STL file is exported as an xyz file to generate a point cloud (Figure 7c).

(iii)

The xyz file contains 3D coordinate data of surface points (Figure 7d), which are formatted using Excel or Python (Figure 7e).

(iv)

The formatted data is saved as a data file and imported into DEFORM 3D to enable material point backtracking through the simulated deformation process.

These material points act as virtual markers for tracking deformation and enable the reconstruction of the preform geometry by identifying the location of these points in the undeformed billet.

2.2.2. Reconstruction and Solid Modeling from Point Cloud Data

After backtracking, the result is a set of 3D coordinates defining the boundary of the preform (Figure 8a). To use this in further FE simulations, the point cloud must be converted into a solid model suitable for meshing.

(i)

The backtracked points from DEFORM 3D are saved as an xyz file.

(ii)

The xyz file is imported into SolidWorks 2022 using the Mesh Prep Wizard to construct an initial mesh model (Figure 8b).

(iii)

The raw mesh may contain issues such as overlapping triangles or non-manifold edges. These are resolved using SpaceClaim, where the mesh is smoothed, repaired, and re-meshed (Figure 8c).

(iv)

The final clean geometry is saved as an STL file and used for the next iteration of FE simulation.

This step bridges the gap between simulation data and practical geometry modeling, and it requires an understanding of geometric modeling terms such as “point cloud generation,” “surface triangulation,” “mesh healing,” and “solid body reconstruction.”

It is important to note that in DEFORM 3D, backtracking is not performed directly on finite element nodes. Instead, the user defines a surface or profile of interest, specified by spatial coordinates (x, y, z), and DEFORM tracks that region through prior deformation steps. When re-meshing is used (as is common in large-deformation 3D simulations), the tracked point may not lie exactly on a node. In such cases, DEFORM uses shape function-based interpolation to determine the position of the material point within the element. For tetrahedral elements, interpolation involves the four corner nodes; for higher-order elements, additional mid-side or internal nodes are included. This allows the software to reconstruct material point trajectories across re-meshed domains.

However, frequent re-meshing may introduce artifacts in the reconstructed surface due to small interpolation errors or distortions in the underlying mesh. These may manifest as surface irregularities or jagged edges, particularly in regions with complex, multi-valued flow paths. This effect is illustrated in Figure 8. To address these issues, surface-smoothing algorithms and mesh healing operations are applied during reconstruction to ensure that the resulting preform geometry is continuous and manufacturable. This post-processing step is essential for restoring geometric integrity and enabling reliable input for subsequent FE simulation iterations.

3. Application of the Preform Methodology for 3D Closed Die Forging Processes

The geometric resemblance methodology was applied to three forging case studies involving complex part geometries: (1) a cross-joint, (2) a bevel gear, and (3) a three-lobe drive hub. In all cases, the objective was to design a preform that would achieve full die filling while minimizing flash formation and forging loads, with an emphasis on achieving near-flashless forging conditions. In this work, we define near-flashless forging as a process where flash formation is minimized to the extent that post-forging trimming and material loss are negligible, though not entirely eliminated. This contrasts with fully flashless forging, which may require extremely precise preform control and die alignment.

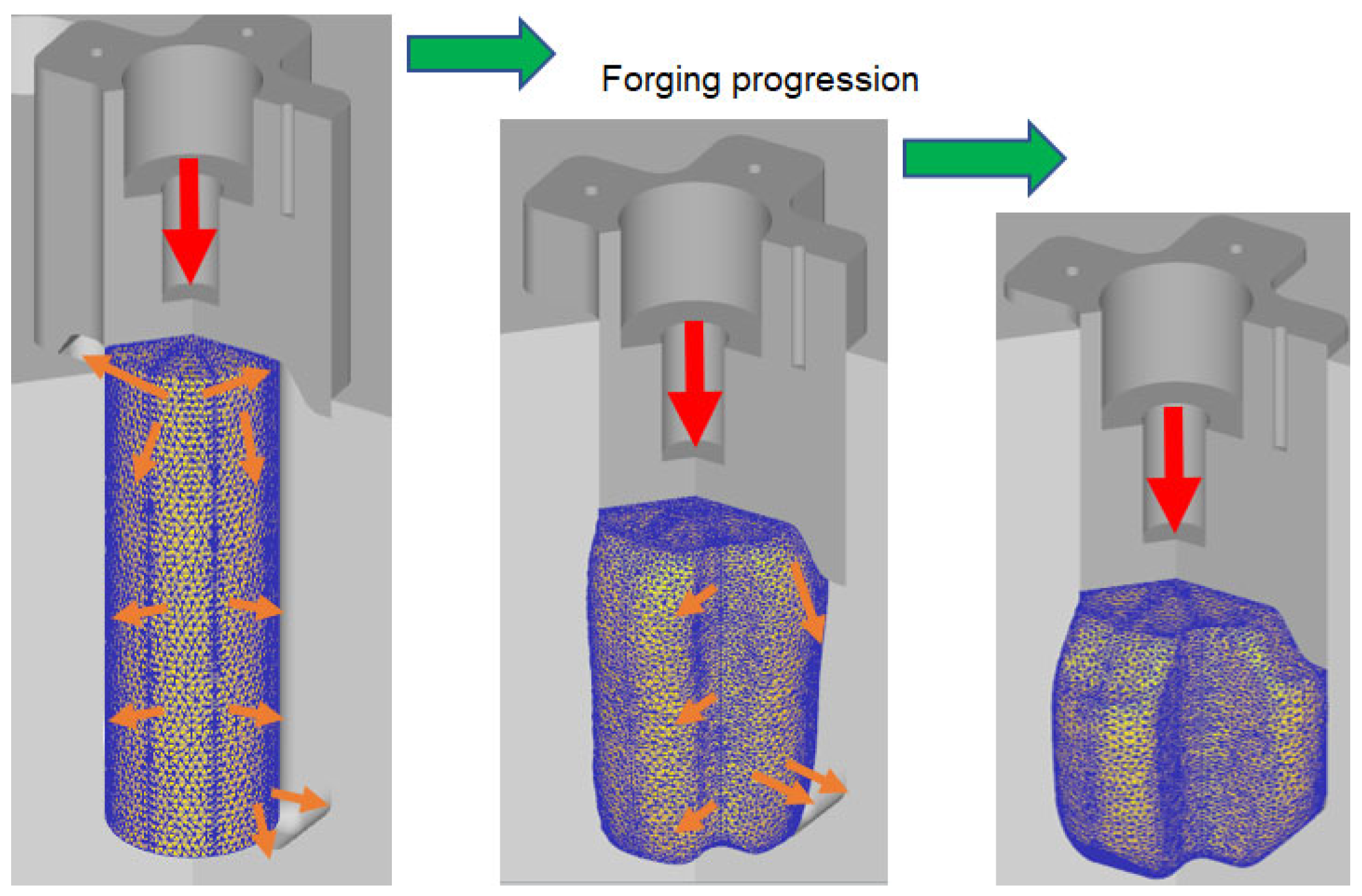
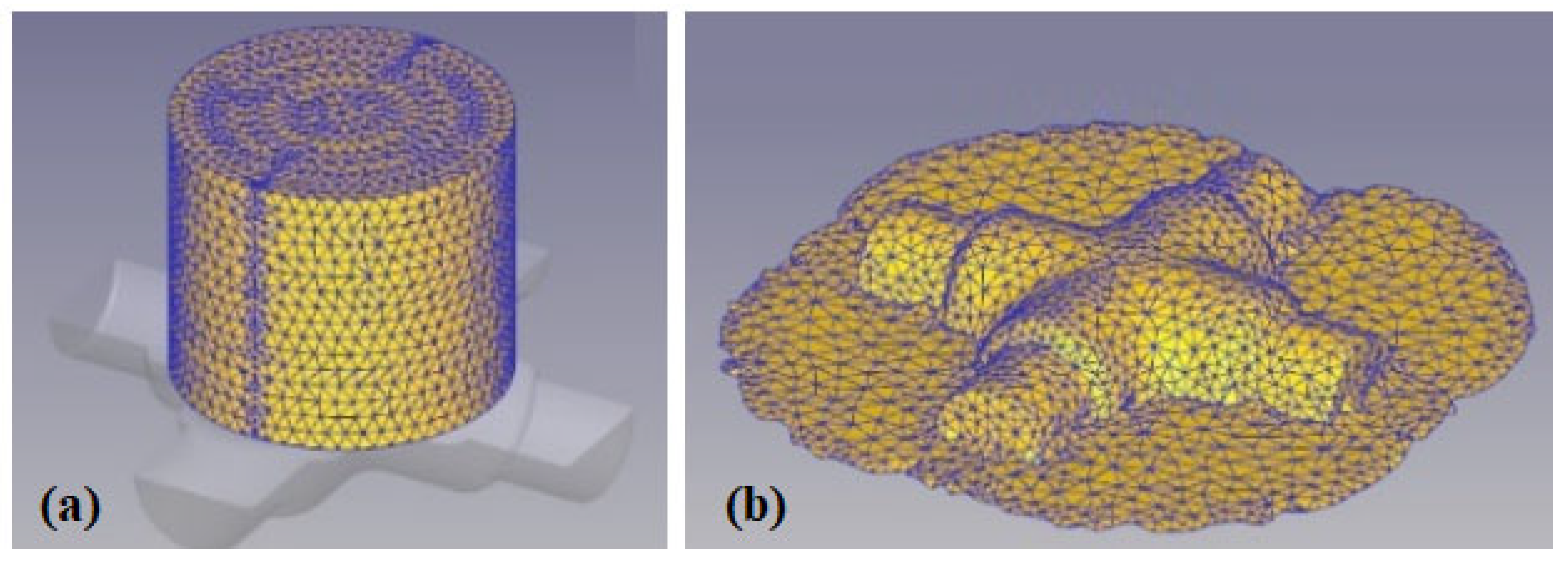
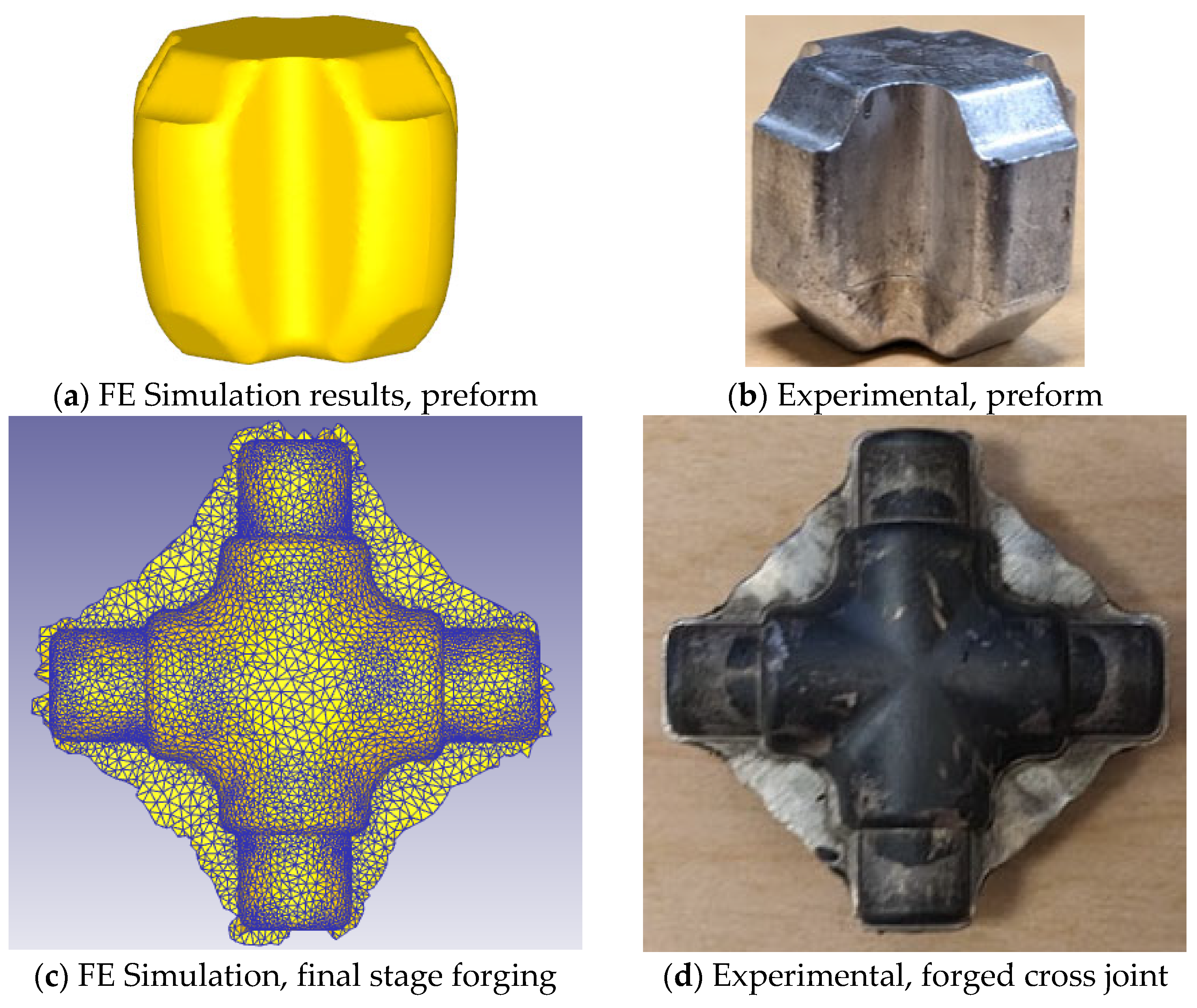
3.1. Cross-Joint Forging

The preform design methodology based on geometrical resemblance was applied to determine a preform for a cross-joint forged from AISI 1016. To evaluate flash formation during single-stage forging, finite element (FE) simulations were conducted using the DEFORM software package. The initial billet measured 50 mm in diameter and 60 mm in length. Forging was performed at a billet temperature of 1000 °C and die temperature of 250 °C, with a friction factor of m = 0.3 at the die–workpiece interface, as given in

Table 2. FE simulation conditions for cross-joint forging.

Parameter	Value/Description
Material Model	AISI 1016 (sourced from DEFORM Material Library)
Billet Temperature	1000 °C
Die Temperature	250 °C
Interface Friction Model	Shear friction law (friction factor m = 0.3)

.

The workpiece’s material flow stress behavior was modeled using data from the DEFORM-3D software’s built-in material library, which is routinely maintained by the software developers and widely used for hot-forging applications.

Figure 9a shows the initial cylindrical billet, and Figure 9b depicts the resulting forged cross-joint with significant flash formation.

To reduce material waste due to flash, the preform design methodology based on geometrical resemblance (outlined in Section 2.1) was used. Larger shapes, Xb and Xc, were constructed, and an estimated preform Pc was established, as illustrated in Figure 10.

FE iterations for preform determination are shown in Figure 11. Due to symmetry, only a half 3D FE model was simulated. In the first iteration, the expanded baseline geometry Pc was used to forge a larger part, Xc, as shown in Figure 11b. Subsequently, the boundary surface of the target part, Xb, was mapped onto Xc to identify the region of interest for backtracking, as depicted in Figure 11c.

Interpreting Figure 11c,d requires some spatial reasoning, as they involve curved 3D surfaces. In Figure 11c, the dark blue region represents material points corresponding to one-eighth of the boundary surface of the target cross-joint Xb, superimposed onto Xc. This 1/8th sector is selected for clarity and computational efficiency, leveraging the multiple symmetry planes inherent to the cross-joint geometry. These mapped material points are then backtracked through the deformation field to reconstruct the original point positions, thereby generating the preform geometry Pb. The resulting point cloud is shown in dark blue in Figure 11d. This 3D procedure closely parallels the 2D backtracking illustration provided earlier in Figure 2C,D, where dark-colored lines were used to indicate mapped and traced boundaries. The consistency between the 2D and 3D examples reinforces the generality of the proposed physics-informed approach.

A second iteration was begun by forging Xb using preform Pb, the simulation results of which are shown in Figure 11f. By backtracking material points from Xb, Pa can be obtained. The last FE iteration involved forging preform Pa, resulting in part Xa with a minimal amount of flash (Figure 11j). The uniformity in the material flow observed in the final part suggests that an additional FE iteration will completely eliminate the flash.

Figure 12 shows the effective strain distribution for forging the cross-joint using the established preform. Flash regions exhibited maximum effective strains around 7.4, while the bulk material exhibited strains near 5. Forging loads for both the preforming and final forging stages are shown in Figure 13. The maximum load obtained for preforming was 480 tons, whereas the maximum load for the final stage was 1000 tons. It should be noted that at the end of the stroke, the load jumps, indicating that the actual forming load should be lower than what is reported here. It can be observed that by using the intermediate preform stage, the volume of the billet is reduced by approximately 13.5%.

While constructing the initial expanded baseline geometry is relatively straightforward for simple parts, significant challenges arise when dealing with complex geometries that exhibit intricate three-dimensional material flow. In such cases, achieving an adequately oversized preform shape may necessitate the non-proportional scaling of boundary surfaces rather than uniform expansion. In this study, all geometries tested employed proportional scaling; however, future applications may require more sophisticated scaling strategies to accommodate localized geometric features. It is also important to recognize that, despite being informed by the underlying physics of deformation, some backtracked preform shapes may prove impractical to forge due to geometric intricacies or manufacturing constraints. In such instances, the initial expanded geometry may need to be revised or simplified to ensure manufacturability while preserving the intended flow characteristics. Furthermore, during the preform reconstruction for the cross-joint forging case, surface smoothing was applied to the backtracked geometry due to insufficient point cloud resolution, highlighting the importance of adequately sampled data in obtaining usable CAD models.

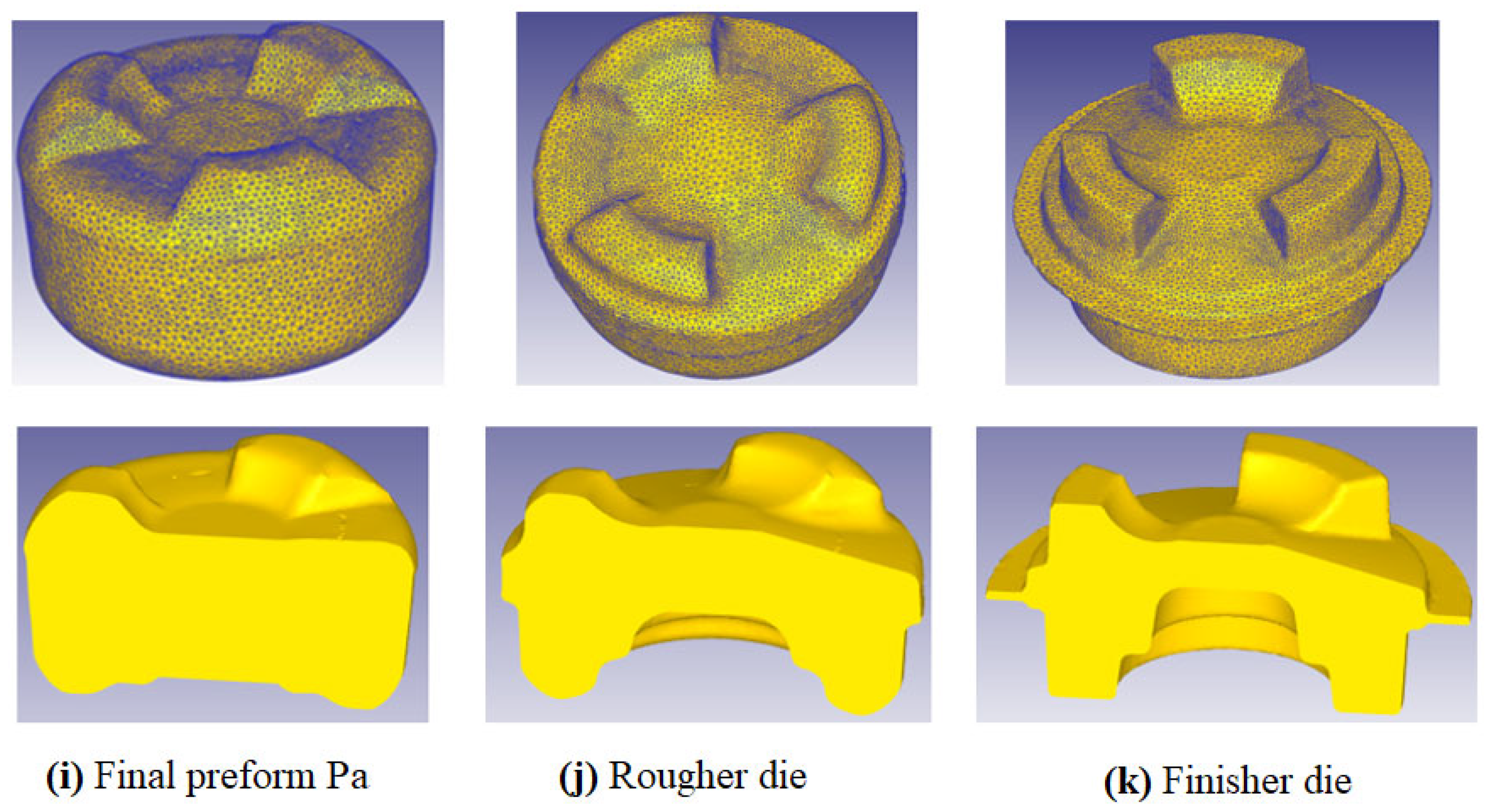
3.2. Three-Lobe Drive Hub Forging

The preform design methodology was further applied to a three-lobe drive hub featuring lobes on one side and an axisymmetric cup shape on the other. As the forging is carried out using a cylindrical billet, the deformation of the material during forging is such that the three lobes will be extruded out on one side, and the other side will feature backward cup extrusion. Due to the presence of three lobes, the material flow exhibits complex three-dimensional flow. Figure 14 shows the target hub geometry (Xa) and its geometrically enlarged counterparts (Xb and Xc) which were used in the preform search scheme. One of the goals for this case study was to utilize the preform design methodology based on geometrical resemblance to establish a preform that will result in minimal flash formation.

The procedures for determining the preform die are the same as those used for the cross-joint forging presented earlier. The study was conducted on AISI 1035 cylindrical billet material measuring 48 mm in diameter and 100 mm in height. Forging simulations were performed at 1200 °C for the billet and 150 °C for the dies, and with a friction factor of m = 0.3 (

Table 3. FE simulation conditions for three-lobe drive hub forging.

Parameter	Value/Description
Material Model	AISI 1035 (sourced from DEFORM Material Library
Billet Temperature	1200 °C
Die Temperature	150 °C
Interface Friction Model	Shear friction law (friction factor m = 0.3)

). Due to symmetry, only one sixth of the part was modeled.

In the first iteration (Figure 15a–d), a pancake-shaped billet was employed as the initial expanded geometry or oversized billet, to forge the intermediate part Xc. The boundary of the target geometry, Xb, was then overlaid onto Xc to identify the relevant deformation region. By backtracking the material points from Xc, the corresponding preform geometry, Pb, was reconstructed. This mapped configuration became the initial estimate of the preform shape. As with the earlier cross-joint case presented in Section 3.1, interpreting Figure 15c,d requires some spatial visualization, given the complexity of 3D surface mapping. In Figure 15c, the dark blue region represents 1/6th of the boundary surface of Xb, projected onto the forged part Xc. This fraction was selected to reflect the part’s threefold rotational symmetry. In Figure 15d, the dark blue region illustrates the backtracked material points, traced from Xc back to the initial billet, which defines the geometry of preform Pb. This approach mirrors the conceptual strategy outlined in the 2D example of Figure 2C,D, but adapted here to a three-dimensional, lobed geometry.

The second iteration starts with the meshing of Pb obtained from iteration 1, as shown in Figure 15e–h. However, the geometry from back tracing required smoothing. It should be noted that the Pb is extracted from inside the bulk of Pc as a point cloud and must undergo triangulation as discussed in Section 2.2.1 and Section 2.2.2. During reconstruction, tiny geometric features may be lost in the process. After the Xb part is simulated, Xa is overlaid on the simulation results, followed by tracing back of the material points of Xa onto Xb. Backtracking these points produced the final preform Pa. Figure 15i shows Pa, with the three lobes oriented upward. Figure 15j,k shows forgings obtained from the rougher and finisher dies for the three-lobe drive hub.

Effective strain distributions for preforming and final forging are shown in Figure 16. The preform resulted in a maximum effective strain of 2.81, where the final stage forging exhibited a maximum strain of 4.85. The forging load versus stroke is shown in Figure 17, where the maximum forging load for preforming was 130 tons, and for the final stage, the force rose to 545 tons. Although minor flash remained at the end of forging, the flash volume was significantly reduced compared to conventional forging practices. Further refinements could achieve fully flashless forging.

4. Experimental Validation

As discussed in the previous sections, the goals for preform forging are threefold: (a) eliminate flash during forging, (b) reduce flash formation (near-flashless forging), and (c) enable the forging of complex parts that would otherwise be impossible to forge in a single stage. It is important to evaluate the efficiency of the preform design methodology to determine how well the preforming stage contributes to reducing flash and improving overall forging efficiency.

To validate the effectiveness of the proposed preform methodology, forging tests were conducted on a downscaled cross-joint component made from AL6061. This validation primarily aimed to minimize material utilization by reducing the amount of flash. Preliminary finite element (FE) simulations were carried out for different billet sizes to establish the billet volume limit below which a cross-joint could not be forged successfully in a single stage.

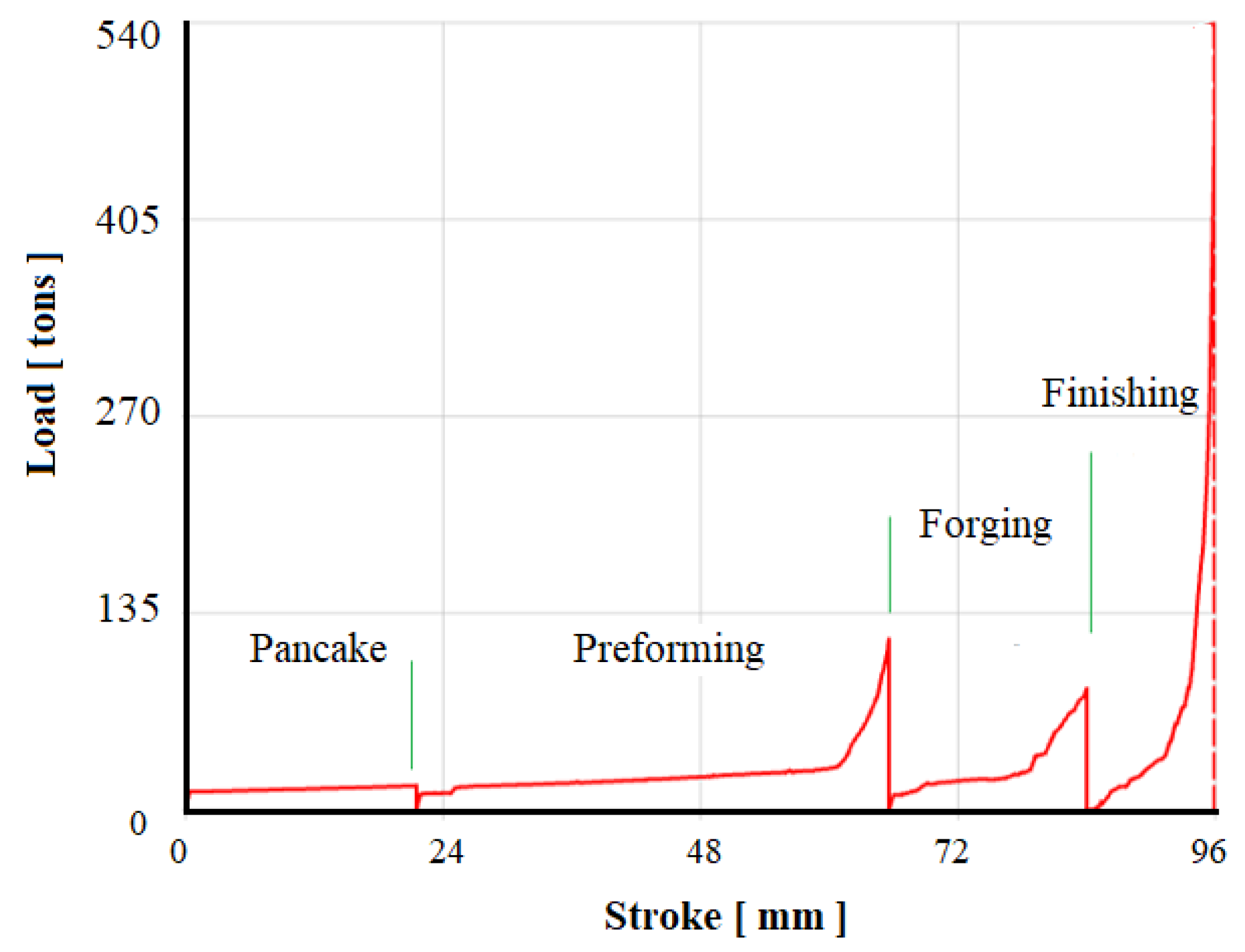
4.1. Preliminary FE Forging Simulations

Several forging simulations were conducted to determine the billet volume threshold that would require multi-stage forging for an AL6061 cross-joint. Billets with a diameter of 11 mm and varying lengths were evaluated. These simulations were necessary because cross-joints can typically be forged with flash in a single stage, and the major benefit of preform use is to reduce flash while maintaining part soundness. The FE simulation conditions are summarized in

Table 4. FE simulation conditions for cross-joint forging.

Parameter	Value/Description
Material Model	AL6061 (sourced from DEFORM Material Library)
Billet Temperature	400 °C
Die Temperature	150 °C
Interface Friction Model	Shear friction law (friction factor m = 0.3)
Billet transfer	15 s set for billet heat loss (air heat transfer)

. The simulation workflow accounted for billet cooling during manual transfer from the heating furnace to the forging dies, with an estimated transfer time of 15 s. A constant shear friction model was employed, using a friction factor of m = 0.3, which is representative of hot forging conditions with copper-based lubricants.

Figure 18 summarizes the simulation results for three billet sizes: (a) 3478 mm³ (110% of the net part volume), (b) 3379 mm³ (107% of the net part volume), and (c) 3326 mm³ (105% of the net part volume). At 110% billet volume (Figure 18A(a)), the cross-joint was fully formed but with approximately 10% material lost as flash. Reducing the billet size to 107% and 105% (Figure 18A(b,c)) led to underfill, indicating that successful forging with these billet sizes would require the use of a preform. Using the preform methodology discussed in Section 3, a sound cross-joint was produced in two stages, as shown in Figure 18 B.

The cross-joint example demonstrates that by introducing a preform stage, at least 5% of billet material can be conserved. While this comes with the added complexity of a multi-stage forging process, the improvement in material utilization can be substantial, particularly for geometrically complex forgings where flash losses are typically significant. In such cases, preforming may be the only technically viable approach to achieving full die fill and sound part formation. The experimental validation presented below was based on the FE model shown in Figure 18B.

4.2. Laboratory-Scale Forging Tests

4.2.1. Test Setup Design

To experimentally validate the preform methodology, downscaled cross-joints were forged in two stages using a 150-ton hydraulic press. Based on FE results, dies and punches for both the preforming and final forging stages were fabricated from H13 tool steel and heat-treated to a hardness of 56 HRC.

Figure 19 shows the preforming die set, where a cross-hole in the top die guides the punch. The bottom of the punch features a cavity that shapes the preform. The top cylinder is fastened to the punch, and it transfers the forging load from the ram of the press. The final forging die set (Figure 20) consists of a top and bottom die with matching cavity configurations. Both die sets include holes for securing the assembly. The set of holes located near the die cavities is specifically designed for aligning the top and bottom dies using dowel pins. The assembled die set (Figure 21) was mounted on the press table. Since the forging was conducted at elevated temperatures, both top and bottom dies were heated to 150 °C using band heaters. A heat insulation mat was placed between the bottom die and the tooling base to minimize heat loss through metal-to-metal contact.

4.2.2. Test Procedures

Cylindrical AL6061 billets were heated to 400 °C in a furnace and soaked for 15 min to ensure uniform temperature distribution. The dies were simultaneously heated to 150 °C. A copper paste lubricant was applied to the die surfaces before forging. Once the target temperatures were reached, billets were transferred using tongs into the preform dies, and the ram was immediately activated.

In industrial settings, preforming and final forging are performed sequentially without reheating. However, due to laboratory limitations, multiple billets were preformed first, then reheated to 400 °C before the final forging step was carried out.

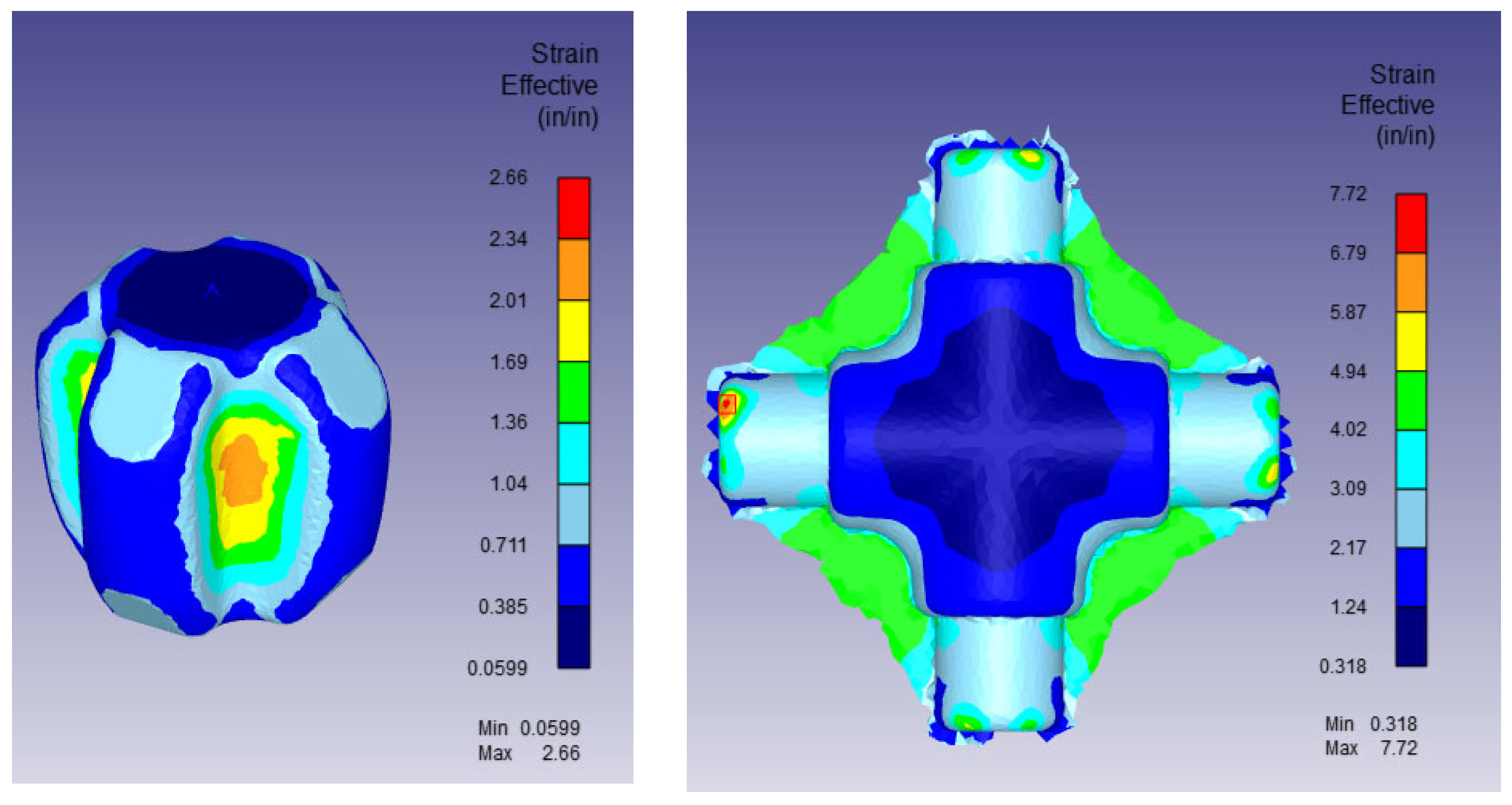
4.2.3. Test Results and Discussions

Figure 22a–c present the forged preforms, the final forged cross-joint, and a cross-sectional view, respectively. Visual inspection revealed no surface defects or underfill. A total of nine cross-joints were forged, and dimensional measurements, including overall part dimensions and flash thickness, were obtained using micrometers. The results demonstrated excellent repeatability across all samples. The final forged cross-joint exhibited full die filling, with no visible laps, folds, or discontinuities.

Figure 23 compares the material flow behavior predicted by the FE simulations with that observed in the preforms and final forged parts. The flash formation in the experimental samples closely matched the simulation predictions, indicating good agreement between numerical and physical outcomes. Strain distribution maps for both the preform and final forging are shown in Figure 24. During the preforming stage, the maximum effective strain was approximately 2.66, while the final forging reached a maximum strain of 7.2. However, the bulk of the cross-joint exhibited an average effective strain of around 3.0.

The forging load profiles from both FE simulations and experiments are presented in Figure 25. During the physical experiments, the peak load for the preforming stage was approximately 12 tons, while the final forging stage reached a peak load of 40 tons. In contrast, the FE simulations predicted a peak preforming load of 7 tons and a final forging load of 32 tons. Although the differences in peak load between the simulations and experiments are notable, it is important to emphasize that these peak values occur near the end of the stroke, precisely when the material is expelled from the die cavity as flash. At this stage, even a small variation in flash thickness can lead to a significant discrepancy in predicted load.

Overall, the experimental loads were consistently higher than those predicted by the simulations. A plausible explanation for this discrepancy is the assumed friction condition in the FE model. All simulations used a constant shear friction model with a friction factor of m = 0.3. While this value is considered reasonable for hot forging with copper-based lubricants, it may underestimate actual interface friction. In practice, frictional behavior in closed-die forging can vary substantially due to factors such as die temperature, surface oxidation, lubricant breakdown, and contact pressure. These variations can significantly affect forming loads, especially in the late stages of the stroke.

5. Discussion on Viability, Limitations, and Prospects of the Proposed Method

The primary objective of the preform design methodology is to reduce or eliminate flash formation and to produce high-quality parts free of defects. By improving material utilization and potentially reducing energy demands, this approach contributes to more sustainable and resource-efficient forging operations. At the heart of the method is a material point backtracking strategy informed by finite element analysis (FEA). The approach capitalizes on the predictive power of FEA, which captures complex interactions between die geometry, material flow behavior, interfacial friction, and thermal gradients. The process begins with a systematically expanded baseline geometry, rather than a blind or arbitrary guess. This geometry is deliberately constructed to ensure sufficient material availability across the part’s features and is subjected to a forward FE simulation. The simulation yields a deformation history that enables the tracing of material points from the final geometry back to their origin in the billet. This results in a physics-informed preform estimate, one that inherently reflects key physical phenomena such as localized strain accumulation, thermal heterogeneity, and anisotropic deformation modes. Compared to traditional geometric or empirical inverse methods, this strategy offers a significantly more realistic basis for preform design.

For two-dimensional problems, such as axisymmetric and plane strain configurations, the computational effort remains relatively low, as the FE iterations involve only linear or curvilinear boundary reconstructions. However, in three-dimensional forging models, the computational burden increases significantly. The iterative process involves material point tracking, surface mapping, reconstruction, and solid modeling from point cloud data. In the case of complex, asymmetric 3D parts, the material flow behavior becomes highly non-linear, often necessitating the non-proportional scaling of boundary surfaces to generate an appropriately oversized preform geometry. For the cross-joint and three-lobe drive hub case studies presented earlier, a uniform boundary scaling approach was adopted. Nevertheless, it is important to note that for both cases, reconstructing a manufacturable and continuous preform during the FE iterations required extensive surface smoothing operations to ensure geometric continuity and forgeability.

Figure 26 illustrates an example of irregularities encountered when reconstructing a preform from backtracked material points for the cross-joint. Surface defects can result from multiple factors, including insufficient point cloud density, mesh distortion during forging simulations, multi-valued material flow paths, and limitations inherent to CAD modeling platforms.

Some of these challenges could be addressed by adopting a hybrid design workflow that combines backtracking-based preform generation with Design of Experiments (DOE) and surrogate modeling techniques. In this hybrid approach, the backtracked preform geometry serves as the initial candidate, providing a physically consistent “seed” that captures the essential material flow characteristics. This shape is then used to define a local design space, wherein key geometric parameters, such as radii, fillet curvatures, and preform heights, are systematically varied using DOE strategies. Surrogate models, such as response surface models (RSM) or Kriging functions, can be employed to efficiently explore the design space. Objectives such as minimizing flash, ensuring complete die filling, or reducing forging energy consumption can be targeted. By combining the high-fidelity insights of FEA-driven backtracking with the flexibility and robustness of parametric optimization, this hybrid strategy promises to generate preform designs that are both physically accurate and practically manufacturable.

6. Conclusions and Future Work

This study presented a preform design methodology for forging processes based on geometrical resemblance, focusing specifically on hot forgings that exhibit three-dimensional deformation behavior. The approach exploits the ability of modern finite element (FE) software to track material points throughout the deformation process. Two case studies, hot forging of a cross-joint and a three-lobe drive hub, were used to demonstrate the methodology. Because 3D forgings involve the tracking of voluminous material data points during each FE iteration, a systematic scheme was developed to manage data effectively, including material point generation, backtracking, surface reconstruction, and solid modeling from point cloud data.

Major conclusions drawn from this study

• Preform search for complex 3D forgings requires careful handling of point cloud data. Unlike 2D forging problems, finding an optimal preform for complex geometries demands a more refined mesh to capture sufficient data points. However, since extremely fine meshes are often impractical, geometry smoothing techniques must be adopted, which may result in the loss of some minor geometric details on the determined preform.
• The cross-joint case study demonstrated material savings of approximately 13.5% through the introduction of an intermediate preform stage developed using the proposed scheme.
• Substantial material waste reduction is attainable even in highly complex 3D forging scenarios, as evidenced by the three-lobe drive hub case study, where iterative refinement of the preform during FE simulation significantly minimized flash formation.
• While data handling remains a potential challenge, advances in computational speed and the integration of DOE and optimization techniques into metal forming software have greatly reduced these concerns. The methodology is thus becoming increasingly practical for industrial applications.

Future Work: Future work will focus on the following directions:

• Conducting a sensitivity analysis on the influence of different initial expanded geometries to quantify their impact on the convergence behavior and accuracy of the final preform obtained through the iterative backtracking and optimization process.
• Automating key steps in the workflow, particularly point generation, surface smoothing, and solid geometry reconstruction from point cloud data, by implementing advanced algorithms and automation tools.
• Developing a hybrid workflow that combines FEA-based material point backtracking with DOE and surrogate modeling techniques. In this approach, the backtracked preform would serve as a physically accurate initial design, which would then be refined through parametric optimization strategies such as Response Surface Methodology or Kriging models. This hybrid method would accelerate convergence toward flashless, fully filled forgings while maintaining manufacturability.
• By addressing these areas, the proposed methodology can evolve into a powerful and practical tool for forging preform design across a wide range of industrial applications.