Investigation of the Effect of Tool Rotation Rate in EDM Drilling of Ultrafine Grain Tungsten Carbide Using Predictive Machine Learning

Abstract

Electric discharge machining (EDM) is widely employed for machining hard, conductive materials. Tool rotation has emerged as an effective strategy to enhance debris flushing and improve stability during deep-hole EDM drilling. This study proposes a machine learning-based approach to evaluate the influence of tool rotation and predict the unstable machining conditions in EDM of ultrafine grained tungsten carbide. A structured analytical workflow, combining Taguchi–Grey optimization, regression analysis, and classification models, was designed to capture discharge dynamics across macro- and micro-timescales. Classification models trained on raw and processed electrical signal features achieved over 88% accuracy and 90% recall. SHAP analysis revealed that the relationship between key discharge events such as sparks and short circuits varied significantly across stable and unstable machining phases, underscoring the importance of phase-specific modeling. While correlation analysis showed weak global associations, phase-dependent SHAP values revealed opposing feature effects, allowing the context-informed interpretation of model behavior. Phase segmentation revealed that, compared to 1000 RPM, short circuits were reduced by about 40% during stable machining at 8000–9000 RPM. Conversely, during unstable phases, spark effectiveness dropped by nearly 45%, and secondary discharges increased throughout this range. These insights support the design of adaptive control strategies that adjust the rotation rate in response to detected phase changes, aiming to sustain machining stability. The findings support the development of dynamic control frameworks to improve EDM performance, particularly for mold fabrication using tungsten carbide.

1. Introduction

Electrical discharge machining (EDM) is a non-traditional machining process that removes material through controlled electrical discharges between a tool and a workpiece, both submerged in a dielectric fluid [1]. Due to its non-contact nature and ability to machine hard, brittle, and conductive materials, EDM is widely used in the aerospace [2], biomedical [3,4], and mold industries [5,6].

Rotary EDM, wherein the tool is rotated during machining, has emerged as an effective strategy to enhance debris flushing, stabilize the discharge process, and improve machining performance. Studies have reported improvements in material removal rates [7,8], surface finish [9], and tool life [10] with tool rotation assistance. However, while a moderate increase in the rotation rate can enhance performance, at a higher rate the benefits plateau or even diminish due to excessive turbulence or arc formation [11,12]. This introduces complexity in selecting the optimal tool rotation rate, especially because differences in the machining behavior at different rotation rates are often subtle and non-linear.

Moreover, EDM is inherently a pseudo-random process at the micro-timescale, governed by complex interactions between electrical, thermal, and fluid dynamic phenomena [13]. Traditional performance metrics, such as the material removal rate (MRR), tool wear rate (EWR), and surface roughness (Ra, Sa), provide limited insight into the underlying process stability. Consequently, there is growing interest in analyzing internal discharge characteristics to better understand and optimize EDM operations.

To model and optimize EDM performance, various approaches have been developed, including Response Surface Methodology (RSM) [14,15], and Taguchi methods with ANOVA-based analysis [16,17]. The Taguchi–Grey relational analysis [18,19] in particular offers a structured framework to handle multi-objective optimization problems and has been effectively applied in EDM parameter optimization. However, in most previous studies, these methods primarily relate input parameters such as voltage, current, and pulse frequency directly to output metrics, without a deeper exploration of the discharge dynamics.

Recent advances in on-machine process monitoring have enabled the segmentation and classification of individual electrical events into types such as clean sparks, arcs, and short circuits [20,21]. Discharge classification provides a richer, physically interpretable view of the EDM process beyond conventional current and voltage waveform analysis. While pulse-based breakout detection using discharge behavior has been explored, primarily in wire EDM, where breakout is a critical event [22,23], such approaches are often limited to sudden, extreme transitions. In contrast, die-sinking EDM under rotational conditions induces more gradual and subtle changes, where the traditional feed rate or voltage variations cause noticeable differences but the rotation rate variation affects the internal discharge dynamics more subtly.

This highlights a critical research gap: the need to understand how the tool rotation rate variation influences discharge patterns and machining stability in die-sinking EDM, where differences are not easily captured by classical threshold-based models. Tungsten carbide, particularly ultrafine-grained cobalt-bonded grades, is widely used in mold fabrication due to its high hardness and thermal resistance, but it is also difficult to machine, making it a particularly relevant material for this investigation [24].

We hypothesize that variation in tool rotation rate leads to measurable changes in discharge event patterns and phase-dependent machining stability, which can be detected and predicted using machine learning models trained on on-machine electrical measurements. To test this hypothesis, we develop a multi-stage methodology that combines process optimization, data-driven classification, and phase-aware analysis of electrical discharges.

First, Taguchi–Grey analysis is applied to optimize machining parameters excluding rotation rate, establishing baseline process performance. Next, regression modeling with process indicators is employed to refine the understanding of input–output relationships. Machine learning classification models (Random Forest and XGBoost) are then developed to predict machining stability based on both raw electrical signal features and classified discharge-type features. Finally, dynamic discharge trends across varying rotation rates are examined to uncover behaviors indicative of process instability, forming the foundation for data-driven control strategies. The objective is not only to improve the prediction accuracy but also to enhance physical interpretability by linking signal characteristics and discharge phenomena to machining outcomes.

This study aims to advance a physically grounded understanding of the stability phenomena in rotational EDM through the integration of traditional optimization techniques and modern machine learning. The findings support improved process stability and productivity in the deep hole drilling of challenging mold materials such as tungsten carbide.

2. Methodology

2.1. Experimental Setup and Data Acquisition

2.1.1. Materials and Machining Configuration

Electric discharge machining (EDM) experiments were performed on ultrafine grain cobalt-bonded tungsten carbide (KM10), produced by Toyo Tool, Osaka, Japan. The material had an average grain size of 0.7 $\mathsf{\mu }$m and a binder concentration of 8 %, with its mechanical properties listed in

Table 1. Material properties.

Material	Hardness [HRA]	Tensile Strength [GPa]	Toughness [GPa]
WC-Co (KM10)	91.5	3.4	11.2

. Copper electrodes with a diameter of 1 mm, supplied by Nilaco, Tokyo, Japan, were used as tools. The experiments were conducted using the Mitsubishi EA8PV die-sinking EDM machine.

Tool rotation was controlled using a Nakanishi E2280 pneumatic air spindle, with the rotational rate regulated via an Arduino Uno and ADC-based system. The dielectric fluid used was Shell Paraol 250, equipped with a custom filtration system operating in two stages: 10 $\mathsf{\mu }$m and 0.5 $\mathsf{\mu }$m.

Waveform data were acquired using an Iwatsu SS-0130R voltage probe and an Iwatsu SS-240A current probe, connected to a Picoscope 3403D MSO oscilloscope. A sampling interval of 504 ns was used to capture short-duration pulses with high precision. The data were recorded in binary format using Python wrappers from the PicoSDK library. A schematic of the complete machining setup is shown in Figure 1.

2.1.2. Waveform Capture and Discharge Classification

To reduce the impact of electrical noise, both inductive and capacitive, a weighted moving average filter was applied to voltage and current signals. The kernel used was (0.05, 0.15, 0.6, 0.15, 0.05), which effectively smoothed high-frequency fluctuations while preserving the underlying discharge shape.

The EDM system employed in this study features an always-on voltage and a pulsed current profile. A switched-capacitor (SC) circuit was used, in which the current rises gradually for each discharge. The discharge pulse duration was defined as the interval during which the current exceeds 60% of its local peak, capturing the effective energy delivery window.

Discharge events were flagged whenever this 60% threshold was crossed. For each event, the start time, average voltage, average current, discharge duration, and inter-discharge delay were computed. A schematic of the event detection methodology is shown in Figure 2, and classification criteria are provided in Table 2.

In addition to the standard discharge categories established in previous studies [20,25], two new classes are introduced: Unstable Sparks (USs) and Secondary Discharges (SDs). These capture events with pulse-off durations shorter than the nominal off-time, a common feature in circuits with continuously applied voltage and pulsed current. This categorization was necessary, as a substantial proportion of discharges were found to occur under these conditions as seen in Figure A1.

Table 2. Key conditions for the classification of detected discharges.

Class	Symbol	Key Conditions
Short circuit	SC	$V<0.01V_o$
Clean Sparks	SP	$V>0.01V_o;I>0.75I_p;0.9T_{\mathrm{on}}\ge T\ge 1.1T_{\mathrm{on}};$
		$\mathrm{Delay}\ge T_{\mathrm{off}}$
Transient Arcs	TA	$V>0.01V_o;1.1T_{\mathrm{on}}>T\ge 1.4T_{\mathrm{on}}$
Arcs	AR	$V>0.01V_o;T>1.4T_{\mathrm{on}}$
Unstable Spark	US	Same as SP but $\mathrm{Delay}<T_{\mathrm{off}}$
Partial Sparks	PS	Same as SP but $I<0.75I_p$
Secondary Discharges	SD	All other discharges not matching the above categories

Table 2. Key conditions for the classification of detected discharges.

Class	Symbol	Key Conditions
Short circuit	SC	$V<0.01V_o$
Clean Sparks	SP	$V>0.01V_o;I>0.75I_p;0.9T_{\mathrm{on}}\ge T\ge 1.1T_{\mathrm{on}};$
		$\mathrm{Delay}\ge T_{\mathrm{off}}$
Transient Arcs	TA	$V>0.01V_o;1.1T_{\mathrm{on}}>T\ge 1.4T_{\mathrm{on}}$
Arcs	AR	$V>0.01V_o;T>1.4T_{\mathrm{on}}$
Unstable Spark	US	Same as SP but $\mathrm{Delay}<T_{\mathrm{off}}$
Partial Sparks	PS	Same as SP but $I<0.75I_p$
Secondary Discharges	SD	All other discharges not matching the above categories

Where $V_o,I_p,T_{on},T_{off}$ refer to open circuit voltage, peak current, pulse on duration, and pulse off duration, respectively.

2.2. Experimental Design and Optimization

2.2.1. Design of Experiments

Two sets of experiments were conducted to evaluate the effect of tool rotation in EDM. The first was a parameter optimization experiment to establish baseline machining performance, followed by the micro through-hole drilling of tungsten carbide to investigate the influence of different rotation rates. The optimization experiments were conducted under lower settings of the transistor–resistor circuit, representing the semi-finish machining region with discharge energy [1–10 mJ]. Informed by the prior literature [24] and manufacturer recommendations to reduce tool wear, short and frequent pulses with a gradual power rise were applied. To ensure adequate resolution in waveform acquisition, a minimum pulse duration of 4 $\mathsf{\mu }$s (8 samples) was maintained. Subsequently, rotation evaluation experiments were carried out by machining a tungsten carbide plate of thickness 1 mm and varying rotation rates from 1000 to 10,000 RPM. In addition to the standard experiments under fixed rotation rates, two dynamic test cases were introduced to evaluate the model’s robustness under time-varying rotation rates. These test cases simulate practical scenarios with varying rotation rates. They were excluded from training and used solely for independent validation. The rotation rates for the two test cases are defined as

$$Test1=⌊1000+6\times Time\left(s\right)⌋RPM$$

(1)

$$Test2=⌊4000+4.45\times Time\left(s\right)⌋RPM$$

(2)

2.2.2. Taguchi–Grey Optimization

The Taguchi method was employed to determine optimal machining parameters within defined experimental constraints. Five parameters—open circuit voltage ($V_o$), peak discharge current ($I_p$), feed rate (f), pulse-on duration ($T_{on}$), and duty ratio ($DR$)—were each evaluated at four levels using an L16 orthogonal array as shown in

Table 3. Orthogonal array for Taguchi–Grey optimization.

E.ID	Voltage [V]	Feed Rate [μm/min]	Peak Current [A]	Pulse On [μs]	Duty Ratio
1	80	60	1	4	0.2
2	80	120	1.5	8	0.3
3	80	180	2	16	0.4
4	80	240	2.5	32	0.5
5	110	60	1.5	16	0.5
6	110	120	1	32	0.4
7	110	180	2.5	4	0.3
8	110	240	2	8	0.2
9	150	60	2	32	0.3
10	150	120	2.5	16	0.2
11	150	180	1	8	0.5
12	150	240	1.5	4	0.4
13	220	60	2.5	8	0.4
14	220	120	2	4	0.5
15	220	180	1.5	32	0.2
16	220	240	1	16	0.3

. Blind holes of 200 $\mathsf{\mu }$m were machined at a rotation rate of 2000 RPM.

Performance evaluation was categorized into three domains: material removal rate (MRR), surface roughness (Sa and Sz), and profile accuracy, specifically, machining depth (d) and diametric overcut (DOC). Each output metric had a distinct optimization goal: maximizing MRR, minimizing surface roughness, and achieving dimensional accuracy in profile features. To address the multi-objective nature of the problem, the Grey relational analysis (GRA) method was adopted. The procedure includes (1) the normalization of data, (2) the computation of Grey relational coefficients (GRC), and (3) ranking based on Grey relational grade (GRG). Based on the optimization objective, one of three normalization formulas was used: smaller-the-better, larger-the-better, or nominal-the-best (Equations (3)–(5)). The GRC was calculated using Equation (6), and the GRG using Equation (7). The notation was simplified for clarity but remained consistent with standard GRA formulations [26,27]:

$$n_i\left(k\right)={\displaystyle \frac{max{x}_i\left(k\right)-x_i\left(k\right)}{max{x}_i\left(k\right)-min{x}_i\left(k\right)}}$$

(3)

$$n_i\left(k\right)={\displaystyle \frac{x_i\left(k\right)-min{x}_i\left(k\right)}{max{x}_i\left(k\right)-min{x}_i\left(k\right)}}$$

(4)

$$n_i\left(k\right)=1-{\displaystyle \frac{x_i\left(k\right)-obj\left(k\right)}{max\left|x_i\left(k\right)-obj\left(k\right)\right|}}$$

(5)

where $x_i\left(k\right)$ are the values of output k for experiment ID i, and $obj\left(k\right)$ is the goal value of output k:

$$GR{C}_i\left(k\right)={\displaystyle \frac{{\Delta }_{min}+\zeta ·{\Delta }_{max}}{{\Delta }_i\left(k\right)+\zeta ·{\Delta }_{max}}}$$

(6)

where ${\Delta }_i\left(k\right)=\left|x_i\left(k\right)-n_i\left(k\right)\right|$ is the deviation of the sequence. The distinguishing coefficient $\zeta$ was set to 0.5, a commonly used value in the literature, ensuring moderate sensitivity in the GRC calculation:

$$GR{G}_i=\sum _{k=1}^n{\beta }_{k}GR{C}_i\left(k\right)$$

(7)

To balance machining objectives, the five responses were grouped into three categories: machining efficiency (MRR), surface quality (Sa, Sz), and profile accuracy (d, DOC). Equal weight was applied to each category when calculating the GRG, aligning with the study’s goal of balanced optimization.

2.2.3. Regression-Based Parameter Analysis

The empirical relationships between input (X) parameter and output (Y) metrics were further explored through regression modeling. Both linear regression (LR) and non-linear ensemble models, Random Forest (RF) and Extreme Gradient Boosting (XGB), were implemented using the scikit-learn Python library. For linear regression, which is sensitive to multicollinearity, features with a variance inflation factor (VIF) greater than 5 were iteratively removed. To enhance model performance, backward sequential feature selection was employed to identify the most relevant variables. The objective was to retain the maximum number of features while achieving high performance, defined by $R^2>0.85$ and $\mathrm{MAPE}<20\%$.

For the non-linear RF and XGB models (as described in [28]), which are inherently robust to multicollinearity, no VIF filtering was applied. A train–test split ratio of 80:20 was used, unless a predefined test set was available.

These regression models were not intended solely for high-accuracy prediction but were used to evaluate the nature of relationships, linear or non-linear, between input parameters and output metrics, and to identify key influencing variables. In cases where the regression models failed to meet the performance thresholds, a correlation analysis was conducted. The Pearson correlation coefficient between two variables x and y is given by Equation (8):

$$Corr\left(x,y\right)={\displaystyle \frac{Cov\left(x,y\right)}{{\sigma }_x{\sigma }_y}}$$

(8)

2.3. Labeling and Predictive Modeling

2.3.1. End-of-Machining (EOM) Detection

Following data preparation, we first developed a model to detect the End-of-Machining (EOM) phase. This was essential to isolate the effective machining period from the chaotic breakthrough or termination phases, which often introduce labeling noise. The EOM phase is characterized by a decaying discharge signals: highly oscillatory waveforms with gradually diminishing amplitude as illustrated in Figure 3a. To detect this transition, Fast Fourier Transform (FFT) was applied to the total discharge signal, leveraging the observation that EOM regions exhibit significantly lower energy in frequency bands [0.08–0.12 Hz]. A preliminary manual annotation of the EOM onset was made via visual inspection. This initial label was then used to train a Random Forest classifier on features such as FFT band energy Figure 3b and the rolling mean of discharge count over a 25 s window Figure 3c.

The trained model enabled the automatic detection and segmentation of machining and EOM phases, ensuring that subsequent analysis focused only on the machining regime.

2.3.2. Instability Labeling Strategy

Within the machining phase, the term instability may refer to undesirable conditions such as frequent tool oscillations, inefficient material removal, short circuits, or erratic discharge behavior. For effective machine learning-based classification, it is essential to establish a consistent and physically meaningful definition of instability that remains valid across varying rotation rates.

Based on exploratory analysis, two categories of instability were identified: (1) quantitative instability, characterized by a significant deviation in the total number of discharges from typical machining behavior, and (2) qualitative instability, involving compositional shifts in discharge events, such as increased arcing or secondary discharges. This study focuses on the former, quantitative instability hereafter referred to as “unstable machining”.

To define instability in a rotation-invariant manner, the total discharge count distribution was analyzed across all machining batches (1 s each). Batches falling below the 10th percentile were labeled as under-machined, while those exceeding the 85th percentile were labeled as over-machined as seen in Figure 4. These thresholds, selected through iterative testing, ensured a balance between class coverage and label separability. The resulting binary labels: unstable (under- or over-machined) and stable, served as the ground truth for supervised learning.

To classify stable and unstable machining batches based on the defined labels, we used two commonly applied tree-based ensemble learning algorithms: Random Forest (RF) [29,30] and Extreme Gradient Boosting (XGBoost or XGB) [31]. RF builds multiple decision trees using randomly sampled data and features, which helps improve robustness and reduce overfitting. XGBoost, on the other hand, builds trees sequentially, with each tree aiming to correct errors made by the previous ones. These models are often used for structured data classification tasks and are known for their performance in practical applications such as the detection of defects [32,33] or process monitoring in manufacturing [34].

In this study, we applied both models to predict machining stability at the batch level, using features engineered from event statistics and signal-based indicators.

2.3.3. Supervised Classification

Two types of features were extracted for model training. The first set comprises raw waveform derived features, including mean, standard deviation, maximum, and minimum values of voltage, current, discharge duration, inter-discharge delay, and gap, calculated over 1 s batches.

The second set includes classified discharge features, such as the count of each discharge type, 10 s rolling averages, and temporal derivatives. While percentage-based features were initially explored, they were excluded to avoid data leakage, as they directly depend on the total discharge count used for labeling.

In total, over 20 features were considered. To address the potential high dimensionality and multicollinearity, an initial Random Forest model was used to evaluate feature importance. Features with low SHAP (SHapley Additive Explanations) scores and high variance inflation (VIF > 10) were removed, and the top 15 features were selected. Additionally, to address the issue to the class imbalance (unstable batches comprising 25%), the Synthetic Minority Oversampling Technique (SMOTE) was applied during training.

The two classifiers, RF and XGBoost, were evaluated. Hyperparameter tuning was performed using grid search. A conservative decision threshold of 0.4 was adopted to prioritize recall over precision, given the application’s focus on detecting potentially unstable conditions where false negatives are more critical than false positives. The complete machine learning workflow is outlined in Figure 5.

The overall proposed framework to evaluate the effect of rotation rate is shown in Figure 6.

3. Results and Discussion

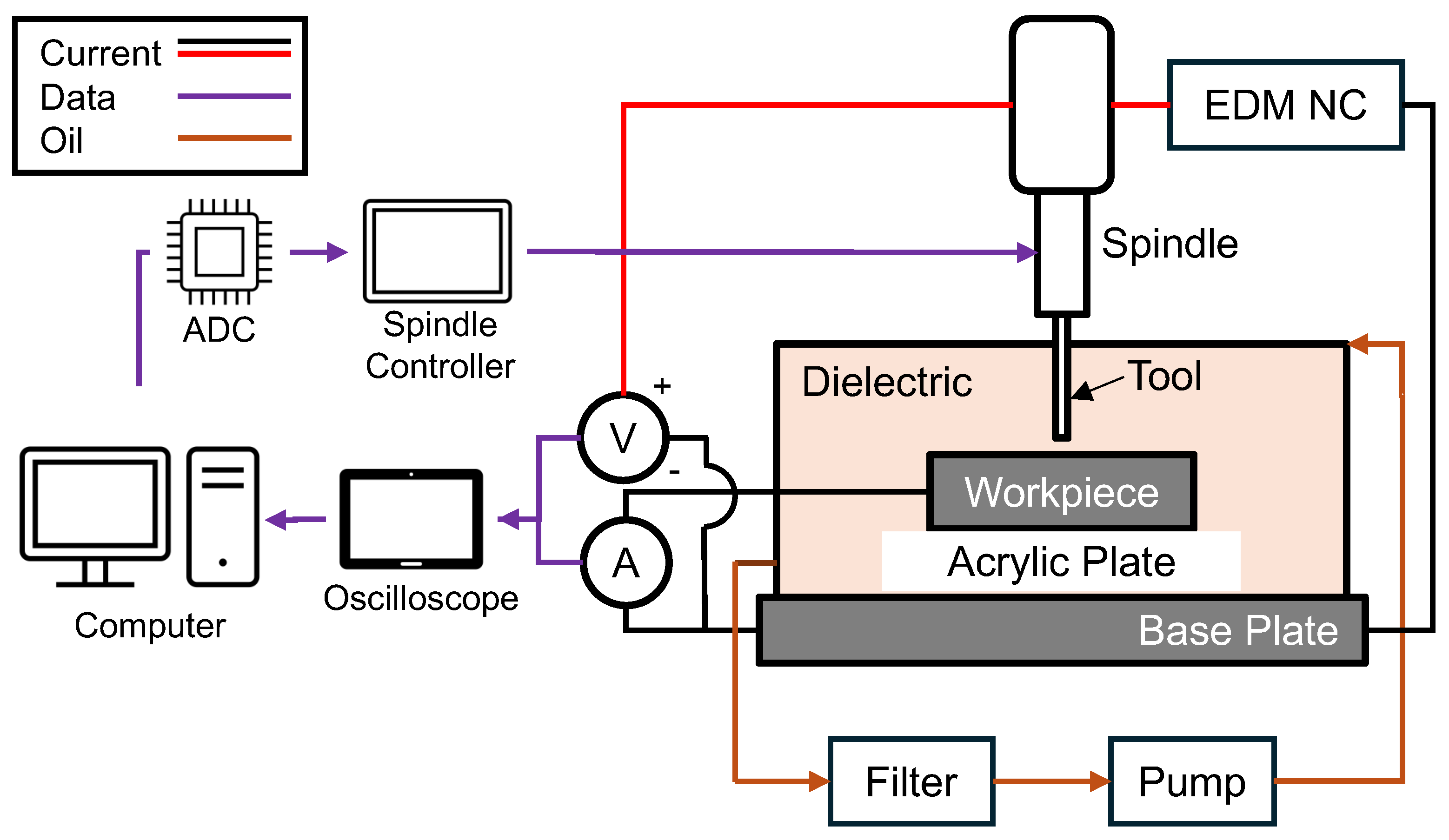
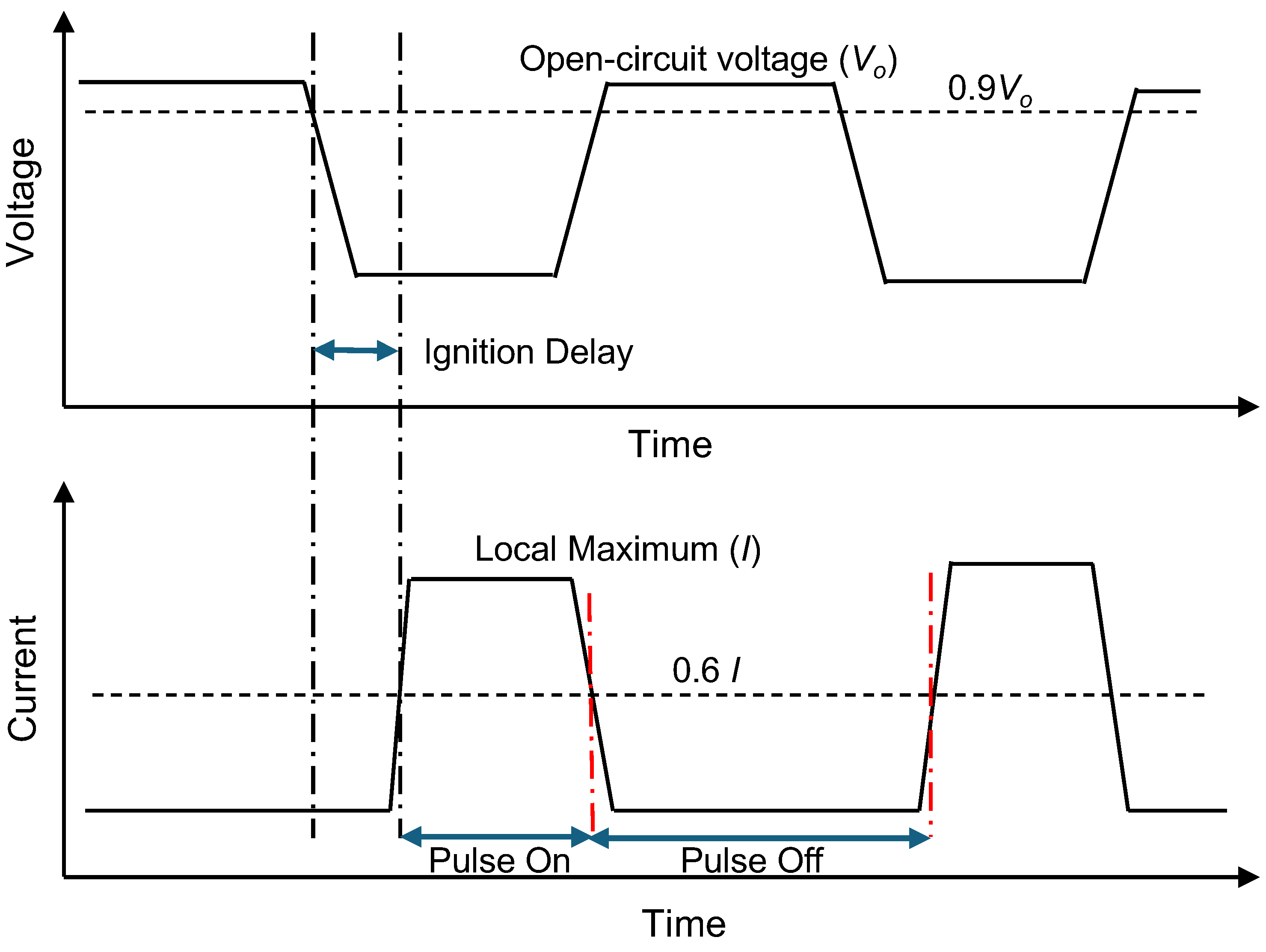
3.1. Parameter Optimization Using Taguchi–Grey and Regression Models

The summary of performance metrics and corresponding Grey relational grades (GRG) for each experimental condition is shown in

Table 4. Summary of results and Grey relational grades (GRG) for each parameter evaluation experiment.

E.ID	Results					GRG	Rank
	MRR	Sa	Sz	DOC	d
	[μm3/min]	[μm]	[μm]	[μm]	[μm]
1	18.74	0.88	15.14	23.59	184.43	0.47	13
2	32.23	1.21	22.35	26.49	197.49	0.62	6
3	66.56	1.82	23.73	30.68	225.31	0.62	5
4	71.84	3.25	39.30	38.17	269.97	0.54	9
5	49.23	1.94	24.89	33.83	276.93	0.47	12
6	24.25	3.07	32.78	33.41	235.20	0.43	15
7	79.90	1.34	20.25	21.37	221.17	0.84	1
8	35.86	0.75	12.78	19.32	192.09	0.74	2
9	26.76	4.42	37.70	40.34	184.15	0.44	14
10	24.00	2.46	30.28	25.98	192.25	0.54	10
11	48.99	1.61	21.95	28.62	189.27	0.60	7
12	63.41	1.45	21.82	25.58	214.76	0.67	3
13	37.43	1.86	26.58	25.83	220.97	0.54	8
14	58.89	1.57	24.94	22.55	227.19	0.64	4
15	16.07	3.38	36.51	27.53	209.60	0.49	11
16	17.21	2.41	26.08	31.76	154.30	0.43	16

. Experiments 7 and 8 exhibited the highest GRG values. Subsequent SEM-based surface inspections, as seen in Figure 7, revealed minimal surface defects such as micro-cracks in these samples, validating the selection. Experiment 7 was ultimately chosen for rotation rate evaluation experiments. The table for data normalization and Grey relational coefficients is shown in

Table A1. Summary of normalized values and Grey relational coefficients (GRCs) for each parameter evaluation experiment.

E.ID	Normalized Results					Grey Relational Coefficients
	MRR	Sa	Sz	DOC	d	MRR	Sa	Sz	DOC	d
1	0.04	0.96	0.91	0.80	0.80	0.34	0.93	0.85	0.71	0.76
2	0.25	0.87	0.64	0.66	0.97	0.40	0.80	0.58	0.59	1.00
3	0.79	0.71	0.59	0.46	0.67	0.71	0.63	0.55	0.48	0.64
4	0.87	0.32	0.00	0.10	0.09	0.80	0.42	0.33	0.36	0.38
5	0.52	0.67	0.54	0.31	0.00	0.51	0.61	0.52	0.42	0.36
6	0.13	0.37	0.25	0.33	0.54	0.36	0.44	0.40	0.43	0.56
7	1.00	0.84	0.72	0.90	0.72	1.00	0.75	0.64	0.84	0.69
8	0.31	1.00	1.00	1.00	0.90	0.42	1.00	1.00	1.00	0.88
9	0.17	0.00	0.06	0.00	0.79	0.38	0.33	0.35	0.33	0.75
10	0.12	0.53	0.34	0.68	0.90	0.36	0.52	0.43	0.61	0.89
11	0.52	0.76	0.65	0.56	0.86	0.51	0.68	0.59	0.53	0.83
12	0.74	0.81	0.66	0.70	0.81	0.66	0.72	0.59	0.63	0.77
13	0.33	0.70	0.48	0.69	0.73	0.43	0.62	0.49	0.62	0.69
14	0.67	0.77	0.54	0.85	0.65	0.60	0.69	0.52	0.76	0.62
15	0.00	0.28	0.11	0.61	0.88	0.33	0.41	0.36	0.56	0.85
16	0.02	0.55	0.50	0.41	0.41	0.34	0.52	0.50	0.46	0.49

.

Based on the methodologies described in Section 2.2.3, linear regression models were evaluated using $R^2$ and MAPE as shown in

Table 5. Linear regression results for each target output.

Target	R2	MAPE
MRR	0.861	15.970
Sa	0.948	12.355
Sz	0.496	18.384
Depth	0.172	11.635
Overcut	0.771	8.988

. Only MRR and Sa achieved the target thresholds of $R^2$ > 0.85 and MAPE < 20% and were considered suitable for interpretation. The MRR showed strong dependence on peak current and pulse-on duration (Equation (9)). For Sa, as seen in Equation (10), lower voltage, shorter pulse durations, and higher feed rates were found to be favorable for achieving better surface quality. These findings align with prior studies on the semi-finish EDM of hard materials [35,36,37].

$$MRR=6.471+1.717I_p+0.065T_{on}+0.062DR$$

(9)

$$Sa=-0.017+0.008T_{on}+0.011V_p-0.002f$$

(10)

3.2. Exploratory Modeling and Feature Selection for Bad Condition Labeling

To evaluate machining performance across different rotation rates, an evaluation study was conducted, summarized in

Table 6. Summary of machining metrics.

Rotation Rate	Mach. Time	Top Dia.	Bot Dia.	Top Rou.	Bot Rou.	GRG	Rank
[RPM]	[min]	[μm]	[μm]	[μm]	[μm]
1000	17.18	1075.38	946.09	23.57	3.92	0.76	1
2000	17.62	1106.06	945.98	26.26	5.81	0.63	5
3000	18.70	1107.25	939.29	22.17	5.92	0.55	7
4000	18.42	1112.93	968.52	23.93	18.84	0.53	8
5000	18.37	1071.83	950.82	3.37	10.88	0.68	3
6000	17.97	1123.92	953.23	22.82	3.71	0.64	4
7000	19.32	1116.01	960.14	25.97	11.72	0.50	10
8000	18.98	1120.61	971.63	26.59	14.28	0.52	9
9000	16.93	1126.05	978.17	19.34	17.17	0.75	2
10,000	19.10	1098.28	953.79	21.81	3.46	0.60	6

. Since the material removal rate for through-holes is directly influenced by both top and bottom diameters, machining time (Mach.Time) was considered as an independent metric. Additionally, as illustrated in Figure 8d,e, inlet chipping was observed for some conditions, prompting the inclusion of roundness metrics (Top Rou, Bot Rou). Three distinct temporal surfaces (B1, B2, B3) were observed in the hole cross-sections (Figure 8b,e), and were therefore excluded from quantitative analysis. Equal weights were assigned to the machining time, diameter, and roundness in the Grey relational grade (GRG) computation.

From the results, the best performance was observed at 1000 and 9000 RPM, which emerged as potential optima. Normalized data and Grey relation coefficients for these conditions are shown in

Table A2. Summary of normalized values and Grey relational coefficients (GRCs) for each parameter evaluation experiment.

E.ID	Normalized Results					Grey Relational Coefficients
	Mach. Time	Top Dia	Bot Dia	Top Rou.	Bot Rou.	Mach. Time	Top Dia	Bot Dia	Top Rou.	Bot Rou.
1	0.42	0.93	0.18	0.13	0.97	0.46	0.88	0.38	0.36	0.94
2	0.45	0.37	0.17	0.01	0.85	0.48	0.44	0.38	0.34	0.77
3	0.09	0.35	0.00	0.19	0.84	0.35	0.43	0.33	0.38	0.76
4	0.36	0.24	0.75	0.11	0.00	0.44	0.40	0.67	0.36	0.33
5	0.05	1.00	0.30	1.00	0.52	0.35	1.00	0.42	1.00	0.51
6	0.48	0.04	0.36	0.16	0.98	0.49	0.34	0.44	0.37	0.97
7	0.07	0.19	0.54	0.03	0.46	0.35	0.38	0.52	0.34	0.48
8	0.25	0.10	0.83	0.00	0.30	0.40	0.36	0.75	0.33	0.42
9	1.00	0.00	1.00	0.31	0.11	1.00	0.33	1.00	0.42	0.36
10	0.00	0.51	0.37	0.21	1.00	0.33	0.51	0.44	0.39	1.00

.

To explore empirical modeling, linear and non-linear regression models were applied using the rotation rate as a sole input variable as seen in

Table 7. Model $R^2$ scores for different feature sets.

Output	R2 Rotation			R2 Signal Features			R2 Classified Features
	LinReg	RF	XGB	LinReg	RF	XGB	LinReg	RF	XGB
Mac. Time	−20.20	−18.27	−17.99	−58.28	0.69	−0.67	−4.08	0.10	−0.22
Top Dia.	−0.63	−1.81	−3.86	−9.00	0.28	−0.14	−713.80	−0.22	0.00
Bot Dia.	0.46	0.72	0.92	−177.40	−0.62	−0.15	−3141.73	−0.74	−0.78
Top Rou.	−0.83	−0.99	−1.50	−35.22	0.01	−0.43	−1080.21	−0.46	−1.77
Bot Rou.	−0.08	0.47	0.82	−748.46	−0.46	−0.83	−17641.0	−1.33	−2.25

. However, most models yielded negative $R^2$ scores, indicating they performed worse than simple mean-based prediction. This suggests either insufficient data points or a non-monotonic (i.e., non-consistently increasing or decreasing) relationship between rotation rate and output metrics. We then explored whether including on-machine measurements could improve model performance by incorporating two feature sets: Z1 (raw electrical signals) and Z2 (discharge classifications), as described in Section 2.1.2.

Despite these enhancements, regression models (especially linear ones) still performed poorly. For example, the linear model trained on raw signal features produced an implausibly negative $R^2$ (e.g., −748 for bottom roundness), indicating poor model generalization and potential issues with input scaling or multicollinearity. While ensemble models (e.g., Random Forests) achieved marginal improvements (e.g., $R^2$ = 0.69 for machining time), the overall prediction remained weak.

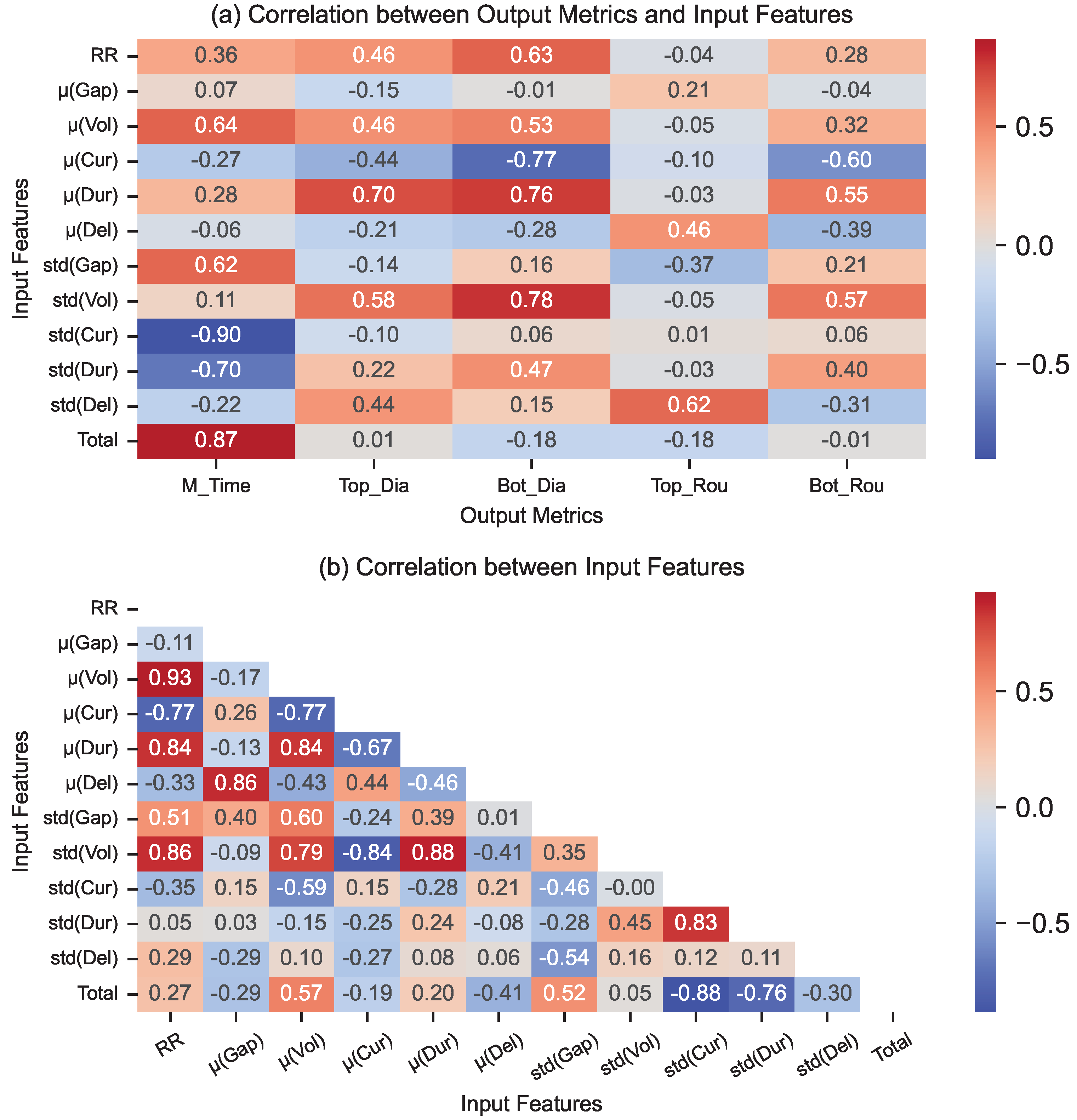
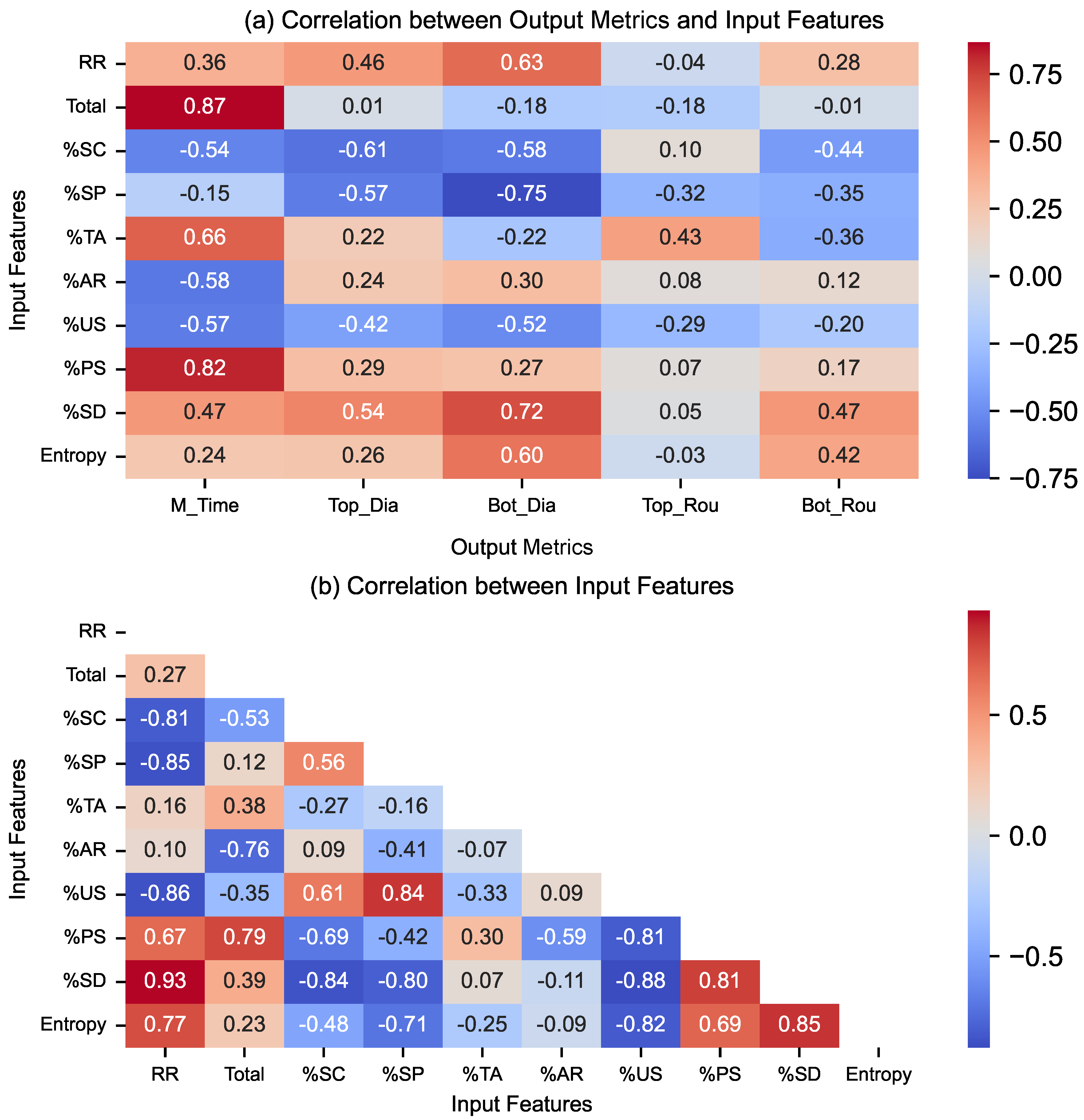
Due to these limitations, the focus shifted from regression modeling to correlation-based analysis. Pearson correlation coefficients were computed both between input features and output metrics ($Z-Y$), and among input features themselves ($Z-Z$), along with the rotation rate [RR] for classified data as visualized in Figure 9. A correlation threshold of $\left|r\right|\ge 0.6$ was used to denote strong associations.

The findings revealed several key relationships between discharge types and machining outcomes. An increase in weak partial sparks and transient arcs was significantly correlated with longer machining times, suggesting inefficiencies in energy transfer. A higher count of secondary discharges, likely resulting from poor flushing, was associated with enlarged top and bottom diameters, leading to pronounced overcuts. In contrast, clean sparks consistently aligned with improved machining efficiency and reduced top and bottom diameters thereby reducing overcuts, reaffirming their role as desirable discharges.

Interestingly, short circuits also showed negative correlation with overcut (top and bottom diameters). This counterintuitive trend is interpreted as a secondary effect arising from increased clean spark frequency and the suppression of secondary discharges. Despite these insights, extensive multicollinearity among the features substantially weakened the explanatory power of regression-based models.

An important physical insight emerged: increasing the rotation rate tends to raise the frequency of partial sparks and secondary discharges, likely due to increased fluid shear disrupting discharge channels. At the same time, increasing rotation helps break down short circuits more rapidly. In summary, the increased rotation rate increases chaos or entropy within the discharge gap as seen in Figure 9b. These inferences were further supported by correlations derived from raw signal features (Figure A2).

These results underscore the value of time-resolved discharge pattern analysis over aggregate statistics when evaluating the influence of rotation. To reduce feature dimensionality and address multicollinearity among discharge categories, we propose condensing discharge types into two interpretable classification schemes: one based on the discharge timing (henceforth on discharge timing)-derived features (

Table 8. Class 1: based on discharge timing-derived features.

Category	Constituents	Description
D1	SC	Non-machining discharges with variable duration
D2	AR, TA	Long-duration discharges; typically indicate overcut or high energy
D3	US, SD	Short-duration discharges with minimal inter-discharge delay
D4	SP, PS	Sparks with optimal duration and delay, may vary in energy

) and the other based on the impact of the discharge event (

Table 9. Class 2: based on impact of the discharge event.

Category	Constituents	Description
E1	SC	Dominant failure mode; produces minimal or no material removal
E2	AR, SD	High energy or erratic discharges; increase tool wear or cause interruptions
E3	TA, PS, US	Spark-like discharges with sub-optimal energy, duration or delay characteristics
E4	SP	Clean sparks; primary contributors to efficient and stable material removal

).

This categorization is used in the next stage of our machine learning framework to reduce feature complexity while preserving physical interpretability.

3.3. Supervised Classification Using Machine Learning

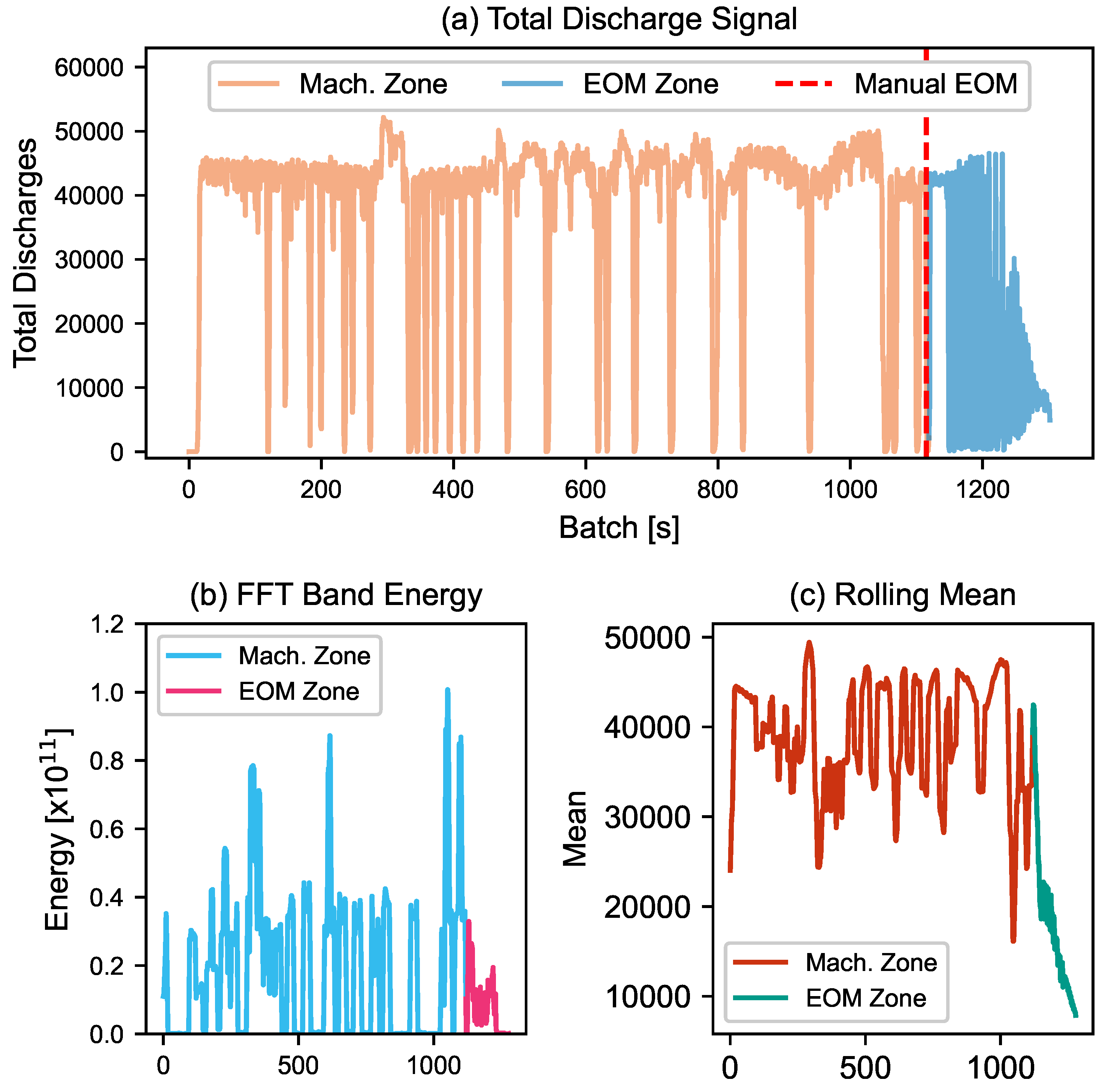
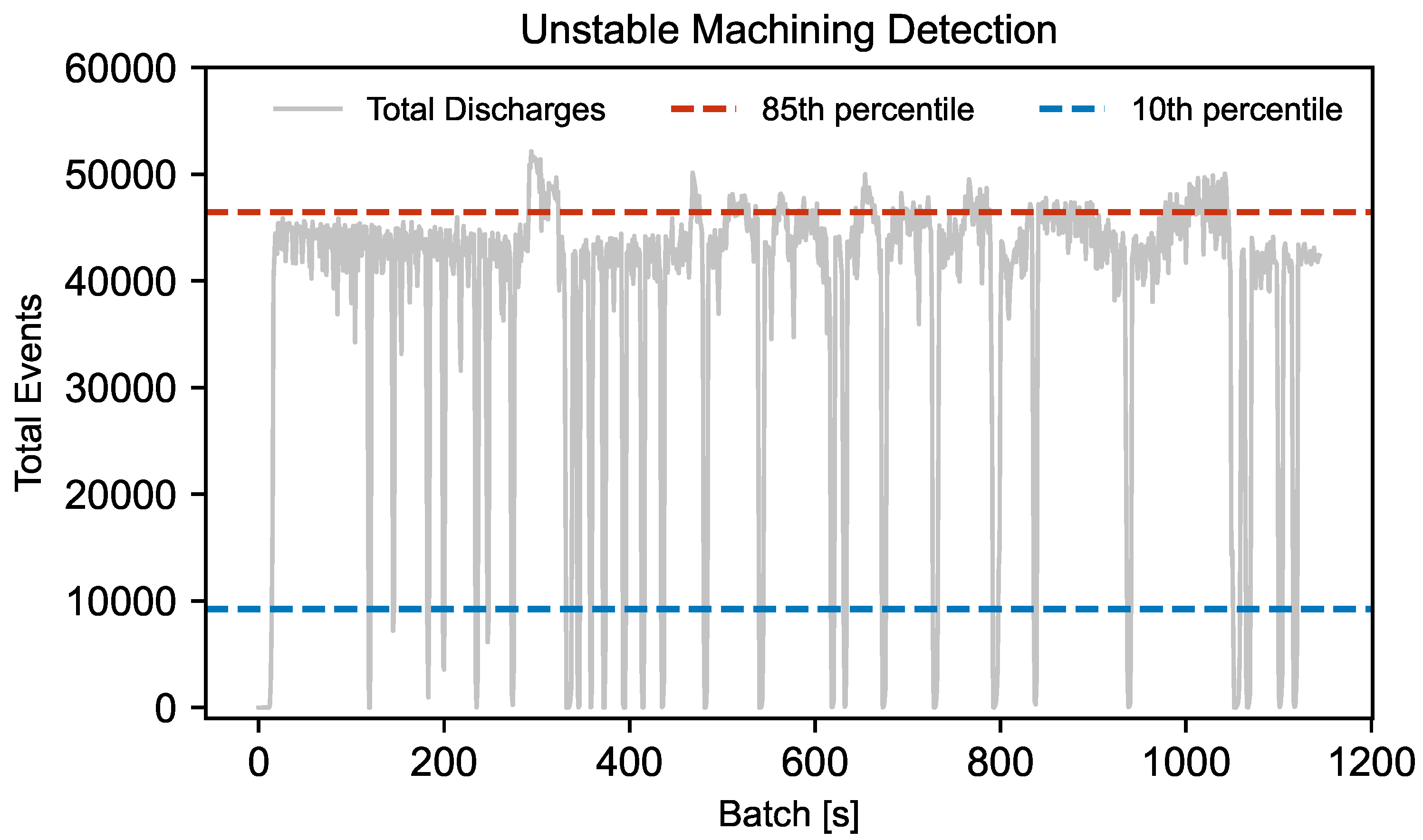
The End-of-Machining (EOM) detection model achieved an overall accuracy of 98%, with a precision of 0.85 and recall of 0.89 for detecting the EOM class. The confusion matrix in

Table 10. Confusion matrix results for EOM detection.

	Predicted: Not EOM	Predicted: EOM
Actual: Not EOM	2254	32
Actual: EOM	22	176

shows that only 22 batches were misclassified as EOM before the actual onset, while the majority of false positives occurred after the true EOM point as seen in Figure 10 (Predicted EOM Phase), indicating the model’s conservative behavior. To avoid premature deactivation in a proposed dynamic control system, a post-EOM misclassification tolerance of 10 batches was adopted. While early false positives could impact control decisions, post-EOM misclassifications are acceptable since control would already be disengaged after detection. This conservative buffer ensures safe and robust labeling in anticipation of future deployment.

The model metrics and global temporal characteristics for the machine learning models in the segmented machining zone are summarized in

Table 11. Performance metrics for different feature types and classifiers.

Metric	Raw Features		Class 1 Features		Class 2 Features
	RF	XGB	RF	XGB	RF	XGB
Precision	0.694	0.729	0.816	0.760	0.710	0.696
Recall	0.907	0.858	0.448	0.544	0.885	0.907
F1-score	0.787	0.788	0.578	0.634	0.788	0.788
Accuracy	0.877	0.885	0.836	0.843	0.881	0.878

and Figure 11, respectively.

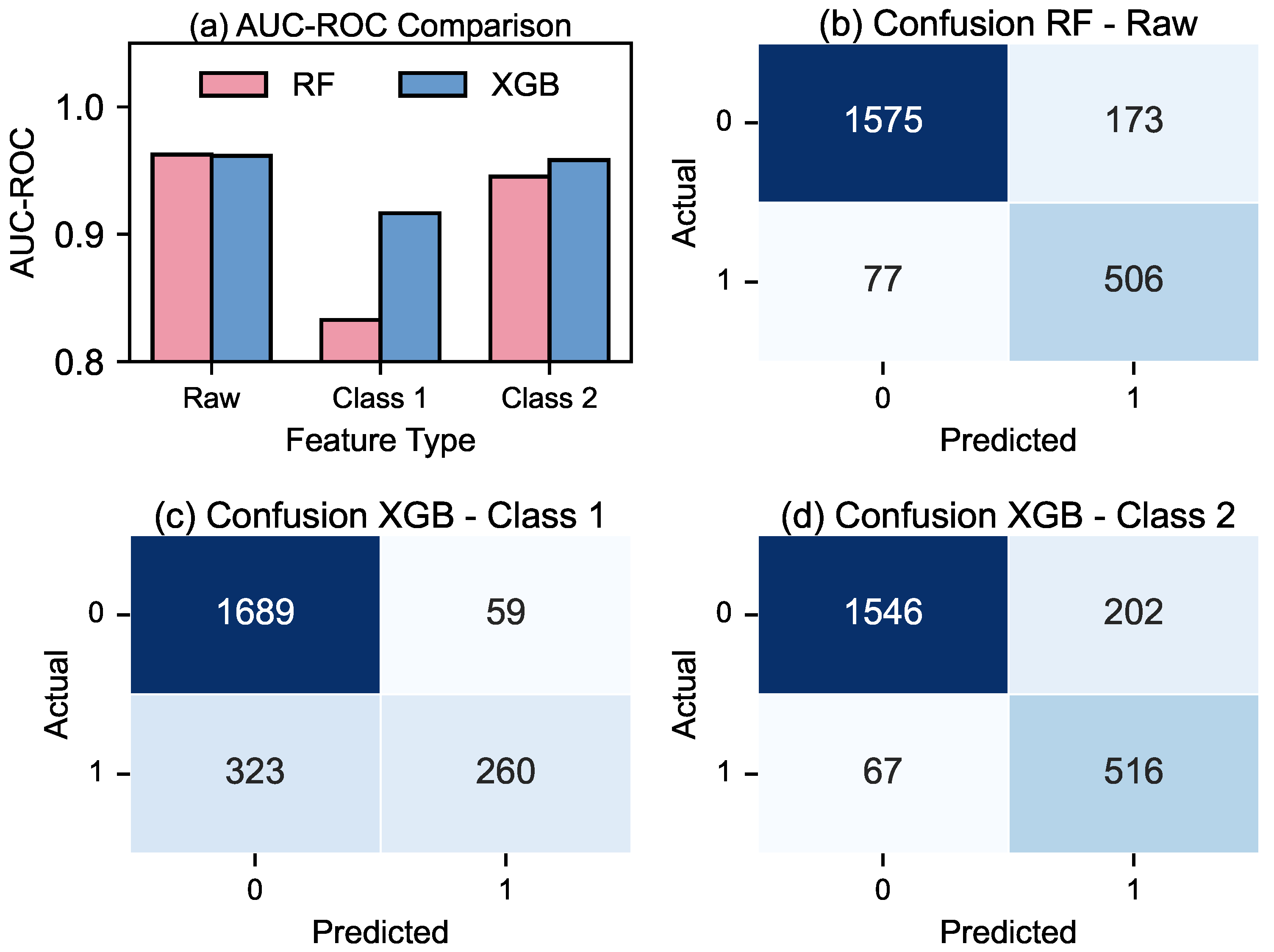
In general, the Extreme Gradient Boosting (XGB) classifier outperformed the Random Forest (RF) classifier in terms of both accuracy, the proportion of correctly predicted batches, and F1-score, which balances precision and recall, making it particularly useful under class imbalance. As shown in Figure 11a, most models achieved high confidence levels (ROC-AUC > 0.9), indicating that small changes in the probability threshold are unlikely to significantly affect classification outcomes.

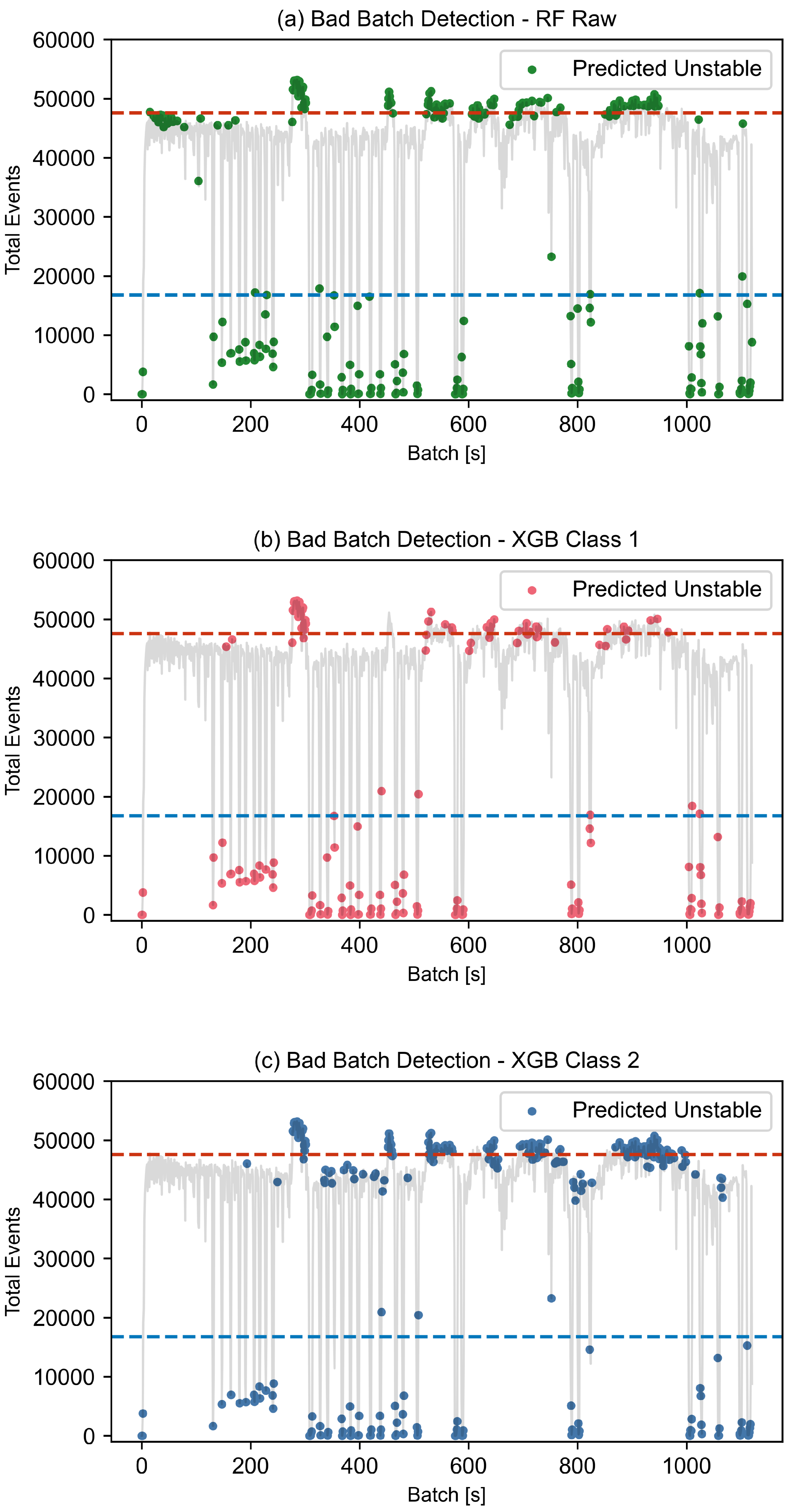
Additional insights are drawn from the confusion matrices in Figure 11b–d and the batch-level prediction overlays in Figure 12a–c. The model trained on raw electrical signal features exhibits a more sensitive prediction behavior, flagging a larger number of unstable batches, including those with subtle variations in discharge characteristics. This is particularly evident during the early machining periods (Figure 12a). In contrast, models based on discharge timing or impact features (Class 1) produce more conservative predictions, mainly identifying the most severe instances of instability but fail to capture sustained over-machining. Meanwhile, the model using discharge impact based features (Class 2) offers a more balanced prediction across different instability patterns.

This comparison highlights a key trade-off. Raw signal-based models are highly sensitive and computationally efficient due to minimal preprocessing but are also more prone to noise and false positives. Classification-based models, built on features like discharge timing or impact, offer greater physical interpretability and targeted detection, albeit with increased computational effort. For real-time monitoring, the RF model with raw features may be better suited for early anomaly detection. However, for corrective interventions, the discharge classification-based models provide more robust and interpretable predictions.

Given that this study aims to enable adaptive control of tool rotation, the model based on discharge impact features (Class 2) is recommended. While it achieves only moderate accuracy, its consistently high recall ensures the dependable detection of potentially unstable conditions, critical for preventive control, even if it occasionally sacrifices precision.

Additionally, we analyzed the model’s prediction methodology by examining the SHAP values of the five most important features as shown in Figure 13. In the plot, the dot color represents the actual feature value, while the SHAP value indicates the (unitless) magnitude and direction of that feature’s contribution toward predicting instability. In this study, both under-machining and over-machining conditions were collectively labeled as unstable machining. This broad classification can introduce non-monotonic behavior in the relationships between features and predicted outcomes.

Such non-monotonicity was evident in the top raw signal feature, gap mean (Figure 13a), where both low values could correspond to either stable or unstable conditions depending on contextual factors. In contrast, stable machining zones were generally associated with higher current levels. The short delay pulses (D3), despite exhibiting the high feature importance, likely due to its dominance in discharge counts (Figure A1), did not show a strong association with stable machining, as seen in Figure 13, also demonstrating a non-monotonic trend. Meanwhile, category E3, comprising ‘almost spark’ discharges such as Transient Arcs (TAs), Partial Sparks (PSs), and Unstable Sparks (USs), showed a consistently strong association with stable machining, as seen in Figure 13b,c. These observations underscore the importance of discharge type grouping in determining model interpretability and efficiency, and also highlight the potential multicollinearity between discharge categories.

Moreover, while the correlation analysis shows only a weak positive relationship between short circuits and sparks in Figure 9b, the SHAP summary from the classification model reveals a strong opposing effect; stable machining is associated with a higher occurrence of sparks and a lower presence of short circuits (D1, E1 and D4, E4).

Overall, although clear monotonic trends were not consistently observed, the SHAP analysis provided valuable insights into the model’s internal decision making and the relative importance of individual features in identifying machining instability.

3.4. Correction Strategy Exploration

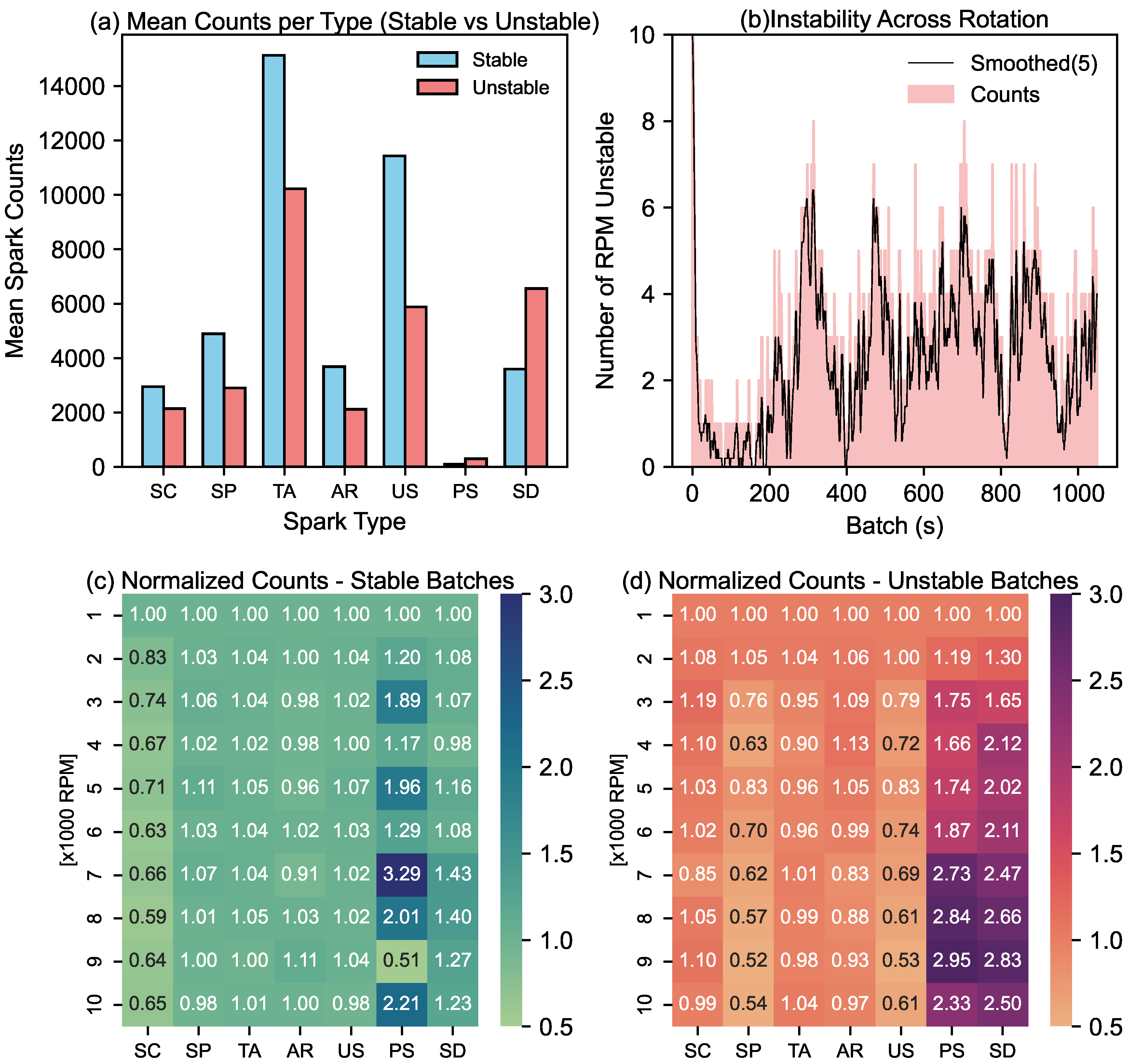
Based on the prediction model derived above, unstable machining zones were re-predicted for different tool rotation rates. Figure 14a shows the aggregate count of discharges for each spark type in stable and unstable machining phases. It was observed that during instability, there was a significant drop in the total number of discharges. However, there was a noticeable increase in secondary discharges, which are likely responsible for over-machining.

To better understand the role of rotation, the counts of different spark types for each rotation rate were normalized with respect to the 1000 RPM baseline. As shown in Figure 14c,d, transient arcs and arcs remain relatively constant (within 10% variation) across all rotation rates, indicating that long duration discharges are not significantly influenced by rotation. Two key observations emerged: First, increasing rotation rate was found to reduce short circuits by up to 40% during stable machining, while it remained unchanged during unstable machining. Contrarily, while clean spark counts decreased significantly during instability at higher rotation rates (more than 45%), they remained unaffected during stable phases. Furthermore, secondary discharges increased at higher rotation rates under both stable and unstable conditions, likely due to fluid shear that disrupted the discharge channels.

These contrasting behaviors help reconcile the earlier discrepancy between correlation and SHAP-based analysis: while short circuits and sparks showed a weak positive correlation overall, their opposing trends across stable and unstable phases at different rotation rates led to compensating effects in the aggregate data.

From these findings, we infer that during stable machining, increasing the rotation rate can suppress short circuits, whereas during unstable machining, a higher rotation rate may transform effective clean sparks into secondary discharges.

This insight forms the basis for a dynamic rotation control strategy: increase rotation rate during stable phases to improve flushing efficiency, and decrease it upon detecting instability to preserve spark effectiveness. Moreover, Figure 14b reveals that temporal evolution of instability occurs across all rotation rates, suggesting time-dependent patterns in machining behavior. Such trends are difficult to capture using static models like Random Forests and XGBoost. Future work could employ sequence-based models, such as recurrent neural networks (RNNs), to learn and predict these evolving patterns, potentially enabling earlier and more adaptive control.

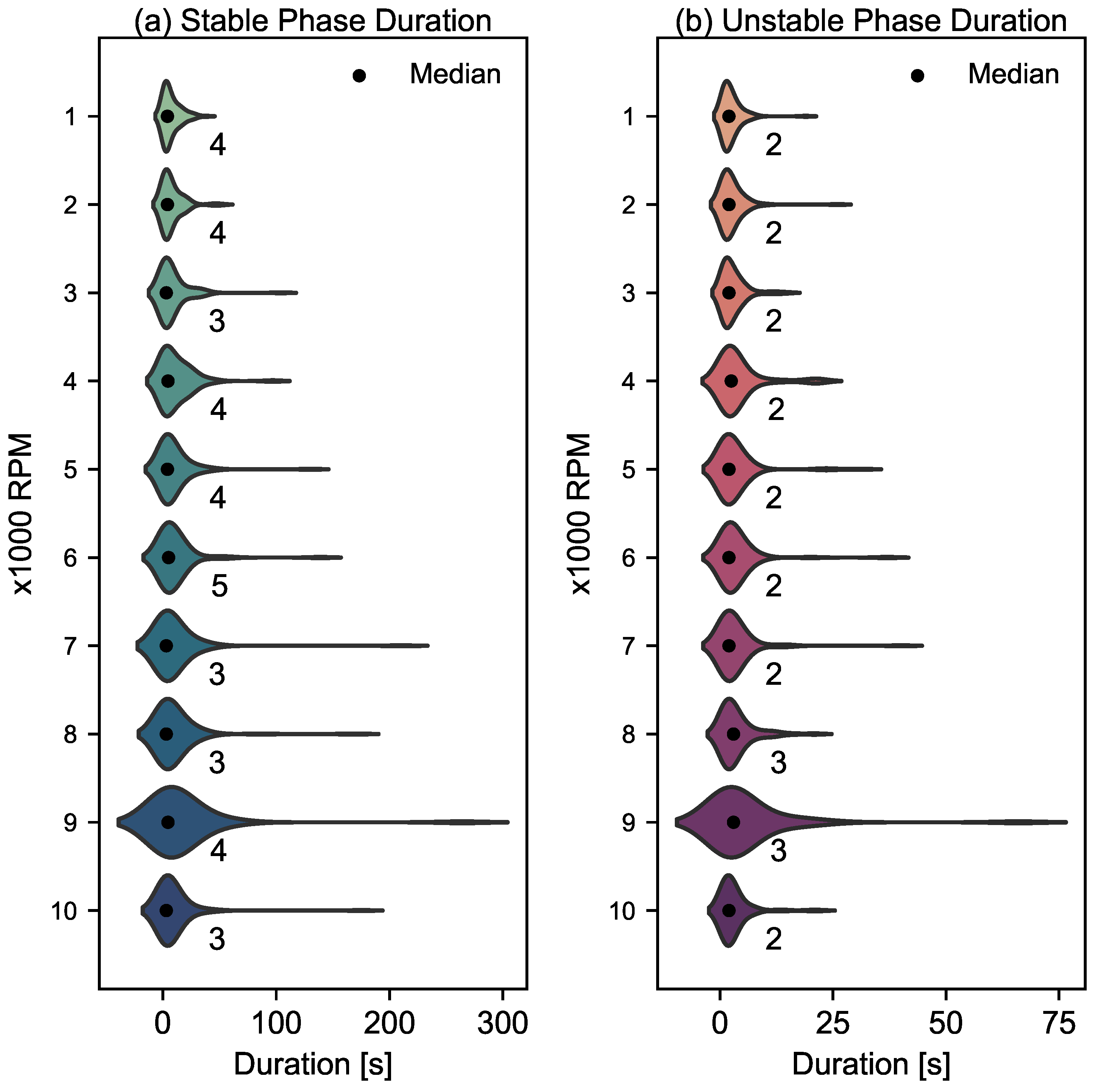
Violin plots in Figure 15 show that higher rotation rates are associated with longer tailed distributions in both stable and unstable phase durations. This suggests that once a particular phase is established at a higher rotation rate, it tends to persist for a longer duration. In contrast, lower rotation rates exhibit more compact distributions, indicative of shorter lived phases. This observation highlights the potential of rotation rate as a means to modulate machining phase stability.

Based on these two analyses, we propose a simple framework for real-time control. During machining, if stable conditions persist, increase the rotation incrementally every 4 s (the median duration of stable phases). If instability persists beyond 2 s, decrease the rotation rate sharply to achieve a more stable machining condition.

However, this study also recognizes certain limitations. The proposed control strategy is based on a limited number of observed rotation transitions and should be regarded as preliminary. Moreover, the predictive modeling employed in this work operates on a batch size of 1 s, which is comparable to the proposed control adjustment timescale of 2 s. This temporal proximity may limit the responsiveness of the current model in capturing finer grained transitions. To overcome this, future investigations should explore time-sequence modeling approaches, such as recurrent neural networks (RNNs), which can identify evolving patterns at subsecond resolutions. These models may enable the earlier detection of instability onset and better accommodate time delays introduced by data acquisition, feature computation, prediction, and spindle actuation delays. Additionally, since this study focused exclusively on ultrafine-grained tungsten carbide, the applicability of the proposed models and control strategies to other electrode or workpiece materials remains to be validated.

4. Conclusions

This study developed a multi-level framework to evaluate the effect of tool rotation in electric discharge machining (EDM) of tungsten carbide. Parameter optimization, tool rotation effect clarification, machining stability prediction, and feature importance analysis were performed. Additionally, a feedback informed framework for adaptive control was explored. The key findings are summarized as follows:

• Taguchi–Grey relational analysis successfully identified optimal parameter combinations for EDM in the semi-finish machining region with discharge energy [1–10 mJ]. Regression models validated strong relationships between electrical parameters and machining performance for material removal rate and surface roughness. However, regression approaches failed to capture the complex (non-monotonic) effects of tool rotation rates on machining outcomes, motivating the shift toward feature based classification.
• Three types of features: raw waveform, discharge timing based, and discharge impact based were used to train Random Forest and XGBoost classifiers. The best-performing model (RF on raw features) achieved 88.5% accuracy and over 90% recall. While raw features offered high sensitivity, discharge impact-based classification yielded better interpretability through SHAP analysis, despite the non-monotonic trends driven by the unified labeling of under- and over-machining as instability.
• SHAP analysis revealed that the relationship between short circuits and sparks is context-dependent. Although the global correlation matrix showed weak association, phase-specific analysis and SHAP plots highlighted their opposing roles in stability. This dual layer interpretation illustrates the strength of our framework in both predictive accuracy (downstream) and explaining aggregate trends through localized behavior (upstream).
• Tool rotation significantly influenced the discharge behavior. During stable machining, increasing the rotation rate from 1000 to 9000 RPM reduced short circuits by over 40%, while clean sparks remained consistent. However, under unstable conditions, higher rotation diminished spark counts and increased secondary discharges, indicating a shift in process dynamics.
• Higher rotation rates also resulted in longer stable and unstable phase durations (e.g., maximum stable phase duration increased from 38 s at 1000 RPM to 264 s at 9000 RPM). Based on these temporal dynamics, a control strategy was proposed: incrementally increase rotation every 4 s during extended stability, and reduce it within 2 s of instability detection, to extend productive phases and suppress deterioration.

The proposed framework is particularly applicable to deep hole EDM for glass molding dies, where improved surface integrity, dimensional consistency, and reduced electrode wear are essential. By dynamically controlling the tool rotation based on real-time discharge monitoring, this methodology supports the fabrication of cleaner, deeper holes in tungsten carbide, enhancing mold quality and service life.