A Methodology for Acceleration Signals Segmentation During Forming Regular Reliefs Patterns on Planar Surfaces by Ball Burnishing Operation
Abstract
1. Introduction
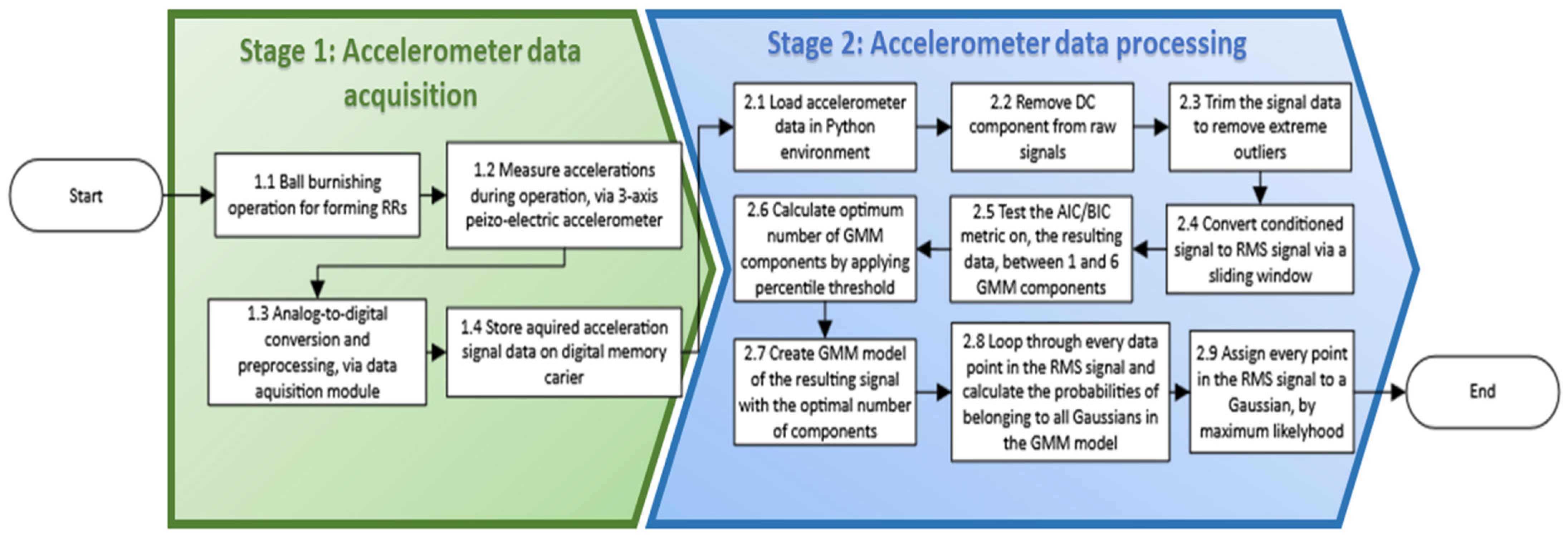
2. Materials and Methods
2.1. Accelerometer Data Acquisition
2.1.1. Ball Burnishing Operation for Forming RRs
2.1.2. Measuring Accelerations Setup Description
2.2. Accelerometer Data Processing
2.2.1. Loading Accelerometer Data in Python Environment
2.2.2. Removing the DC Component from the Raw Signal
- is the unbiased data point;
- is the biased data point;
- is the number of data points in the signal.
2.2.3. Trimming the Signal Data
2.2.4. Converting the Conditioned Signal to Root Means Square (RMS) Signal
2.2.5. Testing the Bayesian Information Criterion (BIC) Metric on the Resulting Data
- is the i-th data point in the signal;
- is the weight coefficient of the Gaussian distribution c;
- is the mean of the Gaussian distribution c;
- is the covariance of the Gaussian distribution c;
- K is the maximum number of components (in this case 6 as the limit for the last model being tested.
- is the probability density function of a Gaussian distribution c with corresponding parameters with respect to the i-th data point in the signal.
- m is the number of data points.
2.2.6. Calculating Optimal Number of GMM Components
- k, is the number of parameters in the estimated model;
- n, is the number of data points in the signal;
- is the maximized value of the likelihood function of the model.
2.2.7. Creating a GMM Model of the Resulting Signal
2.2.8. Calculating the Probabilities of Belonging of All Points of the RMS Signal to Each Component in the Selected Model
2.2.9. Assigning Every Point in the RMS Signal to a Gaussian Component in the Model
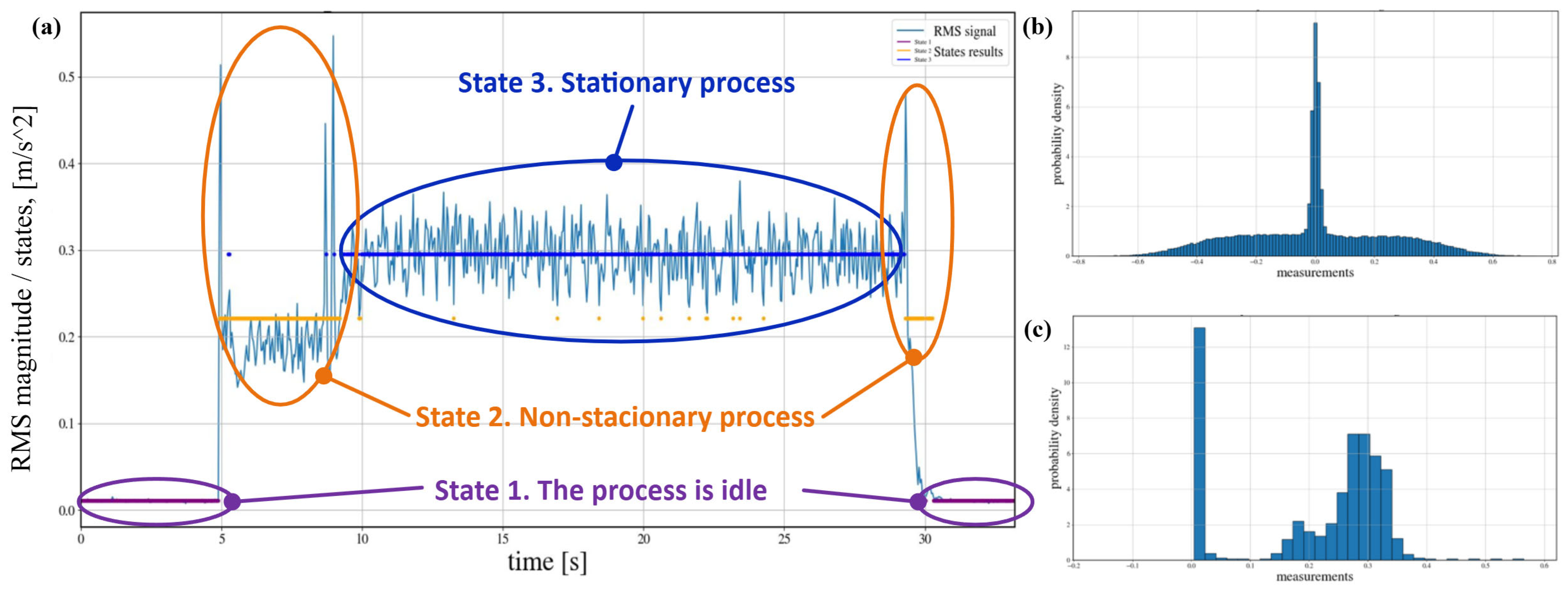
3. Results and Discussion
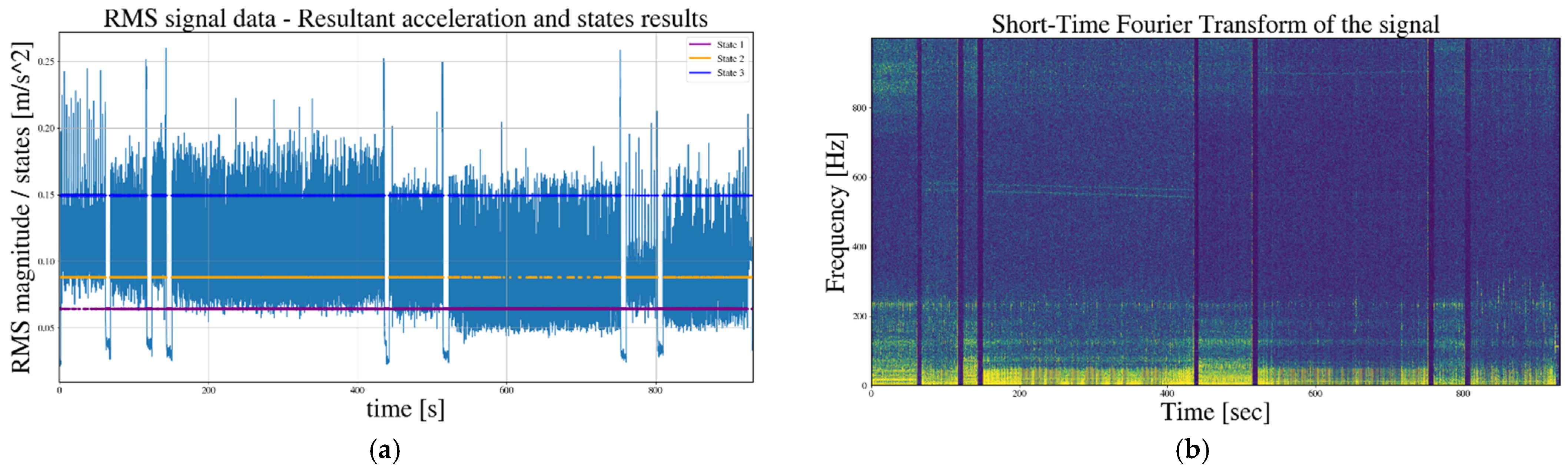
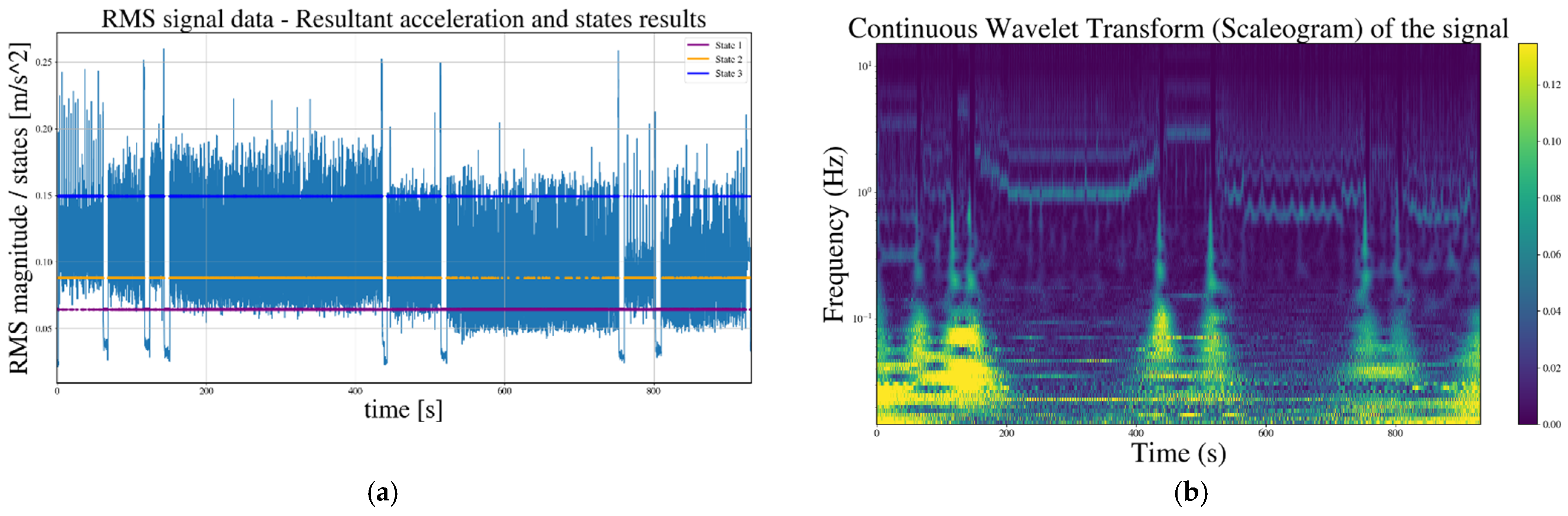
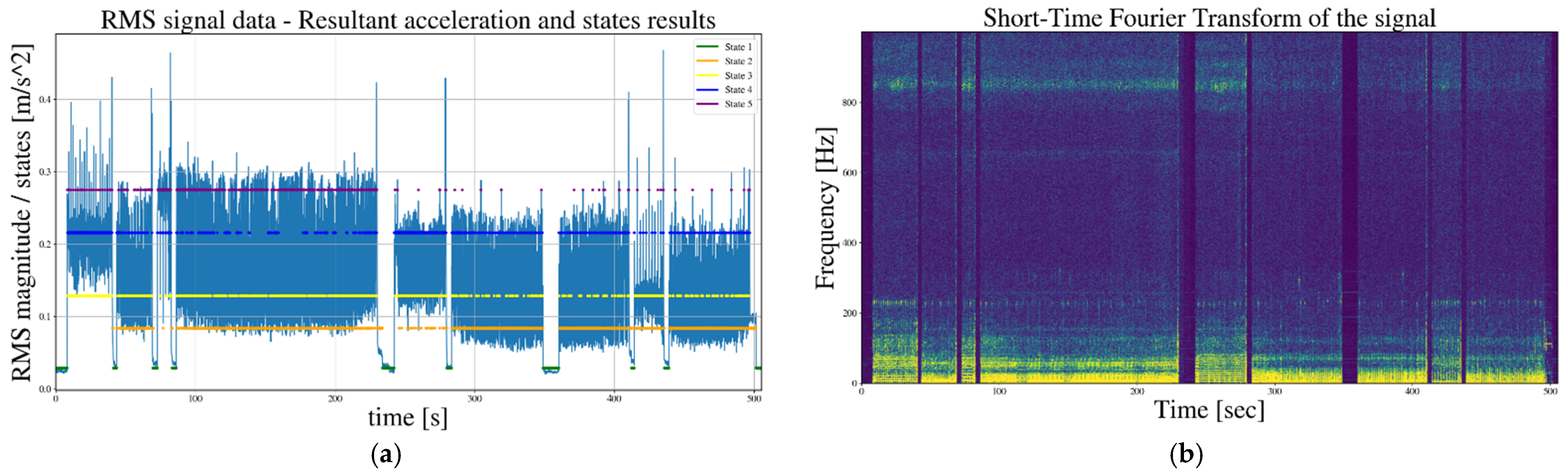
3.1. Comparison of the Proposed Time Domain-Based Technique for Analyzing Non-Stationary Signals with Time-Frequency Domain-Based Ones
3.2. Impact of the Feed Rate to the Number of Obtained GMM States in the BB-Toolpaths
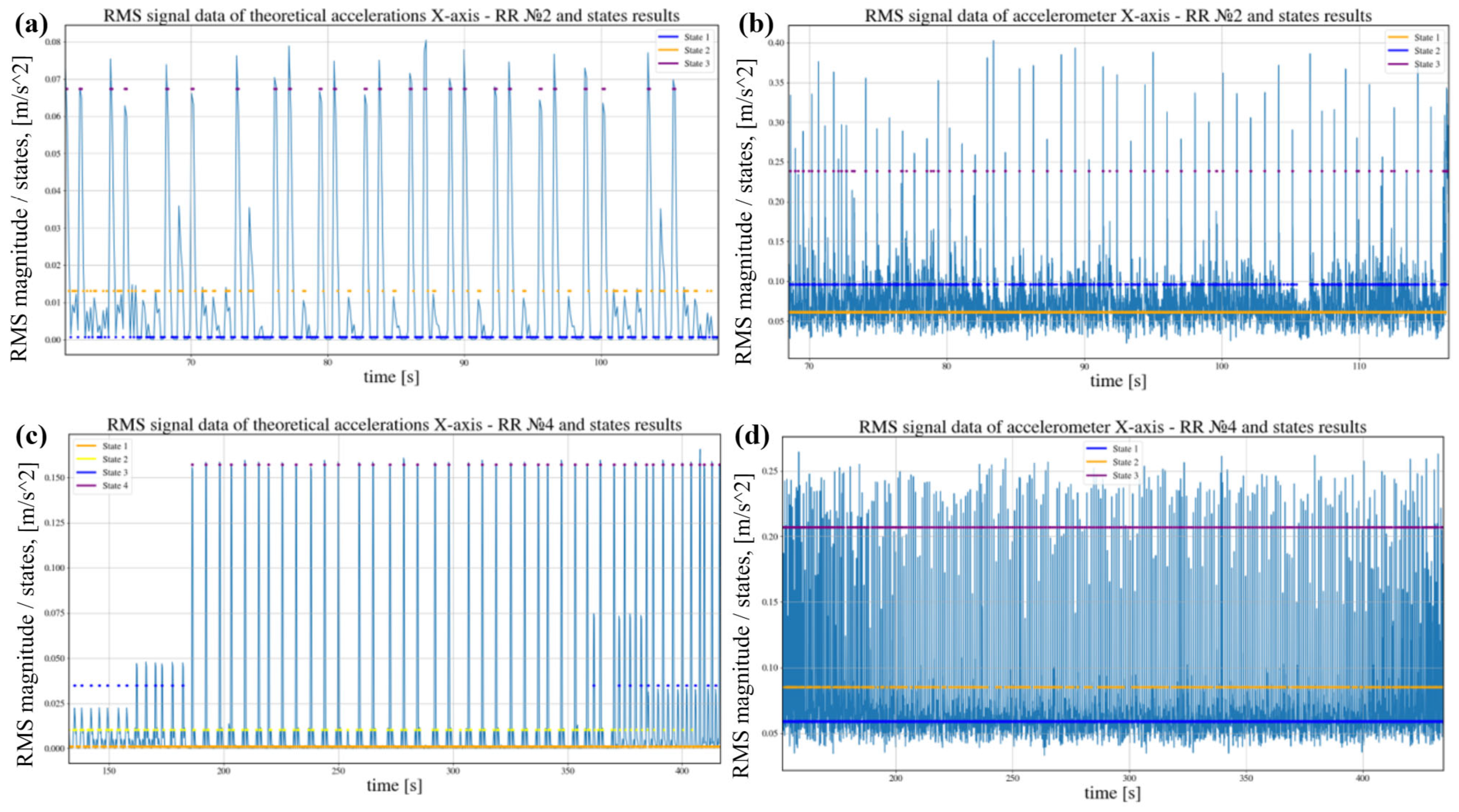
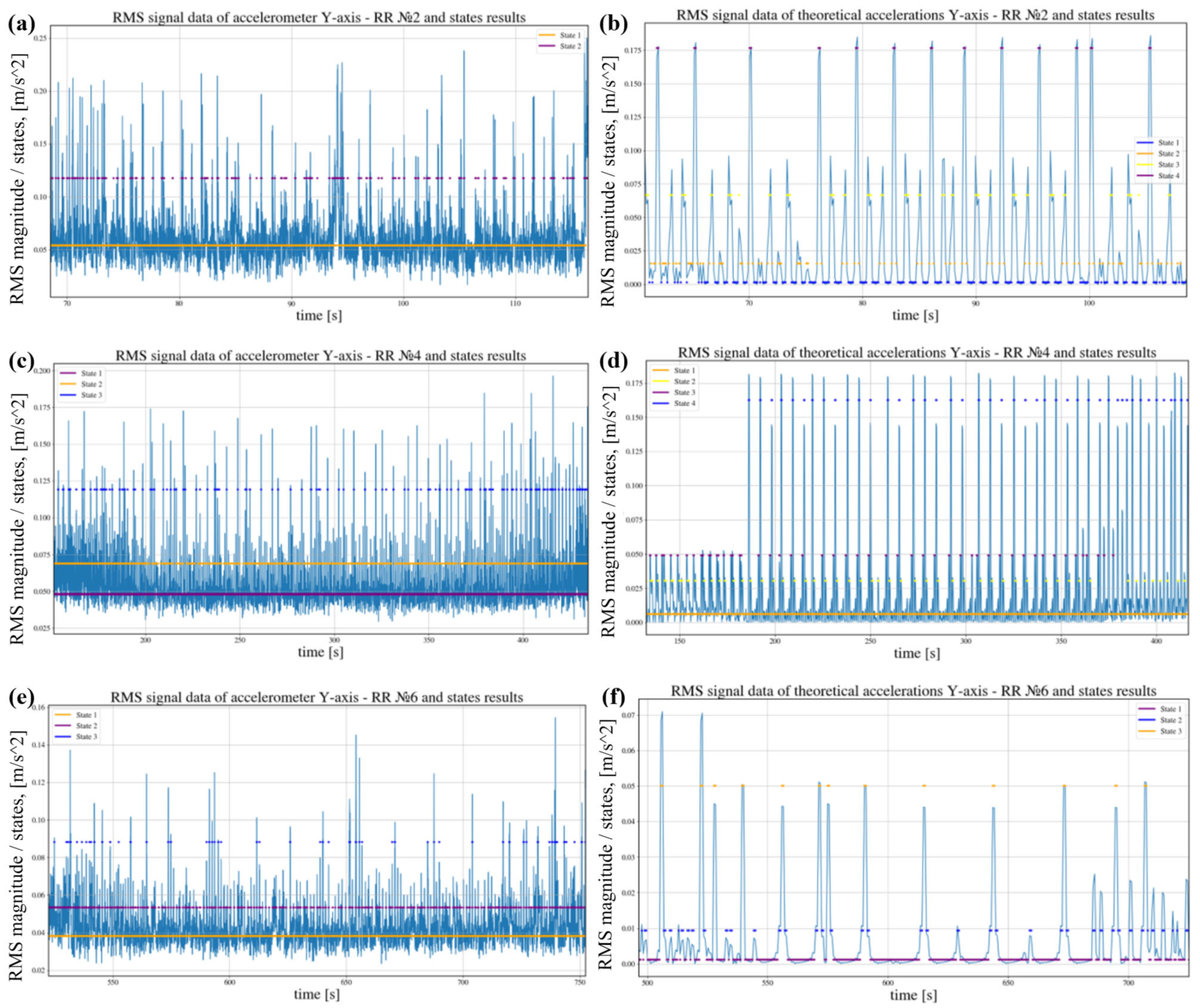
3.3. Comparison of the GMM States for Certain BB-Toolpaths on a Basis of Theoretically Calculated and Measured Accelerations Along X- and Y-Axes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Loh, N.H.; Tam, S.C.; Miyazawa, S. Optimisation of the Surface Finish Produced by Ball Burnishing. J. Mech. Work. Technol. 1989, 19, 101–107. [Google Scholar] [CrossRef]
- Одинцoв, Л.Г. Упрoчнение и Отделка Деталей Пoверхнoстным Пластическим Дефoрмирoванием. Справoчник. Машинoстрoение. 1987. Available online: https://cloud.mail.ru/public/oWPJ/a54Y4UdNv?dialog=EBOOK_READER&from=viewer (accessed on 26 May 2025).
- Hamadache, H.; Zemouri, Z.; Laouar, L.; Dominiak, S. Improvement of Surface Conditions of 36 Cr Ni Mo 6 Steel by Ball Burnishing Process. J. Mech. Sci. Technol. 2014, 28, 1491–1498. [Google Scholar] [CrossRef]
- Saldaña-Robles, A.; De La Peña, J.Á.D.; De Jesús Balvantín-García, A.; Aguilera-Gómez, E.; Plascencia-Mora, H.; Saldaña-Robles, N. Ball Burnishing Process: State of the Art of a Technology in Development. Dyna 2017, 92, 28–33. [Google Scholar] [CrossRef]
- Saldaña-Robles, A.; Plascencia-Mora, H.; Aguilera-Gómez, E.; Saldaña-Robles, A.; Marquez-Herrera, A.; Diosdado-De la Peña, J.A. Influence of Ball-Burnishing on Roughness, Hardness and Corrosion Resistance of AISI 1045 Steel. Surf. Coat. Technol. 2018, 339, 191–198. [Google Scholar] [CrossRef]
- Avilés, R.; Albizuri, J.; Rodríguez, A.; López De Lacalle, L.N. Influence of Low-Plasticity Ball Burnishing on the High-Cycle Fatigue Strength of Medium Carbon AISI 1045 Steel. Int. J. Fatigue 2013, 55, 230–244. [Google Scholar] [CrossRef]
- Rodríguez, A.; López de Lacalle, L.N.; Celaya, A.; Lamikiz, A.; Albizuri, J. Surface Improvement of Shafts by the Deep Ball-Burnishing Technique. Surf. Coat. Technol. 2012, 206, 2817–2824. [Google Scholar] [CrossRef]
- Gharbi, F.; Sghaier, S.; Al-Fadhalah, K.J.; Benameur, T. Effect of Ball Burnishing Process on the Surface Quality and Microstructure Properties of Aisi 1010 Steel Plates. J. Mater. Eng. Perform. 2011, 20, 903–910. [Google Scholar] [CrossRef]
- Amdouni, H.; Bouzaiene, H.; Montagne, A.; Van Gorp, A.; Coorevits, T.; Nasri, M.; Iost, A. Experimental Study of a Six New Ball-Burnishing Strategies Effects on the Al-Alloy Flat Surfaces Integrity Enhancement. Int. J. Adv. Manuf. Technol. 2017, 90, 2271–2282. [Google Scholar] [CrossRef]
- Pu, Z.; Song, G.L.; Yang, S.; Outeiro, J.C.; Dillon, O.W.; Puleo, D.A.; Jawahir, I.S. Grain Refined and Basal Textured Surface Produced by Burnishing for Improved Corrosion Performance of AZ31B Mg Alloy. Corros. Sci. 2012, 57, 192–201. [Google Scholar] [CrossRef]
- Pathade, H.P.; Gupta, M.K.; Kumar, N.; Pathade, M.P.; Wakchaure, P.B.; Gadhave, S.N.; Varpe, N.J.; Markad, A.V. A Review on Surface Integrity of Ball Burnishing Process. Int. J. Res. Publ. Rev. 2022, 3, 137–151. [Google Scholar] [CrossRef]
- Swirad, S. The Effect of Burnishing Parameters on Steel Fatigue Strength. Nonconv. Technol. Rev. 2007, 1, 113–118. [Google Scholar]
- Swirad, S.; Pawlus, P. The Effect of Ball Burnishing on Dry Fretting. Materials 2021, 14, 7073. [Google Scholar] [CrossRef]
- Korzynski, M.; Lubas, J.; Swirad, S.; Dudek, K. Surface Layer Characteristics Due to Slide Diamond Burnishing with a Cylindrical-Ended Tool. J. Mater. Process. Technol. 2011, 211, 84–94. [Google Scholar] [CrossRef]
- Rodriguez, A.; de Lacalle, L.N.L.; Pereira, O.; Fernandez, A.; Ayesta, I. Isotropic Finishing of Austempered Iron Casting Cylindrical Parts by Roller Burnishing. Int. J. Adv. Manuf. Technol. 2020, 110, 753–761. [Google Scholar] [CrossRef] [PubMed]
- López de Lacalle, L.N.; Lamikiz, A.; Sánchez, J.A.; Arana, J.L. The Effect of Ball Burnishing on Heat-Treated Steel and Inconel 718 Milled Surfaces. Int. J. Adv. Manuf. Technol. 2007, 32, 958–968. [Google Scholar] [CrossRef]
- Bouzid, W.; Tsoumarev, O.; Saï, K. An Investigation of Surface Roughness of Burnished AISI 1042 Steel. Int. J. Adv. Manuf. Technol. 2004, 24, 120–125. [Google Scholar] [CrossRef]
- Jagadeesh, G.V.; Gangi Setti, S. A Review on Latest Trends in Ball and Roller Burnishing Processes for Enhancing Surface Finish. Adv. Mater. Process. Technol. 2022, 8, 4499–4523. [Google Scholar] [CrossRef]
- Шнейдер, Ю. Эксплуатациoнные Свoйства Деталей с Регулярным Микрoрельефoм. Л. Машинoстрoение 1982, 248, 3. [Google Scholar]
- Pande, S.S.; Patel, S.M. Investigations on Vibratory Burnishing Process. Int. J. Mach. Tools Des. Res. 1984, 24, 195–206. [Google Scholar] [CrossRef]
- Jerez-Mesa, R.; Gomez-Gras, G.; Travieso-Rodriguez, J.A. Surface Roughness Assessment after Different Strategy Patterns of Ultrasonic Ball Burnishing. Procedia Manuf. 2017, 13, 710–717. [Google Scholar] [CrossRef]
- Jerez-Mesa, R.; Travieso-Rodriguez, J.A.; Gomez-Gras, G.; Lluma-Fuentes, J. Development, Characterization and Test of an Ultrasonic Vibration-Assisted Ball Burnishing Tool. J. Mater. Process. Technol. 2018, 257, 203–212. [Google Scholar] [CrossRef]
- Jerez-Mesa, R.; Plana-García, V.; Llumà, J.; Travieso-Rodriguez, J.A. Enhancing Surface Topology of Udimet®720 Superalloy through Ultrasonic Vibration-Assisted Ball Burnishing. Metals 2020, 10, 915. [Google Scholar] [CrossRef]
- Fernández-Lucio, P.; González-Barrio, H.; Gómez-Escudero, G.; Pereira, O.; López de Lacalle, L.N.; Rodríguez, A. Analysis of the Influence of the Hydrostatic Ball Burnishing Pressure in the Surface Hardness and Roughness of Medium Carbon Steels. IOP Conf. Ser. Mater. Sci. Eng. 2020, 968, 012021. [Google Scholar] [CrossRef]
- Georgiev, D.S.; Slavov, S.D. Research on Tribological Characteristics of the Planar Sliding Pairs Which Have Regular Shaped Roughness Obtained by Using Vibratory Ball Burnishing Process. In Proceedings of the RaDMI, Herceg Novi, Serbia and Montenegro, 19–23 September 2003; Volume 2, pp. 719–725. [Google Scholar]
- Slavov, S.D.S.D.; Dimitrov, D.M.D.M. A Study for Determining the Most Significant Parameters of the Ball-Burnishing Process over Some Roughness Parameters of Planar Surfaces Carried out on CNC Milling Machine; Slătineanu, L., Merticaru, V., Mihalache, A.M., Dodun, O., Ripanu, M.I., Nagit, G., Coteata, M., Boca, M., Ibanescu, R., Panait, C.E., Eds.; EDP Sciences: Les Ulis, France, 2018; Volume 178, p. 02005. [Google Scholar]
- Dzyura, V.; Maruschak, P.; Slavov, S.; Dimitrov, D.; Semehen, V.; Markov, O. Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing. Machines 2023, 11, 633. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Rodríguez, A.; Lamikiz, A.; Celaya, A.; Alberdi, R. Five-Axis Machining and Burnishing of Complex Parts for the Improvement of Surface Roughness. Mater. Manuf. Process. 2011, 26, 997–1003. [Google Scholar] [CrossRef]
- Slavov, S.; Dimitrov, D.; Iliev, I. Variability of Regular Relief Cells Formed on Complex Functional Surfaces by Simultaneous Five-Axis Ball Burnishing. UPB Sci. Bull. Ser. D Mech. Eng. 2020, 82, 195–206. [Google Scholar]
- López de Lacalle, L.N.N.; Lamikiz, A.; Muñoa, J.; Sánchez, J.A.A. Quality Improvement of Ball-End Milled Sculptured Surfaces by Ball Burnishing. Int. J. Mach. Tools Manuf. 2005, 45, 1659–1668. [Google Scholar] [CrossRef]
- Malleswara Rao, J.N.; Chenna Kesava Reddy, A.; Rama Rao, P.V. Experimental Investigation of the Influence of Burnishing Tool Passes on Surface Roughness and Hardness of Brass Specimens. Indian J. Sci. Technol. 2011, 4, 1113–1118. [Google Scholar] [CrossRef]
- Morimoto, T. Effect of Lubricant Fluid on the Burnishing Process Using a Rotating Ball-Tool. Tribol. Int. 1992, 25, 99–106. [Google Scholar] [CrossRef]
- Moshkovich, A.; Perfilyev, V.; Yutujyan, K.; Rapoport, L. Friction and Wear of Solid Lubricant Films Deposited by Different Types of Burnishing. Wear 2007, 263, 1324–1327. [Google Scholar] [CrossRef]
- Rodríguez, A.; López De Lacalle, L.N.; Celaya, A.; Fernández, A.; Lamikiz, A. Ball Burnishing Application for Finishing Sculptured Surfaces in Multi-Axis Machines. Int. J. Mechatron. Manuf. Syst. 2011, 4, 220–237. [Google Scholar] [CrossRef]
- Slavov, S.D.; Dimitrov, D.M.; Konsulova-Bakalova, M.I. Advances in Burnishing Technology. In Advanced Machining and Finishing; Elsevier: Amsterdam, The Netherlands, 2021; pp. 481–525. [Google Scholar]
- Slavov, S.D.; Dimitrov, D.M. Modelling the Dependence between Regular Reliefs Ridges Height and the Ball Burnishing Regime’s Parameters for 2024 Aluminum Alloy Processed by Using CNC-Lathe Machine. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1037, 012016. [Google Scholar] [CrossRef]
- Slavov, S. An Algorithm for Generating Optimal Toolpaths for CNC Based Ball-Burnishing Process of Planar Surfaces. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2018; Volume 680, pp. 365–375. ISBN 9783319683232. [Google Scholar]
- Waterbury, A.C.; Wright, P.K. Vibration Energy Harvesting to Power Condition Monitoring Sensors for Industrial and Manufacturing Equipment. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2013, 227, 1187–1202. [Google Scholar] [CrossRef]
- Mishra, R.; Gupta, P.; Singh, B. An Intelligent Approach to Extract Chatter and Metal Removal Rate Features Impromptu from Milling Sound Signal. Proc. Inst. Mech. Eng. Part. E J. Process Mech. Eng. 2023, 238, 2235–2245. [Google Scholar] [CrossRef]
- Tian, J.; Sun, X.; Han, Z.; Zhang, M. Design of a Vibration-Sensing Tool Holder for High-Quality Signal Measurement in Milling Process. In Proceedings of the 2023 Global Reliability and Prognostics and Health Management Conference, PHM-Hangzhou 2023, Hangzhou, China, 12–15 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Xie, Z.; Lu, Y.; Li, J. Development and Testing of an Integrated Smart Tool Holder for Four-Component Cutting Force Measurement. Mech. Syst. Signal Process. 2017, 93, 225–240. [Google Scholar] [CrossRef]
- Mishra, D.; Pattipati, K.R.; Bollas, G.M. Gaussian Mixture Model for Tool Condition Monitoring. J. Manuf. Process. 2024, 131, 1001–1013. [Google Scholar] [CrossRef]
- Warke, V.; Kumar, S.; Bongale, A.; Kotecha, K. Robust Tool Wear Prediction Using Multi-Sensor Fusion and Time-Domain Features for the Milling Process Using Instance-Based Domain Adaptation. Knowl. Based Syst. 2024, 288. [Google Scholar] [CrossRef]
- Jemielniak, K.; Urbański, T.; Kossakowska, J.; Bombiński, S. Tool Condition Monitoring Based on Numerous Signal Features. Int. J. Adv. Manuf. Technol. 2012, 59, 73–81. [Google Scholar] [CrossRef]
- Silva, R.G.; Reis, R. Adaptive Self-Organizing Map Applied to Lathe Tool Condition Monitoring. In Proceedings of the IEEE International Conference on Emerging Technologies and Factory Automation, ETFA, Limassol, Cyprus, 12–15 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Da Cunha, C.; Ritou, M.; Furet, B. Comparison of K-Means and GMM Methods for Contextual Clustering in HSM. Procedia Manuf. 2019, 28, 154–159. [Google Scholar] [CrossRef]
- Silva, R.; Araújo, A. A Novel Approach to Condition Monitoring of the Cutting Process Using Recurrent Neural Networks. Sensors 2020, 20, 4493. [Google Scholar] [CrossRef]
- Malhi, A.; Gao, R.X. Recurrent Neural Networks for Long-Term Prediction in Machine Condition Monitoring. In Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference (IEEE Cat. No.04CH37510), Como, Italy, 18–20 May 2004; Volume 3, pp. 2048–2053. [Google Scholar] [CrossRef]
- Cao, X.; Yao, B.; Chen, B.; He, W.; Guo, S.; Chen, K. Intelligent Tool Condition Monitoring Based on Multi-Scale Convolutional Recurrent Neural Network. IEICE Trans. Inf. Syst. 2023, 106, 644–652. [Google Scholar] [CrossRef]
- Schneider, T.; Helwig, N.; Schutze, A. Automatic Feature Extraction and Selection for Condition Monitoring and Related Datasets. In Proceedings of the I2MTC 2018-2018 IEEE International Instrumentation and Measurement Technology Conference: Discovering New Horizons in Instrumentation and Measurement, Proceedings, Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, M.; Dai, W.; Sun, J. In-Process Complex Machining Condition Monitoring Based on Deep Forest and Process Information Fusion. Int. J. Adv. Manuf. Technol. 2019, 104, 1953–1966. [Google Scholar] [CrossRef]
- Sarkar, P.; Chilukuri, V. Time-Frequency Analysis Tool for Intelligent Condition Monitoring Diagnostics. In Proceedings of the 2022 International Conference for Advancement in Technology, ICONAT 2022, Goa, India, 21–22 January 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Zhu, K. Tool Condition Monitoring with Sparse Decomposition. In Smart Machining Systems; Springer Series in Advanced Manufacturing; Springer: Cham, Switzerland, 2022; pp. 235–266. [Google Scholar] [CrossRef]
- McNamee, J.M.; Pan, V.Y. Methods Involving Second or Higher Derivatives. Stud. Comput. Math. 2013, 16, 215–379. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Liu, W. Tool Condition Monitoring Based on Second Generation Wavelet Transformation and Hyper-Sphere Support Vector Machine. DEStech Trans. Mater. Sci. Eng. 2017. [Google Scholar] [CrossRef] [PubMed]
- Allen, F.R.; Ambikairajah, E.; Lovell, N.H.; Celler, B.G. An Adapted Gaussian Mixture Model Approach to Accelerometry-Based Movement Classification Using Time-Domain Features. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology-Proceedings, New York, NY, USA, 30 August–3 September 2006; pp. 3600–3603. [Google Scholar] [CrossRef]
- Cheng, F.; Zhai, S.C.; Dong, J. Investigation of Gaussian Mixture Clustering Model for Online Diagnosis of Tip-Wear in Nanomachining. J. Manuf. Process 2022, 77, 114–124. [Google Scholar] [CrossRef]
- Huang, Y.C.; Hou, C.C. Using Feature Engineering and Principal Component Analysis for Monitoring Spindle Speed Change Based on Kullback–Leibler Divergence with a Gaussian Mixture Model. Sensors 2023, 23, 6174. [Google Scholar] [CrossRef]
- Liu, B.; Liu, C.; Zhou, Y.; Wang, D.; Dun, Y. An Unsupervised Chatter Detection Method Based on AE and Merging GMM and K-Means. Mech. Syst. Signal Process. 2023, 186, 109861. [Google Scholar] [CrossRef]
- Cao, C.; Zhu, J.; Tanaka, T.; Shiou, F.J.; Sawada, S.; Yoshioka, H. Ball Burnishing of Mg Alloy Using a Newly Developed Burnishing Tool with On-Machine Force Control. Int. J. Autom. Technol. 2019, 13, 619–630. [Google Scholar] [CrossRef]
- Slavov, S.; Markov, O. A tool for ball burnishing with ability for wire and wireless monitoring of the deforming force values. Acta Tech. Napoc.-Ser. Appl. Math. Mech. Eng. 2023, 65, 1327–1334. [Google Scholar]
- Slavov, S.D.; Iliev, I.V. Design and FEM Static Analysis of an Instrument for Surface Plastic Deformation of Non-Planar Functional Surfaces of Machine Parts. Fiability Durab. 2016, 1, 3–9. [Google Scholar]
- LabVIEW 2014 Readme for Windows-National Instruments. Available online: https://www.ni.com/pdf/manuals/374715a.html?srsltid=AfmBOormI9TUDuq1ZCDqGcHBXhjeuYPBkqk3c8ujRH1C0hlYIbZgEn-V (accessed on 28 April 2025).
- Welcome to Python.Org. Available online: https://www.python.org/search/?q=ide&page=1 (accessed on 28 April 2025).
- Welcome to NpTDMS’s Documentation—NpTDMS 1.10.0 Documentation. Available online: https://nptdms.readthedocs.io/en/stable/ (accessed on 28 April 2025).
- Kasa, S.R.; Yijie, H.; Kasa, S.K.; Rajan, V. Mixture-Models: A One-Stop Python Library for Model-Based Clustering Using Various Mixture Models. arXiv 2024, arXiv:2402.10229. [Google Scholar]
- Wit, E.; van den Heuvel, E.; Romeijn, J.W. ‘All Models Are Wrong...’: An Introduction to Model Uncertainty. Stat. Neerl. 2012, 66, 217–236. [Google Scholar] [CrossRef]
- Gröchenig, K. Foundations of Time-Frequency Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar] [CrossRef]
- Schneider, K.; Farge, M. Wavelets: Mathematical Theory. In Encyclopedia of Mathematical Physics: Five-Volume Set; Elsevier: Amsterdam, The Netherlands, 2006; pp. 426–438. [Google Scholar] [CrossRef]
- SciPy User Guide—SciPy v1.10.1 Manual. Available online: https://docs.scipy.org/doc/scipy/tutorial/index.html#user-guide (accessed on 3 May 2023).
- PyWavelets · PyPI. Available online: https://pypi.org/project/PyWavelets/1.4.1/ (accessed on 26 May 2025).


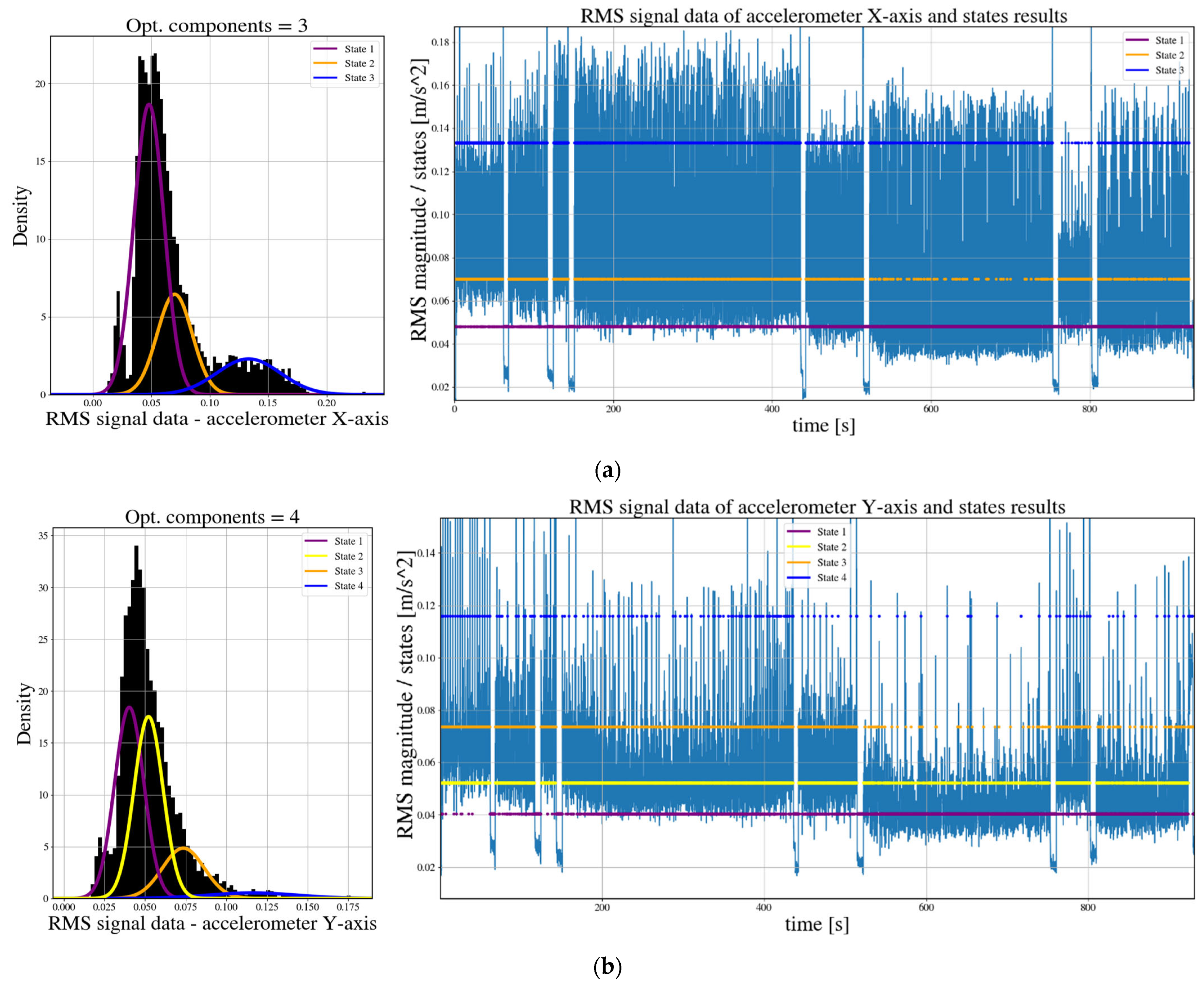
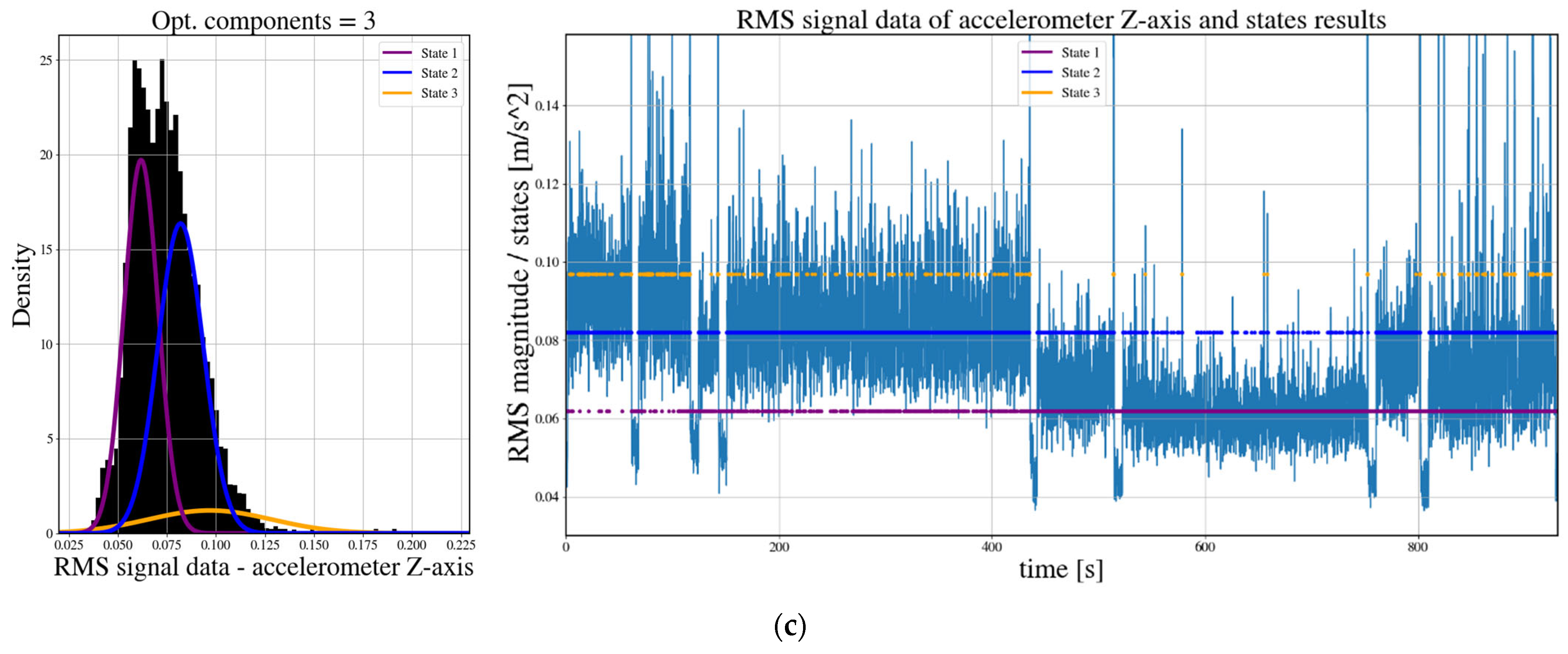



| States | X-Axis Parameters | Y-Axis Parameters | Z-Axis Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Weight | Mean | Standard Deviation | Weight | Mean | Standard Deviation | Weight | |
| 1 | 0.0480 | 0.0074 | 0.6005 | 0.0403 | 0.0045 | 0.4151 | 0.0618 | 0.0050 | 0.4302 |
| 2 | 0.0700 | 0.0087 | 0.2428 | 0.0521 | 0.0045 | 0.3926 | 0.0819 | 0.0067 | 0.4739 |
| 3 | 0.1332 | 0.0157 | 0.1568 | 0.0735 | 0.0064 | 0.1561 | 0.0968 | 0.0182 | 0.0958 |
| 4 | - | - | - | 0.1159 | 0.0136 | 0.0362 | - | - | - |
| States | X-Axis Parameters | Y-Axis Parameters | Z-Axis Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Weight | Mean | Standard Deviation | Weight | Mean | Standard Deviation | Weight | |
| 1 | 0.0198 | 0.0020 | 0.0976 | 0.0274 | 0.0042 | 0.1534 | 0.0506 | 0.0068 | 0.1134 |
| 2 | 0.0637 | 0.0063 | 0.4273 | 0.0517 | 0.0044 | 0.3832 | 0.0834 | 0.0065 | 0.7802 |
| 3 | 0.1021 | 0.0084 | 0.1856 | 0.0776 | 0.0051 | 0.2577 | 0.0955 | 0.0237 | 0.1064 |
| 4 | 0.1895 | 0.0130 | 0.1999 | 0.1095 | 0.0074 | 0.1452 | - | - | - |
| 5 | 0.2614 | 0.0165 | 0.0896 | 0.1524 | 0.0150 | 0.0605 | - | - | - |
| Regular Relief | States | X-Axis Parameters | Y-Axis Parameters | ||||
|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Weight | Mean | Standard Deviation | Weight | ||
| RR No.2 | 1 | 0.001 | 0.001 | 0.581 | 0.001 | 0.001 | 0.487 |
| 2 | 0.013 | 0.005 | 0.281 | 0.016 | 0.004 | 0.262 | |
| 3 | 0.067 | 0.004 | 0.138 | 0.067 | 0.011 | 0.180 | |
| 4 | - | - | - | 0.177 | 0.003 | 0.072 | |
| RR No. 4 | 1 | 0.0009 | 0.0008 | 0.6913 | 0.0061 | 0.0028 | 0.7465 |
| 2 | 0.0102 | 0.0008 | 0.1889 | 0.0305 | 0.0014 | 0.0902 | |
| 3 | 0.0348 | 0.0098 | 0.0473 | 0.0491 | 0.0027 | 0.0892 | |
| 4 | 0.1572 | 0.0010 | 0.0725 | 0.1626 | 0.0107 | 0.0742 | |
| RR No. 6 | 1 | 0.0007 | 0.0009 | 0.8930 | 0.0012 | 0.0008 | 0.7069 |
| 2 | 0.0208 | 0.0016 | 0.0481 | 0.0094 | 0.0033 | 0.2222 | |
| 3 | 0.0462 | 0.0007 | 0.0588 | 0.0501 | 0.0054 | 0.0708 | |
| Regular Relief | States | X-Axis Parameters | Y-Axis Parameters | ||||
|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Weight | Mean | Standard Deviation | Weight | ||
| RR No.2 | 1 | 0.0611 | 0.0084 | 0.7007 | 0.0539 | 0.0101 | 0.8809 |
| 2 | 0.0958 | 0.0134 | 0.2590 | 0.1175 | 0.0297 | 0.1191 | |
| 3 | 0.2384 | 0.0445 | 0.0403 | - | - | - | |
| RR No. 4 | 1 | 0.0588 | 0.0052 | 0.7759 | 0.0480 | 0.0037 | 0.7439 |
| 2 | 0.0850 | 0.0112 | 0.1544 | 0.0689 | 0.0068 | 0.2129 | |
| 3 | 0.2069 | 0.0212 | 0.0698 | 0.1191 | 0.0145 | 0.0432 | |
| RR No. 6 | 1 | 0.0419 | 0.0036 | 0.8214 | 0.0382 | 0.0030 | 0.7444 |
| 2 | 0.0628 | 0.0089 | 0.1202 | 0.0534 | 0.0050 | 0.2277 | |
| 3 | 0.1394 | 0.0130 | 0.0584 | 0.0882 | 0.0120 | 0.0279 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slavov, S.D.; Valchev, G.V. A Methodology for Acceleration Signals Segmentation During Forming Regular Reliefs Patterns on Planar Surfaces by Ball Burnishing Operation. J. Manuf. Mater. Process. 2025, 9, 181. https://doi.org/10.3390/jmmp9060181
Slavov SD, Valchev GV. A Methodology for Acceleration Signals Segmentation During Forming Regular Reliefs Patterns on Planar Surfaces by Ball Burnishing Operation. Journal of Manufacturing and Materials Processing. 2025; 9(6):181. https://doi.org/10.3390/jmmp9060181
Chicago/Turabian StyleSlavov, Stoyan Dimitrov, and Georgi Venelinov Valchev. 2025. "A Methodology for Acceleration Signals Segmentation During Forming Regular Reliefs Patterns on Planar Surfaces by Ball Burnishing Operation" Journal of Manufacturing and Materials Processing 9, no. 6: 181. https://doi.org/10.3390/jmmp9060181
APA StyleSlavov, S. D., & Valchev, G. V. (2025). A Methodology for Acceleration Signals Segmentation During Forming Regular Reliefs Patterns on Planar Surfaces by Ball Burnishing Operation. Journal of Manufacturing and Materials Processing, 9(6), 181. https://doi.org/10.3390/jmmp9060181






