Online Tool Wear Monitoring via Long Short-Term Memory (LSTM) Improved Particle Filtering and Gaussian Process Regression

Abstract

Accurate prediction of tool wear plays a vital role in improving machining quality in intelligent manufacturing. However, traditional Gaussian Process Regression (GPR) models are constrained by linear assumptions, while conventional filtering algorithms struggle in noisy environments with low signal-to-noise ratios. To address these challenges, this paper presents an innovative tool wear prediction method that integrates a nonlinear mean function and a multi-kernel function-optimized GPR model combined with an LSTM-enhanced particle filter algorithm. The approach incorporates the LSTM network into the state transition model, utilizing its strong time-series feature extraction capabilities to dynamically adjust particle weight distributions, significantly enhancing the accuracy of state estimation. Experimental results demonstrate that the proposed method reduces the mean absolute error (MAE) by 47.6% and improves the signal-to-noise ratio by 15.4% compared to traditional filtering approaches. By incorporating a nonlinear mean function based on machining parameters, the method effectively models the coupling relationships between cutting depth, spindle speed, feed rate, and wear, leading to a 31.09% reduction in MAE and a 42.61% reduction in RMSE compared to traditional linear models. The kernel function design employs a composite strategy using a Gaussian kernel and a 5/2 Matern kernel, achieving a balanced approach that captures both data smoothness and abrupt changes. This results in a 58.7% reduction in MAE and a 64.5% reduction in RMSE. This study successfully tackles key challenges in tool wear monitoring, such as noise suppression, nonlinear modeling, and non-stationary data handling, providing an efficient and stable solution for tool condition monitoring in complex manufacturing environments.

1. Introduction

In high-speed cutting, precision machining, and automated production, the development of tool wear significantly influences the surface quality and machining accuracy of the workpiece [1,2,3,4]. High-performance evaluation and prediction of tool wear prediction can help reduce production downtime, tool replacement frequency, and costs and enhance overall machining efficiency [5]. With advancements in intelligent manufacturing and Industry 4.0, data-driven techniques for tool wear prediction have emerged as research and technique focuses [6]. Conventional methods, including empirical formulas, physical modeling, and statistical analysis, are capable of providing the off-line prediction of tool wear conditions, whereas such methods struggle to adapt to the complexities of practical machining environments with high-dimensional feature data [7,8,9]. In high-precision and high-efficiency automated manufacturing, tool wear is influenced by a combination of cutting parameters, material properties, and coolant/lubrication types [10,11,12]. The nonlinear and dynamic nature of these factors makes it difficult for conventional methods to meet the requirement of accuracy and efficiency for practical applications [13].

In response to these challenges, machine learning (ML)-based models for tool wear prediction have gained considerable traction. ML models offer distinct advantages in improving predictive accuracy and efficiency. Regression techniques [14,15] and support vector machines (SVM) [16,17] provide basic predictive capabilities but require predefined model assumptions, which are less effective in handling intricate nonlinear relationships and high-dimensional datasets. For example, linear regression develops a direct linear correlation between variables, which fails to capture the complex and dynamic nature of tool wear. Although SVM addresses nonlinear patterns, it remains highly sensitive to parameter tuning and suffers from inefficiencies in high-dimensional data processing. To overcome these limitations, deep learning (DL) methods have emerged as a powerful alternative for tool wear prediction. Convolutional neural networks (CNN) [18,19] and deep neural networks (DNN) [20,21] have proven highly effective in automatic feature extraction and pattern recognition. CNN is good at identifying spatial characteristics in images or visualized data, while DNN leverages multi-layer nonlinear mappings to model complex input–output relationships, making the algorithms particularly well-suited for tool wear prediction. However, deep learning models require large amounts of labeled training data [22] and come with high computational costs, posing challenges related to data availability and processing resources in industrial applications. Recently, Gaussian Process Regression (GPR) [23] has gained significant attention due to its non-parametric nature and Bayesian inference framework. Different from traditional regression methods, GPR does not rely on rigid model assumptions, which leverage kernel functions to automatically capture complex nonlinear relationships. Compared to DL algorithms, GPR is more adaptable to limited datasets, as it does not require large amounts of labeled data. Furthermore, by using appropriate kernel functions, GPR can effectively model diverse nonlinear relationships [24]. However, standard GPR methods are limited due to predicting instability and noise sensitivity when applied to dynamically evolving wear data. Enhancing GPR with dynamic processing mechanisms and improving its predictive performance remain critical research challenges.

According to the reviewed studies, online tool wear monitoring currently faces two pivotal challenges: (1) in practical machining, sensor-captured signals—such as cutting forces and vibrations—are frequently impacted by a variety of noise sources, e.g., mechanical vibrations, electromagnetic interference, and background noise from the sensors. Effective filtering strategies that extract tool wear-relevant information remain a core technical hurdle in enhancing the accuracy and reliability of monitoring systems. (2) Existing monitoring models often struggle to adapt to complex machining scenarios, largely because mainstream approaches rely on single-kernel function mappings between input signals and wear states. This restricts their ability to accurately capture the nonlinear evolution of tool wear and, eventually, the generalizability and robustness.

To tackle the critical challenges of severe signal noise interference and limited model adaptability in online tool wear monitoring, this study introduces a Gaussian Process Regression (GPR) model enhanced with a machining-parameter-based nonlinear mean function and a composite kernel function alongside an LSTM-enhanced particle filter algorithm for preprocessing input signals. The main contributions of this work are summarized as follows:

(1)

A nonlinear mean function that incorporates key machining parameters such as spindle speed, feed rate, and cutting depth is designed, which overcomes the limitations imposed by the linear assumptions inherent in traditional GPR models.

(2)

To further enhance the model’s capability in handling complex wear patterns, a composite kernel function is constructed by integrating a Gaussian kernel with a 5/2 Matern kernel, which is effective in capturing abrupt changes and non-stationary behaviors.

(3)

An LSTM-enhanced particle filter algorithm is developed to address the degradation of state estimation under high-noise industrial conditions, which adaptively corrects particle distributions through gated recurrent units.

Through the synergistic integration of these techniques, the proposed approach significantly advances the accuracy and reliability of tool wear prediction, providing a precise and robust solution for tool condition monitoring in complex manufacturing scenarios.

2. Experiment and Data Collection

The experiment was performed on a VDL600A CNC machining center (Figure 1) for dry face milling of Inconel 718 alloy (

Table 1. Physical and mechanical properties of Inconel 718 [26,27,28].

Physical Properties	Values
Density (g/cm3)	8.19
Melting Point (°C)	1260–1320
Thermal Conductivity (W/m·K)	11.4
Specific Heat Capacity (J/kg·K)	435
Elastic Modulus (GPa)	205
Shear Modulus (GPa)	79.6
Electrical Resistivity (μΩ·m)	1.29
Poisson’s Ratio	0.33
Coefficient of Thermal Expansion (µm/m·K)	11.8 (20–1000 °C)

). The workpiece had dimensions of 80 × 80 × 20 mm³. In compliance with ISO 3685 standards [25], a four-flute TiAlN-coated carbide end mill (Φ6 mm) was used, with machining parameters listed in

Table 2. Machining conditions of the experiments.

No.	$\mathbf{Spindle} \mathbf{Speed} \mathit{n}$ (rpm)	Feed Rate f (mm/r)	$\mathbf{Cutting} \mathbf{Depth} {\mathit{a}}_{\mathit{p}}$ (mm)	Replications
1	2000	0.04	0.2	3
2	3000	0.06	0.2	3
3	2000	0.04	0.3	3
4	3000	0.06	0.3	3

. To leverage the high sensitivity of cutting force signals in tool condition monitoring, this study employed a YDCB-III05 tri-axial piezoelectric dynamometer (manufacturer: Ningbo Lingyuan Measurement and Control Engineering Co., Ltd., Ningbo, China) to acquire real-time dynamic force signals at a 20 kHz sampling rate. This sensor demonstrated significantly superior resistance to environmental interference compared to conventional temperature and acoustic emission sensors. During machining, the flank wear (VB) of the cutting edge was measured every 200 s using a VHX-7000 microscope system (manufacturer: Keyence Corporation, Osaka, Japan), with the average wear across the four flutes serving as the characteristic value. Experimental observations indicated that when VB exceeded 0.10 mm, edge chipping occurred. Consequently, the tool life criterion was adjusted to ${VB}_{max}$ = 0.15 mm, reducing the standard threshold by 50%. Over a total machining duration of 2000 s, a mapping database was established to correlate the time-frequency domain features of force signals with tool wear using machine learning algorithms.

In the cutting experiments, force signals were obtained via a piezoelectric dynamometer, and 30,000 data points were selected as the sampling dataset in each cutting trail. Raw signals were subsequently processed using a particle filtering algorithm optimized by LSTM, aiming to extract effective metrics reflecting the development of tool wear. Time-domain features were extracted from the filtered force signals, including mean value, standard deviation, root mean square, skewness, kurtosis, and peak value. For the frequency-domain metrics, spectral features such as spectral variance, spectral skewness, spectral kurtosis, and center frequency were calculated through Fast Fourier Transform (FFT) analysis. Additionally, three-level wavelet packet decomposition was conducted using the db1 wavelet basis, and eight wavelet packet energy features were extracted. In total, 54 features were derived from the cutting force signals in three axes to construct the initial feature space. Subsequently, the Pearson correlation coefficient was calculated between each feature and tool wear, and features with a correlation coefficient greater than 0.6 were selected as input variables for tool wear monitoring.

3. Methodology

3.1. LSTM Improved Particle Filtering Algorithm

At the initial stage of the particle filter algorithm, the particle set must first be initialized. The particle filter approximates the system’s true state by incorporating many particles, where each particle’s initial position and velocity significantly influence the algorithm’s convergence rate and accuracy. The initialized particle set is generally uniformly distributed across the state space to ensure comprehensive coverage of all possible system states. Additionally, each particle is assigned an initial weight, representing its contribution to the system state at the current time step. Initially, all particles are typically assigned equal weights.

$$x_0^{\left(i\right)}=x_{init},{\omega }_0^{\left(i\right)}={\displaystyle \frac{1}{N}},i=\mathrm{1,2},\dots ,N$$

(1)

At each time step, an LSTM network is utilized to predict the system state at the current time t. The LSTM takes observed data $X_t$ from both the current and past time steps as input and, through forward propagation, computes the predicted future state ${\widehat{x}}_{t+1|t}$. This prediction serves as the prior estimate for the particle filter, forming the basis for updating particle states in the next step.

$${\widehat{x}}_{t+1|t}=\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}\left(X_t\right)$$

(2)

For each particle $x_t^{\left(i\right)}$, the system’s state transition function is applied to generate the predicted state at time t.

$$x_t^{\left(i\right)}=f\left(x_{t-1}^{\left(i\right)},u_t\right)+{ϵ}_t^{\left(i\right)}$$

(3)

where $f(x_{t-1}^{\left(i\right)},u_t)$ represents the state transition function, and ${ϵ}_t^{\left(i\right)}$ denotes the process noise associated with particle $i$.

The discrepancy between each particle’s predicted state and the actual observation is quantified using the observation model, which is then used to update particle weights. Throughout this process, the particle weights reflect the degree of consistency between the predicted and observed states. The weight update formula is given as follows:

$${\omega }_t^{\left(i\right)}={\displaystyle \frac{{\omega }_{t-1}^{\left(i\right)}·p\left(z_t|x_t^{\left(i\right)}\right)}{{\sum }_{i=1}^N{\omega }_{t-1}^{\left(i\right)}·p\left(z_t|x_t^{\left(i\right)}\right)}}$$

(4)

Resampling is performed based on the particle weights ${\omega }_t^{\left(i\right)}$, redistributing weight toward particles that better align with actual observations, thereby generating an updated particle set.

$$x_t^{\left(i\right)}~{\omega }_t^{\left(i\right)},i=\mathrm{1,2},\dots ,N$$

(5)

Finally, the state estimation at the current time step is derived using a weighted average. By integrating all particle states along with their respective weights, the particle filter produces a refined and comprehensive state estimate, leading to improved prediction accuracy.

$$x_t^{\left(i\right)}={\displaystyle \frac{{\sum }_{i=1}^N{\omega }_t^{\left(i\right)}·x_t^{\left(i\right)}}{{\sum }_{i=1}^N{\omega }_t^{\left(i\right)}}}$$

(6)

By implementing these steps, the LSTM-enhanced particle filter algorithm enables high-precision state estimation in complex, nonlinear, and non-Gaussian noise environments. It is particularly well-suited for state tracking and prediction tasks in dynamic systems. The algorithm workflow is illustrated in Figure 2.

3.2. Nonlinear Mean Function for Machining Parameter-Based Tool Wear Prediction

Conventional GPR models often employ simple mean functions, such as constant or linear functions, while relying on basic kernel functions like the Radial basis function kernel (RBF) or Matern kernel. However, in real-world machining processes, the relationship between machining parameters and tool wear is rarely linear. Tool wear is influenced by multiple interacting machining parameters, exhibiting nonlinear behavior that cannot be effectively captured by conventional models. When using a single kernel function, the RBF kernel excels in modeling smooth variations, while the Matern kernel is particularly effective at handling local fluctuations. However, when used independently, neither kernel can fully encapsulate the diverse characteristics of tool wear, especially in machining processes with varying scales of influence. The conventional GPR model is expressed as follows:

$$f\left(x\right)~gp\left(\mu \left(x\right),k\left(x,x^{\prime }\right)\right)$$

(7)

where $\mu \left(x\right)$ is the mean function, and $k(x,x^{\prime })$ denotes the kernel function.

In this study, a nonlinear mean function that integrates linear terms, quadratic terms, and interaction terms of machining parameters: spindle speed $n$, feed rate $f$, and cutting depth $a_p$ is developed, which enhances the model’s ability to capture intricate wear dynamics:

$$\mu \left(x\right)={\beta }_1+{\beta }_{2}n+{\beta }_{3}f+{\beta }_3{a}_p+{\beta }_4{n}^2+{\beta }_5{f}^2+{\beta }_6{a}_p^2+{\beta }_{7}nf+{\beta }_{8}n{a}_p+{\beta }_{9}f{a}_{p }$$

(8)

The parameter $\beta$ is estimated by maximizing the marginal likelihood function:

$$\widehat{\beta }=arg\underset{\beta }{\min }\left[\right(y-\mu {\left(X\right))}^T{K}^{-1}(y-\mu (X\left)\right)]$$

(9)

where K represents the kernel matrix, and X denotes the feature matrix of training data.

The inclusion of interaction terms is important because machining conditions often exhibit synergistic effects, such as joint effects of n and f on tool wear development. By explicitly modeling these interactions, the nonlinear mean function not only improves data fitting accuracy but also better reflects the underlying physical mechanisms of tool wear. In addition, kernel selection plays a crucial role in determining the predictive capability of the GPR model.

Table 3. GPR kernel function.

Kernel Function	Math Equation
Gaussian Kernel	$k\left(x_i,x_j\right)={\sigma }_f^{2}exp(-{\displaystyle \frac{{‖x_i-x_j‖}^2}{{2l}^2}})$
Rational Quadratic Kernel	$k\left(x_i,x_j\right)={{\sigma }_f^2(1+{\displaystyle \frac{{‖x_i-x_j‖}^2}{2\alpha l^2}})}^{-\alpha }$
$\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{è}\mathrm{r}\mathrm{n}$ 5/2 Kernel	$k\left(x_i,x_j\right)={\sigma }_f^2(1+\sqrt{5}‖x_i-x_j‖+{5‖x_i-x_j‖}^2/3)exp(-\sqrt{5}‖x_i-x_j‖)$
Periodic Kernel	$k\left(x_i,x_j\right)={\sigma }_f^{2}exp(-{\displaystyle \frac{\left(2{sin}^2\left(\pi \left|x_i-x_j\right|\right)/p\right)}{l^2}})$
Linear Kernel	$k\left(x_i,x_j\right)={({x_i}^T{x}_j+c)}^d$

lists the commonly used kernel functions.

In the listed equations, $l$ represents the length-scale parameter, which controls the similarity between data points diminishes and ${\sigma }_f^2$ is the amplitude parameter governing the overall magnitude of the kernel function.

To enhance prediction accuracy, this study develops a multi-kernel function that dynamically integrates the RBF and Matern kernels, allowing the model to fit different data patterns:

$$k\left(x,x^{\prime }\right)=k_{\mathrm{R}\mathrm{B}\mathrm{F}}\left(x,x^{\prime }\right)+\gamma ·k_{\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{r}\mathrm{n}5/2}\left(x,x^{\prime }\right)$$

(10)

where $\mathsf{\gamma }$ is a learned adaptive parameter that dynamically adjusts the contribution of RBF and Matern kernels at each predicted point.

The form of the Radial basis function (RBF) kernel is given by

$$k_{\mathrm{R}\mathrm{B}\mathrm{F}}\left(x,x^{\prime }\right)={\sigma }_f^{2}exp\left(-{\displaystyle \frac{{‖x-x^{\prime }‖}^2}{2l_g^2}}\right)$$

(11)

The Matern 5/2 kernel is formulated as

$$k_{\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}5/2}\left(x,x^{\prime }\right)={\sigma }_m^2\left(1+{\displaystyle \frac{\sqrt{5}‖x-x^{\prime }‖}{l_m}}+{\displaystyle \frac{5{‖x-x^{\prime }‖}^2}{3l_m^2}}\right)exp\left(-{\displaystyle \frac{\sqrt{5}‖x-x^{\prime }‖}{l_m}}\right)$$

(12)

The hyperparameters $\theta =\left\{{\sigma }_f,l_g,{\sigma }_m,l_m,\gamma \right\}$ are optimized by maximizing the log marginal likelihood function.

$$logp\left(y|X,\theta \right)=-{\displaystyle \frac{1}{2}}{y}^T{K}_{\theta }^{-1}y-{\displaystyle \frac{1}{2}}log\left|K_{\theta }\right|-{\displaystyle \frac{N}{2}}log2\pi$$

(13)

With the advantages of RBF and Matern kernels, this hybrid kernel function effectively balances smooth global trends and localized variations in tool wear data. The composite kernel provides a robust, flexible, and adaptive framework, making it particularly well-suited for modeling complex, multi-scale machining processes with diverse wear patterns.

For a new input $x_{*}$, the predictive posterior distribution is

$$p\left(f_{*}|X,y,x_{*}\right)=N\left({\mu }_{*},{\sigma }_{*}^2\right)$$

(14)

where the predictive mean ${\mu }_{*}$ and variance ${\sigma }_{*}^2$ are given by

$${\mu }_{*}=\mu \left(x_{*}\right)+k_{*}^T{K}^{-1}\left(y-\mu \left(X\right)\right)$$

(15)

$${\sigma }_{*}^2=k\left(x_{*},x_{*}\right)-k_{*}^T{K}^{-1}{k}_{*}$$

(16)

$$k_{*}={\left[k\left(x_{*},x_1\right),\dots ,k\left(x_{*},x_n\right)\right]}^T$$

(17)

The improved GPR framework integrates physical mechanisms with data-driven insights to achieve synergistic optimization of modeling accuracy and interpretability for tool wear prediction. In the design of the mean function, a nonlinear structure incorporating quadratic and interaction terms based on the coupling effects of machining parameters is explicitly constructed. As for the kernel function, a synthesized kernel architecture enables multi-scale feature extraction, where the Gaussian kernel captures global smooth trends, and the Matern kernel adapts to local abrupt changes. A dynamic weight adjustment mechanism autonomously balances their contributions based on the data distribution characteristics, significantly improving the model’s adaptability across different stages of tool wear.

4. Experimental Results and Analysis

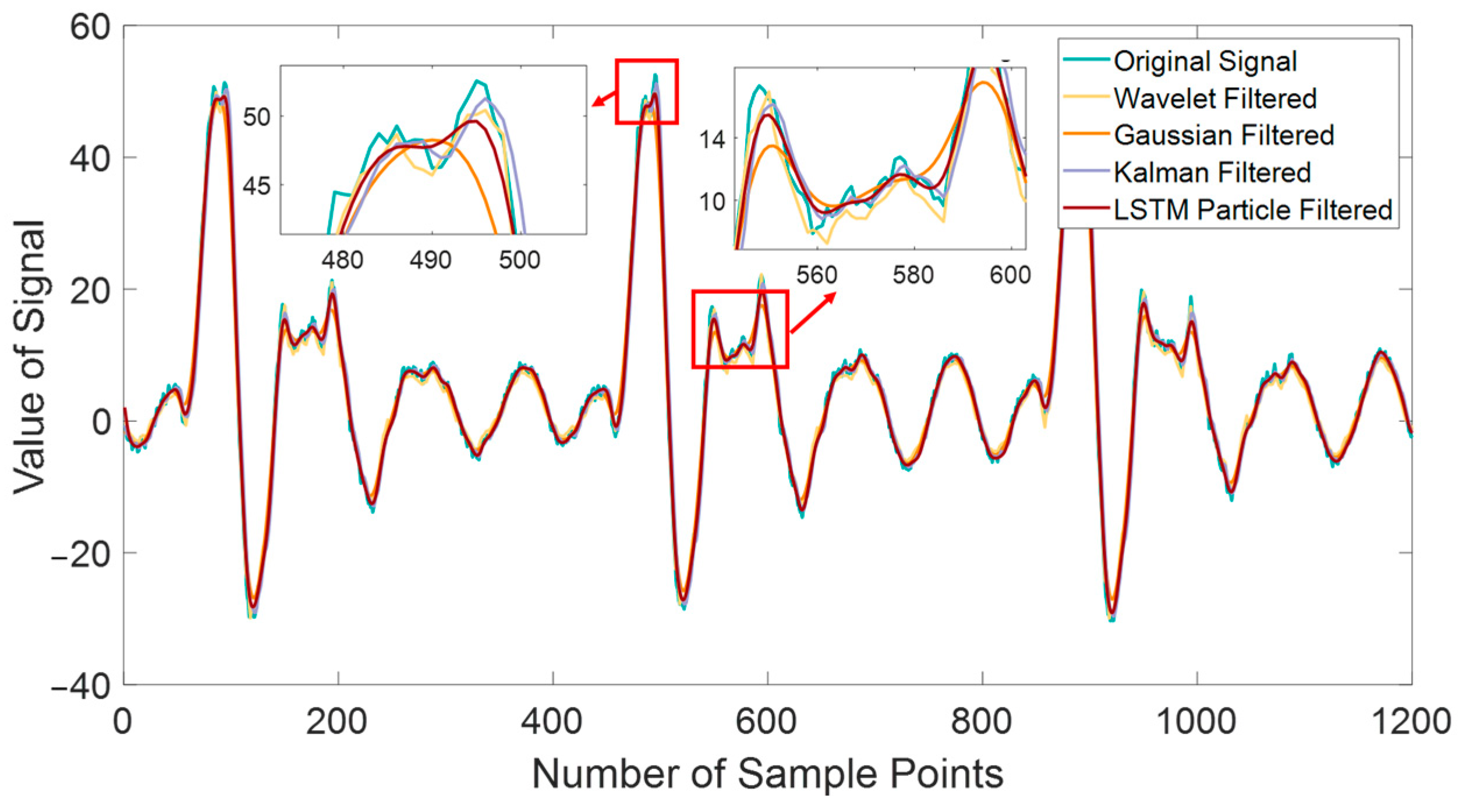
Figure 3 illustrates the performance of different filtering methods, highlighting the limitations of conventional approaches. The wavelet filter exhibits noticeable fluctuations due to its thresholding strategy, which struggles to differentiate between sharp transients in the signal and noise. When significant variations occur, improper threshold selection compromises denoising effectiveness, preventing the complete restoration of high-frequency components.

The Gaussian filter suffers from excessive smoothing, resulting in signal distortion—especially at pulse peaks—where amplitude attenuation leads to the loss of critical high-frequency features. Meanwhile, the Kalman filter reveals its inherent limitations when applied to complex dynamic systems. As a linear predictive model, it fails to handle nonlinear or non-Gaussian noise effectively. Over time, accumulated errors exacerbate phase shifts, causing a marked decline in performance.

By comparison, the LSTM particle filter demonstrates a substantial advantage over traditional methods in both mean absolute error (MAE) and signal-to-noise ratio (SNR). As shown in

Table 4. Evaluation indicators of different filtering methods under low noise.

	MAE	SNR
Wavelet Filter	1.217	18.566
Gaussian Filter	1.375	18.035
Kalman Filter	1.674	17.181
LSTM Particle Filter	0.633	21.408

, the LSTM particle filter achieves a 47.6% reduction in MAE compared to the wavelet filter, 54.2% compared to the Gaussian filter, and 62.2% compared to the Kalman filter. Additionally, it increases the SNR by approximately 15.4%, significantly outperforming other filtering techniques. These results highlight the superior denoising precision and signal reconstruction capability of the LSTM particle filter. The LSTM network, with its advanced gating mechanisms, effectively captures long-term temporal dependencies, allowing it to model intricate variations within the signal. Meanwhile, the particle filter dynamically updates particle weights, ensuring more accurate tracking of the true system state. This integration of deep learning and probabilistic filtering techniques enhances both estimation accuracy and robustness, making the LSTM particle filter a highly effective solution for complex signal-processing tasks.

As illustrated in Figure 4, the Mean Squared Error (MSE) of the LSTM particle filter increased by 75% compared to Figure 3, while other filtering methods exhibited significantly larger increases: 111% for the wavelet filter, 105% for the Gaussian filter, and 126% for the Kalman filter. These results indicate that the LSTM particle filter possesses superior generalization ability, maintaining stable performance across varying noise conditions. Unlike traditional methods, LSTM’s gradient optimization mechanism dynamically adjusts state transition parameters, reducing bias from manual tuning. Additionally, its nonlinear activation functions enhance the model’s ability to distinguish intricate signal variations, ensuring stable performance even in high-noise environments.

By integrating deep learning’s advanced feature extraction with the probabilistic framework of particle filtering, the LSTM particle filter simultaneously optimizes both error reduction and signal-to-noise ratio (SNR) in complex noise scenarios, as shown in

Table 5. Evaluation indicators of different filtering methods under high noise.

	MAE	SNR
Wavelet Filter	1.351	21.953
Gaussian Filter	2.826	18.747
Kalman Filter	3.792	17.470
LSTM Particle Filter	1.106	22.818

. The key advantages of this approach include robust dynamic modeling, allowing it to accurately capture long-term temporal dependencies. Superior nonlinear adaptability, enabling effective handling of complex signal fluctuations and varying noise characteristics.

Compared to conventional filtering techniques, the LSTM particle filter surpasses the limitations of fixed parameter assumptions and linear model constraints, delivering a highly flexible and precise state estimation approach for nonlinear, non-Gaussian systems. Experimental results confirm that the LSTM particle filter provides a superior solution for state estimation in complex systems, demonstrating exceptional performance in dynamic environments.

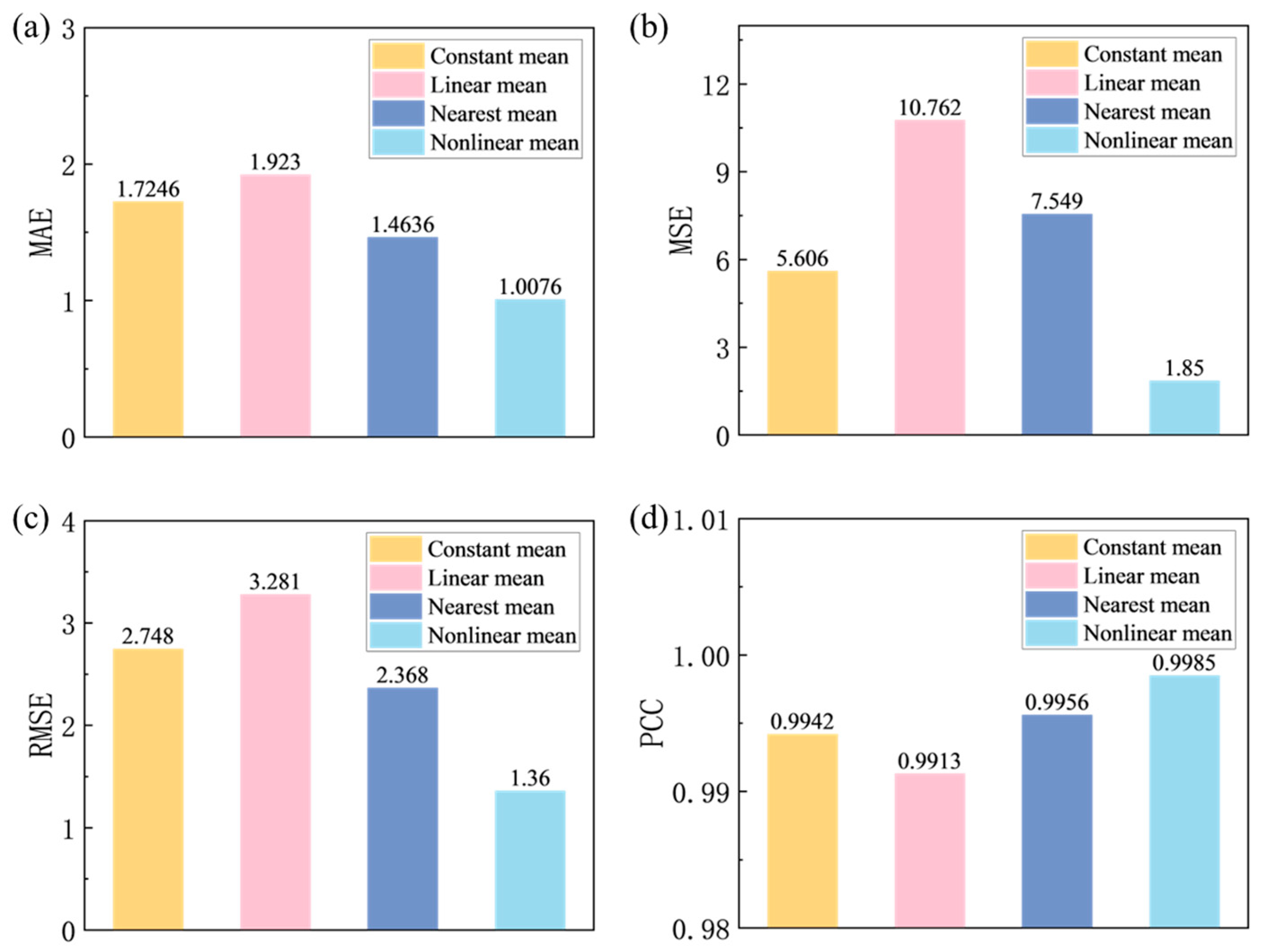
As depicted in Figure 5, the nonlinear mean function exhibits superior performance in both mean absolute error (MAE) and Root Mean Squared Error (RMSE). Compared with the constant mean function, linear mean function, and neighboring mean function, the MAE decreases by 41.78%, 47.72%, and 31.09%, respectively, while the RMSE is reduced by 50.47%, 58.45%, and 42.61%, respectively. These results underscore the effectiveness of the nonlinear mean function in improving data fitting and significantly reducing prediction errors. 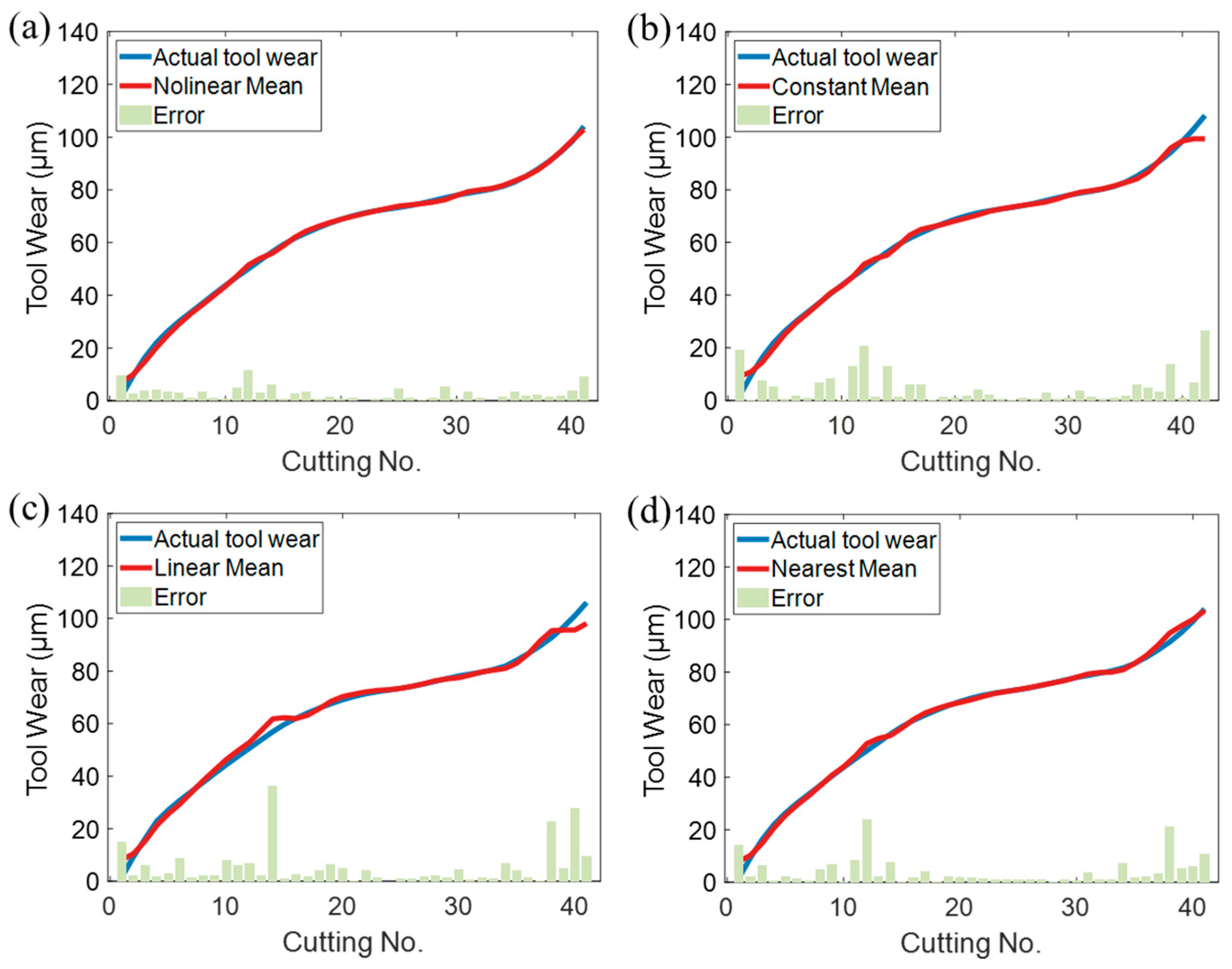Figure 6 further highlights the limitations of traditional mean functions. The constant mean function can only approximate a fixed value, failing to reflect trends and complex variations in data, leading to poor predictive accuracy. The linear mean function, although capable of basic linear fitting, lacks the flexibility to model nonlinear relationships, limiting its applicability. While the neighboring mean function provides some improvement in fitting, it remains restricted to localized similarity patterns and simple approximations, preventing it from capturing global nonlinear structures in the data. The nonlinear mean function overcomes these limitations by incorporating machining parameters, which have a direct physical correlation with tool wear. By embedding these parameters into the model, the nonlinear mean function not only enhances the representation of real machining processes but also minimizes prediction errors, providing a more accurate and reliable tool wear prediction model.

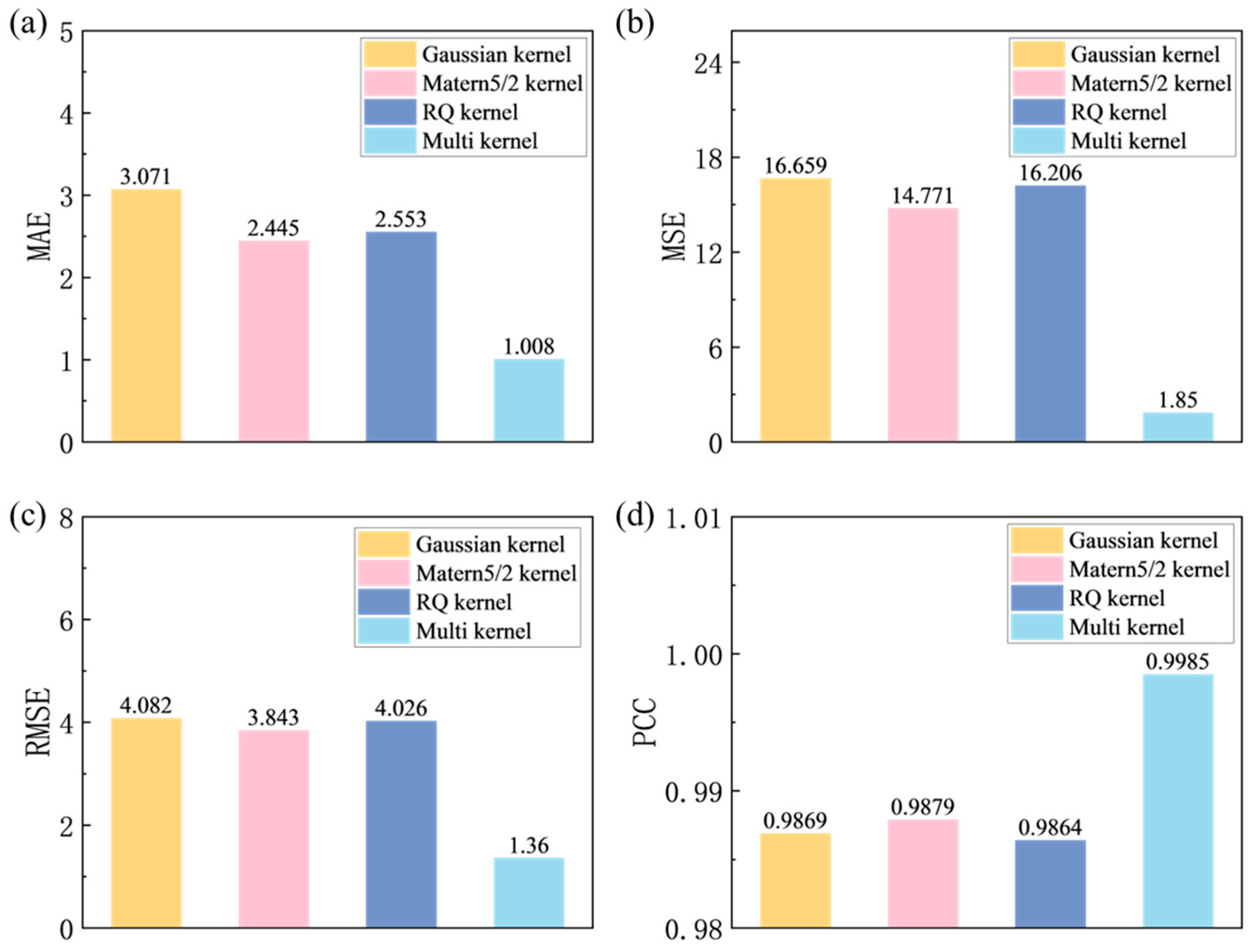
As shown in Figure 7, the multi-kernel function significantly outperforms other kernel functions in Gaussian Process Regression (GPR). Compared to the Gaussian kernel, 5/2 Matern kernel, and covariance kernel, the composite kernel reduces mean absolute error (MAE) by 67.2%, 58.7%, and 60.5%, respectively, and Root Mean Squared Error (RMSE) by 66.7%, 64.5%, and 66.3%, respectively. Figure 8 demonstrates that the Gaussian kernel produces larger fluctuations in the predictions, particularly where the data exhibits strong nonlinear characteristics, leading to more noticeable prediction errors. On the other hand, the Matern kernel delivers smoother predictions, especially across broader data ranges. Its smoothness helps mitigate the overfitting issue commonly associated with the Gaussian kernel. However, the Matern kernel still experiences larger errors at the prediction endpoints, indicating challenges in handling boundary conditions or regions with substantial data fluctuations. The Rational Quadratic (RQ) kernel shows larger discrepancies in some localized regions, especially where sharp changes occur in the data. This results in difficulty fitting accurate predictions, leading to potential error accumulation.

In contrast, the multi-kernel function, by combining the advantages of both kernels, achieves a better balance between global and local features. It minimizes fluctuations, improves the smoothness of the predictions, and maintains lower errors across a larger data range. Notably, the composite kernel performs better than individual kernels in boundary regions, offering a more robust and accurate solution for tool wear prediction.

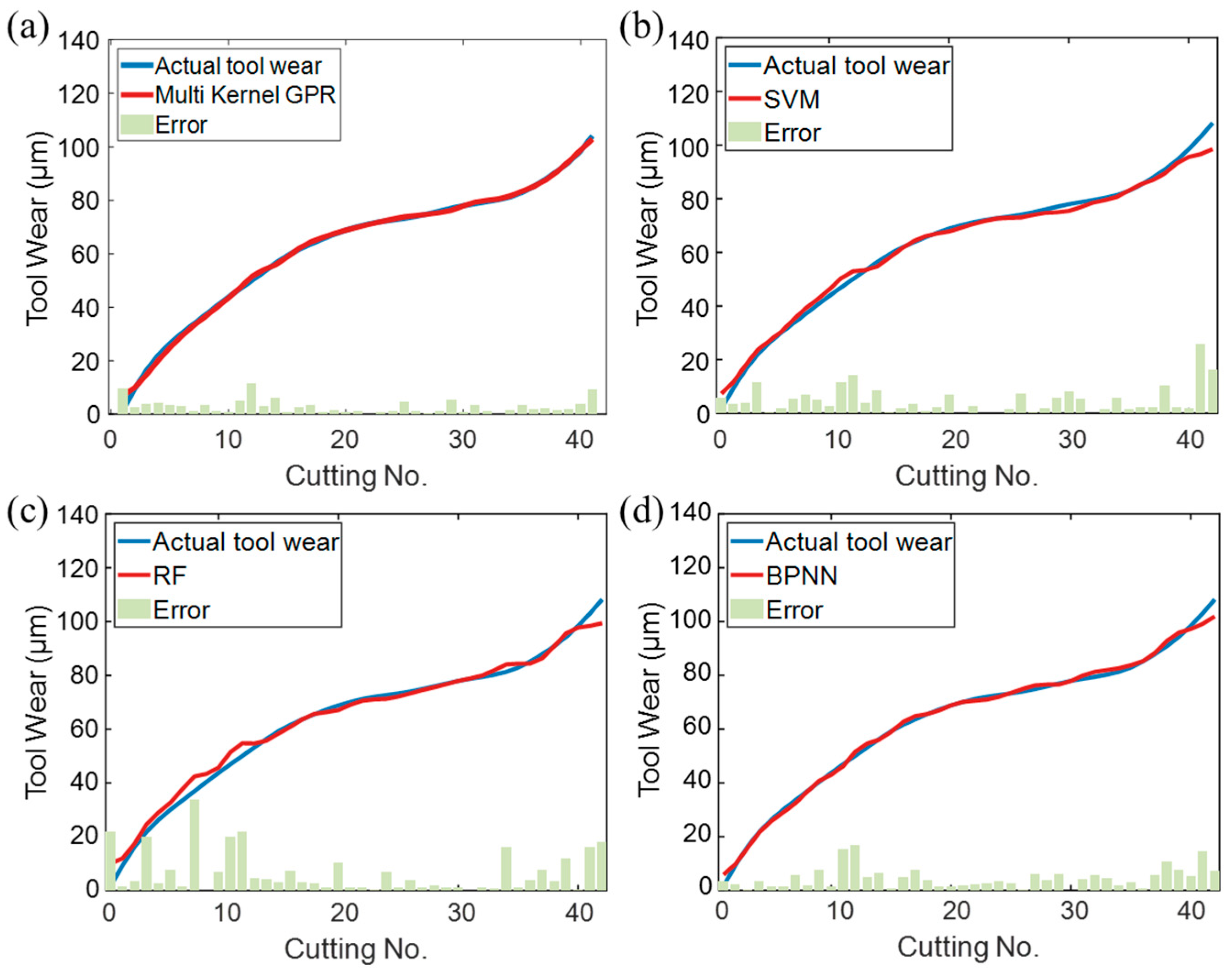
The comparison of the performance among the algorithms of the proposed multi-kernel GPR and representative ML algorithms, SVM, Random Forests (RF), and Backpropagation Neural Networks (BPNN), is implemented. For SVM, a nonlinear regression framework is established using a Gaussian kernel function, with model complexity and generalization ability balanced through a regularization parameter. To enhance robustness, a tight loss function is employed, and the kernel bandwidth is optimized in a data-driven manner. RF constructs a strong learner by integrating multiple regression trees. To mitigate overfitting, a minimum sample constraint at leaf nodes is applied. Full-dimensional feature sampling is retained to effectively capture multi-source feature interactions related to tool wear. For BPNN, a dual-hidden-layer topology is designed to strengthen nonlinear mapping capabilities. Bayesian regularization is introduced to autonomously optimize model complexity, and an early stopping criterion is used to dynamically control the training process. Optimal hyperparameters for each algorithm are determined through parameter sensitivity analysis to ensure fair comparison.

Figure 9 presents the predicted results of different algorithms. Although SVM can achieve nonlinear modeling through the Gaussian kernel and balance complexity via regularization, it exhibits limited dynamic response to severe cutting force fluctuations. The RF benefits from ensemble learning and feature interaction capturing; however, it still suffers from monitoring lag during the rapid tool wear phase. BPNN enhances nonlinear expressiveness through its dual-hidden-layer structure but remains constrained by local optimum convergence. As summarized in

Table 6. Experimental results of different prediction methods for tool wear prediction.

	MAE	MSE	RMSE	PCC
Multi Kernel GPR	1.01	1.85	1.36	0.9985
SVM	1.93	7.73	2.78	0.9956
RF	2.61	16.26	4.03	0.9887
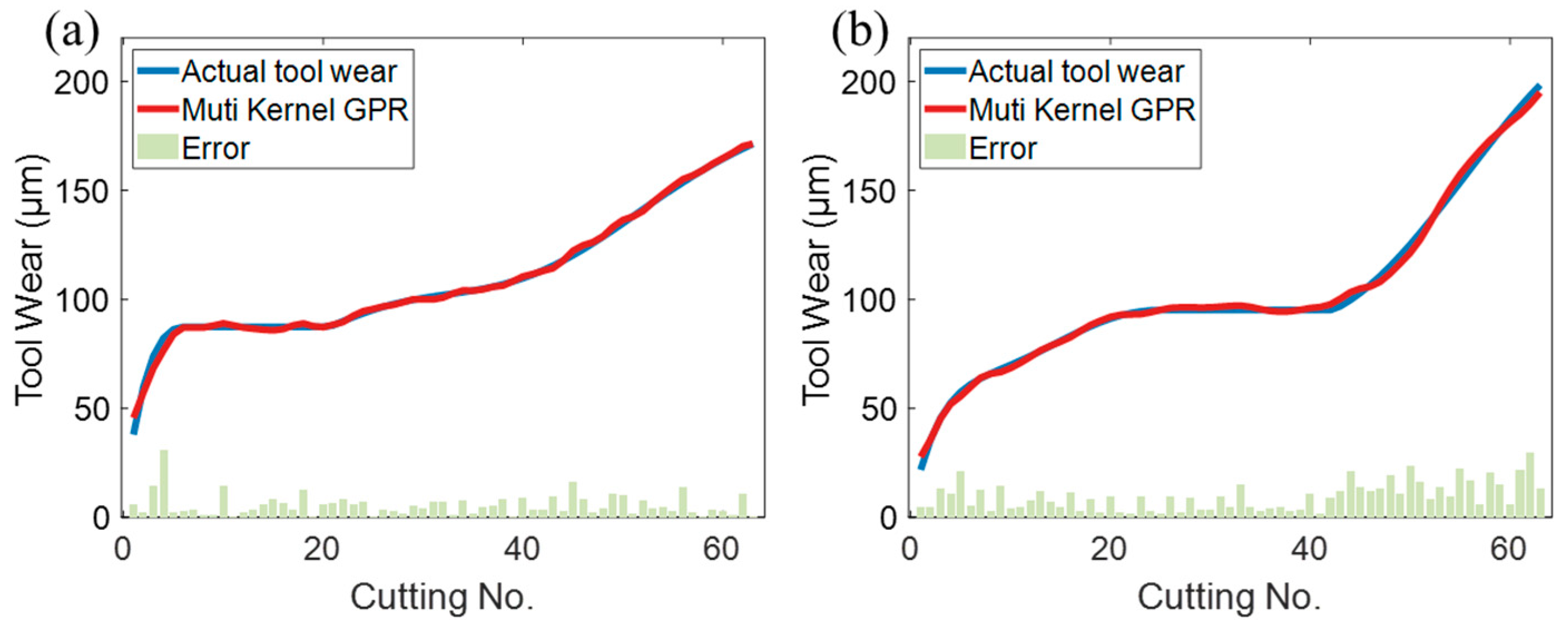
BPNN	1.82	5.61	2.37	0.9956

, the modified GPR achieves substantial improvements over the traditional models, with reductions in mean absolute error (MAE) by 47.67%, 61.30%, and 44.51%, and decreases in Root Mean Square Error (RMSE) by 51.08%, 66.25%, and 42.62%, respectively. Particularly during the rapid wear stage near the end of tool life, the multi-kernel GPR demonstrates superior adaptability, with its prediction curve exhibiting a 0.29–0.99% higher Pearson correlation coefficient (PCC) compared to other models. To further validate the generalizability of the modified GPR, verification was conducted using the standardized and publicly available PHM2010 dataset. Specifically, datasets C1 and C4 were selected for evaluation. As shown in Figure 10, the model achieved mean absolute errors of 1.264 and 2.176, Mean Squared Errors of 2.895 and 6.906, Root Mean Square Errors of 1.7015 and 2.628, and Pearson correlation coefficients of 0.9984 and 0.9976, respectively. These results demonstrate that the proposed model maintains excellent adaptability across varying operational conditions.

5. Conclusions

This study proposes a tool wear monitoring system based on the fusion of multi-kernel Gaussian Process Regression (GPR) and intelligent filtering, achieving a notable breakthrough in the engineering applicability of process condition monitoring in manufacturing. By addressing the noise suppression limitations and nonlinear modeling deficiencies of traditional approaches, the proposed system demonstrates significant engineering value:

(1) To accommodate the complex industrial conditions commonly encountered in workshops—such as vibration and electromagnetic interference—this study employs an LSTM-enhanced particle filter algorithm. By learning temporal features, the algorithm adaptively adjusts particle weights in real time. Experimental results show that under typical industrial environments, this method reduces the mean absolute error (MAE) of state estimation by 47.6% and improves the signal-to-noise ratio (SNR) by 15.4%, compared with traditional wavelet and Gaussian filtering methods. This significant improvement greatly enhances the reliability of online monitoring for CNC equipment and provides robust technical support for real-time condition tracking in industrial production.

(2) A nonlinear mean function was constructed to model the mathematical relationships between key process parameters—such as cutting depth, spindle speed, and feed rate—and tool wear. The results indicate that the proposed model outperforms conventional linear approaches, achieving a 31.09% reduction in MAE. This advancement provides a solid theoretical foundation for process optimization and supports accurate control and maintenance decision-making in industrial machining operations.

(3) By combining Gaussian and Matern kernels, the system not only maintains stability in modeling smooth signal trends but also significantly improves the capability to capture abrupt feature changes. In the context of challenging tasks such as high-hardness material machining, the prediction model achieves reductions of 58.7% in MAE and 64.5% in RMSE, greatly enhancing its stability and reliability for real-world industrial applications.

This research offers a scalable and engineering-practical approach to predictive maintenance in intelligent manufacturing. The proposed algorithmic framework is versatile and adaptable to various CNC machining scenarios. However, several real-world challenges must still be addressed in practical applications, such as physical constraints in sensor deployment and the impact of fluctuating data quality on model performance. To further enhance the system’s stability and generalization capability in complex industrial environments, future work will focus on the fast reconstruction of adaptive kernel functions and model updating strategies under dynamic operating conditions. In addition, we will explore the deep integration of heterogeneous multi-source sensor data—including vibration, acoustic emission, and current signals—to construct a more robust multi-modal perception framework. This will strengthen the model’s adaptability to unknown and extreme conditions, ultimately enabling stable deployment and long-term operation in real production environments.