Abstract
Machining deformation is a key bottleneck that restricts the improvement of manufacturing accuracy of aviation thin-walled structural components, such as frames, beams, and wall panels. The initial residual stress of the workblank and the cutting load are the direct factors leading to machining deformation. Based on the initial residual stress measurement and the milling force test, a finite element prediction model for milling deformation of frame-type thin-walled parts with integrated consideration of initial residual stress and the milling force was established and experimentally verified in this study. Then, the influence of milling process factors, such as the frame processing sequence (FPS), the cutting path, and the single frame one-time removal depth (SFORD), on the milling deformation of frame-type parts was studied. The results showed that the established prediction model had high reliability and the prediction accuracy was improved by 6.7% compared with that when only considering the initial residual stress. A smaller machining deformation can be achieved through the use of the FPS to prioritize the width, direction, and symmetrical milling, as well as the inner loop cutting path, and the smaller SFORD. This study can provide a technical reference for the prediction and control of milling deformation of aviation thin-walled structural parts, especially frame-type thin-walled parts.
1. Introduction
With the continuous development of the aviation manufacturing industry, lightweighting has become an important development trend for aircraft and other aviation equipment. The large-scale application of thin-walled aviation structural parts enables aircraft to reduce their own weight sufficiently while maintaining structural strength, thereby improving maneuverability, load capacity, and flight distance [1]. Common aviation thin-walled structural parts mainly include frames, beams, wall panels, and edge strips, among others. Most of these parts are made of light metals, such as aluminum alloys and titanium alloys. The structure is composed of thin plates in the form of polygonal frames and reinforcement ribs. The wall thickness is usually between 1.5 and 3 mm, which is a typical weak rigidity structure [2]. In order to ensure the overall rigidity of the parts, aviation thin-walled parts are generally manufactured using a whole piece of material as a workblank, which is obtained by removing more than 90% of the machining allowance through end milling. Therefore, milling deformation is the main source of machining errors in aviation thin-walled parts, which seriously reduces the manufacturing accuracy of such parts, and even causes them to be scrapped [3].
Theoretically, all the factors of the machining system, such as the machine tool, the cutting tool, the workblank, the fixture, and the milling process, will affect the machining deformation. From the perspective of the action mechanism on the machining deformation, the above factors are broadly divided into two categories: direct and indirect factors. The first, direct factors, include the workblank initial residual stress, the cutting load, and the clamping force, among others, which directly lead to deformation, and determine the deformation characteristics of thin-walled parts. The second, indirect factors, include workblank size, workpiece structure, tool material, tool size, machining parameter, milling process, and clamping method, among others, which indirectly affect milling deformation by changing the distribution and size of residual stress, milling load, and clamping force [4,5].
In recent years, some scholars have conducted a lot of research on the direct factors affecting the milling deformation, such as the initial residual stress and the cutting load. Different milling deformation prediction methods have been established, and the formation mechanism of milling deformation of aviation thin-walled structural parts has been preliminarily revealed [6]. Aurrekoetxea et al. [7] established a hybrid model combining analytical formulas and finite element modeling, which can easily and quickly predict processing deformation using BIRS estimated from simplified LR. The model is suitable for different rib geometries typical in aerospace structures, and enables deformation analysis in the process planning stage. Wang and Padmanaban [8] used the “element deletion method” to establish a finite element prediction method for machining deformation of large plate parts, and carried out related research. The results showed that the workpiece machining deformation is mainly caused by the redistribution and rebalancing of the workblank initial residual stresses during the material removal process. Chen et al. [9] proposed an analytical prediction model for the milling deformation of U-shaped and H-shaped crossbeams based on the theory of equivalent bending stiffness, and investigated the redistribution of initial residual stress during material removal and its influence on workpiece deformation. Yang et al. [10] established a milling deformation analysis model of aircraft crossbeam through the fitting method, and carried out the relevant research. The results showed that, in order to reduce the milling deformation, a workblank with a smaller fluctuation amplitude of initial residual stress should be selected. Wang et al. [11] established a functional relationship between the milling deformation of the frame parts and the workblank initial residual stress, thereby optimizing the position of thin-walled parts in the workblank and reducing the machining deformation of the parts. Based on plate-shell theory, Gao et al. [12,13] proposed an analytical prediction method for milling deformation of plate parts considering initial residual stress, and proved the feasibility of this method through experiments. However, this method is not suitable for machining deformation prediction with high removal rates. On this basis, the authors proposed a semi-analytical prediction model to investigate the influence of equivalent thickness and equivalent bending stiffness on milling deformation during the machining of aviation thin-walled parts. Based on the finite element method, Saleem et al. [14] established a machining deformation prediction model for aluminum alloy frame-type parts that only considered the workblank initial residual stress, but the method is only suitable for large-size thin-walled parts. Ma et al. [15] combined finite element simulation and theoretical calculations to propose a method for analyzing the machining deformation of large-size thin-walled parts, which achieved good computational efficiency and prediction accuracy within the linear elastic range. The study also showed that, in addition to the workblank initial residual stress, the cutting loads, such as the milling force and the milling heat, are also the main causes of workpiece deformation. The research of D’Alvise et al. [16] showed that, due to the high material removal rate during the machining of aviation structural parts, the thermodynamic coupling effect has a great influence on the rebalancing of residual stresses inside the workpiece. Huang et al. [17] studied the influence of the workblank initial residual stress and the milling thermodynamic coupling effect on the deformation of thin-walled frame parts by using the finite element method. The results showed that the workblank initial residual stress is the main influencing factor of the workpiece deformation, and the thermodynamic coupling in the process of milling further aggravates the deformation of the workpiece. Aurrekoetxea et al. [18] proposed an upgraded formula for an improved layer removal method based on 2D BIRS characterization to achieve the prediction of sheet metal processing deformation. This method takes into account multiple factors, such as BIRS, MIRS and original geometry (initial deformation) of the workblank. Tang et al. [19] established a finite element prediction model for the machining deformation of frame-type structural parts by considering multiple factors, such as workblank initial residual stress and clamping force. The results showed that the workblank initial residual stress caused the bending deformation of the parts, while the clamping force caused the torsional deformation.
In addition to the direct factors, the control of machining deformation based on milling process optimization, tool path planning, and milling parameter optimization is also the main research direction in this field. Madariaga et al. [20] developed an FEM model for predicting milling deformation of large-size structural parts of aluminum alloy, and analyzed the influence of the milling processes. The results showed that milling process optimization can significantly minimize machining deformation. Zheng et al. [21] investigated the milling deformation of aluminum alloy thin-walled parts under different tool paths by finite element simulation and experimental methods. The results showed that the deformation is sensitive to the machining path.
In summary, the workblank initial residual stress and the cutting load are the direct causes of milling deformation of aviation thin-walled parts. Milling process optimization, tool path planning, and milling parameter optimization are important ways to restrain and reduce milling deformation. The current research on prediction and control of milling deformation is mainly realized by the analytical method and the finite element method. The analytical method has the advantages of high efficiency and low cost, but the analytical model is usually established based on more simplified assumptions, which has the shortcomings of low prediction accuracy and small scope of application. With the development of computer technology, the function, efficiency, and prediction accuracy of the finite element method have been continuously improved, so that it can gradually meet the needs of studying the complex working conditions.
In this research, the milling deformation of frame-type thin-walled parts was studied by using a method that combines experiments and finite element simulation. Firstly, the workblank initial residual stress and milling force are obtained through X-ray stress measurement and milling tests. Then, a finite element prediction model, which integrally takes into account the initial residual stress, the milling force, and the clamping mode, was established and verified by experiments. Finally, the model is used to analyze the influence of milling process factors such as the frame processing sequence (FPS), the tool path, and the single frame one-time removal depth (SFORD) on the milling deformation of thin-walled parts. This research can realize the prediction of milling deformation of frame-type thin-walled parts and reveal the mechanism and changing law of milling deformation, so as to provide methods and technical references for improving the manufacturing accuracy and reducing the scrap rate of aviation thin-walled parts.
2. Measurement of Workblank Initial Residual Stress and Milling Force
The workblank was a rectangular cold-extruded aluminum alloy sheet with a size of 204 mm × 102 mm × 20 mm, as shown in Figure 1. The material type is Al6061-T6 that is mainly composed of aluminum, magnesium, and other elements, with low density, high specific strength, and corrosion resistance, among other advantages. This material is widely used to manufacture aviation thin-walled parts such as aircraft frames, beams and wall panels. Its chemical composition and main mechanical properties are listed in Table 1 and Table 2 [22].

Figure 1.
Aluminum alloy 6061-T6 cold-extruded workblank.

Table 1.
Chemical composition of aluminum alloy 6061-T6.

Table 2.
Mechanical properties of aluminum alloy 6061-T6.
2.1. Determination of the Workblank Initial Residual Stress Field
Initial residual stress refers to the internal stress caused by some factors such as metal phase change and plastic deformation under the action of temperature and pressure during the production of the workblank, which is the most important factor directly leading to the machining deformation of thin-walled structural parts [23]. According to the theory of material mechanics and the related literature, the initial residual stress field of high-quality aluminum alloy sheets usually has the following characteristics [9,11,24,25]:
- (1)
- Self-balance. In the absence of external forces, the vector sums of stress and torque in all directions inside the workblank are zero, and the internal residual stress field is in static equilibrium.
- (2)
- Uniform distribution in the same layer. The residual stresses along the length and width direction within the same thickness layer of the material can be regarded as equal.
- (3)
- Symmetrical distribution. The residual stress of the material in the thickness direction can be considered to be equal to zero, and the residual stress in the length and width directions is distributed symmetrically about the midplane of the blank.
As shown in Figure 2, a combination method of experiment and analysis was used to determine the workblank initial residual stress field. Firstly, according to the above characteristics of the initial residual stress field and the size of the workblank, the characteristic points on the workblank for residual stress measurement are determined. Secondly, the residual stress at the characteristic points is measured by using the PROTO X-ray stress analyzer. Lastly, according to the characteristics of the initial residual stress, the distribution curve of the initial residual stress field is obtained by curve fitting of the measured data [18]. As shown in Figure 2c, the workblank initial residual stress field generally exhibits the characteristics of “external tension and internal pressure”, in which the surface layer at a depth of 4 mm showed tensile stress, and the σxx and σyy of the outermost layer were 39.01 MPa and 32.67 MPa, respectively. The inner layer exhibited compressive stress, in which the σxx and σyy of the mid-plane are −34.58 MPa and −27.73 MPa, respectively.
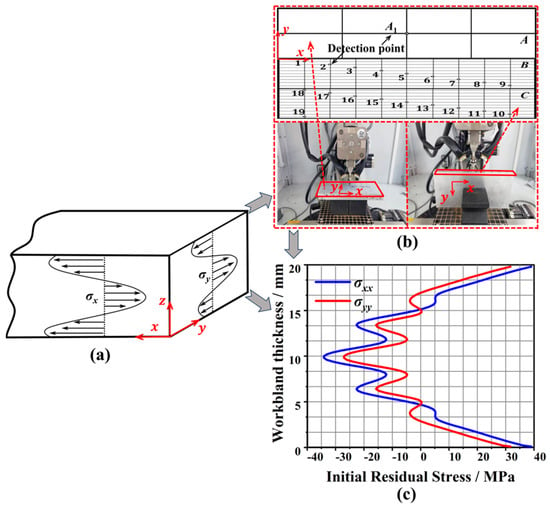
Figure 2.
Determination of workblank initial residual stress field: (a) distribution characteristics of the initial residual stress field; (b) measurement of the residual stress at characteristic points; (c) distribution curve of the workblank initial residual stress field.
2.2. Experiments for Milling Forces
The cutting loads during the machining include the cutting force, the cutting heat, the machining vibration, etc., among which the cutting force and the cutting heat are two important aspects. In the case of aluminum alloys, machining temperatures have a relatively small effect due to their light weight, excellent thermal conductivity, and good cutting properties. In addition, during the milling process of framed parts, coolant is usually used to cool the workpiece so that the workpiece is always at a lower temperature during machining. Therefore, only the influence of force load was considered in this research [26]. The milling force was measured by a milling test of the aluminum alloy Al6061-T6.
As shown in Figure 3, the experiment of end milling was carried out on the JT-VL850B vertical machining center. After screening the machining parameters by orthogonal tests, the milling parameters were determined, as listed in Table 3. The tool and milling parameters were the same as those for the machining of frame-type thin-walled parts. The tool was a Φ10 mm three-flute carbide end mill; its structural parameters are listed in Figure 4 and Table 4. During the machining, a 5% emulsion was applied as cooling fluid, and the milling force was measured by using a Kistler 9272 cutting dynamometer. As can be seen in Figure 3, the workpiece is subjected to three-dimensional forces from the tool during the milling, in which the feed force Fx is the largest, the normal force Fy is the second largest, and the axial force Fz is the smallest. With the rotation of the tool, the workpiece material was removed continuously in wedge-shaped units, so that Fx, Fy, and Fz all show the trend of cyclic fluctuations [27].
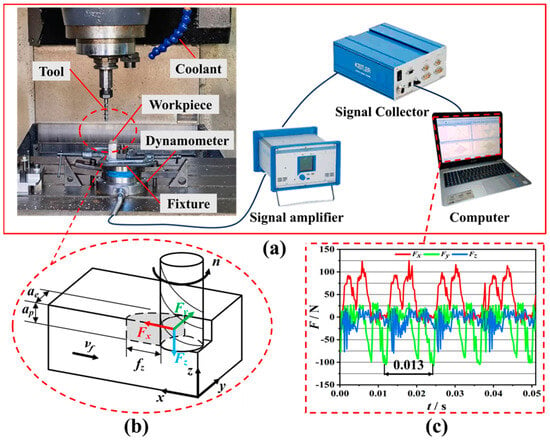
Figure 3.
Milling force test and results: (a) milling force test setup; (b) schematic diagram of end milling; (c) milling force experimental results.

Table 3.
Milling parameters.

Figure 4.
Schematic diagram of tool structure.

Table 4.
Structural parameters of end mill.
3. Establishment of the Deformation Prediction Method for Frame-Type Thin-Walled Parts
In this research, a four-frame thin-walled part was selected as the analysis object, and the “element deletion method” in finite element simulation was used to simulate the milling deformation. Figure 5 shows the flow chart of finite element simulation for milling deformation. Firstly, a three-dimensional model of the workblank was established by the finite element software ABAQUS, then the material properties were set, and the initial residual stress field was loaded. Secondly, the constraints were imposed on the workblank model according to the actual clamping mode. Thirdly, the milling force was loaded on the workpiece model. Lastly, the prediction of the machining deformation was conducted, and the experimental validation for the predicted resulted was carried out.
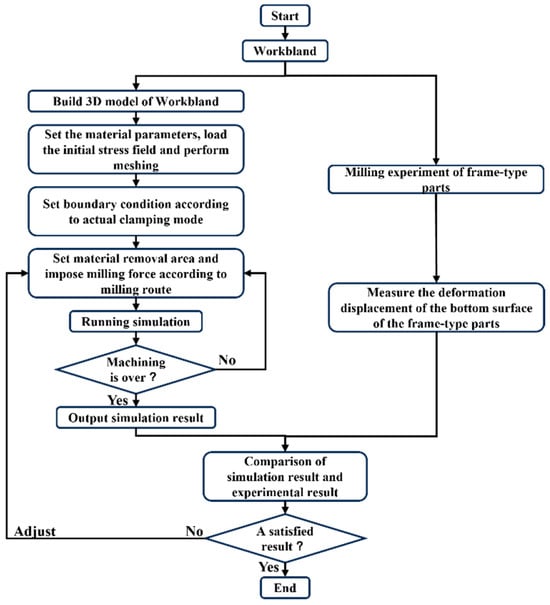
Figure 5.
Flow chart of finite element simulation.
3.1. Establishment of the Workblank Model and Loading of the Initial Stress Field
The workblank 3D model is shown in Figure 6. This model was built according to the actual dimensions of the workblank, where the x-axis, y-axis and z-axis represent the length direction, the width direction, and the thickness direction, respectively. The rib and base thickness of the frame-type parts were set to 2 mm. Since the dimension of the workblank was 204 mm × 102 mm × 20 mm, the removal material size of a single frame should be 99 mm × 48 mm × 18 mm. The material properties of the workblank model are defined according to the material parameters listed in Table 1 and Table 2. The model is meshed by the manually controlled mapping method, which generates 416,160 elements, and the mesh type is the C3D8R element. Subsequently, the initial stress field obtained in the part of 2.1 was scattered and loaded to the corresponding layers of the workblank model by the SIGINI subroutine.
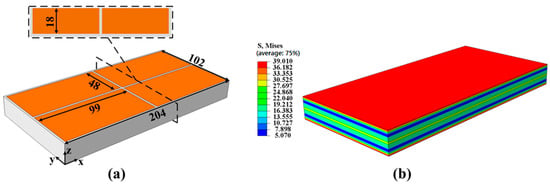
Figure 6.
3D model of the workblank: (a) geometric model of the workblank; (b) initial stress distribution inside the workblank.
3.2. Setting of Boundary Conditions for the Workblank Model
As shown in Figure 7, the constraint for the workblank model was set according to the actual clamping mode. During actual machining, the workblank was positioned by its bottom and clamped on the workbench of the machining center. Therefore, the constraint for the workblank model was set to a completely fixed mode at the bottom. After the simulation was finished, the constraint was transformed into a three-node constraint (XYZ–YZ–Z) mode with non-collinear bottom surface. This method not only takes into account the constraint during actual machining, but allows the workpiece to deform freely after unloading.
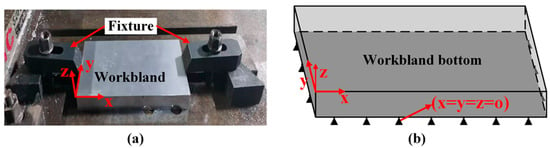
Figure 7.
Setting of boundary conditions for the workblank model: (a) actual clamping mode; (b) constraint for the workblank model.
3.3. Division of the Milling Removal Region and Application of Milling Force
In the existing studies, the machining deformation simulation of thin-walled parts generally has been carried out by the element deletion method (EDM). First, multiple analysis steps are created based on tool trajectory and machining parameters. Next, the material removal region is set up in each sub-step and the force load is applied to the element nodes of the corresponding region in turn, and the milling force is unloaded after the region material is removed. In this study, the force load was set as the body force, which avoided the unloading of the milling force and thus improved the simulation efficiency. Assuming that the body force was uniformly distributed in each removal region, it can be obtained as follows:
where FBi is the body force (N/mm3), F is the experimental milling force (N), and V is the volume of the removal unit in the actual milling (mm3). According to Equation (1), the three-dimensional maximum milling forces obtained in the part of 2.2 were equivalently converted into three-dimensional body forces: FBix = 32.78 N/mm3, FBiy = −28.89 N/mm3, and FBiz = −19.44 N/mm3.
In order to simplify the calculation, the removal unit shape of the actual end milling needs to be simplified. The simplification of the cutting layer is generally based on two principles: firstly, the simplified area should facilitate the realization of the material removal and the application of loads; secondly, it should significantly improve the computational efficiency. As shown in Figure 8, the wedge-shaped removal unit was simplified to a rectangular unit of the same size, which is not only convenient for meshing, but is conducive to loading the milling force [28]. During the simulation, the material removal length in each analysis step was defined as 10 fz; that is, each simulation analysis step was 10 times the feed per tooth of fz in the actual milling. As a result, the three-dimensional milling forces applied to each analysis step were also scaled up in equal proportion. Figure 9 shows the schematic diagram of removal of the machined material by the element deletion method. The material removal in each analysis step was realized by three steps, including selecting the region, applying the force load, and deleting the region. Then, the analysis steps were set according to the tool path and the frame processing sequence to achieve the complete removal of machining allowance.
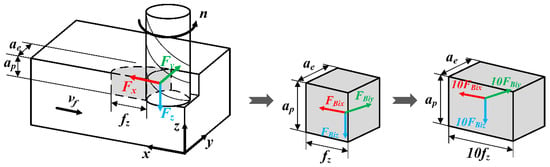
Figure 8.
Schematic diagram of the loading method of milling force.
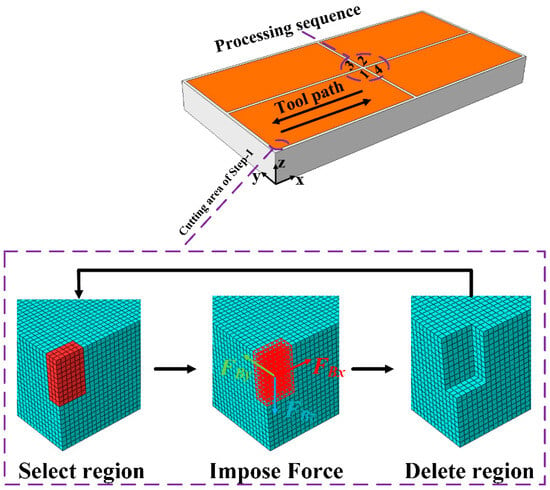
Figure 9.
Schematic diagram of removal machined material by element deletion method.
3.4. Finite Element Simulation of Milling Deformation for Frame-Type Thin-Walled Parts
Using the above method, the milling deformation simulation of the frame-type thin-walled parts was carried out according to the tool path and the frame processing sequence, as shown in Figure 9. Figure 10 shows the milling deformation cloud maps. It can be seen from Figure 10 that the deformation characteristics of the frame-type parts was the same regardless of whether or the milling force was applied, but their deformation amounts were different. When the milling force was applied, the maximum deformation in the end of the part was 0.2029 mm, which was 37.5% higher than that without the milling force. The reasons why the force load changed the deformation amount mainly depend on two aspects. On the one hand, the milling force induces the machining residual stress, which changes the residual stress field inside the workpiece. On the other hand, the milling force causes the plastic deformation of the workpiece along the weak rigidity direction. Therefore, the milling force had an important influence on the prediction accuracy of machining deformation.
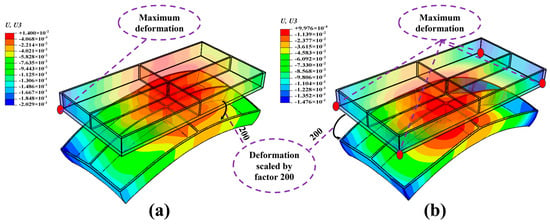
Figure 10.
Milling deformation cloud maps of the frame-type parts: (a) with milling force applied; (b) without milling force applied.
3.5. Experimental Verification of the Simulation Method
In order to verify the simulation method, a milling test for the four-frame thin-walled parts was carried out. After the milling was completed, the relative displacements of the characteristic points at the bottom of the parts were measured using a micrometer. Figure 11 shows the deformation measurement method and a comparison of the experimental simulation results. The results show that the simulation and the experimental results were in good agreement, and the frame-type parts presented the deformation characteristics of “convex in the middle and bending along the long side”.
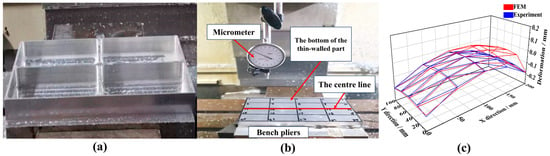
Figure 11.
Deformation measurement method and comparison of results: (a) machined four-frame part; (b) measurement of the deformation displacement; (c) comparison of experimental and simulation results.
In order to quantitatively compare the deformation, based on the above deformation characteristics, the center line mean curvature, , in the direction of the length of the frame-type parts was calculated. The smaller the mean curvature of , the closer the curve is to a straight line and the smaller the degree of deformation; whereas the larger mean curvature of , the greater the degree of deformation. The derivation is given below.
Firstly, based on the finite element simulation results, the bending equation for the center line in the direction of the length of the frame-type parts is derived as follows:
where x is the distribution coordinate of the feature point at the center line in the direction of the length and y is the deformation displacement of the point in the thickness direction of the workpiece. The center line mean curvature, , in the direction of the length of the frame-type parts was calculated using Formula (3).
where C represents the center line length and its definition domain is [0, 204], k is the local curvature, ds is the element of arc length, and L is the total length of the center line. Figure 12 shows a comparison between the simulation and the experimental results of the center line mean curvature. From Figure 12, it can be seen that the deformation prediction result of the combined consideration of the workblank initial residual stress and the force load was closer to the experimental result. The simulation results of the mean curvature of with and without force load were 2.62 × 10−5/mm and 2.46 × 10−5/mm, respectively, and the experimental mean curvature of was 3.11 × 10−5/mm. Therefore, the deformation prediction accuracy can be improved by 6.7% when the milling force load is considered.
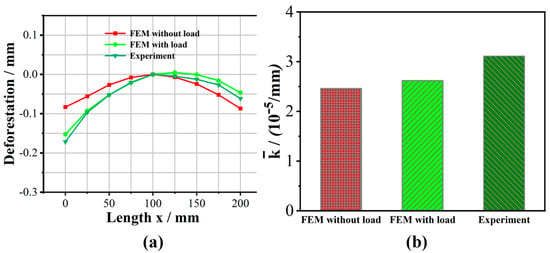
Figure 12.
Comparison of simulation and experimental results of the center line mean curvature: (a) deformation curves; (b) mean curvature of .
4. Influence of Process Strategy on Milling Deformation of Frame-Type Parts
As mentioned above, indirect factors, such as process strategy, affect the milling deformation of thin-walled parts by changing the distribution and size of residual stresses and cutting loads. Optimizing the milling process is an important way to reduce and suppress the deformation. Based on the established finite element prediction method, the influence of milling process factors, such as the frame processing sequence (FPS), the tool path, and the single frame one-time removal depth (SFORD), on the deformation of frame-type parts are discussed.
4.1. Influence of FPS on the Milling Deformation
Figure 13 shows the influence of an FPS on the milling deformation. For the four-frame thin-walled parts, there are six possible FPSs (as shown in Figure 13a). During this simulation, the milling parameters were unchanged, as shown in Table 3, and the tool path is a reciprocating type. Figure 13b shows the deformation cloud maps of the bottom of the parts, from which the deformation curves corresponding to the long center line and the mean curvatures could be obtained (see Figure 13c).
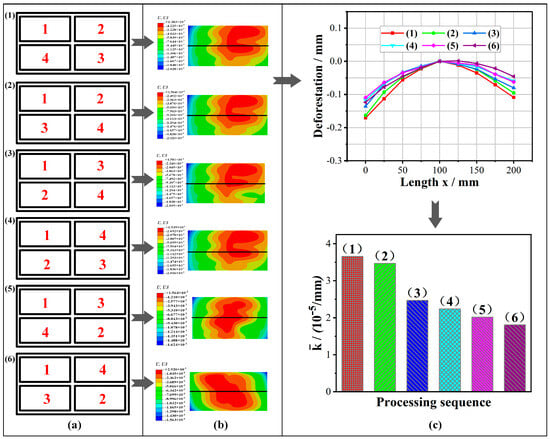
Figure 13.
Influence of FPSs on the milling deformation: (a) FPS; (b) deformation cloud maps; (c) deformation curves and mean curvatures.
According to Figure 13c, the FPSs had significant effect on the milling deformation. The deformation with FPS (1) and (2) was evidently greater than those with the other FPSs, and the mean curvatures in both cases were 3.66 × 10−5/mm and 3.47 × 10−5/mm, respectively. The deformation with FPS (3) and (4) was in the middle, and the mean curvatures were 2.57 × 10−5/mm and 2.24 × 10−5/mm, respectively. It had the smallest deformation with FPS (5) and (6), the mean curvatures in these two cases were 2.02 × 10−5/mm and 1.81 × 10−5/mm. This result shows that smaller machining deformation can be obtained by using the FPSs of prioritizing the width direction and symmetrical milling. This is due to the fact that asymmetric milling leads to uneven release of the initial residual stresses, which results in increasing deformation. In addition, the short side of the frame-type part has higher rigidity than the long side, and the workpiece is more resistant to deformation caused by stress release when the symmetrical milling along the width is performed first.
4.2. Influence of Tool Path on Milling Deformation
Figure 14 shows the influence of the tool path on the milling deformation. As shown in Figure 14a, tool paths include four types: (1) single way, (2) reciprocating type, (3) inner loop, and (4) outer loop. The milling parameters remain unchanged and the FPS was case (6) in Figure 13.
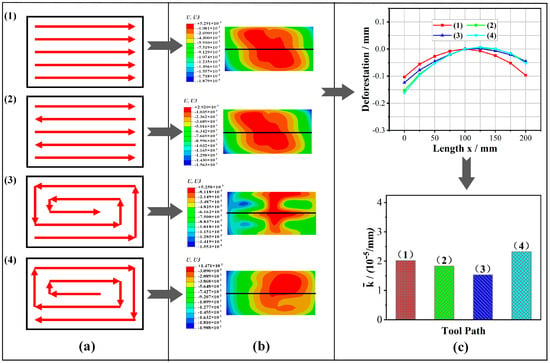
Figure 14.
Influence of tool path on the milling deformation: (a) tool path; (b) deformation cloud maps; (c) deformation curves and mean curvatures.
From Figure 14c, it can be seen that the deformation under the four tool paths also has a big difference, and their mean curvatures are 1.91 × 10−5/mm, 1.81 × 10−5/mm, 1.53 × 10−5/mm, 2.02 × 10−5/mm, respectively. The deformation of the inner loop tool path was the smallest, followed by the reciprocating type tool path, and the deformation of the outer loop tool path was the largest. The reason for this result is that the inner loop tool path provides more space for stress release, which facilitates a more uniform distribution of stress within the workpiece.
4.3. Influence of SFORD on the Machining Deformations
Figure 15 shows the effect of the SFORD on the milling deformation. The so-called SFORD refers to the depth of continuous machining for a single frame when the milling parameters, the FPS, and the tool path remain unchanged. As shown in Figure 15a, four SFORDs of 1 mm, 3 mm, 6 mm, and 9 mm were selected. The milling parameters and the FPS remain unchanged. Figure 15b shows the deformation cloud maps of the bottom of the parts, and Figure 15c shows the comparison of deformation curves and mean curvatures.
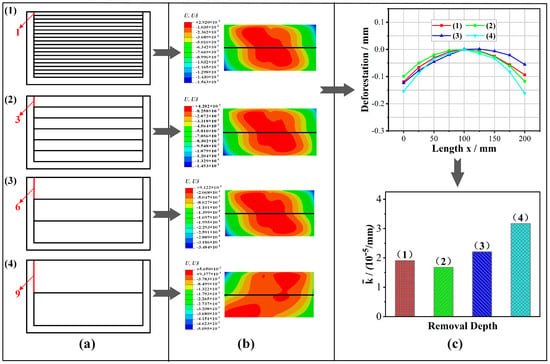
Figure 15.
Influence of the SFORD on the milling deformation: (a) SFORD; (b) deformation cloud maps; (c) deformation curves and mean curvatures.
As shown in Figure 15c, the mean curvatures with the four cases were 1.81 × 10−5/mm, 1.68 × 10−5/mm, 2.21 × 10−5/mm, and 3.17 × 10−5/mm, respectively, in which the deformation was the smallest when the SFORD was 3 mm, and the deformation was the largest at the SFORD of 9 mm. In order to reduce the milling deformation, a smaller SFORD should be chosen. This is because a small SFORD has less influence on the residual stress field of the workpiece, which results in a smaller stress imbalance distribution within the workpiece.
5. Conclusions
Based on the experimental results of the workblank initial residual stress and milling force, a prediction method for the milling deformation of the frame-type thin-walled parts was established by using the “element deletion method” in the finite element simulation, and experimental verification was carried out. On this basis, the model was used to explore the effect of the milling process strategy on milling deformation of frame-type thin-walled parts. The results show the following:
- (1)
- A reliable prediction result can be obtained by this method, and the prediction results of the deformation characteristics for the frame-type parts are in good agreement with the experiment results.
- (2)
- When milling frame parts, smaller machining deformation can be obtained by using the FPS of prioritizing the width direction and symmetrical milling.
- (3)
- The deformation of the framed part is the smallest in the inner loop under four different machining paths: single way, reciprocating type, inner loop, and outer loop.
- (4)
- The milling deformation of the framed parts decreases and then increases with the increase of the removal depth, where the deformation is the smallest when the SFORD is 3 mm.
Author Contributions
Conceptualization, L.M., Y.Z., and S.B.; methodology, L.M. and S.B.; software, S.B., Y.Z., and H.L.; validation, S.B., L.L., and F.G.; investigation, S.B. and Y.Z.; resources, F.Z. and J.M.; writing—original draft preparation, S.B. and Y.Z.; writing—review and editing, L.M. and S.B.; supervision, L.M., F.Z., and J.M. All authors have read and agreed to the published version of the manuscript.
Funding
L.M. acknowledges support from the Henan province key R&D project (No. 251111221900.), the National Natural Science Foundation of China (No.52175397.) and the State Department project of China (No. JF2020-1-0422.).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FPS | Frame processing sequence |
| SFORD | Single frame one-time removal depth |
| FEM | Finite element method |
| EDM | Element deletion method |
References
- Yue, C.; Zhang, J.; Liu, X.; Chen, Z.; Liang, S.; Wang, L. Research progress on machining deformation of thin-walled parts in milling process. Acta Aeronaut. Astronaut. Sin. 2022, 43, 525164. [Google Scholar]
- Del Sol, I.; Rivero, A.; López de Lacalle, L.N.; Gamez, A.J. Thin-wall machining of light alloys: A review of models and industrial approaches. Materials 2019, 12, 12. [Google Scholar] [CrossRef] [PubMed]
- Aurrekoetxea, M.; Llanos, I.; Zelaieta, O.; López de Lacalle, L.N. Towards advanced prediction and control of machining distortion: A comprehensive review. Int. J. Adv. Manuf. Technol. 2022, 122, 2823–2848. [Google Scholar] [CrossRef]
- Santos, M.C.; Machado, A.R.; Sales, W.F.; Barrozo, M.A.; Ezugwu, E.O. Machining of aluminum alloys: A review. Int. J. Adv. Manuf. Technol. 2016, 86, 3067–3080. [Google Scholar] [CrossRef]
- Yiyang, Z.; Jian, M.; Gang, L.; Man, Z. A review on error generation and control in efficient precision machining of thin-walled parts. Int. J. Adv. Manuf. Technol. 2024, 133, 2083–2101. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, B.; Ding, W.; Pu, C.; Wang, X.; Peng, S.; Ma, F. A short review on machining deformation control of aero-engine thin-walled casings. Int. J. Adv. Manuf. Technol. 2022, 121, 2971–2985. [Google Scholar] [CrossRef]
- Aurrekoetxea, M.; López de Lacalle, L.N.; Zelaieta, O.; Llanos, I. In-Process Machining Distortion Prediction Method Based on Bulk Residual Stresses Estimation from Reduced Layer Removal. J. Manuf. Mater. Process. 2024, 8, 9. [Google Scholar] [CrossRef]
- Wang, S.P.; Padmanaban, S. A new approach for FEM simulation of NC machining processes. AIP Conf. Proc. 2004, 712, 1371–1376. [Google Scholar]
- Chen, Z.; Yue, C.; Xu, Y.; Liu, X.; Liang, S.Y. An analytical machining deformation model of H-section multi-frame beam integral components. J. Mater. Process. Technol. 2023, 314, 117907. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X.; Li, L.; He, N.; Zhao, G.; Chen, N.; Lan, H.; Zhou, Z. Investigation on deformation of single-sided stringer parts based on fluctuant initial residual stress. J. Mater. Process. Technol. 2019, 271, 623–633. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, J.; Liu, L.; Wang, R.; Chen, W. An analytical model to predict the machining deformation of frame parts caused by residual stress. J. Mater. Process. Technol. 2019, 274, 116282. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Wu, Q.; Song, J. An analytical model for predicting the machining deformation of a plate blank considers biaxial initial residual stresses. Int. J. Adv. Manuf. Technol. 2017, 93, 1473–1486. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Wu, Q.; Li, B. Investigation on influences of initial residual stress on thin-walled part machining deformation based on a semi-analytical model. J. Mater. Process. Technol. 2018, 262, 437–448. [Google Scholar] [CrossRef]
- Saleem, W.; Ijaz, H.; Zain-ul-Abdein, M.; Taimoor, A.A.; Wang, Y. Studying control strategies for dimensional precision in aerospace parts machining. Int. J. Adv. Manuf. Technol. 2017, 18, 39–47. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, J.; Yu, D.; Feng, P.; Xu, C. Modeling of machining distortion for thin-walled components based on the internal stress field evolution. Int. J. Adv. Manuf. Technol. 2019, 103, 3597–3612. [Google Scholar] [CrossRef]
- D’Alvise, L.; Chantzis, D.; Schoinochoritis, B.; Salonitis, K. Modelling of part distortion due to residual stresses relaxation: An aeronautical case study. Procedia Cirp 2015, 31, 447–452. [Google Scholar] [CrossRef]
- Huang, X.; Sun, J.; Li, J. Effect of initial residual stress and machining-induced residual stress on the deformation of aluminium alloy plate. Stroj. Vestn-J. Mech. E 2015, 61, 131–137. [Google Scholar] [CrossRef]
- Aurrekoetxea, M.; López de Lacalle, L.N.; Llanos, I. Machining stresses and initial geometry on bulk residual stresses characterization by on-machine layer removal. Materials 2020, 13, 1445. [Google Scholar] [CrossRef]
- Tang, Z.T.; Yu, T.; Xu, L.Q.; Liu, Z.Q. Machining deformation prediction for frame components considering multifactor coupling effects. Int. J. Adv. Manuf. Technol. 2013, 68, 187–196. [Google Scholar] [CrossRef]
- Madariaga, A.; Perez, I.; Arrazola, P.J.; Sanchez, R.; Ruiz, J.J.; Rubio, F.J. Reduction of distortions in large aluminium parts by controlling machining-induced residual stresses. Int. J. Adv. Manuf. Technol. 2018, 97, 967–978. [Google Scholar] [CrossRef]
- Zheng, J.Y.; Voyle, R.; Tang, H.P.; Mannion, A. Study of distortion on milled thin-wall aluminum parts influenced by initial residual stress and toolpath strategy. Int. J. Adv. Manuf. Technol. 2023, 127, 237–251. [Google Scholar] [CrossRef]
- Rajaa, S.M.; Abdulhadi, H.A.; Jabur, K.S.; Mohammed, G.R. Aging time effects on the mechanical properties of Al 6061-T6 alloy. Eng. Technol. Appl. Sci. 2018, 8, 3113–3115. [Google Scholar] [CrossRef]
- Yi, S.; Wu, Y.; Gong, H.; Peng, C.; He, Y. Experimental analysis and prediction model of milling-induced residual stress of aeronautical aluminum alloys. Appl. Sci. 2021, 11, 5881. [Google Scholar] [CrossRef]
- Weber, D.; Kirsch, B.; D ‘Elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Simulation-Based Investigation of the Distortion of Milled Thin-Walled Aluminum Structural Parts Due to Residual Stresses. In Proceedings of the 3rd Conference on Physical Modeling for Virtual Manufacturing Systems and Processes; Springer International Publishing: Cham, Switzerland, 2023; pp. 149–169. [Google Scholar]
- Weber, D.; Kirsch, B.; Jonsson, J.E.; D’Elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Simulation based compensation techniques to minimize distortion of thin-walled monolithic aluminum parts due to residual stresses. CIRP J. Manuf. Sci. Technol. 2022, 38, 427–441. [Google Scholar] [CrossRef]
- Bi, Y.B.; Cheng, Q.L.; Dong, H.Y.; Ke, Y.L. Machining distortion prediction of aerospace monolithic components. J. Zhejiang Univ.-Sci. A. 2009, 10, 661–668. [Google Scholar] [CrossRef]
- Liping, W.A.N.G.; Hao, S.I.; Liheng, G.U. Prediction of cutting forces in flank milling of parts with non-developable ruled surfaces. Chin. J. Aeronaut. 2019, 32, 1788–1796. [Google Scholar]
- Sanz-Calle, M.; Iglesias, A.; de Lacalle, L.L.; Dombovari, Z.; Munoa, J. Optimal milling cutter helix selection for period doubling chatter suppression. Int. J. Mach. Tool. Manu. 2024, 202, 104211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).