Permea-Design: An Innovative Tool for Generating Triply Periodic Minimal Surface Scaffolds with Tailored Permeability
Abstract
:1. Introduction
2. Materials and Methods
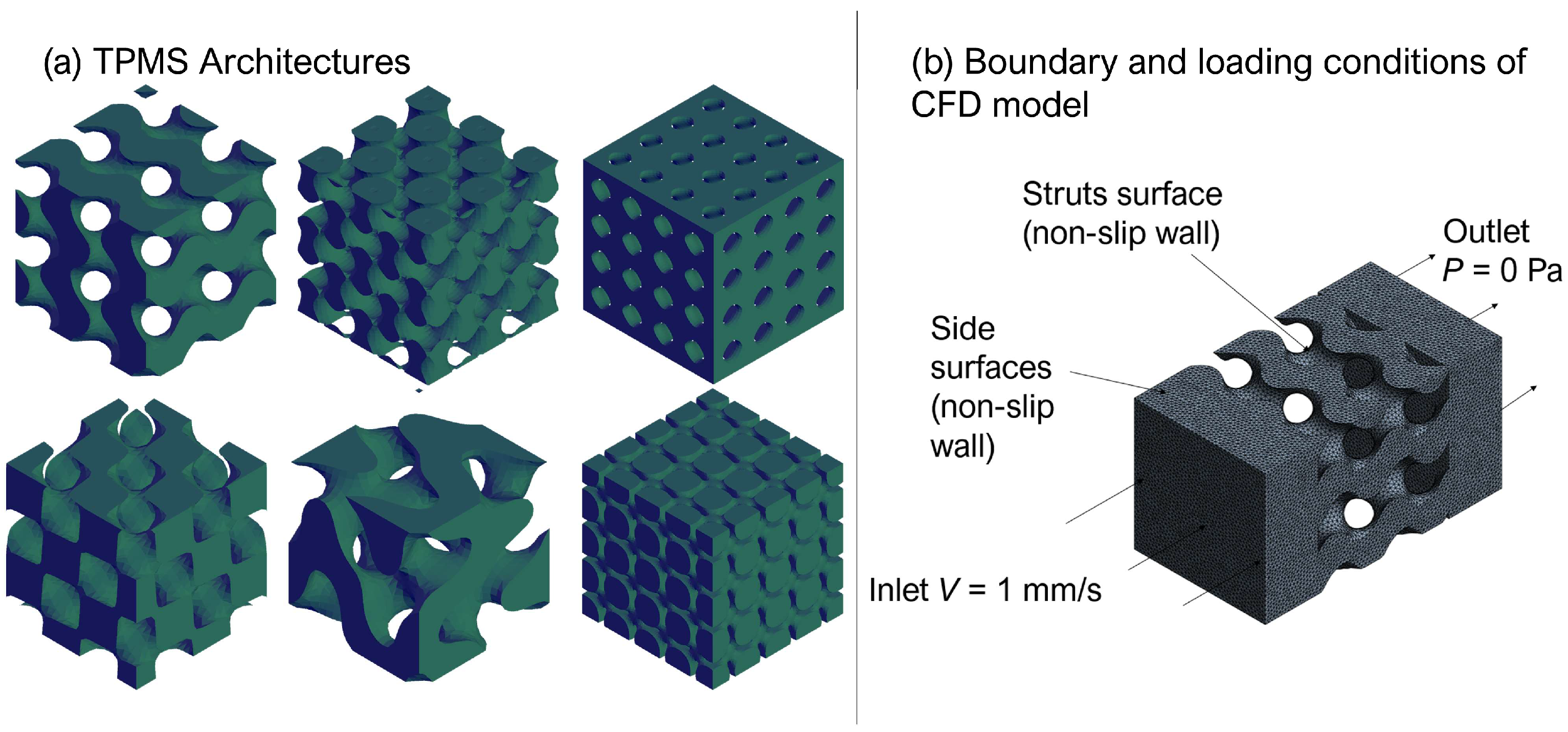
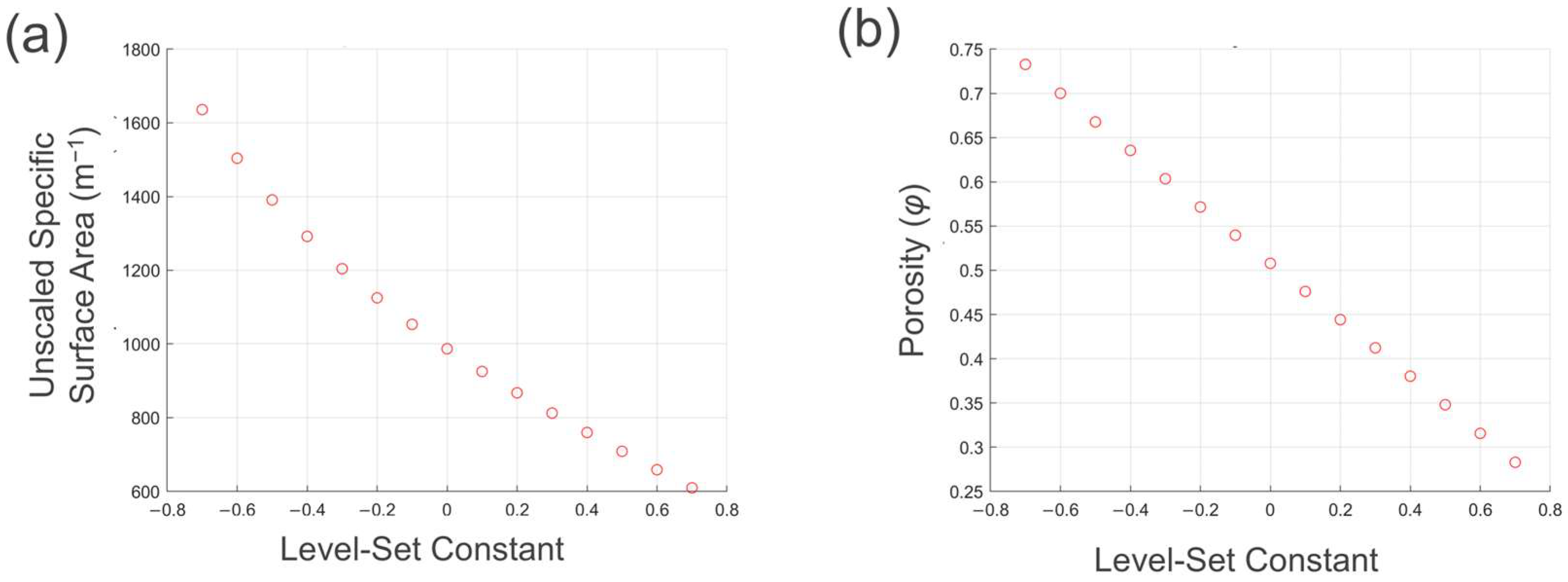
2.1. Topology Analysis
2.2. CFD Simulation to Determine Kozeny Constant β
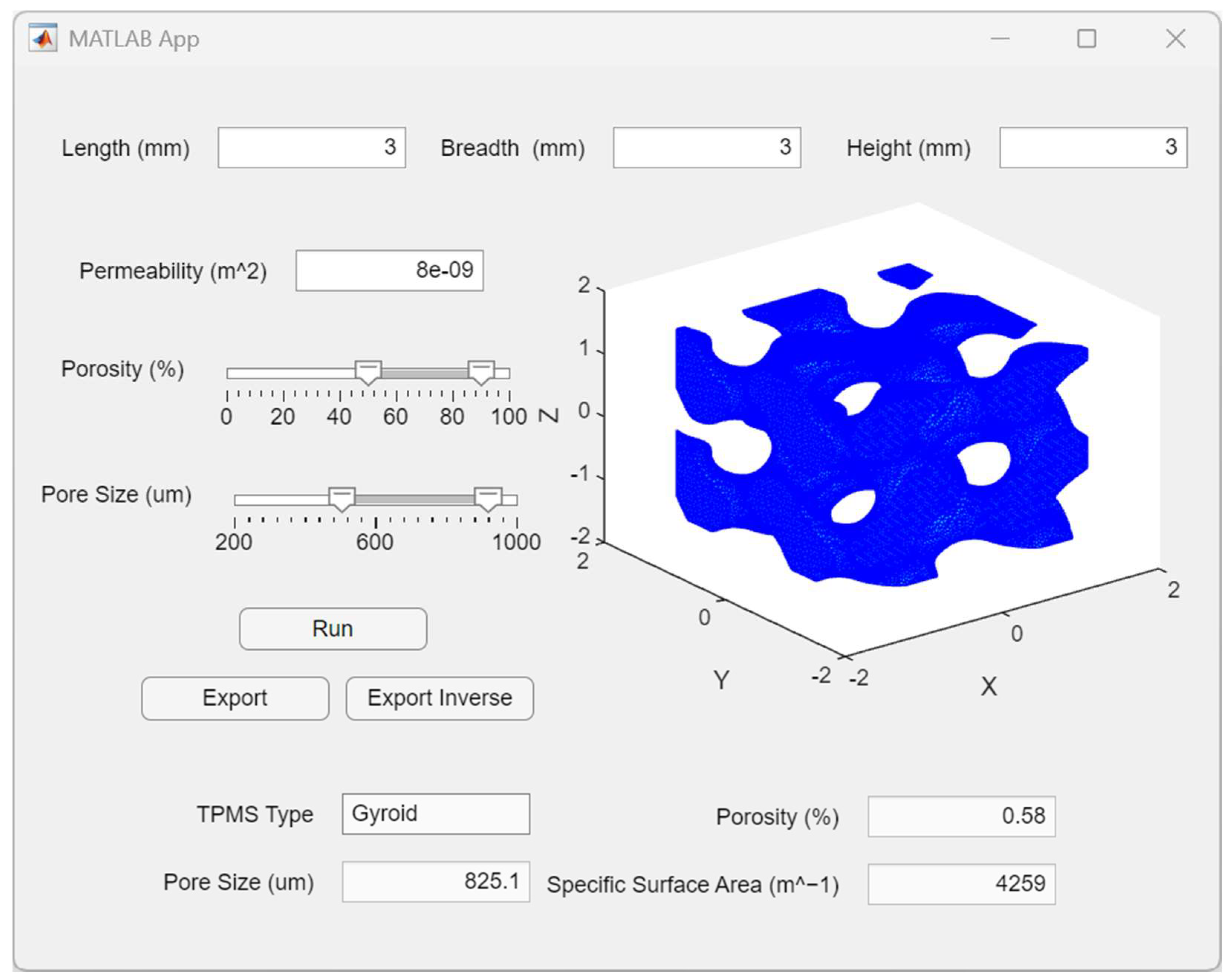
2.3. Development of Scaffold Design Toolbox
3. Results
3.1. Updated Kozeny–Carman Equation
3.2. MATLAB Toolbox for Scaffold Design
4. Discussion
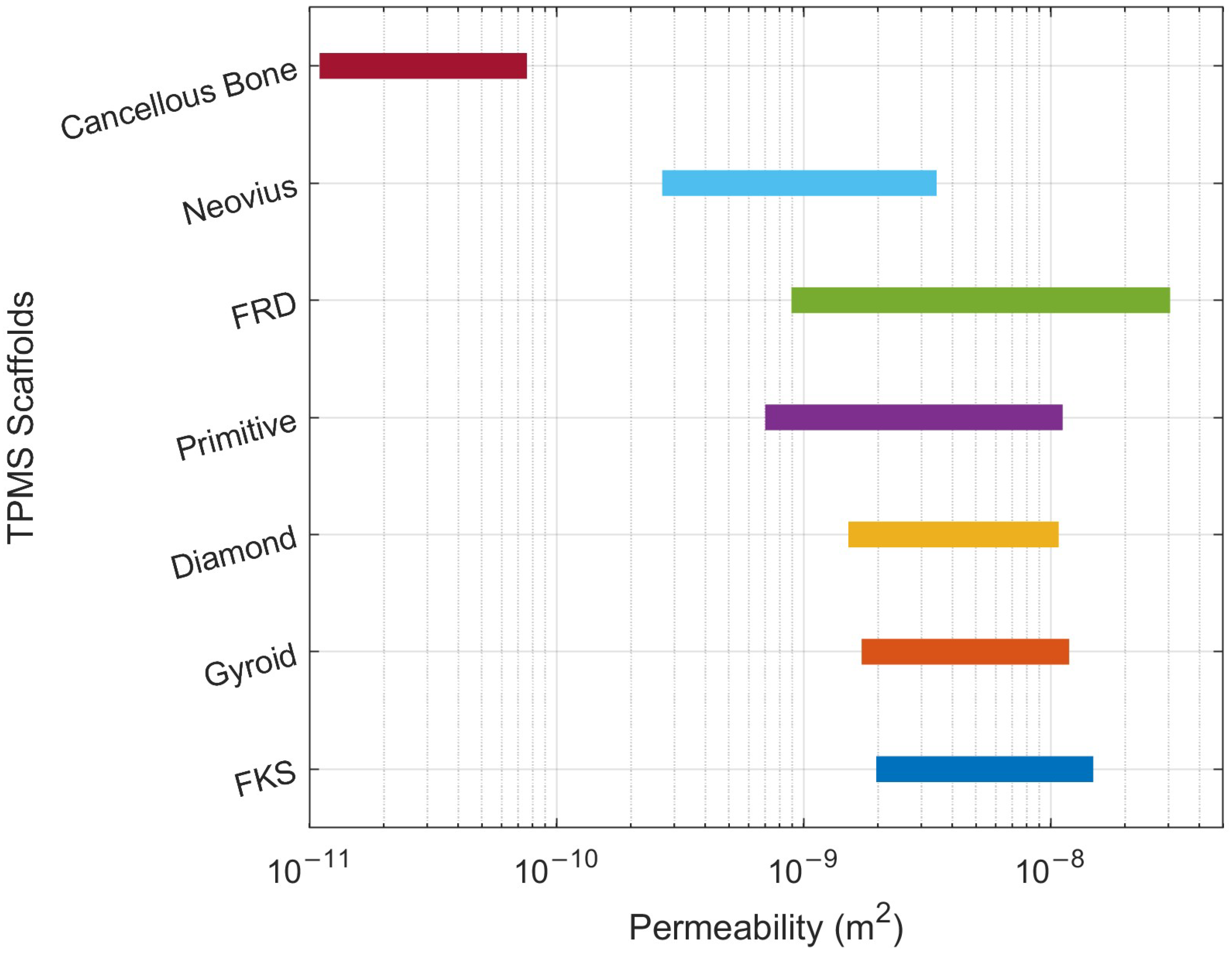
4.1. Permeability Comparison of TPMS Architectures
4.2. Limitations and Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, F.; van Rietbergen, B.; Ito, K.; Hofmann, S. Flow rates in perfusion bioreactors to maximise mineralisation in bone tissue engineering In Vitro. J. Biomech. 2018, 79, 232–237. [Google Scholar] [CrossRef] [PubMed]
- Frantz, C.; Stewart, K.M.; Weaver, V.M. The extracellular matrix at a glance. J. Cell Sci. 2010, 123, 4195–4200. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Zhao, X. Application of TPMS structure in bone regeneration. Eng. Regen. 2021, 2, 154–162. [Google Scholar] [CrossRef]
- Sokollu, B.; Gulcan, O.; Konukseven, E.I. Mechanical Properties Comparison of Strut-Based and Triply Periodic Minimal Surface Lattice Structures Produced by Electron Beam Melting. Addit. Manuf. 2022, 60, 103199. [Google Scholar]
- Lehder, E.F.; Ashcroft, I.A.; Wildman, R.D.; Ruiz-Cantu, L.A.; Maskery, I. A multiscale optimisation method for bone growth scaffolds based on triply periodic minimal surfaces. Biomech. Model. Mechanobiol. 2021, 20, 2085–2096. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.P.G.; Pires, T.; Santos, J.E.; Gouveia, B.P.; Fernandes, P.R. Permeability versus design in TPMS scaffolds. Materials 2019, 12, 1313. [Google Scholar] [CrossRef] [PubMed]
- Ochoa, I.; Sanz-Herrera, J.A.; García-Aznar, J.M.; Doblaré, M.; Yunos, D.M.; Boccaccini, A.R. Permeability evaluation of 45S5 Bioglass®-based scaffolds for bone tissue engineering. J. Biomech. 2009, 42, 257–260. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Xiong, Y.; Ito, K.; van Rietbergen, B.; Hofmann, S. Porous Geometry Guided Micro-mechanical Environment Within Scaffolds for Cell Mechanobiology Study in Bone Tissue Engineering. Front. Bioeng. Biotechnol. 2021, 9, 736489. [Google Scholar] [CrossRef] [PubMed]
- Berg, C.F. Permeability Description by Characteristic Length, Tortuosity, Constriction and Porosity. Transp. Porous Media 2015, 107, 713–726. [Google Scholar] [CrossRef]
- Rabbani, A.; Jamshidi, S. Specific surface and porosity relationship for sandstones for prediction of permeability. Int. J. Rock Mech. Min. Sci. 2014, 71, 25–32. [Google Scholar] [CrossRef]
- Mauri, A.; Bertola, M. Alvascience: A New Software Suite for the QSAR Workflow Applied to the Blood–Brain Barrier Permeability. Int. J. Mol. Sci. 2022, 23, 12882. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.L.; Yu, H.; Yuan, X.H.; Xu, H.Y.; Micheal, M.; Zhang, J.N.; Shu, H.L.; Wang, G.C.; Wu, H.A. Permeability prediction of low-resolution porous media images using autoencoder-based convolutional neural network. J. Pet. Sci. Eng. 2022, 208, 109589. [Google Scholar] [CrossRef]
- The Carman-Kozeny Equation. Available online: https://www.doitpoms.ac.uk/tlplib/powder/carman.php (accessed on 22 May 2024).
- Blanquer, S.B.G.; Werner, M.; Hannula, M.; Sharifi, S.; Lajoinie, G.P.R.; Eglin, D.; Hyttinen, J.; Poot, A.A.; Grijpma, D.W. Surface curvature in triply-periodic minimal surface architectures as a distinct design parameter in preparing advanced tissue engineering scaffolds. Biofabrication 2017, 9, 025001. [Google Scholar] [CrossRef] [PubMed]
- Knödler, P.; Dreissigacker, V. Fluid Dynamic Assessment and Development of Nusselt Correlations for Fischer Koch S Structures. Energies 2024, 17, 688. [Google Scholar] [CrossRef]
- Abou-Ali, A.M.; Lee, D.W.; Abu Al-Rub, R.K. On the Effect of Lattice Topology on Mechanical Properties of SLS Additively Manufactured Sheet-, Ligament-, and Strut-Based Polymeric Metamaterials. Polymers 2022, 14, 4583. [Google Scholar] [CrossRef] [PubMed]
- Abou-Ali, A.M.; Al-Ketan, O.; Lee, D.W.; Rowshan, R.; Abu Al-Rub, R.K. Mechanical behavior of polymeric selective laser sintered ligament and sheet based lattices of triply periodic minimal surface architectures. Mater. Des. 2020, 196, 109100. [Google Scholar] [CrossRef]
- Zou, S.; Mu, Y.; Pan, B.; Li, G.; Shao, L.; Du, J.; Jin, Y. Mechanical and biological properties of enhanced porous scaffolds based on triply periodic minimal surfaces. Mater. Des. 2022, 219, 110803. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, Y.; Aziz, M.; Wen, P.; Zhang, C.; Shen, Q.; Chen, F. Mechanical behaviors of multidimensional gradient gyroid structures under static and dynamic loading: A numerical and experimental study. Addit. Manuf. 2022, 59, 103187. [Google Scholar] [CrossRef]
- Walker, J.M.; Bodamer, E.; Kleinfehn, A.; Luo, Y.; Becker, M.; Dean, D. Design and mechanical characterization of solid and highly porous 3D printed poly(propylene fumarate) scaffolds. Prog. Addit. Manuf. 2017, 2, 99–108. [Google Scholar] [CrossRef]
- Ansys CFX-Pre User’s Guide. 2021. Available online: https://dl.cfdexperts.net/cfd_resources/Ansys_Documentation/CFX/Ansys_CFX-Solver_Theory_Guide.pdf (accessed on 17 February 2025).
- Sven. Stlwrite-Write ASCII or Binary STL Files. MATLAB Central File Exchange. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/20922-stlwrite-write-ascii-or-binary-stl-files (accessed on 11 January 2025).
- Prakoso, A.T.; Basri, H.; Adanta, D.; Yani, I.; Ammarullah, M.I.; Akbar, I.; Ghazali, F.A.; Syahrom, A.; Kamarul, T. The Effect of Tortuosity on Permeability of Porous Scaffold. Biomedicines 2023, 11, 427. [Google Scholar] [CrossRef] [PubMed]


| TPMS Type | Gyroid | Diamond | FKS | FRD | Primitive | Neovius |
|---|---|---|---|---|---|---|
| β | 0.12 ± 0.021 | 0.13 ± 0.022 | 0.12 ± 0.019 | 0.17 ± 0.019 | 0.15 ± 0.032 | 0.12 ± 0.032 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedding-Tyrrell, M.; Sandnes, B.; Nithiarasu, P.; Zhao, F. Permea-Design: An Innovative Tool for Generating Triply Periodic Minimal Surface Scaffolds with Tailored Permeability. J. Manuf. Mater. Process. 2025, 9, 72. https://doi.org/10.3390/jmmp9030072
Bedding-Tyrrell M, Sandnes B, Nithiarasu P, Zhao F. Permea-Design: An Innovative Tool for Generating Triply Periodic Minimal Surface Scaffolds with Tailored Permeability. Journal of Manufacturing and Materials Processing. 2025; 9(3):72. https://doi.org/10.3390/jmmp9030072
Chicago/Turabian StyleBedding-Tyrrell, Matthew, Bjornar Sandnes, Perumal Nithiarasu, and Feihu Zhao. 2025. "Permea-Design: An Innovative Tool for Generating Triply Periodic Minimal Surface Scaffolds with Tailored Permeability" Journal of Manufacturing and Materials Processing 9, no. 3: 72. https://doi.org/10.3390/jmmp9030072
APA StyleBedding-Tyrrell, M., Sandnes, B., Nithiarasu, P., & Zhao, F. (2025). Permea-Design: An Innovative Tool for Generating Triply Periodic Minimal Surface Scaffolds with Tailored Permeability. Journal of Manufacturing and Materials Processing, 9(3), 72. https://doi.org/10.3390/jmmp9030072







