Bayesian Optimization-Based Parameter Identification for Discrete Element Method Simulation of Consolidation and Its Application to Powder Spreading Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials Used
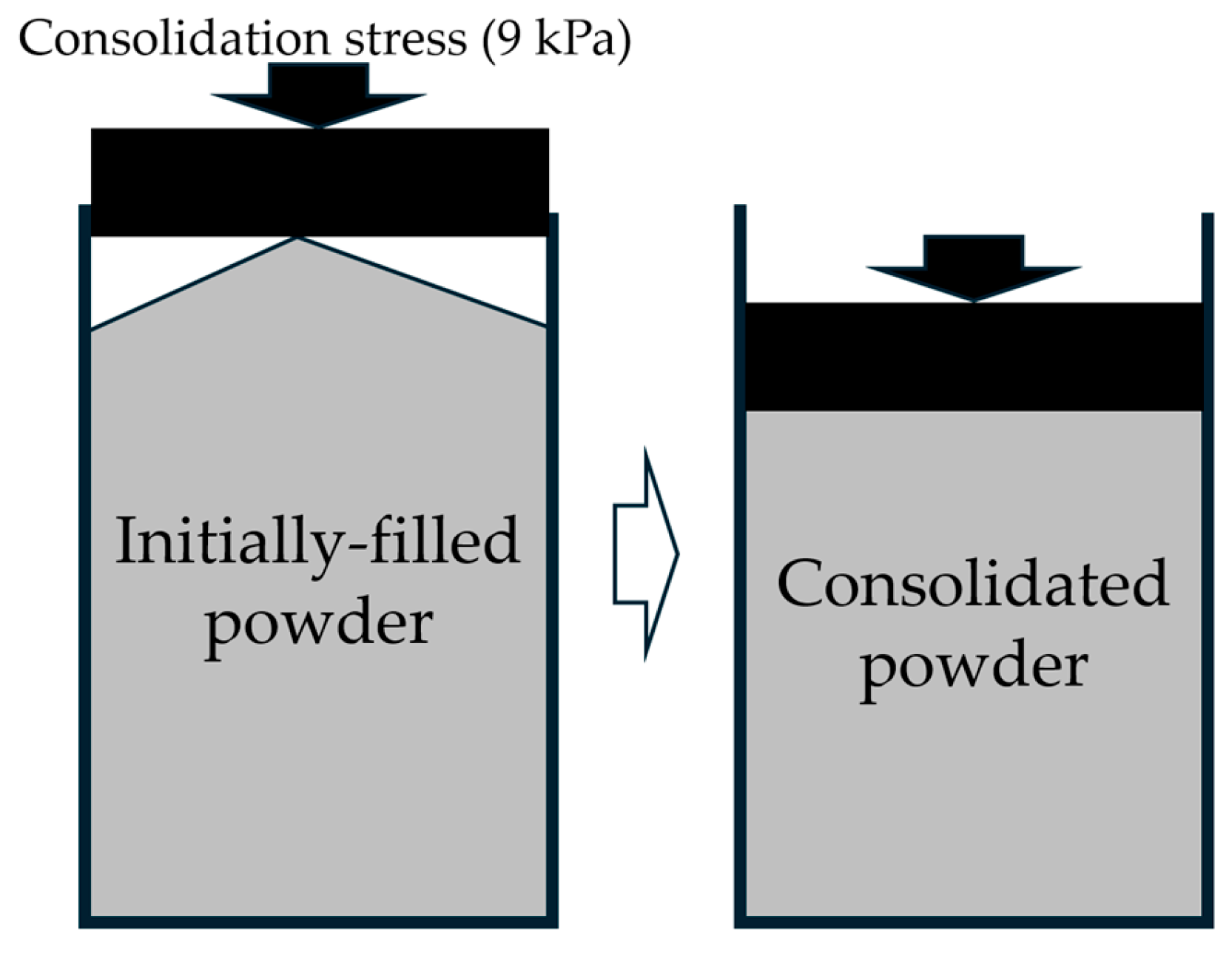
2.2. Consolidation Experiment
2.3. Discrete Element Method Overview
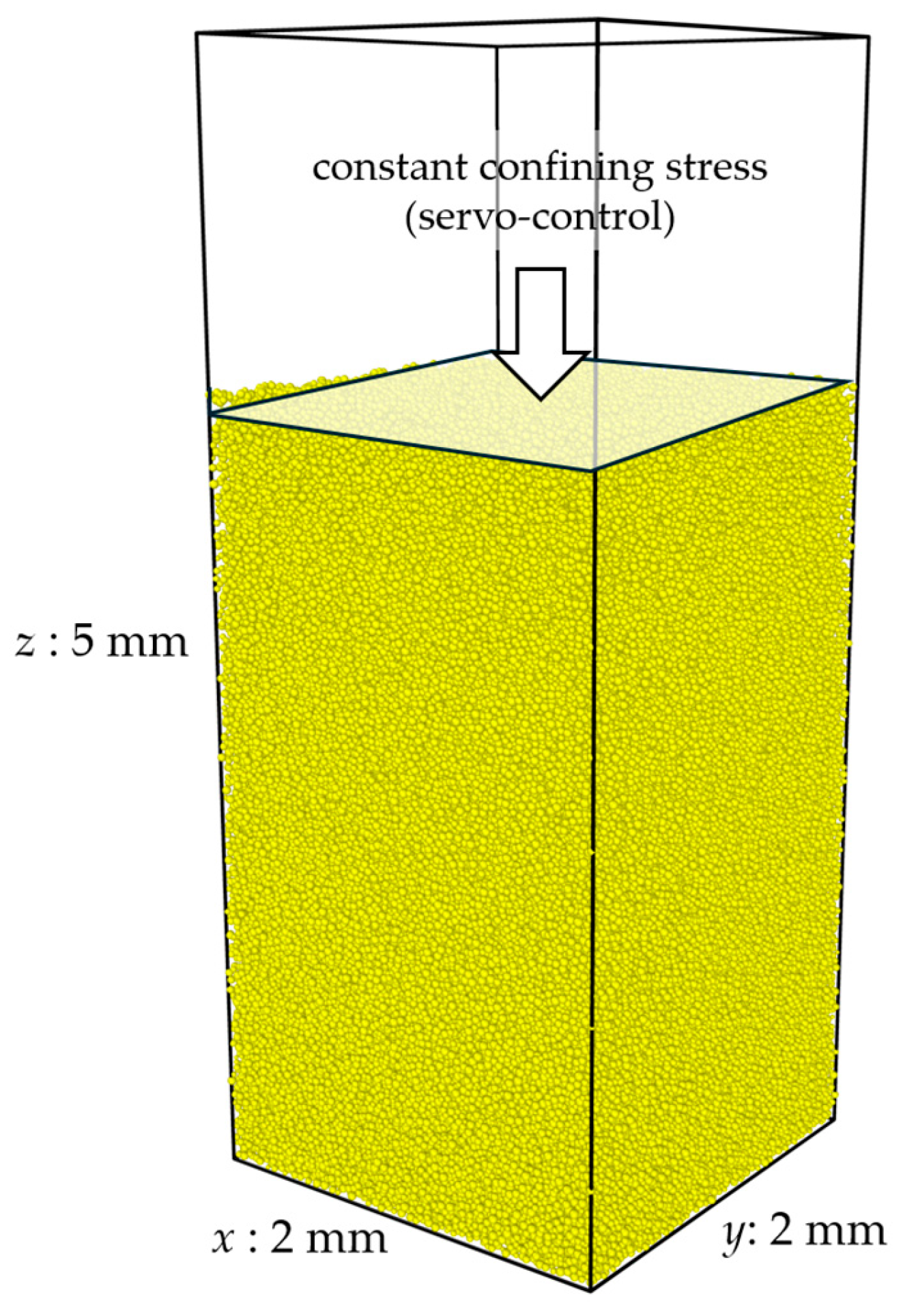
2.4. Consolidation Simulation
2.5. Bayesian Optimization
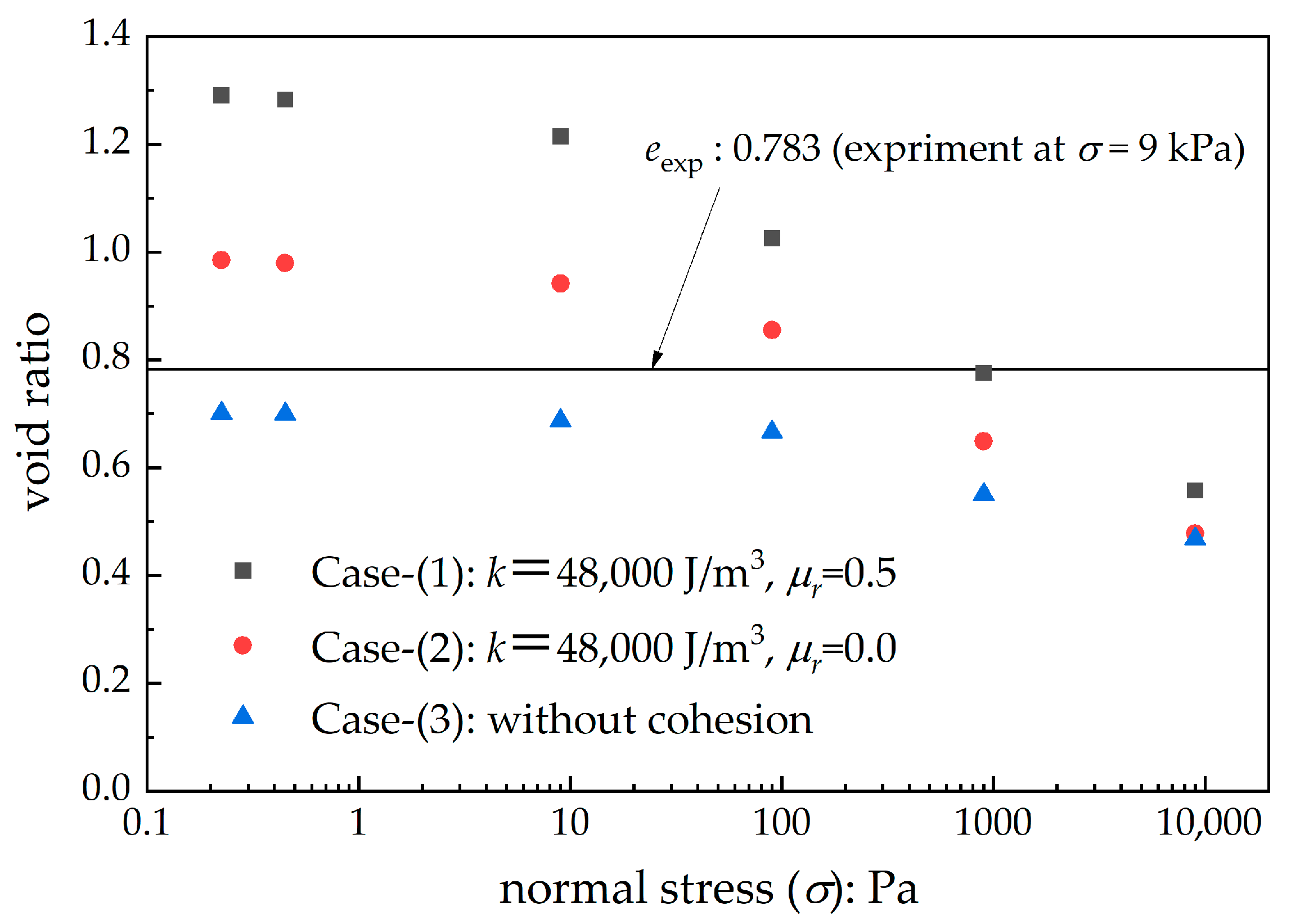
| Case | k [J/m3] | μr [-] | Void Ratio |
|---|---|---|---|
| 0–1 | 102 | 0.05 | 0.575 |
| 0–2 | 105 | 0.7 | 1.459 |
| 0–3 | 102 | 0.7 | 0.566 |
| 0–4 | 105 | 0.05 | 1.120 |
| 0–5 | 5 × 102 | 0.4 | 0.568 |
| 1 | 5570 | 0.13 | 0.569 |
| 2 | 70,500 | 0.37 | 1.064 |
| 3 | 9100 | 0.24 | 0.565 |
| 4 | 36,900 | 0.63 | 0.658 |
| 5 | 42,800 | 0.31 | 0.721 |
| 6 | 55,400 | 0.66 | 0.889 |
| 7 | 17,500 | 0.68 | 0.566 |
| 8 | 56,400 | 0.49 | 0.897 |
| 9 | 69,800 | 0.56 | 1.080 |
| 10 | 55,400 | 0.56 | 0.886 |
| 11 | 42,800 | 0.55 | 0.716 |
| 12 | 56,400 | 0.46 | 0.897 |
| best | 47,500 | 0.5 | 0.776 |
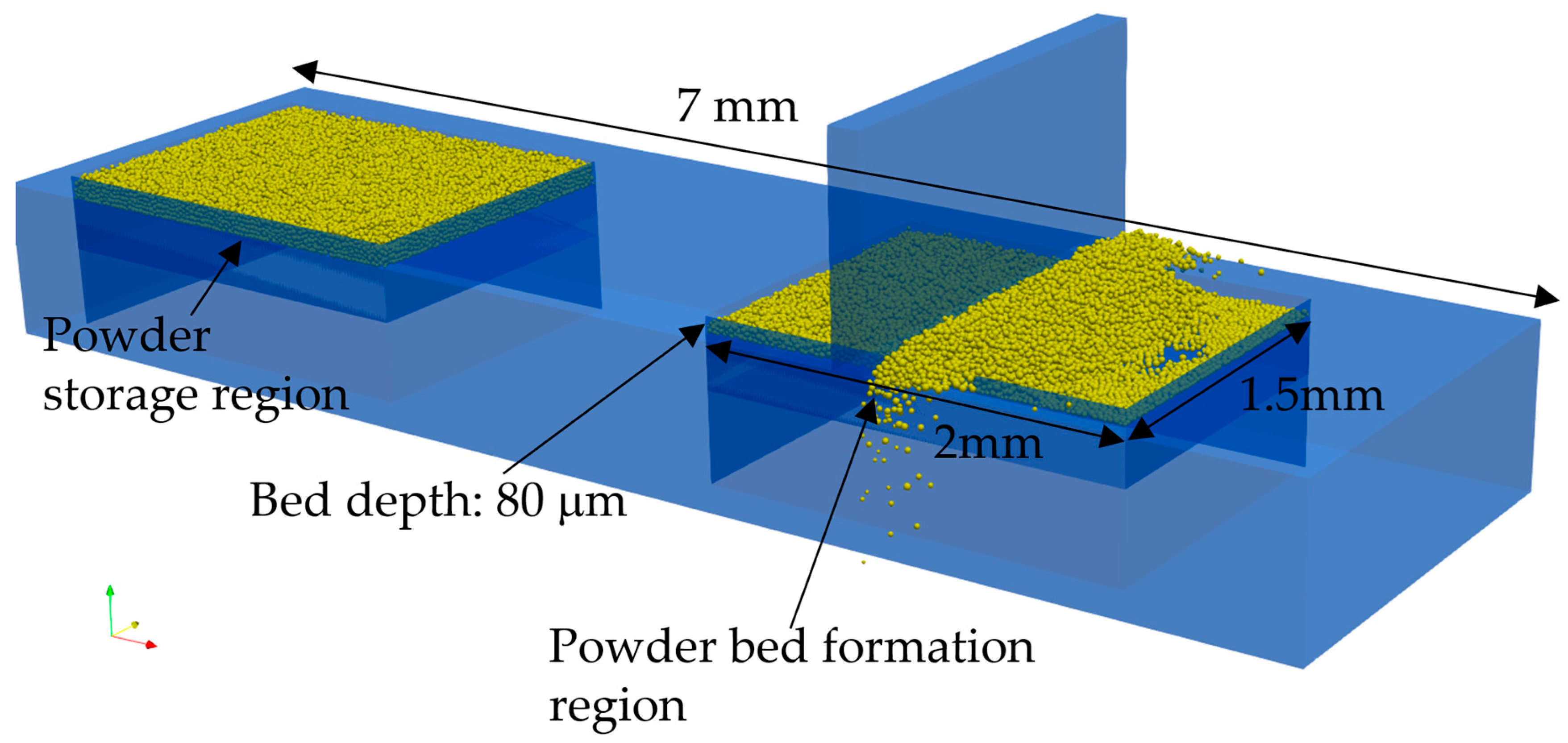
2.6. Powder Spreading Simulation
3. Results
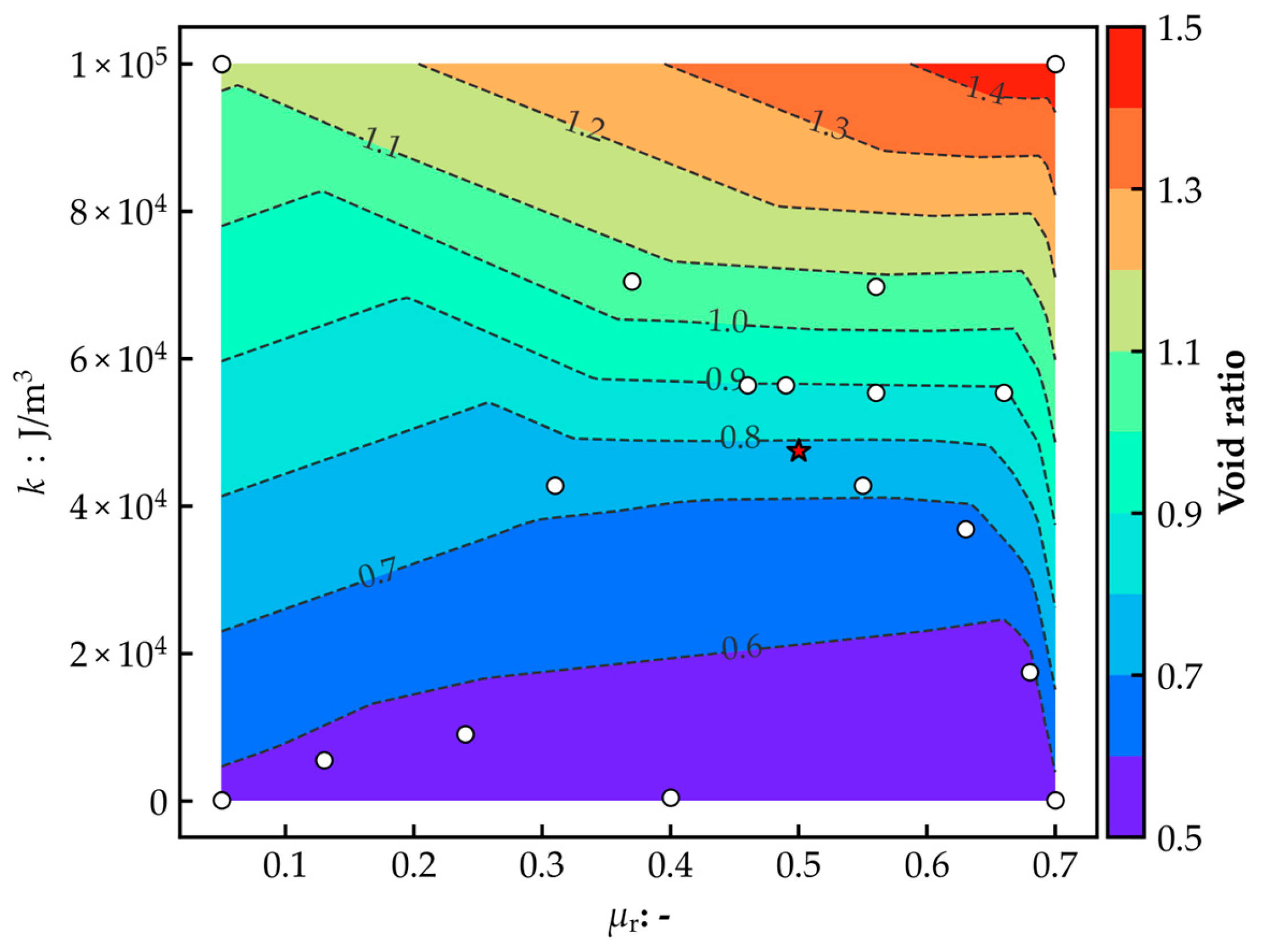
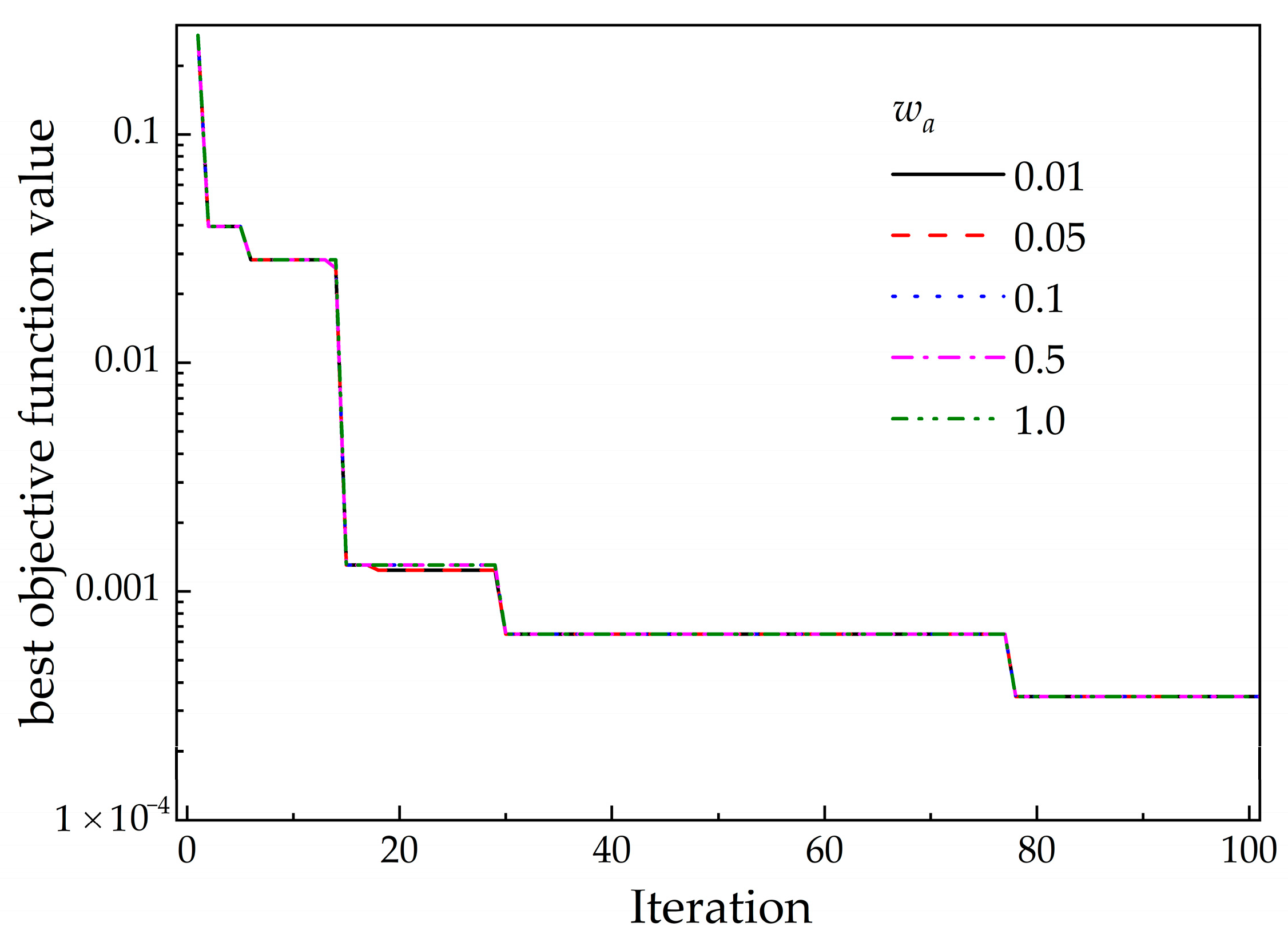
3.1. Optimization Results
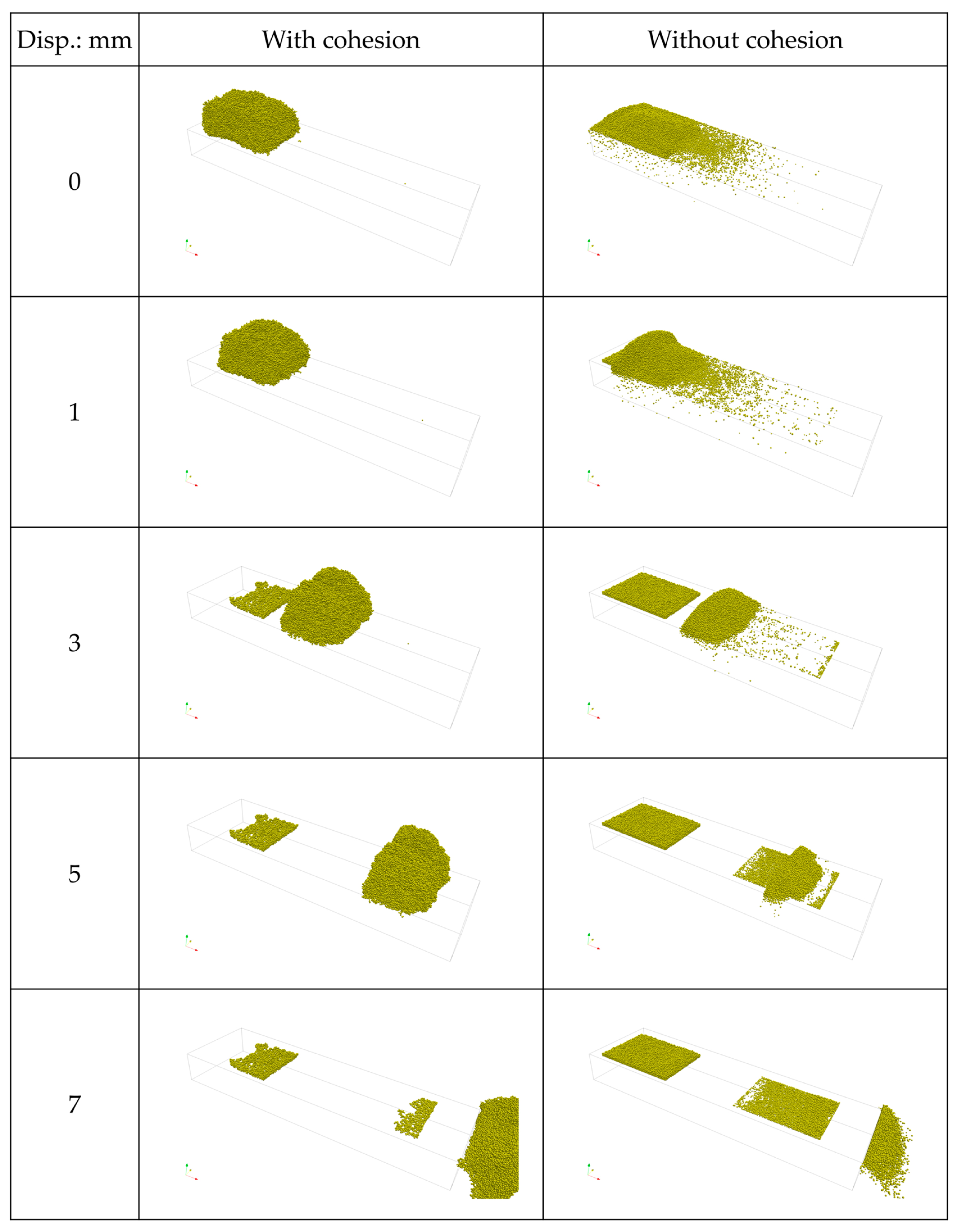
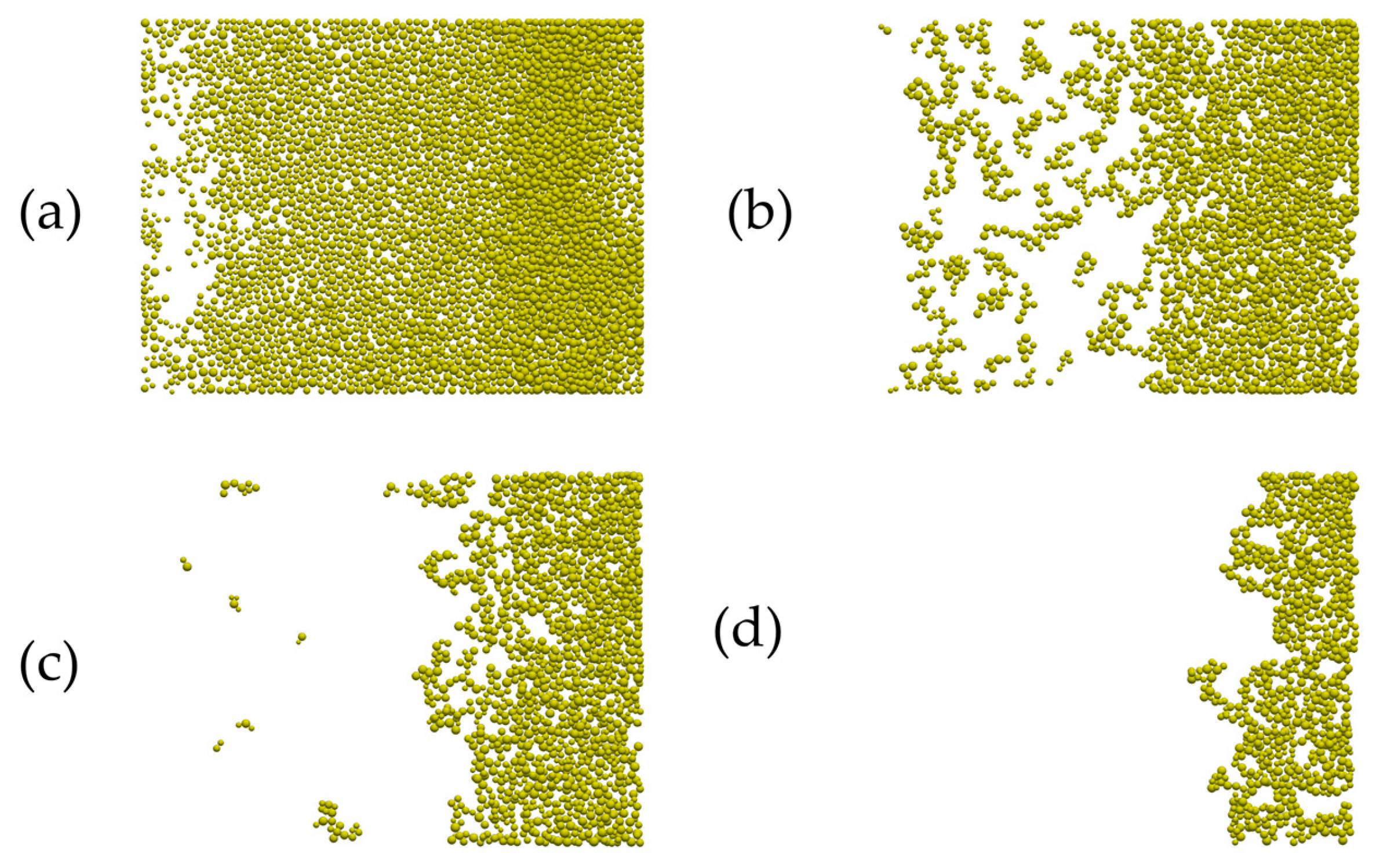
3.2. Powder Spreading Simulation Using the Parameters Estimated
4. Discussions
4.1. Scaling
4.2. Difference in Particle-Scale Dynamics
5. Conclusions
- A sequential optimization process was conducted utilizing Bayesian optimization. Although the optimal parameter set was not directly identified within twelve trials, several parameter sets close to the optimum were obtained as early as the fifth trial.
- Proposing the next candidate parameter sets based on the user’s judgment rather than relying solely on Gaussian process regression resulted in the successful attainment of a parameter set consistent with the experimental values.
- The parameter set identified for reproducing consolidation, in which inter-particle normal forces were dominant, was found to be incapable of reproducing the powder bed formation.
- This inconsistency may be caused by two main aspects: (1) the scaling law (the ratio of Young’s modulus to consolidation stress) between the experiments and DEM does not match and (2) there is a difference between the particle-scale dynamics between consolidation and direct shear in powder spreading.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PBF-LM | Powder bed fusion laser melting |
| BO | Bayesian optimization |
| DEM | Discrete element method |
| HX | Hastelloy X |
| SJKR | Simplified Johnson–Kendall–Roberts |
| HITL | Human in the loop |
References
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Seede, R.; Shoukr, D.; Zhang, B.; Whitt, A.; Gibbons, S.; Flater, P.; Elwany, A.; Arroyave, R.; Karaman, I. An ultra-high strength martensitic steel fabricated using selective laser melting additive manufacturing: Densification, microstructure, and mechanical properties. Acta Mater. 2020, 186, 199–214. [Google Scholar] [CrossRef]
- Fürstenau, J.-P.; Wessels, H.; Weißenfels, C.; Wriggers, P. Generating virtual process maps of slm using powder-scale sph simulations. Comput. Part. Mech. 2020, 7, 655–677. [Google Scholar] [CrossRef]
- Grange, D.; Queva, A.; Guillemot, G.; Bellet, M.; Bartout, J.D.; Colin, C. Effect of processing parameters during the laser beam melting of inconel 738: Comparison between simulated and experimental melt pool shape. J. Mater. Process. Technol. 2021, 289, 116897. [Google Scholar] [CrossRef]
- Alphonso, W.; Baier, M.; Carmignato, S.; Hattel, J.; Bayat, M. On the possibility of doing reduced order, thermo-fluid modelling of laser pow- der bed fusion (l-pbf)—Assessment of the importance of recoil pressure and surface tension. J. Manuf. Process. 2023, 94, 564–577. [Google Scholar] [CrossRef]
- Katagiri, J.; Kusano, M.; Minamoto, S.; Kitano, H.; Daimaru, K.; Tsujii, M.; Watanabe, M. Melt pool shape evaluation by single-track experiments and finite-element thermal analysis: Balling and lack of fusion criteria for generating process window of inconel738lc. Materials 2023, 16, 1729. [Google Scholar] [CrossRef]
- Katagiri, J.; Nomoto, S.; Kusano, M.; Watanabe, M. Particle size effect on powder packing properties and molten pool dimensions in laser powder bed fusion simulation. J. Manuf. Mater. Process. 2024, 8, 71. [Google Scholar] [CrossRef]
- Masuda, H. Adhesion of powder particles. Denshi Shashin Gakkaishi (Electrophotogr.) 1997, 36, 169–174. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete element model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Li, T.; Peng, Y.; Zhu, Z.; Zou, S.; Yin, Z. Discrete Element Method Simulations of the Inter-Particle Contact Parameters for the Mono-Sized Iron Ore Particles. Materials 2017, 10, 520. [Google Scholar] [CrossRef]
- Yim, S.; Bian, H.; Aoyagi, K.; Yamanaka, K.; Chiba, A. Spreading behavior of Ti–48Al–2Cr–2Nb powders in powder bed fusion additive manufacturing process: Experimental and discrete element method study. Addit. Manuf. 2022, 49, 102489. [Google Scholar] [CrossRef]
- Geer, S.; Bernhardt-Barry, M.L.; Garboczi, E.J.; Whiting, J.; Donmez, A. A more efficient method for calibrating discrete element method parameters for simulations of metallic powder used in additive manufacturing. Granul. Matter 2018, 20, 77. [Google Scholar] [CrossRef]
- Lupo, M.; Ajabshir, S.Z.; Sofia, D.; Barletta, D.; Poletto, M. Discrete element method model calibration and validation for the spreading step of the powder bed fusion process to predict the quality of the layer surface. Particuology 2024, 94, 261–273. [Google Scholar] [CrossRef]
- Kitano, H.; Kusano, M.; Tsujii, M.; Yumoto, A.; Watanabe, M. Process parameter optimization framework for the selective laser melting of hastelloy x alloy considering defects and solidification crack occurrence. Crystals 2021, 11, 578. [Google Scholar] [CrossRef]
- Freeman, R. Measuring the flow properties of consolidated, conditioned and aerated powders—A comparative study using a powder rheometer and a rotational shear cell. Powder Technol. 2007, 174, 25–33. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, X.; Lu, H.; Gong, X. An investigation of the effect of particle size on the flow behavior of pulverized coal. Procedia Eng. 2015, 102, 698–713. [Google Scholar] [CrossRef]
- Koynov, S.; Duda, K.; Santos, P.A.D.L.; Goldfarb, D.J. Comparative evaluation of peschl and ft4 full-bed rotational shear cells for powder flow characterization. Powder Technol. 2025, 456, 120810. [Google Scholar] [CrossRef]
- DCS Computing GmbH. Liggghts-Public Documentation, Version 3.x. 2025. Available online: https://www.cfdem.com/media/DEM/docu/Manual.html (accessed on 15 August 2025).
- Haynes International. Hastelloy-X. 2025. Available online: https://haynesintl.com/en/alloys/alloy-portfolio/high-temperature-alloys/hastelloy-x/#physical-properties (accessed on 15 August 2025).
- The GpyOpt Authors. Gpyopt: A Bayesian Optimization Framework in Python. 2016. Available online: http://github.com/SheffieldML/GPyOpt (accessed on 15 August 2025).
- Kim, M.; Ding, Y.; Malcolm, P.; Speeckaert, J.; Siviy, C.J.; Walsh, C.J.; Kuindersma, S. Human-in-the-loop bayesian optimization of wearable device parameters. PLoS ONE 2017, 12, e0184054. [Google Scholar] [CrossRef]
- Sousa, J.; Sousa, A.; Brueckner, F.; Reis, L.P.; Reis, A. Hu-man-in-the-loop multi-objective bayesian optimization for directed energy deposition with in-situ monitoring. Robot. Comput.-Integr. Manuf. 2025, 92, 102892. [Google Scholar] [CrossRef]
- Kim, D.B.; Bajestani, M.S.; Lee, J.Y.; Shin, S.-J.; Kim, G.-Y.; Sajadieh, S.M.M.; Noh, S. Human-in-the-loop in smart manufacturing (h-sm): A review and perspective. J. Manuf. Syst. 2025, 82, 178–199. [Google Scholar] [CrossRef]
- Kikuchi, K.; Tanifuji, Y.; Zhou, W.; Nomura, N.; Kawasaki, A. Experimental characterization and computational simulation of powder bed for powder bed fusion additive manufacturing. Mater. Trans. 2022, 63, 931–938. [Google Scholar] [CrossRef]
- Okugawa, M.; Isono, Y.; Koizumi, Y.; Nakano, T. Raking process for powder bed fusion of ti–6al–4v alloy powder analyzed by discrete element method. Mater. Trans. 2023, 64, 37–43. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Contact law | Hertz–Mindlin (no history) |
| Density | 8220 kg/m3 |
| Young’s modulus | 5 × 106 Pa |
| Poisson’s ratio | 0.3 |
| Restitution coefficient | 0.4 |
| Particle–particle friction coefficient | 0.3 |
| Particle–wall friction coefficient | 0.3 |
| Time increment | 1 × 10−6 s |
| Gravity | 9.81 m/s2 |
| Neighbor list radius | 40 μm |
| Integrator | nve/sphere |
| Boundary condition | x: periodic, y: periodic, z: fixed |
| Wall consolidation stress | 0.9 kPa |
| Servo wall maximum velocity | 0.1 m/s |
| Wall servo control parameters (kp) | 0.1 |
| Parameter | Value |
|---|---|
| Acquisition (acquisition_type) | Expected improvement (EI) |
| Model type (model_type) | Gaussian process (GP) |
| Allowance of duplicate proposals (de_duplication) | True |
| Inclusion of noise in objective function (exact_feval) | False |
| Acquisition weight: wa (acquisition_weight) | 0.01–1.0 |
| Objective function | (eexp − eDEM)2 |
| Optimization type | Minimization |
| Initial cases (initial_design_num_data, X, Y) | 5 (0–1 to 0–5 in Table 3) |
| Range of k | 102–105 J/m3 |
| Range of μr | 0.05–0.7 |
| Number of iterations | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katagiri, J.; Kusano, M.; Watanabe, M. Bayesian Optimization-Based Parameter Identification for Discrete Element Method Simulation of Consolidation and Its Application to Powder Spreading Analysis. J. Manuf. Mater. Process. 2025, 9, 383. https://doi.org/10.3390/jmmp9120383
Katagiri J, Kusano M, Watanabe M. Bayesian Optimization-Based Parameter Identification for Discrete Element Method Simulation of Consolidation and Its Application to Powder Spreading Analysis. Journal of Manufacturing and Materials Processing. 2025; 9(12):383. https://doi.org/10.3390/jmmp9120383
Chicago/Turabian StyleKatagiri, Jun, Masahiro Kusano, and Makoto Watanabe. 2025. "Bayesian Optimization-Based Parameter Identification for Discrete Element Method Simulation of Consolidation and Its Application to Powder Spreading Analysis" Journal of Manufacturing and Materials Processing 9, no. 12: 383. https://doi.org/10.3390/jmmp9120383
APA StyleKatagiri, J., Kusano, M., & Watanabe, M. (2025). Bayesian Optimization-Based Parameter Identification for Discrete Element Method Simulation of Consolidation and Its Application to Powder Spreading Analysis. Journal of Manufacturing and Materials Processing, 9(12), 383. https://doi.org/10.3390/jmmp9120383






