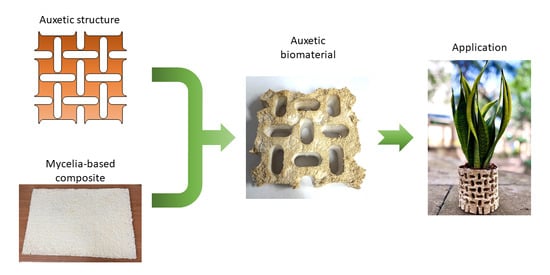
Auxetic Systems Fabricated Using Mycelia-Based Composites
Abstract
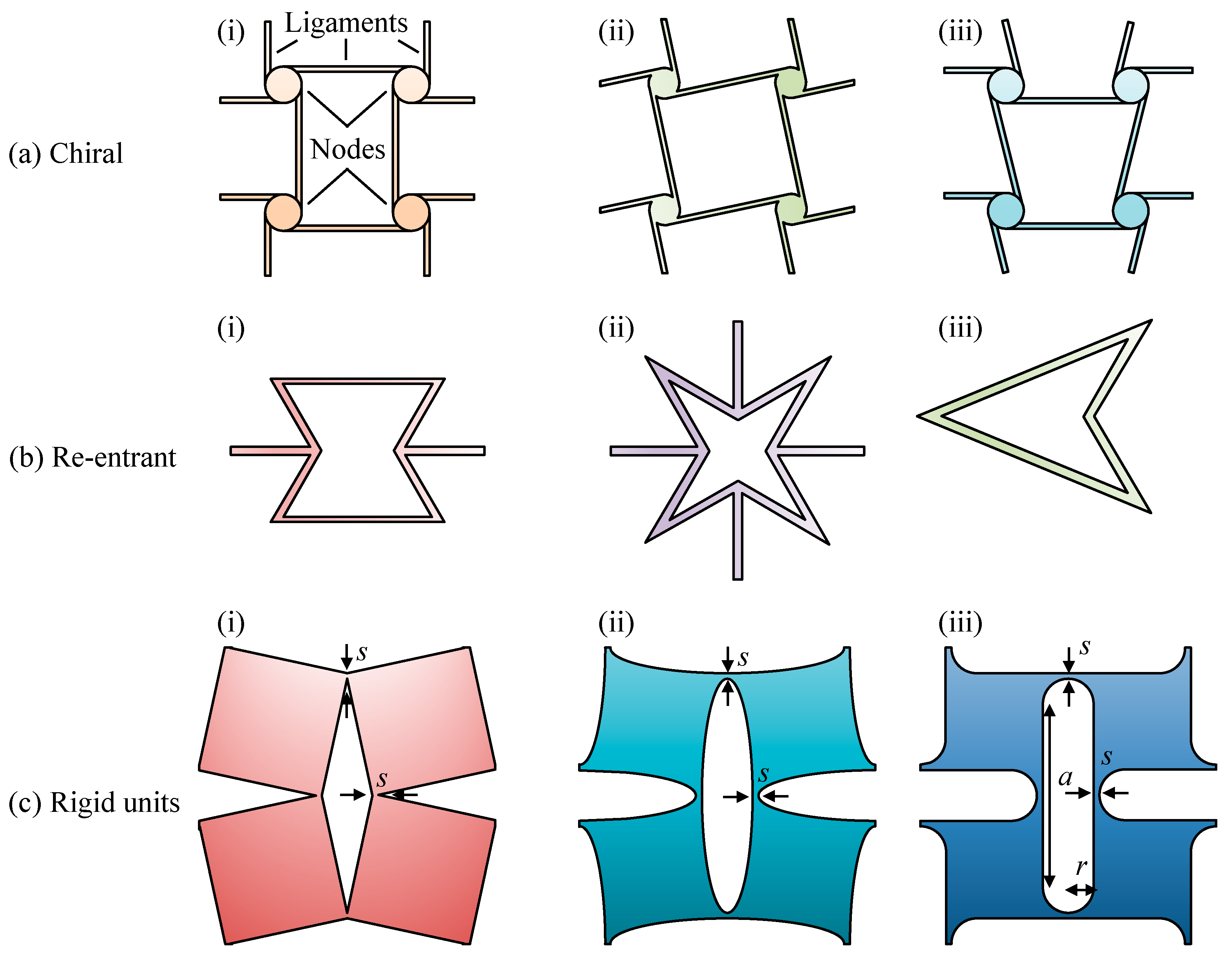
1. Introduction
2. Materials and Methods
2.1. Design and Fabrication of the Molds
2.2. Procedure Followed for Auxetic MBCs Grown on an In-House Substrate Mix
2.2.1. Substrate and Inoculum Preparation
2.2.2. Scaffoldings and Substrate Enhancements
2.2.3. Specimen Preparation
- Inclusion of S-pattern: Three grids were placed in the mold, positioned between layers of approximately 5 g, 10 g, 10 g, and 5 g of inoculated substrate.
- Inclusion of C-pattern: Only two grids were placed in the mold, positioned between 10 g layers of the inoculated substrate, as the C-pattern scaffolding was thicker than the S-pattern one.
- Inclusion of fiber reinforcements: Two layers of hay, each containing approximately 0.2 g, were distributed like a mesh between 10 g layers of the inoculated substrate.
| Samples Name | Substrate | Scaffoldings and Substrate Enhancements |
|---|---|---|
| A1 | S1—Fine granulation sawdust substrate | S-pattern |
| A2 | ||
| B1 | Hay | |
| B2 | ||
| C1 | C-pattern | |
| C2 | ||
| D1 | S2—High wheat bran substrate | S-pattern |
| D2 | ||
| E1 | S3—High gypsum substrate | |
| E2 | ||
| F1 | S4—High wheat bran and gypsum substrate | |
| F2 | ||
| G1 | S5—Mixed granulation substrate | |
| G2 |
2.3. Procedures Using Subtractive Manufacturing on Ready-Made Mycelia Panels
2.4. Mechanical Tests in Compression
3. Results and Discussion
3.1. Qualitative Assessment of the Samples
3.1.1. Samples Produced Using the In-House Mixes
3.1.2. Samples Produced Using Subtractive Manufacturing
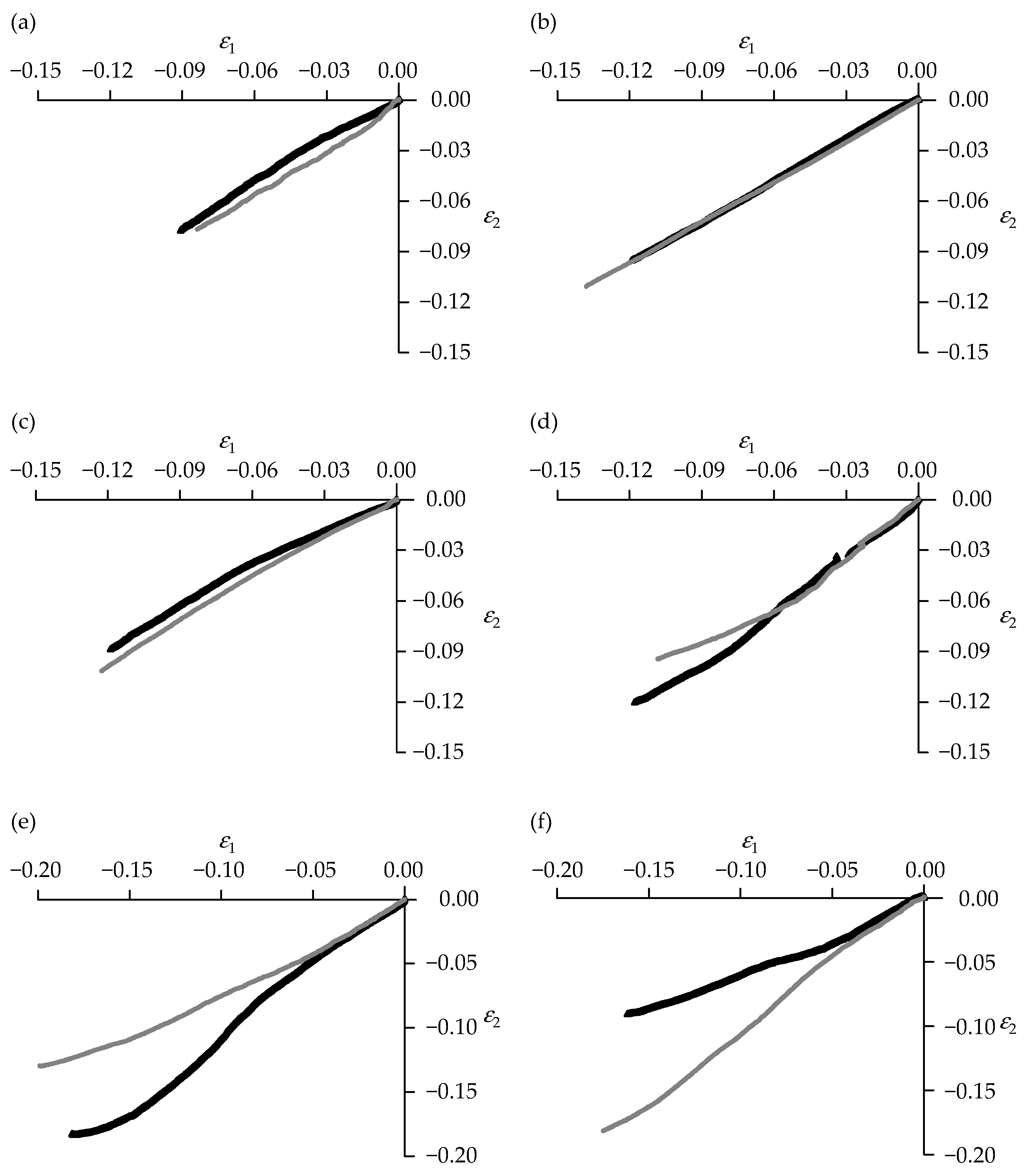
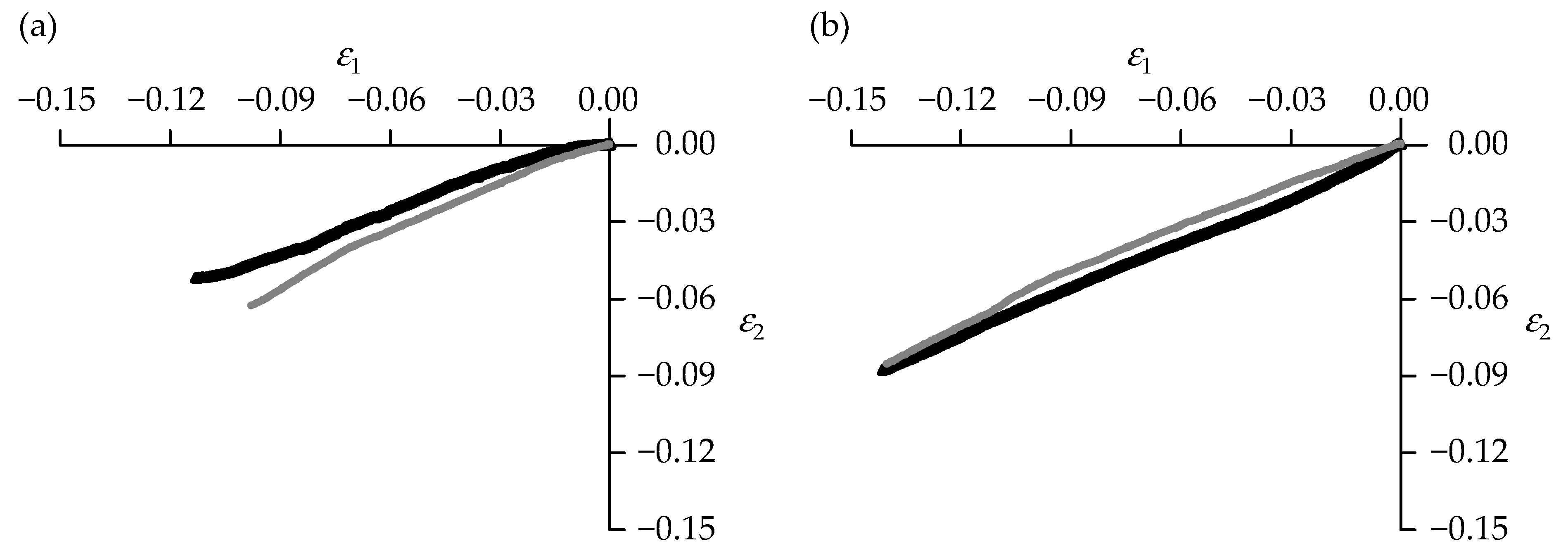
3.2. Mechanical Properties Under Compression
3.2.1. Samples Produced Using the In-House Mixes
3.2.2. Samples Produced Using Subtractive Manufacturing
3.2.3. Further Considerations
4. Conclusions
- -
- Auxetic biocomposites can effectively be manufactured.
- -
- The specimens tested exhibit a negative Poisson’s ratio that can be close to −1 under compression, the theoretical value for the ideal rotating squares model.
- -
- The samples can show a constant Poisson’s ratio over relatively large compressive strains.
- -
- The prototypes can recover to their original shape after the loading is removed.
- -
- Various enhancements can be used to improve the cohesion and elastic properties of the composites, including the use of finer granulation sawdust, scaffoldings, fiber reinforcements in the form of hay, and increased nutrients.
- -
- Production of auxetic biomaterials through direct growth appears to be more viable than using subtractive manufacturing.
- -
- Specimens grown using finer granulation sawdust and relatively thin scaffolds seemed to provide better results.
- -
- It is possible to grow mycelia-based composites in molds that have complex shapes.
- -
- The possibility of creating an auxetic pot made of mycelia-based composites.
- -
- Cohesion of the biomaterial can easily lead to its breakup under mechanical loading.
- -
- The use of relatively thick scaffolds prevents proper bonding of the mycelia across them.
- -
- The growth time of the fungi is relatively long, limiting the production rates and requiring extensive storage.
- -
- The use of finer sawdust requires good-quality hydration methodologies.
- -
- Further studies are required to determine the best substrate and enhancements leading to optimal cohesion and mechanical properties of the auxetic biomaterials.
- -
- Determine the extent of colonization of the substrate by the mycelia.
- -
- Optimize the design of the scaffolds.
- -
- Quantitatively assess the efficacy of each enhancement used.
- -
- Enhancing the cohesion of the substrate.
- -
- Investigate how substrate composition and enhancements affect the elastic behavior and Young’s modulus of the auxetic biomaterials.
- -
- Derive methodologies for the fabrication of large-sized auxetic biomaterials on a large scale, having consistent mechanical properties.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lenkiewicz, Z.; Bernardes, F.; Halpaap, A.; Louzada, L.; Ramola, A.; Filho, C.S.; Souza, H.H.S.; Smith, J.; Ternald, D.; Wilson, D. Global Waste Management Outlook 2024; The United Nations Environment Programme (UNEP): Nairobi, Kenya; The International Solid Waste Association (ISWA): Rotterdam, The Netherlands, 2024; p. 116. [Google Scholar]
- Ferdous, W.; Manalo, A.; Siddique, R.; Mendis, P.; Zhuge, Y.; Wong, H.S.; Lokuge, W.; Aravinthan, T.; Schubel, P. Recycling of Landfill Wastes (Tyres, Plastics and Glass) in Construction—A Review on Global Waste Generation, Performance, Application and Future Opportunities. Resour. Conserv. Recycl. 2021, 173, 105745. [Google Scholar] [CrossRef]
- Wünsch, C.; Tsybina, A. Municipal Solid Waste Management in Russia: Potentials of Climate Change Mitigation. Int. J. Environ. Sci. Technol. 2022, 19, 27–42. [Google Scholar] [CrossRef]
- Abubakar, I.R.; Maniruzzaman, K.M.; Dano, U.L.; AlShihri, F.S.; AlShammari, M.S.; Ahmed, S.M.S.; Al-Gehlani, W.A.G.; Alrawaf, T.I. Environmental Sustainability Impacts of Solid Waste Management Practices in the Global South. Int. J. Environ. Res. Public Health 2022, 19, 12717. [Google Scholar] [CrossRef] [PubMed]
- Kaza, S.; Yao, L.; Bhada-Tata, P.; Van Woerden, F. What a Waste 2.0: A Global Snapshot of Solid Waste Management to 2050; World Bank Publications: Washington, DC, USA, 2018. [Google Scholar]
- Wilts, H. Germany on the Road to a Circular Economy? Friedrich-Ebert-Stiftung, Division for Economic and Social Policy: Bonn, Germany, 2016. [Google Scholar]
- Fehrer, J.A.; Kemper, J.A.; Baker, J.J. Shaping Circular Service Ecosystems. J. Serv. Res. 2024, 27, 49–68. [Google Scholar] [CrossRef]
- Halkos, G.E.; Petrau, K.N. Moving Towards a Circular Economy: Rethinking Waste Management Practices. J. Econ. Soc. Thought 2016, 3, 220–240. [Google Scholar]
- Lee, P.; Sims, E.; Bertham, O.; Symington, H.; Bell, N.; Pfaltzgraff, L.; Sjögren, P.; Wilts, H.; O’Brien, M.; Benke, J. Towards a Circular Economy: Waste Management in the EU 2017; European Union: Brussels, Belgium, 2017. [Google Scholar]
- Nguyen, P.Q.; Courchesne, N.-M.D.; Duraj-Thatte, A.; Praveschotinunt, P.; Joshi, N.S. Engineered Living Materials: Prospects and Challenges for Using Biological Systems to Direct the Assembly of Smart Materials. Adv. Mater. 2018, 30, 1704847. [Google Scholar] [CrossRef]
- Aiduang, W.; Chanthaluck, A.; Kumla, J.; Jatuwong, K.; Srinuanpan, S.; Waroonkun, T.; Oranratmanee, R.; Lumyong, S.; Suwannarach, N. Amazing Fungi for Eco-Friendly Composite Materials: A Comprehensive Review. J. Fungi 2022, 8, 842. [Google Scholar] [CrossRef]
- Etinosa, O.P. Design and Testing of Mycelium Biocomposite. Master’s Thesis, African University of Science and Technology, Galadima, Nigeria, 2019. [Google Scholar]
- Alemu, D.; Tafesse, M.; Mondal, A.K. Mycelium-Based Composite: The Future Sustainable Biomaterial. Int. J. Biomater. 2022, 2022, 8401528. [Google Scholar] [CrossRef]
- Zhao, L.; Schaefer, D.; Xu, H.; Modi, S.J.; LaCourse, W.R.; Marten, M.R. Elastic Properties of the Cell Wall of Aspergillus Nidulans Studied with Atomic Force Microscopy. Biotechnol. Prog. 2005, 21, 292–299. [Google Scholar] [CrossRef]
- Islam, M.R.; Tudryn, G.; Bucinell, R.; Schadler, L.; Picu, R.C. Morphology and Mechanics of Fungal Mycelium. Sci. Rep. 2017, 7, 13070. [Google Scholar] [CrossRef]
- Elsacker, E.; Zhang, M.; Dade-Robertson, M. Fungal Engineered Living Materials: The Viability of Pure Mycelium Materials with Self-Healing Functionalities. Adv. Funct. Mater. 2023, 33, 2301875. [Google Scholar] [CrossRef]
- Elsacker, E.; Vandelook, S.; Brancart, J.; Peeters, E.; De Laet, L. Mechanical, Physical and Chemical Characterisation of Mycelium-Based Composites with Different Types of Lignocellulosic Substrates. PLoS ONE 2019, 14, e0213954. [Google Scholar] [CrossRef]
- Appels, F.V.W.; Camere, S.; Montalti, M.; Karana, E.; Jansen, K.M.B.; Dijksterhuis, J.; Krijgsheld, P.; Wösten, H.A.B. Fabrication Factors Influencing Mechanical, Moisture- and Water-Related Properties of Mycelium-Based Composites. Mater. Des. 2019, 161, 64–71. [Google Scholar] [CrossRef]
- Zimele, Z.; Irbe, I.; Grinins, J.; Bikovens, O.; Verovkins, A.; Bajare, D. Novel Mycelium-Based Biocomposites (MBB) as Building Materials. J. Renew. Mater. 2020, 8, 1067–1076. [Google Scholar] [CrossRef]
- Aiduang, W.; Kumla, J.; Srinuanpan, S.; Thamjaree, W.; Lumyong, S.; Suwannarach, N. Mechanical, Physical, and Chemical Properties of Mycelium-Based Composites Produced from Various Lignocellulosic Residues and Fungal Species. J. Fungi 2022, 8, 1125. [Google Scholar] [CrossRef]
- Jones, M.; Mautner, A.; Luenco, S.; Bismarck, A.; John, S. Engineered Mycelium Composite Construction Materials from Fungal Biorefineries: A Critical Review. Mater. Des. 2020, 187, 108397. [Google Scholar] [CrossRef]
- Alaneme, K.K.; Anaele, J.U.; Oke, T.M.; Kareem, S.A.; Adediran, M.; Ajibuwa, O.A.; Anabaranze, Y.O. Mycelium Based Composites: A Review of Their Bio-Fabrication Procedures, Material Properties and Potential for Green Building and Construction Applications. Alex. Eng. J. 2023, 83, 234–250. [Google Scholar] [CrossRef]
- Scarpa, F.; Bullough, W.A.; Lumley, P. Trends in Acoustic Properties of Iron Particle Seeded Auxetic Polyurethane Foam. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 241–244. [Google Scholar] [CrossRef]
- Scarpa, F.; Yates, J.R.; Ciffo, L.G.; Patsias, S. Dynamic Crushing of Auxetic Open-Cell Polyurethane Foam. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 1153–1156. [Google Scholar] [CrossRef]
- Scarpa, F.; Ciffo, L.G.; Yates, J.R. Dynamic Properties of High Structural Integrity Auxetic Open Cell Foam. Smart Mater. Struct. 2004, 13, 49. [Google Scholar] [CrossRef]
- Evans, K.E. Auxetic Polymers: A New Range of Materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Qi, C.; Remennikov, A.; Pei, L.-Z.; Yang, S.; Yu, Z.-H.; Ngo, T.D. Impact and Close-in Blast Response of Auxetic Honeycomb-Cored Sandwich Panels: Experimental Tests and Numerical Simulations. Compos. Struct. 2017, 180, 161–178. [Google Scholar] [CrossRef]
- Lakes, R.S.; Elms, K. Indentability of Conventional and Negative Poisson’s Ratio Foams. J. Compos. Mater. 1993, 27, 1193–1202. [Google Scholar] [CrossRef]
- Chen, C.P.; Lakes, R.S. Micromechanical Analysis of Dynamic Behavior of Conventional and Negative Poisson’s Ratio Foams. J. Eng. Mater. Technol. 1996, 118, 285–288. [Google Scholar] [CrossRef]
- Scarpa, F.; Tomlinson, G. Theoretical Characteristics of the Vibration of Sandwich Plates with In-Plane Negative Poisson’s Ratio Values. J. Sound Vib. 2000, 230, 45–67. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L. Auxetic Materials. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 565–575. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Auxetic, Partially Auxetic, and Nonauxetic Behaviour in 2D Crystals of Hard Cyclic Tetramers. Phys. Status Solidi (RRL)—Rapid Res. Lett. 2020, 14, 2000198. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W.; Tretiakov, K.V.; Smardzewski, J.; Scarpa, F.; Piglowski, P.M.; Kowalik, M.; Imre, A.R.; Bilski, M. Auxetic Properties of a f.c.c. Crystal of Hard Spheres with an Array of [001]-Nanochannels Filled by Hard Spheres of Another Diameter. Phys. Status Solidi (B) 2019, 256, 1800611. [Google Scholar] [CrossRef]
- Pigłowski, P.M.; Wojciechowski, K.W.; Tretiakov, K.V. Partial Auxeticity Induced by Nanoslits in the Yukawa Crystal. Phys. Status Solidi (RRL)—Rapid Res. Lett. 2016, 10, 566–569. [Google Scholar] [CrossRef]
- Kolat, P.; Maruszewski, B.M.; Wojciechowski, K.W. Solitary Waves in Auxetic Plates. J. Non-Cryst. Solids 2010, 356, 2001–2009. [Google Scholar] [CrossRef]
- Kołat, P.; Maruszewski, B.T.; Tretiakov, K.V.; Wojciechowski, K.W. Solitary Waves in Auxetic Rods. Phys. Status Solidi (B) 2011, 248, 148–157. [Google Scholar] [CrossRef]
- Ho, V.H.; Ho, D.T.; Kwon, S.-Y.; Kim, S.Y. Negative Poisson’s Ratio in Periodic Porous Graphene Structures. Phys. Status Solidi (B) 2016, 253, 1303–1309. [Google Scholar] [CrossRef]
- Hoover, W.G.; Hoover, C.G. Searching for Auxetics with DYNA3D and ParaDyn. Phys. Status Solidi (B) 2005, 242, 585–594. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Non-Chiral, Molecular Model of Negative Poisson Ratio in Two Dimensions. J. Phys. A Math. Gen. 2003, 36, 11765. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Piglowski, P.M.; Hyzorek, K.; Wojciechowski, K.W. Enhanced Auxeticity in Yukawa Systems Due to Introduction of Nanochannels in [001]-Direction. Smart Mater. Struct. 2016, 25, 054007. [Google Scholar] [CrossRef]
- Bui Dinh, T.; Long, V.C.; Xuan, K.D.; Wojciechowski, K.W. Computer Simulation of Solitary Waves in a Common or Auxetic Elastic Rod with Both Quadratic and Cubic Nonlinearities. Phys. Status Solidi (B) 2012, 249, 1386–1392. [Google Scholar] [CrossRef]
- Bui Dinh, T.; Cao Long, V.; Wojciechowski, K.W. Solitary Waves in Auxetic Rods with Quadratic Nonlinearity: Exact Analytical Solutions and Numerical Simulations. Phys. Status Solidi (B) 2015, 252, 1587–1594. [Google Scholar] [CrossRef]
- Ho, D.T.; Nguyen, C.T.; Kwon, S.-Y.; Kim, S.Y. Auxeticity in Metals and Periodic Metallic Porous Structures Induced by Elastic Instabilities. Phys. Status Solidi (B) 2019, 256, 1800122. [Google Scholar] [CrossRef]
- Overvelde, J.T.B.; Shan, S.; Bertoldi, K. Compaction Through Buckling in 2D Periodic, Soft and Porous Structures: Effect of Pore Shape. Adv. Mater. 2012, 24, 2337–2342. [Google Scholar] [CrossRef] [PubMed]
- Bertoldi, K.; Reis, P.M.; Willshaw, S.; Mullin, T. Negative Poisson’s Ratio Behavior Induced by an Elastic Instability. Adv. Mater. 2010, 22, 361–366. [Google Scholar] [CrossRef]
- Grima, J.N.; Mizzi, L.; Azzopardi, K.M.; Gatt, R. Auxetic Perforated Mechanical Metamaterials with Randomly Oriented Cuts. Adv. Mater. 2016, 28, 385–389. [Google Scholar] [CrossRef]
- Poźniak, A.A.; Wojciechowski, K.W.; Grima, J.N.; Mizzi, L. Planar Auxeticity from Elliptic Inclusions. Compos. Part B Eng. 2016, 94, 379–388. [Google Scholar] [CrossRef]
- Galea, R.; Farrugia, P.-S.; Dudek, K.K.; Attard, D.; Grima, J.N.; Gatt, R. A Novel Design Method to Produce 3D Auxetic Metamaterials with Continuous Pores Exemplified through 3D Rotating Auxetic Systems. Mater. Des. 2023, 226, 111596. [Google Scholar] [CrossRef]
- Wojciechowski, K. Constant Thermodynamic Tension Monte Carlo Studies of Elastic Properties of a Two-Dimensional System of Hard Cyclic Hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Lakes, R. Deformation Mechanisms in Negative Poisson’s Ratio Materials: Structural Aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Gatt, R.; Attard, D.; Farrugia, P.-S.; Azzopardi, K.M.; Mizzi, L.; Brincat, J.-P.; Grima, J.N. A Realistic Generic Model for Anti-Tetrachiral Systems. Phys. Status Solidi (B) 2013, 250, 2012–2019. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Attard, D.; Evans, K.E.; Gatt, R.; Grima, J.N.; Miller, W.; Ravirala, N.; Smith, C.W.; Zied, K. Elastic Constants of 3-, 4- and 6-Connected Chiral and Anti-Chiral Honeycombs Subject to Uniaxial in-Plane Loading. Compos. Sci. Technol. 2010, 70, 1042–1048. [Google Scholar] [CrossRef]
- Sigmund, O.; Torquato, S.; Aksay, I. On the Design of 1-3 Piezocomposites Using Topology Optimization. J. Mater. Res. 1998, 13, 1038–1048. [Google Scholar] [CrossRef]
- Wojciechowski, K. Two-Dimensional Isotropic System with a Negative Poisson Ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Masters, I.G.; Evans, K.E. Models for the Elastic Deformation of Honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A.; Christian, F.R. Auxetic Two-Dimensional Polymer Networks. An Example of Tailoring Geometry for Specific Mechanical Properties. J. Chem. Soc. Faraday Trans. 1995, 91, 2671–2680. [Google Scholar] [CrossRef]
- Gibson LJ, A.M. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Larsen, U.D.; Signund, O.; Bouwsta, S. Design and Fabrication of Compliant Micromechanisms and Structures with Negative Poisson’s Ratio. J. Microelectromech. Syst. 1997, 6, 99–106. [Google Scholar] [CrossRef]
- Farrugia, P.-S.; Gatt, R.; De Vrieze, S.; Mellos, C.; Grima, J.N. Edge Effects of a Hexagonal Honeycomb on the Poisson’s Ratio and Young’s Modulus. Phys. Status Solidi (B) 2020, 257, 1900511. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic Behavior from Rotating Squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.-S.; Gatt, R.; Attard, D. On the Auxetic Properties of Rotating Rhombi and Parallelograms: A Preliminary Investigation. Phys. Status Solidi (B) 2008, 245, 521–529. [Google Scholar] [CrossRef]
- Sigmund, O. Tailoring Materials with Prescribed Elastic Properties. Mech. Mater. 1995, 20, 351–368. [Google Scholar] [CrossRef]
- Ishibashi, Y.; Iwata, M. A Microscopic Model of a Negative Poisson’s Ratio in Some Crystals. J. Phys. Soc. Jpn. 2000, 69, 2702–2703. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P. On the Properties of Auxetic Meta-Tetrachiral Structures. Phys. Status Solidi (B) 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The Mechanics of Two-Dimensional Cellular Materials. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Attenborough, F.R. The Modelling of Network Polymers. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 1997. [Google Scholar]
- Theocaris, P.S.; Stavroulakis, G.E.; Panagiotopoulos, P.D. Negative Poisson’s Ratios in Composites with Star-Shaped Inclusions: A Numerical Homogenization Approach. Arch. Appl. Mech. 1997, 67, 274–286. [Google Scholar] [CrossRef]
- Taylor, M.; Francesconi, L.; Gerendás, M.; Shanian, A.; Carson, C.; Bertoldi, K. Low Porosity Metallic Periodic Structures with Negative Poisson’s Ratio. Adv. Mater. 2014, 26, 2365–2370. [Google Scholar] [CrossRef]
- Fallah, A.S.; Mehreganian, N. Computational Optimisation of the Cassini Oval Aperture Auxetic Metamaterial. Results Eng. 2025, 28, 107559. [Google Scholar] [CrossRef]
- Galea Mifsud, R. An Investigation of Smart, Inclusion-Based Mechanical Metamaterials. Doctoral Dissertation, University of Malta, Msida, Malta, 2023. [Google Scholar]
- Grima, J.N.; Farrugia, P.S.; Caruana, C.; Gatt, R.; Attard, D. Auxetic Behaviour from Stretching Connected Squares. J. Mater. Sci. 2008, 43, 5962–5971. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R. Perforated Sheets Exhibiting Negative Poisson’s Ratios. Adv. Eng. Mater. 2010, 12, 460–464. [Google Scholar] [CrossRef]
- Elsacker, E.; Vandelook, S.; Wylick, A.V.; Ruytinx, J.; Laet, L.D.; Peeters, E. A Comprehensive Framework for the Production of Mycelium-Based Lignocellulosic Composites. Sci. Total Environ. 2020, 725, 138431. [Google Scholar] [CrossRef]
- Stamets, P. Growing Gourmet and Medicinal Mushrooms, 3rd ed.; Ten Speed Press: New York, NY, USA, 2000. [Google Scholar]
- Stamets, P.; Chilton, J.S. The Mushroom Cultivator: A Practical Guide to Growing Mushrooms at Home; Agariikon Press: Washington, DC, USA, 1983. [Google Scholar]
- Stamets, P. Mycelium Running: How Mushrooms Can Help Save the World; Ten Speed Press: Berkeley, CA, USA, 2005. [Google Scholar]
- Lingam, D.; Narayan, S.; Mamun, K.; Charan, D. Engineered Mycelium-Based Composite Materials: Comprehensive Study of Various Properties and Applications. Constr. Build. Mater. 2023, 391, 131841. [Google Scholar] [CrossRef]
- Cai, J.; Han, J.; Ge, F.; Lin, Y.; Pan, J.; Ren, A. Development of Impact-Resistant Mycelium-Based Composites (MBCs) with Agricultural Waste Straws. Constr. Build. Mater. 2023, 389, 131730. [Google Scholar] [CrossRef]
- Biby, S.R.; Surendran, V.; Kundanati, L. Mycelium Biocomposites from Agricultural and Paper Waste: Sustainable Alternative to Plastic Foam Based Secondary Packaging. Bioresour. Technol. Rep. 2025, 31, 102177. [Google Scholar] [CrossRef]
- Peng, L.; Yi, J.; Yang, X.; Xie, J.; Chen, C. Development and Characterization of Mycelium Bio-Composites by Utilization of Different Agricultural Residual Byproducts. J. Bioresour. Bioprod. 2023, 8, 78–89. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, S.; Poh, L.H.; Shao, Y.; Wang, Q. Enhanced Hexa-Missing Rib Auxetics for Achieving Targeted Constant NPR and in-Plane Isotropy at Finite Deformation. Smart Mater. Struct. 2020, 29, 045030. [Google Scholar] [CrossRef]
- Wan, H.; Ohtaki, H.; Kotosaka, S.; Hu, G. A Study of Negative Poisson’s Ratios in Auxetic Honeycombs Based on a Large Deflection Model. Eur. J. Mech.—A/Solids 2004, 23, 95–106. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.-P.; Poh, L.H. Auxetic Hexachiral Structures with Wavy Ligaments for Large Elasto-Plastic Deformation. Smart Mater. Struct. 2018, 27, 055001. [Google Scholar] [CrossRef]
- Caddock, B.D.; Evans, K.E. Microporous Materials with Negative Poisson’s Ratios. I. Microstructure and Mechanical Properties. J. Phys. D Appl. Phys. 1989, 22, 1877. [Google Scholar] [CrossRef]
- Gao, Q.; Tan, C.A.; Hulbert, G.; Wang, L. Geometrically Nonlinear Mechanical Properties of Auxetic Double-V Microstructures with Negative Poisson’s Ratio. Eur. J. Mech.—A/Solids 2020, 80, 103933. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Wojciechowski, K.W. The Influence of Large Deformations on Mechanical Properties of Sinusoidal Ligament Structures. Smart Mater. Struct. 2016, 25, 054002. [Google Scholar] [CrossRef]
- Schenk, M.; Guest, S.D.; McShane, G.J. Novel Stacked Folded Cores for Blast-Resistant Sandwich Beams. Int. J. Solids Struct. 2014, 51, 4196–4214. [Google Scholar] [CrossRef]
- Imbalzano, G.; Tran, P.; Ngo, T.D.; Lee, P.V.S. A Numerical Study of Auxetic Composite Panels under Blast Loadings. Compos. Struct. 2016, 135, 339–352. [Google Scholar] [CrossRef]
- Novak, N.; Starčevič, L.; Vesenjak, M.; Ren, Z. Blast Response Study of the Sandwich Composite Panels with 3D Chiral Auxetic Core. Compos. Struct. 2019, 210, 167–178. [Google Scholar] [CrossRef]

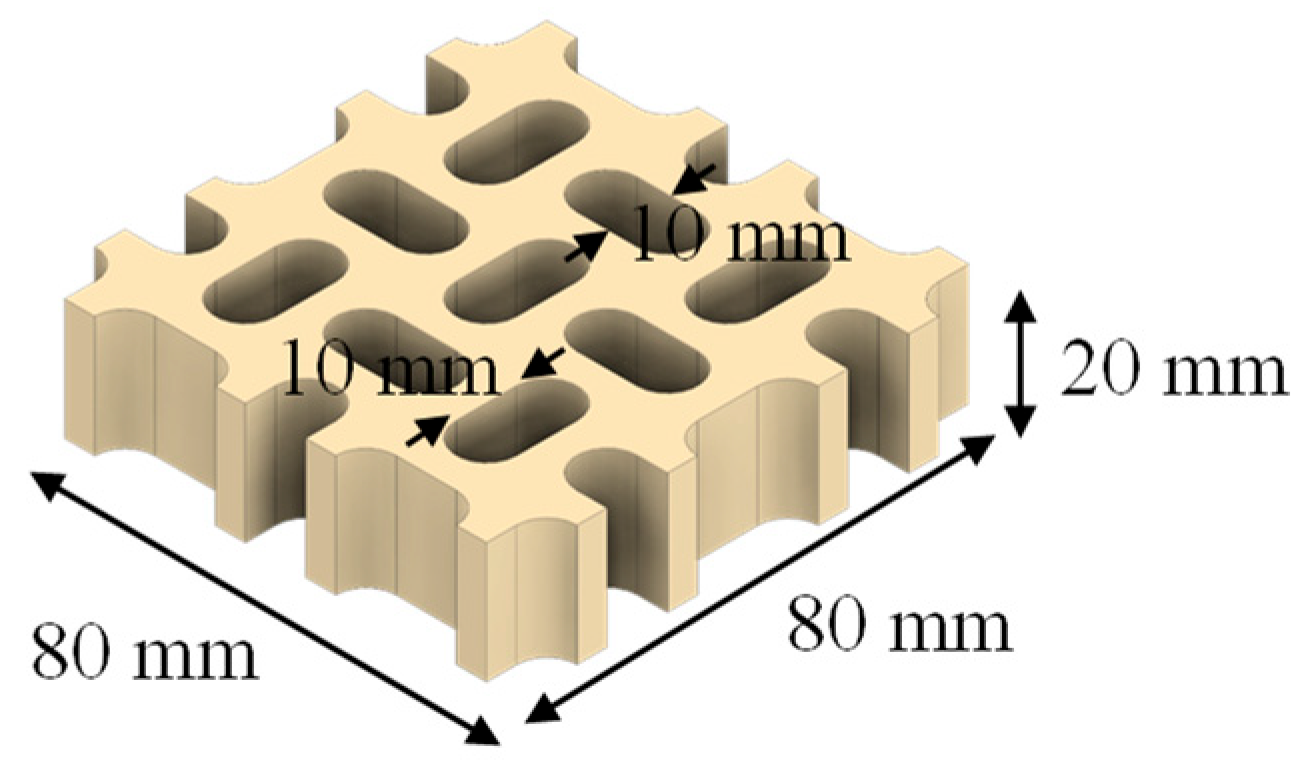
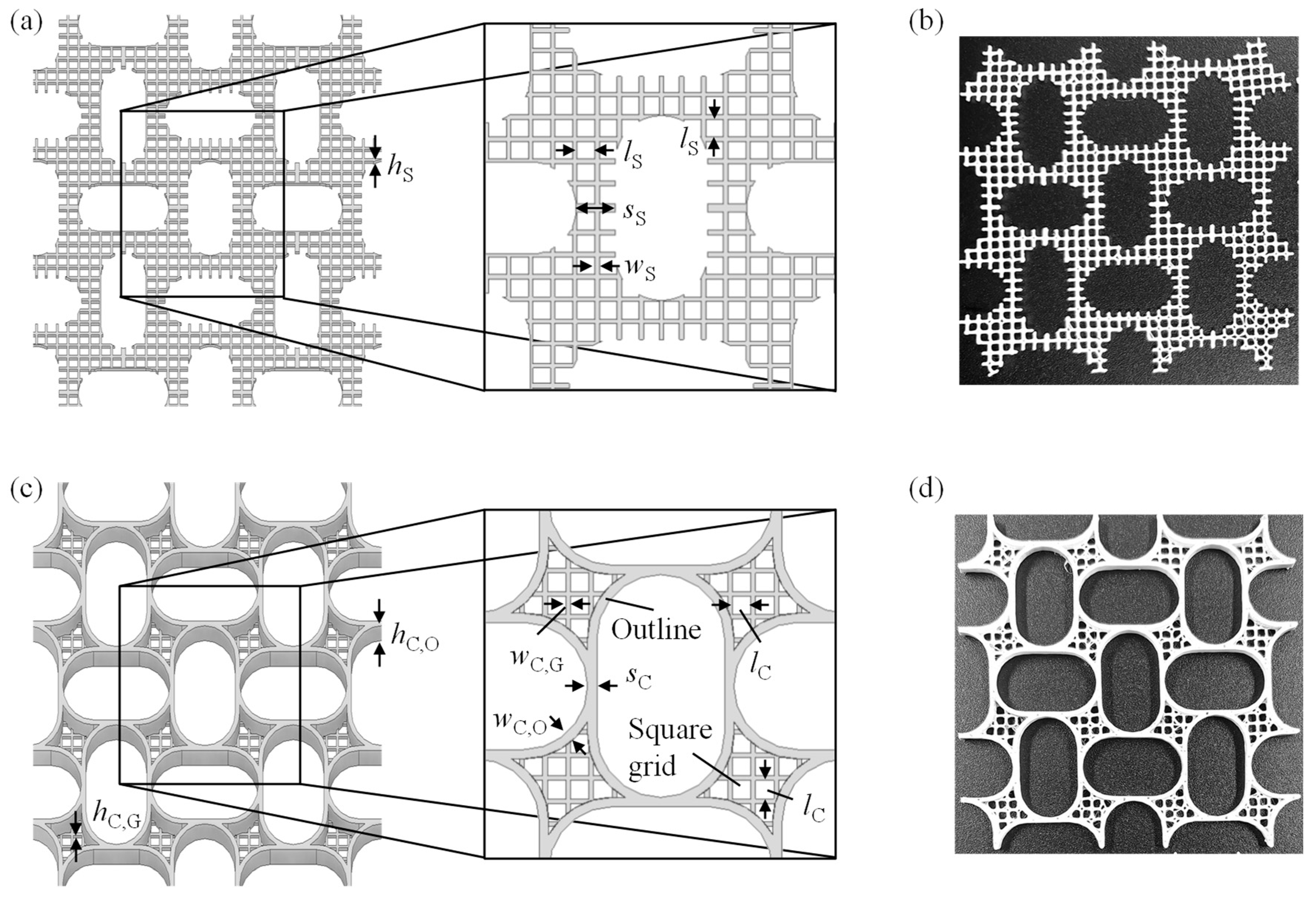







| Substrate Symbol and Name | Fine Sawdust (Particle Size < 180 μm)/g | Regular Sawdust (Particle Size < 710 μm)/g | Wheat Bran/g | Gypsum/g | Water/g |
|---|---|---|---|---|---|
| S1—Fine granulation sawdust substrate | 260.95 | - | 215.40 | 67.43 | 456.22 |
| S2—High wheat bran substrate | 126.35 | - | 350.00 | 67.43 | 456.22 |
| S3—High gypsum substrate | 248.37 | - | 215.41 | 80.00 | 456.22 |
| S4—High wheat bran and gypsum substrate | 113.78 | - | 350.00 | 80.00 | 456.22 |
| S5—Mixed granulation substrate | 130.47 | 130.47 | 215.41 | 67.43 | 456.22 |
| Samples Name | Poisson’s Ratio | Uncertainty | Pearson Correlation Coefficient |
|---|---|---|---|
| A1 | −0.876 | 0.001 | 0.9997 |
| A2 | −0.811 | 0.001 | 1.0000 |
| B1 * | BDL | n/a | n/a |
| B2 * | BDL | n/a | n/a |
| C1 | −0.758 | 0.003 | 0.9979 |
| C2 ** | BDL | n/a | n/a |
| D1 | −0.987 | 0.005 | 0.9947 |
| D2 | −0.885 | 0.003 | 0.9975 |
| E1 ** | BDL | n/a | n/a |
| E2 *** | BDL | n/a | n/a |
| F1 *** | BDL | n/a | n/a |
| F2 *** | BDL | n/a | n/a |
| G1 *** | BDL | n/a | n/a |
| G2 | −0.844 | 0.001 | 0.9996 |
| Samples | Poisson’s Ratio | Uncertainty | Pearson Correlation Coefficient |
|---|---|---|---|
| P1 | −0.563 | 0.002 | 0.9969 |
| P2 | −0.602 | 0.001 | 0.9993 |
| P3 | BDL | n/a | n/a |
| P4 | BDL | n/a | n/a |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cadinu, C.; Gatt, R.; Blundell, R.; Grima, J.N.; Farrugia, P.-S. Auxetic Systems Fabricated Using Mycelia-Based Composites. J. Manuf. Mater. Process. 2025, 9, 353. https://doi.org/10.3390/jmmp9110353
Cadinu C, Gatt R, Blundell R, Grima JN, Farrugia P-S. Auxetic Systems Fabricated Using Mycelia-Based Composites. Journal of Manufacturing and Materials Processing. 2025; 9(11):353. https://doi.org/10.3390/jmmp9110353
Chicago/Turabian StyleCadinu, Claudia, Ruben Gatt, Renald Blundell, Joseph N. Grima, and Pierre-Sandre Farrugia. 2025. "Auxetic Systems Fabricated Using Mycelia-Based Composites" Journal of Manufacturing and Materials Processing 9, no. 11: 353. https://doi.org/10.3390/jmmp9110353
APA StyleCadinu, C., Gatt, R., Blundell, R., Grima, J. N., & Farrugia, P.-S. (2025). Auxetic Systems Fabricated Using Mycelia-Based Composites. Journal of Manufacturing and Materials Processing, 9(11), 353. https://doi.org/10.3390/jmmp9110353