Multi-Scale Model of Mid-Frequency Errors in Semi-Rigid Tool Polishing of Diamond-Turned Electroless Nickel Mirror
Abstract
1. Introduction
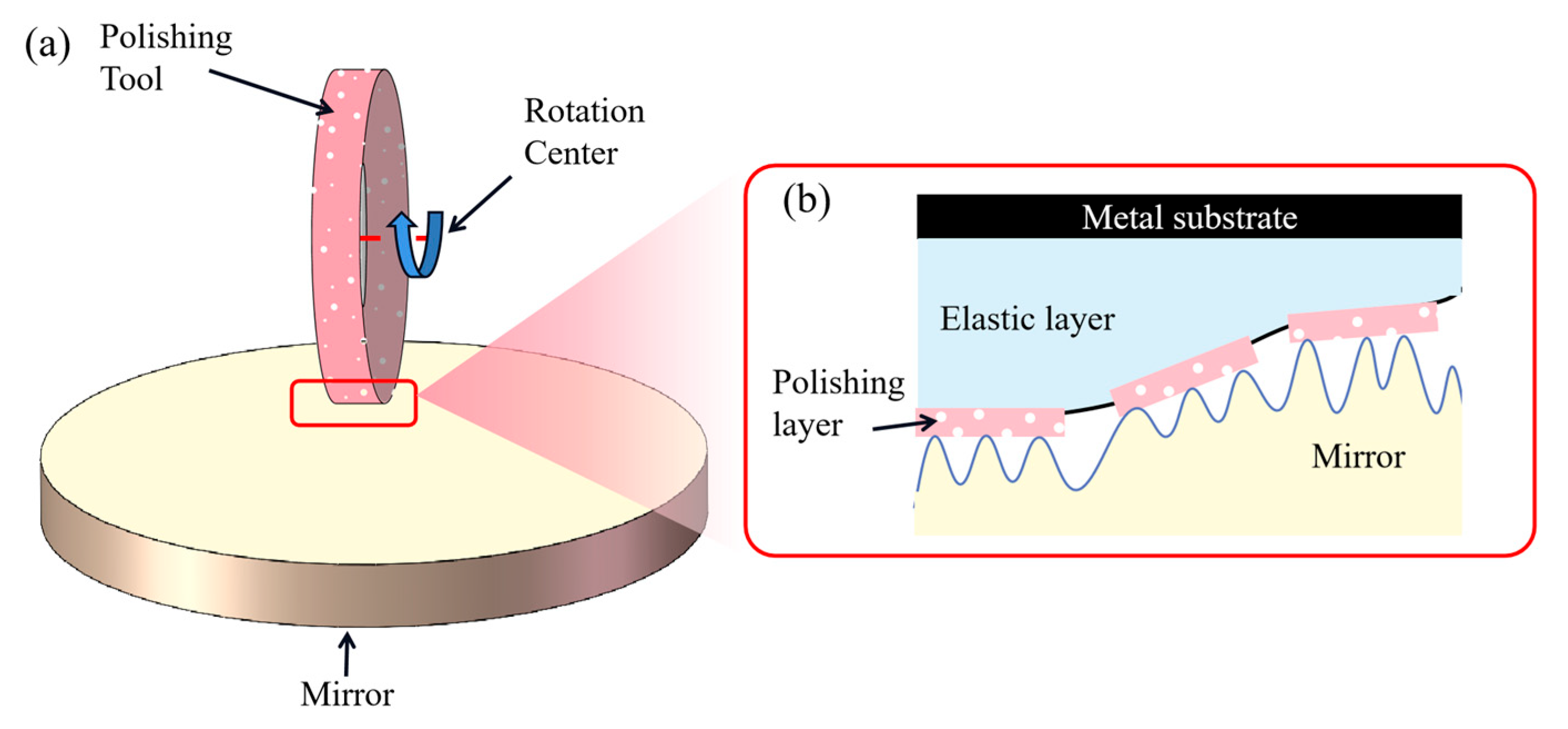
2. Theory and Modeling of MFEs
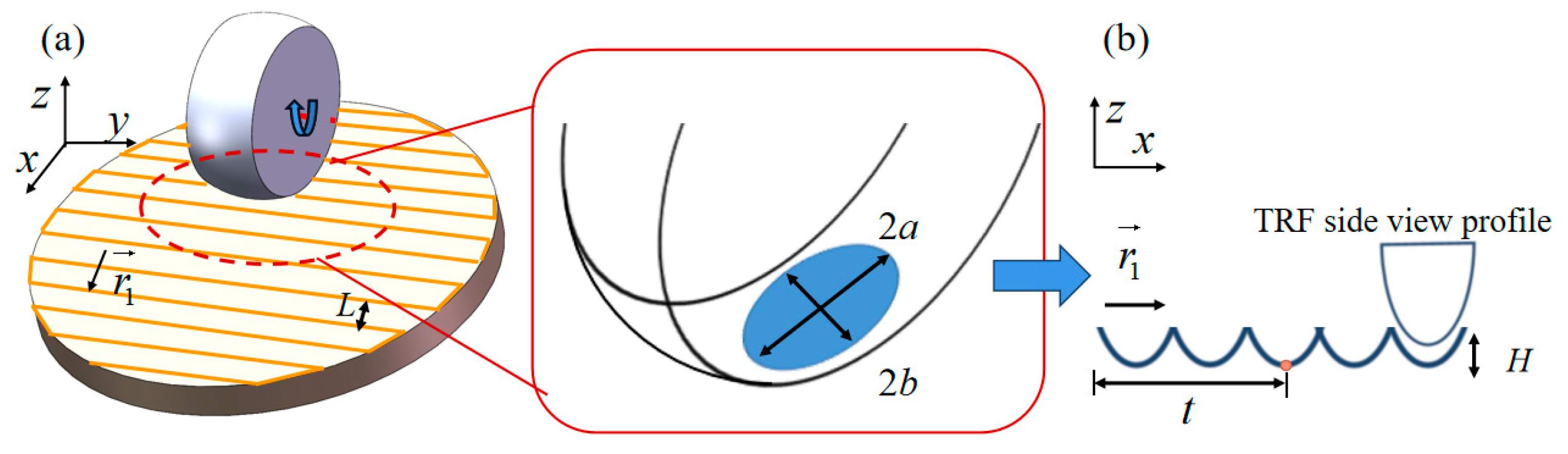
2.1. Hertzian Contact and Polishing Path-Introduced Marks
2.2. Bridging Contact and Smooth Limitation
- When the spatial frequency of the error is sufficiently high, the smoothing effect can reduce the profile error to nearly zero;
- The smoothing limit is directly proportional to the applied pressure q, and inversely proportional to the flexural rigidity D;
- This implies that the smoothing effect described by the bridging model can be considered analogous to a low-pass filter.
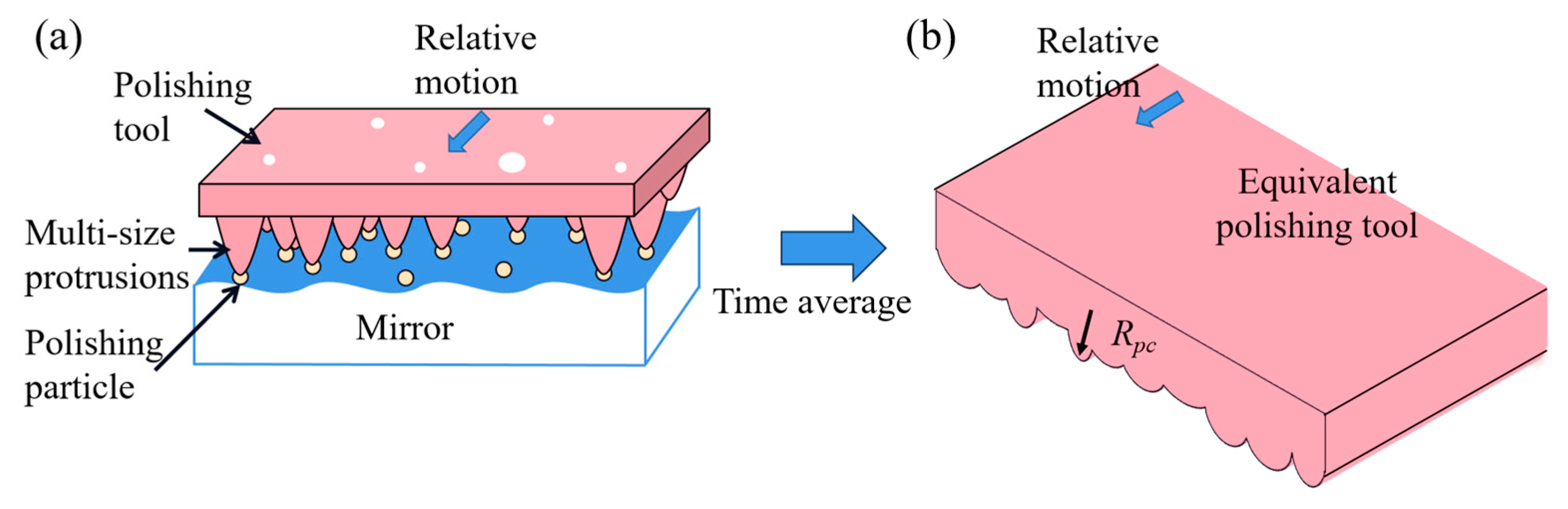
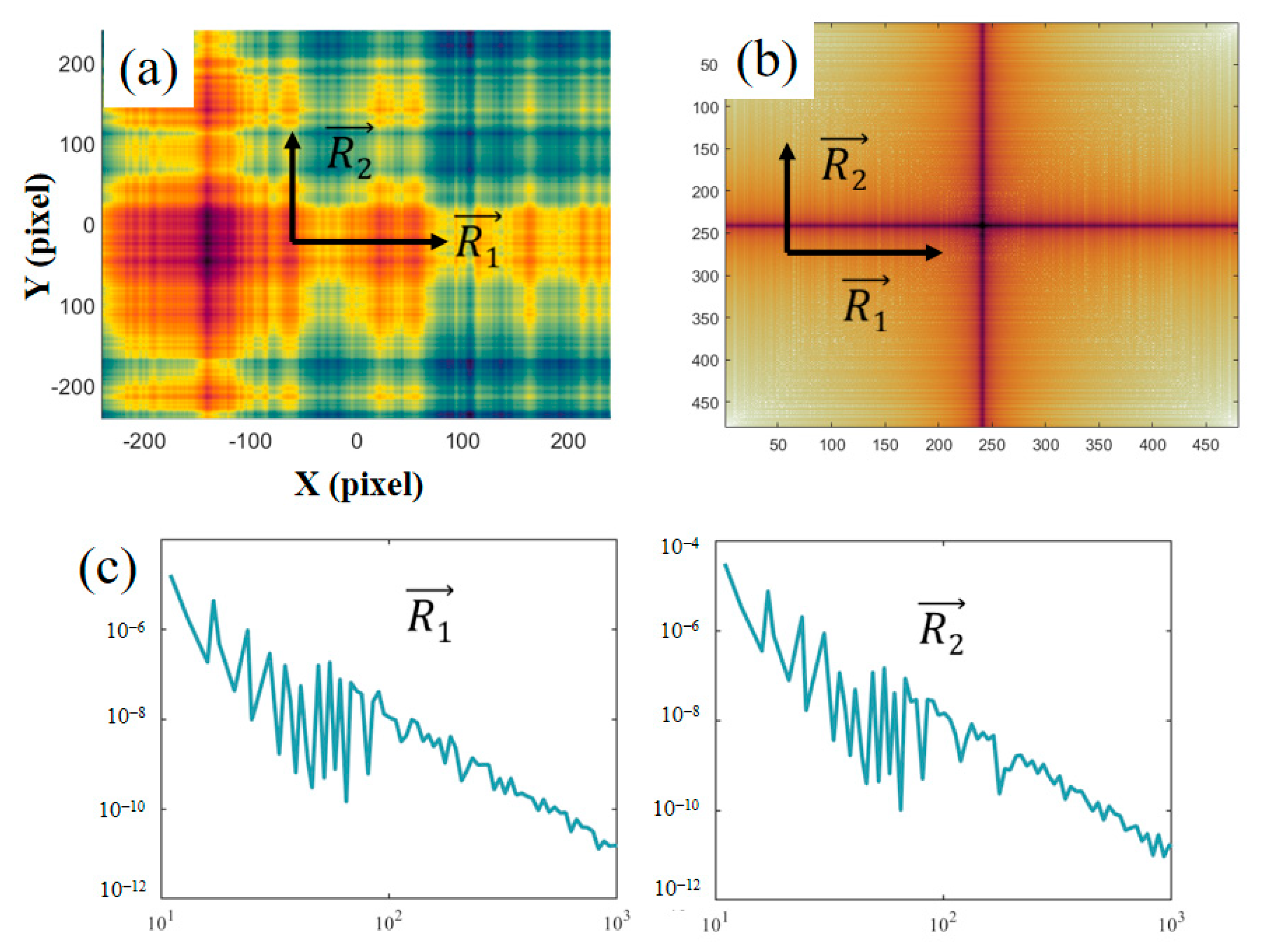
2.3. Rough Contact Introduced Mid-Frequency Errors
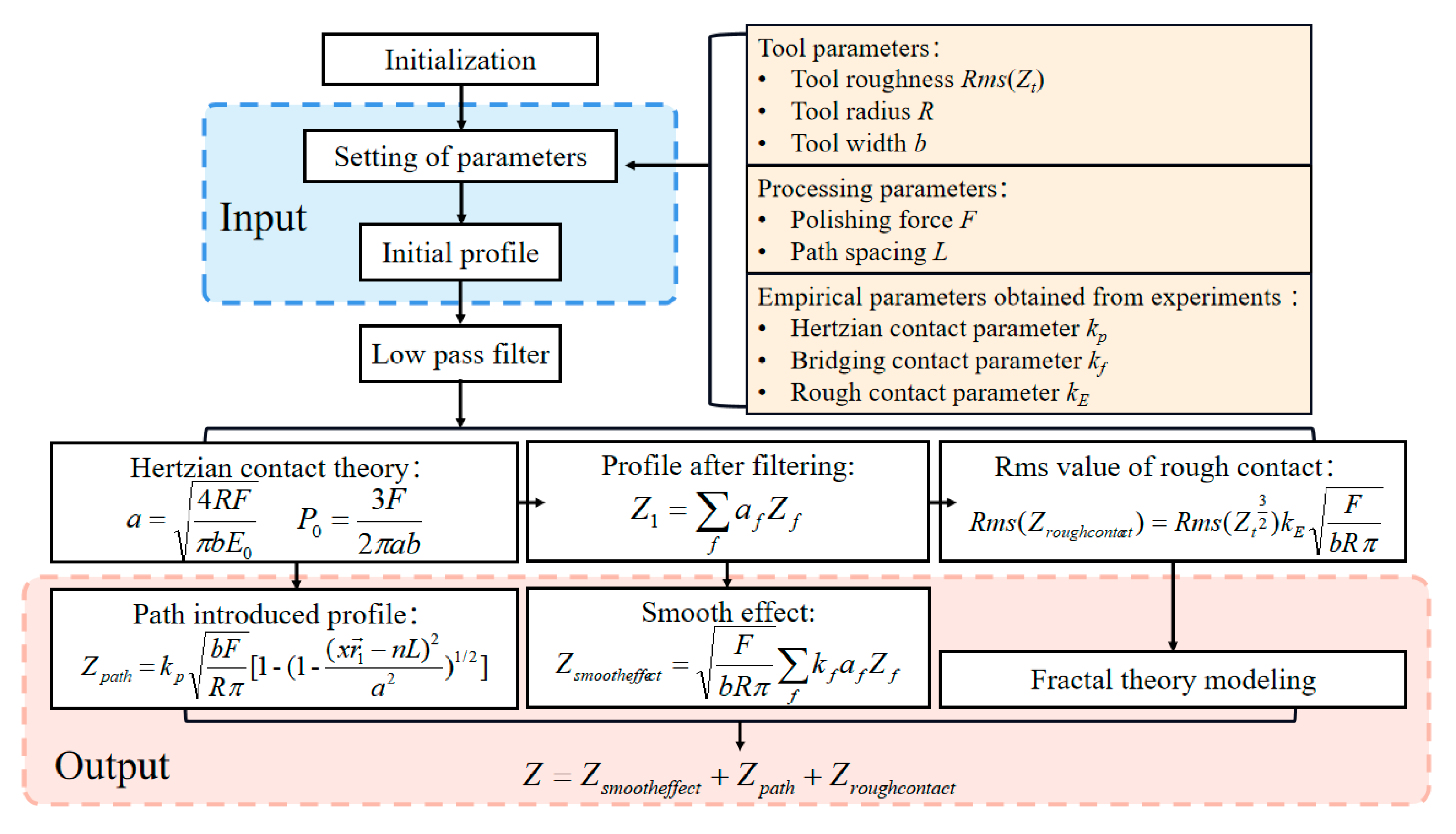
2.4. MFEs Predication Model
- Tool parameters, including tool roughness, tool radius, and tool width;
- Polishing parameters, including path spacing and polishing force;
- Empirical parameters obtained by experiments, including fh, kp, kf and kE.
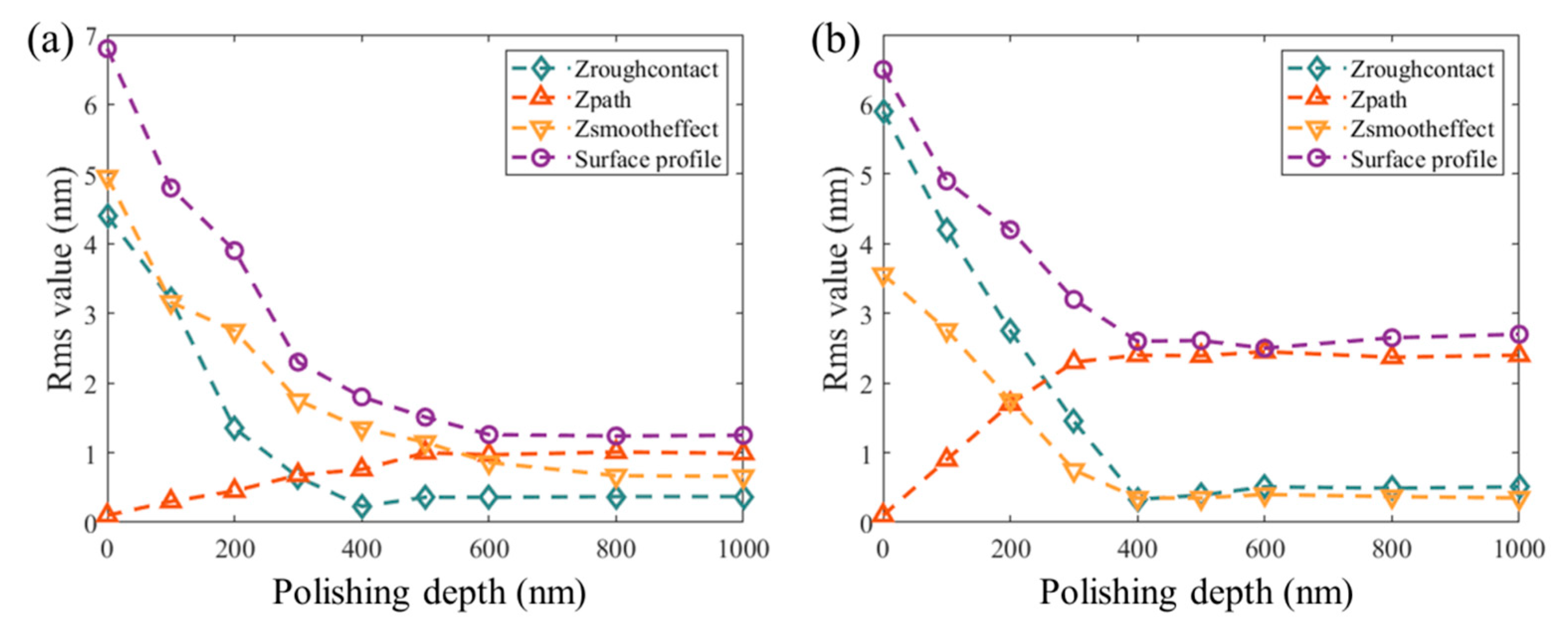
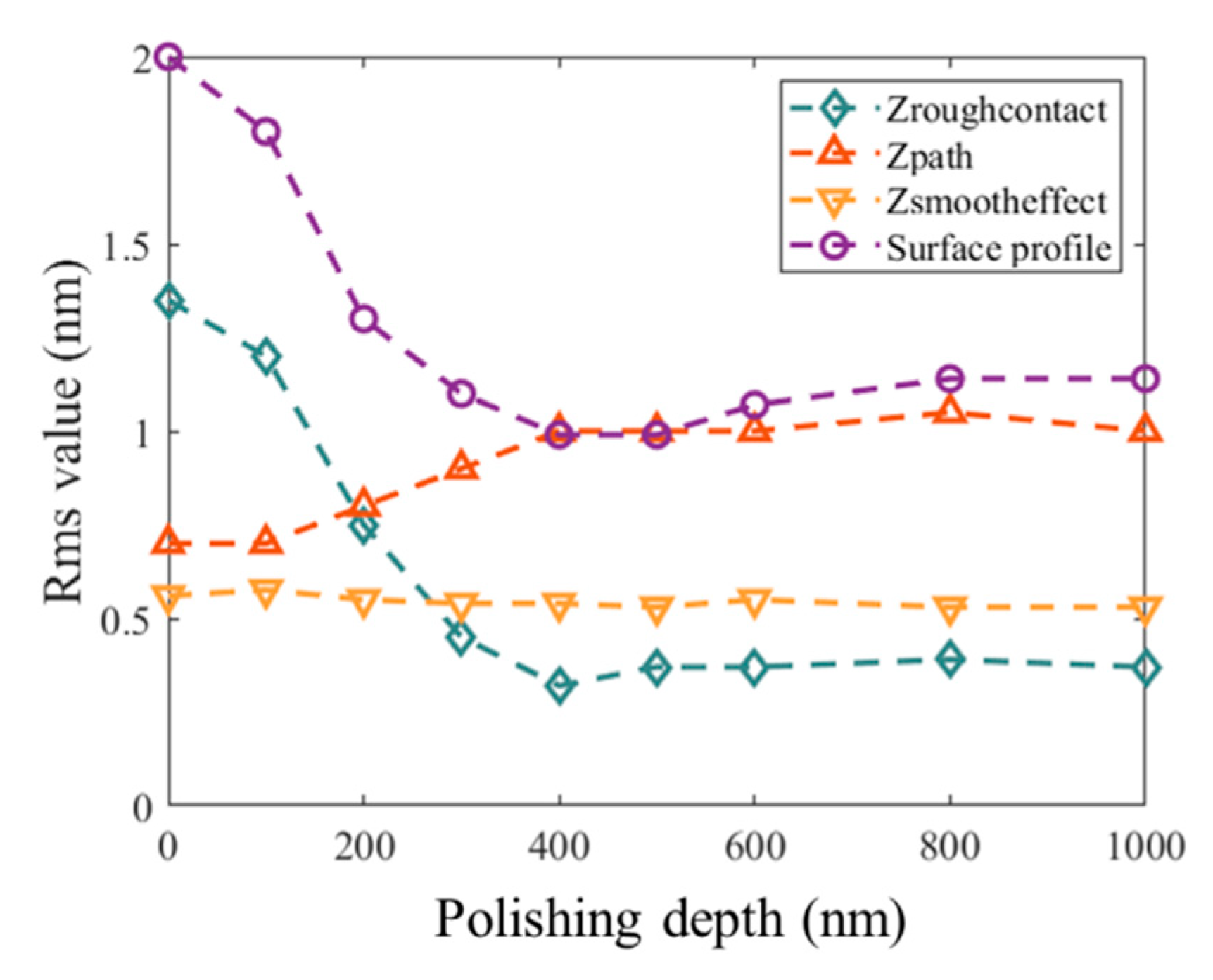
2.5. Error Analysis
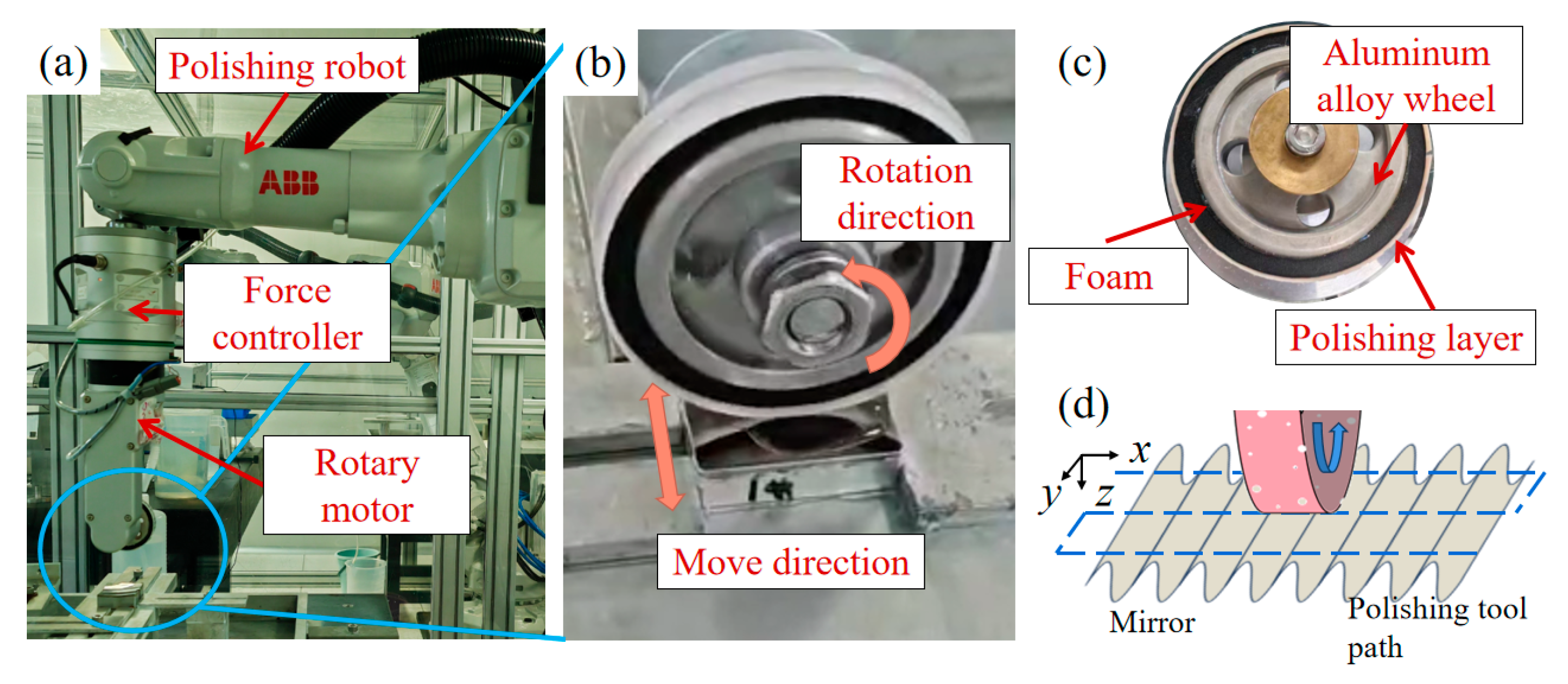
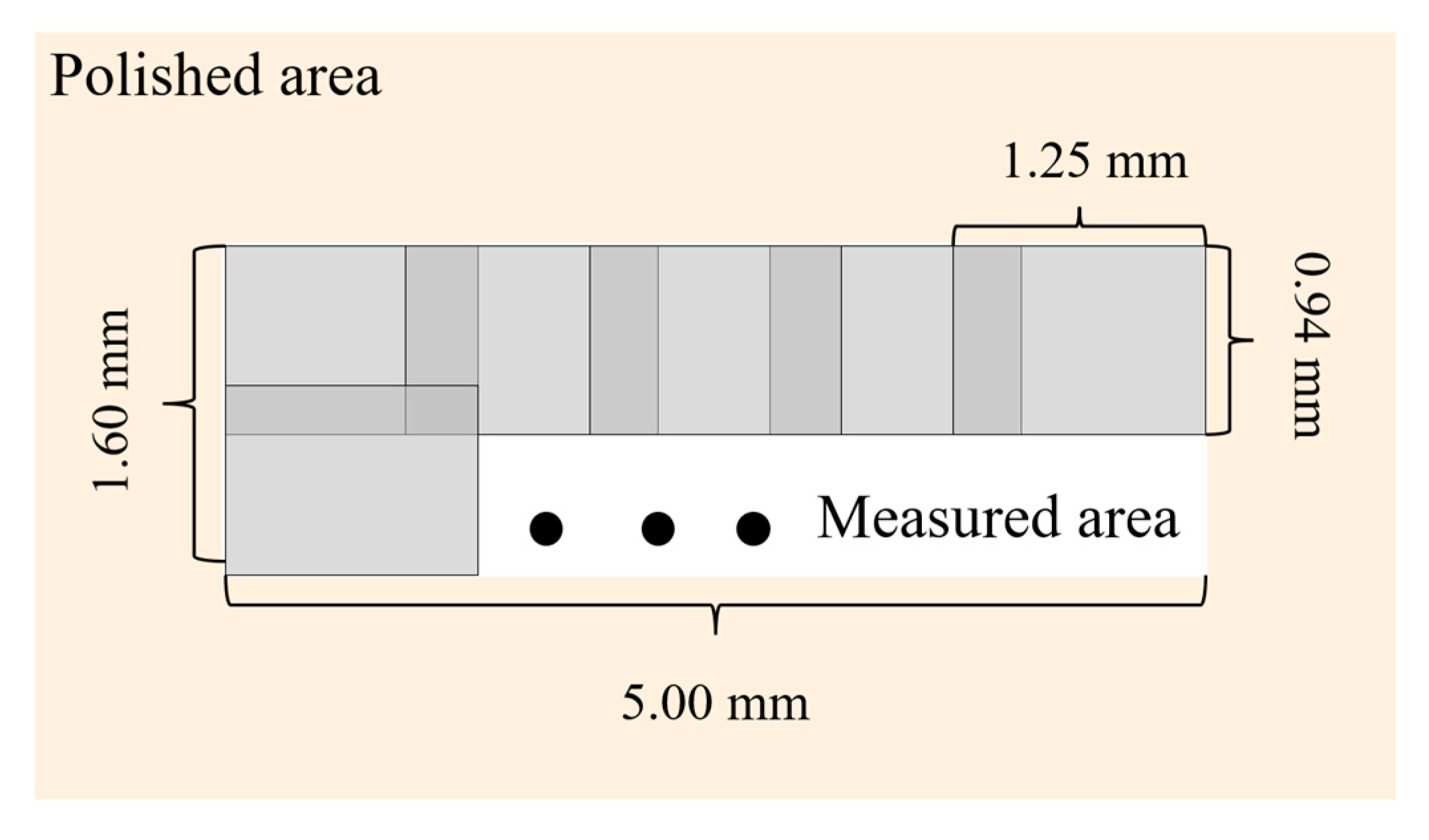
3. Experiment Design
3.1. Parameters Acquisition Experiments
3.2. Model Validation Experiments
4. Results and Discussion
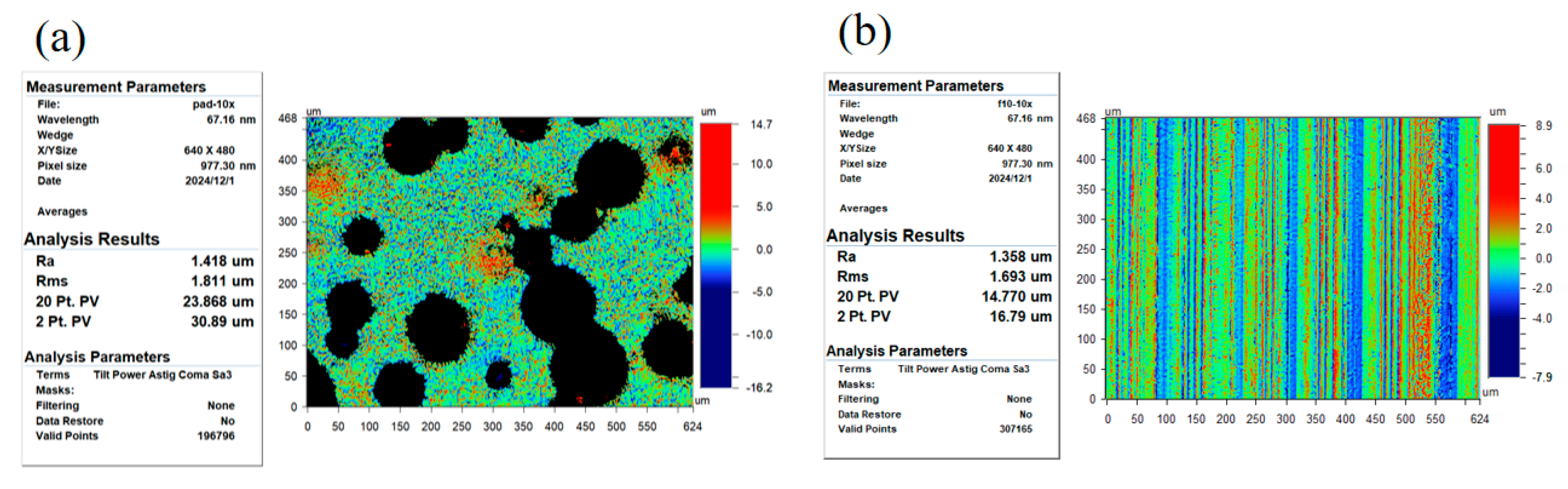
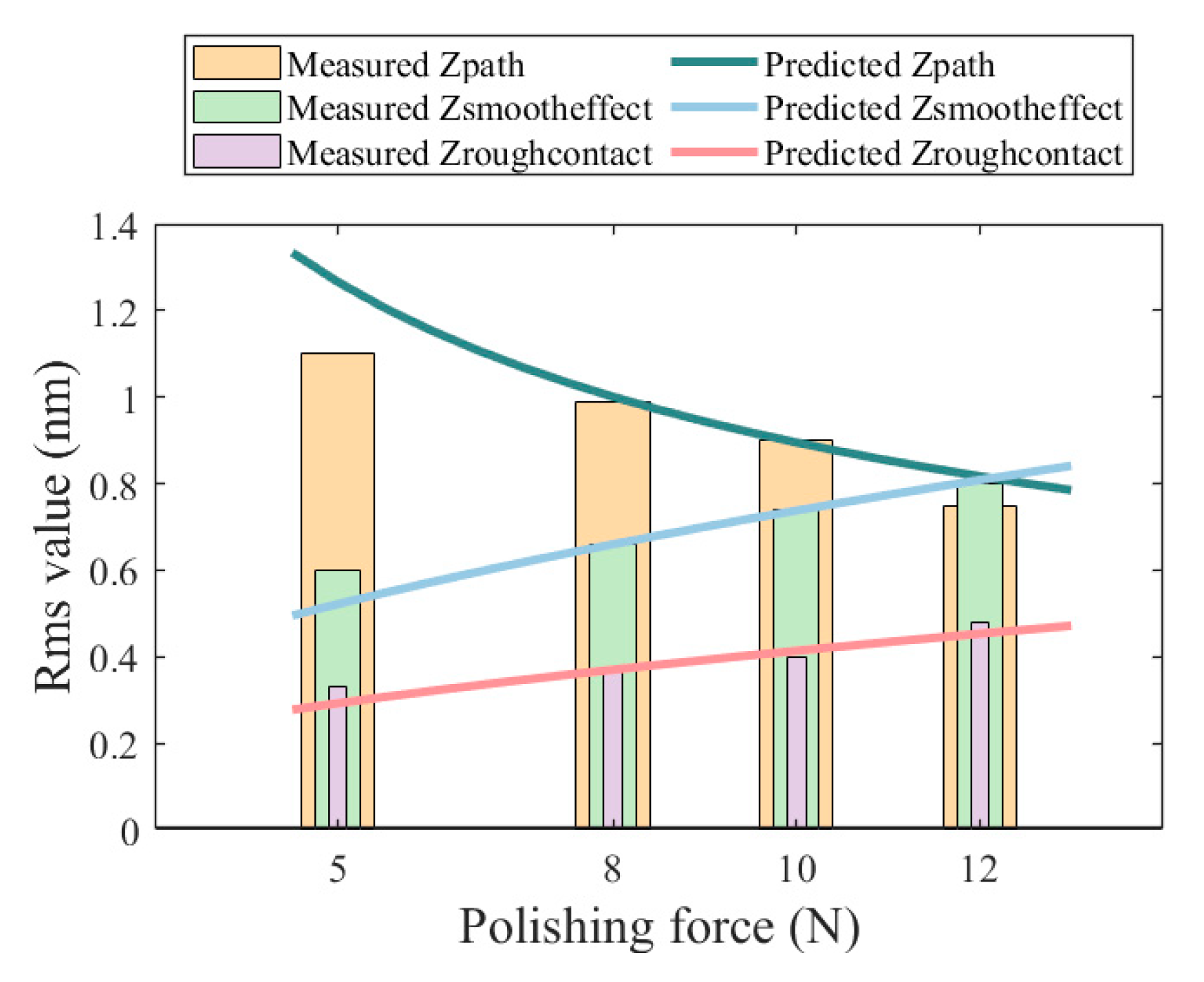
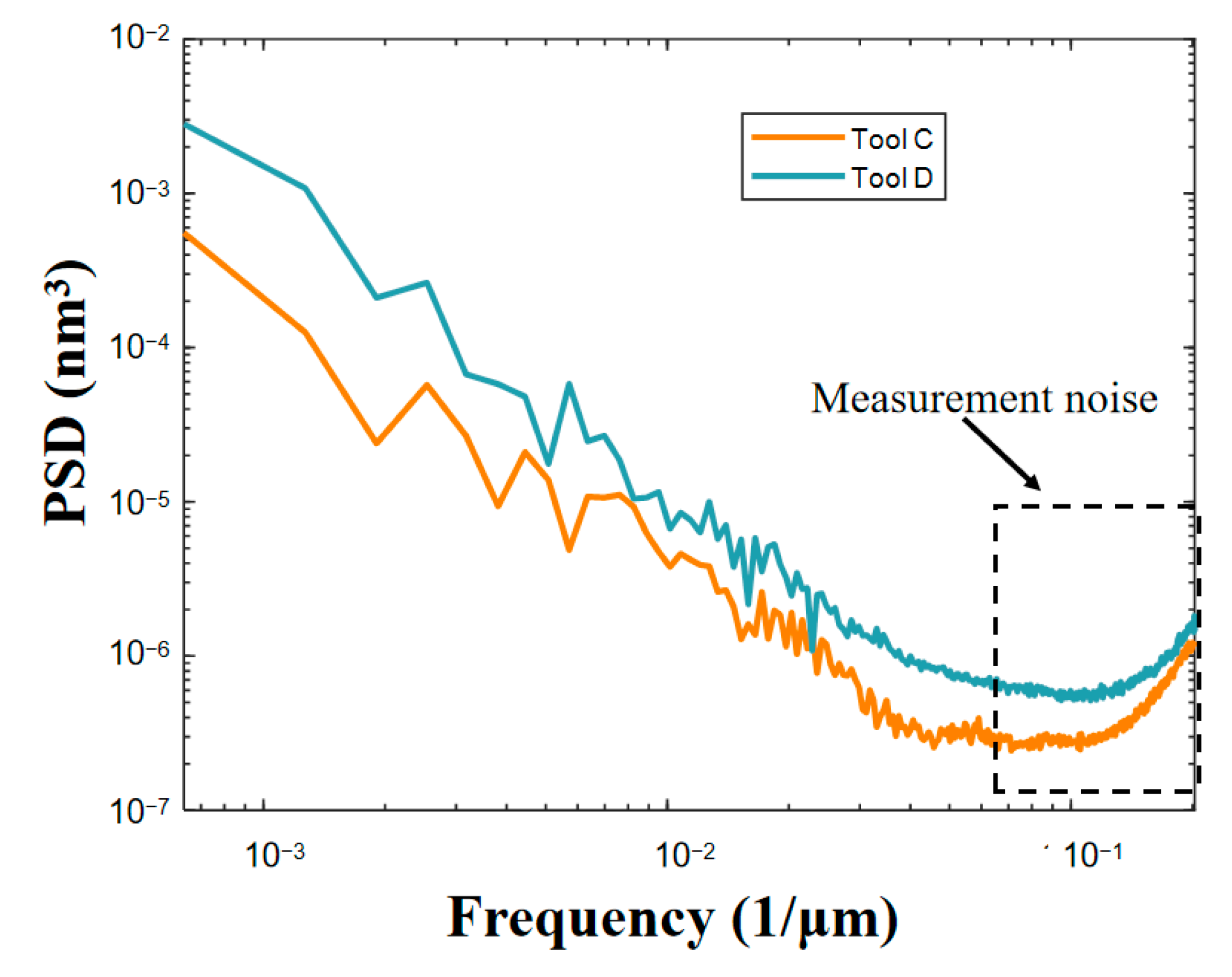
4.1. Parameters Acquisition
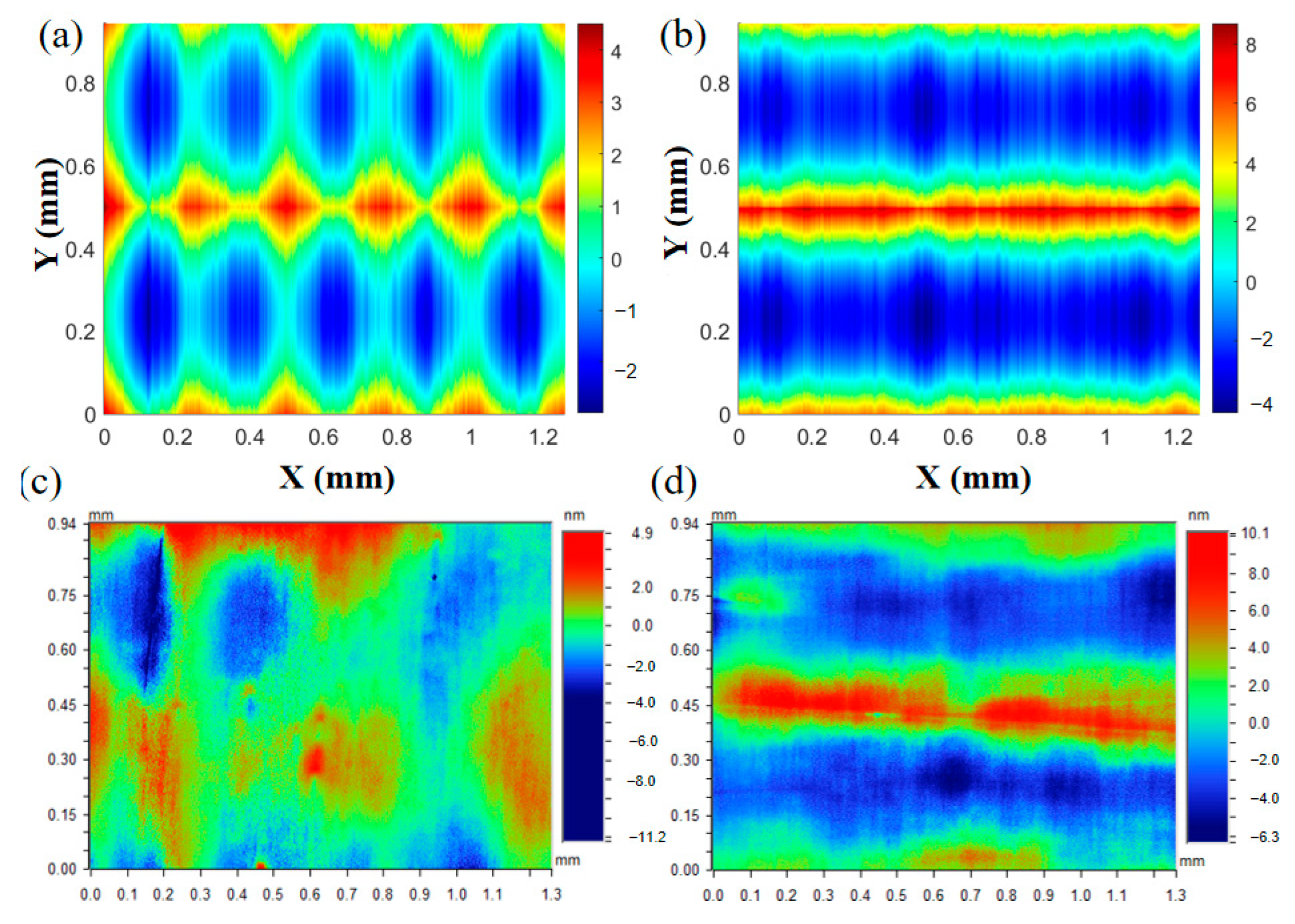
4.2. Model Validation
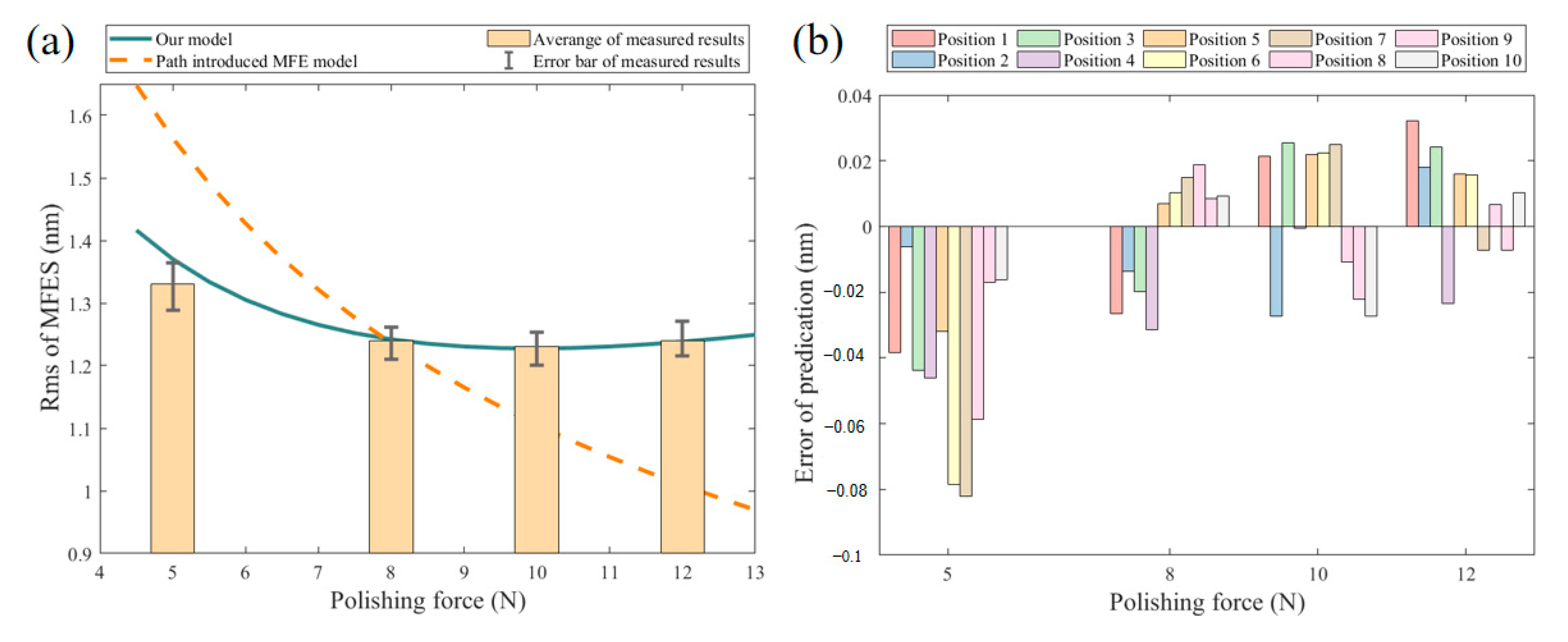
4.2.1. The Influence of Polishing Force
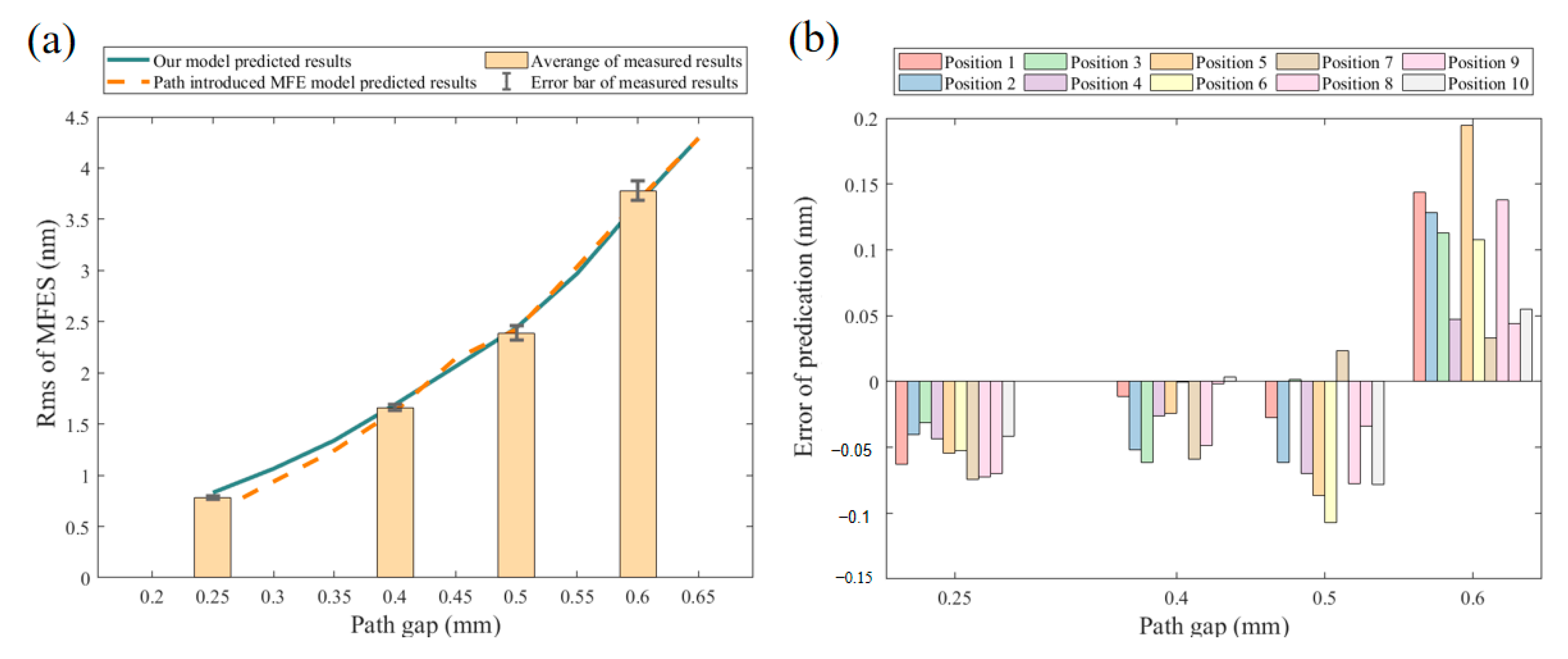
4.2.2. The Influence of Path Spacing
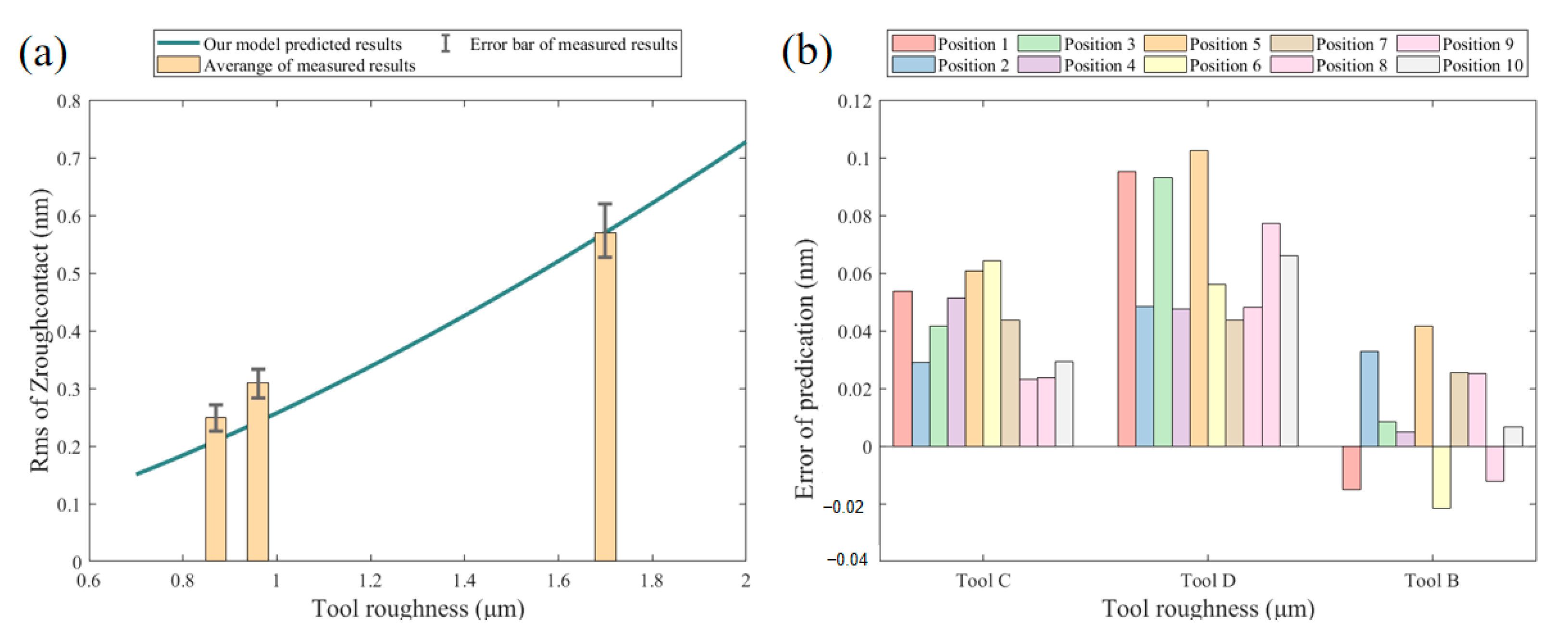
4.2.3. The Influence of Tool Roughness
4.3. Further Discussion: Engineering Application of Model
5. Conclusions
- The MFE prediction model was developed by incorporating a Hertzian contact, rough surface contact, and bridging model. The key parameters were categorized into three groups: tool parameters, polishing parameters, and empirical parameters. The empirical parameters are associated with the structural properties of the polishing tool and the characteristics of the polishing slurry. Once these empirical parameters are determined through polishing experiments, the model can be used to guide the optimized selection of polishing and tool parameters for improved process performance;
- The effects of tool roughness, polishing force, and path spacing were systematically investigated in this study. The model indicates that reduced tool roughness and smaller path spacing contribute to MFEs. In contrast, the relationship between the polishing force and MFEs is non-linear: The MFEs initially decrease with increasing force but begin to rise once the force is larger than a certain value;
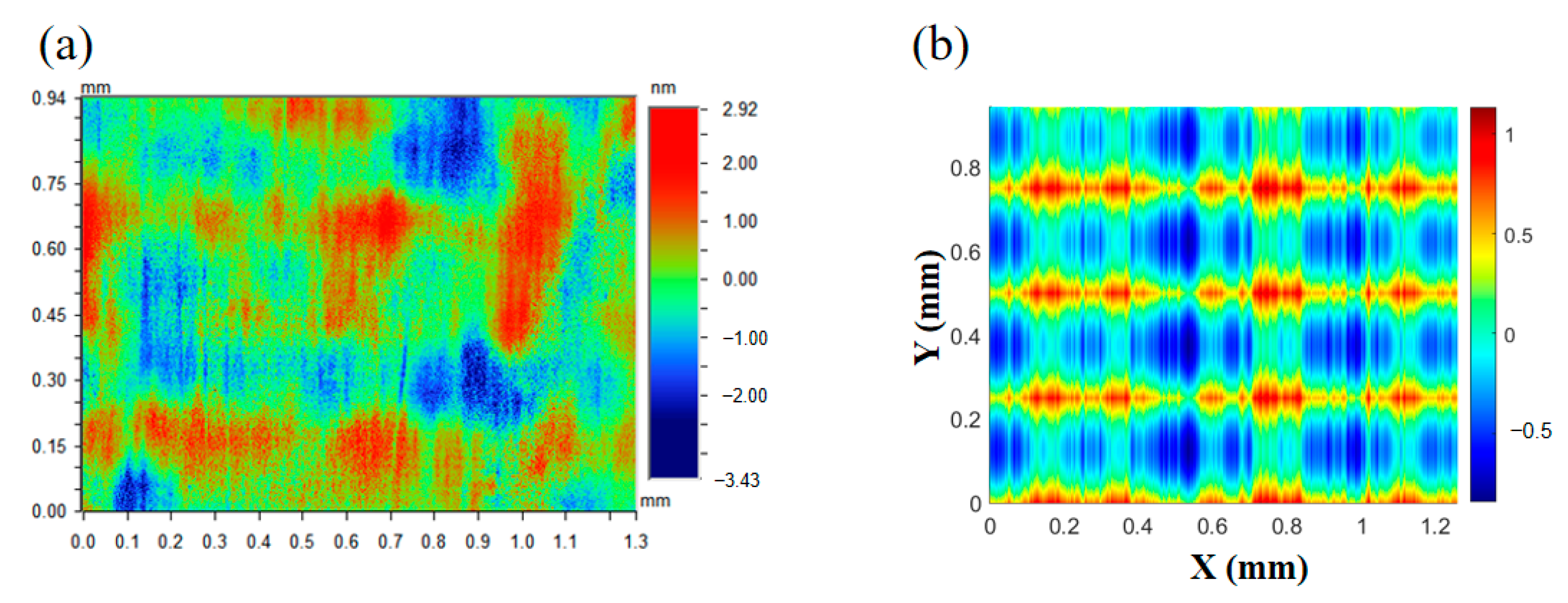
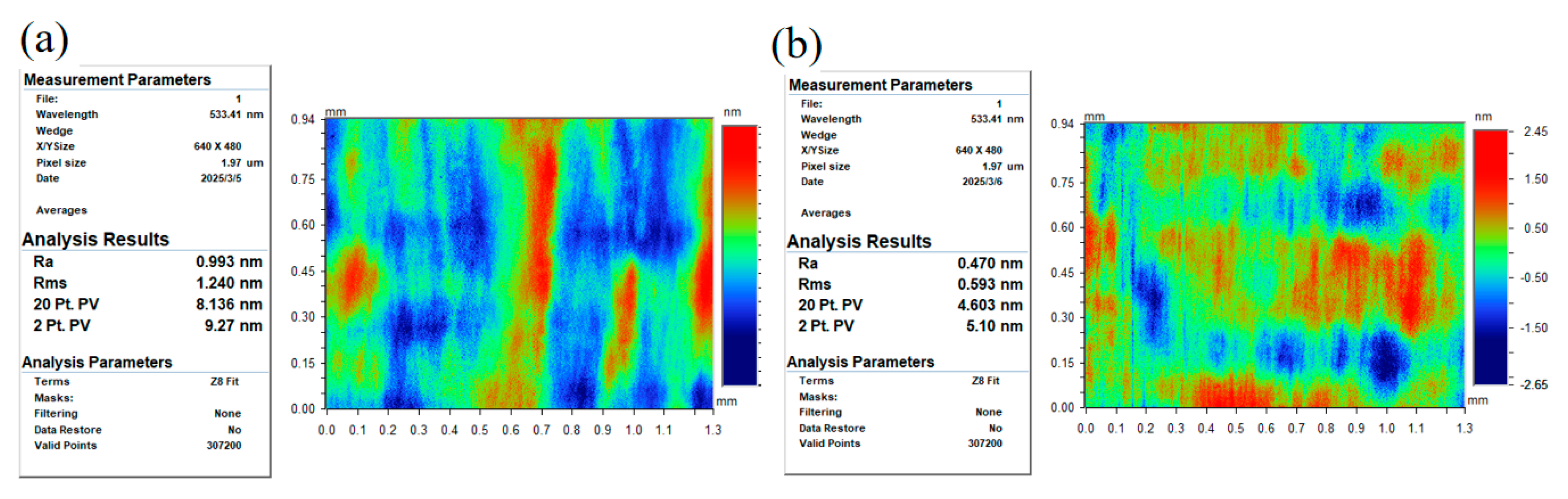
- Polishing experiments were carried out on diamond-turned electroless nickel plates to validate the proposed model. The predicted results show good agreement with the experimental data. Guided by this model, the “best roughness” polishing parameter within the limitations of our processing instrument was selected for the polishing experiments. The surface roughness achieved was 0.59 nm (Rms), measured over a 1.26 mm × 0.94 mm area, which closely matched the predicted value of 0.64 nm (Rms).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EN | Electroless nickel |
| LFEs | Low-frequency errors |
| MFEs | Mid-frequency errors |
| HFEs | High-frequency errors |
| Rms | Root-mean-square |
| PV | Peak-to-valley |
| CMP | Chemical-mechanical polishing |
| TRF | Tool removal function |
| GW | Greenwood–Williamson |
| STP | Small-tool polishing |
| PSD | Power spectral density |
| 2D | Two-dimensional |
| 1D | One-dimensional |
References
- Civitani, M.M.; Basso, S.; Incorvaia, S.; Lessio, L.; Pareschi, G.; Toso, G.; Vecchi, G. A novel approach for fast and effective realization of high-resolution x-ray optics in metal. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 1–5 August 2021; Volume 11822, pp. 258–270. [Google Scholar]
- Bachrach, R.Z.; Flodstrom, S.A.; Bauer, R.S.; Rehn, V.; Jones, V.O. Evaluation of the soft X-ray spectral throughput of platinum-coated, copper, synchrotron-radiation collection mirrors. Nucl. Instrum. Methods 1978, 152, 135–139. [Google Scholar] [CrossRef]
- Yamaguchi, G.; Motoyama, H.; Owada, S.; Kubota, Y.; Egawa, S.; Kume, T.; Takeo, Y.; Yabashi, M.; Mimura, H. Copper electroforming replication process for soft x-ray mirrors. Rev. Sci. Instrum. 2021, 92, 123106. [Google Scholar] [CrossRef] [PubMed]
- Xue, L.; Si, S.; Zhang, H.; He, Y.; Tian, N.; Zhao, C.; Zhang, Y.; Mo, Q.; Sun, H.; Li, Z.; et al. X-ray optics development and metrology at Shanghai synchrotron radiation facility. In Proceedings of the International Conference on Optical and Photonic Engineering (icOPEN 2023), Singapore, 27 November–1 December 2023; Volume 13069, pp. 313–321. [Google Scholar]
- Pimenov, D.Y.; Kiran, M.; Khanna, N.; Pintaude, G.; Vasco, M.C.; da Silva, L.R.R.; Giasin, K. Review of improvement of machinability and surface integrity in machining on aluminum alloys. Int. J. Adv. Manuf. Technol. 2023, 129, 4743–4779. [Google Scholar] [CrossRef]
- Hibbard, D.L. Electroless nickel for optical applications. In Proceedings of the Optical Science, Engineering and Instrumentation ′97, San Diego, CA, USA, 27 July–1 August 1997; Volume 10289, pp. 173–199. [Google Scholar]
- Signorato, R.; del Rio, M.S. Structured slope errors on real x-ray mirrors: Ray tracing versus Experiment. In Proceedings of the Optical Science, Engineering and Instrumentation ′97, San Diego, CA, USA, 27 July–1 August 1997; Volume 3152, pp. 136–147. [Google Scholar]
- Raimondi, L.; Spiga, D. Mirrors for X-ray telescopes: Fresnel diffraction-based computation of point spread functions from metrology. Astron. Astrophys 2015, 573, A22. [Google Scholar] [CrossRef]
- Werzer, O.; Kowarik, S.; Gasser, F.; Jiang, Z.; Strzalka, J.; Nicklin, C.; Resel, R. X-ray diffraction under grazing incidence conditions. Nat. Rev. Methods Primers 2024, 4, 15. [Google Scholar] [CrossRef]
- Soufli, R.; Fernandez-Perea, M.; Baker, S.L.; Robinson, J.C.; Gullikson, E.M.; Heimann, P.; Yashchuk, V.V.; McKinney, W.R.; Schlotter, W.F.; Rowen, M. Development and calibration of mirrors and gratings for the soft x-ray materials science beamline at the Linac Coherent Light Source free-electron laser. Appl. Opt. 2012, 51, 2118–2128. [Google Scholar] [CrossRef]
- Windt, D.L.; Waskiewicz, W.K.; Griffith, J.E. Surface finish requirements for soft x-ray mirrors. Appl. Opt. 1994, 33, 2025–2031. [Google Scholar] [CrossRef]
- Pramanik, A.; Neo, K.S.; Rahman, M.; Li, X.P.; Sawa, M.; Maeda, Y. Cutting performance of diamond tools during ultra-precision turning of electroless-nickel plated die materials. J. Mater. Process. Technol. 2003, 140, 308–313. [Google Scholar] [CrossRef]
- Chon, K.S.; Namba, Y. Single-point diamond turning of electroless nickel for flat X-ray mirror. J. Mech. Sci. Technol. 2010, 24, 1603–1609. [Google Scholar] [CrossRef]
- Pramanik, A.; Neo, K.S.; Rahman, M.; Li, X.P.; Sawa, M.; Maeda, Y. Ultraprecision turning of electroless nickel: Effects of crystal orientation and origin of diamond tools. Int. J. Adv. Manuf. Technol. 2009, 43, 681–689. [Google Scholar] [CrossRef]
- Pradhan, P.; Shurvinton, R.; Bourgenot, C.; Wang, H.; Sawhney, K. Ultra-high precision NiP mirror fabrication using ion beam figuring for space applications. Opt. Express 2025, 33, 17721–17734. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.G.; Jeong, S.K.; Jeon, M.; Jeong, B.; Yeo, W.J.; Choi, H.J.; Kwon, Y.E.; Ham, J.; Kim, J.H.; Lee, W. Magnetorheological finishing of electroless nickel-phosphorus-plated mold for ultraprecision injection molding. Int. J. Adv. Manuf. Technol. 2024, 131, 1705–1716. [Google Scholar] [CrossRef]
- Shurvinton, R.; Wang, H.; Pradhan, P.; Nistea, I.T.; Alcock, S.; Bazan Da Silva, M.; Majhi, A.; Sawhney, K. Ion beam figuring for X-ray mirrors: History, state-of-the-art and future prospects. J. Synchrotron Radiat. 2024, 31, 655–669. [Google Scholar] [CrossRef]
- Wang, W.; Ji, S.; Zhao, J. Review of magnetorheological finishing on components with complex surfaces. Int. J. Adv. Manuf. Technol. 2024, 131, 3165–3191. [Google Scholar] [CrossRef]
- Jones, R.A.; Rupp, W.J. Rapid optical fabrication with computer-controlled optical surfacing. Opt. Eng. 1991, 30, 1962–1968. [Google Scholar] [CrossRef]
- Xue, J.; Wang, B.; Liao, Q.; Wu, K.; Liu, Y.; Wu, Y.; Chen, W.; Qiao, Z.; Jin, Y.; Ding, F.; et al. Precision Manufacturing in China of Replication Mandrels for Ni-Based Monolithic Wolter-I X-ray Mirror Mandrels. Aerospace 2024, 11, 849. [Google Scholar] [CrossRef]
- Li, F.; Bai, Y.; Hu, H.; Li, L.; Li, L.; Zhang, F.; Luo, X.; Zhang, X. Elastoplastic contact model of pitch-based rough surface and its polishing characteristics. Opt. Express 2024, 31, 42150–42164. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Song, J.; Liu, X.; Lee, C.H.; Marinescu, I.D.; Hui, J.; Guo, L. Precision and ultra-precision machining with elastic polishing tools: A review. Surf. Sci. Technol. 2025, 3, 9. [Google Scholar] [CrossRef]
- Beaucamp, A.T.; Freeman, R.R.; Matsumoto, A.; Namba, Y. Fluid jet and bonnet polishing of optical moulds for application from visible to x-ray. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 21–25 August 2011; Volume 8126, pp. 240–247. [Google Scholar]
- Namba, Y.; Shimomura, T.; Fushiki, A.; Beaucamp, A.; Inasaki, I.; Kunieda, H.; Ogasaka, Y.; Yamashita, K. Ultra-precision polishing of electroless nickel molding dies for shorter wavelength applications. CIRP Ann. 2008, 57, 337–340. [Google Scholar] [CrossRef]
- Beaucamp, A.; Namba, Y. Super-smooth finishing of diamond turned hard X-ray molding dies by combined fluid jet and bonnet polishing. CIRP Ann. 2013, 62, 315–318. [Google Scholar] [CrossRef]
- Xue, J.; Chu, Y.; Liu, Y.; Liao, Q.; Chen, W.; Wu, Y.; Ding, F.; Wang, B.; Li, G.; Wang, D.; et al. Influence analysis of surface particulate and molecular contamination in CMP process of mandrel for EP focusing mirror. Radiat. Detect. Technol. Methods 2025, 9, 344–354. [Google Scholar] [CrossRef]
- Ghosh, G.; Sidpara, A.; Bandyopadhyay, P.P. Brittle-ductile transition in compliant finishing of HVOF sprayed hard WC-Co coating. Int. J. Refract. Met. H. 2021, 99, 105610. [Google Scholar] [CrossRef]
- Feng, H.; Huang, L.; Huang, P.; Liu, J.; He, X.; Peng, Y. Review on high efficiency and high precision compliant polishing method. Int. J. Adv. Manuf. Technol. 2024, 132, 2091–2128. [Google Scholar] [CrossRef]
- Wang, X.; Gao, H.; Yuan, J. Experimental investigation and analytical modelling of the tool influence function of the ultra-precision numerical control polishing method based on the water dissolution principle for KDP crystals. Precis. Eng. 2020, 65, 185–196. [Google Scholar] [CrossRef]
- Yang, K.; Di, H.; Huang, N.; Hou, C.; Zhou, P. Surface microtopography evolution of monocrystalline silicon in chemical mechanical polishing. J. Mater. Process. Technol. 2024, 328, 118387. [Google Scholar] [CrossRef]
- Deng, Y.; Hou, X.; Li, B.; Wang, J.; Zhang, Y. Review on mid-spatial frequency error suppression in optical components manufacturing. Int. J. Adv. Manuf. Technol. 2023, 126, 4827–4847. [Google Scholar] [CrossRef]
- He, Z.; Hai, K.; Li, K.; Yu, J.; Wu, L.; Zhang, L.; Su, X.; Cai, L.; Huang, W.; Hang, W. Research on the influence of the material removal profile of a spherical polishing tool on the mid-spatial frequency errors of optical surfaces. Micromachines 2024, 15, 654. [Google Scholar] [CrossRef]
- Li, S.; Wang, K.; Ai, H.; Ren, P.; Wang, Z. Middle–high spatial frequency error suppression of a self-organizing map pseudorandom path planning method in complex surface polishing. Appl. Opt. 2025, 64, 3936–3946. [Google Scholar] [CrossRef] [PubMed]
- Tam, H.Y.; Cheng, H. An investigation of the effects of the tool path on the removal of material in polishing. J. Mater. Process. Technol. 2010, 210, 807–818. [Google Scholar] [CrossRef]
- Liao, D.; Yuan, Z.; Tang, C.; Xie, R.; Chen, X. Mid-Spatial Frequency Error (PSD-2) of optics induced during CCOS and full-aperture polishing. J. Eur. Opt. Soc.-Rapid 2013, 8, 13031. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Vlassak, J.J. A model for chemical–mechanical polishing of a material surface based on contact mechanics. J. Mech. Phys. Solids 2004, 52, 847–873. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Daamen, R.; van Kranenburg, H.; van der Velden, P.; Woerlee, P.H. A physical model for dishing during metal CMP. J. Electrochem. Soc. 2003, 150, G689. [Google Scholar] [CrossRef]
- Luo, J.; Dornfeld, D.A. Material removal mechanism in chemical mechanical polishing: Theory and modeling. IEEE Trans. Semicond. Manuf. 2001, 14, 112–133. [Google Scholar] [CrossRef]
- Jones, R.A. Optimization of computer controlled polishing. Appl. Opt. 1997, 16, 218–224. [Google Scholar] [CrossRef]
- Johnson, K.L. One hundred years of Hertz contact. Proc. Inst. Mech. Eng. 1982, 196, 363–378. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Liang, Y.; Meng, F.; Cui, Z.; Chen, T.; Yang, Y.; Fan, C.; Yu, T.; Zhao, J. Modelling of polyurethane polishing pad surface topography and fixed-point polished surface profile. Tribol. Int. 2024, 195, 109646. [Google Scholar] [CrossRef]
- Zhang, L.; Wan, S.; Li, H.; Guo, H.; Wei, C.; Zhang, D.; Shao, J. Modeling and in-depth analysis of the mid-spatial-frequency error influenced by actual contact pressure distribution in sub-aperture polishing. Opt. Express 2023, 31, 14414–14431. [Google Scholar] [CrossRef] [PubMed]
- Seok, J.; Sukam, C.P.; Kim, A.T.; Tichy, J.A.; Cale, T.S. Multiscale material removal modeling of chemical mechanical polishing. Wear 2003, 254, 307–320. [Google Scholar] [CrossRef]
- Cao, Z.C.; Cheung, C.F. Multi-scale modeling and simulation of material removal characteristics in computer-controlled bonnet polishing. Int. J. Mech. Sci. 2016, 106, 147–156. [Google Scholar] [CrossRef]
- Lu, A.; Jin, T.; Liu, Q.; Guo, Z.; Qu, M.; Luo, H.; Han, M. Modeling and prediction of surface topography and surface roughness in dual-axis wheel polishing of optical glass. Int. J. Mach. Tools Manuf. 2019, 137, 13–29. [Google Scholar] [CrossRef]
- Yao, W.; Chu, Q.; Lyu, B.; Wang, C.; Shao, Q.; Feng, M.; Wu, Z. Modeling of material removal based on multi-scale contact in cylindrical polishing. Int. J. Mech. Sci. 2022, 223, 107287. [Google Scholar] [CrossRef]
- Meng, F.; Cui, Z.; Liang, Y.; Wang, Z.; Yu, T.; Ma, Z.; Zhao, J. Multiscale model of material removal for ultrasonic assisted polishing of cylindrical surfaces. Tribol. Int. 2025, 202, 110383. [Google Scholar] [CrossRef]
- Kang, H.; Li, Z.M.; Liu, T.; Zhao, G.; Jing, J.; Yuan, W. A novel multiscale model for contact behavior analysis of rough surfaces with the statistical approach. Int. J. Mech. Sci. 2021, 212, 106808. [Google Scholar] [CrossRef]
- Savio, G.; Meneghello, R.; Concheri, G. A surface roughness predictive model in deterministic polishing of ground glass moulds. Int. J. Mach. Tools Manuf. 2009, 49, 1–7. [Google Scholar] [CrossRef]
- Zhang, C.; Qu, S.; Liang, Y.; Chen, X.; Zhao, J.; Yu, T. Predictive modeling and experimental study of polishing force for ultrasonic vibration-assisted polishing of K9 optical glass. Int. J. Adv. Manuf. Technol. 2022, 119, 3119–3139. [Google Scholar] [CrossRef]
- Peng, W.; Jiang, L.; Huang, C.; Chen, Y.; Tian, Y.; Han, Y.; Zhang, S.; Qian, L. Surface roughness evolution law in full-aperture chemical mechanical polishing. Int. J. Mech. Sci. 2024, 277, 109387. [Google Scholar] [CrossRef]
- Deng, Y.; Hou, X.; Li, B.; Wang, J.; Zhang, Y. Experimental studies on smoothing process for aspheric optical components. In Proceedings of the 8th Asia Pacific Conference on Optics Manufacture & 3rd International Forum of Young Scientists on Advanced Optical Manufacturing, Shenzhen, China, 4–6 August 2023; Volume 12976, pp. 175–180. [Google Scholar]
- Suratwala, T.; Tham, G.; Steele, R.; Wong, L.; Menapace, J.; Ray, N.; Bauman, B. Smoothing tool design and performance during subaperture glass polishing. Appl. Opt. 2023, 62, 2061–2072. [Google Scholar] [CrossRef] [PubMed]
- Lei, P.; Hou, J.; Wang, J.; Deng, W.; Zhong, B. Smoothing of mid-spatial frequency errors by computer controlled surface processing. High Power Laser Part. Beams 2019, 31, 111002. [Google Scholar]
- Mehta, P.K.; Reid, P.B. Mathematical model for optical smoothing prediction of high-spatial-frequency surface errors. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 18–23 July 1999; Volume 3786, pp. 447–459. [Google Scholar]
- Burge, J.H.; Anderson, B.; Benjamin, S.; Cho, M.K.; Smith, K.Z.; Valente, M.J. Development of optimal grinding and polishing tools for aspheric surfaces. In Proceedings of the International Symposium on Optical Science and Technology, San Diego, CA, USA, 29 July–3 August 2001; Volume 4451, pp. 153–164. [Google Scholar]
- Liu, S.W.; Wang, H.X.; Zhang, Q.H.; Hou, J.; Chen, X.H.; Xu, Q.; Wang, C. Smoothing process of conformal vibration polishing for mid-spatial frequency errors: Characteristics research and guiding prediction. Appl. Opt. 2021, 60, 3925–3935. [Google Scholar] [CrossRef]
- Shu, Y.; Nie, X.; Shi, F.; Li, S. Smoothing evolution model for computer controlled optical surfacing. J. Opt. Technol. 2014, 81, 164–167. [Google Scholar] [CrossRef]
- Li, X.; Wei, C.; Zhang, S.; Xu, W.; Shao, J. Theoretical and experimental comparisons of the smoothing effects for different multi-layer polishing tools during computer-controlled optical surfacing. Appl. Opt. 2019, 58, 4406–4413. [Google Scholar] [CrossRef] [PubMed]
- Nie, X.; Li, S.; Shi, F.; Hu, H. Generalized numerical pressure distribution model for smoothing polishing of irregular midspatial frequency errors. Appl. Opt. 2014, 53, 1020–1027. [Google Scholar] [CrossRef] [PubMed]
- Khatri, N.; Manjunath, K.; Tewary, S.; Kang, W.; Liang, R. Measurement of mid-spatial frequencies of diamond turned optics by using dual-mode snapshot interferometry. In Proceedings of the Optical Engineering + Applications, San Diego, CA, USA, 18–22 August 2024; Volume 13134, pp. 182–190. [Google Scholar]
- Xia, J.; Yu, J.; Lu, S.; Xue, C.; Zhu, Y.; Feng, Y.; Sheng, P.; Wang, Z. Extraction of isotropic and anisotropic components for optical surface micro-metrology based on the two-dimensional power spectral density analysis. Precis. Eng. 2024, 91, 344–357. [Google Scholar] [CrossRef]


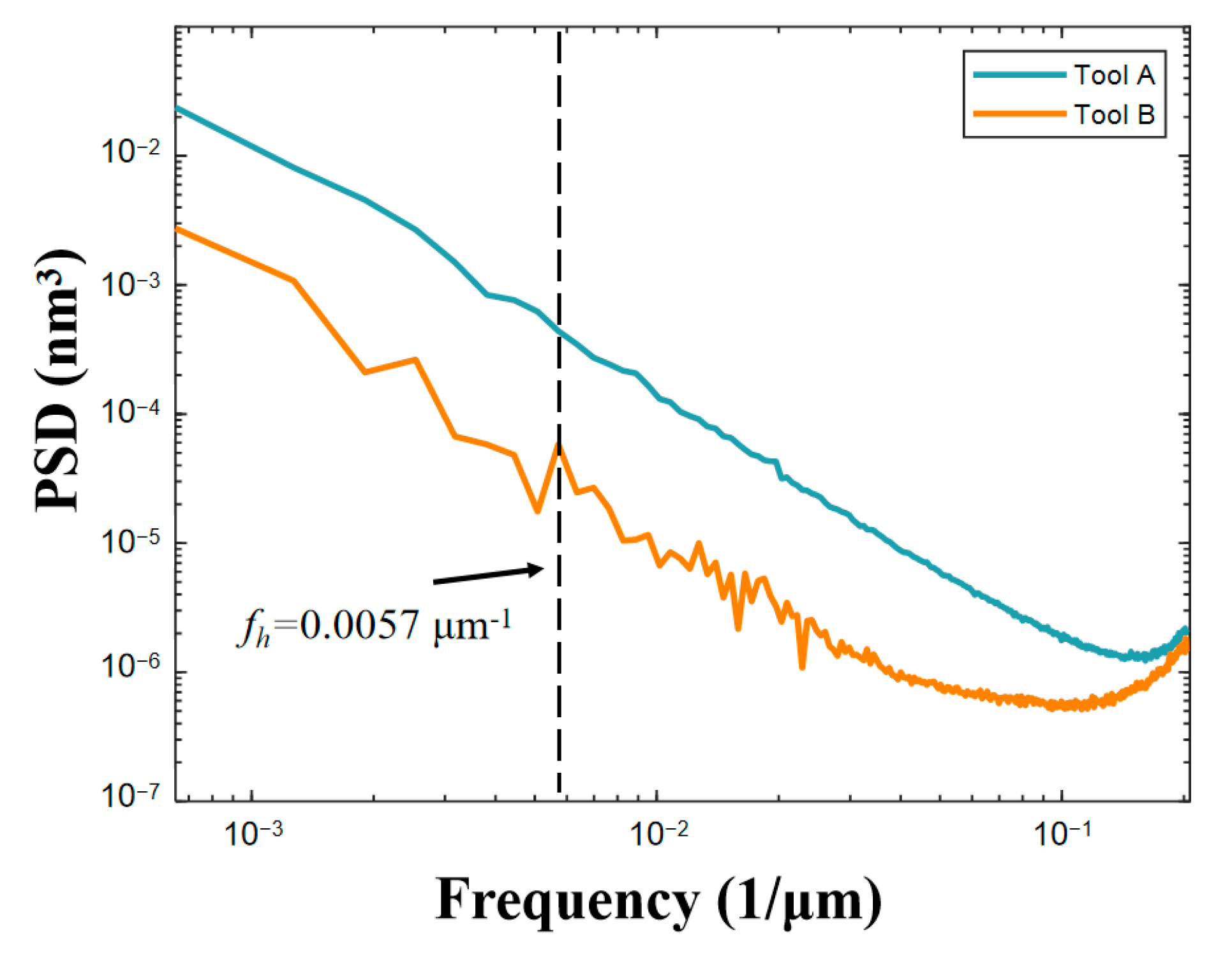

| Tool A | Tool B | |
|---|---|---|
| Aluminum wheel radius | 25 mm | 25 mm |
| Foam layer thickness | 5 mm | 5 mm |
| Polishing layer thickness | 1.20 mm | 1.20 mm |
| Polishing layer material | LP87 | SL4387 |
| Rms tool roughness | 1.81 μm | 1.70 μm |
| Tool B | Tool C | Tool D | |
|---|---|---|---|
| Aluminum wheel radius | 25 mm | 25 mm | 25 mm |
| Foam layer thickness | 5 mm | 5 mm | 5 mm |
| Polishing layer thickness | 1.20 mm | 1.20 mm | 1.20 mm |
| Polishing layer material | SL4387 | SL4387 | SL4387 |
| Rms tool roughness | 1.70 μm | 0.87 μm | 0.96 μm |
| Tool A | Tool B | |
|---|---|---|
| Rms(Zpath) | 0.95 nm | 2.41 nm |
| Rms(Zroughcontact) | 0.33 nm | 0.51 nm |
| Rms(Zsmootheffect) | 0.69 nm | 0.35 nm |
| Force (N) | 5 | 8 | 10 | 12 |
|---|---|---|---|---|
| Measure MFEs (nm) | 1.33 ± 0.04 | 1.25 ± 0.03 | 1.23 ± 0.02 | 1.24 ± 0.03 |
| Predicted MFEs (nm) | 1.37 | 1.26 | 1.24 | 1.25 |
| Error of predication (nm) | −0.04 ± 0.04 | 0.00 ± 0.03 | −0.01 ± 0.02 | −0.01 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, P.; Xia, J.; Yu, J.; Wang, K.; Wang, Z. Multi-Scale Model of Mid-Frequency Errors in Semi-Rigid Tool Polishing of Diamond-Turned Electroless Nickel Mirror. J. Manuf. Mater. Process. 2025, 9, 325. https://doi.org/10.3390/jmmp9100325
Sheng P, Xia J, Yu J, Wang K, Wang Z. Multi-Scale Model of Mid-Frequency Errors in Semi-Rigid Tool Polishing of Diamond-Turned Electroless Nickel Mirror. Journal of Manufacturing and Materials Processing. 2025; 9(10):325. https://doi.org/10.3390/jmmp9100325
Chicago/Turabian StyleSheng, Pengfeng, Jingjing Xia, Jun Yu, Kun Wang, and Zhanshan Wang. 2025. "Multi-Scale Model of Mid-Frequency Errors in Semi-Rigid Tool Polishing of Diamond-Turned Electroless Nickel Mirror" Journal of Manufacturing and Materials Processing 9, no. 10: 325. https://doi.org/10.3390/jmmp9100325
APA StyleSheng, P., Xia, J., Yu, J., Wang, K., & Wang, Z. (2025). Multi-Scale Model of Mid-Frequency Errors in Semi-Rigid Tool Polishing of Diamond-Turned Electroless Nickel Mirror. Journal of Manufacturing and Materials Processing, 9(10), 325. https://doi.org/10.3390/jmmp9100325






