Abstract
The paper presents an innovative theoretical concept of a bio-inspired soft gripper system with two parallel jaws, a fixed and a mobile one. It is conceived for gripping fragile or soft objects with complex, irregular shapes that are easily deformable. This novel gripper is designed for handling small objects of masses up to 0.5 kg. The maximum gripping stroke of the mobile jaw is 13.5 mm. The driving motor is a pneumatic muscle, an actuator with inherently compliant, spring-like behavior. Compliance is the feature responsible for the soft character of the gripper system, ensuring its passive adaptability to the nature of the object to be gripped. The paper presents the structural, kinematic, static, and dynamic models of the novel gripper system and describes the compliant behavior of the entire assembly. The results of the dynamic simulation of the gripper have confirmed the attaining of the imposed motion-related performance.
1. Introduction
Gripper systems are defined as mechanisms conceived for retaining and manipulating objects. These devices are essential in robotics, in numerous industrial processes, and various other applications, acting like the “hands” of the machines or assisting tasks requiring gripping and moving of objects. Robotic gripper systems are essentially useful when deployed for repetitive and occasionally dangerous tasks. Examples of applications can be found in many areas, like food industry and agriculture [1,2,3], marine robotics [4,5], aerospace technology, such as drones for transportation [6], as well as in the field of miniaturization [7].
Gripper systems must cumulate a number of characteristics, such as high energy efficiency, compactness, easy utilization, being made from innovative, light materials, ensuring a compliant behavior, and being adaptable to human–robot interaction. Research conducted over the last years has been aimed at developing gripper systems with a small number of degrees of mobility, while being compliant and adaptable to the complex shapes of the manipulated objects. An additional requirement is obtaining these characteristics at the smallest possible costs.
A current trend of particular interest concerns developing soft gripper systems that support not only complex, irregular shapes of the objects to be manipulated but also their consistency. Fragile and soft objects (e.g., eggs, cakes, fruit) are often damaged because of an excessive gripping force or consequently to great deformation. Developing compliant gripper systems that ensure soft gripping represents a challenge [8]. A solution to these problems is the soft robotic gripper that comes with promising benefits, like excellent flexibility [9], high adaptability to the environment [10], and human–machine safety [11]. From injection molding to harvesting fruit and even robotic surgery, soft gripper technology facilitates the gripping and manipulation of any type of object. While conventional grippers require intensive processing and calculations to handle small or fragile objects, soft grippers can do it more safely, efficiently, and effectively [12]. Soft grippers, made from compliant and flexible materials, are able to conform better to various shapes. They are also more suitable for delicate grasping tasks, as they typically apply gentler forces compared to rigid grippers [5].
Soft gripper systems currently available on the marketplace are widely varied in several aspects, such as their dimensions, number of jaws, stroke lengths, gripping force, and type of actuation. They benefit from dexterity and gentleness to pick and place even the most delicate of objects. Soft grippers are a great option because they are simpler and more flexible than more complicated or specialized end-of-arm tooling [12].
Nature is the main source of inspiration for developing novel compliant gripper systems. The role of bionics as a branch of science is to transfer knowledge from biology to engineering with the purpose of developing novel products and technologies [13]. Thus, for example, the study of the effector organs of birds, fish, and land animals has led to the development of robotic soft grippers for handling delicate and irregularly shaped objects without causing damage [14]. Similarly to bird claws, many soft grippers use between two and four hydraulically or pneumatically actuated fingers. In the case of pneumatic systems, for example, the fingers made from soft rubber are hollow (tubular). When the fingers are subject to interior pressure, they flex and wrap around the object to be gripped. The gripping force is adjusted by the pressure of the compressed air.
Birglen et al. [15] delivered a comprehensive study on various types of gripper systems. Based on information taken from the catalogs of several known companies, the authors devised an analysis of the characteristics of industrial grippers. Included in the specifications under scrutiny in this article were stroke, force, and weight. The analysis yielded the conclusion that pneumatic actuation of soft grippers is preferable to actuation by cables or shape memory alloys [16,17]. The main reasons for this choice are based on certain advantages offered by pneumatic actuation, like the compactness of the driving elements, the favorable power-to-weight ratio, low costs, easy maintenance, clean work environment, etc. Another important characteristic required for the manipulation of delicate objects is compliance, or the spring-like behavior found in biological systems. Compliant mechanisms are based on the elastic deformation of their flexible components in order to complete the transformation of motion and force. Adaptable compliance is used to make the interaction between robots and their environment more natural. Compliant mechanisms are used on a large scale in minimally invasive surgery, also for high-precision assembling, and the manipulation of fragile and deformable objects [18,19].
Many variants of pneumatically actuated soft grippers have been developed that can grip not only regular-shaped, but also irregular-shaped objects such as bottles, glasses, and scissors [20,21,22]. Examples of soft grippers are those actuated by McKibben artificial muscles, passive compliant actuators that include an elastic element. A compliant actuator will allow deviations from its own equilibrium position, depending on the applied external force. The compressibility of air makes the pneumatic muscle inherently compliant, behaving in a spring-like fashion. The company Festo, Germany, has proposed such a gripper system modeled on the complex kinematics of a bird’s beak. The construction of the gripper is based on Watt linkages, and the actuator is a pneumatic muscle [23]. In [24] the authors present an innovative soft gripper conceived for automated assembling operations. This robotic soft gripper too utilizes a linear pneumatic muscle as its motor.
Most grippers installed on robots are two-jaw (finger) mechanisms that are used for both manipulation and assembling. Two-jaw grippers are the most frequent due to the simple configuration of object grasping, simple installation and deployment. A two-jaw gripper provides an equal amount of force at each finger and is easier to automate due to its simple design.
In industry, repetitive manufacturing tasks like grasping irregular and/or fragile objects, manipulation of delicate objects, and automated assembly are frequent and require the deployment of compliant gripper systems. Thus, in automated assembly for instance, the non-homogeneity of the dimensional characteristics of the surfaces to be paired is compensated by soft gripper systems. Their structure includes a Remote Centre Compliance mechanism (RCC) that ensures the necessary adaptive behavior such as to compensate for the frequently inevitable misalignment of the parts to be assembled. Soft, compliant gripper systems can be utilized with robotic arms that have a lower positioning precision, thus allowing for a more cost-effective technical solution.
The reviewed specialist literature while presenting many variants of pneumatically actuated soft grippers, is however indicative of that fact, that the concept of integrating pneumatic muscles in industrial manufacturing has not been sufficiently exploited. This is due to the relatively recent emergence of such actuators, as well as to insufficient knowledge of their performance. For this reason, this paper proposes a soft gripper with two parallel jaws, a fixed and a mobile one, actuated by a pneumatic muscle. Upon being charged with compressed air, the pneumatic muscle contracts axially and controls the gripping of the object by means of a rack and pinion mechanism. The device does not require sensors or complex controllers, as it is the mechanical system itself that provides the required adaptive behavior. The proposed gripper system can be used in various applications such as human–robot interaction and collaboration in performing manufacturing tasks. The concrete manufacturing application this system has been designed for and that is analyzed and discussed in this paper is to grasp objects of various consistencies, fragile or deformable.
Specifically, this article is organized as follows: Section 2 discusses the main characteristic required of a soft gripper, namely compliance. Further presented are the necessary phases of the gripping process of an object and the required variation mode of a gripper’s compliance during the travel of its jaws. Section 3 of the paper presents the modeling of the gripper. The structural, kinematic, static and dynamic models of the proposed gripper are presented. Model-Based-Design techniques via MatLab R2021b software are used to analyze and validate the system’s behavior. Section 4 presents the calculation of the gripper’s rigidity and compliance and the corresponding characteristic curves. These are in agreement with the hypotheses formulated in Section 2. Section 5 is dedicated to the main conclusions yielded by the study.
2. Soft Gripping Requirements
Humans use their fingers to grasp objects of various consistencies, fragile or deformable, such as eggs, fruit, and glass. This happens instinctively by using the tactile sense in order to apply adequate force. For a robotic hand, however, the safe manipulation of delicate or deformable objects is an extremely difficult task. This is due to the fact that robots generally lack a well-developed tactile sense, relying upon complex vision and computational schemes [25].
Understanding the mechanics of the motions required for gripping and manipulating an object resorts to the principles of analogical bionics (a top-down approach). In this case, the sequence of steps are as follows: 1. defining the problem; 2. identifying and analyzing analogies in nature; and 3. identifying technical solutions for the formulated problem based on the identified natural models.
This approach requires decomposing the gripping process into phases and elementary motions. Thus, the action of gripping is broken down into standard phases, specific to all natural or artificial gripping systems (including animals, birds, insects, mechanical systems, etc.). Generally, the manipulation of an object goes through the following standard phases:
- Initiation of contact; the gripper jaws approach the object, and their dedicated surfaces touch the target.
- Achieving contact and orientation of the object grasped between the jaws.
- Fixing the object firmly between the jaws, by increasing the holding force. For fragile objects, the retaining forces must adapt to the concrete case.
- Releasing the object either by gravity or with the help of special systems.
Figure 1 shows the necessary phases for grasping an object in the case of a gripper with a fixed and a mobile jaw:
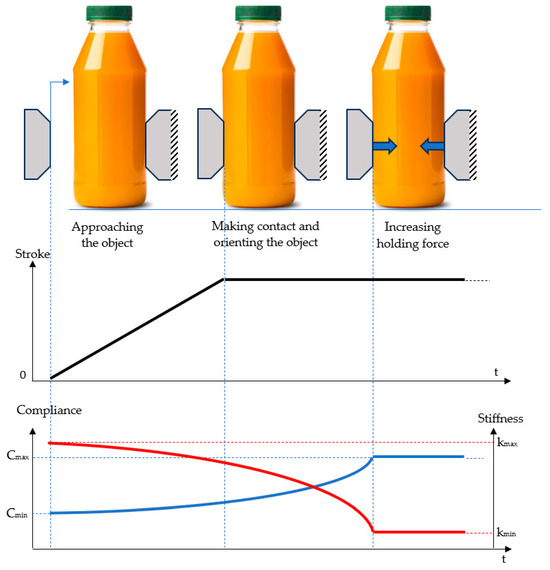
Figure 1.
Decomposition of the gripping process.
In order to avoid causing damage to fragile or easily deformable objects, their gripping between jaws requires the use of adaptable grippers. The characteristic that ensures the adaptability of the gripper to the complex shape and/or the consistency of the object to be gripped is compliance, the inverse of rigidity. A system that benefits from this characteristic allows deviations from a certain position of equilibrium when subject to exterior forces.
Starting from the phases of the gripping process of an object, Figure 1 shows also how compliance and rigidity of the gripper should vary in time (blue and red curves, respectively). In the approaching phase of the jaws to the object to be gripped, the rigidity of the system has to be great, and the compliance minimal. After achieving the contact between the jaws and the object to be gripped, in order to prevent its deforming, the compliance of the system has to reach its maximum, and the rigidity has to tend towards its minimum. The form of the compliance curve has to be concave, indicative of the fact that at the beginning of the gripping process the gradient of compliance increase is small. In phase of firm fixing of the object between the jaws by increasing the holding force, compliance has to increase rapidly, tending towards maximum values.
A modality of achieving compliant behavior is using soft fluidic actuation. In this case, the holding forces of a deformable object are generated by the controlled pressure increase in a fluid that is introduced into a hermetically closed chamber. The configuration of this chamber allows its deformation from a certain direction, resulting in a displacement caused by either an elongation or a contraction [26]. The idea of the directed deformation of a fluidic actuator originates in the analogy with biological muscles that contract in response to stimuli. Pneumatic muscles are examples of such actuators working similarly to the human muscle, namely ensuring an axial contraction by modifying their geometrical form. The compressibility of air makes them inherently compliant, behaving in a spring-like fashion [27,28]. Pneumatic muscles are variable stiffness actuators (VSAs), also known as adjustable compliant actuators (ACAs).
Knowing the sequence of the necessary phases for gripping an object, further on presented is a bioinspired constructive variant of a gripper actuated by a pneumatic muscle. The selected solution is a gripper with two parallel jaws, a mobile and a fixed one.
3. Modeling of the Gripper
3.1. Structural, Kinematic, and Static Modeling of the Gripper
The constructive variant shown in Figure 2 proposes an asymmetrical solution with a single mobile jaw, gripping being achieved by form and friction. Between the motor (the pneumatic muscle) and the end elements (the jaws), a mechanism consisting of rigid elements is interposed, namely two rack and pinion mechanisms.
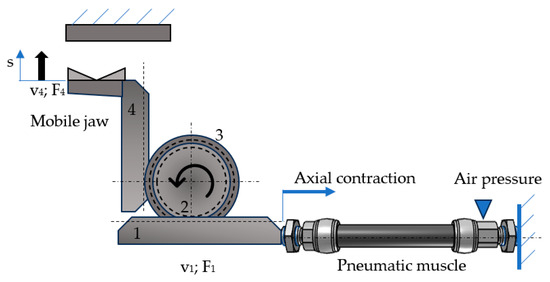
Figure 2.
Kinematic diagram of the gripper.
The input quantities of the system are the speed (v1) and the force (F1) developed by the pneumatic muscle. These are transmitted to the jaws via two rack and pinion mechanisms (1–2 and 3–4, respectively). The output of the system represents its exterior connection to the jaws of the gripper and is characterized by speed v4 and force F4.
The block diagram of the gripper is shown in Figure 3.

Figure 3.
Block diagram of the gripper.
The analyzed system consists of a single linkage with series-connected components, with a number of two exterior links: L = 2. The input of the system consists of its connection to the pneumatic muscle, while its output is represented by the connection to an element supporting the jaw. The system consisting of the two mechanisms that are not connected to each other has a degree of mobility calculated by Equation (1):
where j is the number of component mechanisms.
By connecting the two mechanisms, the resulting degree of freedom of the system is given by Equation (2), where the number of couplings LC = 1 is as follows:
The relationship above is indicative of the fact that the studied mechanism is characterized by an independent exterior motion (speed v1) and by a dependent input force (F1). Consequently, the remaining exterior motion (v4) is dependent, and the remaining exterior force is (F4) independent.
Later, the motion transmission function v4 = f(v1) and the transmission function of the forces F1 = f(F4) will be determined.
The transmission ratio i14 is calculated by Equation (3):
Taking into account the couplings of the mechanisms and that ω2 = ω3, the transmission ratio from above can be written as
where z2 and z3 denote the number of teeth of gears 2 and 3 (z2 = 20; z3 = 30).
From Equations (3) and (4), follow the expression of :
In order to determine the transmission function, friction and the inertial effects of the moving masses were assumed neglectable:
In the calculations, the efficiency of the rack and pinion mechanisms was estimated at η = 0.97 [29]:
The total efficiency of the gripper is determined by Equation (8):
where β is a distribution coefficient equal to 1 (for a series-connected system with a single power branch). The global efficiency η14 is
where
Returning to Equation (6), the transmission function of the force is determined:
or
3.2. The Geometrical Model of the Gripper System
The geometrical model of the gripper is presented in Figure 4. For this constructive solution, gripping is achieved by form and friction.
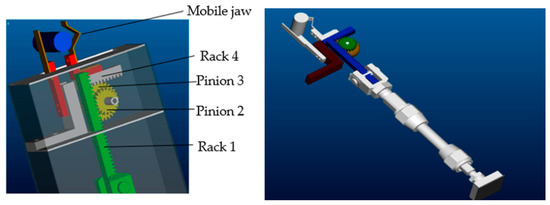
Figure 4.
Geometrical model of the gripper.
The utilized pneumatic muscle (not represented in the figure) is manufactured by Festo AG & Co., Esslingen am Neckar, Germany (DMSP-5-45N-RM-CM). The interior diameter of the tube is 5 mm, and the length of the active part is 45 mm. The maximum shortening of the muscle is 9 mm, at a charging pressure of 6 bar. Figure 5 shows the curves that describe the maximum forces developed by this pneumatic muscle versus air pressure and its axial contraction (stroke).
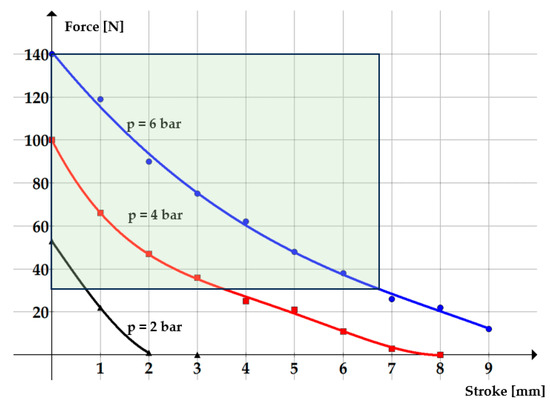
Figure 5.
Variation in the force versus the stroke and charging pressure.
The gripper was dimensioned considering a mass of m = 0.5 kg of the object to be gripped. The object is to be lifted with an acceleration of a = 5 m/s2. Further input data are gravitational acceleration: g = 9.81 m/s2; friction coefficient jaw/object: µ = 0.2; safety coefficient: S = 2; V-jaw angle 2∙α = 120° (Figure 6). For these values, the necessary force for retaining the object, FG, is determined by Equation (13):
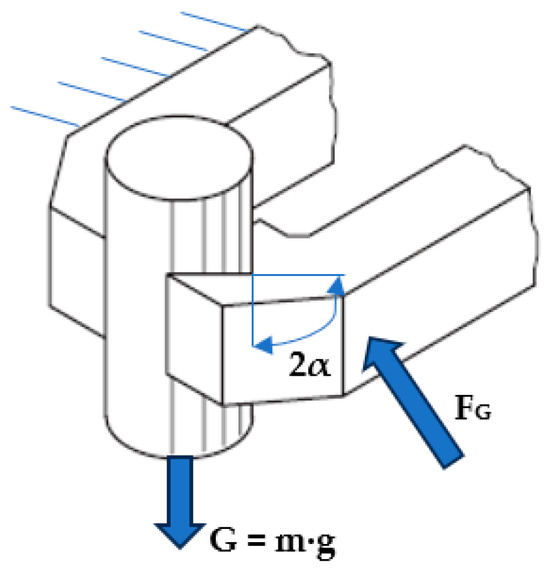
Figure 6.
Schematic of object gripping.
The selected pneumatic muscle is required to have the capacity of generating a force of at least 32.064 N; its operational range is marked green in Figure 5. Thus, for example, at a charging pressure of 6 bar of the compressed air, the maximum stroke of the pneumatic muscle is about 6.7 mm, and at a charging pressure of 4 bar, the stroke is 3.5 mm.
3.3. Functional Model of the Gripper
The functioning of the dynamic gripper system—currently in the development phase—was analyzed and validated by Model-Based Design (MBD) techniques available by means of the graphic extension Simulink® of Matlab® R2021b. One of the components of Simulink® is Simscape™ that uses mathematical models/algorithms and graphic/visual representations to identify design errors.
The functional model of the gripper (Figure 7) was conceived by means of Simscape™ Fluids™ that provides a set of specific components for the simulation of fluidic systems. The model of the gripper includes the kinematic structure of the mechanical assembly and the dimensional parameters of its components.
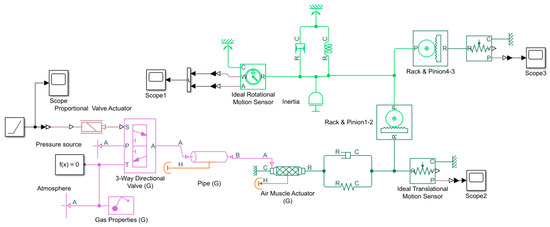
Figure 7.
Functional model of the soft gripper system.
The motion of rack 4 (the mobile jaw) is simulated by considering a 5 s gripping task of an object. This is possible by generating a ramp-type signal of the shape shown in Figure 8. The shape of this signal is visualized by means of the Scope block.
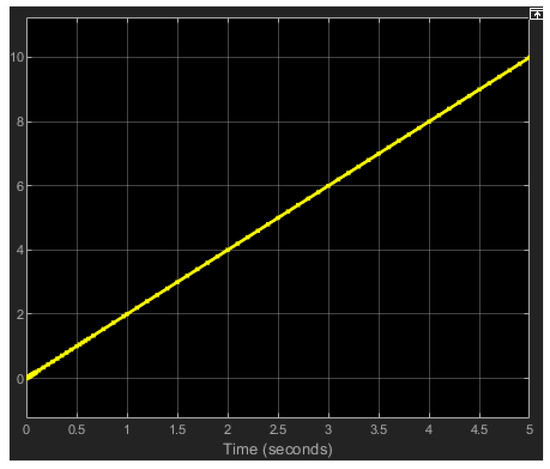
Figure 8.
Ramp-type input signal.
This signal is transmitted to the assembly consisting of the Proportional Valve Actuator and 3-Way Directional Valve blocks that together model a proportional pressure regulator. All blocks used for modeling are included by and taken form the Simulink Library.
The compressed air further reaches the Air Muscle Actuator block with characteristics in accordance with the Chou and Hannaford model [30]. The charging with compressed air of the pneumatic muscle determines its axial contraction, the variation in that versus time being shown by the Scope2 block (Figure 9).
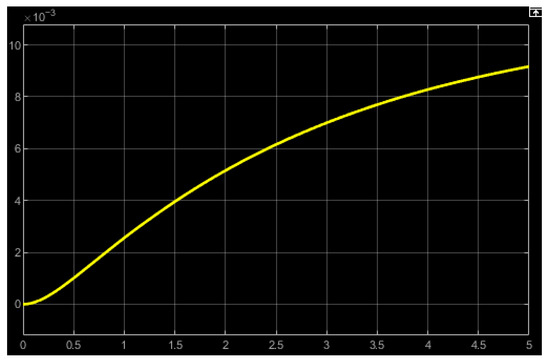
Figure 9.
Variation versus time of the axial contraction of the pneumatic muscle.
Charging the pneumatic muscle with compressed air at a pressure of 6 bar causes a displacement of its free end and implicitly of rack 1 by 9 mm. On its turn, the rack determines the rotation of gears 2 and 3. The variation versus time of the rotation angle is shown in Figure 10.
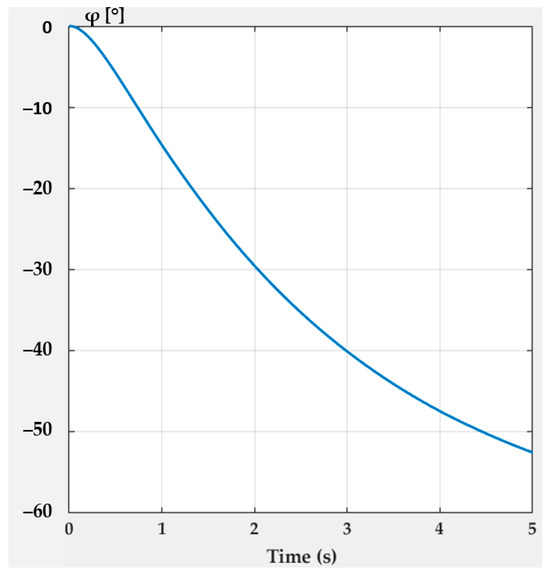
Figure 10.
Variation versus time of the rotation angle of gears 2 and 3.
The displacement of rack 4 is monitored by the Scope 3 block (Figure 11). It can be noticed that its displacement is amplified to 13.5 mm, determined by the assembly of the two gears with different numbers of teeth.
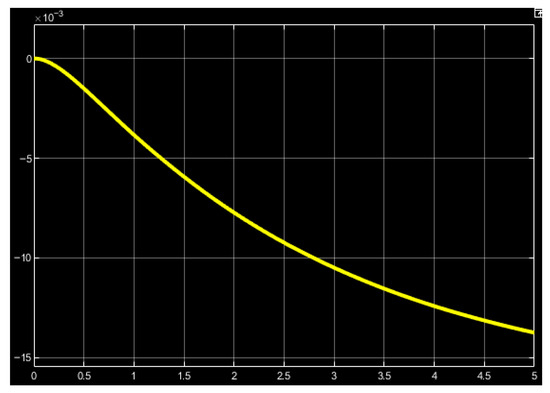
Figure 11.
Variation versus time of the displacement of rack 4.
The variation versus time of the speed of rack 4 is shown in Figure 12.
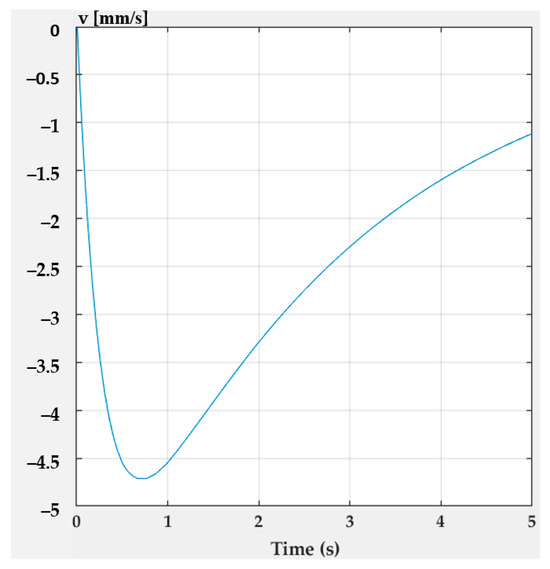
Figure 12.
Variation versus time of the speed of rack 4.
In this operational sequence, in the first part of the movement, when the jaw approaches the object without having made contact yet, a rapid increase in the velocity up to 4.7 mm/s can be noticed. Close to the jaw/object contact, the speed decreases to values that do not represent a risk for the integrity of the object to be gripped.
4. Analysis of the Compliant Behavior of the Gripper
The regression functions corresponding to the variation curves of the forces developed by the pneumatic muscle, with respect to stroke and charging pressure (as shown in Figure 5), have the following mathematical forms:
The above equations show a nonlinear dependency of the developed forces (F) on the stroke (s), which determines the compliant behavior of the analyzed system. Under these conditions, the rigidity k and its inverse, compliance C, will be variable and described mathematically by the following equations:
Of particular interest in analyzing this gripper system is the high-pressure range 4 and 6 bar (the area marked green in Figure 5). For these two pressures, Figure 13 and Figure 14 show the variation in rigidity and compliance, respectively, versus the stroke of the jaw.
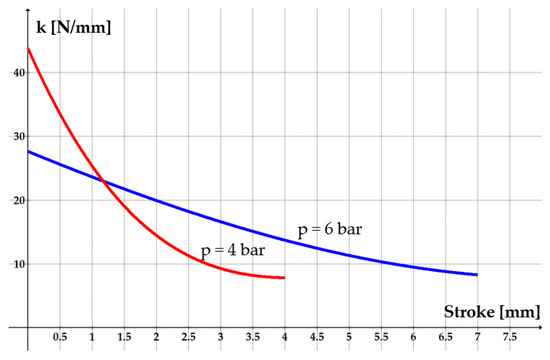
Figure 13.
Variation in rigidity versus the stroke of the jaw.
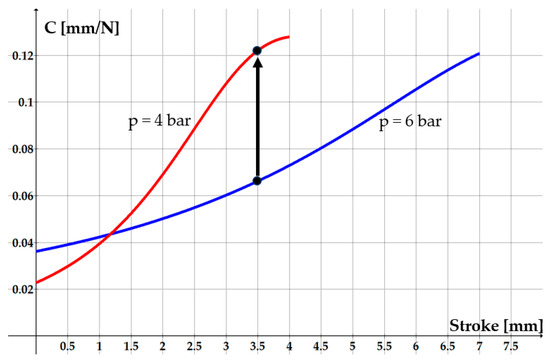
Figure 14.
Variation in compliance versus the stroke of the jaw.
The requirements for rigidity and compliance to be met by a soft gripper are presented in Figure 1. Figure 13 and Figure 14 show that the analyzed system meets these requirements, meaning that rigidity has a decreasing trend as the jaw approaches the object, while compliance increases. The shape of the compliance curve is concave, its tilt becoming steeper as the stroke progresses. The gripper’s compliance reaches increasingly higher values when firm gripping of the object is required.
An example of the gripper’s compliance modification is presented in Figure 14. For a jaw stroke of 3.5 mm, decreasing the air pressure from 6 to 4 bar increases compliance from 0.0633 to 0.122 mm/N—almost a twofold increase. Thus, the gripper is more adequate for grasping and fixing delicate, fragile, or easily deformable objects. Decreasing pressure from 6 to 4 bar entails a decrease in the gripping force from 67.475 N to 31.01 N. This force, however, is sufficient to grip a 0.5 L deformable plastic bottle, as studies indicate that an average grip strength of around 10 N is required.
The obtained results presented above were compared to those measured on the gripper prototype presented by the authors in [24]. In that device, a 1 mm jaw stroke with a reduction in air pressure from 6 to 4 bar increases compliance from 0.0215 to 0.0244 mm/N. It can be observed that, in the case of the new gripper system discussed here, the increase in compliance is greater, which is an advantage. A further advantage is the simpler construction, which entails lower costs.
The ability to adjust gripper compliance by modifying compressed air pressure enables control of the contact forces and keeps them within acceptable limits for safe manipulation, without the need for a feedback loop. In addition to adjustable feed pressure, the inherently compliant nature of the pneumatic muscle enables the soft gripping of fragile objects.
5. Conclusions
Modern gripper systems need to adapt to various applications that involve the manipulation of fragile, easily deformable objects. This paper proposed a soft gripper that meets these requirements and benefits from a simple structure that is achievable at low manufacturing costs. The motor used for actuation is a pneumatic muscle with an inherently compliant behavior. The compliance of a gripper system is responsible for its soft characteristics, allowing passive adaptation to the form of the object to be gripped. The proposed system can be used to perform various delicate manufacturing tasks, using compressed air as a working medium, contributing to the implementation of sustainable and eco-friendly manufacturing practices. The proposed system can also ensure the necessary adaptability for compensating misalignments in automated assembling, robustness in situations of minor impacts, as well as operator safety, all based on a simple design and at reduced costs. Furthermore, this soft gripper system lends itself to utilization with robotic arms that have a lower positioning precision, thus allowing for a more cost-effective technical solution.
The paper presents a novel concept of a soft parallel gripper with two jaws, a fixed and a mobile one. The structural, kinematic, static, and dynamic models of the gripper are described. An important aspect to be analyzed is the system’s behavior with regard to rigidity and compliance. Compliance values are modified by varying air pressure in the pneumatic muscle by means of a proportional pressure regulator. The compliant behavior meets the requirements for such a system, achieving soft gripping of an object without causing deformation.
Author Contributions
Conceptualization, T.D.; methodology, A.D.; validation, A.D. and T.D.; investigation, A.D. and T.D.; writing—original draft preparation, A.D.; writing—review and editing, A.D. and T.D.; supervision, T.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, B.; Xie, Y.; Zhou, J.; Wang, K.; Zhang, Z. State-of-the-art robotic grippers, grasping and control strategies, as well as their applications in agricultural robots: A review. Comput. Electron. Agric. 2020, 177, 105694. [Google Scholar] [CrossRef]
- Navas, E.; Fernández, R.; Sepúlveda, D.; Armada, M.; Gonzalez-de Santos, P. Soft grippers for automatic crop harvesting: A review. Sensors 2021, 21, 2689. [Google Scholar] [CrossRef] [PubMed]
- Elfferich, J.F.; Dodou, D.; Della Santina, C. Soft robotic grippers for crop handling or harvesting: A review. IEEE Access 2022, 10, 75428–75443. [Google Scholar] [CrossRef]
- Mazzeo, A.; Aguzzi, J.; Calisti, M.; Canese, S.; Vecchi, F.; Stefanni, S.; Controzzi, M. Marine Robotics for Deep-Sea Specimen Collection: A Systematic Review of Underwater Grippers. Sensors 2022, 22, 648. [Google Scholar] [CrossRef]
- Cortinovis, S.; Vitrani, G.; Maggiali, M.; Romeo, R.A. Control Methodologies for Robotic Grippers: A Review. Actuators 2023, 12, 332. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Huang, Z.; Liu, H.; Huang, T. Earthworm-Inspired Multimodal Pneumatic Continuous Soft Robot Enhanced by Winding Transmission. Cyborg Bionic Syst. 2025, 6, 0204. [Google Scholar] [CrossRef]
- Schmelter, T.; Bade, L.; Kuhlenkötter, B. A Two-Finger Gripper Actuated by Shape Memory Alloy for Applications in Automation Technology with Minimized Installation Space. Actuators 2024, 13, 425. [Google Scholar] [CrossRef]
- Huang, S.J.; Chang, W.; Su, J.-Y. Intelligent robotic gripper with adaptive grasping force. Int. J. Control Autom. 2017, 15, 2272–2282. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Q.; Chen, X. Design and analysis of a flexible robotic hand with soft fingers and a changeable palm. Adv. Robot. 2020, 34, 1041–1054. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Ren, Y.; Jin, G.; Zhang, C.; Chen, W.; Yan, F. Poly (ionic liquid) hydrogel-based anti-freezing ionic skin for a soft robotic gripper. Mater. Horiz. 2020, 7, 919–927. [Google Scholar] [CrossRef]
- Zhang, H.; Kumar, A.S.; Fuh, J.Y.H.; Wang, M.Y. Design and development of a topology-optimized three-dimensional printed soft gripper. Soft Robot. 2018, 5, 650–661. [Google Scholar] [CrossRef]
- Robotics Tomorrow. Soft Grippers Can Handle Small and Delicate Parts with Greater Ease. Available online: https://www.roboticstomorrow.com/story/2022/05/soft-grippers-can-handle-small-and-delicate-parts-with-greater-ease/18746/ (accessed on 24 May 2025).
- Bar-Cohen, Y. Biomimetics—Using nature to inspire human innovation. J. Bioinspir. Biomim. 2006, 1, 1. [Google Scholar] [CrossRef] [PubMed]
- Dieter, G.E. Engineering Design: A Material and Processing Approach, 3rd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Birglen, L.; Schlicht, T. A statistical review of industrial robotic grippers. Robot. Comput.-Integr. Manuf. 2018, 49, 88–97. [Google Scholar] [CrossRef]
- Yin, H.; Kong, C.; Li, J.; Yang, G. Modeling of grasping force for a soft robotic gripper with variable stiffness. Mech. Mach. Theory 2018, 128, 254–274. [Google Scholar] [CrossRef]
- Akbari, S.; Sakhaei, A.H.; Panjwani, S.; Kowsari, K.; Serjouei, A.; Ge, Q. Multimaterial 3D printed soft actuators powered by shape memory alloy wires. Sensors Actuators A Phys. 2019, 290, 177–189. [Google Scholar] [CrossRef]
- Sigmund, O. On the design of compliant mechanisms using topology optimization. Mech. Struct. Mach. 1997, 25, 493–524. [Google Scholar] [CrossRef]
- Ai, W.; Xu, Q. New structural design of a compliant gripper based on the Scott-Russell mechanism. Int. J. Adv. Robot. Syst. 2014, 11, 192. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, S.; Wang, Z. A soft-robotic gripper with enhanced object adaptation and grasping reliability. IEEE Robot. Autom. Lett. 2017, 2, 2287–2293. [Google Scholar] [CrossRef]
- Liu, S.; Wang, F.; Liu, Z.; Zhang, W.; Tian, Y.; Zhang, D. A two-finger soft-robotic gripper with enveloping and pinching grasping modes. IEEE ASME Trans. Mech. 2021, 26, 146–155. [Google Scholar] [CrossRef]
- Li, H.; Yao, J.; Zhou, P.; Chen, X.; Xu, Y.; Zhao, Y. High-load soft grippers based on bionic winding effect. Soft Robot. 2019, 6, 276–288. [Google Scholar] [CrossRef]
- PowerGripper. Available online: https://www.festo.com/gb/en/e/about-festo/research-and-development/bionic-learning-network/highlights-from-2010-to-2012/powergripper-id_33664/ (accessed on 25 May 2025).
- Deaconescu, A.; Deaconescu, T. Compliant Parallel Asymmetrical Gripper System. Technologies 2025, 13, 86. [Google Scholar] [CrossRef]
- Shea, H.R.; Shintake, J.; Floreano, D. Soft Compliant Gripper for Safe Manipulation of Extremely Fragile Objects. Available online: https://www.spie.org/news/6409-soft-compliant-gripper-for-safe-manipulation-of-extremely-fragile-objects (accessed on 24 May 2025).
- Digumarti, K.M.; Conn, A.T.; Rossiter, J. Euglenoid-inspired giant shape change for highly deformable soft robots. IEEE Robot. Autom. Lett. 2017, 2, 2302–2307. [Google Scholar] [CrossRef]
- Van Ham, R.; Sugar, T.G.; Vanderborght, B.; Hollander, K.W.; Lefeber, D. Compliant actuator designs. IEEE Robot. Autom. Mag. 2009, 16, 81–94. [Google Scholar] [CrossRef]
- Deaconescu, T.; Deaconescu, A. Pneumatic muscle actuated equipment for continuous passive motion. In IAENG Transactions on Engineering Technologies; Ao, S.L., Chan, A.H.S., Katagiri, H., Xu, L., Eds.; American Institute of Physics: Melville, NY, USA, 2009; Volume 3/1174, pp. 311–321. [Google Scholar]
- Muşat, M.; Stoica, G. Mechanical Transmissions with One-Step Reduction Gears. Designing Handbook [in Romanian]. Available online: http://www.omtr.pub.ro/didactic/indrumare/indrumar_gstoica.pdf (accessed on 24 May 2025).
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben Pneumatic Artificial Muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).