Flexural Analysis of Additively Manufactured Continuous Fiber-Reinforced Honeycomb Sandwich Structures
Abstract
1. Introduction
1.1. Mechanics of Sandwich Panels with Honeycomb Cores
1.2. Failure Mode Prediction Models for Sandwich Composite Panels
2. Materials and Methods
3. Results
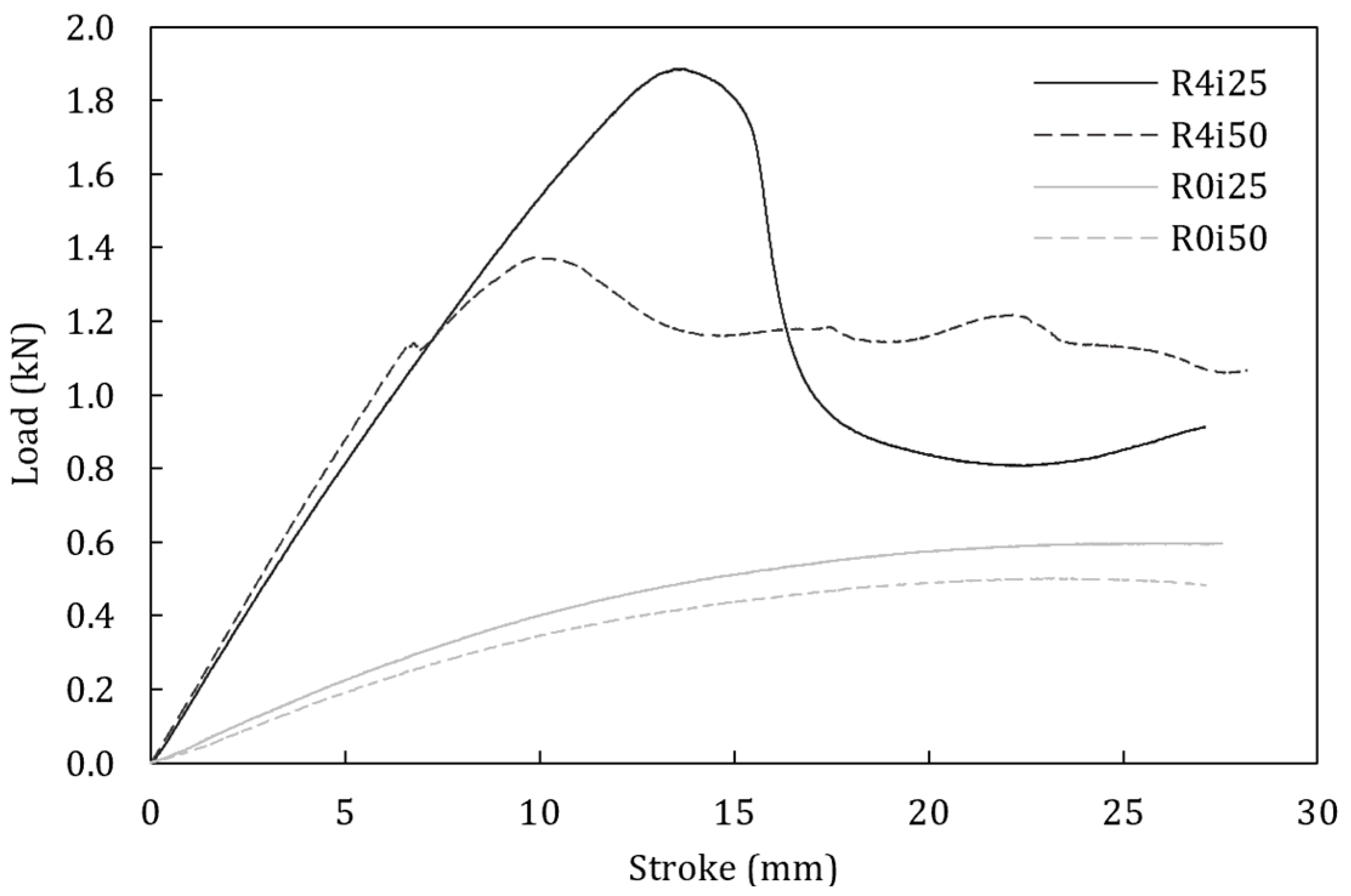
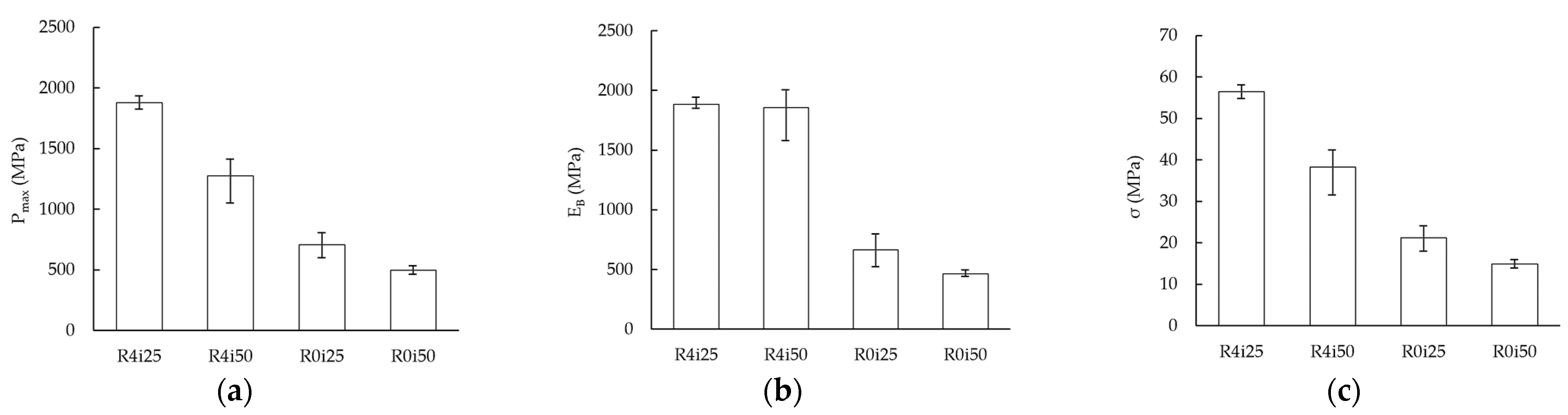
3.1. Mechanical Behavior of CFRC Sandwich Panels with Honeycomb Cores
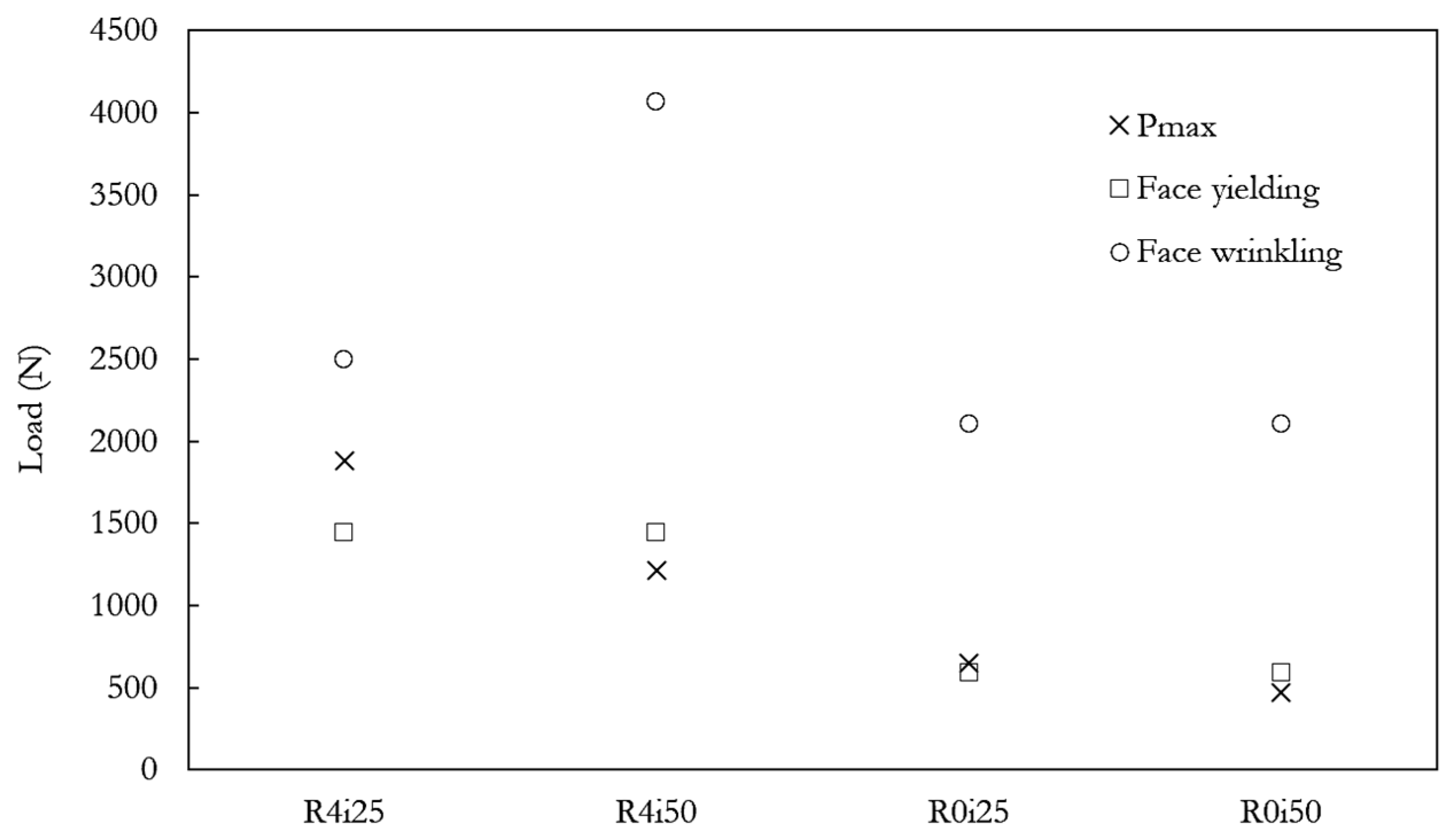
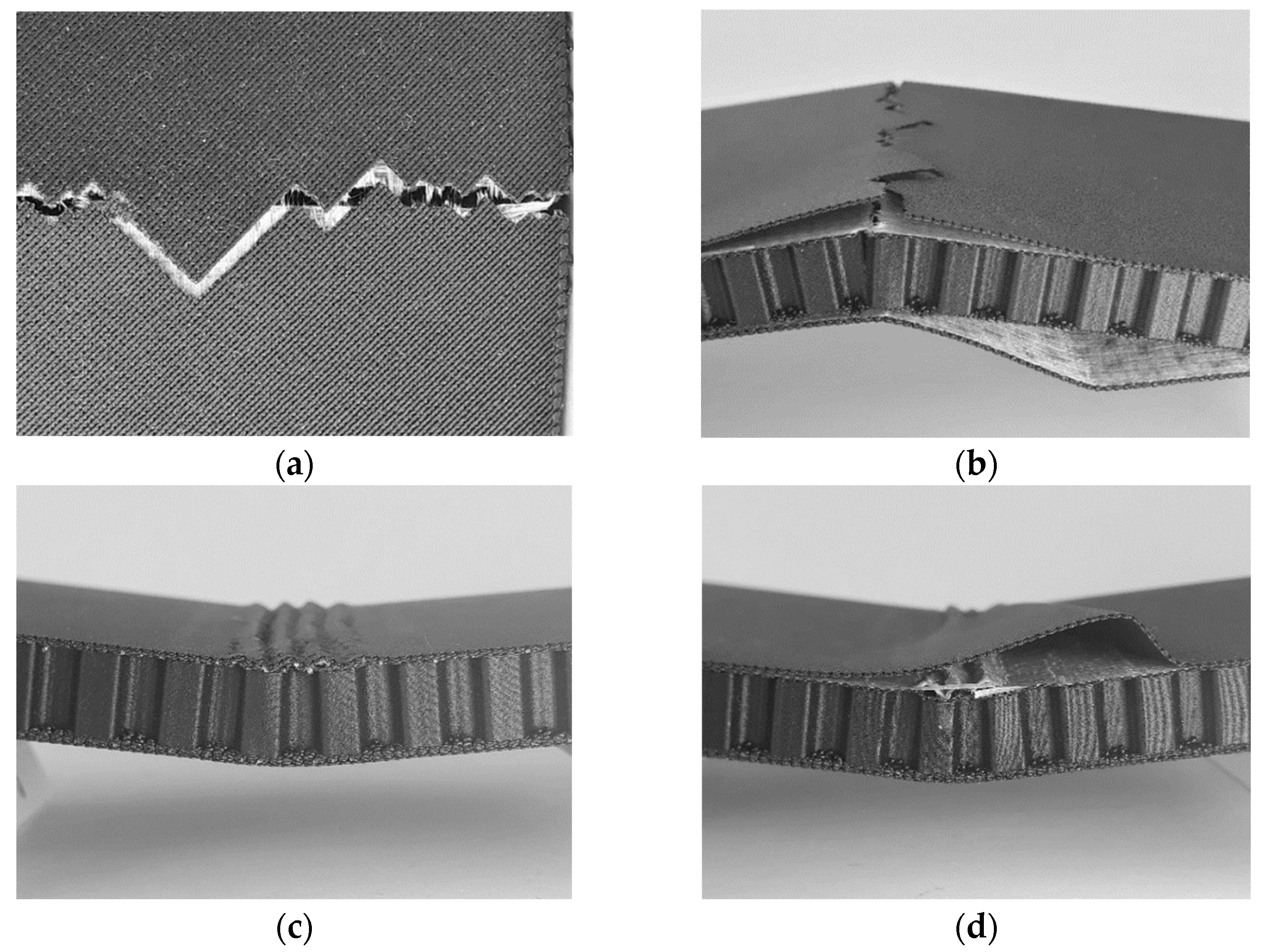
3.2. Failure Analysis of CFRC Sandwich Panels with Honeycomb Cores
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhate, D.; Hayduke, D. Architected Cellular Materials. In Additive Manufacturing Design and Applications; ASM International: Materials Park, OH, USA, 2023; pp. 1–10. [Google Scholar]
- Cuan-Urquizo, E.; Guerra Silva, R. Fused Filament Fabrication of Cellular, Lattice and Porous Mechanical Metamaterials: A Review. Virtual Phys. Prototyp. 2023, 18, e2224300. [Google Scholar] [CrossRef]
- Bru, J.; Leite, M.; Ribeiro, A.R.; Reis, L.; Deus, A.M.; Fátima Vaz, M. Bioinspired Structures for Core Sandwich Composites Produced by Fused Deposition Modelling. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 379–393. [Google Scholar] [CrossRef]
- Monteiro, J.G.; Sardinha, M.; Alves, F.; Ribeiro, A.R.; Reis, L.; Deus, A.M.; Leite, M.; Vaz, M.F. Evaluation of the Effect of Core Lattice Topology on the Properties of Sandwich Panels Produced by Additive Manufacturing. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 235, 1312–1324. [Google Scholar] [CrossRef]
- Antony, S.; Cherouat, A.; Montay, G. Fabrication and Characterization of Hemp Fibre Based 3D Printed Honeycomb Sandwich Structure by FDM Process. Appl. Compos. Mater. 2020, 27, 935–953. [Google Scholar] [CrossRef]
- Araújo, H.; Leite, M.; Ribeiro, A.R.; Deus, A.M.; Reis, L.; Vaz, M.F. The Effect of Geometry on the Flexural Properties of Cellular Core Structures. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 338–347. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. Honeycomb Sandwich Specimens Made of PLA and Produced Via 3D FDM Printing Process: An Experimental Study. J. Aircr. Spacecr. Technol. 2020, 4, 54–69. [Google Scholar] [CrossRef]
- Brischetto, S.; Ferro, C.G.; Torre, R.; Maggiore, P. 3D FDM Production and Mechanical Behavior of Polymeric Sandwich Specimens Embedding Classical and Honeycomb Cores. Curved Layer. Struct. 2018, 5, 80–94. [Google Scholar] [CrossRef]
- Gullapalli, H.; Massod, S.H.; Riza, S.; Ponnusamy, P. Flexural Behaviour of 2D Cellular Lattice Structures Manufactured by Fused Deposition Modelling. In Advances in Structures, Systems and Materials; Springer: Singapore, 2020; pp. 109–117. [Google Scholar]
- Gajdoš, I.; Kaščák, L.; Spišák, E.; Slota, J. Flexural Properties of FDM Prototypes Made with Honeycomb and Sparse Structure. Key Eng. Mater. 2015, 635, 169–173. [Google Scholar] [CrossRef]
- Beloshenko, V.; Beygelzimer, Y.; Chishko, V.; Savchenko, B.; Sova, N.; Verbylo, D.; Voznyak, A.; Vozniak, I. Mechanical Properties of Flexible Tpu-Based 3d Printed Lattice Structures: Role of Lattice Cut Direction and Architecture. Polymers 2021, 13, 2986. [Google Scholar] [CrossRef]
- Essassi, K.; Rebiere, J.L.; El Mahi, A.; Ben Souf, M.A.; Bouguecha, A.; Haddar, M. Experimental and Analytical Investigation of the Bending Behaviour of 3D-Printed Bio-Based Sandwich Structures Composites with Auxetic Core under Cyclic Fatigue Tests. Compos. Part A Appl. Sci. Manuf. 2020, 131, 105775. [Google Scholar] [CrossRef]
- Yazdani Sarvestani, H.; Akbarzadeh, A.H.; Mirbolghasemi, A.; Hermenean, K. 3D Printed Meta-Sandwich Structures: Failure Mechanism, Energy Absorption and Multi-Hit Capability. Mater. Des. 2018, 160, 179–193. [Google Scholar] [CrossRef]
- Lu, C.; Qi, M.; Islam, S.; Chen, P.; Gao, S.; Xu, Y.; Yang, X. Mechanical Performance of 3D-Printing Plastic Honeycomb Sandwich Structure. Int. J. Precis. Eng. Manuf. Green. Technol. 2018, 5, 47–54. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Fernandez, E.; Uribe-Lam, E. Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials 2022, 15, 1841. [Google Scholar] [CrossRef]
- Hou, Y.; Tai, Y.H.; Lira, C.; Scarpa, F.; Yates, J.R.; Gu, B. The Bending and Failure of Sandwich Structures with Auxetic Gradient Cellular Cores. Compos. Part A Appl. Sci. Manuf. 2013, 49, 119–131. [Google Scholar] [CrossRef]
- Cao, D.; Bouzolin, D.; Lu, H.; Griffith, D.T. Bending and Shear Improvements in 3D-Printed Core Sandwich Composites through Modification of Resin Uptake in the Skin/Core Interphase Region. Compos. B Eng. 2023, 264, 110912. [Google Scholar] [CrossRef]
- Travieso-Rodriguez, J.A.; Zandi, M.D.; Jerez-Mesa, R.; Lluma-Fuentes, J. Fatigue Behavior of PLA-Wood Composite Manufactured by Fused Filament Fabrication. J. Mater. Res. Technol. 2020, 9, 8507–8516. [Google Scholar] [CrossRef]
- Dong, Y.; Milentis, J.; Pramanik, A. Additive Manufacturing of Mechanical Testing Samples Based on Virgin Poly (Lactic Acid) (PLA) and PLA/Wood Fibre Composites. Adv. Manuf. 2018, 6, 71–82. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal Design and Modeling of Gyroid-Based Functionally Graded Cellular Structures for Additive Manufacturing. Comput.-Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Forés-Garriga, A.; Gómez-Gras, G.; Pérez, M.A. Lightweight Hybrid Composite Sandwich Structures with Additively Manufactured Cellular Cores. Thin-Walled Struct. 2023, 191, 111082. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive Manufacturing of Carbon Fiber Reinforced Thermoplastic Composites Using Fused Deposition Modeling. Compos. B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Dey, A.; Roan Eagle, I.N.; Yodo, N. A Review on Filament Materials for Fused Filament Fabrication. J. Manuf. Mater. Process. 2021, 5, 69. [Google Scholar] [CrossRef]
- Ferreira, I.; Machado, M.; Alves, F.; Torres Marques, A. A Review on Fibre Reinforced Composite Printing via FFF. Rapid Prototyp. J. 2019, 25, 972–988. [Google Scholar] [CrossRef]
- Penumakala, P.K.; Santo, J.; Thomas, A. A Critical Review on the Fused Deposition Modeling of Thermoplastic Polymer Composites. Compos. B Eng. 2020, 201, 108336. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Álvarez-Trejo, A.; Robles Gil, A.; Tejada-Ortigoza, V.; Camposeco-Negrete, C.; Uribe-Lam, E.; Treviño-Quintanilla, C.D. Effective Stiffness of Fused Deposition Modeling Infill Lattice Patterns Made of PLA-Wood Material. Polymers 2022, 14, 337. [Google Scholar] [CrossRef]
- Li, J.; Durandet, Y.; Huang, X.; Sun, G.; Ruan, D. Additively Manufactured Fiber-Reinforced Composites: A Review of Mechanical Behavior and Opportunities. J. Mater. Sci. Technol. 2022, 119, 219–244. [Google Scholar] [CrossRef]
- Safari, F.; Kami, A.; Abedini, V. 3D Printing of Continuous Fiber Reinforced Composites: A Review of the Processing, Pre- and Post-Processing Effects on Mechanical Properties. Polym. Polym. Compos. 2022, 30, 096739112210987. [Google Scholar] [CrossRef]
- Pandelidi, C.; Bateman, S.; Piegert, S.; Hoehner, R.; Kelbassa, I.; Brandt, M. The Technology of Continuous Fibre-Reinforced Polymers: A Review on Extrusion Additive Manufacturing Methods. Int. J. Adv. Manuf. Technol. 2021, 113, 3057–3077. [Google Scholar] [CrossRef]
- Cheng, P.; Peng, Y.; Li, S.; Rao, Y.; Le Duigou, A.; Wang, K.; Ahzi, S. 3D Printed Continuous Fiber Reinforced Composite Lightweight Structures: A Review and Outlook. Compos. B Eng. 2023, 250, 110450. [Google Scholar] [CrossRef]
- Krajangsawasdi, N.; Blok, L.G.; Hamerton, I.; Longana, M.L.; Woods, B.K.S.; Ivanov, D.S. Fused Deposition Modelling of Fibre Reinforced Polymer Composites: A Parametric Review. J. Compos. Sci. 2021, 5, 29. [Google Scholar] [CrossRef]
- Wong, J.; Altassan, A.; Rosen, D.W. Additive Manufacturing of Fiber-Reinforced Polymer Composites: A Technical Review and Status of Design Methodologies. Compos. B Eng. 2023, 255, 110603. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.F.M. A Critical Review on 3D Printed Continuous Fiber-Reinforced Composites: History, Mechanism, Materials and Properties. Compos. Struct. 2020, 232, 111476. [Google Scholar] [CrossRef]
- van de Werken, N.; Tekinalp, H.; Khanbolouki, P.; Ozcan, S.; Williams, A.; Tehrani, M. Additively Manufactured Carbon Fiber-Reinforced Composites: State of the Art and Perspective. Addit. Manuf. 2020, 31, 100962. [Google Scholar] [CrossRef]
- Adil, S.; Lazoglu, I. A Review on Additive Manufacturing of Carbon Fiber-Reinforced Polymers: Current Methods, Materials, Mechanical Properties, Applications and Challenges. J. Appl. Polym. Sci. 2023, 140, e53476. [Google Scholar] [CrossRef]
- Rimkus, A.; Farh, M.M.; Gribniak, V. Continuously Reinforced Polymeric Composite for Additive Manufacturing—Development and Efficiency Analysis. Polymers 2022, 14, 3471. [Google Scholar] [CrossRef]
- Justo, J.; Távara, L.; García-Guzmán, L.; París, F. Characterization of 3D Printed Long Fibre Reinforced Composites. Compos. Struct. 2018, 185, 537–548. [Google Scholar] [CrossRef]
- Dickson, A.N.; Barry, J.N.; McDonnell, K.A.; Dowling, D.P. Fabrication of Continuous Carbon, Glass and Kevlar Fibre Reinforced Polymer Composites Using Additive Manufacturing. Addit. Manuf. 2017, 16, 146–152. [Google Scholar] [CrossRef]
- Pertuz, A.D.; Díaz-Cardona, S.; González-Estrada, O.A. Static and Fatigue Behaviour of Continuous Fibre Reinforced Thermoplastic Composites Manufactured by Fused Deposition Modelling Technique. Int. J. Fatigue 2020, 130, 105275. [Google Scholar] [CrossRef]
- Naranjo-Lozada, J.; Ahuett-Garza, H.; Orta-Castañón, P.; Verbeeten, W.M.H.; Sáiz-González, D. Tensile Properties and Failure Behavior of Chopped and Continuous Carbon Fiber Composites Produced by Additive Manufacturing. Addit. Manuf. 2019, 26, 227–241. [Google Scholar] [CrossRef]
- Sugiyama, K.; Matsuzaki, R.; Ueda, M.; Todoroki, A.; Hirano, Y. 3D Printing of Composite Sandwich Structures Using Continuous Carbon Fiber and Fiber Tension. Compos. Part A Appl. Sci. Manuf. 2018, 113, 114–121. [Google Scholar] [CrossRef]
- An, D.-S.; Kim, T.H.; Lee, E.-H. Analytical and Experimental Investigation into the Relative Influence of Core and Side Parts on Structures Laminated by Fused Deposition Modeling. Int. J. Precis. Eng. Manuf.-Green. Technol. 2021, 8, 13–27. [Google Scholar] [CrossRef]
- Feng, J.; Yao, L.; Lyu, Z.; Wu, Z.; Zhang, G.; Zhao, H. Mechanical Properties and Damage Failure of 3D-printed Continuous Carbon Fiber-reinforced Composite Honeycomb Sandwich Structures with Fiber-interleaved Core. Polym. Compos. 2023, 44, 1980–1992. [Google Scholar] [CrossRef]
- ASTM C393; Standard Test Method for Core Shear Properties of Sandwich Constructions by Beam Flexure 1. ASM International: Materials Park, OH, USA, 2006.
- ASTM D790-17; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials 1. ASM International: Materials Park, OH, USA, 2017. [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997; ISBN 9781139878326. [Google Scholar]
- Staal, R.A.; Horrigan, D.P.W.; Mallinson, G.D. Wrinkling Stresses in Honeycomb Sandwich Panels Using Discrete and Continuum Core Representations. In Proceedings of the 13th European Conference on Composite Materials; European Society for Composite Materials, Stockholm, Sweden, 2–5 June 2008. [Google Scholar]
- Tolf, G.; Clarin, P. Comparison between Flexural and Tensile Modulus of Fibre Composites. Fibre Sci. Technol. 1984, 21, 319–326. [Google Scholar] [CrossRef]
- Callister, W. Materials Science and Engineering: An Introduction, 5th ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Markforged. An Introductory Guide Carbon Fiber 3D Printing; Markforged: Waltham, MA, USA; Available online: https://3d.markforged.com/carbon-fiber-3d-printing-whitepaper.html (accessed on 5 October 2024).
- Markforged Composites—Material Datasheet. Available online: https://static.markforged.com/downloads/composites-data-sheet.pdf (accessed on 21 July 2023).
- Saeed, K.; McIlhagger, A.; Harkin-Jones, E.; McGarrigle, C.; Dixon, D.; Ali Shar, M.; McMillan, A.; Archer, E. Characterization of Continuous Carbon Fibre Reinforced 3D Printed Polymer Composites with Varying Fibre Volume Fractions. Compos. Struct. 2022, 282, 115033. [Google Scholar] [CrossRef]
- Tekoglu, C.; Onck, P.R. Size Effects in the Mechanical Behavior of Cellular Materials. J. Mater. Sci. 2005, 40, 5911–5917. [Google Scholar] [CrossRef]
- Andrews, E.W.; Gioux, G.; Onck, P.; Gibson, L.J. Size Effects in Ductile Cellular Solids. Part II: Experimental Results. Int. J. Mech. Sci. 2001, 43, 701–713. [Google Scholar] [CrossRef]
- Tekoglu, C.; Gibson, L.J.; Pardoen, T.; Onck, P.R. Size Effects in Foams: Experiments and Modeling. Prog. Mater. Sci. 2011, 56, 109–138. [Google Scholar] [CrossRef]
- Cofaru, N.F.; Pascu, A.; Oleksik, M.; Petruse, R. Tensile Properties of 3D-Printed Continuous-Fiber-Reinforced Plastics. Mater. Plast. 2022, 58, 271–282. [Google Scholar] [CrossRef]
- Caminero, M.A.; Chacón, J.M.; García-Moreno, I.; Reverte, J.M. Interlaminar Bonding Performance of 3D Printed Continuous Fibre Reinforced Thermoplastic Composites Using Fused Deposition Modelling. Polym. Test. 2018, 68, 415–423. [Google Scholar] [CrossRef]
- Abdullah Aloyaydi, B.; Sivasankaran, S.; Rizk Ammar, H. Influence of Infill Density on Microstructure and Flexural Behavior of 3D Printed PLA Thermoplastic Parts Processed by Fusion Deposition Modeling. AIMS Mater. Sci. 2019, 6, 1033–1048. [Google Scholar] [CrossRef]
- Baich, L.; Manogharan, G. Study of Infill Print Parameters on Mechanical Strength and Production Cost-Time of 3D Printed ABS Parts. In Proceedings of the 26th Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, SFF 2015, Austin, TX, USA, 10–12 August 2015; pp. 209–218. [Google Scholar]
- Ashby, M.F. Designing Hybrid Materials. In Materials Selection in Mechanical Design; Elsevier: Amsterdam, The Netherlands, 2011; pp. 299–340. [Google Scholar]
- Goh, G.D.; Dikshit, V.; Nagalingam, A.P.; Goh, G.L.; Agarwala, S.; Sing, S.L.; Wei, J.; Yeong, W.Y. Characterization of Mechanical Properties and Fracture Mode of Additively Manufactured Carbon Fiber and Glass Fiber Reinforced Thermoplastics. Mater. Des. 2018, 137, 79–89. [Google Scholar] [CrossRef]
- Caminero, M.A.; Rodríguez, G.P.; Muñoz, V. Effect of Stacking Sequence on Charpy Impact and Flexural Damage Behavior of Composite Laminates. Compos. Struct. 2016, 136, 345–357. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; Núñez, P.J.; García-Plaza, E.; García-Moreno, I.; Reverte, J.M. Additive Manufacturing of Continuous Fibre Reinforced Thermoplastic Composites Using Fused Deposition Modelling: Effect of Process Parameters on Mechanical Properties. Compos. Sci. Technol. 2019, 181, 107688. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Y.; Long, H.; Baghani, M.; Rao, Y.; Peng, Y. Hygrothermal Aging Effects on the Mechanical Properties of 3D Printed Composites with Different Stacking Sequence of Continuous Glass Fiber Layers. Polym. Test. 2021, 100, 107242. [Google Scholar] [CrossRef]
- Chabaud, G.; Castro, M.; Denoual, C.; Le Duigou, A. Hygromechanical Properties of 3D Printed Continuous Carbon and Glass Fibre Reinforced Polyamide Composite for Outdoor Structural Applications. Addit. Manuf. 2019, 26, 94–105. [Google Scholar] [CrossRef]
- Iragi, M.; Pascual-González, C.; Esnaola, A.; Lopes, C.S.; Aretxabaleta, L. Ply and Interlaminar Behaviours of 3D Printed Continuous Carbon Fibre-Reinforced Thermoplastic Laminates; Effects of Processing Conditions and Microstructure. Addit. Manuf. 2019, 30, 100884. [Google Scholar] [CrossRef]
- Somireddy, M.; Singh, C.V.; Czekanski, A. Analysis of the Material Behavior of 3D Printed Laminates Via FFF. Exp. Mech. 2019, 59, 871–881. [Google Scholar] [CrossRef]
- Rajpurohit, S.R.; Dave, H.K.; Bodaghi, M. Classical Laminate Theory for Flexural Strength Prediction of FDM 3D Printed PLAs. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Saeed, K.; McIlhagger, A.; Harkin-Jones, E.; Kelly, J.; Archer, E. Predication of the In-Plane Mechanical Properties of Continuous Carbon Fibre Reinforced 3D Printed Polymer Composites Using Classical Laminated-Plate Theory. Compos. Struct. 2021, 259, 113226. [Google Scholar] [CrossRef]
- Yavas, D.; Zhang, Z.; Liu, Q.; Wu, D. Interlaminar Shear Behavior of Continuous and Short Carbon Fiber Reinforced Polymer Composites Fabricated by Additive Manufacturing. Compos. B Eng. 2021, 204, 108460. [Google Scholar] [CrossRef]
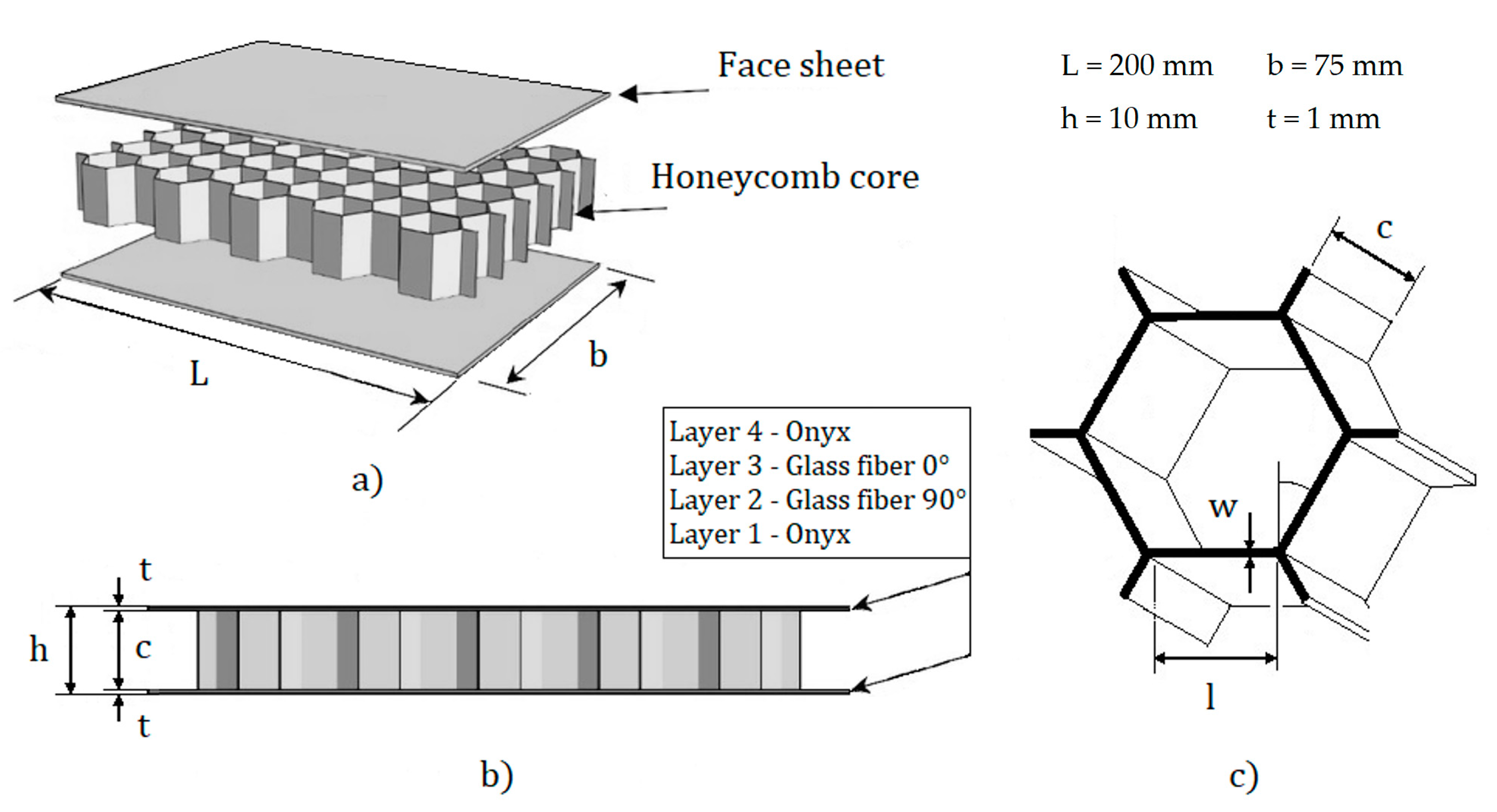


| ID | Infill Density (Core) | Reinforcement Layers (Facing) | Fiber Orientation |
|---|---|---|---|
| R4i25 | 25% | 4 (2 per face) | 0°/90° |
| R4i50 | 50% | 4 (2 per face) | 0°/90° |
| R0i25 | 25% | 0 | - |
| R0i50 | 50% | 0 | - |
| Material | ρ (g/cm3) | Tensile Strength (MPa) | Tensile Modulus (GPa) |
|---|---|---|---|
| Onyx | 1.2 | 40 | 2.4 |
| Glass fiber | 1.5 | 590 | 21 |
| ID | l (mm) | w (mm) | ρc (g/cm3) | Ec (GPa) | σfc (MPa) | Vr | Vr0 | Ef (GPa) | σfy (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| R4i25 | 4.17 | 1.10 | 0.29 | 0.127 | 1.86 | 0.21 | 0.105 | 5.0 | 97.8 |
| R4i50 | 3.04 | 1.40 | 0.40 | 0.674 | 5.66 | 0.21 | 0.105 | 5.0 | 97.8 |
| R0i25 | 4.17 | 1.10 | 0.29 | 0.127 | 1.86 | - | - | 2.4 | 40 |
| R0i50 | 3.04 | 1.40 | 0.40 | 0.674 | 5.66 | - | - | 2.4 | 40 |
| ID | Experiment (Equation (3)) | EHM (Equation (6)) | Relative Error | Tolf and Clarin (Equation (7)) | Relative Error |
|---|---|---|---|---|---|
| R4i25 | 1885.1 ± 38.8 | 1580.6 | 19.3% | 1127.0 | 40.2% |
| R4i50 | 1856.3 ± 197.3 | 1580.6 | 17.4% | 1407.2 | 24.2% |
| R0i25 | 666.0 ± 112.2 | 871.4 | 23.6% | 650.4 | 2.3% |
| R0i50 | 463.1 ± 22.7 | 871.4 | 46.9% | 930.7 | 101.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerra Silva, R.; Gonzalez, E.; Inostroza, A.; Morales Pavez, G. Flexural Analysis of Additively Manufactured Continuous Fiber-Reinforced Honeycomb Sandwich Structures. J. Manuf. Mater. Process. 2024, 8, 226. https://doi.org/10.3390/jmmp8050226
Guerra Silva R, Gonzalez E, Inostroza A, Morales Pavez G. Flexural Analysis of Additively Manufactured Continuous Fiber-Reinforced Honeycomb Sandwich Structures. Journal of Manufacturing and Materials Processing. 2024; 8(5):226. https://doi.org/10.3390/jmmp8050226
Chicago/Turabian StyleGuerra Silva, Rafael, Esteban Gonzalez, Andres Inostroza, and Gustavo Morales Pavez. 2024. "Flexural Analysis of Additively Manufactured Continuous Fiber-Reinforced Honeycomb Sandwich Structures" Journal of Manufacturing and Materials Processing 8, no. 5: 226. https://doi.org/10.3390/jmmp8050226
APA StyleGuerra Silva, R., Gonzalez, E., Inostroza, A., & Morales Pavez, G. (2024). Flexural Analysis of Additively Manufactured Continuous Fiber-Reinforced Honeycomb Sandwich Structures. Journal of Manufacturing and Materials Processing, 8(5), 226. https://doi.org/10.3390/jmmp8050226








