Design, Fabrication, and Commissioning of Transonic Linear Cascade for Micro-Shock Wave Analysis
Abstract
1. Introduction
2. Materials and Methods
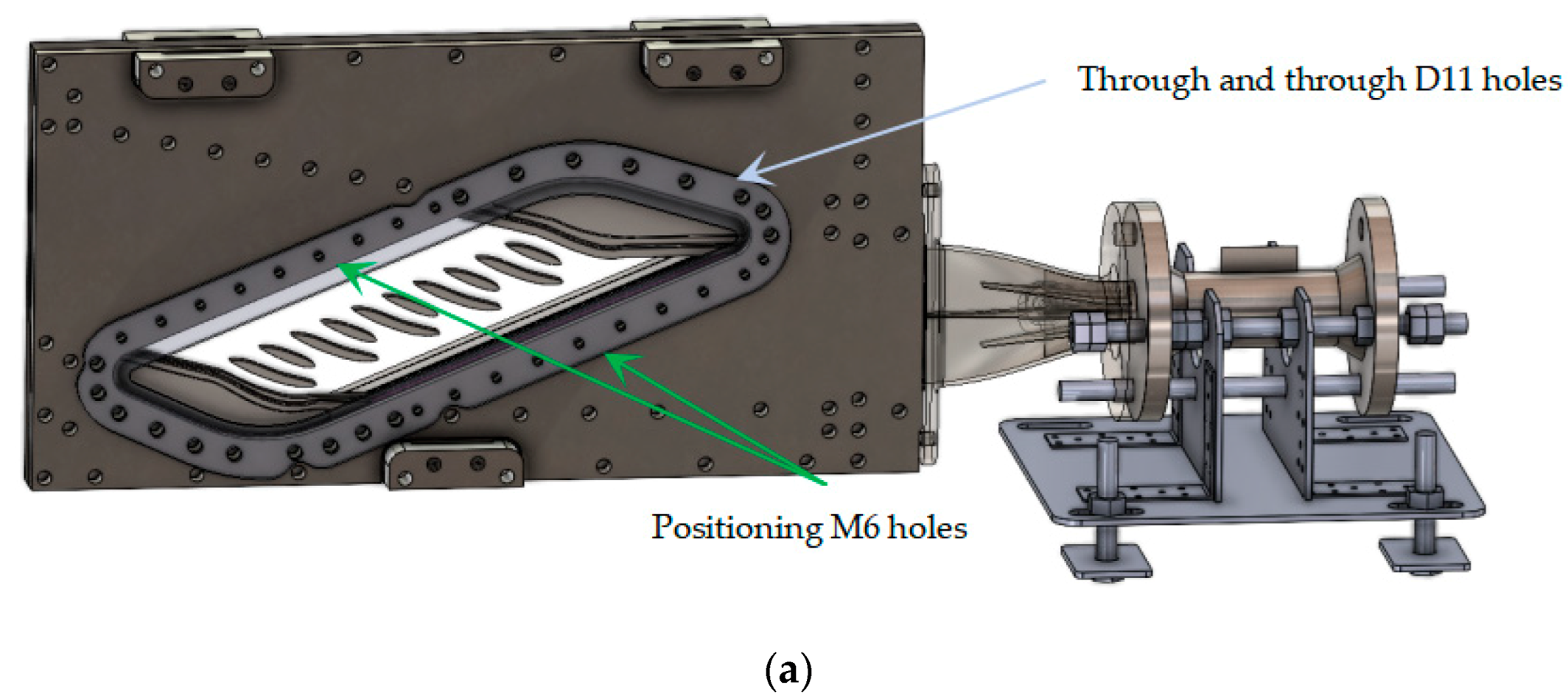
2.1. Linear Cascade Design and Manufacturing
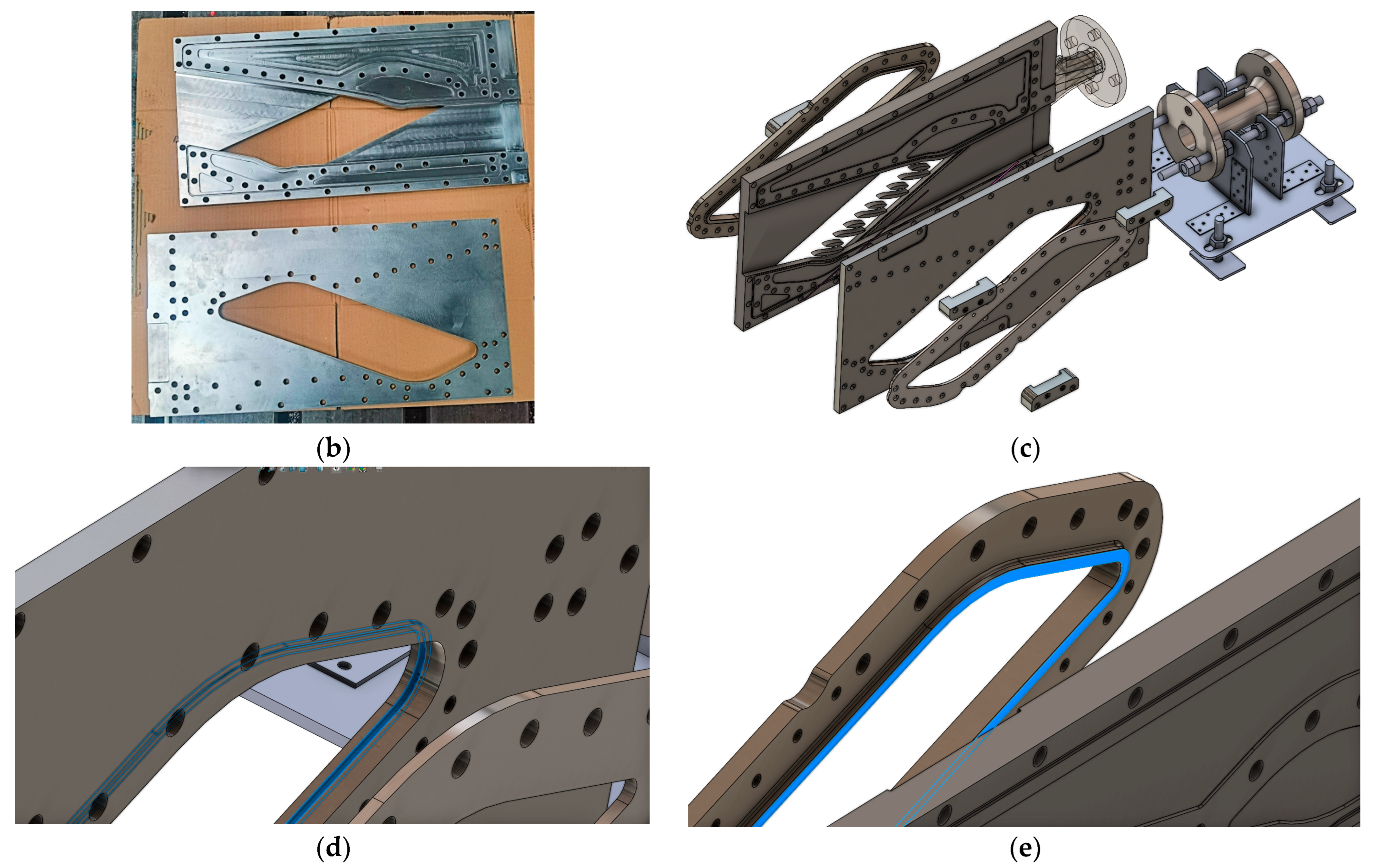
2.2. Vane Design and Manufacturing
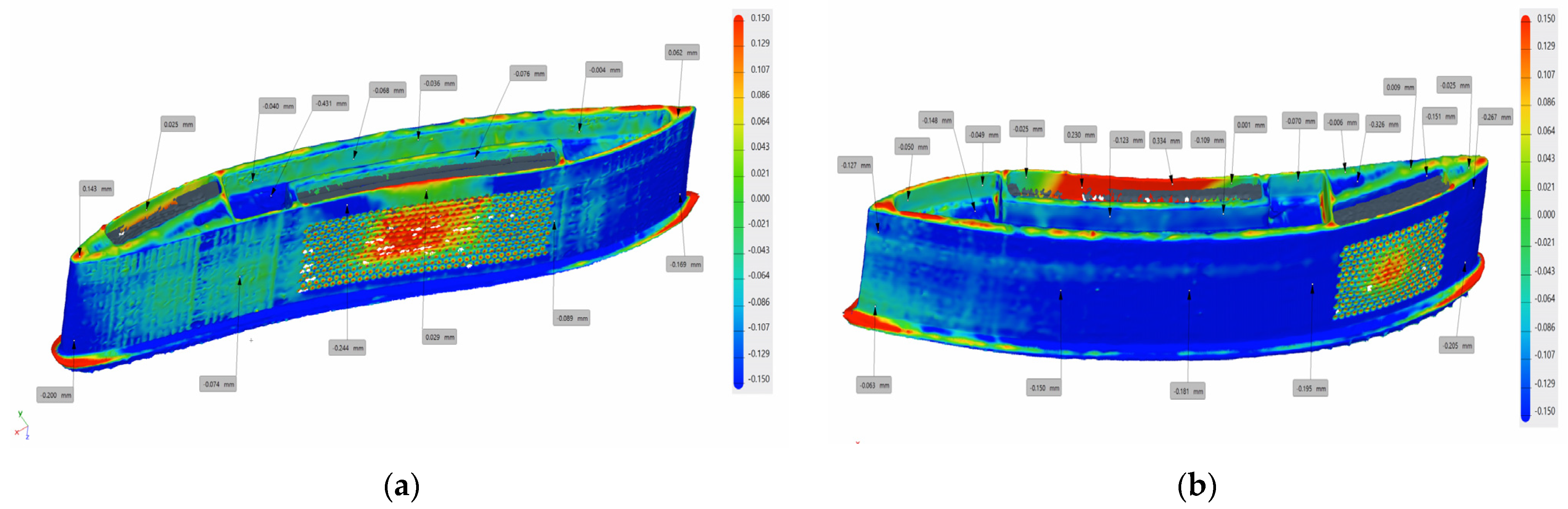
2.2.1. Blade Manufacturing, Orifice Size of the Porous Wall: 0.5 mm
- Increasing the size of the perforations and spacing: the size of the perforations in the airfoil models and the distance between them needed to be increased to reduce their number and avoid manufacturing issues;
- Material additions for enhanced dimensional accuracy: to achieve a dimensional accuracy superior to the values recorded in the first test, additional material had to be added to all model elevations to allow machining;
- Designing a platform for CNC clamping: a platform needed to be added to the models’ bases to facilitate clamping them onto the CNC machine fixtures for further processing.
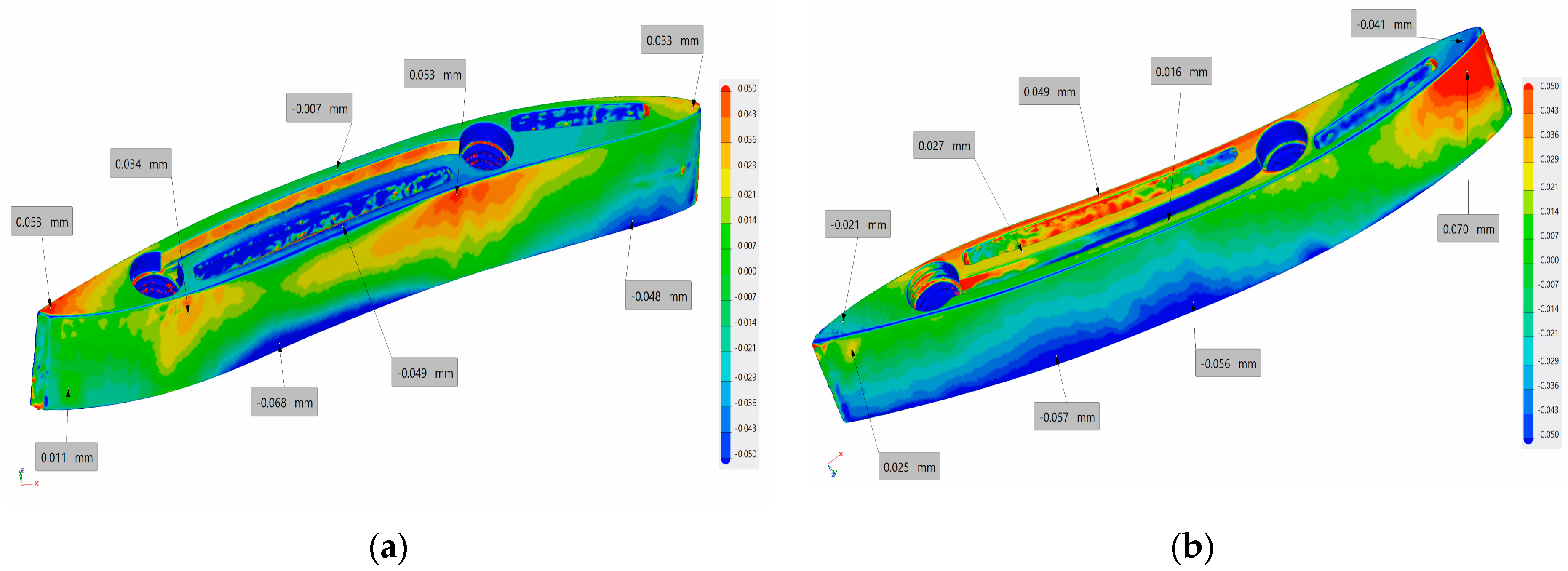
2.2.2. Blade Manufacturing, Orifice Size of the Porous Wall: 0.75 mm
2.2.3. Blade Manufacturing, Orifice Size of the Porous Wall: 0.75 mm (Rounding the Ends of the Platform Base)
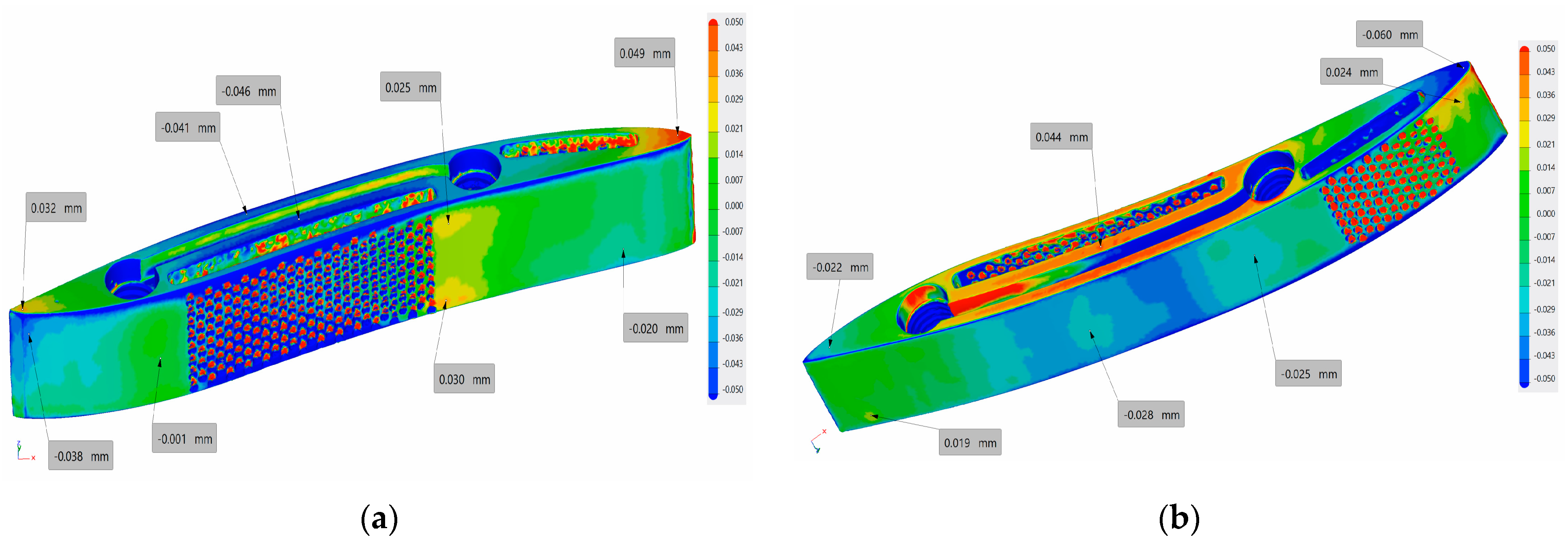
- On the main vane, two areas with porous walls were implemented: one near the leading edge on the suction side with a depth of 2 mm and a length of 12 mm, and another on the pressure side with the same depth but a length of 27 mm. The grid configurations are 8 × 7 holes for the leading edge and 13 × 8 holes for the pressure side;
- On the secondary vane, two porous areas with a depth of 2 mm, a length of 22 mm, and a grid of 11 × 8 holes were positioned in the middle of the vane.
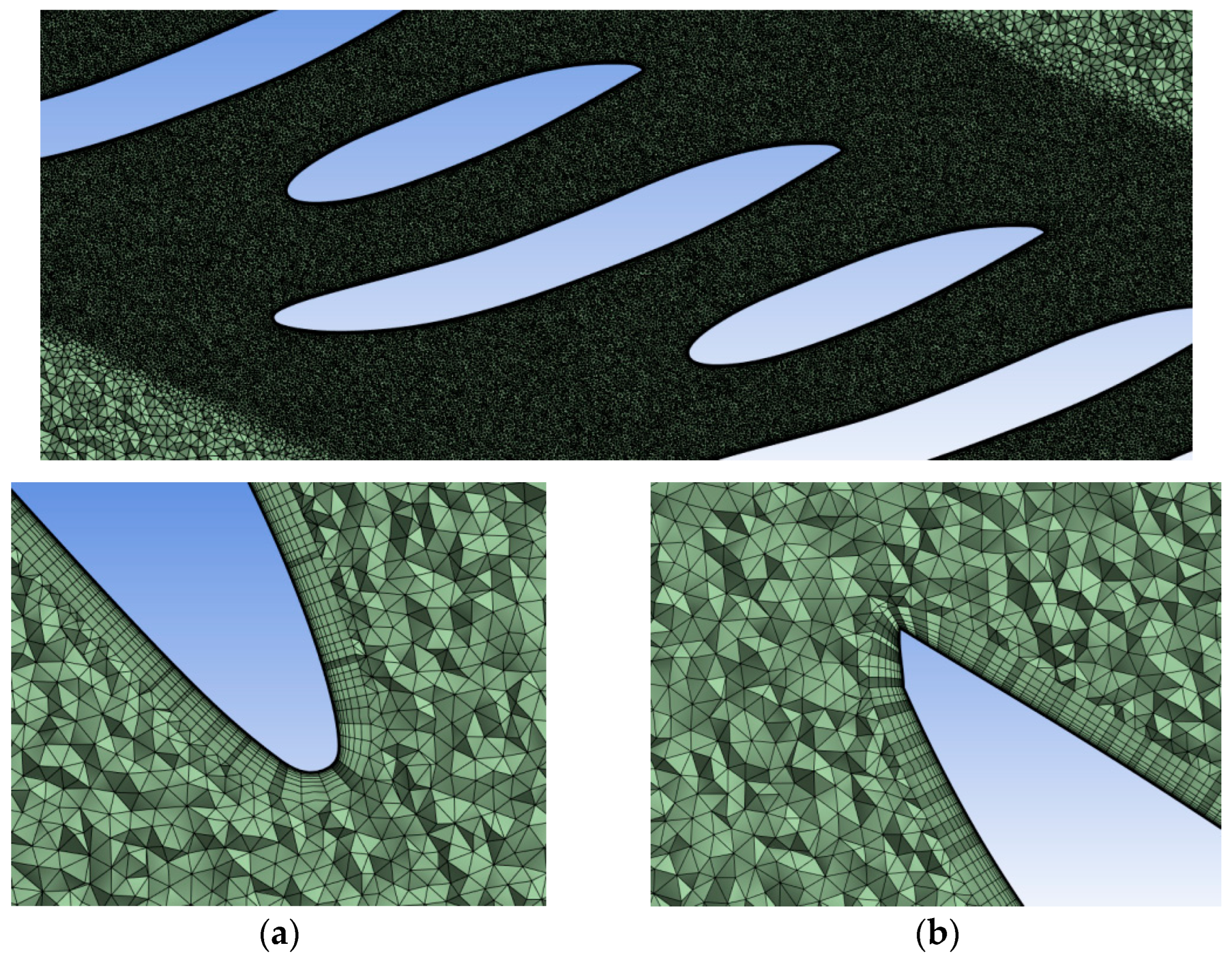
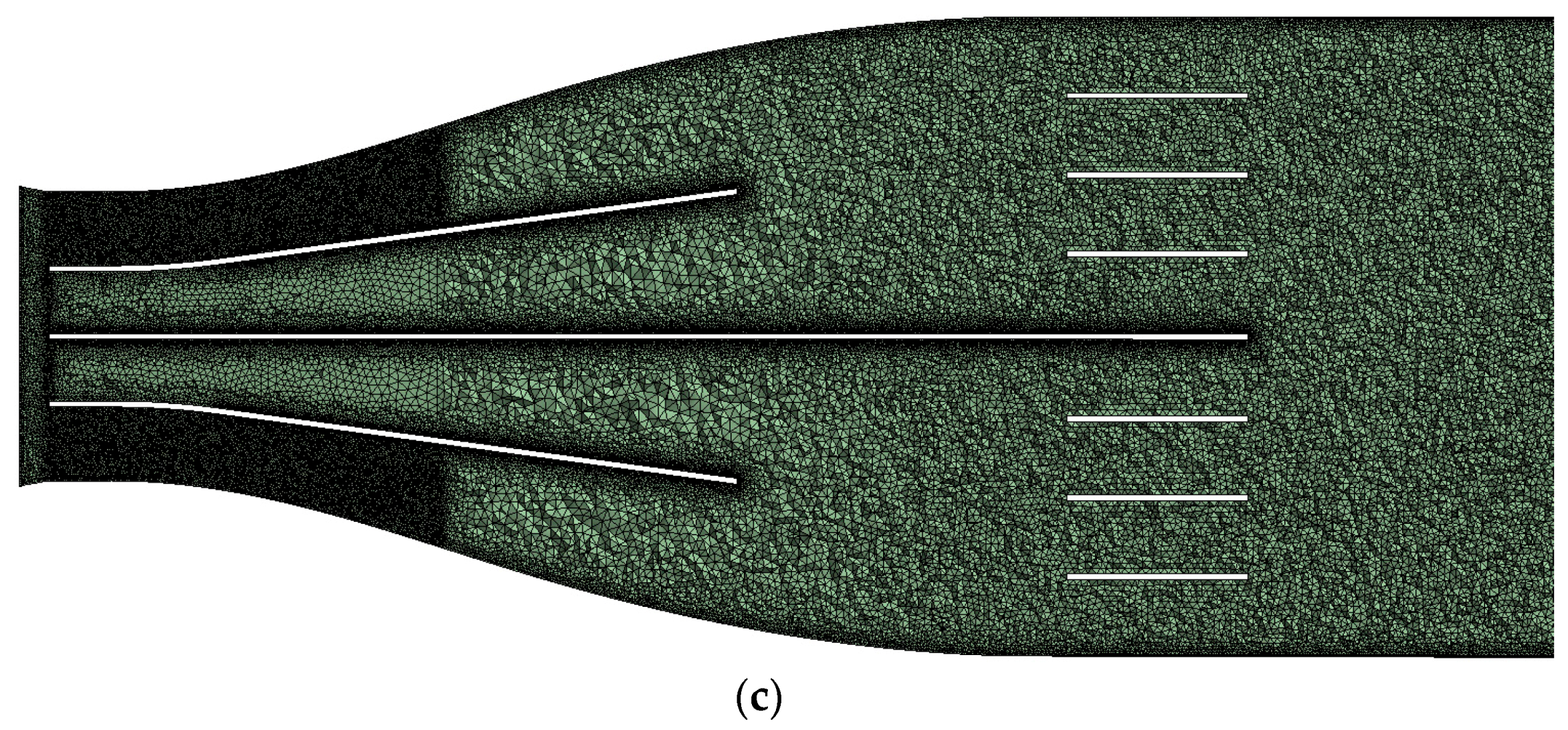
2.3. Computational Setup of the Linear Cascade
3. Results
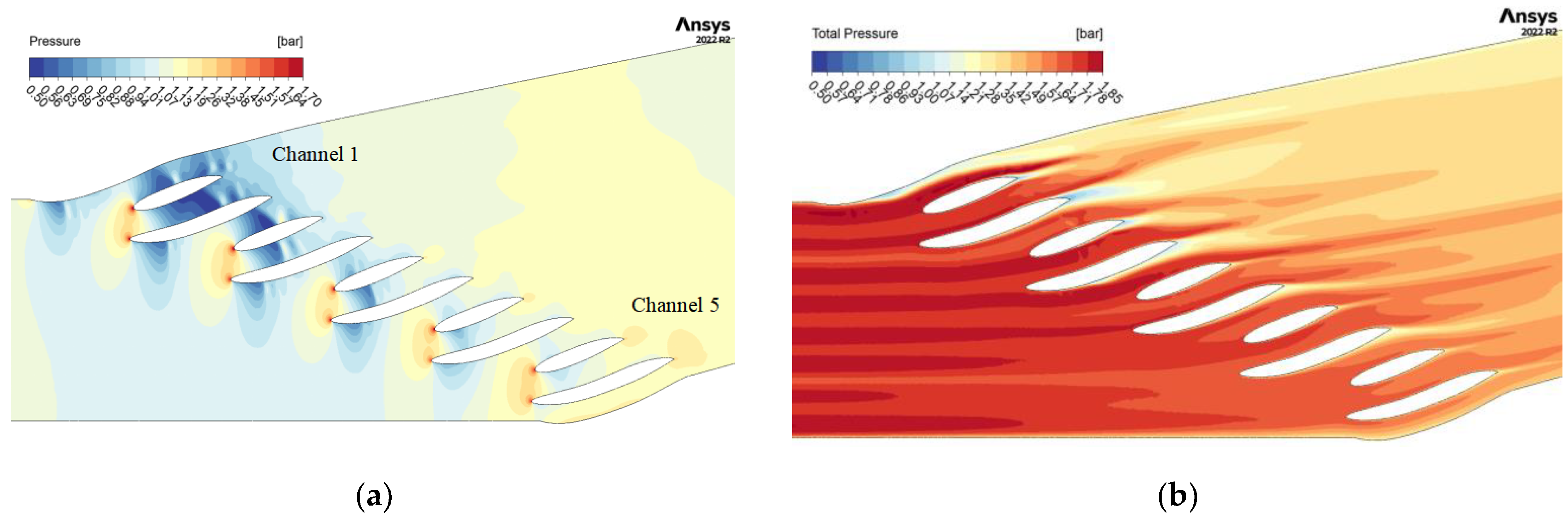
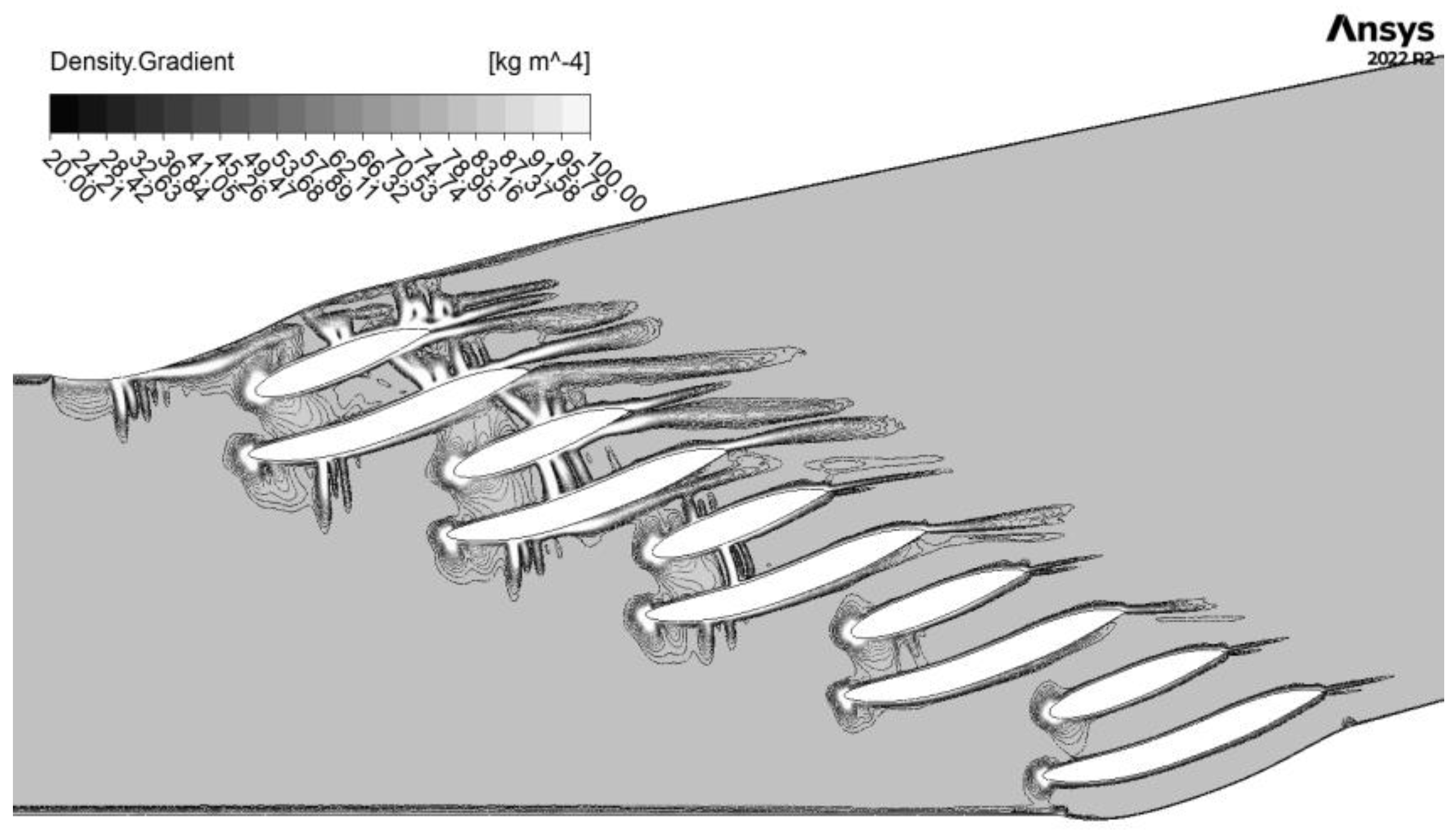
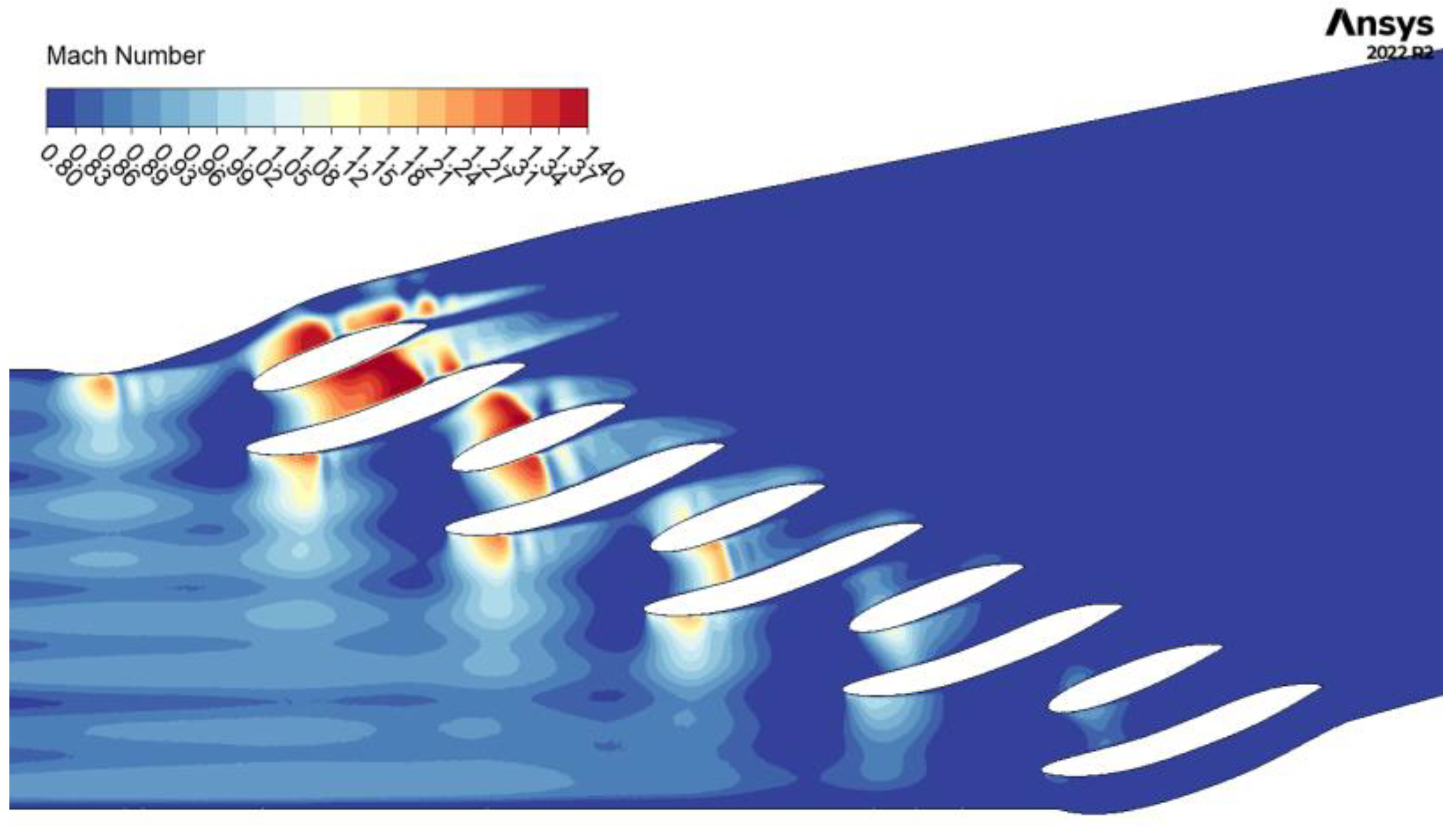
3.1. Numerical Analysis of the Linear Cascade
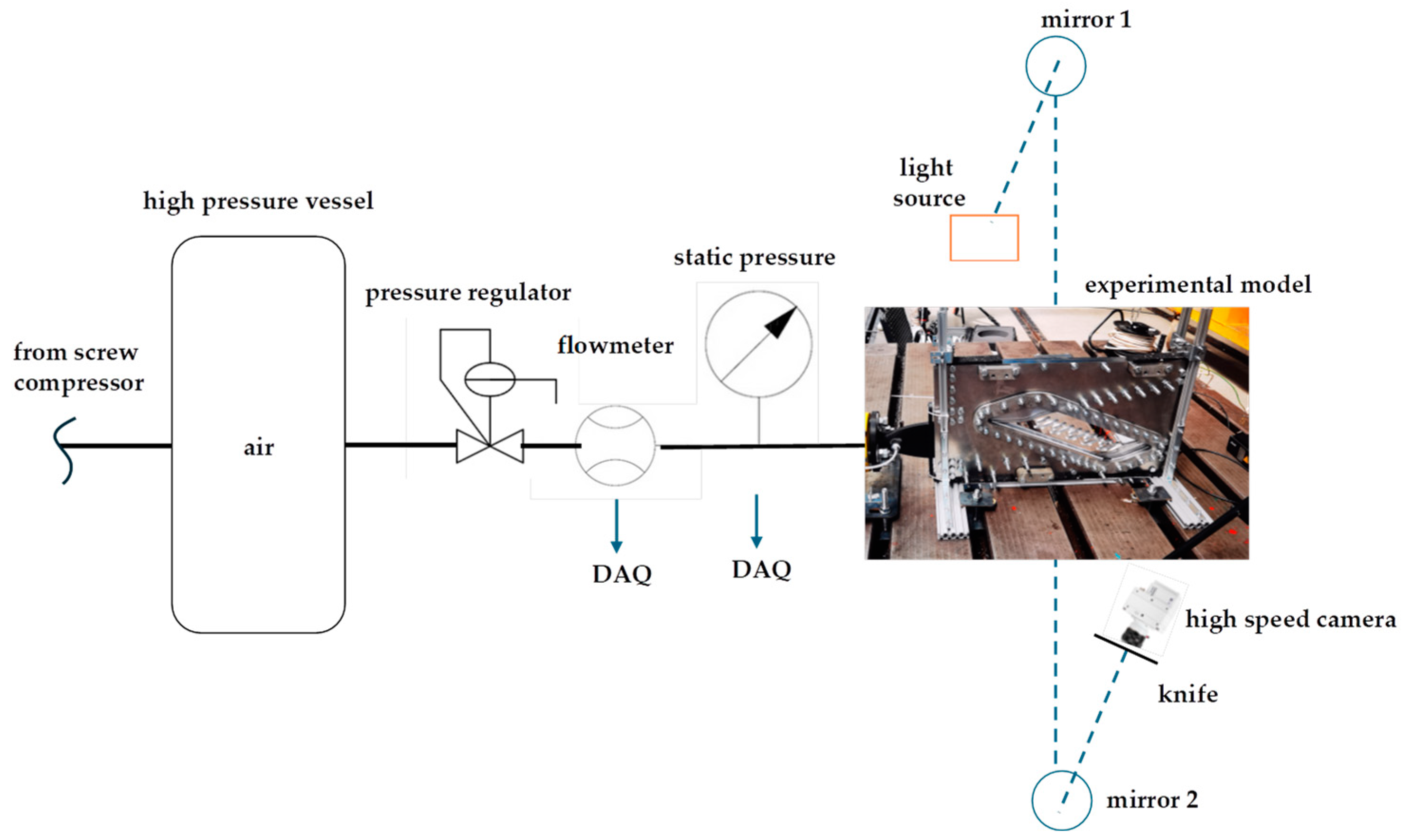
3.2. Installation Commissioning and Testing
4. Conclusions
- Blade manufacturing—The blades were produced using a combination of additive manufacturing, electroerosion, and CNC milling, with each method compensating for the limitations of the others. The size, number, placement, and orientation of the holes required for each blade would have been prohibitively expensive using traditional drilling methods. Furthermore, the material, a nickel-based superalloy (Inconel), posed challenges due to its hardness, which would have significantly increased the cost of drilling and milling. Choosing this material enhances the relevance of the design for the aviation industry, as Inconel is commonly used in turbine blades. Blade alignment within the blade row was achieved using two Teflon bolts, which gently pressed the blades against the quartz window, reducing vibration. A control curve etched into the periphery of the window provided a means of visually monitoring the blade alignment while also functioning as a miniature plenum chamber, aiding the air seal between the two parts;
- Test rig design and fabrication—The rig posed several engineering challenges, such as ensuring that the blades are both removable and air-tight, while consistently placed in the same position. Furthermore, blade mounting was constrained to the perimeter to avoid obstructing visualization. To ensure air tightness, the contact surfaces were machined with high precision and aligned in the same plane. Additionally, the top visualization window was allowed some spanwise play to ensure contact with the blade tips;
- While the numerical simulations using Ansys CFX with an implicit pressure-based solver and high-order numerical schemes provided a broadly accurate representation of the shock wave characteristics, there were some limitations. The simulations captured the macrolevel shock wave positions and intensities effectively but missed some finer flow structures observed in the experimental data. This indicates the need for the further refinement of the numerical models to fully capture all the detailed flow phenomena;
- The shock wave intensity and position are highly sensitive to changes in the inlet pressure. Higher inlet pressures result in stronger and more extensive shock waves across the cascade channels. Specifically, relative inlet pressures of 0.7-bar gauge, 0.8-bar gauge, and 0.9-bar gauge at an inlet temperature of 21 °C demonstrated varying shock wave characteristics, with the most pronounced effects observed at the highest pressure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hergt, A.; Klinner, J.; Wellner, J.; Willert, C.; Grund, S.; Steinert, W.; Beversdorff, M. The Present Challenge of Transonic Compressor Blade Design. ASME. J. Turbomach. 2019, 141, 091004. [Google Scholar] [CrossRef]
- Gaitonde, D.V.; Adler, M.C. Dynamics of Three-Dimensional Shock-Wave/Boundary-Layer Interactions. Annu. Rev. Fluid Mech. 2023, 55, 291–321. [Google Scholar]
- Hou, W.T.; Qiao, W.Y.; Luo, H.L. Shock-Wave/Boundary-Layer Interaction in a Transonic Turbine Cascade. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2011, 225, 77–85. [Google Scholar] [CrossRef]
- Ligrani, P.M.; McNabb, E.; Collopy, H.; Anderson, M.; Marko, S.M. Recent investigations of shock wave effects and interactions. Adv. Aerodyn. 2020, 2, 4. [Google Scholar] [CrossRef]
- Giannelis, N.F.; Vio, G.A.; Levinski, O. A review of recent developments in the understanding of transonic shock buffet. Prog. Aerosp. Sci. 2017, 92, 39–84. [Google Scholar] [CrossRef]
- Liu, B.; Shi, H.; Yu, X. A new method for rapid shock loss evaluation and reduction for the optimization design of a supersonic compressor cascade. Proc. IMechE Part G J. Aerosp. Eng. 2018, 232, 2458–2476. [Google Scholar]
- Wang, Z.; Chang, J.; Li, Y.; Kong, C. Investigation of shock wave control by suction in a supersonic cascade. Aerosp. Sci. Technol. 2021, 108, 106382. [Google Scholar] [CrossRef]
- Meng, F.; Tang, J.; Li, J.; Gong, C.; Guo, P. Variations of the shock and secondary flow structure in a transonic compressor cascade with outlet back pressure. Phys. Fluids 2024, 36, 066114. [Google Scholar] [CrossRef]
- Gad-el-Hak, M. Flow Control: Passive, Active, and Reactive Flow Management; Cambridge University Press: Cambridge, UK, 2009; ISBN 13978-0511529535. [Google Scholar] [CrossRef]
- Klinner, J.; Hergt, A.; Grund, S.; Willert, C.E. Experimental investigation of shock-induced separation and fow control in a transonic compressor cascade. Exp. Fluids 2019, 60, 96. [Google Scholar] [CrossRef]
- Šimurda, D.; Luxa, M.; Šafařík, P.; Synáč, J.; Rudas, B. Measurements on supersonic turbine cascades—Methodical approach. In Proceedings of the XXII Symposium on Measuring Techniques in Turbomachinery Transonic and Supersonic Flow in Cascades and Turbomachines, Lyon, France, 4–5 September 2014. [Google Scholar]
- Zhang, Z.; Wen, C.; Zhang, W.; Liu, Y.; Jiang, Z. A theoretical method for solving shock relations coupled with chemical equilibrium and its applications. Chin. J. Aeronaut. 2022, 35, 47–62. [Google Scholar] [CrossRef]
- Sabnis, K.; Babinsky, H. A review of three-dimensional shock wave–boundary-layer interactions. Prog. Aerosp. Sci. 2023, 143, 100953. [Google Scholar] [CrossRef]
- Okada, M.; Simonassi, L.; Lopes, G.; Lavagnoli, S. Particle Image Velocimetry Measurements in a High-Speed Low-Reynolds Low-Pressure Turbine Cascade. ASME. J. Turbomach. 2024, 146, 031010. [Google Scholar] [CrossRef]
- Jiang, H.; Peng, X.; Xie, W.; Lu, S.; Gu, Y. Development of a Large-Scale High-Speed Linear Cascade Rig for Turbine Blade Tip Heat Transfer Study. Aerospace 2022, 9, 695. [Google Scholar] [CrossRef]
- Humble, R.A.; Scarano, F.; van Oudheusden, B.W. Particle Image Velocimetry Measurements of a Shock Wave/Turbulent Boundary Layer Interaction. Exp. Fluids 2007, 43, 173–183. [Google Scholar] [CrossRef]
- Wang, Z.; Chang, J.; Hou, W.; Yu, D. Throttling process of a supersonic cascade studied by high-frequency response pressure and high-speed schlieren. Sci. Rep. 2021, 11, 13550. [Google Scholar] [CrossRef]
- Gao, L.; Yang, G.; Gao, T.; Li, R.; Hu, X. Experimental Investigation of a Linear Cascade with Large Solidity Using Pressure Sensitive Paint and Dual-Camera System. J. Therm. Sci. 2021, 30, 682–695. [Google Scholar] [CrossRef]
- Lei, X.; Gao, L.; Chang, L.; Yang, G.; Mao, X. Application of Pressure-Sensitive Paint Measurement Technology in Pressure Measurement of Cascade Blade Surface. In Proceedings of the 9th Asian Joint Workshop on Thermophysics and Fluid Science, Utsunomiya, Japan, 27–30 November 2022; Suryan, A., Yaga, M., Ko, H.S., Guang, Z., Eds.; AJWTF2022 2022; Springer Proceedings in Physics. Springer: Singapore, 2022; Volume 396. [Google Scholar] [CrossRef]
- Jing, W.; Hui, C.; Qiong, W.; Hongbo, L.; Zhanjun, L. Surface modification of carbon fibers and the selective laser sintering of modified carbon fiber/nylon 12 composite powder. Mater. Des. 2017, 116, 253–260. [Google Scholar] [CrossRef]
- Gao, Y.; Lalevée, J.; Simon-Masseron, A. An Overview on 3D Printing of Structured Porous Materials and Their Applications. Adv. Mater. Technol. 2023, 8, 2300377. [Google Scholar] [CrossRef]
- Guddati, S.; Kiran, A.S.K.; Leavy, M.; Ramakrishna, S. Recent advancements in additive manufacturing technologies for porous material applications. Int. J. Adv. Manuf. Technol. 2019, 105, 193–215. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-1-4939-2112-6. [Google Scholar]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Kumar, S.; Kruth, J.P. Composites by rapid prototyping technology. Mater. Des. 2010, 31, 850–856. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P. Ti-6Al-4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J. Mech. Behav. Biomed. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef]
- Wendel, B.; Rietzel, D.; Kühnlein, F.; Feulner, R.; Horsch, C.; Schmachtenberg, E. Additive processing of polymers. Macromol. Mater. Eng. 2008, 293, 799–809. [Google Scholar] [CrossRef]
- Torrado, A.R.; Shemelya, C.M. Effects of PolyLactic Acid properties on 3D printed structures: Tensile strength, ductility, and malleability. J. Mater. Res. 2016, 31, 2387. [Google Scholar] [CrossRef]
- Dumitrescu, O.; Gall, M.; Dragan, V. A Three-Dimensional Design to Study the Shock Waves of Linear Cascade with Reduced Mass Flow Requirements. Appl. Sci. 2023, 13, 11029. [Google Scholar] [CrossRef]
- Shimazaki, T.; Ichihara, S.; Tagawa, Y. Background oriented schlieren technique with fast Fourier demodulation for measuring large density-gradient fields of fluids. Exp. Therm. Fluid Sci. 2022, 134, 110598. [Google Scholar] [CrossRef]
- Tateishi, A.; Watanabe, T.; Himeno, T.; Uzawa, S. Numerical method for an assessment of steady and motion-excited flowfields in a transonic cascade wind tunnel. J. Glob. Power Propuls. Soc. 2017, 1, 171–183. [Google Scholar] [CrossRef]
- Jutur, P.; Govardhan, R.N. Flutter in Started and Unstarted Transonic Linear Cascades: Simultaneous Measurements of Unsteady Loads and Shock Dynamics. ASME J. Turbomach. 2019, 141, 121004. [Google Scholar] [CrossRef]
- Pressure Transmitters Type MBS 33. Available online: https://assets.danfoss.com/documents/184624/AI308949780206en-000202.pdf (accessed on 4 April 2024).
- Yue, S.; Wang, Y.; Wang, H. Design and Optimization of Tandem Arranged Cascade in a Transonic Compressor. J. Therm. Sci. 2018, 27, 349–358. [Google Scholar]
- Tweedt, D.L.; Schreiber, H.A.; Starken, H. Experimental Investigation of the Performance of a Supersonic Compressor Cascade. ASME J. Turbomach. 1988, 110, 456–466. [Google Scholar]
- Casoni, M.; Magrini, A.; Benini, E. Supersonic Compressor Cascade Shape Optimization under Multiple Inlet Mach Operating Conditions. Aerospace 2019, 6, 64. [Google Scholar] [CrossRef]
- Watanabe, T.; Aotsuka, M. Unsteady aerodynamic characteristics of oscillating cascade with separation bubble in high subsonic flow. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, NV, USA, 6–9 June 2005; International Gas Turbine Institute: Houston, TX, USA, 2005; pp. 625–633. [Google Scholar] [CrossRef]
- Vogt, D.M.; Fransson, T.H. Experimental investigation of mode shape sensitivity of an oscillating low-pressure turbine cascade at design and off-design conditions. J. Eng. Gas Turbines Power 2006, 129, 530–541. [Google Scholar] [CrossRef]
- Kazawa, J.; Watanabe, T. Active suppression of cascade flutter with piezoelectric device. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; International Gas Turbine Institute: Houston, TX, USA, 2006; pp. 1091–1100. [Google Scholar] [CrossRef]
- Aotsuka, M.; Watanabe, T.; Machida, Y. Role of shock and boundary layer separation on unsteady aerodynamic characteristics of oscillating transonic cascade. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA, 16–19 June 2003; International Gas Turbine Institute: Houston, TX, USA, 2003; pp. 349–356. [Google Scholar] [CrossRef]
- Jadhav, A.; Jadhav, V.S. A review on 3D printing: An additive manufacturing technology. Mater. Today Proc. 2022, 62, 2094–2099. [Google Scholar] [CrossRef]
- Available online: https://www.metronicnet.com/uploads/archivos/20240111_zeiss_atos-compact-scan_brochure_en.pdf (accessed on 22 January 2024).
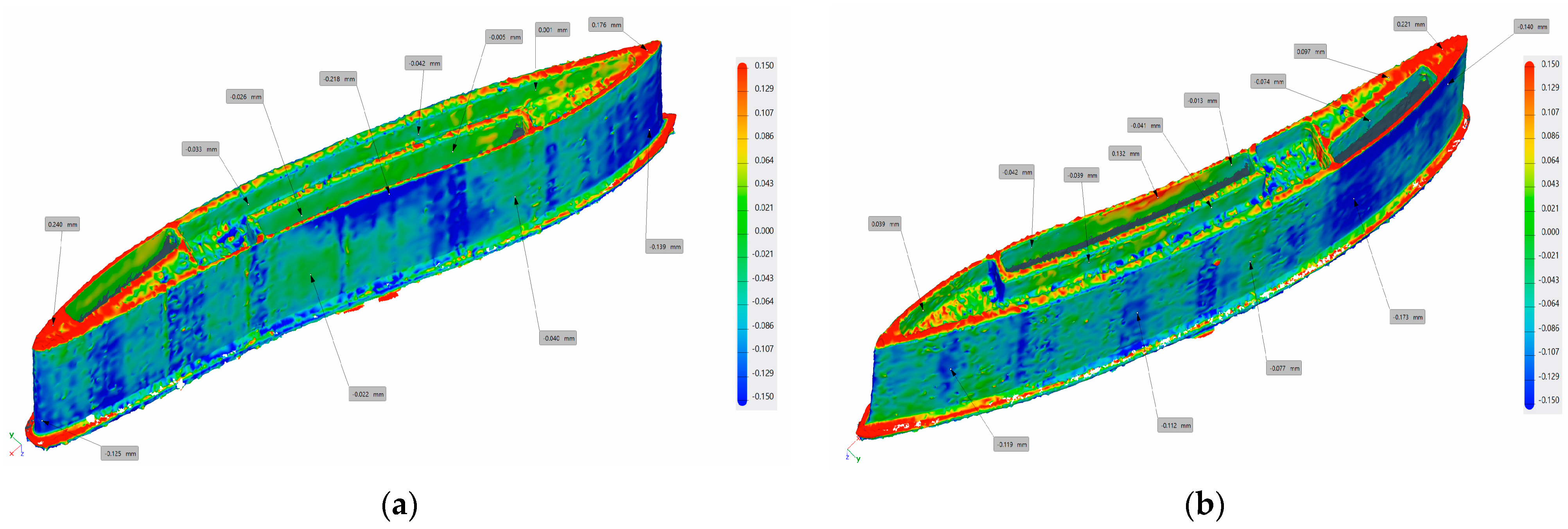
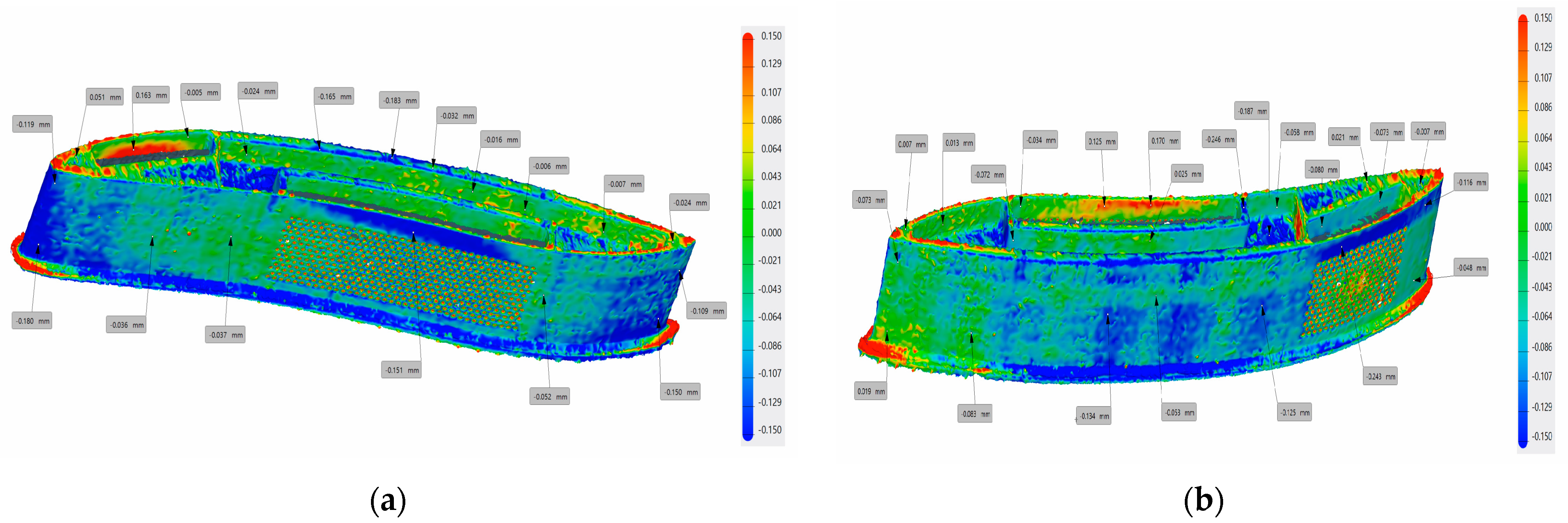
- Zhang, L.; Zhang, S.; Zhu, H.; Hu, Z.; Wang, G.; Zeng, X. Horizontal dimensional accuracy prediction of selective laser melting. Mater. Des. 2018, 160, 9–20. [Google Scholar] [CrossRef]
- Minetola, P.; Galati, M.; Calignano, F.; Iuliano, L.; Rizza, G.; Fontana, L. Comparison of dimensional tolerance grades for metal AM processes. Procedia CIRP 2020, 88, 399–404. [Google Scholar] [CrossRef]
- Gibson, L.; Galloway, L.; Kim, S.I.; Spence, S. Assessment of turbulence model predictions for a centrifugal compressor simulation. J. Glob. Power Propuls. Soc. 2017, 1, 142–156. [Google Scholar] [CrossRef]
- Balasubramanian, R.; Barrows, S.; Chen, J. Investigation of Shear-Stress Transport Turbulence Model for Turbomachinery Applications. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NA, USA, 7–10 January 2008; p. 212. [Google Scholar] [CrossRef]
- Prisăcariu, E.-G.; Prisecaru, T. Quantitative Color Schlieren for an H2–O2 Exhaust Jet Developing in Air. Fluids 2024, 9, 19. [Google Scholar] [CrossRef]
- Zhu, W.; Bons, J.; Gregory, J. Boundary layer and near wake measurements of a two-dimensional airfoil with background-oriented schlieren method. Exp. Fluids 2023, 64, 7. [Google Scholar] [CrossRef]
- Anand, P.; Zhang, J.; Rajendran, L.K.; Bane, S.P.; Vlachos, P.P. Quantifying numerical uncertainty in background-oriented schlieren. Exp. Fluids 2024, 65, 1. [Google Scholar] [CrossRef]
- Gall, M.; Dumitrescu, O.; Drăgan, V.; Crunțeanu, D.E. Effects of Perforated Plates on Shock Structure Alteration for NACA0012 Airfoils. Inventions 2024, 9, 28. [Google Scholar] [CrossRef]

















| Symbol | Parameter | Main Blade | Splitter Blade |
|---|---|---|---|
| c | Blade chord length [mm] | 71.16 | 45.22 |
| s | Pitch width [mm] | 52 | 52 |
| l | Blade span [mm] | 10 | 10 |
| σ | Solidity | 1.368 | 0.869 |
| γ | Stagger angle [°] | 51.55 | 49.23 |
| First Batch | Final Blade Model | |
|---|---|---|
| Main Blade |  |  |
 |  | |
| Secondary Blade |  | 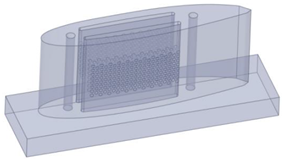 |
 |  |
| Main Blade | Secondary Blade | |
|---|---|---|
| Length [mm] | 73 | 48 |
| Maximum thickness [mm] | 7 | 7 |
| Height [mm] | 10 | 10 |
| Length of the porous-wall area—suction side [mm] | 15 | 23 |
| Length of the porous-wall area—pressure side [mm] | 30 | 23 |
| Number of orifices—pressure side | 88 | 104 |
| Number of orifices—suction side | 88 | 56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gall, M.; Drăgan, V.; Dumitrescu, O.; Prisăcariu, E.G.; Condruz, M.R.; Paraschiv, A.; Petrescu, V.; Vlăduț, M. Design, Fabrication, and Commissioning of Transonic Linear Cascade for Micro-Shock Wave Analysis. J. Manuf. Mater. Process. 2024, 8, 201. https://doi.org/10.3390/jmmp8050201
Gall M, Drăgan V, Dumitrescu O, Prisăcariu EG, Condruz MR, Paraschiv A, Petrescu V, Vlăduț M. Design, Fabrication, and Commissioning of Transonic Linear Cascade for Micro-Shock Wave Analysis. Journal of Manufacturing and Materials Processing. 2024; 8(5):201. https://doi.org/10.3390/jmmp8050201
Chicago/Turabian StyleGall, Mihnea, Valeriu Drăgan, Oana Dumitrescu, Emilia Georgiana Prisăcariu, Mihaela Raluca Condruz, Alexandru Paraschiv, Valentin Petrescu, and Mihai Vlăduț. 2024. "Design, Fabrication, and Commissioning of Transonic Linear Cascade for Micro-Shock Wave Analysis" Journal of Manufacturing and Materials Processing 8, no. 5: 201. https://doi.org/10.3390/jmmp8050201
APA StyleGall, M., Drăgan, V., Dumitrescu, O., Prisăcariu, E. G., Condruz, M. R., Paraschiv, A., Petrescu, V., & Vlăduț, M. (2024). Design, Fabrication, and Commissioning of Transonic Linear Cascade for Micro-Shock Wave Analysis. Journal of Manufacturing and Materials Processing, 8(5), 201. https://doi.org/10.3390/jmmp8050201






