Figure 1.
Material removal mechanism in die-sink electric discharge machining.
Figure 1.
Material removal mechanism in die-sink electric discharge machining.
Figure 2.
Die-sink electric discharge machining setup.
Figure 2.
Die-sink electric discharge machining setup.
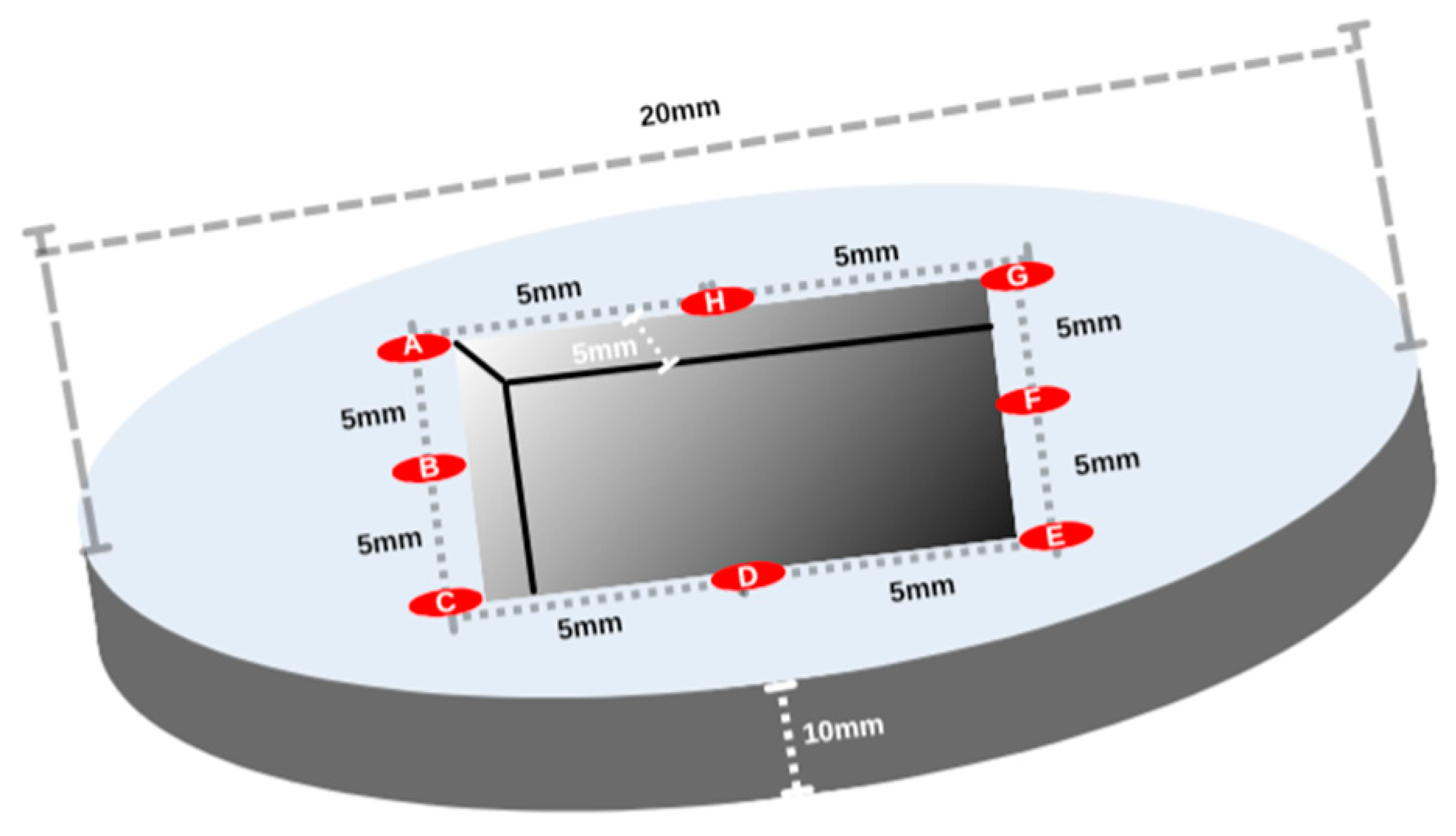
Figure 3.
Visualization of the sample with X-ray target spots for residual stress measurement.
Figure 3.
Visualization of the sample with X-ray target spots for residual stress measurement.
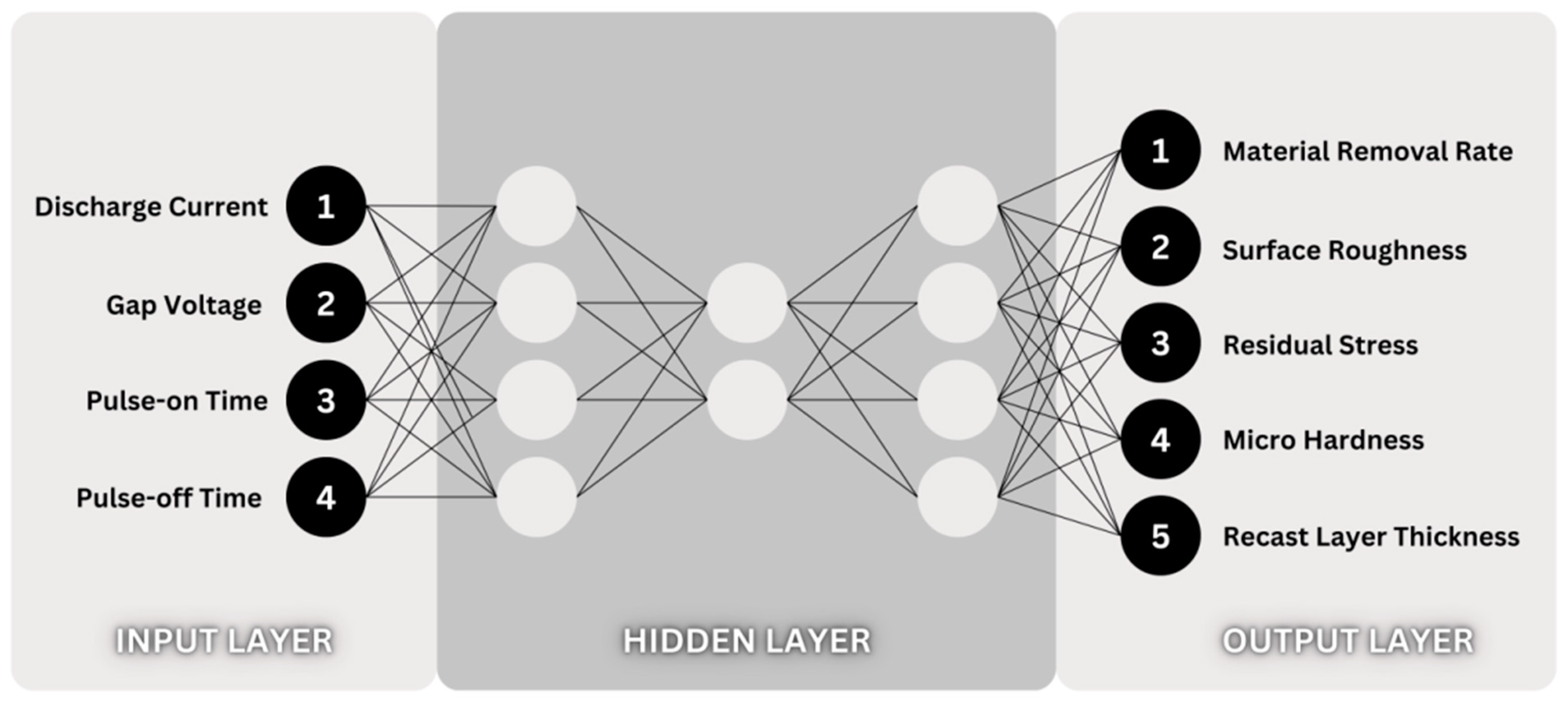
Figure 4.
Schematic representation of the multi-layered feed-forward artificial neural network.
Figure 4.
Schematic representation of the multi-layered feed-forward artificial neural network.
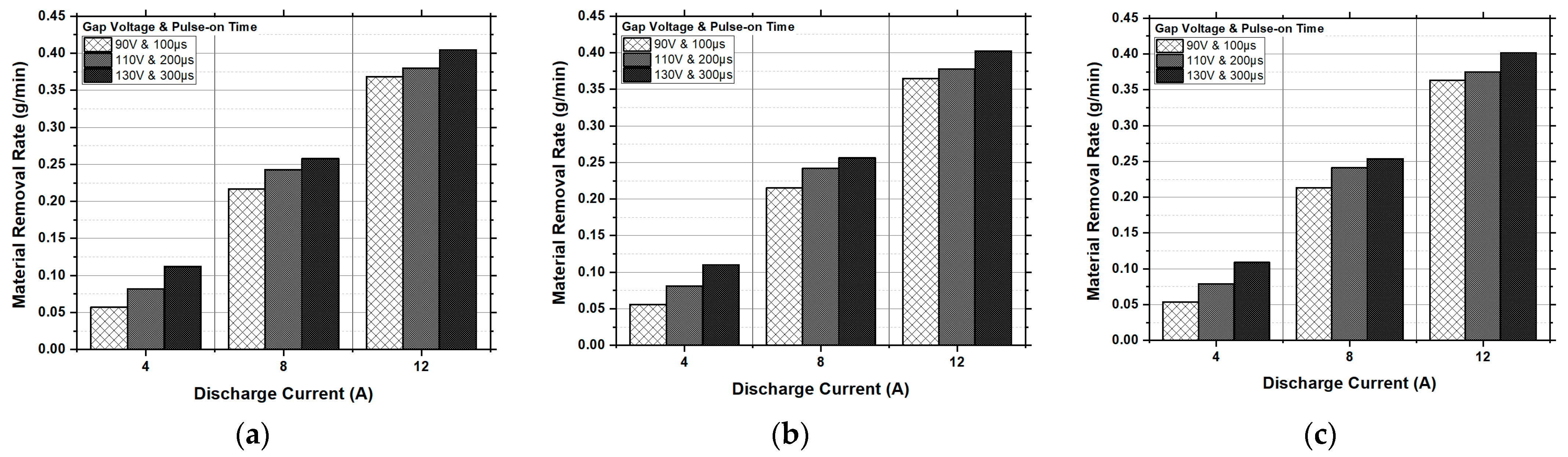
Figure 5.
Experimental results of the material removal rate (g/min) vs. the discharge current, gap voltage and pulse-on time for the (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 5.
Experimental results of the material removal rate (g/min) vs. the discharge current, gap voltage and pulse-on time for the (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 6.
Electric discharge-machined holes of dimensions 10 mm × 10 mm × 10 mm on AISI 316L stainless steel using the Ti-6Al-4V-SiCp electrode under (a) A—4 A, B—130 V, C—300 µs, D—5 µs; (b) A—8 A, B—130 V, C—100 µs, D—5 µs; and (c) A—12 A, B—130 V, C—200 µs, D—5 µs.
Figure 6.
Electric discharge-machined holes of dimensions 10 mm × 10 mm × 10 mm on AISI 316L stainless steel using the Ti-6Al-4V-SiCp electrode under (a) A—4 A, B—130 V, C—300 µs, D—5 µs; (b) A—8 A, B—130 V, C—100 µs, D—5 µs; and (c) A—12 A, B—130 V, C—200 µs, D—5 µs.
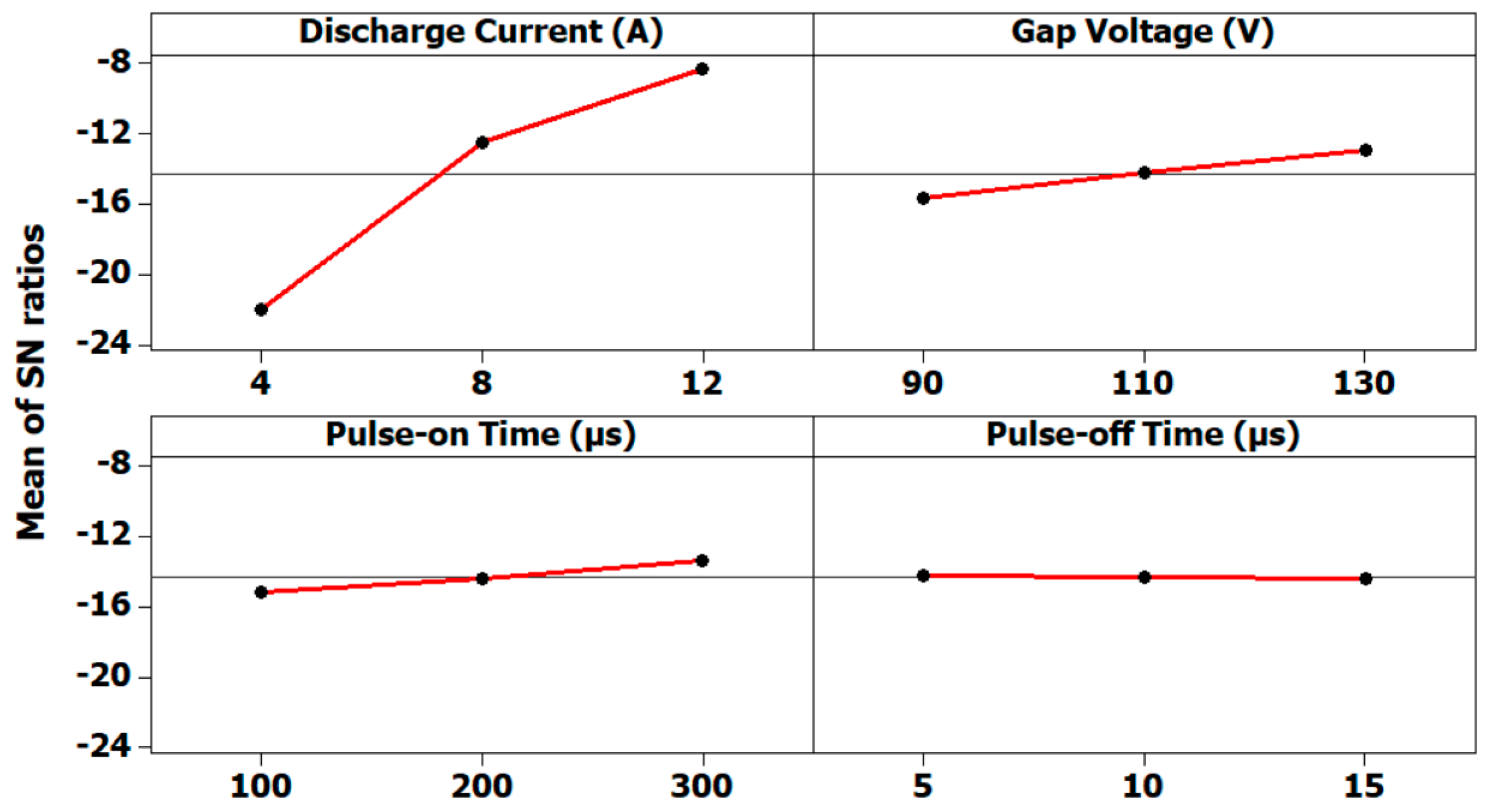
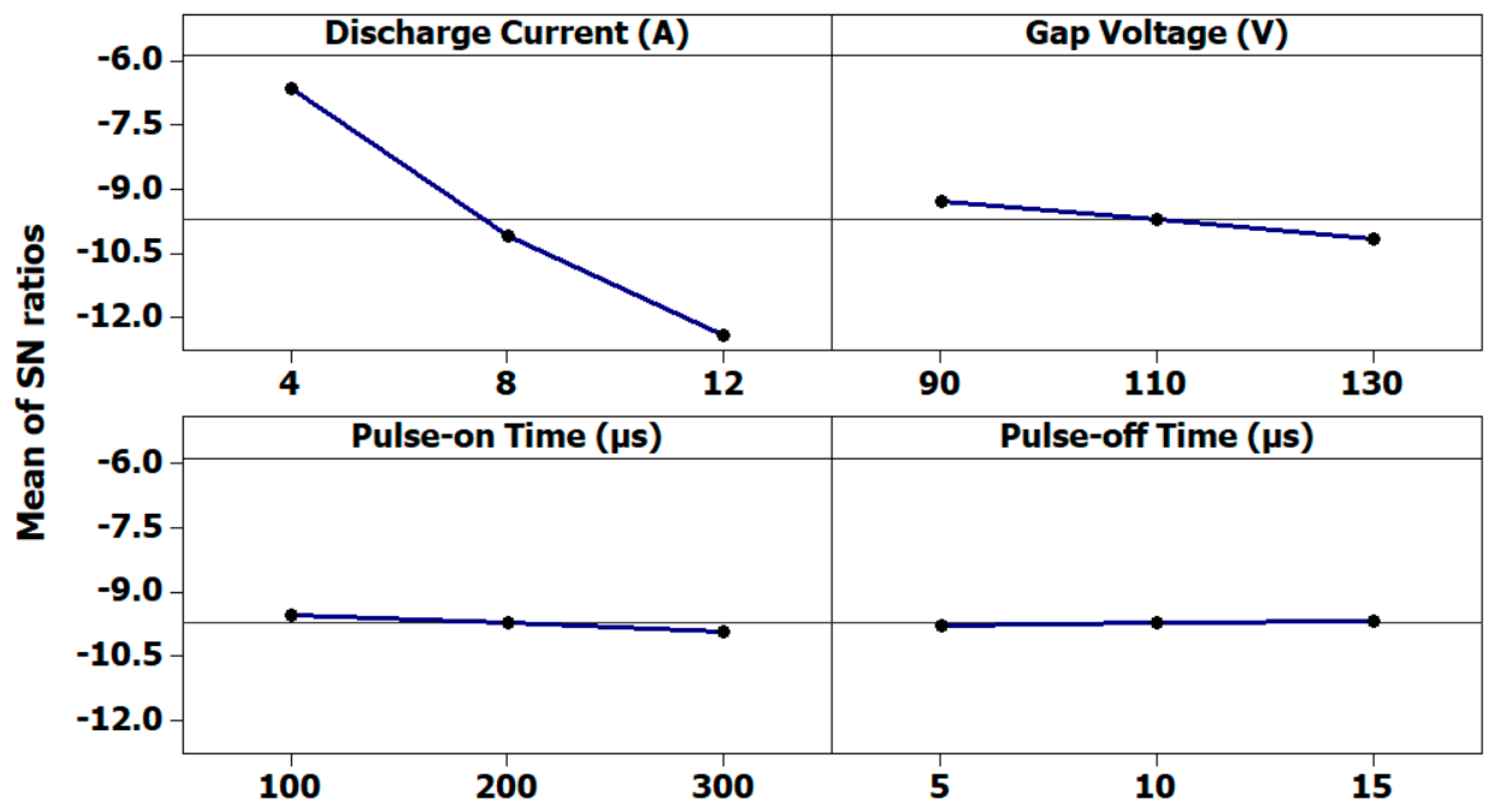
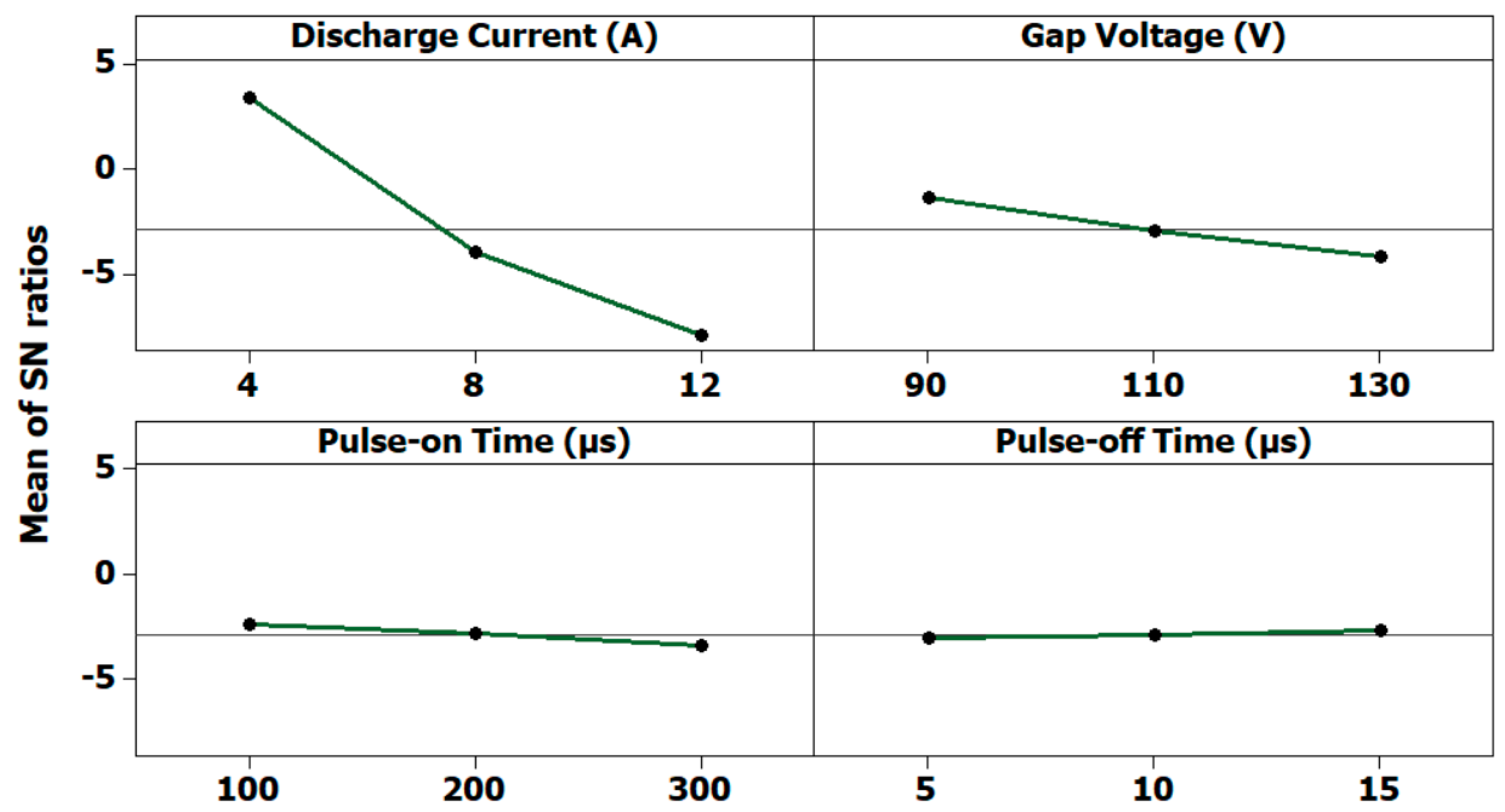
Figure 7.
Main effects plot for the signal–noise ratio for the material removal rate.
Figure 7.
Main effects plot for the signal–noise ratio for the material removal rate.
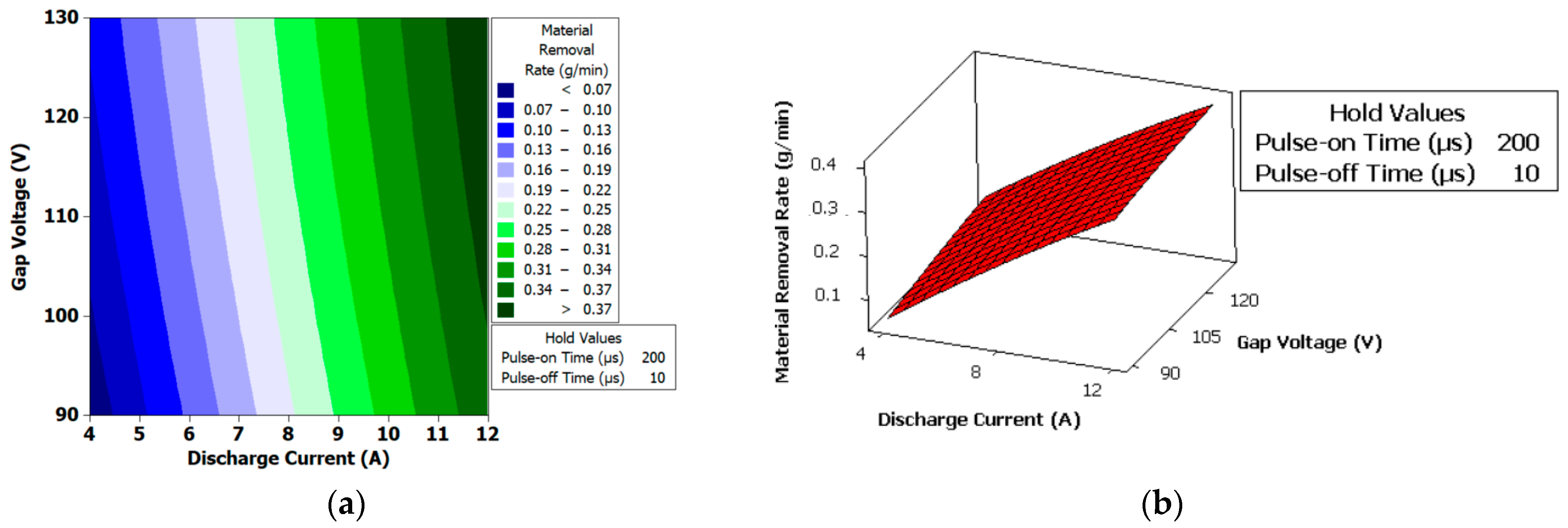
Figure 8.
(a) Contour plot for the material removal rate (g/min). (b) Surface plot for the material removal rate (g/min).
Figure 8.
(a) Contour plot for the material removal rate (g/min). (b) Surface plot for the material removal rate (g/min).
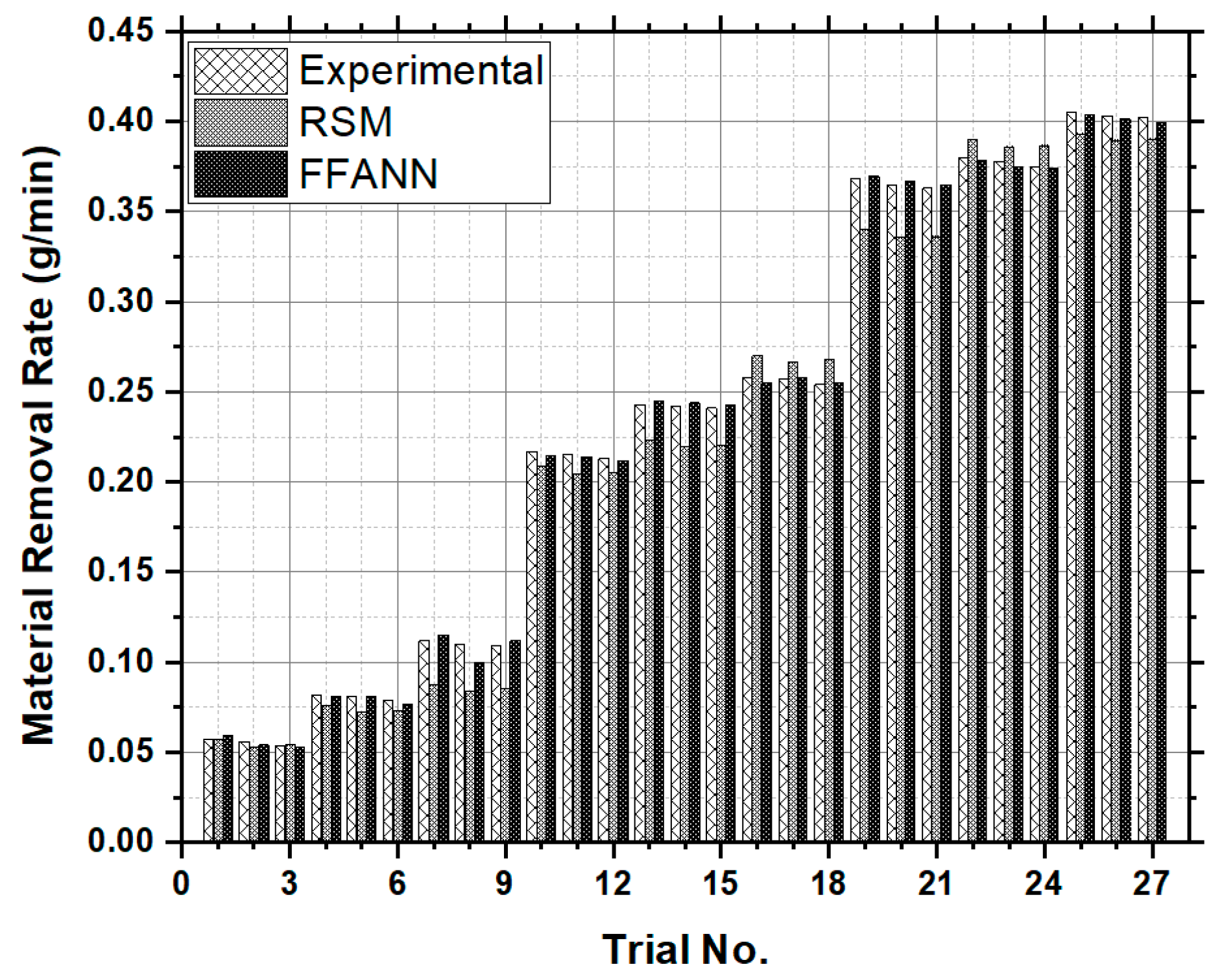
Figure 9.
Comparison of the RSM and FFANN predictions against the experimental results for the material removal rate (g/min).
Figure 9.
Comparison of the RSM and FFANN predictions against the experimental results for the material removal rate (g/min).
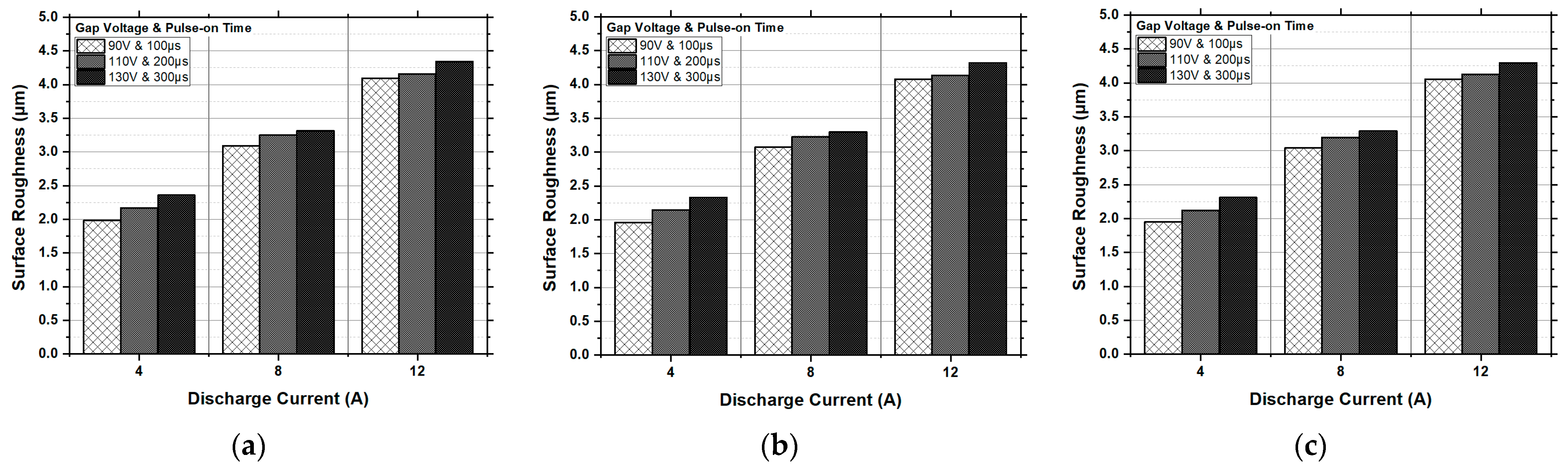
Figure 10.
Experimental results of the surface roughness (µm) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 10.
Experimental results of the surface roughness (µm) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 11.
Scanning electron images of AISI 316L stainless steel samples after die-sink electric discharge machining under (a) 4A discharge current, 90 V gap voltage, 100 µs pulse-on time and 5 µs pulse-off time; (b) 8 A discharge current, 110 V gap voltage, 200 µs pulse-on time and 10 µs pulse-off time; and (c) 12A discharge current, 130 V gap voltage, 300 µs pulse-on time and 15 µs pulse-off time.
Figure 11.
Scanning electron images of AISI 316L stainless steel samples after die-sink electric discharge machining under (a) 4A discharge current, 90 V gap voltage, 100 µs pulse-on time and 5 µs pulse-off time; (b) 8 A discharge current, 110 V gap voltage, 200 µs pulse-on time and 10 µs pulse-off time; and (c) 12A discharge current, 130 V gap voltage, 300 µs pulse-on time and 15 µs pulse-off time.
Figure 12.
Main effects plot for the signal–noise ratio for the surface roughness.
Figure 12.
Main effects plot for the signal–noise ratio for the surface roughness.
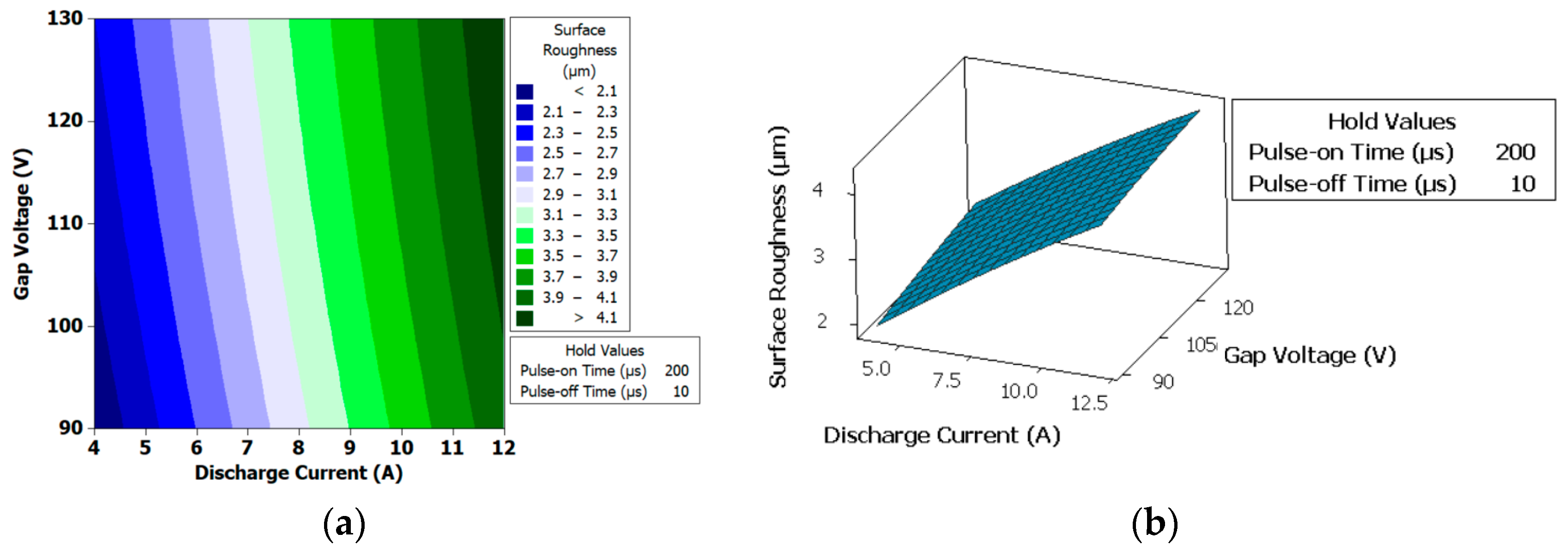
Figure 13.
(a) Contour plot for the surface roughness (µm). (b) Surface plot for the surface roughness (µm).
Figure 13.
(a) Contour plot for the surface roughness (µm). (b) Surface plot for the surface roughness (µm).
Figure 14.
Comparison of the RSM and FFANN predictions against the experimental results for the surface roughness (µm).
Figure 14.
Comparison of the RSM and FFANN predictions against the experimental results for the surface roughness (µm).
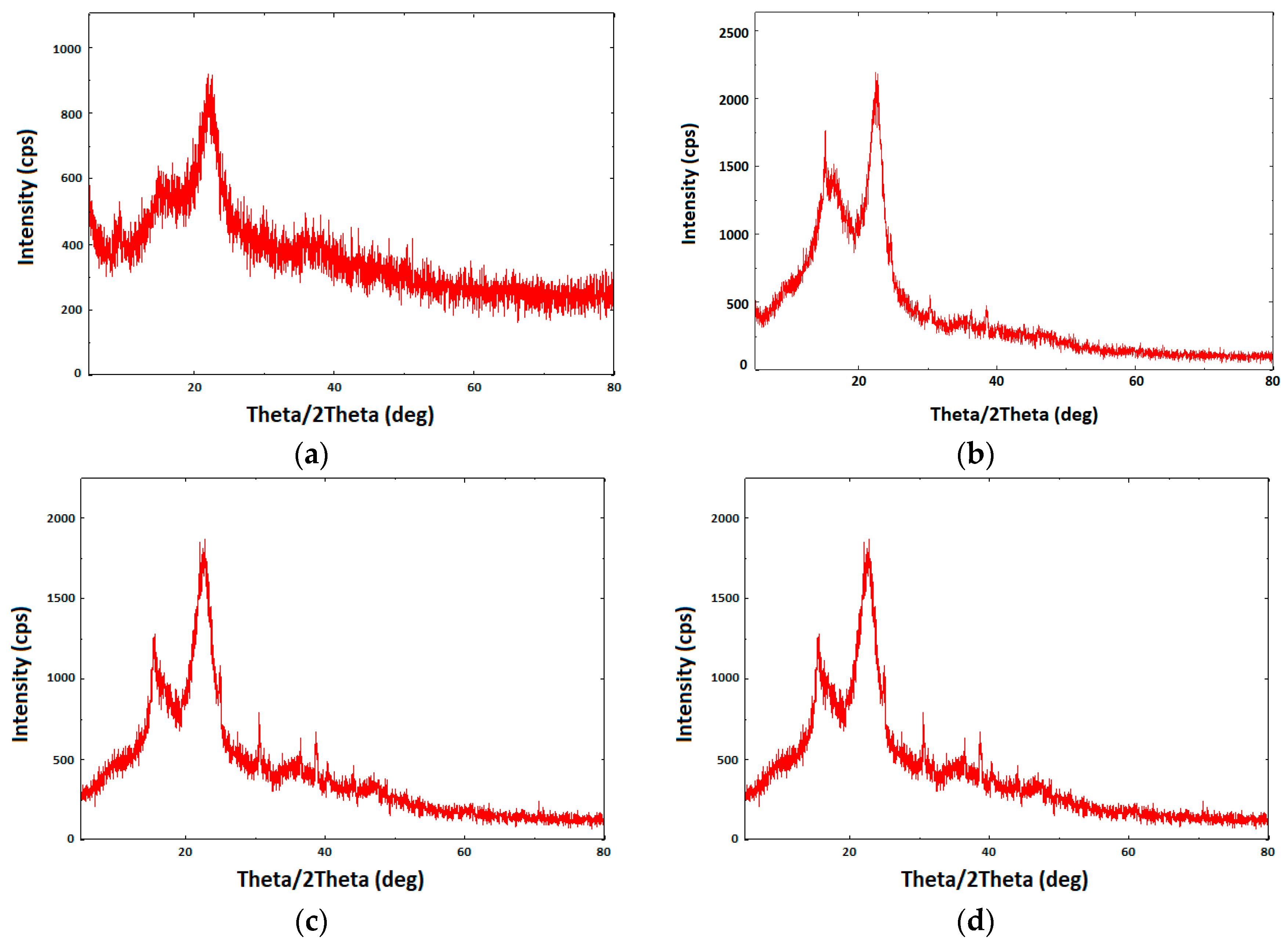
Figure 15.
Intensity vs. theta/2theta plots for the measurement of the residual stress for the (a) control sample; and samples machined under (b) A—12 A, B—130 V, C—300 µs, D—15 µs {target point A}; (c) A—10 A, B—110 V, C—200 µs, D—10 µs {target Point D}; and (d) A—8 A, B—90 V, C—100 µs, D—5 µs {target point G}.
Figure 15.
Intensity vs. theta/2theta plots for the measurement of the residual stress for the (a) control sample; and samples machined under (b) A—12 A, B—130 V, C—300 µs, D—15 µs {target point A}; (c) A—10 A, B—110 V, C—200 µs, D—10 µs {target Point D}; and (d) A—8 A, B—90 V, C—100 µs, D—5 µs {target point G}.
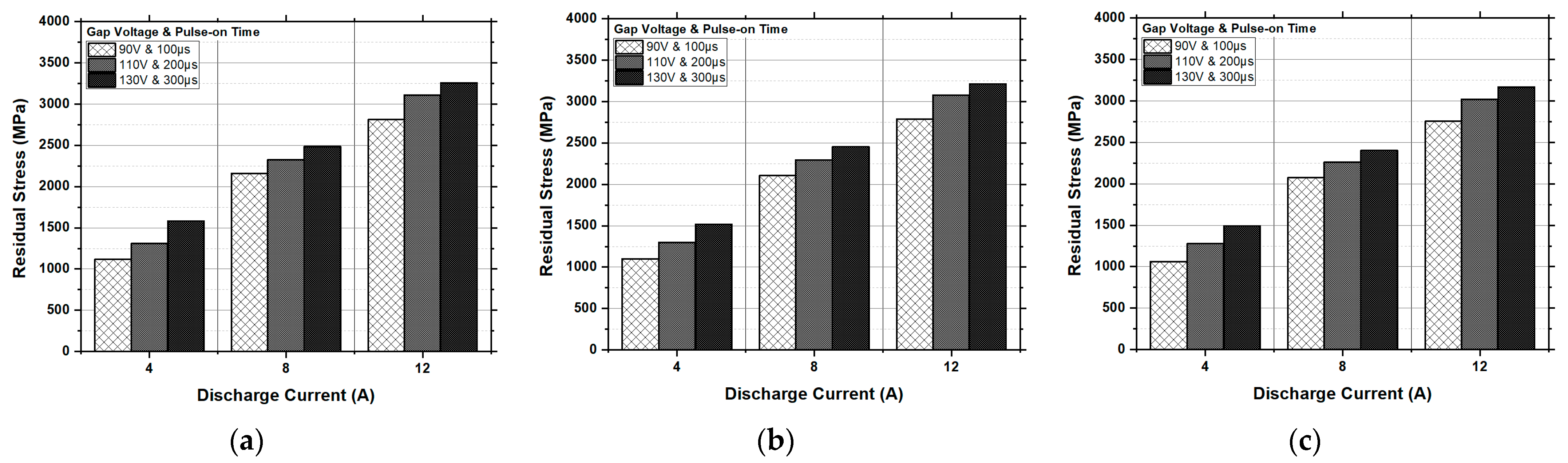
Figure 16.
Experimental results of the residual stress (MPa) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 16.
Experimental results of the residual stress (MPa) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
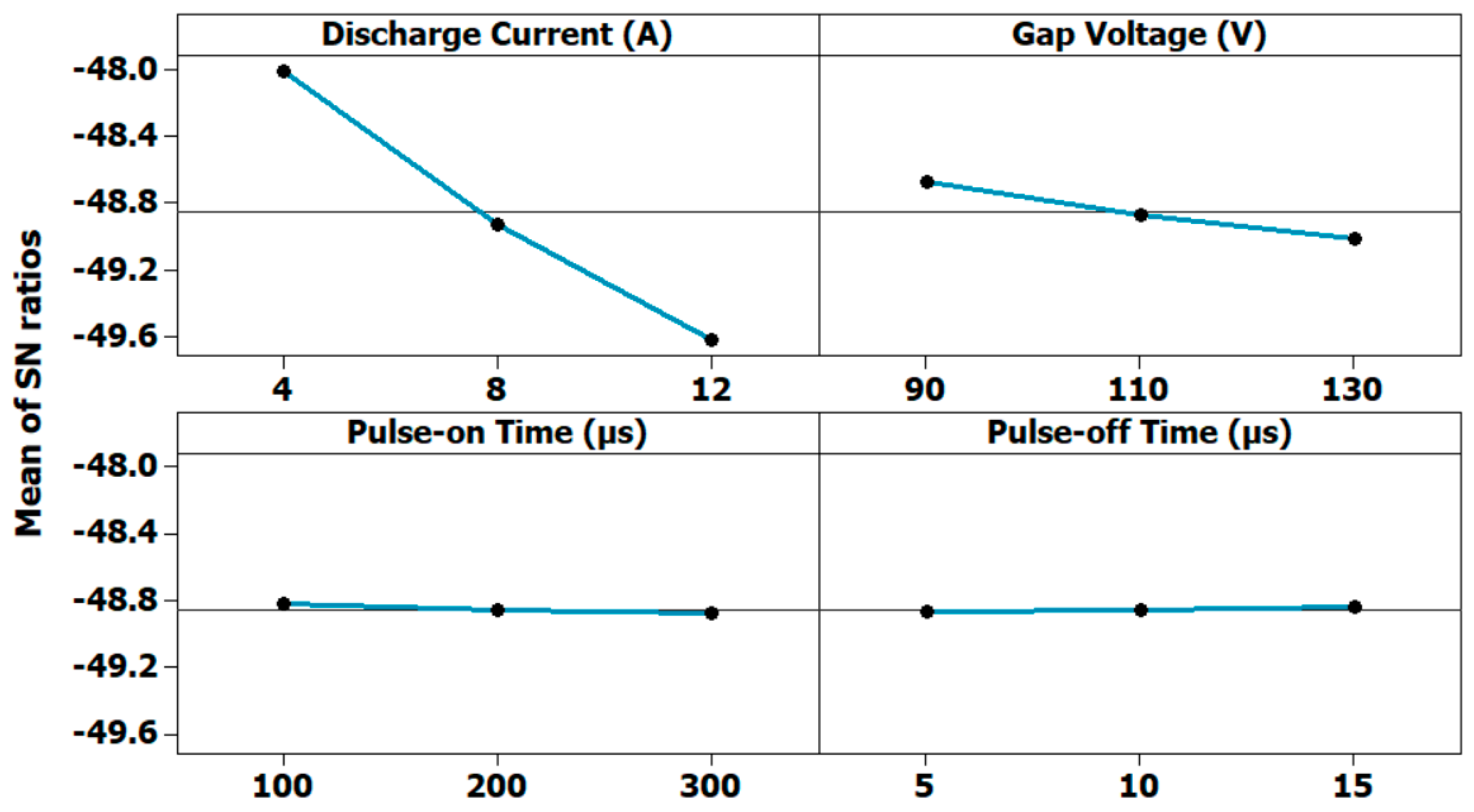
Figure 17.
Main effects plot of the signal–noise ratio for the residual stress (MPa).
Figure 17.
Main effects plot of the signal–noise ratio for the residual stress (MPa).
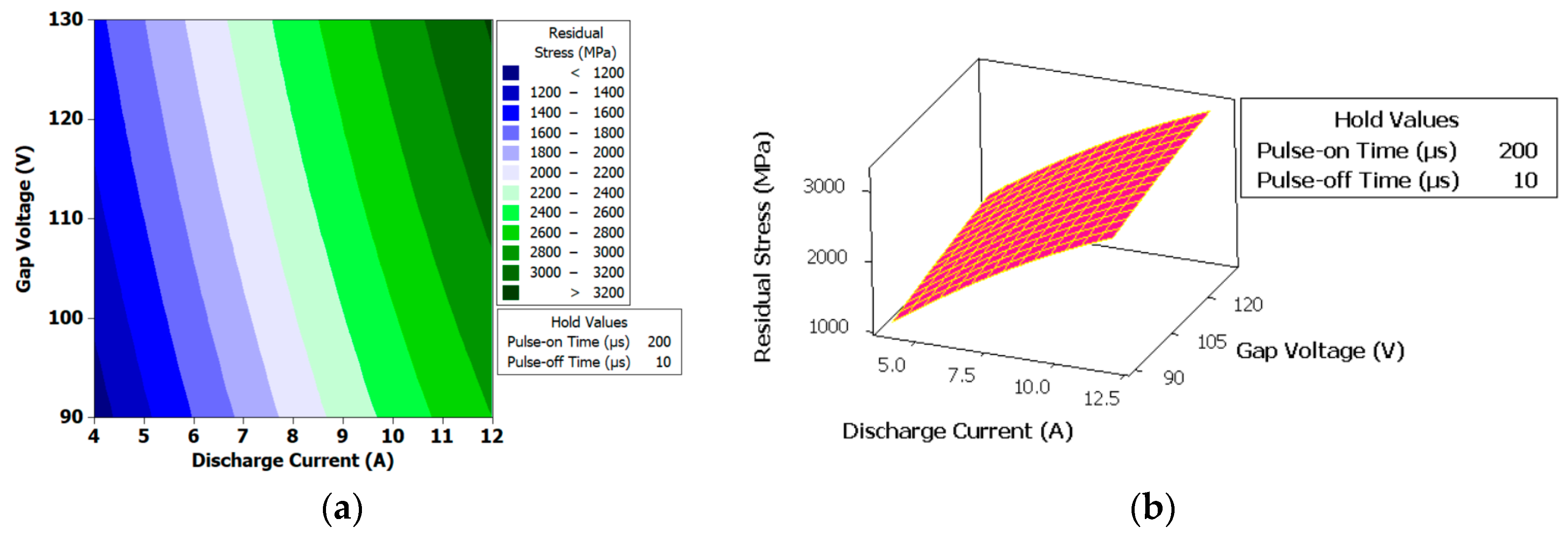
Figure 18.
(a) Contour plot for the residual stress (MPa). (b) Surface plot for the residual stress (MPa).
Figure 18.
(a) Contour plot for the residual stress (MPa). (b) Surface plot for the residual stress (MPa).
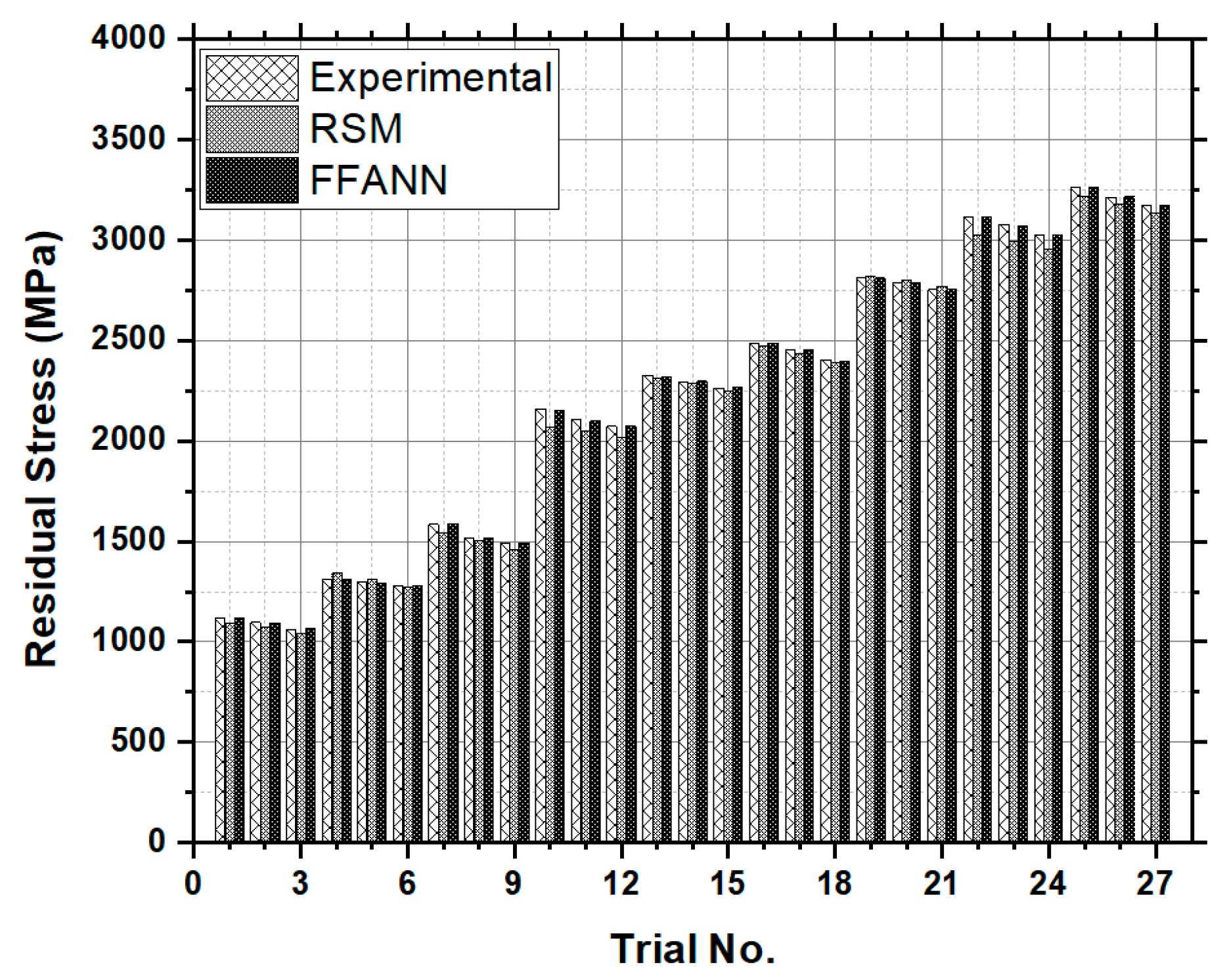
Figure 19.
Comparison of the RSM and FFANN prediction against the experimental results for the residual stress (MPa).
Figure 19.
Comparison of the RSM and FFANN prediction against the experimental results for the residual stress (MPa).
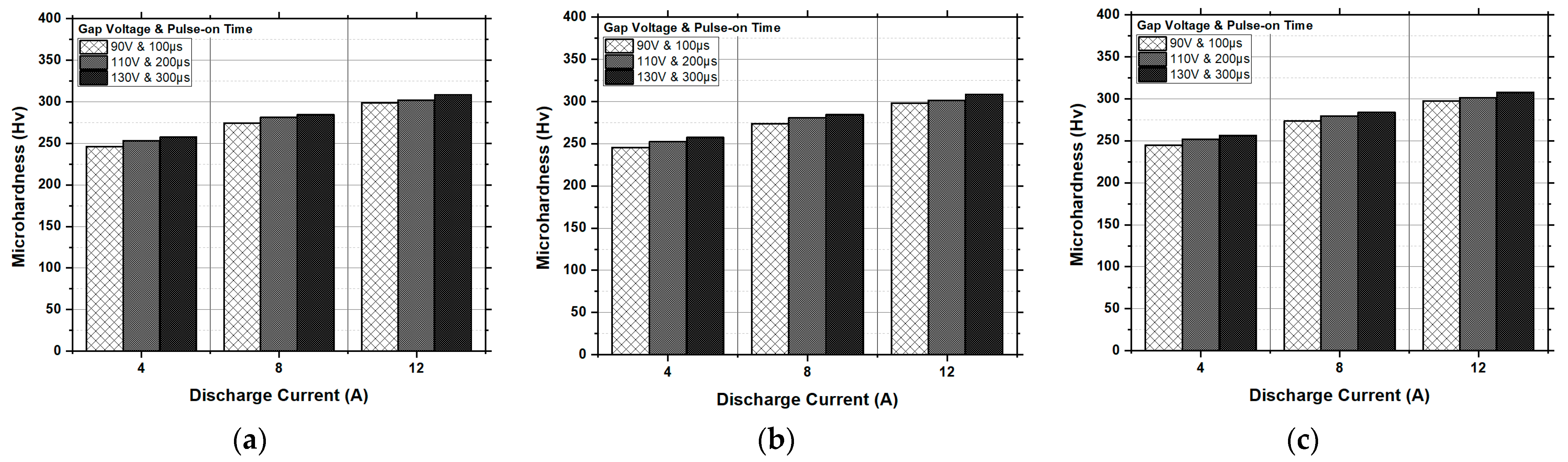
Figure 20.
Experimental results of the microhardness (Hv) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 20.
Experimental results of the microhardness (Hv) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 21.
Main effects plot of the signal to noise ratio for the microhardness (Hv).
Figure 21.
Main effects plot of the signal to noise ratio for the microhardness (Hv).
Figure 22.
(a) Contour plot of the microhardness (Hv). (b) Surface plot of the microhardness (Hv).
Figure 22.
(a) Contour plot of the microhardness (Hv). (b) Surface plot of the microhardness (Hv).
Figure 23.
Comparison of the RSM and FFANN prediction against the experimental results for the microhardness.
Figure 23.
Comparison of the RSM and FFANN prediction against the experimental results for the microhardness.
Figure 24.
Experimental results of the recast layer thickness (µm) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 24.
Experimental results of the recast layer thickness (µm) vs. the discharge current, gap voltage and pulse-on time for a (a) pulse-off time of 5 µs; (b) pulse-off time of 10 µs; and (c) pulse-off time of 15 µs.
Figure 25.
Recast layer thickness measurement using the trinocular vertical microscope for samples processed under (a) A—4 A, B—130 V, C—300 µs, D—5 µs; (b) A—8 A, B—130 V, C—100 µs, D—5 µs; and (c) A—12 A, B—130 V, C—200 µs, D—5 µs.
Figure 25.
Recast layer thickness measurement using the trinocular vertical microscope for samples processed under (a) A—4 A, B—130 V, C—300 µs, D—5 µs; (b) A—8 A, B—130 V, C—100 µs, D—5 µs; and (c) A—12 A, B—130 V, C—200 µs, D—5 µs.
Figure 26.
Main effects plot of the signal to noise ratio for the recast layer thickness (µm).
Figure 26.
Main effects plot of the signal to noise ratio for the recast layer thickness (µm).
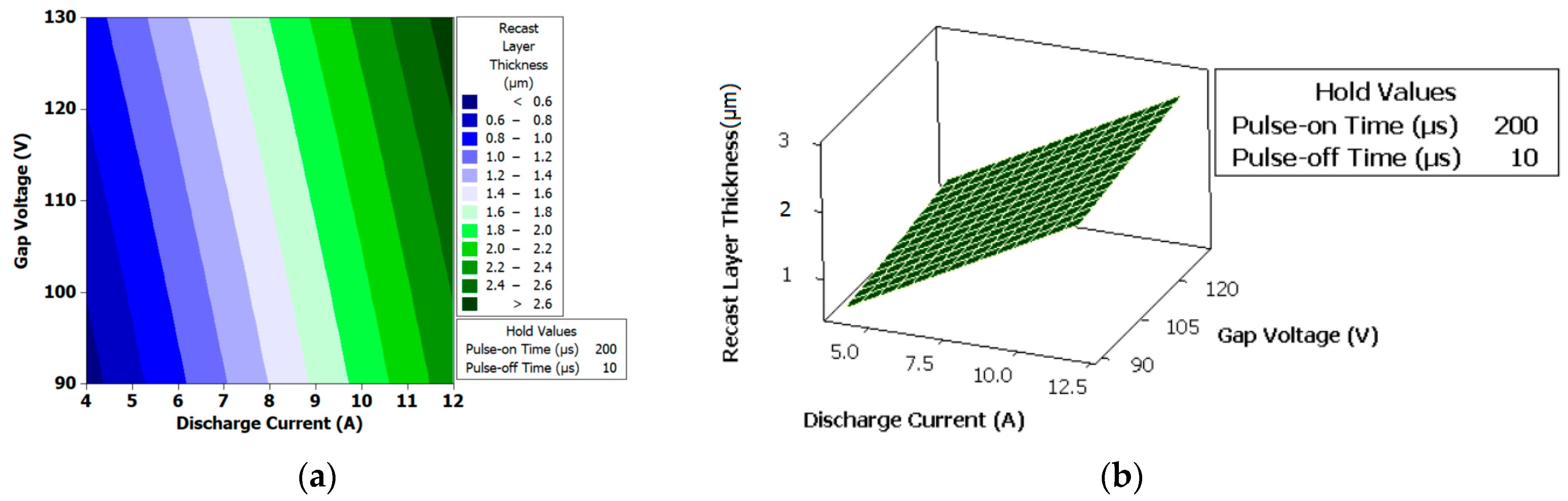
Figure 27.
(a) Contour plot for the recast layer thickness (µm). (b) Surface plot for the recast layer thickness (µm).
Figure 27.
(a) Contour plot for the recast layer thickness (µm). (b) Surface plot for the recast layer thickness (µm).
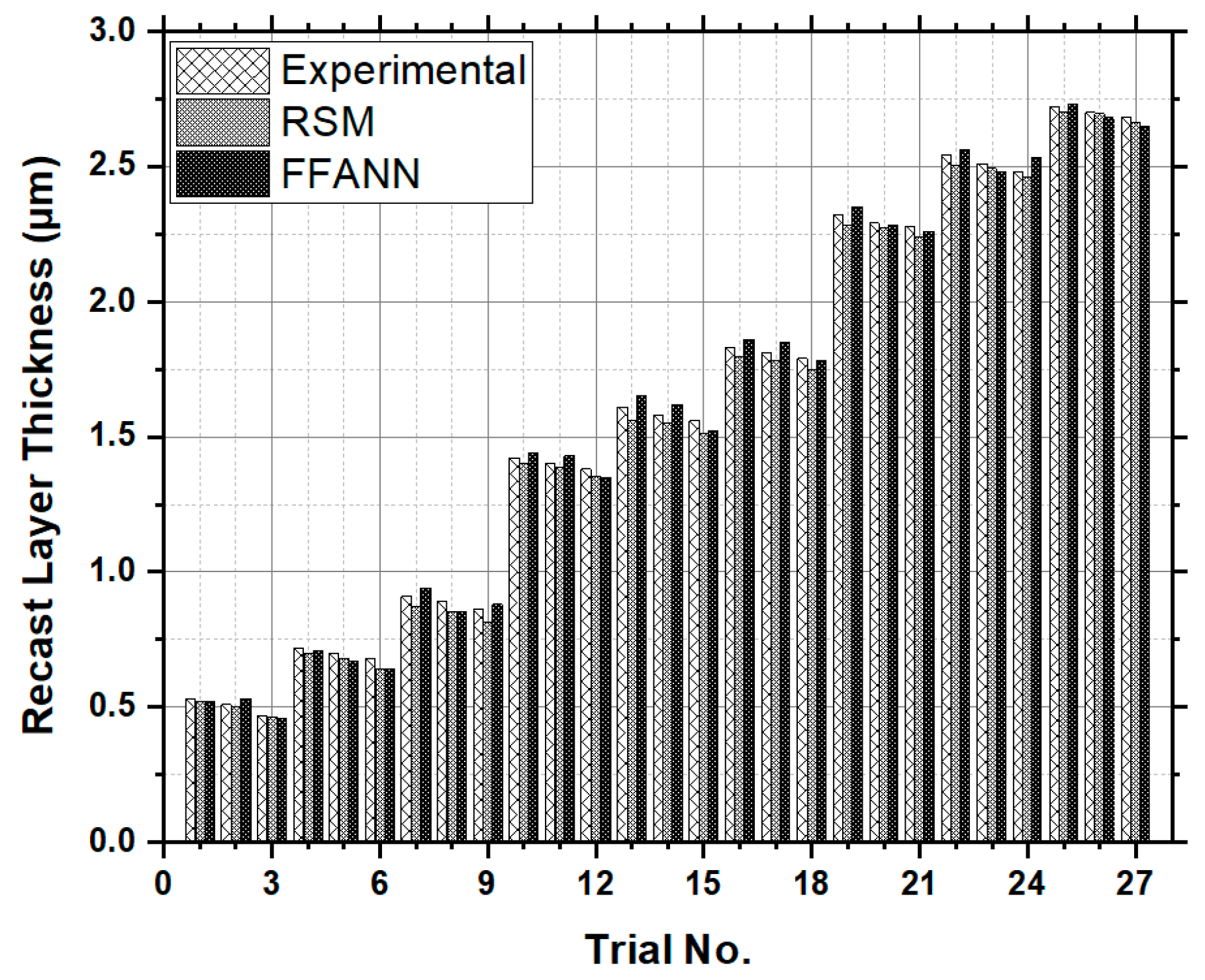
Figure 28.
Comparison of the RSM and FFANN prediction against the experimental results for the recast layer thickness (µm).
Figure 28.
Comparison of the RSM and FFANN prediction against the experimental results for the recast layer thickness (µm).
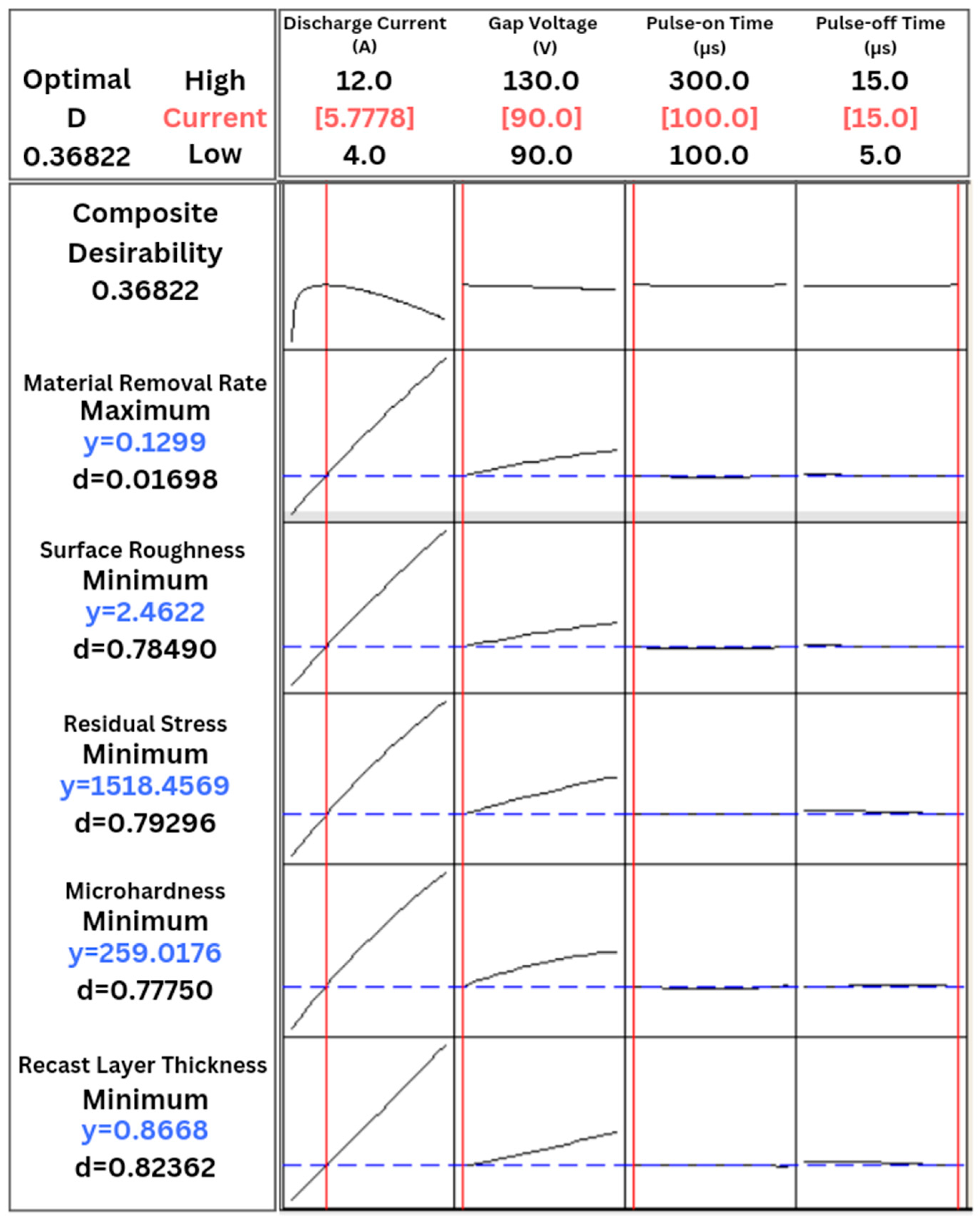
Figure 29.
Desirability function analysis for optimum results.
Figure 29.
Desirability function analysis for optimum results.
Table 1.
Overview of the relevant literature.
Table 1.
Overview of the relevant literature.
| Name of Researcher and Year | Material Used—Workpiece (W) and Tool (T) | Parameters | Limitations |
|---|
| Input | Response |
|---|
| MRR | SR |
|---|
| T. A. El-Taweel et al., 2009 [7] | C k 45 Steel (W) and Al-Cu-Si-TiC Powder Metallurgy Composite (T) | TiC Wt.%, Current, Flushing pressure, Pulse-on time | 0.6056 g/min | - | The study’s focus on a specific range of TiC percentages and peak currents may limit the applicability of the findings to broader EDM settings, and the effects of varying dielectric flushing pressures were found to be minimal, potentially overlooking other influential factors. |
| Raj Mohan et al., 2012 [52] | AISI 304 Stainless Steel (W) and Copper/Brass (T) | Pulse-on time, Pulse-off time, Current, Voltage | 36.56 mm3/min | - | The study is constrained to a specific range of EDM parameters and does not account for potential variations in other material types or complex parameter interactions, which may limit the generalizability of the findings to different EDM applications. |
| Nikalje et al., 2013 [53] | MDN 300 Steel (W) and Copper (T) | Current, Pulse-on time, Pulse-off time | 52.29 mm3/min | 5.58 µm | The study could benefit more from detailed analysis of more input parameters and the output response. |
| Chandramouli et al., 2017 [54] | 17–4 PH Steel (W) and Copper Tungsten (T) | Current, Pulse-on time, Pulse-off time, Lift time | 189.27 mg/min | 3.46 µm | The research focuses primarily on optimizing process parameters without addressing the thermal effects or metallurgical changes in the material, which are crucial for understanding the long-term performance of machined components. |
| Koteswararao 2017 [55] | EN-31 Steel (W) and Copper (T) | Electrode diameter, Current, Pulse-on time | 0.2921 g/min | - | The study focuses predominantly on MRR, TWR, and OC, leaving out the microstructural analysis and surface integrity aspects, which are crucial for high-precision applications in material science. |
| Buschaiah et al., 2018 [56] | AISI 304 Steel (W) and Copper (T) | Current, Pulse-on time, Electrode diameter | - | 2.24 µm | The research is primarily focused on surface roughness as the response parameter, without considering other important factors like material removal rate, electrode wear, or microstructural changes that could impact overall machining performance. |
| Muthuramalingam et al., 2014 [57] | AISI 202 Steel (W) and Copper, Brass, Tungsten Carbide (T) | Voltage, Current, Duty factor, Tool material | 16.621 mm3/min | 0.326 µm | The research focuses on specific process parameters and electrode materials, limiting the generalization of results to other materials or conditions. |
| Nandurkar et al., 2022 [58] | Oil-Hardened and Non-Shrinking Steel (W) and Copper/Brass (T) | Current, Pulse-on time, Pulse-off time | 0.5083 g/min | - | The research does not address other critical aspects, such as the surface integrity, residual stress, or thermal effects during machining, which are essential for comprehensive evaluation of EDM performance on tool steels. |
| Sonker et al., 2022 [59] | Die Steel (W) and Copper, Graphite (T) | Current, Pulse-on time, Pulse-off time | 5.9042 mm3/min | 2.6612 µm | The research primarily focuses on MRR, SR, and white layer formation without exploring microstructural changes or the potential long-term impact of the white layer on material properties, which are critical for die-steel applications. |
| Phani et al. 2023 [60] | HCHCr Steel (W) and Copper (T) | Current, Pulse-on time, Pulse-off time | 31.32 mm3/min | 0.79 µm | The research mainly focuses on electrical parameters without providing insights into the microstructural or thermal impacts on the material post-machining, which are crucial for ensuring long-term durability in industrial applications. |
| Naveed 2024 [61] | Die Steel (W) and Copper, Copper–Tungsten, Graphite (T) | Tool material, Relief angle | 302.36 × 106 µm3/s | - | The study does not explore the impact of varying relief angles beyond 20 degrees or the potential effects of tool wear on long-term EDM performance and dimensional accuracy. |
| Kumar et al., 2020 [62] | AISI 420 Steel (W) and Copper (T) | Current, Voltage, Pulse-on time | 0.0387 g/min | - | The study’s focus on AISI420 steel and copper electrodes limits its applicability to other materials and tool types, and does not consider the effects of dielectric fluid properties or long-term tool degradation. |
| Muthuramalingam et al., 2013 [63] | AISI 202 Steel (W) and Tungsten Carbide, Brass, Copper (T) | Current, Voltage, Duty Factor | 20.1 mm3/min | 0.25 µm | The study does not explore the influence of the dielectric fluid properties or long-term electrode wear, limiting the understanding of their combined effects on EDM performance. |
| Shukry et al., 2016 [64] | AISI 316 Steel (W) and Copper (T) | Current, Pulse-on time, Pulse-off time | 48.16 mm3/min | - | The study does not address the effects of varying dielectric fluid types or conditions over extended machining periods, which may influence the long-term performance and accuracy of the EDM process. |
| Makwana et al., 2015 [65] | AISI 316 Steel (W) and Copper (T) | Current, Pulse-on time, Pulse-off time | 91.615 mm3/min | 9.8 µm | The study primarily focuses on a fixed cross-sectional area and does not explore the effects of varying electrode sizes or materials, which could limit the generalizability of the findings to other EDM applications or electrode designs. |
Table 2.
Chemical composition (Wt.%) of the AISI 316L stainless steel as procured.
Table 2.
Chemical composition (Wt.%) of the AISI 316L stainless steel as procured.
| Element | Fe | Cr | Ni | Mo | Mn | Si | C | P | S |
|---|
| Wt.% | 66 | 17 | 13.2 | 2.1 | 1.2 | 0.4 | 0.01 | 0.0042 | 0.008 |
Table 3.
Properties of the AISI 316L stainless steel [
51].
Table 3.
Properties of the AISI 316L stainless steel [
51].
| Properties | Values |
|---|
| Density | 8000 kg/m3 |
| Hardness | 180 Hv |
| Young’s Modulus | 193 GPa |
| Bulk Modulus | 160 GPa |
| Tensile Strength | 510 MPa |
| Thermal Conductivity at 500 °C | 21.5 W/m·K |
Table 4.
Properties of the Ti-6Al-4V-SiCp electrode material [
51].
Table 4.
Properties of the Ti-6Al-4V-SiCp electrode material [
51].
| Properties | Ti-6Al-4V-SiCp |
|---|
| Hardness | 440 BHN |
| Thermal Conductivity at 500 °C | 36.15 (W/m·K) |
| Electrical Conductivity at 500 °C | 2.347 × 10−7 (Ω·m) |
Table 5.
Control factors and levels for the EDM (DoE).
Table 5.
Control factors and levels for the EDM (DoE).
| Control Factors | Levels |
|---|
| 1 | 2 | 3 |
|---|
| A | 4 | 8 | 12 |
| B | 90 | 110 | 130 |
| C | 100 | 200 | 300 |
| D | 5 | 10 | 15 |
Table 6.
Averaged experimental results from the electric discharge machining of AISI 316L stainless steel.
Table 6.
Averaged experimental results from the electric discharge machining of AISI 316L stainless steel.
| Trial. No. | A | B | C | D | Material
Removal Rate (g/min) | Surface Roughness
(µm) | Residual Stress (MPa) | Microhardness
(Hv) | Recast Layer Thickness (µm) |
|---|
| 1 | 4 | 90 | 100 | 5 | 0.057 | 1.98 | 1115.56 | 245.9 | 0.53 |
| 2 | 4 | 90 | 100 | 10 | 0.056 | 1.96 | 1098.32 | 245.4 | 0.51 |
| 3 | 4 | 90 | 100 | 15 | 0.054 | 1.95 | 1063.74 | 244.8 | 0.47 |
| 4 | 4 | 110 | 200 | 5 | 0.082 | 2.17 | 1310.47 | 253.1 | 0.72 |
| 5 | 4 | 110 | 200 | 10 | 0.081 | 2.15 | 1298.31 | 252.6 | 0.70 |
| 6 | 4 | 110 | 200 | 15 | 0.079 | 2.12 | 1278.39 | 252.2 | 0.68 |
| 7 | 4 | 130 | 300 | 5 | 0.112 | 2.36 | 1584.91 | 257.6 | 0.91 |
| 8 | 4 | 130 | 300 | 10 | 0.110 | 2.33 | 1515.83 | 257.1 | 0.89 |
| 9 | 4 | 130 | 300 | 15 | 0.109 | 2.31 | 1490.58 | 256.5 | 0.86 |
| 10 | 8 | 90 | 200 | 5 | 0.217 | 3.09 | 2158.62 | 274.1 | 1.42 |
| 11 | 8 | 90 | 200 | 10 | 0.215 | 3.07 | 2104.47 | 273.7 | 1.40 |
| 12 | 8 | 90 | 200 | 15 | 0.213 | 3.04 | 2071.54 | 273.2 | 1.38 |
| 13 | 8 | 110 | 300 | 5 | 0.243 | 3.25 | 2326.71 | 281.3 | 1.61 |
| 14 | 8 | 110 | 300 | 10 | 0.242 | 3.23 | 2295.74 | 281.1 | 1.58 |
| 15 | 8 | 110 | 300 | 15 | 0.241 | 3.20 | 2262.56 | 279.6 | 1.56 |
| 16 | 8 | 130 | 100 | 5 | 0.258 | 3.32 | 2486.64 | 284.6 | 1.83 |
| 17 | 8 | 130 | 100 | 10 | 0.257 | 3.30 | 2451.15 | 284.2 | 1.81 |
| 18 | 8 | 130 | 100 | 15 | 0.254 | 3.29 | 2404.38 | 283.9 | 1.79 |
| 19 | 12 | 90 | 300 | 5 | 0.368 | 4.09 | 2808.83 | 298.3 | 2.32 |
| 20 | 12 | 90 | 300 | 10 | 0.365 | 4.08 | 2785.34 | 297.8 | 2.29 |
| 21 | 12 | 90 | 300 | 15 | 0.363 | 4.05 | 2750.65 | 297.5 | 2.28 |
| 22 | 12 | 110 | 100 | 5 | 0.380 | 4.16 | 3112.57 | 302.1 | 2.54 |
| 23 | 12 | 110 | 100 | 10 | 0.378 | 4.14 | 3078.41 | 301.8 | 2.51 |
| 24 | 12 | 110 | 100 | 15 | 0.375 | 4.13 | 3023.40 | 301.5 | 2.48 |
| 25 | 12 | 130 | 200 | 5 | 0.405 | 4.35 | 3260.01 | 308.7 | 2.72 |
| 26 | 12 | 130 | 200 | 10 | 0.403 | 4.32 | 3212.53 | 308.3 | 2.70 |
| 27 | 12 | 130 | 200 | 15 | 0.402 | 4.30 | 3169.71 | 307.9 | 2.68 |
Table 7.
Analysis of variance for the SN ratios of the material removal rate.
Table 7.
Analysis of variance for the SN ratios of the material removal rate.
| Source | DF | Seq.SS | Adj.SS | Adj.MS | F | P | p% |
|---|
| A | 2 | 884.745 | 884.745 | 442.373 | 271.96 | 0.000 | 93.83 |
| B | 2 | 34.795 | 34.795 | 17.397 | 10.70 | 0.011 | 3.69 |
| C | 2 | 13.356 | 13.356 | 6.678 | 4.11 | 0.075 | 1.416 |
| D | 2 | 0.161 | 0.161 | 0.081 | 0.05 | 0.952 | 0.017 |
| A × D | 4 | 0.055 | 0.055 | 0.014 | 0.01 | 1.000 | 0.005 |
| B × D | 4 | 0.010 | 0.010 | 0.003 | 0.00 | 1.000 | 0.001 |
| C × D | 4 | 0.011 | 0.011 | 0.003 | 0.00 | 1.000 | 0.001 |
| Residual Error | 6 | 9.760 | 9.760 | 1.627 | | | |
| Total | 26 | 942.892 | | | | | |
Table 8.
Estimated regression coefficients for the material removal rate (g/min).
Table 8.
Estimated regression coefficients for the material removal rate (g/min).
| Term | Coef. | SE Coef. | T | P |
|---|
| Constant | −0.358355 | 0.040604 | −8.826 | 0.000 |
| A | 0.053816 | 0.001711 | 31.444 | 0.000 |
| B | 0.003597 | 0.000803 | 4.478 | 0.000 |
| C | −0.000132 | 0.000068 | −1.931 | 0.071 |
| D | −0.002330 | 0.001369 | −1.702 | 0.108 |
| A × A | −0.000639 | 0.000091 | −7.059 | 0.000 |
| B × B | −0.000009 | 0.000004 | −2.571 | 0.021 |
| C × C | 0.000000 | 0.000000 | 2.263 | 0.038 |
| D × D | 0.000091 | 0.000058 | 1.573 | 0.135 |
| A × B | −0.000053 | 0.000007 | −7.287 | 0.000 |
| A × C | −0.000000 | 0.000001 | −0.000 | 1.000 |
| A × D | −0.000013 | 0.000029 | −0.429 | 0.674 |
| B × C | 0.000000 | 0.000000 | 0.000 | 1.000 |
| B × D | 0.000003 | 0.000006 | 0.429 | 0.674 |
| C × D | 0.000000 | 0.000001 | 0.000 | 1.000 |
Table 9.
ANOVA for the material removal rate (g/min).
Table 9.
ANOVA for the material removal rate (g/min).
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|
| Regression | 14 | 0.418227 | 0.418227 | 0.029873 | 5489.13 | 0.000 |
| Residual Error | 16 | 0.000087 | 0.000087 | 0.000005 | | |
| Total | 30 | 0.418314 | | | | |
Table 10.
Analysis of variance for the SN ratios of the surface roughness.
Table 10.
Analysis of variance for the SN ratios of the surface roughness.
| Source | DF | Seq.SS | Adj.SS | Adj.MS | F | P | p% |
|---|
| A | 2 | 153.519 | 153.519 | 76.7593 | 1867.97 | 0.000 | 97.13 |
| B | 2 | 3.546 | 3.546 | 1.7729 | 43.14 | 0.000 | 2.243 |
| C | 2 | 0.662 | 0.662 | 0.3310 | 8.05 | 0.020 | 0.418 |
| D | 2 | 0.070 | 0.070 | 0.0352 | 0.86 | 0.471 | 0.044 |
| A × D | 4 | 0.006 | 0.006 | 0.0016 | 0.04 | 0.996 | 0.003 |
| B × D | 4 | 0.001 | 0.001 | 0.0002 | 0.00 | 1.000 | 0.0006 |
| C × D | 4 | 0.003 | 0.003 | 0.0008 | 0.02 | 0.999 | 0.001 |
| Residual Error | 6 | 0.247 | 0.247 | 0.0411 | | | |
| Total | 26 | 158.054 | | | | | |
Table 11.
Estimated regression coefficients for the surface roughness (µm).
Table 11.
Estimated regression coefficients for the surface roughness (µm).
| Term | Coef. | SE Coef. | T | P |
|---|
| Constant | −0.865430 | 0.380068 | −2.277 | 0.037 |
| A | 0.361282 | 0.016020 | 22.552 | 0.000 |
| B | 0.025126 | 0.007519 | 3.341 | 0.004 |
| C | −0.000966 | 0.000641 | −1.508 | 0.151 |
| D | −0.010919 | 0.012816 | −0.852 | 0.407 |
| A × A | −0.004124 | 0.000847 | −4.868 | 0.000 |
| B × B | −0.000065 | 0.000034 | −1.917 | 0.073 |
| C × C | 0.000002 | 0.000001 | 1.772 | 0.096 |
| D × D | 0.000561 | 0.000542 | 1.034 | 0.317 |
| A × B | −0.000359 | 0.000068 | −5.266 | 0.000 |
| A × C | 0.000000 | 0.000014 | 0.000 | 1.000 |
| A × D | −0.000063 | 0.000273 | −0.229 | 0.822 |
| B × C | 0.000000 | 0.000003 | 0.000 | 1.000 |
| B × D | −0.000037 | 0.000055 | −0.687 | 0.502 |
| C × D | 0.000000 | 0.000011 | 0.000 | 1.000 |
Table 12.
ANOVA for the surface roughness (µm).
Table 12.
ANOVA for the surface roughness (µm).
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|
| Regression | 14 | 19.2113 | 19.2113 | 1.372238 | 2877.81 | 0.000 |
| Residual Error | 16 | 0.0076 | 0.007629 | 0.000477 | | |
| Total | 30 | 19.2190 | | | | |
Table 13.
X-ray diffraction data captured at target point A for a sample processed under A—8 A, B—90 V, C—100 µs, and D—5 µs.
Table 13.
X-ray diffraction data captured at target point A for a sample processed under A—8 A, B—90 V, C—100 µs, and D—5 µs.
| Peak No. | Diffraction Angle (2ϴ) | Crystallographic Plane | Lattice Spacing (Ǻ) (Control) | Lattice Spacing (Ǻ) (Sample) | Lattice Strain (ɛ) | Residual Stress (MPa) |
|---|
| 1 | 15.4 | (111) | 3.6 | 3.612 | 0.003333333 | 653.33 |
| 2 | 17.8 | (200) | 2.521 | 2.528 | 0.002776676 | 544.22 |
| 3 | 18.3 | (220) | 1.802 | 1.809 | 0.003884573 | 761.37 |
| 4 | 18.6 | (311) | 1.456 | 1.462 | 0.004120879 | 807.69 |
| 5 | 19.2 | 222 | 1.351 | 1.359 | 0.00592154 | 1160.62 |
| 6 | 20.1 | 400 | 1.257 | 1.261 | 0.00318218 | 623.70 |
| 7 | 20.8 | 331 | 1.183 | 1.188 | 0.004226543 | 828.40 |
| 8 | 21.4 | 420 | 1.127 | 1.131 | 0.003549246 | 695.65 |
| 9 | 25.3 | 422 | 1.016 | 1.023 | 0.006889764 | 1350.39 |
| 10 | 26.8 | 511 | 0.922 | 0.929 | 0.007592191 | 1488.06 |
| 11 | 30.2 | 440 | 0.839 | 0.842 | 0.003575685 | 700.83 |
| 12 | 41.4 | 620 | 0.671 | 0.676 | 0.007451565 | 1460.50 |
| 13 | 45.6 | 622 | 0.624 | 0.628 | 0.006410256 | 1256.41 |
| 14 | 52.1 | 333 | 0.554 | 0.559 | 0.009025271 | 1768.95 |
| 15 | 55.7 | 622 | 0.528 | 0.531 | 0.005681818 | 1113.63 |
| 16 | 63.8 | 553 | 0.459 | 0.462 | 0.006535948 | 1281.04 |
| 17 | 68.2 | 440 | 0.428 | 0.432 | 0.009345794 | 1831.77 |
| 18 | 72.1 | 444 | 0.405 | 0.408 | 0.007407407 | 1451.85 |
| 19 | 73.5 | 622 | 0.395 | 0.399 | 0.010126582 | 1984.81 |
| 20 | 74.2 | 553 | 0.389 | 0.392 | 0.007712082 | 1511.56 |
| Average Residual Stress (Mpa) | 1163.74 |
Table 14.
X-ray diffraction data captured at target point D for a sample processed under A—10 A, B—110 V, C—200 µs, and D—10 µs.
Table 14.
X-ray diffraction data captured at target point D for a sample processed under A—10 A, B—110 V, C—200 µs, and D—10 µs.
| Peak No. | Diffraction Angle (2ϴ) | Crystallographic Plane | Lattice Spacing (Ǻ) (Control) | Lattice Spacing (Ǻ) (Sample) | Lattice Strain (ɛ) | Residual Stress (MPa) |
|---|
| 1 | 15.4 | 111 | 3.6 | 3.62 | 0.005555556 | 1088.88 |
| 2 | 17.8 | 200 | 2.521 | 2.534 | 0.005156684 | 1010.71 |
| 3 | 18.3 | 220 | 1.802 | 1.811 | 0.004994451 | 978.91 |
| 4 | 18.6 | 311 | 1.456 | 1.468 | 0.008241758 | 1615.38 |
| 5 | 19.2 | 222 | 1.351 | 1.368 | 0.012583272 | 2466.32 |
| 6 | 20.1 | 400 | 1.257 | 1.268 | 0.008750994 | 1715.19 |
| 7 | 20.8 | 331 | 1.183 | 1.196 | 0.010989011 | 2153.84 |
| 8 | 21.4 | 420 | 1.127 | 1.138 | 0.009760426 | 1913.04 |
| 9 | 25.3 | 422 | 1.016 | 1.025 | 0.008858268 | 1736.22 |
| 10 | 26.8 | 511 | 0.922 | 0.934 | 0.013015184 | 2550.97 |
| 11 | 30.2 | 440 | 0.839 | 0.85 | 0.013110846 | 2569.72 |
| 12 | 41.4 | 620 | 0.671 | 0.68 | 0.013412817 | 2628.91 |
| 13 | 45.6 | 622 | 0.624 | 0.631 | 0.011217949 | 2198.71 |
| 14 | 52.1 | 333 | 0.554 | 0.563 | 0.016245487 | 3184.11 |
| 15 | 55.7 | 622 | 0.528 | 0.535 | 0.013257576 | 2598.48 |
| 16 | 63.8 | 553 | 0.459 | 0.466 | 0.015250545 | 2989.10 |
| 17 | 68.2 | 440 | 0.428 | 0.434 | 0.014018692 | 2747.66 |
| 18 | 72.1 | 444 | 0.405 | 0.412 | 0.017283951 | 3387.65 |
| 19 | 73.5 | 622 | 0.395 | 0.402 | 0.017721519 | 3473.41 |
| 20 | 74.2 | 553 | 0.389 | 0.396 | 0.017994859 | 3526.99 |
| Average Residual Stress (Mpa) | 2326.71 |
Table 15.
X-ray diffraction data captured at target point G for a sample processed under A—12 A, B—130 V, C—300 µs, and D—15 µs.
Table 15.
X-ray diffraction data captured at target point G for a sample processed under A—12 A, B—130 V, C—300 µs, and D—15 µs.
| Peak No. | Diffraction Angle (2ϴ) | Crystallographic Plane | Lattice Spacing (Ǻ) (Control) | Lattice Spacing (Ǻ) (Sample) | Lattice Strain (ɛ) | Residual Stress (MPa) |
|---|
| 1 | 15.4 | 111 | 3.6 | 3.67 | 0.019444444 | 3811.11 |
| 2 | 17.8 | 200 | 2.521 | 2.556 | 0.01388338 | 2721.14 |
| 3 | 18.3 | 220 | 1.802 | 1.829 | 0.014983352 | 2936.73 |
| 4 | 18.6 | 311 | 1.456 | 1.475 | 0.013049451 | 2557.69 |
| 5 | 19.2 | 222 | 1.351 | 1.369 | 0.013323464 | 2611.39 |
| 6 | 20.1 | 400 | 1.257 | 1.275 | 0.014319809 | 2806.68 |
| 7 | 20.8 | 331 | 1.183 | 1.199 | 0.013524937 | 2650.88 |
| 8 | 21.4 | 420 | 1.127 | 1.14 | 0.011535049 | 2260.86 |
| 9 | 25.3 | 422 | 1.016 | 1.03 | 0.013779528 | 2700.78 |
| 10 | 26.8 | 511 | 0.922 | 0.936 | 0.015184382 | 2976.13 |
| 11 | 30.2 | 440 | 0.839 | 0.852 | 0.015494636 | 3036.94 |
| 12 | 41.4 | 620 | 0.671 | 0.682 | 0.016393443 | 3213.11 |
| 13 | 45.6 | 622 | 0.624 | 0.635 | 0.017628205 | 3455.12 |
| 14 | 52.1 | 333 | 0.554 | 0.564 | 0.018050542 | 3537.90 |
| 15 | 55.7 | 622 | 0.528 | 0.537 | 0.017045455 | 3340.90 |
| 16 | 63.8 | 553 | 0.459 | 0.466 | 0.015250545 | 2989.10 |
| 17 | 68.2 | 440 | 0.428 | 0.435 | 0.01635514 | 3205.60 |
| 18 | 72.1 | 444 | 0.405 | 0.412 | 0.017283951 | 3387.65 |
| 19 | 73.5 | 622 | 0.395 | 0.402 | 0.017721519 | 3473.41 |
| 20 | 74.2 | 553 | 0.389 | 0.396 | 0.017994859 | 3526.99 |
| Average Residual Stress (Mpa) | 3060.01 |
Table 16.
Analysis of variance for the SN ratios of the residual stress.
Table 16.
Analysis of variance for the SN ratios of the residual stress.
| Source | DF | Seq.SS | Adj.SS | Adj.MS | F | P | p% |
|---|
| A | 2 | 252.684 | 252.684 | 126.342 | 454.93 | 0.000 | 93.254 |
| B | 2 | 15.002 | 15.002 | 7.501 | 27.01 | 0.001 | 5.536 |
| C | 2 | 1.153 | 1.153 | 0.577 | 2.08 | 0.206 | 0.425 |
| D | 2 | 0.415 | 0.415 | 0.207 | 0.75 | 0.513 | 0.153 |
| A × D | 4 | 0.020 | 0.020 | 0.005 | 0.02 | 0.999 | 0.007 |
| B × D | 4 | 0.015 | 0.015 | 0.004 | 0.01 | 1.000 | 0.005 |
| C × D | 4 | 0.008 | 0.008 | 0.002 | 0.01 | 1.000 | 0.002 |
| Residual Error | 6 | 1.666 | 1.666 | 0.278 | | | |
| Total | 26 | 270.963 | | | | | |
Table 17.
Estimated regression coefficients for the residual stress (MPa).
Table 17.
Estimated regression coefficients for the residual stress (MPa).
| Term | Coef. | SE Coef. | T | P |
|---|
| Constant | −1813.12 | 394.987 | −4.590 | 0.000 |
| A | 328.40 | 16.649 | 19.725 | 0.000 |
| B | 24.44 | 7.815 | 3.127 | 0.006 |
| C | 0.13 | 0.666 | 0.191 | 0.851 |
| D | 7.70 | 13.319 | 0.578 | 0.571 |
| A × A | −7.00 | 0.880 | −7.951 | 0.000 |
| B × B | −0.06 | 0.035 | −1.601 | 0.129 |
| C × C | −0.00 | 0.001 | −0.229 | 0.822 |
| D × D | −0.23 | 0.563 | −0.407 | 0.690 |
| A × B | −0.04 | 0.071 | −0.571 | 0.576 |
| A × C | 0.00 | 0.014 | 0.000 | 1.000 |
| A × D | −0.01 | 0.284 | −0.051 | 0.960 |
| B × C | 0.00 | 0.003 | 0.000 | 1.000 |
| B × D | −0.09 | 0.057 | −1.644 | 0.120 |
| C × D | 0.00 | 0.011 | 0.000 | 1.000 |
Table 18.
ANOVA for the residual stress (MPa).
Table 18.
ANOVA for the residual stress (MPa).
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|
| Regression | 14 | 13,920,138 | 13,920,138 | 994,295.6 | 1930.65 | 0.000 |
| Residual Error | 16 | 8240 | 8240 | | | |
| Total | 30 | 13,928,378 | | | | |
Table 19.
Analysis of variance for the SN ratios of the residual stress.
Table 19.
Analysis of variance for the SN ratios of the residual stress.
| Source | DF | Seq.SS | Adj.SS | Adj.MS | F | P | p% |
|---|
| A | 2 | 11.6280 | 11.6280 | 5.81402 | 11748.71 | 0.000 | 95.39 |
| B | 2 | 0.5365 | 0.5365 | 0.26827 | 542.12 | 0.000 | 4.401 |
| C | 2 | 0.0166 | 0.0166 | 0.00831 | 16.79 | 0.003 | 0.136 |
| D | 2 | 0.0042 | 0.0042 | 0.00208 | 4.20 | 0.072 | 0.034 |
| A × D | 4 | 0.0003 | 0.0003 | 0.00007 | 0.13 | 0.965 | 0.0024 |
| B × D | 4 | 0.0001 | 0.0001 | 0.00002 | 0.04 | 0.996 | 0.0008 |
| C × D | 4 | 0.0002 | 0.0002 | 0.00004 | 0.09 | 0.982 | 0.0016 |
| Residual Error | 6 | 0.0030 | 0.0030 | 0.00049 | | | |
| Total | 26 | 12.1888 | | | | | |
Table 20.
Estimated regression coefficients for the microhardness (Hv).
Table 20.
Estimated regression coefficients for the microhardness (Hv).
| Term | Coef. | SE Coef. | T | P |
|---|
| Constant | 129.329 | 18,3442 | 7.050 | 0.000 |
| A | 9.627 | 0.7732 | 12.450 | 0.000 |
| B | 1.309 | 0.3629 | 3.607 | 0.002 |
| C | −0.019 | 0.0309 | −0.604 | 0.555 |
| D | 0.424 | 0.6186 | 0.686 | 0.502 |
| A × A | −0.219 | 0.0409 | −5.347 | 0.000 |
| B × B | −0.004 | 0.0016 | −2.672 | 0.017 |
| C × C | 0.000 | 0.0001 | 1.379 | 0.187 |
| D × D | −0.010 | 0.0262 | −0.379 | 0.710 |
| A × B | −0.001 | 0.0033 | −0.166 | 0.870 |
| A × C | 0.001 | 0.0007 | 1.067 | 0.302 |
| A × D | 0.018 | 0.0132 | 1.352 | 0.195 |
| B × C | −0.000 | 0.0001 | −1.067 | 0.302 |
| B × D | −0.003 | 0.0026 | −1.067 | 0.302 |
| C × D | −0.001 | 0.0005 | −1.067 | 0.302 |
Table 21.
ANOVA for the microhardness (Hv).
Table 21.
ANOVA for the microhardness (Hv).
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|
| Regression | 14 | 12,502.8 | 12,502.8 | 693.0596 | 803.96 | 0.000 |
| Residual Error | 16 | 17.8 | 17.8 | 1.1108 | | |
| Total | 30 | 12,520.6 | | | | |
Table 22.
Analysis of variance for the SN ratios of the recast layer thickness (µm).
Table 22.
Analysis of variance for the SN ratios of the recast layer thickness (µm).
| Source | DF | Seq.SS | Adj.SS | Adj.MS | F | P | p% |
|---|
| A | 2 | 594.813 | 594.813 | 297.406 | 301.06 | 0.000 | 92.51 |
| B | 2 | 36.789 | 36.789 | 18.394 | 18.62 | 0.003 | 5.721 |
| C | 2 | 4.511 | 4.511 | 2.255 | 2.28 | 0.183 | 0.701 |
| D | 2 | 0.583 | 0.583 | 0.291 | 0.30 | 0.755 | 0.09 |
| A × D | 4 | 0.243 | 0.243 | 0.061 | 0.06 | 0.991 | 0.037 |
| B × D | 4 | 0.039 | 0.039 | 0.010 | 0.01 | 1.000 | 0.006 |
| C × D | 4 | 0.039 | 0.039 | 0.010 | 0.01 | 1.000 | 0.006 |
| Residual Error | 6 | 5.927 | 5.927 | 0.988 | | | |
| Total | 26 | 642.943 | | | | | |
Table 23.
Estimated regression coefficients for the recast layer thickness (µm).
Table 23.
Estimated regression coefficients for the recast layer thickness (µm).
| Term | Coef. | SE Coef. | T | P |
|---|
| Constant | −0.952350 | 0.114253 | −8.335 | 0.000 |
| A | 0.210341 | 0.004816 | 43.677 | 0.000 |
| B | 0.004631 | 0.002260 | 2.049 | 0.057 |
| C | 0.000245 | 0.000193 | 1.271 | 0.222 |
| D | 0.001467 | 0.003853 | 0.381 | 0.708 |
| A × A | 0.000538 | 0.000255 | 2.111 | 0.051 |
| B × B | 0.000021 | 0.000010 | 2.111 | 0.051 |
| C × C | −0.000001 | 0.000000 | −1.571 | 0.136 |
| D × D | −0.000456 | 0.000163 | −2.798 | 0.013 |
| A × B | 0.000047 | 0.000021 | 2.285 | 0.036 |
| A × C | 0.000000 | 0.000004 | 0.000 | 1.000 |
| A × D | 0.000188 | 0.000082 | 2.285 | 0.036 |
| B × C | 0.000000 | 0.000001 | 0.000 | 1.000 |
| B × D | 0.000012 | 0.000016 | 0.762 | 0.457 |
| C × D | 0.000000 | 0.000003 | 0.000 | 1.000 |
Table 24.
ANOVA for the recast layer thickness(µm).
Table 24.
ANOVA for the recast layer thickness(µm).
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|
| Regression | 14 | 15.4178 | 15.4178 | 1.101273 | 25,557.34 | 0.000 |
| Residual Error | 16 | 0.0007 | 0.0007 | 0.000043 | | |
| Total | 30 | 15.4185 | | | | |