A Toolpath Generator Based on Signed Distance Fields and Clustering Algorithms for Optimized Additive Manufacturing
Abstract
1. Introduction
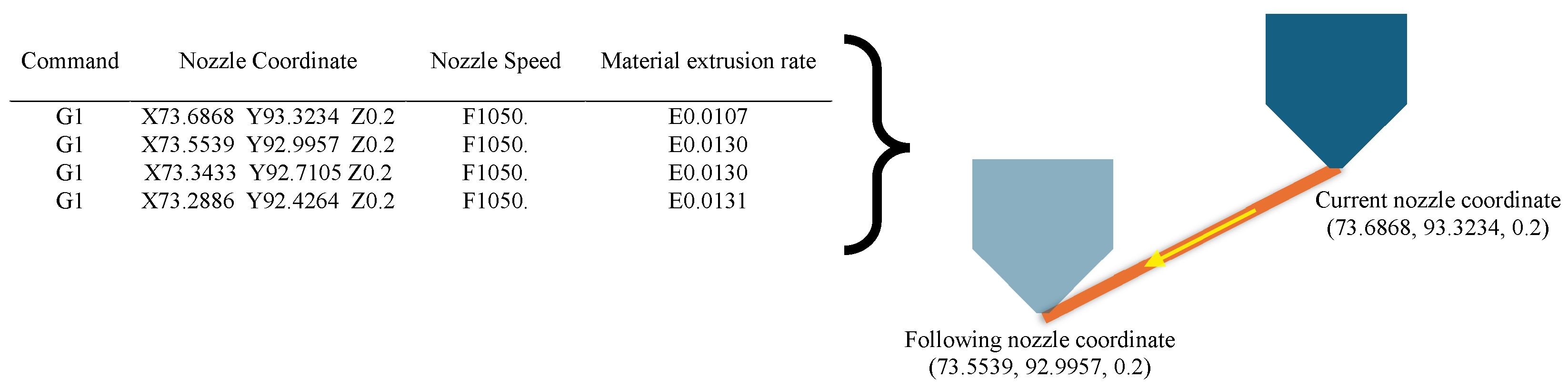
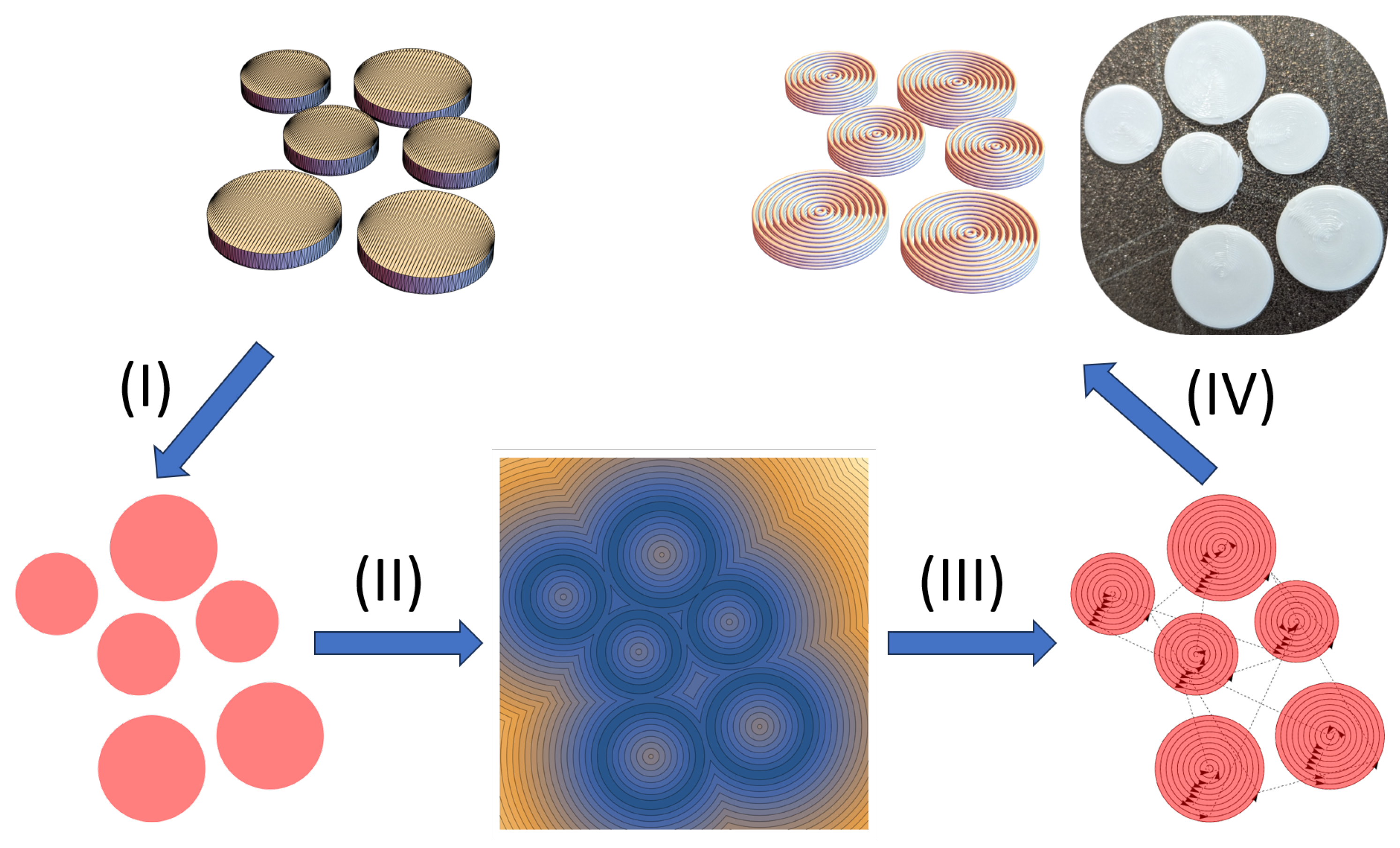
2. Materials and Methods
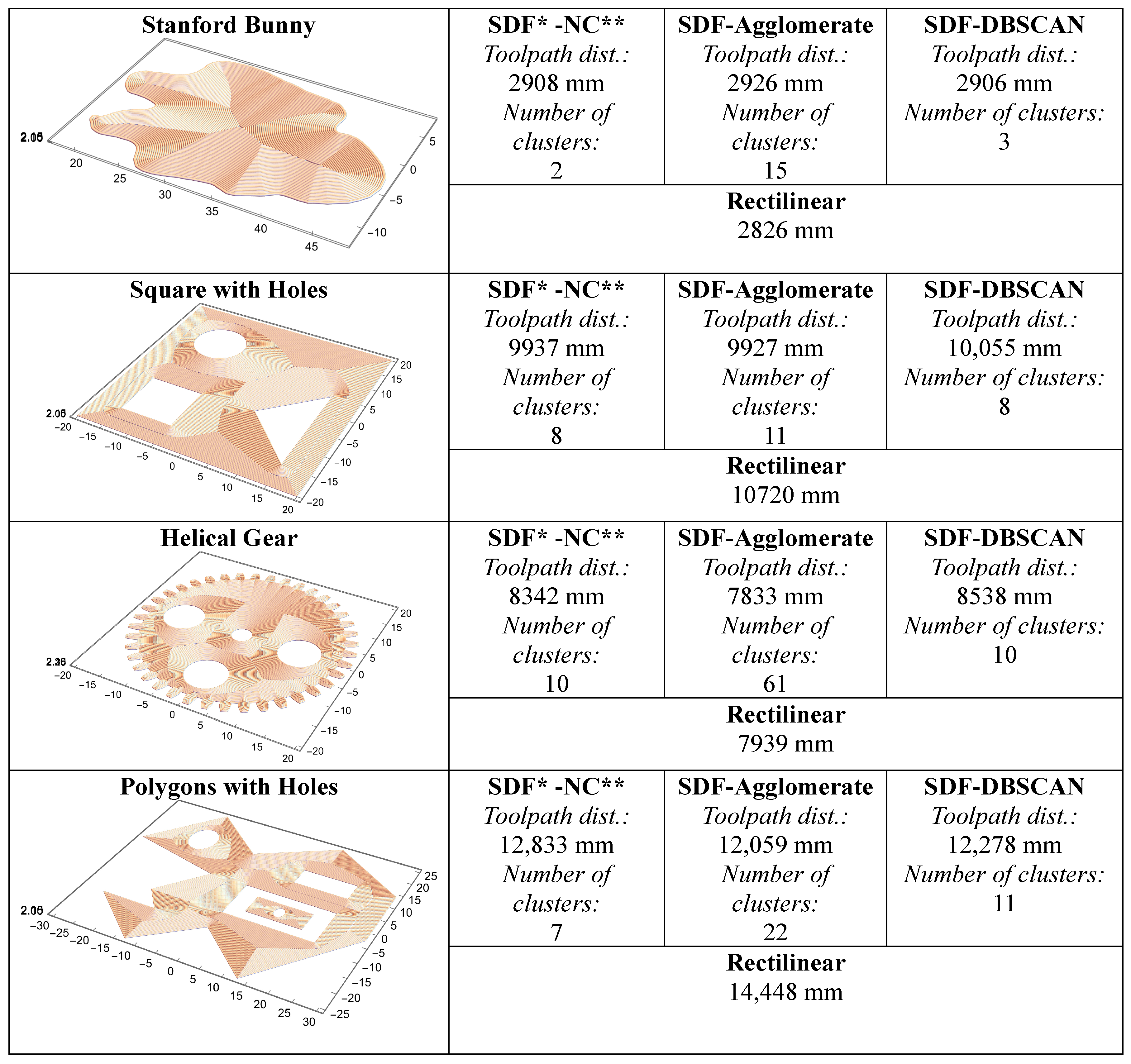
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wong, K.V.; Hernandez, A. A review of additive manufacturing. Int. Sch. Res. Not. 2012, 2012, 208760. [Google Scholar] [CrossRef]
- Huang, S.H.; Liu, P.; Mokasdar, A.; Hou, L. Additive manufacturing and its societal impact: A literature review. Int. J. Adv. Manuf. Technol. 2013, 67, 1191–1203. [Google Scholar] [CrossRef]
- Keleş, Ö.; Blevins, C.W.; Bowman, K.J. Effect of build orientation on the mechanical reliability of 3D printed ABS. Rapid Prototyp. J. 2017, 23, 320–328. [Google Scholar] [CrossRef]
- Rafiee, M.; Abidnejad, R.; Ranta, A.; Ojha, K.; Karakoç, A.; Paltakari, J. Exploring the possibilities of FDM filaments comprising natural fiber-reinforced biocomposites for additive manufacturing. AIMS Mater. Sci. 2021, 8, 524–537. [Google Scholar] [CrossRef]
- Liu, W.; Chen, L.; Mai, G.; Song, L. Toolpath planning for additive manufacturing using sliced model decomposition and metaheuristic algorithms. Adv. Eng. Softw. 2020, 149, 102906. [Google Scholar] [CrossRef]
- Zakirov, A.; Belousov, S.; Bogdanova, M.; Korneev, B.; Stepanov, A.; Perepelkina, A.; Levchenko, V.; Meshkov, A.; Potapkin, B. Predictive modeling of laser and electron beam powder bed fusion additive manufacturing of metals at the mesoscale. Addit. Manuf. 2020, 35, 101236. [Google Scholar] [CrossRef]
- Karakoç, A. RegionTPMS—Region based triply periodic minimal surfaces (TPMS) for 3-D printed multiphase bone scaffolds with exact porosity values. SoftwareX 2021, 16, 100835. [Google Scholar] [CrossRef]
- Altıparmak, S.C.; Yardley, V.A.; Shi, Z.; Lin, J. Extrusion-based additive manufacturing technologies: State of the art and future perspectives. J. Manuf. Process. 2022, 83, 607–636. [Google Scholar] [CrossRef]
- Djurović, S.; Lazarević, D.; Ćirković, B.; Mišić, M.; Ivković, M.; Stojčetović, B.; Petković, M.; Ašonja, A. Modeling and Prediction of Surface Roughness in Hybrid Manufacturing–Milling after FDM Using Artificial Neural Networks. Appl. Sci. 2024, 14, 5980. [Google Scholar] [CrossRef]
- Keleş, Ö.; Anderson, E.H.; Huynh, J.; Gelb, J.; Freund, J.; Karakoç, A. Stochastic fracture of additively manufactured porous composites. Sci. Rep. 2018, 8, 15437. [Google Scholar] [CrossRef]
- Patel, A.; Taufik, M. Extrusion-based technology in additive manufacturing: A comprehensive review. Arab. J. Sci. Eng. 2024, 49, 1309–1342. [Google Scholar] [CrossRef]
- Kam, M.; Saruhan, H.; İpekçi, A. Investigation the effect of 3D printer system vibrations on surface roughness of the printed products. Düzce Üniversitesi Bilim Teknol. Derg. 2019, 7, 147–157. [Google Scholar] [CrossRef]
- Çevik, Ü.; Kam, M. A review study on mechanical properties of obtained products by FDM method and metal/polymer composite filament production. J. Nanomater. 2020, 2020, 6187149. [Google Scholar] [CrossRef]
- Dei Rossi, J.; Keles, O.; Viswanathan, V. Fused deposition modeling with induced vibrations: A study on the mechanical characteristics of printed parts. Appl. Sci. 2022, 12, 9327. [Google Scholar] [CrossRef]
- Jensen, N.; Parker, G.; Blough, J. Base vibration effects on additive manufactured part quality. Exp. Tech. 2024, 48, 159–170. [Google Scholar] [CrossRef]
- Kayali, Y.; Ding, M.; Hamdallah, S.; Qi, S.; Bibb, R.; Gleadall, A. Effect of printing parameters on microscale geometry for 3D printed lattice structures. Mater. Today Proc. 2022, 70, 31–37. [Google Scholar] [CrossRef]
- Fleming, C.; Walker, S.; Branyan, C.; Nicolai, A.; Hollinger, G.; Mengüç, Y. Toolpath Planning for Continuous Extrusion Additive Manufacturing; Oregon State University: Corvallis, OR, USA, 2017. [Google Scholar]
- Lalegani Dezaki, M.; Mohd Ariffin, M.K.A. The effects of combined infill patterns on mechanical properties in fdm process. Polymers 2020, 12, 2792. [Google Scholar] [CrossRef]
- Eryildiz, M. The effects of infill patterns on the mechanical properties of 3D printed PLA parts fabricated by FDM. Ukr. J. Mech. Eng. Mater. Sci. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Yahya, A. Effects of 3D printing parameters on mechanical properties of ABS samples. Designs 2023, 7, 136. [Google Scholar] [CrossRef]
- Birosz, M.T.; Ledenyak, D.; Ando, M. Effect of FDM infill patterns on mechanical properties. Polym. Test. 2022, 113, 107654. [Google Scholar] [CrossRef]
- Ambati, S.S.; Ambatipudi, R. Effect of infill density and infill pattern on the mechanical properties of 3D printed PLA parts. Mater. Today Proc. 2022, 64, 804–807. [Google Scholar] [CrossRef]
- Hussam, H.; Abdelrhman, Y.; Soliman, M.E.S.; Hassab-Allah, I.M. Effects of a new filling technique on the mechanical properties of ABS specimens manufactured by fused deposition modeling. Int. J. Adv. Manuf. Technol. 2022, 121, 1639–1650. [Google Scholar] [CrossRef]
- Kim, S.; Andreu, A.; Kim, I.; Kim, J.H.; Lee, J.; Yoon, Y.J. Continuously varied infill pattern (ConVIP): Improvement of mechanical properties and printing speed of fused filament fabrication (FFF) 3D printing. J. Mater. Res. Technol. 2022, 18, 1055–1069. [Google Scholar] [CrossRef]
- Jin, G.; Li, W.D.; Gao, L. An adaptive process planning approach of rapid prototyping and manufacturing. Robot.-Comput.-Integr. Manuf. 2013, 29, 23–38. [Google Scholar] [CrossRef]
- Habib, A.; Ahsan, N.; Khoda, B. Optimizing material deposition direction for functional internal architecture in additive manufacturing processes. Procedia Manuf. 2015, 1, 378–392. [Google Scholar] [CrossRef][Green Version]
- Bui, H.; Pierson, H.A.; Nurre, S.G.; Sullivan, K.M. Tool path planning optimization for multi-tool additive manufacturing. Procedia Manuf. 2019, 39, 457–464. [Google Scholar] [CrossRef]
- Evjemo, L.D.; Langelandsvik, G.; Moe, S.; Danielsen, M.H.; Gravdahl, J.T. Wire-arc additive manufacturing of structures with overhang: Experimental results depositing material onto fixed substrate. CIRP J. Manuf. Sci. Technol. 2022, 38, 186–203. [Google Scholar] [CrossRef]
- Rauch, M.; Hascoet, J.Y.; Querard, V. A multiaxis tool path generation approach for thin wall structures made with WAAM. J. Manuf. Mater. Process. 2021, 5, 128. [Google Scholar] [CrossRef]
- R.W. Selby & Co., Inc. Mathematica Version 13.0; R.W. Selby & Co., Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Toolpath and GCode Generator. Available online: https://github.com/metudust/Toolpath_and_GCode_Generator (accessed on 10 September 2024).
- Duan, J.; Haines, B.; Ward, W.O.; Bai, L. Surface reconstruction from point clouds using a novel variational model. In Proceedings of the Research and Development in Intelligent Systems XXXII: Incorporating Applications and Innovations in Intelligent Systems XXIII 32, Cambridge, UK, 5–17 December 2015; Springer: Cham, Switzerland, 2015; pp. 135–146. [Google Scholar]
- Oleynikova, H.; Millane, A.; Taylor, Z.; Galceran, E.; Nieto, J.; Siegwart, R. Signed distance fields: A natural representation for both mapping and planning. In Proceedings of the RSS 2016 Workshop: Geometry and Beyond-Representations, Physics, and Scene Understanding for Robotics, Ann Arbor, MI, USA, 19 June 2016; University of Michigan: Ann Arbor, MI, USA, 2016. [Google Scholar]
- Sanchez, M.; Fryazinov, O.; Fayolle, P.A.; Pasko, A. Convolution filtering of continuous signed distance fields for polygonal meshes. In Proceedings of the Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2015; Volume 34, pp. 277–288. [Google Scholar]
- Gonzalez, T.F. Clustering to minimize the maximum intercluster distance. Theor. Comput. Sci. 1985, 38, 293–306. [Google Scholar] [CrossRef]
- Pourbahrami, S.; Balafar, M.A.; Khanli, L.M.; Kakarash, Z.A. A survey of neighborhood construction algorithms for clustering and classifying data points. Comput. Sci. Rev. 2020, 38, 100315. [Google Scholar] [CrossRef]
- Yu, X.; Long, W.; Li, Y.; Gao, L.; Shi, X. Trajectory dimensionality reduction and hyperparameter settings of DBSCAN for trajectory clustering. IET Intell. Transp. Syst. 2022, 16, 691–710. [Google Scholar] [CrossRef]
- İnkaya, T.; Kayalıgil, S.; Özdemirel, N.E. An adaptive neighbourhood construction algorithm based on density and connectivity. Pattern Recognit. Lett. 2015, 52, 17–24. [Google Scholar] [CrossRef]
- Zhou, S.; Zhao, Y.; Guan, J.; Huang, J. A neighborhood-based clustering algorithm. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Hanoi, Vietnam, 18–20 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 361–371. [Google Scholar]
- Lodhi, S.S.; Kumar, N.; Pandey, P.K. Autonomous vehicular overtaking maneuver: A survey and taxonomy. Veh. Commun. 2023, 42, 100623. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, K.; Keller, J.M.; Bezdek, J.C. A possibilistic fuzzy c-means clustering algorithm. IEEE Trans. Fuzzy Syst. 2005, 13, 517–530. [Google Scholar] [CrossRef]
- Sasirekha, K.; Baby, P. Agglomerative hierarchical clustering algorithm-a. Int. J. Sci. Res. Publ. 2013, 83, 83. [Google Scholar]
- Campello, R.J.; Moulavi, D.; Sander, J. Density-based clustering based on hierarchical density estimates. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Gold Coast, Australia, 14–17 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 1996 Knowledge Discovery and Data Mining (KDD’96) International Conference, Portland, Oregon, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Karakoç, A.; Paltakari, J.; Taciroglu, E. Data-driven computational homogenization method based on Euclidean bipartite matching. J. Eng. Mech. 2020, 146, 04019132. [Google Scholar] [CrossRef]
- Chen, D.; Heyer, S.; Ibbotson, S.; Salonitis, K.; Steingrímsson, J.G.; Thiede, S. Direct digital manufacturing: Definition, evolution, and sustainability implications. J. Clean. Prod. 2015, 107, 615–625. [Google Scholar] [CrossRef]
- Somade, D.K. Part Design Geometry-Driven Toolpath Optimization for Additive Manufacturing Energy Sustainability Improvement. Master’s Thesis, Northern Illinois University, DeKalb, IL, USA, 2023. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakoç, A. A Toolpath Generator Based on Signed Distance Fields and Clustering Algorithms for Optimized Additive Manufacturing. J. Manuf. Mater. Process. 2024, 8, 199. https://doi.org/10.3390/jmmp8050199
Karakoç A. A Toolpath Generator Based on Signed Distance Fields and Clustering Algorithms for Optimized Additive Manufacturing. Journal of Manufacturing and Materials Processing. 2024; 8(5):199. https://doi.org/10.3390/jmmp8050199
Chicago/Turabian StyleKarakoç, Alp. 2024. "A Toolpath Generator Based on Signed Distance Fields and Clustering Algorithms for Optimized Additive Manufacturing" Journal of Manufacturing and Materials Processing 8, no. 5: 199. https://doi.org/10.3390/jmmp8050199
APA StyleKarakoç, A. (2024). A Toolpath Generator Based on Signed Distance Fields and Clustering Algorithms for Optimized Additive Manufacturing. Journal of Manufacturing and Materials Processing, 8(5), 199. https://doi.org/10.3390/jmmp8050199





