Study on Extraordinarily High-Speed Cutting Mechanics and Its Application to Dry Cutting of Aluminum Alloys with Non-Coated Carbide Tools
Abstract
1. Introduction
2. Mechanics/Application of Extraordinarily High-Speed Cutting and Analysis of Cutting Temperature in EHS Cutting
2.1. Understanding of Mechanics and Application to Dry Cutting of Aluminum Alloy with Non-Coated Tool
2.2. Analysis of Cutting Temperature in EHS Cutting of Heat-Softening Region
3. Experimental Method
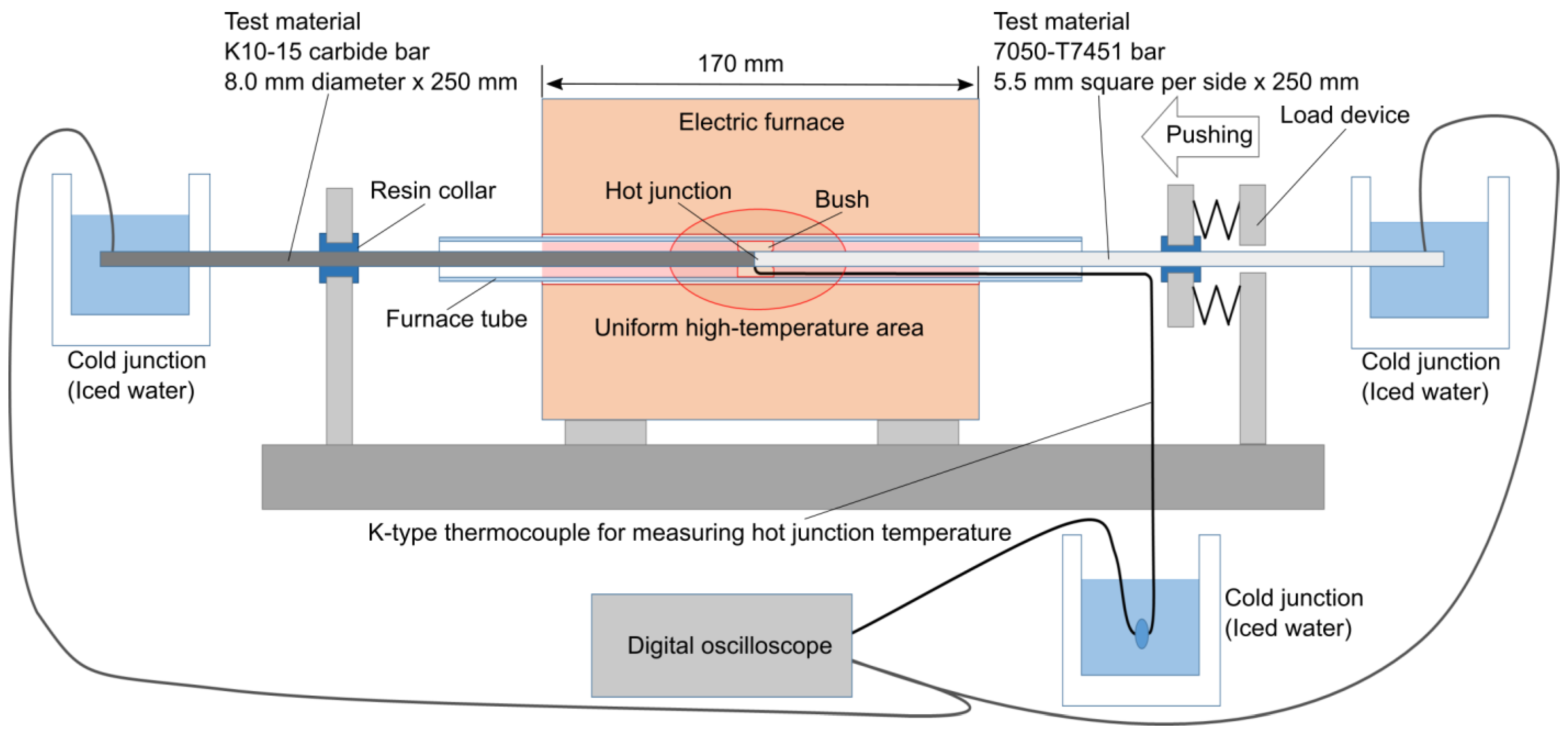
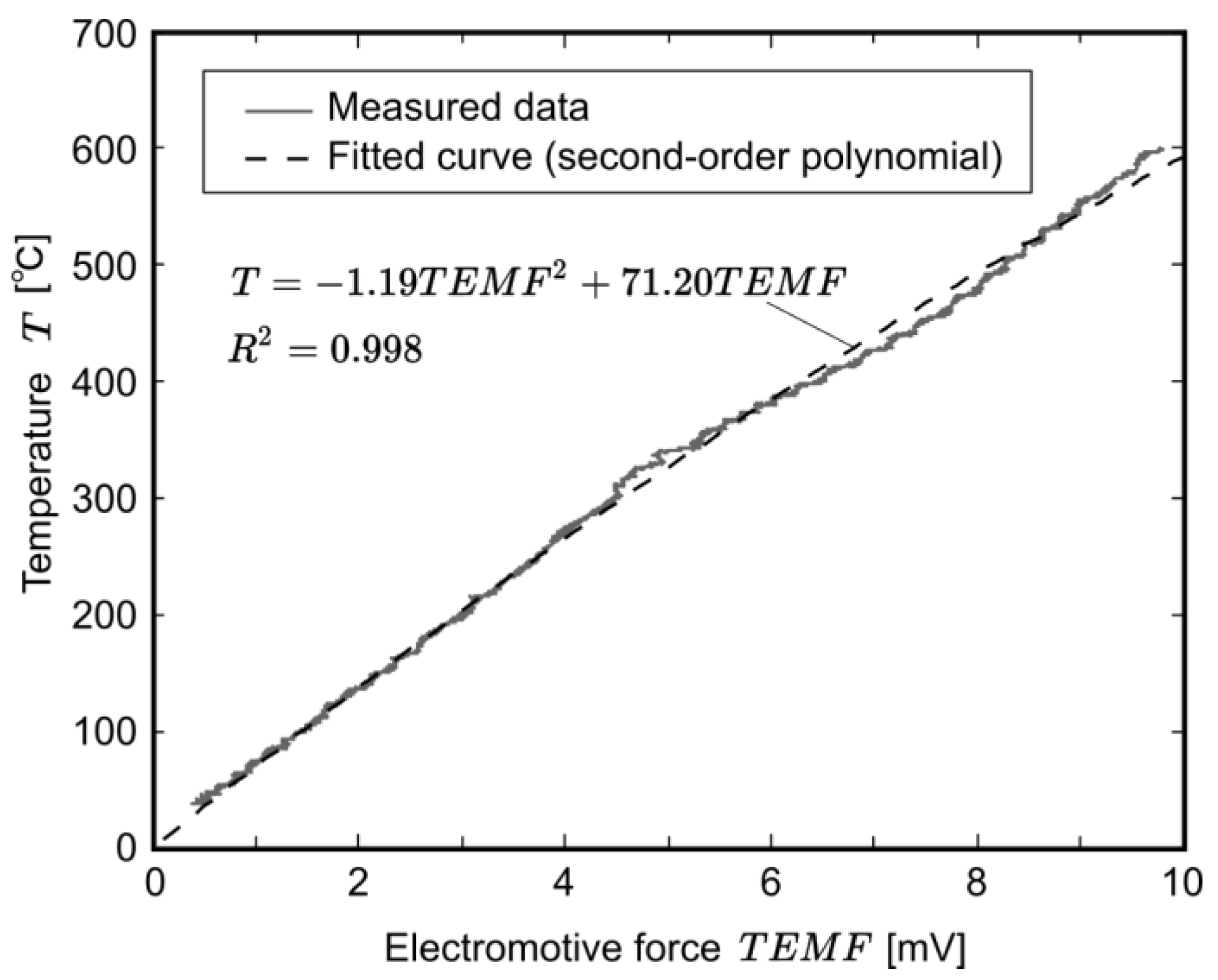
3.1. Thermoelectromotive Force Calibration
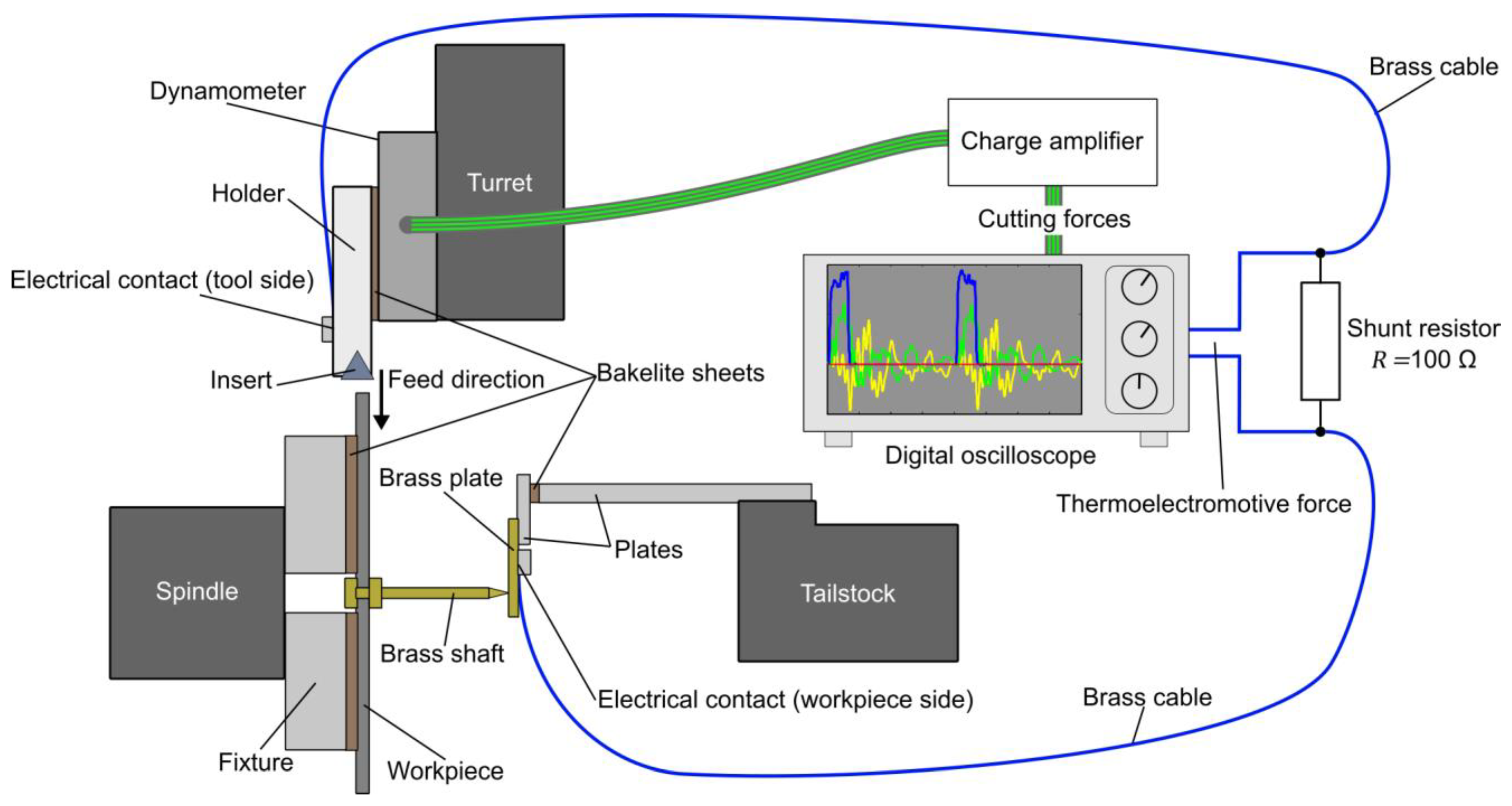
3.2. Experimental Setup and Conditions
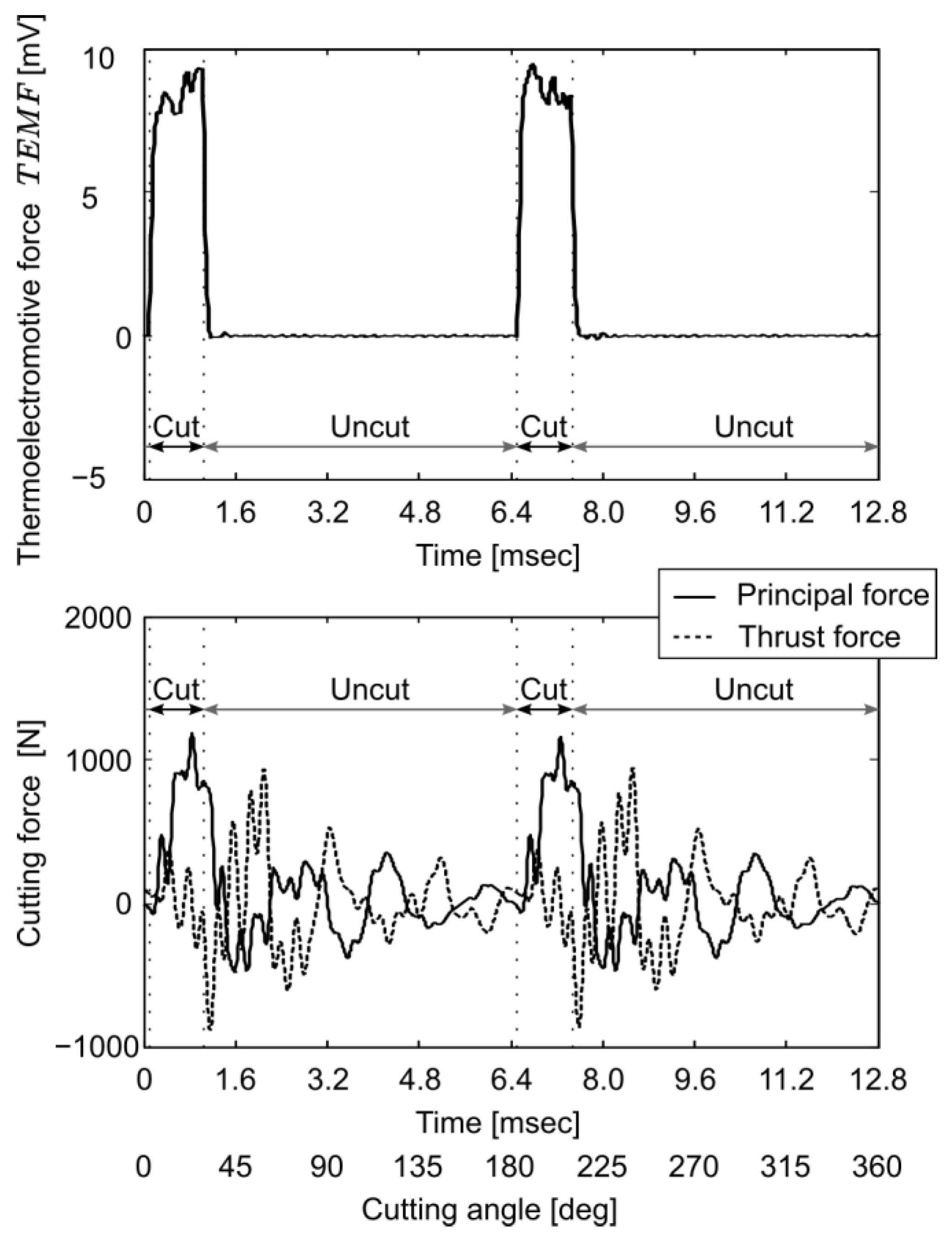
4. Results and Discussion
4.1. Effect of Cutting Speed and Comparison between Measured and Analyzed Cutting Temperatures
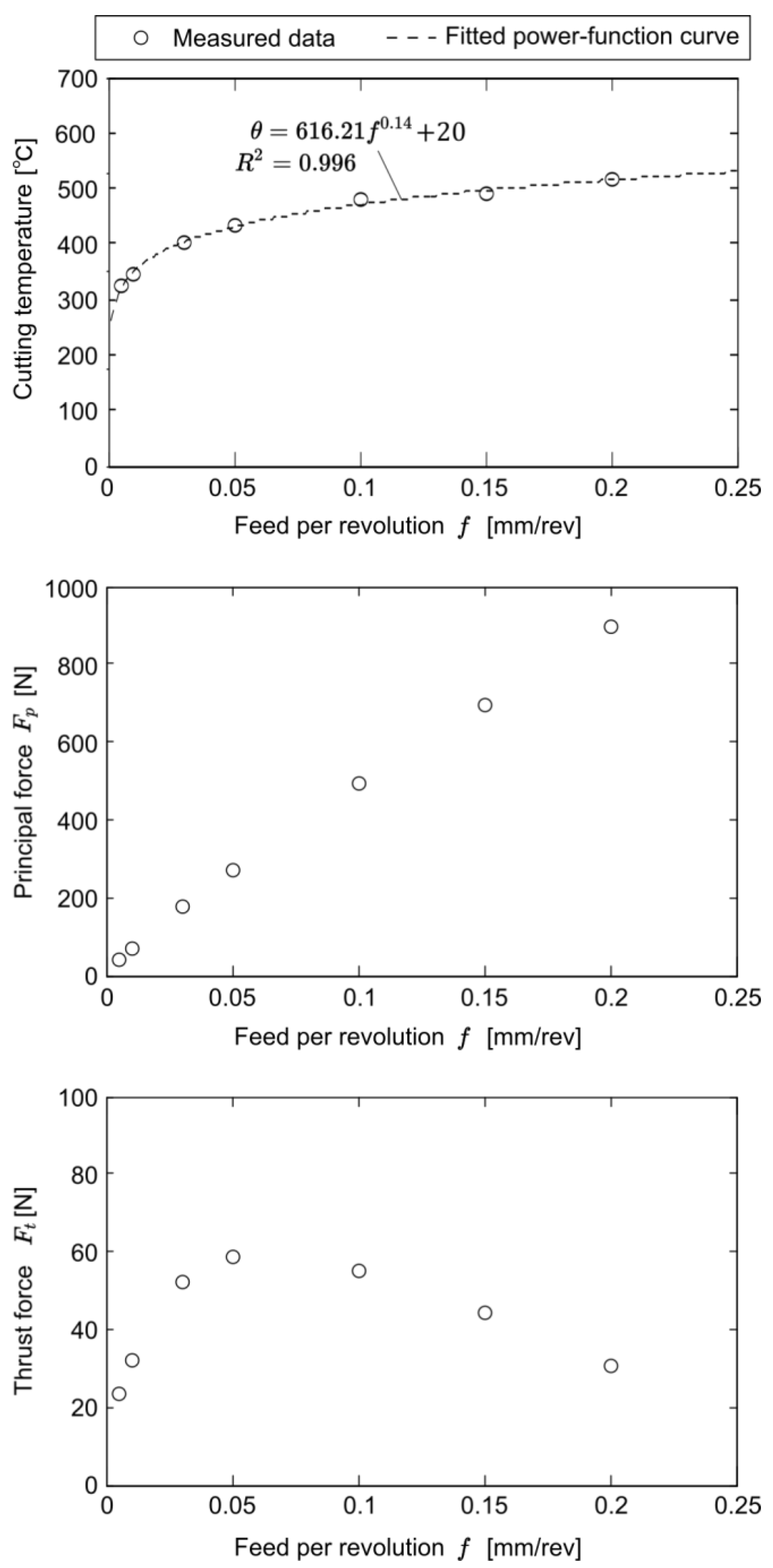
4.2. Effect of Feed Per Revolution
4.3. Effect of Rake Angle
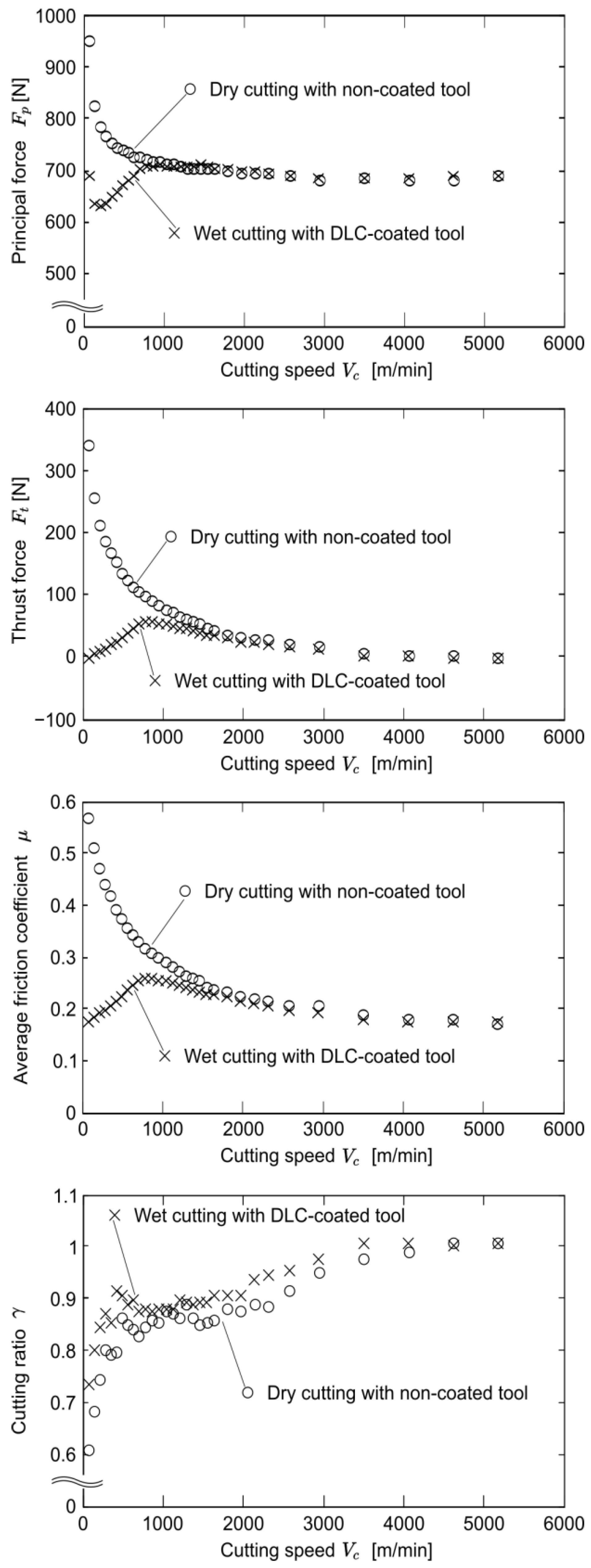
4.4. Comparison between Dry Cutting with Non-Coated Tool and Wet Cutting with Coated Tool
5. Conclusions
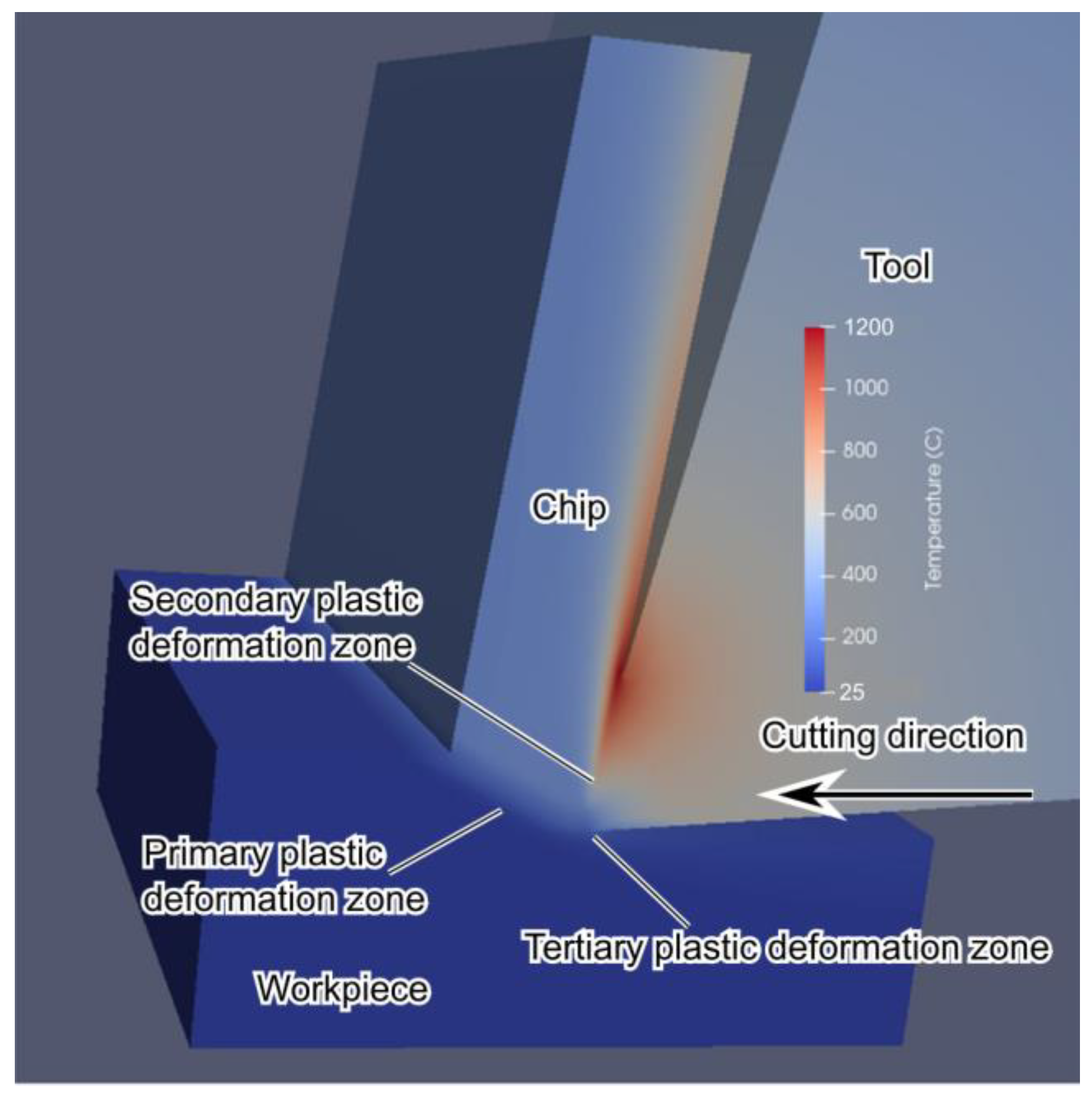
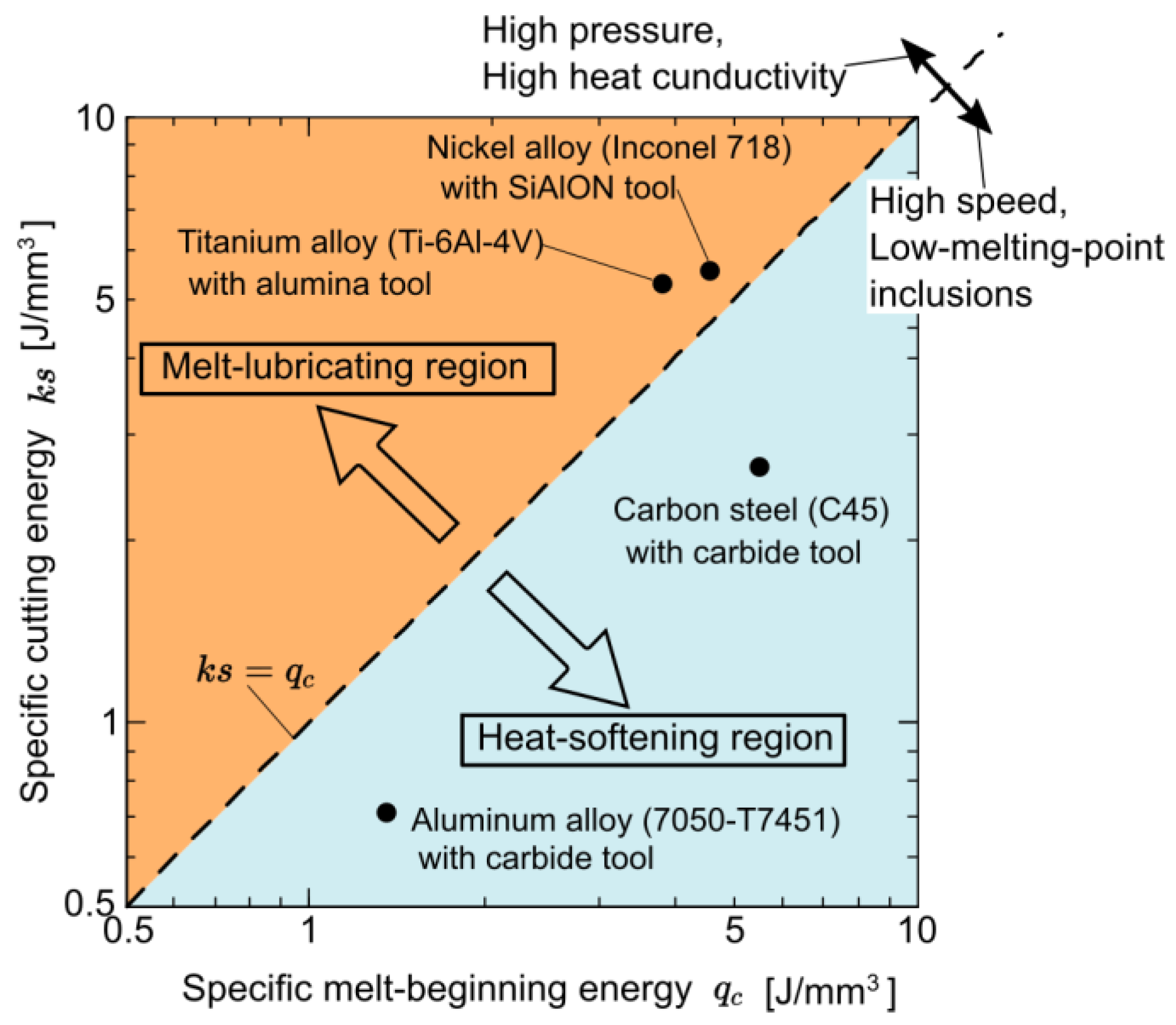
- EHS cutting was categorized into two regions focusing on the specific cutting energy and specific melt-beginning energy : (1) melt-lubricating region () in which partial melting occurs and (2) heat-softening region () in which heat softening occurs. This research mainly focused on the latter region, and it was determined that a sufficiently high cutting temperature causes heat softening at the secondary plastic deformation zone rather than at the primary plastic deformation zone.
- A simple analysis of the cutting temperature and experiments on soft and highly heat-conductive aluminum alloy were conducted to observe the mechanics. In the experiments, the cutting temperature and cutting forces were measured with varied cutting speed, feed per revolution, and rake angle. In the cutting-speed region of m/min, the cutting temperature showed a power function-like trend, and at the region of , it changed to a gradually increasing trend.
- The trend of gradual increase in cutting temperature agreed well with the analytical one based on Jaeger’s theory with assumptions that 100% of the shear and friction heat flow into the chip and that the chip thickness is large enough, and the increased friction speed and the intensifying heat/temperature gradient in the thickness direction of the chip were responsible for the gradual increase.
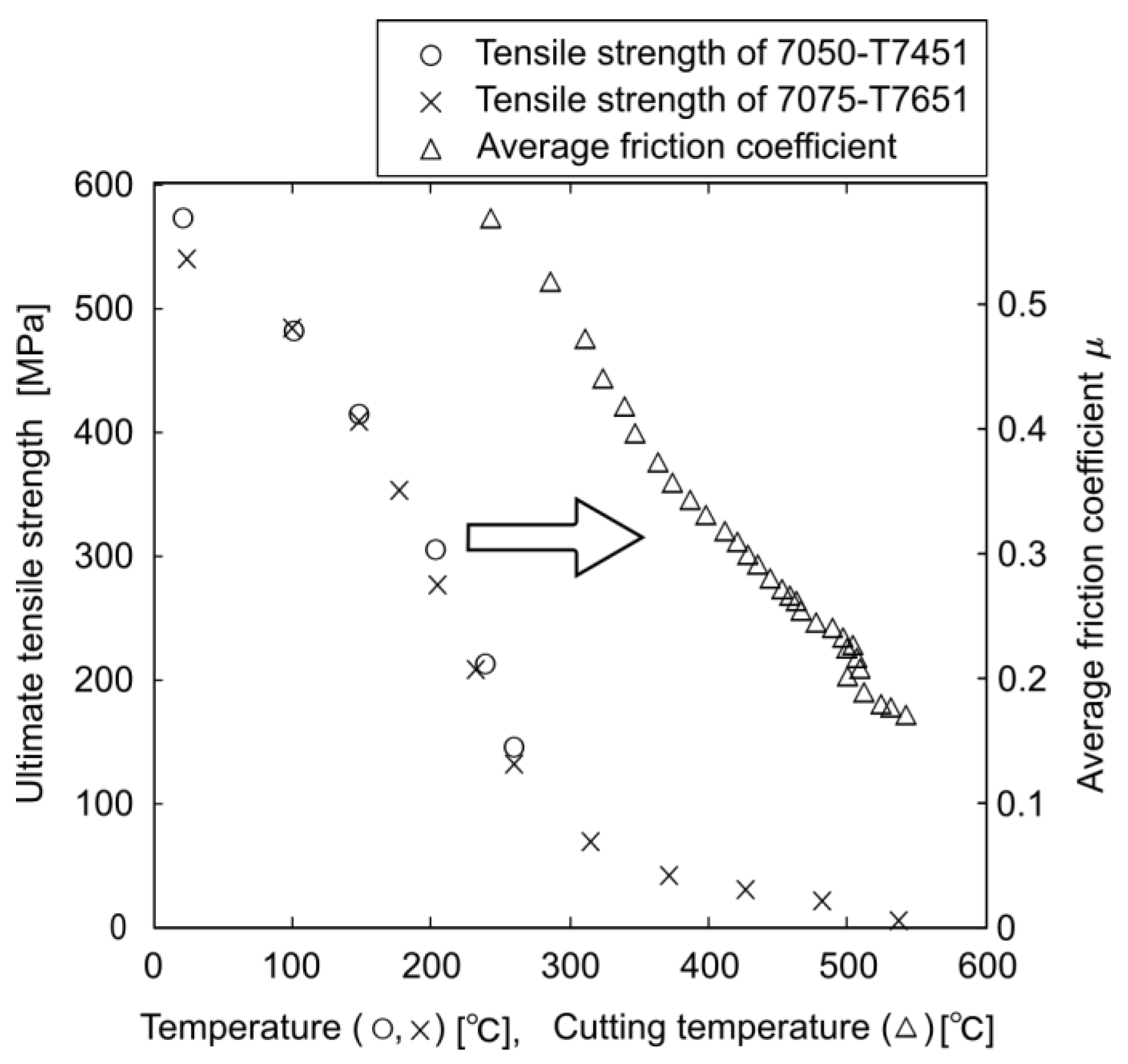
- The average friction coefficient dropped from 0.569 at the lowest cutting speed to 0.170 in the EHS cutting region, whereas the average shear stress at the shear plane did not change much. Due to these facts, it was confirmed that heat softening in the tool–chip interface was responsible for the friction coefficient decrease. It was also shown that a larger feed per revolution and smaller rake angle increased the cutting temperature and reachability of EHS cutting.
- Application to dry cutting of aluminum alloys with non-coated carbide tools was proposed, focusing on the low friction coefficient in EHS cutting. Experiments were conducted to compare dry cutting with a non-coated carbide tool and wet cutting with a DLC-coated carbide tool, and it was confirmed that the cutting fluid and coating had an effect in the relatively low-cutting-speed region of m/min. However, it was also shown that in the EHS cutting region of m/min, there was almost no difference between the two conditions; the cutting fluid and coating could be eliminated. Although other advanced methods in the literature, e.g., high-pressure coolant systems and laser-assisted machining, can improve the cutting process, they require enormous additional energy compared to conventional wet cutting using coated tools. On the other hand, EHS cutting improves the cutting process greatly in an energy-friendly manner owing to the eliminated cutting fluid and coating. Hence, the proposed application can contribute to carbon-neutral manufacturing. Note that chipping of the carbide tool during long-run cutting in high speeds may be a future task as reported in the literature.
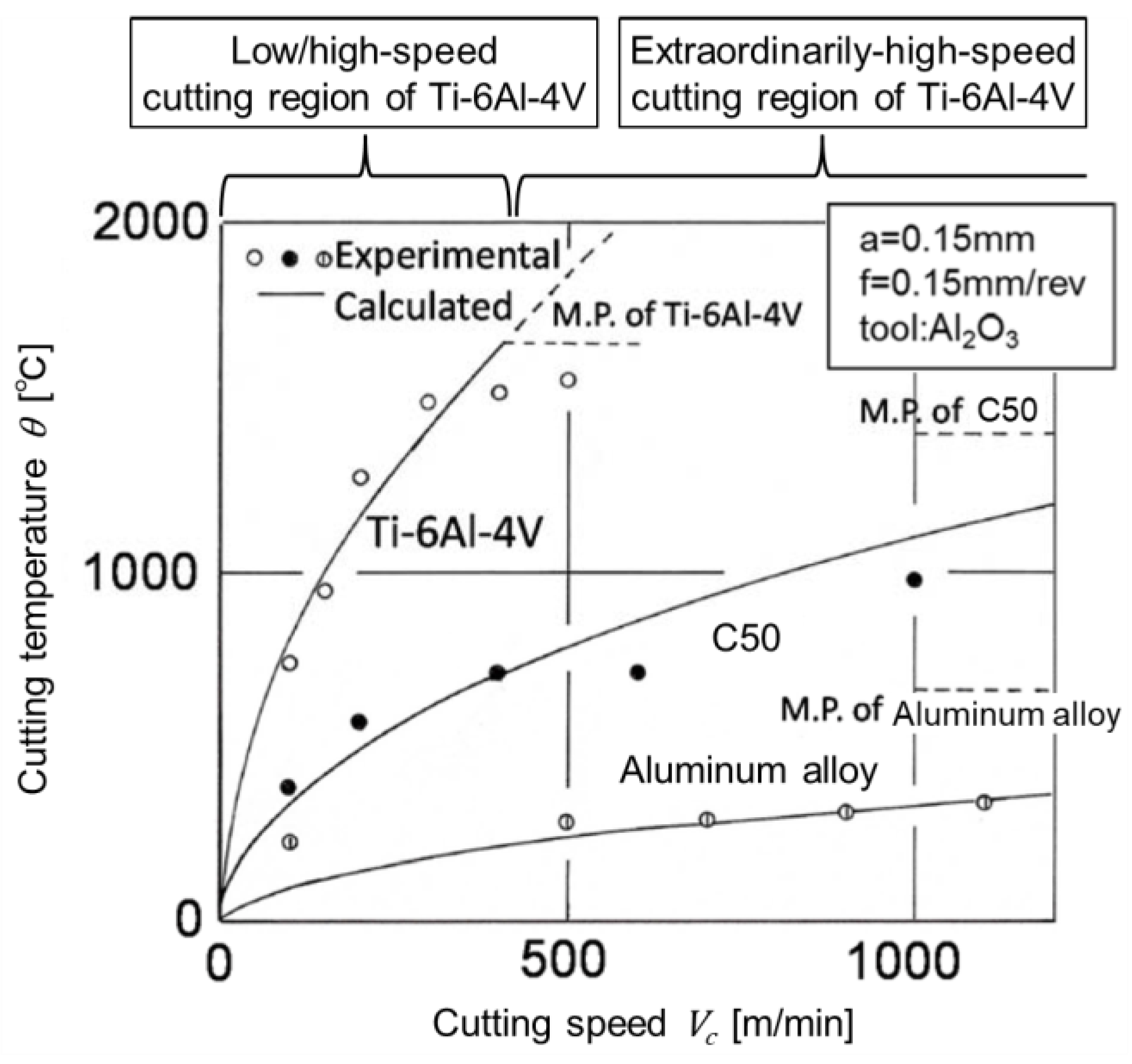
- In this research, EHS cutting was applied to aluminum alloys. As for other soft and highly heat-conductive materials, e.g., copper alloy and magnesium alloy, EHS cutting should be able to be realized as it was for aluminum alloy. As for hard and lowly heat-conductive materials, e.g., titanium alloys and high-strength steels, the heat-softening points of these are usually large, e.g., around 600 °C for titanium alloy [36] and around 700 °C for (stainless) steel [37]. Although EHS cutting should be realized for these materials, tool wear may become a problem at such high temperatures. In those situations, utilizing highly heat-resistant tool materials such as ceramic and cBN may be one solution, where tool properties such as sharpness of the cutting edge and thermal conductivity should also be considered since they affect the reachability of EHS cutting.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grzesik, W. Experimental investigation of the influence of adhesion on the frictional conditions in the cutting process. Tribol. Int. 1999, 32, 15–23. [Google Scholar] [CrossRef]
- Xia, Q.; Gillespie, D.R. Quasi-static finite element modelling of thermal distribution and heat partitioning for the multi-component system of high speed metal cutting. J. Mater. Process. Technol. 2020, 275, 116389. [Google Scholar] [CrossRef]
- Zemzemi, F.; Rech, J.; Salem, W.B.; Dogui, A.; Kapsa, P. Identification of a friction model at tool/chip/workpiece interfaces in dry machining of AISI4142 treated steels. J. Mater. Process. Technol. 2009, 209, 3978–3990. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Song, Q.; Wan, Y.; Shi, Z. Proper selection of cutting parameters and cutting tool angle to lower the specific cutting energy during high speed machining of 7050-T7451 aluminum alloy. J. Clean. Prod. 2016, 129, 292–304. [Google Scholar] [CrossRef]
- Santos, M.C.; Machado, A.R.; Sales, W.F.; Barrozo, M.A.; Ezugwu, E.O. Machining of aluminum alloys: A review. Int. J. Adv. Manuf. Technol. 2016, 86, 3067–3080. [Google Scholar] [CrossRef]
- Abele, E.; Sielaff, T.; Schiffler, A.; Rothenbücher, S. Analyzing energy consumption of machine tool spindle units and identification of potential for improvements of efficiency. In Glocalized Solutions for Sustainability in Manufacturing: Proceedings of the 18th CIRP International Conference on Life Cycle Engineering, Technische Universität Braunschweig, Braunschweig, Germany, 2–4 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 280–285. [Google Scholar]
- Gontarz, A.; Züst, S.; Weiss, L.; Wegener, K. Energetic machine tool modeling approach for energy consumption prediction. In Proceedings of the GCSM 2012 10th Global Conference on Sustainable Manufacturing, Istanbul, Turkey, 31 October–2 November 2012; Institute of Machine Tools and Manufacturing (IWF), Swiss Federal Institute of Technology: Zürich, Switzerland, 2012. [Google Scholar] [CrossRef]
- Kouam, J.; Songmene, V.; Balazinski, M.; Hendrick, P. Effects of minimum quantity lubricating (MQL) conditions on machining of 7075-T6 aluminum alloy. Int. J. Adv. Manuf. Technol. 2015, 79, 1325–1334. [Google Scholar] [CrossRef]
- Denkena, B.; Dittrich, M.A.; Jacob, S. Energy efficiency in machining of aircraft components. Procedia CIRP 2016, 48, 479–482. [Google Scholar] [CrossRef]
- Naves, V.T.G.; Da Silva, M.B.; Da Silva, F.J. Evaluation of the effect of application of cutting fluid at high pressure on tool wear during turning operation of AISI 316 austenitic stainless steel. Wear 2013, 302, 1201–1208. [Google Scholar] [CrossRef]
- Anderson, M.; Patwa, R.; Shin, Y.C. Laser-assisted machining of Inconel 718 with an economic analysis. Int. J. Mach. Tools Manuf. 2006, 46, 1879–1891. [Google Scholar] [CrossRef]
- Sutter, G.; Molinari, A. Analysis of the cutting force components and friction in high speed machining. J. Manuf. Sci. Eng. 2005, 127, 245–250. [Google Scholar] [CrossRef]
- Philippon, S.; Sutter, G.; Molinari, A. An experimental study of friction at high sliding velocities. Wear 2004, 257, 777–784. [Google Scholar] [CrossRef]
- Ozlu, E.; Budak, E.; Molinari, A. Analytical and experimental investigation of rake contact and friction behavior in metal cutting. Int. J. Mach. Tools Manuf. 2009, 49, 865–875. [Google Scholar] [CrossRef]
- Recht, R.F. A Dynamic Analysis of High Speed, Machining. ASME J. Eng. Ind. 1985, 107, 309–315. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Cai, Y.; Luo, X.; Ma, H.; Song, Q.; Xiong, Z. Advancements in material removal mechanism and surface integrity of high speed metal cutting: A review. Int. J. Mach. Tools Manuf. 2021, 166, 103744. [Google Scholar] [CrossRef]
- Ueda, T.; Hirai, Y.; Shamoto, E. Experimental studies on cutting temperature and its effect in high speed turning of difficult-to-cut materials with ceramic tool. Trans. JSME 2017, 83, 17-00344. (In Japanese) [Google Scholar] [CrossRef]
- Richardson, D.J.; Keavey, M.A.; Dailami, F. Modelling of cutting induced workpiece temperatures for dry milling. Int. J. Mach. Tools Manuf. 2006, 46, 1139–1145. [Google Scholar] [CrossRef]
- Ueda, T.; Hirai, Y.; Uto, S.; Shamoto, E. Studies on cutting temperature by dimensional analysis (Influence of cutting conditions in turning with Al2O3 cutting tool). Trans. JSME 2019, 85, 18-00284. (In Japanese) [Google Scholar] [CrossRef]
- Ueda, T.; Sato, M.; Nakayama, K. The temperature of a single crystal diamond tool in turning. CIRP Ann. 1998, 47, 41–44. [Google Scholar] [CrossRef]
- Ueda, T.; Uto, S.; Hirai, Y.; Shamoto, E. Studies on cutting temperature by dimensional analysis (2nd report: Influence of thermal properties of workpiece and tool materials). Trans. JSME 2020, 86, 20-00100. (In Japanese) [Google Scholar] [CrossRef]
- Hayasaka, T.; Jung, H.; Azuma, K.; Shamoto, E. Consolidated chatter stability prediction model considering material removing and ploughing processes. Precis. Eng. 2019, 59, 120–133. [Google Scholar] [CrossRef]
- Suzuki, N.; Enmei, R.; Hashimoto, Y.; Shamoto, E.; Hatano, Y. Tool failure mechanism in high-speed milling of Inconel 718 by use of ceramic tools. Int. J. Autom. Technol. 2014, 8, 837–846. [Google Scholar] [CrossRef]
- Minamino, Y.; Yamane, T.; Miyake, T.; Koizumi, M.; Miyamoto, Y. Effect of high pressure on diffusion reactions and phase diagram in Al–Mg system. Mater. Sci. Technol. 1986, 2, 777–783. [Google Scholar] [CrossRef]
- Deel, O.L.; Ruff, P.E.; Mindlin, H. Engineering Data on New Aerospace Structural Materials; AFML-TR-73-114; Battelle’s Columbus Laboratories: Columbus, OH, USA, 1973. [Google Scholar]
- Kaufman, J.G. (Ed.) Properties of Aluminum Alloys: Tensile, Creep, and Fatigue at High and Low Temperatures; ASM International: Almere, The Netherlands, 1999; pp. 206–217. [Google Scholar]
- Subroto, T.; Miroux, A.G.; Eskin, D.G.; Katgerman, L. Tensile mechanical properties, constitutive parameters and fracture characteristics of an as-cast AA7050 alloy in the near-solidus temperature regime. Mater. Sci. Eng. A 2017, 679, 28–35. [Google Scholar] [CrossRef]
- Battelle Memorial Institute; William J. Hughes Technical Center (U.S.). Metallic Materials Properties Development and Standardization—MMPDS-14; Federal Aviation Administration: Washington, DC, USA, 2019.
- Aluminum Standards and Data Metric SI; The Aluminum Association: Arlington, VA, USA, 2017; Available online: https://www.aluminum.org/aluminum-standards-and-data (accessed on 11 August 2024).
- Chao, B.T.; Trigger, K.J. The Significance of the Thermal Number in Metal Machining. Trans. ASME 1953, 75, 109–115. [Google Scholar] [CrossRef]
- Jaeger, J.C. Moving sources of heat and the temperature of sliding contacts. Proc. R. Soc. New South Wales 1942, 76, 203–224. [Google Scholar] [CrossRef]
- Loewen, E.G.; Shaw, M.C. On the analysis of cutting-tool temperatures. Trans. ASME 1954, 76, 217–225. [Google Scholar] [CrossRef]
- Herbert, E.G. The Measurement of Cutting Temperatures. Proc. Inst. Mech. Eng. 1926, 110, 289–329. [Google Scholar] [CrossRef]
- Kato, S.; Yamaguchi, K.; Yamada, M. Stress Distribution at the Interface Between Tool and Chip in Machining. ASME J. Eng. Ind. 1972, 94, 683–689. [Google Scholar] [CrossRef]
- Calatoru, V.D.; Balazinski, M.; Mayer, J.R.R.; Paris, H.; L’Esperance, G. Diffusion wear mechanism during high-speed machining of 7475-T7351 aluminum alloy with carbide end mills. Wear 2008, 265, 1793–1800. [Google Scholar] [CrossRef]
- Boyer, R.; Welsch, G.; Collings, E.W. Materials Properties Handbook: Titanium Alloys; ASM International: Almere, The Netherlands, 1994; Volume 76. [Google Scholar]
- Chen, J.; Young, B. Stress-strain curves for stainless steel at elevated temperatures. Eng. Struct. 2006, 28, 229–239. [Google Scholar] [CrossRef]





| Cutting conditions | Feed per revolution [mm/rev] | 0.15 |
| Cutting width [mm] | 6.4 | |
| Identified parameter | Specific cutting force in principal direction [MPa] | 713.54 |
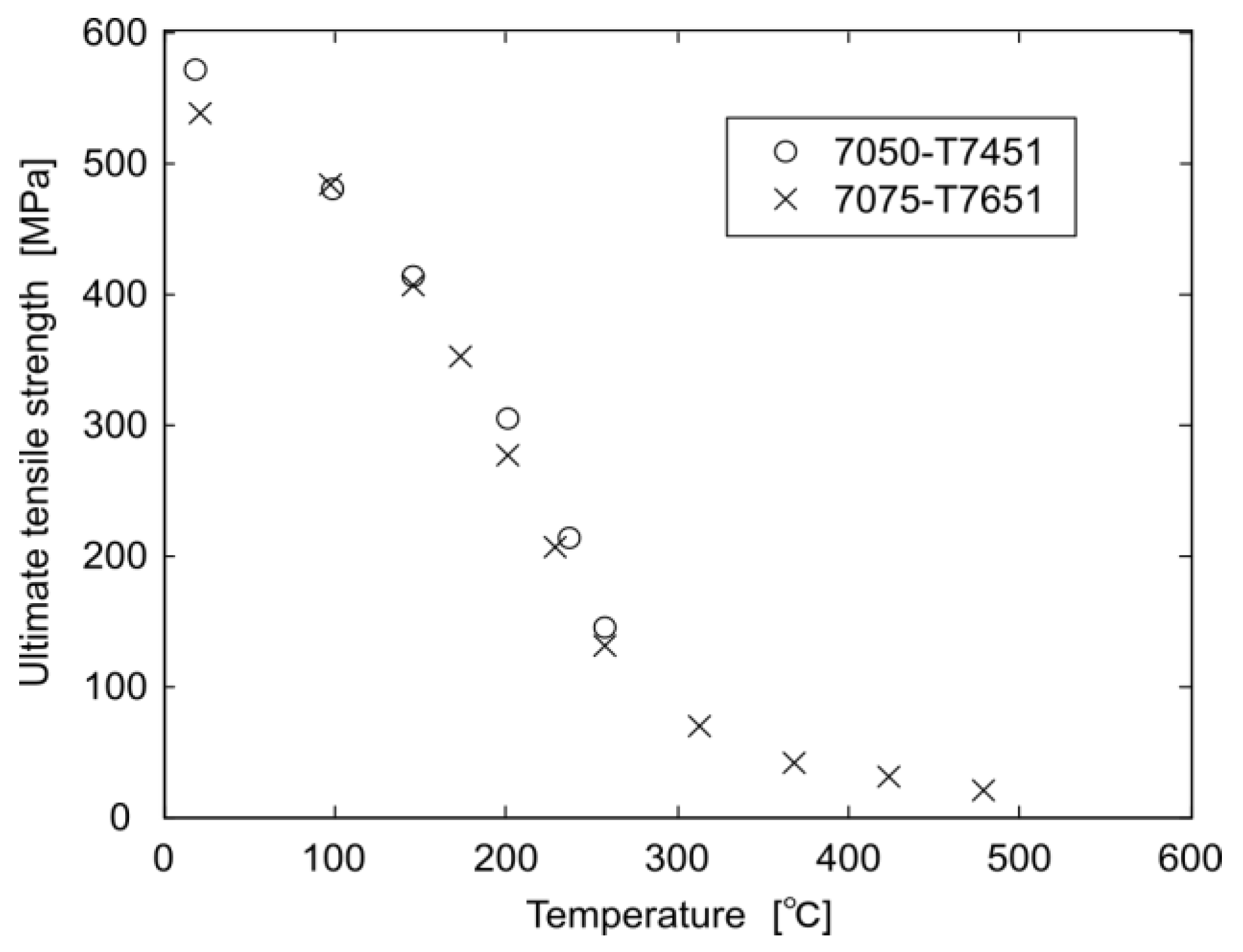
| Properties of 7050-T7451 | Density [g/cc] | 2.823 |
| Specific heat capacity [J/(kg∙°C)] | 962.964 | |
| Thermal conductivity [W/(m∙°C)] | 157.497 | |
| Thermal diffusivity [mm2/s] | 57.936 | |
| Melting (solidus) temperature [°C] | 490 |
| Fixture Type | Large | Small |
|---|---|---|
| Fixture diameter [mm] | 290 | 160 |
| Fixture mass [kg] | 13.26 | 4.41 |
| Cutting speed range [m/min] | >1500 | <1500 |
| Workpiece diameter range [mm] | 354 to 292 | 255 to 162 |
| Cutting angle range (one end) [deg] | 26.1 to 31.8 | 36.6 to 59.2 |
| Tool Type | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| Rake angle [deg] | 10 | 0 | −10 | 10 |
| Clearance angle [deg] | 17 | 17 | 17 | 17 |
| Coating | Non-coated | DLC | ||
| Cutting edge radius [µm] | Approximately 5 | Approximately 6 | ||
| Rake surface | Lapped ( | Lapped and then coated | ||
| Experiment Type | Tool Types | Fixture Types | Fixed Conditions | Varied Conditions |
|---|---|---|---|---|
| Cutting speed | T1 | Large, Small | Dry cutting Feed per revolution : 0.15 mm/rev Rake angle : +10 deg | Cutting speed : 70 to 5184 m/min |
| Feed per revolution | T1 | Small | Dry cutting Cutting speed : 1465 m/min Rake angle : +10 deg | Feed per revolution : 0.005 to 0.2 mm/rev |
| Rake angle | T1, T2, T3 | Large, Small | Dry cutting Feed per revolution : 0.15 mm/rev | Cutting speed : 70 to 5184 m/min Rake angle : +10, 0, −10 deg |
| Cutting fluid and coating | T1, T4 | Large, Small | Feed per revolution : 0.15 mm/rev Rake angle : +10 deg | Cutting speed : 70 to 5184 m/min Cutting fluid: dry, wet Tool coating: non-coated, DLC-coated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eto, J.; Hayasaka, T.; Shamoto, E.; Xu, L. Study on Extraordinarily High-Speed Cutting Mechanics and Its Application to Dry Cutting of Aluminum Alloys with Non-Coated Carbide Tools. J. Manuf. Mater. Process. 2024, 8, 198. https://doi.org/10.3390/jmmp8050198
Eto J, Hayasaka T, Shamoto E, Xu L. Study on Extraordinarily High-Speed Cutting Mechanics and Its Application to Dry Cutting of Aluminum Alloys with Non-Coated Carbide Tools. Journal of Manufacturing and Materials Processing. 2024; 8(5):198. https://doi.org/10.3390/jmmp8050198
Chicago/Turabian StyleEto, Jun, Takehiro Hayasaka, Eiji Shamoto, and Liangji Xu. 2024. "Study on Extraordinarily High-Speed Cutting Mechanics and Its Application to Dry Cutting of Aluminum Alloys with Non-Coated Carbide Tools" Journal of Manufacturing and Materials Processing 8, no. 5: 198. https://doi.org/10.3390/jmmp8050198
APA StyleEto, J., Hayasaka, T., Shamoto, E., & Xu, L. (2024). Study on Extraordinarily High-Speed Cutting Mechanics and Its Application to Dry Cutting of Aluminum Alloys with Non-Coated Carbide Tools. Journal of Manufacturing and Materials Processing, 8(5), 198. https://doi.org/10.3390/jmmp8050198