Process Optimization and Distortion Prediction in Directed Energy Deposition
Abstract
1. Introduction
2. Constitutive Model
2.1. Thermal Model
2.1.1. Gaussian Model
2.1.2. Goldak Model
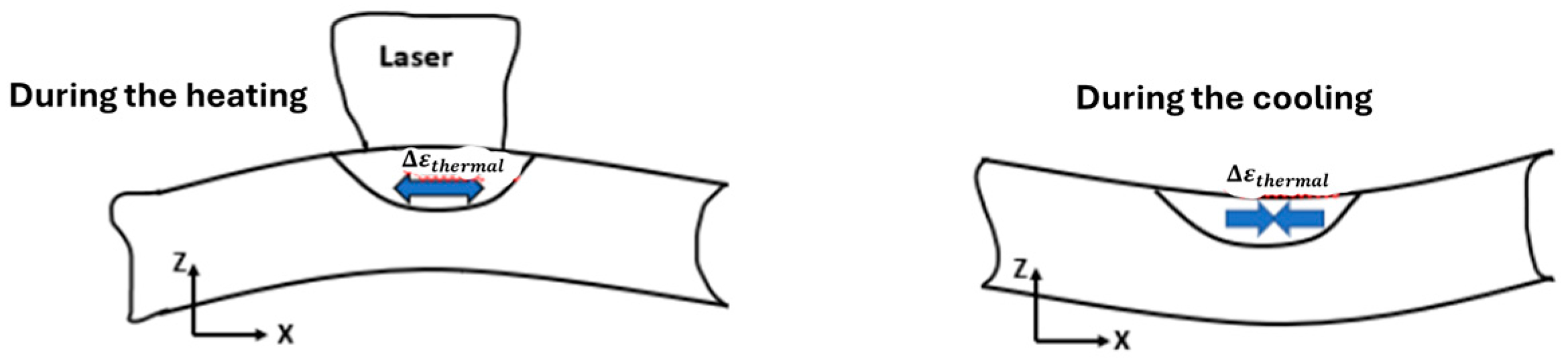
2.2. Structural Analysis
3. Numerical Finite Element Model
3.1. Geometry Description
3.2. Thermomechanical Simulation
3.2.1. Mesh Description
3.2.2. Material Proprieties
4. Results and Discussion
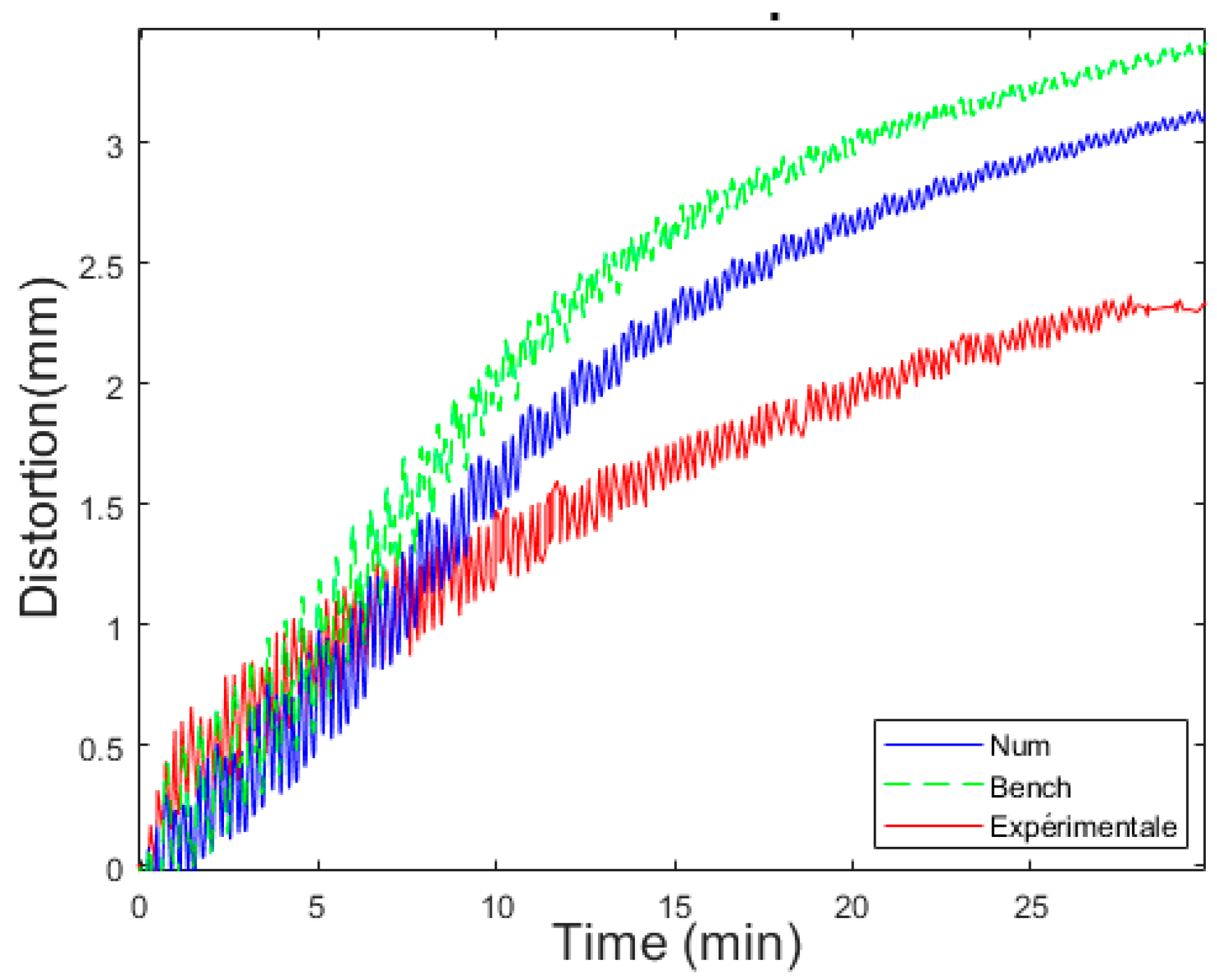
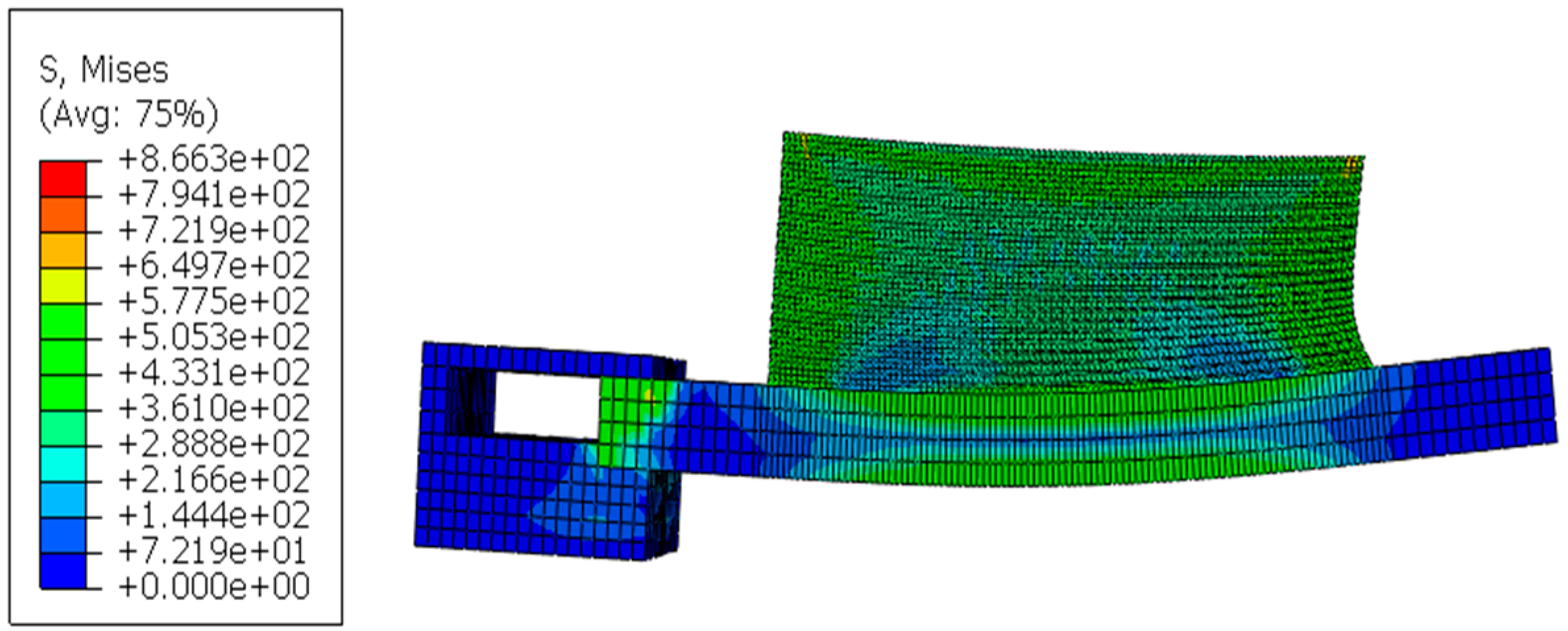
4.1. Model Validation
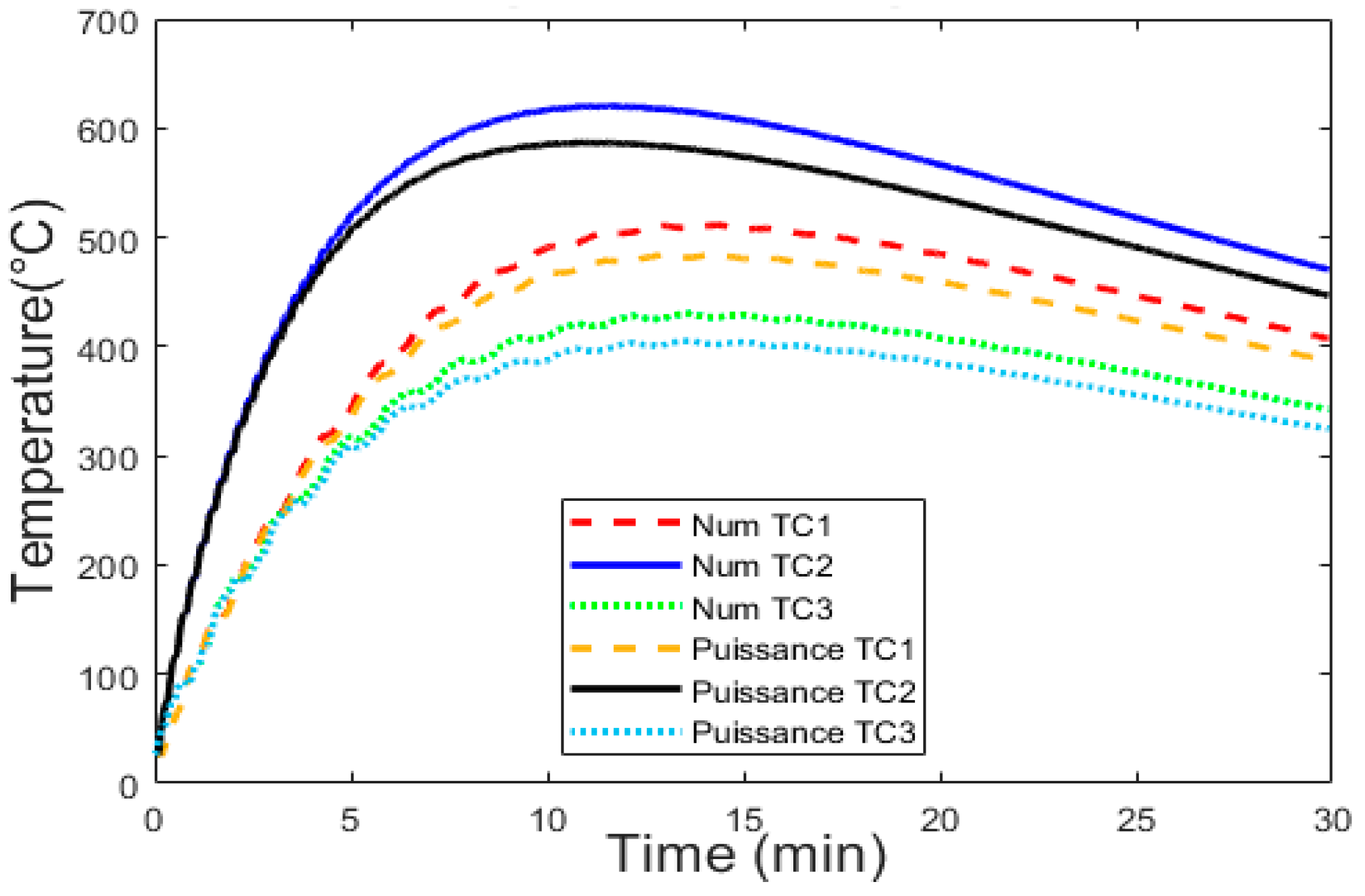
4.1.1. Thermal Results
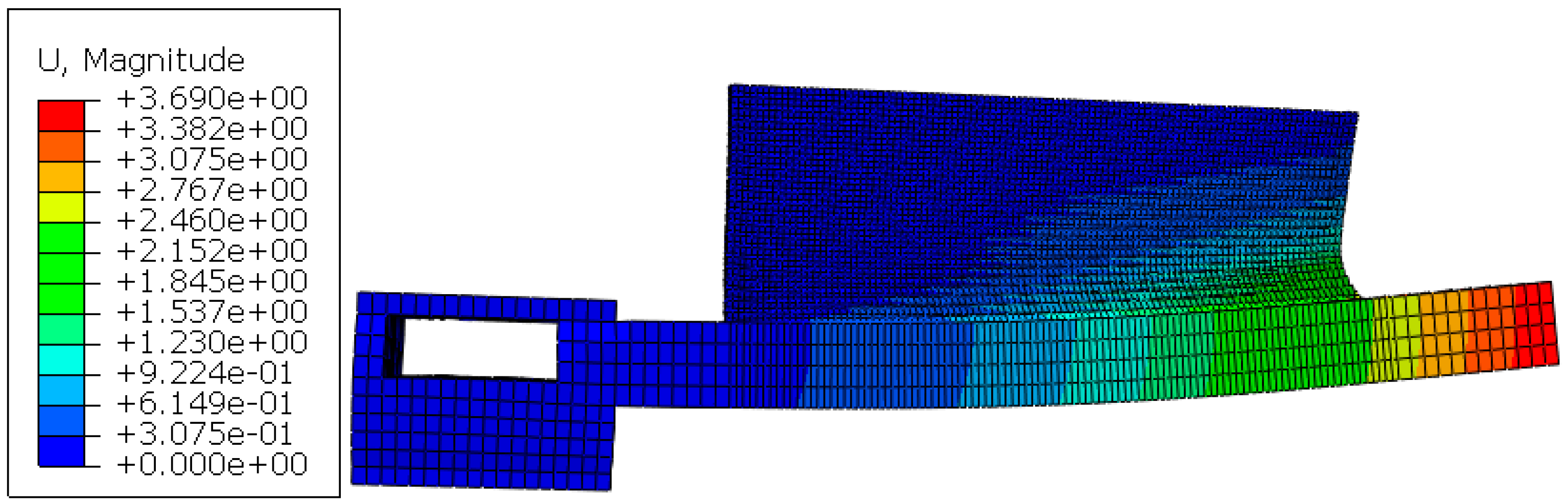
4.1.2. Distortion Prediction Using Thermal–Mechanical Coupling
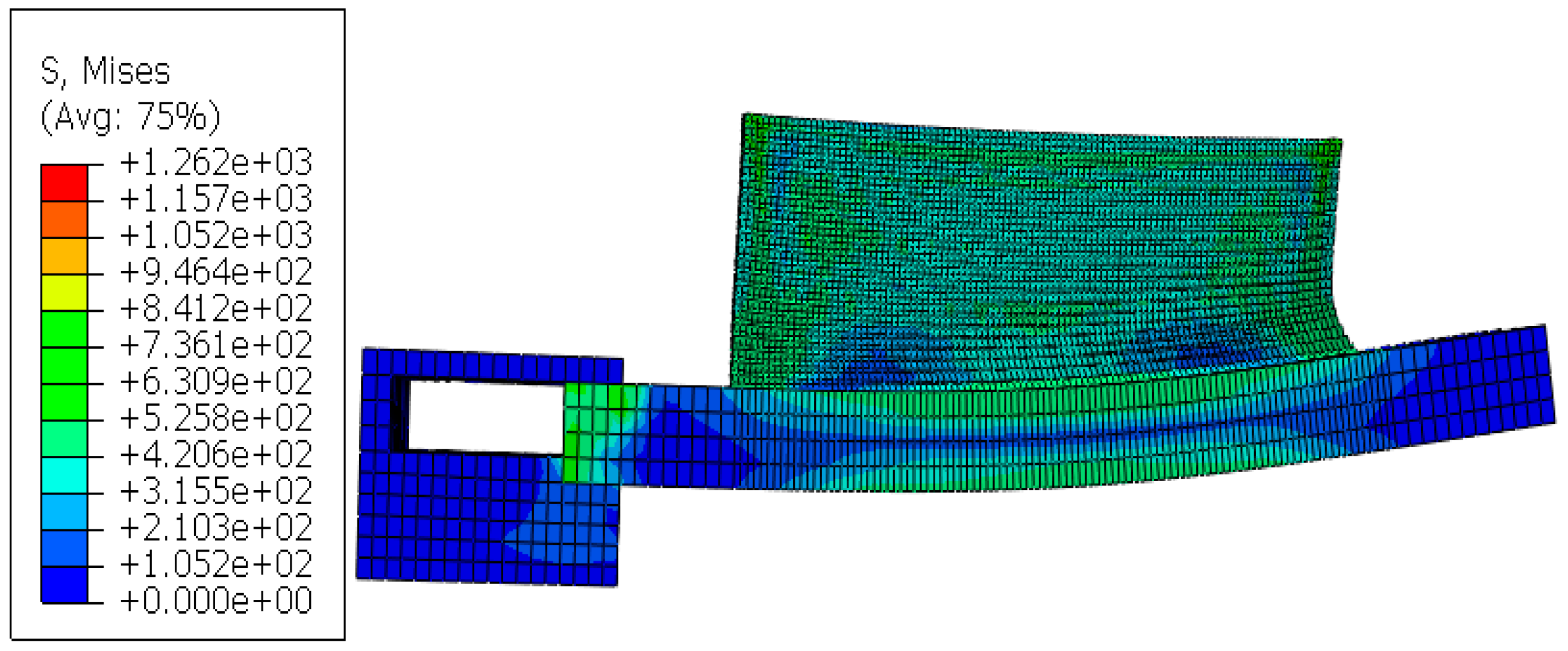
4.1.3. Stress Distribution
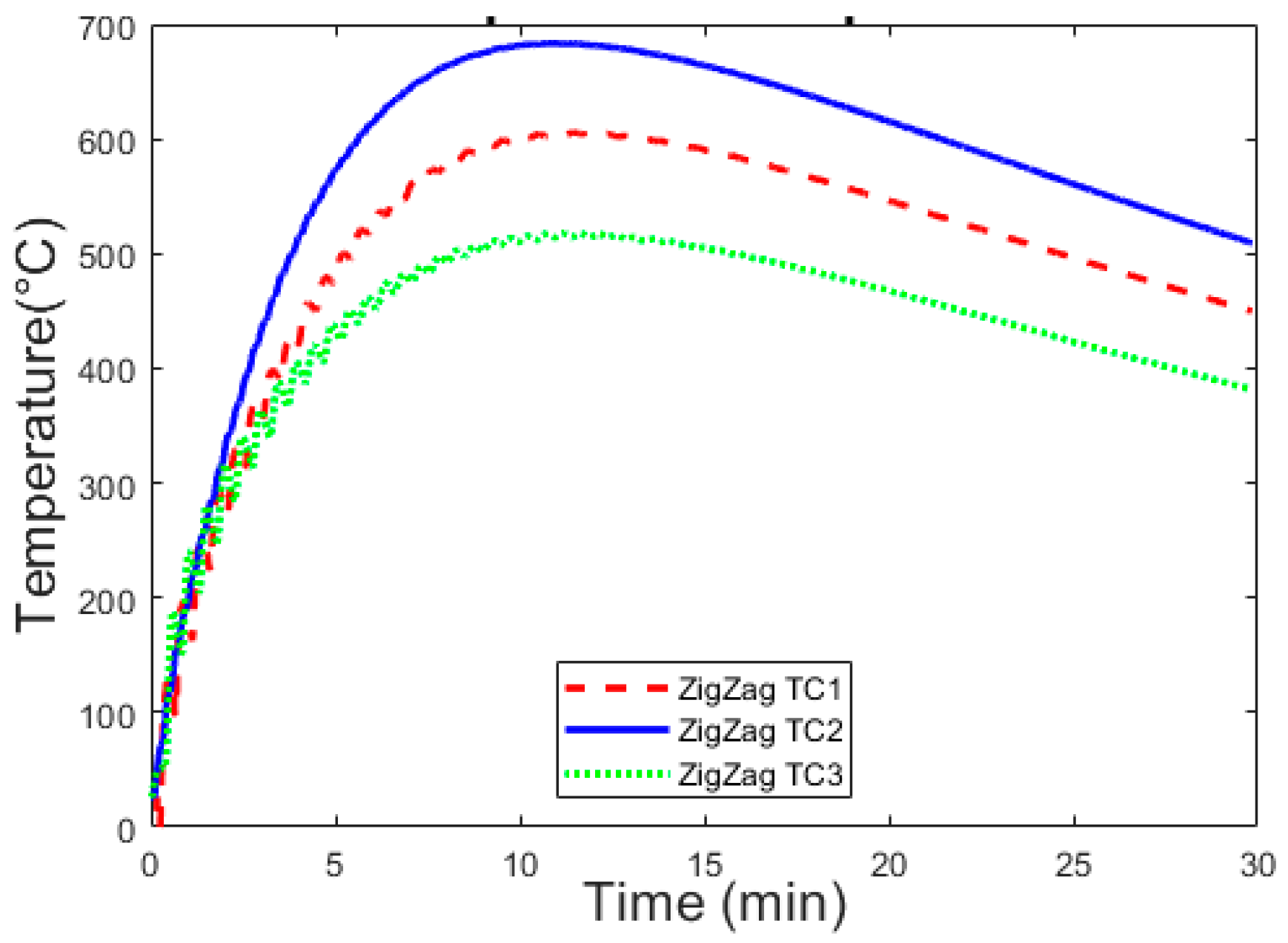
4.2. Effect of Zig-Zag Strategy
4.2.1. Thermal Results
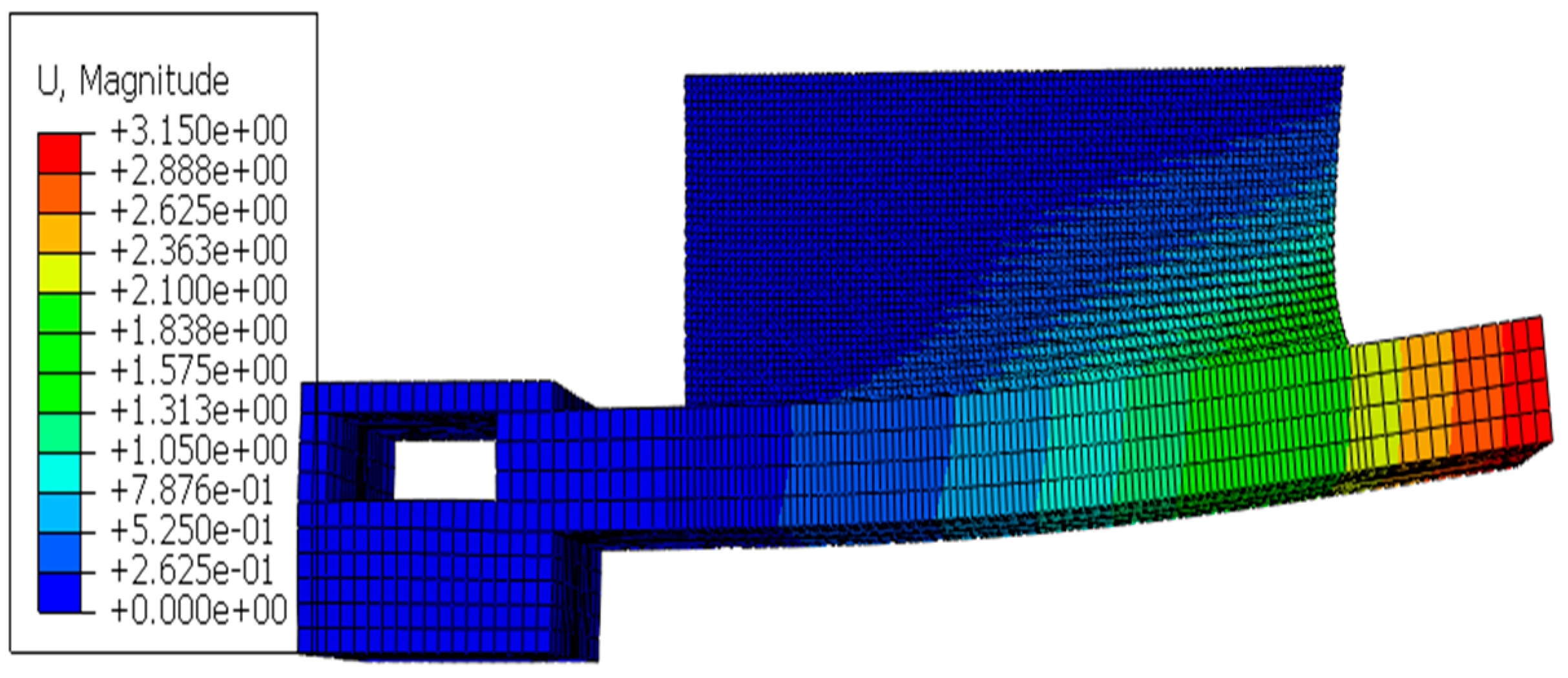
4.2.2. Distortion Results
4.2.3. Stress Distributions
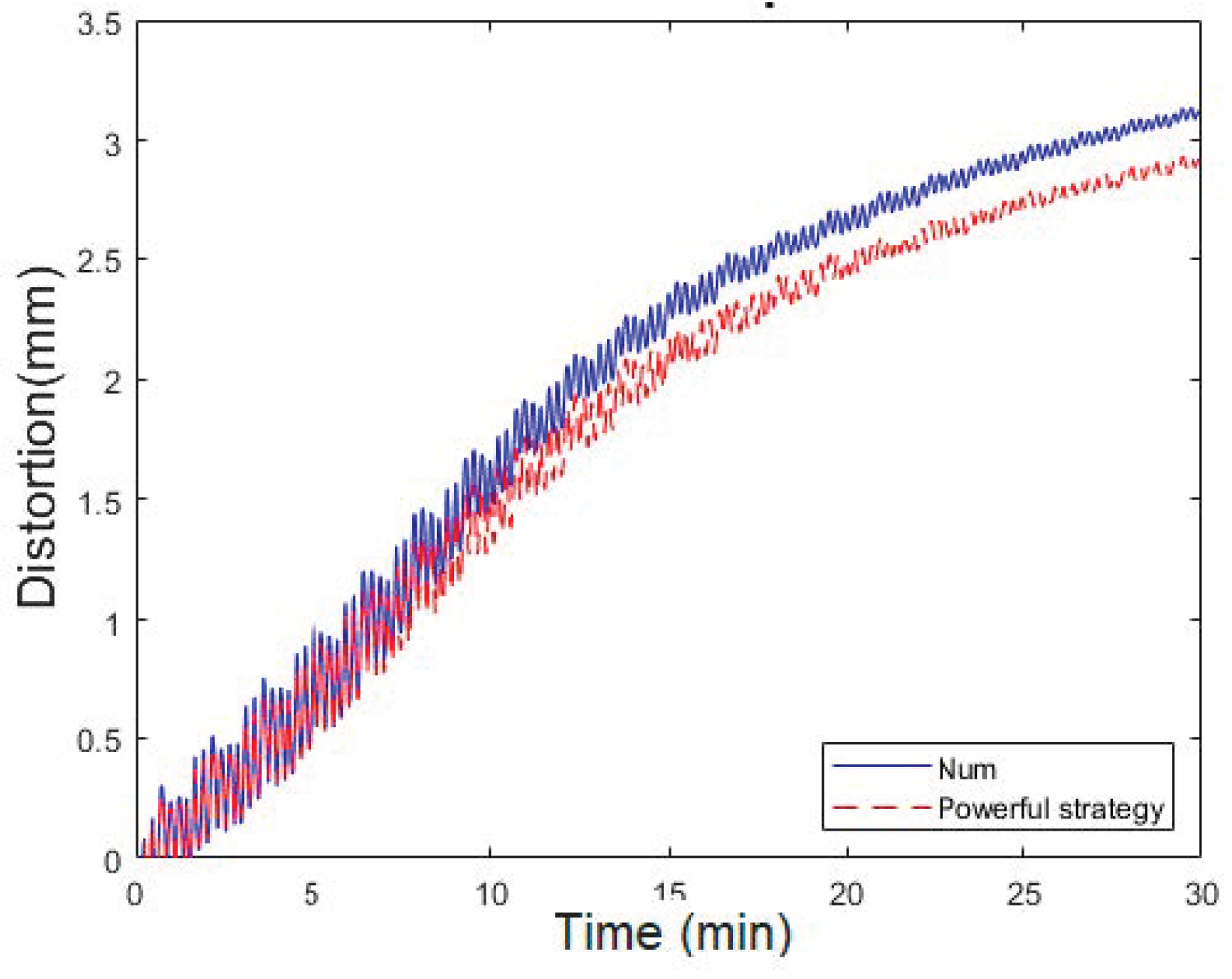
4.3. Effect of Low-Power Strategy
4.3.1. Thermal Results
4.3.2. Distortion Evolution
4.3.3. Stress Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jafari-Marandi, R.; Khanzadeh, M.; Tian, W.; Smith, B.; Bian, L. From in-situ monitoring toward high-throughput process control: Cost-driven decision-making framework for laser-based additive manufacturing. J. Manuf. Syst. 2019, 51, 29–41. [Google Scholar] [CrossRef]
- Grasso, M.; Gallina, F.; Colosimo, B.M. Data fusion methods for statistical process monitoring and quality characterization in metal additive manufacturing. Procedia CIRP 2018, 75, 103–107. [Google Scholar] [CrossRef]
- Ahn, D.G. Directed Energy Deposition (DED) Process: State of the Art. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 703–742. [Google Scholar] [CrossRef]
- Dass, A.; Moridi, A. State of the art in directed energy deposition: From additive manufacturing to materials design. Coatings 2019, 9, 418. [Google Scholar] [CrossRef]
- Yao, B.; Imani, F.; Yang, H. Markov Decision Process for Image-Guided Additive Manufacturing. IEEE Robot. Autom. Lett. 2018, 3, 2792–2798. [Google Scholar] [CrossRef]
- Al-Meslemi, Y. Predictive Modeling for Metal Additive Manufacturing: Key Characteristics and Porosity Characterization. Doctoral Dissertation, Université Paris-Saclay, Paris, France, 2021. [Google Scholar]
- Chen, Y.; Peng, X.; Kong, L.; Dong, G.; Remani, A.; Leach, R. Defect inspection technologies for additive manufacturing. Int. J. Extreme Manuf. 2021, 3, 022002. [Google Scholar] [CrossRef]
- Ren, W.; Mazumder, J. In-situ porosity recognition for laser additive manufacturing of 7075-Al alloy using plasma emission spectroscopy. Sci. Rep. 2020, 10, 19493. [Google Scholar] [CrossRef] [PubMed]
- Whiting, J.; Springer, A.; Sciammarella, F. Real-Time Acoustic Emission Monitoring of Powder Mass Flow Rate for Directed Energy Deposition. Addit. Manuf. 2018, 23, 312–318. [Google Scholar] [CrossRef] [PubMed]
- Svetlizky, D.; Das, M.; Zheng, B.; Vyatskikh, A.L.; Bose, S.; Bandyopadhyay, A.; Schoenung, J.M.; Lavernia, E.J.; Eliaz, N. Directed energy deposition (DED) additive manufacturing: Physical characteristics, defects, challenges and applications. Mater. Today 2021, 49, 271–295. [Google Scholar] [CrossRef]
- Khanzadeh, M.; Tian, W.; Yadollahi, A.; Doude, H.R.; Tschopp, M.A.; Bian, L. Dual process monitoring of metal-based additive manufacturing using tensor decomposition of thermal image streams. Addit. Manuf. 2018, 23, 443–456. [Google Scholar] [CrossRef]
- Michaleris, P.; Debiccari, A. Prediction of Welding Distortion A two-step numerical analysis technique was developed to predict welding- induced distortion and the structural integrity of large and complex structures. In Proceedings of the 12th International Symposium on Zirconium in the Nuclear Industry, Toronto, ON, Canada, 15–18 June 1998. [Google Scholar]
- Ninpetch, P.; Kowitwarangkul, P.; Chalermkarnnon, P.; Promoppatum, P.; Chuchuay, P.; Rattanadecho, P. Numerical Modeling of Distortion of Ti-6Al-4V Components Manufactured Using Laser Powder Bed Fusion. Metals 2022, 12, 1484. [Google Scholar] [CrossRef]
- Mughal, M.P.; Fawad, H.; Mufti, R.A. Three-dimensional finite-element modelling of deformation in weldbased rapid prototyping. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 875–885. [Google Scholar] [CrossRef]
- Corbin, D.J.; Nassar, A.R.; Reutzel, E.W.; Beese, A.M.; Michaleris, P. Effect of Substrate Thickness and Preheating on the Distortion of Laser Deposited Ti–6Al–4V. J. Manuf. Sci. Eng. 2018, 140, 061009. [Google Scholar] [CrossRef]
- Knüttel, D.; Baraldo, S.; Valente, A.; Carpanzano, E.; Wegener, K. Height prediction in Directed Metal Deposition with Artificial Neural Networks. Procedia CIRP 2022, 113, 312–317. [Google Scholar] [CrossRef]
- Yang, Y.P.; Jamshidinia, M.; Boulware, P.; Kelly, S.M. Prediction of microstructure, residual stress, and deformation in laser powder bed fusion process. Comput. Mech. 2018, 61, 599–615. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Michaleris, P. Effect of stress relaxation on distortion in additive manufacturing process modeling. Addit. Manuf. 2016, 12, 51–59. [Google Scholar] [CrossRef]
- Smith, J.; Xiong, W.; Yan, W.; Lin, S.; Cheng, P.; Kafka, O.L.; Wagner, G.J.; Cao, J.; Liu, W.K. Linking process, structure, property, and performance for metal-based additive manufacturing: Computational approaches with experimental support. Comput. Mech. 2016, 57, 583–610. [Google Scholar] [CrossRef]
- Marion, G.; Cailletaud, G.; Colin, C.; Mazière, M. A finite element model for the simulation of direct metal deposition. In International Congress on Applications of Lasers & Electro-Optics; AIP Publishing: San Diego, CA, USA, 2014; pp. 834–841. [Google Scholar] [CrossRef]
- Mi, G.; Li, C.; Gao, Z.; Zhao, D.; Niu, J. Finite element analysis of welding residual stress of aluminum plates under different butt joint parameters. Eng. Rev. 2014, 34, 161–166. [Google Scholar]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Goldak, J.A.; Akhlaghi, M. (Eds.) Thermal Analysis of Welds. In Computational Welding Mechanics; Springer: Boston, MA, USA, 2005; pp. 71–117. [Google Scholar] [CrossRef]
- Israr, R.; Buhl, J.; Elze, L.; Bambach, M. Simulation of different path strategies for wire-arc additive manufacturing with Lagrangian finite element methods Chair of Mechanical Design and Manufacturing. In Proceedings of the LS-DYNA Forum 2018, Bamberg, Germany, 15–17 October 2018. [Google Scholar]
- Wang, J.; Wang, Y.; Su, Y.; Shi, J. Evaluation of in-situ alloyed Inconel 625 from elemental powders by laser directed energy deposition. Mater. Sci. Eng. A 2022, 830, 142296. [Google Scholar] [CrossRef]
- Tsirkas, S.A.; Papanikos, P.; Kermanidis, T. Numerical simulation of the laser welding process in butt-joint specimens. J. Mater. Process. Technol. 2003, 134, 59–69. [Google Scholar] [CrossRef]
- Lundbäck, A. Finite Element Modelling and Simulation of Welding of Aerospace Components. Doctoral Dissertation, Luleå tekniska universitet, Luleå, Sweden, 2003; p. 50. [Google Scholar]
- Ulbricht, A.; Altenburg, S.J.; Sprengel, M.; Sommer, K.; Mohr, G.; Fritsch, T.; Mishurova, T.; Serrano-Munoz, I.; Evans, A.; Hofmann, M.; et al. Separation of the Formation Mechanisms of Residual Stresses in LPBF 316L. Metals 2020, 10, 9. [Google Scholar] [CrossRef]
- Dunbar, A.J.; Denlinger, E.R.; Gouge, M.F.; Simpson, T.W.; Michaleris, P. Comparisons of laser powder bed fusion additive manufacturing builds through experimental in situ distortion and temperature measurements. Addit. Manuf. 2017, 15, 57–65. [Google Scholar] [CrossRef]
- Benzley, S.E.; Perry, E.; Merkley, K.; Clark, B.; Sjaardama, G. A Comparison of All Hexagonal and All Tetrahedral Finite Element Meshes for Elastic and Elasto-plastic Analysis. In Proceedings, 4th International Meshing Roundtable; Sandia National Laboratories: Albuquerque, NM, USA, 1995; p. 13. [Google Scholar]
- Shoemaker, L.E. Alloys 625 and 725: Trends in Properties and Applications. Superalloys 2005, 718, 409–418. [Google Scholar] [CrossRef]
- Lu, X.; Cervera, M.; Chiumenti, M.; Lin, X. Residual Stresses Control in Additive Manufacturing. J. Manuf. Mater. Process. 2021, 5, 138. [Google Scholar] [CrossRef]
- Ivanov, S.; Artinov, A.; Zemlyakov, E.; Karpov, I.; Rylov, S.; Em, V. Spatiotemporal Evolution of Stress Field during Direct Laser Deposition of Multilayer Thin Wall of Ti-6Al-4V. Materials 2021, 15, 263. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Zou, X.; Li, S.; Luo, G.; Song, L. A Study on the Thermo-Mechanical History, Residual Stress, and Dynamic Recrystallization Mechanisms in Additively Manufactured Austenitic Stainless Steels. Metals 2022, 12, 1109. [Google Scholar] [CrossRef]
- Filho, C.M.; Caicedo-Silva, M.; Cervera, M.; Chiumenti, M.; Baiges, J. A Robust h-Adaptive Finite Element Framework for Industrial Part-Scale Thermal Analysis in Additive Manufacturing Processes. Eng. Comput. 2022, 38, 4791–4813. [Google Scholar] [CrossRef]
- Du, L.; Gu, D.; Dai, D.; Shi, Q.; Ma, C.; Xia, M. Relation of thermal behavior and microstructure evolution during multi-track laser melting deposition of Ni-based material. Opt. Laser Technol. 2018, 108, 207–217. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Yang, H.; Huang, W. Residual stress and distortion of rectangular and S-shaped Ti-6Al-4V parts by Directed Energy Deposition: Modelling and experimental calibration. Addit. Manuf. 2019, 26, 166–179. [Google Scholar] [CrossRef]
- Glaspell, A.; De la Peña, J.A.D.; Ryu, J.J.; Choo, K. Thermal Stress Characteristics of Dissimilar Joints Joining Ti-64 and CCM via Linear Friction Welding. Energies 2022, 15, 5588. [Google Scholar] [CrossRef]
- Mukherjee, T.; Zhang, W.; DebRoy, T. An improved prediction of residual stresses and distortion in additive manufacturing. Comput. Mater. Sci. 2017, 126, 360–372. [Google Scholar] [CrossRef]
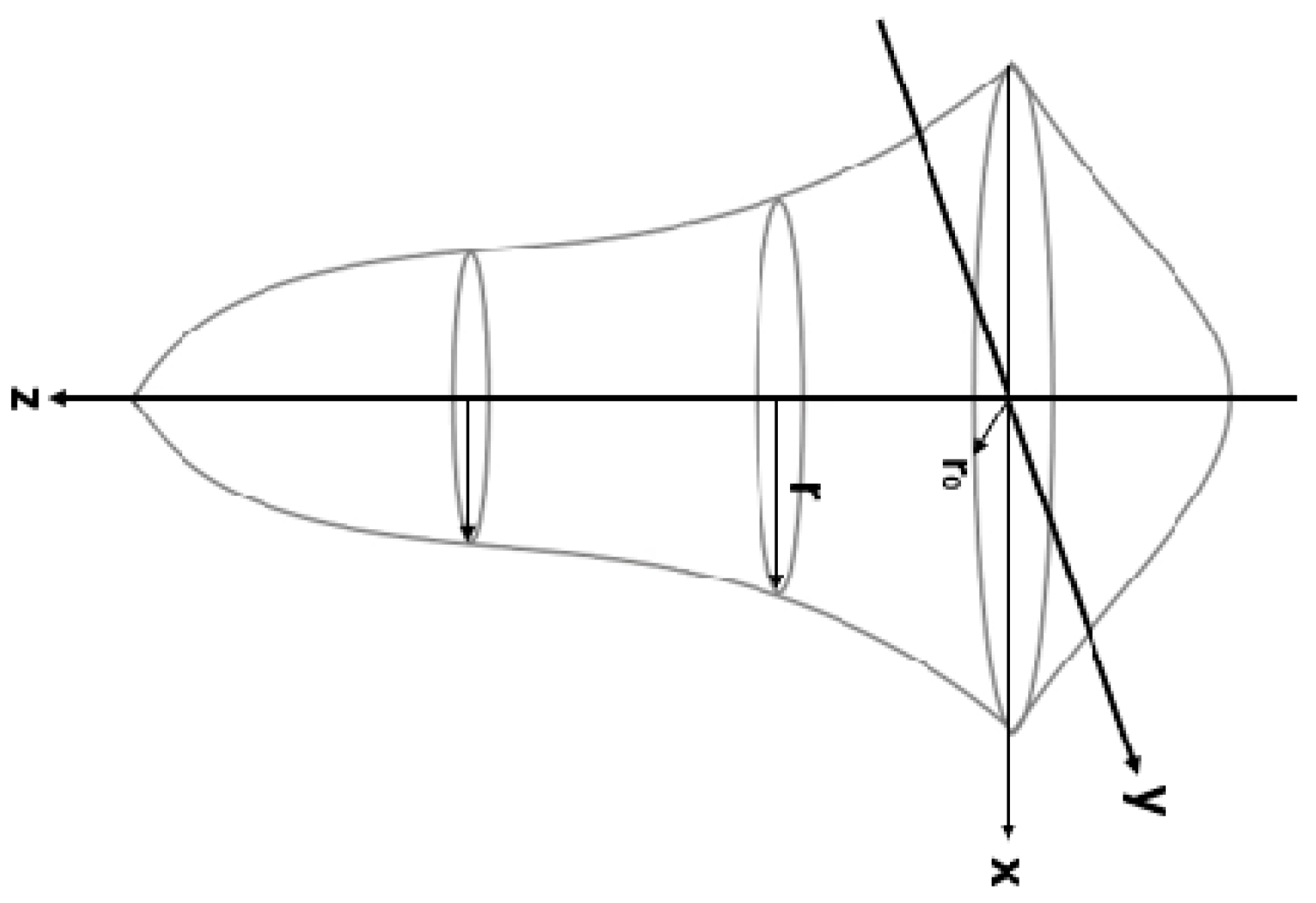
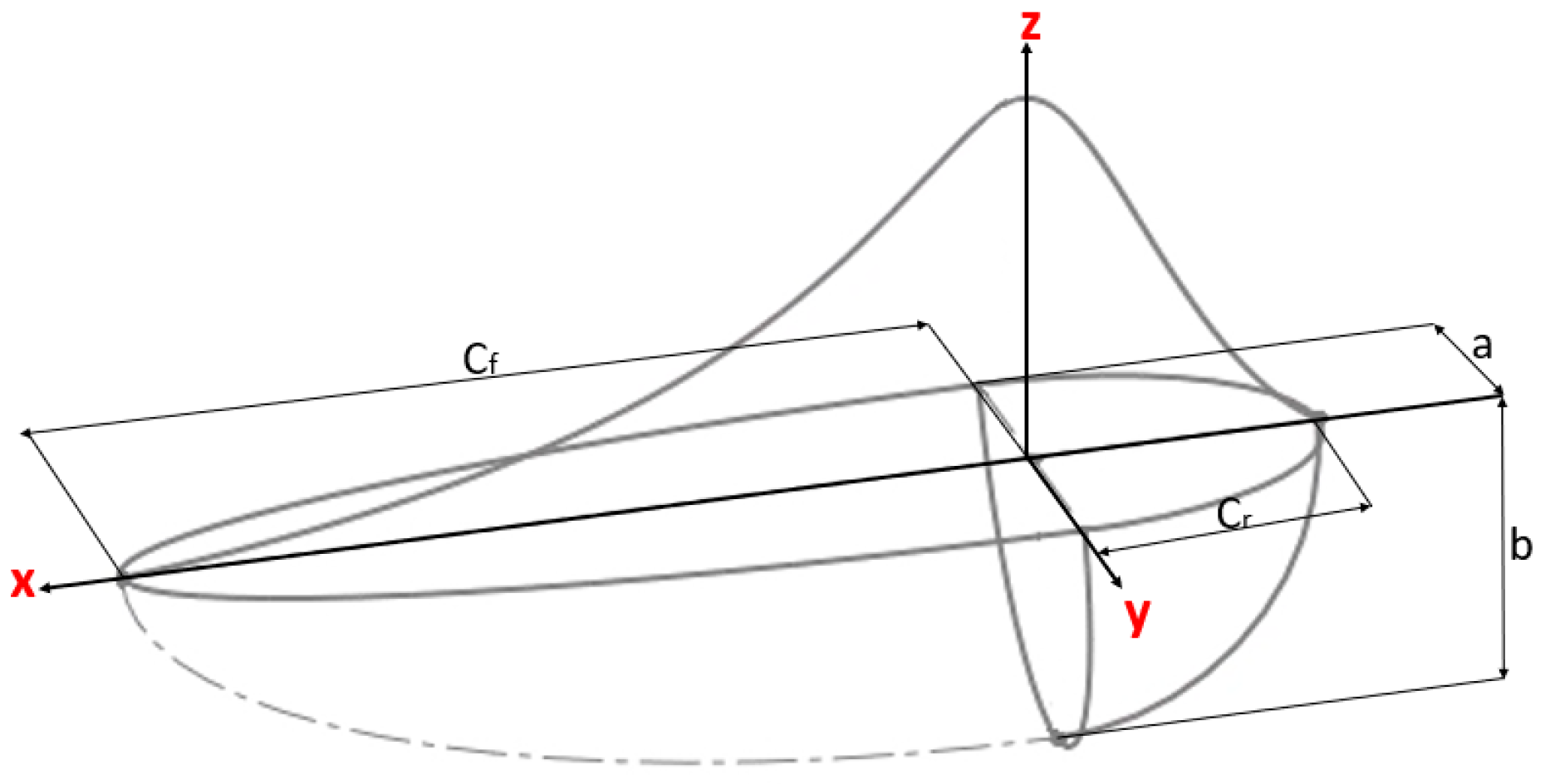
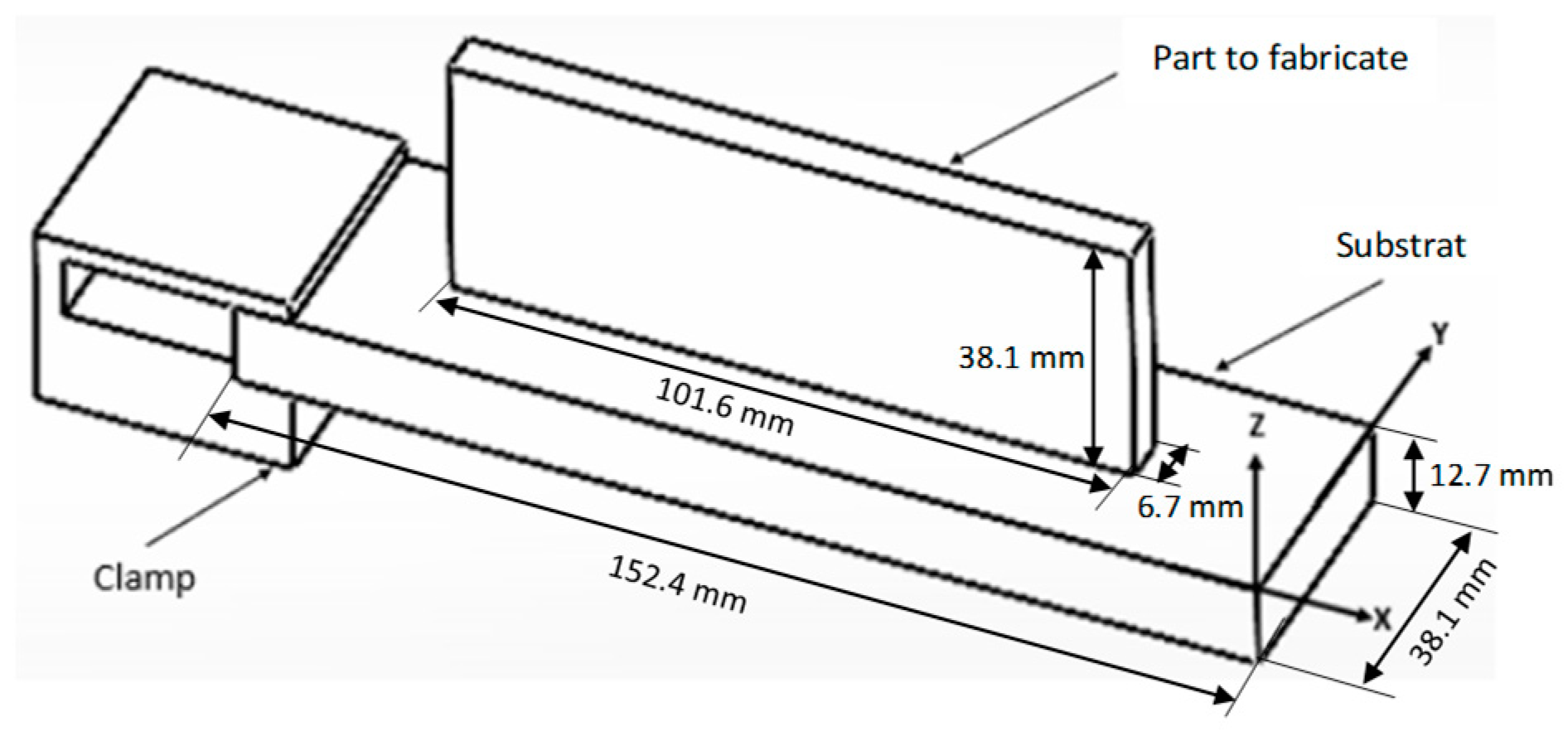


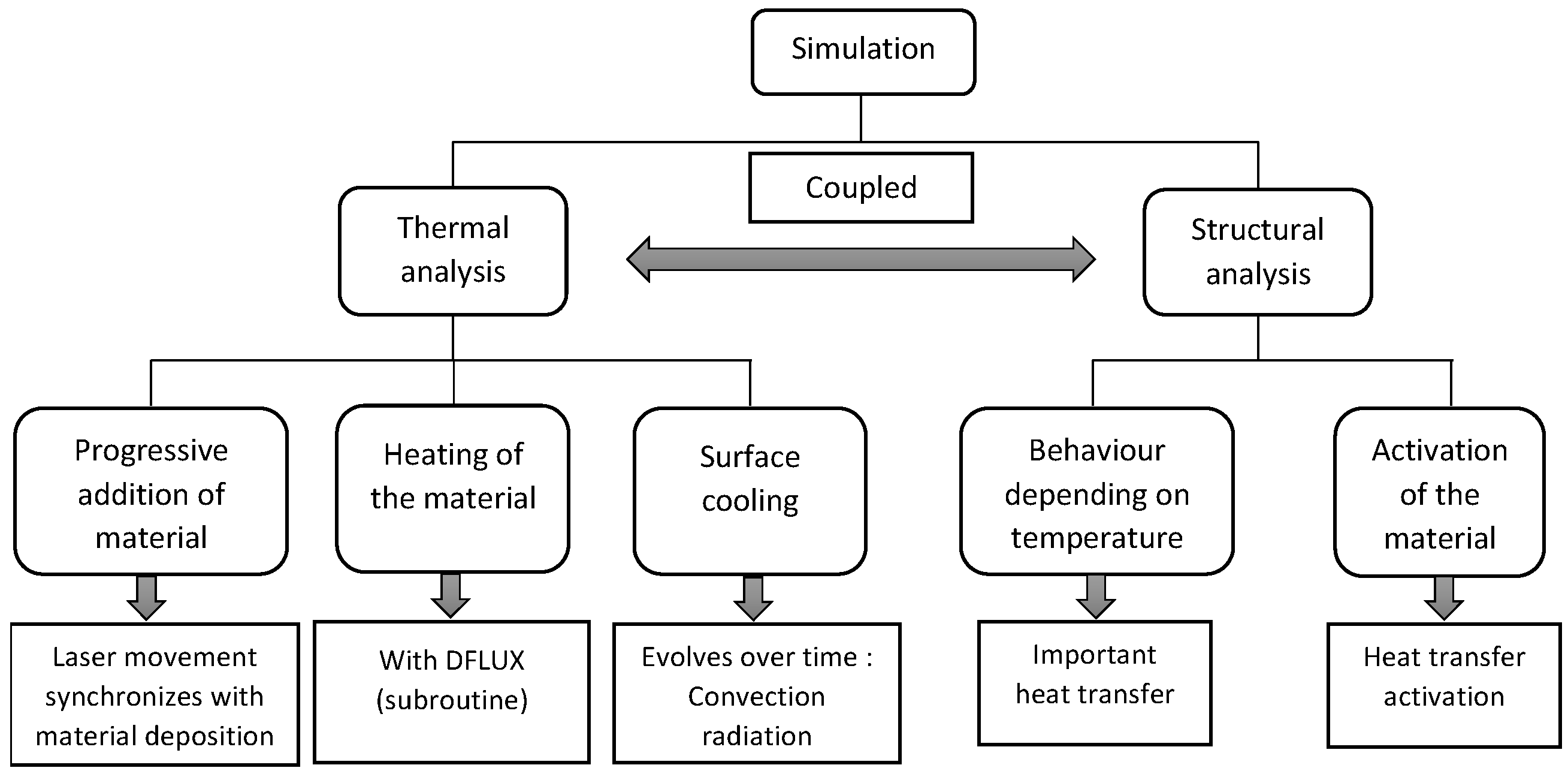










| Parameter | Value |
|---|---|
| Weld pool width, a | 2.0 mm |
| Weld pool depth, b | 1.1 mm |
| Forward weld pool, cf | 2.0 mm |
| Rearward weld pool, cr | 2.0 mm |
| Forward heat factor, ff | 1.0 |
| Rearward heat factor, fr | 1.0 |
| Exponent constant, n | 1.0 |
| The laser beam spot size, D | 4 mm |
| Weld pool energy, Q | 2000 W |
| Laser scan speed, v | 10.6 mm/s |
| Designation | Symbol |
|---|---|
| Strategy of standard model | Num |
| Experimental results | Exp |
| Simulation benchmark Abaqus | Bench |
| Strategy of power variation | Power |
| Strategy of scan pattern for Zig-Zag | Zig-Zag |
| Laser displacement sensor | LDS |
| Thermocouple 1 at the free end of the substrate | TC1 |
| Thermocouple 2 at the center of the substrate | TC2 |
| Thermocouple 3 at the clamp end of the substrate | TC3 |
| Element | Cr | Mo | Nb | Fe | Ni |
|---|---|---|---|---|---|
| Percentage (%) | 22 | 9 | 3.5 | 3 | - |
| T (°C) | Conductivity (mW/(mm·°C)) | Specific Heat (mJ/(ton·°C)) | α (1/°C) | E (MPa) | Yield Stress (MPa) |
|---|---|---|---|---|---|
| 20 | 9.9 | 4.10 × 108 | 1.28 × 10–5 | 2.08 × 105 | 493 |
| 205 | 12.5 | 4.56 × 108 | 1.31 × 10–5 | 1.98 × 105 | 443 |
| 315 | 14.1 | 4.81 × 108 | 1.33 × 10–5 | 1.92 × 105 | 430 |
| 425 | 15.7 | 5.11 × 108 | 1.37 × 10–5 | 1.86 × 105 | 424 |
| 540 | 17.5 | 5.36 × 108 | 1.40 × 10–5 | 1.79 × 105 | 423 |
| 650 | 19.0 | 5.65 × 108 | 1.48 × 10–5 | 1.70 × 105 | 422 |
| 760 | 20.8 | 5.90 × 108 | 1.53 × 10–5 | 1.61 × 105 | 415 |
| 870 | 22.8 | 6.20 × 108 | 1.58 × 10–5 | 1.48 × 105 | 386 |
| Clamp | Inconel 625 |
|---|---|
| Density | 2.70 × 10−9 ton/mm3 |
| Conductivity | 237 mW/(mm·°C) |
| Specific heat | 9.1 × 108 mJ/(ton·°C) |
| Elastic modulus | 70 × 103 MPa |
| Poisson’s ratio | 0.366 |
| Thermal expansion coefficient | 2.31 × 10−5/°C |
| Solidus temperature | 1290 °C |
| Liquidus temperature | 1350 °C |
| Emissivity | 0.28 |
| Film coefficient | 0.018 mW/(mm2·°C) |
| Feed rate | 16 g/min |
| Latent heat | 272 × 109 |
| Abaqus. Bench | Exp. | Num. Model | |
|---|---|---|---|
| TC1 (°C) | 480 | 510 | 505 |
| TC2 (°C) | 565 | 505 | 620 |
| Zig-Zag | Ref | |
|---|---|---|
| TC1 (°C) | 610 | 505 |
| TC2 (°C) | 680 | 620 |
| TC3 (°C) | 510 | 430 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Hammouda, A.; Mrad, H.; Marouani, H.; Frikha, A.; Belem, T. Process Optimization and Distortion Prediction in Directed Energy Deposition. J. Manuf. Mater. Process. 2024, 8, 116. https://doi.org/10.3390/jmmp8030116
Ben Hammouda A, Mrad H, Marouani H, Frikha A, Belem T. Process Optimization and Distortion Prediction in Directed Energy Deposition. Journal of Manufacturing and Materials Processing. 2024; 8(3):116. https://doi.org/10.3390/jmmp8030116
Chicago/Turabian StyleBen Hammouda, Adem, Hatem Mrad, Haykel Marouani, Ahmed Frikha, and Tikou Belem. 2024. "Process Optimization and Distortion Prediction in Directed Energy Deposition" Journal of Manufacturing and Materials Processing 8, no. 3: 116. https://doi.org/10.3390/jmmp8030116
APA StyleBen Hammouda, A., Mrad, H., Marouani, H., Frikha, A., & Belem, T. (2024). Process Optimization and Distortion Prediction in Directed Energy Deposition. Journal of Manufacturing and Materials Processing, 8(3), 116. https://doi.org/10.3390/jmmp8030116







