1. Introduction
Joining by plastic deformation has gained considerable relevance in recent years due to its advantages in terms of its cost, productivity, application range and environmental friendliness compared to conventional joining methods such as welding, adhesive bonding and bolted joints [
1]. This joining technology is particularly attractive due to the possibility of joining parts made of different materials, thus enabling lightweight construction approaches, as well as the integration of functional elements into massive metallic structures [
2,
3]. In particular, the development of sensory structures and machine elements involves the integration of sensors into mechanical structures. The joint connecting the host structure to the sensor plays a critical role in determining the sensory properties of the resulting sensor structure, including aspects such as sensor linearity and measurement resolution, as discussed in detail in [
4].
The advantages of integrating sensors into metallic structures using forming techniques range from the flexibility to create form-fit or form- and force-fit joints, as demonstrated by Schubert et al. [
3,
5], to the benefits of joining sensitive functional materials without heat. This is particularly advantageous, as it ensures that the quality, accuracy and reliability of the joined parts are not affected by temperature variations [
2]. This contrasts sharply with the demanding requirements for protecting sensitive sensors and their electronics from elevated temperatures when using high-temperature processes, as illustrated in [
6], for the integration of strain gauge sensors through high-pressure die casting.
On the other hand, adhesive joining has limitations, including extended processing times, expensive surface preparation, prolonged curing times and restricted temperature ranges for application. Moreover, specific surface conditions are required to achieve the optimal joining strength [
7]. Investigations on sensor integration into metal sheets have shown a deterioration in the sensory behavior during the post-processing phase of the sensor sheet compound [
8].
In the specific case of the incremental forming process of rotary swaging, the gradual formation of the joint and the tool oscillation, which results in known loaded and non-loaded process phases, demonstrate significant advantages in terms of adjusting the sensor pre-load conditions during the joining process and consequently influencing the resulting sensory properties. Previous works on sensor integration using recess and infeed rotary swaging show the process ability for target-oriented pre-stress conditions [
9,
10]. Moreover, in situ measuring of the preload at the integrated sensor enables process control and in-process calibration of the sensory structures produced [
11,
12]. However, these investigations have underscored the challenge of integrating axial-force- and torque-measuring strain-gauge-based sensors. Achieving specific pre-load conditions for axial force measurement results in a reduced measuring range for torque measurement and vice versa, as discussed in [
13]. This challenge is attributed to the required pre-load conditions for electromechanical sensors, such as strain-gauge-based and piezo-based sensors, as shown in [
4].
To overcome this limitation, extension of the measuring axis is achieved through a novel optical non-contact measurement concept, as presented in [
14]. However, substituting optical elements for electromechanical transducers poses new challenges for the design of the joining process. Unlike electromechanical transducers, which require specific pre-load conditions during the joining process, the integration of optical transducers requires high positional accuracy. Although joining by forming is sometimes used when a precise final geometry is required, as shown in [
15,
16], a reduction in the geometry deviation in the final products is achieved by optimizing the process design to control the material flow during joining, as shown in [
17]. Nevertheless, such approaches are mainly limited to certain processes, like boss forming.
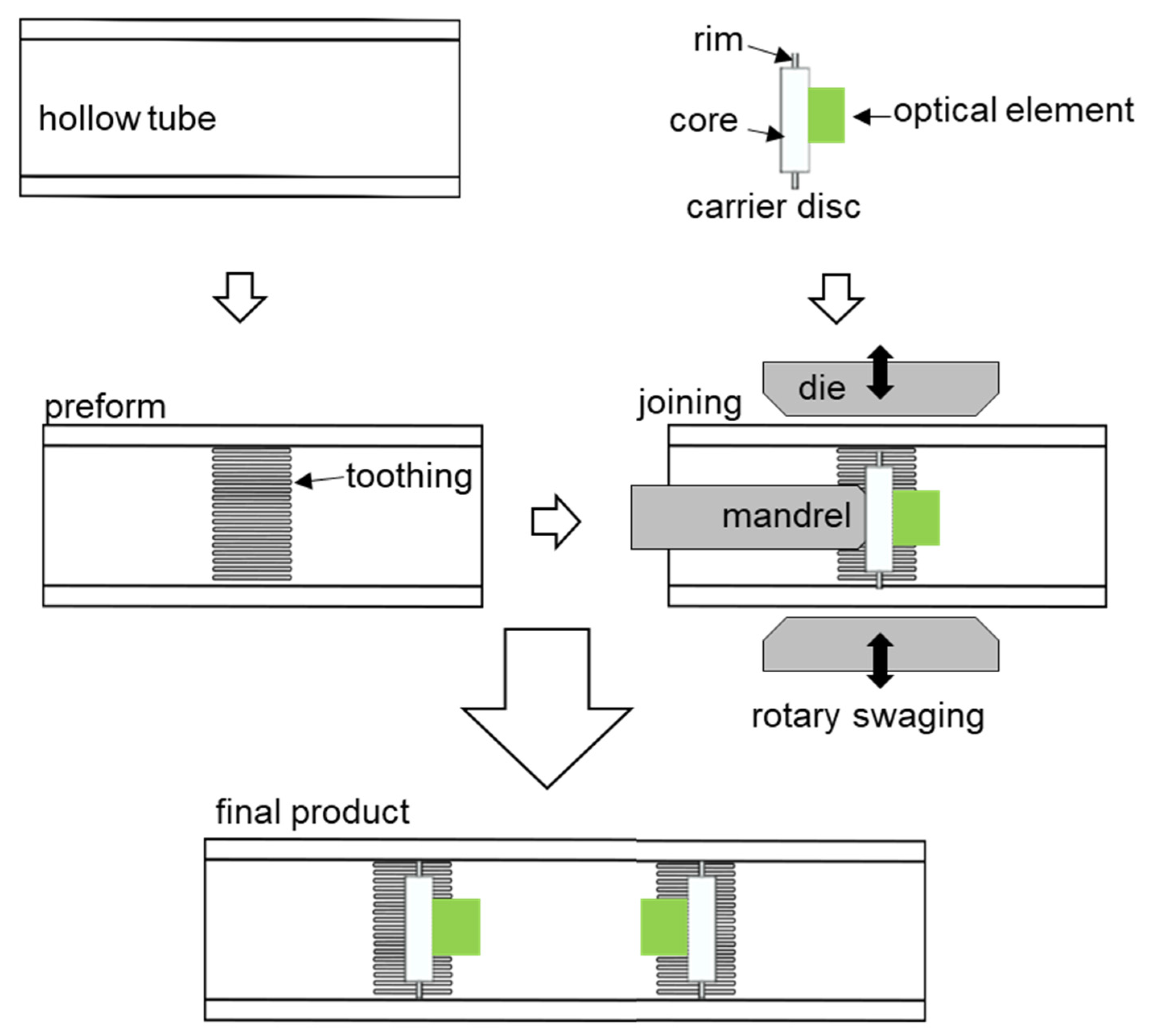
In this paper, we investigate the feasibility and the process phenomena of rotary-swaging-based joining by forming for the integration of a developed two-part multiaxial optical sensor.
The paper is structured as follows: First, the optical image-based sensor is introduced, and the positioning accuracy requirements for sensor integration into tubular structures are specified. A process design for form- and force-fit joining of the sensor parts with minimal joining forces is then presented. Subsequently, the key process parameters are investigated numerically, and their influence on the joining mechanism is discussed. The numerically determined optimal process parameters are then investigated experimentally, and sensor integration tests are carried out. Finally, the paper presents the results of numerical simulations for a potential approach to position-controlled sensor joining by forming.
3. Numerical Process Simulation
The stiffness ratio between the components being joined is influenced by their material properties or geometric design. To prevent premature plastic deformation of the rim as it engages with the teeth, the disc is assumed to be constructed from 1.2379 steel with a high yield strength (σ_y = 990 MPa), while the tube is made of S355J2G3, which has a relatively lower yield strength (σ_y = 385 MPa). The numerical simulation considered two configurations for the rim edge: one with a chamfered edge and one without. The number of teeth was also varied, with configurations featuring 4, 6 and 8 teeth, as detailed in
Table 1.
Table 1 shows the simulated parameters of the joining partners. The teeth have a height of 0.7 mm, a base of 1.73 mm and a flank angle of 100°. The integration is simulated with 4, 6 and 8 teeth. The sensor-bearing disc consists of a core diameter of 10 mm and a rim diameter of 22 mm. The disc edge is simulated as chamfered and not chamfered. Increasing the number of teeth increases the required force for the disc’s penetration and reduces the form-fit of the joint. A similar behavior can be observed when increasing the contact surface on the disc’s rim. With the aid of numerical investigations, the geometric design of the carrier disc and the internal toothing are analyzed with respect to the resulting force and the form-fit.
To set up the simulation model, preliminary investigations are undertaken on a small segment of the entire model using the explicit Abaqus solver. Furthermore, to reduce the computational time for numerical investigation of the complex rotary swaging process, only 10 tool strokes are set to achieve the final diameter reduction.
3.1. Preliminary Simulation and Basics of the Model Parameters
Due to the high deformation of the teeth during the disc’s penetration, the mesh shape and the mass scaling need to be optimized to improve the accuracy of the simulation. In a standard Abaqus mesh algorithm, the inner elements become very small in a triangular shape, like a tooth. As a result, these elements become completely flat at larger deformations, and the simulation will be aborted. In order to avoid this problem, internal paths with specific node distribution are created.
Figure 3a shows the standard mesh at the top with the internal elements becoming smaller and the created mesh with the designed nodes paths in red at the bottom. Furthermore, the Arbitrary Lagrangian–Eulerian Algorithm for remeshing (ALE) was used to create a more uniform aspect ratio within the mesh.
Figure 3b,c show the simulation parameters and the resulting deformation behavior during the joining process.
The different materials allow the tooth to undergo plastic deformation earlier, making it easier for the rim to penetrate. When the rim reaches the bottom of the tooth, the compressive stress increases, and the rim begins to deflect; see
Figure 3c. To accurately simulate the joining behavior of the disc between the teeth and the disc, a 3D section with a thickness and a height of 5 mm of the tube is modeled,
Figure 4a. This allows the joining behavior to be modeled with a higher accuracy in both the axial and radial directions. The modeled tube section includes a variable number of teeth, the carrier disc and the four tools. Since torsional loads occur during workpiece rotation when the forming tools are closed during rotary swaging, the influence of torsion during rotary swaging is neglected, and the simulation model is set up for torsion-free rotary swaging of the tube, so that the workpiece only rotates when the tools are open; see
Figure 4b.
Figure 4b shows the movement of the tools. After ten forming strokes, four calibration strokes are carried out to ensure a uniform stress distribution between the disc and the tube teeth. At the end of the forming process, the boundary condition that fixes the disc is removed. Due to the stress relief and the resulting spring-back, which manifests as minimal axial disc displacement, the disc reaches its final position.
3.2. Investigating the Effect of the Rim Geometry
As shown in
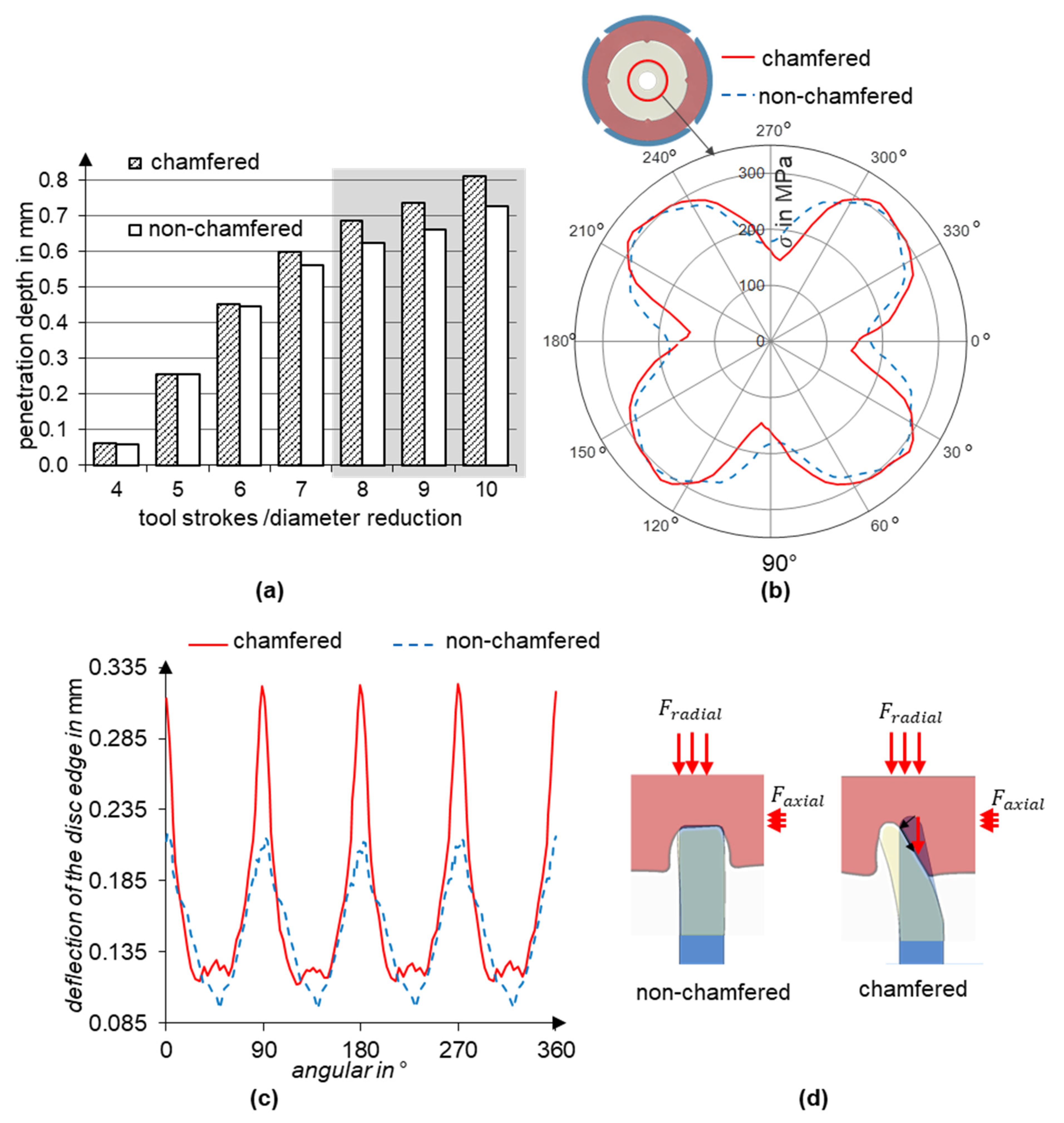
Table 1, the influence of the geometry of the rim edge is investigated by comparing two main variants: a chamfered and a non-chamfered rim edge. In the non-chamfered rim edge variant, the contact surface is twice as large as in the variant with the chamfered edge. Therefore, it is expected to require a higher radial joining force and achieve a lower penetration depth in this case.
In addition to evaluating the deformations, the force fit is also analyzed using the radial stress. The simplifying assumption is made that after the integration of the carrier disc, only radial stresses appear at the boundary between the thick core and the rim, as visualized in
Figure 5b.
Evaluation of the penetration depth shows that the chamfered rim achieves only about a 10% higher penetration depth (
Figure 5a) and about a 3% lower maximum radial stress (
Figure 5b) compared to the non-chamfered edge. However, a significant difference can be observed in the axial deflection behavior of the two rim geometries shown in
Figure 5c.
As can be seen in
Figure 5c, both disc variants show wave-like axial deflection, with the peaks at the teeth resulting from the disc’s penetration. However, the chamfered variant shows significantly higher peaks. An increased alternate rim deflection between the toothed and non-toothed areas indicates a higher axial disc grip within the teeth. Both disc variants are subjected to nearly identical radial and axial forces, whereby the radial force results from the radial forming tools and the axial force results from the material flow in the axial direction. However, the chamfered rim variant experiences a higher axial deflection due to the chamfer geometry; see
Figure 5d. Due to the higher penetration depth and the correlated increase in the alternate axial rim deflection, the chamfered disc variant is considered in subsequent investigations.
3.3. Investigating the Number of Teeth
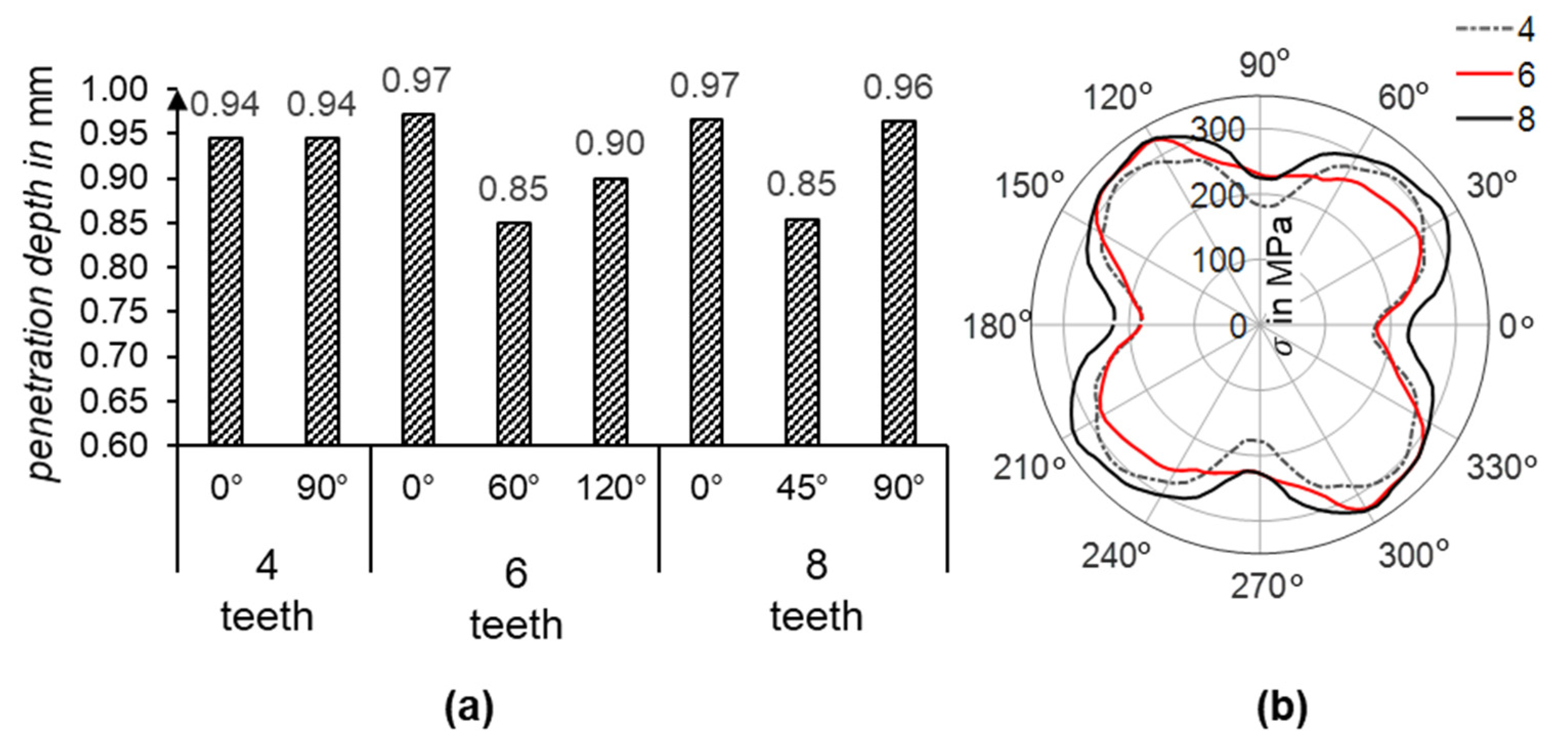
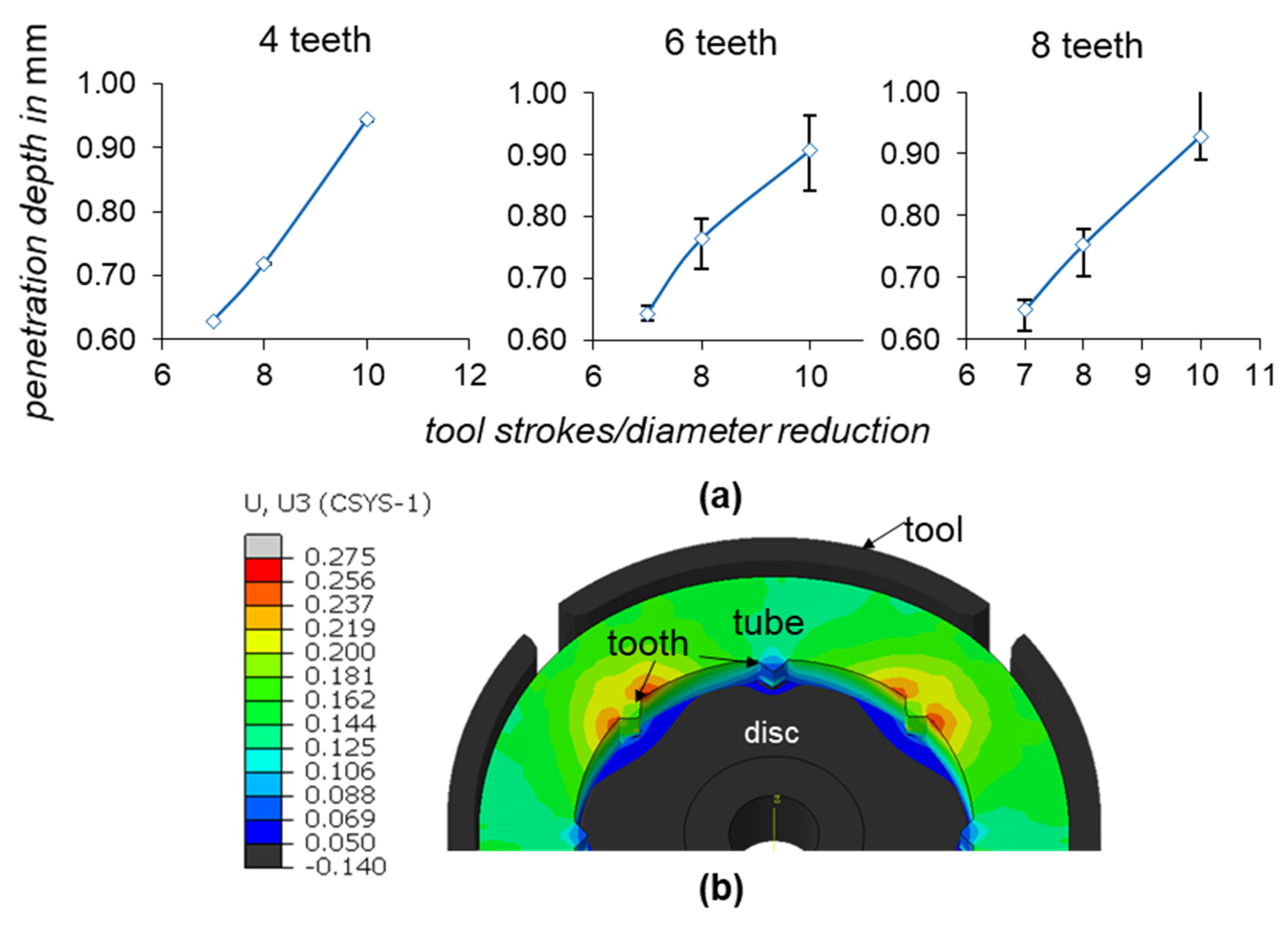
Increasing the number of teeth obviously increases the contact area between the teeth and the disc, which increases the required joining force and decreases the achievable penetration depth. To investigate the effect of the number of teeth on the formation of the joint, the number of teeth is varied between 4, 6 and 8 in the following tests. In this variant, the disc with the chamfered rim was used. The simulation results show no significant differences in the depth of the disc’s penetration; see
Figure 6a. On the other hand, the radial stress distribution is more dependent on the number of teeth, as can be seen in
Figure 6b. The difference in radial stress between four and eight teeth is approximately 40 MPa.
However, the results indicate that increasing the number of teeth seems to lead to asymmetrical disc penetration into the teeth, as well as an inhomogeneous distribution of radial stress onto the disc. The radial stress distribution appears to have four distinct amplitudes regardless of the number of teeth. To clarify this behavior, both the disc’s penetration and the development of radial stress during the rotary swaging process were analyzed. See
Figure 7.
The average penetration of all the teeth (blue curve) and the deviation in the tooth penetration (error bars) are shown in
Figure 7a for the three cases. It can be seen that in the case of four teeth, linear progression of the disc penetration occurs at almost the same level for all the teeth, and the deviation in the penetration depth is almost zero. In the case of 6 and 8 teeth, the penetration becomes less linear and shows significant deviation between the teeth. This deviation is even more distinct in the case of 6 teeth, and the progression of the penetration appears to be more non-linear.
The reason for this behavior was identified as radial force propagation from the tools into the tube during the rotary swaging process. Since only four oscillating tools strike the tube each time, some of the teeth are located outside the path of the acting radial force. At this point, the tube material starts to flow into the unloaded gap between the tools, causing the previously established radial stress to be released.
Figure 7b illustrates the material flow at three teeth in the case of eight teeth during a forming increment.
As can be seen in
Figure 7b, the axial material flow at the teeth in the area of the gaps between the tools is much higher than at the teeth in the tool engagement zone. This alternating reduction in the previously established radial stress through incremental tool striking and workpiece rotation explains why, regardless of the teeth variants, the resulting stress distribution shows the same pattern. This pattern is determined by the number of rotary swaging tools.
Although this typically has less effect on the roundness and surface finish of rotary swaging workpieces, it leads to a distortion in the radial stress created between the disc and the die. To mitigate this issue, the teeth should ideally be arranged so that they remain within the effective tool area during rotation.
5. Future Work
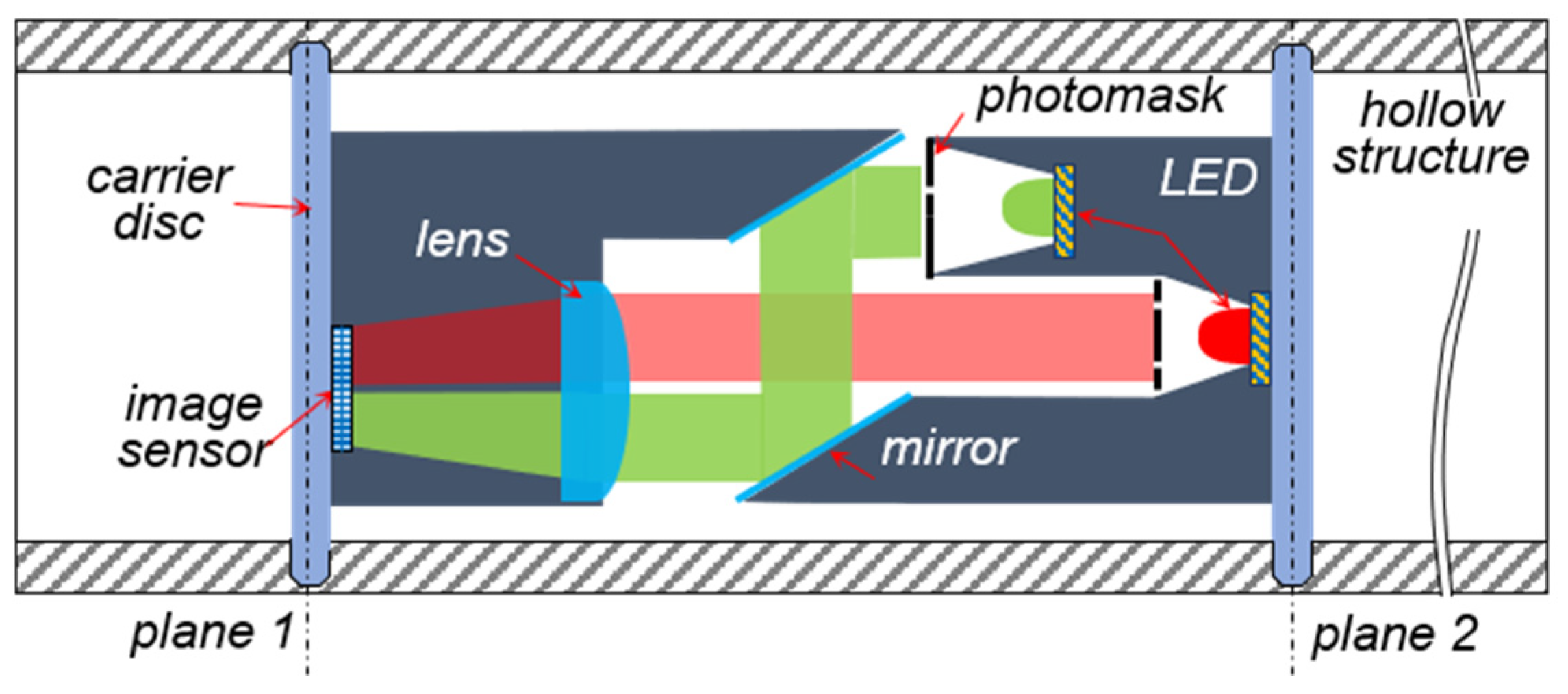
Ensuring the required parallel alignment of the built-in mirrors in the presented sensor design (
Figure 1) is the key challenge during integration into the tube. To address this challenge, it is imperative to prevent or control possible disc tilting during the rotary swaging process through the implementation of a closed-loop controller, as discussed in [
19]. In the case of closed-loop position control, a critical aspect is the ability to manipulate the disc’s position inside the tube during the joining process. Assuming this ability, numerical simulations were conducted to investigate the possibility of compensating for disc tilting and to examine the available time window for correcting the disc position during disc joining. In the numerical investigation, the disc is initially tilted by
and
. See
Figure 13a. For an initial tilt of 1°, the disc tilt is corrected at four different advance times in the process, which was driven by the previous investigations. See
Figure 13b.
Figure 13c shows the results for an initial tilt of 2° for two candidate process times.
As can be seen in
Figure 13, the simulation results demonstrate that the earlier the misalignment is corrected and the smaller the error is, the smaller the remaining angle error. The stiffness ratios between the two joining partners ensure a form-fit connection despite the subsequent change in position for tilt correction.
6. Conclusions
This study presents a novel approach to integrating non-contact optical sensors into metallic structures using metal forming technology. Within the paper, we investigated the possibility of integrating highly sensitive optical sensors with the required high positional accuracy using rotary swaging. The investigations have demonstrated the possibilities offered by appropriate design of the joining parameters and the joining process. Additionally, the studies have shown that the number of tools and the contact area during rotary swaging directly affect the distribution of radial stresses in the integrated disc. When a tooth is located in the gap between the tools during a forming increment, the material flow at that point results in a partial reduction in the previously created radial stress. As the tube rotates and the gap between the teeth changes, non-linear radial stress is created, which increases with the depth of penetration. The integration of the two discs at a specific distance from each other resulted in a deviation of only 0.6% from the desired distance, but the total tilt of the discs was 0.8°. Permitting higher tilting of the carrying the discs required simplification of the design of the optical sensor to ensure its functionality. Full functionality with no hysteresis is provided by the integrated sensor for bending force and torque measurement. To achieve higher positional accuracy during the disc joining process, position-controlled disc joining can be applied to improve the achievable positional accuracy. The numerical results show the potential to correct possible angle tilt errors during the joining process. Future work will implement and experiment with this control approach. In addition, the increased stiffness of the teeth during their pre-forming needs to be reduced, for example, by applying hot rotary swaging during the pre-toothing process.