Minimizing Dimensional Defects in FFF Using a Novel Adaptive Slicing Method Based on Local Shape Complexity
Abstract
1. Introduction
2. Related Works
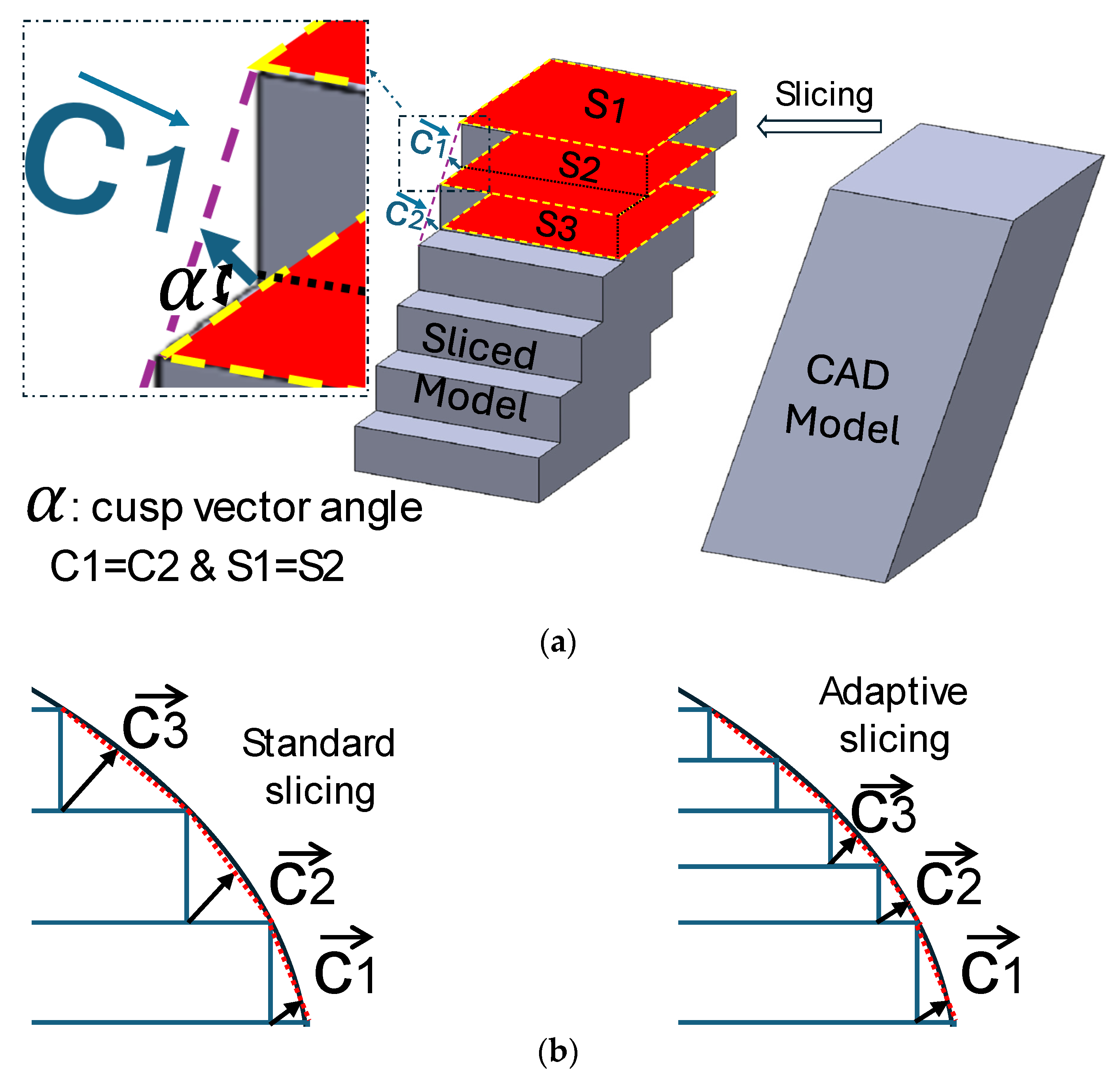
3. FFF Layering Errors
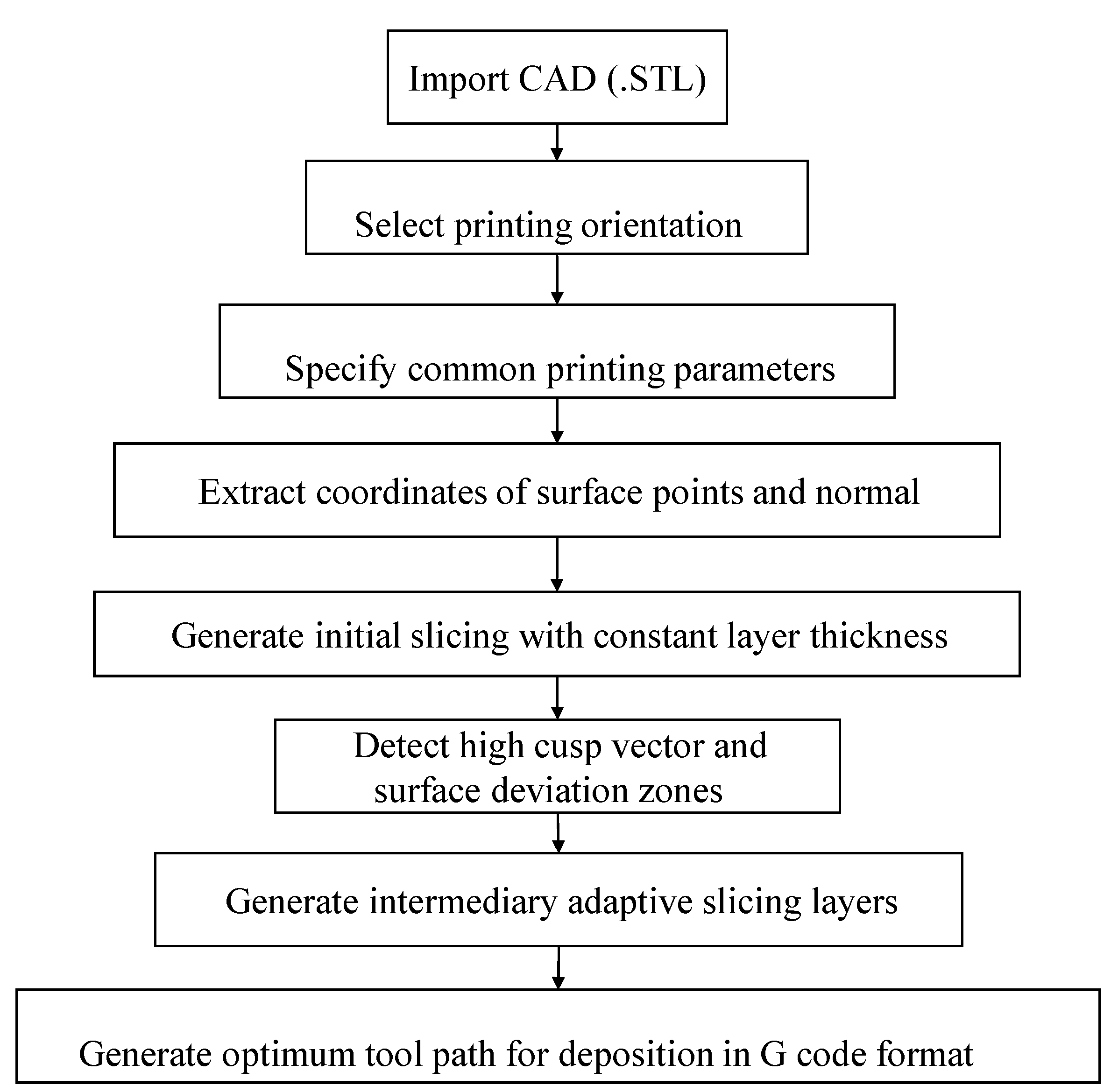
4. Proposed Method
4.1. File Preparation
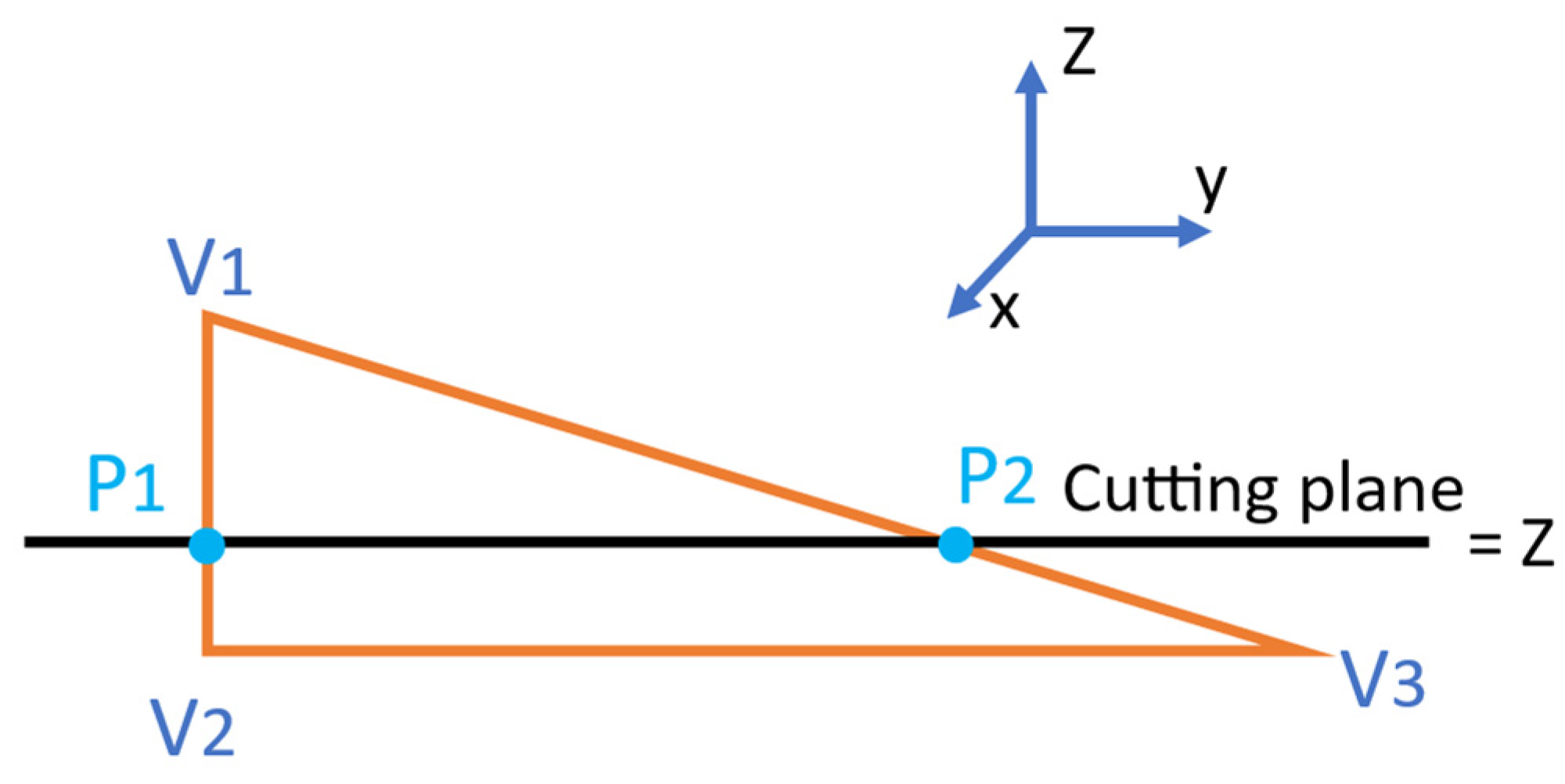
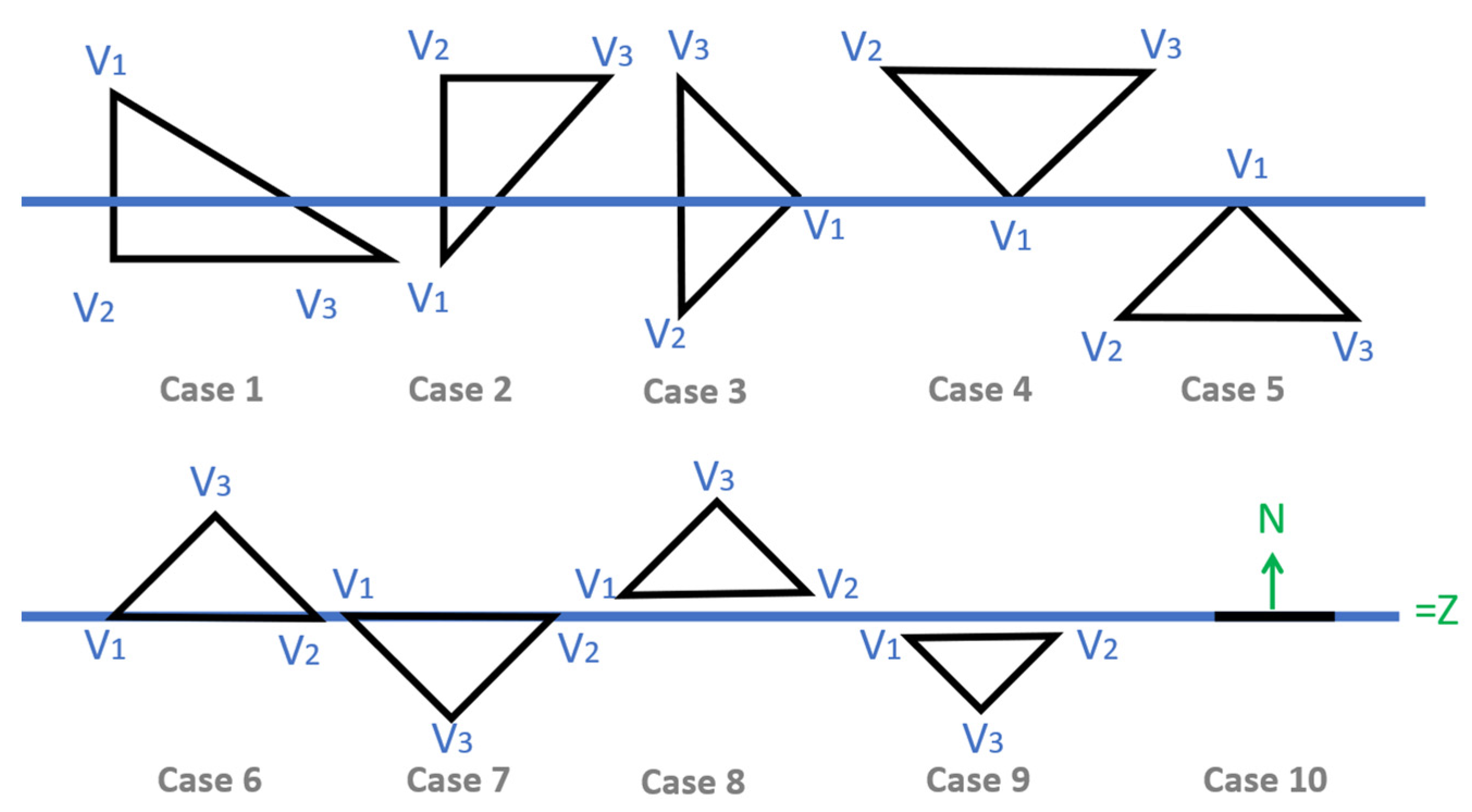
4.2. Extraction of Points Resulting from Facet Intersection
4.3. Polygon Creation
4.4. Layer Thickness Determination
4.5. Generation of the Raster Pattern
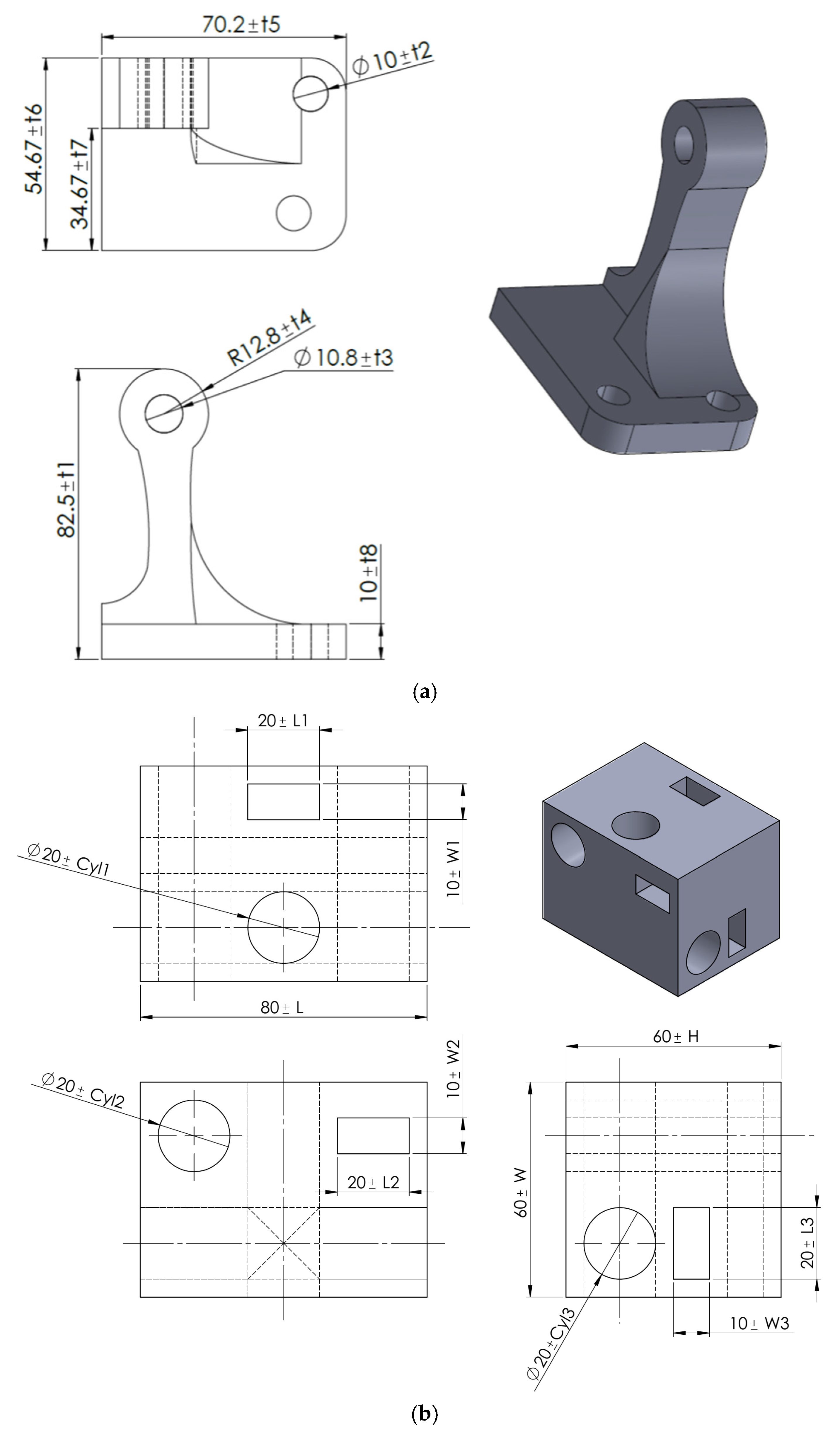
5. Case Study
5.1. Design and Manufacturing Results
5.2. Measurement Results
6. Discussion
- The improvement in the algorithm efficiency in terms of printing time could be achieved by carefully selecting the range of layer thickness. The outcomes of the study could inform this selection by employing a multi-optimization algorithm to achieve a balanced solution between required the dimensional accuracy and printing time.
- The algorithm serves as a guideline for considering dimensional tolerances during the slicing process, presenting a new challenge for parts including features with different tolerance values in the part drawing. The proposed algorithm smoothly accommodates the allocation of specific values of the cusp height and surface deviation threshold to layers containing features according to their assigned tolerance values.
- In addition to layer thickness, several FFF parameters, such as build orientation, printing speed, nozzle temperature, and pressure conditions, significantly influence part dimensional accuracy. Moreover, achieving enhanced dimensional accuracy must also align with the desired mechanical properties and surface quality of the printed functional parts. Therefore, further investigations employing multi-objective optimization approaches are necessary to address these interconnected requirements simultaneously.
- Zones with lower material density are observed when having many low-thickness layers gathered in the adaptive slicing part. This phenomenon may lead to diminished mechanical properties due to inadequate material adhesion. Algorithm inputs such as cusp height, surface deviation, and layer thickness thresholds should be determined through a multi-optimization approach that considers dimensional accuracy, mechanical properties, and build orientation. The development of a multi-criteria decision model (MCDM) that articulates product requirements concerning manufacturing cost, part accuracy, quality, and mechanical properties will enhance the durability of the product.
7. Conclusions
- The result analysis demonstrates the promising capability of the slicing approach to improve the dimensional accuracy of FFF parts. Compared to standard slicing, the proposed method led to enhancements in dimensional accuracy, with average gains of 0.1% and 0.3% observed using RE and CMM processes, respectively. Similarly, in the second case study, average gains of 0.58% and 0.76% were achieved using RE and CMM processes.
- The method effectively reduces the stair-stepping effect on curved shapes and minimizes heat shrinkage along the printing direction. It is particularly effective in improving the dimensional accuracy of features with highly curved shapes compared to linear contours.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Klahn, C.; Leutenecker, B.; Meboldt, M. Design for Additive Manufacturing—Supporting the Substitution of Components in Series Products. Procedia CIRP 2014, 21, 138–143. [Google Scholar] [CrossRef]
- Emmelmann, C.; Kranz, J.; Herzog, D.; Wycisk, E. Laser Technology in Biomimetics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Shi, S.; Jiang, Y.; Ren, H.; Deng, S.; Sun, J.; Cheng, F.; Jing, J.; Chen, Y. 3D-Printed Carbon-Based Conformal Electromagnetic Interference Shielding Module for Integrated Electronics. Nano-Micro Lett. 2024, 16, 85. [Google Scholar] [CrossRef] [PubMed]
- Colorado, H.A.; Velásquez, E.I.G.; Monteiro, S.N. Sustainability of Additive Manufacturing: The Circular Economy of Materials and Environmental Perspectives. J. Mater. Res. Technol. 2020, 9, 8221–8234. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive Manufacturing (3D Printing): A Review of Materials, Methods, Applications and Challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Dey, A.; Yodo, N. A Systematic Survey of FDM Process Parameter Optimization and Their Influence on Part Characteristics. J. Manuf. Mater. Process. 2019, 3, 64. [Google Scholar] [CrossRef]
- Solomon, I.J.; Sevvel, P.; Gunasekaran, J. A Review on the Various Processing Parameters in FDM. Mater. Today Proc. 2020, 37, 509–514. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Chen, T.; Lin, Y.-C. 3D Printer Selection for Aircraft Component Manufacturing Using a Nonlinear FGM and Dependency-Considered Fuzzy VIKOR Approach. Aerospace 2023, 10, 591. [Google Scholar] [CrossRef]
- Sharma, A.; Rai, A. Fused Deposition Modelling (FDM) Based 3D & 4D Printing: A State of Art Review. Mater. Today Proc. 2022, 62, 367–372. [Google Scholar] [CrossRef]
- Tlija, M.; Al-Tamimi, A.A. Combined Manufacturing and Cost Complexity Scores-Based Process Selection for Hybrid Manufacturing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 237, 1473–1484. [Google Scholar] [CrossRef]
- Angrish, A. A Critical Analysis of Additive Manufacturing Technologies for Aerospace Applications. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA; 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Sun, B.; Ma, Q.; Wang, X.; Liu, J.; Rejab, M.R.M. Additive Manufacturing in Medical Applications: A Brief Review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1078, 012007. [Google Scholar] [CrossRef]
- Carvalho, J.R.G.; Conde, G.; Antonioli, M.L.; Santana, C.H.; Littiere, T.O.; Dias, P.P.; Chinelatto, M.A.; Canola, P.A.; Zara, F.J.; Ferraz, G.C. Long-Term Evaluation of Poly(Lactic Acid) (PLA) Implants in a Horse: An Experimental Pilot Study. Molecules 2021, 26, 7224. [Google Scholar] [CrossRef]
- Alrasheedi, N.H.; Tlija, M.; Elloumi, N.; Louhichi, B. A Critical Review of 3D Printed Orthoses towards Workflow Implementation in the Clinical Practice. J. Eng. Res. 2024, in press. [Google Scholar] [CrossRef]
- Schuh, G.; Bergweiler, G.; Fiedler, F.; Bickendorf, P.; Schumacher, P. Small Series Production and Geometric Analysis of Sheet Metal Car Body Parts Using Forming Tools Made of Fused Filament Fabricated PLA. In Proceedings of the 2020 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 14–17 December 2020; Volume 2020, pp. 156–160. [Google Scholar]
- Berni, A.; Borgianni, Y.; Obi, M.; Pradel, P.; Bibb, R. Investigating Perceived Meanings and Scopes of Design for Additive Manufacturing. Proc. Des. Soc. 2021, 1, 1937–1946. [Google Scholar] [CrossRef]
- Quan, Z.; Wu, A.; Keefe, M.; Qin, X.; Yu, J.; Suhr, J.; Byun, J.H.; Kim, B.S.; Chou, T.W. Additive Manufacturing of Multi-Directional Preforms for Composites: Opportunities and Challenges. Mater. Today 2015, 18, 503–512. [Google Scholar] [CrossRef]
- Tolosa, I.; Garciandía, F.; Zubiri, F.; Zapirain, F.; Esnaola, A. Study of Mechanical Properties of AISI 316 Stainless Steel Processed by “Selective Laser Melting”, Following Different Manufacturing Strategies. Int. J. Adv. Manuf. Technol. 2010, 51, 639–647. [Google Scholar] [CrossRef]
- Caulfield, B.; McHugh, P.E.; Lohfeld, S. Dependence of Mechanical Properties of Polyamide Components on Build Parameters in the SLS Process. J. Mater. Process. Technol. 2007, 182, 477–488. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J.P. Residual Stresses in Selective Laser Sintering and Selective Laser Melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Lieneke, T.; Denzer, V.; Adam, G.A.O.; Zimmer, D. Dimensional Tolerances for Additive Manufacturing: Experimental Investigation for Fused Deposition Modeling. Procedia CIRP 2016, 43, 286–291. [Google Scholar] [CrossRef]
- Zhu, Z.; Anwer, N.; Huang, Q.; Mathieu, L. Machine Learning in Tolerancing for Additive Manufacturing. CIRP Ann. 2018, 67, 157–160. [Google Scholar] [CrossRef]
- Calignano, F.; Manfredi, D.; Ambrosio, E.P.; Biamino, S.; Pavese, M.; Fino, P. Direct Fabrication of Joints Based on Direct Metal Laser Sintering in Aluminum and Titanium Alloys. Procedia CIRP 2014, 21, 129–132. [Google Scholar] [CrossRef]
- Liu, H.; Liu, L.; Li, D.; Huang, R.; Dai, N. An Approach to Partition Workpiece CAD Model towards 5-Axis Support-Free 3D Printing. Int. J. Adv. Manuf. Technol. 2020, 106, 683–699. [Google Scholar] [CrossRef]
- Goguelin, S.; Dhokia, V.; Flynn, J.M. Bayesian Optimisation of Part Orientation in Additive Manufacturing. Int. J. Comput. Integr. Manuf. 2021, 34, 1263–1284. [Google Scholar] [CrossRef]
- Angelo, L.D.; Stefano, P.D.; Guardiani, E. Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review. J. Manuf. Mater. Process. 2020, 4, 71. [Google Scholar] [CrossRef]
- Spišák, E.; Nováková-Marcinčínová, E.; Majerníková, J.; Mulidrán, P.; Nováková-Marcinčínová, Ľ. Experimental and Numerical Study of Printing Strategy Impact on the Mechanical Properties of Sustainable PLA Materials. Polymers 2023, 15, 4639. [Google Scholar] [CrossRef]
- Ritter, T.; McNiffe, E.; Higgins, T.; Sam-Daliri, O.; Flanagan, T.; Walls, M.; Ghabezi, P.; Finnegan, W.; Mitchell, S.; Harrison, N.M. Design and Modification of a Material Extrusion 3D Printer to Manufacture Functional Gradient PEEK Components. Polymers 2023, 15, 3825. [Google Scholar] [CrossRef]
- O’Connor, H.J.; Dowling, D.P. Evaluation of the Influence of Low Pressure Additive Manufacturing Processing Conditions on Printed Polymer Parts. Addit. Manuf. 2018, 21, 404–412. [Google Scholar] [CrossRef]
- Boschetto, A.; Bottini, L. Accuracy Prediction in Fused Deposition Modeling. Int. J. Adv. Manuf. Technol. 2014, 73, 913–928. [Google Scholar] [CrossRef]
- Byun, H.S.; Lee, K.H. Determination of Optimal Build Direction in Rapid Prototyping with Variable Slicing. Int. J. Adv. Manuf. Technol. 2006, 28, 307–313. [Google Scholar] [CrossRef]
- Al-Tamimi, A.A.; Tlija, M.; Abidi, M.H.; Anis, A.; Abd Elgawad, A.E.E. Material Extrusion of Multi-Polymer Structures Utilizing Design and Shrinkage Behaviors: A Design of Experiment Study. Polymers 2023, 15, 2683. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Laperrière, L. Adaptive Direct Slicing of the Solid Model for Rapid Prototyping. Int. J. Prod. Res. 2000, 38, 69–83. [Google Scholar] [CrossRef]
- Di Angelo, L.; Di Stefano, P.; Marzola, A. Surface Quality Prediction in FDM Additive Manufacturing. Int. J. Adv. Manuf. Technol. 2017, 93, 3655–3662. [Google Scholar] [CrossRef]
- Angelo, L.D.; Di Stefano, P.; Dolatnezhadsomarin, A.; Guardiani, E.; Khorram, E.; Stefano, P.D. A Reliable Build Orientation Optimization Method in Additive Manufacturing: The Application to FDM Technology. Int. J. Adv. Manuf. Technol. 2020, 108, 263–276. [Google Scholar] [CrossRef]
- Shao, M.; Wei, C.; Cui, B.; Li, Y.; Zheng, T. An Adaptive Slicing Approach for Processing STL Massive Data Model in Batches Based on Layer Merging. J. Phys. Conf. Ser. 2021, 1884, 012025. [Google Scholar] [CrossRef]
- Elayeb, A.; Korbi, A.; Tlija, M.; Louhichi, B. Optimal Part Orientation in the Additive Manufacturing Process Based on Tolerancing. In Advances in Mechanical Engineering and Mechanics II; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2022; pp. 217–225. [Google Scholar]
- Tagore, G.R.N.; Anjikar, S.D.; Venu Gopal, A. Multi Objective Optimisation of Build Orientation for Rapid Prototyping with Fused Deposition Modeling (FDM). In Proceedings of the 18th Solid Freeform Fabrication Symposium, Austin, TX, USA, 6–8 August 2007; pp. 246–255. [Google Scholar]
- Kulkarni, P.; Dutta, D. An Accurate Slicing Procedure for Layered Manufacturing. Comput. Des. 1996, 28, 683–697. [Google Scholar] [CrossRef]
- Ben Amor, S.; Zongo, F.; Eltaief, A.; Maatki, A.; Louhichi, B.; Tahan, A. A New Method to Select Optimal Part Building Orientation for Additive Manufacturing Processes Based on Geometric Complexity and Heat Shrinkage. Prog. Addit. Manuf. 2023, 8, 211–222. [Google Scholar] [CrossRef]
- Hyndhavi, D.; Babu, G.R.; Murthy, S.B. Investigation of Dimensional Accuracy and Material Performance in Fused Deposition Modeling. Mater. Today Proc. 2018, 5, 23508–23517. [Google Scholar] [CrossRef]
- Hanon, M.M.; Zsidai, L.; Ma, Q. Accuracy Investigation of 3D Printed PLA with Various Process Parameters and Different Colors. Mater. Today Proc. 2021, 42, 3089–3096. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L.; Nikzad, M.; Azadmanjiri, J. Effect of Process Parameters on Dynamic Mechanical Performance of FDM PC/ABS Printed Parts Through Design of Experiment. J. Mater. Eng. Perform. 2016, 25, 2922–2935. [Google Scholar] [CrossRef]
- Xinhua, L.; Shengpeng, L.; Zhou, L.; Xianhua, Z.; Xiaohu, C.; Zhongbin, W. An Investigation on Distortion of PLA Thin-Plate Part in the FDM Process. Int. J. Adv. Manuf. Technol. 2015, 79, 1117–1126. [Google Scholar] [CrossRef]







| Authors | Responses | Methods/Tools |
|---|---|---|
| O’Connor et al. [29] | Mechanical proprieties, thermal behavior, and surface roughness | Experimental comparisons of printing performances under low and atmospheric pressure conditions. |
| Boschetto et al. [30] | Dimensional deviations | Mathematical modeling of dimensional accuracy prediction for filament deposition, considering deposition angle and layer thickness dependencies. Validation-based experimental tests. |
| Byun et al. [31] | Surface roughness (Ra), printing time, and part cost | Muti-attribute decision-making method-based optimization of printing orientation with variable slicing thickness. Mathematic modeling of Ra as a function of layer thickness. |
| Zhao et al. [33] | Reduce the number of layers while conserving staircase tolerance | Cusp height-based adaptative slicing. |
| Di Angelo et al. [34] | Surface roughness (Pa) | A geometrical modeling-based Pa prediction considering deposing filament shape and a constant layer thickness. |
| Di Angelo et al. [35] | Build cost and surface roughness (Pa) | Prediction of build time, surface quality (Pa), and support volume as functions of the build orientation. SMS-EMOA and Pareto front for build orientation selection. |
| Lieneke et al. [21] | Dimensional deviations | Experimentally exploring the relationship between dimensional tolerances and nominal dimension values. |
| Al-Tamimi et al. [32] | Mechanical properties, surface roughness, and dimensional deviations | Experimental investigationsbased Taguchi method and signal-to-noise ratio. |
| Shao et al. [36] | Printing time and surface profile errors | A layer merging-adaptive slicing method. |
| Case | Positional Relationships | Interpretation |
|---|---|---|
| 1, 2, 3 | such as |
|
| 4, 5 | or | F contacts Sp at a single point, which is useless information for the code. |
| 6, 7 | F contacts Sp with its two vertices P1 and P2. | |
| 8, 9 |
| |
| 10 |
|
| Parts | Standard Slicing (s) | Adaptative Slicing (s) | Time Loss (%) |
|---|---|---|---|
| A | 21.3203 | 21.7954 | 2.2 |
| B | 47.4834 | 47.4834 | 2.0 |
| Printing Parameters | Values |
|---|---|
| Filament diameter | 1.75 mm |
| Infill density | 10% |
| Raster angle | 0°/90° |
| Shell thickness | 1mm |
| Nozzle diameter | 0.4 mm |
| Fusion temperature | 200 °C |
| Bed temperature | 60 °C |
| Printing speed | 60 mm/s |
| Parts | Parameters | Standard Slicing | Adaptative Slicing |
|---|---|---|---|
| Design A | Layer height | 0.2 mm | 0.2–0.05 mm |
| Number of layers | 414 layers | 439 layers | |
| Printing time | 2 h 22 min 20 s | 2 h 29 min 53 s | |
| Filament weight used | 22.11 g | 18.54 g | |
| Design B | Layer height | 0.2 mm | 0.2–0.05 mm |
| Number of layers | 151 layers | 282 layers | |
| Printing time | 3 h 20 min | 5 h 54 min | |
| Filament weight used | 78.9 g | 81.2 g |
| Tolerances | RE | CMM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Errors of PartA1 | Errors of PartA2 | Gain | Errors of PartA1 | Errors of PartA2 | Gain | |||||
| mm | % | mm | % | % | mm | % | mm | % | % | |
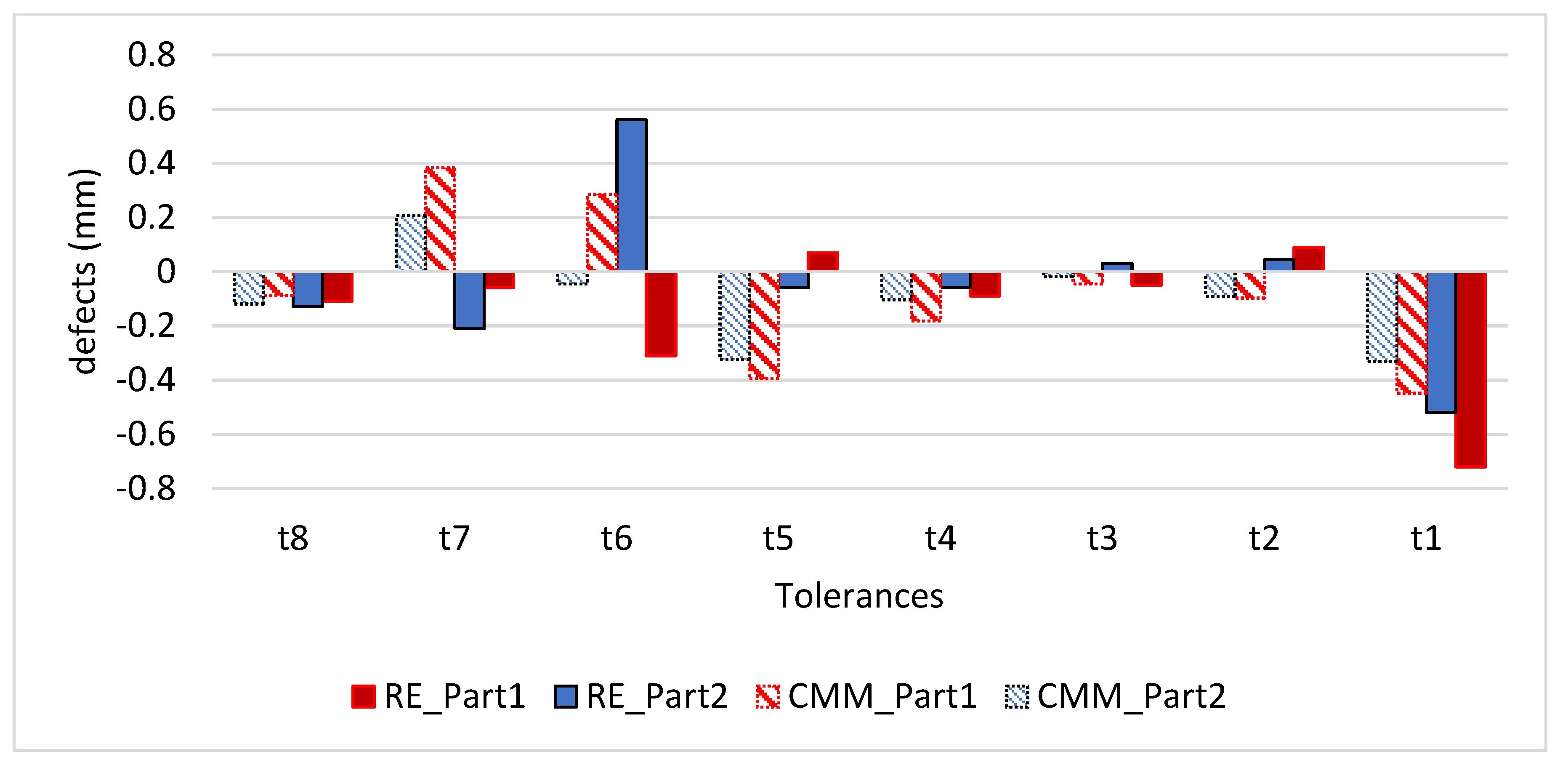
| t1 | −0.72 | 0.87% | −0.52 | 0.63% | 0.24% | −0.448 | 0.54% | −0.331 | 0.40% | 0.14% |
| t2 | 0.09 | 1.80% | 0.045 | 0.90% | 0.90% | −0.097 | 1.94% | −0.091 | 1.82% | 0.12% |
| t3 | −0.05 | 0.93% | 0.03 | 0.56% | 0.37% | −0.045 | 0.83% | −0.019 | 0.35% | 0.48% |
| t4 | −0.09 | 0.71% | −0.06 | 0.47% | 0.24% | −0.182 | 1.43% | −0.103 | 0.81% | 0.62% |
| t5 | 0.07 | 0.10% | −0.06 | 0.09% | 0.01% | −0.395 | 0.56% | −0.323 | 0.46% | 0.10% |
| t6 | −0.31 | 0.57% | 0.56 | 1.02% | −0.45% | 0.285 | 0.52% | −0.045 | 0.08% | 0.44% |
| t7 | −0.06 | 0.17% | −0.21 | 0.61% | −0.44% | 0.383 | 1.10% | 0.206 | 0.59% | 0.51% |
| t8 | −0.11 | 1.09% | −0.129 | 1.29% | −0.20% | −0.088 | 0.88% | −0.12 | 1.19% | −0.31% |
| Tolerances | RE | CMM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Errors of PartB1 | Errors of PartB2 | Gain | Errors of PartB1 | Errors of PartB2 | Gain | |||||
| mm | % | mm | % | % | mm | % | mm | % | % | |
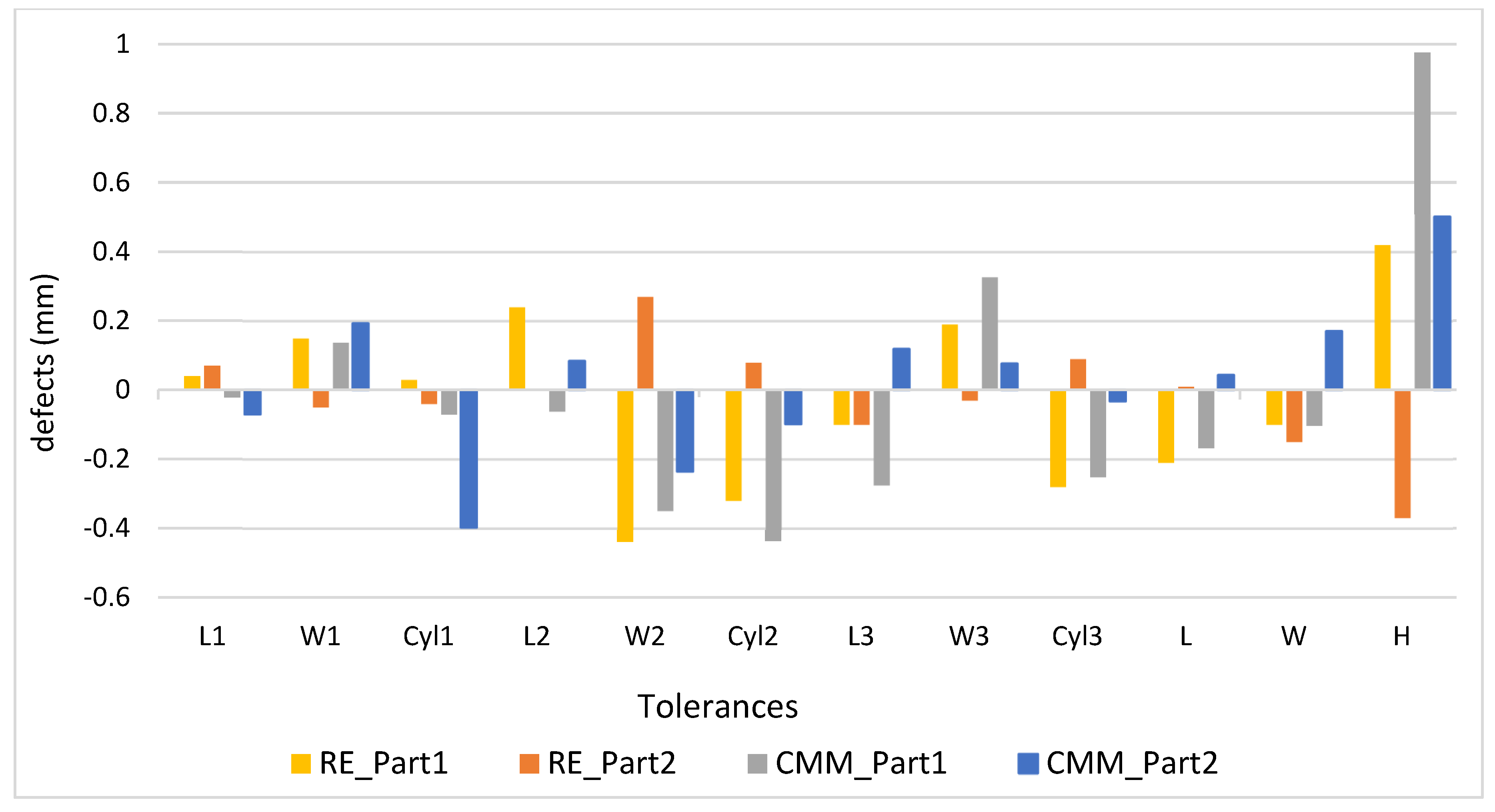
| L1 | 0.04 | 0.43% | 0.07 | 0.02% | 0.17% | −0.022 | 0.11% | −0.07 | 0.35% | −0.24% |
| W1 | 0.15 | 0.61% | −0.05 | 1.45% | 0.02% | 0.1375 | 1.37% | 0.19 | 1.93% | −0.55% |
| Cyl1 | 0.03 | 0.27% | −0.04 | 2.21% | −2.05% | −0.071 | 0.36% | −0.40 | 1.99% | −1.64% |
| L2 | 0.24 | 1.32% | 0 | 0.40% | 0.79% | −0.062 | 0.31% | 0.08 | 0.42% | −0.11% |
| W2 | −0.44 | 5.48% | 0.27 | 0.37% | 4.03% | −0.3495 | 3.49% | −0.24 | 2.36% | 1.13% |
| Cyl2 | −0.32 | 2.26% | 0.08 | 0.09% | 1.51% | −0.437 | 2.19% | −0.10 | 0.50% | 1.69% |
| L3 | −0.1 | 0.79% | −0.1 | 0.08% | 0.42% | −0.2755 | 1.38% | 0.12 | 0.59% | 0.79% |
| W3 | 0.19 | 2.32% | −0.03 | 0.48% | 1.42% | 0.327 | 3.27% | 0.08 | 0.76% | 2.51% |
| Cyl3 | −0.28 | 0.59% | 0.09 | 0.30% | 1.08% | −0.252 | 1.26% | −0.03 | 0.17% | 1.09% |
| L | −0.21 | 0.26% | 0.01 | 0.06% | 0.20% | −0.168 | 0.21% | 0.043 | 0.05% | 0.16% |
| W | −0.1 | 0.17% | −0.15 | 0.03% | 0.13% | −0.103 | 0.17% | 0.17 | 0.28% | −0.11% |
| H | 0.42 | 0.70% | −0.37 | 0.21% | 0.49% | 0.975 | 1.63% | 0.501 | 0.83% | 0.79% |
| Items | A1 | A2 | B1 | B2 |
|---|---|---|---|---|
| Equipment purchase cost (USD) | 6795 | 6804 | ||
| Cmh (USD) | 0.920 | 0.921 | ||
| Cr (USD) | 1.726 | 1.448 | 6.161 | 6.340 |
| Cm (USD) | 2.182 | 2.297 | 3.069 | 5.433 |
| Cp (USD) | 3.908 | 3.745 | 9.230 | 11.773 |
| Ct (USD) | 9.593 | 4.107 | 9.593 | 12.136 |
| PLA filament cost per Kg (USD) | 78.08 | |||
| T (h) | 2400 | |||
| Labor cost per hour (USD) | 0.363 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elayeb, A.; Tlija, M.; Eltaief, A.; Louhichi, B.; Zemzemi, F. Minimizing Dimensional Defects in FFF Using a Novel Adaptive Slicing Method Based on Local Shape Complexity. J. Manuf. Mater. Process. 2024, 8, 59. https://doi.org/10.3390/jmmp8020059
Elayeb A, Tlija M, Eltaief A, Louhichi B, Zemzemi F. Minimizing Dimensional Defects in FFF Using a Novel Adaptive Slicing Method Based on Local Shape Complexity. Journal of Manufacturing and Materials Processing. 2024; 8(2):59. https://doi.org/10.3390/jmmp8020059
Chicago/Turabian StyleElayeb, Ahmed, Mehdi Tlija, Ameni Eltaief, Borhen Louhichi, and Farhat Zemzemi. 2024. "Minimizing Dimensional Defects in FFF Using a Novel Adaptive Slicing Method Based on Local Shape Complexity" Journal of Manufacturing and Materials Processing 8, no. 2: 59. https://doi.org/10.3390/jmmp8020059
APA StyleElayeb, A., Tlija, M., Eltaief, A., Louhichi, B., & Zemzemi, F. (2024). Minimizing Dimensional Defects in FFF Using a Novel Adaptive Slicing Method Based on Local Shape Complexity. Journal of Manufacturing and Materials Processing, 8(2), 59. https://doi.org/10.3390/jmmp8020059







