Predicting the Dynamic Parameters for Milling Thin-Walled Blades with a Neural Network
Abstract
1. Introduction
2. Modeling of Thin-Walled Blade Dynamics Based on the Removal Process
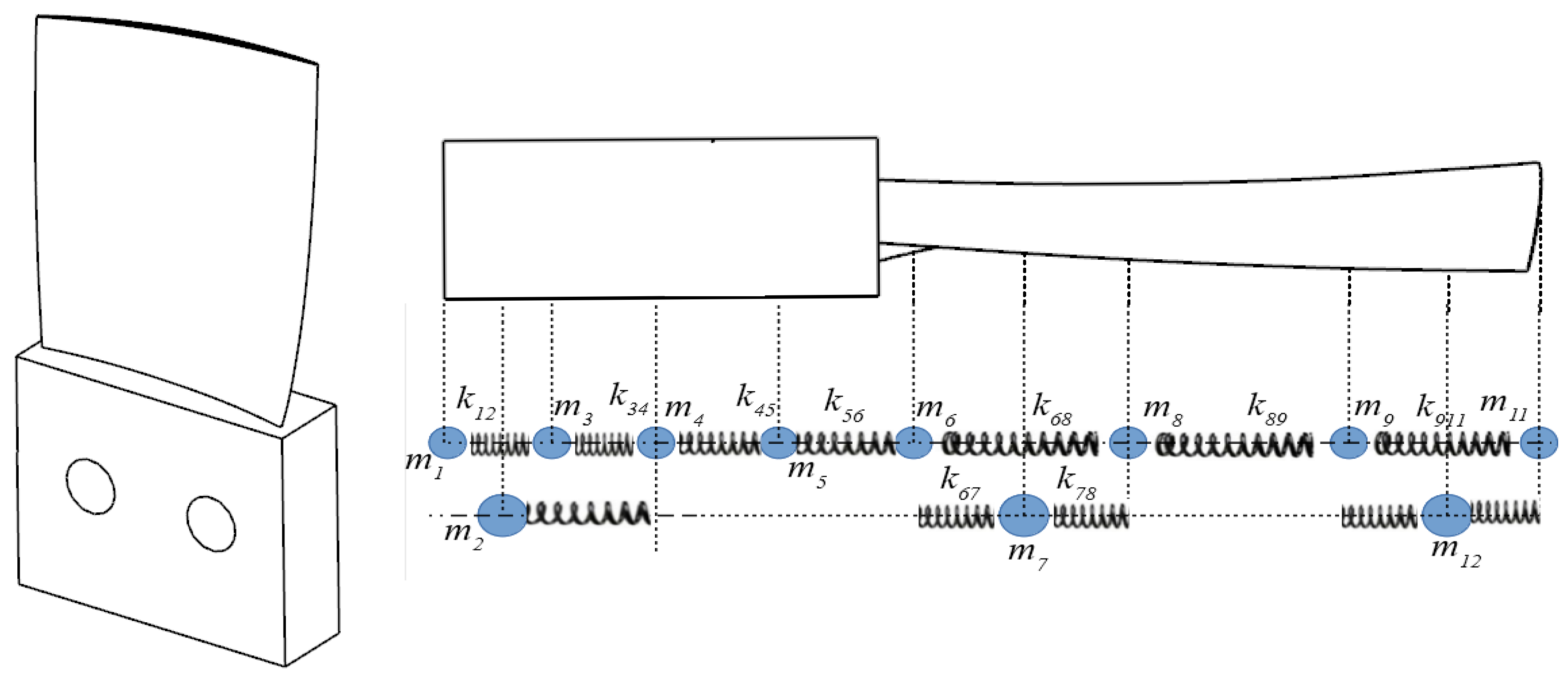
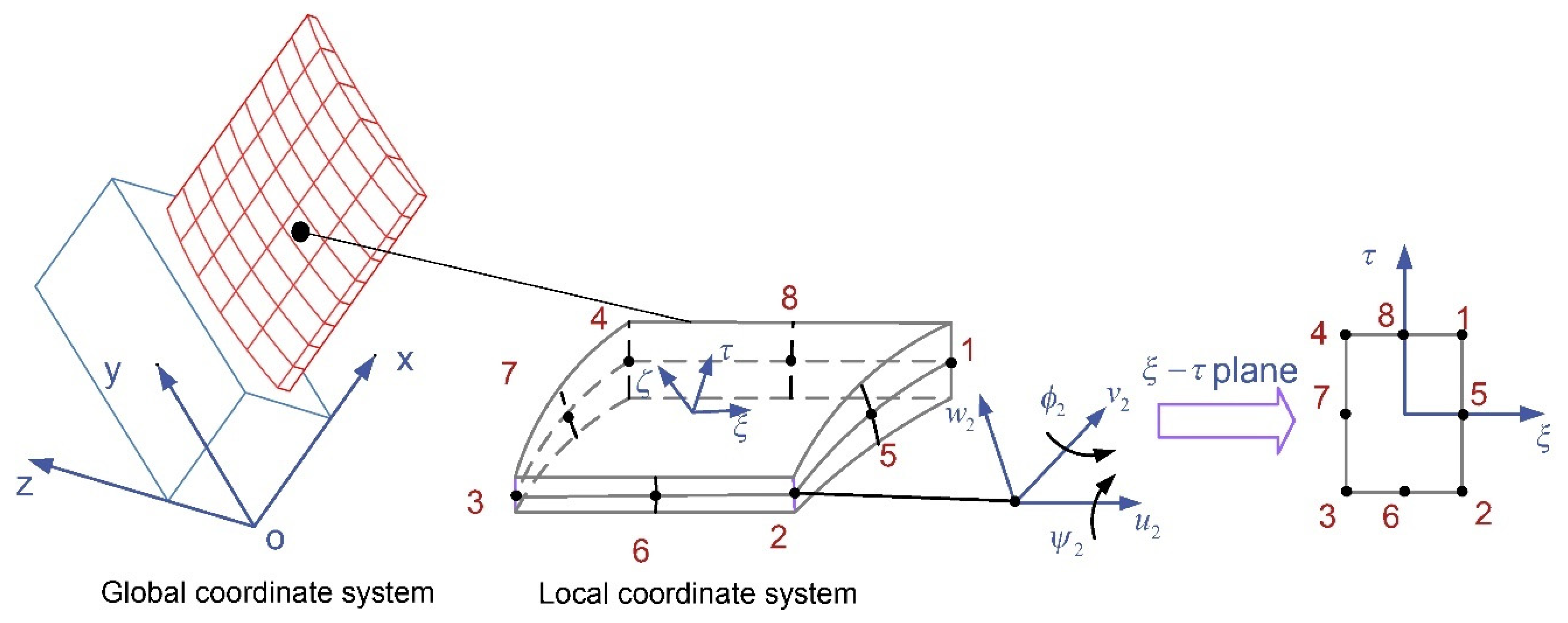
2.1. Dynamic Model of the Thin-Walled Blade Structure
2.2. Milling Process Grid Cell Definitions
2.3. Solving for the Kinetic Parameters
- (1)
- Establish a three-dimensional model of the thin-walled blade in NX;
- (2)
- Insert the point sets in the U and V directions of the basin and the back of the thin-walled blade, and set the number of points in the U direction to 11 and the number of points in the V direction to 19;
- (3)
- Compile the UG secondary development plug-in in C++, and export the point sets on the same cross-section to the same file through the function UC4524;
- (4)
- Take the exported point set from step (3) through the curve fitting to generate the two curves above and below the blade’s cross-section;
- (5)
- Calculate the coordinates of the discrete points on the mid-arc and the thickness of the blade through the mid-arc solution algorithm, and generate the mid-arc curves through the curve fitting;
- (6)
- Generate the mid-arc face through the mid-arc curve fitting;
- (7)
- Use C++ to compile the UG secondary development plug-ins, obtain the coordinates of the discrete points of the mid-arc surface through the UG/Open function UF_MODL_ask_face_parm, and obtain the normal vector of the mid-arc surface through the function UF_MODL_ask_face_props.
- (1)
- Use the same number of units to discretize the uncut workpiece and the machined workpiece, and use the method shown in Figure 3 to calculate the coordinates of the nodes on the arc surface of the discrete unit, the thickness of the blade corresponding to the nodes, and the normal vector of the mid-arc surface, and store them in the file.
- (2)
- Adopt the discrete method in step (1) to discretize the workpiece in the cutting process into the machined units and uncut units, and then number them.
- (3)
- According to the discrete unit number of the workpiece in the cutting process in step (2), read the corresponding geometric parameters in step (1), establish a finite element model of the workpiece in the cutting process based on the shell unit, and calculate the stiffness matrix and mass matrix of the workpiece.
- (4)
- Using the calculated stiffness matrix and mass matrix of the workpiece, the nature frequency and mode shapes of the workpiece in the cutting process are calculated by solving the characteristic equations.
3. Neural Network-Based Prediction of Kinetic Parameters
- (1)
- Take the thickness of the unit node as the input quantity and the first three orders of the workpiece’s nature frequency as the output variable, and define the forward computation model with a fixed frequency, as shown in Equations (23)–(25).
- (2)
- Using the mean square deviation between the predicted values and nominal values of the workpiece’s nature frequency as the loss function, the prediction of the milling dynamic parameters of thin-walled parts is transformed into an optimization problem, as shown in Equation (27).
- (3)
- Iterative solution parameters, i.e., the neural network weight matrix and offset vectors , are used through the most rapid descent method to calculate the nature frequency of the thin-walled parts.
4. Prediction and Validation of Milling Dynamic Parameters for Thin-Walled Parts
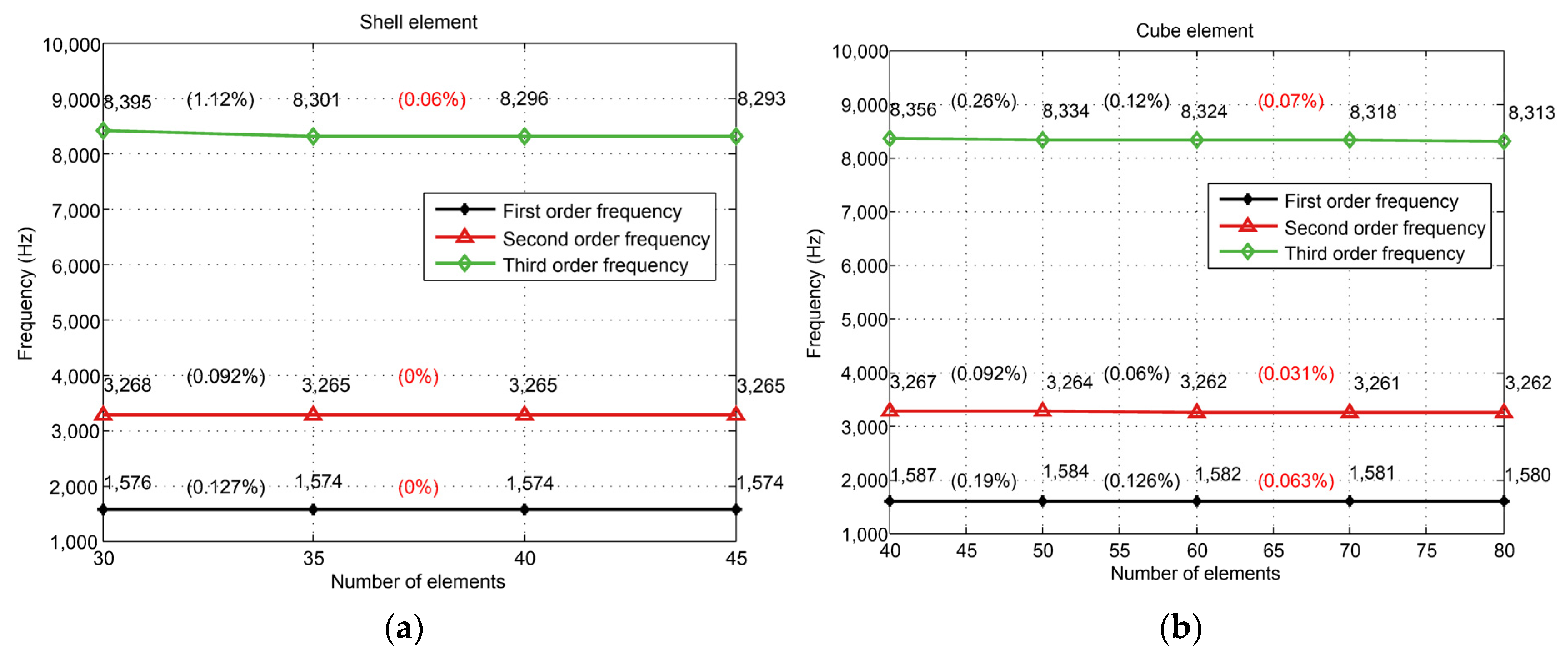
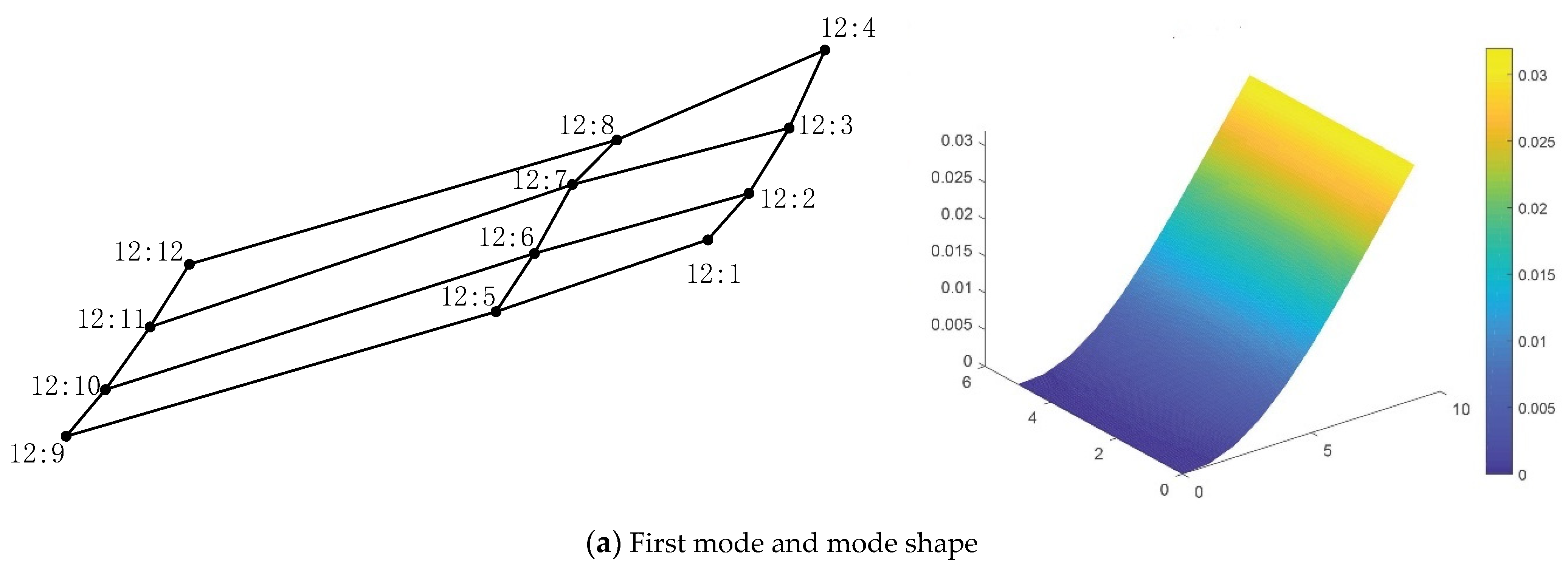
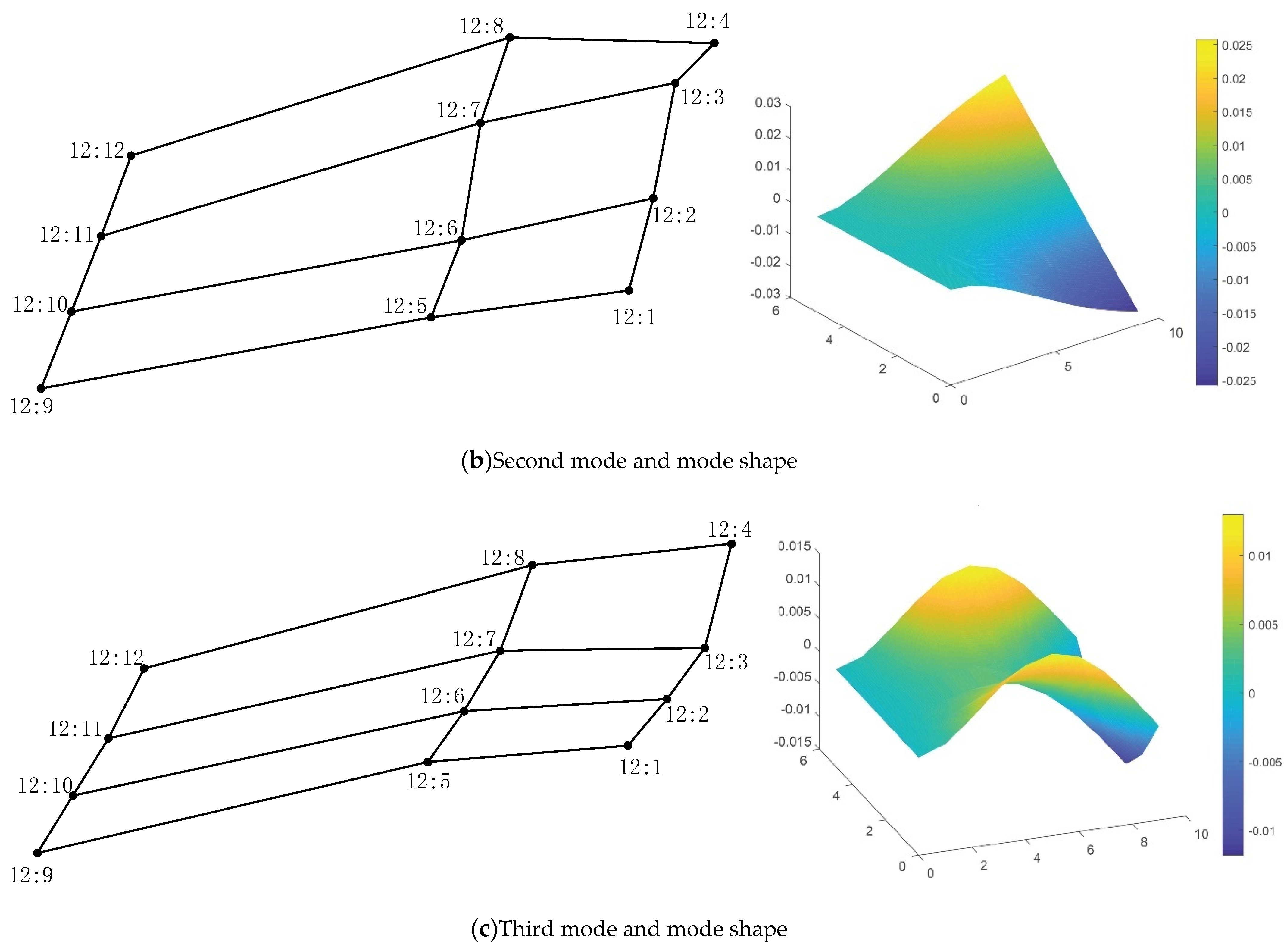
4.1. Finite Element Model Calculation and Test Verification
4.2. Neural Network Model Predictive Analysis
5. Conclusions
- (1)
- The proposed method only needs to mesh the initial workpiece and the machined workpiece once, and it only needs to calculate the geometric parameters of the initial workpiece and the machined workpiece. It does not need to re-mesh the thin-walled parts at each cutting position and to repeatedly calculate the geometric parameters of the workpiece during the cutting process. Meanwhile, in comparison with the three-dimensional cube elements, the shell elements can reduce the number of degrees of freedom of the FEM model by 74%, which leads to about nine times faster computation of the characteristic equation.
- (2)
- Modal test results show that the maximum prediction error of the workpiece nature frequency of the built shell FEM is about 4%.
- (3)
- Compared with the calculation results of the FEM, the maximum prediction error of the neural network model is 0.409%. It can be inferred that compared with the modal test results, the maximum prediction error of the neural network model is about 4%.
- (4)
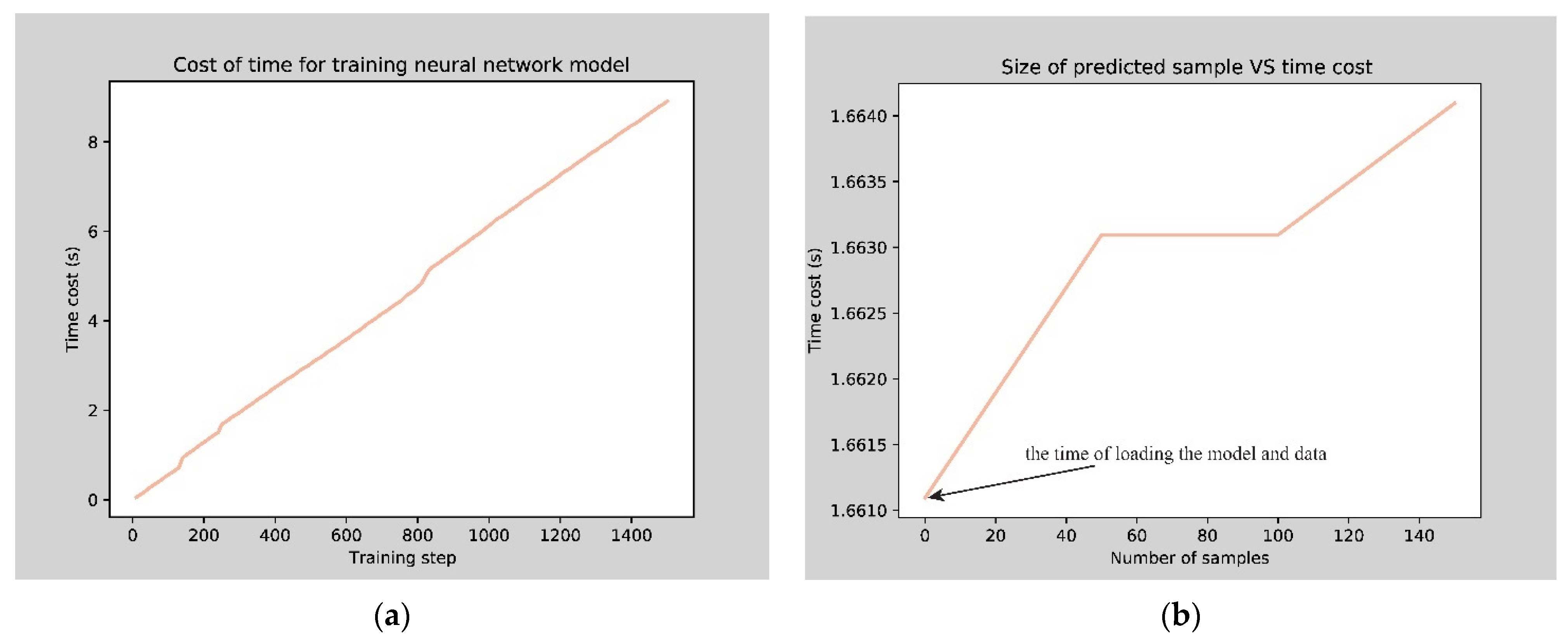
- When the training samples are 132, the epoch is 300, the batch size is 30, and the CPU is used for calculation, the training time is about 9 s. When using the model to batch-calculate the dynamic parameters of a thin-wall part at different cutting stages, the loading time of the neural network model and the model input data is about 1.6611 s. When the number of predicted cutting states is 150, the prediction time is only 0.00315 s. Therefore, the three-layer neural network model can highly improve calculation efficiency while ensuring calculation accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, G.L.; Zhao, B.; Ding, W.F.; Xin, L.J.; Nian, Z.W.; Peng, J.H.; He, N.; Xu, J.H. Nontraditional energy-assisted mechanical machining of difficult-to-cut materials and components in aerospace community: A comparative analysis. Int. J. Extreme Manufacturing 2023, 6, 022007. [Google Scholar] [CrossRef]
- Bravo, U.; Altuzarra, O.; De Lacalle, L.N.L.; Sánchez, J.A.; Campa, F.J. Stability limits of milling considering the flexibility of the workpiece and the machine. Int. J. Mach. Tools Manuf. 2005, 45, 1669–1680. [Google Scholar]
- Seguy, S.; Campa, F.J.; De Lacalle, L.N.L.; Arnaud, L.; Dessein, G.; Aramendi, G. Toolpath dependent stability lobes for the milling of thin-walled parts. Int. J. Mach. Mach. Mater. 2008, 4, 377. [Google Scholar] [CrossRef]
- Arnaud, L.; Gonzalo, O.; Seguy, S.; Jauregi, H.; Peigné, G. Simulation of low rigidity part machining applied to thin-walled structures. Int. J. Adv. Manuf. Technol. 2011, 54, 479–488. [Google Scholar] [CrossRef]
- Thevenot, V.; Arnaud, L.; Dessein, G.; Cazenave-Larrocheet, G. Influence of material removal on the dynamic behavior of thin-walled structures in peripheral milling. Mach. Sci. Technol. 2006, 10, 275–287. [Google Scholar] [CrossRef]
- Song, Q.H.; Ai, X.; Tang, W.X. Prediction of simultaneous dynamic stability limit of time–variable parameters system in thin-walled workpiece high-speed milling processes. Int. J. Adv. Manuf. Technol. 2011, 55, 883–889. [Google Scholar] [CrossRef]
- Meshreki, M.; Attia, H.; Kövecses, J. Development of a new model for the varying dynamics of flexible pocket-structures during machining. J. Manuf. Sci. Eng. Am. Soc. Mech. Eng. 2011, 133, 41002. [Google Scholar] [CrossRef]
- Song, Q.H.; Liu, Z.Q.; Wan, Y.; Ju, G.G.; Shi, J.H. Application of Sherman-Morrison-Woodbury formulas in instantaneous dynamic of peripheral milling for thin-walled component. Int. J. Mech. Sci. 2015, 96, 79–90. [Google Scholar] [CrossRef]
- Song, Q.H.; Shi, J.H.; Liu, Z.Q.; Wan, Y. A time-space discretization method in milling stability prediction of thin-walled component. Int. J. Adv. Manuf. Technol. 2017, 89, 2675–2689. [Google Scholar] [CrossRef]
- Ahmadi, K. Finite strip modeling of the varying dynamics of thin-walled pocket structures during machining. Int. J. Adv. Manuf. Technol. 2017, 89, 2691–2699. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Frequency domain updating of thin-walled workpiece dynamics using reduced order substructuring method in machining. J. Manuf. Sci. Eng. Am. Soc. Mech. Eng. 2017, 139, 71013. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.H.; Ma, Y.C.; Wan, M. Chatter prediction for the peripheral milling of thin-walled workpiece with curved surfaces. Int. J. Mach. Tools Manuf. 2016, 109, 36–48. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.H.; Ma, Y.C.; Wan, M.; Dang, X.B. An efficient decomposition-condensation method for chatter prediction in milling large-scale thin-walled structures. Mech. Syst. Signal Process. 2019, 121, 58–76. [Google Scholar] [CrossRef]
- Dang, X.B.; Wan, M.; Yang, Y.; Zhang, W.H. Efficient prediction of varying dynamic characteristics in thin-wall milling using freedom and mode reduction methods. Int. J. Mech. Sci. 2019, 150, 202–216. [Google Scholar] [CrossRef]
- Budak, E.; Tun, L.T.; Alan, S.; Nevzat-Özgüvenet, H. Prediction of workpiece dynamics and its effects on chatter stability in milling. CIRP Ann. 2012, 61, 339–342. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, L.; Ding, H. Matrix perturbation method for predicting dynamic modal shapes of the workpiece in high-speed machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 177–183. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, D.H.; Wu, B.H.; Tang, M. Modeling and analysis effects of material removal on machining dynamics in milling of thin-walled workpiece. Adv. Mater. Res. 2011, 223, 671–678. [Google Scholar] [CrossRef]
- Tian, W.J.; Ren, J.X.; Zhou, J.H.; Wang, D.Z. Dynamic modal prediction and experimental study of thin-walled workpiece removal based on perturbation method. Int. J. Adv. Manuf. Technol. 2018, 94, 2099–2113. [Google Scholar] [CrossRef]
- Ju, G.G. Research on Instability Characteristics of Thin-walled Parts with Complex Curved Surface and Variable Thickness during Multi-Axis Milling. Master’s Thesis, Shandong University, Jinan, China, 2016. [Google Scholar]
- Tuysuz, O.; Altintas, Y. Time-domain modeling of varying dynamic characteristics in thin-wall machining using perturbation and reduced-order substructuring methods. J. Manuf. Sci. Eng. 2018, 140, 011015. [Google Scholar] [CrossRef]
- Liu, Y.L. Analysis of Milling Dynamics and Chatter Detection and Control Methods for Thin-Walled Workpiece. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2017. [Google Scholar]
- Kim, D.H.; Kim, T.Y.; Wang, X.L.; Kim, M.; Quan, Y.J.; Oh, J.W.; Min, S.H.; Kim, H.J.; Bhandari, B.; Yang, I.; et al. Smart Machining Process Using Machine Learning: A Review and Perspective on Machining Industry. Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 555–568. [Google Scholar] [CrossRef]
- Yeganefar, A.; Niknam, S.A.; Asadi, R. The use of support vector machine, neural network, and regression analysis to predict and optimize surface roughness and cutting forces in milling. Int. J. Adv. Manuf. Technol. 2019, 105, 951–965. [Google Scholar] [CrossRef]
- Pavlenko, I.; Saga, M.; Kuric, I.; Kotliar, A.; Basova, Y.; Trojanowska, J.; Ivanov, V. Parameter identification of cutting forces in crankshaft grinding using artificial neural networks. Materials 2020, 13, 5357. [Google Scholar] [CrossRef]
- SK, T.; Shankar, S.; T, M.; K, D. Tool wear prediction in hard turning of EN8 steel using cutting force and surface roughness with artificial neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 329–342. [Google Scholar] [CrossRef]
- Vasanth, X.A.; Paul, P.S.; Varadarajan, A.S. A neural network model to predict surface roughness during turning of hardened SS410 steel. Int. J. Syst. Assur. Eng. Manag. 2020, 11, 704–715. [Google Scholar] [CrossRef]
- Wang, J.; Zou, B.; Liu, M.; Li, Y.; Ding, H.; Xue, K. Milling force prediction model based on transfer learning and neural network. J. Intell. Manuf. 2021, 32, 947–956. [Google Scholar] [CrossRef]
- Heitz, T.; He, N.; Ait-Mlouk, A.; Bachrathy, D.; Chen, N.; Zhao, G.; Li, L. Investigation on eXtreme Gradient Boosting for cutting force prediction in milling. J. Intell. Manuf. 2023. [Google Scholar] [CrossRef]
- Zhu, B.F. ; The Finite Element Method Theory and Applications; China Institute of Water Resources and Hydropower Research: Beijing, China, 2018. [Google Scholar]
- Logan, D.L. A First Course in the Finite Element Method; Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]



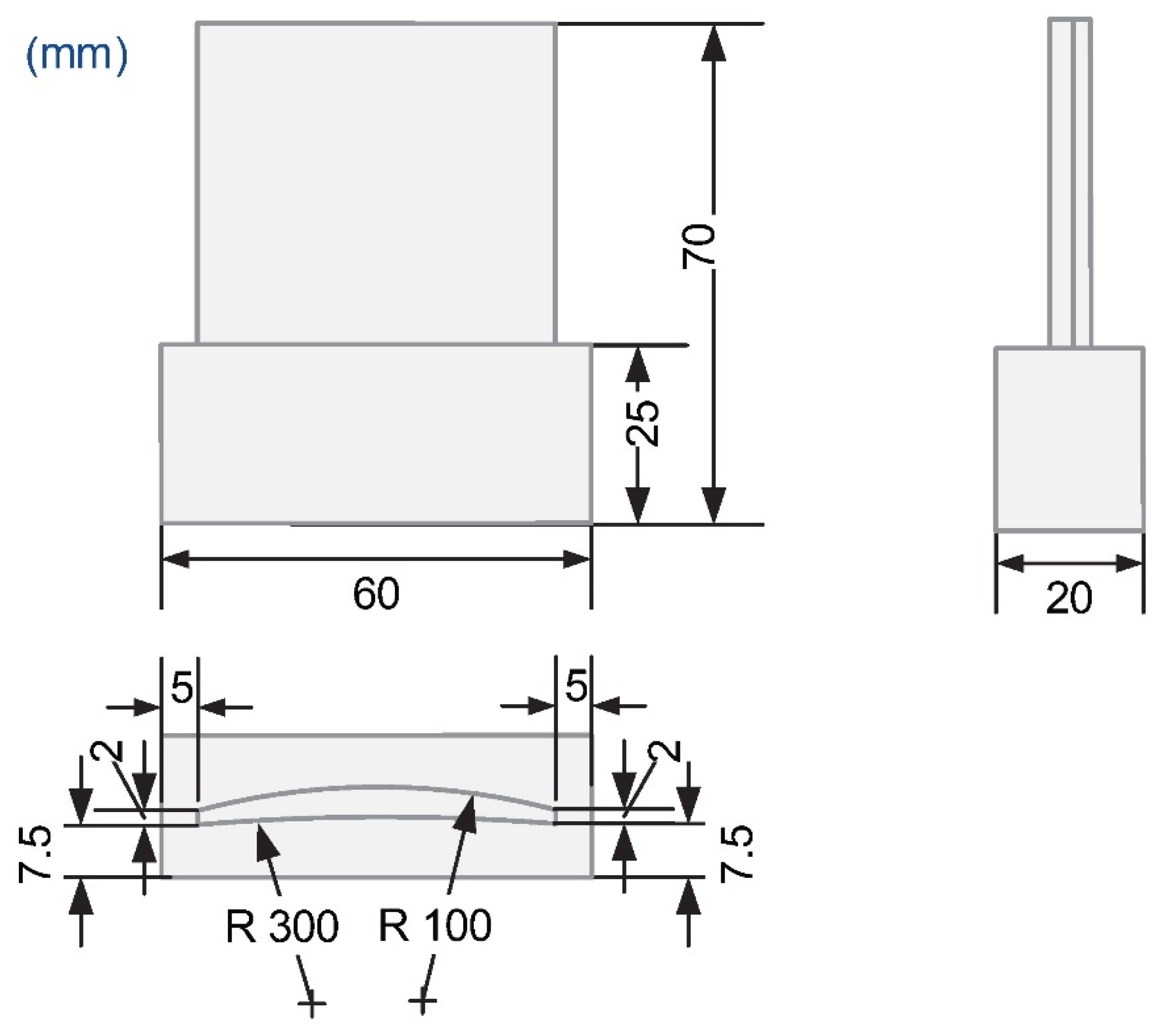


| Spindle Speed (rpm) | Feed Rate (mm/min) | Axial Depth of Cut (mm) | Radial Depth of Cut (mm) |
|---|---|---|---|
| 3000 | 300 | 5 | 0.2 |
| Steps | Modes | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | Tests | 1535 | 3290 | 8152 |
| FEM | 1574 | 3265 | 8293 | |
| (%) | (2.51) | (−0.76) | (1.72) | |
| 1 | Tests | 1552 | 3313 | 8094 |
| FEM | 1591 | 3289 | 8233 | |
| (%) | (2.53) | (−0.73) | (1.71) | |
| 2 | Tests | 1551 | 3312 | 8101 |
| FEM | 1604 | 3302 | 8299 | |
| (%) | (3.42) | (−0.32) | (2.45) | |
| 3 | Tests | 1548 | 3268 | 7972 |
| FEM | 1611 | 3301 | 8244 | |
| (%) | (4.04) | (1.02) | (3.41) | |
| 4 | Tests | 1551 | 3239 | 7965 |
| FEM | 1613 | 3286 | 8174 | |
| (%) | (4.01) | (1.44) | (2.62) | |
| 5 | Tests | 1550 | 3210 | 7867 |
| FEM | 1609 | 3259 | 8112 | |
| (%) | (3.81) | (1.52) | (3.11) |
| State | Modes | 1 | 2 | 3 | State | Modes | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | FEM | 1536 | 3002 | 7538 | 7 | FEM | 1589 | 3032 | 7370 |
| NN | 1534 | 3004.5 | 7545.1 | NN | 1584 | 3037.1 | 7368.6 | ||
| (%) | (−0.12) | (0.082) | (0.095) | (%) | (−0.31) | (0.168) | (−0.019) | ||
| 2 | FEM | 1512 | 2965 | 7523 | 8 | FEM | 1557 | 2957 | 7322 |
| NN | 1510 | 2967 | 7526.4 | NN | 1556 | 2964.6 | 7333.7 | ||
| (%) | (−0.11) | (0.067) | (0.046) | (%) | (−0.03) | (0.255) | (0.16) | ||
| 3 | FEM | 1553 | 3099 | 7806 | 9 | FEM | 1505 | 2881 | 7289 |
| NN | 1549 | 3098 | 7821.4 | NN | 1509 | 2889.6 | 7296.3 | ||
| (%) | (−0.29) | (−0.001) | (0.197) | (%) | (0.25) | (0.298) | (0.099) | ||
| 4 | FEM | 1581 | 3131 | 7748 | 10 | FEM | 1496 | 2954 | 7487 |
| NN | 1576 | 3131.9 | 7766.3 | NN | 1500 | 2960.9 | 7517.1 | ||
| (%) | (−0.30) | (0.0027) | (0.236) | (%) | (0.28) | (0.233) | (0.401) | ||
| 5 | FEM | 1598 | 3131 | 7624 | 11 | FEM | 1511 | 2970 | 7459 |
| NN | 1593 | 3132.5 | 7628.7 | NN | 1514 | 2977.3 | 7489.5 | ||
| (%) | (−0.31) | (0.047) | (0.062) | (%) | (0.20) | (0.247) | (0.409) | ||
| 6 | FEM | 1602 | 3095 | 7479 | 12 | FEM | 1519 | 2969 | 7400 |
| NN | 1598 | 3094.3 | 7486.3 | NN | 1522 | 2977.6 | 7420.7 | ||
| (%) | (−0.23) | (−0.023) | (0.098) | (%) | (0.23) | (0.291) | (0.28) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ding, F.; Wang, D.; Tian, W.; Zhou, J. Predicting the Dynamic Parameters for Milling Thin-Walled Blades with a Neural Network. J. Manuf. Mater. Process. 2024, 8, 43. https://doi.org/10.3390/jmmp8020043
Li Y, Ding F, Wang D, Tian W, Zhou J. Predicting the Dynamic Parameters for Milling Thin-Walled Blades with a Neural Network. Journal of Manufacturing and Materials Processing. 2024; 8(2):43. https://doi.org/10.3390/jmmp8020043
Chicago/Turabian StyleLi, Yu, Feng Ding, Dazhen Wang, Weijun Tian, and Jinhua Zhou. 2024. "Predicting the Dynamic Parameters for Milling Thin-Walled Blades with a Neural Network" Journal of Manufacturing and Materials Processing 8, no. 2: 43. https://doi.org/10.3390/jmmp8020043
APA StyleLi, Y., Ding, F., Wang, D., Tian, W., & Zhou, J. (2024). Predicting the Dynamic Parameters for Milling Thin-Walled Blades with a Neural Network. Journal of Manufacturing and Materials Processing, 8(2), 43. https://doi.org/10.3390/jmmp8020043








