Next-Gen Manufacturing: Machine Learning for Surface Roughness Prediction in Ti-6Al-4V Biocompatible Alloy Machining

Abstract

Mechanical engineering plays an important role in the design and manufacture of medical devices, implants, prostheses, and other medical equipment, where the machining of bio-compatible materials have a special place. There are a lot of different conventional and non-conventional types of machining of biocompatible materials. One of the most frequently used methods is milling. The first part of this research explores the machining parameters optimization minimizing surface roughness in milling titanium alloy Ti-6Al-4V. A full factorial design involving four factors (cutting speed, feed rate, depth of cut, and the cooling/lubricating method), each having three levels, implies the 81 experimental runs. Using the Taguchi method, the number of experimental runs was reduced from 81 to 27 through an orthogonal design. According to the analysis of variance (ANOVA), the most significant parameter for surface roughness is feed rate. The second part explores the possibilities of using different ML techniques to create a predictive model for average surface roughness using the previously created small datasets. The paper presents a comparative analysis of several commonly used techniques for handling small datasets and regression problems. The best results indicate that the widely used machine learning algorithm Random Forest excels in handling regression problems and small datasets.

1. Introduction

Mechanical engineering holds a crucial role in the design and production of medical devices, implants, prostheses, and various other medical equipment, with a particular emphasis on the machining of biocompatible materials [1,2]. Biocompatible materials are acceptable for contact with biological tissue, such as human skin, muscles, bones, or organs. After being integrated into the body, they do not cause rejection or damage to the surrounding tissue or other harmful effects on the body. Biocompatible materials are used in medicine to make implants, prostheses, surgical sutures, and other medical devices. There are many types of biocompatible materials, and some of them are [3,4]:

• Polymers (polyurethanes, polycarbonates, and polyesters);
• Ceramic materials;
• Metals (titanium, cobalt, chromium and their alloys, as well as stainless steels);
• Biological materials (collagen, hyaluronic acid, and fibrin);
• Composites;
• Nanomaterials.

There are many different conventional and non-conventional types of machining of biocompatible materials. The most commonly used traditional machining types are turning, drilling, and milling. In contrast, the most widely used non-conventional machining types are abrasive jet machining, ultrasonic machining, dry ice machining, laser beam machining, electrical discharge machining (EDM), and electron beam machining [5]. This paper analyzes the machining of the biocompatible material titanium alloy Ti-6Al-4V (titanium alloy). Alloy Ti-6Al-4V belongs to the group of alloys, i.e., difficult-to-machine (DTM) materials. Namely, high strength and low thermal conductivity make it challenging to machine this alloy. Surgeons and dentists use Ti-6Al-4V implants for crafting endoprostheses, dental implants in dentistry, and surgical tools. In addition to biomedicine, the aviation industry frequently employs this alloy because of its high strength, corrosion resistance, and low specific gravity [6].

2. Literature Review

Milling is a prevalent conventional machining type of this material. This paper analyzes the effects of machining parameters (cutting speed, feed rate, depth of cut) and cooling/lubricating on surface roughness in Ti-6Al-4V alloy milling.

Optimizing cutting parameters is crucial to achieving an efficient material removal rate, prolonging tool life, and having better surface quality, i.e., lower average surface roughness (Ra). Optimal cutting parameters can vary based on different factors, such as the machine tool, tool holder, jigs and fixtures, and other factors.

Cutting speed. Titanium alloys have low thermal conductivity, so it is important to manage heat generation. Generally, moderate cutting speeds are preferred to avoid excessive tool wear. In general, tool manufacturers recommend that alloys be produced at lower cutting speeds, so recommendations are often in the range of 30 to 90 m per minute (m/min). Reviewing the relevant literature reveals that researchers utilize various cutting speeds for milling titanium alloys, primarily falling within the range of 30 m/min to 200 m/min [7,8,9,10,11,12,13,14,15,16].

Feed rate. The feed rate is significant to strike a balance between material removal rate and tool life. The relationship between maximum surface roughness and feed rate is also well known for the straight turning using a single-point cutting tool.The maximum surface roughness is directly related to the square of the feed rate and inversely associated with the radius of the nose. Feed rate is the factor that, in most cases, has the most significant influence on average surface roughness (Ra) on milling titanium alloy. Lower feed rates are usually recommended for titanium alloys to reduce the risk of tool wear and breakage. On milling titanium alloys, feed rates typically range from 0.05 to 0.15 mm/tooth [7,11,12,13].

Depth of cut. Many prefer smaller values for the depth of cut when machining titanium alloys due to their low thermal conductivity. Numerous researchers primarily utilize end mill tools for milling titanium alloy, either solid end mills or end mills with inserts [7,8,9,10,11,12,13,15,16]. Consequently, the radial depth of the cut (width of cut) is approximately half the end mill diameter [9,11], while the axial depth of the cut varies.

A literature review indicates that numerous experts have extensively investigated the milling of titanium alloy Ti-6Al-4V.

Table 1. Predicting the arithmetic mean roughness (Ra) in the milling of the Ti-6Al-4V alloy.

Author, Year	Process	Cutting Conditions
Shokrani et al. (2006) [7]	Solid carbide end mill $\Phi$8	Experimental input parameters: Cutting speed 30, 115, 200 m/min, feed rate 0.03, 0.055, 0.1 mm/tooth, radial depth of cut 1, 3, 5 mm, cooling/lubricating: cryogenic, flood, dry
Iqbal et al. (2020) [8]	Solid carbide end mill $\Phi$8	Experimental input parameters: Cutting speed 100, 175 m/min, Cutter’s helix angle: 30, 42 deg, Milling orientation: up, down, Cutting fluid: LN2, CO2, MQL
Tešić et al. (2020) [9]	Indexable end mill $\Phi$16	Experimental input parameters: Cutting speed 40, 80, 160 m/min, feed rate 0.05, 0.1, 0.2 mm/tooth, radial depth of cut 8 mm, axial depth of cut 0.5, 1.0 and 2 mm
Danish et al. (2022) [10]	Indexable end mill	Experimental input parameters: Cutting speed 140, 150 m/min, feed rate 0.1, 0.2 mm/tooth, axial depth of cut 0.5 mm, dry cutting
Ginting et al. (2006) [11]	Indexable ball end mill $\Phi$16	Experimental input parameters: Cutting speed 60, 75, 100, 125, 150 m/min, feed rate 0.1, 0.15 mm/tooth, radial depth of cut 8.8 mm, axial depth of cut 2 mm, dry cutting
Paschoalinoto et al. (2020) [12]	Indexable end mill	Experimental input parameters: Cutting speed 80, 90, 100 m/min, feed rate 0.06, 0.08, 0.1 mm/tooth, radial depth of cut 0.5, 0.75, 1 mm, cooling/lubricating: air, MQL, MQL+graphite
Sun et al. (2009) [13]	Solid carbide end mill	Experimental input parameters: Cutting speed 50, 65, 80, 95, 110 m/min, feed rate 0.06, 0.08, 0.1, 0.12, 0.14 mm/tooth, radial depth of cut 2, 3, 4, 5, 6 mm, axial depth of cut 1.5 mm
Rahman Al Mazedur et al. (2021) [14]	Face mill	Experimental input parameters: Cutting speed 50, 57.5, 65 m/min, feed rate 0.2, 0.25, 0.3 mm/tooth, radial depth of cut 7.5, 10, 12 mm, axial depth of cut 2.54 mm
Karkalos et al. (2016) [15]	Solid carbide end mill $\Phi$6	Experimental input parameters: Cutting speed 26.39, 32.05, 37.70 m/min, feed rate 75, 100, 125 mm/min, radial depth of cut 0.3, 0.6, 0.9
Bai et al. (2019) [16]	End mill	Experimental input parameters: 1200 rpm, feed rate 500 mm/min, axial depth of cut 0.25 mm, radial depth of cut 10 mm, cooling/lubricating: nanofluids

provides an overview of the cutting parameters in relevant studies. An analysis of this data reveals variations in the ranking of cutting parameters.

Cooling/lubricating technique. Since titanium alloy belongs to the group of difficult- to-cut material, the cooling/lubricating method is significant and have a considerable influence on tool life and surface quality. Cutting fluids provides good cooling and lubricating properties. However, considering that there is considerable evidence that cutting fluids harms human health and the environment, efforts are being made to replace them with other cooling/lubricating methods [17].

Over the past few decades, novel solutions have emerged to address the primary limitations of cutting fluids. Principal alternatives encompass dry cutting, minimal quantity lubrication (MQL), cryogenic cooling, solid lubrication, environmentally friendly cutting fluids, and nanofluids. Dry machining presents several potential benefits, such as a decreased environmental impact by eliminating coolant waste and reduced operational costs linked to the procurement, upkeep, and disposal of cutting fluids. Danish et al. [10] examined the machinability performance of a coated carbide insert tool during dry machining in turning operations. They concluded that average surface roughness (Ra) has lower values at higher cutting speed and lower feed rate, but flank wear was more intensive at a lower feed rate (0.1 rev/min) compared to a higher value (0.2 rev/min). Ginting et al. [11] utilized uncoated cemented carbide tools for ball-end milling of the titanium alloy Ti6242S under dry machining conditions. Sun et al. [13] experimented with turning titanium alloy in dry conditions using PCD and PCBN inserts. They concluded that the PCBN tool’s life was much shorter than that of the PCD tool under the same cutting conditions.

Narasimhulu et al. [18] have studied machining parameters and rake angle on the average surface roughness (Ra) and cutting force on turning titanium alloy. Their conclusion highlighted that the most influential factors on cutting force are feed and depth of cut, while feed and cutting velocity significantly impact surface roughness. The absence of cooling and lubrication can lead to higher temperatures at the cutting zone, potentially causing thermal damage to the workpiece and tool. Machining Ti-6Al-4V under dry conditions is possible, but it requires careful planning, selection of appropriate tools and parameters, and considerations for heat management and chip control to achieve successful results. Minimum quantity of liquid (MQL) entails the application of a small quantity of lubricant or coolant directly to the cutting zone during machining operations. This method aims to provide the necessary lubrication and cooling to improve tool life and machining performance while minimizing the amount of lubricant used compared to traditional flood coolant systems.

Iqbal et al. [8] investigated the influence of the MQL and several types of cryogenic coolants and lubricants on tool wear, cutting forces, and surface roughness. They found that MQL is more effective than LN₂ and Co2 in reducing tool wear and providing better surface quality.

Cryogenic cooling is a technique that entails subjecting the workpiece and the cutting tool to extremely low temperatures during machining, and it is particularly engaging when machining challenging materials such as titanium alloys, e.g., Ti-6Al-4V. These coolants have extremely low temperatures and rapidly evaporate upon contact with the heat generated during machining. Cryogenic cooling rapidly removes heat from the cutting zone, reducing the risk of thermal damage to both the tool and the workpiece, significantly extending the life of cutting tools by reducing tool wear, improving surface finish due to reduced friction and heat-induced distortion, and decreasing cutting force. Cryogenic coolants are environmentally friendly because they evaporate quickly without leaving behind residues or generating harmful waste. Negative aspects of using this technology are related to costs since it can be expensive to set up and maintain due to the need for specialized equipment and cryogenic fluids, the need for careful adjustment of coolant flow rates, and finally, extremely low temperatures can make some materials, including certain tool materials, more brittle. Many researchers investigate the effects of cryogenic cooling on milling titanium alloys. Jerold et al. [19] investigated the influence of cryogenic coolants LN₂ and CO₂ in the machining of Ti-6Al-4V and how it affects surface roughness, cutting temperature, tool wear, and cutting forces. Cryogenic cooling decreases significantly cutting force and cutting temperature compared to flood machining and dry machining. LN₂ (liquid nitrogen) achieves lower cutting temperatures and lower forces than CO₂ (carbon dioxide). Shokrani et al. [7] investigated the effects of cryogenic cooling on surface roughness on milling Ti–6Al–4V titanium alloy. They reported that with cryogenic cooling, surface roughness is 39% lower than dry cutting and 31% compared to flood cooling. Xiufang et al. [16] evaluated the lubrication performances of different nanofluids in milling titanium alloy Ti-6Al-4V using the following nanofluids: graphite, Al₂O₃, MoS₂, SiC, SiO₂, and CNTs. They discussed the effects of using nanofluids on surface roughness and milling force.

A vortex tube offers an alternative to traditional liquid coolants by providing a clean air stream to cool cutters and workpieces during machining. The vortex tube (Ranque–Hilsch vortex tube) is a mechanical device separating compressed gas into two distinct streams of air, hot and cold. The vortex tube can reduce ambient temperature by −40 $°$C, depending on the air pressure supplied to the tube. This device has no moving element of an external heat source to achieve temperature separation. Šterpin Valić et al. [20] investigated the influence of cooling using MQL in combination with the vortex tube on surface roughness and tool life while turning stainless steel. Yüksel et al. [21] used a vortex tube to investigate the effects of cooling on the turning parameters. They found that lower temperatures decrease surface roughness significantly, while the influence on cutting force is negligible.

Singh et al. [22] use a vortex tube implemented into the MQL in turning titanium alloy grade 2. The research focuses on average surface roughness, power consumption, cutting force, and tool flank wear. The authors reported that this technology (VMQL) reduced surface roughness by 15–18% compared to MQL, and a reduction in cutting force was also achieved.

In metal cutting, spatially difficult-to-cut materials such as Ti-6Al-4V, working with big datasets is not always practical. Using AI can help predict outcomes even with smaller datasets. Choosing the proper AI technique is very important, as there are many options to consider. Recently, applying AI techniques in metal cutting for various output factors, such as average surface roughness and cutting forces, has become an appealing and active area of interest. Particularly interesting is the utilization of small datasets, which is common in metal cutting due to the challenges of numerous and costly experiments.

Several suthors [23,24,25,26,27,28,29] employed neural networks featuring one or two hidden layers to predict surface roughness using a relatively small dataset of 27 samples. They experimented by adjusting the number of hidden layers, varying the number of neurons within those layers, and employing different training algorithms to identify the neural network configuration that yielded the best performance.

Some researchers, such as Kosarac et al. [27], leveraged neural networks and relatively small datasets to predict phenomena beyond surface roughness. They employed an Artificial Neural Network (ANN) model to analyze how working conditions influence the thermal behavior of a motorized grinder spindle. Their investigation focused on four key factors: the number of revolutions, motor coolant flow, bearing coolant flow, and the type of coolant. The dataset comprised 40 sets of data. Their findings revealed that the 4-8-8-3 network topology exhibited the lowest Root Mean Square Error (RMSE) value, signifying that this model demonstrated the most outstanding performance.

Dubey et al. [28] conducted an experiment focusing on surface roughness in the machining of AISI 304 Steel. The experiment consisted of 27 samples, each involving various combinations of input parameters: depth of cut, feed rate, cutting speed, and nanofluid concentration. Based on the experimental data, Dubey developed three machine-learning models to predict surface roughness based on the input parameters: Linear Regression (LR), Random Forest (RF), and Support Vector Machine (SVM). The study revealed that the Random Forest (RF) model surpassed the other two models in accurately predicting surface roughness.

Agrawal et al. [29] conducted an experiment involving AISI 4340 steel, where they varied the depth of cut, feed rate, cutting speed, and measured surface roughness. They collected a dataset of 39 samples and developed three regression models: Multiple regression, Random forest, and Quantile regression. The study results concluded that the Random Forest regression model outperformed the other models in predicting surface roughness and may be the superior choice for predicting surface roughness in such problems.

3. Exprerimental Setup

This study explores the impact of four variables on surface roughness: cutting speed (v), feed rate (f), axial depth of cut (a), and the various types of coolants/lubricants, each with three distinct levels. All experimental runs took place under uniform machining conditions and on the same machine tool, utilizing the milling center Emco Concept Mill 250. The experiment utilized the spindle milling cutter HF 16E2R030A16-SBN10-C by PRAMET, which incorporated two BNGX 10T308SR-MM: M8345 inserts designed for superalloy cutting. The Mitutoyo SJ-210 measuring device, shown in Figure 1, measured the arithmetic mean roughness Ra. For this experiment, measuring parameters are set according to the expected value of the Ra to $\lambda$f = 2.5 $\mathsf{\mu }$m, $\lambda$c = 0.8 mm, ln = 4 mm. After machining, the workpiece undergoes three measurements, each at three different positions. The machining process involved clamping the workpiece with dimensions of 35 × 25 × 20 using a versatile milling vise. The machining operation involved both sides of the sample parts and utilized the climb milling method, chosen to improve the quality of the machined surface.

The chemical composition of Ti-6Al-4V super alloy is given in

Table 2. The chemical composition of Ti-6Al-4 super alloy.

Elements	V	Al	Sn	Zr	Mo	C	Si	Ti
Chemical composition (wt%)	4.22	5.48	0.0625	0.0028	0.05	0.369	0.0222	Balance

.

The selection of cutting parameter levels resulted from considering recommendations from the tool manufacturer, which aligned with the characteristics of both the workpiece and the tool material. Furthermore, machining parameters used in research systematized in Table 1 played a role in demanding a range of factors.

Table 3. Experimental factors and their levels.

Factors	Levels
	Low Level	Middle Level	High Level
	−1	0	1
Cutting speed (m/min)	50	100	150
Feed rate per tooth (mm/tooth)	0.05	0.125	0.2
Axial depth of cut (mm)	0.5	0.8	1.2
Cooling/lubricating technique	Emulsion	Dry cutting	Vortex tube

shows the factors and their levels.

The rpm values used in the experiment ($n_1$ = 1000 rpm, $n_2$ = 2000 rpm, and $n_3$ = 3000 rpm) were calculated based on adopted upper and lower cutting speeds (Table 3):

$$n=\frac{1000·v}{D·\pi }=\frac{1000·50}{16·\pi }=1000\mathrm{rpm}$$

(1)

where D is the cutter diameter and v is the cutting speed.

The calculation of the feed rate per minute involves the determined rpm, the feed per tooth value (Table 3), and the number of inserts of the cutting tool. The lowest feed rate is associated with the lowest rpm ($n_1$ = 1000 rpm) and the lowest feed per tooth ($s_{z_1}$ = 0.05 mm/tooth). On the other hand, the highest feed rate ($s_{max}$ = 1200 mm/min) coincides with the maximum rpm ($n_3$ = 3000 rpm) and the the highest value of the feed per tooth ($s_{z_3}$ = 0.2 mm/tooth):

$$s_{min}=n_1·s_{z_1}·z=1000·0.05·2=100\mathrm{rpm}$$

(2)

where $n_1$ is calculated spindle speed, $s_{z_1}$ feed per tooth, and z number of inserts in the cutting tool. The axial depth of the cut had values of a = 0.5, 0.8, and 1.2 mm, while the radial depth of the cut is constant for all experimental runs and equal to one-half of the tool diameter, i.e., 8 mm.

The following cooling/lubricating methods are considered in this experiment: emulsion, dry cutting, and vortex tube, as depicted in Figure 2.

For wet machining, the semi-synthetic fluid BIOL MIN-E with a quality level of ISO 6743/7 [30] was chosen. The vortex tube, known as the Ranque–Hilsch vortex tube, is a device capable of dividing compressed gas into cold and hot streams without requiring any moving components, Figure 2. Easy to mount with a magnetic base and flexible hose, the vortex tube creates instant cold air by reducing ambient air temperatures by $-40°\mathrm{C}$.

4. Utilizing the Taguchi Method for Optimizing Cutting Parameters

Experimentation assessed the influence of various factors on surface quality. While a full factorial plan necessitates conducting the maximum number of experimental runs, contingent upon the factors and their levels, this can lead to increased time and costs. In contrast, the Taguchi method, a widely adopted approach in experimental design, allows for fewer experimental runs than the full factorial plan. The primary objective of the Taguchi method is to determine the minimum number of experimental runs required to identify the optimal combination of factors and their respective levels. The following data analysis employs statistical methods. 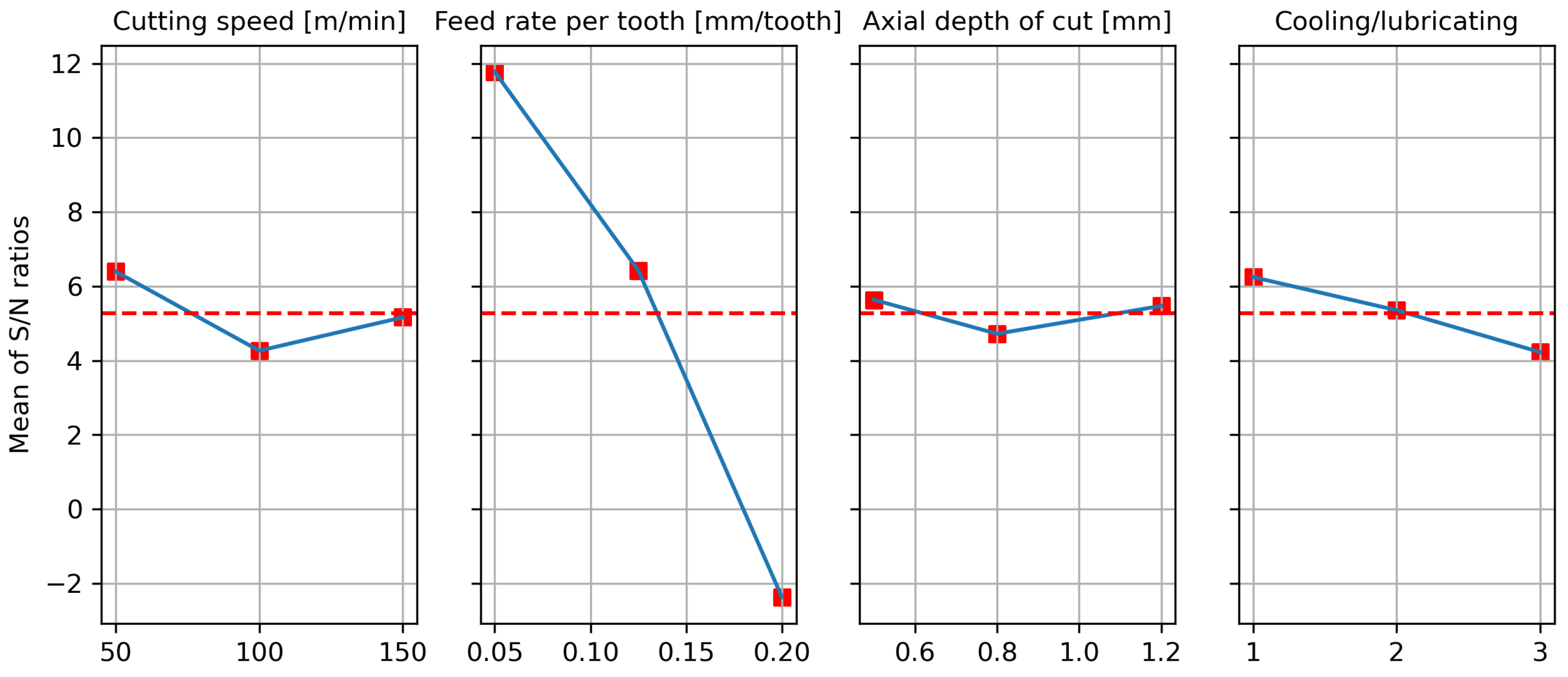The Taguchi optimization method is applied to attain low surface roughness in various cutting operations, as evidenced by References [9,14,31,32,33,34]. Furthermore, the signal-to-noise ratio, serving as a metric for assessing quality characteristics, is closely monitored. This ratio quantifies the deviation from the desired value. In the context of addressing static problems, three common signal-to-noise ratios find use: “smaller is better”, “bigger is better”, and “nominal is the best”. In this particular experiment, the objective was to determine the arithmetic mean roughness (Ra), focusing on the “smaller is better” criterion for the selected S/N ratio of interest.

$$\frac{S}{N}=-100·log\left(\sum _{i=1}^n{y}_i^2\right)$$

(3)

In the provided equation, S/N represents the signal-to-noise ratio, ‘n’ signifies the number of responses, and ‘y_i’ denotes the response associated with a specific factor/level combination. In this scenario, a complete factorial experiment involved $3^4=81$ experimental runs. By implementing the Taguchi method, the number of experiments was streamlined from 81 to 27 runs using an orthogonal design. The orthogonal matrix, as depicted in

Table 4. Experimental plan—L27 orthogonal array (Taguhci method).

No. of Trials	Cutting Speed (m/min)	Feed per Tooth (mm/tooth)	Axial Depth of Cut (mm)	Cooling/Lubricating Technique	Ra1 $\mathsf{\mu }$m	Ra2 $\mathsf{\mu }$m	Ra3 $\mathsf{\mu }$m	Aver. Ra $\mathsf{\mu }$m	S/N (dB)
1	50	0.05	0.5	Emulsion	0.173	0.211	0.199	0.194	14.229
2	50	0.05	0.8	Dry machining	0.233	0.257	0.277	0.255	11.846
3	50	0.05	1.2	Vortex tube	0.234	0.26	0.254	0.2493	12.064
4	50	0.125	0.5	Dry machining	0.327	0.378	0.307	0.337	9.4388
5	50	0.125	0.8	Vortex tube	0.467	0.521	0.509	0.499	6.037
6	50	0.125	1.2	Emulsion	0.326	0.33	0.292	0.316	10.006
7	50	0.2	0.5	Vortex tube	1.345	1.225	1.32	1.296	−2.256
8	50	0.2	0.8	Emulsion	1.341	1.315	1.402	1.352	−2.623
9	50	0.2	1.2	Dry machining	1.225	1.106	1.094	1.141	−1.150
10	100	0.05	0.5	Emulsion	0.232	0.278	0.248	0.252	11.949
11	100	0.05	0.8	Dry machining	0.286	0.233	0.297	0.272	11.308
12	100	0.05	1.2	Vortex tube	0.34	0.271	0.334	0.315	10.033
13	100	0.125	0.5	Dry machining	0.668	0.657	0.498	0.607	4.3266
14	100	0.125	0.8	Vortex tube	0.607	0.489	0.505	0.533	5.4545
15	100	0.125	1.2	Emulsion	0.446	0.519	0.602	0.522	5.6410
16	100	0.2	0.5	Vortex tube	1.479	1.556	1.565	1.533	−3.712
17	100	0.2	0.8	Emulsion	1.662	1.337	1.673	1.557	−3.8476
18	100	0.2	1.2	Dry machining	1.279	1.272	1.57	1.373	−2.7576
19	150	0.05	0.5	Emulsion	0.21	0.21	0.21	0.21	13.555
20	150	0.05	0.8	Dry machining	0.412	0.22	0.169	0.267	11.469
21	150	0.05	1.2	Vortex tube	0.351	0.36	0.291	0.334	9.525
22	150	0.125	0.5	Emulsion	0.494	0.572	0.491	0.519	5.696
23	150	0.125	0.8	Dry machining	0.703	0.707	0.624	0.678	3.375
24	150	0.125	1.2	Vortex tube	0.298	0.429	0.487	0.404	7.858
25	150	0.2	0.5	Vortex tube	1.492	1.187	1.317	1.332	−2.490
26	150	0.2	0.8	Emulsion	0.804	1.194	1.188	1.062	−0.522
27	150	0.2	1.2	Dry machining	1.168	1.421	1.176	1.255	−1.972

, consists of 27 rows corresponding to the number of conducted experimental runs.

The last column in Table 4 contains S/N values derived from measuring Ra values, using the “smaller is better” criterion outlined in Equation (3). These S/N values are instrumental in identifying the most influential parameters to the arithmetic mean roughness, Ra. An aggregated S/N ratio for the arithmetic mean roughness (Ra) across all factors was computed and is presented in Table 4. A higher S/N value indicates better performance. The cutting speed of 50 m/min (level 1), a feed rate of 0.05 mm/tooth (level 1), an axial depth of cut of 0.5 mm (level 1), and machining with emulsion (level 1) yielded the highest S/N value, representing the optimal setting for the arithmetic mean roughness Ra, as shown in Figure 3 and

Table 5. S/N ratio of the arithmetic mean roughness Ra.

Factors	Levels			Delta	Rank
	1	2	3
Cutting speed (m/min)	6.399 *	4.266	5.166	2.133	2
Feed rate per tooth (mm/tooth)	11.776 *	6.426	−2.371	14.146	1
Axial depth of cut (mm)	5.637 *	4.722	5.472	0.915	4
Cooling/lubricating technique	6.249 *	5.356	4.226	2.024	3

* Optimal level.

. It is worth noting that the feed rate had a more pronounced impact on the arithmetic mean roughness, Ra, compared to cutting speed, depth of cut, and the choice of cooling/lubrication techniques, which exhibited relatively less influence. Optimization based on the “smaller is better” criterion led to the identification of the optimal combination, coded as 1-1-1-1, signifying the following input parameters: cutting speed of 50 m/min, feed rate of 0.05 mm/tooth, depth of cut of 0.5 mm, and machining with emulsion (

Table 6. Optimum factor levels.

Level	v (m/min)	sz (mm/tooth)	a (mm)	Cooling/Lubricating	Ra Measured ($\mathsf{\mu }$m)
1	50	0.05	0.5	Emulsion	0.194

).

A confirmation experiment is unnecessary because the orthogonal array includes the 1-1-1-1 combination. Combination 1-1-1-1 has minimal values Ra = 0.194 $\mathsf{\mu }$m.

5. Analysis of Variance (ANOVA)

Analysis of variance (ANOVA), as a statistical technique, was used to test the significance of the main factors compared to a mean square. A goal of the ANOVA is to estimate the experimental flaw at a certain confidence level. This paper utilizes ANOVA for analyzing experimentally obtained arithmetic mean roughness (Ra). ANOVA illustrates the degree of importance of the four factors that influenced the arithmetic mean roughness (Ra).

Table 7. Results of ANOVA for the arithmetic mean roughness.

Factor	DOF	Sum of Squares	Variance	F
A	2	0.102	0.051	5.490
B	2	5.615	2.808	302.467
C	2	0.018	0.009	0.989
D	2	0.051	0.026	2.760
Error	18	0.17	0.009
Total	26	5.95

shows the results of the ANOVA for the arithmetic mean roughness (Ra).

The F-test magnitude for the depth of cut is less than 1, indicating limited significance for this specific value. Consequently, the consideration of factor C is reassessed, and upon its exclusion, the F-test value is recalculated, as shown in Table 7.

Columns 5 and 6 in

Table 8. Final ANOVA table.

Factor	DOF	Sum of Squares	Variance	F	Percent
A	2	0.0833	0.051	5.496	1.4%
B	2	5.596	2.808	302.8	94%
D	2	0.032	0.026	2.73	0.55%
Error	20	0.241	0.00927		4.05%

present the significance levels of the process parameters concerning the arithmetic mean roughness Ra, indicating whether the factors had a discernible impact on Ra. According to the F distribution tables, the thresholds for significance at 95% and 99% confidence levels are as follows: ${\mathrm{F}}_{0.05,2.20}$= 3.49 and ${\mathrm{F}}_{0.01,2.20}$ = 5.848. That means that only one factor, feed rate, presents physical and statistical significance corresponding to 95% and 99% confidence levels, since F > F$\alpha$ = 5% and F > F$\alpha$ = 1% for that factor. Factor A, cutting speed, presents physical and statistical significance corresponding to 95%, but not to 99% confidence. The colling lubricating technique shows physical and statistical insignificance for a confidence level of 95% and, therefore, for a confidence level of 99%. Extensive research has consistently demonstrated that the feed rate stands out as the most impactful factor, showing the most substantial influence on determining the arithmetic mean roughness (Ra) [7,11,14,15].

6. Utilizing Machine Learning (ML) for Predicting Surface Roughness in Milling

In the field of ML, working with small datasets can be challenging. Many ML models require large amounts of data for training. However, just a few ML algorithms can deal successfully with small datasets. The required size of a dataset for training an ML model can vary widely depending on several factors, the complexity of the problem and the specific requirements of the model. There is no fixed threshold for the “ideal” dataset size, but there are some general guidelines for different ML algorithms. This study conducts a comparative analysis employing various machine learning algorithms to predict surface roughness in milling using regression techniques. Each of these algorithms has strengths and weaknesses, making them suitable for different data types and problem scenarios. Given the dataset’s specific characteristics, which comprise a modest 27 samples and entail a regression task with four input features and one output, the following machine-learning approaches can be considered.

Neural Networks often require substantial data but can still be effective with small datasets. Regularization techniques can help prevent overfitting.

Decision trees can work well with small datasets because they partition the data into subsets based on simple rules. They are less likely to overfit, making them suitable for limited data.

Random forests build multiple decision trees and aggregate their predictions, improving accuracy and reducing overfitting. This ensemble approach is practical with small datasets.

Linear regression can be practical when there are transparent linear relationships between input and output. It is relatively simple and less prone to overfitting with small datasets.

K-Nearest Neighbors (KNN) makes predictions based on nearby data points. With small datasets, it identifies meaningful neighbors, leading to accurate predictions.

Ridge, Lasso, and Elastic Net Regression regularization techniques can prevent overfitting by introducing penalty terms into the regression process, which is particularly beneficial when data are scarce.

Support Vector Machine (SVM) Regression aims to find the best-fitting hyperplane. With a small dataset, SVM can still find a well-defined boundary between classes, avoiding overfitting.

Gradient boosting builds models sequentially, focusing on data points that were previously mispredicted. This targeted learning from limited data can lead to predictive solid performance.

The abovementioned techniques are less prone to overfitting and can effectively handle limited data. The appropriateness of each algorithm hinges on the distinct attributes of the dataset and the inherent relationships among variables. This paper will evaluate each of the mentioned algorithms, and by analyzing their performances, we will determine the most suitable choice for a small dataset. Evaluating the model performance quality involves various metrics that assess its performance and capabilities. To evaluate and access the quality of neural networks for regression tasks, the most often used are:

• Mean Squared Error (MSE) and Mean Absolute Error (MAE), as a measure of the magnitude of prediction errors;
• R-squared (Coefficient of Determination, which indicates the proportion of variance in the dependent variable that is predictable from the independent variables;

R-squared (R2) and Mean Squared Error (MSE) serve as critical metrics for evaluating the performance of regression models, yet they offer distinct insights. R-squared quantifies the proportion of predictability in the dependent variable (target) from the independent variables (features). It indicates how well the model’s predictions match the actual values. A higher R-squared value indicates a better fit of the model to the data. MSE measures the average squared difference between the predicted values and the actual values. It quantifies the average magnitude of errors, with smaller values indicating better performance. MSE provides a direct measure of the quality of predictions regarding their proximity to the actual values. In terms of evaluation, it is generally a good practice to consider both R-squared and MSE together to get a comprehensive understanding of the model’s performance: a good model should have a low MSE and a high R-squared value. In practice, it is common to consider both metrics and potentially other relevant metrics depending on the context of the problem.

The dataset utilized to train and evaluate the neural network model consists of 27 samples generated through an experiment conducted using a Taguchi-designed experimental plan, see Table 4.

Notably, the training phase involved 80% of these samples, resulting in 21 instances for training and six samples for testing and validation.

Sets of samples for training and testing vary based on different random states, which can result in a range of neural network performances. To address this issue, testing multiple seeds through a loop determines the best network performance, including metrics such as MSE and R-squared.

Consequently, the neural network that demonstrates the most optimal performance, as indicated by the highest R-squared value and the lowest MSE, is chosen for further testing and analysis.

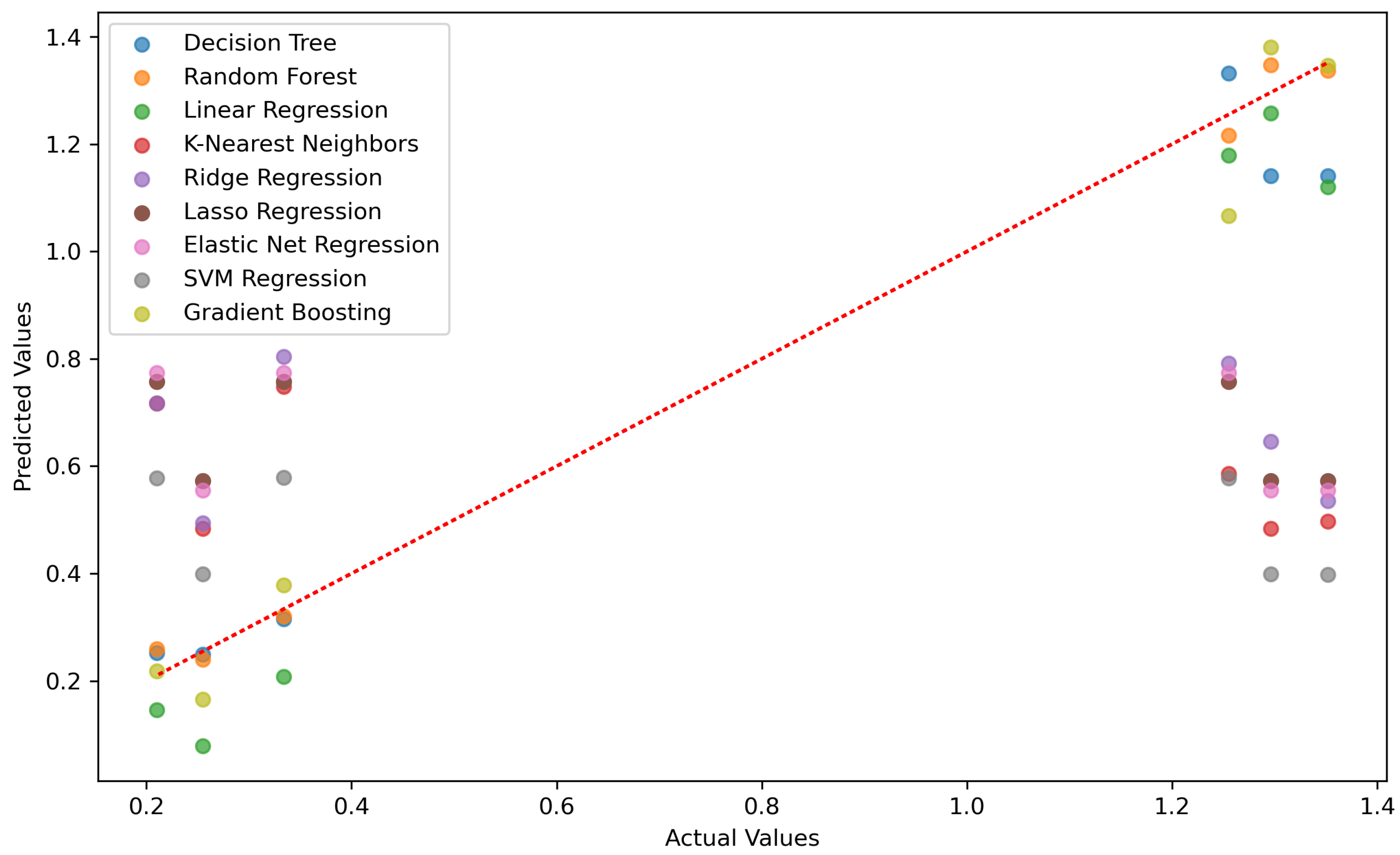
An additional experiment was conducted involving a dataset comprising 12 distinct sets, as presented in

Table 9. Experimental plan—L27 orthogonal array (Taguchi method).

No. of Trials	Cutting Speed (m/min)	Feed per Tooth (mm/tooth)	Axial Depth of Cut (mm)	Cooling/Lubricating Technique	Ra1 $\mathsf{\mu }$m	Ra2 $\mathsf{\mu }$m	Ra3 $\mathsf{\mu }$m
1	50	0.05	0.5	Vortex tube	0.247	0.227	0.247
2	50	0.2	0.5	Emulsion	1.244	1.14	1.165
3	50	0.125	0.8	Dry machining	0.425	0.444	0.42
4	50	0.2	0.8	Vortex tube	1.38	1.314	1.509
5	50	0.2	1.2	Emulsion	1.274	1.233	1.272
6	100	0.05	0.5	Dry machining	0.227	0.223	0.279
7	100	0.2	0.8	Dry machining	1.198	1.13	1.068
8	100	0.05	1.2	Emulsion	0.22	0.272	0.248
9	100	0.2	1.2	Vortex tube	1.365	1.406	1.581
10	150	0.2	0.8	Dry machining	1.005	1.253	1.092
11	150	0.05	1.2	Emulsion	0.313	0.267	0.28
12	150	0.125	1.2	Vortex tube	0.786	0.555	0.594

, to enhance the assessment of the neural network’s performance. The network’s training, testing, and validation stages did not include this dataset.

Its purpose lies in its utilization for simulating the models. As a result, the subsequent evaluation of these simulations will be visually showcased through graphical charts that display the Mean Squared Error (MSE) and R-squared (R2) values.

Cooling and lubricating techniques encompass various methods, including emulsion, dry, and vortex tubes. However, these descriptions are not suitable for machine learning. To make them usable, the get_dummies function is employed, as illustrated in

Table 10. Dummy variable mapping.

v	f	a	ra	Emulsion	Dry	Vortex Tube
50	0.05	0.5	0.194	1	0	0
50	0.05	0.8	0.255	0	1	0
50	0.05	1.2	0.249	0	0	1
50	0.125	0.5	0.337	0	1	0

.

This function transforms the textual representations of these techniques into numerical codes, allowing categorical variables to be represented as binary values. This enables these techniques to be utilized as input features for machine learning algorithms, enhancing the overall predictive capability of the models.

7. Deep Neural Network Evaluation—Model Performance Visualization and Validation Loss

Deep neural networks can be powerful and challenging to use with small datasets. While deep neural networks have the potential to extract valuable insights from small datasets, they also require careful consideration of overfitting and the appropriate use of regularization and hyperparameter tuning.

Constructing a robust machine-learning model entails a two-step process. Initially, it demands the provisioning of an initial dataset for training, which serves as the foundation upon which the model acquires its knowledge. Subsequently, the model’s capabilities are assessed by exposing it to previously unseen data, thereby evaluating its performance.

This paper shows an examination and comparison of the effects of two specific cross-validation techniques on model performance:

• Holdout Cross-Validation Technique: This approach involves partitioning the dataset into two distinct subsets: one for training and the other for validation. The model undergoes training on the training set, and its performance is subsequently evaluated on the validation set. This technique is known for its simplicity and speed, making it a common choice for initial model assessment.
• KFold Cross-Validation Technique: In contrast, the KFold cross-validation method involves dividing the dataset into ‘K’ equally sized subsets or “folds”. The model is trained ‘K’ times, each using a different fold for validation and the remaining folds for training. This process is repeated ‘K’ times, ensuring that each fold includes the validation set once. The results are averaged to provide a robust assessment of the model’s performance. KFold cross-validation is especially useful for assessing a model’s consistency and reducing the risk of overfitting.

The choice between these cross-validation techniques can significantly impact the performance and reliability of a machine learning model, and this paper aims to compare the effects of Holdout and KFold techniques on model outcomes.

Table 11. Neural network parameters assessed on test and simulation dataset, Holdout cross-validation.

Network Topology	R-Squared (Test)	MSE (Test)	R-Squared (Simulation)	MSE (Simulation)
4-8-1	0.9599	0.0093	0.3202	0.1534
4-10-1	0.9507	0.0144	0.2144	0.1773
4-12-1	0.9710	0.0071	0.6767	0.0730
4-8-8-1	0.9591	0.0058	0.1492	0.1920
4-10-10-1	0.9100	0.0186	0.6675	0.0750
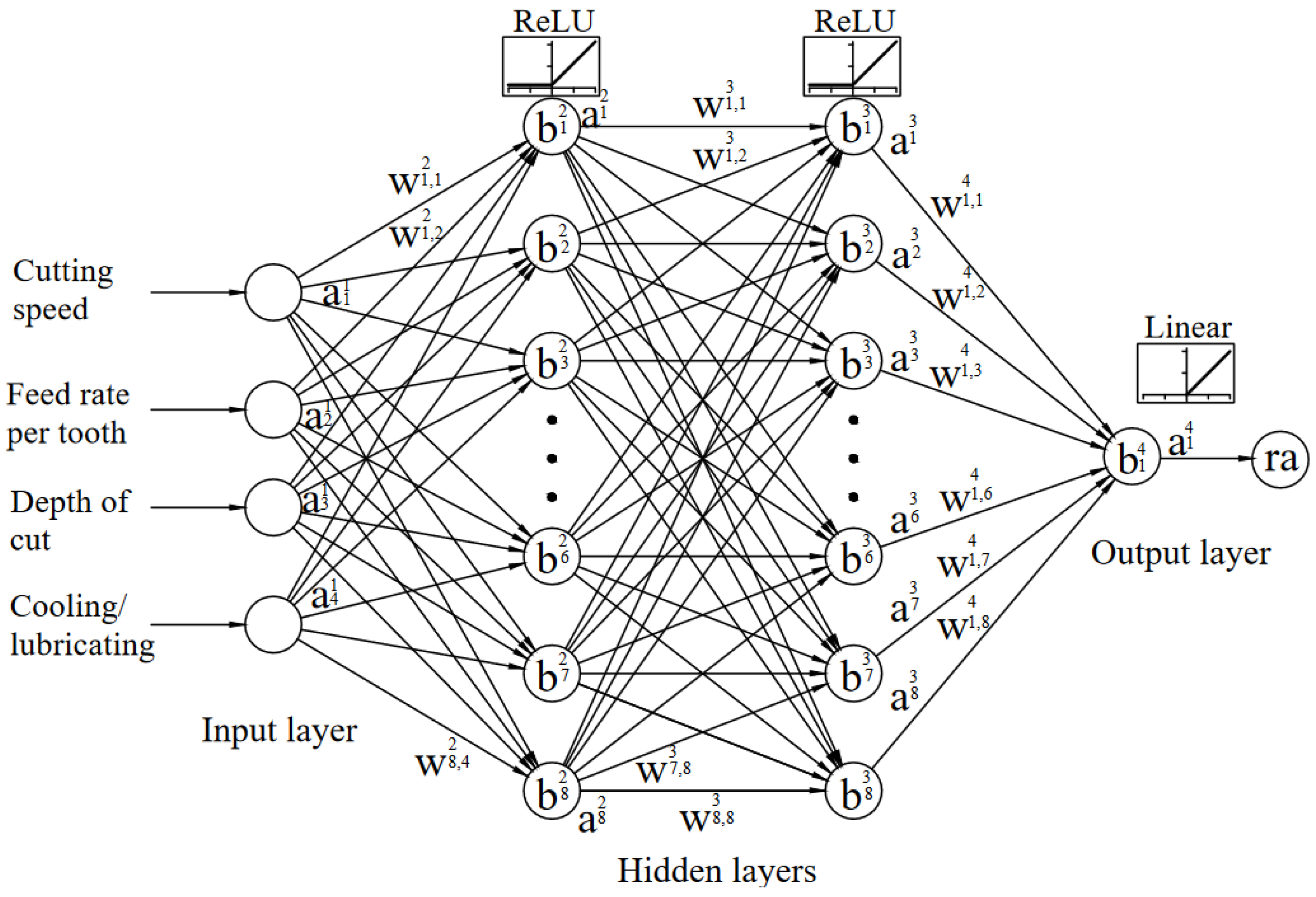
4-12-12-1	0.8603	0.0310	0.3512	0.1464

and

Table 12. Neural network parameters assessed on test and simulation dataset, KFold cross-validation.

Network Topology (Num. Fold)	R-Squared (Test)	MSE (Test)	R-Squared (Simulation)	MSE (Simulation)
4-12-1 (5)	0.5562	0.0819	0.5229	0.1077
4-12-1 (10)	0.3052	0.1181	-0.4100	0.3182
4-12-12-1 (5)	0.2623	0.1195	0.7444	0.0577
4-12-12-1 (10)	−0.5683	0.0803	0.6004	0.0902

show tested neural network topologies. All neural network architecture comprises one or two hidden layers, trained using the Adam optimization algorithm. The learning rate, set at 0.001, guides the network’s parameter updates. Each hidden layer comprises 8, 10, or 12 neurons, and the ReLU activation function facilitates the network’s nonlinear transformations and feature extraction. As evident from Table 11 and Table 12, holdout cross-validation provided a more unambiguous indication of the network’s performance on the test dataset. The 4-12-1 neural network topology with holdout cross-validation appears to be the best-performing model for an existing dataset regarding R-squared and MSE on the test dataset. KFold cross-validation results varied depending on the number of folds, making it essential to choose an appropriate number based on specific needs. Additionally, the performance on the simulation dataset may indicate overfitting, so further analysis and regularization techniques may be necessary to improve generalization. However, it is essential to consider the application and significance of these metrics in the specific problem domain. In summary, while holdout cross-validation provided more consistent and interpretable results, KFold cross-validation can help assess model stability and generalization across different subsets of the data. The choice between the two techniques should depend on specific goals and the trade-offs between model performance and computational resources.

Figure 4 visually illustrates the neural network configuration, offering insights into the specific architectural topology it utilizes.

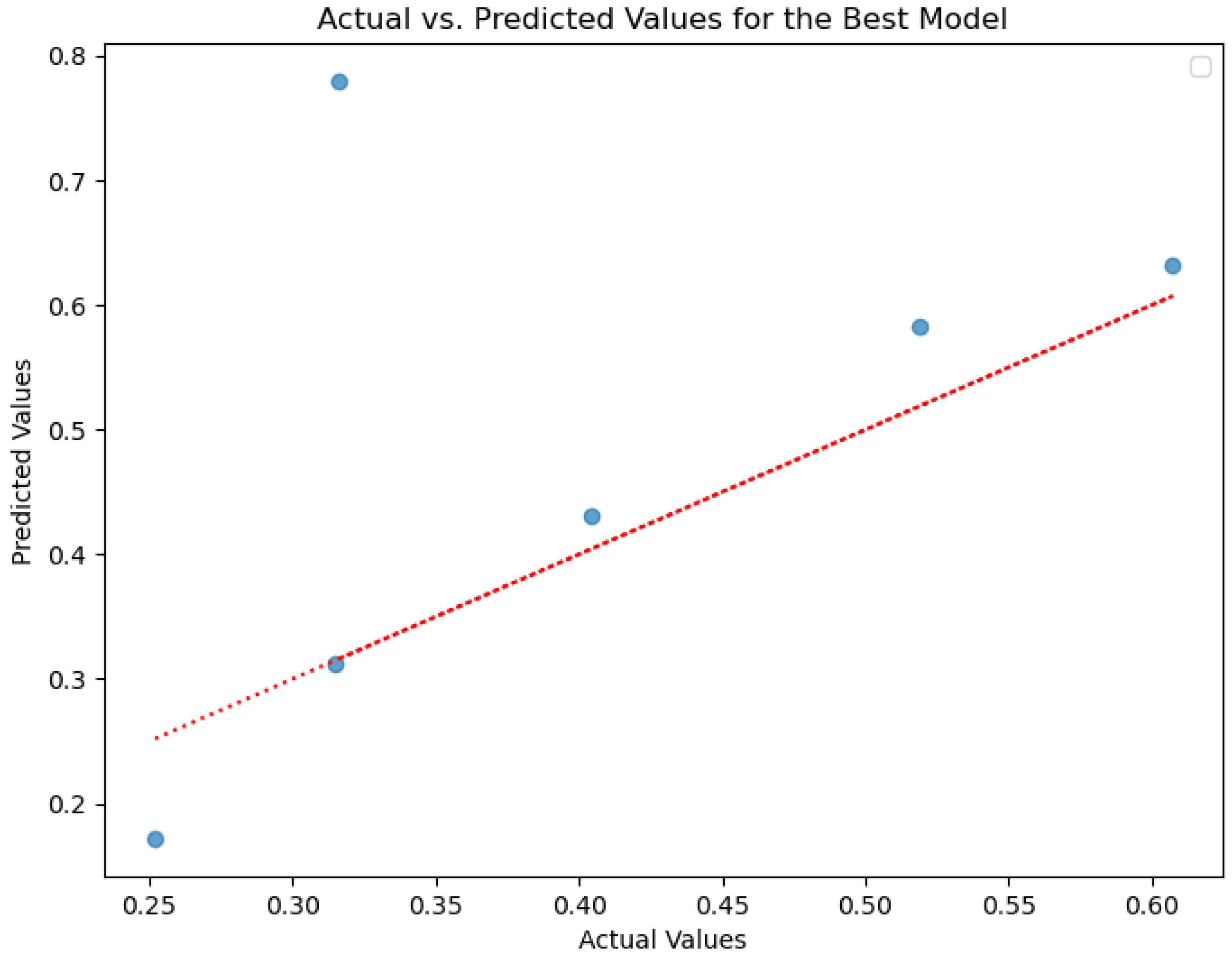
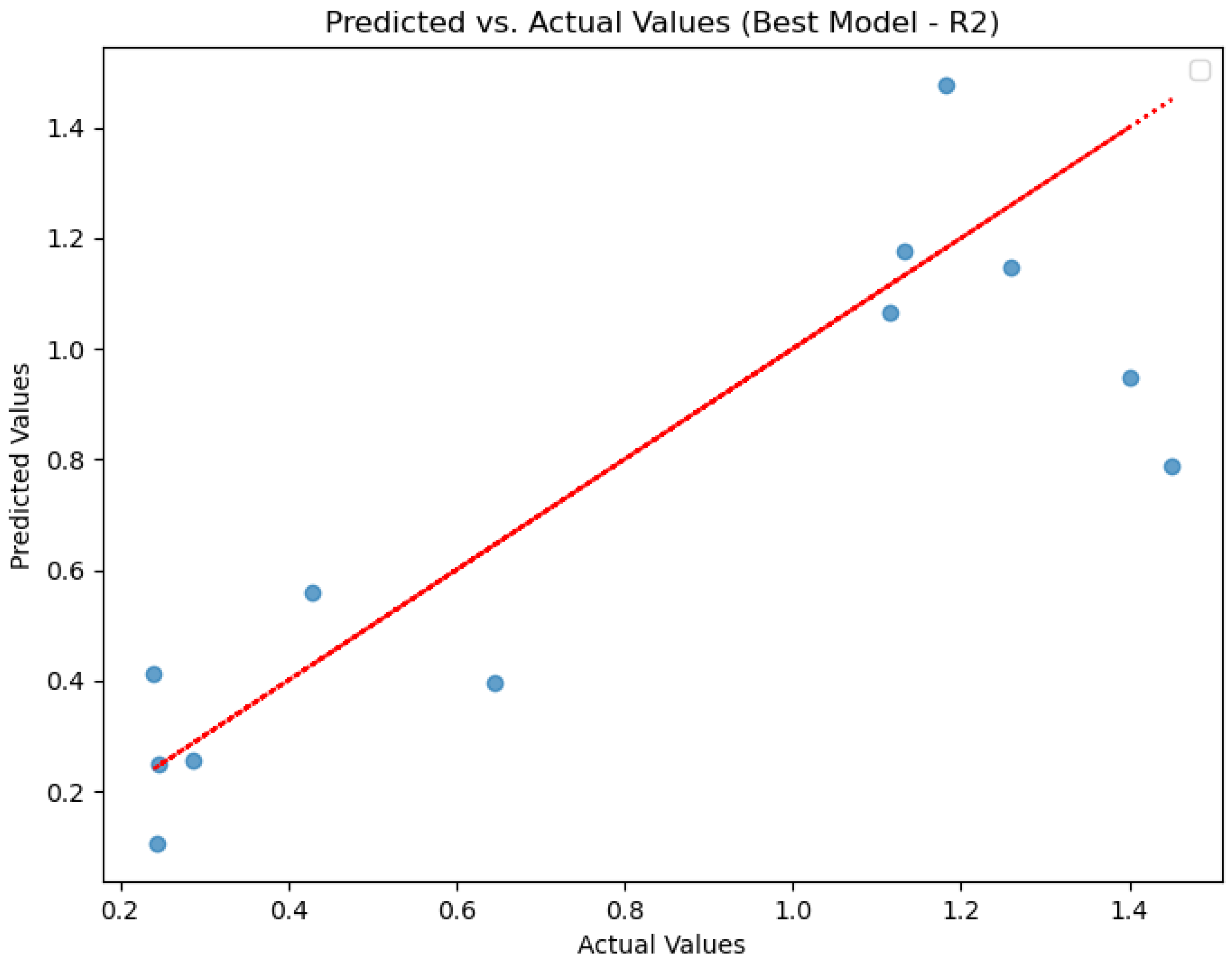
Figure 5 displays an actual vs. predicted values diagram generated by a neural network (NN) for testing the dataset. This type of diagram typically consists of scatter points that represent the valid (actual) values on one axis and the predicted values on the other axis. Each point corresponds to a data instance, where its position on the graph indicates how close the expected value is to the actual value. The ideal scenario would be a diagonal line (y = x), indicating perfect predictions where all points lie on that line. In this case, the coefficient of determination (R-squared) for the data in Figure 5 is 0.9710, suggesting that the predicted values from the deep neural network can explain approximately 97.1% of the variability in the actual values. 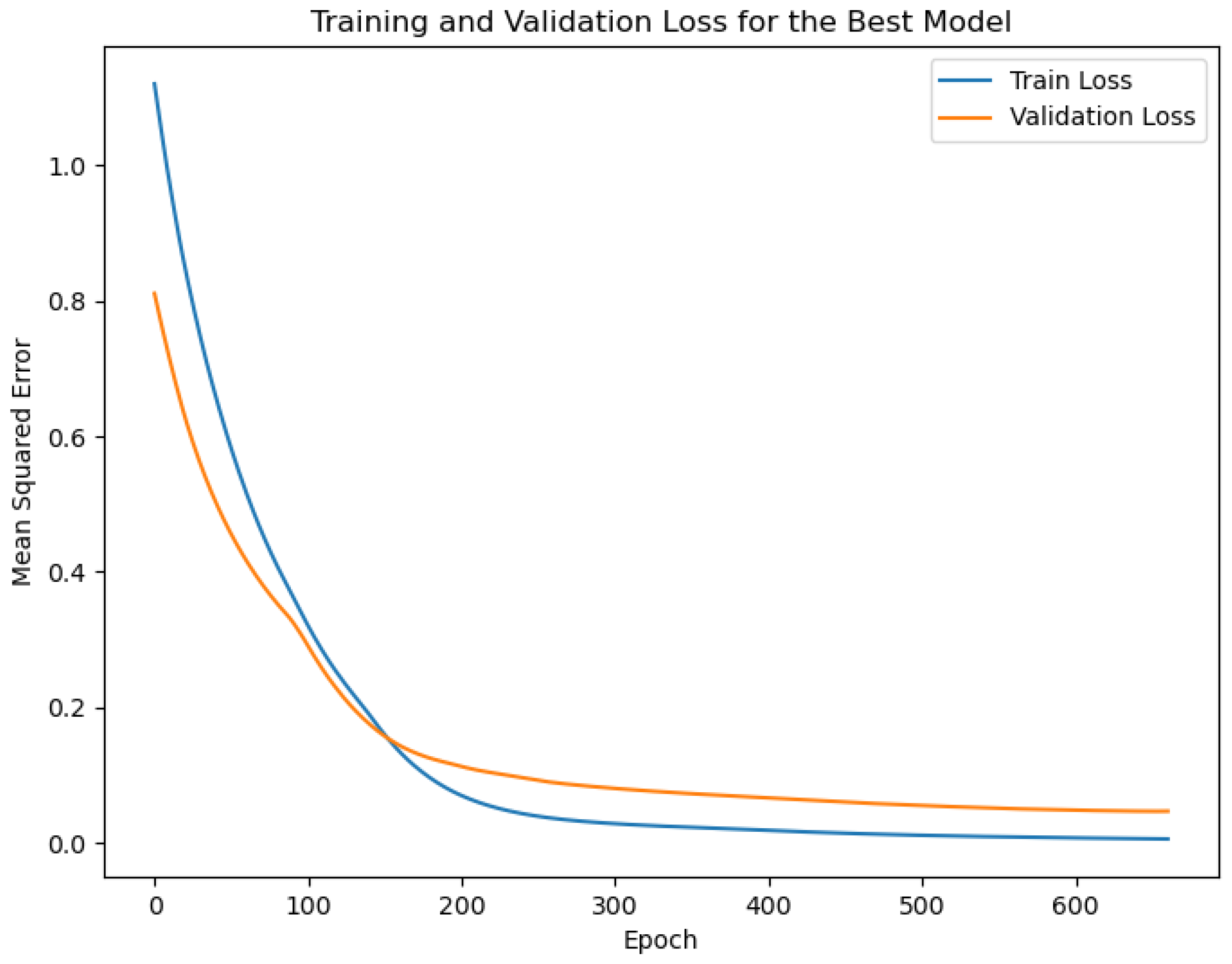Figure 6 displays the trend of validation loss throughout the training of the deep neural network. The calculated Mean Squared Error (MSE) for this model is 0.0071, signifying the average deviation of predicted values from the actual values in the validation dataset. The validation loss curve in Figure 6 starts at the beginning of training and is observed up to 661 epochs. Despite setting a total of 2000 epochs for training, an early stop function halted the training process when the validation loss no longer significantly improved. This technique helps prevent overfitting and ensures that the model’s generalization ability is not compromised.

In this case, with early stopping, the training was stopped at the 661st epoch, suggesting that the model achieved a good balance between capturing patterns and avoiding overfitting. An MSE of 0.0071 indicates that, on average, the squared difference between the predicted and actual values is relatively low, suggesting that the model’s predictions are reasonably close to the real values in the validation dataset and provide a well-regulated training process that helps produce a model with solid generalization capabilities. Figure 7 showcases the performance of the deep neural network model on a previously unseen dataset through a diagram depicting actual vs. predicted values. The Mean Squared Error (MSE) of the model is 0.073, suggesting a moderately accurate level of prediction. An R-squared value of 0.6767 indicates that the model’s predictions explain approximately 67.67% of the variability in the actual values. While the model’s performance could be more robust during the training and validation, it demonstrates a reasonable ability to capture patterns in new, unseen data.

8. Comparative Evaluation of Performances: Regression Algorithms Analysis

Keeping in mind that the best model was found through a loop, aiming for a minimum MSE and maximum R-squared, and dealing with variability in model performance between runs, as well as experimenting with various training processes, layer configurations, and optimization methods, it is indeed a complex and iterative process. Exploring alternative algorithms or methodologies is a natural step when confronted with challenges such as these. While deep neural networks have shown great promise in various domains, they are sometimes the best fit for specific problems.

Figure 8 provides a comparative view of actual vs. predicted values for a range of commonly used regression algorithms, each designed to address overfitting concerns. Through an iterative process, including training loops, the best-performing models were selected. Among these models, the Best Random Forest algorithm stands out with a low Mean Squared Error (MSE) of 0.0007, indicative of precise predictions, and a high R-squared value of 0.9958, showcasing a robust explanation of the variance in the data. Low MSE and high R-squared highlight the effectiveness of the Random Forest method in capturing complex relationships within the dataset while resisting overfitting. Other algorithms also display varying performance levels, underlining the importance of method selection based on specific problem characteristics.

Figure 9 displays the evaluation of the performance of various regression algorithms that underwent optimization through iterative loops. The bar chart diagram provides a visual depiction of the Mean Squared Error (MSE) and R-squared scores for each algorithm. These optimized models have been fine-tuned to strike a balance between precision and generalization, and their representation in this figure illustrates their effectiveness in addressing overfitting concerns and capturing the underlying patterns in the data.

Figure 10 shows a model’s performance by presenting a bar chart comparison of Mean Squared Error (MSE) and R-squared scores for the simulated best models. The chart provides a clear visual representation of how these models stack up against each other, shedding light on the nuances of their predictive capabilities and their capacity to explain the variability within the data.

9. Conclusions

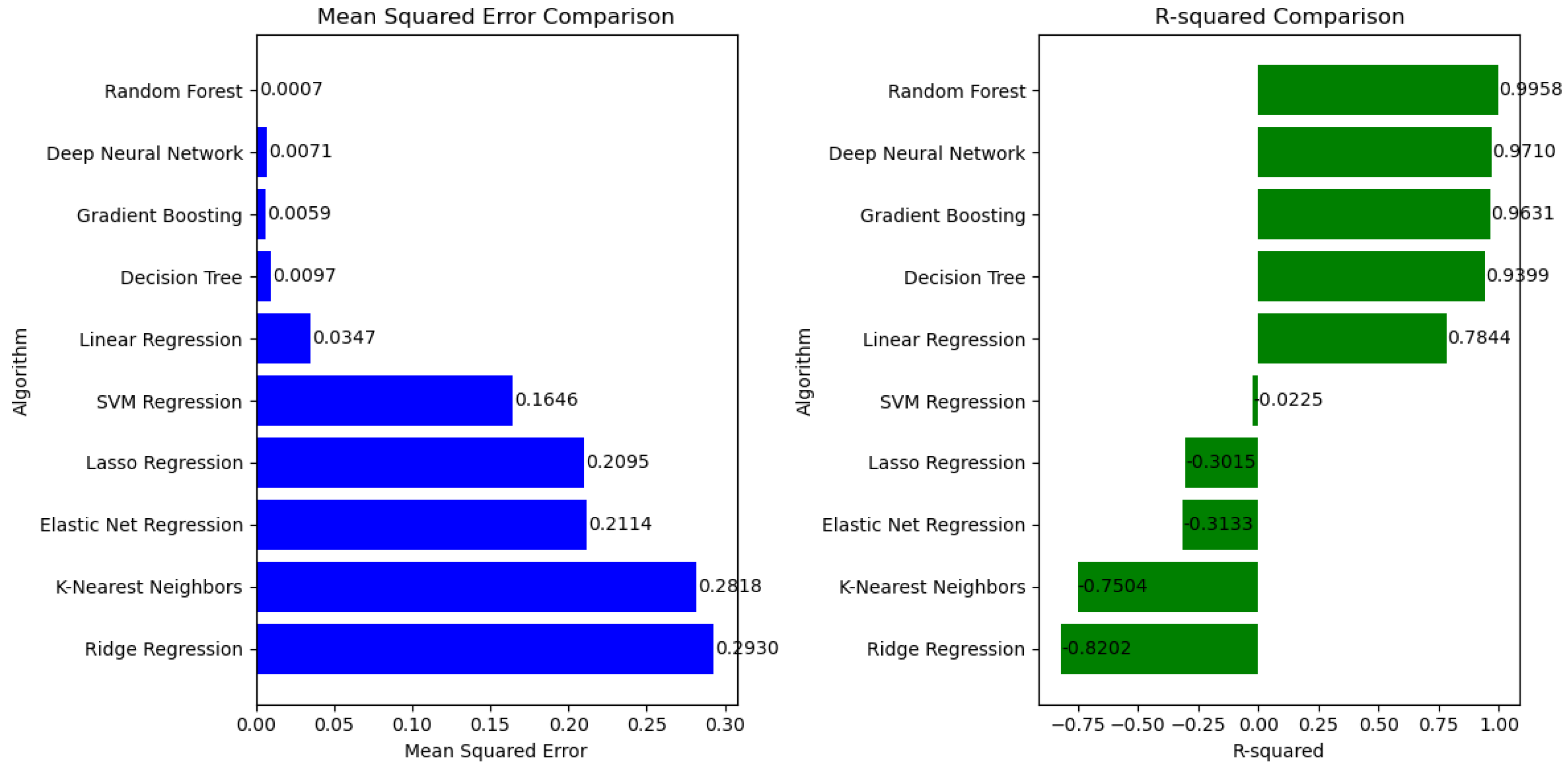
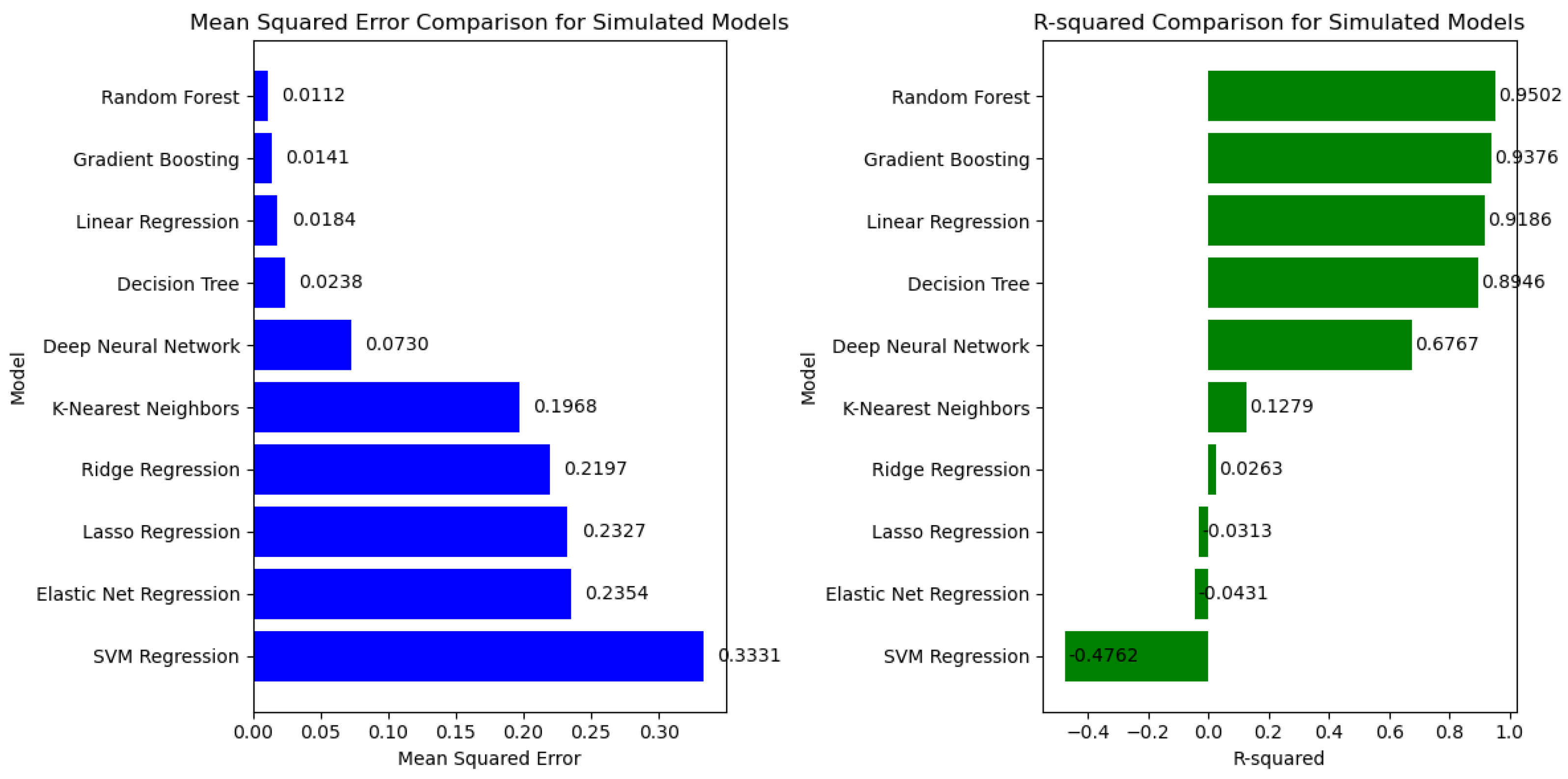
This paper consists of two distinct parts. In the initial phase, the research investigated the impact of cutting parameters and a range of factor levels on average surface roughness (Ra) during the milling process of the biocompatible titanium alloy Ti-6Al-4V. The considered machining parameters included cutting speed, feed rate, depth of cut, and the chosen cooling/lubricating method. Using the Taguchi methodology in the design of the experiment led to the execution of an experiment involving 27 individual runs, which produced a dataset of 27 sets. The outcomes highlighted a notable influence of the feed rate, as evident from the ANOVA analysis, which indicated the relative insignificance of other factors. In the subsequent phase, the dataset, which consists of the 27 sets from the first experiment, was used to train various neural networks. In the second part of the research, an extensive comparative analysis was conducted to assess the performance of several neural network algorithms in addressing regression problems. This analysis unveiled the most effective models, achieved through iterative loops and model simulation on previously unseen data. Among the array of algorithms explored, the Best Random Forest algorithm demonstrated superior performance in terms of metrics. It achieved a notably low Mean Squared Error (MSE) of 0.0007, coupled with a relatively high R-squared value of 0.9958 when tested on the dataset. Additionally, the simulation dataset exhibited commendable performance with an MSE of 0.0112 and an R-squared of 0.9502. These results underscore the robustness of Random Forests in effectively addressing the challenges posed by small datasets. On the other hand, the Neural Network showcased slightly lower performance, achieving an MSE of 0.0071 and an R-squared value of 0.9710. However, its performance on the simulation dataset was comparatively less promising, with an MSE of 0.0730 and an R-squared of 0.6767. Given these findings, the Random Forest algorithm emerges as a preferable choice, given its more consistent and reliable performance across both datasets. This success highlights its potential as a tool for similar tasks. The Best Gradient Boosting algorithm delivered impressive results with a low Mean Squared Error (MSE) of 0.0059, accompanied by a commendable R-squared value of 0.9631, achieved with a seed of 18. This performance on the test dataset showcases its efficacy. On the simulation dataset, it maintained its strength with an R-squared value of 0.9376 and a Mean Squared Error (MSE) of 0.0141. Notably, this performance is right behind the Random Forest algorithm. While the Decision Tree and Linear Regression algorithms show respectable performance, they slightly trail behind the top-performing algorithms. In contrast, the outlook for the other algorithms appears less promising, as they have yet to demonstrate competitive results. Nonetheless, it is imperative to acknowledge that selecting the optimal algorithm depends on the specific problem context, which underscores the importance of meticulous model selection and fine-tuning based on the inherent characteristics of the problem. In essence, this investigation underscores the versatility of a diverse range of regression techniques, thereby serving as a guide for decision-making in the model selection and evaluation.