Abstract
This work investigates the efficacy of high-pressure torsion (HPT), as a severe plastic deformation mechanism for processing plain and silicon-carbide-reinforced AA6061, with the broader objective of using the technique for improving the properties of lightweight materials for a range of objectives. The interactions between input variables, such as the pressure and equivalent strain (εeq) applied during HPT processing, and the presence of SiCp and response variables, like the relative density, grain refinement, homogeneity of the structure, and the mechanical properties of the AA6061 aluminum matrix, were investigated. Hot compaction (HC) of the mixed powders followed by HPT were employed to produce AA6061 discs with and without 15% SiCp. The experimental findings were then analyzed statistically using the response surface methodology (RSM) and a machine learning (ML) approach to predict the output variables and to optimize the input parameters. The optimum combination of HPT process parameters was confirmed by the genetic algorithm (GA) and ML approaches. Furthermore, the constructed ML and RSM models were validated experimentally by HPT processing the same material under new conditions not fed into the models and comparing the experimental results to those predicted by the model. From the ML and RSM models, it was found that processing the AA6061/SiCp composite HPT via four revolutions at 3 GPa produced the highest mechanical properties coupled with significant grain refinement compared to the HC condition. ML analysis revealed that the equivalent strain induced by the number of revolutions was the most effective parameter for grain refinement, whereas the presence of SiCp played the highest role in improving both the hardness values and the compressive strength of the AA6061 matrices.
1. Introduction
Due to their low density and good workability, aluminum alloys stand out for their wide range of industrial applications; nonetheless, their usage is constrained by their comparatively low yield strength and poor wear resistance. The study of aluminum matrix composites (AMCs) has been prompted to obtain better mechanical behavior for specific applications, such as defense, aerospace, automotive, and aeronautic industries [1,2]. Significant AMC attributes, such as its superior strength-to-weight ratio, energy efficiency, and greater wear resistance, increase its potential to outperform traditional aluminum alloys [3]. One type of these composites—AMC reinforced with SiC particles—promises to be more useful than other metal matrix composites (MMCs) because of its distinct qualities, including a higher strength, elastic modulus, wear resistance, electrical conductivity, and a lower thermal expansion coefficient than conventional alloys [4,5]. Engine pistons and cylinder liners, brake rotors for automobiles, bearing surfaces, tank tracks, maritime winch drums, and wear-resistant coatings are some of the most frequent places where components are exposed to mechanical damage [6]. One of the many methods used to create aluminum–SiC composites is the powder metallurgy (PM) approach, which has a strong reputation in terms of regulated material behavior due to careful microstructure control [7]. Due to its excellent formability and weldability among the many AMCs, the 6xxx Al alloy is frequently used in a variety of engineering sectors [8]. Furthermore, it has recently come to light that by adjusting the grain refinement procedures, a better knowledge of the strengthening and flow behavior of the Al alloys of the 6xxx family can provide more efficient manipulation of these alloys [9].
Production of ultrafine-grained (UFG) and nanocrystalline (NC) materials is in high demand due to their superior mechanical qualities and greater strength-to-weight ratio. As a result, much early research has focused on various methods for producing UFG materials with improved physical, mechanical, tribological, thermal, electrochemical, and electrical characteristics [9,10]. Processing of materials through various techniques of severe plastic deformation (SPD), commonly equal-channel angular pressing (ECAP) [10] and high-pressure torsion (HPT) [11], and multi-channel spiral twist extrusion (MCSTE) [12] offered the opportunity to achieve much finer grain sizes than those obtained by conventional processes including rolling and extrusion. HPT is a more efficient process that is capable of producing ultrafine grain sizes and high strength levels [13,14]. For example, AA6061 HPT-processed samples display grain sizes 22–30% finer than those processed by ECAP as a result of the severe strain imposed during processing [15]. Moreover, HPT is used for the recycling of monolithic metal chips and composite metal chips [16], which improves friction and wear performance [17]. HPT is also used for powder consolidating [9] and enhances the hydrogenation kinetics among various hydrogen storage materials [18]. During HPT processing, a cylindrical-shaped sample is pressed in the middle of two rotating anvils relative to one another, which subjects the disc to severe torsional stress [11]. The applied strain fluctuates over the disc’s radius, and the shear strain and equivalent strain may be calculated as shown in Equations (1) and (2), respectively.
where γ, εeq, r, N, ho, and h are the shear strain, equivalent strain, the distance from the center of the disc, number of revolutions, original disc thickness, and the final disc thickness, respectively [11].
Extensive research has been conducted to develop various material design techniques, such as the design of experiment methodologies, optimization procedures, and physical-based models, in order to examine and produce unique materials with distinct properties [19,20,21]. To investigate the right links between intricate material attributes and design concepts, these traditional approaches usually require thorough physics-based analysis. In this sense, it was essential to first study a number of fundamental physical and chemical laws that govern material properties. Machine learning (ML) models, which require just a database to capture the complex relationship between material properties and design parameters, were another option. They are regarded as an innovative approach that has lately gained great success in the material design sector [22].
ML models with high prediction performance aided in the discovery of material property correlations several orders of magnitude quicker than any other conventional material design approach. The ML area has recently experienced a rising interest in many industrial applications, owing to the fast increase in computer performance and capabilities as well as the availability of massive datasets and successfully implemented complex algorithms. As a result, ML approaches are increasingly being utilized effectively to tackle large datasets with high-dimensional inputs and accomplish various difficult tasks such as regression, classification, data clustering, and dimensionality reduction. In addition, ML technology has the potential to manage and expose complex material systems quickly, including rapid functional changes, extracting information from available data, and predicting system performance. When new datasets are fed into trained and well-tested ML models, they can act as a data analysis tool, extracting results autonomously [23,24].
On the other hand, in modern computing database technology, the development and expansion of applicable mathematical insights is a vital requirement. Earlier studies adopted the response surface methodology (RSM) with the aim of optimizing severe plastic deformation (SPD) techniques. RSM is an experimental system of mathematical and statistical techniques that are used to simulate and improve experiments [25]. In order to prevent local optimum solutions, the genetic algorithm (GA) is also employed in optimization. GA is a technique that is frequently utilized in industry and science. GA offers the best algorithms in each individual through a common convention method that creates a single point and adopts a predetermined technique to choose the following generation. Each generation assesses individual fitness capabilities. GA uses specific methods to obtain a solution targeting a global minimum for a fitness function, which ensures convergence of the findings [26,27].
In light of the above survey and with the goal of optimization of the HPT processing parameters for the enhancement of the mechanical properties of lightweight materials for a spectrum of applications, this work presents a detailed investigation. In particular, the influence of addition of SiC particles on the structural evolution and mechanical properties of AA6061 as a function of the HPT processing pressure and εeq induced by variable number of revolutions was investigated and compared to the plain alloy. Additionally, prediction of the output variables and optimization of the input parameters were developed using ML and statistical approaches. The experimental data in this study were analyzed using ANOVA to identify the input parameters’ most significant effects on the output responses’ relative density, grain size, compressive strength, and hardness. Furthermore, the ML, GA, and hybrid design of experiment-GA (DOE-GA) algorithms were used to identify the HPT optimum processing parameters. In addition, the constructed ML and RSM models were validated experimentally by HPT processing AA6061/SiCp composite through different parameters, and the experimental results were compared with the predicted findings. Figure 1 demonstrates the flow diagram of the detailed work strategy of this study.
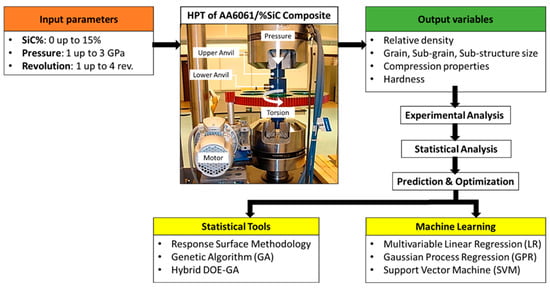
Figure 1.
Experimental procedure flow diagram.
2. Methodology
2.1. Materials and Experimental Procedures
AA6061 aluminum alloy (0.9% Mg, 0.6% Si, 0.5% Fe, 0.3% Cu, 0.25% Cr, 0.2% Zn, 0.1% Ti, 0.05% Mn, and Al balance) and a reinforced 15 vol% SiCp metal matrix composite (MMC) variant were fabricated with powder metallurgy. The as-received AA6061 powder was supplied by Aluminum Powders Company limited (APC), and SiC powder was supplied by American Elements Company (AEC). AA6061 particles were characterized by irregularity in shape, size variation from 10 to 75 µm and an average particle size of 30 µm. The as-received SiC powders were characterized by non-uniformity in shape with particles size ranging from 1 to 5 µm and an average size of 2 µm. The two powders were mixed in a vacuum glove box and then blended for three hours at 96 rpm in a turbula mixer. Discs with a diameter of 10 mm and a thickness of 9.7 mm were prepared through a single-sided uniaxial hot compaction (HC) process that lasted for 30 min at 400 °C and 525 MPa compaction pressure by means of an ARMSTRONG 100-ton hydraulic press. Each disc was HPT processed under either 1 or 3 GPa pressure on the upper anvil and for 1, 2, or 4 revolutions on the lower anvil at room temperature. The HPT and HC dies were manufactured from high strength tool steel (AISI-W302), hardened until 55 HRC, and purchased and treated at Böhler, Egypt.
The microstructural evolution, density, and compressive properties were investigated before and after HPT for both AA6061 and AA6061–SiCp. The disc was prepared by mounting, grinding, appropriate polishing until a mirror-like gloss was achieved with an alumina fluid, and lastly, treating it with “Keller” adhesive. Grain structure was investigated using LEO field emission scanning electron microscopy (FESEM), and the average size of the grains and sub-grains was calculated using the average grain intercept (AGI) method. Density was measured using a Mettler Toledo XS 205 digital densitometer that uses the Archimedean principle to determine density. The hardness of the HPT-processed discs was measured using a Vickers hardness (HV) tester at three locations along the disc’s cross-section: at the center, the half radius mark, and periphery. The hardness readings collected and displayed are the average of 5 equidistant indentations. Hv tests were conducted using a load of 1 kg applied for 15 s. A compression test was conducted at room temperature using a Materials Testing System (MTS) machine with an applied force of 500 KN and a strain rate of 1 × 10−5 S−1. Three compression specimens per condition were tested, and the average values of the mechanical properties were recorded.
2.2. Machine Learning (ML) Approach
There are several types of ML methodologies, including supervised learning, unsupervised learning, semi-supervised learning, and reinforcement learning. The most common form of ML technique is supervised learning, which utilizes training data to identify patterns and predict future outcomes based on past results [28,29]. Many critical phases are included in the unsupervised learning framework, such as data preprocessing, data standardization, feature extraction, algorithm selection, model training, validation, and testing. The model learning process starts with the training dataset being used to formulate an initial model that is capable of matching the input data with adjusted variables. The majority of model learning strategies are implemented by searching within the training data for empirical correlations that may achieve best-fit relationships that properly predict the targeted output of the model. The validation dataset is used to fine-tune the model’s variable structure for further accuracy. The model is then trained by maximizing its performance, which is frequently measured using some sort of cost function. This usually necessitates modifying model hyperparameters that influence the training process, model structure, and characteristics. Ideally, the validation and testing sets should both be distinct from the training set, yet all three should share the same probability distribution.
Overfitting is an issue that may arise during model training in which the model perfectly fits all of the points in the dataset while ignoring the regularization criterion. In this situation, the trained model almost always fails to perform well in the testing phase. To overcome this problem, especially with a small dataset, as in this study, the cross-validation (CV) approach is applied. The k-fold CV method splits the dataset into smaller subsets, which are identified as “folds” and are randomly chosen. All folds except one are used as the training dataset the model is validated with, and the residual fold is used as a test set to calculate and evaluate its implementation. This process is performed k times within an iterative loop that cycles through all unique folds to validate the model. Model performance metrics are computed using the average of the metrics acquired in the whole loop. This method is computationally costly; however, it preserves the need for excessive data, particularly when training is to be performed on a small set of data. Cross-validation has the benefit of providing a more trustworthy assessment of the model’s performance than a single train/test split. By testing the model on numerous subsets of the data, the potential of overfitting to a specific subset or bias in the data is reduced. However, cross-validation does not always offer improved prediction results. Rather, it estimates the model’s performance on new, previously unseen data. This may be used to compare model performance or to tune the hyperparameters of a single model. It is also worth mentioning that cross-validation results might vary based on the precise subsets of data utilized in each fold. Therefore, in this work, we optimized the number of k-folds to be five folds (i.e., k = 5). The flow chart of a typical machine learning workflow that includes cross-validation is summarized as follows:
- Data preparation: This step includes collecting the data, cleaning, feature engineering, and normalization.
- Data splitting: The data are split into training and testing sets. Optionally, the data can also be split into validation sets to tune hyperparameters.
- Model defining: This step includes choosing a machine learning algorithm and defining the model architecture.
- Model training: The model is trained on the training dataset using the chosen algorithm and hyperparameters.
- Model evaluation: The model is tested on the testing dataset to evaluate its performance. Optionally, the validation set can also be used to tune hyperparameters.
- Cross-validation: k-fold cross-validation is performed to estimate the performance of the model on new, unseen data. This step is repeated with different random splits of the data, and the results are averaged to increase the reliability of the estimate.
- Hyperparameter tuning: The results of cross-validation are used to tune the hyperparameters of the model, such as the learning rate, regularization strength, or number of layers.
- Evaluation of the final model: after training the final model on the entire dataset using the optimized hyperparameters, it is important to test the final model on a holdout dataset to evaluate its performance on new, unseen data.
- Model deployment: The final model is deployed in production, and its performance over time is monitored.
To evaluate prediction performance of ML, the most commonly used performance metrics are the root mean square error (RMSE) and the coefficient of determination (R2-score). RMSE measures the average deviation of the predicted values from the actual values, expressed in the same units as the target variable. RMSE is a popular metric because it penalizes large errors more heavily than small errors and is sensitive to outliers. A lower RMSE value indicates better model performance, as it means the model’s predictions are closer to the actual values. The coefficient of determination measures the proportion of the variance in the target variable that is explained by the model. R2-score produces values between 0 and 1, with higher values indicating better model performance.
In this study, multiple ML algorithms were used, including multivariable linear regression (LR), Gaussian process regression (GPR), and support vector machine (SVM) regression (SVR). The adopted approaches are briefly introduced in the following section.
2.2.1. Multivariable Linear Regression
Linear regression models are commonly used to characterize the connection between a set of predictive input variables and an outcome response variable. The linear regression approach employs supervised ML to determine the most appropriate linear connection between the predictor(s) and the outcome response. It is valuable for explaining and foreseeing the response of intricate systems, in addition to interpreting data resulting from experiments and from fields like biology, finance, and chemistry. When there are several independent variables (X), linear regression (Equation (3)) yields an answer vector (Y) in the form of:
where βn signifies the estimated linear parameters, β0 signifies the constant, and indicates the error terms.
2.2.2. Regression Gaussian Process
The GPR regression technique is a nonparametric Bayesian regression methodology that was the result of recent significant breakthroughs in ML [29,30]. The methodology possesses many benefits, such as the capability to work adequately on a limited amount of data and generate predictions of uncertainty.
Considering the training dataset (xi, yi); i = 1, 2, …, n, where xi ϵ ℝd and yi ϵ ℝ are derived from an unknown distribution, a GPR model is used to predict the value of a response variable y* given the new input vector x* and the training data. Equation (4), a linear regression model, has the following structure:
where the β vector is the estimated coefficient that fits the model, and the error term is denoted as ε ∼ N(0, σ2), where N( ) indicates a normal distribution of the error with a mean of zero and a variance of σ2. In general, a Gaussian process (GP) is described via its mean function m(x) and covariance function (or kernel function) k(x, x′), where x and x′ are two instances in the input feature matrix x. Therefore, Equation (5) presents the predicted values of y* reformulated as a GP:
It should be noted that the covariance function must be properly chosen or created since it is critical in deciding the performance of GPR. In reality, there are multiple common covariance functions in the GPR; however, choosing one is a case-by-case decision. One of the famous kernels commonly utilized with GPR is the radial basis function, Equation (6), which is written as [31]:
where represents the Euclidean distance among the two feature vectors, and σ signifies the dispersion of the kernel function’s distribution.
2.2.3. Support Vector Machine
The SVM method is usually adopted with classification or regression cases [31]. Support vector machine regression (SVR) is based on classification procedures identical to the SVM albeit with minor modifications [32,33,34,35]. A tolerance margin (ε) is provided whenever regression must be conducted. It represents a region around the predicted function where errors within this region are considered to be acceptable and have zero loss function. In addition, there is a more complex justification is that the algorithm is more sophisticated and must be accounted for. The SVM method works by finding the hyperplane that best divides data into many classes with the maximum margin. The function f(x) is implemented to effectively estimate the provided training dataset (xi, yi), i = 1, 2, ……, N, where xn is a multivariate collection. In the most basic form, the function f(x) is written as (Equation (7)) [31]:
Minimizing the following formula [31], Equations (8) and (9), yields the optimum values of the weight w and the bias term b:
where and are slack variables that introduced in the SVM method to produce a regression function with soft margin. The slack variables are non-negative variables that allow some data points to be on the wrong side of the margin or the hyperplane. C is a balance between the empirically estimated error and generic term. The objective function of the SVM is then modified to minimize the sum of the slack variables, subject to the constraint that the classification errors are limited by a certain threshold.
Subject to:
where is an ε-insensitive tube expressing an acceptable error tolerance with negligible loss. Using the optimal constraints along with Lagrangian multipliers, the regression function may be expressed as follows in Equation (10) [31]:
where K(xi, x) is referred to as the kernel function. The resulting objective function is then optimized with respect to both the hyperplane coefficients and the Lagrange multipliers ( and ). The Lagrange multipliers act as weights that determine the importance of each data point in defining the hyperplane. The linear, polynomial, sigmoidal, Gaussian, and radial basis functions are some of the most well-known kernel functions that are commonly used with SVR.
2.2.4. Analysis of ML Approach
Correlation coefficients quantify the strength of a link between two variables. Pearson’s correlation coefficient (r) is the most commonly used to identify the linear relation between features and the target model output in ML models utilizing linear regression computation. It is the slope of the least-squares-estimated straight line describing the linear association of two variables. It is a statistical measure that describes the intensity and direction of that connection and is calculated by obtaining the covariance of the two variables and dividing it by the multiplication product of both variables’ standard deviations. It has a range of outcomes from −1 to +1, where the positive values indicate a direct relationship with an increasing proportional slope line and vice versa. Strong correlations are shown by coefficient values approaching 1, regardless of the sign, while weak correlations approach 0.0. Values smaller than 0.3 are considered weak correlations, those ranging from 0.3 to 0.5 are considered to be medium correlations, and those between 0.5 and 1 reflect strong correlations. Figure 2 shows the correlation chart for the input variables representing the model parameters and the measured outcomes of the calculated responses. It provides a visual and numerical display of the overall correlations among all inputs and outcomes in pairs based on r values, as depicted in the input data matrix. Each off-diagonal subplot has a scatterplot of a pair of variables, and each diagonal subplot reveals a histogram to give an indication of the variables’ distribution.
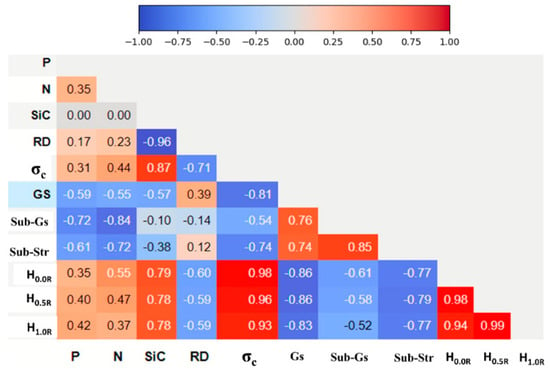
Figure 2.
Correlation plots of all response composite properties (RD, GS, Sub-Gs, Sub-Str, σc, and Vicker’s microhardness at H0.0R, H0.5R, and H1.0R versus process feature parameters (P, N, and SiC content).
Figure 2 shows that grain size (GS), sub-grain size (Sub-Gs), and sub-structure size (Sub-Str) strongly correlated with both HPT pressure (P) and the number of revolutions (N). The former inputs had high negative significant correlations with P of −0.59, −0.72, and −0.61, respectively and also high negative significant correlations with the N of −0.55, −0.84, and −0.72, respectively. On the other hand, only GS had a high correlation of -0.57 with SiC content, while Sub-Gs and Sub-Str showed moderately low correlations of -0.10 and -0.38 with SiC content, respectively. In addition, it was noted that the SiC content affected the relative density (RD) strongly, as it revealed a high negative significant correlation of −0.96, while it showed an insignificant positive correlation with P and N of 0.17 and 0.23, respectively. It was also clear that increasing P, N, and SiC content had positively affected the compressive strength (σc). SiC content showed a high and significant positive correlation of 0.87 for σc. On the other hand, P and N showed a moderately positive correlation as well. It is worth mentioning here that SiC content was the most significant parameter in increasing the hardness of AA6061 alloy at the center (H0.0R), midway between the center and edge (H0.5R), and near the peripheries (H1.0R) of the AA6061 discs with high positive significant correlations of 0.79, 0.78, and 0.78, respectively. Furthermore, P and N showed moderately positive correlations.
2.3. Statistical Analysis
The experimental data in this study were analyzed using ANOVA to identify the input parameters’ most significant effects on the output responses’ relative density, grain size, sub-grain size, sub-structure size, compressive properties, and hardness. The adopted software package used to perform the analysis was Design–Expert, version 13.0.5. The ANOVA statistics are presented in Table 1, showing the F-value, p-value, adequate precision, R2, adjusted R2, and predicted R2 at a 95% confidence level. All the model independent input parameters as well as the interaction terms had a substantial impact on the responses, as indicated by the p-values of all responses being less than 0.05. These results suggested that the predicted models were adequate. It was found that the most significant factor affecting the microstructure characteristics and the fracture strain is the number of revolutions, while the percentage of SiC had the most effect on the relative density, hardness, yield, and compression strengths. The model showed that it could be capable of navigating the design space, as the resulting response outcomes had an adequate precision of more than four, which indicates that there is a sufficient signal.

Table 1.
ANOVA results of HPT responses.
Several types of regression transformations and interactions between independent input parameters were looked into to model the outcome responses. Second-polynomial regression was adopted to model the relationship between the independent input parameters of HPT of AA6061 and the outcome responses. The models created in an experimental study are said to be of statistical significance and are able to be adopted to expect the outcome responses when their coefficient of determination (R2), adjusted R2, and predicted R2 are close to 1 and the values of the adjusted R2 are within or close to 0.2 of the predicted R2 [36]. All the regression models presented in this study were functions of the number of revolutions (N), the pressure (P), the percentage of SiC, and their interactions. Moreover, the plots of experimental values as a function of the matching expected values of outcome responses showed that experimental and expected values agree well because the majority of their intersection points are relatively near the median line, supporting the efficacy of the proposed regression models.
Process optimization is also established to figure out the best parameter combination for the HPT process for the desired outcome responses based on a thorough examination of each independent variable. The optimum combination of HPT independent input parameters that led to the minimum likely GS, Sub-Gs, and Sub-Str and the maximum possible RD, σc, and hardness was determined using the response surface methodology (RSM), genetic algorithm (GA), and hybrid DOE-GA approaches. The obtained regression equations, which were used as the objective functions for each response, using a genetic algorithm technique, were subjected to the HPT boundary conditions of pressure, number of revolutions, and SiC%. The suggested objective functions could be stated as follows:
Minimize (P, N, SiC%)
They were subjected to ranges of HPT conditions:
1 ≤ P ≤ 3 (GPa), 1≤ N ≤ 4 (rev), 0 ≤ SiC ≤ 15 (%)
The performance of the fitness value and run solver view were obtained from MATLAB, as were the corresponding HPT conditions for the best local solution of GS, Sub-Gs, Sub-Str, RD, σc, and hardness for the GA optimization technique. In order to improve the results of GA, a hybrid design of experiment and GA (DOE-GA) was used. Also, hybrid techniques were used to find the best global solution with lowest number of generations. Table A1 (Appendix A) shows the full design of experiment (14 runs) and the HPT responses as well.
3. Results and Discussion
3.1. Relative Density (RD)
The relative densities of AA6061 and AA6061/SiCp composite HC discs were 98.5% and 96.4%, respectively. After processing via HPT, their RD increased with the increase in the induced strain, which is a function of the number of revolutions (N). The previous is illustrated in more detail in Appendix A, Table A1. From Table A1, it can be seen that the densities of the AA6061–SiC discs were lower than those of the plain AA6061 discs due to the presence of hard SiC particles, which have low compressibility, as opposed to the soft AA6061 matrix. Processing for four revolutions at a pressure of 1 GPa yielded an increase in the relative densities of AA6061 and AA6061/SiCp composites discs to 99.5% and 97.4%, respectively. HPT processing of the AA6061 samples for one revolution and increasing the pressure to 3 GPa resulted in a 0.13% increase in their RD compared to their 1 GPa processed counterparts; increasing the revolutions to four at this elevated pressure yielded no significant effect. On the other hand, increasing the HPT processing pressure to 3 Gpa yielded no significant difference in the RD of AA6061/SiCp compared to the 1 GPa counterparts.
The increased relative density of the monolithic Al alloy and composite discs following HPT processing might be caused by the induced intense shear deformation. The latter is thought to have minimized porosity [37] and caused the breakdown of the naturally developing oxide layers found on the edges of Al grains which had impeded efficient binding of the Al-powder during sintering [38]. On the other hand, it is suggested that localized diffusion between AA6061/SiCp was clearly inhibited due to the segregation of SiCp along the boundaries of the Al particles of the matrix. Finally, as the pressure was raised, increases in the densification processes occurred, and hence the RD was increased.
3.1.1. Machine Learning Prediction Models of Relative Density
Several ML techniques were used to describe the characteristics of the AA6061 and AA6061/SiCp composite, including LR, GPR, and SVR. The validity of these models was tested using RMSE and R2-score during the training and testing phases. Figure 3 depicts the expected RD values versus the actual values, derived from experimental data. As listed in Table 2, the three algorithms effectively captured data trends with high accuracy, for both training and testing sets. This implies that the outcomes had a highly linear correlation with the three input elements (P, N, and SiC content). The SiCp percentage in particular showed a strong negative correlation value of −0.96, as illustrated in the correlation chart shown above. Both the training and test sets yielded similar results; the best-fit values among all three models were an RMSE and an R2-score of 0.195 and 0.98, respectively. The ML approach revealed that processing the AA6061/SiCp through HPT via four revolutions at 3 GPa was the optimum condition for maximizing the composite’s RD and led to an improved value of 97.4.
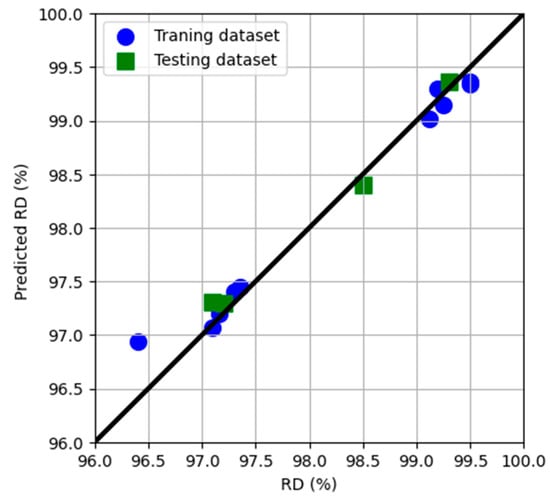
Figure 3.
Expected versus experimental relative density (RD) assessed for the training and the testing datasets.

Table 2.
Model evaluation metrics of AA6061 and AA6061/SiCp composites RD using HPT parameters.
3.1.2. Regression Models and 3D Plots of Relative Density
Regression Equation (11) was used to describe the RD response. Figure 4 is the contrast plot of the RD experimental outcomes against the model estimates where blue points are for minimum output value and gradually changed to red points for maximum output value. In Figure 5, the impact of HPT parameters on the regression-model-predicted RD is illustrated. The number of revolutions and RD showed a proportionate correlation at both SiC percentages. The relative densities at various SiC percentages were slightly affected by the pressure level used in the experiment. Figure 5a illustrates the highest 0% SiC RD, which was 99.5% attained at 3 GPa and four revolutions. The highest possible 15% SiC RD was 97%, attained at 3 GPa and four revolutions, shown in Figure 5b.
RD = +98.90750 + 0.076250 × P + 0.140357 × N − 0.130167 SiC − 0.016250 P × N − 0.002667 P × SiC − 0.002214 × N × SiC
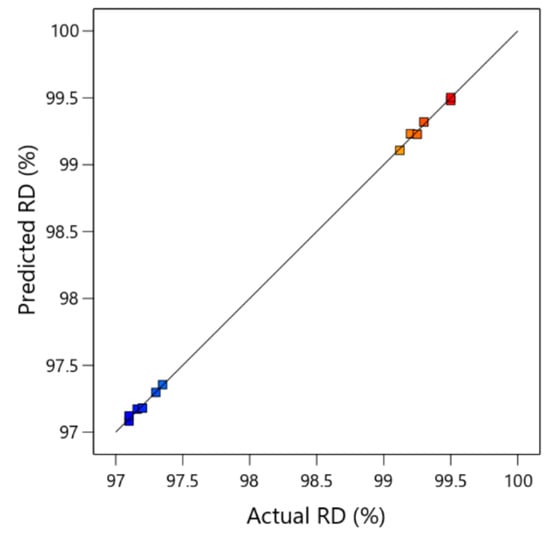
Figure 4.
The contrast of experimental versus estimated outcomes of HPT for RD (blue points are for minimum output value and gradually changed to red points for maximum output value).
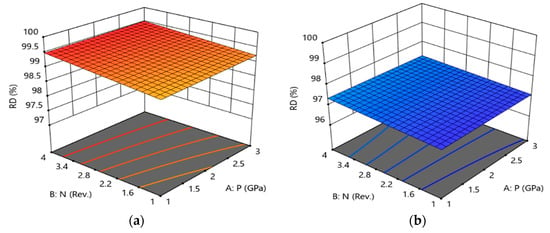
Figure 5.
3D response plot of relative density at (a) 0% SiC and (b) 15% of SiC (b).
3.1.3. Optimization of Relative Density
The maximum RD and its corresponding parameters were found by RSM optimization. “In range” was chosen as the optimization objective, “Maximize” was selected as the solution destination, and “larger-is-better” was anticipated by the desirability function. The maximum RD value was 99.5027, attained with HPT parameters of P (A) = 3 GPa, N (B) = 4 revolutions, and SiC% (C) = 0%. The maximizing of RD suggested in Equation (11) was used as the fitting function, with the application of the HPT boundary conditions. The greatest RD estimate by GA was 99.5027, attained at 3 GPa, four revolutions, and 0% SiC, as demonstrated in Figure A1a, found in Appendix B. Figure A1b illustrated the hybrid DOE-GA findings, which revealed a greatest RD value of 99.5027 at 3 GPa, 4-revolutions, and 0% SiC.
3.2. Microstructural Evolution
An SEM micrograph showing the grain, sub-grains, and sub-structures of AA6061 alloy processed through four revolutions at 3 GPa is displayed in Figure 6. In addition, the microstructural evolution of the disc at the peripheral areas after HPT processing is illustrated in Figure 7 using FESEM used on AA6061 subjected to one revolution (a,e) and four revolutions (c,g) at a pressure of 1 GPa (a,c) and at a pressure of 3 GPa (e,g). In addition, Figure 7 shows comparable micrographs of the composite subjected to one revolution (b,f) and four revolutions (d,h) at pressures of 1 GPa (b,d) and 3 GPa (f,h). The SEM micrographs demonstrated the possibility of obtaining ultrafine sub-grains and sub-structures within the as cast grains following HPT processing. The average GS, Sub-Gs, and Sub-Str of as-HC AA6061/SiCp and after HPT processing through different conditions are listed in Appendix A, Table A1. The micrographs clearly show the increased refinement in the average size of the grains, Sub-Gs and Sub-Str, resulting from increasing the number of revolutions from one to four. The average GS, Sub-Gs, and Sub-Str of the as-HC AA6061 discs were 35, 3.2 µm, and 610 nm, respectively (Table A1). HPT processing at pressures of 1 GPa and one revolution resulted in the refinement of the GS, Sub-Gs, and Sub-Str to 33, 2.8 µm, and 360 nm, respectively (Table A1). HPT with four revolutions under the same pressure of 1 GPa resulted in additional refinement of the GS, Sub-Gs, and Sub-Str to 30, 1.9 µm, and 250 nm (Figure 7c). HPT processing of AA6061 discs at 3 GPa and four revolutions led to the refinement of the GS, Sub-Gs, and Sub-Str to 28, 1.8 µm, and 240 nm, respectively (Figure 7g and Table A1).
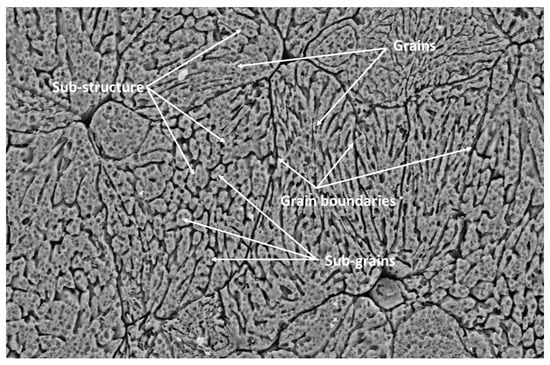
Figure 6.
SEM micrograph showing grains, sub-grains, and sub-structures of AA6061 processed via four revolutions at 3 GPa.

Figure 7.
SEM micrographs of AA6061 (a,c,e,g) and AA6061/SiCp (b,d,f,h) discs processed at 1 GPa (a–d) and 3 GPa (e–h) via one revolution (a,b,e,f) and four revolutions (c,d,g,h).
For the AA6061/SiCp as-HC discs, the GS, Sub-Gs, and Sub-Str of the HC were 33, 3 µm, and 420 nm, respectively, as listed in Table A1. HPT processing through one revolution resulted in refining the GS, Sub-Gs, and Sub-Str of AA6061/SiCp discs to 31.5, 2.7 µm, and 260 nm, respectively (Figure 7d). The increased amount of strain up to four revolutions at 1 GPa led to a reduction in the GS, Sub-Gs, and Sub-Str to 25, 1.9 µm, and 184 nm, respectively (Figure 7d). The accumulation of HPT straining up to four revolutions at 3 GPa yielded UFGs with GS, Sub-Gs, and Sub-Str of 24, 1.5 µm, and 154 nm, respectively (Figure 7h and Table A1).
It is reasonable to assume that the process’s significant torsional straining and relatively high applied pressure were the main causes behind the refined grain sizes produced by HPT. Furthermore, the resulted UFG structure led to an increase in the grain boundaries area which acted as a barrier against dislocation motion that made it more challenging for dislocations to shift their direction of motion due to the different grain orientations. Prior to their slide planes, these pile-ups produced stress concentrations that caused further dislocations in neighboring grains [11,39].
3.2.1. Machine Learning Prediction Models of the Microstructural Evolution
Figure 8 depicts the expected versus actual experimental microstructure evolution data of the alloy, comprising GS, Sub-Gs, and Sub-Str for monolithic AA6061 and AA6061/SiCp composite. For both the training and testing phases, the predicted values were in close agreement with those of the experimental data with high R2-scores. According to Table 3, SVR resulted in the best possible fitting model with a lower RMSE and an R2-score of 0.99 in all cases. Furthermore, ML revealed that the optimum HPT parameters for processing AA6061 and AA6061/SiCp composite was four revolutions at 3 GPa pressure. ML findings showed that these optimum HPT processing parameters should lead to refinements in the GS, Sub-Gs, and Sub-Str by 27%, 45%, and 63%, respectively, compared to the HC counterpart.
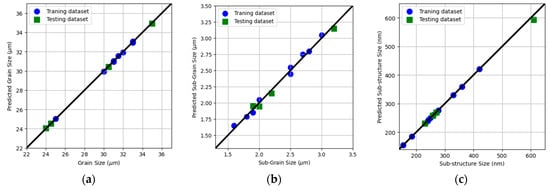
Figure 8.
Predicted versus experimentally measured evaluated for the training and the testing datasets for (a) GS, (b) Sub-Gs, and (c) Sub-Str.

Table 3.
Model evaluation metrics of properties of AA6061–SiC composite using HPT parameters.
3.2.2. Regression Models and 3D Plots of Microstructure Characteristics
Equations (12)–(14) represent the predicted linear models of microstructure responses of GS, Sub-Gs, and Sub-Str.
GS = +34.12500 + 0.520833 × P − 1.08929 × N + 0.094444 × SiC − 1.01786 P × N − 0.291667 × P × SiC + 0.120238 N × SiC + 1.88532 × 10−14 × N2 + 0.060714 P × N × SiC + 0.229167 × P × N2 − 0.052778 × N2 × SiC
Sub-Gs = +3.55000 − 0.475000 × P − 0.392857 × N + 0.003333 × SiC + 0.103571 × P × N + 0.003333 × P × SiC − 0.006667 × N × SiC
Sub-Str = +435.25000 − 52.12500 × P − 30.07143 × N − 11.43333 × SiC + 10.28571 × P × N + 3.81667 × P × SiC + 2.12619 × N × SiC − 3.75000 × N2 − 1.12143 × P × N × SiC + 0.375000 × P × N2 − 0.050000 × N2 × SiC
Figure 9a–c show the experimental against estimated outcome values of GS, Sub-Gs, and Sub-Str, respectively. Figure 10 shows the 3D response plots, which illustrate how HPT parameters such as pressure and number of revolutions had an impact on the microstructure characteristics as a function of HPT parameters (P and N) at various SiC percentages. For GS, as shown in Figure 10a,b, there was an inverse relationship between HPT parameters and GS at 0% and 15% SiC. At a constant SiCp percentage, the increase in both P and N produced finer grains. The minimum GS of 24 µm was obtained at a pressure of 3 GPa, four revolutions, and 15% SiC. Furthermore, Figure 8d and Figure 10c illustrate an inverse relationship between HPT parameters and Sub-Gs at 0% and 15% of SiCp. Increases in both P and N produced finer sub-grains at any given SiCp%. The finest Sub-Gs, measuring 1.6 µm, was attained at 3 GPa, four revolutions, and 15% SiC.
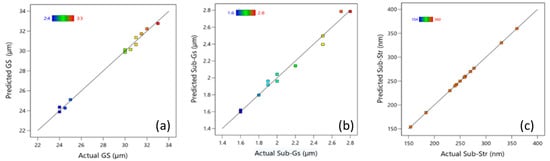
Figure 9.
The contrast of experimental versus estimated outcomes of HPT for (a) GS, (b) Sub-Gs, and (c) Sub-Str.
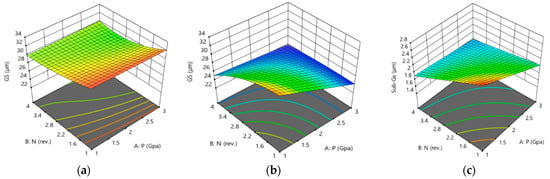
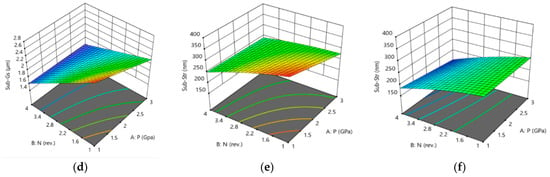
Figure 10.
3D response plot of (a,b) GS (c,d), Sub-Gs, and (e,f) Sub-Str for (a,c,e) AA6061, and (b,d,f) AA6061/SiCp composite.
Finally, an inverse relation between Sub-Str and HPT parameters was also revealed for the 0% and 15% of SiCp, as shown in Figure 10e,f. At a fixed SiCp content, an increase in P and N led to finer Sub-Str. At 3 GPa, 4-revolutions, and 15% SiCp, the absolute finest Sub-Str was 154 nm. This is indicative of the significant influence of SiCp reinforcement on the refinement of the structure compared to the plain AA6061 alloys. In conclusion, the optimum processing conditions for structural refinement are achieved at the highest pressure (3 GPa) and the highest number of revolutions (four revolutions) for the AA6061 with SiCp reinforcement.
3.2.3. Optimization of Microstructure Characteristics
The refinement in microstructure and its corresponding HPT processing parameters for the AA6061/SiC composite was determined using RSM optimization. Based on the fact that low values of GS, Sub-Gs, and Sub-Str are better for microstructure features, “In range” was chosen as the optimization objective, “Minimize” was selected as the solution destination, and “smaller-is-better” was anticipated by the desirability function. The minimum GS, Sub-Gs, and Sub-Str were reached at 23.9 m, 1.6 m, and 154 nm, respectively, with optimal HPT condition parameters of P (A) = 3 GPa, N (B) = 4 revolutions, and SiC% (C) = 15%.
Figure A2, Appendix B, shows the fitness function of microstructure-feature minimization suggested in Equations (12)–(14), and subjected to the HPT boundary conditions. The minimum values of GS, Sub-Gs, and Sub-Str estimated by GA were 23.9 µm, 1.6 µm, and 154 nm, respectively, which were attained at 3 GPa, four revolutions, and 15% SiC, as demonstrated in (Figure A2a,c,e). Based on the optimum HPT conditions of the DOE, the initial population of the hybrid DOE-GA had the following parameters: P = 3 GPa, N = 4 revolutions, and SiC% = 15%. According to the hybrid DOE-GA, the minimum values for GS, Sub-Gs, and Sub-Str were 23.9 µm, 1.6 µm, and 154 nm, respectively, at 3 GPa, four revolutions, and 15% SiC (Figure A2b,d,f).
3.3. Hardness Distribution
Figure 11a,b show HV values measured across different sections of processed and as-HC AA6061 and AA6061/SiCp discs, respectively. The as-HC average Vicker’s hardness values were 63 and 96 for monolithic AA6061 and AA6061/SiCp, respectively. After HPT processing of the plain AA6061 alloy at 1 GPa pressure and one revolution (Figure 11a), the average HV values measured were lowest at the core of the disc (80 HV) and increased up to 122Hv at the peripheries of the disc. This indicates the non-uniformity of the hardness distribution throughout the disc’s cross-section. Increasing the number of revolutions up to four under the same pressure (Figure 11a) yielded a significant increase in the average hardness (125 HV) coupled with a significant enhancement in hardness uniformity across the disc’s cross section. Increasing the HPT processing pressure up to 3 GPa (Figure 11b) resulted in a slightly higher level of homogeneity in hardness distribution in contrast to 1 GPa. Furthermore, HV values increased at the peripheries and near the core of the discs by around 2 and 4%, respectively, compared to those of the AA6061 disc processed at 1 GPa pressure with the same number of passes. The highest recorded HVs in monolithic AA6061 were measured at the peripheries of the discs processed for four revolutions and under a pressure of 3 GPa and had an average of 125. The as-HC disc’s hardness doubled after four revolutions of HPT processing, which is a considerable improvement in hardness.
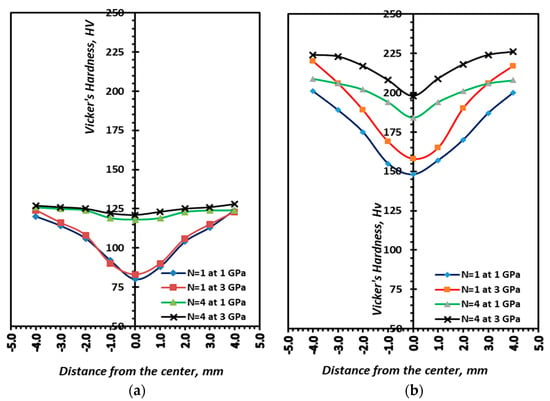
Figure 11.
Variation of HV around the cross-sections of HPT discs for (a) AA6061 and (b) AA6061/SiCp.
For the AA6061/SiCp composite discs, the applied processing strain from HPT led to the increase in the heterogeneity of the hardness distribution throughout the discs’ cross-sectional area. This was demonstrated by distinct absolute minimum values of HV at the middle part of the disc after one revolution (shown in Figure 11b). After HPT processing for one revolution under 1 GPa pressure, the HV values were found to have increased as the distance from the core increased. HV values recorded a maximum of about 210 at the peripheries of the disc, which is significantly higher than that obtained at the core that had an average of 150. When the discs were processed for four revolutions, the results revealed a slight improvement in hardness uniformity across the disc’s cross-sections. It should be noted that, in contrast to the AA6061 discs, the composite AA6061/SiCp discs were not completely homogeneous after four revolutions, and the maximum HV values remained considerably unaltered as the strain increased. It is suggested that the addition of SiCp to the aluminum matrices resulted in increasing friction forces at the disc peripheries at the die wall interface [9]. As a result, the induced strain at the peripheries was much higher compared to the core of the disc, which resulted in excessive strain hardening at the peripheries compared to the core.
A higher processing pressure of 3.0 GPa resulted in a significant increase in the average hardness and a slight enhancement in the hardness uniformity of the disc, compared to the discs processed at 1 GPa pressure for the same number of revolutions (Figure 11b). By increasing the pressure to 3 GPa, the HV values of the composite discs increased by 8.5% at the peripheries and 8% at the core of the disc. The highest Hv values were reported at the peripheries of the disc, with an average of 225 HV. This may be explained by the higher strain hardening at the disc’s peripheries in comparison to its centers due to the increased friction induced by the hard SiCp aggregates at the disc–die wall interface [9]. From the hardness findings, it could be highlighted that the HV values of the HC discs increased by roughly 98% for the alloy and 133% for the composite after HPT processing for four revolutions at 3 GPa.
The variations in HV values observed throughout the cross-section of AA6061 and AA6061/SiC discs processed by HPT were noticeably consistent with the patterns observed by other researchers in face-centered cubic (FCC) shaped materials with low stacking-fault energy (SFE) [40]; the disc cores had lower hardness values, whereas the peripheral regions exhibited higher hardness values. Due to the low SFE of the AA6061 alloy, it recovered slowly with stable growth at the pace of hardening during the preliminary processing phases [41]. In agreement with the findings of Langdon et al., a slow recovery pace led to elevated strain hardening in the preliminary stage, which was related to friction at the disc–die wall juncture, in contrast to the lower hardness values in the middle area [40,41]. When the torsional strain was increased to an extremely high level of total strain, the hardness of the discs became evenly distributed across their cross-section. Furthermore, the observed trend of uniformity in hardness dispersal when increasing the revolutions in HPT processing was consistent with the principles of strain gradient plasticity modeling, the aim of which was to determine how homogeneity changes as the number of revolutions in HPT processing increases [42].
It has been reported that possible SPD-related strengthening processes resulted in increasing the mechanical properties due to strain hardening, grain refinement, and solid solution strengthening mechanisms [43,44,45]. The literature shows that the addition of SiC particles to AA6061 alloy can improve its strength by disrupting the regular arrangement of atoms in its crystal structure, making movement harder for dislocations. It is noteworthy that the inclusion of SiC in AA6061 led to more grain refinement in the processed material. The SiC particles helped increase hardness values by adhering to the grain boundaries, thus limiting the movement towards peripheral areas. The concentration of SiC particles at the grain borders created favorable conditions for impeding dislocation mobility and grain development. On the other hand, the significant grain refinement attained after HPT processing (Figure 7) could be considered one of the most effective mechanisms for strengthening the AA6061 alloy and AA6061/SiCp composite [9].
3.3.1. Machine Learning Prediction Models of Hardness Distribution
Figure 12 displays the predicted hardness values measured at H0.0R, H0.5R, and H1.0R of the alloy against the experimental data. Predicted values showed high degrees of agreement with the experimental data in both the training and testing phases, as indicated by high R2-scores. According to Table 4, SVR achieved the best fitting results with lower RMSE values and an R2-score of 0.99. Moreover, ML revealed that the optimum HPT parameters for the AA6061/SiCp composite was four revolutions at 3 GPa. ML findings showed that processing the composite through four revolutions at 3 GPa resulted in increasing the hardness values at H0.0R, H0.5R, and H1.0R by 106%, 126%, and 133%, respectively, compared to its as-HC counterpart.
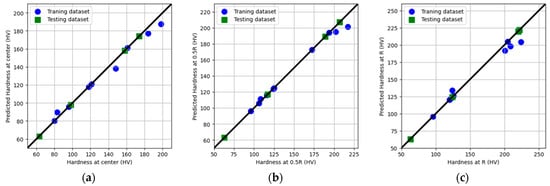
Figure 12.
Predicted hardness versus experimentally measured hardness assessed for the training and the testing datasets at (a) center H0.0R, (b) half radius H0.5R, and (c) radius of disc H1.0R.

Table 4.
Model evaluation metrics of properties of AA6061/SiCp composite using HPT parameters.
3.3.2. Regression Models and 3D Plots of Hardness Distribution
Equations (15)–(17) represent the linear hardness response model at different positions along the specimens’ radius: H0.0R, H0.5R, and H1.0R, respectively. Figure 13 shows the experimental versus estimated hardness distribution outcomes’ contrast plots along the disc’s radius.
H0.0R = +63.333 + 0.166667 × P + 18.96429 × N + 4.011 × SiC + 0.357143 × P × N + 0.3444 × P × SiC + 0.009524 × N × SiC − 1.41667 × N2
H0.5R = +83.70833 + 1.0 × P + 23.64286 × N + 3.98333 × SiC − 0.142857 × P × N + 0.45 × P × SiC + 0.219048 × N × SiC − 3.45833 × N2
H1.0R = +114.625 + 2.54167 × P + 3.71429 × N + 4.8611 × SiC − 0.732143 × P × N + 0.5111 × P × SiC + 0.050 × N × SiC − 0.208333 × N2
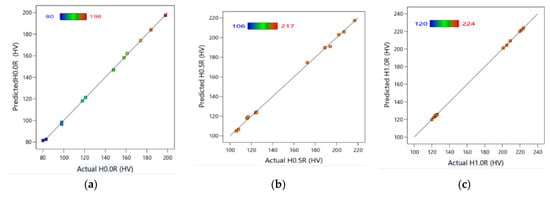
Figure 13.
The contrast of experimental versus estimated outcomes of HPT for hardness distribution along the radius of the specimen (a) at center H0.0R, (b) at half radius H0.5R, and (c) at radius H1.0R.
Figure 14 shows the response surfaces of hardness values at the H0.0R, H0.5R, and H1.0R positions of the specimen against their HPT input parameters as determined by regression models. The HPT input parameters’ impact on hardness for both 0% SiC and 15% SiC was seen to be equivalent. Hardness values at various measurement locations increased as P and N increased. Moreover, it was revealed that interaction plots and experimental findings were consistent with each other, specifically verifying that the highest P and N produced the greatest hardness for both 0% SiC and 15% SiC. The greatest hardness values recorded at the H0.0R, H0.5R, and H1.0R positions of the 0% SiC were 121 HV, 124 HV, and 125 HV, respectively, and were obtained at 3 GPa and four revolutions, as revealed in Figure 14a,c,e. Additionally, at 3 GPa and four revolutions, 15% SiC yielded its greatest H0.0R (197.5 HV), H0.5R (217 HV), and H1.0R (224 HV), as depicted in Figure 14b,d,f.
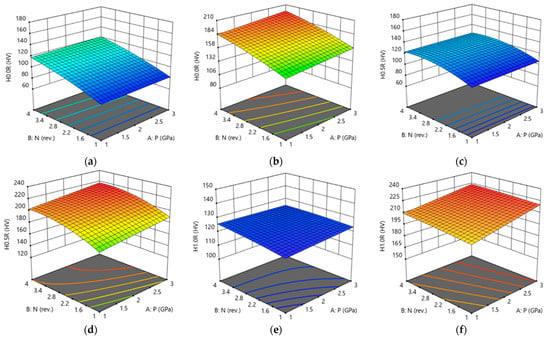
Figure 14.
3D response plot of hardness at (a,b) center H0.0R, (c,d) half radius H0.5R, and (e,f) peripheries H1.0R for (a,c,e) AA6061 and (b,d,f) AA6061/SiCp composite.
3.3.3. Optimization of Hardness Distribution
The maximum hardness values were obtained by RSM optimization of outcomes together with the conditions that correlate to them. The goal was to improve hardness at various locations along the radius to ultimately lead to improved overall specimen hardness; “In range” was chosen as the optimization objective, “Maximize” was selected as the solution destination, and “larger-is-better” was anticipated by the desirability function. The maximum predicted H0.0R, H0.5R, and H1.0R values were 197.55 HV, 217.38 HV, and 223.91 HV, respectively, with processing inputs of with P (A) = 3 GPa, N (B) = 4 revolutions, and SiC% (C) = 15%. The hardness maximization formulas indicated in Equations (15)–(17) were subjected to the HPT boundary constraint. The best hardness values predicted by GA at H0.0R, H0.5R, and H1.0R were found to be 197.55 HV, 217.38 HV, and 223.91 HV, respectively, at three GPa, four revolutions, and 15% SiC, as demonstrated in Figure A3a,c,e. The maximum H0.0R of 197.55 HV was achieved at 3 GPa, four revolutions, and 15% SiC, according to the hybrid DOE-GA data displayed in Figure A3b. Additionally, at 3 GPa, four revolutions, and 15% SiC, the highest H0.5R hardness value of 217.38 was recorded, as demonstrated in Figure A3d. Finally, the highest hardness at H1.0R was 223.91 HV, which was attained at 3 GPa, four revolutions, and 15% SiC, as demonstrated in Figure A3f.
3.4. Compressive Properties
The AA6061 and AA6061/SiC HC discs experienced a σc of 245 and 342 MPa, respectively, as listed in Table A1. In the monolithic AA6061, HPT processing at 1 GPa via one revolution yielded a 13.5% rise in σc compared to the AA6061 as-HC discs (Table A1). Increasing the revolutions up to four showed a 32.6% enhancement in σc compared to the AA6061 as-HC discs. Similar behavior was recorded for the composite; HPT processing at 1 GPa via one revolution resulted in an 18.4% increase in σc compared to the AA6061/SiCp as-HC discs. Increasing the amount of strain by processing for four revolutions resulted in an additional σc increase of 32.5%, compared to the as-HC AA6061/SiCp discs (Table A1).
Increasing the HPT processing pressure up to 3 GPa led to additional increases in the σc of both monolithic AA6061 alloy and AA6061/SiCp composite. HPT processing yielded improved compressive behavior in the AA6061 discs regardless of the number of revolutions, up until the maximum applied of four revolutions. The highest recorded σc value for AA6061 discs was achieved by processing at 3 GPa through four revolutions, which exhibited a 38.5% improvement in σc, when compared with AA6061 HC discs. As for the AA6061/SiCp composite, processing for four revolutions at 3 GPa revealed a 34.8% increase in σc compared to AA6061/SiCp HC discs (Table A1).
The current study highlighted the possibility of attaining nanoscale UFG structures (Figure 7) while increasing the σc of both AA6061 and its SiC-reinforced composite through HPT processing. This noticeable enhancement in strength post-HPT is primarily associated with the development of homogeneous UFG microstructures (Figure 7), which led to substantial enhancements in strength as predicted by the Hall–Petch equation [43,46]. The strength of the HPT processed discs as well as grain refinement improved with the increase in the shear strain in both monolithic AA6061 and AA6061/SiCp composite. The structural refinement of the GS, Sub-Gs, and Sub-Str of the alloy and the composite subsequently resulted in an improved σc.
3.4.1. Machine Learning Prediction Models of Compression Properties
Figure 15 depicts the expected versus actual experimental σc data points for AA6061 and AA6061/SiCp composite. For both the training and testing phases, the predicted values were in great agreement with those of the experimental data with high R2-scores. According to Table 5, SVR showed the best possible fitting model with a lower RMSE and an R2-score of 0.99. ML findings confirmed that processing AA6061/SiCp for four revolutions at 3 GPa was the optimum and had resulted in σc improvements of 35% compared to the HC composite.
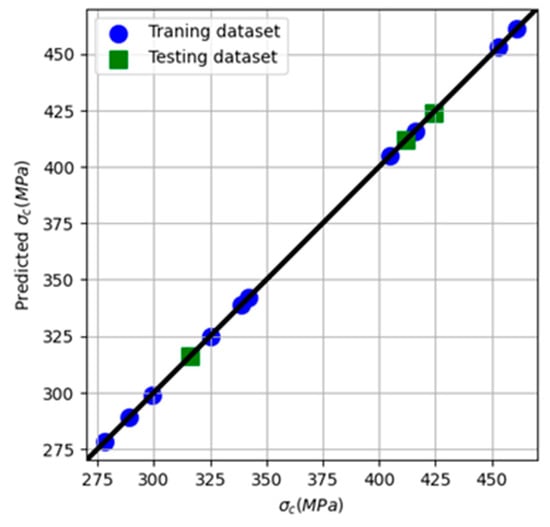
Figure 15.
Predicted versus experimental values evaluated for the training and the testing datasets of σc.

Table 5.
Model evaluation metrics of properties of AA6061–SiC composite using HPT parameters.
3.4.2. Regression Models and 3D Plots of Compression Properties
Equation (18) represents the linear σc model of monolithic AA6061 and its SiC composite. Figure 16 shows the contrast plot of experimental versus estimated outcomes of HPT processing on σc.
σc = +250 + 11.87500 P + 15.85714 N + 8.61667 SiC − 0.660714 P × N − 0.433333 P × SiC + 0.130952 N × SiC
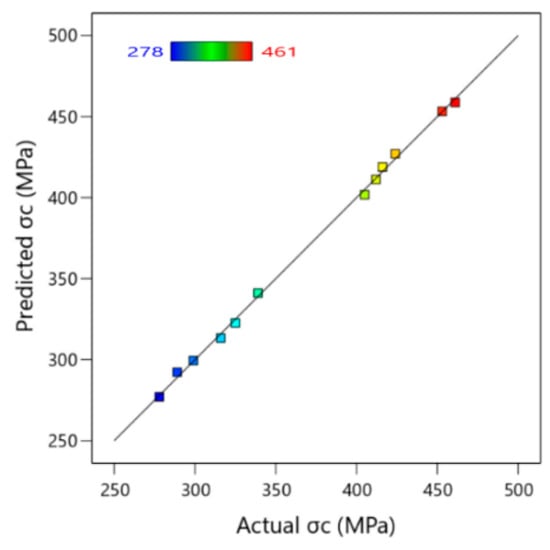
Figure 16.
The contrast of experimental versus estimated outcomes of HPT σc.
Figure 17 shows the response surface of σc to its HPT processing parameters in AA6061 and AA6061/SiC, as determined by regression models. HPT parameters were seen to have had similar effects on σc for both 0% SiC and 15% SiC. The σc values increased with the increase in P and N. Moreover, the response surface results were consistent with those of the interaction plots and experimental findings, specifically corroborating that the highest P and N produced the greatest σc for both 0% SiC and 15% SiC. The greatest monolithic AA6061 σc was 341 MPa, and that of AA6061/SiC was 459 MPa; both were obtained at 3 GPa after four revolutions, as revealed in Figure 15.
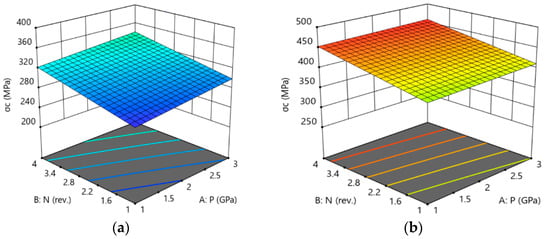
Figure 17.
3D response plot of σc for (a) AA6061 and (b) AA6061/SiCp.
3.4.3. Optimization of Compression Properties
The maximum σc was obtained by RSM optimization of the outcomes as well as the processing input parameters that correlate with them. “In range” was chosen as the optimization objective, “Maximize” was selected as the solution destination, and “larger-is-better” was anticipated by the desirability function. The maximum σc value predicted was 458.73 MPa through HPT parameters of P (A) = 3 GPa, N (B) = 4 revolutions, and SiC% (C) = 15%. The maximization of σc indicated in Equation (18) was constrained by the HPT boundary conditions. The highest σc value obtained by GA was found to be 458.73 MPa, attained at 3 GPa, four revolutions, and 15% SiC, as demonstrated in Figure A4 (Appendix B). The maximum σc predicted the hybrid DOE-GA was 458.73 MPa, achieved at 3 GPa, four revolutions, and 15% SiC, displayed in Figure A4b (Appendix B). Table A2 (Appendix A) summarizes HPT response values extracted from experimental, RSM, GA, and hybrid DOE–GA findings.
4. Validation of ML and RSM Models for AA6061 and AA6061/SiCp Processing through HPT
4.1. Validation of ML Model Inferences
ML model inference is the act of feeding new, unseen data points into a trained and tested model to predict new target data, which should then be validated on a single numerical score. This is also known as “bringing an ML model into production” or “model deployment”. Table 6 lists the experimental results of new, unseen samples processed at a pressure of 1 GPa and through three revolutions and the corresponding model predictions for this unseen data with computed error and relative accuracy. The accuracy scores for these data ranged from 73.5 to 99.9%, depending on the target output property. This range is commonly accepted, especially for models trained using limited data.

Table 6.
ML models performance validation on new unseen data.
4.2. Validation of RSM Models
Table 7 presents the validation of HPT’s regression model for all responses under a specific condition. The validation of the HPT models was obtained at one GPa, three revolutions, and two different percentages of SiC. The results of validation showed that the HPT response models were accurate and had the lowest percentage of error between the experimental and regression models. The HPT conditions examined in the validation were 1 GPa through three revolutions at two percentages of SiC (0% and 15%).

Table 7.
Validation of HPT responses regression models and experimental.
4.3. Validation of HPT Based on Previous Studies
The literature suggests that setting the HPT parameter to 12 revolutions is optimal in light of recent investigations of HPT and the various obtained responses [47]. Table 8 outlines the findings of a genetic algorithm (GA) and a hybrid DOE-GA employed to determine the optimum parameters for HPT processes under multiple conditions.

Table 8.
Validated HPT response based on previous studies.
5. Conclusions
In this study, a detailed investigation was conducted on the feasibility of adopting HPT processing with AA6061/SiCp composites to improve strength and grain refinement. Experiments were conducted to determine the effect of HPT processing conditions (pressure and torsion) with and without 15% SiCp addition to the aluminum matrices on the relative density, grain size refinement, hardness, and compressive properties. A statistical analysis using ANOVA and response surface plots was carried out, followed by ML approaches to determine the output variables and optimize the input parameters. Moreover, results validation was performed to check the accuracy of the response and ML model. The following conclusions could be deduced:
- HPT processing of AA6061/SiCp composite four revolutions at 3 GPa pressures resulted in the refinement of the grain size and sub-grain size by 27% and 46.6%, respectively, compared to the HC counterpart.
- Processing with four revolutions at 3 GPa resulted in improving the hardness and compressive strength of AA6061/SiCp composite by 133% and 34.8%, respectively, compared to the HC counterpart.
- ML results reveals that:
- The correlation plot obtained from ML revealed that SiC content is the most significant parameter in increasing the hardness of AA6061 alloy at H0.0R, H0.5R, H1.0R, and σc of the AA6061 discs with a high positive significant correlation of 0.79, 0.78, 0.78, and 0.87, respectively.
- The correlation plot obtained from ML showed that the GS, Sub-Gs, and Sub-Str were strongly correlated with the number of revolutions of HPT with a high negative significant correlation of −0.55, −0.84, and −0.72, respectively.
- The optimum HPT parameters for AA6061/SiCp composite was four revolutions at 3 GPa.
- Processing the AA6061/SiC composite four revolutions at 3 GPa reduces the grain size and sub-grain size by 27% and 45%, respectively, which resulted in increasing the Vicker’s hardness and compressive strength by 133% and 35%, respectively, compared to the HC counterpart.
- DOE-GA optimization reveals that:
- The minimum GS, Sub-Gs, and Sub-Str were reached at 23.9 µm, 1.6 m, and 154 nm, respectively, with the optimal HPT condition parameters of P = 3 GPa, N = 4 revolutions, and 15% SiC.
- The maximum hardness values at H0.0R, H0.5R, and H1.0R values were calculated to be 197.6 HV, 217.4 HV, and 223.9 HV, respectively, with P = 3 GPa, N = 4 revolutions, and 15% SiC.
- The maximum σc were reached at 458.7 MPa with the optimal HPT condition parameters of P = 3 GPa, N = 4 revolutions, and 15% SiC.
Author Contributions
Conceptualization, W.H.E.-G. and H.G.S.; methodology, W.H.E.-G. and H.G.S.; software, M.S., M.F.A. and H.K.; validation, A.I.A., F.N.A., S.E.-S. and Y.E.-T.; formal analysis, A.I.A. and F.N.A.; investigation, M.S., M.F.A. and F.N.A.; resources, W.H.E.-G. and H.G.S.; data curation, A.I.A., S.E.-S., H.K., Y.E.-T. and M.S.; writing—original draft preparation, W.H.E.-G., S.E.-S., Y.E.-T. and M.S.; writing—review and editing, H.G.S. and W.H.E.-G.; visualization, M.F.A.; supervision, H.G.S.; project administration, W.H.E.-G. funding acquisition, H.G.S. and A.I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All of the raw data supporting the conclusion of this paper were provided by the authors.
Acknowledgments
The researchers would like to thank the Deanship of Scientific Research, Qassim University, for funding the publication of this project.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Design of experiment of ECAP parameters and process response.
Table A1.
Design of experiment of ECAP parameters and process response.
| Run No. | Input | Output | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HPT Conditions | RD (%) | Microstructure | Hardness (HV) | ||||||||
| P (GPa) | N (rev) | SiC% | σc (MPa) | GS (µm) | Sub-Gs (µm) | Sub-Str (nm) | H0.0R | H0.5R | H1.0R | ||
| 1 | as-HC | 0 | 98.5 | 245 | 35 | 3.2 | 610 | 63 | |||
| 2 | as-HC | 15 | 96.4 | 342 | 33 | 3 | 420 | 96 | |||
| 3 | 1 | 1 | 0 | 99.1 | 278 | 33 | 2.8 | 360 | 80 | 106 | 120 |
| 4 | 1 | 2 | 0 | 99.2 | 289 | 31 | 2.5 | 330 | 98 | 116 | 122 |
| 5 | 1 | 4 | 0 | 99.5 | 325 | 30 | 1.9 | 250 | 118 | 124 | 126 |
| 6 | 1 | 1 | 15 | 97.1 | 405 | 31.5 | 2.7 | 260 | 148 | 172.5 | 201 |
| 7 | 1 | 2 | 15 | 97.2 | 416 | 31 | 2.5 | 243 | 161 | 194 | 205 |
| 8 | 1 | 4 | 15 | 97.4 | 453 | 25 | 1.6 | 184 | 184 | 202 | 209 |
| 9 | 3 | 1 | 0 | 99.3 | 299 | 32 | 2 | 277 | 83 | 108 | 124 |
| 10 | 3 | 2 | 0 | 99.3 | 316 | 30.5 | 2 | 270 | 98 | 117 | 124 |
| 11 | 3 | 4 | 0 | 99.5 | 339 | 30 | 1.8 | 240 | 121 | 125 | 125 |
| 12 | 3 | 1 | 15 | 97.1 | 412 | 24.5 | 2.2 | 258 | 158 | 189 | 220 |
| 13 | 3 | 2 | 15 | 97.2 | 424 | 24 | 1.9 | 230 | 174 | 207 | 222 |
| 14 | 3 | 4 | 15 | 97.3 | 461 | 24 | 1.6 | 154 | 198 | 217 | 224 |

Table A2.
Summary results of HPT processing of AA6061 and AA6061/SiC composite.
Table A2.
Summary results of HPT processing of AA6061 and AA6061/SiC composite.
| Response | Experimental | RSM | GA | DOE-GA | |
|---|---|---|---|---|---|
| GS | Value | 24 | 23.88 | 23.88 | 23.88 |
| Cond. | 3P, 4 N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | |
| Sub-Gs | Value | 1.6 | 1.6 | 1.6 | 1.6 |
| Cond. | 3P, 4 N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | |
| Sub-Str | Value | 154 | 154 | 1534 | 154 |
| Cond. | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | |
| RD | Value | 99.5 | 99.5 | 99.5 | 99.5 |
| Cond. | 3P, 4N, 0% | 3P, 4N, 0% | 3P, 4N, 0% | 3P, 4N, 0% | |
| σc | Value | 461 | 458.7 | 458.7 | 458.7 |
| Cond. | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | |
| H0.0R | Value | 198 | 197.55 | 197.55 | 197.55 |
| Cond. | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | |
| H0.5R | Value | 217 | 217.38 | 217.38 | 217.38 |
| Cond. | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | |
| H1.0R | Value | 224 | 223.9 | 223.9 | 223.9 |
| Cond. | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | 3P, 4N, 15% | |
Appendix B
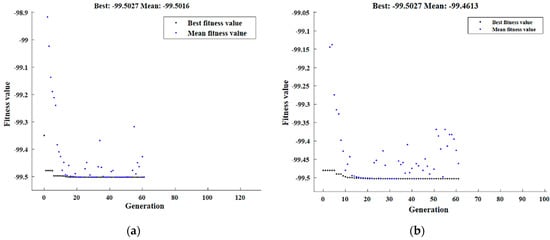
Figure A1.
Optimal relative density with GA (a) and hybrid DOE-GA (b).
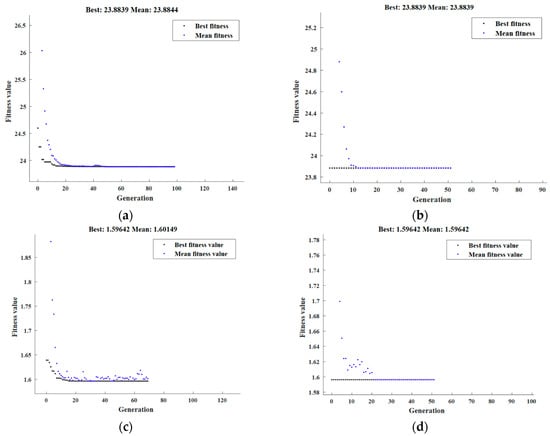
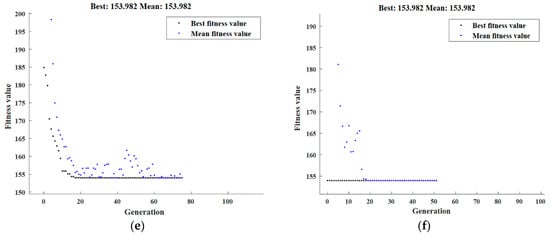
Figure A2.
Optimal microstructure characteristics with GA (a,c,e) and hybrid DOE-GA (b,d,f) of grain size (a,b), sub-grain size (c,d), and sub-structure size (e,f).
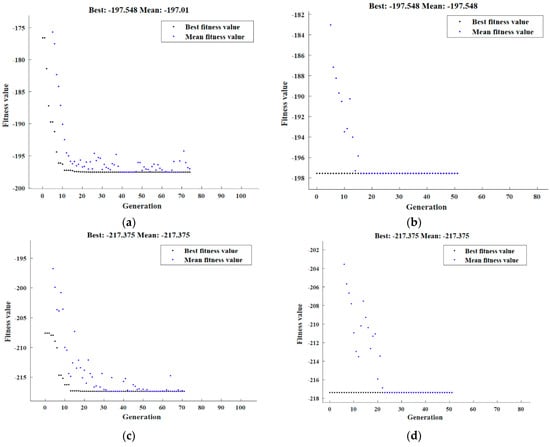
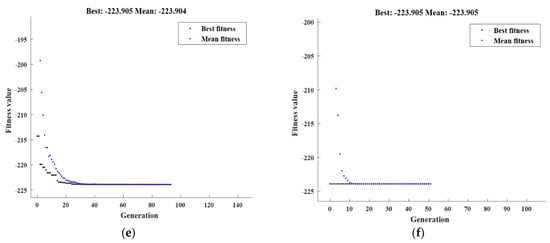
Figure A3.
Optimal hardness with GA (a,c,e) and hybrid DOE-GA (b,d,f) measured at center H0.0R (a,b), half radius H0.5R (c,d), and radius H1.0R (e,f).
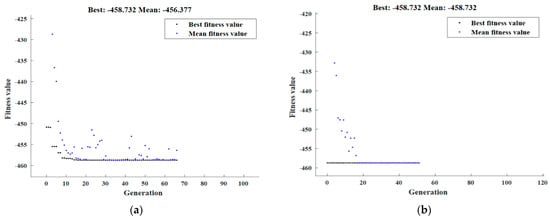
Figure A4.
Optimal σc with GA (a) and hybrid DOE-GA (b).
References
- Flores-Zamora, M.I.; Guel, I.E.; Hernandez, J.G.; Yoshida, M.M.; Sanchez, R.M. Aluminum-graphite composite produced by mechanical milling and hot extrusion. J. Alloys Compd. 2007, 434–435, 518–521. [Google Scholar] [CrossRef]
- Suresha, S.; Sridhara, B.K. Effect of addition of graphite particulates on the wear behavior in aluminum-silicon carbide-graphite composite. Mater. Des. 2010, 31, 1804–1812. [Google Scholar] [CrossRef]
- Suresha, S.; Sridhara, B.K. Wear characteristics of hybrid aluminum matrix composites reinforced with graphite and silicon carbides particulates. Compos. Sci. Technol. 2010, 70, 1652–1659. [Google Scholar] [CrossRef]
- Shorowordi, K.M.; Hasseb, A.S.M.A.; Celis, J.P. Tribo-surface characteristics of Al-B4C and Al-SiC composites worn under different contact pressures. Wear 2006, 261, 634–641. [Google Scholar] [CrossRef]
- Tavakoli, A.H.; Smichi, A.; Reihani, S.M. Study of the compaction behavior of composite powders under monotonic and cyclic loading. Compos. Sci. Technol. 2005, 65, 2094–2104. [Google Scholar] [CrossRef]
- El-Shenawy, M.; Ahmed, M.; Nassef, A.; El-Hadek, M.; Alzahrani, B.; Zedan, Y.; El-Garaihy, W. Effect of ECAP on the Plastic Strain Homogeneity, Microstructural Evolution, Crystallographic Texture and Mechanical Properties of AA2xxx Aluminum Alloy. Metals 2021, 11, 938. [Google Scholar] [CrossRef]
- Salem, H.G.; Sadek, A.A. Fabrication of High-Performance PM Nanocrystalline Bulk AA2124. J. Mater. Eng. Perform. 2009, 19, 356–367. [Google Scholar] [CrossRef]
- Polmear, I.J. Light Alloys-Metallurgy of the Light Metals, 3rd ed.; Arnold: London, UK, 2000. [Google Scholar]
- Salem, H.G.; El-Garaihy, W.H.; Al-Rassoul, E.S.M. Influence of high-pressure torsion on the consolidation behavior and mechanical properties of AA6061-SiCp composite powders. In Supplemental Proceedings; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; pp. 553–560. [Google Scholar] [CrossRef]
- Alateyah, A.I.; Alawad, M.O.; Aljohani, T.A.; El-Garaihy, W.H. Effect of ECAP Route Type on the Microstructural Evolution, Crystallographic Texture, Electrochemical Behavior and Mechanical Properties of ZK30 Biodegradable Magnesium Alloy. Materials 2022, 15, 6088. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Langdon, T.G. Using high-pressure torsion for metal processing: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 893–979. [Google Scholar] [CrossRef]
- El-Garaihy, W.H.; Fouad, D.M.; Salem, H.G. Multi-channel Spiral Twist Extrusion (MCSTE): A Novel Severe Plastic Defor-mation Technique for Grain Refinement. Met. Mater. Trans. A 2018, 49, 2854–2864. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Nurislamova, G.V.; Kim, B.K.; Baró, M.D.; Szpunar, J.A.; Langdon, T.G. Experimental parameters influencing grain refinement and microstructural evolution during high-pressure torsion. Acta Mater. 2003, 51, 753–765. [Google Scholar] [CrossRef]
- Jiang, H.; Zhu, Y.T.; Butt, D.P.; Alexandrov, I.V.; Lowe, T.C. Microstructural evolution, microhardness and thermal stability of HPT-processed Cu. Mater. Sci. Eng. A 2000, 290, 128–138. [Google Scholar] [CrossRef]
- El Aal, M.I.A. The influence of ECAP and HPT processing on the microstructure evolution, mechanical properties and tribology characteristics of an Al6061 alloy. J. Mater. Res. Technol. 2020, 9, 12525–12546. [Google Scholar] [CrossRef]
- El Aal, M.I.A. Recycling of Al chips and Al chips composites using high-pressure torsion. Mater. Res. Express 2021, 8, 056514. [Google Scholar] [CrossRef]
- Deng, N.T.G.; Zhao, X.; Su, L.; Wei, P.; Zhang, L.; Zhan, L.; Chong, Y.; Zhu, H. Effect of high-pressure torsion process on the microhardness, microstructure and tribological property of Ti6Al4V alloy. J. Mater. Sci. Technol. 2021, 94, 183–195. [Google Scholar] [CrossRef]
- Edalati, K.; Akiba, E.; Horita, Z. High-pressure torsion for new hydrogen storage materials. Sci. Technol. Adv. Mater. 2018, 19, 185–193. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.; Botti, S.; Marques, M.A. Recent advances and applications of machine learning in solid-state materials science. Npj Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, Y.; Wang, C.; Xue, D.; Bai, Y.; Antonov, S.; Dai, L.; Lookman, T.; Su, Y. Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Shaban, M.; Alateyah, A.I.; Alsharekh, M.F.; Alawad, M.O.; BaQais, A.; Kamel, M.; Alsunaydih, F.N.; El-Garaihy, W.H.; Salem, H.G. Influence of ECAP Parameters on the Structural, Electrochemical and Mechanical Behavior of ZK30: A Combination of Experimental and Machine Learning Approaches. J. Manuf. Mater. Process. 2023, 7, 52. [Google Scholar] [CrossRef]
- Schleder, G.R.; Padilha, A.C.M.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Recent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar]
- Wang, A.Y.T.; Murdock, R.J.; Kauwe, S.K.; Oliynyk, A.O.; Gurlo, A.; Brgoch, J.; Persson, K.A.; Sparks, T.D. Machine learning for materials scientists: An introductory guide toward best practices. Chem. Mater. 2020, 32, 4954–4965. [Google Scholar]
- Ghaedi, M.; Azad, F.N.; Dashtian, K.; Hajati, S.; Goudarzi, A.; Soylak, M. Central composite design and genetic algorithm applied for the optimization of ultrasonic-assisted removal of malachite green by ZnO Nanorod-loaded activated carbon. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2016, 167, 157–164. [Google Scholar] [CrossRef]
- Dadrasi, A.; Fooladpanjeh, S.; Gharahbagh, A.A. Interactions between HA/GO/epoxy resin nanocomposites: Optimization, modeling and mechanical performance using central composite design and genetic algorithm. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 41–63. [Google Scholar]
- Santhosh, A.J.; Tura, A.D.; Jiregna, I.T.; Gemechu, W.F.; Ashok, N.; Ponnusamy, M. Optimization of CNC turning parameters using face centred CCD approach in RSM and ANN-genetic algorithm for AISI 4340 alloy steel. Results Eng. 2021, 11, 100251. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine learning: Algorithms, real-world applications and research directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Deringer, V.L.; Bartók, A.P.; Bernstein, N.; Wilkins, D.M.; Ceriotti, M.; Csányi, G. Gaussian process regression for materials and molecules. Chem. Rev. 2021, 121, 10073–10141. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2014, 17, 113–126. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar]
- Blanco, V.; Japón, A.; Puerto, J. A mathematical programming approach to SVM-based classification with label noise. Comput. Ind. Eng. 2022, 172, 108611. [Google Scholar]
- Ahmed, N.I.; Nasrin, F. Reducing Error Rate for Eye-Tracking System by Applying SVM. In Machine Intelligence and Data Science Applications; Springer: New York, NY, USA, 2022; pp. 35–47. [Google Scholar]
- Hazir, E.; Ozcan, T. Response surface methodology integrated with desirability function and genetic algorithm approach for the optimization of CNC machining parameters. Arab. J. Sci. Eng. 2019, 44, 2795–2809. [Google Scholar] [CrossRef]
- Bidulska, J.; Kocisko, R.; Bidulsky, R.; Grande, A.; Donic, T.; Martikan, M. Effect of severe plastic deformation on the porosity characteristics of Al-Zn-Mg-Cu PM alloy. Acta Metall. Slovaca 2010, 16, 4–11. [Google Scholar]
- Stolyarov, V.V.; Zhu, Y.T.; Lowe, T.C.; Islamgalive, R.K.; Valiev, R.Z. Processing nanocrystalline Ti and its nanocomposites from micrometer-sized Ti powder using high pressure torsion. Mater. Sci. Eng. A 2000, 282, 78–85. [Google Scholar] [CrossRef]
- Langdon, T.G. The significance of strain reversals during processing by high-pressure torsion. Mater. Sci. Eng. A 2008, 498, 341–348. [Google Scholar] [CrossRef]
- Langdon, T.G.; Xu, C. Three-dimensional representations of hardness distributions after processing by high-pressure torsion. Mater. Sci. Eng. A 2009, 503, 71–74. [Google Scholar] [CrossRef]
- Langdon, T.G.; Xu, C.; Horita, Z. The evolution of homogeneity in an aluminum alloy processed using high-pressure torsion. Acta Mater. 2008, 56, 5168–5176. [Google Scholar] [CrossRef]
- Estrin, Y.; Molotnikov, A.; Davies, C.H.; Lapovok, R. Strain gradient plasticity modelling of high-pressure torsion. J. Mech. Phys. Solids 2008, 56, 1186–1202. [Google Scholar] [CrossRef]
- Moreno-Valle, E.C.; Sabirov, I.; Perez-Prado, M.T.; Murashkin, M.Y.; Bobruk, E.V.; Valiev, R.Z. Effect of the grain refinement via severe plastic deformation on strength properties and deformation behavior of an Al6061 alloy at room and cryogenic temperatures. Mater. Lett. 2011, 65, 2917–2919. [Google Scholar]
- Wetscher, F.; Vorhauer, A.; Pippan, R. Strain hardening during high pressure torsion deformation. Mater. Sci. Eng. A 2005, 410–411, 213–216. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Rovan, H.J.; Liu, M.; Murashkin, M.; Kilmametov, A.R.; Ungar, T.; Balogh, L. Nanostructures and Microhardness in Al and Al–Mg Alloys Subjected to SPD. Mater. Sci. Forum 2009, 604–605, 179–185. [Google Scholar] [CrossRef]
- Alateyah, A.I.; Alawad, M.O.; Aljohani, T.A.; El-Garaihy, W.H. Influence of Ultrafine-Grained Microstructure and Texture Evolution of ECAPed ZK30 Magnesium Alloy on the Corrosion Behavior in Different Corrosive Agents. Materials 2022, 15, 5515. [Google Scholar] [CrossRef] [PubMed]
- Borodachenkova, M.; Wen, W.; de Bastos Pereira, A.M. High-Pressure Torsion: Experiments and Modeling. In Severe Plastic Deformation Techniques; Licensee IntechOpen: London, UK, 2017; pp. 93–112. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).