Theoretical Analysis of Rolling Force during Cold Rolling with Roll Crossing and Shifting System
Abstract
1. Introduction
2. Mill Testing and Experimental Procedure
3. Theoretical Analysis of Rolling Force Considering Roll Crossing with Asymmetric Rolling System
3.1. Rolls Crossing Method
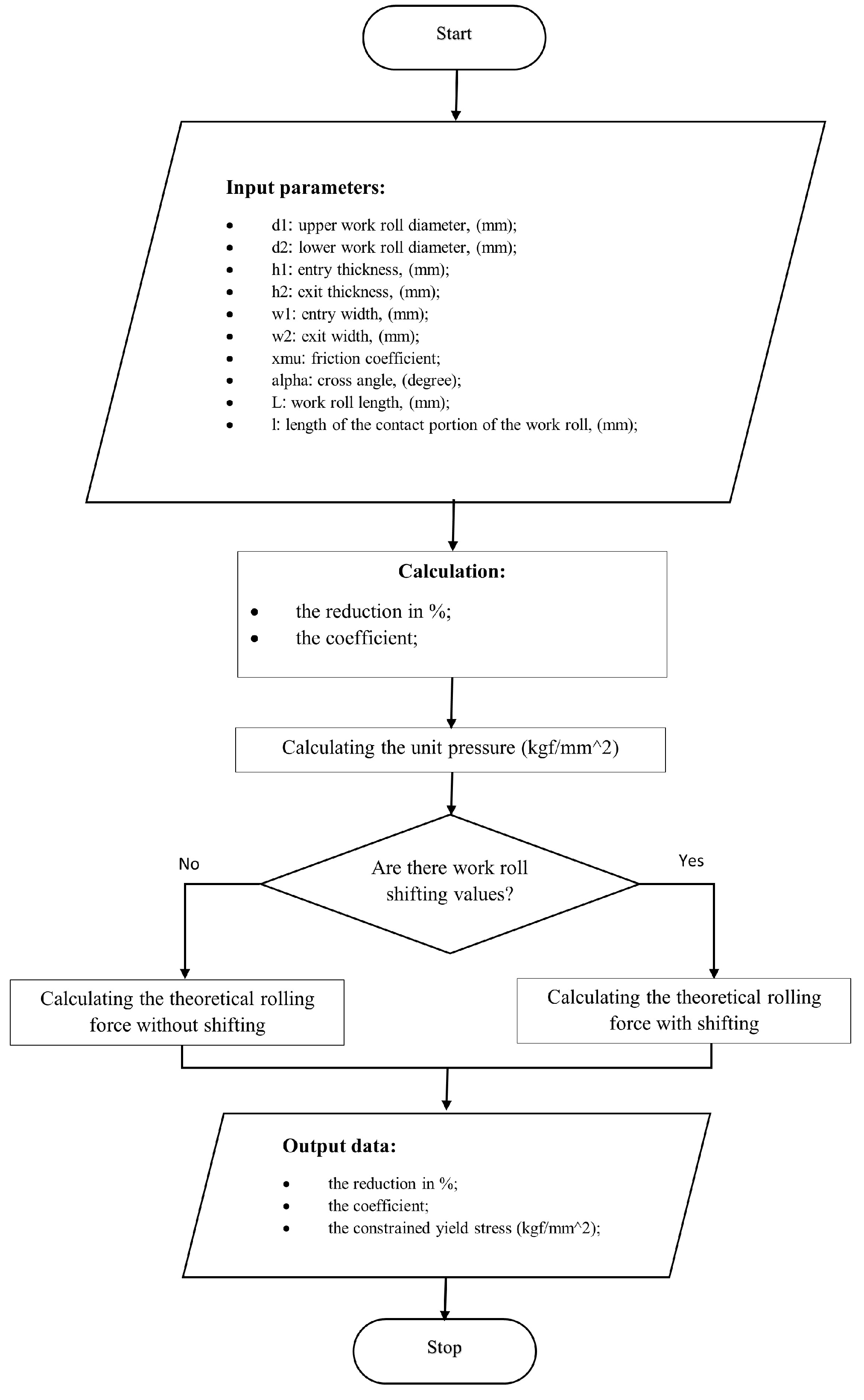
3.1.1. Calculation of Rolling Force Steps
- Compute the coefficient which is related to the and roll diameter and , and can be expressed as
- 2.
- Calculate the reduction ratio (%) value as follows:
- 3.
- 4.
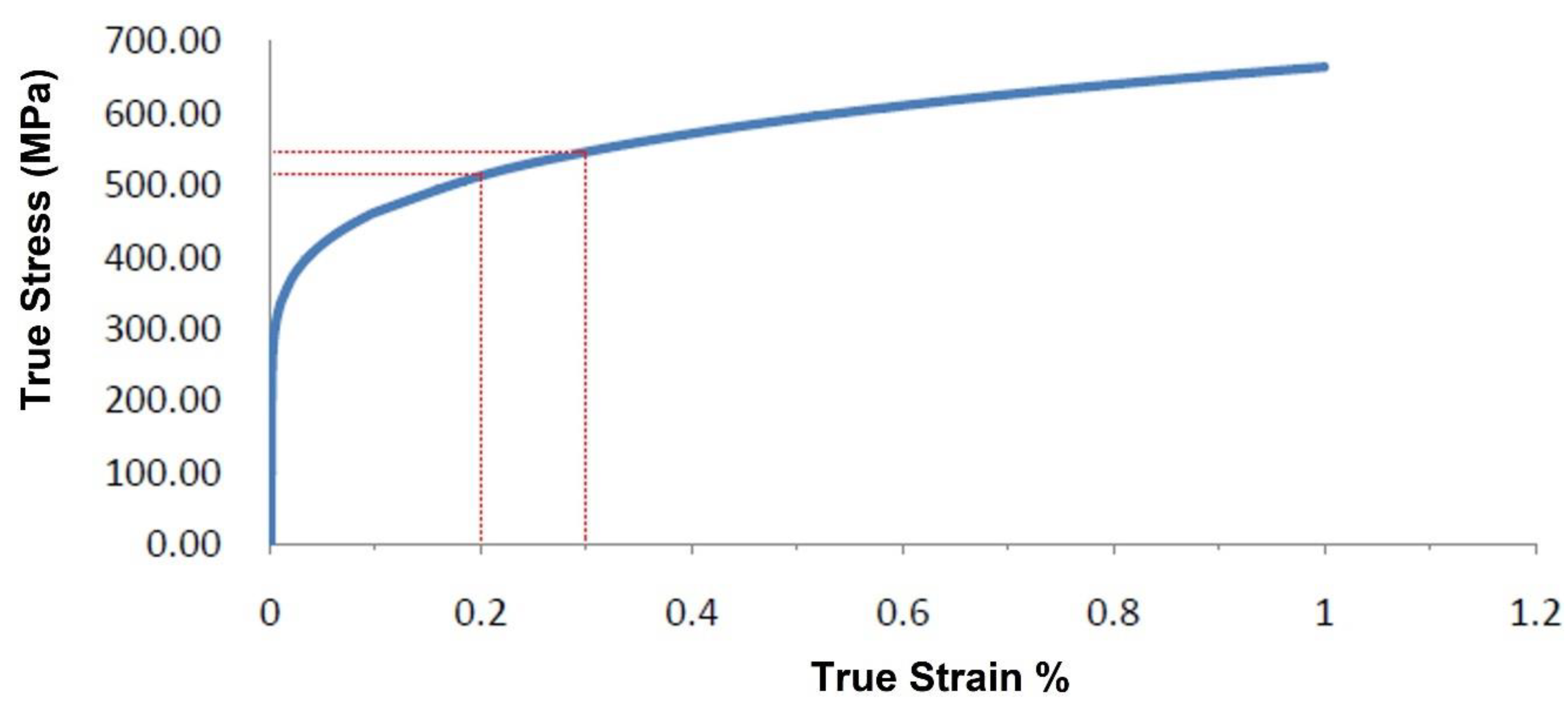
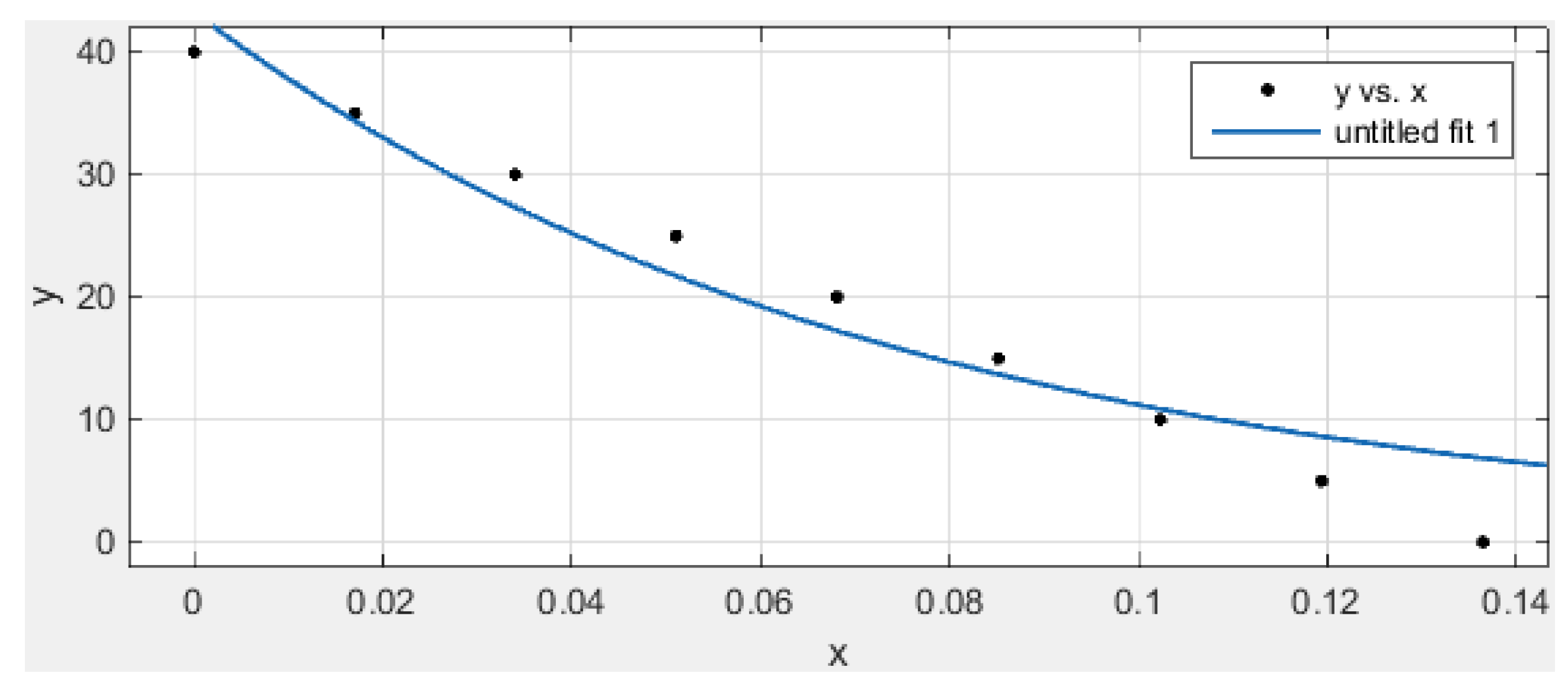
- Check the material yield stress through a tensile test for low-carbon steel alloys as shown in Figure 4.
- 5.
- Calculate the constrained yield stress, K, using Equation (3):
- 6.
- Finally, calculate the unit pressure using Equation (4).
3.1.2. Iteration Method for Calculating the Theoretical Rolling Force (without Consideration of Flattening)
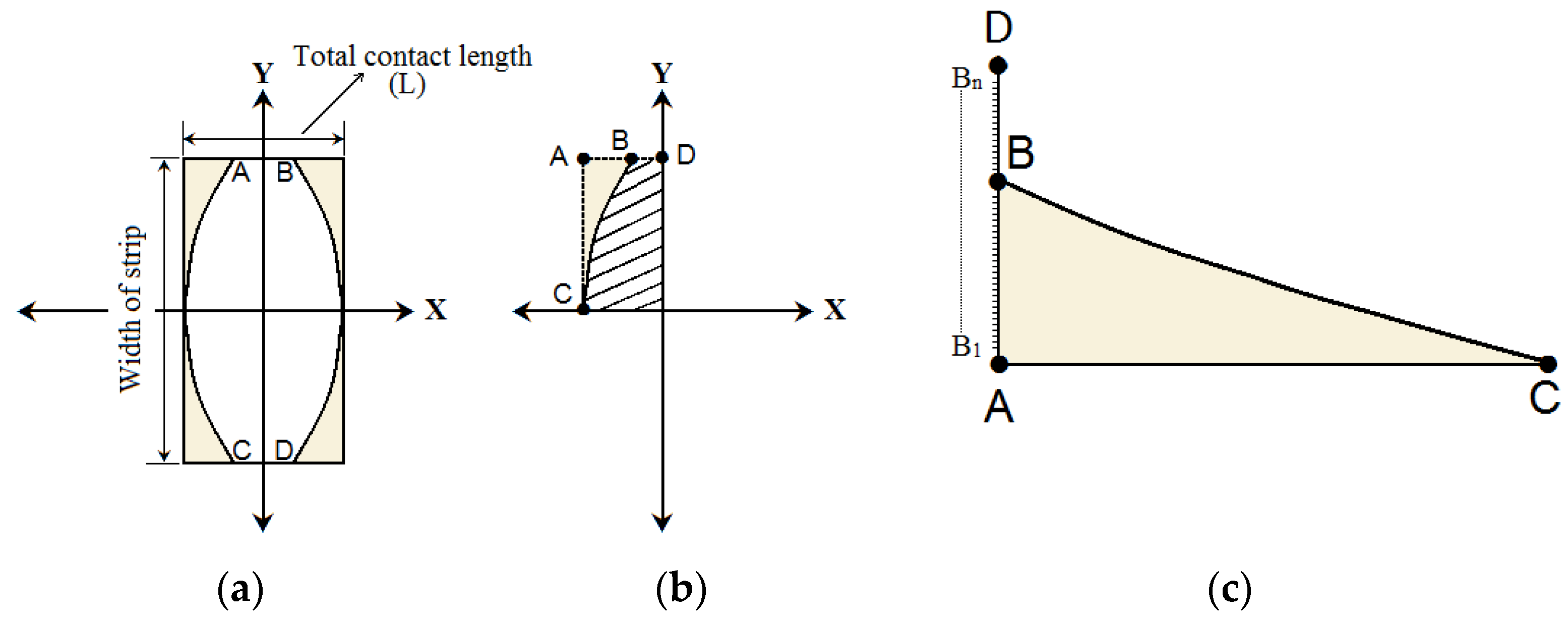
3.1.3. Calculating the Contact Length (with Consideration of Deflection)
3.2. The Mathematical Verification of Convergence of the Calculation
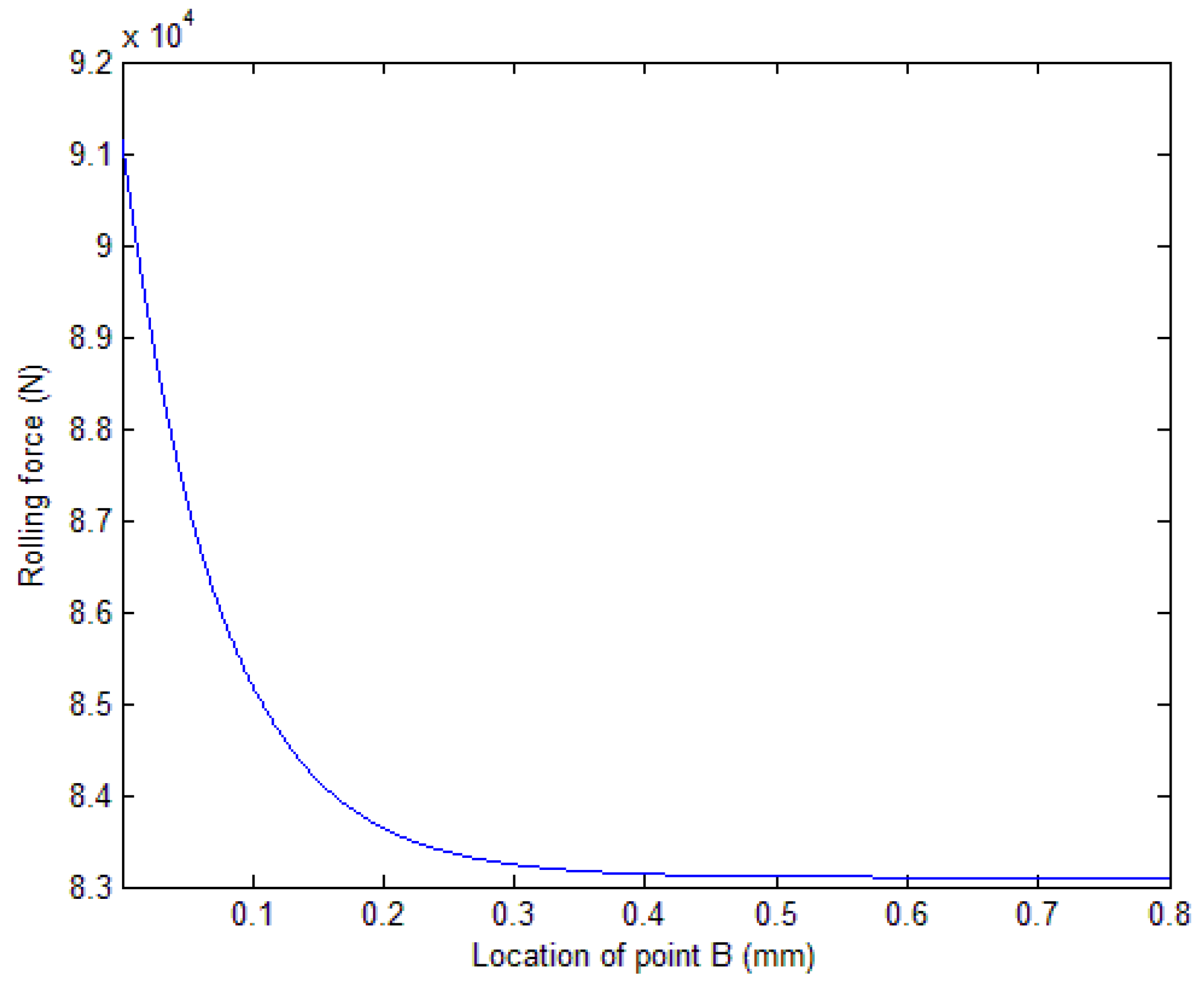
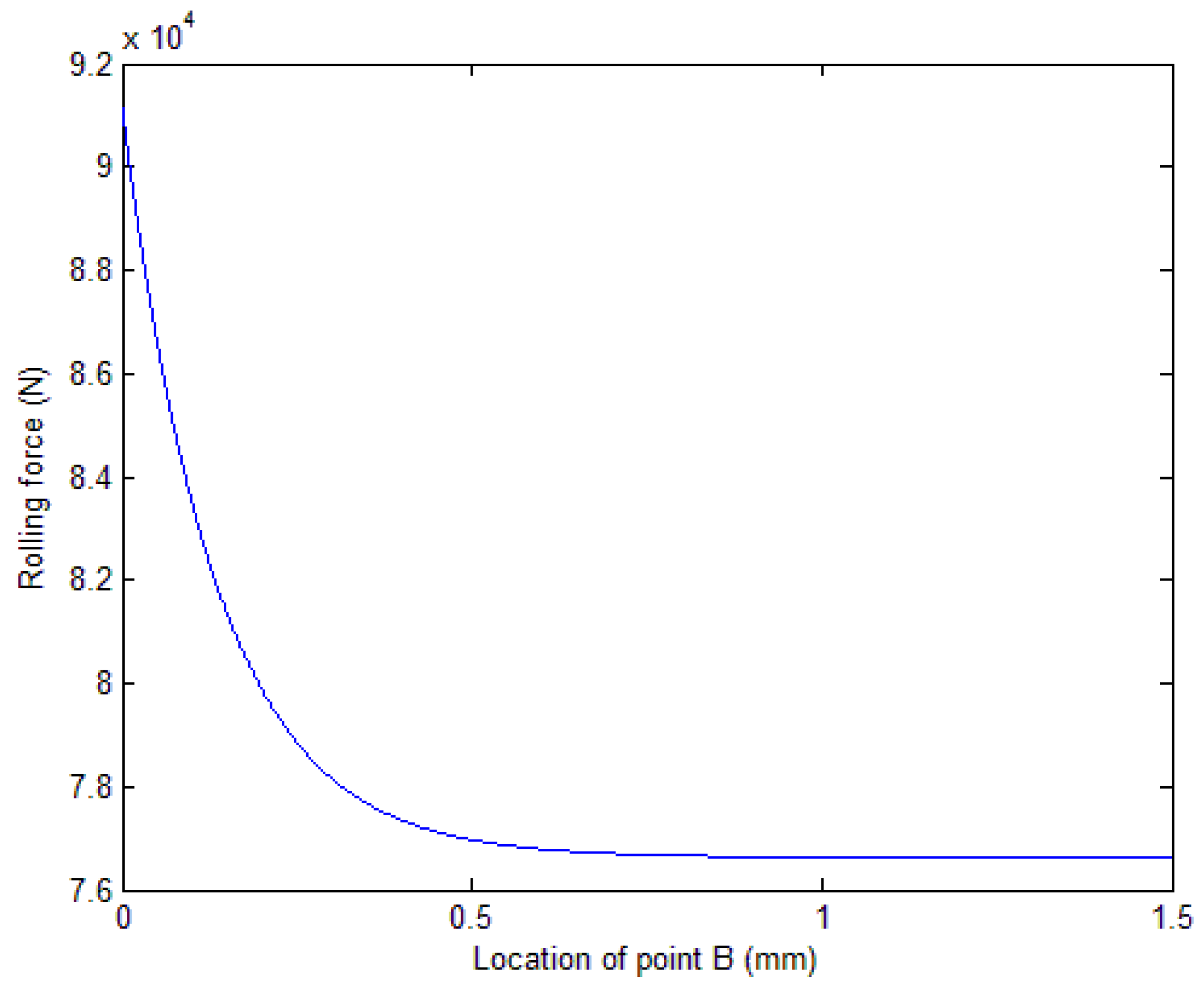
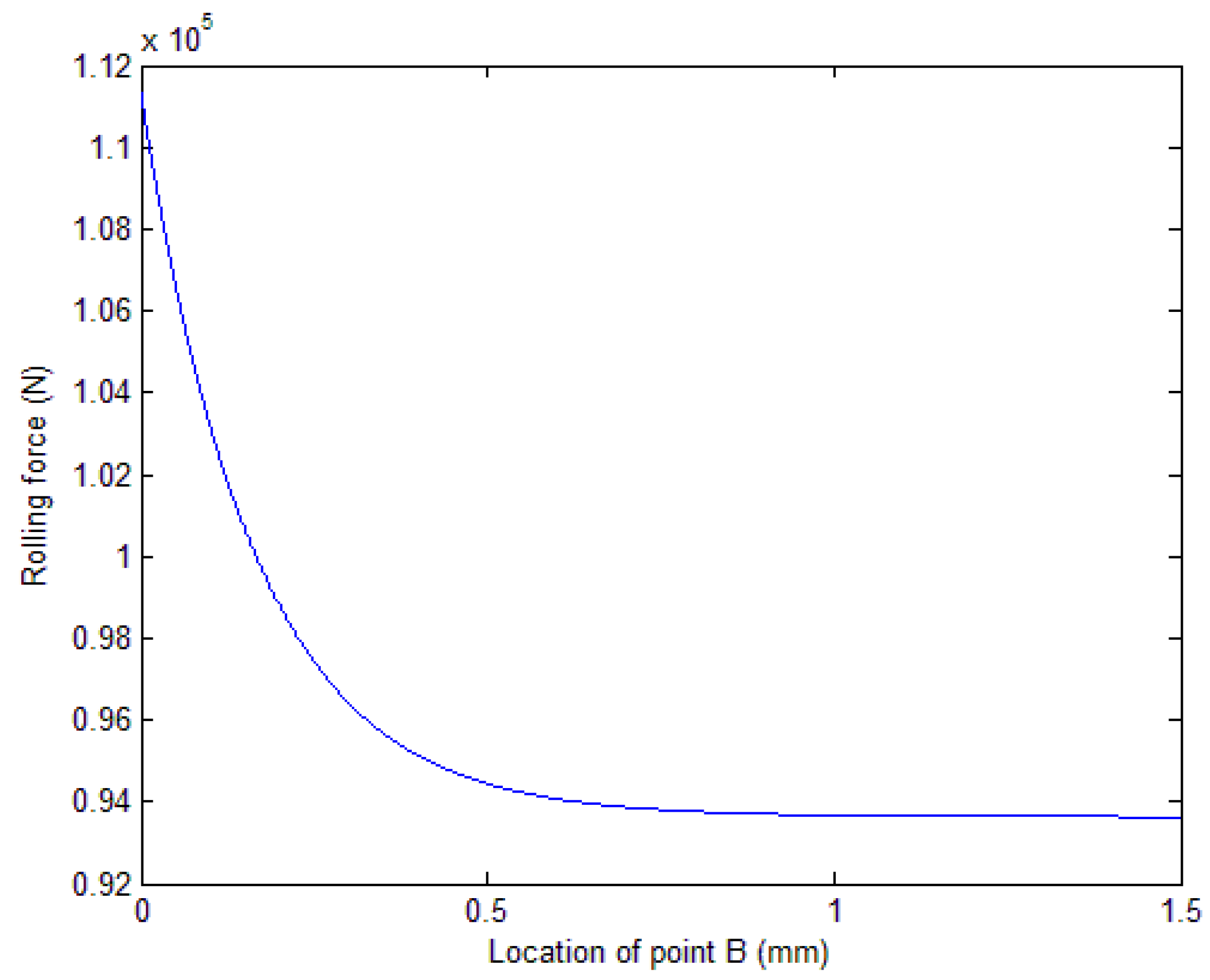
3.2.1. Difference between Two Calculations for the Area of the Four Corners (mm2)
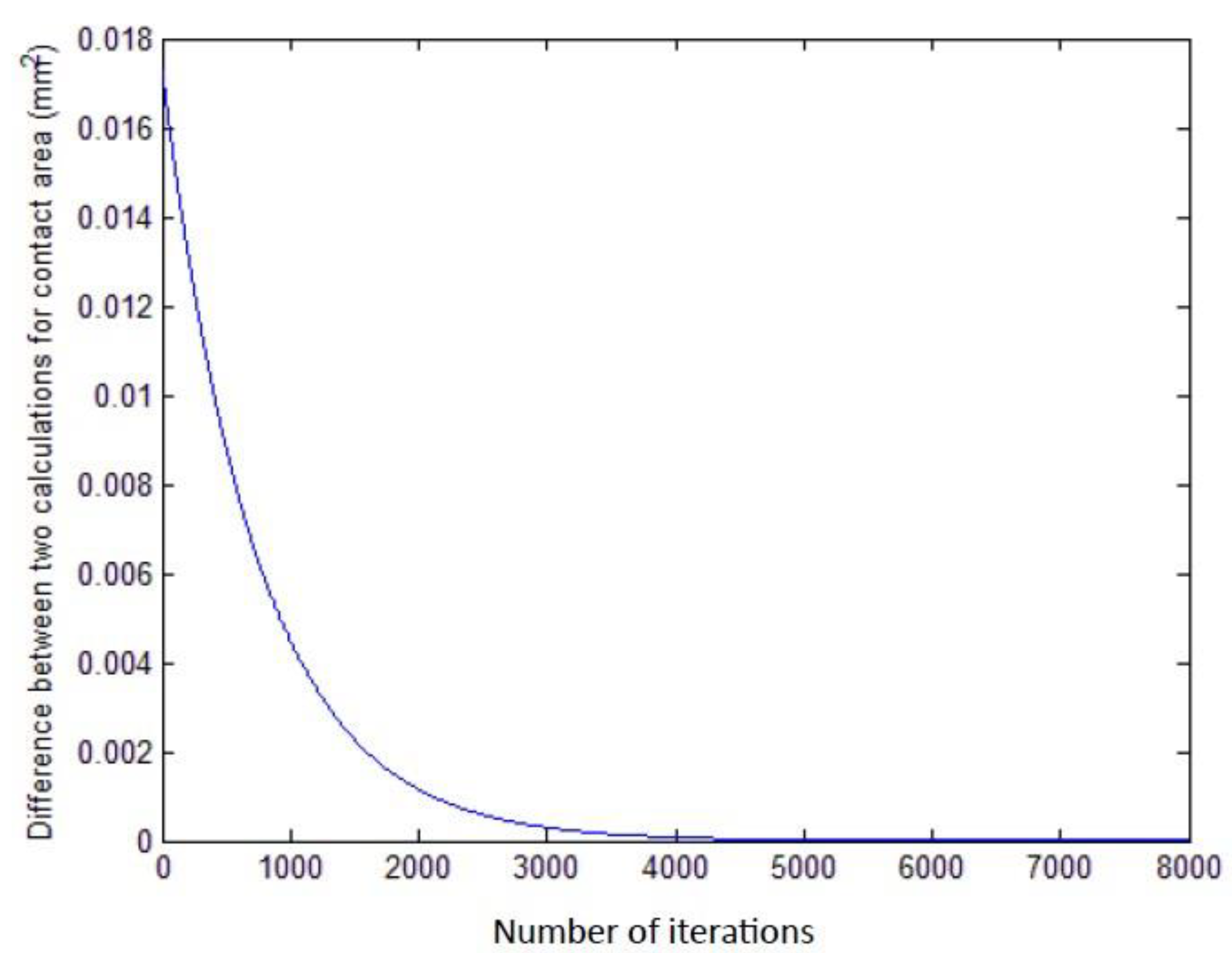
3.2.2. Difference between Two Calculations for Contact Areas (mm2)
3.2.3. Difference between Two Calculations for Rolling Force (N)
4. Results and Discussion
4.1. Calculated Rolling Force Compared to Experimental Rolling Force
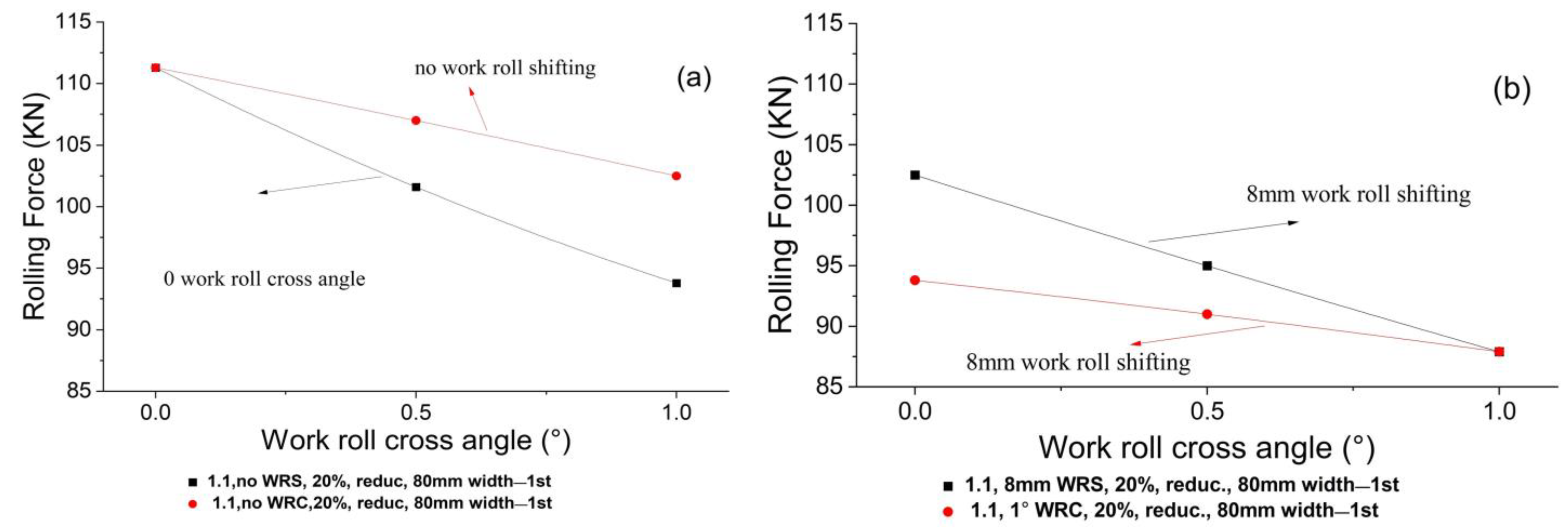
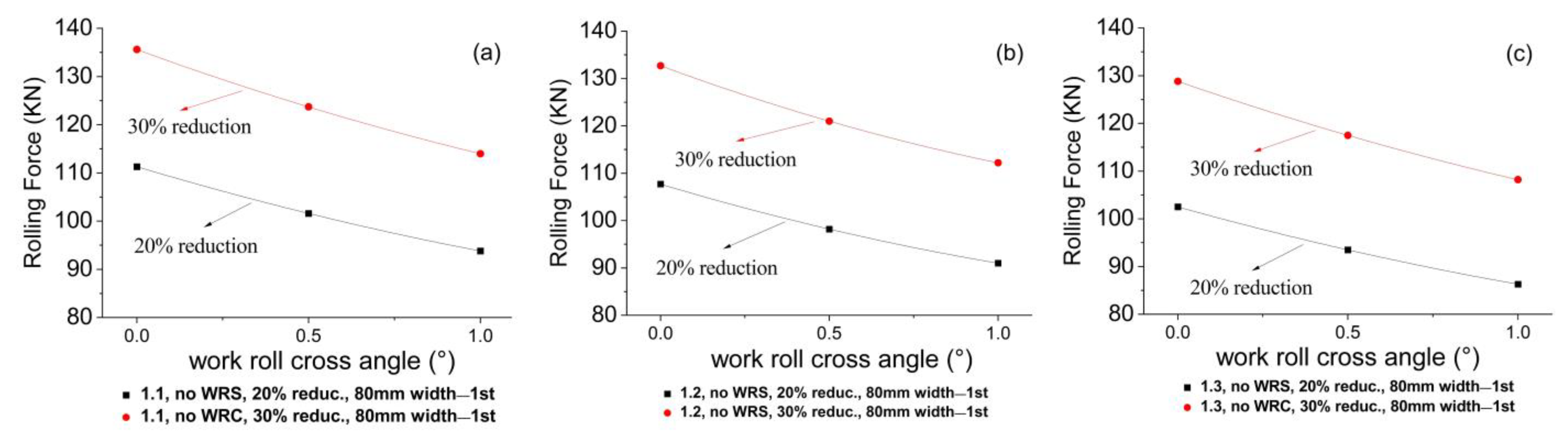
4.1.1. Effect of 1.1 Speed Ratio on Theoretical Rolling Force
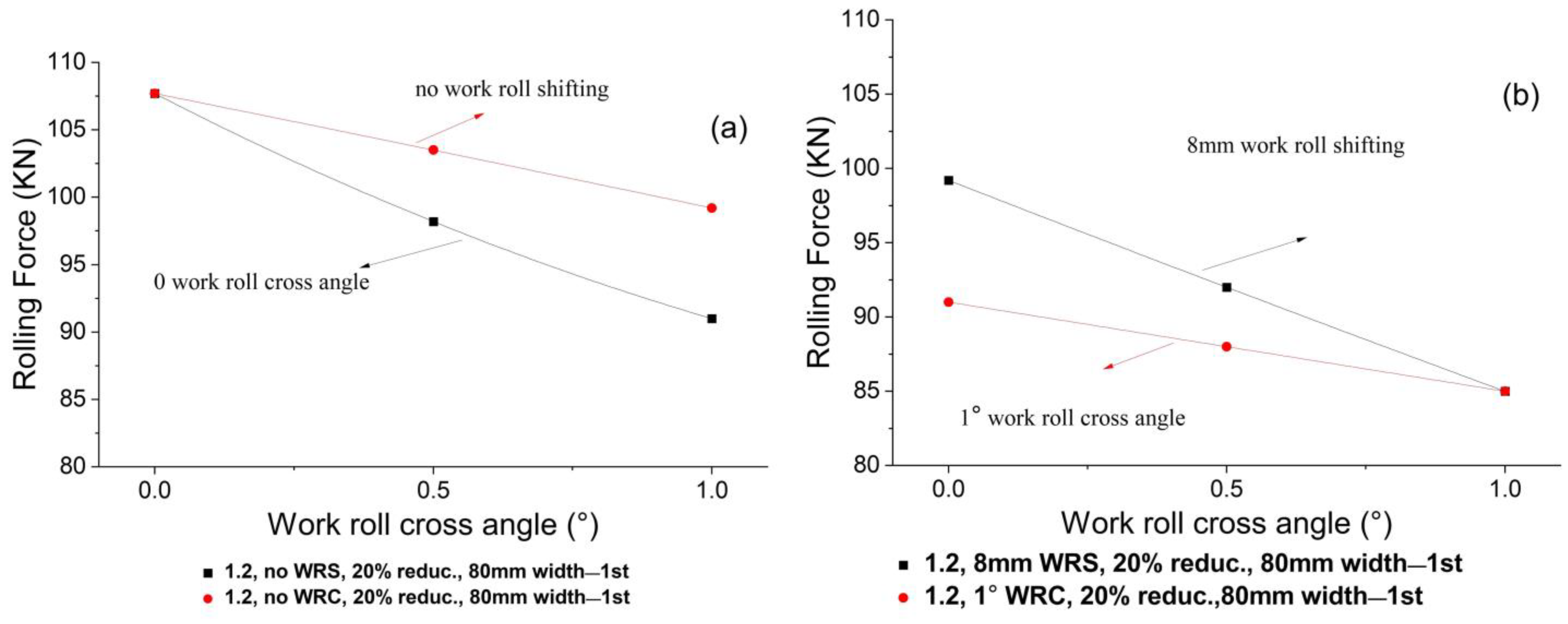
4.1.2. Effect of 1.2 Speed Ratio on the Theoretical Rolling Force
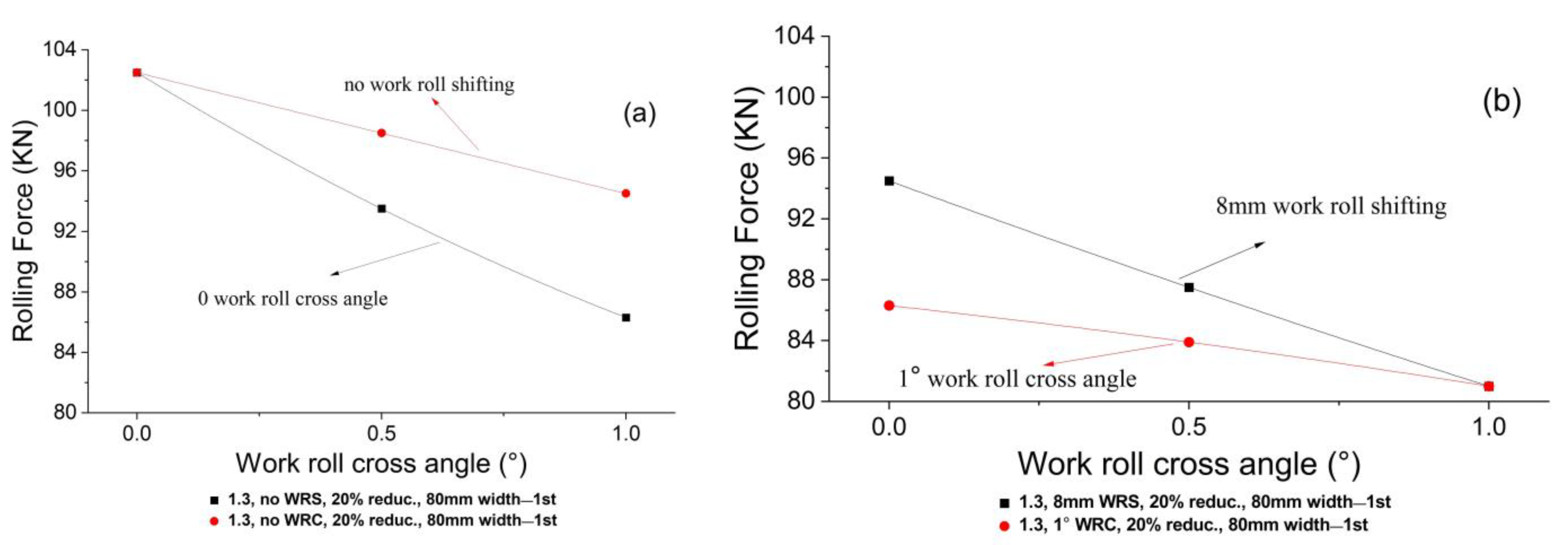
4.1.3. Effect of 1.3 Speed Ratio on the Theoretical Rolling Force
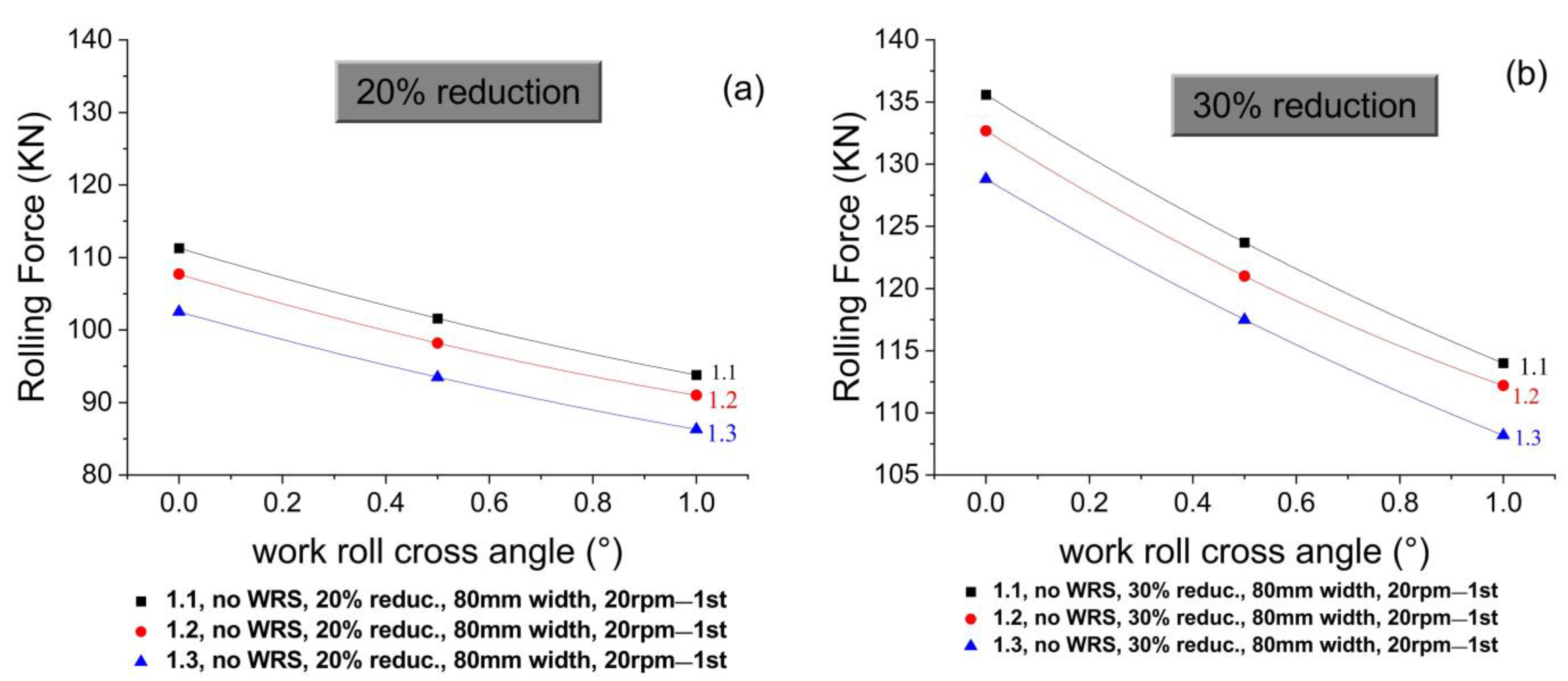
4.1.4. Effect of Reduction Ratio on Theoretical Rolling Force
4.1.5. Effect of Asymmetrical Rolling Process; 1.1 and 1.2 vs. 1.3 on the Theoretical Rolling Force
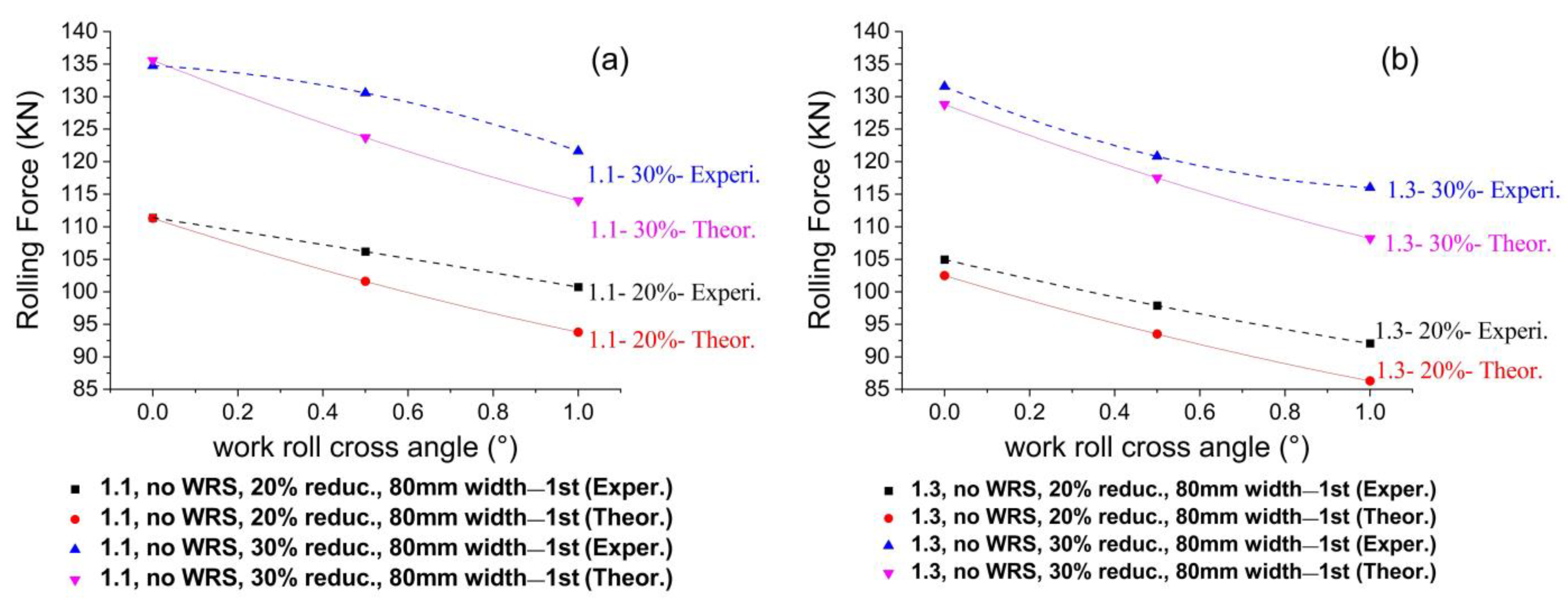
4.1.6. Comparison of Theoretical Rolling Force with Experimental Rolling Force
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| WRC, WRS | The work roll crossing combined with roll shifting for asymmetrical and symmetrical rolling mills |
| PC | The pair-cross mill, in which the backup roll and work roll axes of each top and bottom are crossed |
| h1 | Entry thickness of the strip, (mm) |
| h2 | Exit thickness of the strip, (mm) |
| p | Unit pressure normally acting on the strip surface from the roll, (MPa) |
| P | Roll-separating force, (N) |
| w1, w2 | Entry and exit width of rolled strip, (mm) |
| D1, D2 | The diameter of the top and bottom work rolls respectively, (mm) |
| µ | Coefficient of friction |
| , | Radii of the upper and lower rolls respectively, (mm) |
| The difference between the entry and the exit thickness, (mm) | |
| Coefficient delta | |
| Reduction ratio, (%) | |
| K, | Constrained yield stress and yield stress, respectively, (MPa) |
| n | External friction effect coefficient |
| Total contact length between the work roll and the strip (without work roll crossing angle and work roll shifting), (mm) | |
| Contact length between top and bottom work rolls in case of shifting, (mm) | |
| Theoretical rolling force, (N) | |
| Contact area calculated from the iteration method, (mm2) | |
| AD | ½ of the contact length between the work roll and the strip, (mm) |
| AC | ½ of the strip width, (mm) |
| Deflection of the work rolls, (mm) | |
| Spring-back of the strip, (mm) | |
| Poisson’s ratio |
References
- Wang, Q.; Li, J.; Wang, X.; Yang, Q.; Wu, Z. Evaluation Method and Application of Cold Rolled Strip Flatness Quality Based on Multi-Objective Decision-Making. Metals 2022, 12, 1977. [Google Scholar] [CrossRef]
- Yang, L.; Jiang, Z.; Zhang, Y.; Yu, H. High precision recognition and adjustment of complicated shape details in fine cold rolling process of ultra-thin wide strip. J. Manuf. Process. 2018, 35, 508–516. [Google Scholar] [CrossRef]
- Ren, Z.-K.; Xiao, H.; Yu, C.; Wang, J. Experimental study on transverse displacement of the metal during cold thin strip rolling. Procedia Eng. 2017, 207, 1326–1331. [Google Scholar] [CrossRef]
- Elahi, S.A.; Forouzan, M.R. Increasing the chatter instability speed limit in cold strip rolling using wavy layered composite plates as a damper. Thin-Walled Struct. 2019, 137, 19–28. [Google Scholar] [CrossRef]
- Boemer, D.; Carretta, Y.; Laugier, M.; Legrand, N.; Papeleux, L.; Boman, R.; Ponthot, J.P. An advanced model of lubricated cold rolling with its comprehensive pilot mill validation. J. Mater. Process. Technol. 2021, 296, 117175. [Google Scholar] [CrossRef]
- Shen, S.; Guye, D.; Ma, X.; Yue, S.; Armanfard, N. Multistep networks for roll force prediction in hot strip rolling mill. Mach. Learn. Appl. 2022, 7, 100245. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, Z.; Cao, R.; Zhang, W.; Li, H. Adaptive learning prediction on rolling force in the process of reversible cold rolling mill. In Proceedings of the Intelligent Robotics and Applications: 5th International Conference, Montreal, QC, Canada, 3–5 October 2012; pp. 66–75. [Google Scholar]
- Shan, W.; Chen, Y.; Wang, X.; Yu, C.; Wu, K.; Han, Z. Nonlinear Dynamic Characteristics of Deep Groove Ball Bearings with an Improved Contact Model. Machines 2023, 11, 340. [Google Scholar] [CrossRef]
- Radionov, A.A.; Petukhova, O.I.; Ian, N.; Erdakov, I.N.; Karandaev, A.S.; Boris, M.; Loginov, B.M.; Khramshin, V.R. Developing an Automated System to Control the Rolled Product Section for a Wire Rod Mill with Multi-Roll Passes. J. Manuf. Mater. Process. 2022, 6, 88. [Google Scholar] [CrossRef]
- Tselikov, A. Present state of theory of metal pressure upon rolls in longitudinal rolling. Stahl 1958, 18, 434–441. [Google Scholar]
- Fleck, N.A.; Johnson, K.L.; Mear, M.E.; Zhang, L.C. Cold rolling of foil. Proc. Inst. Mech. Eng. 1992, 206, 119–131. [Google Scholar] [CrossRef]
- Le, H.; Sutcliffe, M. A robust model for rolling of thin strip and foil. Int. J. Mech. Sci. 2001, 43, 1405–1419. [Google Scholar] [CrossRef]
- Wang, X.S.; Peng, Y.; Xu, L.P.; Liu, H.M. A 3-D differential method for solving rolling force of PC hot strip mill. J. Iron Steel Res. Int. 2010, 17, 36–39. [Google Scholar] [CrossRef]
- Han, J.; Cheng, Q.; Hu, P.; Xing, H.; Li, S.; Ge, S.; Hua, X.; Hu, B.; Zhang, W.; Wang, K. Finite Element Analysis of Large Plastic Deformation Process of Pure Molybdenum Plate during Hot Rolling. Metals 2023, 13, 101. [Google Scholar] [CrossRef]
- Aljabri, A.; Jiang, Z.Y.; Wei, D.B.; Wang, X.D.; Tibar, H. Thin strip profile control capability of roll crossing and shifting in cold rolling mill. Mater. Sci. Forum 2014, 773–774, 70–78. [Google Scholar] [CrossRef]
- Aljabri, A.; Jiang, Z.; Wei, D. Analysis of thin strip profile during asymmetrical cold rolling with roll crossing and shifting mill. Adv. Mater. Res. 2014, 894, 212–216. [Google Scholar] [CrossRef]
- Aljabri, A.; Jiang, Z.Y.; Wei, D.B.; Wang, X.D.; Tibar, H. Modeling of thin strip profile during cold rolling on roll crossing and shifting mill. In Proceedings of the 8th Pacific Rim International Congress on Advanced Materials and Processing, Waikoloa, HI, USA, 4–9 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3001–3007. [Google Scholar]
- Aljabri, A.; Jiang, Z.; Wei, D. Analysis of thin strip profile by roll crossing and shifting in asymmetrical cold rolling. Int. J. Mod. Phys. B 2015, 29, 1540032. [Google Scholar] [CrossRef]
- Jiang, Z.; Tieu, A. A 3-D finite element method analysis of cold rolling of thin strip with friction variation. Tribol. Int. 2004, 37, 185–191. [Google Scholar] [CrossRef]
- Wójcik, Ł.; Pater, Z.; Bulzak, T.; Tomczak, J.; Lis, K. A Comparative Analysis of the Physical Modelling of Two Methods of Balls Separation. Materials 2021, 14, 7126. [Google Scholar] [CrossRef]
- Jacobs, L.J.M.; van Dam, K.N.H.; Wentink, D.J.; de Rooij, M.B.; van der Lugt, J.; Schipper, D.J.; Hoefnagels, J.P.M. Effect of asymmetric material entrance on lubrication in cold rolling. Tribol. Int. 2022, 175, 107810. [Google Scholar] [CrossRef]
- Shahani, A.; Setayeshi, S.; Nodamaie, S.A.; Asadi, M.A.; Rezaie, S. Prediction of influence parameters on the hot rolling process using finite element method and neural network. J. Mater. Process. Technol. 2009, 209, 1920–1935. [Google Scholar] [CrossRef]
- Devarajan, K.; Marimuthu, K.P.; Ramesh, A. FEM analysis of effect of rolling parameters on cold rolling process. Bonfring Int. J. Ind. Eng. Manag. Sci. 2012, 2, 35. [Google Scholar]
- Babajamali, Z.; Khabaz, M.K.; Aghadavoudi, F.; Farhatnia, F.; Eftekhari, S.A.; Toghraie, D. Pareto multi-objective optimization of tandem cold rolling settings for reductions and inter stand tensions using NSGA-II. ISA Trans. 2022, 130, 399–408. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Z.J.; Liu, X.; Bu, J. Study of Rolling Force Calculation Models for Cold Rolling Process. Adv. Mater. Res. 2011, 154–155, 882–885. [Google Scholar] [CrossRef]
- Lu, X.; Sun, J.; Li, G.; Wang, Q.; Zhang, D. Dynamic analysis of vibration stability in tandem cold rolling mill. J. Mater. Process. Technol. 2019, 277, 47–57. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, Z.Y.; Tieu, A.K.; Liu, X.H.; Wang, G.D. A method to improve model calculation accuracy of process control in tandem cold mills. In Proceedings of the 2007 2nd IEEE Conference on Industrial Electronics and Applications (ICIEA 2007), Harbin, China, 23–25 May 2007. [Google Scholar]
- Wang, J.; Jiang, Z.Y.; Tieu, K.; Liu, X. Adaptive calculation of deformation resistance model of online process control in tandem cold mill. J. Mater. Process. Technol. 2005, 162, 585–590. [Google Scholar] [CrossRef]
- Hao, P.; Liu, Y.; Wang, Z.; Wang, T.; He, D.; Huang, Q.; Wang, Z. Analysis of force and deformation parameters in corrugated clad rolling. Int. J. Mech. Sci. 2023, 243, 108042. [Google Scholar] [CrossRef]
- Zhao, Z. Metal Plastic Deformation and Rolling Theory; Metallurgical Industry Press: Beijing, China, 1980. [Google Scholar]
- Su, F.; Jiang, J.; Chen, T. An Accurate Mathematical Model of Roll Flattened Arc Length. Acta Metall. Sin. 1984, 1, 17. [Google Scholar]
- Qu, F.; Jiang, Z.; Wei, D.; Chen, Q.; Lu, H. Study of micro flexible rolling based on grained inhomogeneity. Int. J. Mech. Sci. 2017, 123, 324–339. [Google Scholar] [CrossRef]
- Mathematical Constant. Available online: https://en.wikipedia.org/wiki/Mathematical_constant (accessed on 15 October 2022).
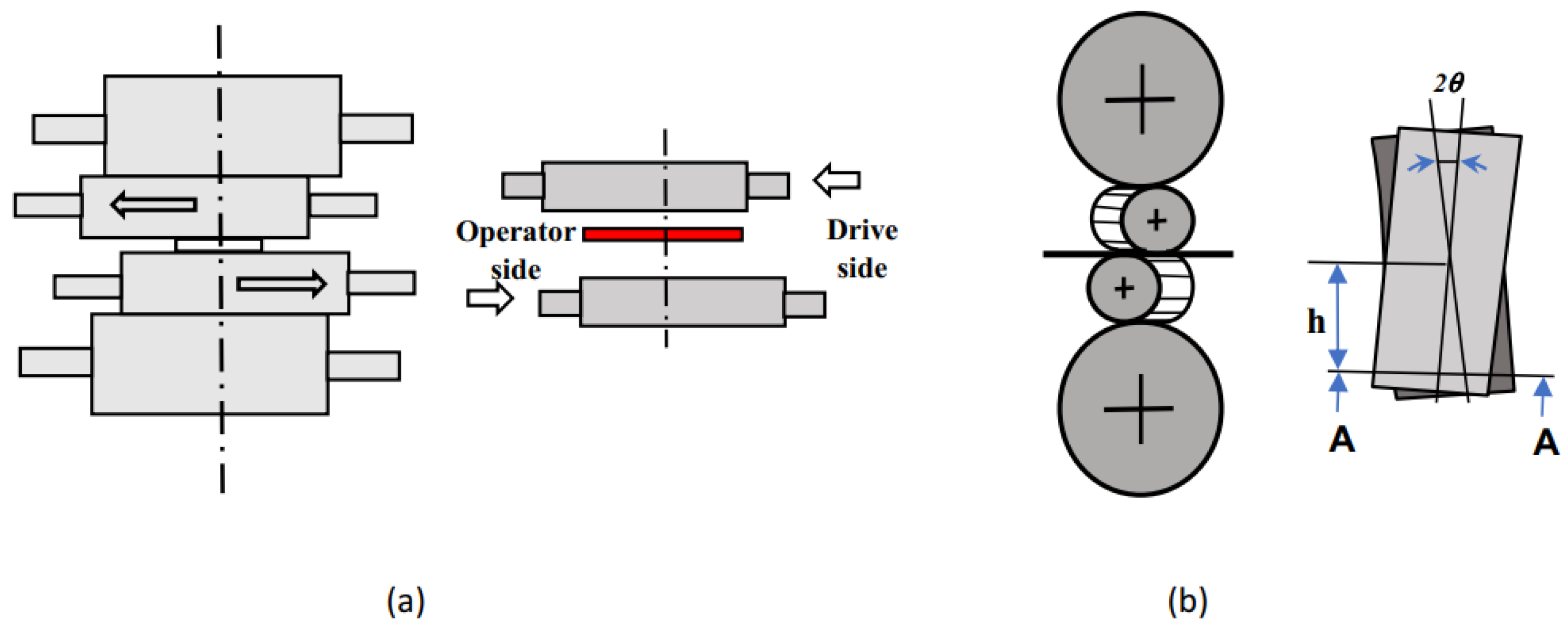



| Mill system | Work roll crossing and shifting |
| Cross angle | 0–1.5° |
| Shifting value | 0–8 mm |
| Work roll | Diameter for upper work roll = 63 mm, lower work roll = 69 mm, length = 250 mm |
| Backup roll | Diameter = 228 mm, length = 250 mm |
| Rolling force | 0–1500 kN |
| Rolling torque | 0–13 kN m |
| Speed Ratio | (20%) | (30%) | n Value (20%) | n Value (30%) | |
|---|---|---|---|---|---|
| 1.1 | 0.09 | 2.31 | 1.89 | 1.05 | 1.03 |
| 1.2 | 0.08 | 2.1 | 1.714 | 1 | 0.99 |
| 1.3 | 0.07 | 1.80 | 1.53 | 0.945 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljabri, A.; Tibar, H.; Mahmoud, E.R.I.; Almohamadi, H.; Qu, F.; Jiang, Z. Theoretical Analysis of Rolling Force during Cold Rolling with Roll Crossing and Shifting System. J. Manuf. Mater. Process. 2023, 7, 104. https://doi.org/10.3390/jmmp7030104
Aljabri A, Tibar H, Mahmoud ERI, Almohamadi H, Qu F, Jiang Z. Theoretical Analysis of Rolling Force during Cold Rolling with Roll Crossing and Shifting System. Journal of Manufacturing and Materials Processing. 2023; 7(3):104. https://doi.org/10.3390/jmmp7030104
Chicago/Turabian StyleAljabri, Abdulrahman, Hasan Tibar, Essam R. I. Mahmoud, Hamad Almohamadi, Feijun Qu, and Zhengyi Jiang. 2023. "Theoretical Analysis of Rolling Force during Cold Rolling with Roll Crossing and Shifting System" Journal of Manufacturing and Materials Processing 7, no. 3: 104. https://doi.org/10.3390/jmmp7030104
APA StyleAljabri, A., Tibar, H., Mahmoud, E. R. I., Almohamadi, H., Qu, F., & Jiang, Z. (2023). Theoretical Analysis of Rolling Force during Cold Rolling with Roll Crossing and Shifting System. Journal of Manufacturing and Materials Processing, 7(3), 104. https://doi.org/10.3390/jmmp7030104










