Investigation of Pressure Fields Generated by Two Simultaneous Discharges in Liquid Initiated by Wires
Abstract
1. Introduction
2. Materials and Methods
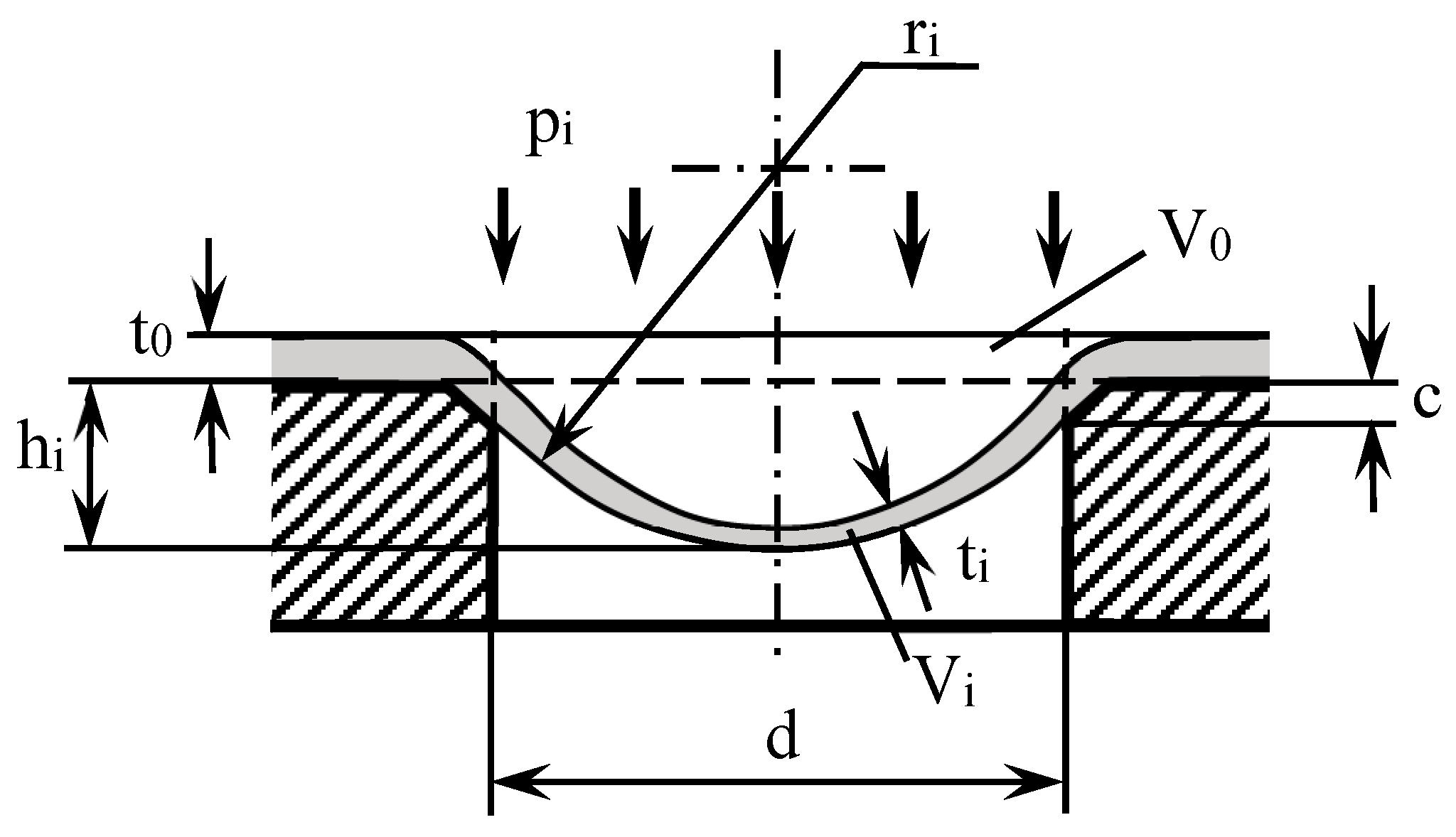
2.1. Test Setup
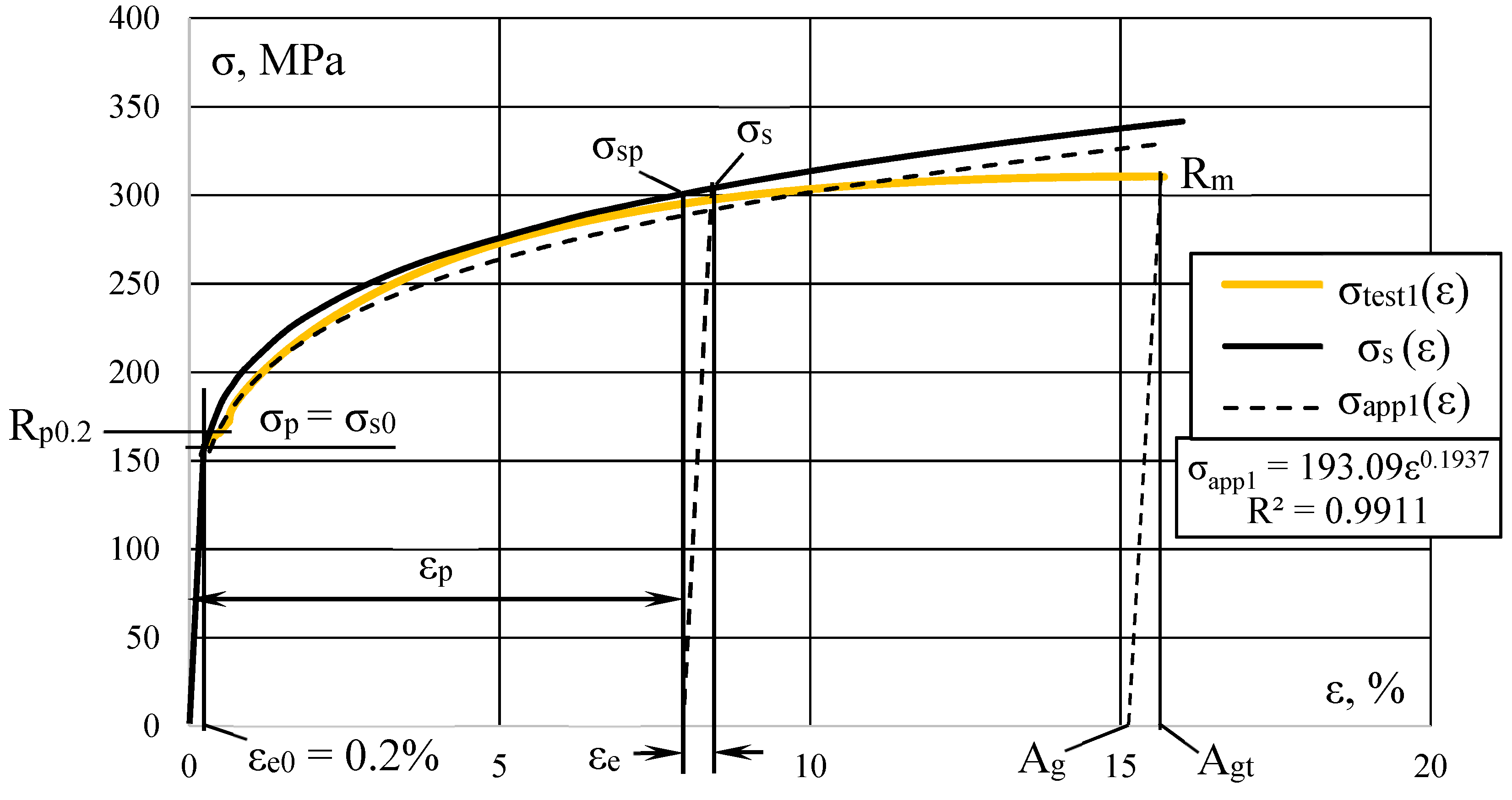
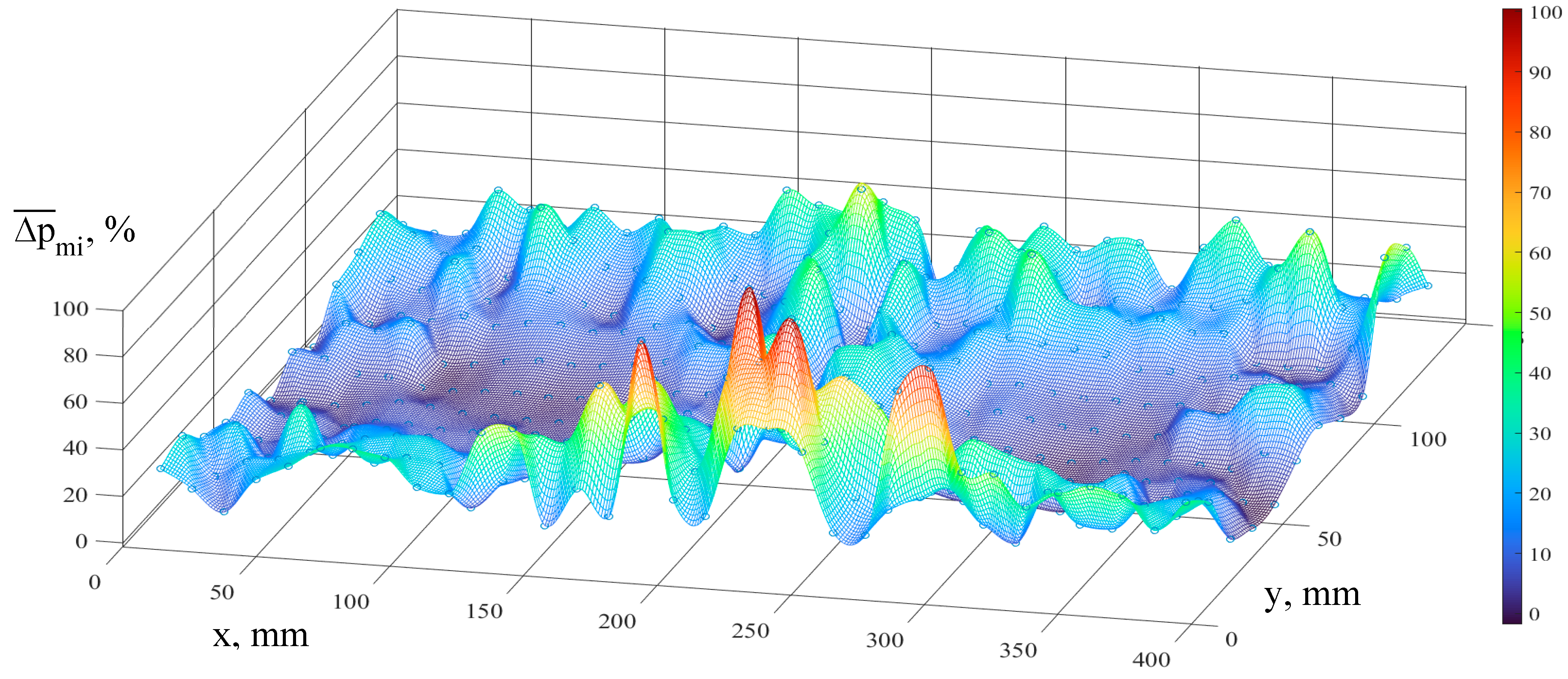
2.2. Processing of Measurement Results
- mean pressure value on the left half-area with the point coordinates at intervals x = 0–200 mm and y = 0–150 mm in the j-membrane
- mean pressure value on the right half-area with the point coordinates at intervals x = 200–400 mm and y = 0–150 mm in the j-membrane
- left-hand FL, right-hand FR and total F forcesFL = pmL × SL; FR = pmR × SR; F = pm × S = FL + FR.
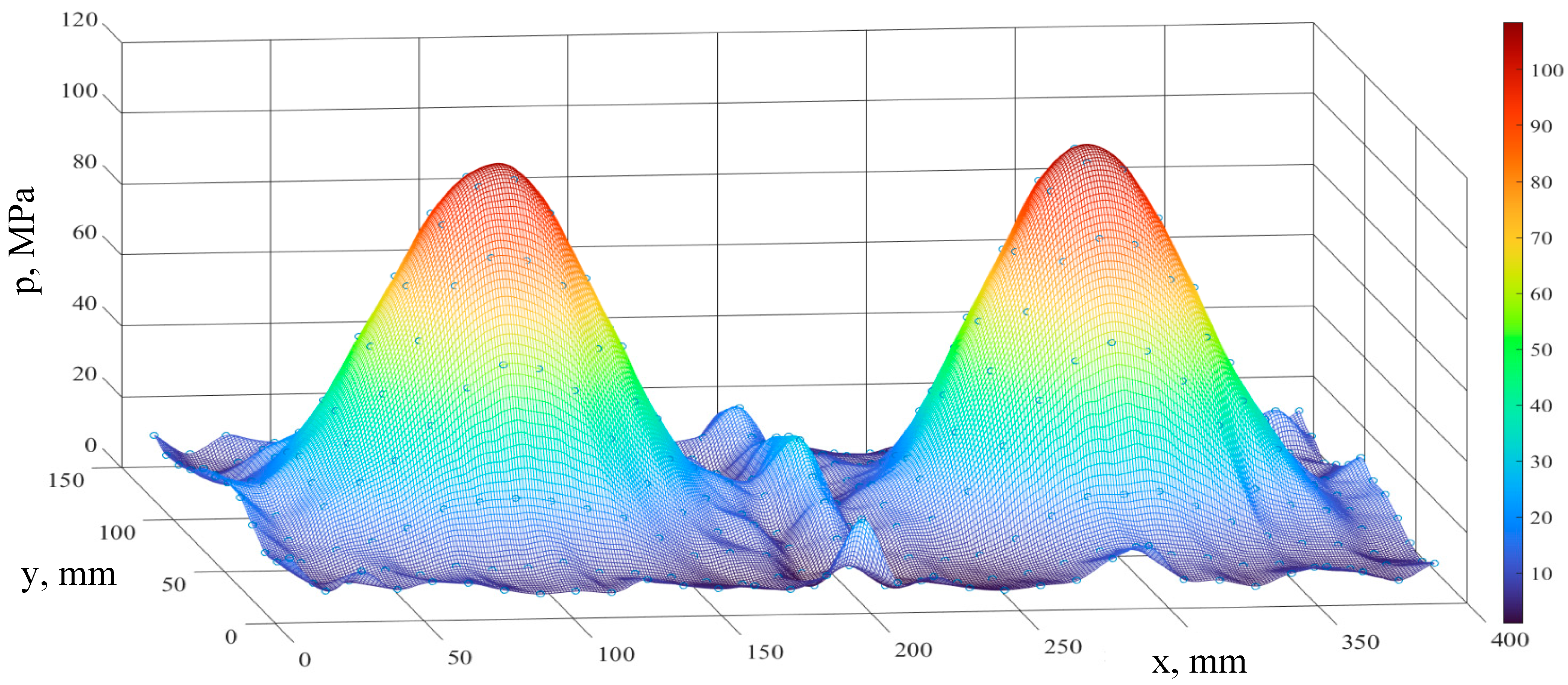
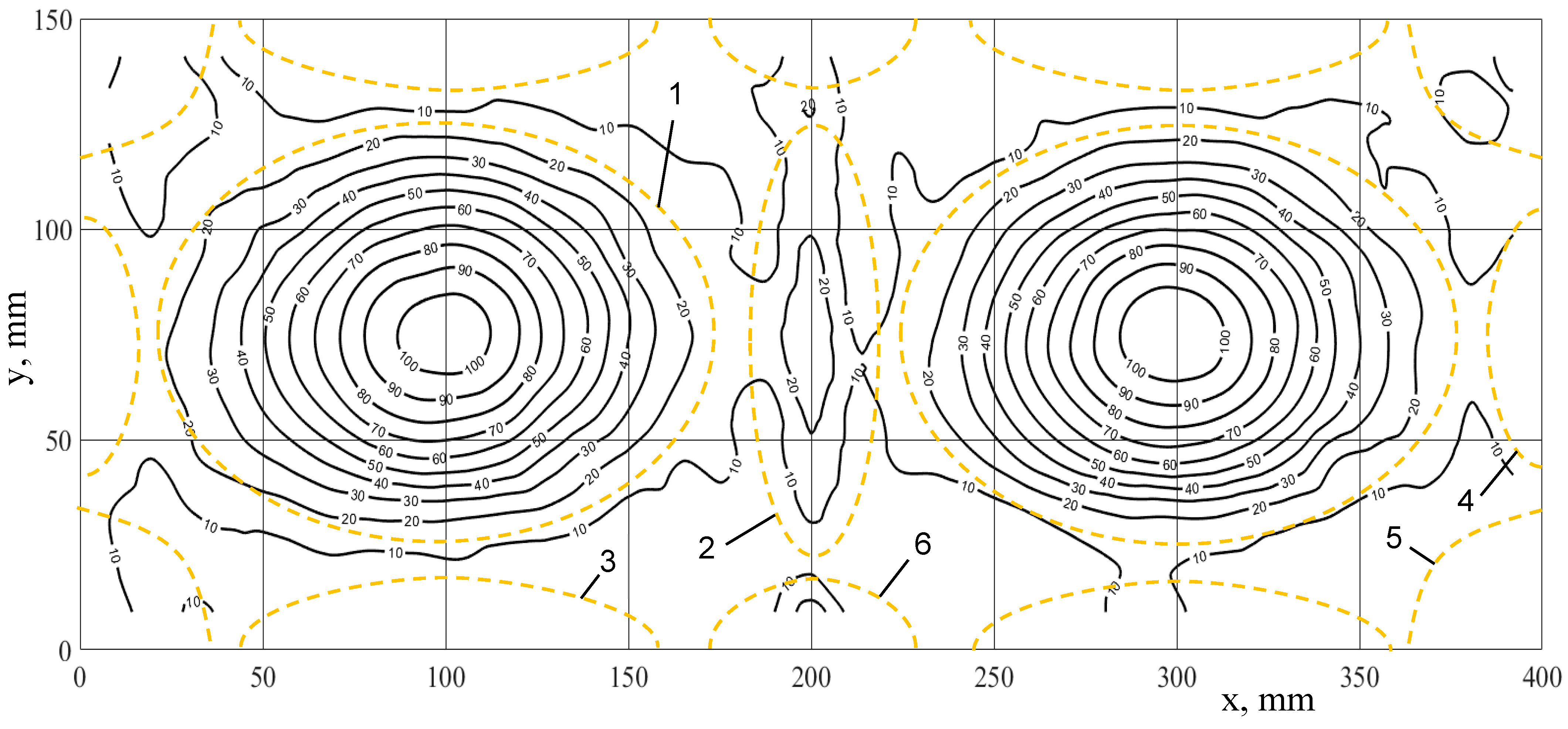
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Avrillaud, G.; Mazars, G.; Cantergiani, E.; Beguet, F.; Cuq-Lelandais, J.-P.; Deroy, J. Examples of How Increased Formability through High Strain Rates Can Be Used in Electro-Hydraulic Forming and Electromagnetic Forming Industrial Applications. J. Manuf. Mater. Process. 2021, 5, 96. [Google Scholar] [CrossRef]
- Mamutov, A.V.; Golovashchenko, S.F.; Bessonov, N.M.; Mamutov, V.S. Electrohydraulic Forming of Low Volume and Prototype Parts: Process Design and Practical Examples. J. Manuf. Mater. Process. 2021, 5, 47. [Google Scholar] [CrossRef]
- Cantergiani, E.; Atieh, S.; Léaux, F.; Perez Fontenla, A.T.; Prunet, S.; Dufay-Chanat, L.; Koettig, T.; Bertinelli, F.; Capatina, O.; Favre, G.; et al. Niobium superconducting rf cavity fabrication by electrohydraulic forming. Phys. Rev. Accel. Beams 2016, 19, 114703. [Google Scholar] [CrossRef]
- Naugolnykh, K.A.; Roy, N.A. Elektricheskie Razriady v Vode (Electrical Discharges in Water); Nauka: Moscow, Russia, 1971; p. 155. (In Russian) [Google Scholar]
- Deroy, J.; Claverie, A.; Avrillaud, G.; Boustie, M.; Mazanchenko, E.; Assous, D.; Chuvatin, A. Optical diagnostics for high power pulsed underwater electrical discharge characterization. J. Phys. Conf. Ser. 2014, 500, 142010. [Google Scholar] [CrossRef]
- Barbashova, G.A.; Shomko, V.V. Cyclicity effect of the electrical energy input in a channel of the underwater spark discharge. Surf. Eng. Appl. Electrochem. 2007, 43, 110–115. [Google Scholar] [CrossRef]
- Mamutov, A.V.; Golovashchenko, S.F.; Mamutov, V.S.; Bonnen, J.J.F. Modeling of electrohydraulic forming of sheet metal parts. J. Mater. Process. Technol. 2015, 219, 84–100. [Google Scholar] [CrossRef]
- Surkaev, A.L.; Kul’kov, V.G.; Talyzov, G.N. Experimental Investigation of the Interaction of Two Acoustic Shock Waves. Tech. Phys. Lett. 2001, 27, 487–488. [Google Scholar] [CrossRef]
- Surkaev, A.L. Investigations of High-Energy Impulse Processes in Condensed Media Based on Electric Explosion of Wires; Abstract of Dissertation for Dr. of Eng.; Volgograd State Technical University: Volgograd, Russia, 2018; p. 32. [Google Scholar]
- Knyazyev, M.K. Investigations, Development and Implementation of Manufacturing Processes of Electrohydraulic Forming with Application of Multi-Electrode Discharge Chambers; Dissertation for Candidate of Eng. Sciences; KhAI: Kharkov, Ukraine, 1995; p. 223. [Google Scholar]
- Shi, H.; Yin, G.; Li, X.; Wu, J.; Murphy, A.B.; Zhang, Y.; Qiu, A. Electrical wire explosion as a source of underwater shock waves. J. Phys. D Appl. Phys. 2021, 54, 403001. [Google Scholar] [CrossRef]
- Krivitskii, E.V. Dynamics of Electric Explosion in Liquids; Naukova Dumka: Kiev, Ukraine, 1983. [Google Scholar]
- Khainatskii, S. Conditions for realization of an optimum regime of the electric explosion of conductors in liquid media. Tech. Phys. Lett. 2009, 35, 299–301. [Google Scholar] [CrossRef]
- Homberg, W.; Beerwald, C.; Pröbsting, A. Investigation of the Electrohydraulic Forming Process with respect to the Design of Sharp Edged Contours. In Proceedings of the 4th International Conference on High Speed Forming, Columbus, OH, USA, 9–10 March 2010; pp. 58–64. [Google Scholar]
- Eguia, I.; Jose, J.S.; Knyazyev, M.; Zhovnovatyuk, Y. Pressure Field Stabilisation in High-Voltage Underwater Pulsed Metal Forming Using Wire-Initiated Discharges. Key Eng. Mater. 2011, 473, 965–972. [Google Scholar] [CrossRef]
- Rososhek, A.; Nouzman, D.; Krasik, Y.E. Addressing the symmetry of a converging cylindrical shock wave in water close to implosion. Appl. Phys. Lett. 2021, 118, 174103. [Google Scholar] [CrossRef]
- Maler, D.; Kozlov, M.; Efimov, S.; Krasik, Y.E. Supersonic jet generation by underwater sub-microsecond electrical explosions of wire arrays. Phys. Plasmas 2022, 29, 032705. [Google Scholar] [CrossRef]
- Amer, E.; Wozniak, M.; Jönsson, G.; Arrhén, F. Evaluation of Shock Tube Retrofitted with Fast-Opening Valve for Dynamic Pressure Calibration. Sensors 2021, 21, 4470. [Google Scholar] [CrossRef]
- Available online: https://www.drurylandetheatre.com/si-702s-ultra-high-pressure-transducer/ (accessed on 3 January 2023).
- Available online: https://mueller-instruments.de/en/pressure-measurement/mueller-platte-needle-probe/ (accessed on 3 January 2023).
- Wen, D.Y.; Lin, Q.W. Electrical response of PVDF film under shock loading. Chin. J. High Press. Phys. 2000, 14, 291–297. [Google Scholar]
- Wang, A.; Chen, C.; Qian, J.; Yang, F.; Wang, L.; Zhang, M. Enhanced Electrical Properties of PVDF Thin Film by Addition of NaCl by Near-Electric-Field 3D Printing. J. Electron. Mater. 2021, 50, 4781–4786. [Google Scholar] [CrossRef]
- Tartière, J.; Arrigoni, M.; Nême, A.; Groeneveld, H.; Van Der Veen, S. PVDF Based Pressure Sensor for the Characterisation of the Mechanical Loading during High Explosive Hydro Forming of Metal Plates. Sensors 2021, 21, 4429. [Google Scholar] [CrossRef]
- Cong, J.; Jing, J.; Chen, C.; Dai, Z. Development of a PVDF Sensor Array for Measurement of the Dynamic Pressure Field of the Blade Tip in an Axial Flow Compressor. Sensors 2019, 19, 1404. [Google Scholar] [CrossRef]
- Available online: https://mueller-instruments.de/en/electronic-pressure-films (accessed on 3 January 2023).
- Available online: https://mueller-instruments.de/en/pressure-indicating-film-prescale (accessed on 3 January 2023).
- Vagin, V.A.; Zdor, G.N.; Mamutov, V.S. Metody Issledovaniya Vysokoskorostnogo Deformirovaniya Metallov (Methods of Research of High-Speed Deformation of Metals); Navuka i tekhnika: Minsk, Belarus, 1990; p. 208. [Google Scholar]
- Cole, R.H. Underwater Explosions; Princeton University Press: Princeton, NJ, USA, 1948. [Google Scholar]
- Homberg, W.; Djakow, E.; Damerow, O. Process reliability and reproducibility of pneumomechanical and electrohydraulic forming processes. In Proceedings of the 6th International Conference on High Speed Forming, Daejeon, Korea, 27–29 March 2014; pp. 217–228. [Google Scholar]
- Djakow, E.; Homberg, W.; Tabakajew, D. Combined working media-based forming on a pneumo-mechanical high speed forming machine. In Proceedings of the ICHSF 2016, Dortmund, Germany, 27–28 April 2016; pp. 47–58. [Google Scholar]
- Beerwald, C.; Beerwald, M.; Dirksen, U.; Henselek, A. Impulse Hydroforming Method for Very Thin Sheets from Metallic or Hybrid Materials. In Proceedings of the 4th International Conference on High Speed Forming, Columbus, OH, USA, 9–10 March 2010; pp. 150–158. [Google Scholar]
- Vohnout, V.J.; Fenton, G.; Daehn, G.S. Pressure heterogeneity in small displacement electrohydraulic forming processes. In Proceedings of the 4th International Conference on High Speed Forming, Columbus, OH, USA, 9–10 March 2010; pp. 65–74. [Google Scholar]
- Bedienungsanleitung SSG-0620FS, Version 1.02; letzte Änderung: 04/2012; Poynting GmbH: Dortmund, Germany, 2012.
- ASTM A1008/A1008M; Standard Specification for Steel, Sheet, Cold-Rolled, Carbon, Structural, High-Strength Low-Alloy, High-Strength Low-Alloy with Improved Formability, Solution Hardened, and Bake Hardenable. ASTM International: West Conshohocken, PA, USA, 2021.
- DIN EN 10130; Cold Rolled Low Carbon Steel Flat Products for Cold Forming. Technical Delivery Conditions. DIN: Berlin, Germany, 2007.
- DIN EN 13601; Copper and Copper Alloys—Copper Rod, Bar and Wire for General Electrical Purposes. DIN: Berlin, Germany, 2021.
- Yu, H.; Zheng, Q. Forming limit diagram of DP600 steel sheets during electrohydraulic forming. Int. J. Adv. Manuf. Technol. 2019, 104, 743–756. [Google Scholar] [CrossRef]
- EN ISO 6892-1; Metallic Materials—Tensile Testing Part 1: Method of Test at Room Temperature. International Organization for Standardization: Geneva, Switzerland, 2019; p. 78.
- Farahnak, P.; Urbánek, M.; Konopík, P.; Džugan, J. Influence of thickness reduction on forming limits of mild steel DC01. Int. J. Mater. Form. 2020, 13, 371–381. [Google Scholar] [CrossRef]
- EN ISO 16808:2022; Metallic Materials. Sheet and Strip. Determination of Biaxial Stress-Strain Curve by Means of Bulge Test with Optical Measuring Systems. International Organization for Standardization: Geneva, Switzerland, 2022; p. 24.
- Wang, H.; Xu, T.; Shou, B. Determination of Material Strengths by Hydraulic Bulge Test. Materials 2017, 10, 23. [Google Scholar] [CrossRef]
- Knyazyev, M.K.; Zhovnovatuk, Y.S. Measurements of Pressure Fields with Multi-Point Membrane Gauges at Electrohydraulic Forming. In Proceedings of the 4th International Conference on High Speed Forming, Columbus, OH, USA, 9–10 March 2010; pp. 75–82. [Google Scholar]
- Mazurovsky, B.Y.; Siziov, A.N. Elektrogidravlicheskiy Effect v Listovoi Shtampovke (Electrohydraulic Effect in Sheet Forming); Naukova Dumka: Kiev, Ukraine, 1983; p. 192. [Google Scholar]
- Das, A. High Strain Rate Deformation Behaviour of Automotive Grade Steels. Ph.D. Dissertation, Indian Institute of Technology, Kharagpur, India, 2019; p. 288. [Google Scholar]
- Okitsu, Y.; Tsuji, N. Effect of Ferrite Grain Size on Dynamic Tensile Properties of Ultrafine Grained Low Carbon Steels with Various Chemical Compositions. Mater. Trans. 2014, 55, 78–84. [Google Scholar] [CrossRef]
- Mihalikova, M.; Girman, V.; Liskova, A. Static and dynamic tensile characteristics of S420 and IF steel sheets. Mater. Technol. 2016, 50, 543–546. [Google Scholar] [CrossRef]
- Xiong, R.-G.; Fu, R.-Y.; Yu, S.; Qian, L.; Wei, X.-C.; Lin, L. Tensile Properties of TWIP Steel at High Strain Rate. J. Iron Steel Res. Int. 2009, 16, 81–86. [Google Scholar] [CrossRef]
- Beynon, N.D.; Jones, T.B.; Fourlaris, G. Effect of high strain rate deformation on microstructure of strip steels tested under dynamic tensile conditions. Mater. Sci. Technol. 2005, 21, 103–112. [Google Scholar] [CrossRef]
- Knyazyev, M.K.; Chebanov, Y.I. Multi-Electrode Discharge Blocks for Electrohydraulic Forming and their Capabilities. East. Eur. J. Enterp. Technol. 2004, 3, 13–20. [Google Scholar]


| Test No. | pmaxl, MPa | pmaxr, MPa | % | % | F, MN | FL, MN | % | FR, MN | % |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 103.817 | 98.524 | –0.89 | –5.94 | 1.377 | 0.719 | 52.22 | 0.658 | 47.78 |
| 2 | 100.669 | 112.731 | –3.89 | +7.62 | 1.575 | 0.781 | 49.60 | 0.794 | 50.40 |
| 3 | 105.868 | 106.878 | +1.07 | +2.03 | 1.526 | 0.788 | 51.64 | 0.738 | 48.36 |
| Mean values | 103.451 | 106.044 | –1.24% | +1.24% | 1.492 | 0.762 | 0.730 | ||
| pmaxM = 104.748 | 100% | 51.1% | 48.9% | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knyazyev, M.; Holzmüller, M.; Homberg, W. Investigation of Pressure Fields Generated by Two Simultaneous Discharges in Liquid Initiated by Wires. J. Manuf. Mater. Process. 2023, 7, 40. https://doi.org/10.3390/jmmp7010040
Knyazyev M, Holzmüller M, Homberg W. Investigation of Pressure Fields Generated by Two Simultaneous Discharges in Liquid Initiated by Wires. Journal of Manufacturing and Materials Processing. 2023; 7(1):40. https://doi.org/10.3390/jmmp7010040
Chicago/Turabian StyleKnyazyev, Mykhaylo, Maik Holzmüller, and Werner Homberg. 2023. "Investigation of Pressure Fields Generated by Two Simultaneous Discharges in Liquid Initiated by Wires" Journal of Manufacturing and Materials Processing 7, no. 1: 40. https://doi.org/10.3390/jmmp7010040
APA StyleKnyazyev, M., Holzmüller, M., & Homberg, W. (2023). Investigation of Pressure Fields Generated by Two Simultaneous Discharges in Liquid Initiated by Wires. Journal of Manufacturing and Materials Processing, 7(1), 40. https://doi.org/10.3390/jmmp7010040





