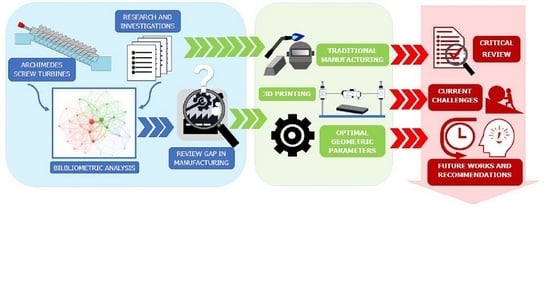
Sustainable Manufacturability of Archimedes Screw Turbines: A Critical Review
Abstract
1. Introduction
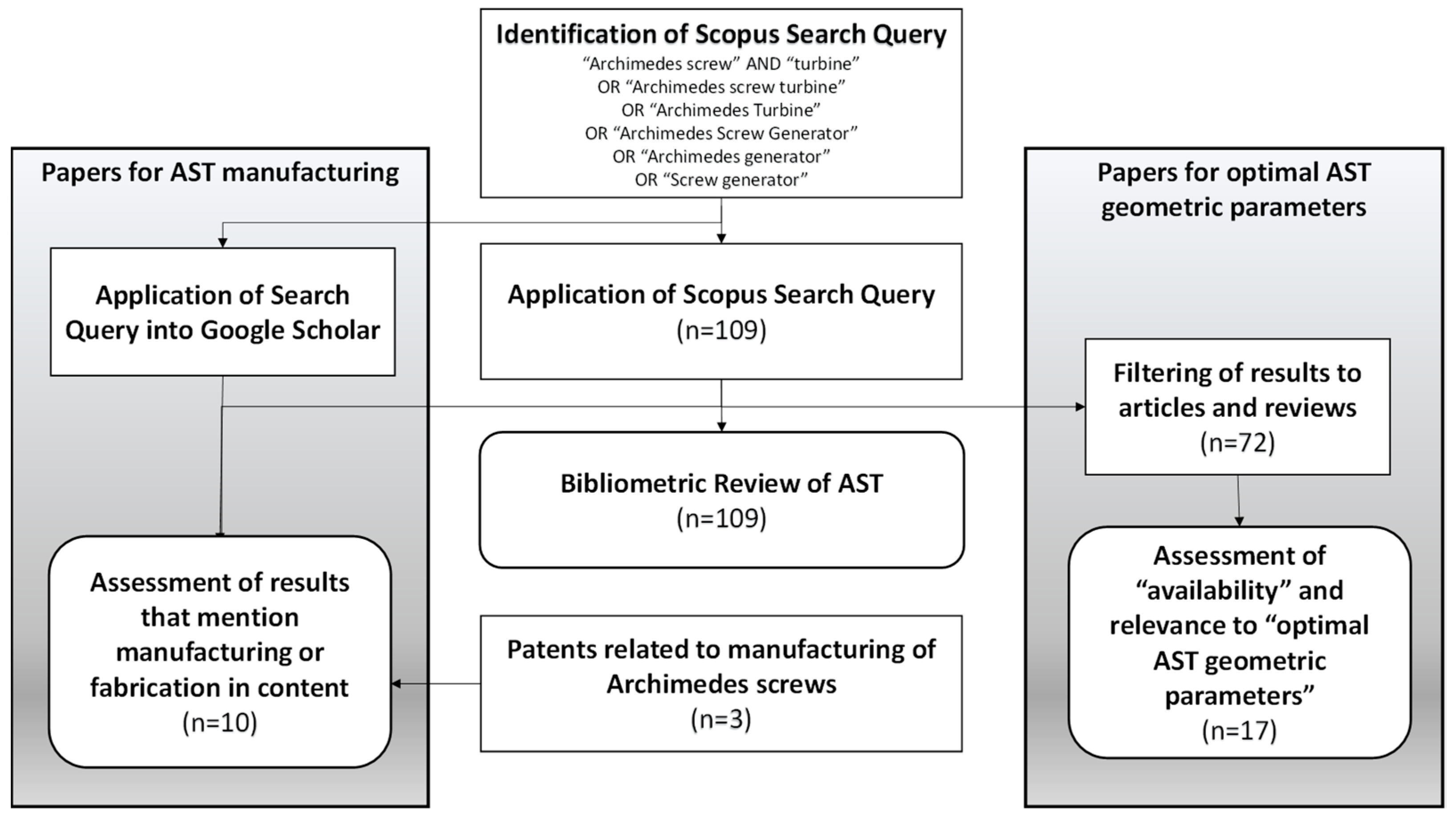
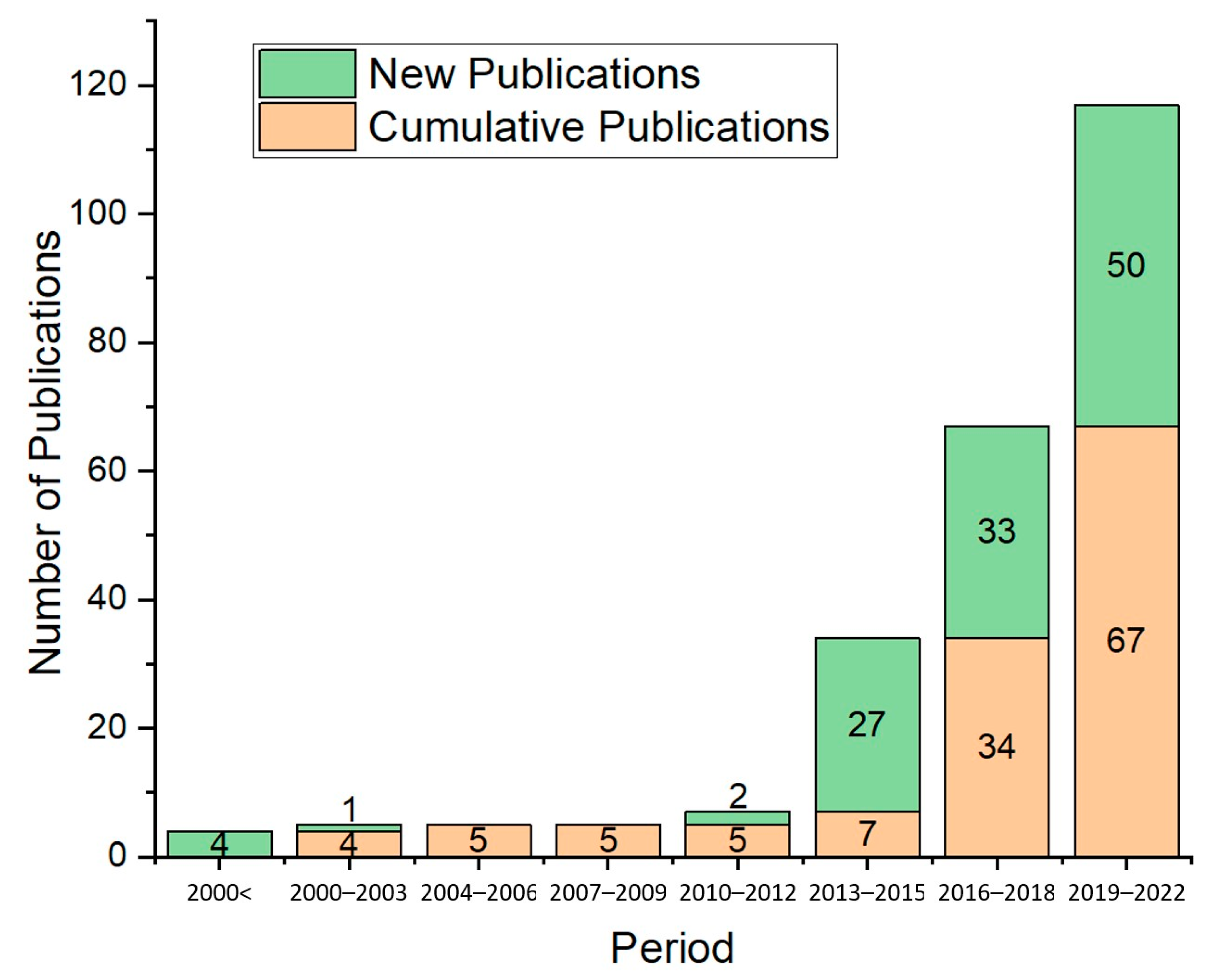
2. Bibliometric Review on Archimedes Screw Turbines
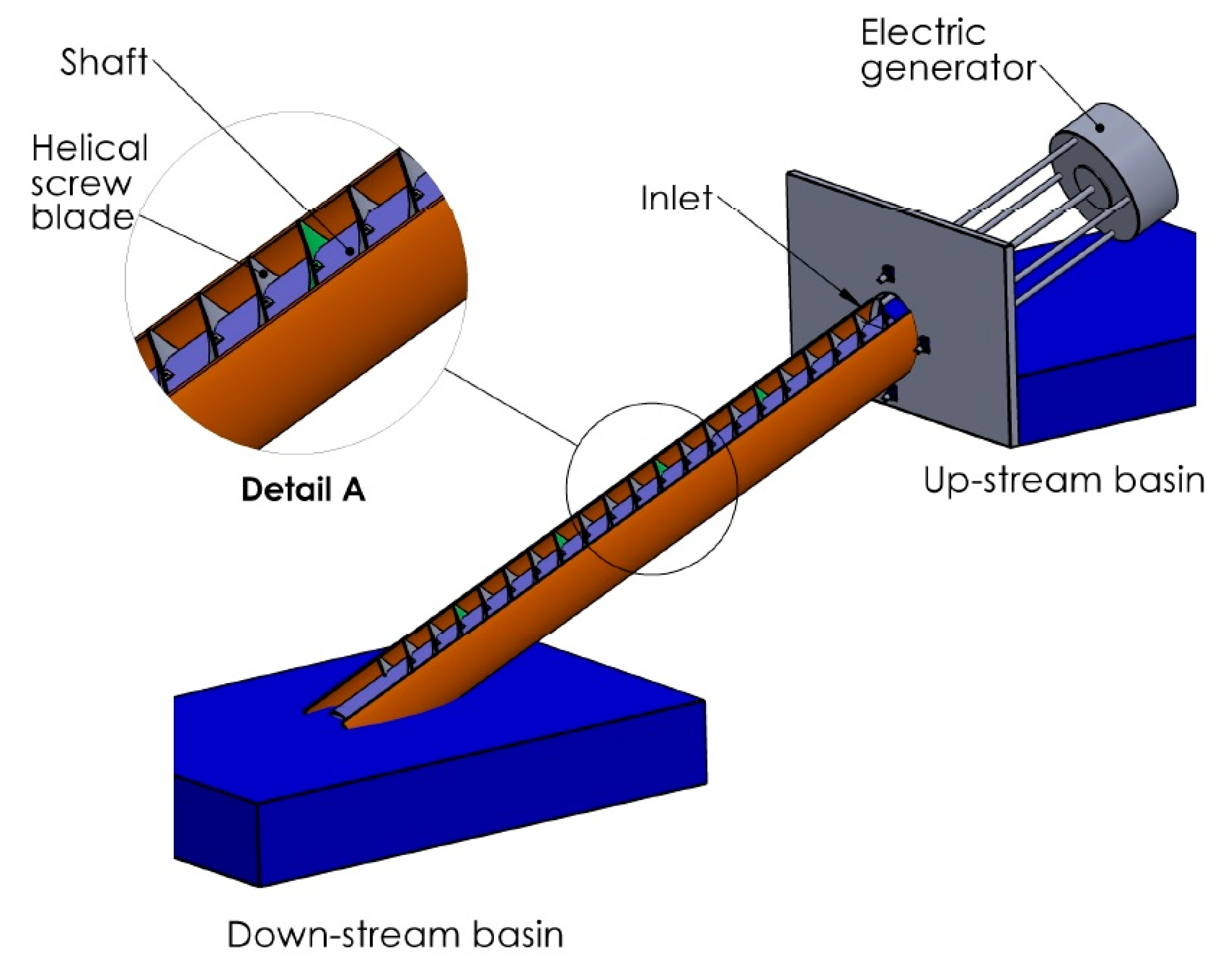
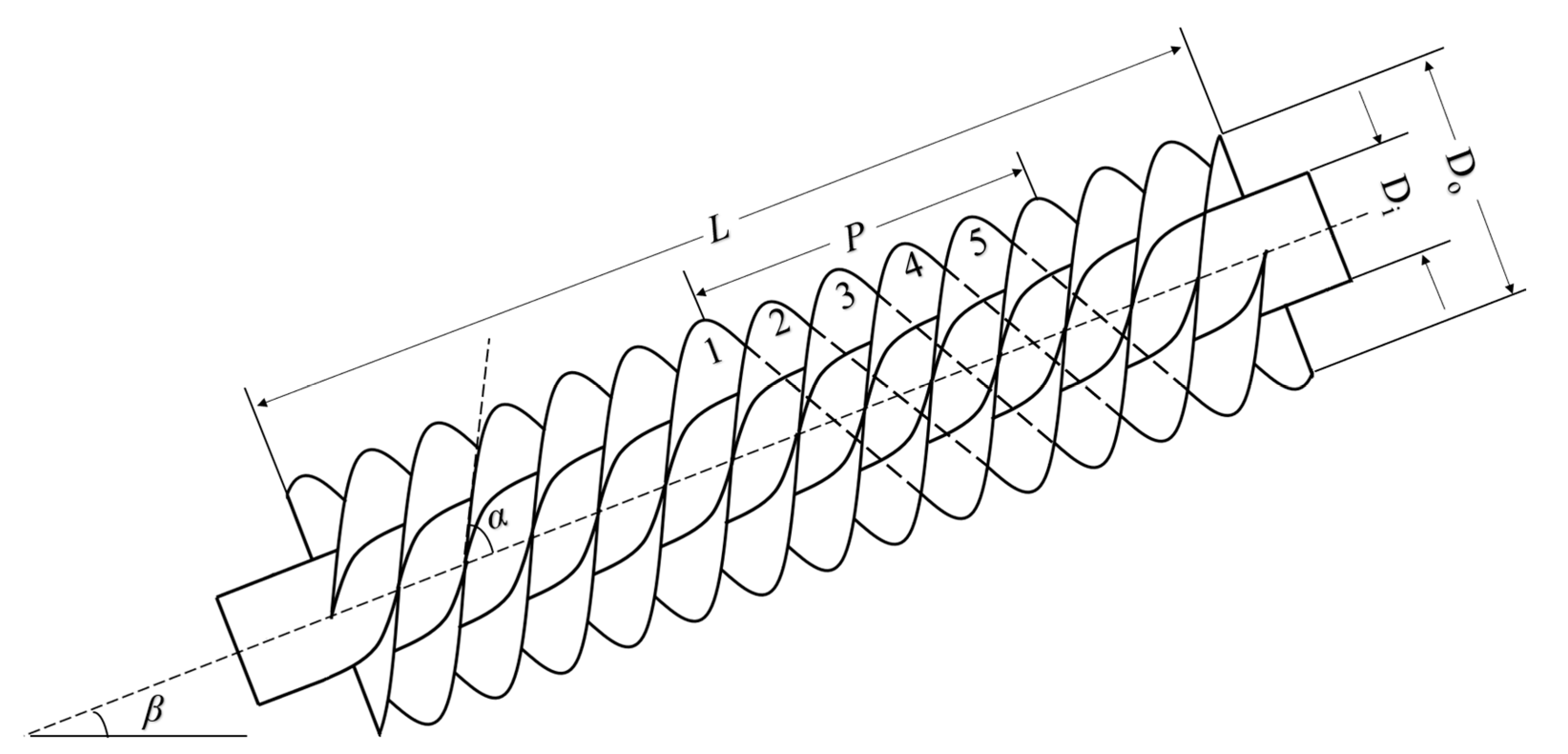
3. Optimal Design Parameters of Archimedes Screw Turbines
4. Manufacturing Methods of Archimedes Screw Turbines
4.1. Traditional Manufacturing
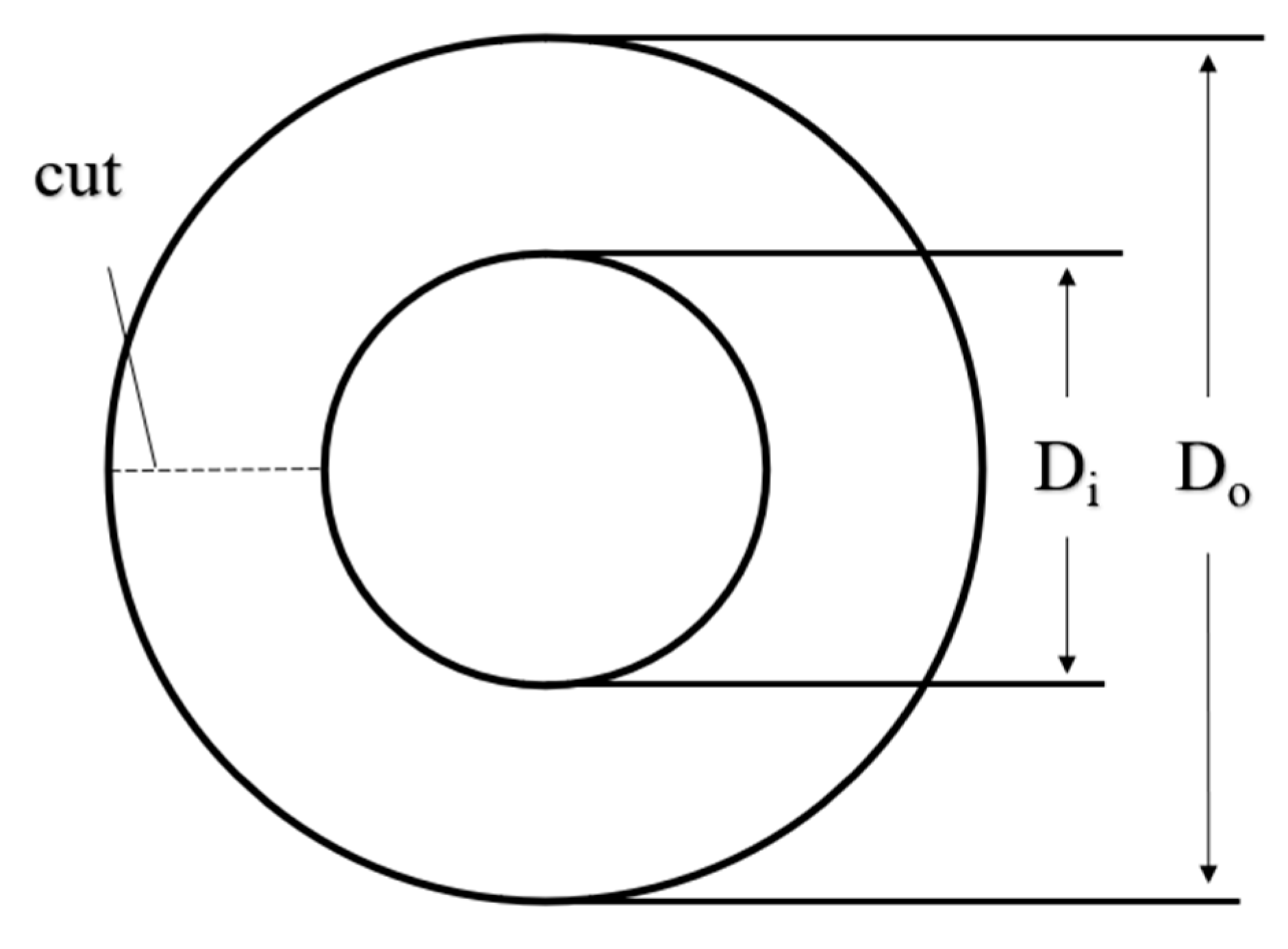
4.1.1. Screw Blade Manufacturing
4.1.2. Assembly of Archimedes Screw Turbine
4.2. CNC Manufacturing
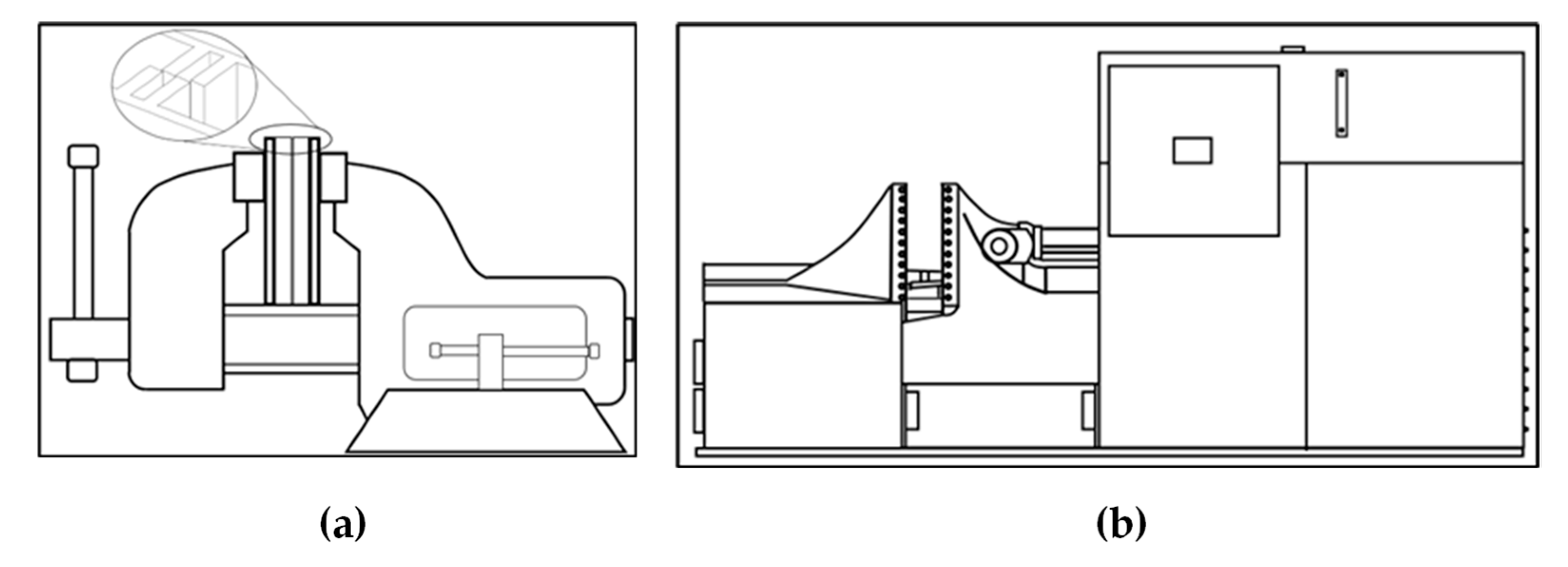
4.3. Molding Manufacturing
4.4. 3D Printing
5. Challenges and Future Perspective
5.1. Discussion of Optimal Geometric Parameters
5.2. Current Limitation of 3D-Printing Manufacturing
5.3. Advantages and Disadvantages of Manufacturing Methods
5.4. Design for Manufacturability
5.5. Recommendation for Future Works
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameters | Archimedes Screw Turbine |
| ro | outer radius (mm) |
| Do | outer diameter (mm) |
| Di | inner diameter (mm) |
| ω | rotational speed (rpm) |
| P | screw pitch (m) |
| L | screw length (m) |
| N | number of blades |
| Q | design flow rate(m3/s) |
| H | hydraulic head (m) |
| ρ | water density (kg/m3) |
| μ | water viscosity (Pa-s) |
| u | inflow velocity (m/s) |
| β | screw angle inclination (°) |
| α | screw blade angle inclination (°) |
| g | gravitational acceleration (m2/s) |
| Φ | specific speed |
| λ | characteristic length |
| Fr | Froude number |
| η | efficiency |
| R | coefficient of determination |
| Radj | adjusted coefficient of determination |
| RSM | response surface methodology |
| DOE | Department of Energy |
| NEA | National Electrification Administration |
| CFD | computational fluid dynamics |
| CAD | computer-aided design |
| AC | alternating current |
| DC | direct current |
| PLA | polyactid acid |
| PVC | polyvinyl chloride |
| MCDM | multicriteria decision method |
References
- IEA. World Energy Outlook; IEA: Paris, France, 2022; CC BY NC SA 4.0 (Annex A); Available online: https://www.iea.org/reports/world-energy-outlook-2022 (accessed on 1 October 2022).
- Liu, X.; Xiao, S.; Pan, H.; Zheng, X.; Han, W.; Huang, C.; Deng, S. Optimizing hydropower plants based on carbon-water-energy-ecosystem nexus. Energy Convers. Manag. 2022, 270, 116191. [Google Scholar] [CrossRef]
- Aviso, K.B.; Marfori, I.A.V.; Tan, R.R.; Ubando, A.T. Optimizing abnormal operations of off-grid community utility systems with fuzzy P-graph. Energy 2020, 202, 117725. [Google Scholar] [CrossRef]
- YoosefDoost, A.; Lubitz, W.D. Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures. Sustainability 2020, 12, 7352. [Google Scholar] [CrossRef]
- Waters, S.; Aggidis, G.A. Over 2000 years in review: Revival of the Archimedes Screw from Pump to Turbine. Renew. Sustain. Energy Rev. 2015, 51, 497–505. [Google Scholar] [CrossRef]
- Koetsier, T.; Blauwendraat, H. The Archimedean Screw-Pump: A Note on Its Invention and the Development of the Theory. In International Symposium on History of Machines and Mechanisms; Springer: Dordrecht, The Netherlands, 2004; pp. 181–194. [Google Scholar]
- Rorres, C. The Turn of the Screw: Optimal Design of an Archimedes Screw. J. Hydraul. Eng. 2000, 126, 72–80. [Google Scholar] [CrossRef]
- Shahverdi, K.; Loni, R.; Maestre, J.M.; Najafi, G. CFD numerical simulation of Archimedes screw turbine with power output analysis. Ocean Eng. 2021, 231, 108718. [Google Scholar] [CrossRef]
- Simmons, S.C.; Elliott, C.; Ford, M.; Clayton, A.; Lubitz, W.D. Archimedes screw generator powerplant assessment and field measurement campaign. Energy Sustain. Dev. 2021, 65, 144–161. [Google Scholar] [CrossRef]
- Bouvant, M.; Betancour, J.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Design optimization of an Archimedes screw turbine for hydrokinetic applications using the response surface methodology. Renew. Energy 2021, 172, 941–954. [Google Scholar] [CrossRef]
- Hoffstaedt, J.P.; Truijen, D.P.K.; Fahlbeck, J.; Gans, L.H.A.; Qudaih, M.; Laguna, A.J.; De Kooning, J.D.M.; Stockman, K.; Nilsson, H.; Storli, P.T.; et al. Low-head pumped hydro storage: A review of applicable technologies for design, grid integration, control and modelling. Renew. Sustain. Energy Rev. 2022, 158, 112119. [Google Scholar] [CrossRef]
- Zhou, D.; Deng, Z. Ultra-low-head hydroelectric technology: A review. Renew. Sustain. Energy Rev. 2017, 78, 23–30. [Google Scholar] [CrossRef]
- Mueller, M.; Knott, J.; Pander, J.; Geist, J. Experimental comparison of fish mortality and injuries at innovative and conventional small hydropower plants. J. Appl. Ecol. 2022, 59, 2360–2372. [Google Scholar] [CrossRef]
- Piper, A.T.; Rosewarne, P.J.; Wright, R.M.; Kemp, P.S. The impact of an Archimedes screw hydropower turbine on fish migration in a lowland river. Ecol. Eng. 2018, 118, 31–42. [Google Scholar] [CrossRef]
- Renardy, S.; Colson, D.; Benitez, J.-P.; Dierckx, A.; Goffaux, D.; Sabbe, J.; Rabouan, A.; Detrait, O.; Nzau Matondo, B.; Sonny, D.; et al. Migration behaviour of Atlantic salmon smolts (Salmo salar L.) in a short and highly fragmented gravel-bed river stretch. Ecol. Freshw. Fish 2022, 31, 499–514. [Google Scholar] [CrossRef]
- Pauwels, I.S.; Baeyens, R.; Toming, G.; Schneider, M.; Buysse, D.; Coeck, J.; Tuhtan, J.A. Multi-Species Assessment of Injury, Mortality, and Physical Conditions during Downstream Passage through a Large Archimedes Hydrodynamic Screw (Albert Canal, Belgium). Sustainability 2020, 12, 8722. [Google Scholar] [CrossRef]
- Renardy, S.; Benitez, J.-P.; Tauzin, A.; Dierckx, A.; Nzau Matondo, B.; Ovidio, M. How and where to pass? Atlantic salmon smolt’s behaviour at a hydropower station offering multiple migration routes. Hydrobiologia 2020, 847, 469–485. [Google Scholar] [CrossRef]
- Simmons, S.C.; Lubitz, W.D. Archimedes screw generators for sustainable micro-hydropower production. Int. J. Energy Res. 2021, 45, 17480–17501. [Google Scholar] [CrossRef]
- Waters, S.; Aggidis, G. Tidal range technologies and state of the art in review. Renew. Sustain. Energy Rev. 2016, 59, 514–529. [Google Scholar] [CrossRef]
- Suraya, A.N.; Ammar, N.M.M.; Kulthum, J.U. The effect of substantive parameters on the efficiency of Archimedes screw microhydro power: A review. IOP Conf. Ser. Mater. Sci. Eng. 2015, 100, 012030. [Google Scholar] [CrossRef]
- Poosti, A.; Lewis, F.M.; Sereno, D.; Redd, K.; Abkian, V. Time for a checkup? Water Environ. Technol. 2003, 15, 66–69. [Google Scholar]
- Siswantara, A.I.; Warjito; Budiarso, B.; Harmadi, R.; Syafei, M.H.; Adanta, D. Investigation of the α angle’s effect on the performance of an Archimedes turbine. Energy Procedia 2019, 156, 458–462. [Google Scholar] [CrossRef]
- Ekström, R.; Ekergård, B.; Leijon, M. Electrical damping of linear generators for wave energy converters—A review. Renew. Sustain. Energy Rev. 2015, 42, 116–128. [Google Scholar] [CrossRef]
- Dellinger, G.; Garambois, P.-A.; Dellinger, N.; Dufresne, M.; Terfous, A.; Vazquez, J.; Ghenaim, A. Computational fluid dynamics modeling for the design of Archimedes Screw Generator. Renew. Energy 2018, 118, 847–857. [Google Scholar] [CrossRef]
- Dellinger, G.; Simmons, S.; Lubitz, W.D.; Garambois, P.-A.; Dellinger, N. Effect of slope and number of blades on Archimedes screw generator power output. Renew. Energy 2019, 136, 896–908. [Google Scholar] [CrossRef]
- Erinofiardi, E.; Syaiful, M.; Prayitno, A. Electric Power Generation from Low Head Simple Turbine for Remote Area Power Supply. J. Teknol. 2015, 74, 5. [Google Scholar] [CrossRef][Green Version]
- Lashofer, A.; Kaltenberger, F.; Kaltenberger, F. Does the Archimedean Screw Turbine Stand the Test? In Wasserkraftprojekte: Ausgewählte Beiträge aus der Fachzeitschrift WasserWirtschaft; Heimerl, S., Ed.; Springer Fachmedien: Wiesbaden, Germany, 2013; pp. 310–318. [Google Scholar]
- Simmons, S.; Songin, K.; Lubitz, W. Experimental Investigation of the Factors Affecting Archimedes Screw Generator Power Output. HYDRO. Available online: https://scottsimmons.ca/wp-content/uploads/2021/07/Preprint-2017-ASG-Experiments.pdf (accessed on 1 October 2022).
- Alonso-Martinez, M.; Suárez Sierra, J.L.; Coz Díaz, J.J.D.; Martinez-Martinez, J.E. A New Methodology to Design Sustainable Archimedean Screw Turbines as Green Energy Generators. Int. J. Environ. Res. Public Health 2020, 17, 9236. [Google Scholar] [CrossRef] [PubMed]
- Edirisinghe, D.S.; Yang, H.-S.; Kim, M.-S.; Kim, B.-H.; Gunawardane, S.P.; Lee, Y.-H. Computational Flow Analysis on a Real Scale Run-of-River Archimedes Screw Turbine with a High Incline Angle. Energies 2021, 14, 3307. [Google Scholar] [CrossRef]
- Saroinsong, T.; Soenoko, R.; Wahyudi, S.; Sasongko, M. Fluid Flow Phenomenon in a Three-Bladed Power-Generating Archimedes Screw Turbine. J. Eng. Sci. Technol. Rev. 2016, 9, 72–79. [Google Scholar] [CrossRef]
- Shahverdi, K. Modeling for prediction of design parameters for micro-hydro Archimedean screw turbines. Sustain. Energy Technol. Assess. 2021, 47, 101554. [Google Scholar] [CrossRef]
- Lee, M.D.; Lee, P.S. Modelling the energy extraction from low-velocity stream water by small scale Archimedes screw turbine. J. King Saud Univ.-Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Shahverdi, K.; Loni, R.; Ghobadian, B.; Gohari, S.; Marofi, S.; Bellos, E. Numerical Optimization Study of Archimedes Screw Turbine (AST): A case study. Renew. Energy 2020, 145, 2130–2143. [Google Scholar] [CrossRef]
- Dedić-Jandrek, H.; Nižetić, S. Small scale archimedes hydro power plant test station: Design and experimental investigation. J. Clean. Prod. 2019, 231, 756–771. [Google Scholar] [CrossRef]
- Maulana, M.I.; Syuhada, A.; Kurniawan, R. Experimental Study on the Effect of Flow rate on the Performance of Two-Blade Archimedes Screw Turbine. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 61, 10–19. [Google Scholar]
- Betancour, J.; Velásquez, L.; Jaramillo, L.Y.; Chica, E.; Rubio-Clemente, A. Application of a central composite face-centered design in the optimization of an archimedean hydrokinetic turbine. Renew. Energy Power Qual. J. 2021, 19, 418–422. [Google Scholar] [CrossRef]
- Zitti, G.; Fattore, F.; Brunori, A.; Brunori, B.; Brocchini, M. Efficiency evaluation of a ductless Archimedes turbine: Laboratory experiments and numerical simulations. Renew. Energy 2020, 146, 867–879. [Google Scholar] [CrossRef]
- Rohmer, J.; Knittel, D.; Sturtzer, G.; Flieller, D.; Renaud, J. Modeling and experimental results of an Archimedes screw turbine. Renew. Energy 2016, 94, 136–146. [Google Scholar] [CrossRef]
- Abdullah, O.S.; Kamel, A.H.; Khalil, W.H. Numerical and Experimental Modelling of Small Hydropower Turbine. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 80, 112–127. [Google Scholar] [CrossRef]
- Durrani, A.M.; Mujahid, O.; Uzair, M. Micro Hydro Power Plant using Sewage Water of Hayatabad Peshawar. In Proceedings of the 2019 15th International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 2–3 December 2019; pp. 1–5. [Google Scholar]
- Syam, I.; Maulana, M.; Syuhada, A. Design and Performance of Archimedes Single Screw Turbine as Micro Hydro Power Plant with Flow Rate Debit Variations (Case Study in Air Dingin, Samadua-South Aceh). J. Inotera 2019, 4, 13. [Google Scholar] [CrossRef]
- Thakur, N.K.; Thakur, R.; Kashyap, K.; Goel, B. Efficiency enhancement in Archimedes screw turbine by varying different input parameters–An experimental study. Mater. Today Proc. 2022, 52, 1161–1167. [Google Scholar] [CrossRef]
- Simmons, S.C.; Lubitz, W.D. Analysis of internal fluid motion in an Archimedes screw using computational fluid mechanics. J. Hydraul. Res. 2021, 59, 932–946. [Google Scholar] [CrossRef]
- Lashofer, A.; Hawle, W.; Kampel, I.; Kaltenberger, F.; Pelikan, B. State of technology and design guidelines for the Archimedes screw turbine. In Proceedings of the Hydro 2012—Innovative Approaches to Global Challenges, Bilbao, Spain, 29–31 October 2012. [Google Scholar]
- Rosly, C.; Jamaludin, U.; Azahari, N.; Nik Mutasim, M.; Oumer, A.; Rao, N.T. Parametric study on efficiency of archimedes screw turbine. ARPN J. Eng. Appl. Sci. 2016, 11, 10904–10908. [Google Scholar]
- Lubitz William, D.; Lyons, M.; Simmons, S. Performance Model of Archimedes Screw Hydro Turbines with Variable Fill Level. J. Hydraul. Eng. 2014, 140, 04014050. [Google Scholar] [CrossRef]
- Songin, K.J.; Lubitz, W.D. Measurement of fill level and effects of overflow in power-generating Archimedes screws. J. Hydraul. Res. 2019, 57, 635–646. [Google Scholar] [CrossRef]
- Dellinger, G.; Terfous, A.; Garambois, P.-A.; Ghenaim, A. Experimental investigation and performance analysis of Archimedes screw generator. J. Hydraul. Res. 2016, 54, 197–209. [Google Scholar] [CrossRef]
- Kozyn, A.; Lubitz, W.D. A power loss model for Archimedes screw generators. Renew. Energy 2017, 108, 260–273. [Google Scholar] [CrossRef]
- Saroinsong, T.; Soenoko, R.; Wahyudi, S.; Sasongko, M.N. The effect of head inflow and turbine axis angle towards the three row bladed screw turbine efficiency. Int. J. Appl. Eng. Res. 2015, 10, 16977–16984. [Google Scholar]
- Saroinsong, T.; Soenoko, R.; Wahyudi, S.; Sasongko, M.N. Performance of three-bladed Archimedes screw turbine. ARPN J. Eng. Appl. Sci. 2016, 11, 9491–9495. [Google Scholar]
- Saroinsong, T.; Soenoko, R.; Wahyudi, S.; Sasongko, M.N. Effect of froude number on three-bladed archimedes screw turbine efficiency. Int. J. Renew. Energy Res. 2016, 6, 1153–1158. [Google Scholar]
- Simmons, S.; Dellinger, G.; Lyons, M.; Terfous, A.; Ghenaim, A.; Lubitz William, D. Effects of Inclination Angle on Archimedes Screw Generator Power Production with Constant Head. J. Hydraul. Eng. 2021, 147, 04021001. [Google Scholar] [CrossRef]
- Suraya, N.; Jamaludin, U.; Nik Mutasim, M. Investigation on the effect of drive train system for archimedes screw turbine. ARPN J. Eng. Appl. Sci. 2017, 12, 4809–4812. [Google Scholar]
- DeChambeau, D. On her majesty’s service. Int. Water Power Dam Constr. 2012, 64, 32–34. [Google Scholar]
- Bauyon, J. Archimedes screw turbine as an energy conversion device for a run-of-river micro-hydropower plant. J. Nucl. Energy Sci. Power Gener. Technol. 2018, 7. [Google Scholar]
- Atkin, S. The 21st Century Archimedes Screw: New Materials and Manufacturing Techniques Enable the Turbine’s Highest-Ever Measured Efficiency. 2021. Available online: https://www.energy.gov/eere/water/articles/21st-century-archimedes-screw-new-materials-and-manufacturing-techniques-enable (accessed on 1 October 2022).
- Bloxham, G.J. Apparatus and Method for Forming a Screw Flight. U.S. Patent US9555457B2, 5 July 2012. Available online: https://patents.google.com/patent/US20140196515A1/en (accessed on 1 October 2022).
- Walker, S.; Howell, R.; Hodgson, P.; Griffin, A. Tidal energy machines: A comparative life cycle assessment study. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2013, 229, 124–140. [Google Scholar] [CrossRef]
- Omodara, L.; Saavalainen, P.; Pitkäaho, S.; Pongrácz, E.; Keiski, R.L. Sustainability assessment of products-Case study of wind turbine generator types. Environ. Impact Assess. Rev. 2023, 98, 106943. [Google Scholar] [CrossRef]
- Rueda-Bayona, J.G.; Cabello Eras, J.J.; Chaparro, T.R. Impacts generated by the materials used in offshore wind technology on Human Health, Natural Environment and Resources. Energy 2022, 261, 125223. [Google Scholar] [CrossRef]
- Das, U.; Nandi, C. Life cycle assessment on onshore wind farm: An evaluation of wind generators in India. Sustain. Energy Technol. Assess. 2022, 53, 102647. [Google Scholar] [CrossRef]
- Ozsahin, B.; Elginoz, N.; Germirli Babuna, F. Life cycle assessment of a wind farm in Turkey. Environ. Sci. Pollut. Res. 2022, 29, 71000–71013. [Google Scholar] [CrossRef]
- Hindle, N.; Boersma, B. Archimedean Screw Apparatus. 2016. Available online: https://patentimages.storage.googleapis.com/cf/01/95/9b30ce59aebf2d/EP0161787A2.pdf (accessed on 1 October 2022).
- Bizzarri, M.; Bartoň, M. Manufacturing of Screw Rotors Via 5-axis Double-Flank CNC Machining. Comput.-Aided Des. 2021, 132, 102960. [Google Scholar] [CrossRef]
- Matejic, M.; Dragoi, M.V.; Blagojevic, M.; Filip, A.; Miletic, I. Progressive screw shaft manufacturing technology. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1009, 012038. [Google Scholar] [CrossRef]
- Swetha, R.; Siva Rama Krishna, L.; Hari Sai Kiran, B.; Ravinder Reddy, P.; Venkatesh, S. Comparative study on life cycle assessment of components produced by additive and conventional manufacturing process. Mater. Today Proc. 2022, 62, 4332–4340. [Google Scholar] [CrossRef]
- Lapeyre, J.M. Mould and Process for Manufacturing Helical Shaped Items. U.S. Patent EP0161787A2, 9 April 1985. [Google Scholar]
- Jung, I.D. Process and design optimization for powder injection molding of turbocharger vanes. Met. Powder Rep. 2021, 76, 26–29. [Google Scholar] [CrossRef]
- Bianchi, M.F.; Gameros, A.A.; Axinte, D.A.; Lowth, S.; Cendrowicz, A.M.; Welch, S.T. Regional temperature control in ceramic injection moulding: An approach based on cooling rate optimisation. J. Manuf. Process. 2021, 68, 1767–1783. [Google Scholar] [CrossRef]
- Upadhyayula, V.K.K.; Gadhamshetty, V.; Athanassiadis, D.; Tysklind, M.; Meng, F.; Pan, Q.; Cullen, J.M.; Yacout, D.M.M. Wind Turbine Blades Using Recycled Carbon Fibers: An Environmental Assessment. Environ. Sci. Technol. 2022, 56, 1267–1277. [Google Scholar] [CrossRef] [PubMed]
- Shahbazi, M.; Jäger, H. Current Status in the Utilization of Biobased Polymers for 3D Printing Process: A Systematic Review of the Materials, Processes, and Challenges. ACS Appl. Bio Mater. 2021, 4, 325–369. [Google Scholar] [CrossRef] [PubMed]
- Shashank, L.; Gokul, R.; Rajath, N.R.; Satwik Bhat, S. Theoretical analysis and fabrication of portable Archimedes screw micro hydro generator. Int. J. Adv. Res. Sci. Eng. Technol. 2021, 8, 17993–18002. [Google Scholar]
- Sari, D.; Saputra, M.; Syofii, I.; Adanta, D. A Study of the Developing Archimedes Screw as a Turbine. Int. J. Adv. Res. 2021, 87, 151–160. [Google Scholar] [CrossRef]
- Straalsund Jerry, L.; Harding Samuel, F.; Nuernbergk Dirk, M.; Rorres, C. Experimental Evaluation of Advanced Archimedes Hydrodynamic Screw Geometries. J. Hydraul. Eng. 2018, 144, 04018052. [Google Scholar] [CrossRef]
- Lee, K.T.; Kim, E.-S.; Chu, W.-S.; Ahn, S.-H. Design and 3D printing of controllable-pitch archimedean screw for pico-hydropower generation. J. Mech. Sci. Technol. 2015, 29, 4851–4857. [Google Scholar] [CrossRef]
- Olivera, A.F.; Chica, E.; Colorado, H.A. Evaluation of Recyclable Thermoplastics for the Manufacturing of Wind Turbines Blades H-Darrieus. In Characterization of Minerals, Metals, and Materials 2022; Springer: Cham, Switzerland, 2022; pp. 341–348. [Google Scholar]
- Gomes, T.E.P.; Cadete, M.S.; Dias-de-Oliveira, J.; Neto, V. Controlling the properties of parts 3D printed from recycled thermoplastics: A review of current practices. Polym. Degrad. Stab. 2022, 196, 109850. [Google Scholar] [CrossRef]
- Serra, A.; Malarco, M.; Musacchio, A.; Buia, G.; Bartocci, P.; Fantozzi, F. Comparing environmental impacts of additive manufacturing vs. Investment casting for the production of a shroud for gas turbine. In Proceedings of the ASME Turbo Expo, Virtual, 7–11 June 2021. [Google Scholar]
- Torres-Carrillo, S.; Siller, H.R.; Vila, C.; López, C.; Rodríguez, C.A. Environmental analysis of selective laser melting in the manufacturing of aeronautical turbine blades. J. Clean. Prod. 2020, 246, 119068. [Google Scholar] [CrossRef]
- Chang, J.; He, J.; Mao, M.; Zhou, W.; Lei, Q.; Li, X.; Li, D.; Chua, C.-K.; Zhao, X. Advanced Material Strategies for Next-Generation Additive Manufacturing. Materials 2018, 11, 166. [Google Scholar] [CrossRef]
- Kankala, R.K.; Zhu, K.; Li, J.; Wang, C.-S.; Wang, S.-B.; Chen, A.-Z. Fabrication of arbitrary 3D components in Cardiac Surgery: From Macro-, Micro- to Nanoscale. Biofabrication 2017, 9, 032002. [Google Scholar] [CrossRef] [PubMed]
- Sarraf, F.; Hadian, A.; Churakov, S.V.; Clemens, F. EVA-PVA binder system for polymer derived mullite made by material extrusion based additive manufacturing. J. Eur. Ceram. Soc. 2022, 43, 530–541. [Google Scholar] [CrossRef]
- Spiller, S.; Berto, F.; Javad Razavi, S.M. Mechanical behavior of Material Extrusion Additive Manufactured components: An overview. Procedia Struct. Integr. 2022, 41, 158–174. [Google Scholar] [CrossRef]
- Miclette, O.; Côté, R.; Demers, V.; Brailovski, V. Material extrusion additive manufacturing of low-viscosity metallic feedstocks: Performances of the plunger-based approach. Addit. Manuf. 2022, 60, 103252. [Google Scholar] [CrossRef]
- Dezaki, M.L.; Serjouei, A.; Zolfagharian, A.; Fotouhi, M.; Moradi, M.; Ariffin, M.K.A.; Bodaghi, M. A review on additive/subtractive hybrid manufacturing of directed energy deposition (DED) process. Adv. Powder Mater. 2022, 1, 100054. [Google Scholar] [CrossRef]
- Markus, D.; Lorin, A.; Thomas, N.; Sven, M. Identifying an opportunistic method in design for manufacturing: An experimental study on successful a on the manufacturability and manufacturing effort of design concepts. Procedia CIRP 2021, 100, 720–725. [Google Scholar] [CrossRef]
- Tessarolo, A.; Luise, F.; Pieri, S.; Benedetti, A.; Bortolozzi, M.; De Martin, M. Design for Manufacturability of an Off-Shore Direct-Drive Wind Generator: An Insight into Additional Loss Prediction and Mitigation. IEEE Trans. Ind. Appl. 2017, 53, 4831–4842. [Google Scholar] [CrossRef]
- Premkumar, V.; Krishnamurty, S.; Wileden, J.C.; Grosse, I.R. A semantic knowledge management system for laminated composites. Adv. Eng. Inform. 2014, 28, 91–101. [Google Scholar] [CrossRef]
- Pietropaoli, M.; Ahlfeld, R.; Montomoli, F.; Ciani, A.; D’Ercole, M. Design for Additive Manufacturing: Internal Channel Optimization. J. Eng. Gas Turbines Power 2017, 139, 102101. [Google Scholar] [CrossRef]
- Clemens, F.; Sarraf, F.; Borzì, A.; Neels, A.; Hadian, A. Material extrusion additive manufacturing of advanced ceramics: Towards the production of large components. J. Eur. Ceram. Soc. 2022, in press. [Google Scholar] [CrossRef]
- Adhikary, P.; Roy, P.; Mazumdar, A. Selection of hydro-turbine blade material-Application of Fuzzy Logic (MCDA). Int. J. Eng. Res. Appl. 2013, 3, 426–430. [Google Scholar]
- Okokpujie, I.P.; Okonkwo, U.C.; Bolu, C.A.; Ohunakin, O.S.; Agboola, M.G.; Atayero, A.A. Implementation of multi-criteria decision method for selection of suitable material for development of horizontal wind turbine blade for sustainable energy generation. Heliyon 2020, 6, e03142. [Google Scholar] [CrossRef] [PubMed]
- Kathwadia, A.; Parmar, K.; Acharya, G. Life Cycle Assessment of Turbine Blade. In Proceedings of the 3rd Afro-Asian International Conference on Science, Engineering & Technology, Gujarat, India, 27–28 March 2015. [Google Scholar]
- Walker, S.R.J.; Thies, P.R. A life cycle assessment comparison of materials for a tidal stream turbine blade. Appl. Energy 2022, 309, 118353. [Google Scholar] [CrossRef]
- Oliveira, P.; Martins, N.; Fontes, P.; Covas, D. Hydroenergy Harvesting Assessment: The Case Study of Alviela River. Water 2021, 13, 1764. [Google Scholar] [CrossRef]
- Ceran, B.; Jurasz, J.; Wróblewski, R.; Guderski, A.; Złotecka, D.; Kaźmierczak, Ł. Impact of the Minimum Head on Low-Head Hydropower Plants Energy Production and Profitability. Energies 2020, 13, 6728. [Google Scholar] [CrossRef]
- Musacchio, A.; Bartocci, P.; Serra, A.; Cencioni, L.; Colantoni, S.; Fantozzi, F. Decarbonizing materials sourcing and machining in the gas turbine sector, through a cost-carbon footprint nexus analysis. J. Clean. Prod. 2021, 310, 127392. [Google Scholar] [CrossRef]
- Miklautsch, P.; Hoffelner, M.; Woschank, M. Harmonizing “Smart” Life Cycle Assessment in Manufacturing Companies: Literature Review and Preliminary Morphological Analysis. IFAC-PapersOnLine 2022, 55, 1483–1490. [Google Scholar] [CrossRef]
- Ammar, M.; Haleem, A.; Javaid, M.; Walia, R.; Bahl, S. Improving material quality management and manufacturing organizations system through Industry 4.0 technologies. Mater. Today Proc. 2021, 45, 5089–5096. [Google Scholar] [CrossRef]
- Paturi, U.M.R.; Cheruku, S.; Reddy, N.S. Artificial neural networks modelling for power coefficient of Archimedes screw turbine for hydropower applications. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 447. [Google Scholar] [CrossRef]
- Kozyn, A.; Songin, K.; Gharabaghi, B.; Lubitz William, D. Predicting Archimedes Screw Generator Power Output Using Artificial Neural Networks. J. Hydraul. Eng. 2018, 144, 05018002. [Google Scholar] [CrossRef]
- Lisicki, M.; Lubitz, W.; Taylor, G.W. Optimal design and operation of Archimedes screw turbines using Bayesian optimization. Appl. Energy 2016, 183, 1404–1417. [Google Scholar] [CrossRef]
- YoosefDoost, A.; Lubitz, W.D. Archimedes Screw Design: An Analytical Model for Rapid Estimation of Archimedes Screw Geometry. Energies 2021, 14, 7812. [Google Scholar] [CrossRef]

| References | Main Contributions |
|---|---|
| Dellinger et al. [25] |
|
| Rorres [7] |
|
| Lashofer et al. [27] |
|
| Simmons et al. [28] |
|
| Alonso-Martinez [29] |
|
| |
| Edirisinghe et al. [30] |
|
| Saroinsong et al. [31] |
|
| Shahverdi [32] |
|
| Lee and Lee [33] |
|
| Shahverdi et al. [34] |
|
| Dedić-Jandrek and Nižetić [35] |
|
| Maulana et al. [36] |
|
| Betancour et al. [37] |
|
| Bouvant et al. [10] |
|
| Reference | Type of Study | L m | P m | N Blades | β ° | α ° | Di mm | Do mm | Q L/s | H m | ω rpm | η % |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dellinger et al. [24] | Numerical | 0.40 | 0.19 | 3 | 24.0 | 104 | 192 | 2.8 | 84.6 | 77.0 | ||
| Zitti et al. [38] | Experimental | 0.32 | 0.16 | 0.0 | 70.0 | 20 | 50 | 28.6 | 23.8 | |||
| Rohmer et al. [39] | Numerical | 0.96 | 3 | 30.0 | 420 | 840 | 90 | 40 | 84.0 | |||
| Erinofiardi et al. [26] | Experimental | 45 | 0.68 | 0.05 | 946 | 92.0 | ||||||
| Abdullah et al. [40] | Experimental | 1.0 | 0.07 | 1 | 35 | 70 | 130 | 1.12 | 165 | 81.4 | ||
| Durrani et al. [41] | Numerical | 1.71 | 3 | 26 | 640 | 1200 | 240 | 1.5 | 27.6 | 77.0 | ||
| Syam et al. [42] | Experimental | 2.0 | 0.26 | 1 | 30 | 140 | 260 | 20 | 1.0 | 236.4 | 57.0 | |
| Dellinger et al. [25] | Numerical | 5 | 24.5 | 50.0 | 85.8 | |||||||
| Thakur et al. [43] | Experimental | 1.63 | 0.30 | 22.0 | 80 | 200 | 1.0 to 4.0 | 74.3 | ||||
| Edirisinghe et al. [30] | Numerical | 7.78 | 0.84 | 3 | 45.0 | 1296 | 2400 | 200 | 5.2 | 54.6 | 82.1 | |
| Saroinsong et al. [31] | Experimental | 0.92 | 0.13 | 3 | 25.0 | 30.0 | 600 | 1100 | 50 | 89.0 | ||
| Shahverdi [32] | Numerical | 4 | 27.3 | 78 | 156 | 0.95 | 0.27 | 106 | 83.4 | |||
| Lee and Lee [33] | Experimental | 1.50 | 0.15 | 1 | 45.0 | 60 | 120 | 0.3 to 1.7 | 1.0 | 179.8 | 94.6 | |
| Shahverdi et al. [34] | Numerical | 6.00 | 1.50 | 1 | 20 | 750 | 1500 | 1200 | 1.8 | 91.1 | 90.8 | |
| Dedić-Jandrek and Nižetić [35] | Experimental | 1.00 | 0.30 | 3 | 21 | 160 | 300 | 10 | 0.5 | 70 | 67.0 | |
| Maulana et al. [36] | Experimental | 2.00 | 0.29 | 2 | 30 | 77 | 144 | 12.5 | 1.0 | 177 | 55% | |
| Betancour et al. [37] | Numerical | 0.12 | 0.30 | 50.6 | ||||||||
| Bouvant et al. [10] | Numerical | 0.36 | 0.22 | 73.9 | 55.2 |
| References | Manufacturing Method | Material | Head (m) | Outer Radius (mm) | Length (m) | Power (W) | Scale |
|---|---|---|---|---|---|---|---|
| Rohmer et al. [39] | Traditional Manufacturing | -- | 0.8 | -- | -- | 200–3000 | Pico |
| Erinofiardi et al. [26] | Aluminum | -- | 53 | 0.7 | 0.1–0.3 | Pico | |
| Abdullah et al. [40] | Stainless steel | -- | 65 | 1.0 | 1.5–2.5 | Pico | |
| Durrani et al. [41] | Galvanized iron | 1.5 | 600 | 3.4 | 2000 | Pico | |
| Syam et al. [42] | Stainless steel | 1.0 | 130 | 2.9 | 110 | Pico | |
| Bauyon [57] | -- | -- | -- | -- | 200 | Pico | |
| Sari et al. [75] | 3D Printing | PLA | 0.4 | -- | -- | 123 | Pico |
| Dellinger et al. [24] | ABS | -- | 96 | -- | 1–3 | Pico | |
| Zitti et al. [38] | PLA | -- | 50 | 0.32 | 30 × 10−3–50 × 10−3 | Pico | |
| Shashank et al. [74] | PLA | 0.1 | 50 | -- | 1–5 | Pico |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ubando, A.T.; Marfori, I.A.V., III; Peradilla, M.S.; Sy, C.L.; Calapatia, A.M.A.; Chen, W.-H. Sustainable Manufacturability of Archimedes Screw Turbines: A Critical Review. J. Manuf. Mater. Process. 2022, 6, 161. https://doi.org/10.3390/jmmp6060161
Ubando AT, Marfori IAV III, Peradilla MS, Sy CL, Calapatia AMA, Chen W-H. Sustainable Manufacturability of Archimedes Screw Turbines: A Critical Review. Journal of Manufacturing and Materials Processing. 2022; 6(6):161. https://doi.org/10.3390/jmmp6060161
Chicago/Turabian StyleUbando, Aristotle T., Isidro Antonio V. Marfori, III, Marnel S. Peradilla, Charlle L. Sy, Andre Marvin A. Calapatia, and Wei-Hsin Chen. 2022. "Sustainable Manufacturability of Archimedes Screw Turbines: A Critical Review" Journal of Manufacturing and Materials Processing 6, no. 6: 161. https://doi.org/10.3390/jmmp6060161
APA StyleUbando, A. T., Marfori, I. A. V., III, Peradilla, M. S., Sy, C. L., Calapatia, A. M. A., & Chen, W.-H. (2022). Sustainable Manufacturability of Archimedes Screw Turbines: A Critical Review. Journal of Manufacturing and Materials Processing, 6(6), 161. https://doi.org/10.3390/jmmp6060161