Abstract
This paper describes the dynamic stability evaluation of a constrained-motion dynamometer (CMD) with passive damping. The CMD’s flexure-based design offers an alternative to traditional piezoelectric cutting force dynamometers, which can exhibit adverse effects of the complex structural dynamics on the measurement accuracy. In contrast, the CMD system’s structural dynamics are nominally single degree of freedom and are conveniently altered by material selection, flexure element geometry, and element arrangement. In this research, a passive damping approach is applied to increase the viscous damping ratio and, subsequently, the stability limit. Cutting tests were completed and the in situ CMD displacement and velocity signals were sampled at the spindle rotating frequency. The periodic sampling approach was used to determine if the milling response was synchronous with the spindle rotation (stable) or not (chatter) by constructing Poincaré maps for both experiment and prediction (time-domain simulation). It was found that the viscous damping coefficient was increased by 130% and the critical stability limit was increased from 4.3 mm (no damping) to 15.4 mm (with damping).
1. Introduction
In manufacturing research, several factors influence part accuracy, including machine tool accuracy, dynamic motion loads, thermal conditions, and cutting forces [1,2,3]. The mechanics of the milling process have been extensively studied; in this context, the cutting force is a considerable area of research interest. As a result of the high sensitivity and rapid response of the cutting force signal to changes in cutting condition [4,5,6,7,8], the force signal can be processed for various tasks to optimize machine tool usage, such as: (1) adaptive feed rate control to keep the applied force at a predetermined level [1,2,3,4]; (2) tool wear evaluation from a comparative force level [9,10,11,12,13]; (3) force monitoring for the detection of chatter vibrations [1,2,4,5,6,7,8,9,10,11,12,13]; and (4) force monitoring for the detection of tool breakage in milling [9,10,11,12,13].
The dynamometer’s measurand, in this case, force, must be transformed into a physical quantity with a known input–output relationship which is realized by at least one principle of measurement in the transducer; see Table 1. Cutting forces are always estimated by using indirect methods, i.e., by measuring the effects of cutting forces such as local deformations, displacements, or accelerations of mechanical elements composing the machining system [8,9,10]. In practice, multi-axis dynamometers based on piezoelectric sensors provide the most common solution for cutting force measurement. A typical dynamometer consists of three or four piezoelectric transducers compressed under high preloads between two stiff plates [8,9].

Table 1.
Comparison of different measurement principles for cutting force measurement.
The transducers consist of thin slabs of the piezoelectric material cut in a precise orientation to the crystal axes depending on the application [10]. The dynamic deflections of the dynamometer’s piezoelectric transducers during machining operations produce a charge which is converted into a voltage proportional to the force that caused the deformation [1,2,8,9,10]. During the machining process, the boundary conditions of the dynamometer such as the connection to the machine tool structure and size and placement of the work material on the dynamometer will lead to variations in the structural response of the dynamometer system. Under forced vibration, the dynamic properties of the dynamometer’s limited bandwidth result in systematic errors which cause erroneous cutting force measurements that do not accurately reflect the physical machining process. The correction of the systematic errors caused by the dynamometer structural dynamics has been extensively researched [1,2,4,5,6,7].
Alternatively, multiple authors have presented various approaches to improved dynamometer designs which consider the dynamic response of the measuring system. Schmitz et al. [14] developed a dynamometer concept where the bandwidth was defined by a bracketed frequency range (10–16 kHz). The high frequency was achieved by designing a pair of nested, coupled single degree-of-freedom (SDOF) tungsten carbide flexure mechanisms. Korkut [15] developed a dynamometer which used four octagonal rings placed between two plates. Strain gauges were mounted on the octagonal rings and the cutting force was inferred from the strain gauge measurements. Yaldiz et al. [16,17] described the development of a four-component dynamometer to measure static and dynamic cutting forces and torque employing strain-gauge based sensors for milling and turning operations using similar octagonal rings. Transchel et al. [18] developed a high-frequency (up to 5 kHz) dynamometer where sensitive piezoelectric sensors were pre-loaded with a common bolt resulting in an improved dynamic stiffness. The mass of the workpiece holder plate was minimized by using a titanium alloy. Totis et al. [19,20,21] developed a plate-type dynamometer using three high-sensitivity tri-axial piezoelectric force sensors for milling and drilling applications. The novel sensor configuration provided higher natural frequencies and, therefore, increased bandwidth. Integration of force sensors into the machine spindle/tool have been explored comprehensively [22,23,24,25]. Smith et al. [25] developed a spindle-based torque dynamometer which was placed between the tool and holder on conventional tooling. The strain gauge-based sensor provided a bandwidth up to 2 kHz. Altintas and Park [26,27] developed a spindle-integrated force sensor system where the cutting forces were measured from six piezoelectric sensors embedded in the spindle housing using a circular arrangement. A disturbance Kalman filter was designed to estimate the high-frequency harmonics of the cutting forces applied at the tool tip. Aoyama and Ishii [28] utilized the Villari effect to determine cutting force components, cutting torque, and tool deflections. This was performed by detecting the intensity and direction of the magnetic field related to the material strain which was used to identify the applied force. An interesting cutting force system was developed by Ettrichratz et al. [29] which required a piezoceramic thick-film sensor plate mounted behind the cutting insert on an indexable end mill. The combination of material selection and placement resulted in accurate force measurements with limited influence on the cutting tool structural response.
To compliment these efforts, a monolithic CMD was designed and constructed to measure milling forces [30,31,32]. The design includes a moving platform for workpiece mounting and four leaf-type flexure elements in a symmetric dual four-bar linkage arrangement; see Figure 1. Simple parallel rectilinear springs exhibit sufficient linearity over a limited displacement range. In this design, the kinematic over-constraint is leveraged to provide elastic averaging of errors in bar lengths without introducing assembly errors. The strains along the flexure length are resisted by the frame [33,34,35,36,37,38,39]. Here, the flexure elements guide the moving platform in the compliant direction resulting in SDOF rectilinear motion. To avoid geometric non-linearities which occur for doubly clamped flexure elements, such as stress stiffening, the deflections must not exceed half the flexure thickness, t. This is a critical design constraint that must be considered to avoid non-linear stiffness behavior [33,39]. An optical interrupter (ROHM RPI-0352E) was selected as the measurement transducer ($0.33–$1.04/sensor). This simple LED-photodetector pair is used to measure displacement with high resolution at low cost using a knife edge [30,31,32,40,41,42,43] to partially block the light beam and, therefore, change the light intensity on the detector. The sensor has the added benefit of a compact footprint and fast response time (10 µs) without the need for an additional amplifier.
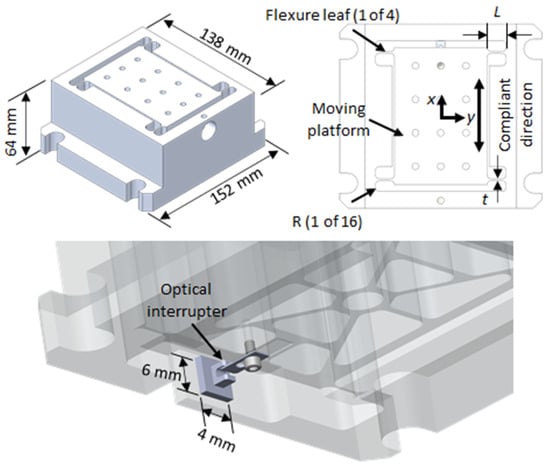
Figure 1.
Constrained-motion dynamometer design and optical interrupter placement for displacement measurement.
The CMD concept was proposed and prototyped by Gomez and Schmitz [30,31,32] where the flexure-based strategy was implemented in the milling setup and the structural deconvolution was carried out by filtering the measured displacement signals to obtain the cutting force. The measured cutting forces were compared to an industry-standard piezoelectric dynamometer (Kistler 9257B) and it was found that the cutting forces were accurately and successfully measured. The focus of this work is to explore the stability behavior of two alternative CMD systems.
For any dynamometer system, a limitation on the allowable axial depth of cut is regenerative chatter. With the ability to modify the dynamic response of a cutting force dynamometer, the stability limit and bandwidth can be significantly augmented either through an increase in stiffness or an increase in viscous damping ratio. In this section, a passive damping approach was selected to modify the viscous damping ratio to increase the critical stability limit of a CMD compared to its original counterpart.
There are many types of passive damping approaches, including: shear film damping, constrained layer damping (CLD), damping by addition of energy-absorbing foams and viscoelastic materials, and dynamic absorbers [33]. For this application, a viscoelastic material was sandwiched between the CMD flexure elements and the mechanism frame. As a milling force is applied to the CMD, energy is dissipated through the viscoelastic medium due to the relative motion between the movable platform and mechanism frame. The advantage of this approach is the ability to obtain a relatively high amount of energy dissipation in a flexure mechanism without compromising the stiffness or mass of the dynamometer. Additionally, it allows for a general strategy of reducing the vibration amplitude at a low-cost. For this study, a widely available silicone rubber sealant was used to demonstrate its benefits as a passive damping medium for the CMD.
2. Materials and Methods
2.1. Time-Domain Simulation
The simulation implemented in this study is based on the “regenerative force, dynamic deflection” model described by Smith and Tlusty [1,44]. The simulation provides both modeling and predictive capabilities which will enable a quantitative comparison between the cutting force dynamometers. Time-domain simulation is selected for this work to:
- enable the force/deflection amplitudes to be predicted and validated;
- allows for a variety of tool geometries including an arbitrary number of cutting teeth, variable teeth spacing, variable helix angles, and cutter teeth runout;
- discern signal quality between alternative dynamometer systems using the force/deflection frequency content.
The simulation proceeds as described by Schmitz and Smith [1]:
- The instantaneous chip thickness is calculated based on the nominal, tooth angle-dependent chip thickness, the current normal vibration, and the vibration of the previous tooth at the same angle.
- The tangential (t) and rotating-normal (n) components of the cutting force is determined by (1) and (2), where b is the axial depth of cut, and h(t), is the instantaneous chip thickness. The cutting (shearing) force coefficients are denoted by ktc and knc while the edge (rubbing) coefficients are denoted by kte and kne:
Ft = ktcbh(t) + kteb
Fn = kncbh(t) + kneb
- The force components are used to find the new displacements by numerical solution of the differential equations of motion in the x (feed) and y directions, shown by (3) and (4):
- The tooth angle, φ, is incremented, and the process is repeated. Modal parameters are used to describe the system dynamics in the x (feed) and y directions, where multiple degrees of freedom in each direction can be incorporated; see Figure 2.
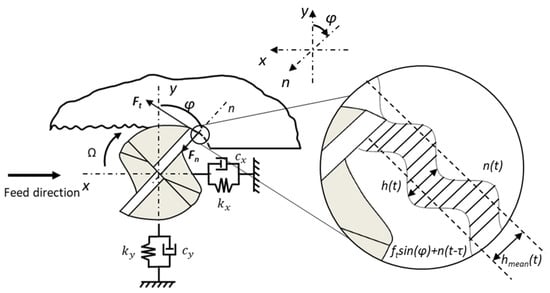 Figure 2. Chip regeneration in milling. The feed direction is identified, and the tool rotation is assumed to be clockwise with respect to the fixed x-y coordinate system.
Figure 2. Chip regeneration in milling. The feed direction is identified, and the tool rotation is assumed to be clockwise with respect to the fixed x-y coordinate system.
2.2. Milling Stability
Since the time-domain simulation approach provides local, rather than global, information about the process behavior for a given axial depth of cut and spindle speed; a once-per-tooth (OPT) sampling strategy can be implemented to calculate a stability metric. The absolute values of the differences in pairs of sequentially sampled points are summed and then normalized to the number of sample points (5). For forced synchronous vibration, the points repeat so this metric is ideally zero. For other behaviors, it is greater than zero [45,46].
In (5), xs is the vector of OPT sampled x displacements and N is the length of the xs vector. For a stable cut, the absolute value of the difference between subsequent points is zero; as a result, their normalized sum remains zero. For an unstable cut, the difference between subsequent points is non-zero and their normalized sum is greater than zero [45,46]. For this research, the metric, M, was selected to be 1 µm.
2.3. Experimental Setup
The experimental setup for the milling stability validation is shown in Figure 3. Cutting tests were performed on a Haas TM-1 CNC vertical milling machine. A 6061-T6 aluminum workpiece was mounted to the CMD. A single flute, 15.88 mm diameter endmill (Kennametal M1D062E1401W075L150) was used to perform up-milling machining passes at a 3 mm radial depth of cut and a variable axial depth of cut. The tool description and cutting parameters for the milling stability validation tests are summarized in Table 2.

Figure 3.
Experimental setup for the milling stability validation tests.

Table 2.
Tool description and cutting parameters for the milling stability validation tests.
Once-per-tooth sampling was achieved using a laser tachometer, where a reflective target was attached to the rotating tool holder. In situ displacement and velocity signals were collected using a laser Doppler vibrometer. The tool and workpiece FRFs were measured by impact testing, where an instrumented hammer is used to excite the structure and the response is measured using a linear low-mass accelerometer. The detailed modal fitting parameters, in addition to the measured and fit FRFs for the tool and workpiece, are presented in Appendix A. The modal parameters for the CMDs x direction are presented in Table 3 to emphasize the increased modal viscous damping coefficient. For brevity, the modal fitting results are presented in Figure 4 and Figure 5 for an Al 6061-T6 CMD (no damping) and the Al 6061-T6 CMD (with damping) x (feed) direction, respectively. Note that the addition of the silicone medium resulted in a 130% increase in damping with negligible change to the modal mass and stiffness parameters.

Table 3.
x-direction modal parameters for the single degree of freedom (SDOF) constrained-motion dynamometers (CMDs).
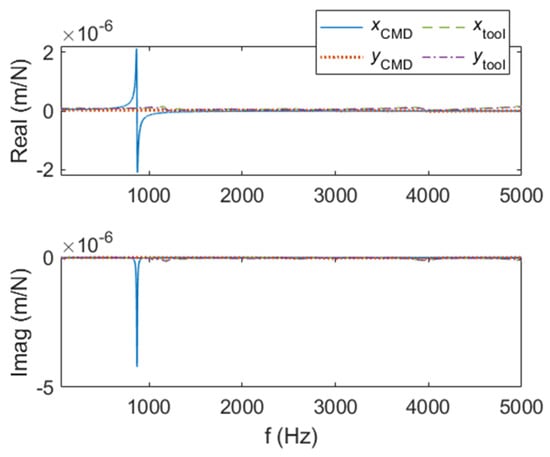
Figure 4.
Modal fit FRFs of the tool and CMD (no damping) for the stability validation setup.
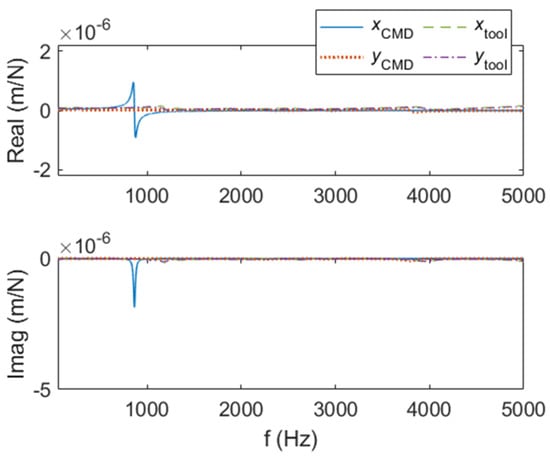
Figure 5.
Modal fit FRFs of the tool and CMD (with damping) for the stability validation setup.
The natural frequency for the CMDs x (feed) direction changed slightly after each cut because the material was removed from the workpiece; therefore, the workpiece was replaced after every test cut. The aluminum 6061-T6 workpiece dimensions were nominally 30 mm × 70 mm × 30 mm with a mass of 164 ± 1 g. The nominal flexure leaf length, width, and thickness were 10 mm, 44.5 mm, and 1.27 mm, respectively.
To explore the stability behavior in detail, a grid of time-domain simulations was completed at spindle speeds of 4000 rpm to 5000 rpm (10 rpm steps) and axial depth from 0.1 mm to 20 mm (0.1 mm steps). The stability behavior was automatically determined by the synchronous sampling strategy outlined in Section 2.2. The results of this strategy are represented by the stability maps in Figure 6 and Figure 7. As mentioned previously, stable cutting behavior can be identified form a distribution of periodically sampled points. If the points repeat with each revolution, then only forced vibration is present and the cut is stable. If the points do not repeat with each revolution, then either secondary Hopf or period-n bifurcations are present. For an unstable cut, the difference between subsequent points is non-zero and their normalized sum is greater than zero [45,46]. For this research, the metric, M, was selected to be 1 µm. To interpret the stability map, stable zones are represented by the white area bounded by the stability contour, where M < 1 µm; the stability boundary is represented by the dark stability contour, where M = 1 µm; and unstable zones are represented by the dark green region bounded by the stability contour, where M > 1 µm.
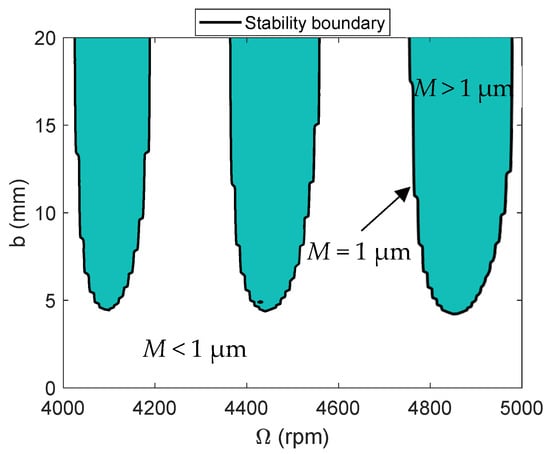
Figure 6.
Time-domain stability limit (TDS), solid black line with teal infill, expressed as a function of spindle speed, Ω, for the CMD (no damping).
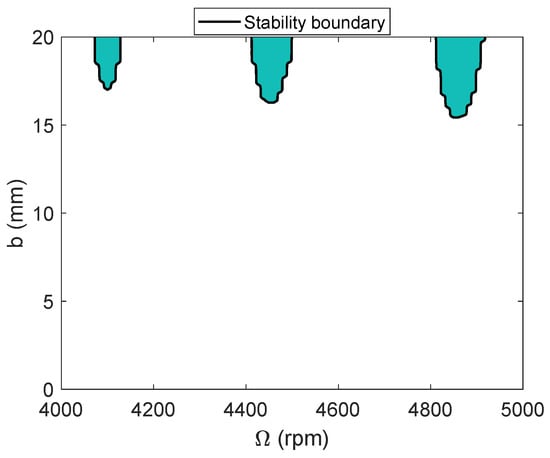
Figure 7.
Time-domain stability limit (TDS), solid black line with teal infill, expressed as a function of spindle speed, Ω, for the CMD (with damping).
3. Results
The milling stability validation proceeded by completing tests cuts on the CMD (no damping) until the critical depth of cut was reached. Afterwards, the same procedure was performed for the CMD (with damping) to demonstrate the increase in the stability limit due to the modification of the viscous damping coefficient by the addition of the passive damping medium.
A Poincaré sectioning strategy was selected to determine if the milling response was stable (synchronous) or unstable (non-synchronous) with the spindle rotating frequency. Practically, this was achieved by measuring the x (feed) direction displacement and velocity signals of the CMD at the spindle’s once-per-revolution (OPR) rotating frequency. The OPR sampled points are plotted on the displacement–velocity plane and used to determine the milling stability. Stable cutting conditions are represented by discrete sampled points which repeat at each spindle revolution. Unstable cutting conditions result in an elliptical distribution of the sampled points caused by the combination of chatter frequency, fc, and the tooth passing frequency, ft, and its integer harmonics, N. The cutting test cases for the CMDs are presented in Table 4 and Table 5.

Table 4.
Cutting conditions and calculated stability metric, M, for the CMD (no damping).

Table 5.
Cutting conditions and calculated stability metric, M, for the CMD (with damping).
The time-dependent displacement and velocity profiles for the first table entry in Table 4 {4900 rpm, 1 mm} are presented in the top two rows of Figure 8 to demonstrate the good agreement between the simulated (left column–blue line color) and experimental (right column, green line) results. The simulated OPT sampled points (red circles) and experimental points (black circles) are superimposed on the profiles, where the entry and exit transients were removed before plotting. The Poincaré maps are displayed in the bottom row. These maps are able to separate stable and chatter conditions because the OPT samples repeat for forced vibration (stable) and do not repeat for self-excited vibration (chatter). The Poincaré maps for the remaining test cases are provided in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. Good agreement is observed in each case. It was found that the Al 6061-T6 CMD (no damping) had a critical stability limit of approximately 4.3 mm. For cases of regenerative chatter, Figure 12 and Figure 13, the displacement amplitude approaches, and in some cases exceeds, the permissible displacement before exceeding the yield strength.
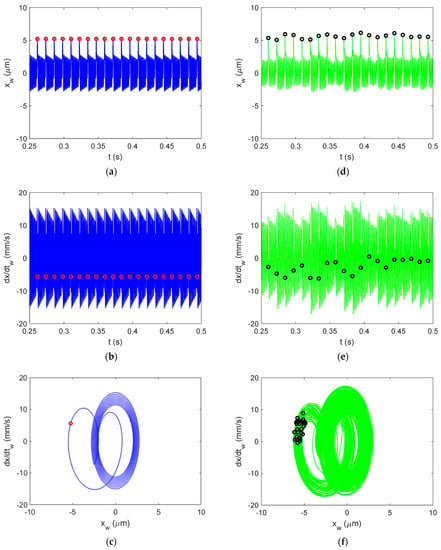
Figure 8.
Al-6061-T6 CMD (no damping) vibration behavior for stable cutting at {4900 rpm, 1 mm}. Predicted displacement (a), velocity (b), and once-per-tooth (OPT) Poincaré map (c) and measured displacement (d), velocity (e), and OPT Poincaré map (f).
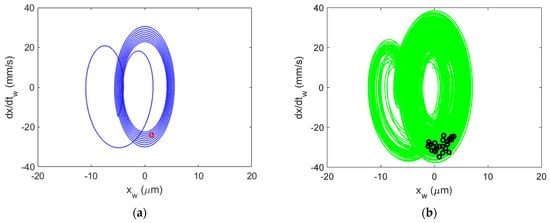
Figure 9.
Al 6061-T6 CMD (no damping) Poincaré maps for stable cutting at {4900 rpm, 2 mm}. Predicted (a) and measured (b).
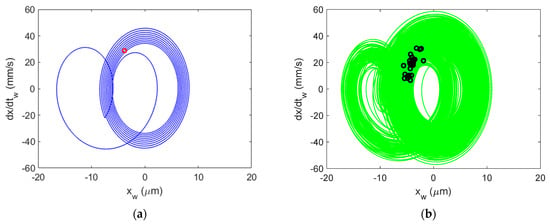
Figure 10.
Al 6061-T6 CMD (no damping) Poincaré maps for stable cutting at {4900 rpm, 3 mm}. Predicted (a) and measured (b).
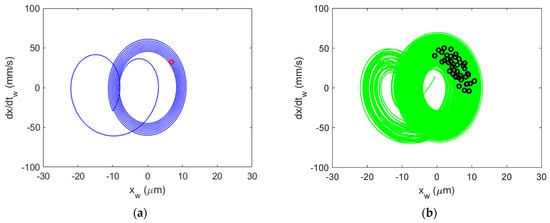
Figure 11.
Al 6061-T6 CMD (no damping) Poincaré maps for stable cutting at {4900 rpm, 4 mm}. Predicted (a) and measured (b).
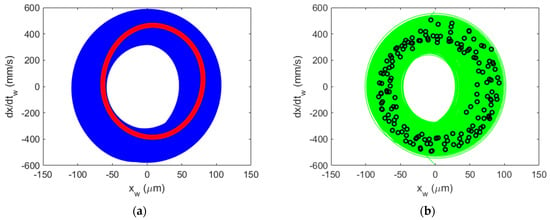
Figure 12.
Al 6061-T6 CMD (no damping) Poincaré maps for regenerative chatter (secondary Hopf bifurcation) at {4900 rpm, 5 mm}. Predicted (a) and measured (b). Note the difference in scale from Figure 11.
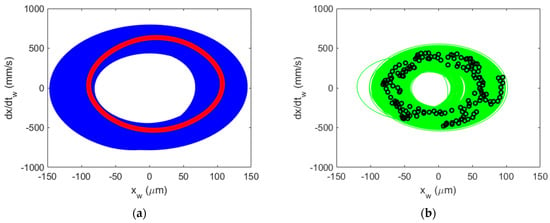
Figure 13.
Al 6061-T6 CMD (no damping) Poincaré maps for regenerative chatter (secondary Hopf bifurcation) at {4900 rpm, 6 mm}. Predicted (a) and measured (b).
Next, the stability results are presented for the damped Al 6061-T6 CMD (with damping), see Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27. Again, good agreement between prediction and measurement was observed at all test locations. There was a significant increase in the stability limit with respect to its undamped counterpart. The maximum allowable depth of cut for the cutting tool was reached without an unstable result. The critical depth of cut for the damped Al 6061-T6 CMD was predicted to be 15.4 mm.
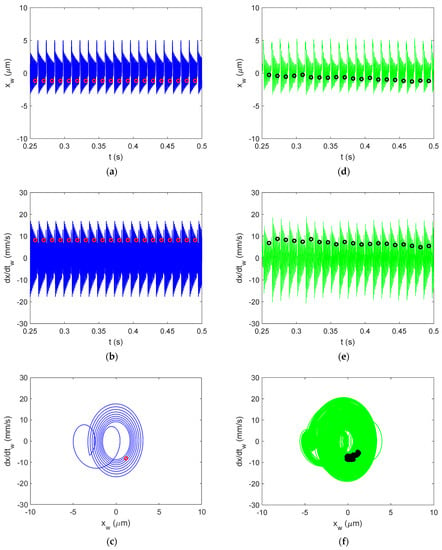
Figure 14.
Al-6061-T6 CMD (with damping) vibration behavior for stable cutting at {4900 rpm, 1 mm}. Predicted displacement (a), velocity (b), and OPT Poincaré map (c) and measured displacement (d), velocity (e), and OPT Poincaré map (f).
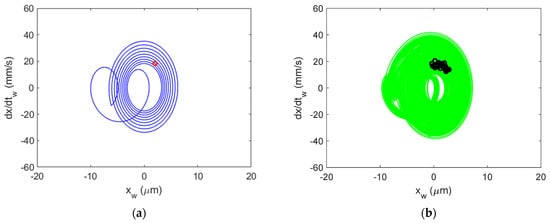
Figure 15.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 2 mm}. Predicted (a) and measured (b).
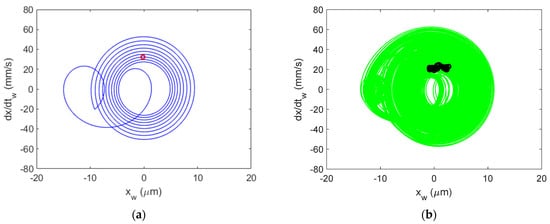
Figure 16.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 3 mm}. Predicted (a) and measured (b).
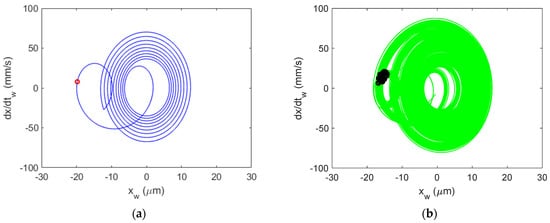
Figure 17.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 4 mm}. Predicted (a) and measured (b).
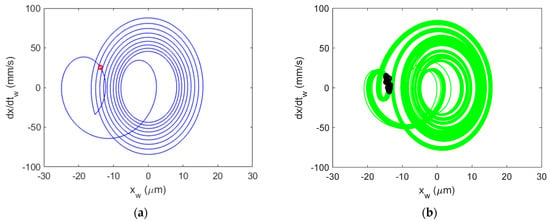
Figure 18.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 5 mm}. Predicted (a) and measured (b).
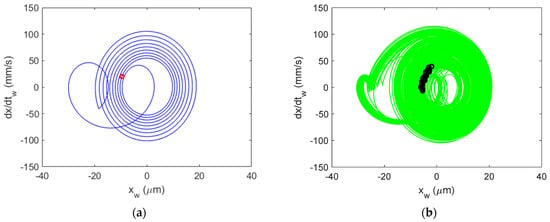
Figure 19.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 6 mm}. Predicted (a) and measured (b).
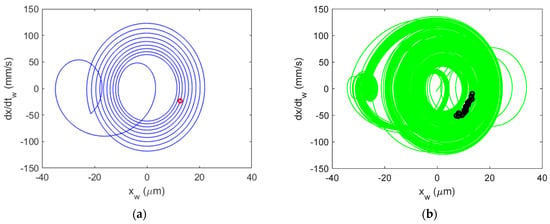
Figure 20.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 7 mm}. Predicted (a) and measured (b).
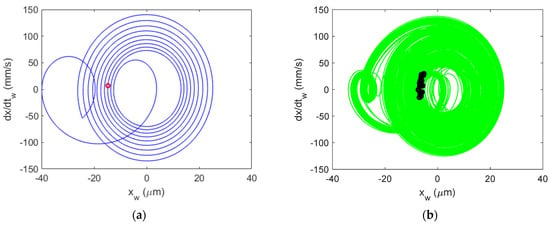
Figure 21.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 8 mm}. Predicted (a) and measured (b).
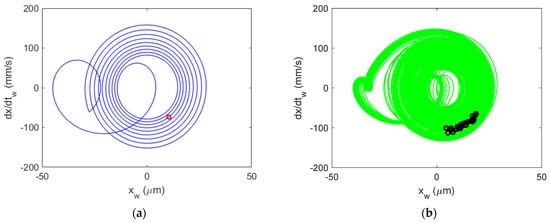
Figure 22.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 9 mm}. Predicted (a) and measured (b).
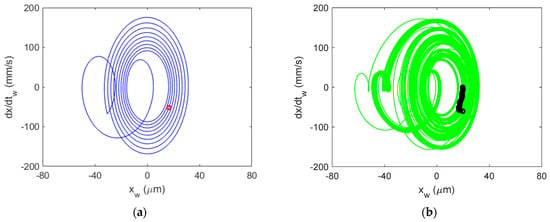
Figure 23.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 10 mm}. Predicted (a) and measured (b).
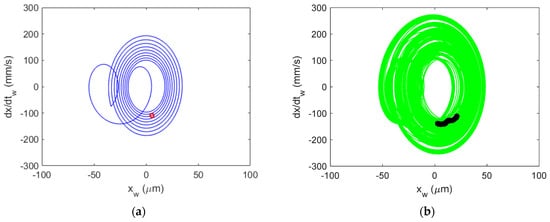
Figure 24.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 11 mm}. Predicted (a) and measured (b).
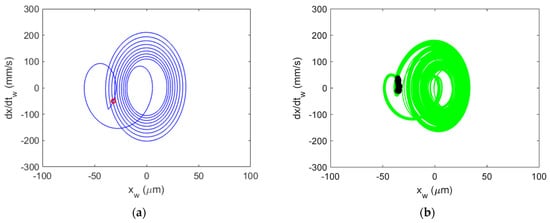
Figure 25.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 12 mm}. Predicted (a) and measured (b).
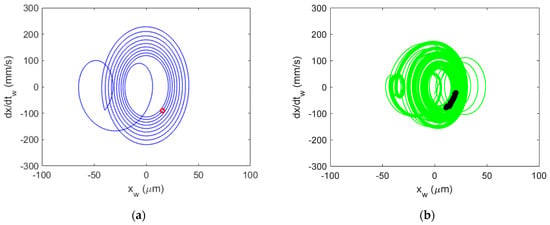
Figure 26.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 13 mm}. Predicted (a) and measured (b).
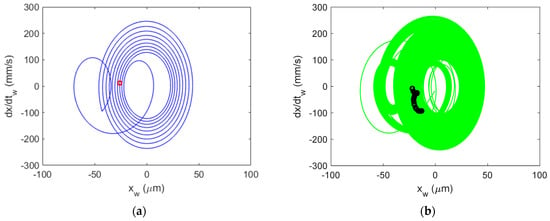
Figure 27.
Al 6061-T6 CMD (with damping) Poincaré maps for stable cutting at {4900 rpm, 14 mm}. Predicted (a) and measured (b).
The milling process model simulation revealed that the critical stability limit increased from 4.3 mm to 15.4 mm, Figure 28. The simulation results were validated using measured displacement and velocity signals to construct Poincaré maps. Good agreement was observed for all test cases.
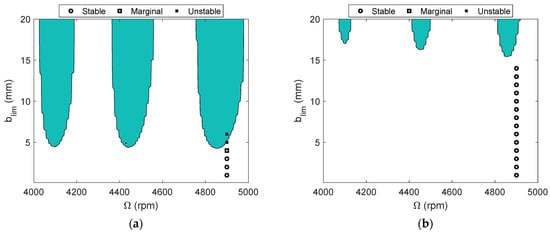
Figure 28.
Milling stability validation for the CMD (no damping) (a) and the CMD (with damping) (b).
While there are numerous models for predicting regions of stable and unstable behavior, a popular strategy remains the frequency domain Fourier series approach presented by Altintas and Budak [2,47]. In this approach, the time-varying coefficients of the dynamic milling equations, which depend on the angular orientation of the cutter as it rotates through the cut, are expanded into a Fourier series, and then truncated to include only the average component to provide a time-invariant analytical solution. The results of this analytical stability lobe diagram (red solid line) are superimposed over the time-domain simulation results (black solid circles); see Figure 29. To interpret the results, the black solid circles represent stable cutting zones while the white area represents regions of unstable cutting. The area below the Fourier series approach boundary predicts stable cutting, while the area above the boundary predicts unstable cutting (chatter).
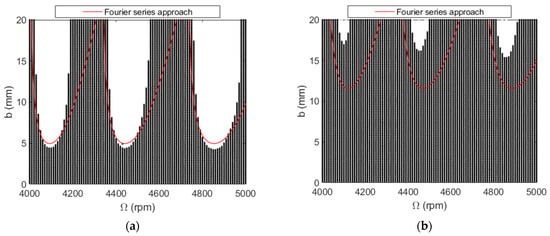
Figure 29.
Milling stability lobe comparison for the CMD (no damping) (a) and the CMD (with damping) (b).
The agreement is good for the CMD with no additional damping (left panel), but less so for the CMD with added damping (right panel). The time-domain simulation identifies the stability boundary using many local simulations, 20,000 in this case. Its accuracy was validated by the test results shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27. Due to the strong asymmetry in the CMD structural dynamics, the time-domain simulation results are more accurate than the Fourier series approach [47]. However, the penalty is additional computation time.
4. Conclusions
A constrained-motion dynamometer (CMD) was designed and developed to measure cutting forces for milling applications. This research leveraged several advantages of flexure-based mechanisms, including monolithic design resulting in wear-free behavior, negligible backlash, smooth and continuous displacement characteristics, and a linear relationship between forces generated by known displacements. The dynamometer was a monolithic design with constrained-motion of a moving platform defined by four leaf-type flexure elements arranged in the traditional H-bar configuration. An optical interrupter (fixed emitter–detector pair with a moving knife edge to partially interrupt the beam) was used to measure the moving platform’s motion during milling. Prior efforts have shown that the CMD can be successfully used for accurate force measurement compared to an industry-standard cutting force dynamometer (Kistler 9257B) [41,42,43]. Given the compliant nature of the CMD, it was necessary to explore the stability behavior.
In all machining applications, a limitation on the allowable axial depth of cut is regenerative chatter. Alternative dynamometer systems rely on specific piezoelectric transducer arrangements and the structural dynamics of the system are often ignored. Here, the system structural dynamics are a principal element in the design space which are easily altered with material selection, flexure element geometry, and flexure element arrangement. The use of flexure mechanisms can reduce the workpiece dynamic static stiffness; however, this provides an important ability to modify the dynamic response of the cutting force dynamometer and, subsequently, the stability limit and bandwidth. This is enabled by modifying the flexure stiffness, moving platform mass, and damping. A passive damping approach was used to modify the viscous damping ratio to increase the critical stability limit of an Al 6061-T6 CMD compared to its original counterpart. It was shown that the viscous damping coefficient increased by 130%. For cases of regenerative chatter, Figure 12 and Figure 13, the displacement amplitude approaches, and in some cases exceeds, the permissible displacement before exceeding the yield strength. This becomes a critical design parameter which should be considered when using a CMD as described by this research.
Author Contributions
Conceptualization, T.S. and M.G.; methodology, T.S. and M.G.; validation, M.G.; formal analysis, M.G.; investigation, T.S. and M.G.; resources, T.S.; data curation, M.G.; writing—original draft preparation, M.G. and T.S.; writing—review and editing, T.S.; visualization, M.G.; supervision, T.S.; project administration, T.S.; funding acquisition, T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a non-exclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan. Accessed on 8 February 2022.)
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
The modal fitting parameters are presented for the stability validation experimental setup; see Figure 3.

Table A1.
Tool tip modal parameters for the x (feed) direction.
Table A1.
Tool tip modal parameters for the x (feed) direction.
| Direction | m (kg) | k (N/m) | c (N-s/m) |
|---|---|---|---|
| x | 190.873 | 3.38 × 107 | 120,529 |
| 1457.395 | 2.21 × 109 | 20,952 | |
| 1170.143 | 2.20 × 109 | 97,233 | |
| 376.291 | 9.51 × 108 | 46,771 | |
| 111.083 | 3.36 × 108 | 12,033 | |
| 99.394 | 4.12 × 108 | 17,079 | |
| 27.683 | 1.81 × 108 | 12,348 | |
| 12.988 | 3.38 × 108 | 10,606 | |
| 40.247 | 1.38 × 109 | 13,900 | |
| 2.455 | 1.35 × 108 | 907 | |
| 109.275 | 7.70 × 109 | 10,239 | |
| 2.061 | 1.54 × 108 | 1975 | |
| 11.237 | 1.05 × 109 | 6515 | |
| 6.408 | 6.78 × 108 | 3155 | |
| 3.028 | 4.32 × 108 | 2320 | |
| 15.432 | 3.70 × 109 | 8989 | |
| 1.356 | 3.67 × 108 | 1327 | |
| 10.041 | 5.72 × 109 | 4165 | |
| 0.251 | 1.55 × 108 | 403 | |
| 4.122 | 4.25 × 109 | 2143 | |
| 0.061 | 6.57 × 107 | 158 | |
| 0.174 | 2.22 × 108 | 683 | |
| 1.145 | 1.80 × 109 | 1610 | |
| 0.026 | 4.62 × 107 | 171 | |
| 1.532 | 3.70 × 109 | 1801 |
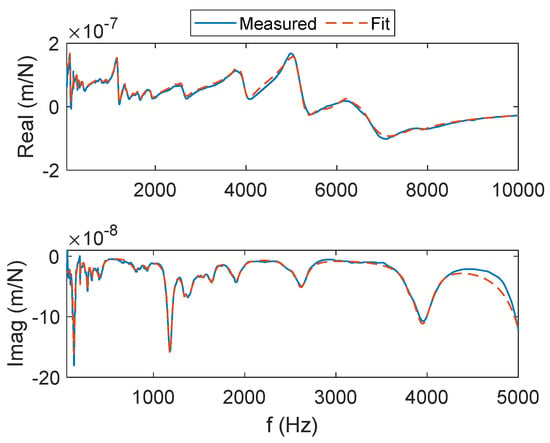
Figure A1.
Tool tip FRF for the x (feed) direction. The real (top) and imaginary (bottom) parts of the complex valued FRF are presented.

Table A2.
Tool tip modal parameters for the y direction.
Table A2.
Tool tip modal parameters for the y direction.
| Direction | m (kg) | k (N/m) | c (N-s/m) |
|---|---|---|---|
| y | 109.319 | 2.18 × 107 | 67,573 |
| 105.099 | 7.15 × 108 | 32,947 | |
| 14.532 | 6.25 × 108 | 4626 | |
| 1.222 | 6.66 × 107 | 1248 | |
| 4.407 | 2.91 × 108 | 35,341 | |
| 4.074 | 3.75 × 108 | 15,300 | |
| 1.204 | 1.91 × 108 | 2594 | |
| 4.211 | 7.78 × 108 | 3286 | |
| 1.938 | 5.36 × 108 | 1840 | |
| 0.284 | 1.75 × 108 | 449 | |
| 0.065 | 7.04 × 107 | 157 | |
| 0.461 | 6.17 × 108 | 1331 | |
| 0.030 | 5.20 × 107 | 193 | |
| 0.153 | 3.75 × 108 | 10,985 | |
| 0.783 | 2.48 × 109 | 42,620 | |
| 2.520 | 8.83 × 109 | 51,484 |
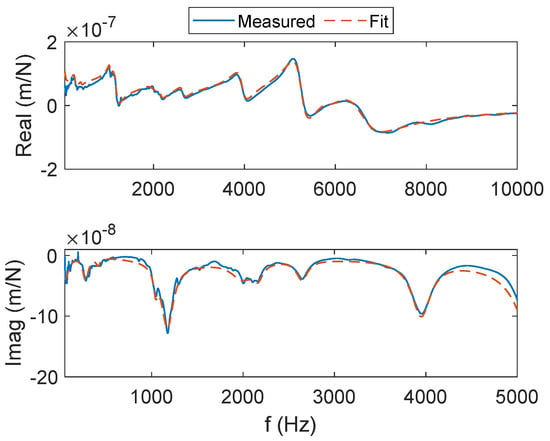
Figure A2.
Tool tip FRF for the y direction. The real (top) and imaginary (bottom) parts of the complex valued FRF are presented.

Table A3.
CMD (no damping) modal parameters for the stability measurement setup in the x (feed) direction.
Table A3.
CMD (no damping) modal parameters for the stability measurement setup in the x (feed) direction.
| Direction | m (kg) | k (N/m) | c (N-s/m) |
|---|---|---|---|
| x | 0.689 | 2.08 × 107 | 43 |
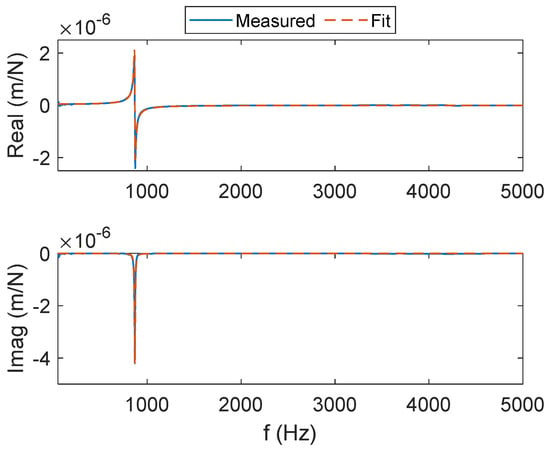
Figure A3.
CMD (no damping) FRF for the x (feed) direction. The real (top) and imaginary (bottom) parts of the complex valued FRF are presented.

Table A4.
CMD (no damping) modal parameters for the stability measurement setup in the y direction.
Table A4.
CMD (no damping) modal parameters for the stability measurement setup in the y direction.
| Direction | m (kg) | k (N/m) | c (N-s/m) |
|---|---|---|---|
| y | 328.120 | 1.03 × 108 | 36,110 |
| 170.733 | 4.99 × 108 | 30,917 | |
| 90.087 | 1.78 × 109 | 16,172 | |
| 126.798 | 5.91 × 109 | 83,599 | |
| 76.151 | 4.45 × 109 | 44,629 | |
| 38.573 | 4.01 × 109 | 48,575 | |
| 11.282 | 2.18 × 109 | 9849 | |
| 4.596 | 1.11 × 109 | 6002 | |
| 4.868 | 1.27 × 109 | 3633 | |
| 64.251 | 1.83 × 1010 | 12,751 | |
| 45.307 | 1.44 × 1010 | 9664 | |
| 66.769 | 2.17 × 1010 | 12,612 | |
| 1.078 | 3.77 × 108 | 1372 | |
| 27.137 | 9.96 × 109 | 11,231 | |
| 3.288 | 1.40 × 109 | 3628 | |
| 9.618 | 4.40 × 109 | 5130 | |
| 2.596 | 1.26 × 109 | 2302 | |
| 7.566 | 4.14 × 109 | 5516 | |
| 1.228 | 7.35 × 108 | 1519 | |
| 2.538 | 1.58 × 109 | 1206 | |
| 17.166 | 1.22 × 1010 | 4618 | |
| 9.875 | 7.96 × 109 | 10,479 |
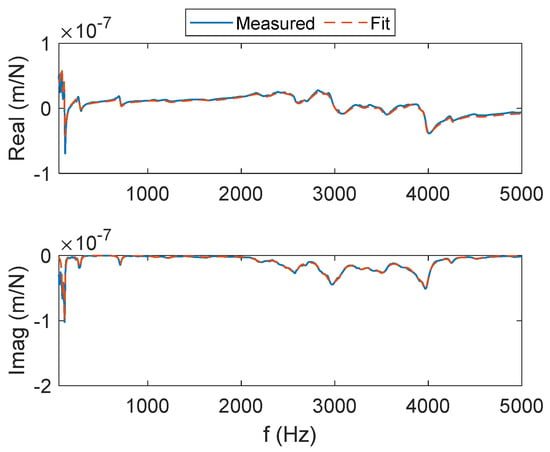
Figure A4.
CMD (no damping) FRF for the y direction. The real (top) and imaginary (bottom) parts of the complex valued FRF are presented.

Table A5.
CMD (with damping) modal parameters for the stability measurement setup in the x (feed) direction.
Table A5.
CMD (with damping) modal parameters for the stability measurement setup in the x (feed) direction.
| Direction | m (kg) | k (N/m) | c (N-s/m) |
|---|---|---|---|
| x | 0.701 | 2.07 × 107 | 99 |
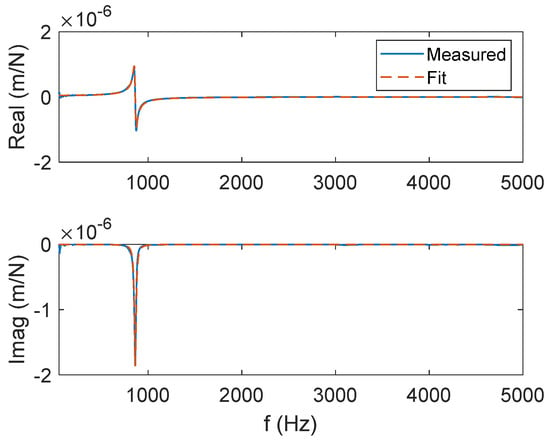
Figure A5.
CMD (with damping) FRF for the x (feed) direction. The real (top) and imaginary (bottom) parts of the complex valued FRF are presented.

Table A6.
CMD (with damping) modal parameters for the stability measurement setup in the y direction.
Table A6.
CMD (with damping) modal parameters for the stability measurement setup in the y direction.
| Direction | m (kg) | k (N/m) | c (N-s/m) |
|---|---|---|---|
| y | 4334.195 | 1.23 × 1010 | 204,353 |
| 182.268 | 5.93 × 108 | 16,828 | |
| 106.509 | 2.14 × 109 | 24,751 | |
| 42.190 | 1.95 × 109 | 60,633 | |
| 152.618 | 8.50 × 109 | 40,556 | |
| 182.646 | 1.44 × 1010 | 53,112 | |
| 14.408 | 1.35 × 109 | 15,197 | |
| 36.573 | 4.42 × 109 | 16,729 | |
| 12.639 | 1.97 × 109 | 21,354 | |
| 1.555 | 3.17 × 108 | 2508 | |
| 43.098 | 9.35 × 109 | 7871 | |
| 453.258 | 1.00 × 1011 | 1,077,191 | |
| 93.694 | 2.23 × 1010 | 30,614 | |
| 25.323 | 6.35 × 109 | 15,557 | |
| 2.805 | 9.32 × 108 | 2065 | |
| 27.777 | 1.14 × 1010 | 22,029 | |
| 2.990 | 1.44 × 109 | 4892 | |
| 1.072 | 5.83 × 108 | 1030 | |
| 9.755 | 5.40 × 109 | 3260 | |
| 177.937 | 1.00 × 1011 | 144,264 | |
| 1.078 | 6.18 × 108 | 449 | |
| 9.715 | 8.46 × 109 | 2695 | |
| 4.884 | 4.71 × 109 | 6702 |
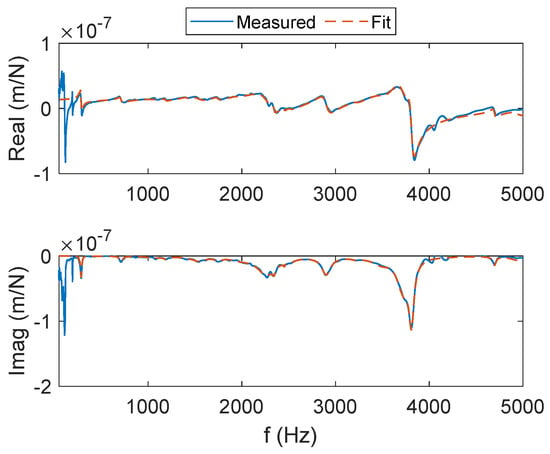
Figure A6.
CMD (with damping) FRF for the y direction. The real (top) and imaginary (bottom) parts of the complex valued FRF are presented.
References
- Schmitz, T.L.; Smith, K.S. Machining Dynamics: Frequency Response to Improved Productivity; Springer: New York, NY, USA, 2009. [Google Scholar]
- Altintas, Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Tlusty, J. Manufacturing Processes and Equipment; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Tlusty, J.; Andrews, G.C. A Critical Review of Sensors for Unmanned Machining. CIRP Ann. 1983, 32, 563–572. [Google Scholar] [CrossRef]
- Byrne, G.; Dornfeld, D.; Denkena, B. Advanced cutting technology. CIRP Ann. 2004, 52, 483–507. [Google Scholar] [CrossRef] [Green Version]
- Tlusty, J.; Jang, D.; Tarng, Y. Measurements of the milling force over a wide frequency range. In Proceedings of the 15th NAMRC, Bethlehem, PA, USA, 27–29 May 1987; pp. 273–280. [Google Scholar]
- Teti, R.; Jemielniak, K.; O’Donnel, G.; Dornfeld, D. Advanced monitoring of machining operations. CIRP Ann. 2010, 59, 707–739. [Google Scholar] [CrossRef] [Green Version]
- Gautschi, G.H. Piezoelectirc Sensorics; Springer: Berlin Heidelberg, Germany, 2002. [Google Scholar]
- Gautschi, G.H. Cutting forces in machining and their routine measurement with multi-component piezo-electric force transducers. In Proceedings of the Twelfth International Machine Tool Design and Research Conference, Manchester, UK, 15–17 September 1971; Macmillan Education UK: London, UK, 1972; pp. 113–120. [Google Scholar]
- Kistler Instrumente AG. The Piezoelectric Effect, Theory, Design and Usage; Company White Paper; Kistler Instrumente AG: Amherst, NY, USA, 2007. [Google Scholar]
- Altintas, Y.; Yellowley, I. The process detection of tool failure in milling using cutting force models. ASME J. Eng. Ind. 1989, 111, 149–157. [Google Scholar] [CrossRef]
- Altintas, Y.; Yellowley, I.; Tlusty, J. Detection of tool breakage in milling. Trans. ASME 1985, 18, 41–48. [Google Scholar]
- Altintas, Y. In process detection of tool breakage using time series monitoring of cutting forces. Int. J. Mach. Tools Manuf. 1988, 28, 157–172. [Google Scholar] [CrossRef]
- Burton, D.; Duncan, G.S.; Ziegert, J.C.; Schmitz, T.L. High frequency, low force dynamometer for micro-milling force measurement. In Proceedings of the 19th American Society for Precision Engineering Annual Meeting, Orlando, Fl, USA, 24–29 October 2004; pp. 221–224. [Google Scholar]
- Korkut, I. A dynamometer design and its construction for milling operation. Mater. Des. 2003, 24, 631–637. [Google Scholar] [CrossRef]
- Yalidz, S.; Unsacar, F. A dynamometer design for measurement of cutting forces on turning. Measurement 2006, 39, 80–89. [Google Scholar] [CrossRef]
- Yaldiz, S.; Unsacar, F.; Haci, S.; Isik, H. Design, development and testing of a four-component milling dynamometer for the measurement of cutting force and torque. Mech. Syst. Signal Process. 2007, 21, 1499–1511. [Google Scholar] [CrossRef]
- Transchel RStirnimann, J.; Blattner, M.; Bill, B.; Thiel, R.; Kuster, F.; Wegener, K. Effective dynamometer for measuring high dynamic process force signals in micro machining operations. Procedia CIRP 2012, 1, 558–562. [Google Scholar] [CrossRef]
- Totis, G.; Sortino, M. Development of a modular dynamometer for triaxial cutting force measurement in milling. Int. J. Mach. Tools Manuf. 2011, 51, 34–42. [Google Scholar] [CrossRef]
- Totis, G.; Adams, O.; Sortino, M.; Veselovac, D.; Klocke, F. Development of an innovative plate dynamometer for advanced milling and drilling applications. Measurement 2014, 49, 164–181. [Google Scholar] [CrossRef]
- Totis, G.; Wirtz, G.; Sortino, M.; Veselovac Kuljanic, F.; DKlocke, F. Development of a dynamometer for measuring individual cutting edge forces in face milling. Mech. Syst. Signal Process. 2010, 24, 1844–1857. [Google Scholar] [CrossRef]
- Jun, M.; Ozdoganlar, B.; DeVor, R.; Kapoor, S.; Kirchheim, K.; Schnaffer, G. Evolution of spindle-based force sensor for monitoring and fault diagnosis of machining operations. Int. J. Mach. Tools Manuf. 2002, 42, 741–751. [Google Scholar] [CrossRef]
- O’Donnel, G.E.; Kelly, K.; Byrne, G. Use of a sensor integrated motor spindle for monitoring of a flexible machining center. In Proceedings of the 2nd CIRP International Seminar on Intelligent Computation in Manufacturing Engineering, Capri, Italy, 21–23 June 2000; pp. 383–388. [Google Scholar]
- Byrne, G.; O’Donnell, G.E. An integrated force sensor solution for process monitoring of drilling operations. CIRP Ann. 2007, 56, 59–62. [Google Scholar] [CrossRef]
- Smith, D.A.; Smith, S.; Tlusty, J. High performance milling torque sensor. J. Manuf. Sci. Eng. 1988, 120, 504–514. [Google Scholar] [CrossRef]
- Park, S.S.; Altintas, Y. Dynamic compensation of spindle-integrated force sensors. CIRP Ann. 2004, 53, 305–308. [Google Scholar]
- Park, S.S. High Frequency Bandwidth Cutting Force Measurements in Milling Using the Spindle Integrated Force Sensor System. Ph.D. Thesis, Department of Mechanical Engineering, University of British Columbia, Vancouver, BC, USA, 2003. [Google Scholar]
- Aoyama, H.; Ishii, T. Sensor to detect cutting force components, cutting torque, and cutting tool deflections. J. Manuf. Process. 2004, 6, 141–147. [Google Scholar] [CrossRef]
- Ettrichrätz, M.; Drossel, W.; Gebhardt, S.; Bucht, A.; Kranz, B.; Schneider, J. Performance of a new piezoceramic thick film sensor for measurement and control of cutting forces during milling. CIRP Ann. 2018, 67, 45–48. [Google Scholar]
- Gomez, M.; Schmitz, T.L. Determination of cutting forces using a flexure-based dynamometer: Deconvolution of structural dynamics using the frequency response function. In Proceedings of the 33rd American Society for Precision Engineering Annual Meeting, Las Vegas, NV, USA, 4–9 November 2018. [Google Scholar]
- Gomez, M.; Schmitz, T.L. Displacement-based dynamometer for milling force measurement. Procedia Manuf. 2019, 34, 867–875. [Google Scholar] [CrossRef]
- Gomez, M.; Schmitz, T.L. Low-cost, constrained-motion dynamometer for milling force measurement. Manuf. Lett. 2020, 25, 34–39. [Google Scholar] [CrossRef]
- Smith, S.T. Flexures: Elements of Elastic Mechanisms; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Smith, S.T.; Chetwynd, D.G. Foundations of Ultraprecision Mechanism Design; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Slocum, A.H. Precision Machine Design; Society of Manufacturing Engineers: Dearborn, MI, USA, 1995. [Google Scholar]
- Awtar, S. Synthesis and Analysis of Parallel Kinematic XY Flexure Mechanisms. Ph.D. Thesis, Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]
- Awtar, S.; Slocum, A.H.; Sevincer, E. Characteristics of beam-based flexure modules. J. Mech. Des. 2007, 129, 625–639. [Google Scholar] [CrossRef] [Green Version]
- Nishawala, V.V. A Study of Large Deflection of Beams and Plates. Master’s Thesis, Department of Mechanical and Aerospace Engineering, Rutgers University, Piscataway, NJ, USA, 2011. [Google Scholar]
- Gu, G.; Shin, Y.; Son, J.; Kim, J. Design and characterization of a photo-sensor based force measuring unit (FMU). Sens. Actuators A 2012, 182, 49–56. [Google Scholar] [CrossRef]
- Lee, C.B.; Lee, S.K.; Tarbutton, J.A. Novel design and sensitivity analysis of displacement measurement system utilizing knife edge diffraction for nanopositioning stages. Rev. Sci. Instrum. 2014, 85, 095113. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.B.; Lee, S.K.; Tarbutton, J.A. Positioning control effectiveness of optical knife edge displacement sensor-embedded monolithic precision stage. Sens. Actuators A 2015, 233, 290–296. [Google Scholar] [CrossRef]
- Lee, C.B.; Mahajan, S.; Zhao, R.; Jeon, S. A curved edge diffraction-utilized displacement sensor for spindle metrology. Rev. Sci. Instrum. 2016, 87, 075113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, K.S.; Tlusty, J. An overview of modeling and simulation of the milling process. ASME J. Eng. Ind. 1991, 113, 169–175. [Google Scholar] [CrossRef]
- Honeycutt, A.; Schmitz, T. A new metric for automated stability identification in time domain milling simulation. ASME J. Manuf. Sci. Eng. 2016, 138, 07450. [Google Scholar] [CrossRef]
- Honeycutt, A.; Schmitz, T. Milling stability interrogation by subharmonic sampling. ASME J. Manuf. Sci. Eng. 2017, 139, 041009. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).