Hybrid Manufacturing of Stiffening Grooves in Additive Deposited Thin Parts
Abstract
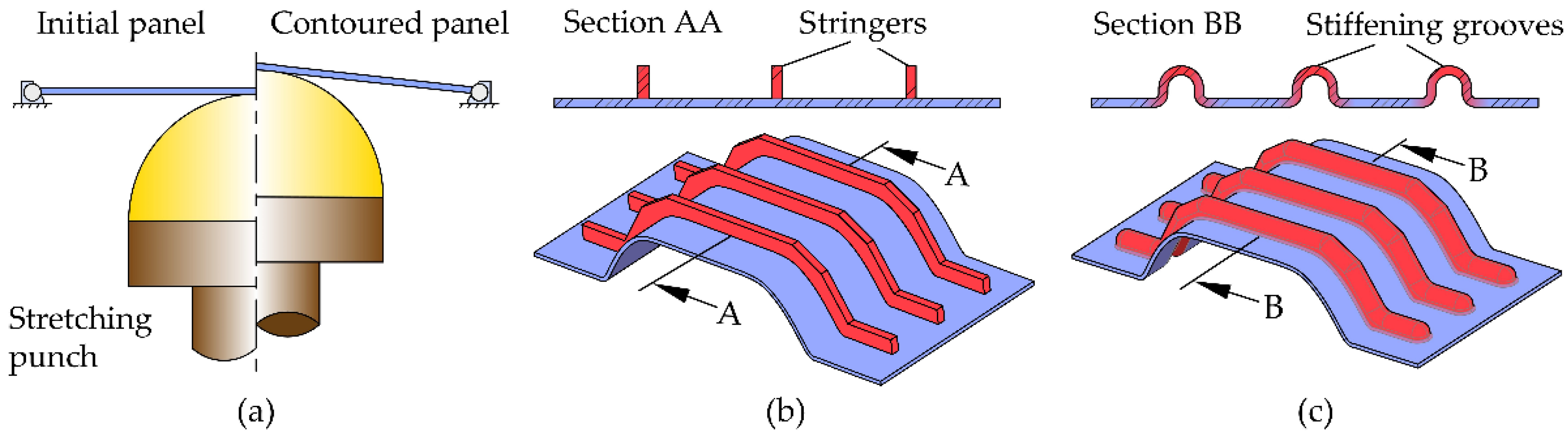
1. Introduction
2. Materials and Methods
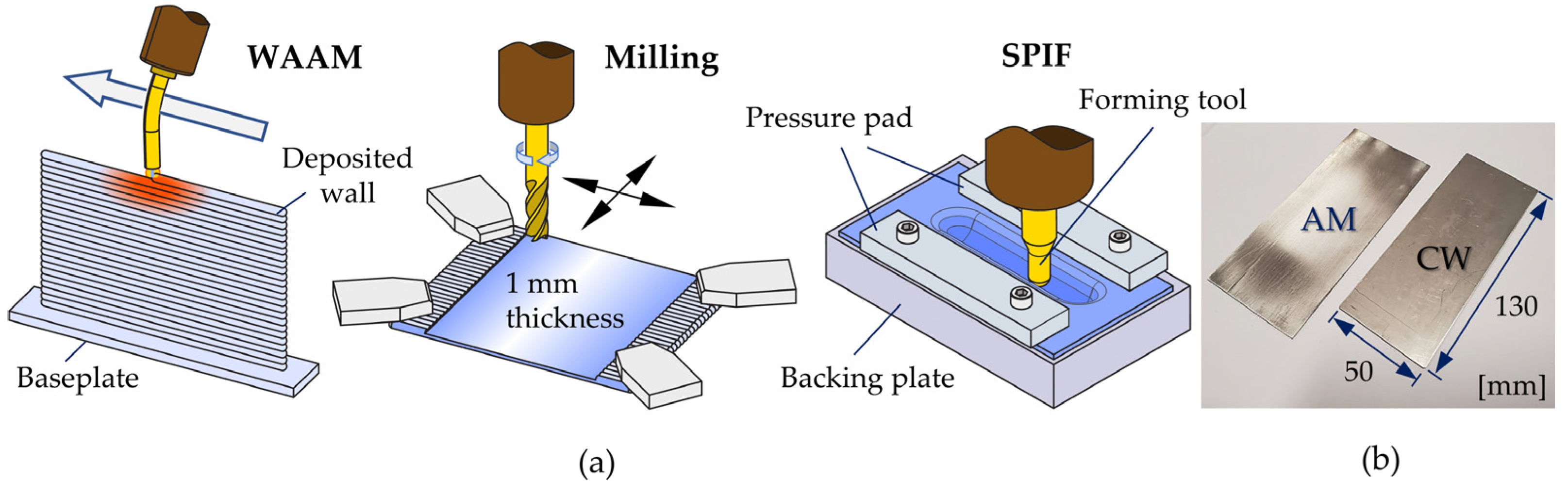
2.1. Additively Deposited and Wrought Commercial Materials
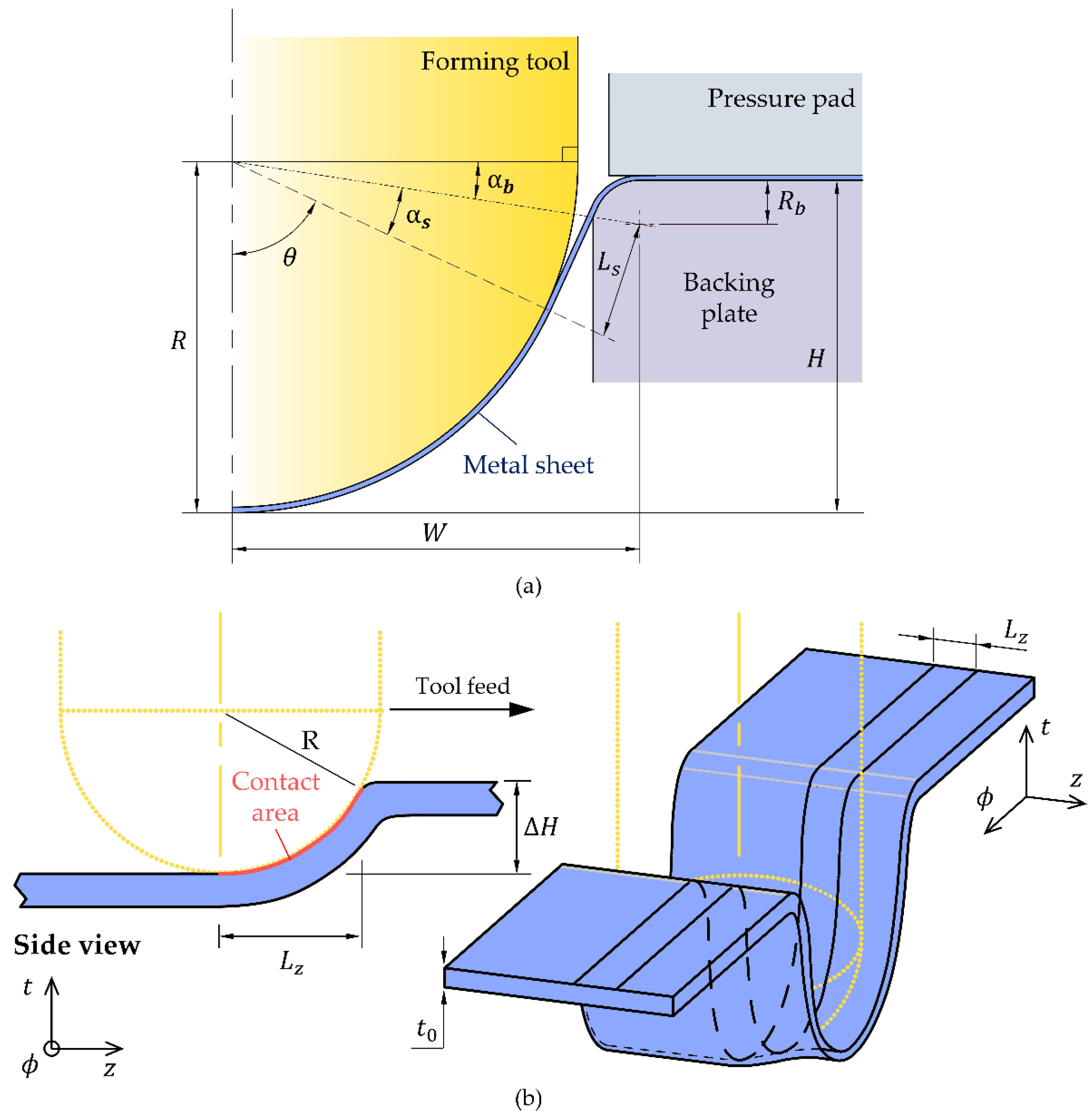
2.2. Single-Point Incremental Forming of the Stiffening Grooves
2.3. Analytical Model for the Incremental Forming of the Stiffening Grooves
2.3.1. Tool Force
2.3.2. Maximum Allowable Depth
3. Results and Discussion
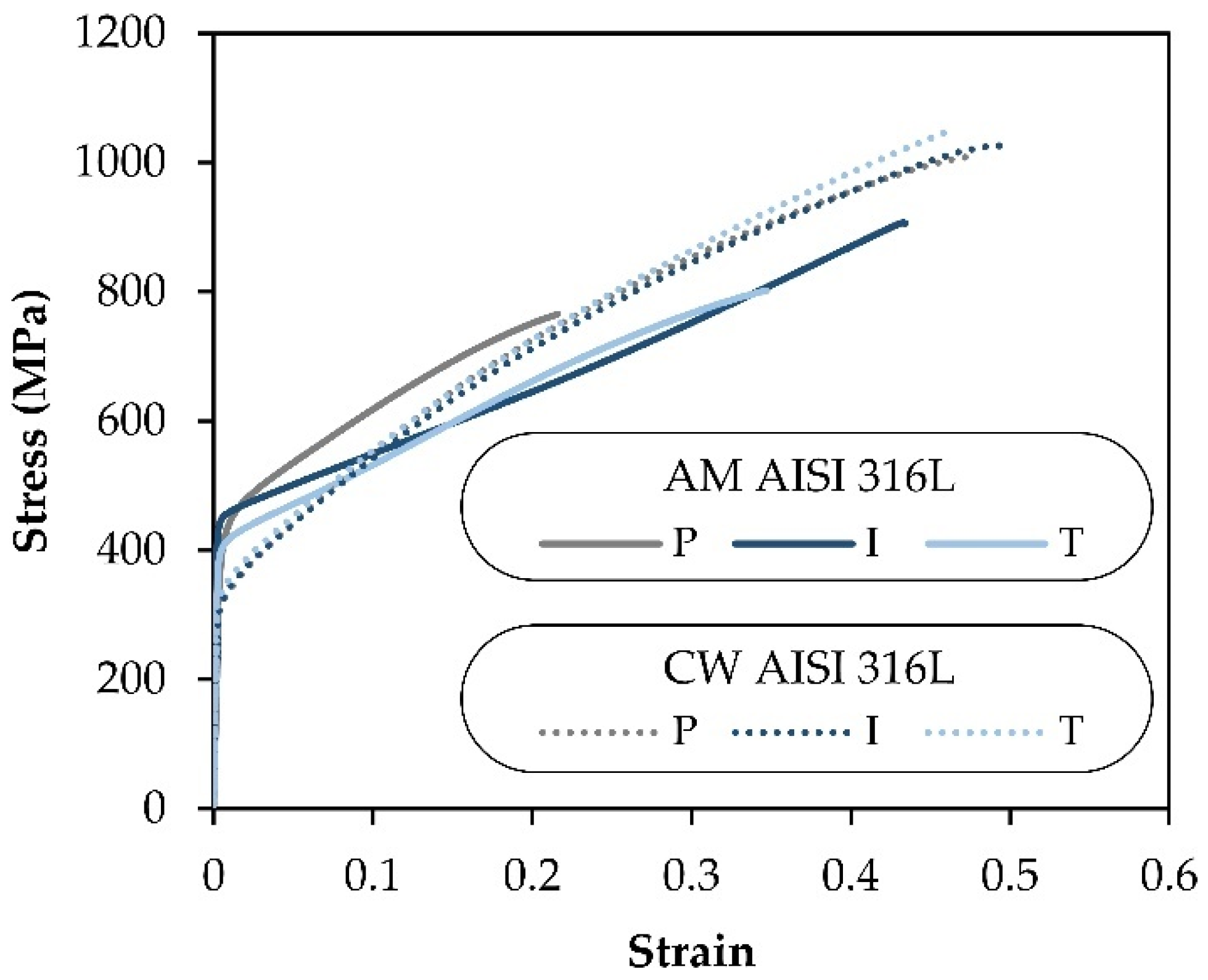
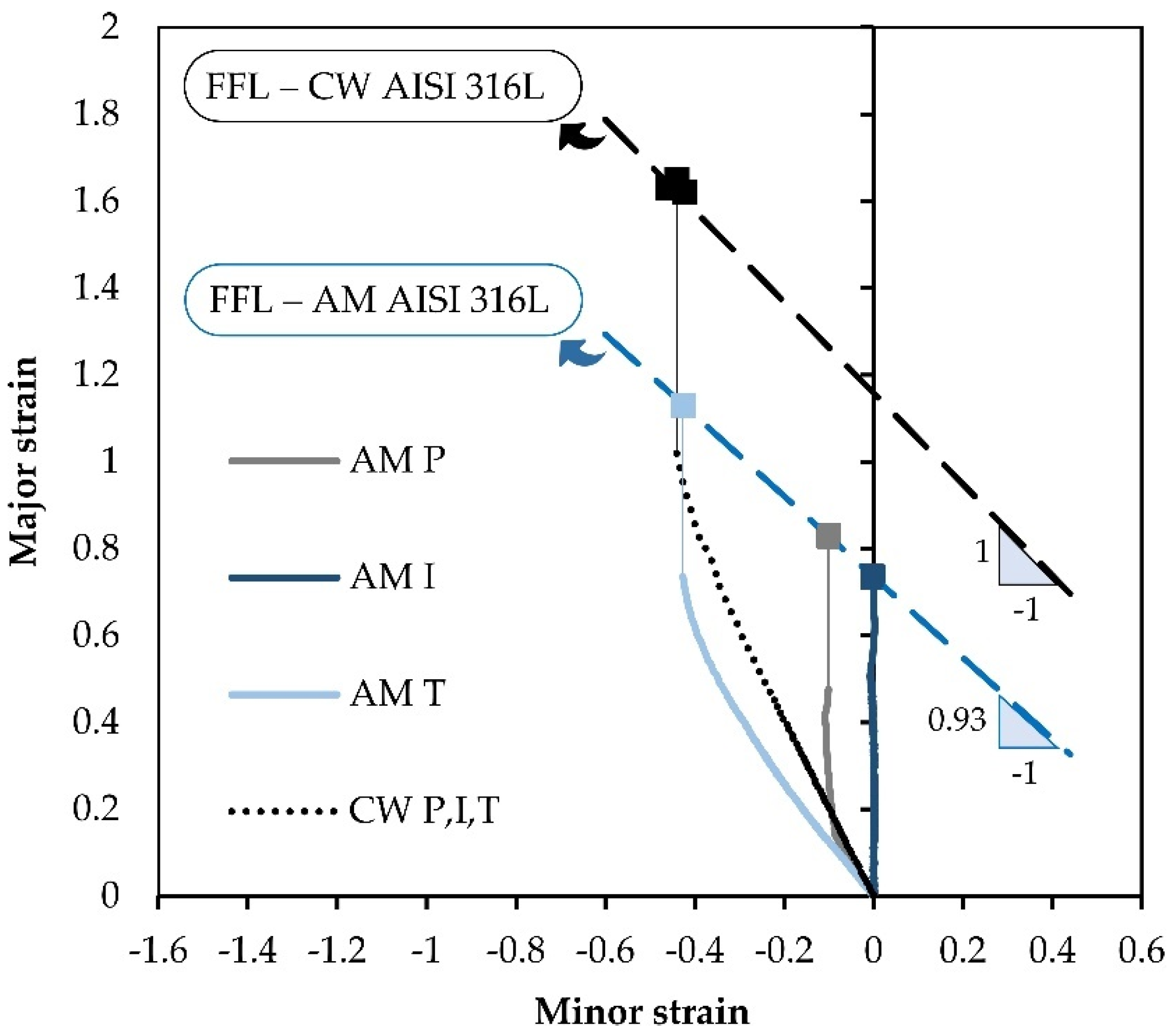
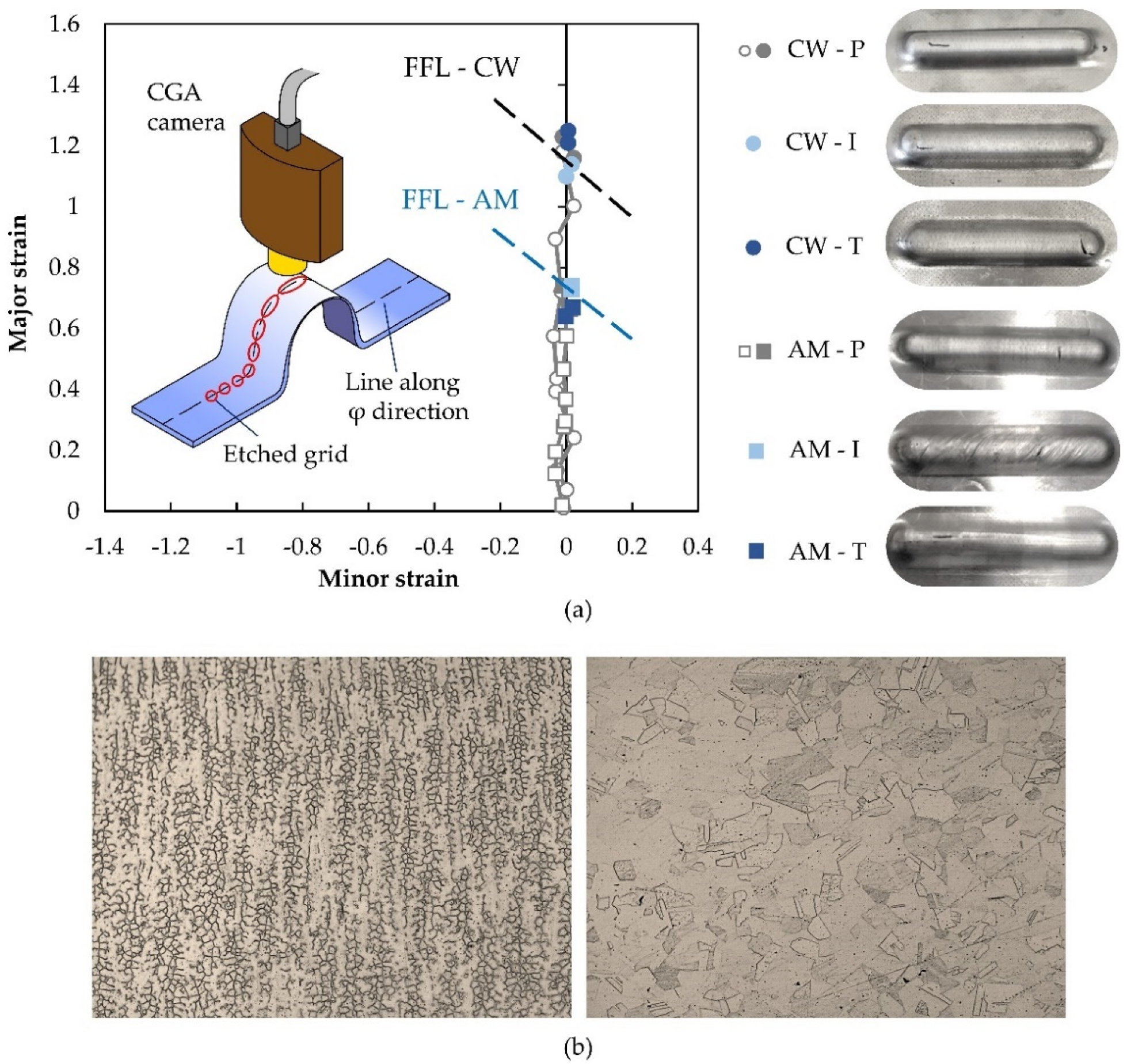
3.1. Strain Paths
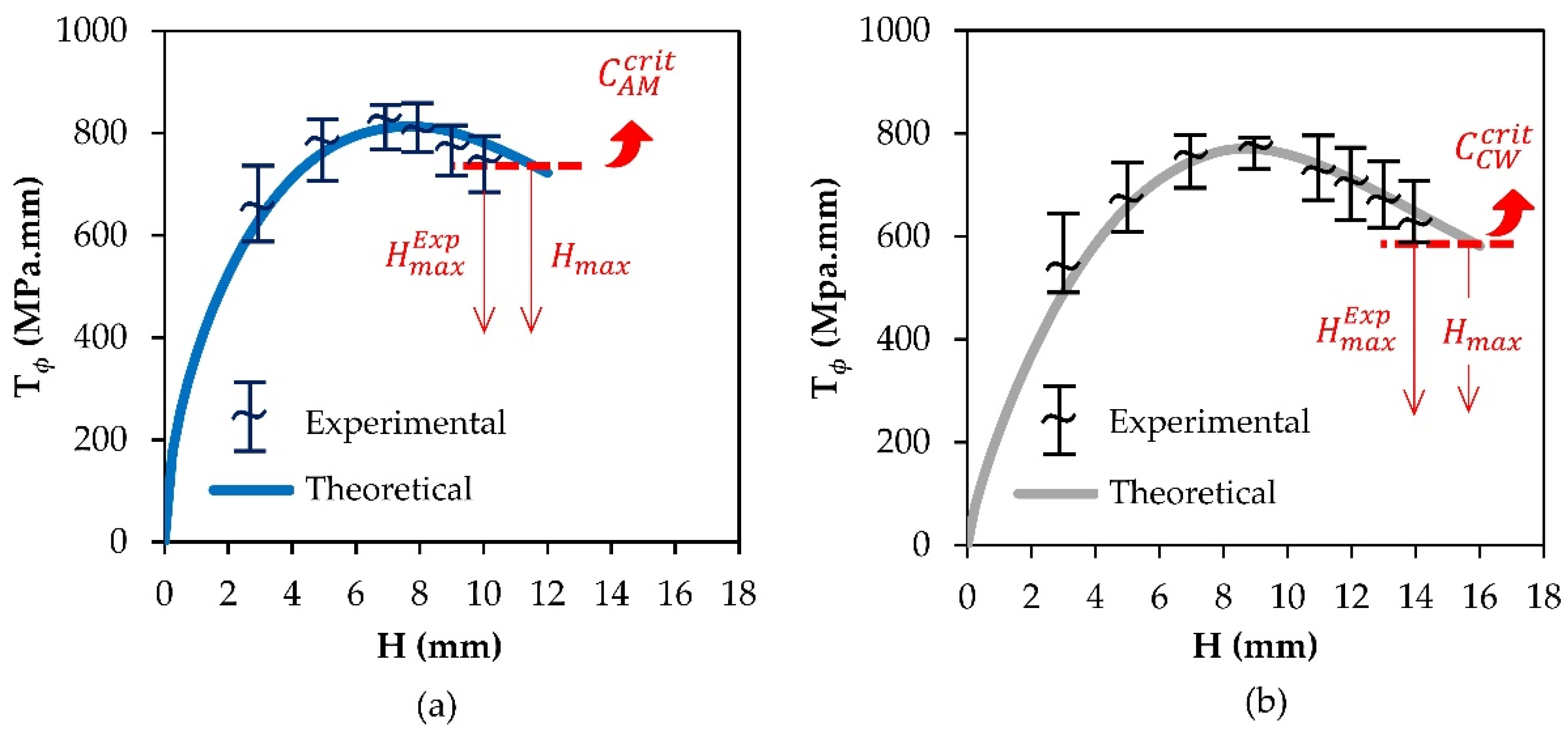
3.2. Maximum Allowable Depths
3.3. Tool Forces
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klocke, F. Manufacturing Processes 4—Forming; Springer: Aachen, Germany, 2013; pp. 332–339. [Google Scholar]
- Köhler, S.; Rohnert, C.; Groche, P. Extension of geometric limits in drawing of stringer sheets. In Proceedings of the 17th International Conference on Metal Forming—Metal Forming 2018, Toyohashi, Japan, 16–19 September 2018; Mori, K.I., Abe, Y., Maeno, T., Eds.; Procedia Manufacturing: Amsterdam, Netherlands, 2018; Volume 15, pp. 693–700. [Google Scholar]
- Seguy, S.; Campa, F.J.; Lacalle, L.N.L.; Arnaud, L.; Dessein, G.; Aramendi, G. Toolpath dependent stability lobes for the milling of thin-walled parts. Int. J. Mach. Mach. Mater. 2009, 4, 377–392. [Google Scholar] [CrossRef]
- Shamsuddin, K.A.; Ab-Kadir, A.R.; Osman, M.H. A comparison of milling cutting path strategies for thin-walled aluminium alloys fabrication. Int. J. Eng. Sci. 2013, 2, 1–8. [Google Scholar]
- World Premiere for Additive Manufacturing: STELIA Aerospace Presents a Demonstrator for Metallic Self-Reinforced Fuselage Panels Manufactured by 3D Impression. Available online: https://additivemanufacturing.com/2018/02/21/world-premiere-for-additive-manufacturing-stelia-aerospace-presents-a-demonstrator-for-metallic-self-reinforced-fuselage-pannels-manufactured-by-3d-impression/ (accessed on 15 February 2018).
- Slota, J.; Kubit, A.; Trzepiecinski, T.; Krasowski, B.; Varga, J. Ultimate load-carrying ability of rib-stiffened 2024-T3 and 7075-T6 aluminium alloy panels under axial compression. Materials 2021, 14, 1176. [Google Scholar] [CrossRef] [PubMed]
- Fusano, L.; Priarone, P.C.; Avalle, M.; Filippi, A.M. Sheet metal plate design: A structured approach to product optimization in the presence of technological constraints. Int. J. Adv. Manuf. Technol. 2011, 56, 31–45. [Google Scholar] [CrossRef][Green Version]
- Lacki, P.; Adamus, J. Numerical analysis of forming sheet panels with stiffening ribs. In Proceedings of the 13rd International Conference on Computational Plasticity. Fundamentals and Applications—COMPLAS XIII, Barcelona, Spain, 1–3 September 2015; pp. 204–215. [Google Scholar]
- Eguia, I.; Mangas, A.; Iturbe, R.; Gutiérrez, M.A. Electromagnetic forming of longitudinal strengthening ribs in roll formed automotive profiles. In Proceedings of the 4th International Conference on High-Speed Forming—ICHSF 2010, Columbus, OH, USA, 9–10 March 2010; pp. 200–207. [Google Scholar]
- Pragana, J.M.P.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. Integration of tube end forming in wire arc additive manufacturing: An experimental and numerical investigation. Int. J. Adv. Manuf. Technol. 2021, 117, 2715–2726. [Google Scholar] [CrossRef]
- Pragana, J.M.P.; Sampaio, R.F.V.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. Hybrid metal additive manufacturing: A state–of–the-art review. Adv. Ind. Manuf. Eng. 2021, 2, 100032. [Google Scholar] [CrossRef]
- Zhu, Z.; Dhokia, V.G.; Nassehi, A.; Newman, S.T. A review of hybrid manufacturing processes–state of the art and future perspectives. Int. J. Comput. Integr. Manuf. 2013, 26, 596–615. [Google Scholar] [CrossRef]
- Pragana, J.P.M.; Rosenthal, S.; Bragança, I.M.F.; Silva, C.M.A.; Tekkaya, A.E.; Martins, P.A.F. Hybrid additive manufacturing of collector coins. J. Manuf. Mater. Process. 2020, 4, 115. [Google Scholar] [CrossRef]
- Pragana, J.P.M.; Bragança, I.M.C.; Reis, L.; Silva, C.M.A.; Martins, P.A.F. Formability of wire-arc deposited AISI 316L sheets for hybrid additive manufacturing applications. J. Mater. Des. Appl. 2021, 235, 2839–2850. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.D.; de Lacalle, L.N.L.; Urbikain, G.; Pereira, O.; Martinez, S.; Bris, J. On the relationship between cutting forces and anisotropy features in the milling of LPBF Inconel 718 for near net shape parts. Int. J. Mach. Tools Manuf. 2021, 170, 103801. [Google Scholar] [CrossRef]
- ASTM E8/E8 M. Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Amini, S.; Gollo, A.H.; Paktinat, H. An investigation of conventional and ultrasonic-assisted incremental forming of annealed AA1050 sheet. Int. J. Adv. Manuf. Technol. 2017, 90, 1569–1578. [Google Scholar] [CrossRef]
- Hill, R. A Theory of yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar]
- Marciniak, Z.; Duncan, J.L. The Mechanics of Sheet Metal Forming, 1st ed.; Edward Arnold: Auckland, New Zealand, 1992; pp. 100–113. [Google Scholar]
- Martins, P.A.F.; Barata Marques, M.J.M. Plane strain rigid plastic finite element formulation for sheet metal forming processes. J. Eng. Manuf. 1993, 207, 167–171. [Google Scholar] [CrossRef]
- Martins, P.A.F.; Bay, N.; Tekkaya, A.E.; Atkins, A.G. Characterization of fracture loci in metal forming. Int. J. Mech. Sci. 2014, 83, 112–123. [Google Scholar] [CrossRef]


| Current (A) | Voltage (V) | Wire Feed Speed (m/min) | Travel Speed (m/min) | Stick-Out Length (mm) | Gas Flow Rate (L/min) | Bead Height (mm) |
|---|---|---|---|---|---|---|
| 100 | 16.5 | 6 | 0.6 | 10 | 10 | 1.8 |
| Material | Direction | Yield Stress (MPa) | Elongation at Break (%) | Anisotropy Coefficient |
|---|---|---|---|---|
| Additively deposited | P | 395.6 ± 5.0 | 23.7 ± 5.1 | 0.81 |
| I | 410.2 ± 5.5 | 54.5 ± 10.1 | 0.02 | |
| T | 392.5 ± 4.5 | 41.4 ± 9.8 | 3.35 | |
| Wrought commercial | P | 320.7 ± 4.4 | 64.9 ± 3.3 | 0.94 |
| I | 313.5 ± 3.1 | 63.6 ± 3.5 | 0.97 | |
| T | 310.5 ± 3.8 | 61.2 ± 4.1 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cristino, V.A.M.; Pragana, J.P.M.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. Hybrid Manufacturing of Stiffening Grooves in Additive Deposited Thin Parts. J. Manuf. Mater. Process. 2021, 5, 140. https://doi.org/10.3390/jmmp5040140
Cristino VAM, Pragana JPM, Bragança IMF, Silva CMA, Martins PAF. Hybrid Manufacturing of Stiffening Grooves in Additive Deposited Thin Parts. Journal of Manufacturing and Materials Processing. 2021; 5(4):140. https://doi.org/10.3390/jmmp5040140
Chicago/Turabian StyleCristino, Valentino A. M., João P. M. Pragana, Ivo M. F. Bragança, Carlos M. A. Silva, and Paulo A. F. Martins. 2021. "Hybrid Manufacturing of Stiffening Grooves in Additive Deposited Thin Parts" Journal of Manufacturing and Materials Processing 5, no. 4: 140. https://doi.org/10.3390/jmmp5040140
APA StyleCristino, V. A. M., Pragana, J. P. M., Bragança, I. M. F., Silva, C. M. A., & Martins, P. A. F. (2021). Hybrid Manufacturing of Stiffening Grooves in Additive Deposited Thin Parts. Journal of Manufacturing and Materials Processing, 5(4), 140. https://doi.org/10.3390/jmmp5040140










