Evaluating Temperature Control in Friction Stir Welding for Industrial Applications
Abstract
:1. Introduction
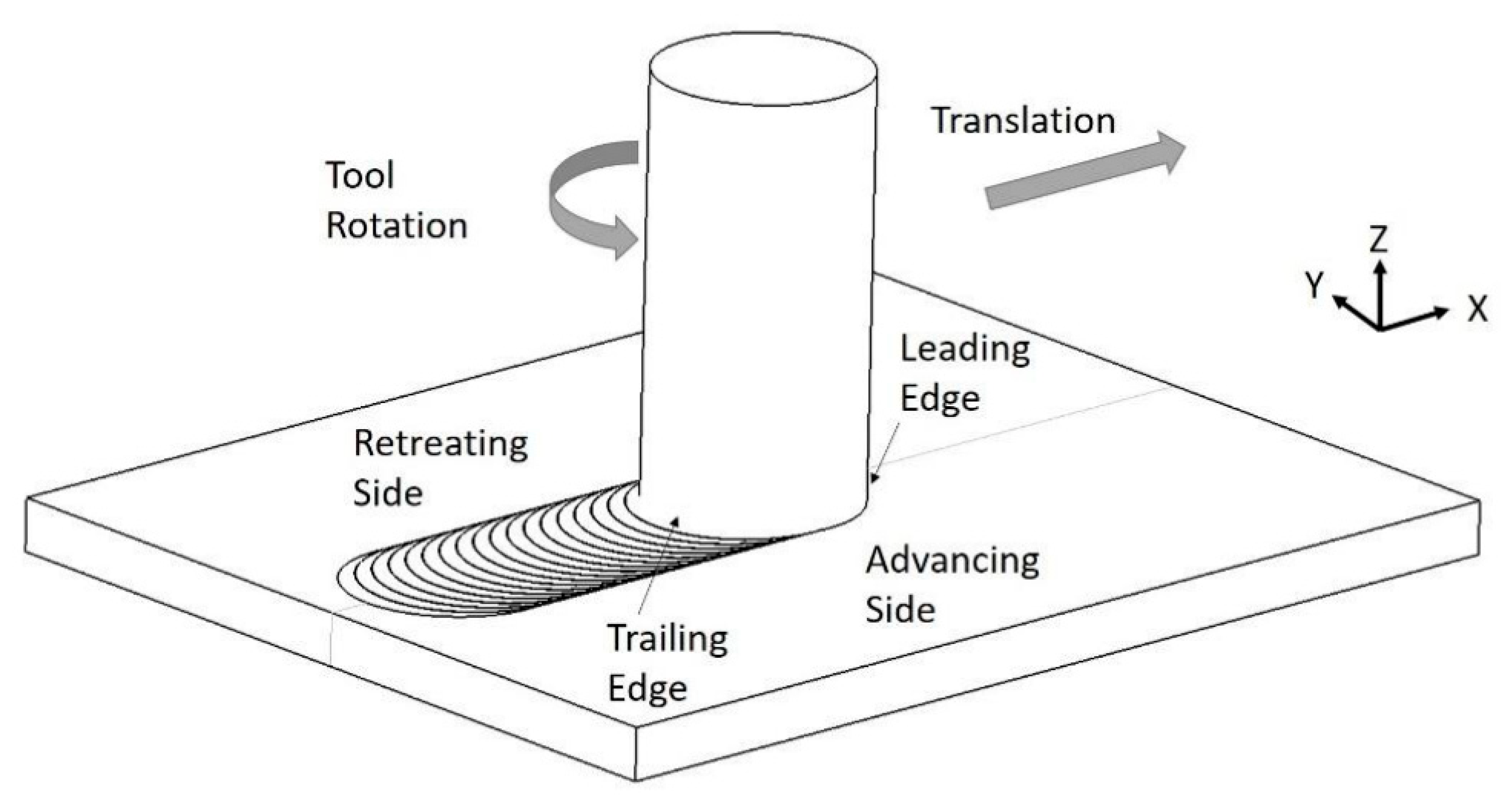
1.1. Friction Stir Welding
1.2. Why Temperature Control?
1.3. History of Temperature Control in FSW
2. Materials and Methods
2.1. Material Properties
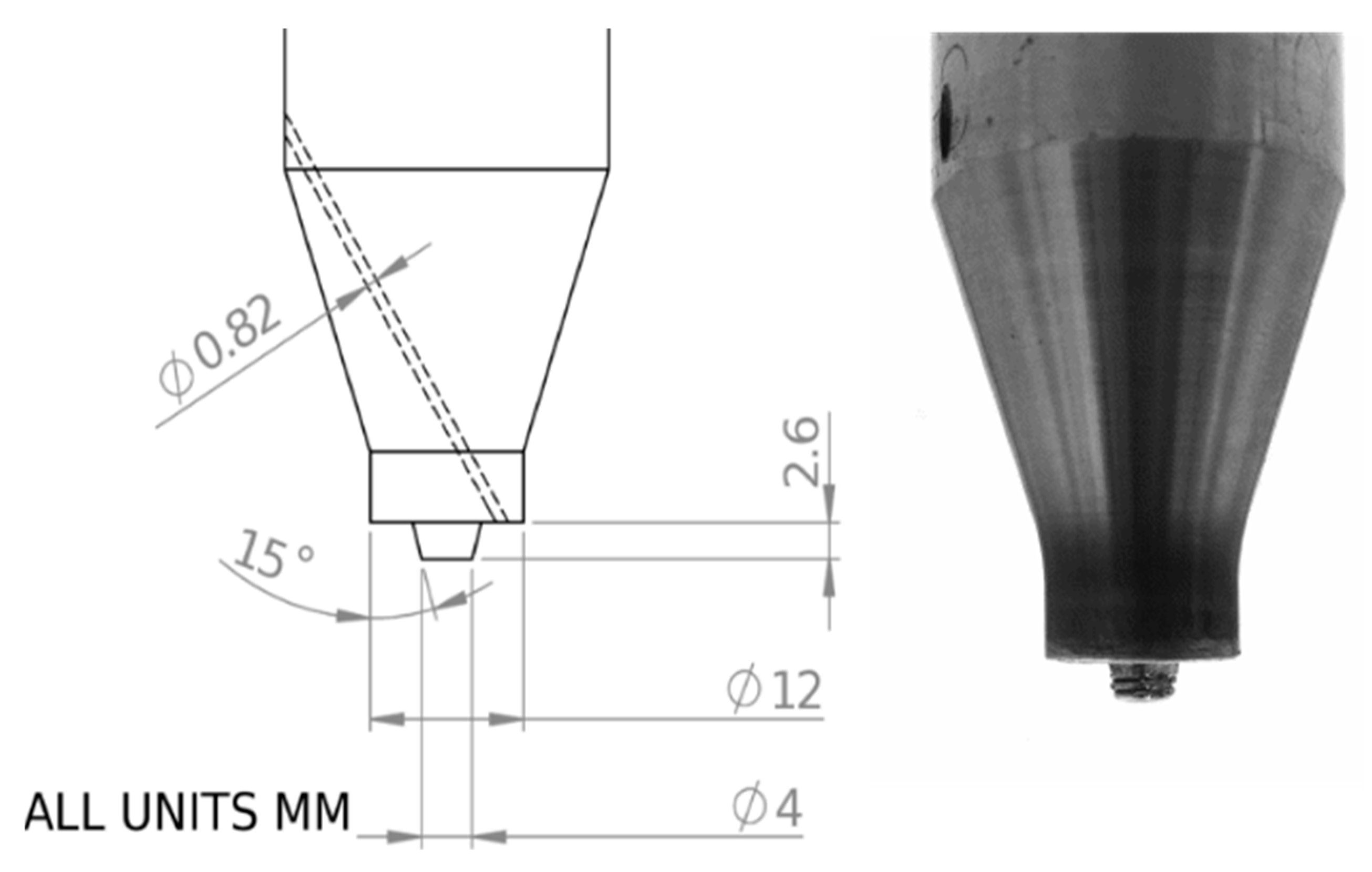
2.2. The Tool
2.3. Temperature Measurement
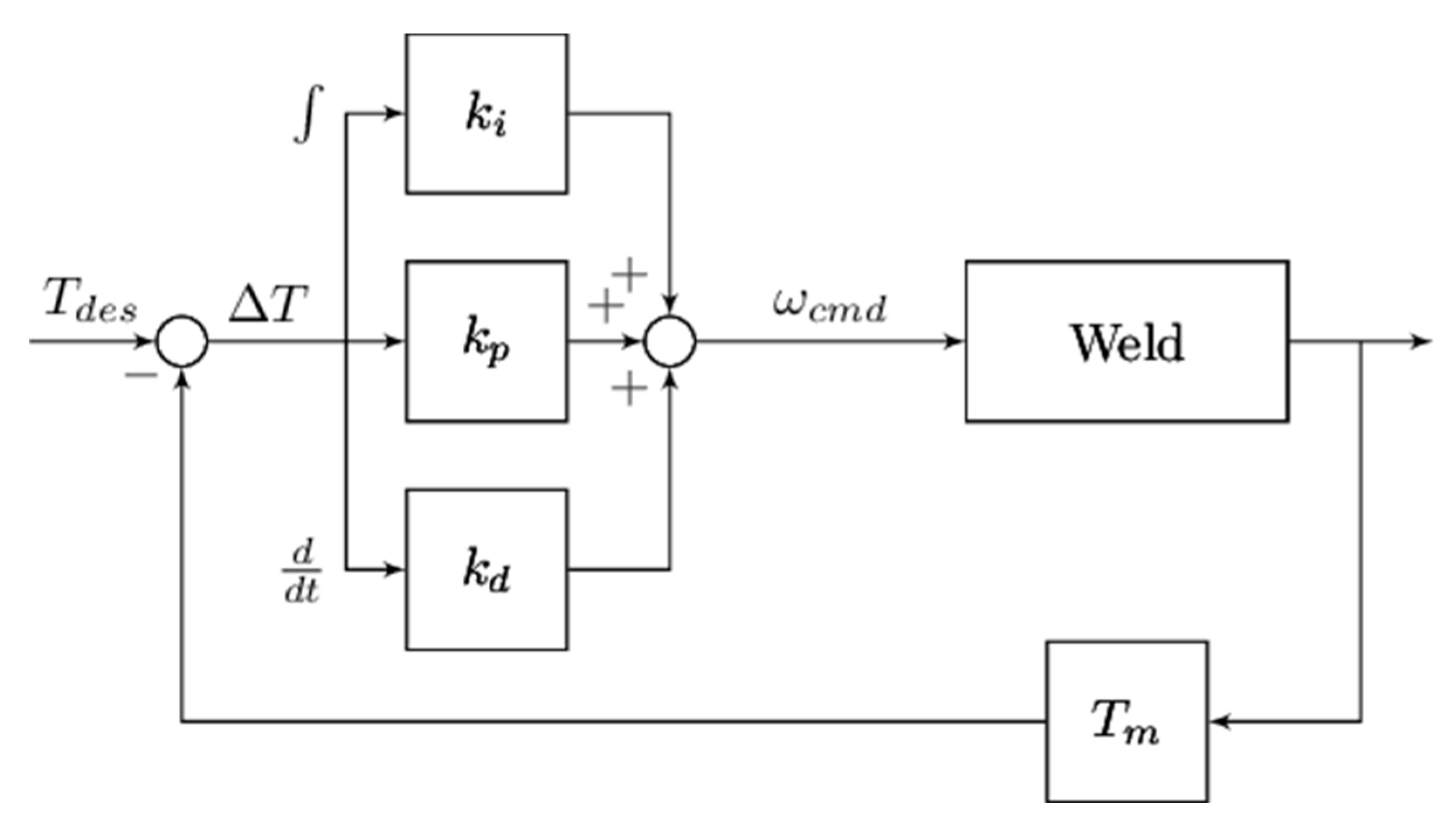
2.4. Temperature Control Method
2.5. Auto-Tuner
2.6. Experimental Design
2.7. Weld Setup
2.8. Tensile Testing
2.9. Fracture Modes
3. Results and Discussion
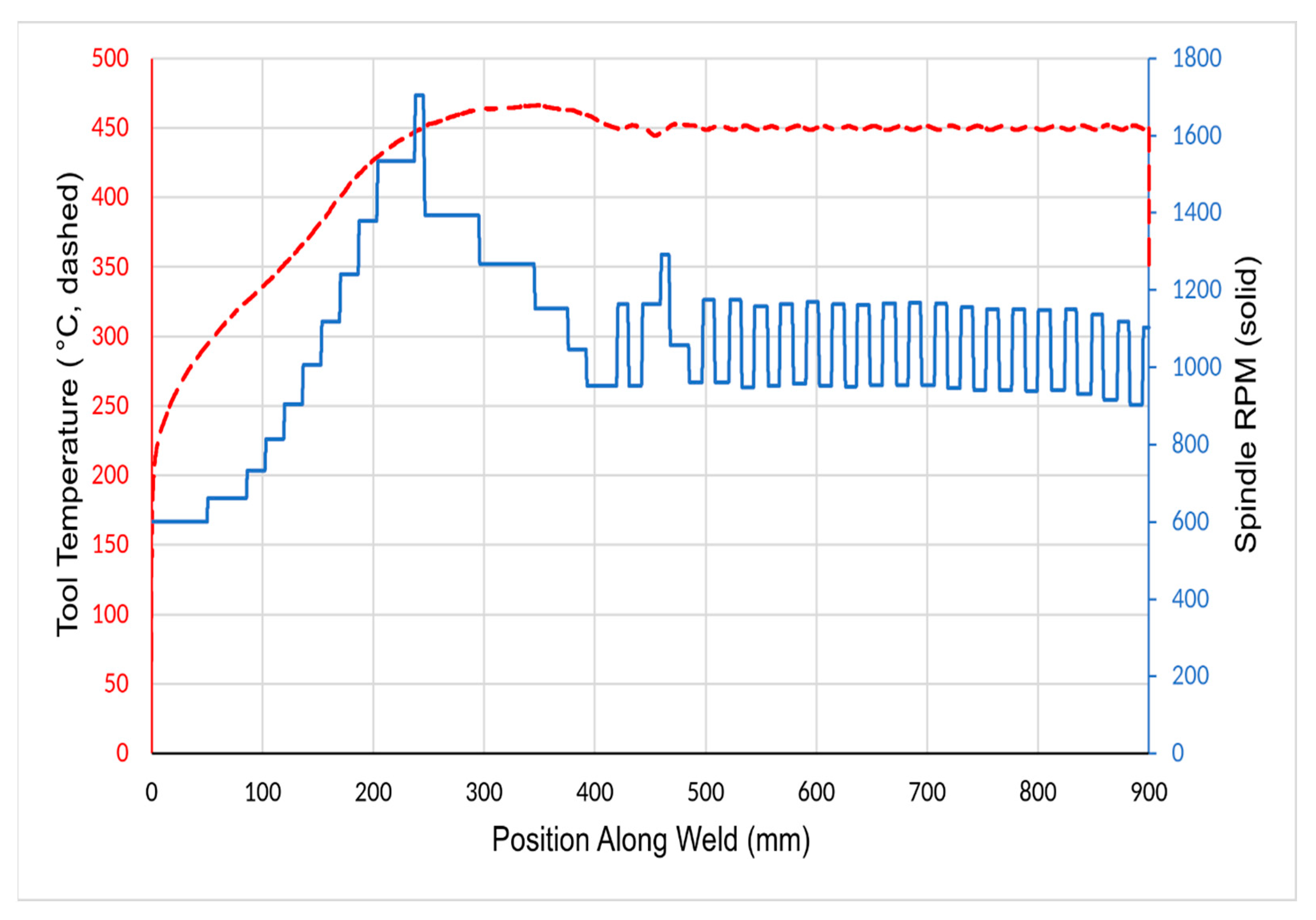
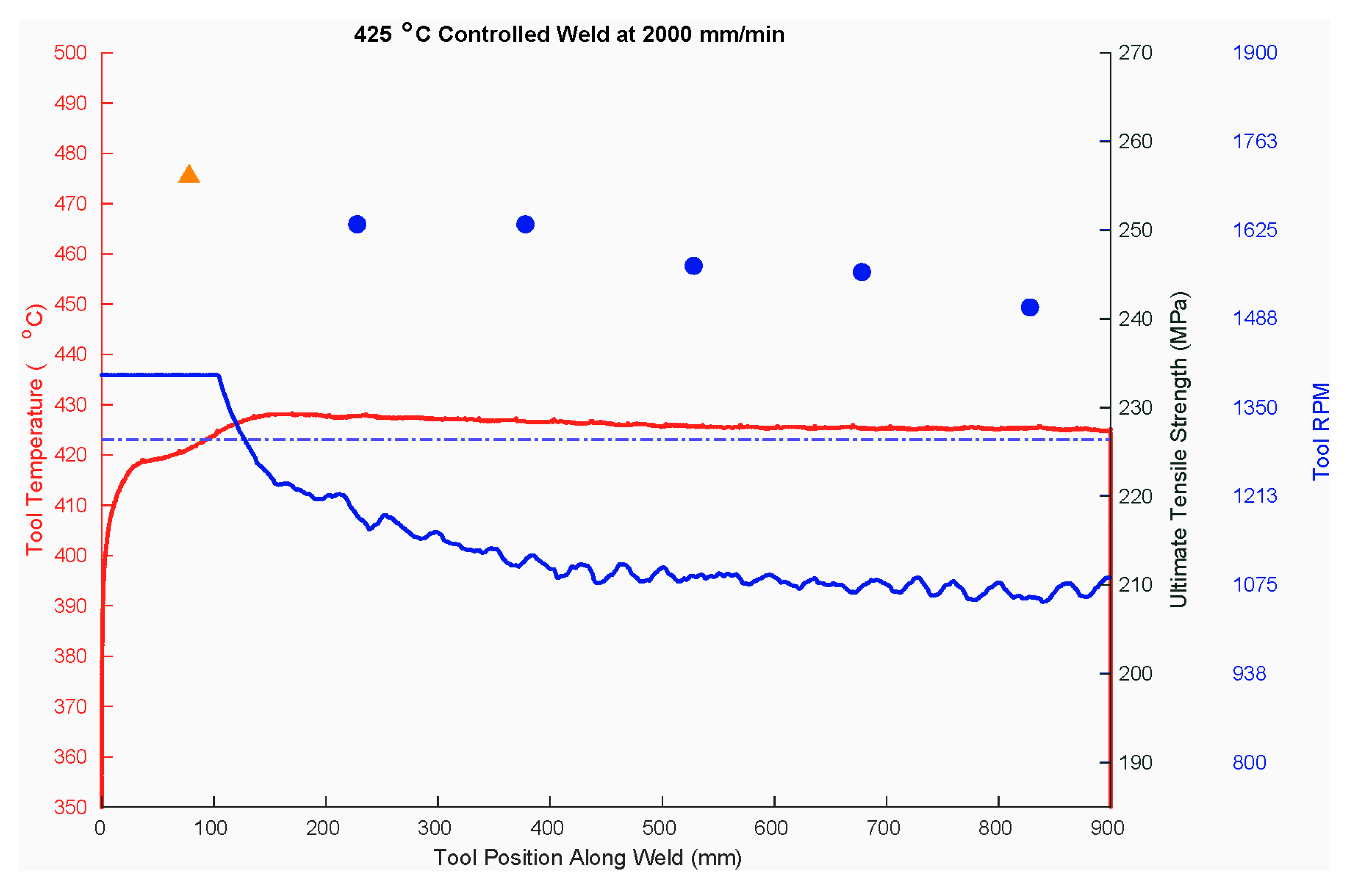
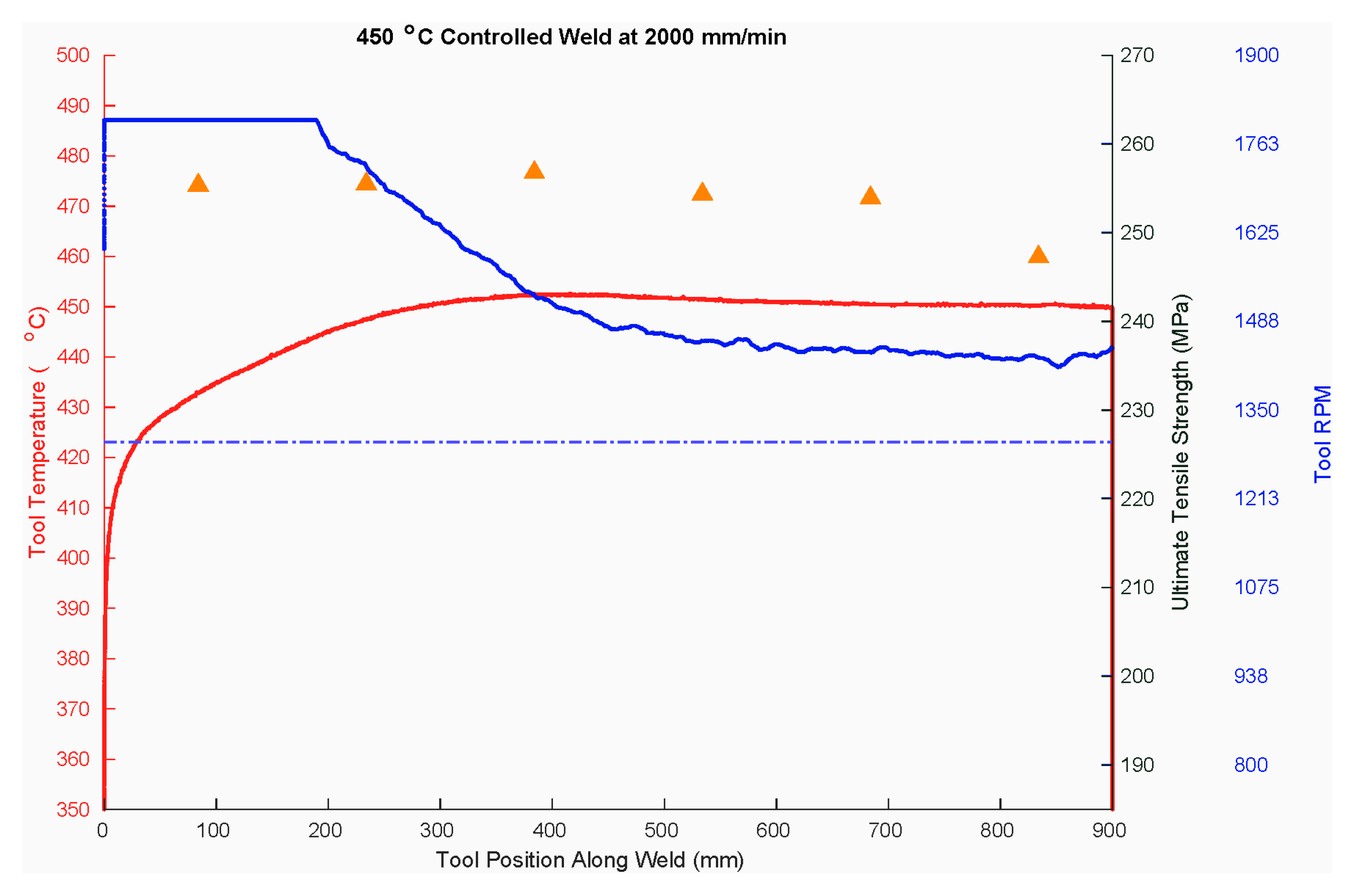
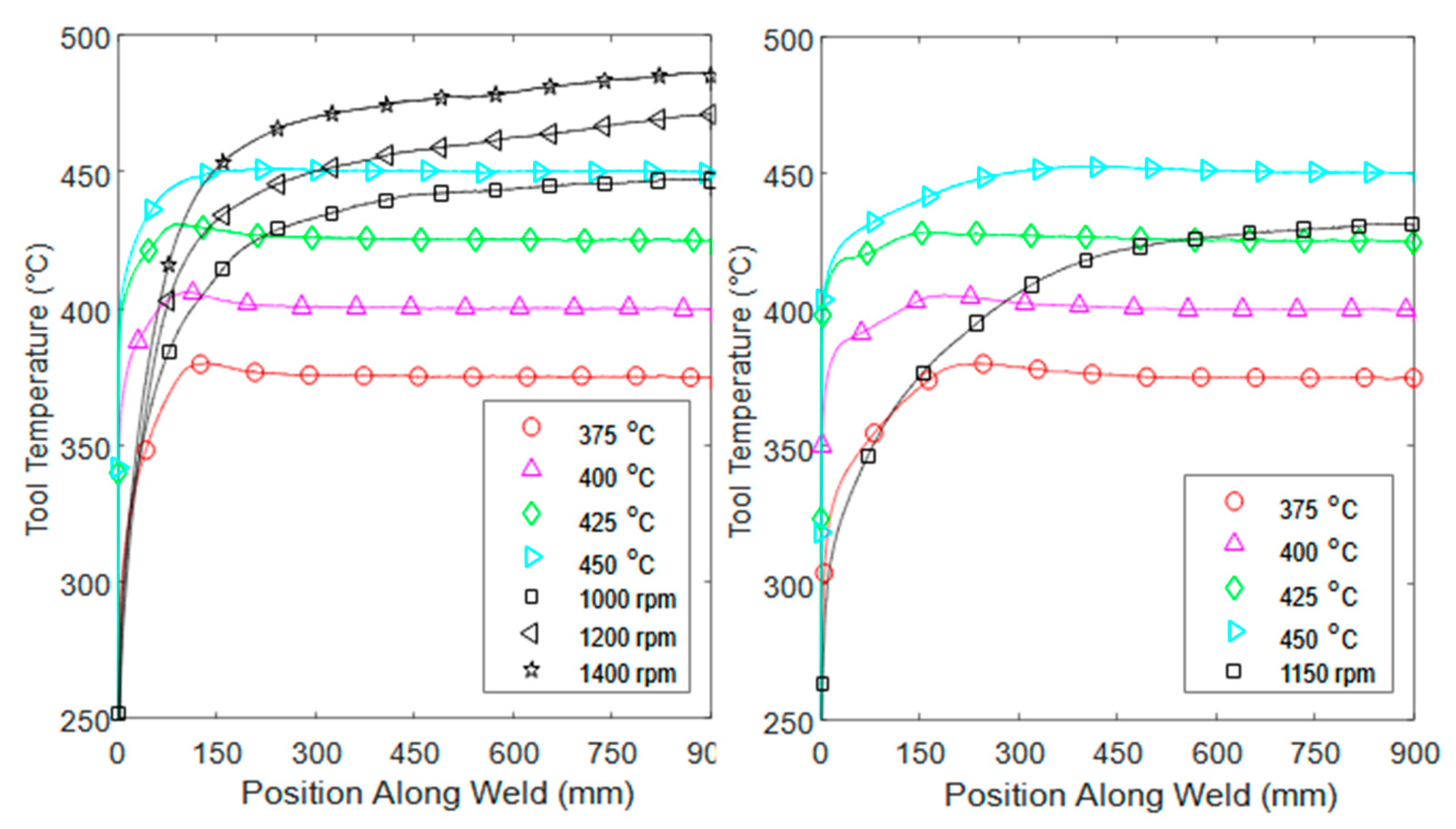
3.1. Temperature Results
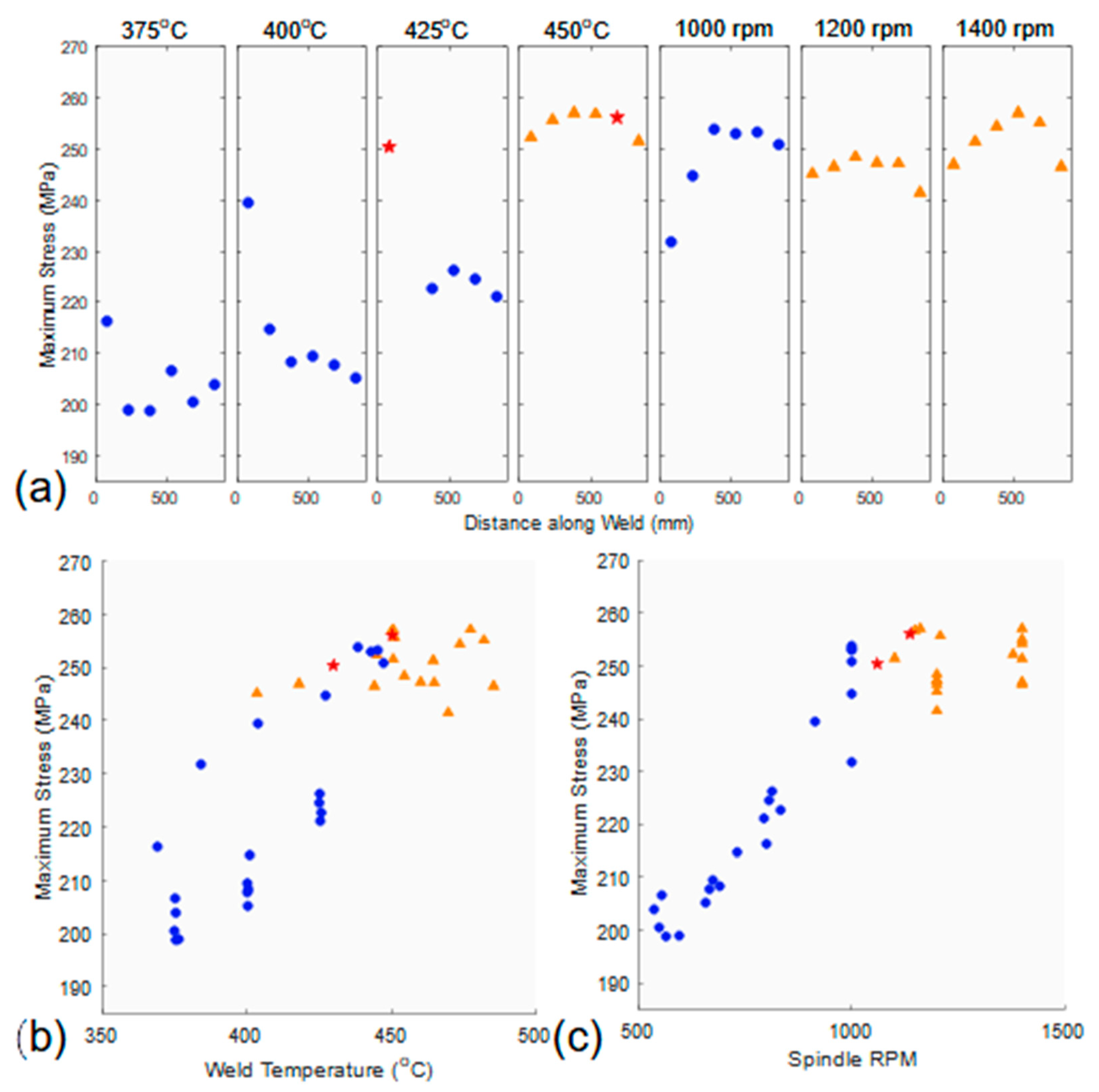
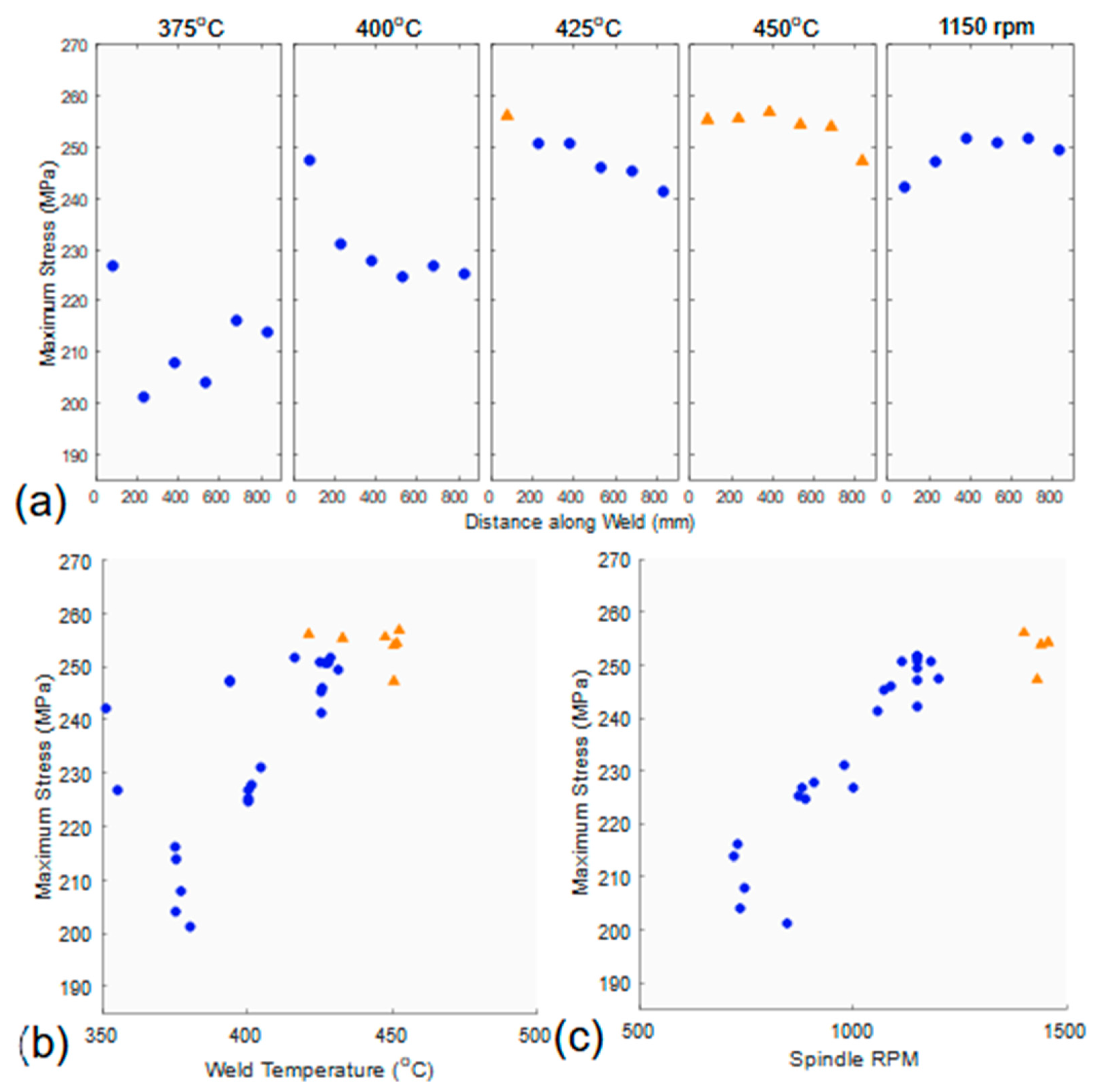
3.2. Weld Strength Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Smith, I.J.; Lord, D.D.R. FSW Patents—A Stirring Story. SAE Trans. 2007, 116, 772–780. [Google Scholar]
- Mishra, R.S.; Mahoney, M.W. Friction Stir Welding and Processing; ASM International: Materials Park, OH, USA, 2007; p. 360. [Google Scholar]
- NASA Marshall Space Flight Center (MSFC). Space Shuttle Technology Summary—Friction Stir Welding; NASA MSFC: Huntsville, AL, USA, 2001.
- Sanders, D.; Edwards, P.; Grant, G.; Ramulu, M.; Reynolds, A. Superplastically Formed Friction Stir Welded Tailored Aluminum and Titanium Blanks for Aerospace Applications. In Proceedings of the 6th EUROSPF Conference, Carcassonne, France, 3–5 September 2008. [Google Scholar]
- Hoyos, E.; Escobar, S.; De Backer, J.; Martin, J.; Palacio, M. Manufacturing Concept and Prototype for Train Component Using the FSW Process. J. Manuf. Mater. Process. 2021, 5, 19. [Google Scholar] [CrossRef]
- Hovanski, Y.; Upadhyay, P.; Carlson, B.; Szymanski, R.; Luzanski, T.; Marshall, D. FSW of Aluminum Tailor Welded Blanks Across Machine Platforms. In Friction Stir Welding and Processing VIII; Springer International Publishing: Cham, Switzerland, 2015; pp. 99–105. [Google Scholar]
- Bachmann, A.; Gamper, J.; Krutzlinger, M.; Zens, A.; Zaeh, M.F. Adaptive model-based temperature control in friction stir welding. Int. J. Adv. Manuf. Technol. 2017, 93, 1157–1171. [Google Scholar] [CrossRef]
- Cederqvist, L.; Garpinger, O.; Hagglund, T.; Robertsson, A. Cascaded control of power input and welding temperature during sealing of spent nuclear fuel canisters. In Proceedings of the ASME Dynamic Systems and Control Conference (DSCC), Cambridge, MA, USA, 12–15 September 2010; pp. 453–460. [Google Scholar]
- Silva-Magalhães, A.; Cederqvist, L.; De Backer, J.; Håkansson, E.; Ossiansson, B.; Bolmsjö, G. A Friction Stir Welding case study using Temperature Controlled Robotics with a HPDC Cylinder Block and dissimilar materials joining. J. Manuf. Process. 2019, 46, 177–184. [Google Scholar] [CrossRef]
- Busu, N.A.; Jaffarullah, M.S.; Low, C.Y.; Shaari, M.S.B.; Armansyah; Jaffar, A. A Review of Force Control Techniques in Friction Stir Process. Procedia Comput. Sci. 2015, 76, 528–533. [Google Scholar] [CrossRef] [Green Version]
- Cederqvist, L.; Johansson, R.; Robertsson, A.; Bolmsjo, G. Faster temperature response and repeatable power input to aid automatic control of friction stir welded copper canisters. In Proceedings of the Friction Stir Welding and Processing V—TMS Annual Meeting & Exhibition, San Francisco, CA, USA, 15–19 February 2009; pp. 39–43. [Google Scholar]
- Cederqvist, L.; Reynolds, A.P.; Sorensen, C.D.; Garpinger, O. Reliable FSW of Copper Canisters Using Improved Process and Regulator Controlling Power Input and Tool Temperature. In Proceedings of the 8th International Symposium on Friction Stir Welding, Timmendorfer Strand, Germany, 18–20 May 2010; pp. 934–943. [Google Scholar]
- Fehrenbacher, A.; Duffie, N.A.; Ferrier, N.J.; Zinn, M.R.; Pfefferkorn, F.E. Temperature Measurement and Closed-loop Control in Friction Stir Welding. In Proceedings of the 8th International Symposium on Friction Stir Welding, Timmendorfer Strand, Germany, 18–20 May 2010; pp. 943–962. [Google Scholar]
- Wright, A.; Smith, D.; Taysom, B.; Hovanski, Y. Transitioning FSW to a Controlled Production Process; Springer International Publishing: Cham, Switzerland; pp. 91–104.
- Ross, K.; Sorensen, C. Advances in Temperature Control for FSP. In Friction Stir Welding and Processing VII; Mishra, R., Mahoney, M.W., Sato, Y., Hovanski, Y., Verma, R., Eds.; Springer International Publishing: Cham, Switzerland, 2013; pp. 301–310. [Google Scholar]
- Ross, K.A. Investigation and Implementation of a Robust Temperature Control Algorithm for Friction Stir Welding; Brigham Young University: Provo, UT, USA, 2012. [Google Scholar]
- Taysom, B.S.; Sorensen, C.D. Advances in Signal Processing for Friction Stir Welding Temperature Control. In Friction Stir Welding and Processing X; Springer International Publishing: Cham, Switzerland, 2019; pp. 135–147. [Google Scholar]
- Taysom, B.S.; Sorensen, C.D. Adaptive relay autotuning under static and non-static disturbances with application to friction stir welding. ISA Trans. 2020, 97, 474–484. [Google Scholar] [CrossRef] [PubMed]
- Albannai, A. Review The Common Defects In Friction Stir Welding. Int. J. Sci. Technol. Res. 2020, 9, 318–329. [Google Scholar]
- Kaufman, J.G. Properties and Applications of Wrought Aluminum Alloys. In ASM Handbook 2B, Properties and Selection of Aluminum Alloys; Anderson, K., Weritz, J., Kaufman, J.G., Eds.; ASM International: Materials Park, OH, USA, 2019; pp. 202–275. [Google Scholar]
- Anderson, K.; Weritz, J.; Kaufman, J.G. (Eds.) Nominal Compositions and Composition Limits for Wrought Aluminum Alloys. In ASM Handbook 2B, Properties and Selection of Aluminum Alloys; ASM International: Materials Park, OH, USA, 2019; pp. 606–611. [Google Scholar]
- Choi, W.; Morrow, J.D.; Pfefferkorn, F.E.; Zinn, M.R. Welding parameter maps to help select power and energy consumption of friction stir welding. J. Manuf. Process. 2018, 33, 35–42. [Google Scholar] [CrossRef]


| 1000 mmpm Welds | Mean UTS (MPa) | Std. Dev (MPa) |
|---|---|---|
| 375 °C | 204.2 | 6.7 |
| 400 °C | 214.1 | 12.8 |
| 425 °C | 230.1 | 11.2 |
| 450 °C | 254.9 | 2.4 |
| 1000 rpm | 247.9 | 8.6 |
| 1200 rpm | 246.0 | 2.5 |
| 1400 rpm | 251.9 | 4.4 |
| 2000 mmpm welds | Mean UTS (MPa) | Std. Dev (MPa) |
| 375 °C | 211.7 | 9.3 |
| 400 °C | 230.5 | 8.6 |
| 425 °C | 248.3 | 5.2 |
| 450 °C | 253.9 | 3.4 |
| 1150 rpm | 248.8 | 3.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wright, A.; Munro, T.R.; Hovanski, Y. Evaluating Temperature Control in Friction Stir Welding for Industrial Applications. J. Manuf. Mater. Process. 2021, 5, 124. https://doi.org/10.3390/jmmp5040124
Wright A, Munro TR, Hovanski Y. Evaluating Temperature Control in Friction Stir Welding for Industrial Applications. Journal of Manufacturing and Materials Processing. 2021; 5(4):124. https://doi.org/10.3390/jmmp5040124
Chicago/Turabian StyleWright, Arnold, Troy R. Munro, and Yuri Hovanski. 2021. "Evaluating Temperature Control in Friction Stir Welding for Industrial Applications" Journal of Manufacturing and Materials Processing 5, no. 4: 124. https://doi.org/10.3390/jmmp5040124
APA StyleWright, A., Munro, T. R., & Hovanski, Y. (2021). Evaluating Temperature Control in Friction Stir Welding for Industrial Applications. Journal of Manufacturing and Materials Processing, 5(4), 124. https://doi.org/10.3390/jmmp5040124






