Modelling and Analysis of Topographic Surface Properties of Grinding Wheels
Abstract
:1. Introduction to Grinding and Wheel Topography
2. State-of-the-Art
2.1. Grinding Wheel Properties
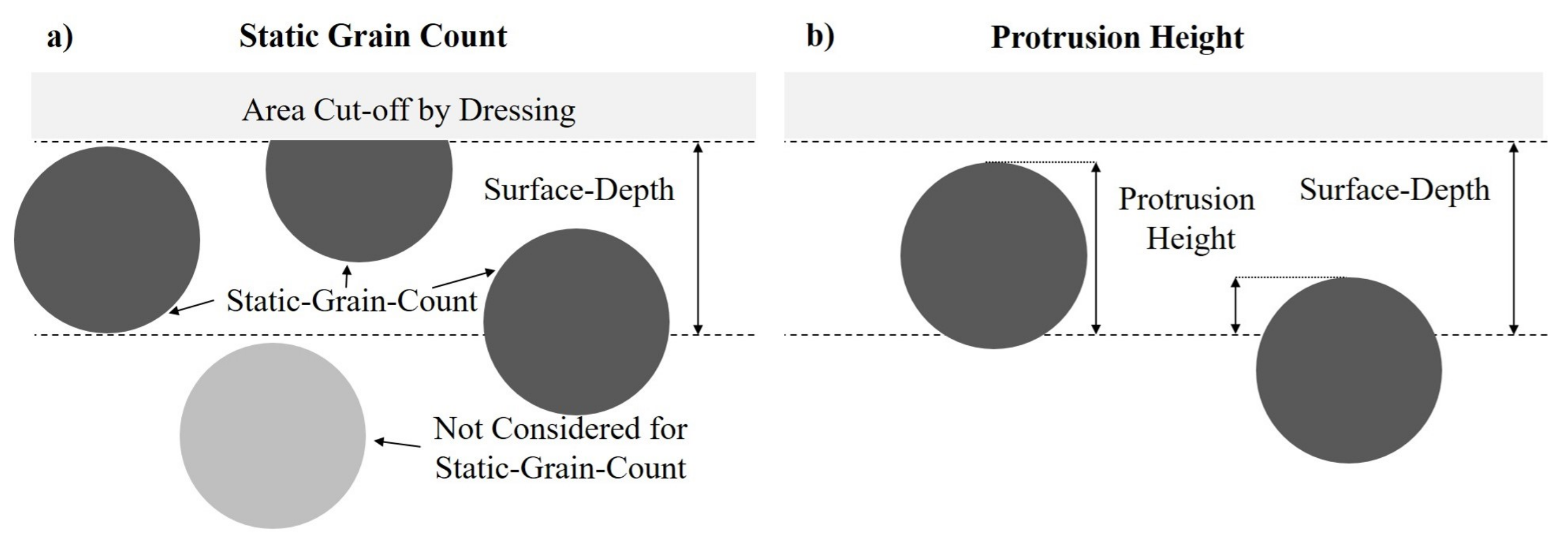
2.2. Grinding Wheel Measures
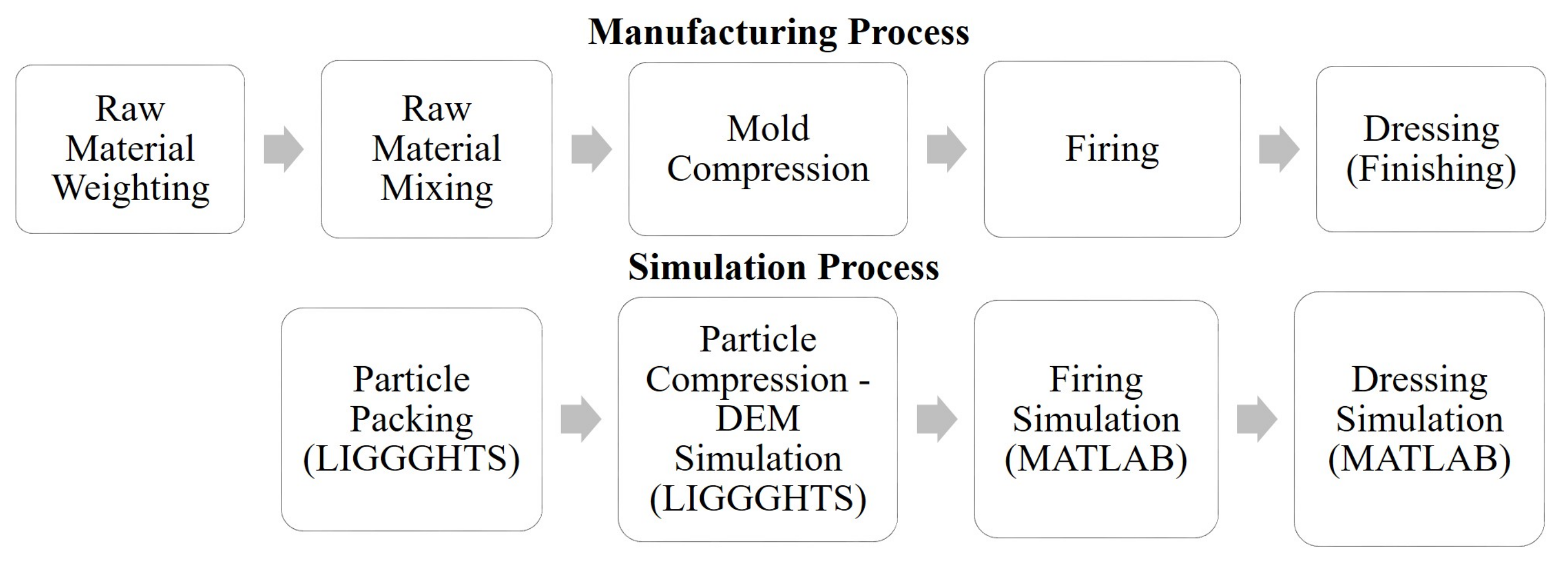
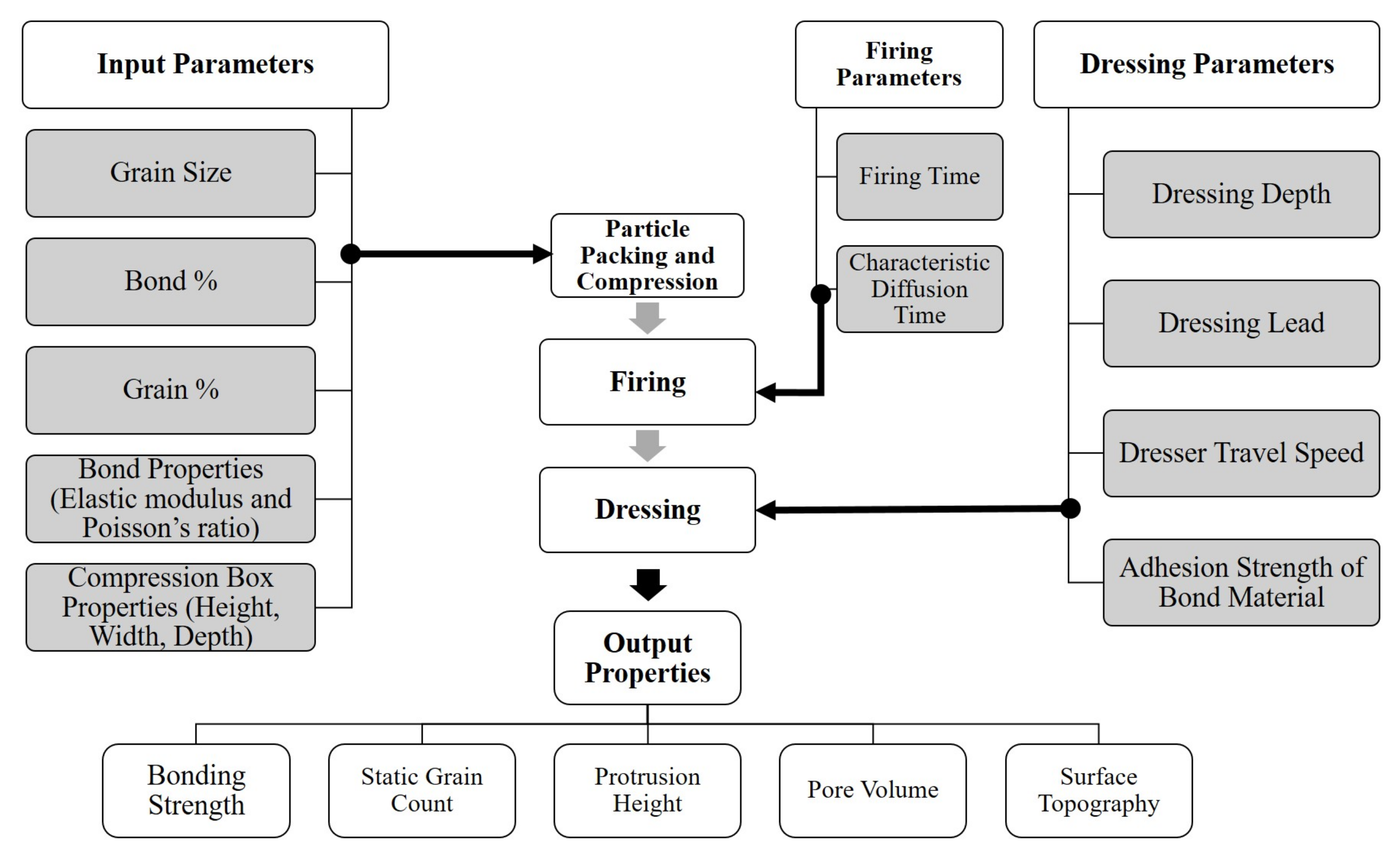
3. Simulation Framework
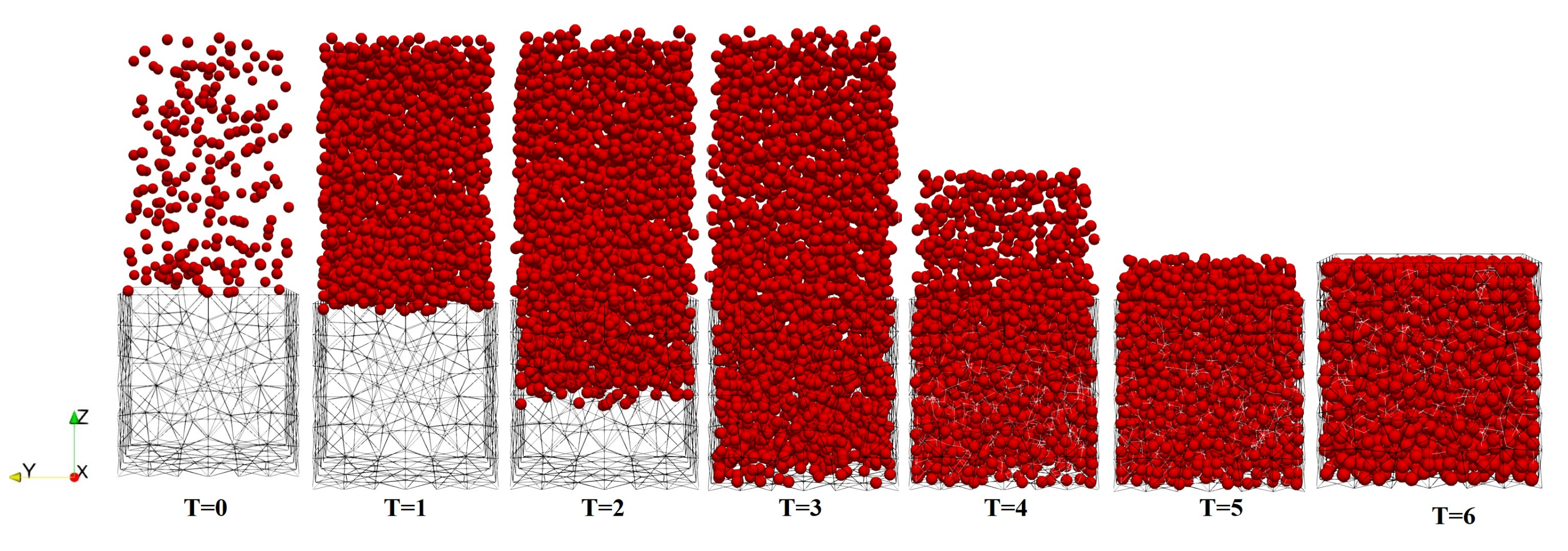
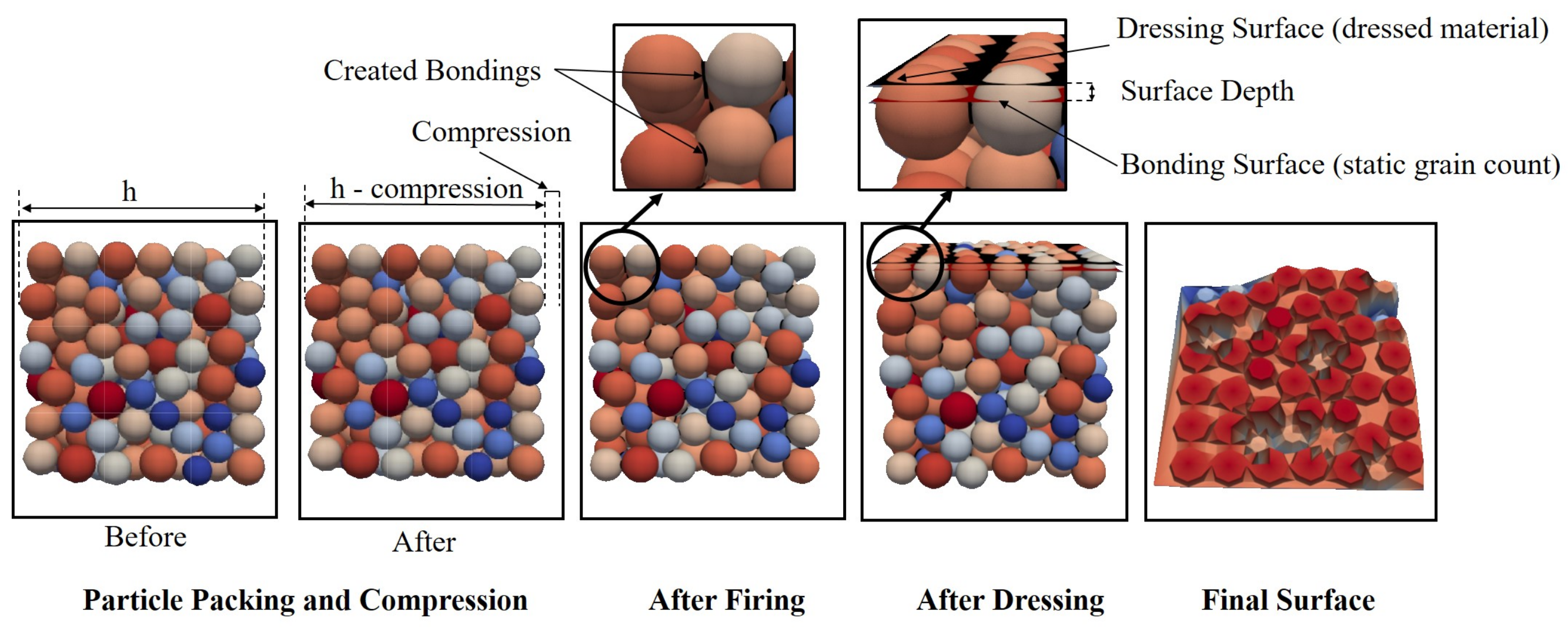
3.1. Particle Mixing and Packing
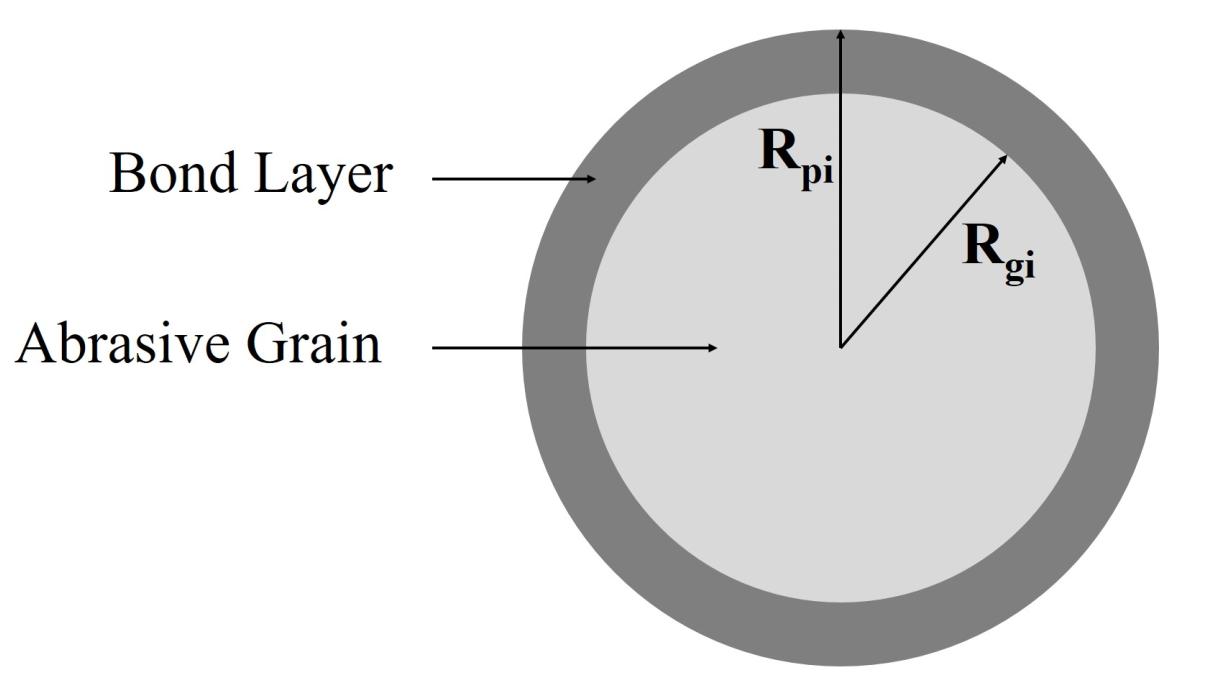
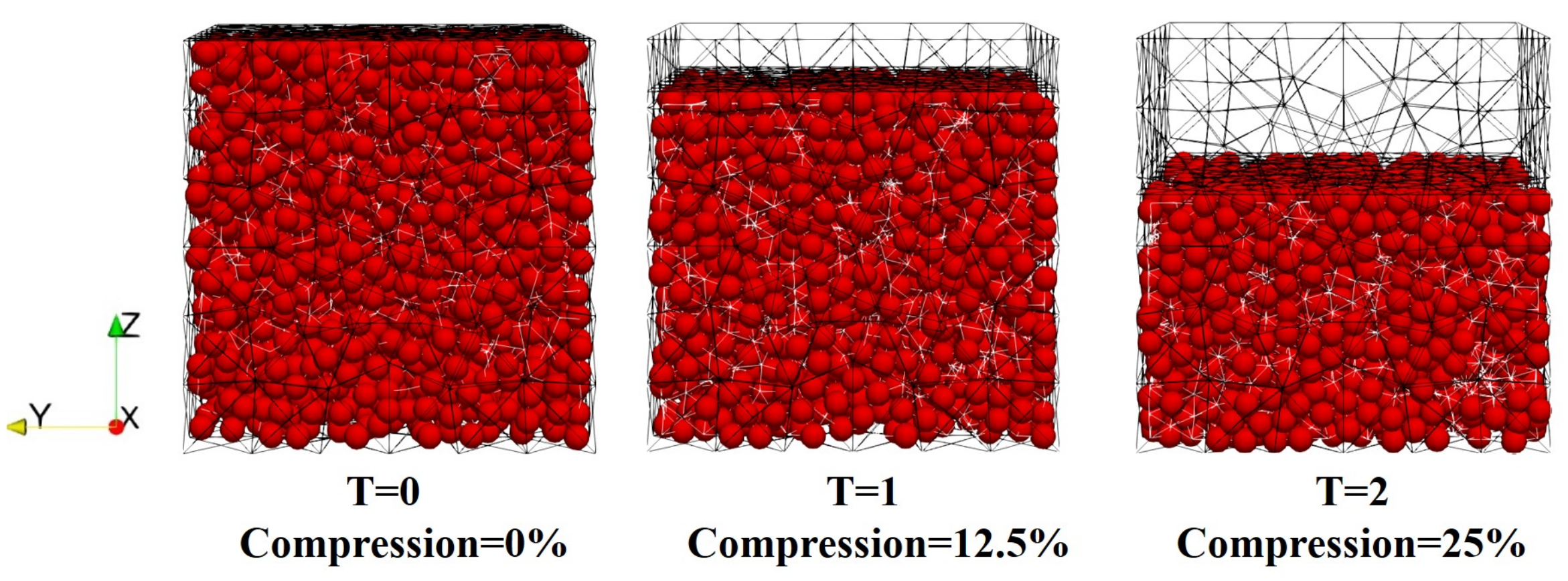
3.2. Particle Compression
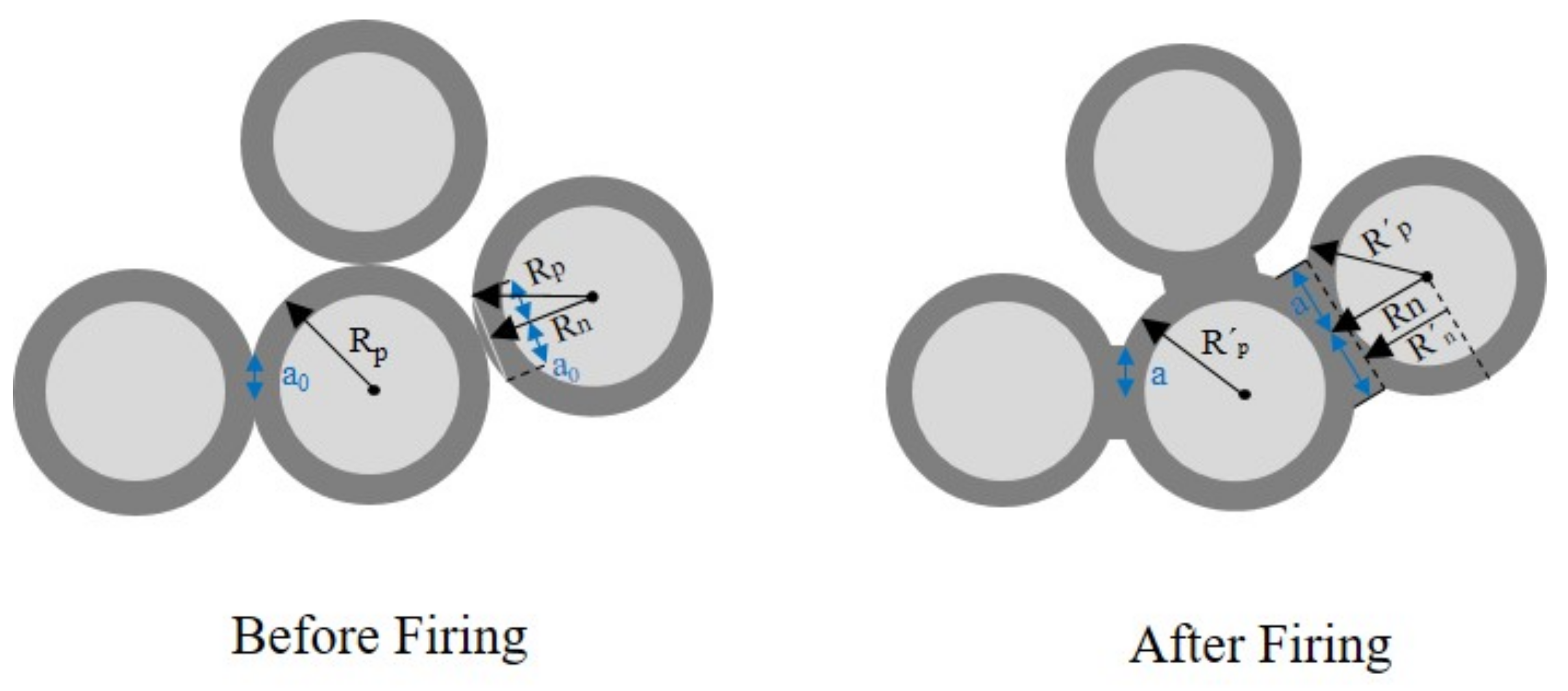
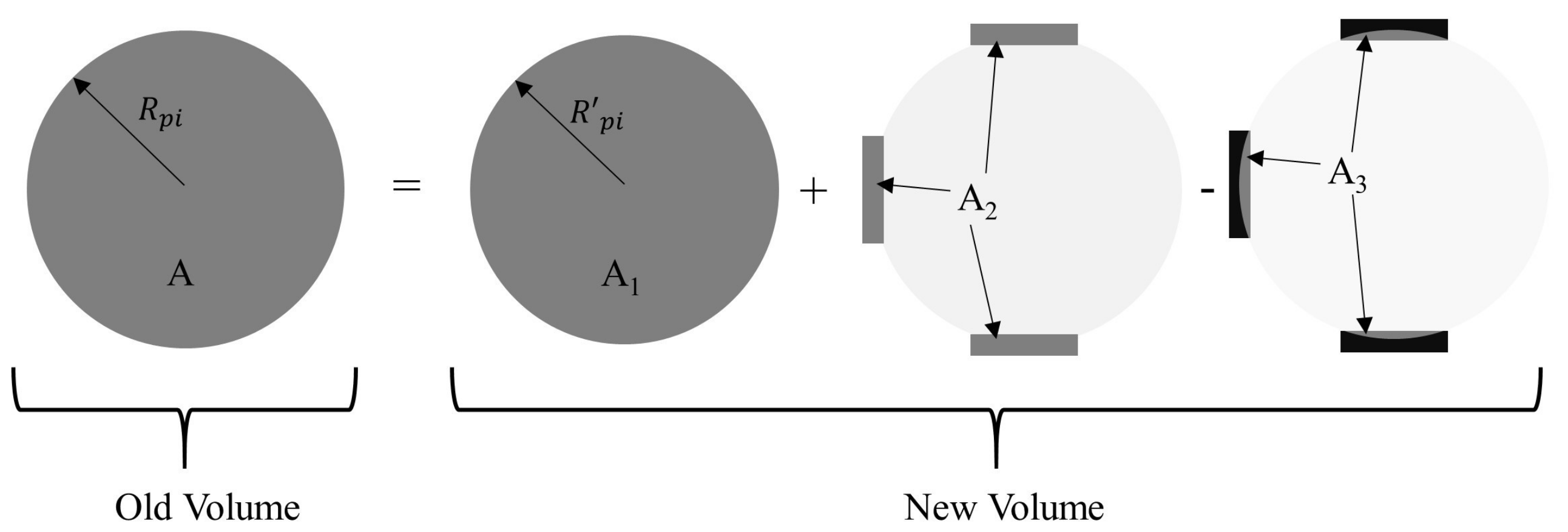
3.3. Firing
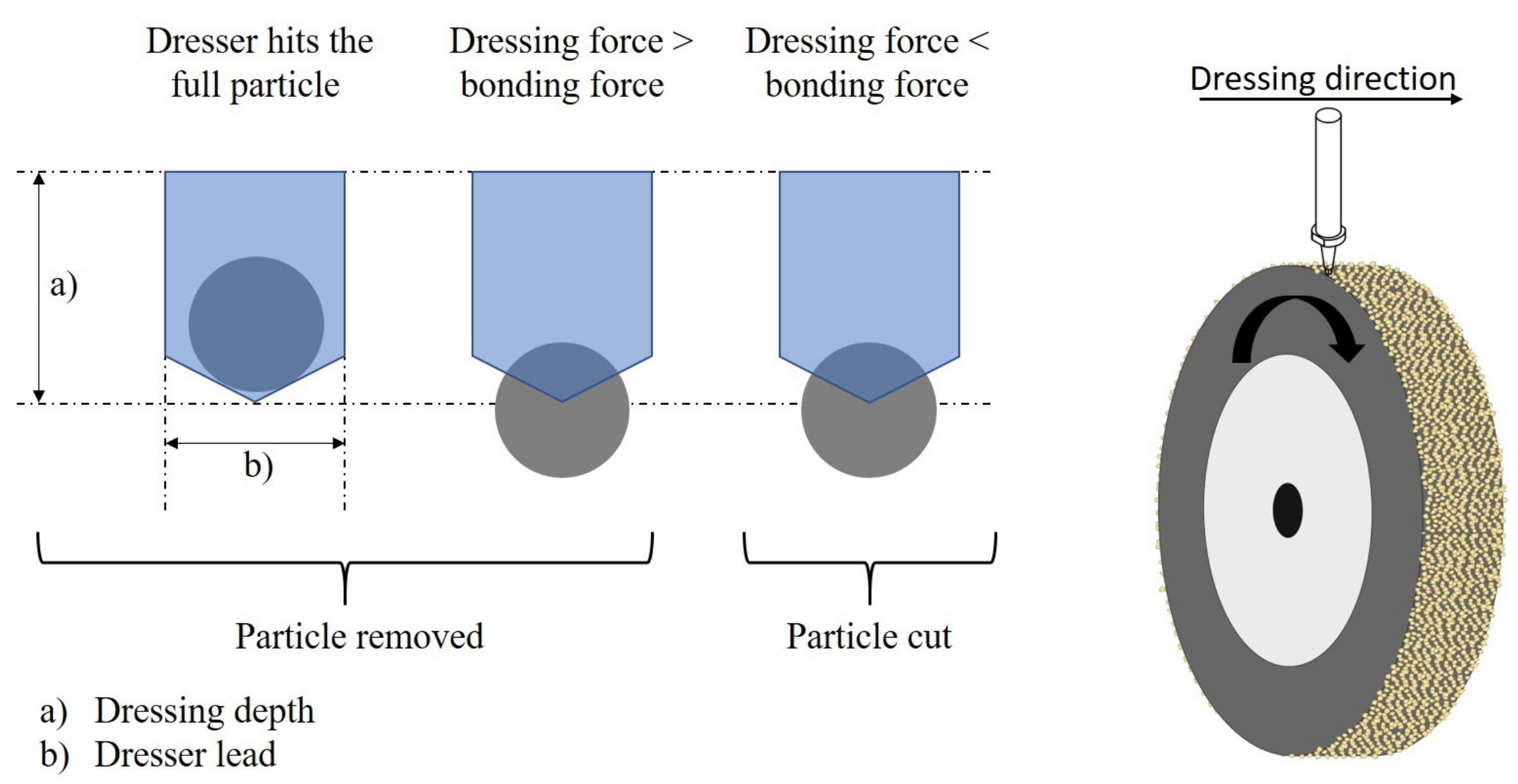
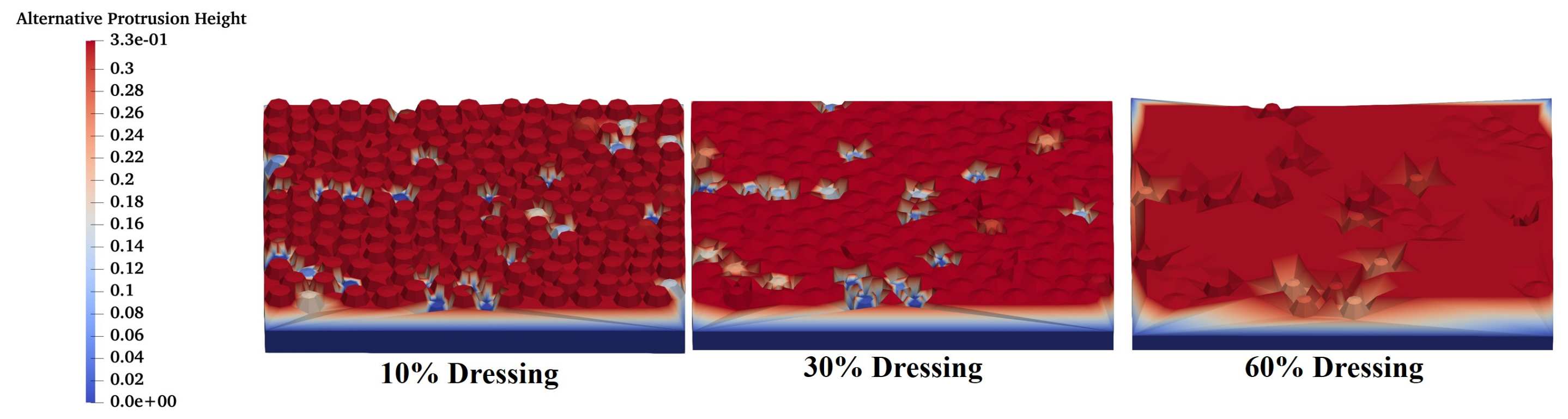
3.4. Dressing
3.5. Calculation of Output Variables
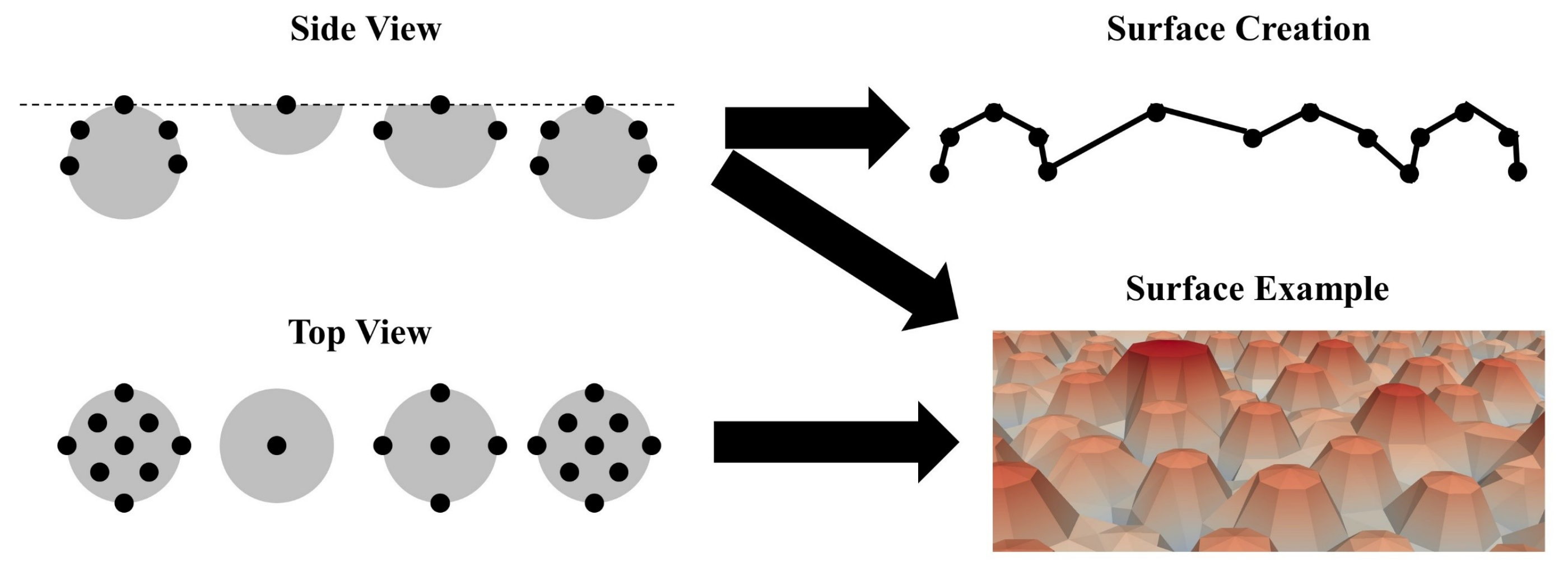
3.6. Surface Calculation and Modelling
4. Results and Discussion
4.1. Analysis of Output Parameters Based on Dressing 10%
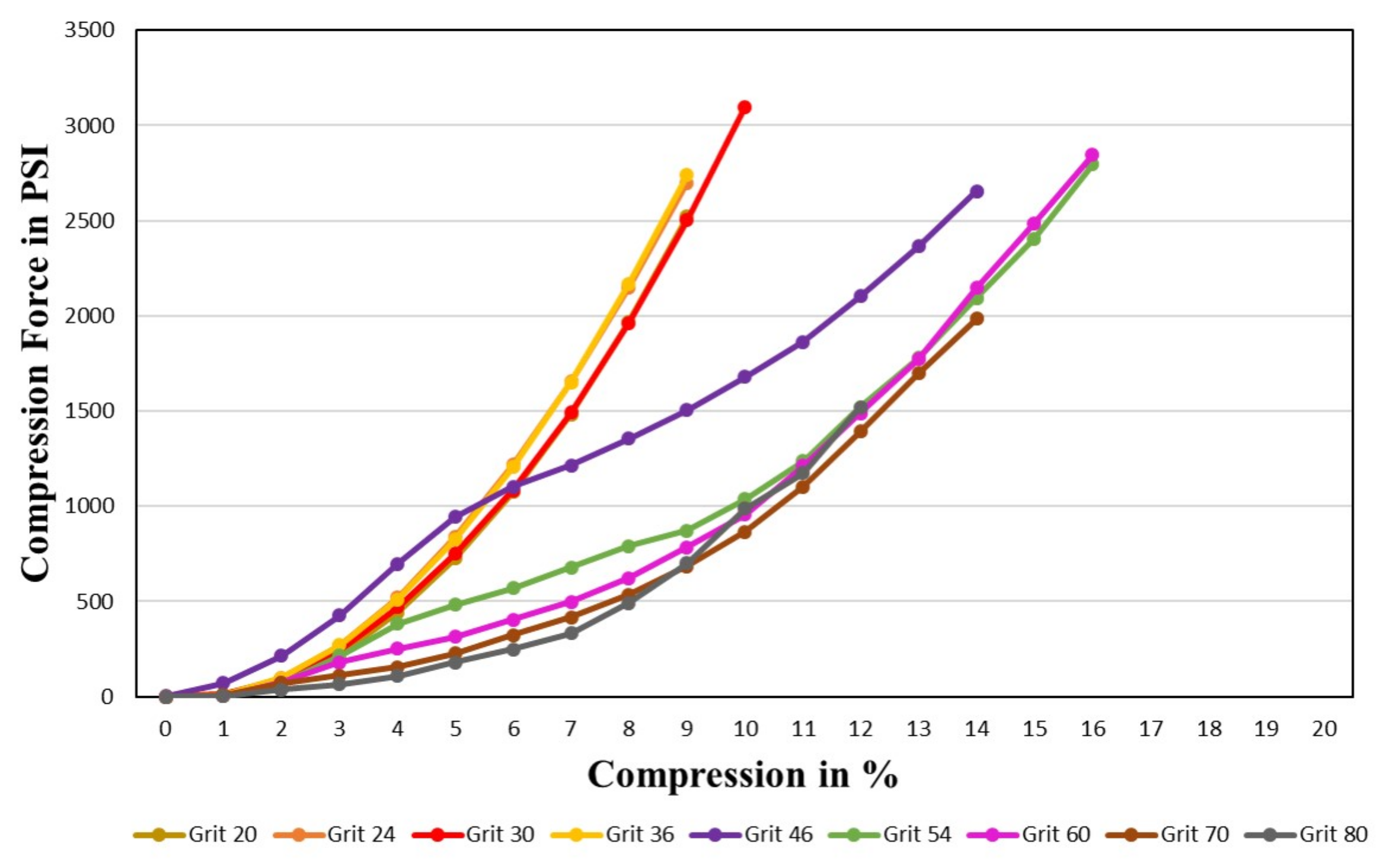
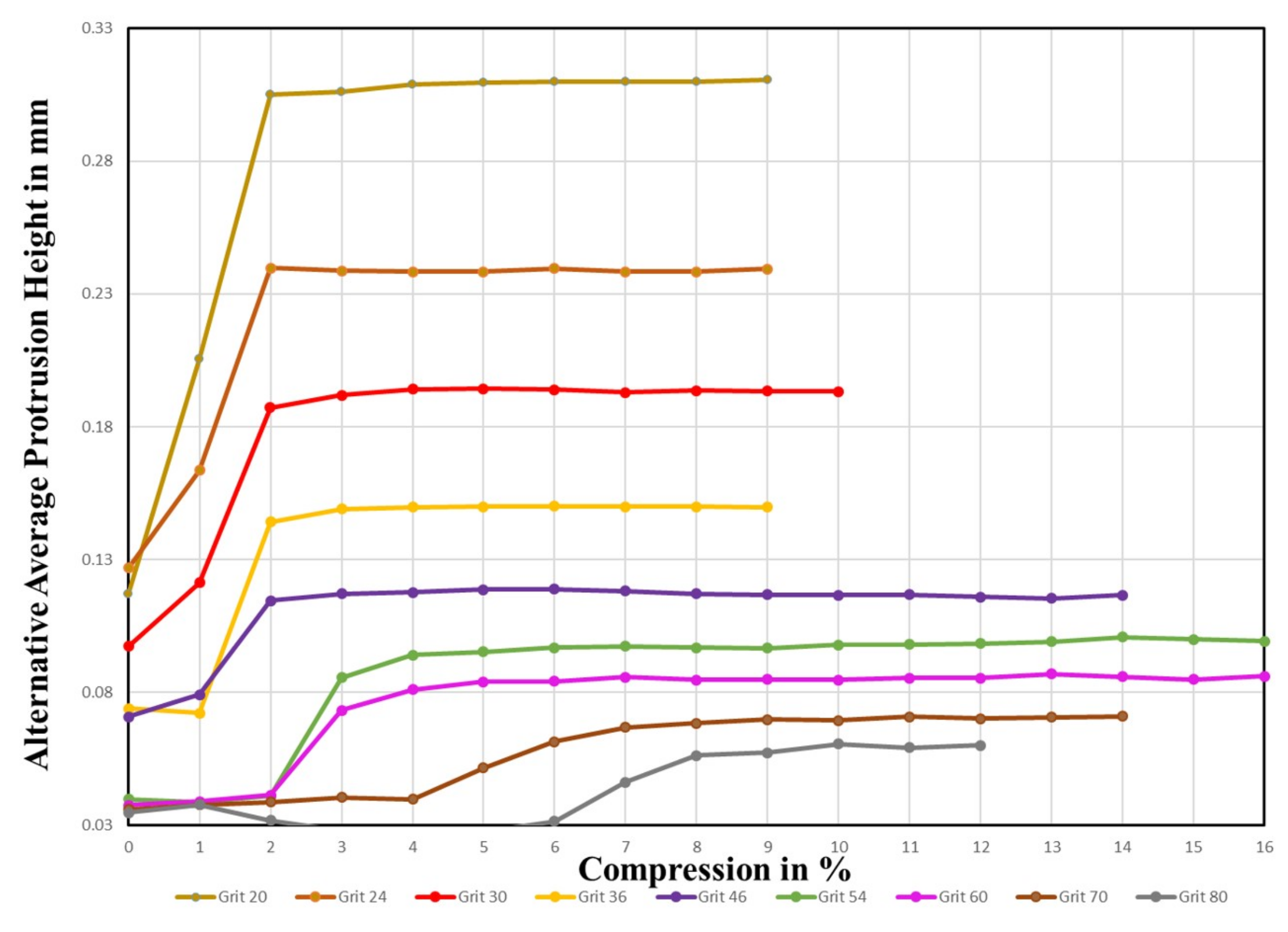
4.1.1. Compression
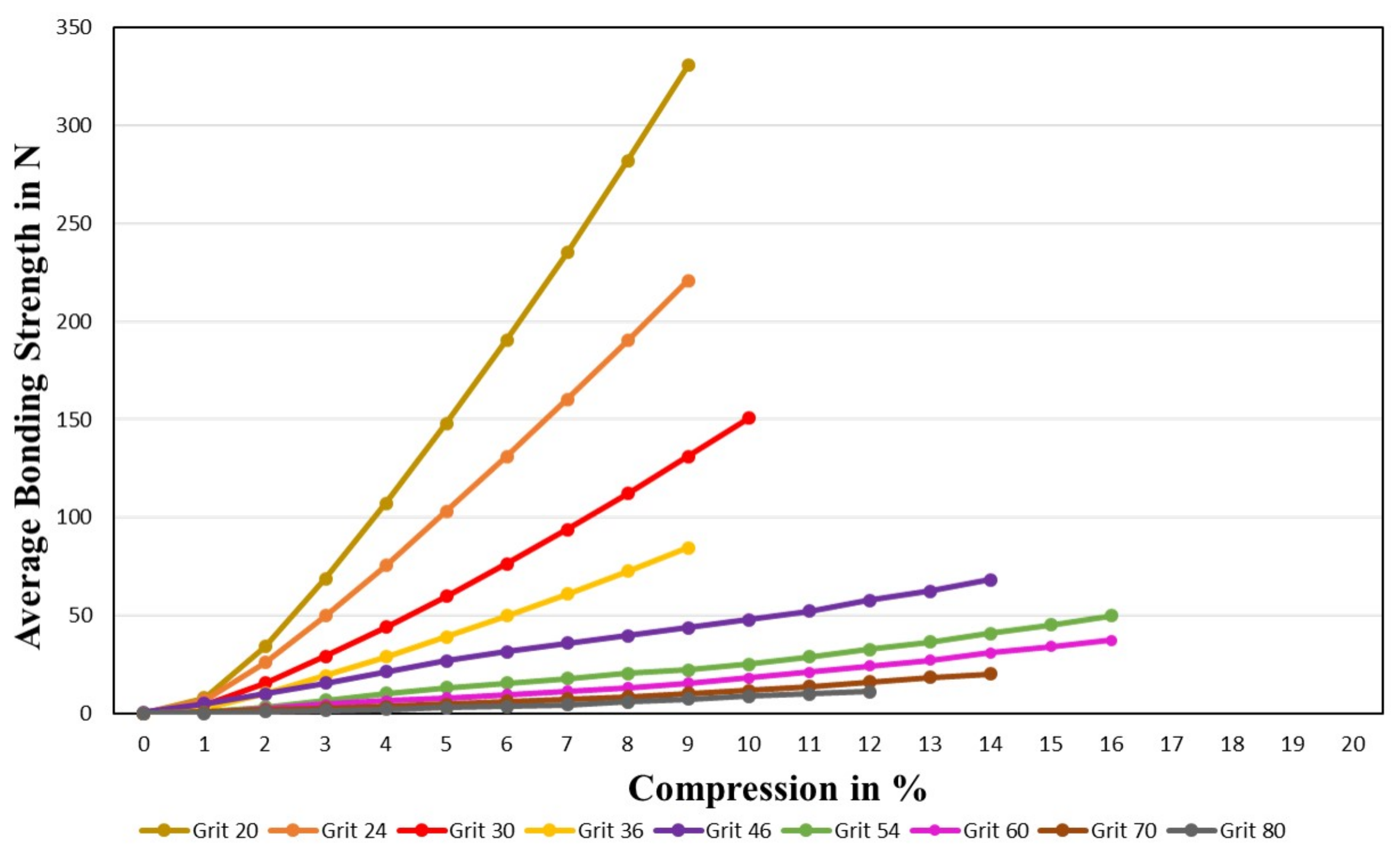
4.1.2. Bonding Strength
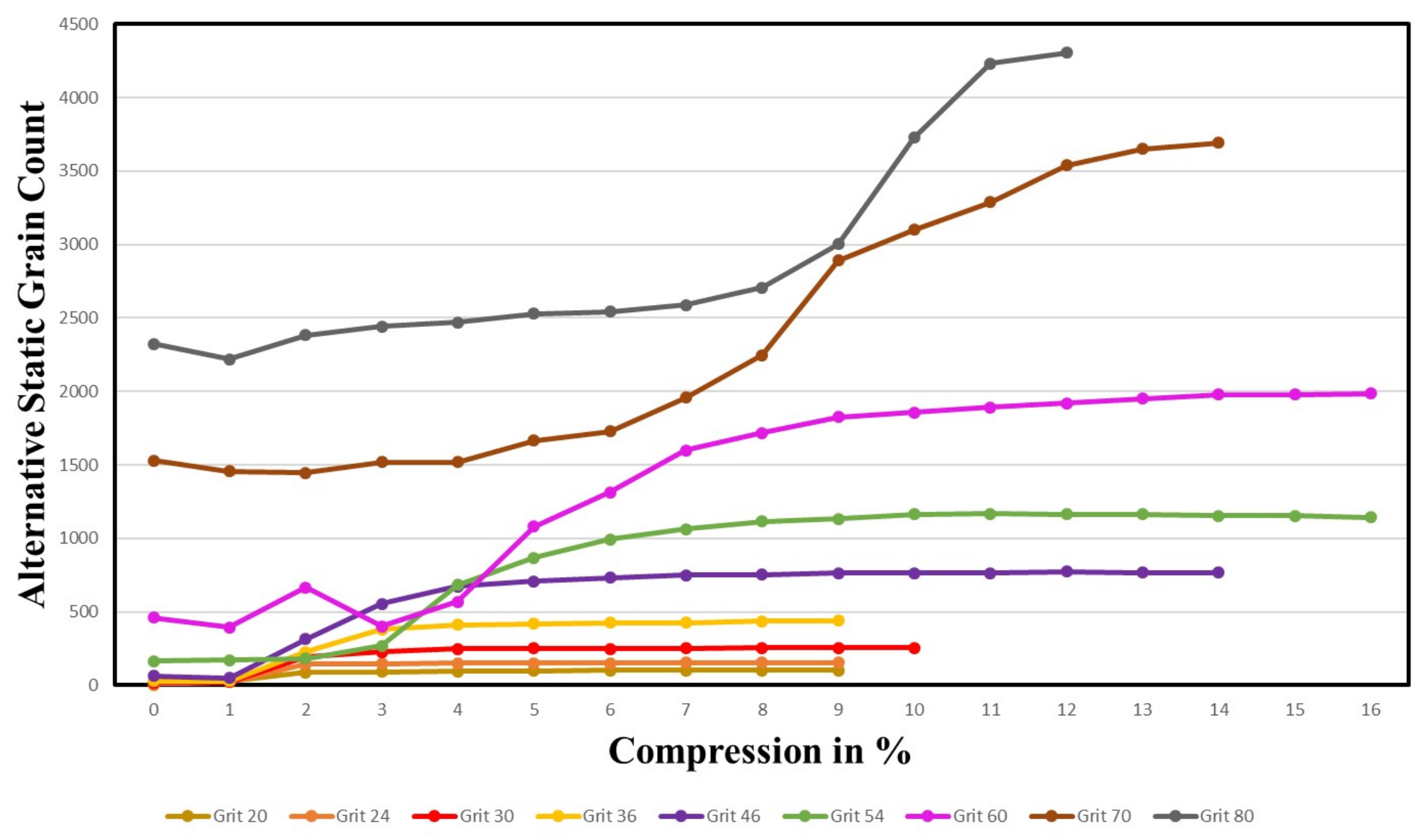
4.1.3. Alternative Static Grain Count
4.1.4. Average Grain Protrusion Height
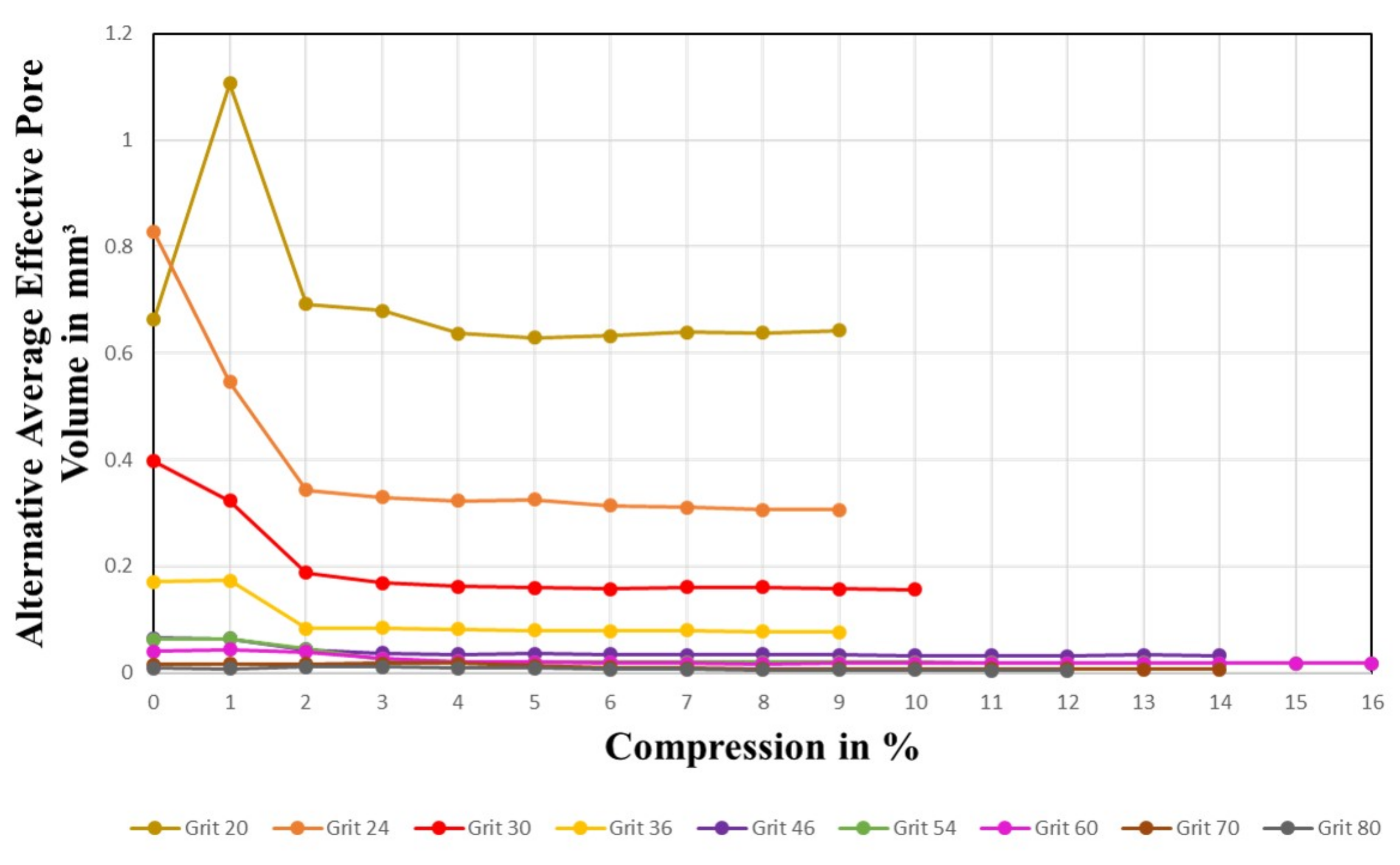
4.1.5. Average Effective Pore Volume
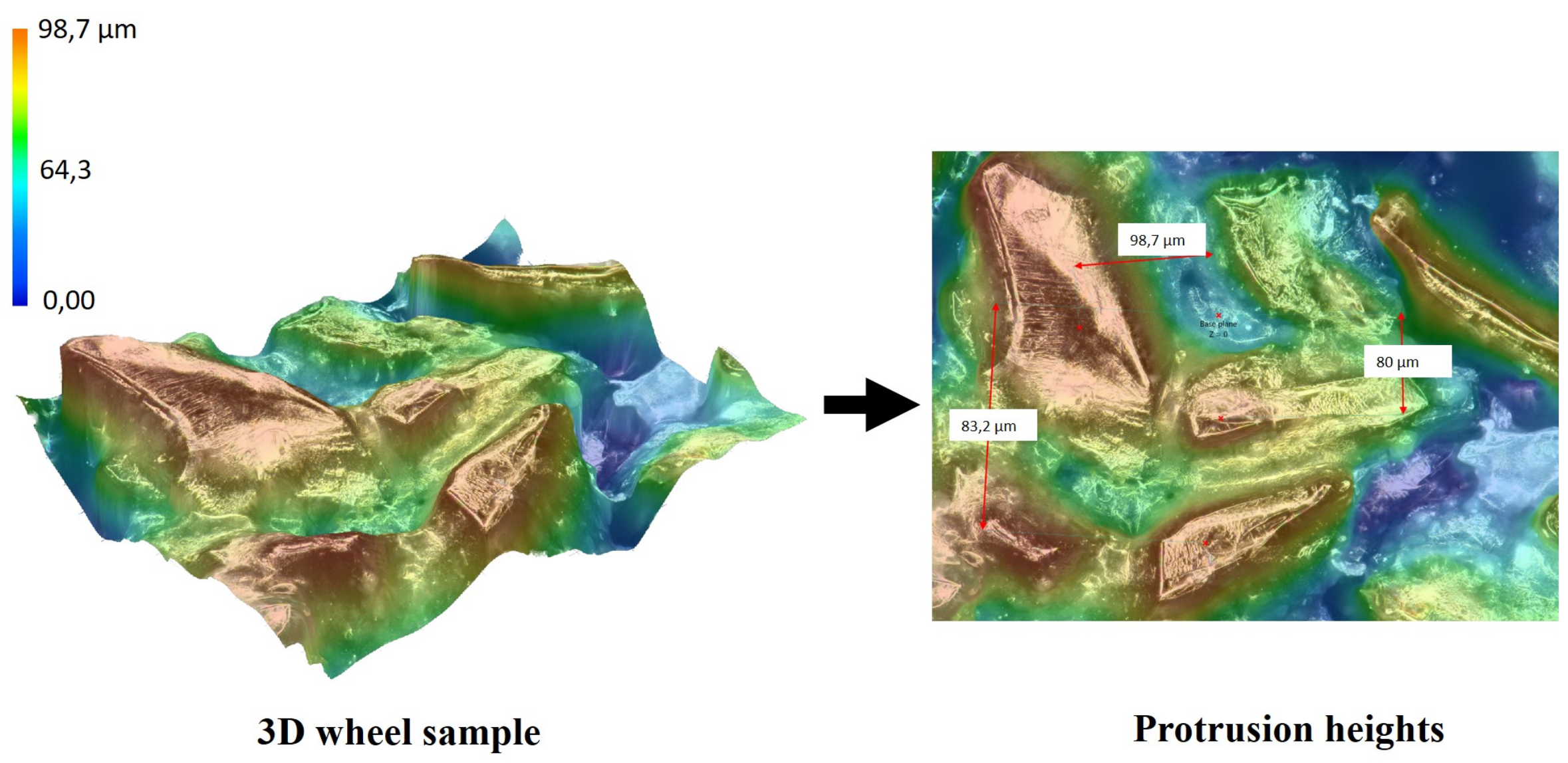
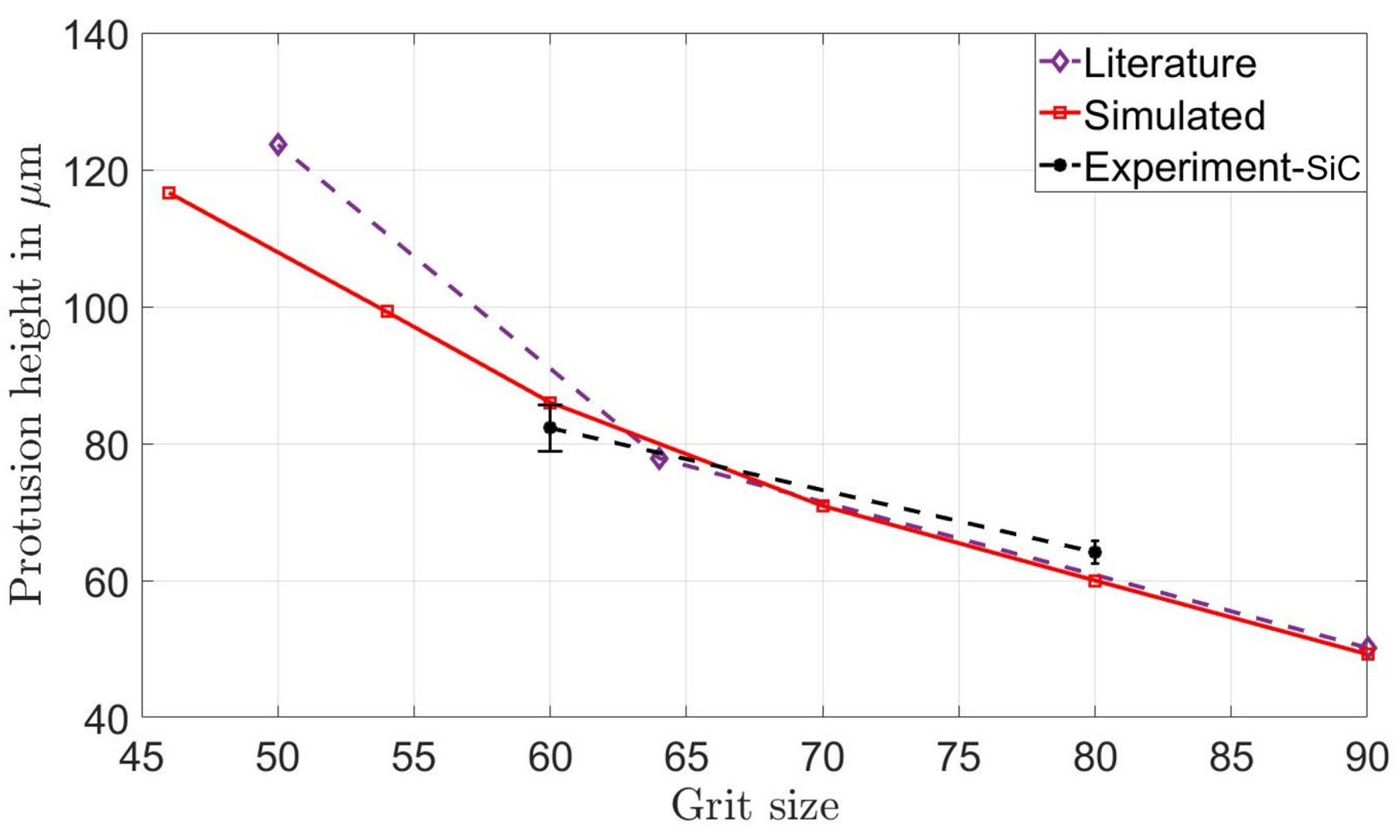
4.2. Grinding Wheel Measurement and Model Verification
4.2.1. Grinding Wheel Measurement Platform
4.2.2. Model Validation
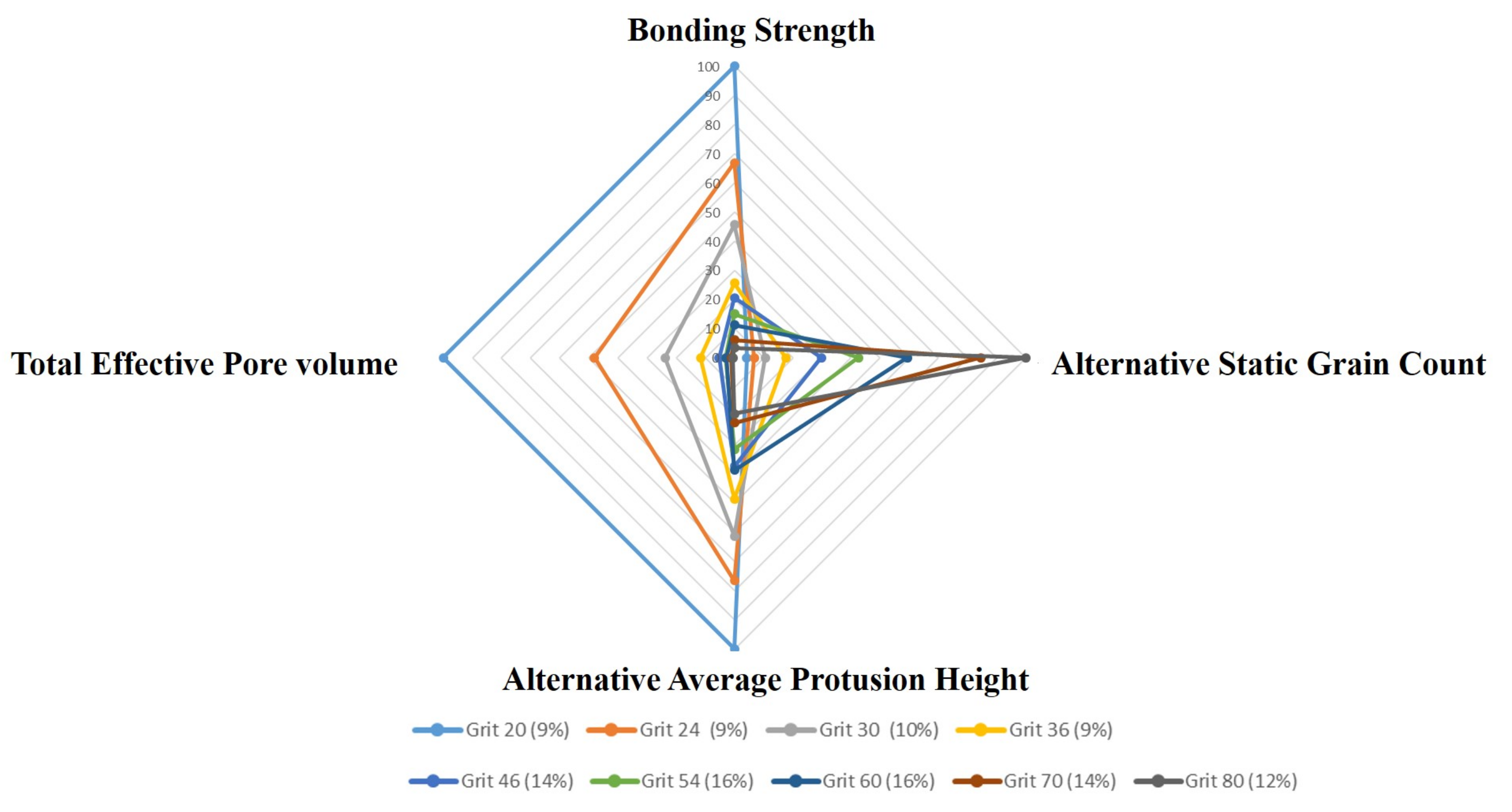
4.3. Effects of Fixed vs. Percentual Dressing (Percentage of Average Grit Diameters)
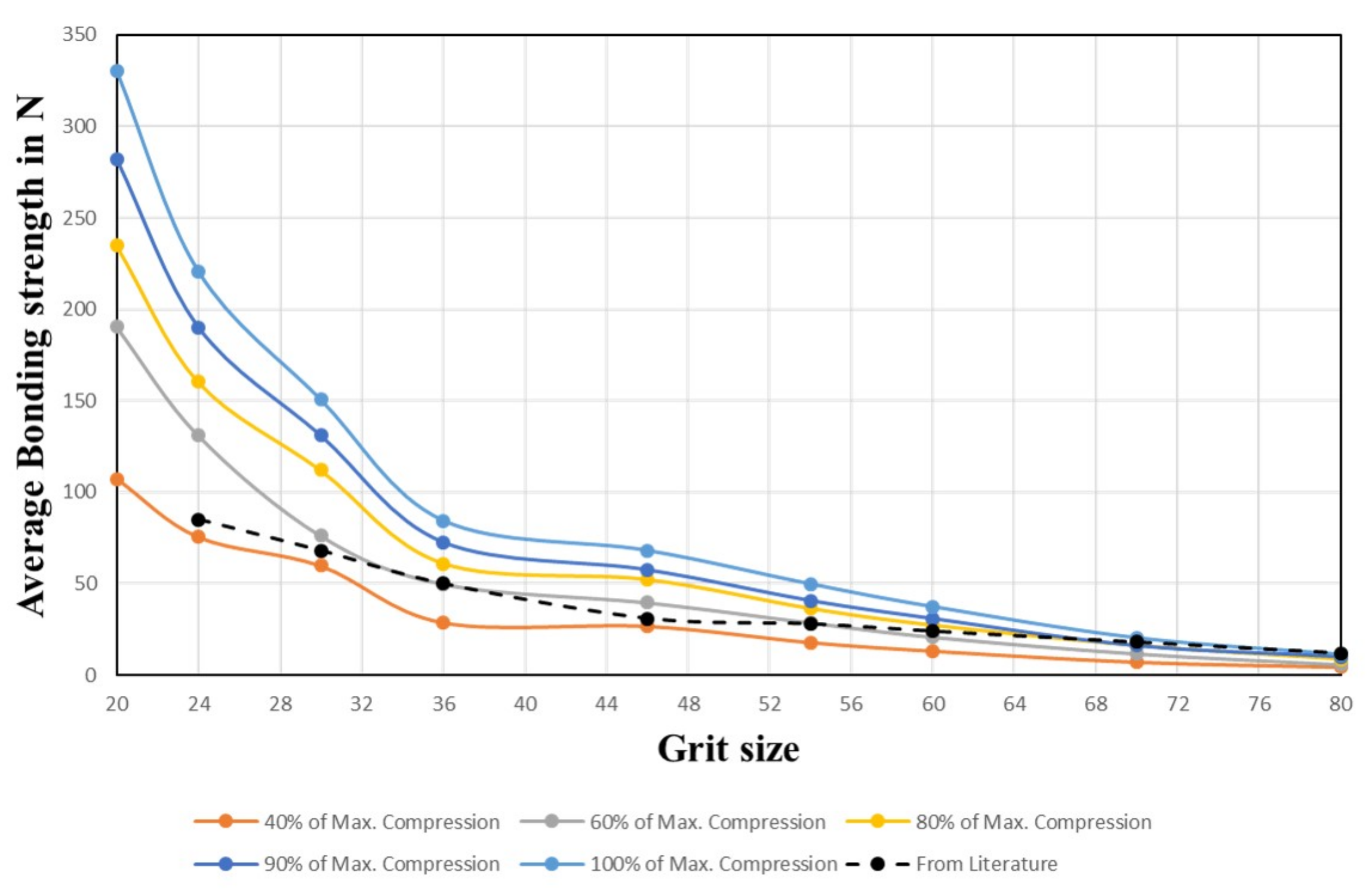
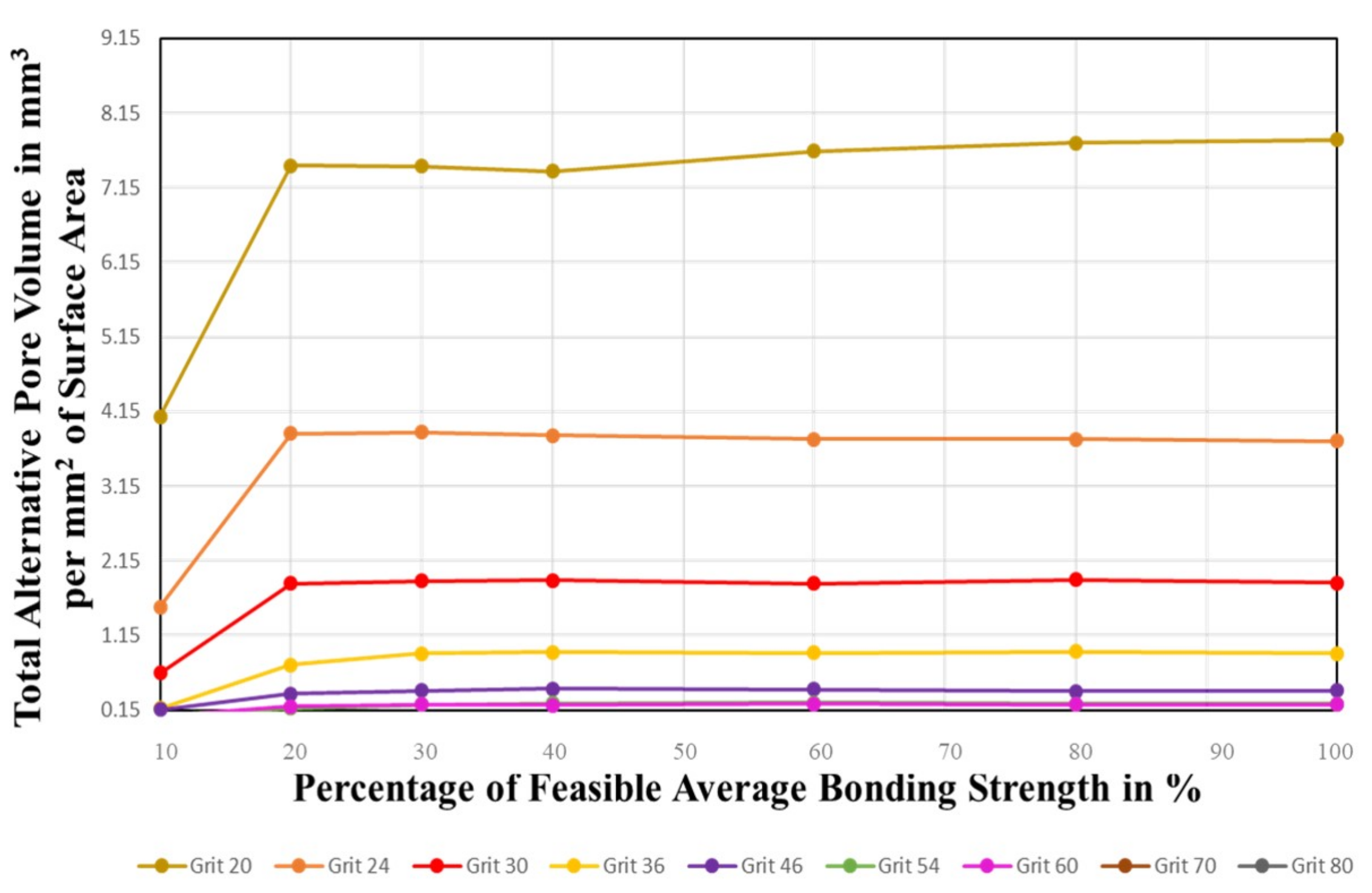
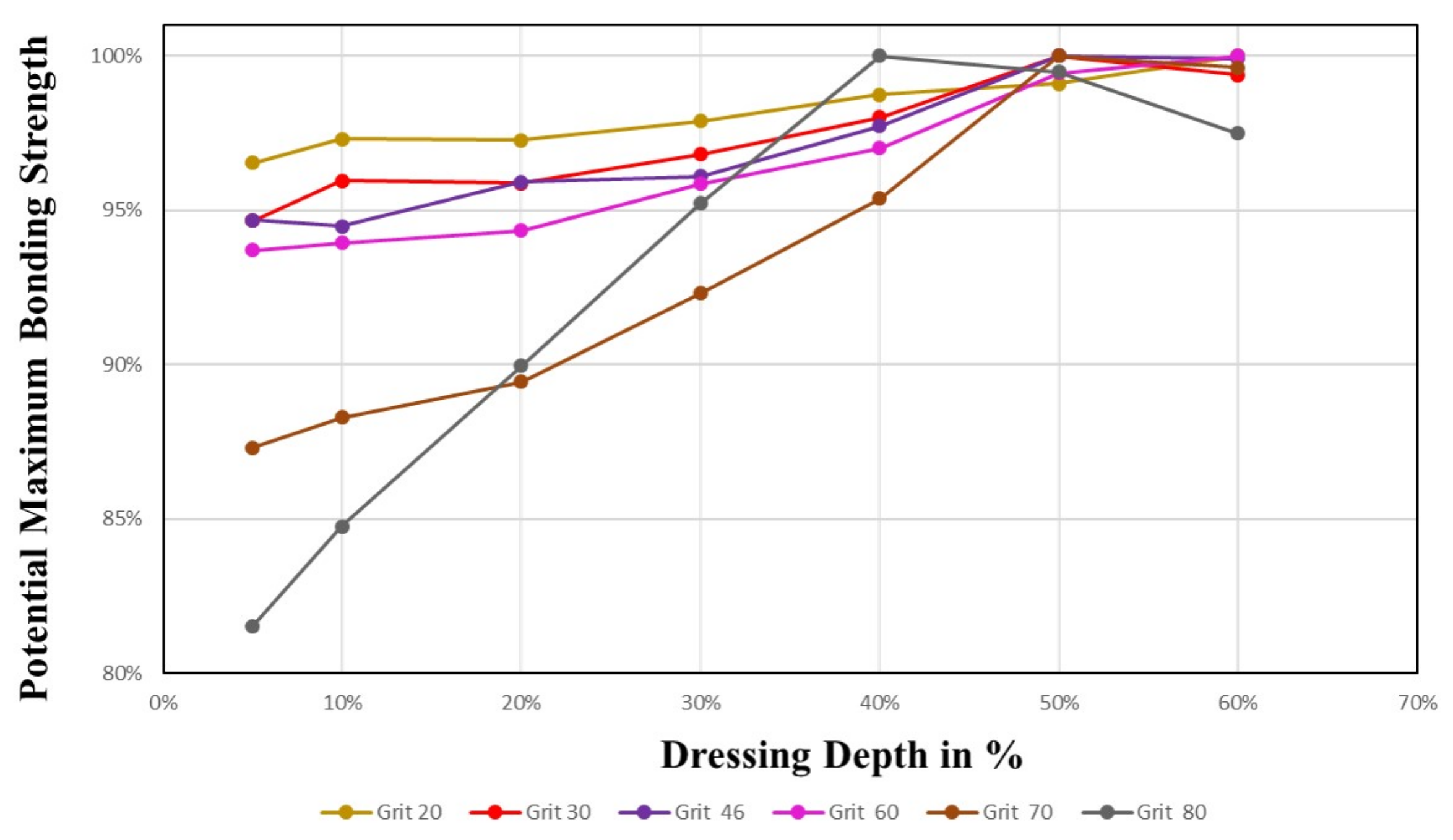
4.3.1. Bonding Strength on Surface
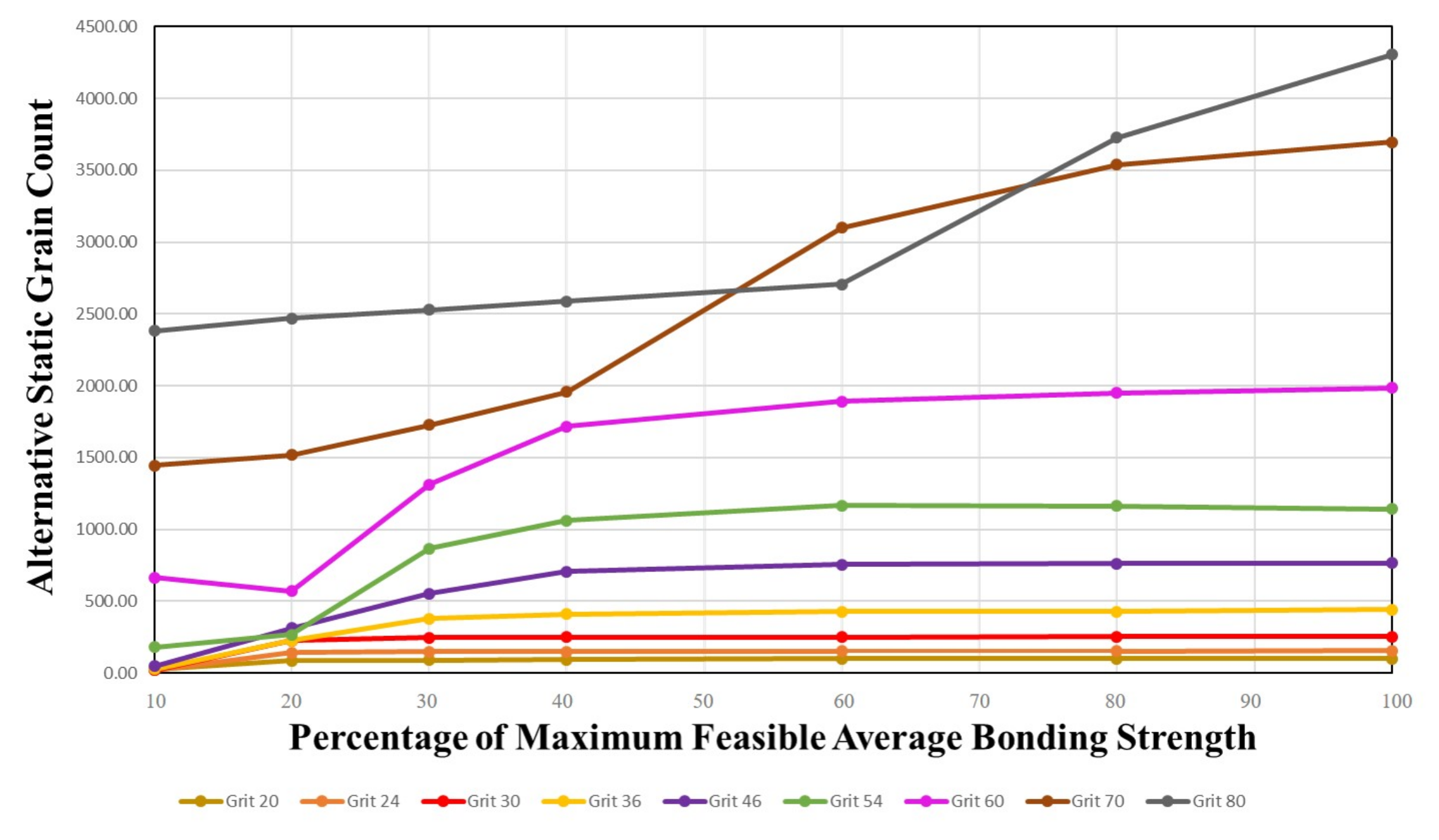
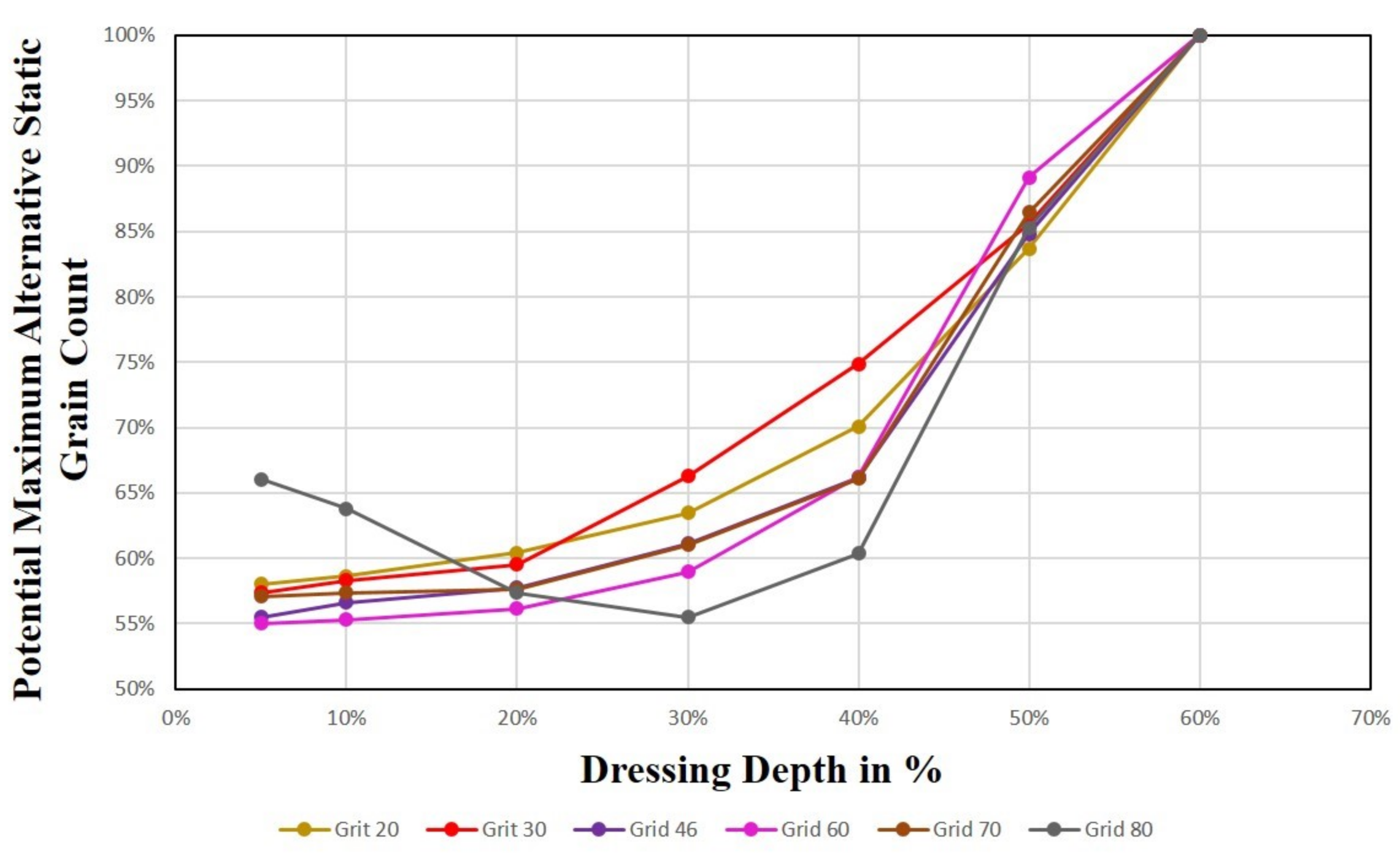
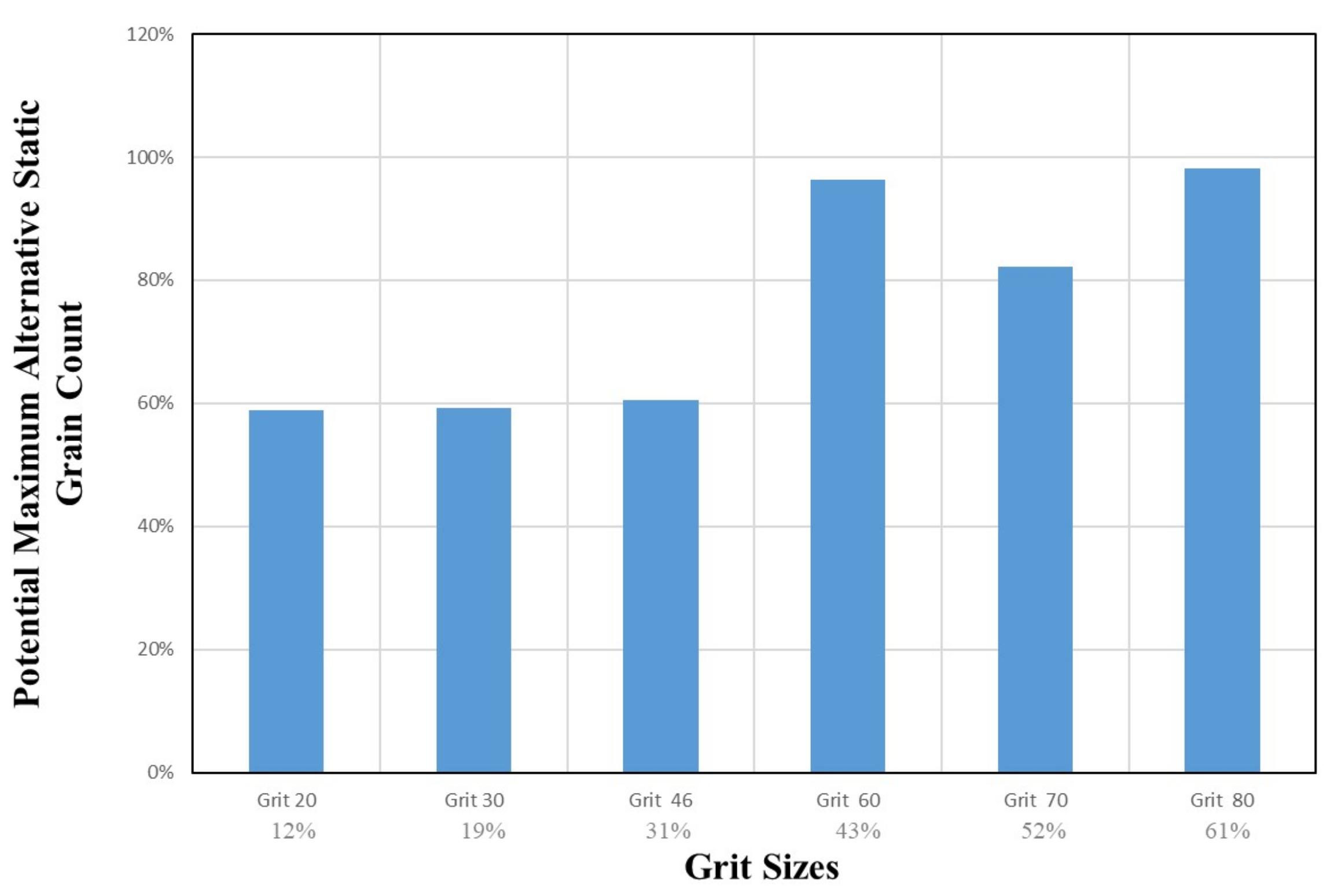
4.3.2. Alternative Static Grain
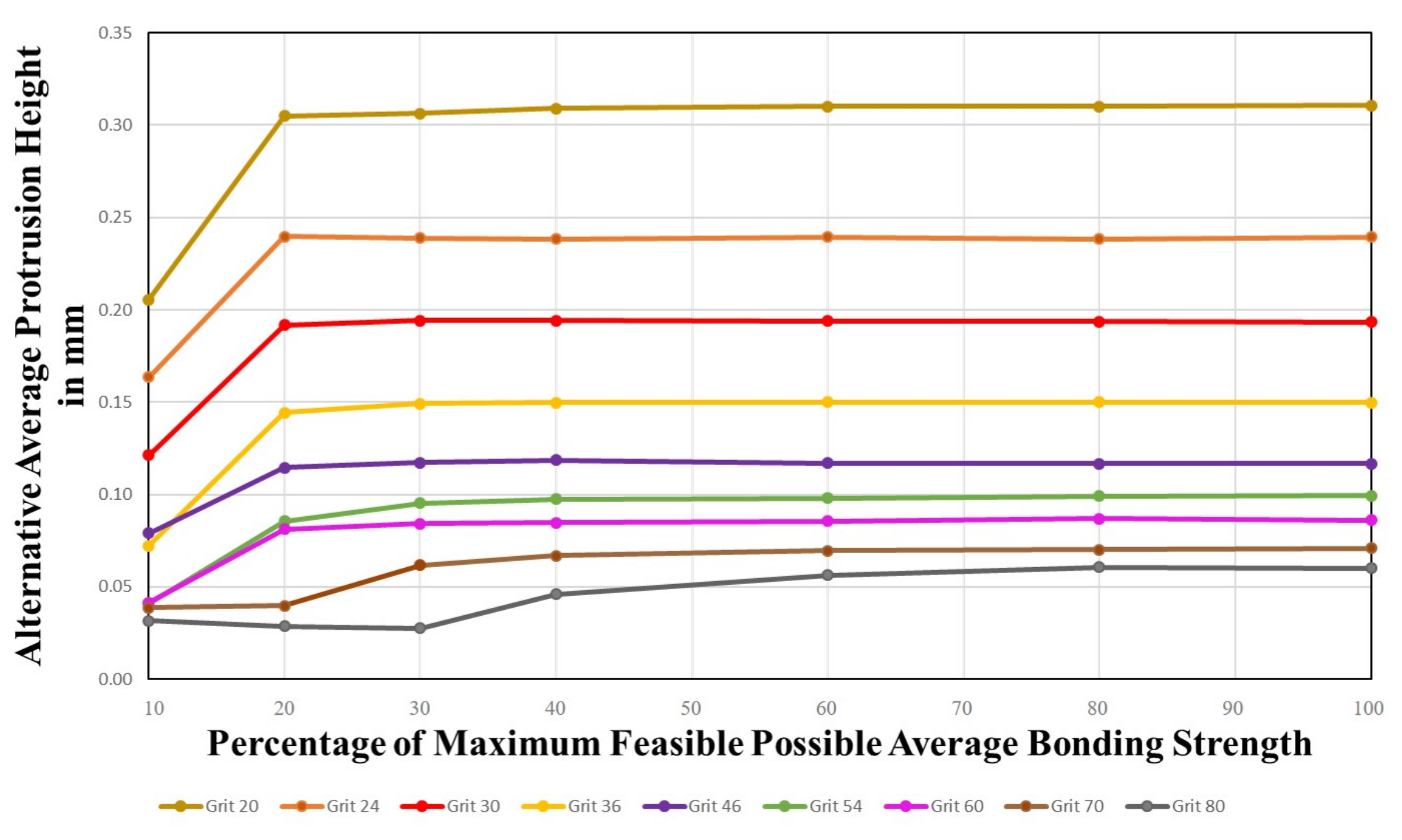
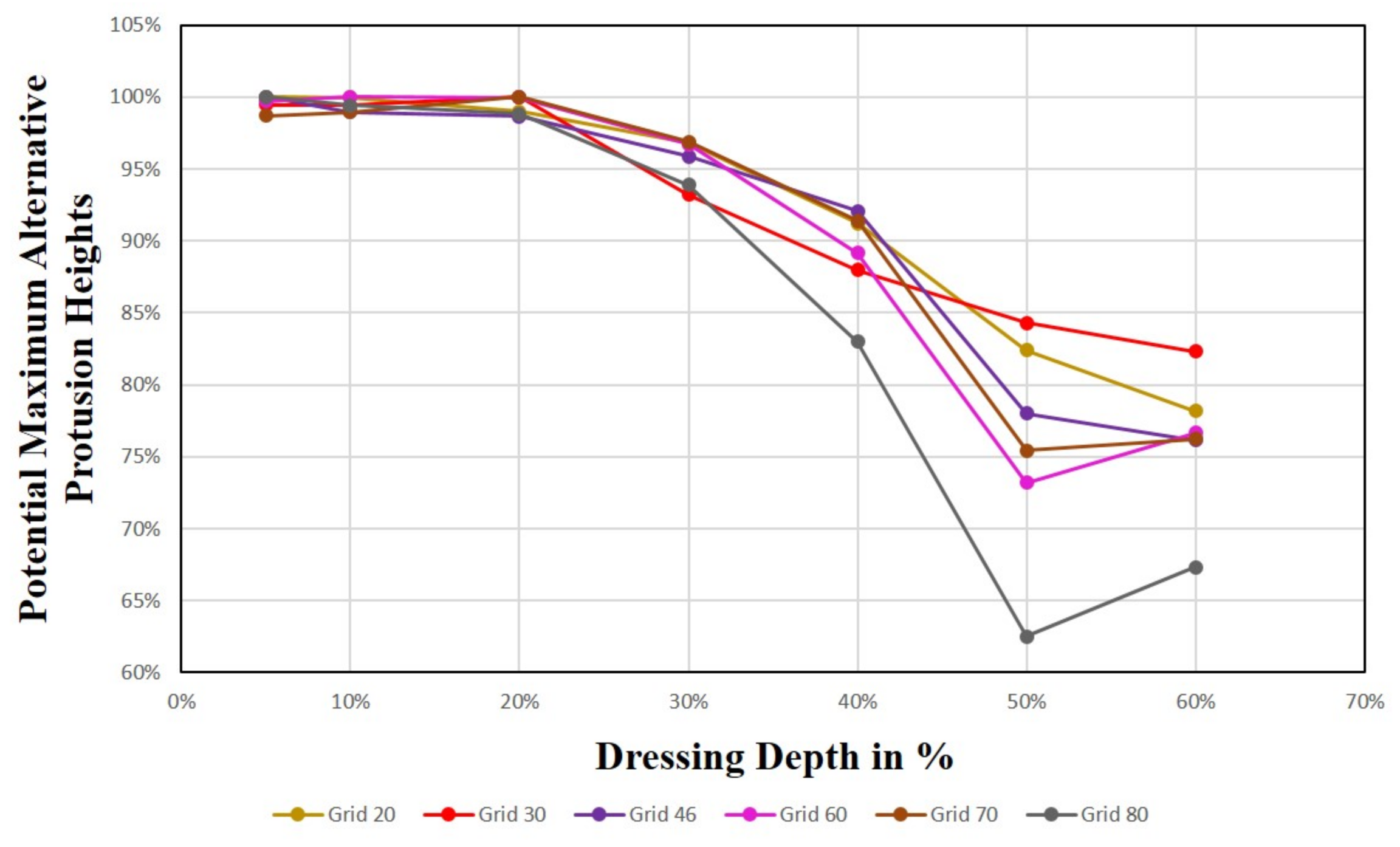
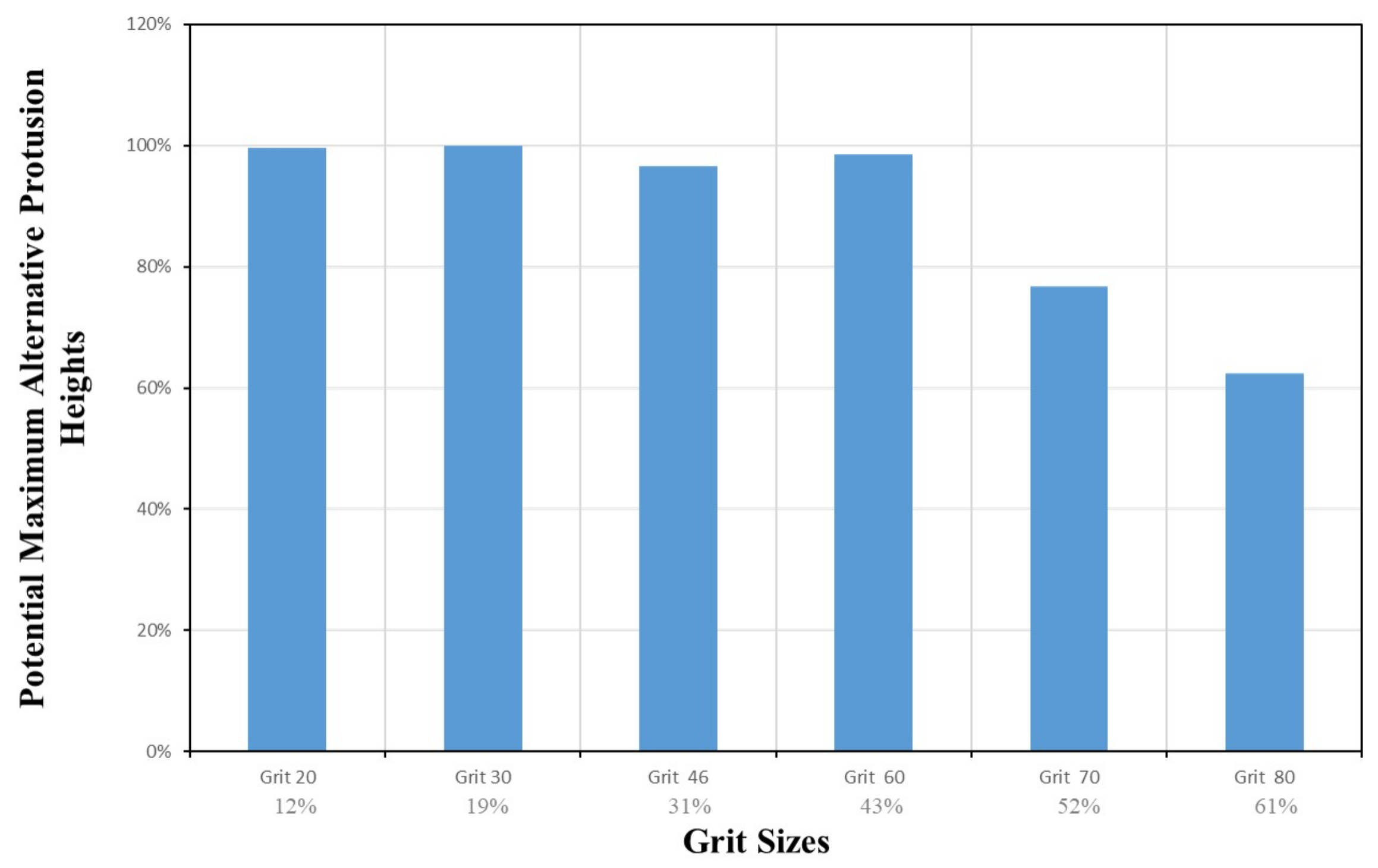
4.3.3. Alternative Protrusion Height
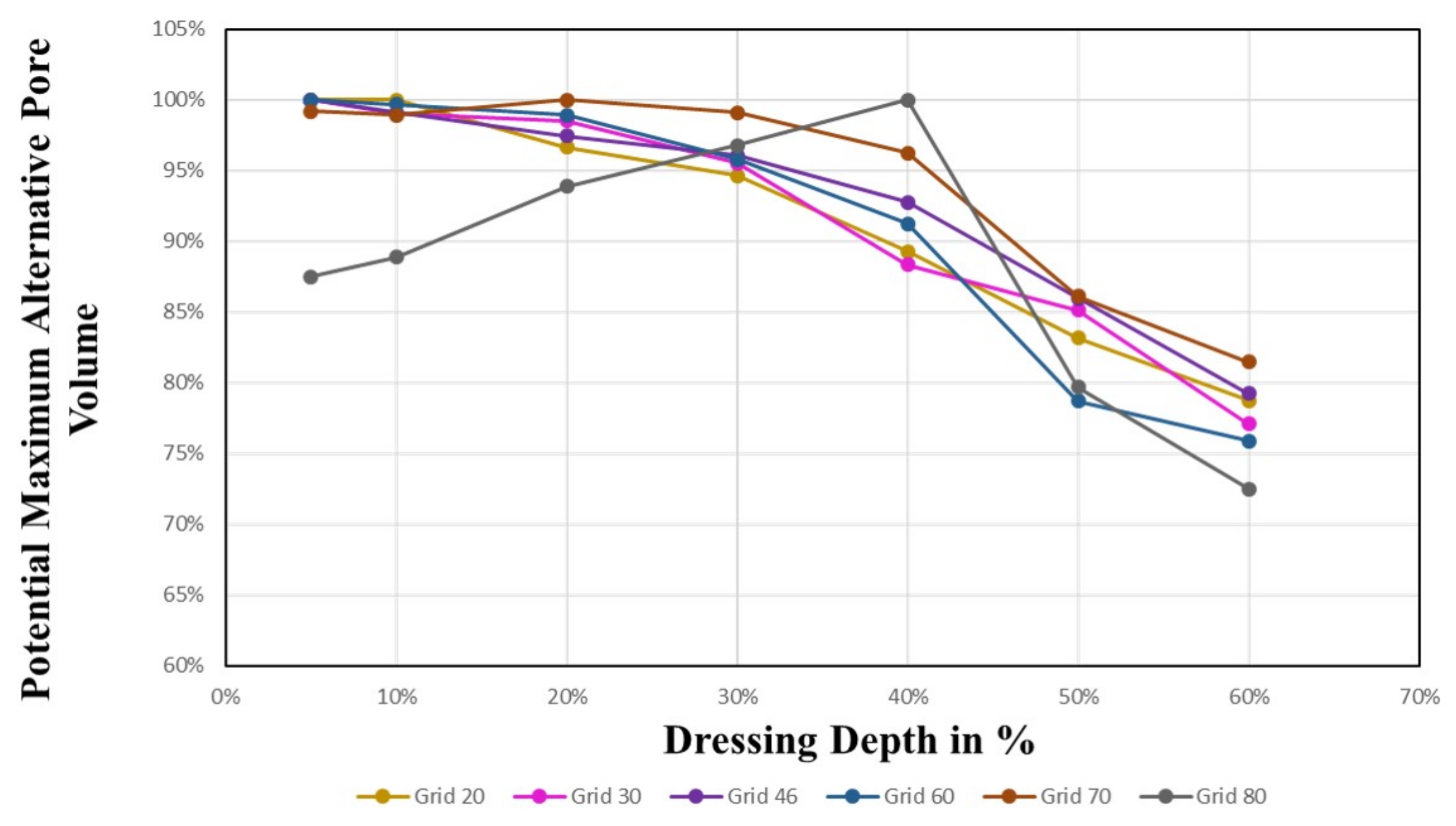
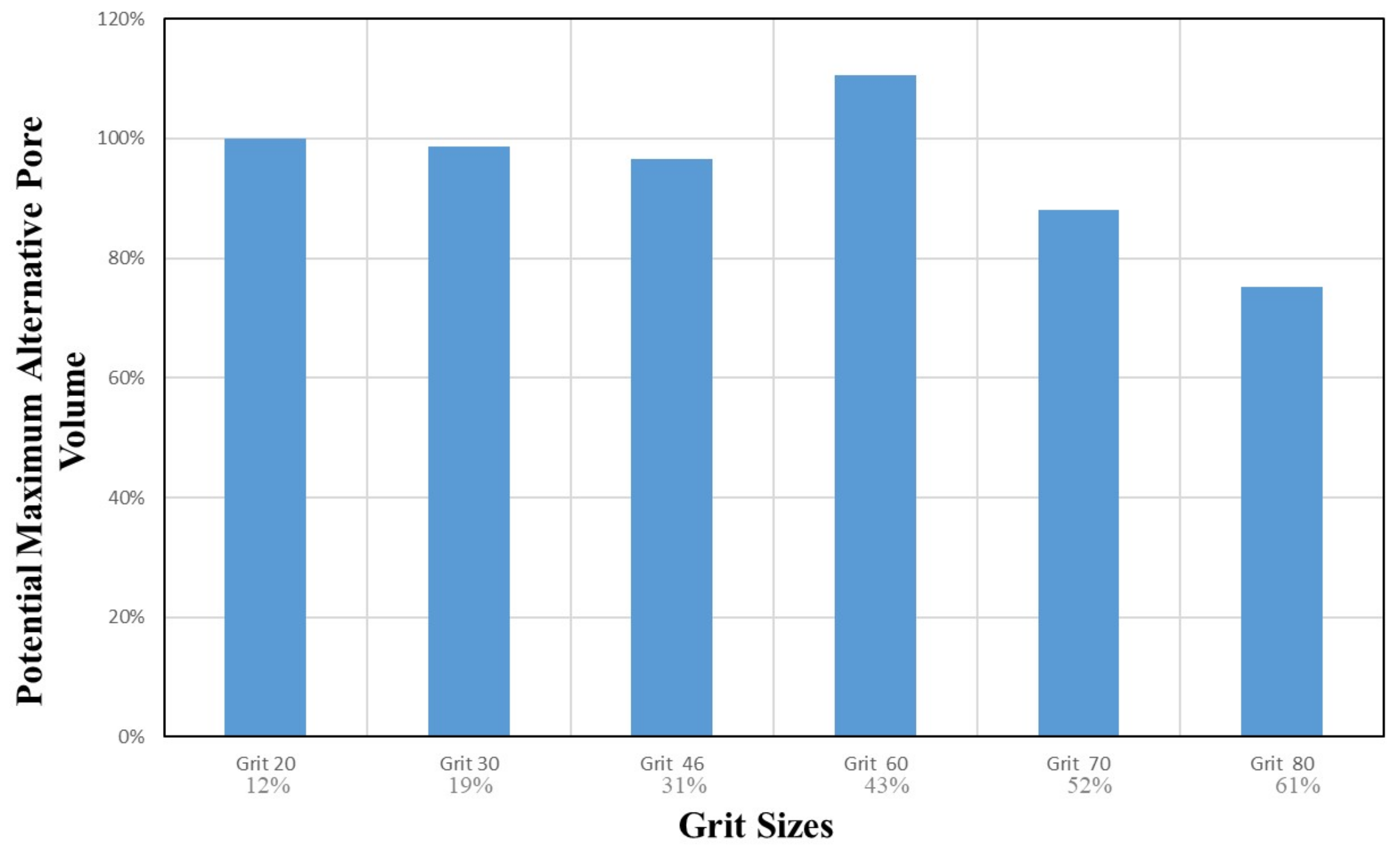
4.3.4. Alternative Pore Volume
4.3.5. Concluding Remarks and Practical Aspects for Variable Dressing
4.4. Grinding Wheel Surface
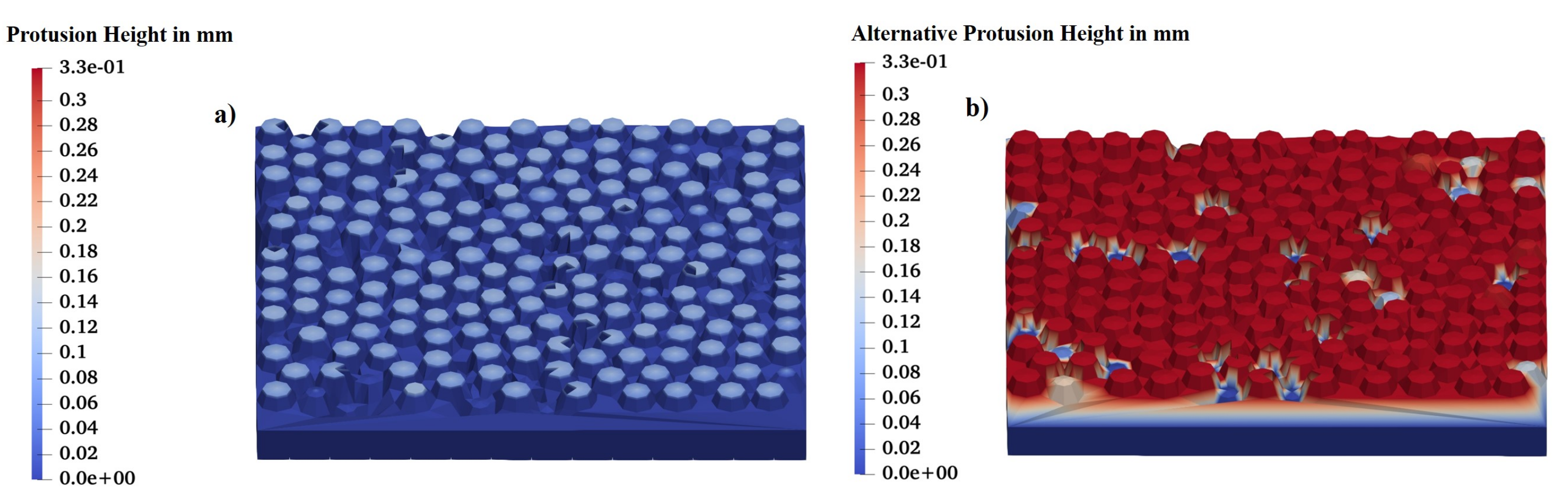
4.4.1. Alternative Protrusion Height
4.4.2. Bonding Strength
4.4.3. Dressing Effects on Topography
4.4.4. Protrusion Height vs. Alternative Protrusion Height
4.5. Practical Applications
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Li, C.; Zhang, Y.; Yang, M.; Zhang, X.; Zhang, N.; Dai, J. Experimental evaluation on tribological performance of the wheel/workpiece interface in minimum quantity lubrication grinding with different concentrations of Al2O3 nanofluids. J. Clean. Prod. 2017, 142, 3571–3583. [Google Scholar] [CrossRef]
- Rubio, E.; Jáuregui-Correa, J. A wavelet approach to estimate the quality of ground parts. J. Appl. Res. Technol. 2012, 10, 28–37. [Google Scholar] [CrossRef]
- Rowe, W.B. Principles of Modern Grinding Technology; William Andrew: Norwich, NY, USA, 2013. [Google Scholar]
- Marinescu, I.D.; Hitchiner, M.P.; Uhlmann, E.; Rowe, W.B.; Inasaki, I. Handbook of Machining with Grinding Wheels; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Doman, D.; Warkentin, A.; Bauer, R. A survey of recent grinding wheel topography models. Int. J. Mach. Tools Manuf. 2006, 46, 343–352. [Google Scholar] [CrossRef]
- Wegener, K.; Hoffmeister, H.W.; Karpuschewski, B.; Kuster, F.; Hahmann, W.C.; Rabiey, M. Conditioning and monitoring of grinding wheels. CIRP Ann. 2011, 60, 757–777. [Google Scholar] [CrossRef]
- Hecker, R.L.; Ramoneda, I.M.; Liang, S.Y. Analysis of wheel topography and grit force for grinding process modeling. J. Manuf. Process. 2003, 5, 13–23. [Google Scholar] [CrossRef]
- Barth, S.; Klocke, F. Influence of the grinding wheel topography on the thermo-mechanical stress collective in grinding. Inventions 2017, 2, 34. [Google Scholar] [CrossRef] [Green Version]
- Weiß, M.; Klocke, F.; Barth, S.; Rasim, M.; Mattfeld, P. Detailed analysis and description of grinding wheel topographies. J. Manuf. Sci. Eng. 2017, 139. [Google Scholar] [CrossRef]
- Osa, J.L.; Sanchez, J.A.; Ortega, N.; Iordanoff, I.; Charles, J.L. Discrete-element modelling of the grinding contact length combining the wheel-body structure and the surface-topography models. Int. J. Mach. Tools Manuf. 2016, 110, 43–54. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Tang, J.; Chen, H.; Zhu, C. Research about modeling of grinding workpiece surface topography based on real topography of grinding wheel. Int. J. Adv. Manuf. Technol. 2017, 93, 2411–2421. [Google Scholar] [CrossRef]
- Liu, W.; Deng, Z.; Shang, Y.; Wan, L. Parametric evaluation and three-dimensional modelling for surface topography of grinding wheel. Int. J. Mech. Sci. 2019, 155, 334–342. [Google Scholar] [CrossRef]
- Liao, D.; Shao, W.; Tang, J.; Li, J.; Tao, X. Numerical generation of grinding wheel surfaces based on time series method. Int. J. Adv. Manuf. Technol. 2018, 94, 561–569. [Google Scholar] [CrossRef]
- Kang, M.; Zhang, L.; Tang, W. Study on three-dimensional topography modeling of the grinding wheel with image processing techniques. Int. J. Mech. Sci. 2020, 167, 105241. [Google Scholar] [CrossRef]
- Gu, Q.; Deng, Z.; Lv, L.; Liu, T.; Teng, H.; Wang, D.; Yuan, J. Prediction research for surface topography of internal grinding based on mechanism and data model. Int. J. Adv. Manuf. Technol. 2021, 113, 821–836. [Google Scholar] [CrossRef]
- Li, X. Modeling and simulation of grinding processes based on a virtual wheel model and microscopic interaction analysis. Worcest. Polytech. Inst. 2010, 4, 38–78. [Google Scholar]
- Li, X.; Rong, Y.K. Kinematics Simulation of Grinding Process Based on Virtual Wheel Model and Micro-Cutting Analysis. Int. Manufact. Sci. Eng. Conf. 2009, 43611, 341–346. [Google Scholar]
- Li, X.; Rong, Y. Framework of grinding process modeling and simulation based on microscopic interaction analysis. Robot. Comput.-Integr. Manuf. 2011, 27, 471–478. [Google Scholar] [CrossRef]
- Koshy, P.; Jain, V.; Lal, G. Stochastic simulation approach to modelling diamond wheel topography. Int. J. Mach. Tools Manuf. 1997, 37, 751–761. [Google Scholar] [CrossRef]
- Doi, T.; Uhlmann, E.; Marinescu, I.D. Handbook of Ceramics Grinding and Polishing; William Andrew: Norwich, NY, USA, 2015. [Google Scholar]
- Marinescu, I.D.; Rowe, W.B.; Dimitrov, B.; Ohmori, H. Tribology of Abrasive Machining Processes; William Andrew: Norwich, NY, USA, 2012. [Google Scholar]
- Jain, R.K.; Jain, V. Stochastic simulation of active grain density in abrasive flow machining. J. Mater. Process. Technol. 2004, 152, 17–22. [Google Scholar] [CrossRef]
- Li, X.; Wolf, S.; Zhi, G.; Rong, Y.K. The modelling and experimental verification of the grinding wheel topographical properties based on the ‘through-the-process’ method. Int. J. Adv. Manuf. Technol. 2014, 70, 649–659. [Google Scholar] [CrossRef]
- Davis, T.D.; DiCorleto, J.; Sheldon, D.; Vecchiarelli, J.; Erkey, C. A route to highly porous grinding wheels by selective extraction of pore inducers with dense carbon dioxide. J. Supercrit. Fluids 2004, 30, 349–358. [Google Scholar] [CrossRef]
- Ravuri, B.P.; Goriparthi, B.K.; Revuru, R.S.; Anne, V.G. Performance evaluation of grinding wheels impregnated with graphene nanoplatelets. Int. J. Adv. Manuf. Technol. 2016, 85, 2235–2245. [Google Scholar] [CrossRef]
- Bhateja, C.; Lindsay, R. The Importance of Abrasive Grinding Wheel Hardness Control for the Productivity of Production Grinding Operations. CIRP Ann. 1981, 30, 247–249. [Google Scholar] [CrossRef]
- Jackson, M.J. A Study of Vitreous-Bonded Abrasive Materials. Ph.D. Thesis, Liverpool John Moores University, Liverpool, UK, 1995. [Google Scholar]
- Kirsch, B.; Effgen, C.; Büchel, M.; Aurich, J. Comparison of the embodied energy of a grinding wheel and an end mill. Procedia CIRP 2014, 15, 74–79. [Google Scholar] [CrossRef] [Green Version]
- Prasad, M.; Kopycinska, M.; Rabe, U.; Arnold, W. Measurement of Young’s modulus of clay minerals using atomic force acoustic microscopy. Geophys. Res. Lett. 2002, 29, 13. [Google Scholar] [CrossRef]
- Zhu, Y.; Liang, S.; Zhan, Z.; Xiao, P.; Fan, Z. Simulation of the change of sintering neck between two grains in two dimensions. Acta Metall. Sin. Engl. Lett. 2006, 19, 397–404. [Google Scholar] [CrossRef]
- Bouvard, D.; McMeeking, R. Deformation of interparticle necks by diffusion-controlled creep. J. Am. Ceram. Soc. 1996, 79, 666–672. [Google Scholar] [CrossRef]
- Li, M.; Ding, W.; Li, B.; Xu, J. Morphological evolution and grinding performance of vitrified bonded microcrystal alumina abrasive wheel dressed with a single-grit diamond. Ceram. Int. 2019, 45, 19669–19678. [Google Scholar] [CrossRef]
- Tawakoli, T.; Rasifard, A. Dressing of grinding wheels. In Machining with Abrasives; Springer: Boston, MA, USA, 2011; pp. 181–244. [Google Scholar]
- Karpuschewski, B.; Lierse, T.; Kaul, T.R.; Schulze, S.; Mueller-Cramm, D. Kinematic process model and investigation of grain breakout for conditioning with CVD diamond dressing disks. CIRP J. Manuf. Sci. Technol. 2018, 22, 21–29. [Google Scholar] [CrossRef]
- Bergs, T.; Ohlert, M.; Prinz, S.; Barth, S. Modeling of the Fracture Behavior of CBN Grains during Single Grain Dressing using FEM. Procedia CIRP 2020, 93, 1514–1519. [Google Scholar] [CrossRef]
- Ding, W.; Linke, B.; Zhu, Y.; Li, Z.; Fu, Y.; Su, H.; Xu, J. Review on monolayer CBN superabrasive wheels for grinding metallic materials. Chin. J. Aeronaut. 2017, 30, 109–134. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.B.; Komanduri, R. On the mechanics of the grinding process–Part I. Stochastic nature of the grinding process. Int. J. Mach. Tools Manuf. 2003, 43, 1579–1593. [Google Scholar] [CrossRef]
- Shaw, M.C. Principles of Abrasive Processing; Oxford University Press on Demand: Demand, UK, 1996. [Google Scholar]
- Eberhardsteiner, J. Approximation of Objects by Spheres for Multisphere Simulations in DEM. Available online: https://www.researchgate.net/profile/Stefan-Amberger/publication/259693012_Approximation_of_Objects_by_Spheres_for_Multisphere_Simulations_in_DEM/links/0a85e52d59a6ea86f5000000/Approximation-of-Objects-by-Spheres-for-Multisphere-Simulations-in-DEM.pdf (accessed on 30 October 2021).
- Mollon, G.; Zhao, J. 3D generation of realistic granular samples based on random fields theory and Fourier shape descriptors. Comput. Meth. Appl. Mech. Eng. 2014, 279, 46–65. [Google Scholar] [CrossRef]












| Particle Properties | |
|---|---|
| Grain fraction | 49% |
| Bond fraction | 10% |
| Young’s modulus of grain | 400 GPa |
| Young’s modulus of bond | 6.2 GPa |
| Poisson’s ratio | 0.3 |
| Maximum particle compression force | |
| Firing properties | |
| Firing time | 20 h |
| Grain-boundary diffusion property | 290 h |
| Dressing settings | |
| Wheel diameter | 250 mm |
| Wheel speed | 20 mm/s |
| Dresser travel speed | 300 mm/min |
| Dressing depth | 10% |
| Dressing lead | 0.19 mm |
| Grid Size | 95% Confidence Interval | |||
|---|---|---|---|---|
| 20 | 0.850 mm | 0.938 mm | 0.762 mm | 0.0440 mm |
| 24 | 0.676 mm | 0.762 mm | 0.589 mm | 0.0432 mm |
| 30 | 0.532 mm | 0.589 mm | 0.476 mm | 0.0282 mm |
| 36 | 0.415 mm | 0.476 mm | 0.354 mm | 0.0305 mm |
| 46 | 0.323 mm | 0.354 mm | 0.291 mm | 0.0157 mm |
| 54 | 0.273 mm | 0.291 mm | 0.255 mm | 0.0090 mm |
| 60 | 0.233 mm | 0.255 mm | 0.211 mm | 0.0110 mm |
| 70 | 0.194 mm | 0.211 mm | 0.178 mm | 0.0082 mm |
| 80 | 0.165 mm | 0.178 mm | 0.152 mm | 0.0065 mm |
| Grit Size | in % of Dressing | |
|---|---|---|
| 20 | 0.85 mm | 12% |
| 30 | 0.532 mm | 19% |
| 46 | 0.323 mm | 31% |
| 60 | 0.233 mm | 43% |
| 70 | 0.194 mm | 52% |
| 80 | 0.165 mm | 61% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sridhar, P.; Mannherz, D.; de Payrebrune, K.M. Modelling and Analysis of Topographic Surface Properties of Grinding Wheels. J. Manuf. Mater. Process. 2021, 5, 121. https://doi.org/10.3390/jmmp5040121
Sridhar P, Mannherz D, de Payrebrune KM. Modelling and Analysis of Topographic Surface Properties of Grinding Wheels. Journal of Manufacturing and Materials Processing. 2021; 5(4):121. https://doi.org/10.3390/jmmp5040121
Chicago/Turabian StyleSridhar, Praveen, Daniel Mannherz, and Kristin M. de Payrebrune. 2021. "Modelling and Analysis of Topographic Surface Properties of Grinding Wheels" Journal of Manufacturing and Materials Processing 5, no. 4: 121. https://doi.org/10.3390/jmmp5040121
APA StyleSridhar, P., Mannherz, D., & de Payrebrune, K. M. (2021). Modelling and Analysis of Topographic Surface Properties of Grinding Wheels. Journal of Manufacturing and Materials Processing, 5(4), 121. https://doi.org/10.3390/jmmp5040121







