Forces Shapes in 3-Axis End-Milling: Classification and Characteristic Equations

Abstract

In 3-axis milling, cutting force analysis represents one of the main methods to increase the quality and productivity of the process. In this context, cutting force shape gives information of both monitoring and prediction of the cutting process. However, the cutting force shape is not unique, and it changes according to the cutting strategy, tool geometry, and cutting parameters. This paper presents a comprehensive approach to predict and classify cutting force shapes in 3-axis milling operations. In detail, the proposed approach starts by classifying the cutting force shapes for a single fluted endmill (i.e., single flute force shape), and, considering how the single flute force shapes may overlap one another, it extends the classification to a general multiple-fluted endmill. Moreover, the method provides, through analytical equations, angles, and magnitude dimensionless parameters of each key point, describing each shape classified. Finally, the proposed approach was experimentally validated through several milling tests in different cutting conditions.

1. Introduction

The milling process is, by far, the most flexible and common machining process in modern manufacturing. The ever-increasing need for high accuracy and productivity has led to the development of advanced monitoring and predictive approaches [1]. The interaction forces between tool and workpiece, known as cutting forces, are an essential input for several of these approaches since they can reveal the effects of different key aspects of the process, such as tool wear [2], engagement conditions [3], vibrations [4], surface error [5,6]. In milling such cutting forces are not constant during the process and their shape and magnitude change significantly with cutting process parameters [7]. Different cutting force models have been proposed in the literature, and most of them relate cutting forces to the chip thickness by utilizing cutting force coefficients [8,9,10]. In peripheral milling, chip thickness can be fairly approximated by sinusoidal functions, however, this simple formulation is valid for straight teeth tools (i.e., zero helix angle) which are practically never adopted in actual operations [11]. Therefore, the approximated cutting forces, computed by such models, are not suitable for force shape prediction, yet they can be only applied to predict surface errors (e.g., surface location error [12]), or vibrations phenomena (e.g., chatter [13,14]), showing several limitations.

Indeed, the tool helix angle changes significantly the cutting force shape since it affects both exit and entry angles, chip area, and it has a direct effect on the surface error variation along with the axial depth of cut [15]. To obtain a reliable and accurate cutting force prediction, including the tool helix angle, chip thickness sinusoidal approximation must be applied to small discs in which the tool should be divided along its axis, leading to cutting force prediction through numerical methods [16,17,18].

However, quick analytical information about the expected cutting forces could be very useful in monitoring solutions (e.g., depth of cut identification [19], feed adjustment [20]). Indeed, measured cutting forces can return high-value information regarding the actual process, and, along with the expected cutting forces, they allow the process to be controlled by adjusting the cutting parameters [21]. Analytical information on cutting forces can be obtained using a frequency domain solution [22,23], but the proposed equations are valid only for a specific cutting force model and require cutting force coefficients [24]. On the other hand, accurate identification of cutting force shape could allow the cutting force to be predicted only at specific instants, dramatically reducing the computational efforts of predictive approaches. Hence, it is clear that an analytical representation of cutting force shape including the effects of cutting parameters could be effectively exploited, even without cutting force magnitude prediction [25,26]. In the last decades, several works have tried to define and classify the cutting force shapes in peripheral milling providing simple equations to represent them.

The work of Choi et al. [27] was one of the first investigations on the relation between force shape and flutes engagements, and the authors developed a method to predict depts of cut in end-milling exploiting this information. Yun et al. [15] computed the position of the peak value of the cutting force through analytical equations. Although effective, their approaches apply only to specific conditions. Yang et al. [28] identified different force shapes with dedicated equations, to detect the depth of cut variations. Their results prove that force shapes are not unique, but, even in this case, only down-milling operations and certain conditions are investigated. Islam et al. [29] and Desai et al. [30] started from these classifications to predict surface error shapes. All the results presented do not give a comprehensive picture of all the force shapes. Indeed, the authors focused their attention only on specific cases: down milling operations with two flutes cutting simultaneously in defined cutting conditions. Moreover, analytical equations for force shape serve to predict characteristic angles without considering the cutting force magnitude variation.

In this work, a comprehensive classification of cutting force shapes is proposed, and specific formulations are presented, considering cutting parameters combinations and different configurations (i.e., up and down milling). Cutting force shapes are classified, and for each type of characteristic equations, which identify the key angles are presented, extending the ones presented by Yang et al. [28]. In addition, magnitude variation was investigated, assigning to each key point, a binary value (i.e., 0 or 1), that allows a simplified representation of the normalized total cutting force shape. The proposed formulations were experimentally validated through cutting tests in several conditions, showing the different force shapes, as classified by the proposed approach.

The proposed classification and formulations return the expected shape of the cutting force without the need for any simulation or cutting force model. For this reason, they could be used to efficiently predict cutting force only on specific points. Moreover, the proposed approach could lay the ground for monitoring solutions based on cutting force signals.

2. Materials and Methods

Cutting force shape is not unique, but it changes according to the tool geometry (tool diameter D, helix angle α_el, number of flutes N), the cutting parameters (radial depth of cut ar, axial depth of cut ap), and the cutting strategy (down-milling or up-milling).

In this work, all the shapes which the total cutting force F (i.e., resultant of cutting force in the x-y plane, as shown in Figure 1) could assume are analyzed and a comprehensive classification is provided, starting from a single fluted endmill (N = 1) to a generical multiple-fluted endmill (N > 1), as partially presented in [7,28].

Each shape is identified by key points, whose coordinates are expressed through the angular position (i.e., key angle) and a binary value (m) which is related to the magnitude of the cutting and defined in this work as:

m = 1 when cutting force is maximum
m = 0 when cutting force is minimum

(1)

These formulations are valid in one period, wide as the tool pitch angle (ϕ_z), which marks the periodicity of the cutting force (neglecting tool run-out). Tool pitch angle, assuming equally spaced flutes for the endmill, can be defined as:

$${\varphi }_z=2\pi /N$$

(2)

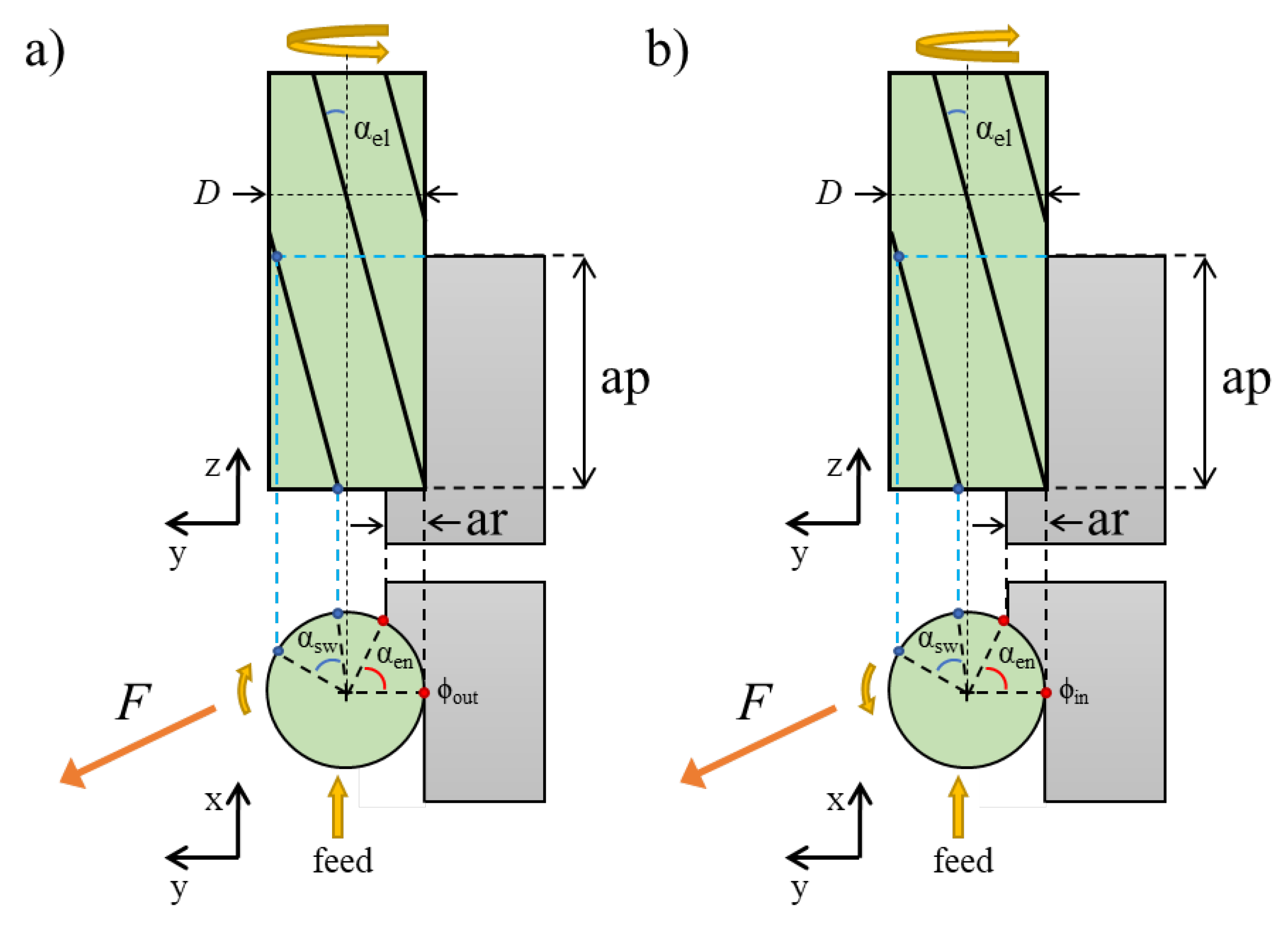
2.1. Shape Classification in Single-Fluted Endmill

The proposed classification starts with the definition of the different types of F shape for a single fluted endmill (N = 1). In this condition, key points’ coordinates (i.e., key angles-m values couples) are based on a set of working angles that can be obtained directly from the cutting parameters (ar, ap) and the tool geometry (D, α_el).

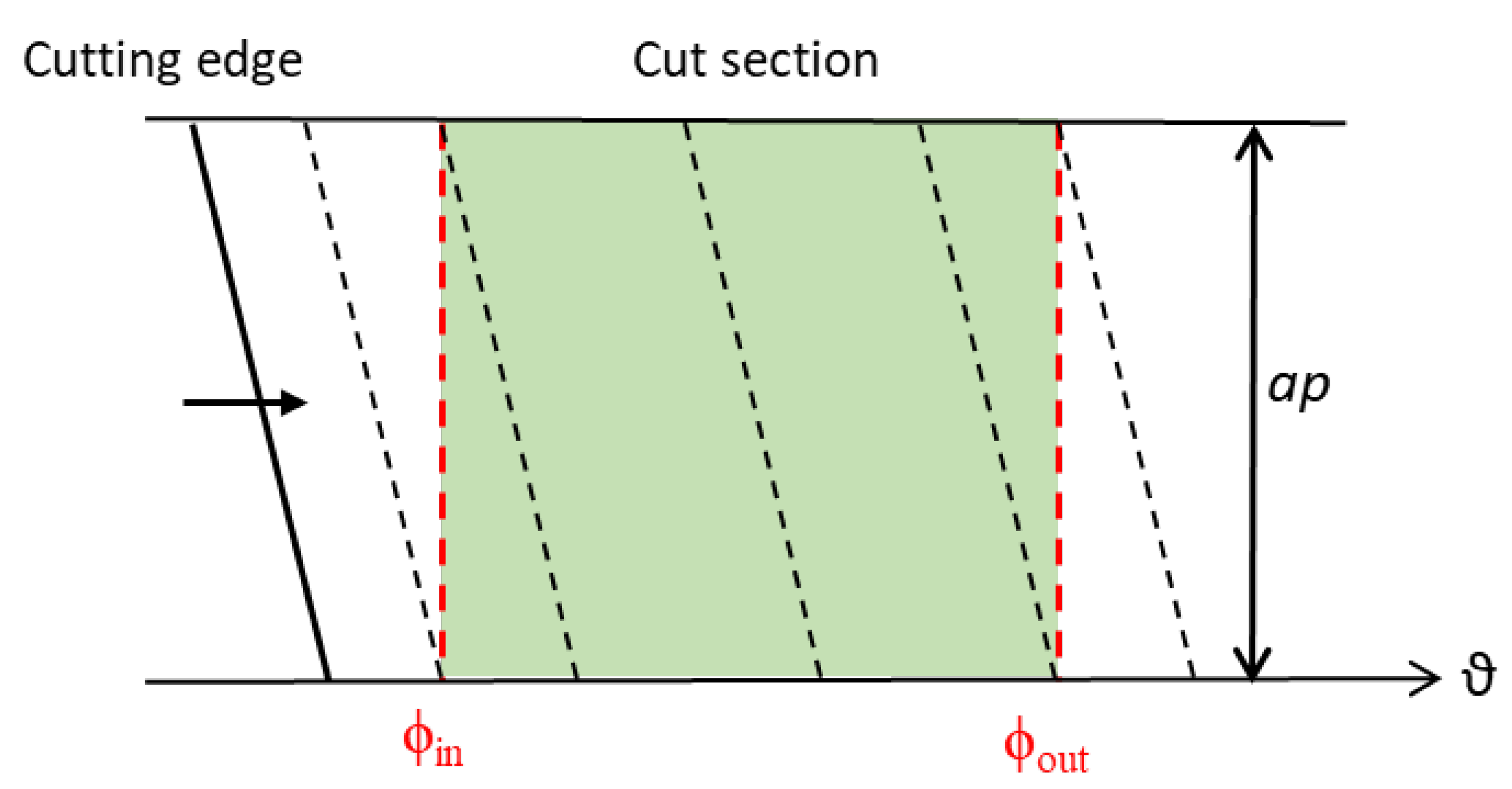
2.1.1. Key Angles

The proposed formulations start from the basic angles already presented by other authors [7,28]. The axial engagement angle α_sw is related to ap and the endmill’s geometry following the equations:

$${\alpha }_{sw}=k_{b}ap$$

(3)

$$k_b=\raisebox{1ex}{$2tan\left({\alpha }_{el}\right)$}\!\left/ \!\raisebox{-1ex}{$D$}\right.$$

(4)

where α_el is the tool helix angle and D is the tool diameter.

The radial engagement angle α_en is defined using radial depth of cut ar with the following equation:

$${\alpha }_{en}={\varphi }_{out}-{\varphi }_{in}=acos\left(1-\raisebox{1ex}{$2ar$}\!\left/ \!\raisebox{-1ex}{$D$}\right.\right)$$

(5)

Moreover, a critical value for both α_en and α_sw is necessary for the classification. The critical axial engagement angle α_swc is the axial engagement angle that equals α_en Equation (6) [28].

$${\alpha }_{swc}={\alpha }_{en}$$

(6)

The critical radial engagement angle α_enc is defined as the engagement angle which identifies the angular position of the maximum of F in a slotting condition. It must be noted that, due to the different kinematic of the cut, α_enc changes from down-milling to up-milling, however, in both cases, it is related to the maximum chip thickness [28].

$${\alpha }_{enc}={\varphi }_{out}+\frac{{\alpha }_{sw}}{2}-\frac{\pi }{2} Down\text{-}milling$$

(7)

$${\alpha }_{enc}=\frac{{\alpha }_{sw}}{2}+\frac{\pi }{2} Up\text{-}milling$$

(8)

These working angles, already presented in other works, are used to express the key angles, which identify the angular position of the key points of the F shape for a single fluted endmill, with the following proposed equations:

$${\vartheta }_1={\varphi }_{in}$$

(9)

$${\vartheta }_2={\varphi }_{in}+{\alpha }_{en}$$

(10)

$${\vartheta }_3={\varphi }_{in}+{\alpha }_{sw}$$

(11)

$${\vartheta }_4={\varphi }_{in}+{\alpha }_{sw}+{\alpha }_{en}$$

(12)

$${\vartheta }_M={\varphi }_{in}+{\alpha }_{sw}+{\alpha }_{en}-{\alpha }_{enc} Down\text{-}milling$$

(13)

$${\vartheta }_M={\varphi }_{in}+{\alpha }_{enc} Up\text{-}milling$$

(14)

Each key angle represents a specific angular position of the cutting process. In detail, the cut starts when the cutting edge reaches ϕ_in, and it ends when the same cutting edge reaches ϕ_out (Figure 2). However, due to the helix angle, the cutting edge reaches these positions at the bottom of ap and the top of ap. Therefore, ϑ₁ represents the angular positions of the cutting edge when it starts cutting at the bottom of ap, while ϑ₃ is the angular position of the cutting edge when it starts cutting at the top of ap.

Following a similar concept, ϑ₂ and ϑ₄ are the angular positions of the cutting edge when it stops cutting at the bottom of the ap and the top of the ap.

On the other hand, ϑ_M, does not represent a particular position of the cutting edge, but it represents the angular position of the maximum value of F. Moreover, ϑ_M is relevant only in those operations where the ar exceeds the tool radius. It is interesting to note that all the key angles are only dependent on the tool’s geometry (α_el, D) and the cutting parameters (ar, ap), without the need for any cutting force model or coefficients.

2.1.2. Magnitude Value

The m value, as defined in Equation (1), corresponding to the key angles ϑ₁ and ϑ₄ is 0, while for ϑ₂, ϑ_3, and ϑ_M the corresponding m value is 1. Indeed, ϑ₁ and ϑ₄ represent the beginning and the ending of the cutting process, therefore they identify a minimum of F. Instead ϑ₂, ϑ₃ and ϑ_M represent angular positions where the cutting edge is fully involved in the cut, thus they identify a maximum of F. However, the key points identified by ϑ₂, ϑ_3, and ϑ_M do not always contribute to the F shape because the angular position corresponds to F maximum changes according to both the cutting parameters (ar, ap) and the cutting strategy (down-milling or up-milling).

2.1.3. Classification

To comprehensively investigate the F shape for a single fluted endmill, the effects of the cutting parameters were studied, exploiting α_sw and α_en and their critical values (α_enc and α_swc) in both down-milling and up-milling. This analysis allows distinguishing three different F shapes, each one defined by a different set of key points. The characteristics of each F shape, referred to as Type, are described as follows:

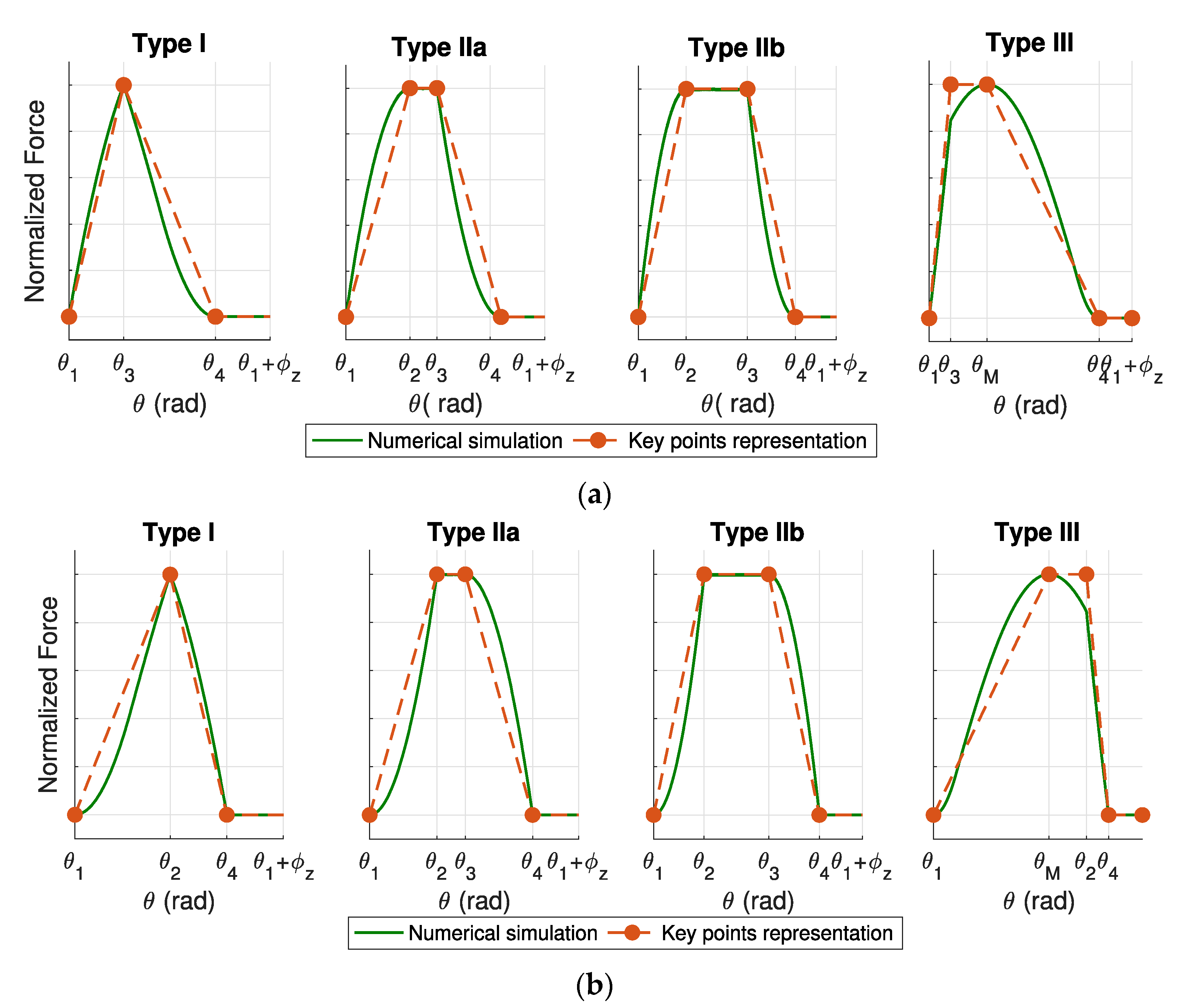
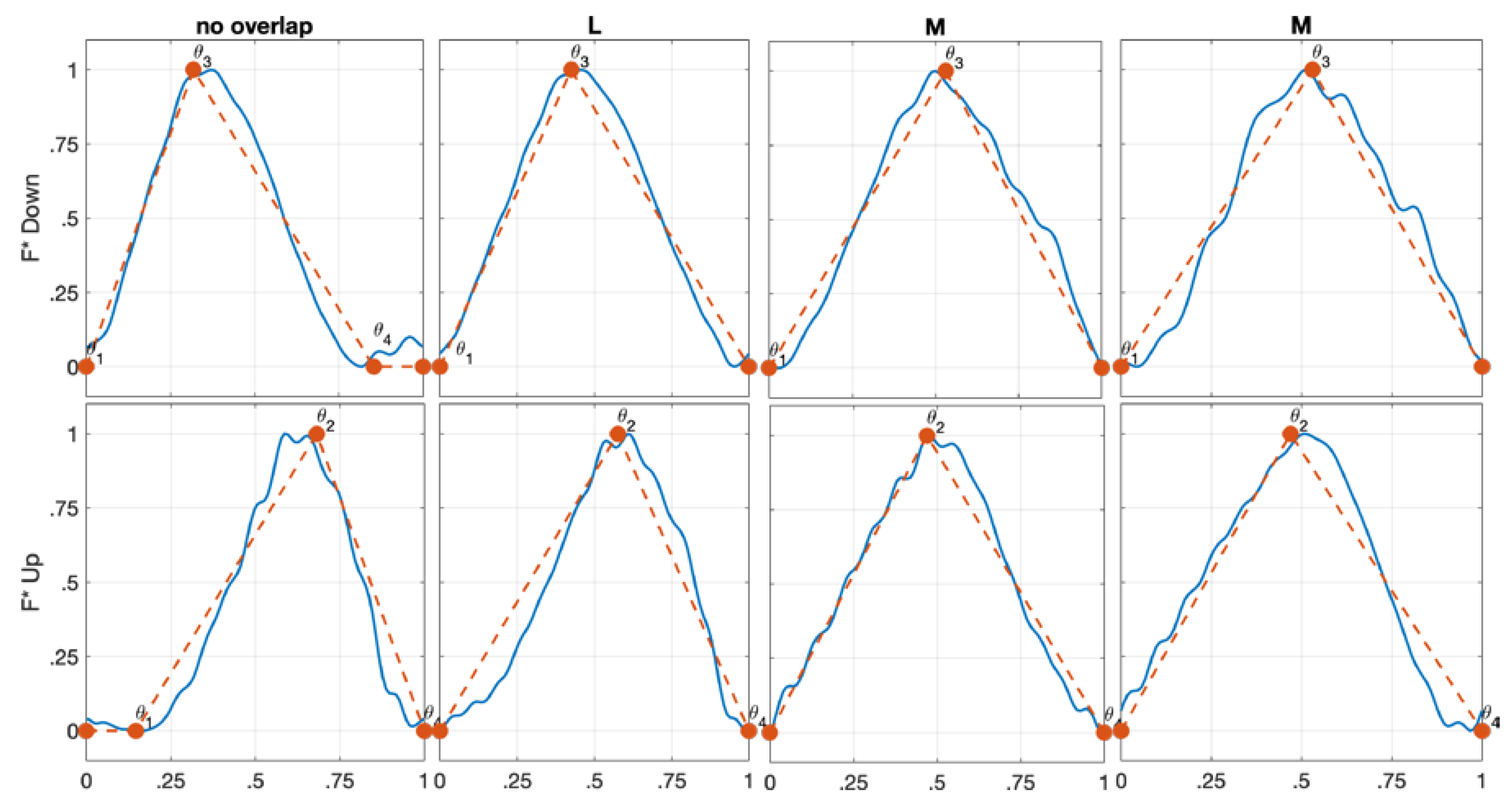
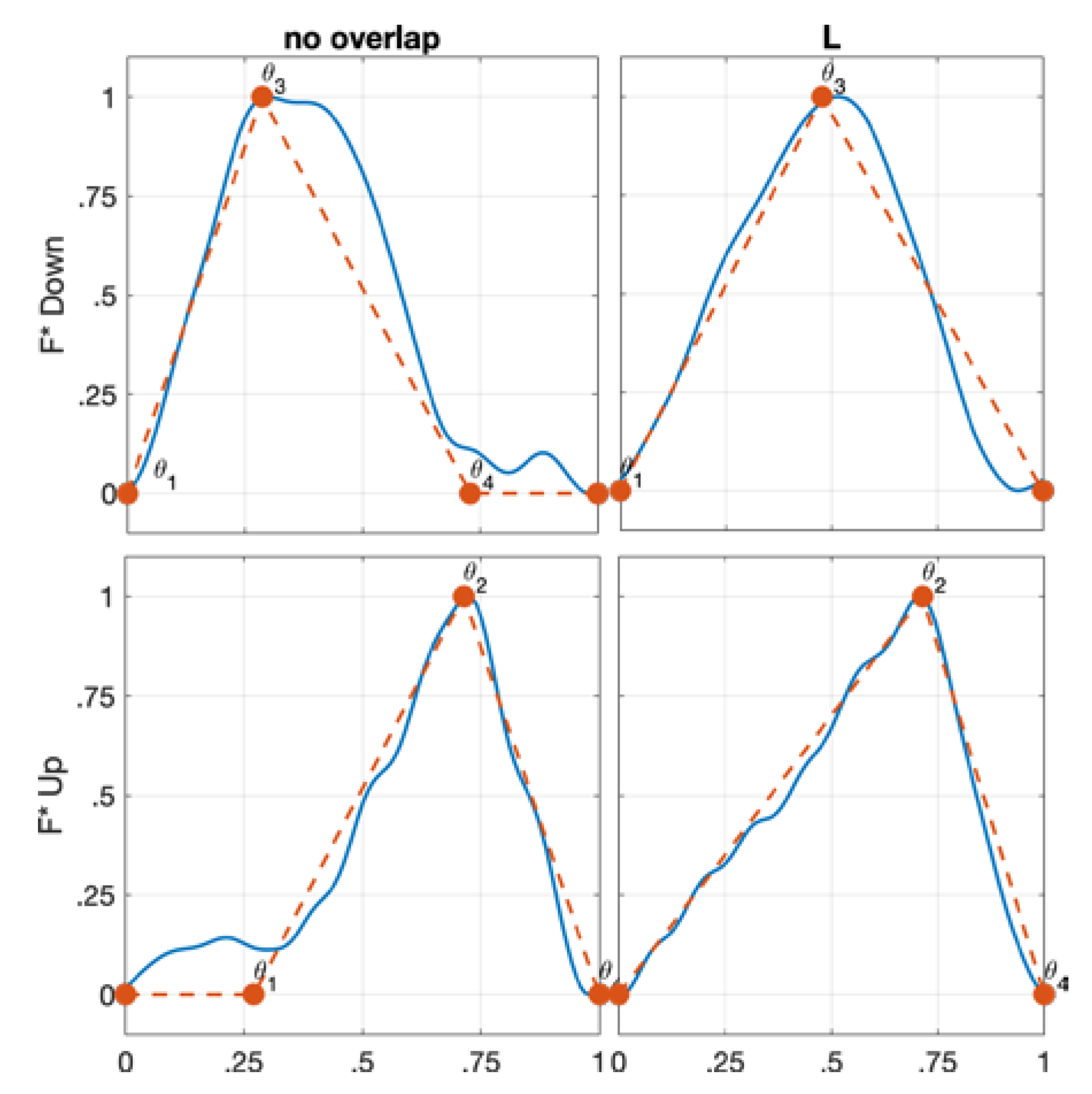
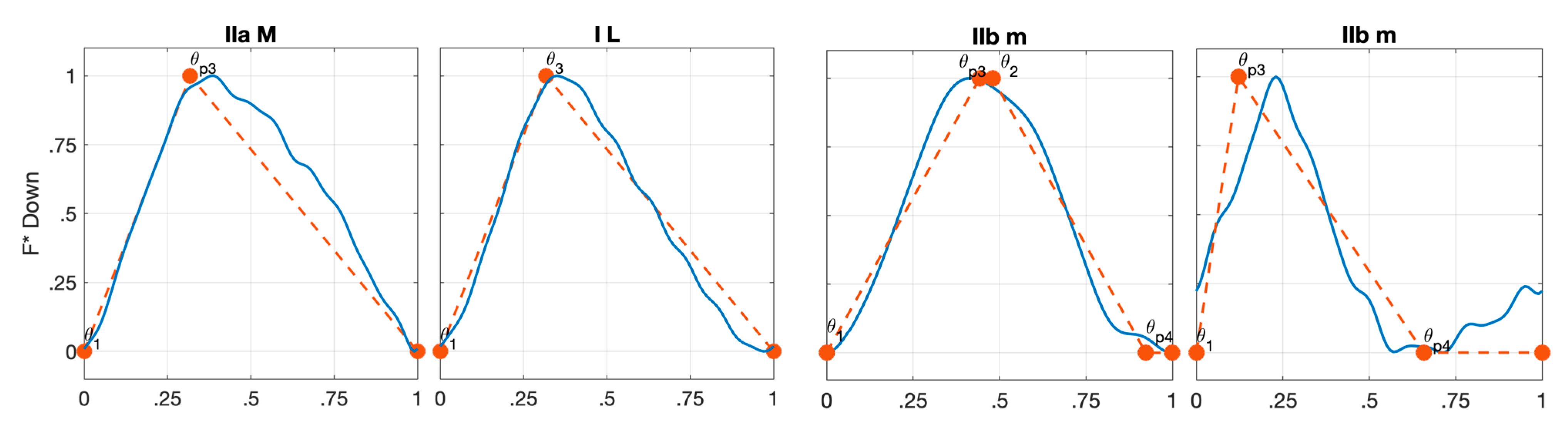
• Type I: This shape occurs when conservative cutting parameters are adopted, and it presents α_en greater than α_sw. In down-milling, this type is identified by three key points (ϑ₁, 0), (ϑ₃, 1), and (ϑ₄, 0). The type I shape reproduces a scalene triangle where the upper vertex, which represents the F maximum, is identified by ϑ₃ because it is the angular position where the cutting edge is fully involved in the cut and the chip thickness is maximum. In up-milling, this type presents a scalene triangle shape defined by three key points (ϑ₁, 0), (ϑ₂, 1), and (ϑ₄, 0). However, in this case, the F maximum is identified by ϑ₂ because this key angle, in up-milling, represents the condition of cutting edge fully engaged and maximum chip thickness.
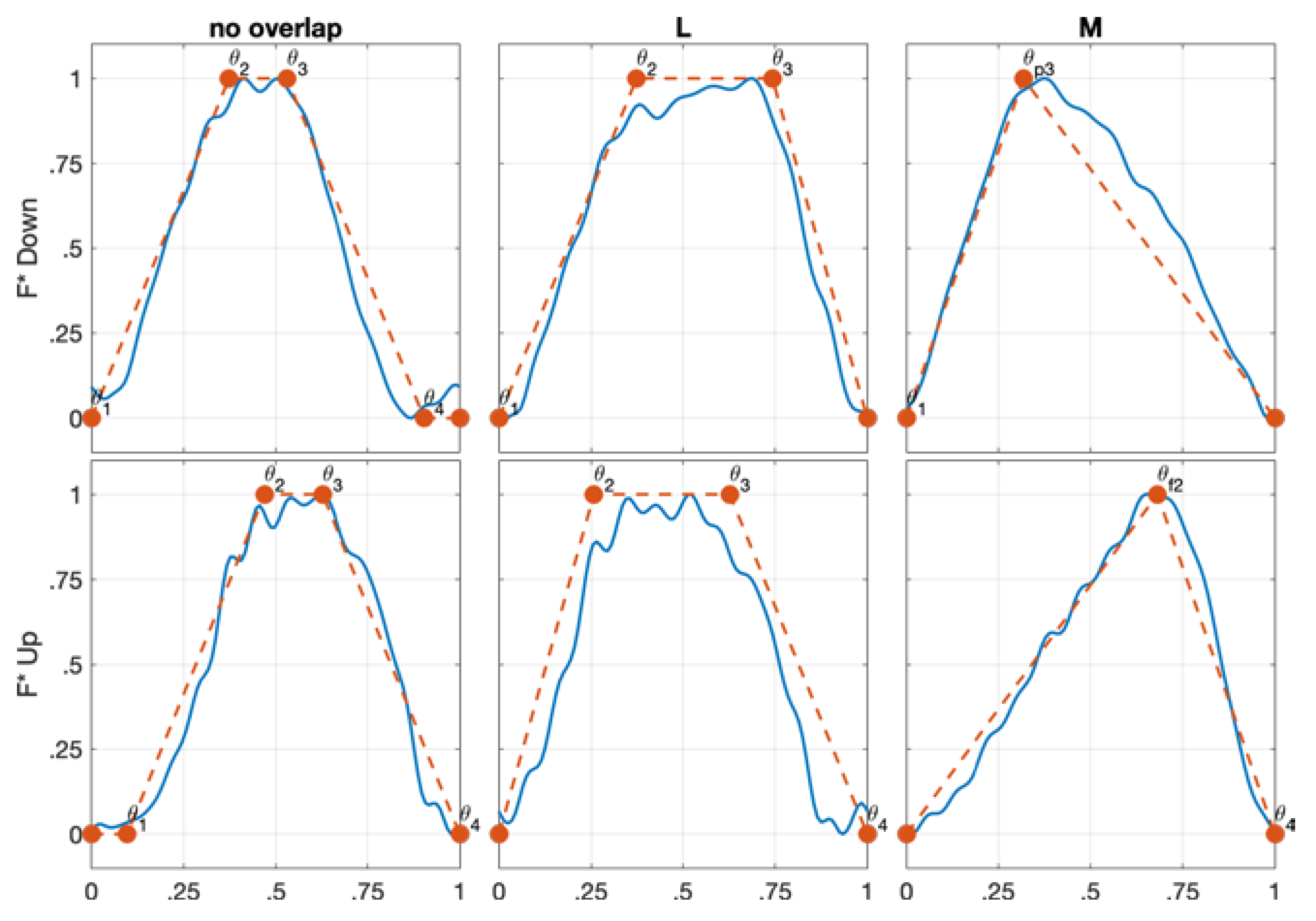
• Type II: This shape occurs when aggressive axial depths of cut are used, and it is characterized by α_sw greater than α_en. In both down-milling and up-milling, this type presents an isosceles trapezoid shape defined by four key points (ϑ₁, 0), (ϑ₂, 1), (ϑ₃, 1) and (ϑ₄, 0). In this case, the F maximum is identified by two different key angles because with high axial depths of cut the condition of cutting edge fully engaged and maximum chip thickness starts at ϑ₂ and continues up to ϑ₃. For this type, two subtypes are defined, IIa and IIb. The difference between type IIa and type IIb is related to the length of the upper base, which is less than half of the lower base length for type IIa and more than half of the lower base length for type IIb.
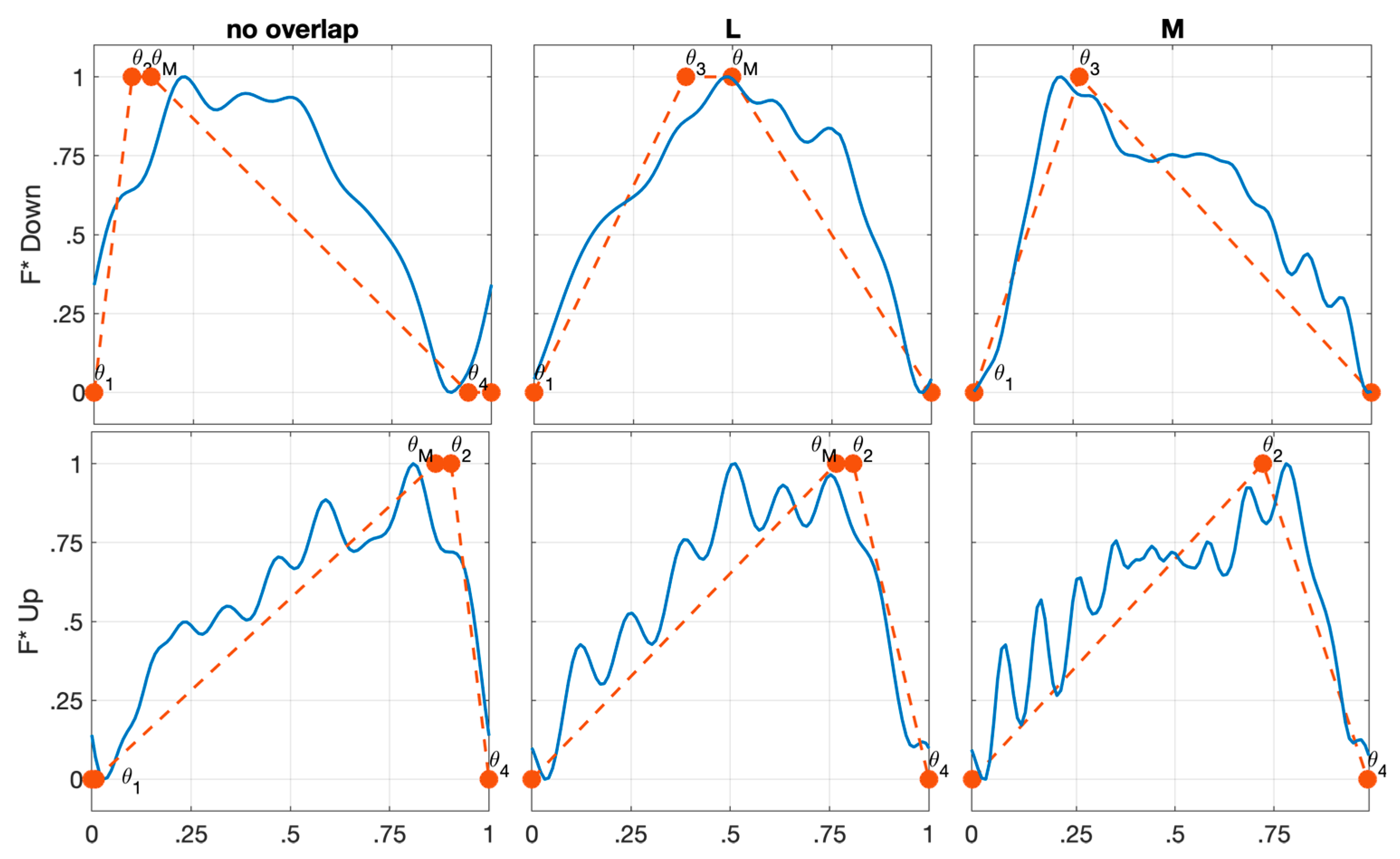
• Type III: This shape occurs when aggressive radial depths of cut are used, and it features α_en greater than α_enc. In down-milling, this type presents an acute trapezoid shape defined by four key points (ϑ₁, 0), (ϑ₃, 1), (ϑ_M, 1) and (ϑ₄, 0). The F maximum is identified by ϑ₃ and ϑ_M, but an important observation must be made. Indeed, ϑ₃ is the angular position where the cutting edge is fully engaged, while ϑ_M is the angular position where the cutting edge is fully engaged, and the chip thickness is maximum. Therefore, the effective value of F at ϑ₃ is smaller than the one at ϑ_M. Moreover, the magnitude value of F at ϑ₃ cannot be known without simulating the cutting force. For this reason, even if F is not effectively maximum at ϑ₃, the m value at ϑ₃ is assumed to be 1. This simplification allows a fairly accurate representation of the type III F shape, without any simulation of the cutting forces. In up-milling type III also presents an acute trapezoid shape identified by four key points (ϑ₁, 0), (ϑ_M, 1), (ϑ₂, 1) and (ϑ₄, 0). The same observation made for ϑ₃ and ϑ_M in down-milling applies to ϑ₂ and ϑ_M in up-milling.

The force profile types are shown in

Table 1. Single flute F type conditions.

	I	IIa	IIb	III
Down-milling	αen < αenc αsw ≤ αswc	αen < αenc αsw > αswc αen < 2αswc	αen < αenc αsw > αswc αen ≥ 2αswc	αen ≥ αenc αsw ≤ αswc
Up-milling	αen ≤ αenc αsw ≤ αswc	αen < αenc αsw > αswc αen < 2αswc	αen < αenc αsw > αswc αen ≥ 2αswc	αen ≥ αenc αsw ≤ αswc

with their occurrence conditions, a comparison between normalized cutting forces and the representation of the key points is shown in Figure 3. In detail, normalized cutting forces were obtained through numerical simulations using the cutting force model presented in [30] using 2000 points discretization for tool rotation and 1500 points discretization in the tool axis direction. Instead, key points for one period (from ϑ₁ to ϑ₁ + ϕ_z in down-milling and from ϑ₄ − ϕ_z to ϑ₄ in up-milling) are provided in

Table 2. Single flute F type key points.

	I	IIa	IIb	III
Down-milling	(ϑ1; 0) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ3; 1) (ϑM; 1) (ϑ4; 0)
Up-milling	(ϑ1; 0) (ϑ2; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑM; 1) (ϑ2; 1) (ϑ4; 0)

. It must be pointed out that a cutting operation characterized by α_en > α_enc and α_sw > α_swc cannot occur, as it is easily verifiable by comparing α_enc Equations (13) and (14) and α_swc Equation (6). The types described are suitable for any 3-axis milling operation in which only one flute is involved in the cut. Nonetheless, milling operations are usually characterized by a concurrent cutting of several flutes, therefore this classification must be extended to a multiple-fluted endmill (N > 1).

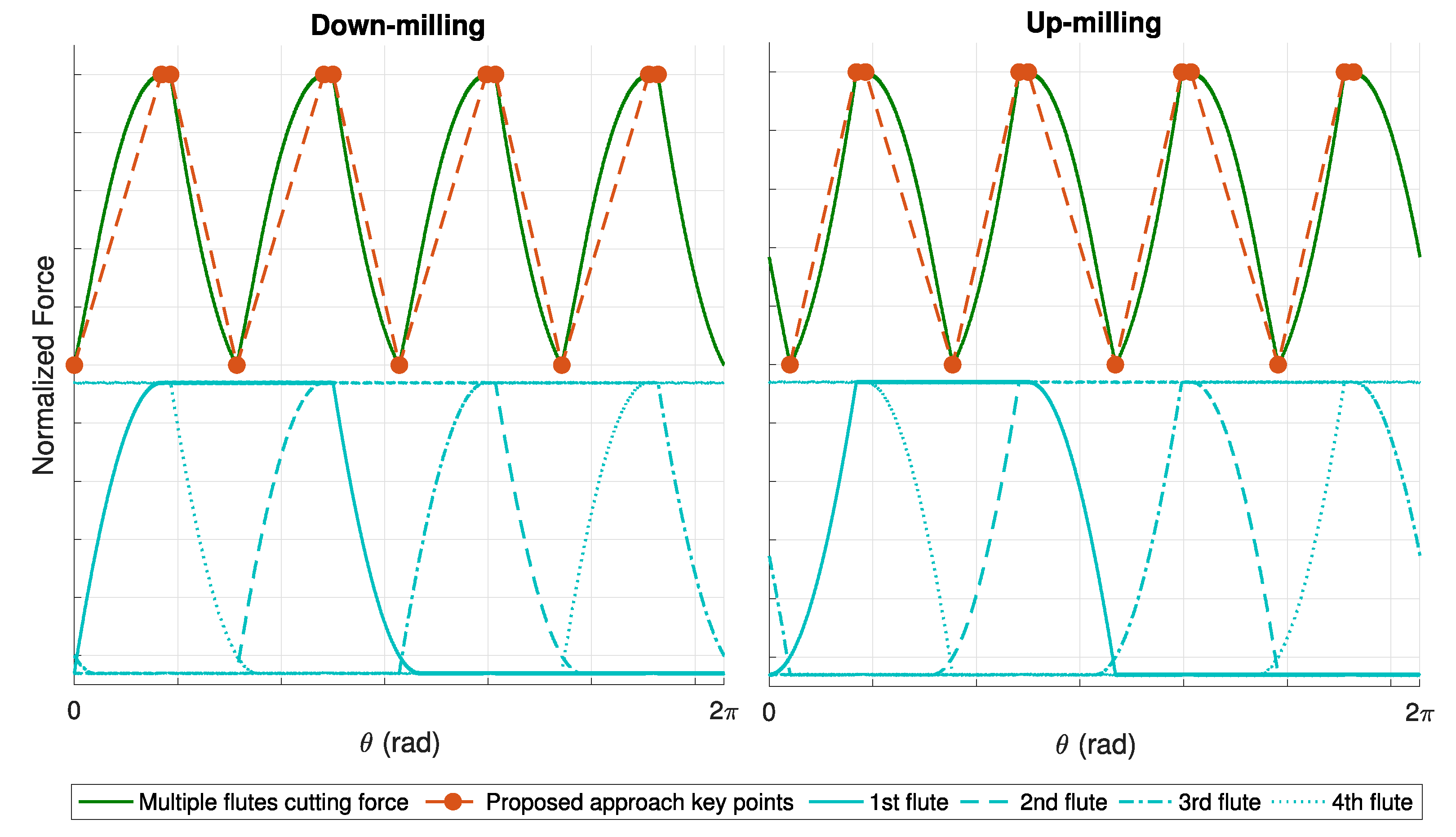
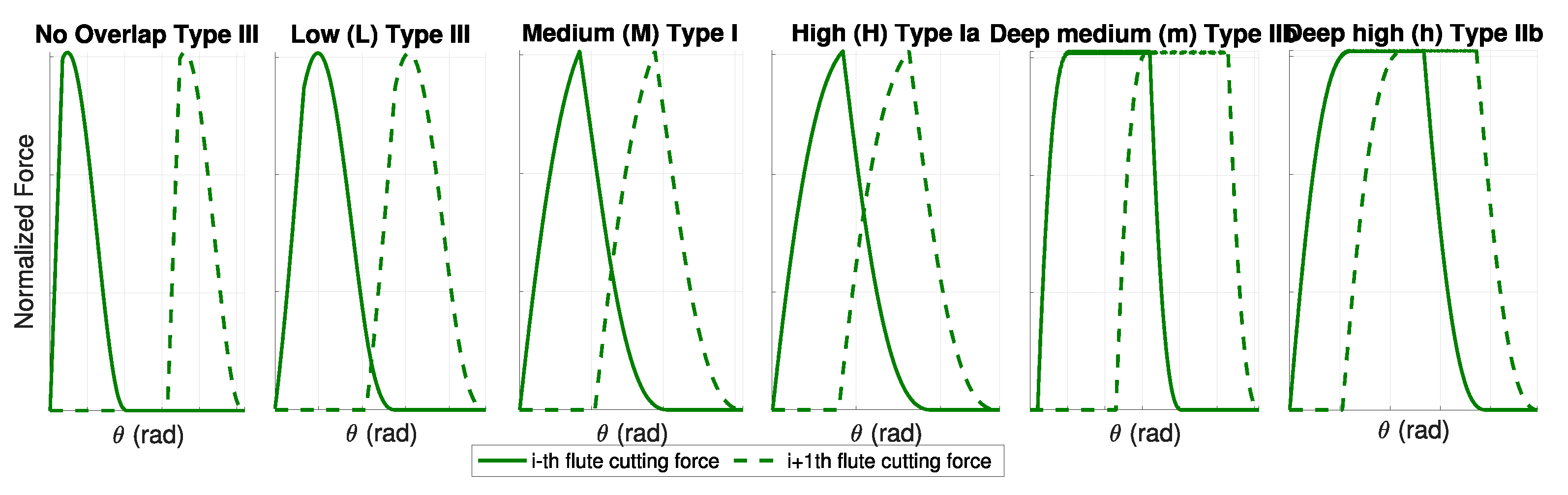
2.2. Shape Classification in Multiple-Fluted Endmill

In the previous section, all the F shapes for a single fluted endmill were distinguished in types. These types are now used to characterize the F shape for a general multiple-fluted endmill (N > 1). Indeed, the F shape for a multiple-fluted endmill can be conceived as the sum of multiple single flute F types as it is shown in Figure 4 for a four-fluted endmill. Hence, the multiple flute F shape can be characterized by analyzing how single flute F shapes of the same type may overlap. Considering the geometric aspects of each type, the amount of overlap between the generic i single flute F shape and the following i + 1 single flute F shape was classified into six different degrees, as it is shown in Figure 5. In detail, the degrees of overlap defined are:

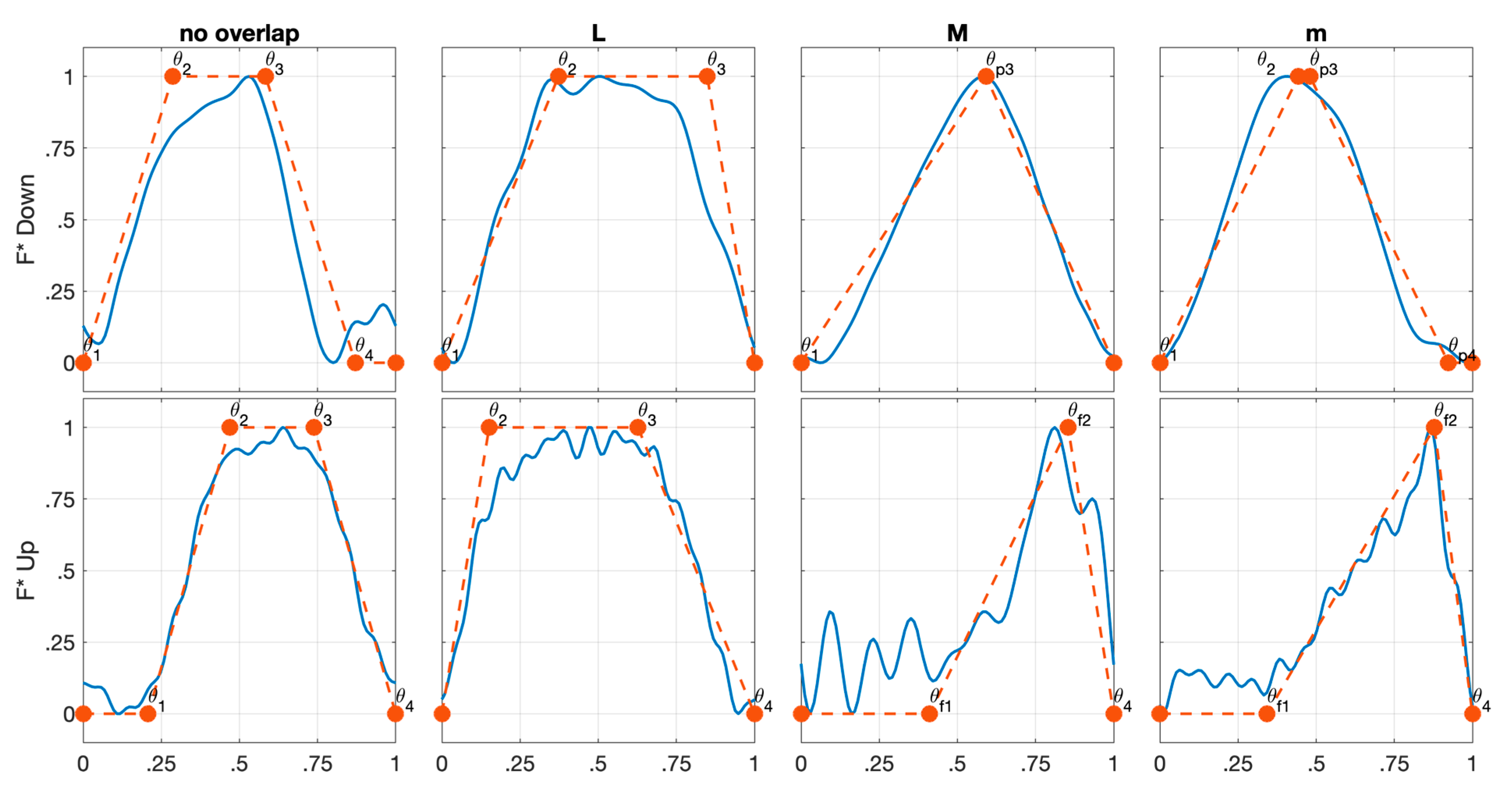
• No Overlap: This configuration applies to every type of single flute F shape, and it occurs when the generic i single flute F shape and the following i + 1 single flute F shape are not intersecting at all.
• Low Overlap (L): The low overlap condition involved all the types of single flute F shape. In detail, the low overlap takes place when the falling edge of the generic i single flute F shape affects the rising edge of the i + 1 single flute F shape.
• Medium Overlap (M): This overlap configuration is possible for every type as well. However, in this condition, the falling edge of the generic i single flute F shape alters two edges, rising and falling edge (type I, type III) or rising and constant portion (type IIa, type IIb), of the i + 1 single flute F shape.
• High Overlap (H): In the high overlap configuration the rising edge of the generic i single flute F shape affects the rising edge of the i + 1 single flute F shape. This case does not apply to type IIb.
• Deep medium overlap (m): The deep medium overlap verifies only for type IIb. In this condition the falling edge of the generic i single flute F shape influences the constant portion of the i + 1 single flute F shape, and, at the same time, the constant portion of the generic i single flute F shape influences the constant portion of the i + 1 single flute F shape.
• Deep high overlap (h): The deep high overlap applies to both type IIb and type IIa. In detail, this overlap occurs when the rising edge of the generic i single flute F shape affects the rising edge of the i + 1 single flute F shape, and, at the same time, the constant portion of the generic i single flute F shape alters the constant portion of the i + 1 single flute F shape.

In addition to type and overlap degree, the number of flutes involved in the cut (n) may significantly impact the multiple flutes F shape, especially in medium and high overlap configurations. Indeed, when n single flute F shapes are overlapping, it is crucial to define which key point of which single flute F shape is relevant for the resultant multiple flute F shape. Therefore, not only n but also the number of flutes involved in the axial engagement (called here v) becomes important to identify the key points for multiple flutes F shapes. For this reason, starting from the key angles for a single fluted endmill, a set of additional key angles for multiple flute F shapes are expressed for both down-milling and up-milling:

$${\vartheta }_{px}={\vartheta }_x-v{\varphi }_z x=1, 2, 3, M, 4 \left(down\text{-}milling\right)$$

(15)

$${\vartheta }_{fx}={\vartheta }_x+v{\varphi }_z x=1, 2, 3, M, 4 \left(up\text{-}milling\right)$$

(16)

$$v ~ {\alpha }_{sw}/{\varphi }_z$$

(17)

The m values corresponding to each additional key angle are defined according to the single flute F shape classification, so 0 is assigned when x is equal to 1 and 4, and 1 when x is equal to 2, 3, and M. The critical aspect for the key point representation of multiple flutes F shapes is related to the cutting parameters (ar, ap). Indeed, both the radial and axial depth of cut directly affect the slope of the edges of the single flute F shapes and, based on a number of flutes involved (n and v), some of the key points which may identify the F maximum for a single flute F shape, becomes irrelevant for the resultant multiple flutes F shapes. Therefore, to identify which key point is necessary to represent the multiple flutes F shape for a specific type/degree of overlap couple, a set of equations are proposed (18)–(23). These equations represent the conditions that must be fulfilled to make a key point relevant for the multiple flutes F shape.

$${\alpha }_{sw}+{\alpha }_{en}<2{\varphi }_z$$

(18)

$${\alpha }_{sw}+{\alpha }_{en}<\left( v+1\right){\varphi }_z$$

(19)

$$\exists i\in \left(0,1,\dots ,n\right) :{\alpha }_{en }+{\alpha }_{sw }-{\varphi }_z<{\vartheta }_2+i{\varphi }_z<{\alpha }_{sw } \left(down\text{-}milling\right)$$

(20)

$$\exists i\in \left(0,1,\dots ,n\right) :{\alpha }_{en }<{\vartheta }_3-i{\varphi }_z<{\varphi }_z \left(up\text{-}milling\right)$$

(21)

The Equations (18) and (19) are valid for both down-milling and up-milling, while the others apply to either down-milling (20) or up-milling (21). Considering the cutting conditions and the type/degree of overlap combination, the key points representing the multiple flutes F shape in one period (from ϑ₁ to ϑ₁ + ϕ_z in down-milling and from ϑ₄ − ϕ_z to ϑ₄ in up-milling) are presented in

Table 3. Multiple flutes F shape key points for one period (ϑ₁; ϑ₁ + ϕ_z) in down-milling.

	I	IIa	IIb	III
No Overlap	(ϑ1; 0) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ3; 1) (ϑM; 1) (ϑ4; 0)
Low (L)	(ϑ1; 0) (ϑ3; 1)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1)	(ϑ1; 0) (ϑ3; 1) (ϑM; 1)
Medium (M)	(ϑ1; 0) (ϑ3; 1)	(ϑ1; 0) (ϑp3; 1) (ϑp4; 0) if (18)	(ϑ1; 0) (ϑp3; 1) (ϑp4; 0) if (18)	(ϑ1; 0) (ϑ3; 1)
High (H)	(ϑ1; 0) (ϑp3; 1)	(ϑ1; 0) (ϑp3; 1)	n/a	(ϑ1; 0) (ϑp3; 1)
Deep medium (m)	n/a	n/a	(ϑ1; 0) (ϑ2; 1) if (20) (ϑp3; 1) (ϑp4; 0) if (19)	n/a
Deep high (h)	n/a	(ϑ1; 0) (ϑp3; 1)	(ϑ1; 0) (ϑp3; 1)	n/a

(down-milling) and

Table 4. Multiple flutes F shape key points for one period (ϑ₄ − ϕ_z; ϑ₄) in up-milling.

	I	IIa	IIb	III
No Overlap	(ϑ1; 0) (ϑ2; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ1; 0) (ϑM; 1) (ϑ2; 1) (ϑ4; 0)
Low (L)	(ϑ2; 1) (ϑ4; 0)	(ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑ2; 1) (ϑ3; 1) (ϑ4; 0)	(ϑM; 1) (ϑ2; 1) (ϑ4; 0)
Medium (M)	(ϑ2; 1) (ϑ4; 0)	(ϑf1; 1) if (18) (ϑf2; 1) (ϑ4; 0)	(ϑf1; 1) if (18) (ϑf2; 1) (ϑ4; 0)	(ϑ2; 1) (ϑ4; 0)
High (H)	(ϑf2; 1) (ϑ4; 0)	(ϑf2; 1) (ϑ4; 0)	n/a	(ϑ2; 1) (ϑ4; 0)
Deep medium (m)	n/a	n/a	(ϑf1; 1) if (19) (ϑf2; 1) (ϑ3; 1) if (21) (ϑ4; 0)	n/a
Deep high (h)	n/a	(ϑ1; 0) (ϑp3; 1)	(ϑ1; 0) (ϑp3; 1)	n/a

(up-milling). In both strategies, for type I and III, the multiple flutes F shape is easily identified by the proposed key points in any configurations, while for the other types (IIa, IIb) the proposed cutting conditions should be considered for the representation of the key points, for medium and deep medium overlap configurations. Furthermore, it is interesting to note that increasing the overlap degree, either by a reduced periodicity (i.e. increasing the number of flutes) or an increase of engagement conditions (i.e., ap and ar), the number of key points required to define the force shape is reduced. The proposed formulations are valid in peripheral milling, in the case of slotting (i.e., full immersion) overlaps may introduce different key points on the profile, caused by the change in the curvature of rising and falling edges.

3. Results and Discussion

3.1. Experimental Set-Up

Several milling tests were carried out to experimentally validate the proposed formulations and present the different force shapes. The tests were performed on a DMU 75 MONOBLOCK machine tool, provided by DMG MORI (Japan), on a stiff workpiece (50 × 80 × 90 mm) made of aluminum (6082-T4), clamped to a table dynamometer from Kitsler (Switzerland), model: 9257A to measure forces during the tests (Figure 6a). The dynamometer’s main characteristics are: ±5000 N of measuring range, 0.1 N resolution, 2.5 kHz resonance frequency (not considering machine-workpiece dynamics). Additional data are provided in the work of Scippa et al. where such device is used [31]. The different tool and cutting parameters combinations are presented in

Table 5. Endmill parameters.

Endmill	Tool ID	D (mm)	N	αhel (deg)	Cutting Length (mm)	fz (mm/Flute)	Spindle Speed (rpm)
202552	1	12	4	45	36	0.1	6366
202274	2	10	3	45	16	0.04	12,732

and

Table 6. Milling tests overview.

Test	Type	Overlap	Strategy	Tool ID	ar (mm)	ap (mm)	Error (%)
1	I	No Overlap	Down	1	2	3	4.2
2	I	Low	Down	1	3	4	3.3
3	I	Medium	Down	1	6	5	4.1
4	I	Medium	Down	1	6.5	5	1.9
5	I	No Overlap	Up	1	2	3	2.8
6	I	Low	Up	1	3	4	2.6
7	I	Medium	Up	1	6	5	0.1
8	I	Medium	Up	1	6.5	5	4.9
9	I	No Overlap	Down	2	2	3	3.9
10	I	Low	Down	2	3	5	2.1
11	I	No Overlap	Up	2	2	3	4.7
12	I	Low	Up	2	3	5	0.1
13	IIa	No Overlap	Down	1	1	5	5.2
14	IIa	Low	Down	1	1	7	6.8
15	IIa	Medium	Down	1	4	12.4	2.9
16	IIa	No Overlap	Up	1	1	5	4.2
17	IIa	Low	Up	1	1	7	9.8
18	IIa	Medium	Up	1	4	12.4	0.4
19	IIb	No Overlap	Down	1	0.6	5.5	13.7
20	IIb	Low	Down	1	1	8	17.1
21	IIb	Medium	Down	1	2.5	15	1.4
22	IIb	Deep Medium	Down	2	2	15	2.7
23	IIb	No Overlap	Up	1	0.5	5	9.5
24	IIb	Low	Up	1	1	8	14.1
25	IIb	Medium	Up	2	2	12	12.1
26	IIb	Deep Medium	Up	1	2	20	3.0
27	III	No Overlap	Down	2	6	1	25.3
28	III	Low	Down	2	8	4	6.3
29	III	Medium	Down	1	7.5	2.5	2.8
30	III	No Overlap	Up	2	6.5	1	18.5
31	III	Low	Up	2	7	2	11.0
32	III	Medium	Up	1	7.5	2.5	12.7
33	I	Low	Down	1	4	3	2.2
34	IIb	Deep Medium	Down	1	2	20	19.7

. These parameters have been designed to test the different categories classified in this work, both in terms of types and overlap degree. In particular:

• Two endmills were used to test different combinations of diameter and number of flutes: a four-fluted 12 mm tool (manufactured by Garant, Germany, model:202552, Figure 6b) and a three-fluted 10 mm tool (manufactured by Garant, Germany, model:202274, Figure 6c). Moreover, the two endmills allow testing of the same type and overlap configuration with different tool characters, as shown in this work for I type.
• The tools are characterized by the same helix angle equal to 45°, this value was selected since it is typical for the tested material (aluminum) and allows to achieve higher overlap degree with less aggressive parameters.
• Spindle speed and feed were selected for each tool according to the parameters suggested by the tool manufacturer and they were not changed in the different tests, since they did not affect the force shape, focus of the work.
• Depths of cut (ap and ar) were designed in order to perform the different types and overlap degrees, as found by the proposed approach. Indeed, as highlighted in the previous sections, it is not important the single value of ap or ar but the combination of both. Therefore, the couple of the depths of cut values were selected together to achieve the different configurations proposed in this work.
• The tests were repeated for Down-milling and Up-milling with slightly different parameters in order to return the same Type and Overlap configuration.
• The high and deep-high overlap configurations were not tested. These conditions required several flutes and aggressive cutting parameters (especially high ar), rarely employed in actual peripheral milling operations. Moreover, the high and deep-high overlap configurations often entail a simple triangle-shaped cutting force profile, less interesting to be investigated.
• Lastly, tests 33 and 34 were performed to highlight some differences between the similar tests, as presented in the discussion section.

Tool proprieties, spindle speed, and feed per tooth used are summarized in Table 5 for both tools. In Table 6 the different tests are reported, including engagement conditions and the combination type and overlap of the specific test. As highlighted in the table, almost all the classified configurations were tested, except for high and deep-high overlap.

For each test, the cutting forces were measured in the three normal directions (X, Y, Z) using the dynamometer. The measured forces were then compensated to reduce the distortion derived by the system dynamics [32,33] using the approach proposed by Scippa et al. [31], and post-processed to reduce measurement noise. As well as this, the impact of tool run-out was compensated as in [8].

Since the focus of the proposed method is the total force (i.e., resultant of the tangential and radial forces), the next step was the computation of such force by combining X-force (feed direction) and Y-force (cross-feed direction).

The measured forces were then normalized to assume values between 0 and 1, obtaining the unity based normalized total forces, called F* which is summarized by the following equation:

$$F^{*}=\frac{F_k-min\left(F\right)}{max\left(F\right)-min\left(F\right)}$$

(22)

where F_k is the generic k value of F in one period, while max (F) and min (F) represent the maximum and minimum values of F in one period.

The computed normalized total forces were grouped based on the type and shown in the next figures (Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10). The different F* were shown in the engagement angle range corresponding to one period, which is equal from ϑ₁ to ϑ₁ + ϕ_z in down-milling and from ϑ₄ − ϕ_z to ϑ₄ in up-milling. To improve the readability of the figures, even engagement angle has been normalized between 0 and 1. For each test key points were predicted, computing their key angles and related magnitude binary values (m). In detail, key points are shown in the figures (red dot line) along with experimental normalized total force (blue solid line). Moreover, the error between the key points and the experimental results was computed as:

$$error=mean\left(F^{*}\left({\vartheta }_x\right)-m\left({\vartheta }_x\right)\right)$$

(23)

where mean is the average value, F* and m are the normalized experimental force and the magnitude value respectively, at the defined ϑ key angles. In Table 6 such error is reported for each test. It is crucial to point out that the proposed method does not aim to predict cutting force in time-domain, indeed it is not a cutting force model, but provides an understanding and classification of the force shapes and the key points that characterize them, without the need of any approximation of modeling approach. Therefore, the error values should not be considered as the only metric to assess the accuracy of the proposed approach. Indeed, measurement issues (e.g., noise in the cutting force measurements) could lead to inaccuracies in normalizing the experimental force, leading to a high value of the error, even in case of good agreement between measured and expected force shape. On the other hand, a low value of error could be computed between key points and measured forces, even in case of poor matching with the expected force shape.

3.2. Experimental Results

Forces for type I with tool 1 (tests 1 to 8) are presented in Figure 7 for different levels of overlap both in down-milling (first row) and up-milling (second row). The typical triangle-like shape is identified for all the forces and the proposed formulations correctly predict the key points of the profile, both in terms of key angles and magnitude (error less than 5%).

In case of no overlap, the number of points characterizing the profile is higher, since the engagement angle is smaller than ϕ_z, highlighting that tool edges are not always in contact with the workpiece. In case of higher degrees of overlap, the shape is characterized only by two points both in down-milling (ϑ₁ and ϑ₃) and up-milling (ϑ₂ and ϑ₄).

It is interesting to underline the differences between the two M overlap profiles both in down and up milling. Indeed, in down-milling passing from test 3 to test 4, the increase of radial depth of cut from 6 mm to 6.5 mm (ap 5 mm), does not move the position of ϑ₃ (affected only by ap). On the contrary, in up-milling, with the same cutting parameters, passing from tests 7 to 8, both ϑ₂ and ϑ₄ positions are affected by the radial depth of cut (α_en), however, since the influence of α_en on the two key points is the same, the cutting force profile in the range between ϑ₄ − ϕ_z and ϑ₄ are not changing. Therefore, the two M cases for both down-milling and up-milling present the same key points, since only the radial depth of cut is changed. This is a crucial aspect, confirming that the key points of the normalized force profile are not a univocal parameter for the engagement conditions identification. Nonetheless, it can be noted that the curvature of the ϑ₁ − ϑ₃ portion in down-milling and the curvature of the ϑ₂ − ϑ₄ portion in up-milling change with the radial depth of cut, suggesting this aspect as an additional parameter to investigate.

In Figure 8 type I with tool 2 (tests 9 to 12) is presented. The same good agreement between experiments and proposed formulations observed for tool 1 can be found with the new tool, as confirmed by the error of less than 5%. In this case, only no overlap and low overlap cases are investigated, since higher degrees of overlap require too aggressive parameters due to the reduced diameter and the low number of flutes.

In Figure 9 cutting forces in both down-milling and up-milling, classified by the proposed approach as IIa type are shown in the three different configurations: no overlap, low overlap (L), and medium overlap (M). As in the previous cases, the proposed key points are in good agreement with the shape of the normalized cutting force, both in terms of error and shape. Higher error (around 10%) is found for the two IIa L configurations, probably because the noise in the force measurement is critical in normalizing cutting force with a large flat zone, leading to an underestimation of such zone with respect to the m value. However, as predicted by the proposed approach, a trapezoidal shape is found in no overlap and low overlap configuration, with the first characterized by an additional point. Starting from medium overlap the shape is characterized by two points, assuming a triangle-like shape as expected. Indeed, the high degree of overlap leads to the superimposition of the single flute profiles, generating this typical profile, as it is found in the experimental results and accurately predicted by the proposed formulations both in terms of angles and normalized magnitude.

Figure 10 shows the F shapes for type IIb in four different configurations, no overlap, low overlap (L) medium overlap (M), and deep medium overlap (m) for both down-milling (first row) and up-milling (second row). The comparison with the predicted shapes shows a very good match, with small deviations in down-milling for no overlap and low overlap. These deviations are found also in the error that in such configuration increase till almost 15%. The reason is the same presented for type IIa (i.e., noise influence in the normalization of the force) but increased since the flat zone in IIb is generally larger. Focusing on shape, for the first two overlap degrees same consideration of IIa type can be made regarding the trapezoidal-like shape of forces. Increasing the degree of overlap, different configurations can be found. Indeed, for M overlap in up-milling Equation (19) is verified and an additional key point (ϑ_f1) is found and predicted (Table 4). Likewise, for the m overlap, engagement conditions in down-milling ensure the presence of two additional points (ϑ₂ ϑ_p4) because both Equations (20) and (21) are verified, while in up-milling only additional ϑ_f1 is predicted since only Equation (20) is verified. The predicted profiles are validated by the experimental results both for angles and normalized magnitude. F shapes for type III in three different configurations (no overlap, L and M overlaps) are presented in Figure 11. Since low ap is adopted in these configurations, a lower signal-to-noise ratio in the cutting forces is experienced and the formulations are found less accurate than the other types (average error of 13% with peak to over 20%). However, experimental forces fairly agree with the predicted key points. Indeed, it must be noted that the points ϑ₃ in down-milling and ϑ₂ in up-milling are expected to be at a lower magnitude position with respect to ϑ_M, as explained in Section 2.1, and this causes an increase of the computed error. Moreover, with high ar, such as the one characterizing the III type, a high curvature in falling (down-milling) or rising (up-milling) edges is expected.

In the no overlap configuration four points are predicted, since the engagement configuration is close to L overlap, the portion of engagement angle corresponding to no cutting is small, especially in up-milling, resulting in high proximity of points (ϑ₁ and ϑ₄). In the L overlap configuration three points are defined by the proposed formulations and accurately found in the experimental cutting forces, considering the expected discrepancy in terms of magnitude for ϑ₃ in down-milling and ϑ₂ in up-milling (as in Figure 3) with respect to ϑ_M. Experimental results for M configurations (tests 29 and 32) confirm the proposed key points, presenting a triangular shape deformed by the high curvature of the falling (down-milling) or rising (up-milling) edge, as expected.

Finally, in Figure 12 two noteworthy comparisons are presented: test 15 with test 33 and test 22 with test 34. In the first comparison (left side in Figure 12), two tests with a different axial depth of cut, type, and overlap but the same radial depth of cut are presented. Although very different, they present the same key points. Indeed, it must be pointed out that, according to the proposed formulations, the same predicted key points can be achieved by increasing the axial depth of the cut of specific values. Of course, experimental cutting forces are not the same in the two cases in terms of both force magnitude (the equivalence is valid for normalized values) and shape of the edges, as is clear from the figure and the previously described results. The second comparison (right side in Figure 12) presents the same type (IIb) and overlap (m) but with different engagement conditions, resulting in different cutting force profiles. This result confirms that the proposed formulations, as it is summarized in Table 3 for down-milling and Table 4 for up-milling, in a specific type and overlap combinations, include the potential occurrence of several points in the cutting force profile, but their presence depends on additional conditions Equations (18)–(21).

In summary, the experimental results show a good agreement with the proposed cutting force shape classification. Moreover, the experimental forces feature similar positions of key points compared to the ones expected. Small errors are found for type I, higher error for types II and III, for most of the results this is probably due to noise in the measurements that affect the normalization of forces and result in a high error, even if the shape was accurately estimated. Indeed, types II and III are characterized by higher depths of cut, resulting in higher forces and hence vibrations.

4. Conclusions

The total cutting force shape is not unique and varies according to cutting strategy, tool geometry, and cutting parameters. In this paper a comprehensive classification of total cutting force shape is presented, proposing four types of single-flute shape (I, IIa, IIb, III) and six configurations of overlap (no overlap, L, M, m, H, h). For each one of the types proposed, analytical formulations to predict force shape, as key points, are provided in terms of both key angles and the normalized magnitude value. The proposed formulations describe the normalized cutting forces (i.e., cutting force transformed in the maximum-minimum range, 0–1), at these characteristic points. These formulations, valid for the single-fluted endmill, are extended to a multiple-fluted endmill, by considering the different degrees of overlap. All the proposed formulations are based only on cutting strategy, tool geometry, and cutting parameters and do not require any cutting force model or cutting coefficients to be used. The main achieved results can be summarized in:

• A comprehensive model-independent classification of total cutting force shapes, including multi-flutes cutting simultaneously;
• Specific depths of cut conditions in which the different shapes occur;
• Analytical equations to predict key points of the total force shapes both in terms of key angles and magnitude;
• Thanks to the proposed formulations, it is possible to know in advance the expected shape of the cutting force without the need for any simulation or cutting force model.

The proposed method has been extensively validated through several milling tests in most of the conditions proposed by the classification. The results show a good agreement between the predicted key points and the actual ones on the measured cutting force profiles in all the tested types and overlaps combinations.

A potential application of such formulations could be the simulation or measurement of cutting forces only at the specific key angles, drastically reducing the time required for these tasks, still returning an accurate representation of the total cutting force.

Furthermore, the characteristic shape of the cutting force identified in this work could form the basis of a monitoring solution for the identification of engagement conditions in milling. However, it is highlighted that the key points of the normalized cutting forces are not unique for a specific set of cutting parameters, cutting strategy, and tool geometry since the same key points could be found in different conditions. Therefore, to fully take advantage of the proposed formulations for monitoring purposes it is suggested to include additional parameters, such as cutting force magnitude or shape characteristics (e.g., rising or falling edge curvature).