An Efficient Methodology towards Mechanical Characterization and Modelling of 18Ni300 AMed Steel in Extreme Loading and Temperature Conditions for Metal Cutting Applications

Abstract

A thorough control of the machining operations is essential to ensure the successful post-processing of additively manufactured components, which can be assessed through machinability tests endowed with numerical simulation of the metal cutting process. However, to accurately depict the complex metal cutting mechanism, it is not only necessary to develop robust numerical models but also to properly characterize the material behavior, which can be a long-winded process, especially for state-of-stress sensitive materials. In this paper, an efficient mechanical characterization methodology has been developed through the usage of both direct and inverse calibration procedures. Apart from the typical axisymmetric specimens (such as those used in compression and tensile tests), plane strain specimens have been applied in the constitutive law calibration accounting for plastic and damage behaviors. Orthogonal cutting experiments allowed the validation of the implemented numerical model for simulation of the metal cutting processes. Moreover, the numerical simulation of an industrial machining operation (longitudinal cylindrical turning) revealed a very reasonably prediction of cutting forces and chip morphology, which is crucial for the identification of favorable cutting scenarios for difficult-to-cut materials.

1. Introduction

The numerical simulation of metal cutting operations has become an everyday practice to assist in the design of better cutting tools and in the optimization of cutting conditions aiming to improve the performance of the machining processes. This is because, in a general sense, numerical simulation of manufacturing processes has scientifically matured and become consolidated as engineering commercial software packages. The quality of the numerical predictions in metal cutting simulation depends mainly on how accurate the constitutive models are to describe the tribo-thermomechanical response of the workpiece materials in a given application. This is of tremendous importance in a context of metal cutting simulation where plastic deformation, fracture, and friction occur under extreme conditions of strain, strain rate, temperature, and complex state-of-stress which make mechanical and tribological testing challenging and leading frequently to intricate the calibration of constitutive parameters by inverse analysis. Similar constitutive model calibration challenges are also being experienced in other manufacturing technologies, such as electromagnetic forming and friction stir welding.

The development of constitutive models and experimental methodologies for the calibration of input data towards the numerical simulation of metal cutting has made significant progress over the last years, especially those considering the state-of-stress influence (i.e., stress invariants) on flow stress and damage [1,2]. Numerical estimates are now closer to laboratory measurements, or even to industrial machining operations measurements. Despite the increasingly good quality of these numerical estimates, the steady progress in materials science and cutting tools promotes the complexity of constitutive modelling, leading frequently to intricate calibration procedures. Typically, a significant number of tests is required to allow the identification of a vast number of model coefficients to better describe the mechanical and tribological response in a given application [3]. In parallel to material improvements, the increasing performances of the manufacturing processes (e.g., high-speed machining) makes input data calibration even more challenging and a time-consuming process each year.

Input data calibration is complex and involves a large number of experimental and theoretical procedures. Some of them are based on long-established laboratory tests, while others use “trial and error” inverse methods to calibrate a constitutive model. Fracture and tribological contributions can significantly expand the already time-consuming calibration procedure of a simple thermo-viscoplastic constitutive model. To put it in another way: calibration should be able for accompanying changes and requirements of the industrial sector, not hindering its development. Therefore, in order to properly handle the model complexity during calibration, the tuning process of the model coefficients requires a deep understanding of the manufacturing process and what assumptions on the mechanical and tribological characterization can be made. Indeed, each manufacturing process has its own specificities, being advantageous to simplify the numerical problem aiming to reduce the computational costs, without penalizing the quality of the theoretical estimates [4]. Likewise, there should be a concern to simplify constitutive model data calibration, which limits the usage of unnecessary experimental and theoretical procedures. This is not an obvious exercise since mechanical and tribological response under typical metal cutting conditions are highly nonlinear, influenced by temperature, state-of-stress invariants (e.g., hydrostatic pressure), and with strong rate dependencies [5].

The uniqueness of the model coefficients values is also of concern, since different coefficients sets can be generated for the same material and constitutive model, depending on the used calibration methodology and experimental techniques. For example, experimental techniques such as the split-Hopkinson pressure bars are commonly employed, despite having a loading signature distinct from the chip formation mechanics [6]. Similarly, pin-on-disc tribometers are regularly employed despite the low contact pressure and existence of metallic oxides, different from the tribological condition in the tool-chip contact interface [7,8]. Even though these traditional mechanical and tribological tests are not able to guarantee the desired accuracy, they are commonly used in the direct calibration of the model coefficients for metal cutting simulation. This is due to scarcity of specific apparatus able to reproduce realistic operative conditions of metal cutting processes under laboratory-controlled conditions and time-consuming experiments. Maybe due to this, most of the published research in metal cutting modelling is based on inverse calibration methodologies [9].

The inverse calibration methodologies are based on the reverse simulation of previously performed experiments in order to determine the best set of coefficients that allows for a better correlation between the numerical estimates and the experimental measurements. Typically, the model coefficients are adjusted in order to replicate the experimental load-time histories and the stress and strain fields. Most of these experiments are based on simulative tests, such as the orthogonal cutting test and even practical metal cutting operations. The accuracy of the constitutive models increases with the diversity of experiments to be replicated by the numerical methods. Although some phenomena are omitted in order to simplify the numerical problem and some coefficients reportedly differ from what should be physically expected, it appears that inverse calibration methodologies are able to collect some of these statistics and can usefully be directed to support numerical modelling of metal cutting processes [10,11].

The majority of constitutive models used in the numerical simulations of metal cutting considers only the plastic deformation contribution to represent the material response during the chip formation, neglecting the damage and consistently omitting the contribution of the ductile fracture. However, the model coefficients are very sensitive to small changes in the metallurgical conditions of the workpiece material. This is particularly relevant for difficult-to-machine materials such as super-alloys, stainless steels, maraging steels, and titanium alloys, among others. The same applies to the process by which the workpiece material is obtained (e.g., additively manufactured materials). The combination of these two factors requires special attention from the point of view of the constitutive modelling. For example, machining post-processing stages of additively manufactured metallic parts bring to focus the importance of machinability assessment. The difficulty in machining such materials with standard tools and cutting parameters has recently been the focus of research as reported in the literature. For example, Marbury et al. [12] reported tool breakage when applying standard cutting parameters thought for conventionally manufactured (CMed) 316 L stainless steel, on the AMed counterpart. On the same alloy, Leça et al. [13] have shown that porosity directly influences the cutting loads and reported a relationship between chip segmentation and relative density. Focusing on the effect of cutting velocity, Bai et al. [14] have compared the machinability of the AMed A131 steel with its conventional counterpart, focusing on the effect of cutting speed. The authors state that the microstructure differences between AMed and CMed materials (existence of melt pools, layer construction, and porosity) impact directly on chip morphology (continuous for the CMed), cutting forces and tool wear (higher for the AMed). Such relative decrease in the machinability of AMed parts has motivated several authors in finding the most appropriate cutting parameters for their processing.

Additively manufactured 18Ni300 maraging steel was selected for this research to better illustrate the need to move in two directions at once: on the one hand, develop an accurate constitutive model calibration for complex thermo-viscoplastic material respons and, on the other hand, optimize the cutting conditions on a new and emerging difficult-to-machine material. In what follows, a combination of experimental tests and adequate numerical methodologies are presented, to help the effective and practical calibration of constitutive models for metal cutting simulation. Therefore, the present study focuses on the mechanical and tribological characterization, accounting for the influence of the strain rate and temperature, as well as the state-of-stress. The choice of the characterization tests and specimen geometries were based on a logical flow to support the input data calibration with physically representative values and its sensitivity to the operative conditions. With the goal of numerically simulate the metal cutting processes, an extensive mechanical characterization of the AMed 18Ni300 maraging steel has been performed. A coupled plastic-damaged model based on Johnson–Cook model was employed and model coefficients determined using a combined direct characterization and inverse calibration procedure. The constitutive model validation was done by comparison of calculated and experimental load and chip curling for orthogonal metal cutting tests. Finally, the validated numerical model has been successfully used in simulations of industrial turning operations performed on AMed 18Ni300 maraging steel.

2. Efficient Methodology for Constitutive Modelling Calibration

This section proposes a progressive and efficient calibration procedure for constitutive modelling and numerical simulation in the metal cutting domain (refer to Figure 1). This procedure seeks a compromise between the direct characterization of physical parameters and the inverse calibration of theoretical models for a quick and effective determination of the constitutive model coefficients. A minimum set of complementary mechanical and tribological tests were selected. These experimental tests allow to reproduce the typical operative conditions similar to those of real metal cutting processes, some allowing to obtain absolute reference values (e.g., yield stress, flow stress under uniaxial compressive loading and friction coefficient at room temperature), whereas others relate to assessing the sensitivity of the mechanical and tribological response to the extreme operative conditions of metal cutting (e.g., strain rate, temperature, triaxiality). Regarding the material modelling, the Johnson–Cook model was selected as the basis since it is one of the mostly used material laws, as well it is available in most of the commercial FE codes. It is commonly believed that the Johnson–Cook model is able to reproduce flow stress behavior of materials under uniaxial impact loading and high temperatures [15].

Tensile testing is one of the most common mechanical tests performed on materials. It provides a simple, accurate, and direct characterization of the material yield stress and flow stress–strain behavior until fracture, which occurs under a positive stress triaxiality (e.g., triaxiality equal to 0.3 or higher) and Lode angle parameter equal to unity. Under these stress conditions, fracture strain is a function of stress triaxiality, being common reduced plastic strains at failure for high stress triaxialities, e.g., effective strains of 0.1, even for ductile metallic alloys. The tensile test is typically performed using universal testing machines capable of being used for a maximum strain rate of 10 s⁻¹ and the occurrence of necking hinders the direct characterization after the necking onset. Non-uniform stress–strain fields during necking impact on stress triaxiality and therefore on the effective strain at failure. After necking, inverse characterization techniques are the most common approaches.

Notwithstanding the foregoing, given the loading signature of metal cutting, it appears logical to complete the mechanical characterization with the uniaxial compression test to undergo high plastic strains (e.g., effective strains up to 1 or above) without cracking due the negative state of stress (e.g., triaxiality of −0.3 or lower and Lode angle of −1). This mechanical test can be carried out using impact testing machines (e.g., strain rates of 10⁴ s⁻¹) inside furnaces (e.g., 750 °C). Contrarily to tensile tests, compression tests allow a direct characterization of the material flow behavior under severe plastic deformation. In addition, they allow for sensitivity analysis concerning the operative conditions influencing the material response rate- and temperature-dependent mechanical characteristics, which is hardly achieved by means of tensile tests under such severe conditions [16].

For reasons of simplification, it is considered that the rate- and temperature-dependent characteristics are independent of the state of stress and can be adequately determined by the uniaxial compression test. These uncoupled effects hypothesis is the basis of the Johnson–Cook constitutive model for the flow stress [17]. This rate- and temperature-dependent response under uniaxial compression can subsequently be generalized to the entire range of triaxialities and Lode angle parameters combinations (axisymmetric tensile and plane strain tests), where the mechanical testing under high strain rates and elevated temperatures are extremely difficult or even impossible to accomplish. As a clear example of this complementarity, the material flow stress which can be determined by the double-notch plane strain test introduced by Abushawashi et al. [18] (quasi-static and room temperature) to better representing the metal cutting conditions, can be further enhanced by the rate- and temperature-dependent sensitivity determined by uniaxial compression testing under high strain rates and elevated temperatures.

Although the compression test simulates the operative conditions (i.e., strain rate and temperature) of the metal cutting processes, the friction between the cylindrical specimen and the compression platen promotes an overestimation for the flow stress. The flow stress should be corrected by subtracting the contribution of the frictional energy. This can be done by performing ring compression tests using the same compression apparatus and thus maintaining constant the tribological interface for all mechanical tests. The ring-shaped specimen is compressed between two flat platens with (similar to the compression test) and without lubrication (similar to dry friction of metal cutting), and the experimental evolution of the inner diameter is measured as a function of the specimen height. The friction coefficient is determined by correlating the experimental measurement of the inner diameter and the friction calibration curves. These calibration curves are inversely determined by numerical simulation, changing the friction coefficient in order to reproduce the experiments. However, an optimization-based procedure is needed for an inverse determination of the flow stress curve under frictionless conditions, and new friction calibration curves and a friction coefficient should be determined. After, the achieved input data for the numerical simulation of the compression test (frictionless flow stress and friction coefficient value) should provide an accurate loading-displacement curve. The method is confirmed to provide flow stress curves within an error of 5%. It is worth noting that the ring test can be carried out in the impact testing machine under the extreme conditions of pressure, strain rate and temperature of the practical machining processes.

The above mentioned procedure has traditionally been considered acceptable for calibrating input data parameters for the numerical simulation of metal cutting processes. However, the radial expansion (compression) and the radial reduction (tensile) of the commonly used mechanical tests may differ from each other, and from the desired plane strain conditions of the chip formation mechanics (refer to Figure 2). This is of relevance when the mechanical response of engineering materials (e.g., flow stress curve, critical damage), which includes the recent AMed metallic alloys, exhibits high sensitivity to the state of stress (e.g., stress triaxiality, Lode angle). The literature shows appropriate procedures to account for the influence of the state-of-stress in the constitutive modelling [19] based on a combination of tensile, compressive and shear tests and inverse calibration methodologies. The geometry of the test specimens plays a determinant role in the resulting state-of-stress of the plastic zone to better replicate the micro cracks initiation and damage propagation occurring in manufacturing processes [20]. The coupled plastic-damage model should be able to capture and reproduce that influence of the triaxiality and Lode angle on the mechanical response of the workpiece material. An adequate selection of the constitutive model and related calibration methodologies can significantly influence the quality of the numerical estimates. The accuracy of the numerical models increases with the range and combination of the triaxiality and Lode angle considered in the inverse calibration procedures [21].

Nevertheless, the cost of implementing a full-range constitutive model valid for any triaxiality and Lode angle parameter is very high, both in terms of the number of tests required as well as in terms of model parameters to be identified thru intricate direct/indirect optimization procedures. In the present research, recognizing the plane strain nature of the metal cutting operations, double notched plane strain specimens introduced by Abushawashi et al. [18] will assume a central role for the constitutive model calibration regarding the reference conditions of temperature and strain rate (e.g., room temperature and quasi-static deformation) based on standard yield theories (e.g., J2 plasticity). The triaxiality of the chip formation mechanism can be well reproduced by the inclined double-notch plane strain tests under controlled laboratory conditions. The triaxiality value is influenced by the tilted notches angle and can be determined based on an optimization-based procedure including physical constraints and initial input values. Thus, given the plane strain deformation of the double-notch plane strain test (aprox. triaxiality ranging from −0.5 to 0.5 and null Lode angle), it appears logical that the optimal solution should be framed between the tensile test (triaxiality 0.3 and Lode angle 1) and the compression test (triaxiality −0.3 and Lode angle −1) for meaningful values. As initial input values the frictionless flow curve obtained from the uniaxial compression test should be used due to its capability to reproduce the extreme conditions of metal cutting, namely the large plastic strain. Using inverse simulation techniques, this kind of test will be used to validate a stress–strain relation. Further, the developed reference flow stress relation can be updated with the thermal and rate dependent influences, from compression testing assuming independent contributions, as underlined by the Johnson–Cook model. Regarding the damage behavior evaluation, the tensile tests covering various triaxialities and the double notched plane strain specimens may provide enough insight covering both positive and negative triaxialities.

The small number of parameters and relatively simple calibration contribute to extensive usage of the Johnson–Cook plasticity model (refer to Equation (1)) in metal cutting simulation. The model describes the equivalent plastic stress ($\sigma$) in function of the uncoupled effects of strain hardening, through material parameters of the equation’s first term $A$, $B$, and $n$, as well as the equivalent plastic strain (${\epsilon }_p$). The viscoplastic response is modelled by the second term through the material parameter $C$ as well as strain rate ($\dot{\epsilon }$) and reference strain rate ($\dot{{\epsilon }_0}$). The temperature softening is modelled by the third term through the definition of the material parameter $m$, room temperature $T_0$, and melting temperature, $T_m$. In addition to the flow stress evolution, the Johnson–Cook damage threshold model (Equation (2)) depicts that the damage initiation strain (${\epsilon }_f$) as a function of stress triaxiality ($\eta$), strain rate, and temperature as well as material parameters $d_1$ to $d_5$. In order to model damage evolution (stiffness degradation), the Hillerborg model (Equation (3)) can be applied due to the idealized combination between damage mechanics and finite element degradation and may be regarded as a material parameter capable of expressing the energy dissipation relative to crack opening. The critical damage dissipation energy, $G_f$, is depicted in function of the characteristic length ($L$), which is associated with an integration point.

$$\sigma =\left(A+B{\epsilon }_p{}^n\right)\left[1+Cln\left(\frac{\dot{\epsilon }}{\dot{{\epsilon }_0}}\right)\right]\left[1-{\left(\frac{T-T_0}{T_m-T_0}\right)}^m\right]$$

(1)

$${\epsilon }_f=\left(d_1+d_2{e}^{d_3\eta }\right)\left[1+d_{4}ln\left(\frac{\dot{\epsilon }}{\dot{{\epsilon }_0}}\right)\right]\left[1+d_5\left(\frac{T-T_0}{T_m-T_0}\right)\right]$$

(2)

$$G_f={{\displaystyle \int }}_{{\epsilon }_0^{}}^{{\epsilon }_f^{}}L\sigma d{\epsilon }_p$$

(3)

The above mentioned direct characterization and inverse calibration methodologies are expected to provide accurate input data parameters for the numerical simulation of the metal cutting processes [22]. Nevertheless, it must be pointed out that assumptions and simplifications have been done in order to allow the development of a progressive and efficient calibration procedure. Thus, an experimental validation concerning metal cutting simulation is also desirable. This can be achieved by comparing the numerical simulation estimates to the experimental measurements on the simple orthogonal cutting test carried out under controlled laboratorial conditions. It should be noted that the tribological condition of metal cutting differs from metal forming due the absence of metallic oxides and thus slight variations in the friction coefficient may occur influencing the chip curling.

3. Additively Manufactured 18Ni300 Maraging Steel

In order to address the characterization requirements, an AMed 18Ni300 material batch was built, through laser powder bed fusion. An ytterbium laser with a spot size of 70 μm was used for processing the material samples, according to the manufacturers’ recommendation for optimal printing conditions and overall quality. This corresponds to a laser power of 400 W, scan speed of 0.86 m/s, hatch spacing of 95 μm and a layer thickness of 40 μm. Additively manufactured parts may present a considerably different mechanical performance, depending on a multitude of aspects in their manufacture. In order to fully understand the materials’ as-built condition, a comprehensive analysis regarding physical, metallurgical and mechanical properties was carried.

The micrograph cross-section method for porosity measurement was adopted in this study. In this technique, AMed samples were cut in two distinct directions (perpendicular and parallel to the build direction), embedded in resin (through compression mount). Manual and semi-automatic grinding using sandpaper, followed by polishing of the cut cross-sections (Struers Pedemax-2, INEGI), allowed for its optical microscope observation (Olympus PMG3 and Zeiss Axiophot). Etchant is not used in these samples, given that the goal is to simply reveal the absence of material (pores) in a polished surface. In order to estimate relative density, metallographic samples were post-processed in ImageJ software for the generation of binary maps that more easily allow for porosity assessment. Figure 3 presents two representative metallographic image samples (one for each direction of interest) for the additively manufactured maraging steel. A computed relative porosity of 99.7% was found, which is identical to the manufacturer’s specification (99.8%). No pattern- or direction-related porosity was found in the analyzed samples.

Microstructural analysis was carried by the same optical equipment used in the porosity analysis. For such task, material samples were etched in order to reveal the melt pool baths as well as the grain morphology. Samples were chemically etched with nital solution (2%) whilst oxalic acid was used for electrolytical etching (6 V DC for 50 s). Grain morphology can easily be observed with chemical etching, whereas melt pool geometry and AMed-related microscopic features, such as laser trace, require electrolytical etching. Figure 4a shows a chemically etched sample of AMed 18Ni300 maraging steel in perpendicular-to-build direction, characterized by an uneven distribution of lath and plate martensite among austenite. Figure 4b shows an electrolytical etched sample in the parallel-to-build direction, where melt pool geometry is evidenced. The melt pool approximate geometry allows for the calculation of an energy density of 122 J/mm³, which is coherent with the literature values for steel alloys processing [23].

Chemical composition analysis was performed using spark emission spectroscopy (SPECTROMAXx). The comparison/verification compliance with material standards, for each alloying element is depicted in

Table 1. Chemical composition (wt%) of 18Ni300 AMed steel with respective reference values [26].

	Ni	Co	Mo	Ti	Si	Mn	C	P	S
Standard min	18.0	8.5	4.6	0.5	-	-	-	-	-
Standard Max	19.0	9.6	5.2	0.8	0.10	0.10	0.03	0.01	0.01
Current	18.80	8.84	5.15	0.65	0.05	0.03	0.02	<0.001	<0.001

, where the low carbon content is noticed. Rather than the typical high carbon content, the martensitic microstructure of AMed 18Ni300 maraging steel is achieved by nickel addition, which is the main element. The lack of carbon enhances weldability, which in turn makes such alloys a good choice for additive processing [24,25].

4. Plastic and Damage Response Determination

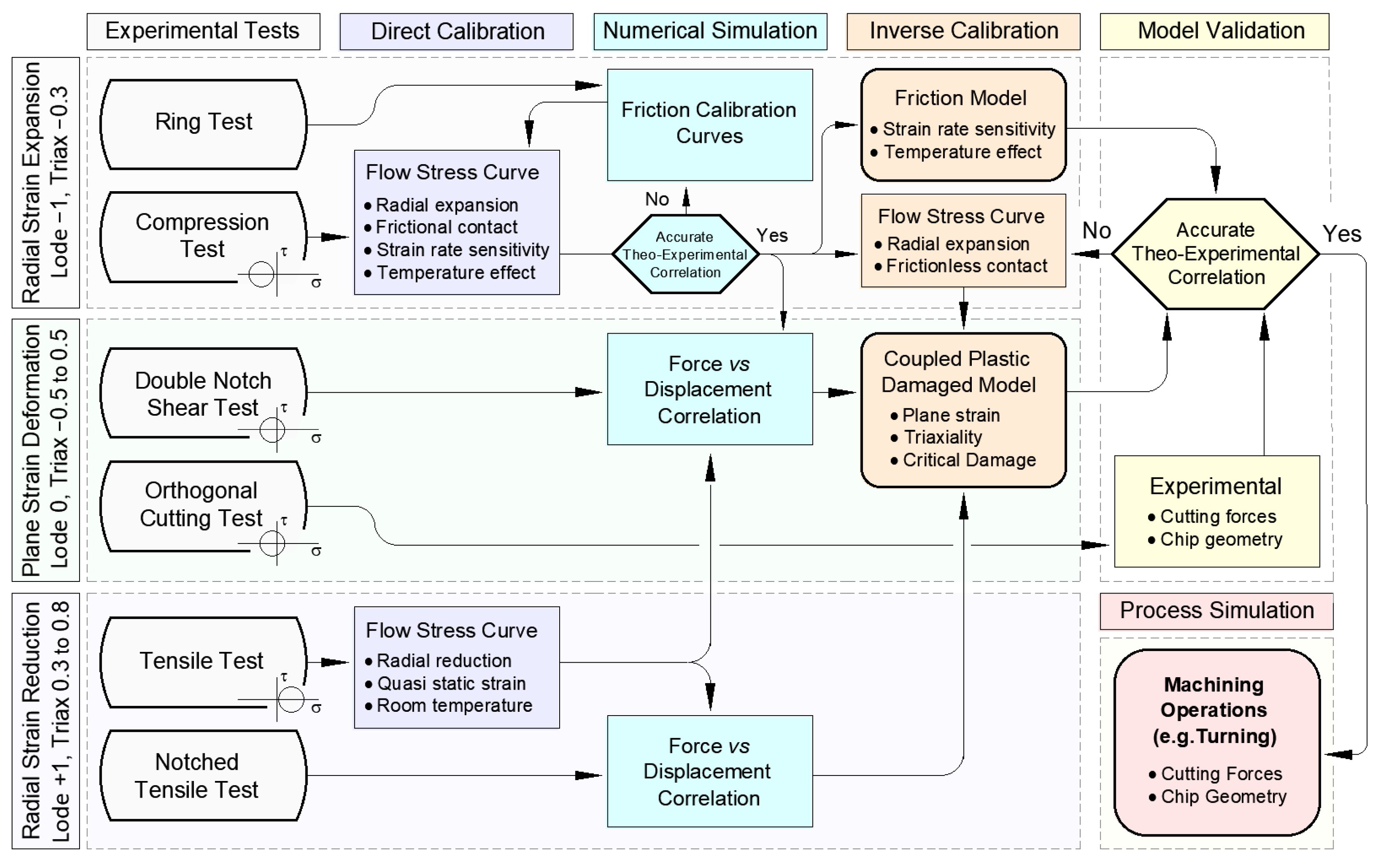
This section focuses on the experimental characterization and inverse calibration methodologies conducted on the AMed 18Ni300 maraging steel to determine its mechanical and tribological behaviors. It begins by introducing the compression tests on both ring and cylindrical specimens. These tests were conducted for a dual purpose: (i) a direct characterization of the material flow stress under radial strain expansion accounting for material sensitivity to strain rate and temperature; and (ii) to estimate friction coefficient at the tool-workpiece interface resorting to a combined experimental-numerical approach. Special emphasis is given to the apparatus that was developed by the authors to perform uniaxial compression tests under extreme thermo-mechanical conditions. In continuation, radial strain reduction tests are performed on both cylindrical and notched cylindrical specimens, tensile tests representing an adequate approach towards identifying the material damage behavior dependence on Lode angle and positive stress triaxialities. Double notch plane strain specimens were also tested for a complementary range of intermediate stress triaxialities at null Lode angle. The inverse analysis of the tests on double notched specimens also allowed establishing the material constitutive plastic law in a more representative state-of-stress to metal cutting. The combined experimental-numerical methodology proposed by the authors requires the inverse analysis of the experimental characterization tests. Thus, ABAQUS FEM software has been used in the full extent of mechanical and tribological characterization modelling, considering an elastoplastic approach with a von Mises (J2) yield criterion with isotropic hardening.

4.1. Initial Definition

The uniaxial compression test and the ring compression test were selected to evaluate the mechanical and tribological properties of the AMed 18Ni300 steel, when submitted to one-dimensional compression and axisymmetric expansion, at different loading rates. These are the most used tests to evaluate the flow stress and friction in metal plasticity [27,28] and can be carried out using the same experimental apparatus, allowing similar tribological conditions between the specimens and the compression platens. Under these experimental conditions and based on adequate inverse analysis procedures, it is possible to identify the individual contribution of plasticity and friction.

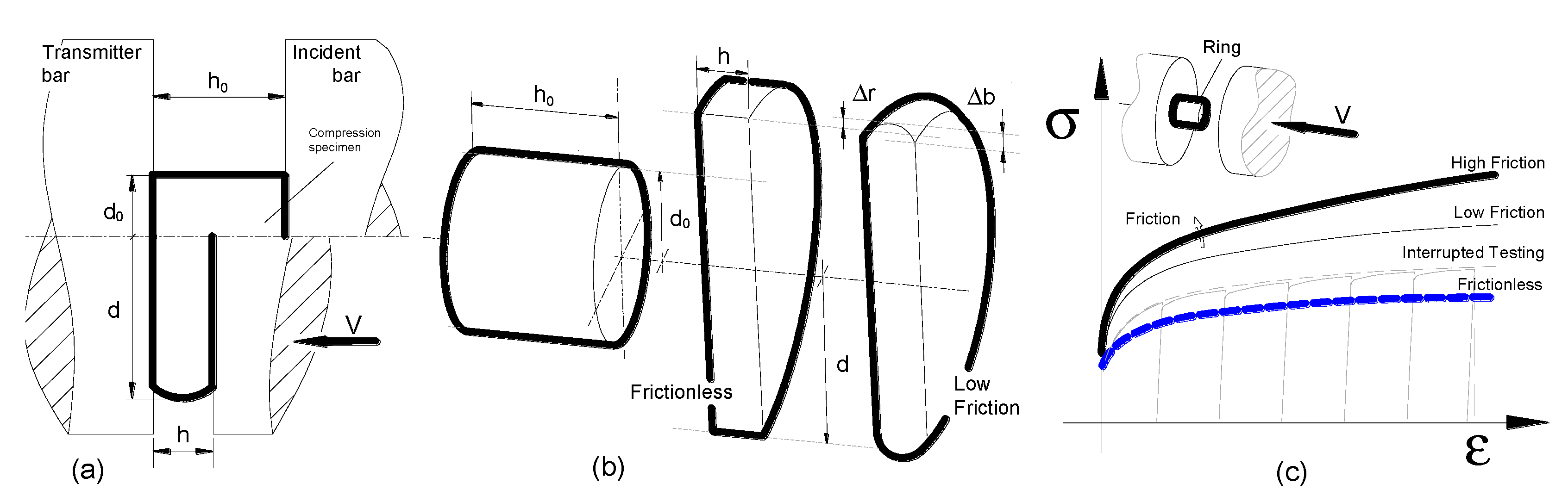
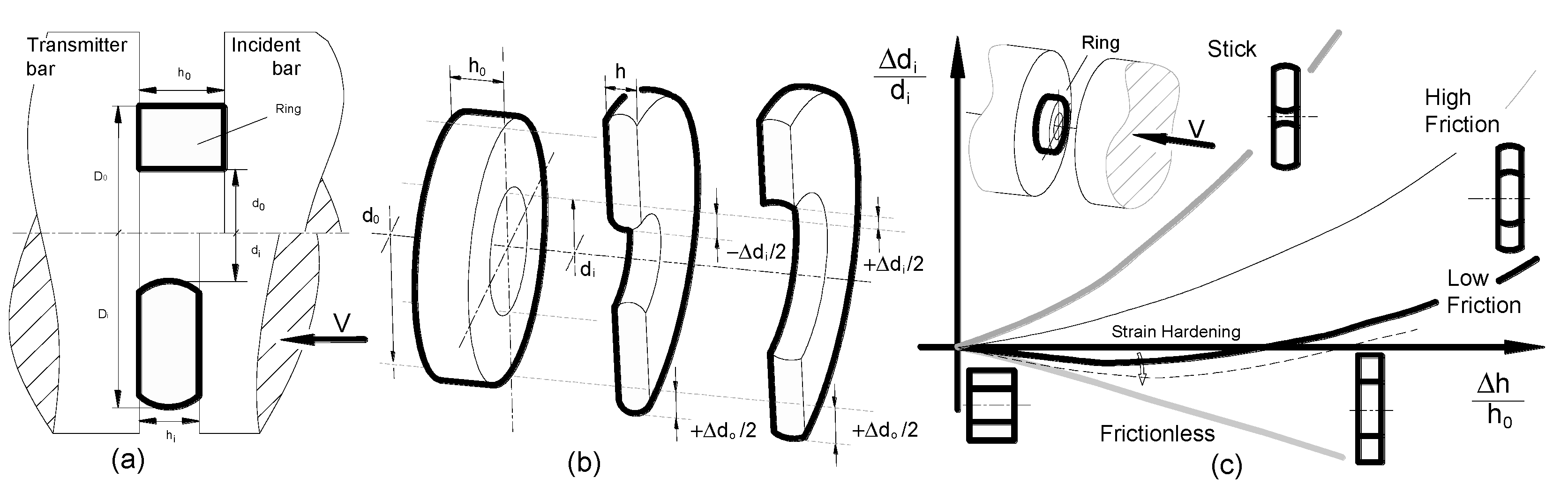
The compression test involves reducing the height of axisymmetric specimens, by uniaxial compression, between two flat and parallel platens (Figure 5a). Compression tests were carried out on cylindrical specimens with a cross-section of 4 mm diameter ($d$) and a height-to-diameter ratio, $h_0/d=1$. In order to evaluate the mechanical response in conditions compelling to those found in metal cutting, tests were conducted for a wide range of strain rates from quasi-static up to 6000 s⁻¹. A thin film of graphite grease was used to lubricate the compression platens. However, despite even the best interface conditioning practices, no homogeneous deformation can be attained due the impossibility to eliminate the frictional shear on both contact interfaces between compression platens and the test specimen (Figure 5b,c). The ideal mechanical response, frictionless flow curve, can be only attained by eliminating the friction contribution on the experimental load–displacement curve using post-processing techniques. To account for tribological phenomenon on the contact interfaces, ring shape specimens were also tested under compression to several pre-determined height decrements (Figure 6a).

As the ring height is reduced, the outer diameter expands radially outwards and the change in inner diameter depends on both compression in the axial direction and the interfacial friction between ring and compression platens. If friction is small, both the inner and the outer diameter expand. However, due to friction hindering of the radial expansion of the specimen material, the inner diameter can become smaller than the original diameter (Figure 6b), for higher values of friction [29]. In this research, the dimensions of the ring specimens were 7, 3.5, and 2.5 mm, corresponding to the outside diameter, inside diameter, and height, respectively (approx. 6:3:2 ratio). The experimental tests were performed for two different lubrication conditions: (i) lubricated contact, in which graphite grease was applied on the compression platens in order to reproduce the tribological conditions of the previously described uniaxial compressions tests, and (ii) dry contact, to study the effect of temperature and loading rate on friction coefficient under similar operative conditions as those observed in machining processes. While for quasi-static conditions it is possible to perform interrupted tests planning various compression stages (several stages and, thus a sequence of experimental measures), in high-speed tests it is not possible to apply such a practice due to the high kinetic energy of the incident bar and thus, only single stages were carried out (a single measure per experimental test). In-between compression stages, the values of specimen’s inner diameter and height were measured using a digital precision caliper gauge and recorded before and after the tests. Each test/experimental measurement produces only one experimental point to be placed on the calibration curves. At least 3 tests were performed for each experimental condition to detect possible gaps in the experimental results that could be attributed to homogeneity and isotropy issues related with the AMed material production and specimens manufacturing.

Friction can be estimated by a comparison of experimental data with friction calibration curves generated in advance by numerical procedures. The calibration curves were obtained by means of finite element-based simulations using Abaqus software. Both compression platens were considered rigid; the bottom platen was considered static, whereas the upper platen motion was set to be consistent with the velocity of the experimental tests. The mechanical behavior (stress–strain data) of the materials to be used in the numerical simulation was determined by means of the compression tests performed on cylindrical specimens, as previously described. The calibration curves for quasi-static conditions are exemplified in Figure 6c and show that low values of friction give rise to increase the inner diameter of the specimens during deformation, whereas high values promote a decrease in the specimen’s inner diameter.

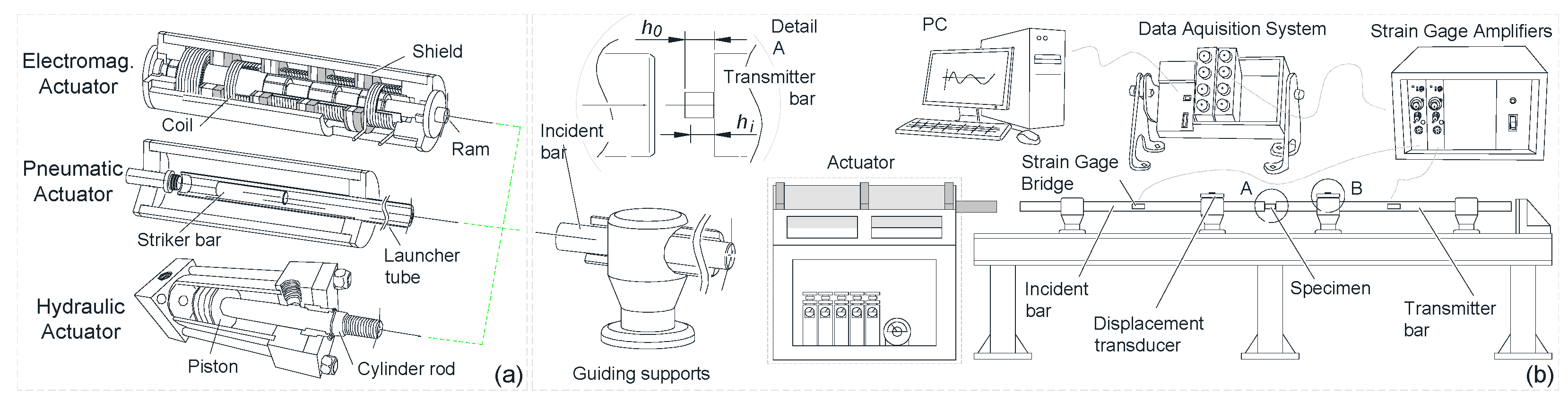
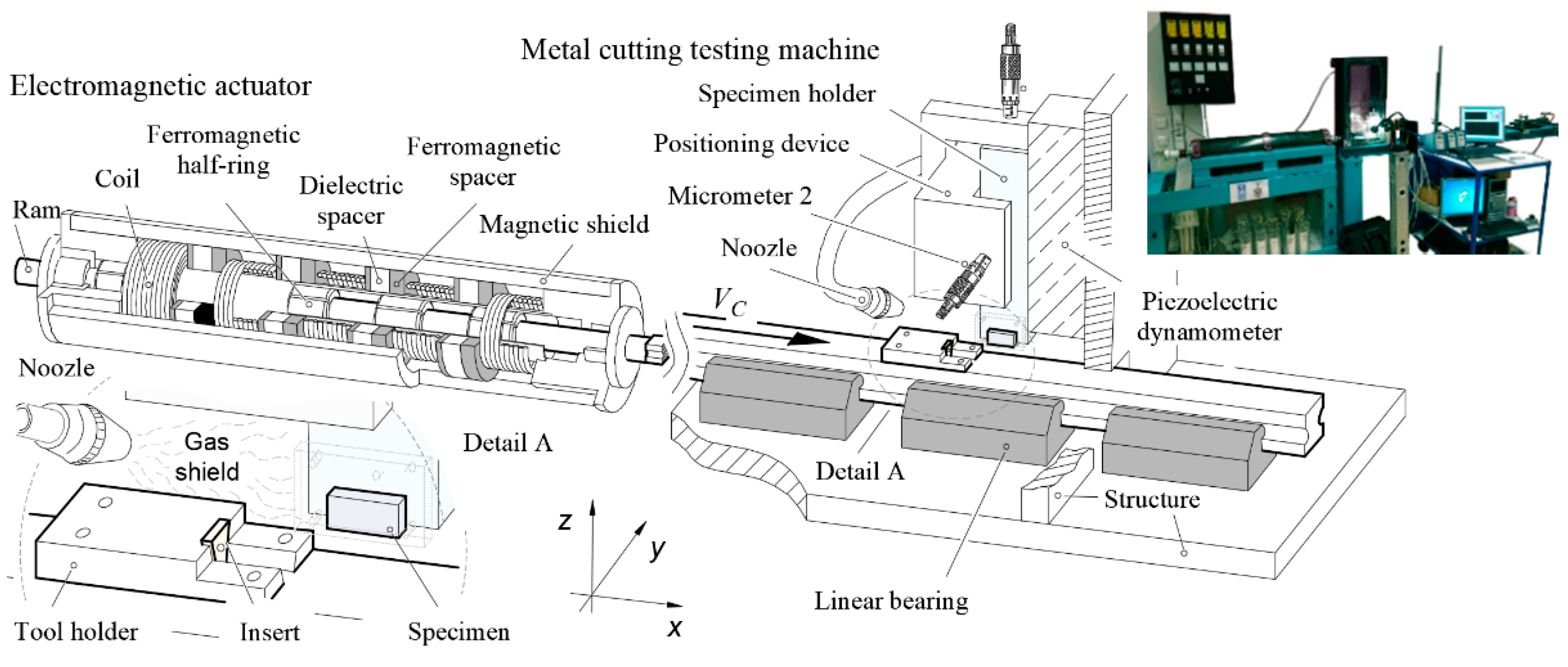
The uniaxial compression tests were carried out in a customized split-Hopkinson pressure bar (SHPB), specially designed to provide a wide range of strain rate conditions and temperatures, schematically shown in Figure 7. This apparatus makes use of a single load cell and specific displacement transducers for all testing conditions, ranging from quasi-static, low strain rates and high strain rates tests, thus eliminating the typical calibration deviations associated with the utilization of different testing machines. The main components can be grouped into three main systems: (i) impact bench, (ii) instrumentation and data acquisition systems, and (iii) rate-based actuators.

The impact bench features basic structural parts, kinematics transmission systems, a thermostatic chamber, and a pair of compression platens. The compression platens were made from a powder metallurgy (PM) composite material consisting of tungsten carbide particles and a cobalt metallic binder (WC–15 wt% Co), that provides the required compromise between hardness and toughness. Thus, assuring that the rigid substrate endures the very demanding conditions of high temperatures and extreme compressive loads but also withstands the shock and vibration of impact tests. In order to limit asperity interlocking contribution to the friction mechanism, the platens’ surface was polished, having shown average roughness values (Ra) in the range of 0.009 to 0.032 µm along the radial direction. Chemical adhesion between the material pair platens-specimen was controlled through the application of a TiAlSiN coating with a thickness of not less than 2.5 µm, using a PVD HiPIMS process.

An electric furnace was used to allow testing temperatures above reference room temperature (Figure 8b). This heating unit was installed directly in the impact zone, surrounding the compression platens, as seen in Figure 8c, allowing testing temperatures up to 900 °C. This furnace consists of a chamber lined with refractory material where the electric heating resistors are located, with the particularity of having a through hole in the sides to permit the compression platens’ action (Figure 8b).

The instantaneous strain, stress and strain-rate are calculated based on the monitorization of the three main physical parameters: time, load, and displacement; being the instant time implicit in the data acquisition systems. A multipurpose data acquisition board, National Instruments PCI-6115 combined with appropriate software (LabView) was used to monitor these parameters, allowing sampling rates of up to 10 MHz. Since the presented experimental technique deviates from the commonly used SHPB in the way that both force and displacement values are taken from direct measurements, special sensors were installed for such purpose. A full Wheatstone bridge arrangement used for load calculation and installed in the first quarter of the transmitter bar, promoting an extended time window without the interference of the reflected wave. The elastic deformation of the bar under compressive loads causes the gauges’ resistance to change and thus, the load cell electrical output signal can be linearly correlated with the applied load. Yet, this voltage output is very low, so a VISHAY 2310B signal conditioning amplification system was required to amplify the electrical signal. For room temperature conditions, inductive position sensors were mounted directly between compression platens in order to promote the precision, accuracy and resolution of the experimental measurements. This experimental technique prescinds of complex data post-processing necessary to account for elastic deformation of the testing machine and allows measuring the distance between compression platens with high resolution under very high velocities and severe accelerations. For compression tests conducted at high temperature, the inductive sensors are no longer viable. To surpass this limitation, linear sliding potentiometer sensors were positioned outside the thermostatic chambers, directly on both incident and transmitter bars and thus, the performance of the sensors is not affected by even the most demanding thermal conditions. A total of 3 potentiometers were installed; 1 on the incident bar and 2 on the transmitter bar and, the distance between compression platens can be measured by correlating the differential value between potentiometers (Figure 7b).

An adequate linear actuator was selected according to the desired strain rate range. For quasi-static and low strain rate compression tests (less than 1 ${\mathrm{s}}^{-1}$), the hydraulic ram cylinder was used (Figure 9a). Dynamic tests can be subdivided into medium strain rate tests (100 to 1000 ${\mathrm{s}}^{-1}$), which were carried out resorting to the electromagnetic actuator (Figure 9b) and, high strain rate tests (above 1000 ${\mathrm{s}}^{-1}$), which were performed using the pneumatic gun (Figure 9c). The electromagnetic actuator comprises several components such as the electrical circuits for charging and firing the banks of energy-storage capacitors and a series of coils that generate the electromagnetic pressure to accelerate the striker bar. The pneumatic gun consists of a pressure vessel that allows precise control of the amount of energy released during compression for a given air pressure. A pneumatic trigger valve allows the stored air volume to flow through a launcher tube, converting pneumatic energy into kinetic energy and, thus, accelerating the striker bar. The impacting velocity is limited by the mass of the striker bar and the strain rate signature of the compression tests depends on the specimen ability to dissipate the corresponding kinetic energy. Despite these fundamentals, it is difficult to achieve an adequate signal noise ratio due to the abrupt pressure impact and wave propagating through the split Hopkinson bar during test monitorization. Thus, a consumable thin nylon sheet of 1 mm was placed between the strike bar and the incident bar for better loading control. With regards to the hydraulic actuator, an electrical pump supplies the required fluid at appropriate flow rates and pressure for the quasi-static and low strain rate compression tests.

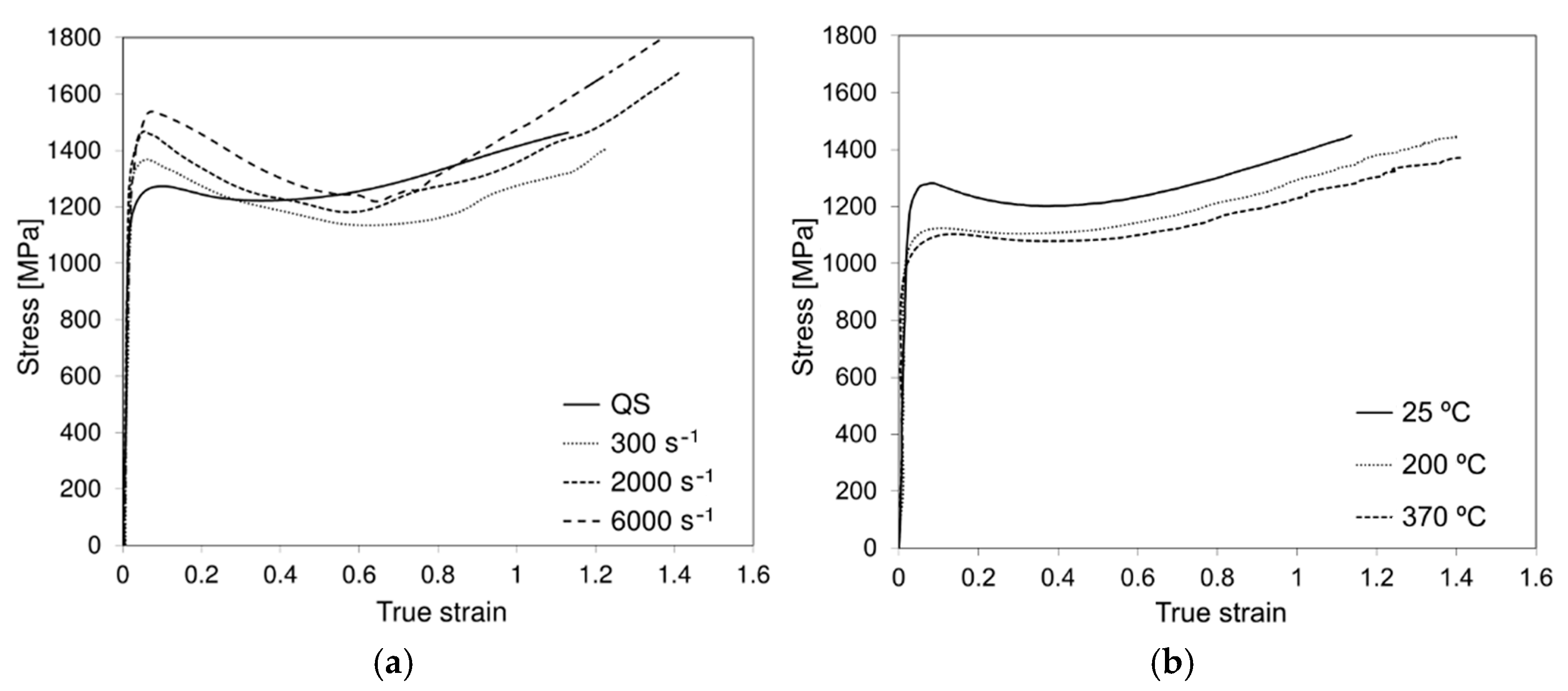
The flow curves obtained from compression tests at room temperature under different strain rate conditions are presented in Figure 10a, where three distinct stages can be observed: (i) for incipient deformation the material exhibits a typical strengthening mechanism up to strains of approximately 0.1, (ii) followed by a sudden softening behavior down to a minimum flow stress value, point after which a (iii) secondary stage of strengthening is observed. Regarding incipient deformation, an increase of 20% in maximum strength is observed from quasi-static conditions to 6000 s⁻¹. It is also worth noticing that the softening behavior seems to be more pronounced with increasing strain rates and, the instant at which the lowest flow stress was measured seems to shift in the positive direction along the strain axis. Moreover, for high strains, the rate-dependent behavior tends to similar stress values of the quasi-static compression tests. In general terms, the results show a peculiar hardening-softening behavior and markedly strain-rate sensitivity with effect on both the flow stress values and curve morphology.

Figure 10b shows the quasi-static high temperature behavior of the AMed 18Ni300 maraging steel. Regarding the relative low temperatures of the workpiece material when submitted to cutting and the aging transformations of the maraging steel starting at 450 °C the maximum tested temperature was of 370 °C [30,31,32]. Apart from the already identified hardening behavior, the stress–strain response of the materials seems to present typical softening for increasing temperature in AMed metallurgical conditions and constant curve morphology.

Based on the results of the mechanical testing and after a probing calibration of the standard Johnson–Cook model (Equation (1)) for the AMed 18Ni300 maraging steel, the limitations of this equation have become clear. Despite its capacity for displaying the strain hardening and thermal softening effects of most materials, the Johnson–Cook model shows itself unable to reproduce the almost perfectly plastic behavior of the maraging steel in simple uniaxial compression, even for room temperature and quasi-static conditions. This is somewhat expected once the standard Johnson–Cook does not account for several important effects, such as the thermal-strain softening phenomena, intrinsic strain-strain rates paths, and temperature- and strain-induced phase transformation, among others. Also, in this calibration procedure the complex plastic deformation which takes place in the specimen (body) resumed as a single collection of data points, does not account for localization problems happening in the real body (e.g., fracture, adiabatic shear bands), which certainly deviate the stress–strain state from the homogenous one assumed to calculate the data originally furnished. Simpler models just Voce equation [33] and Silva equation [6] have proved to be capable to reproduce the sigmoidal stress–strain curve of the AMed 18Ni300 maraging steel. In their standard format, these athermal equations are commonly used at low strain rates with negligible temperature sensitivity and thus strain becomes nearly isothermal [34]. Its application to metal cutting should be clarified, where deformation is almost adiabatic, and heat remains where it is generated. In what follows, the authors consider that conventional metal cutting involves a cold chip formation mechanics, and the high temperature of chip is a result/output parameter of the plastic flow itself. As counterexample, the billet temperature in hot forging is an input parameter achieved prior the forging operation (e.g., by which metallurgical phase transformations may occur). This approach considers that final temperature of a formed chip or deformed cylindrical specimen should be equivalent after the plastic deformation, under comparable operative conditions (e.g., initial room temperature, strain, and strain-rate conditions). The accuracy of the model coefficients can be also improved by considering the loading signature of the process (strain-strain rate history) [6]. Thus, parameters should be obtained using experimental tests considering the signature of the machining process (strain-strain rate history). In other words, the final chip temperature can be estimated by considering the initial temperature of the uncut chip/workpiece (e.g., room temperature, external heating or cryogenic machining), heat transfer mechanisms (e.g., frictional heating, internal heating), and the inelastic heat fraction of plastic work that is converted into heat. As a result, a combined Swift-Voce law will be introduced in what follows to model the isothermal quasi-static hardening of this combined approach for the best fit to the present experimental data of AMed 18Ni300 maraging steel.

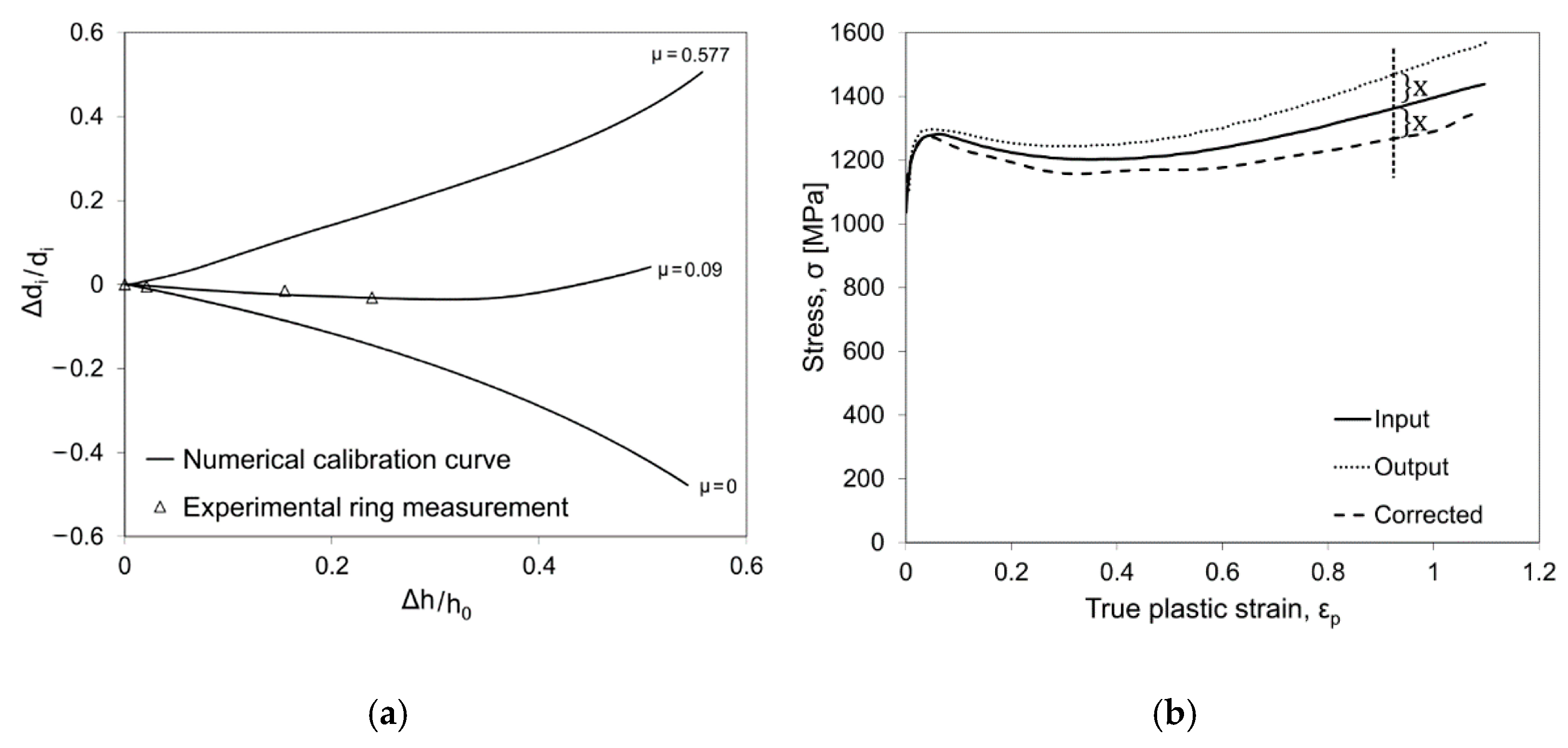
The above mentioned friction estimates method results from an experimental-numerical identification approach in which the first step corresponds to performing compressive tests on cylindrical and ring specimens under the same loading, lubrication and temperature conditions. Compression of cylinder specimens enables the estimation of trial flow stress curves that are used to simulate the corresponding ring compression test (friction calibration curves) for different friction coefficients. An example of friction calibration curves is shown in Figure 11a, where the ring inner diameter variation (Δd_i/d_i) is plotted over ring height variation (Δh/h₀). The comparison of these curves with the experimental results allows the estimation of a friction coefficient μ = 0.09. The strain–stress curves used in the numerical estimative of friction calibration curves are not frictionless, even when contacting interfaces of the compression platen are lubricated. Thus, an iterative process must be applied in order to exclude the friction contribution from the trial flow stress. Furthermore, it helps to reduce the propagation of errors caused by the uncertainties of the tribomechanical calibration. This process consists in the inverse numerical simulation of the compression test using the flow stress as obtained from mechanical testing, labelled as “input” in Figure 11b, and the previously determined friction coefficient (first estimate). The resulting stress–strain curve will be an overestimate of the flow stress curve due to a double contribution of the frictional mechanism (i.e., the unknown experimental friction plus the numerically set friction), labelled as “output” in Figure 11b. By subtracting the friction overestimation, one can derive the corrected frictionless material response. Yet, an iterative process is required since the ring compression simulation is also material-dependent and new friction calibration curves should be determined, allowing a convergence towards the frictionless flow stress curve, labelled as “corrected curve” in Figure 11b, and the final identification of the friction coefficient value. It is relevant to highlight the increasing contribution of friction, for increasing strain rate and temperature, which in turn emphasizes the importance of frictionless flow stress estimation in metal cutting simulation.

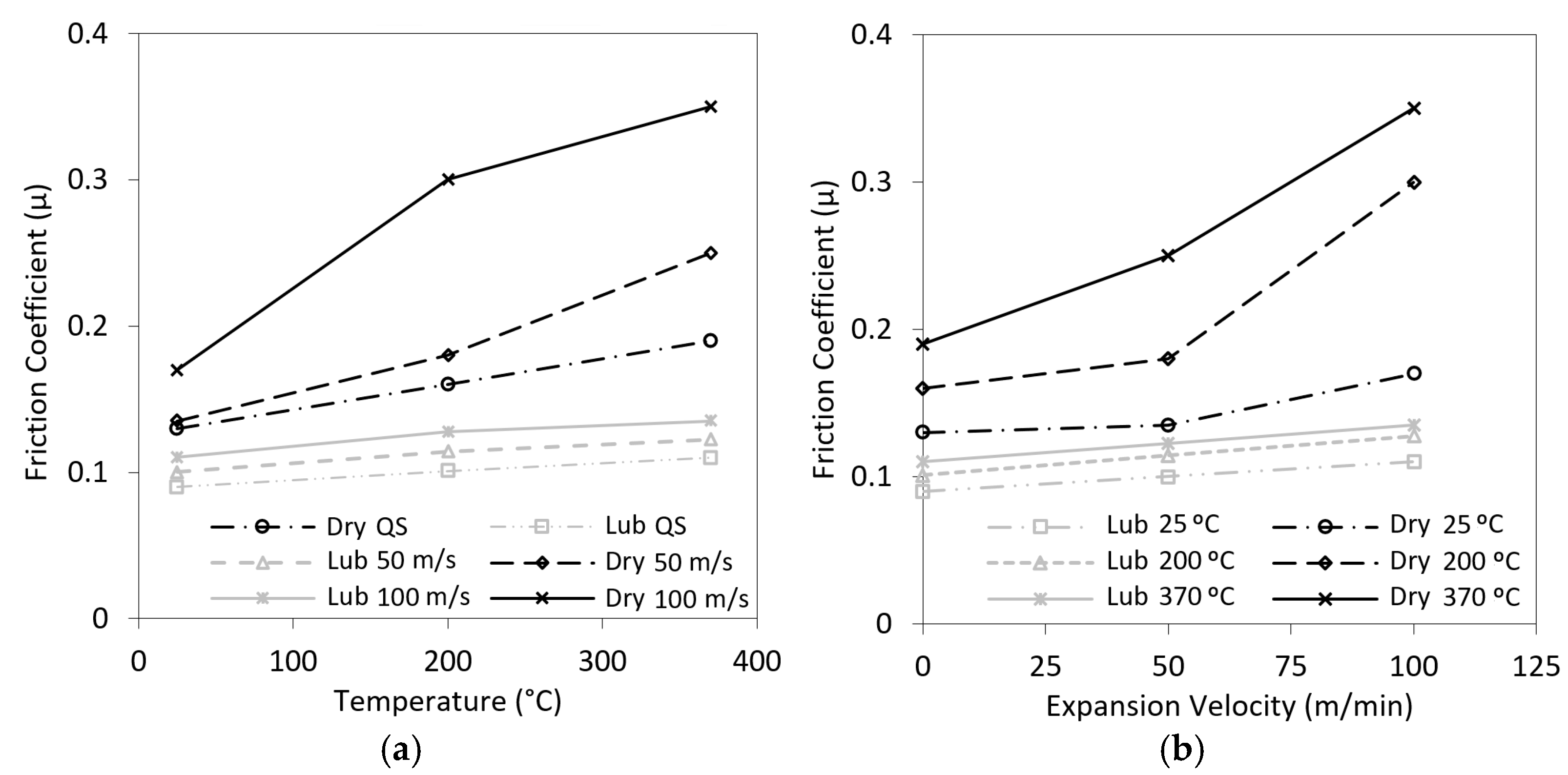
The influence of lubrication, temperature, and strain rate conditions on the friction coefficient value in tool-workpiece contact interface are shown in Figure 12. It is observed that the use of graphite lubricant (labelled as “Lub”) significantly decreases friction adhesion phenomenon for the materials’ interface in all tested conditions. Still with regards to lubricated conditions, a very consistent (yet modest) increasing trend is found for rising temperatures and strain rates. On the other hand, for dry conditions (labelled as “Dry”), friction coefficient tends to double when the temperature rises from room temperature to approximately 370 °C (Figure 12a). Similarly, to temperature, strain rate seems to promote an increasing friction coefficient (Figure 12b). Such results provide evidence of the friction dependence on cutting conditions where the material experiences large strains and high strain rates in the primary deformation zone and most of generated heat due to plastic work to the chip [32], which in turn slides against the tool at the secondary deformation zone.

4.2. Compliance with Metal Cutting Conditions

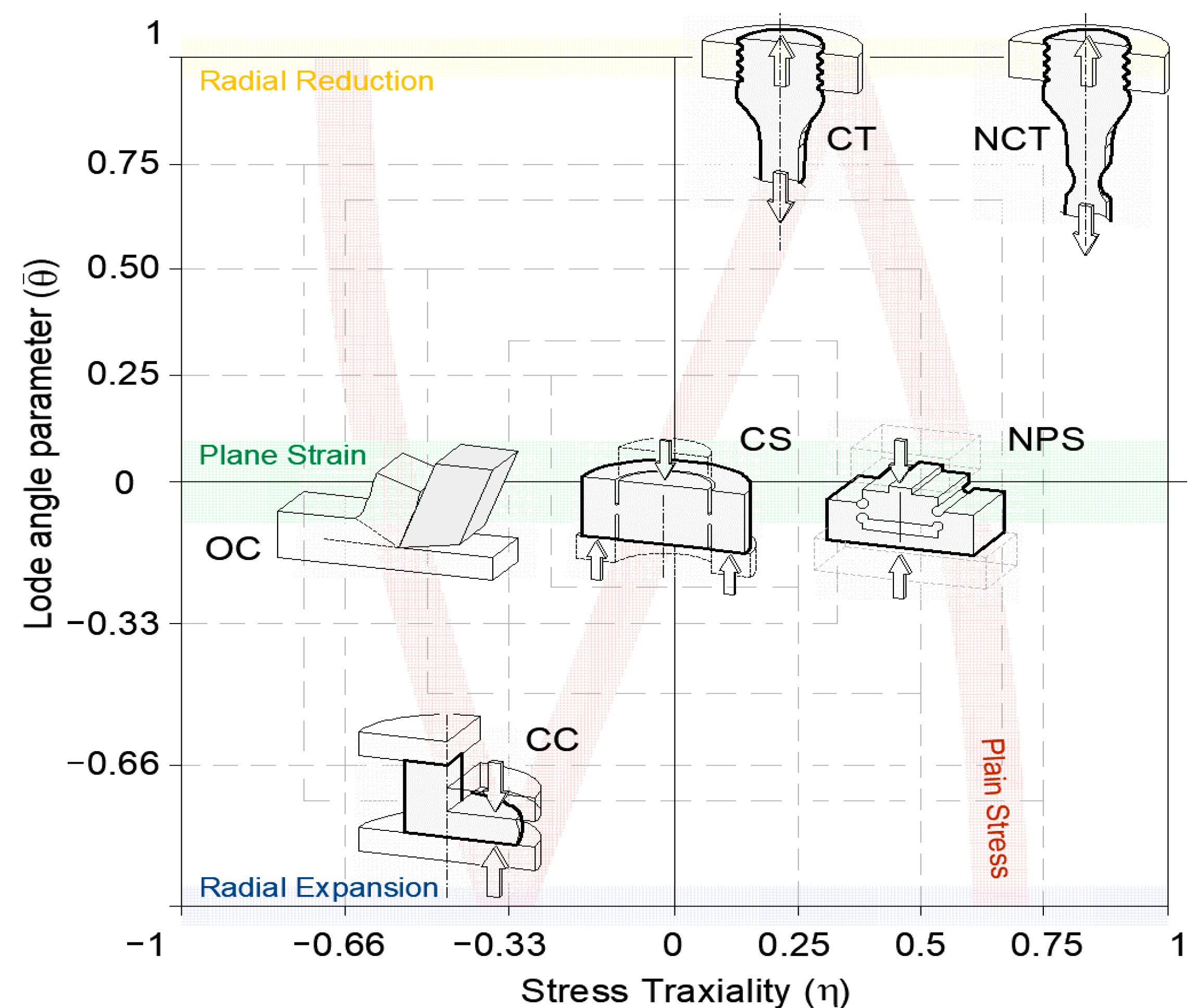
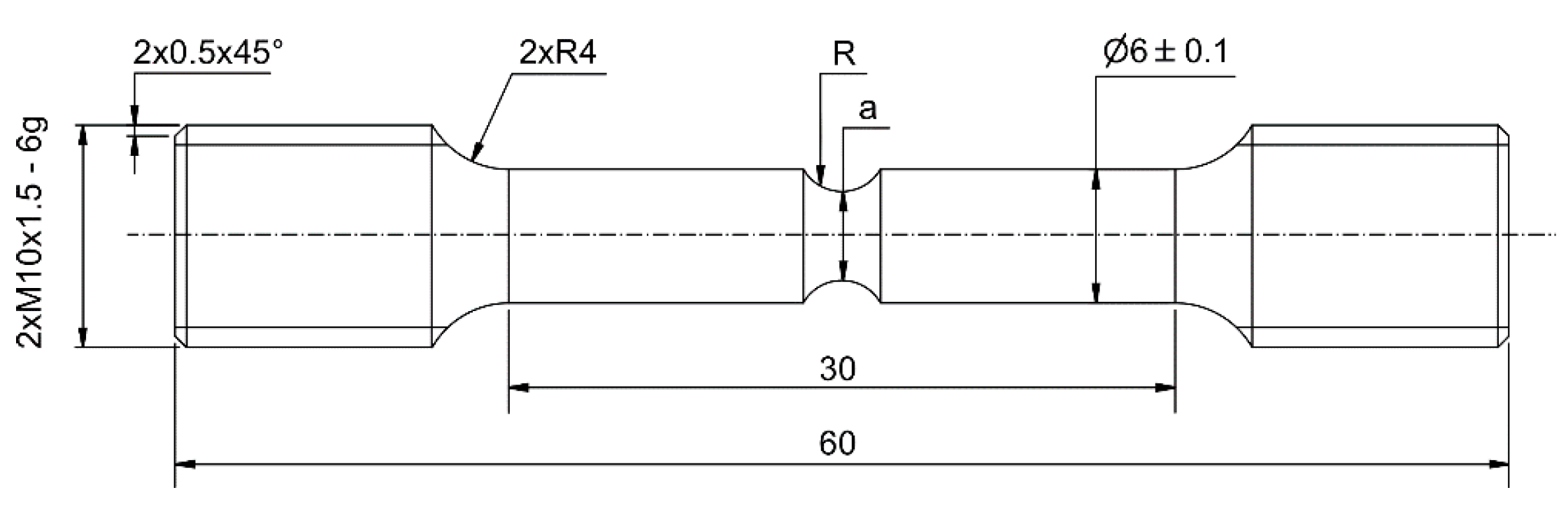
Tensile tests of smooth cylindrical specimens (CT in Figure 2) were conducted in order to evaluate the stress–strain response of the AMed 18Ni300 maraging steel in radial reduction conditions (positive Lode angle parameter and stress triaxiality). Such geometrical-loading configuration allows for an assessment of the state-of-stress influence on the plastic behavior of the alloy, through direct comparison of the stress–strain curves with the ones obtained through radial expansion (compressive loading). Given that the tests were conducted for distinct notch geometries, it is also possible to access the stress triaxiality influence on ductility, enabling damage initiation model identification for a high range of stress triaxiality, which will be further discussed. The general morphology of the tensile specimens is shown in Figure 13 and the parametrized notch dimensions are described in

Table 2. Tested configurations of stress triaxiality according to notch geometry.

Notch Parameter (Refer to Figure 13)	N-∞ (Smooth)	N-5 (Notched)	N-2 (Notched)
a [mm]	6	4	4
R [mm]	∞	5	2
${\eta }_T$	0.33	0.52	0.74

. The theoretical stress triaxiality (${\eta }_T$), assuming unaltered notch contour with deformation, has been calculated according to Bridgman [35] analytical prediction for each tensile specimen geometry. Quasi-static conditions were ensured through the imposition of a 1 mm/min pulling speed to the machine crosshead (Instron 5900R universal servo-hydraulic testing machine), which registered load through the built-in 100 kN load cell and displacement through the usage of an extensometer (MTS 632.12C-20) with a 25 mm gauge length.

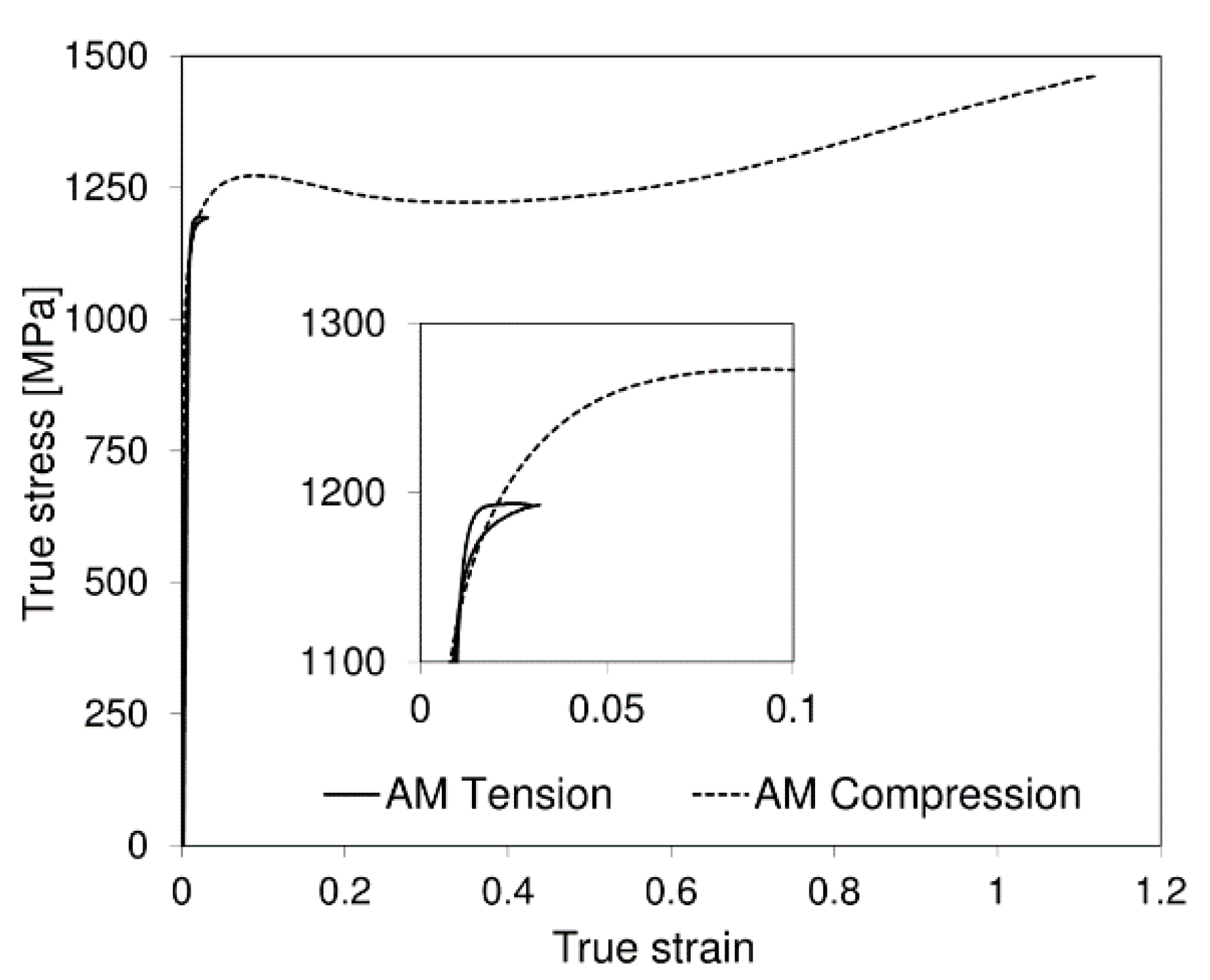
The severe plastic deformation in metal cutting highlights the importance of its thorough characterization, especially since it is widely acknowledged that depending on the state-of-stress, the deformation behavior can significantly differ in certain materials [19]. The comparison between the true stress–strain curves of the AMed 18Ni300 maraging steel obtained from compression and unnotched tensile tests is shown in Figure 14. It is relevant to notice that due to the plastic instability, which leads to non-uniform deformation, the tensile curve is shown up to necking. Despite the very limited extent of uniform plastic deformation of the unnotched tensile tests, a clear plateau that corresponds to plastic yield is noticed, revealing a considerably distinct yield strength depending on loading direction. The observed strength differential effect between compression and tensile loading suggests the sensitivity of the tested alloy to the state-of-stress. Similar behavior has been reported for several AMed alloys [36,37], including the same maraging steel alloy [38]. However, this behavior does not seem to be exclusive of AMed metallurgical condition, given that appreciable differences between compressive and tensile yield strengths have also been noted for martensitic steels [39], including the same maraging steel alloy of conventional manufacturing (wrought) [40]. In addition, the magnitude of the tension/compression strength differential shows similar values (~10%) to that reported for the same material.

In order to accurately portray the plastic deformation during the metal cutting simulation, the mechanical response should be compliant with the plane strain conditions of the chip formation mechanism. 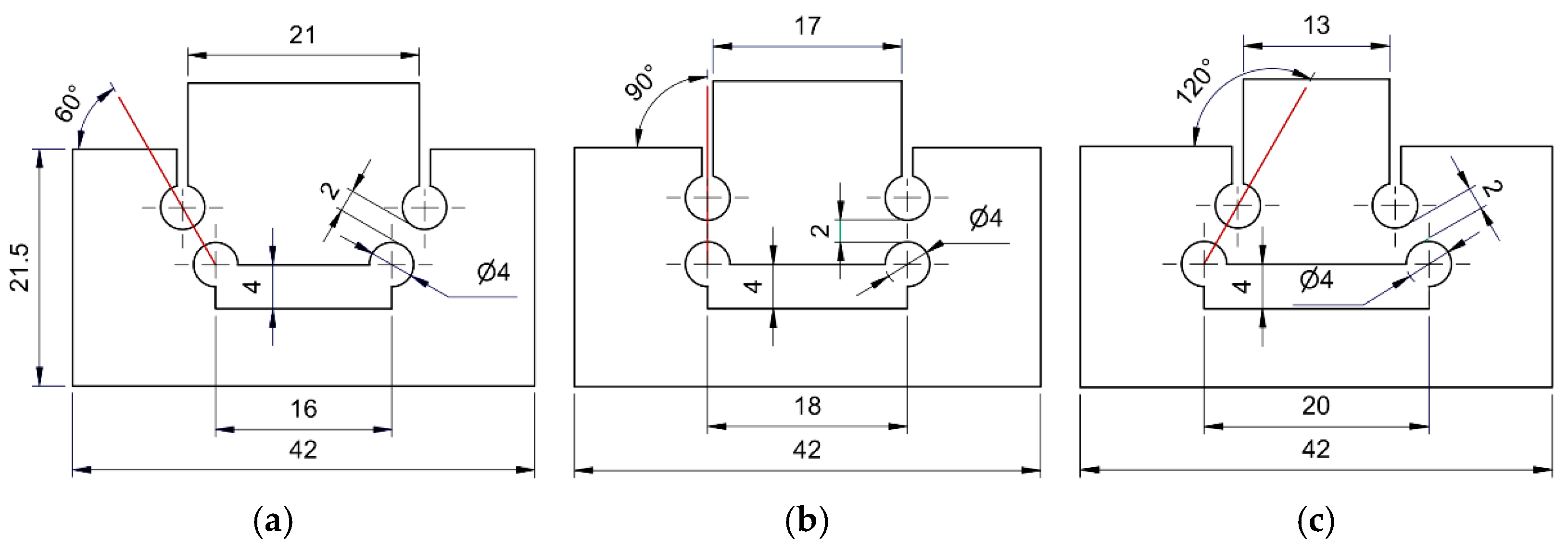Due to its ability to cover an intermediate range of stress triaxialities and null Lode angle parameter, the suitability of the double-notched specimen towards the calibration of plastic and damage models, for cutting applications has been demonstrated by multiple authors [1,18]. These plane strain specimens consist of symmetric double notched geometries (refer to Figure 15), where cylindrical starter cracks have been introduced to create a constant ligament length of 2 mm before loading. The length of the ligament allows to confine plastic deformation to a small region in between the cylindrical notches. The experiments consist in determining the punch shearing load–displacement evolution when the specimen is compressed between compression platens, from which critical damage and flow stress of the material under plane strain conditions may be deduced. Through the variation of the double notch configuration, it is possible to change the specimens’ pressure angle, which is defined by the straight line that is colinear with the centers of the two cylindrical notches. Such modification results in a change of stress triaxiality within the same null Lode angle parameter (plane strain conditions). In the current research work, three distinct pressure angles were tested. For a pressure angle of 90°, null (or close to null) stress triaxiality due to the theoretically pure shear condition is achieved; for a pressure angle of 60° a combination of compression and shear is attained, developing intermediate negative stress triaxialities; for a pressure angle of 120°, a combination of a tensile and shear state-of-stress is achieved, yielding intermediate positive stress triaxialities.

The tests were carried in the same universal testing machine as the tensile tests. A quasi-static compression speed of 1 mm/min was imposed to the machine crosshead and two repetitions were conducted in order to ensure experimental repeatability. Due to specimen symmetry, it was important to ensure not only that the compression plates were parallel between each other (top and bottom), but also perpendicular to crosshead displacement direction. Even though there is a major focus of these specimens towards the identification of the damage initiation and evolution model, they provide very important insight on material’s plasticity and flow stress validity. Given the flaws of typical mechanical characterization methodology, say, for example, friction in compression tests and plastic instability in tensile test, added to the fact that none of both is in identical state-of-stress conditions to cutting (plane strain), the notched bar shear tests allow for a crucial inverse calibration of the plasticity models identified through direct calibration.

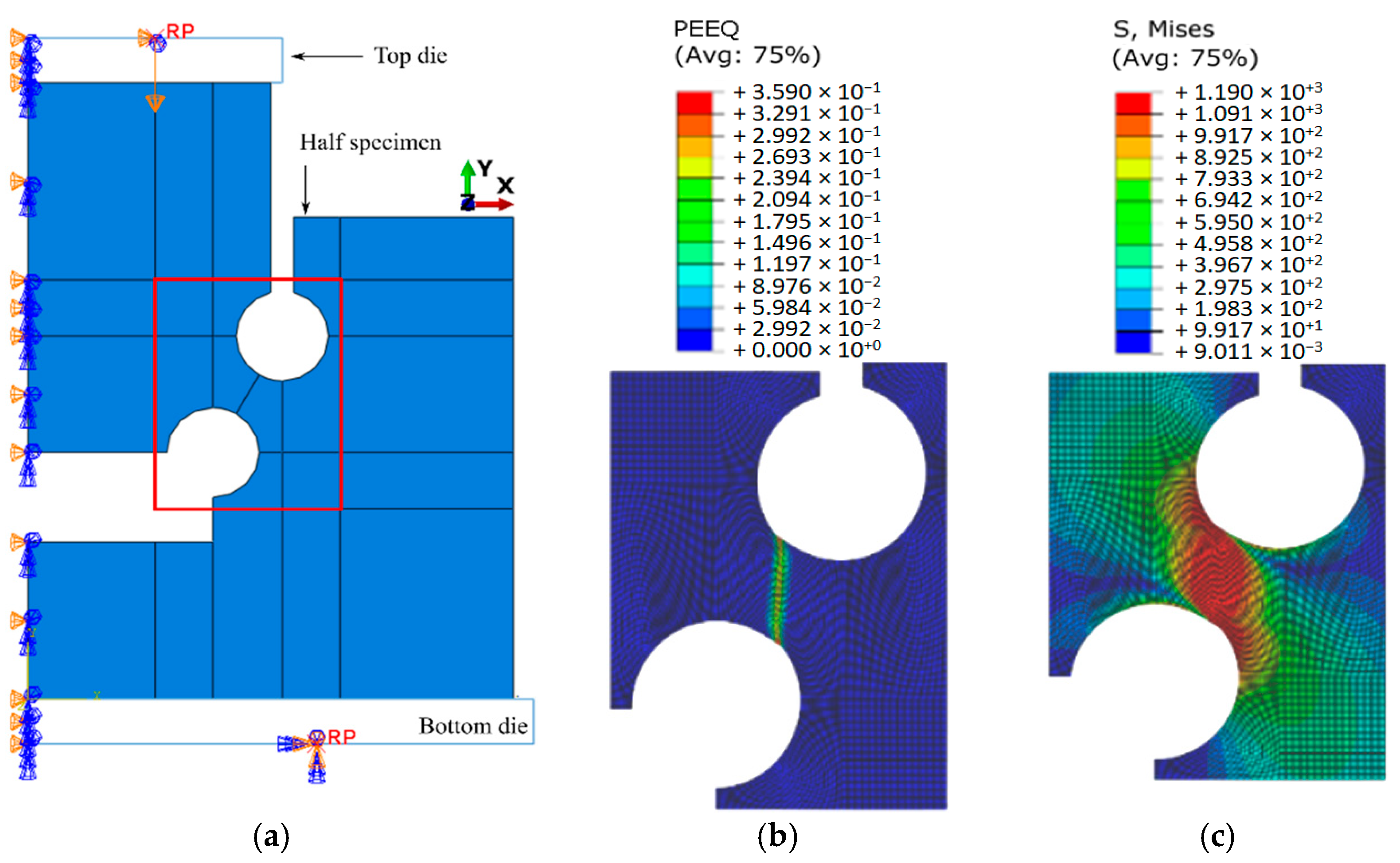
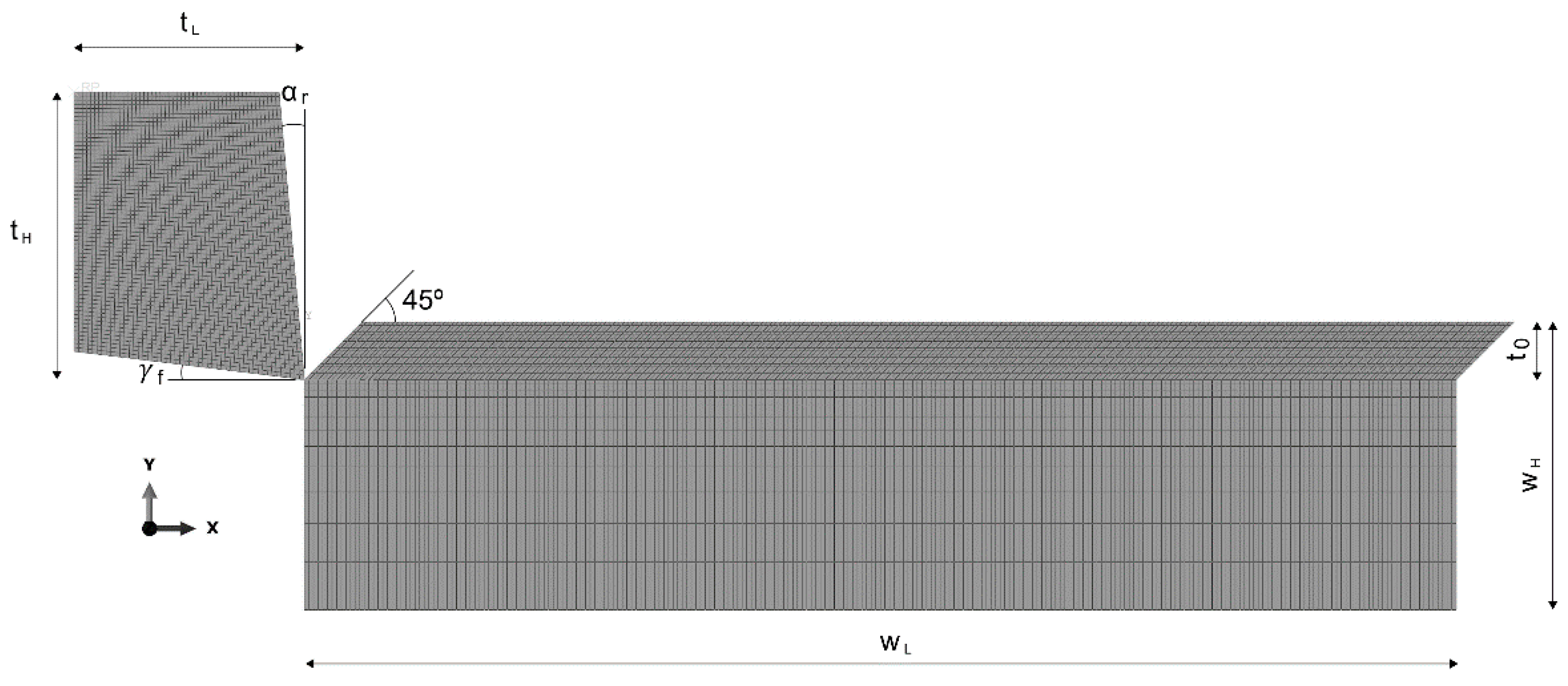
In this research work, a 2D plane strain approach was used for the simulation of the double notched plane strain specimens. Their symmetry enabled the modelling of half-specimen (refer to Figure 16). Four-noded elements with reduced integration (CPE4R) and an element size mesh of 0.05 mm were used. The model consists of a top die (with one degree of freedom in vertical direction) that compresses the specimen onto a bottom die (encastred). Both dies were modelled as rigid bodies.

The successful portrayal of the double notched specimens’ plastic deformation behavior theoretically ensures a material plasticity law in a similar state-of-stress to metal cutting. Such can be achieved through the development of constitutive laws that are sensitive to the state-of-stress or, alternatively, through the inverse calibration of simpler plastic laws with the plane strain specimen. Considering the latter, it is of utmost importance to establish physically admissible upper and lower boundaries for the inverse estimation of the plane strain compliant plastic law, making the direct calibration of the tensile and compression tests a necessary initial step.

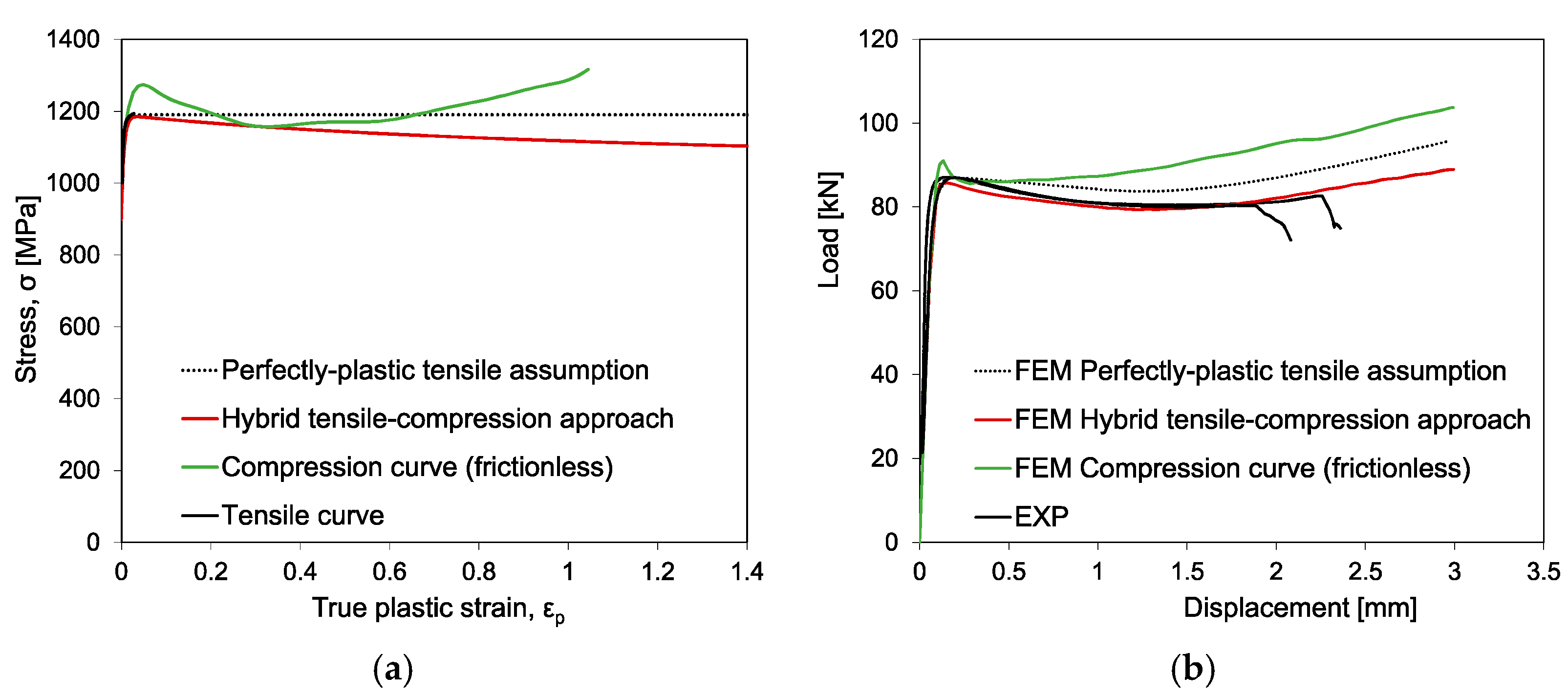
The double notched plane strain specimens have been simulated using distinct flow stresses based on the conducted characterization tests, which are shown in Figure 17a. The green curve corresponds to the (frictionless) compression test and the black dotted curve to the perfectly plastic assumption of the tensile test. An extrapolation of the tensile tests was required, given its limited extent within uniform plastic deformation. In addition, a third curve that corresponds a combined inverse calibration (based on both tensile and compression direct calibration) was built. The curve captures the tensile material response for low strain values and assumes quasi-linear negative strain hardening that is tangent to the minimum stress values obtained by compression testing. Due to allowing for an initial hardening and its saturation (or even softening) the combined Swift-Voce law (Equation (4)) has been selected to model the isothermal quasi-static hardening of this hybrid approach and the parameters are shown in

Table 3. Swift-Voce hardening equation parameters.

$\mathit{K}$ [MPa]	${\mathit{\epsilon }}_0$	$\mathit{n}$	${\mathit{k}}_0\left[\mathbf{MPa}\right]$	$\mathit{Q}$ [MPa]	${\mathit{\beta }}_{\mathit{v}}$	$\mathit{\alpha }$
950	1	−0.7	887.5	362.5	170	0.2

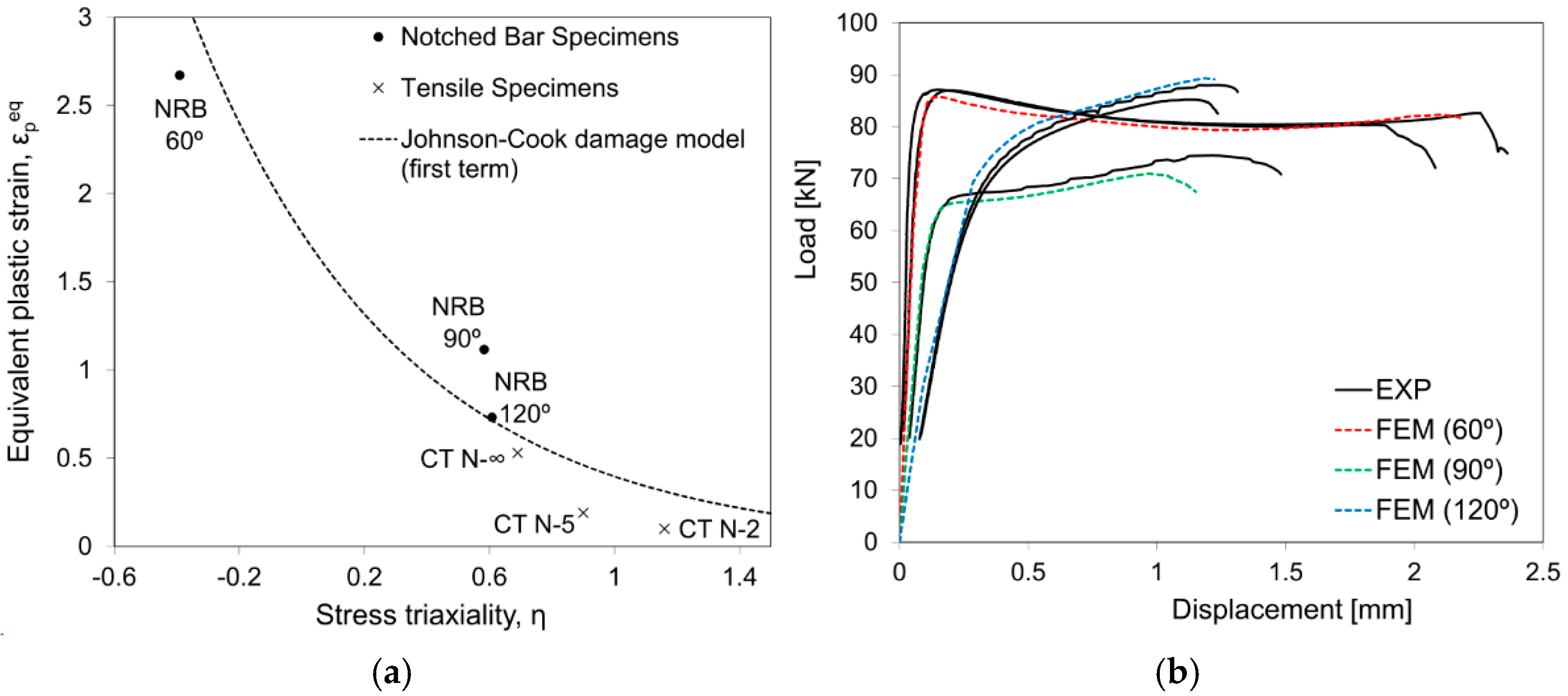
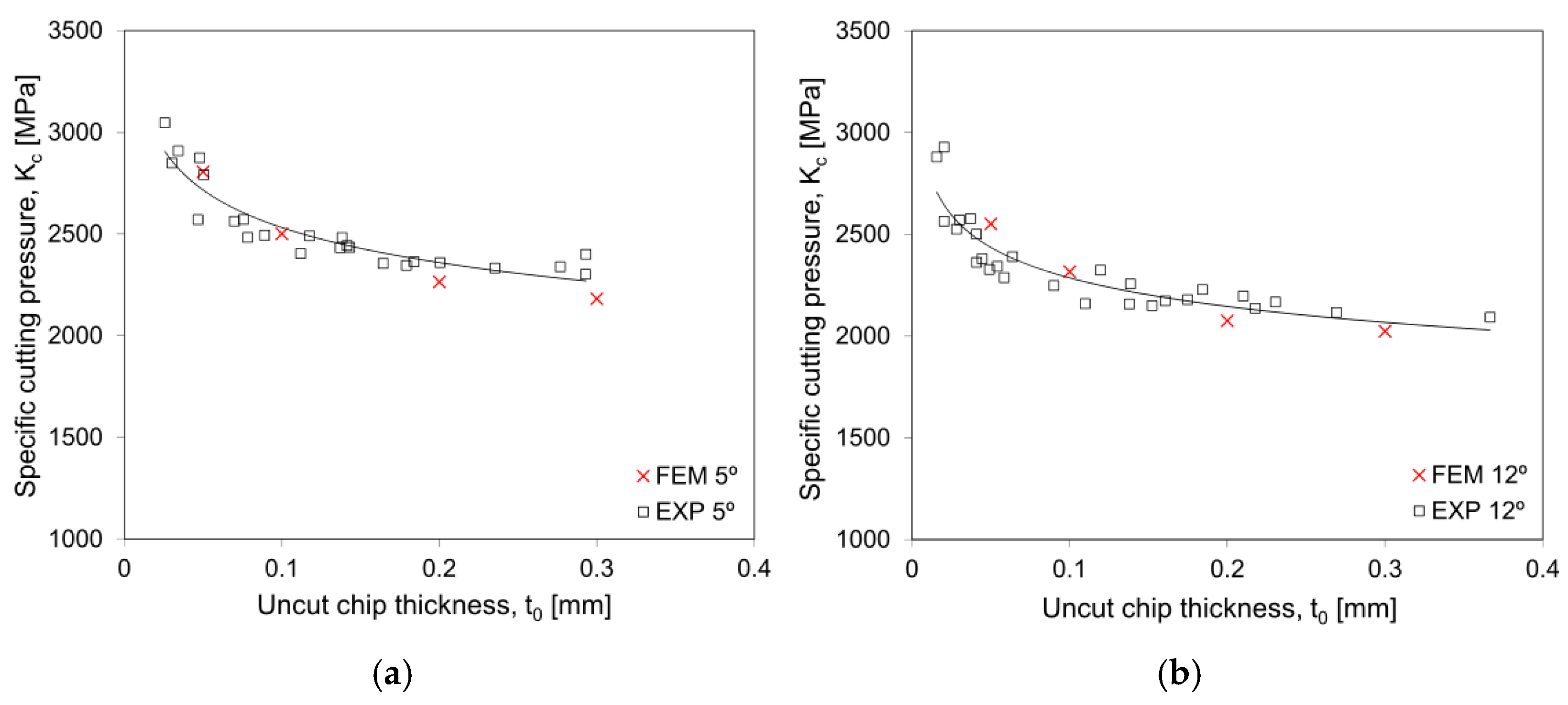
. Figure 17b shows the comparison between the experimental and the numerical load–displacement results for the 60° pressure angle double notched plane strain specimens, using each of the three distinct plastic flow stress evolutions illustrated in Figure 17a. It is important to note that a damage model was not included at this stage, given the initial focus was on the assessment of plastic behavior.

$$\sigma =\alpha \left[K{\left({\epsilon }_0+{\epsilon }_p\right)}^n\right]+\left(1-\alpha \right)\left[k_0-Q\left(1-e^{-{\beta }_v {\epsilon }_p}\right)\right]$$

(4)

The load displacement results show very high sensitivity to the applied plastic load, which can be related with the highly heterogeneous shear strain field. It is observed that the flow stress obtained from frictionless compression testing (green curve) and perfectly plastic tensile assumption overestimate the experimental loads. On the other hand, the combined inverse calibration, inspired on both tensile and compression test data, can accurately depict the plastic behavior of the double-notched plane strain specimens.

As regards to the damage initiation model, the numerical procedure for fracture strain estimation consists in the simulation of both notched and unnotched tensile tests as well as the notched plane strain tests (using the inversely identified model) and comparing the numerical load–displacement curves with the experimentally obtained. Damage initiation was defined as the displacement at which the calibrated FEM plastic prediction and the experimental curve diverge.

For the tensile tests simulation, four-noded axisymmetric elements with reduced integration (CAX4R) were used to mesh the specimens with an element size of 0.1 mm. The adopted boundary conditions include, apart from axisymmetry, null displacement in vertical direction of the bottom nodes and a vertical displacement on the top nodes, as illustrated in Figure 18a. The numerical models were built for the extensometer gauge length, which was of 25 mm. 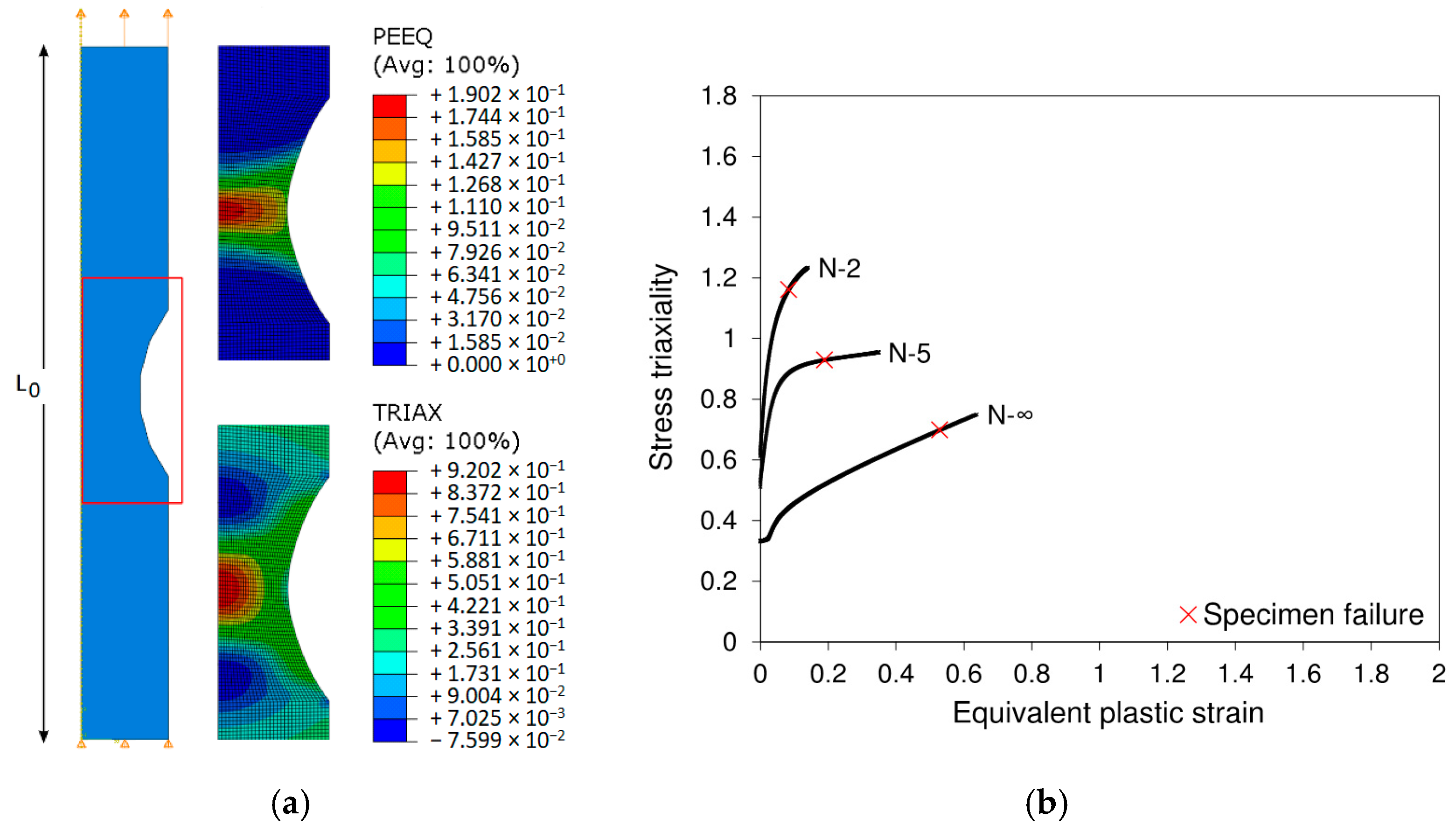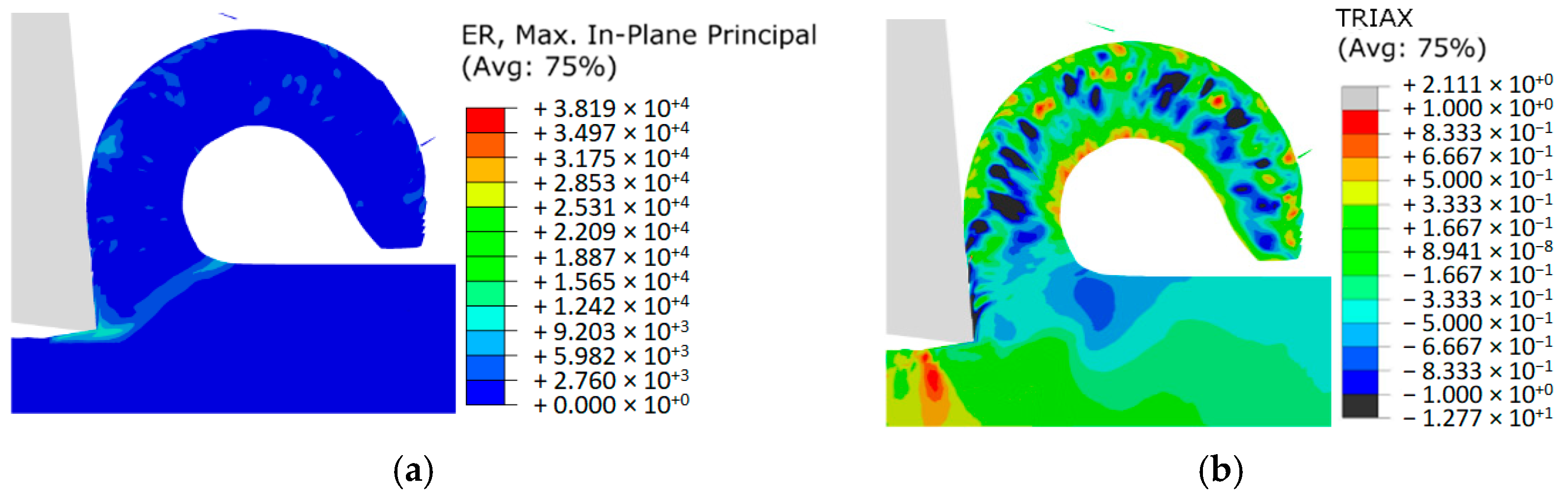Figure 18a additionally shows the field distributions of equivalent plastic strain and stress triaxiality of a notched specimen N-5, refer to Table 2. It is observed that both are localized in the center region of the specimen, where will be maximum. That location has, therefore, been selected for data retrieval as regards the failure strains and respective stress triaxialities, which are shown in Figure 18b, in the function of equivalent plastic strain. The results are in accordance with the predicted trend of lower ductility for higher stress triaxiality (or more pronounced notch geometry). Despite the accurate theoretical prediction of stress triaxiality (${\eta }_T)$ for very incipient strain values, the intense geometrical softening of the specimens (mostly as diffuse necking) results in deviation from initial notch morphology. Thus, a significant evolution of stress triaxiality up to fracture is noticed, highlighting the need for the application of this numerical methodology in order to circumvent plastic deformation localization and instability in tensile loading which hinders direct estimation of fracture strain.

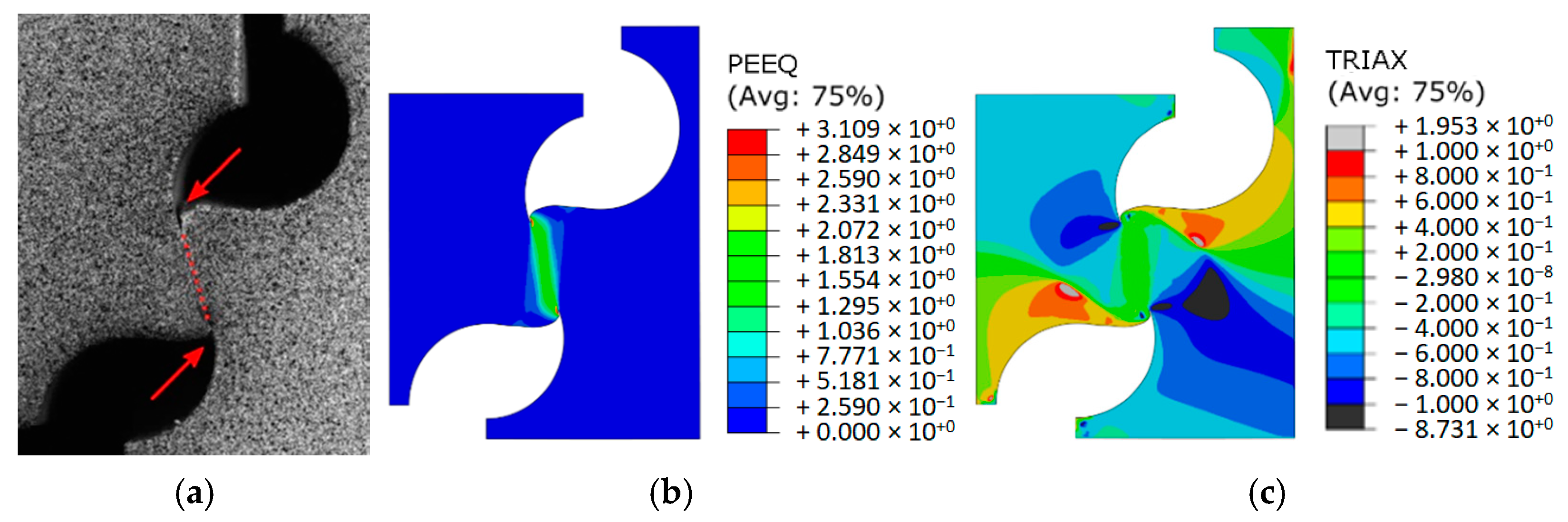
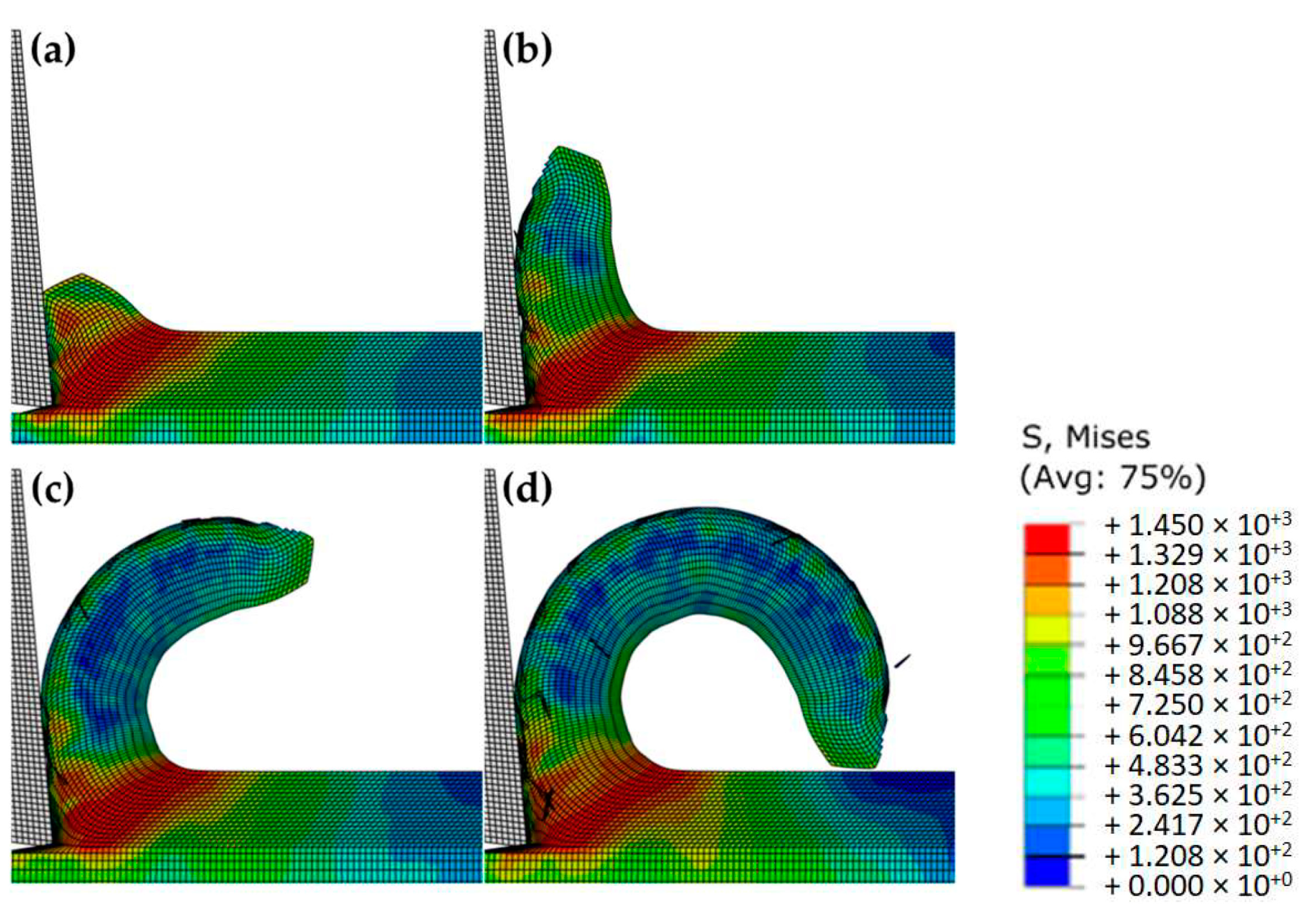
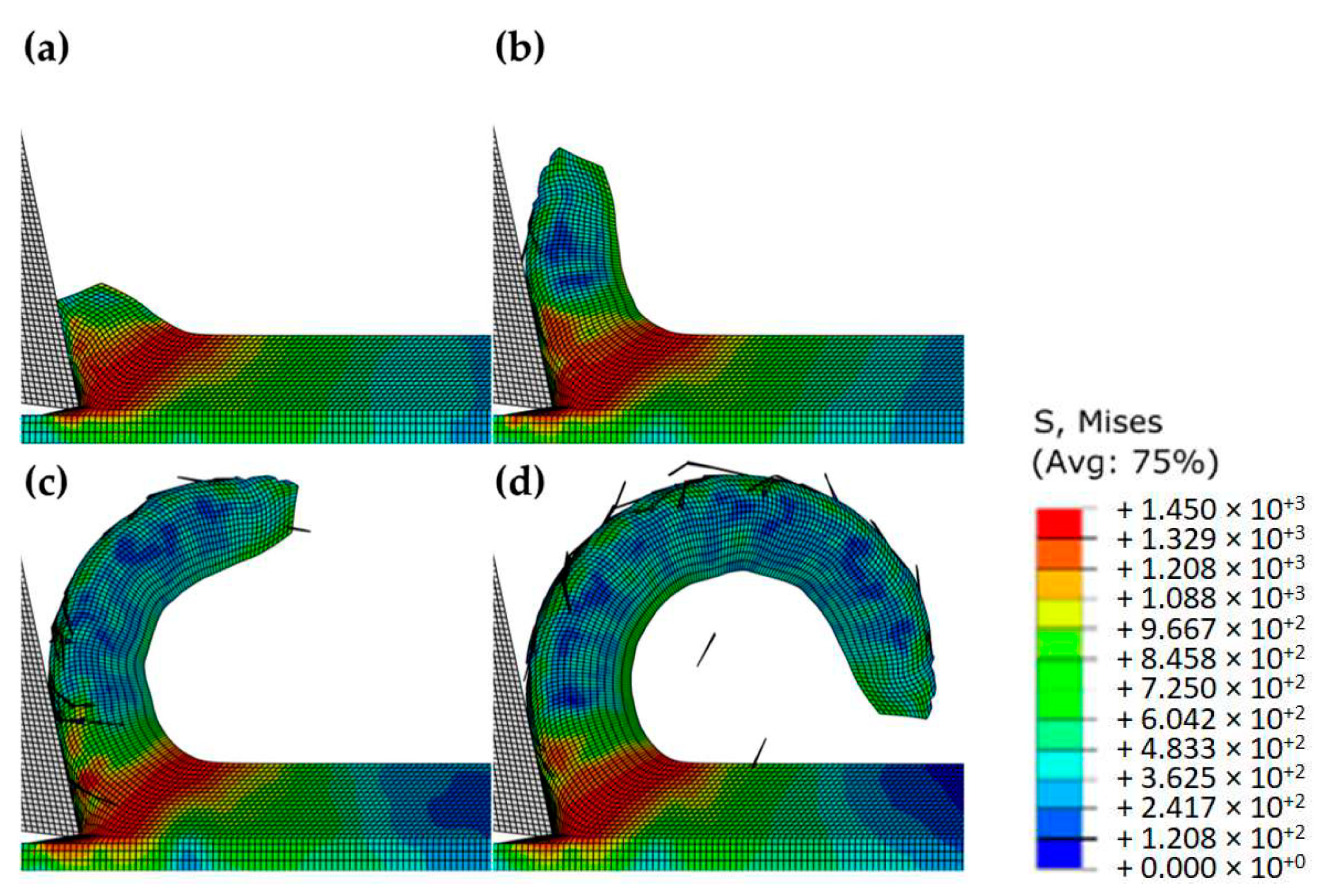
With reference to the double-notch plane strain tests, the determination of fracture strain in function of stress triaxiality and the equivalent plastic strain field distributions was supported by the experimental images of the deformed specimen shapes. Figure 19a illustrates the procedure for the deformed shape of the 60° pressure angle notched bar specimen at the damage onset. Relevant to highlight is the similarity between the numerical and experimental specimen deformed shape, which allows for a further validation of the inversely identified plastic law. In addition, it is possible to notice the beginning of crack propagation (signaled dashed line) which, relying on the numerical model, enables the identification of stress triaxiality (Figure 19c) and equivalent plastic strain (Figure 19b) along the actual experimental crack path. Experimental crack location is in accordance with the maximum equivalent plastic strain at the hole contour surfaces. Such has promoted the propagation of the crack from the surface to the center of the ligament and the identification of the equivalent plastic strain and stress triaxiality fracture thresholds for each notched specimen. Figure 20a shows the identified damage initiation law that was fitted to the experimentally-numerically obtained fracture strains for each distinct specimen. The reduced JC damage law (first term of Equation (2)) was fitted to the identified exponential decrease in fracture strain, for increasing stress triaxiality.

With regards to material damage evolution, element degradation was defined through critical damage dissipation energy definition, as previously presented in Equation (3). It has been inversely estimated for the AMed maraging steel, through the comparison between experimental and numerical results. A critical damage dissipation energy density of $G_f$ = 10 mJ/mm³ was found. The load–displacement curves of Figure 20b present the comparison between the experimental double-notch tests and the constitutive modelling (plasticity and damage) for the AMed maraging steel. Taking into account the significantly distinct load levels and fracture strains, a good agreement seems to be found with the suggested approach and results.

With regards to the viscoplastic behavior of the maraging steel, the C parameter of the second term of Johnson Cook plasticity equation (Equation (1)) was calibrated based on the compression tests, which were conducted for increasing levels of strain rate. Despite the very challenging characterization, it is well known that fracture onset is sensitive to strain rate. In this study, that effect has been inversely identified, based on literature values on the same material. High strain rate tensile tests [41] and Charpy tests [42] are usually applied towards the identification of stain rate influence on fracture strain, which is typically modelled through the $d_4$ parameter in the second term of the Johnson Cook damage initiation model (refer to Equation (2)). An average value was considered ($d_4$ = 0.03), taking into account the range of literature estimation (0.014 > $d_4$ > 0.05). All material properties are summarized in

Table 4. Material properties of AMed 18Ni300 maraging steel used in the built numerical model of orthogonal cutting simulation.

Young’s modulus [GPa]	$E$ = 190
Hardening Law [MPa]	$\sigma =\left[0.2\left[950{\left(1+{\epsilon }_p\right)}^{-0.7}\right]+\left(1-0.2\right)\left[887.5-362.5 \left(1-e^{170{\epsilon }_p}\right)\right] \right]\times \left[1+0.05ln\frac{\dot{\epsilon }}{\dot{{\epsilon }_0}}\right]$
Damage model	${\epsilon }_f=\left[-0.01+1.77e^{-1.5\eta }\right]\left[1+0.03ln\frac{\dot{\epsilon }}{\dot{{\epsilon }_0}}\right]$
Critical energy [mJ/mm3]	$G_f=10$
Friction	$\mu =0.3$
Density [kg/m3]	$\rho =8000$
Thermal cond. [W m−1 °C−1]	$\lambda =0.0206T+15.4$
Specific heat [J kg−1 °C−1]	$c_p=0.374T+437.3$
Thermal expansion [°C−1]	${\alpha }_T=1.12$$\mathrm{E}-3 T-4.03\mathrm{E}-3$

. It is important to note that heat transfer, thermal conductivity, and thermal expansion parameters for this exact material batch were obtained from [43], where a detailed description of its calculation is performed.

5. Validation of the Proposed Methodology

The simulation of the orthogonal cutting mechanism can be seen as a way to validate the found input data values for the plasticity, tribology, and damage laws in (relatively) closer conditions to industrial machining operations. With the plastic, fracture and friction behaviors fully depicted within the previous chapters, the current section focuses on the description of the built numerical orthogonal cutting model and the assessment of the suggested material models under varied, experimentally tested, cutting conditions.

Experimental orthogonal cutting tests were performed in order to enable the validation of the proposed methodology, through comparison with numerical modelling of the cutting process. A specially designed experimental apparatus equipped with load cell instrumentation has been employed. This type of testing machine is relevant towards the experimental representation of the orthogonal cutting due to its robustness and stiffness, that translates into the capability of sustaining high cutting loads in close velocity conditions to cutting. The linear motor is essentially an electromagnetic actuator that allows imposing-controlled velocity and energy to the kinematics transmission systems. A constant cutting velocity of 26 m/min was imposed to all orthogonal cutting tests. A scheme of the testing machine is shown in Figure 21. Load measurement was performed through a three-component piezoelectric dynamometer (Kistler 9257B). A charge amplifier (Kistler 5070A) and a data acquisition system (Advantech 4711A) enabled signal conversion and data collection, with a sampling rate of 5 kHz, which was further analysed using typical processing software. A clamping vice was built for specimen fixation and tightened to the dynamometer, which in turn was bolted to the testing machine table. All components were aligned with the ram movement. The testing machine slide allows for the definition of the uncut chip thickness, $t_0$, through its vertical displacement. A Mitutoyo dial indicator with a 0.001 mm resolution was clamped to the tool slide for improved $t_0$ definition. In order to be able to calculate the effective $t_0$, the height of the specimen was measured beforehand and after each cut, for the whole extent of the cutting length, in 1 mm intervals. A Mitutoyo toolmaker’s microscope (profile projector) with a 2× magnification lens was used for measuring the linear height distances along the specimens’ cutting length. Two distinct tool geometries were tested, varying only the rake angle which was of 5° and 12°. The inserts’ material was tungsten carbide, PVD-coated (TiAlN) with a 3 μm coating layer and their geometry is displayed in Figure 22. With regards to the cutting conditions, $t_0$ values ranging from 0.05 to 0.35 mm have been tested. The inserts were mounted on a tool holder with a V pocket with their inverse geometry (ensuring rigidity), which in turn was fixed to the testing machine ram through a tool holder.

In the current study, a two-dimensional orthogonal cutting numerical model was implemented, using a coupled temperature-displacement (explicit) formulation with a Lagrangian approach. Figure 23 illustrates the implemented numerical model. In order to minimize the high element distortion and eventual non-convergence, distinct aspect ratios were imposed to elements at the uncut chip thickness. Attributing a “pre-deformed” shape to the elements through its diagonal positioning allows for easier convergence of the model [44]. A distinct mesh distribution was also defined, meaning a finer mesh at the uncut chip thickness with decreasing mesh density towards the bottom of the workpiece.

Despite not significantly affecting cutting force, a finer mesh contributes to an improved realistic depiction of chip morphology, at the cost of computing time [45]. In addition, a gradual engagement of the tool was imposed with a chamfered geometry (45°) on the workpiece. An identical tool geometry to the experimental tests was employed in the numerical model, meaning that two rake angles (${\alpha }_r$ = 5° and ${\alpha }_r$ = 12°) were simulated with a fixed relief angle (${\gamma }_f$ = 7°). Workpiece, tool, and mesh sizes were scaled accordingly to the uncut chip thickness value and their parametrized dimensions are shown in

Table 5. Parametrized workpiece, tool and mesh dimensions.

	tH	tL	wH	wL	Element Size
Dimension [mm]	5$t_0$	4$t_0$	5$t_0$	20$t_0$	0.08$t_0$

in accordance with the nomenclature of Figure 23. A theoretically sharp tool was considered in all tool-workpiece geometrical configurations. Four-noded plane strain elements with reduced integration and enhanced hourglass control (CPE4RT) were employed. Tool was considered rigid whilst the workpiece was considered elastoplastic. On the tool, node rotation was null for all degrees of freedom. Identically, displacement was also set to zero in yy direction and experimental cutting speed was imposed in the xx direction. It is important to note that the identified plastic model was not calibrated in function of temperature. In fact, it is assumed that plasticity-generated heat is already accounted in the flow stress obtained by compression tests, meaning that thermal softening, strain and strain-rate hardening are regarded as a coupled effect. Also, it is important to highlight, is that most of the generated heat in the primary deformation zone flows to the chip [32], meaning that at the workpiece and primary cutting zone, temperatures are not high enough to significantly influence material properties [46]. Relying on the assumption that adhesion is the prevailing friction mechanism, the identified friction values have been incorporated in the orthogonal cutting model through Coulomb’s law, motivated by its simplicity and considering the general disagreement of friction modelling in the metal cutting domain. Chip separation has been applied through element deletion. When reaching the fracture strain that is determined by the damage model, elements are disregarded from the mesh. Their degradation was modelled using Equation (3), taking into consideration energy dissipation towards fracture occurrence. Failed elements are deleted from the mesh once the overall damage variable (D) reaches the value of 1. Despite mass loss, this method seemed the most appropriate for the assessment of the identified damage law. In order to promote computational efficiency, the mass of the entire model has been scaled. When used appropriately, this method can significantly decrease simulation time without jeopardizing the degree of accuracy [47].

Figure 24 and Figure 25 show he tchip formation and its evolution at four distinct cutting lengths for an uncut chip thickness of 0.1 mm and tool rake angles of 5° and 12°, respectively. Stress distribution (von Mises) is plotted which shows, as expected, maximum values at the primary deformation zone. Stress concentration is also developed at the secondary deformation zone, due to tool-chip friction. Figure 26a shows that the predicted (numerical) strain rate values at the primary deformation zone is compatible with the dynamic compression tests range. Moreover, in Figure 26b, the stress triaxiality field distribution of the chip is shown. It is interesting to note the highly negative triaxiality values at the secondary shear zone (tool-chip interface) which then evolve into positive stress triaxiality, as the chip is no longer in contact with the tool and is submitted to a bending moment, instead. Despite its tendency to bend (plastically deform) which results in a change of the stress triaxiality values at chip contour, its core still registers the mainly negative values due to the predominant compression loading of the chip formation mechanism.

The study of cutting forces under the most varied machining conditions is a common approach towards cutting process improvement. It can be seen as a benchmarking parameter of cutting efficiency and cutting tool geometry suitability, especially in the development of novel geometries. Such data is typically obtained through extensive experimental testing. Numerical simulation can be highly advantageous in the virtual identification of characteristic cutting constants such as the specific cutting pressure, $K_c$, enabling extrapolation from the numerically validated trends and minimizing experimental machinability tests. Towards the assessment and validation of the implemented FEM models when it comes to load prediction, the experimental range of $t_0$ has been covered numerically for the comparison of specific cutting pressure. Figure 27 presents the numerical and experimental $K_c$ results for the AMed 18Ni300 maraging steel in function of the selected tool geometries. The satisfactory numerical estimation for a wide range of uncut chip thickness in two distinct tool geometries enables the validation of the identified input data values and material laws, as well as the implemented orthogonal cutting numerical model. An approximate maximum error of 4% from the experimental exponential trend has been calculated.

6. Application

The material’s machinability was assessed by means of longitudinal turning tests carried out on a universal lathe EFI DU20 with 5.9 kW power under dry conditions. Given that machining operations are typically performed in additively manufactured components in order to attain better surface quality and to ensure dimensional tolerances for specific applications, the current tests focused only on finishing operations.

The cutting load is significant as an indicator of the operation stability and energy requirements of the machining process. Combined with chip morphology characterization, it allows the identification of favorable cutting scenarios in the post processing stage, envisioning an increase of the production rate and quality of the finished product. When it comes to load measurement and acquisition, the same equipment employed in the orthogonal cutting tests was used. The load cell was mounted on the lathe’s tool carriage and levelled in order to ensure the alignment of the cutting tool with the center of rotation of the fixation chuck. Figure 28 shows a schematic representation and the related nomenclature of the experimental apparatus. An ISO DCGT-11T304-FS cutting insert with a 0.4 mm nose radius, chip-breaking rake surface and the same coating as the orthogonal cutting inserts and compression platens, TiAlN PVD coating, was selected to provide a representative cutting insert to the industrial turning operations and to keep the tribological conditions constant throughout the investigation. It was mounted on a tool holder providing a −3° side cutting edge angle, 0° cutting edge inclination and 7° back relief angle. An unused cutting tool was selected for each segment in order to ensure equal conditions. Regarding the operative parameters, a full factorial combination of two rotational speeds (1800 and 2500 rpm), three feeds (0.05, 0.1 and 0.2 mm/rev) and three depths of cut (0.1, 0.2, and 0.3 mm) were explored. Each specimen is subjected to various cutting passes so the starting point for each cut is an already machined surface. Since the tests were performed under constant rotational speeds, the cutting speeds have evolved along the successive cutting passes due to the diameter reduction. The selected 2500 rpm resulted into cutting speeds between 118 and 77 m/min.

Despite providing valuable insight on metal cutting mechanics, material models validation and simplified kinematics, the orthogonal cutting operation does not accurately represent 3D industrial cutting processes with intricate tool geometries, such as the turning operation. In an attempt of bringing closer the industrial processes with the numerical simulation, the same experimentally tested longitudinal turning operations were numerically modelled. Figure 29a shows the tool and workpiece schematic configuration, illustrating the geometrical cutting parameters. It is important to note that, for kinematics simplification, and similarly to other models in literature [48,49], the workpiece was defined as a rectangular extrusion with the contour of tool nose radius, focusing on a small portion (but steady-state representative) of the cutting process. The chip-breaking insert tool geometry was represented in the model through a rigid body. The workpiece was modelled with 8-node linear elements with reduced integration and hourglass control (C3D8R). In order to be able to apply two distinct structured mesh densities, the workpiece was divided in two regions, labelled as “core” and “envelope” (refer to Figure 29a). In order to ensure continuity between these two parts, a tie constraint was used, ensuring no relative motion between the nodes of each part. Chip separation is modelled through the application of the identified damage model to the whole workpiece. As regards to the tool, a finer mesh density (unstructured) was defined around nose radius. In both tool and workpiece parts, finer meshes correspond to a 0.02 mm seed size, and 0.05 mm for coarser meshes. The workpiece base was clamped and degrees of freedom of the tool were null, except in zz direction, allowing for tool cutting speed definition which was the same as the maximum experimentally tested. With regards to material parameters, the same conditions as orthogonal cutting simulation were applied. Three distinct depths of cut $a_p$ (0.5, 0.3 and 0.1 mm) were simulated for a fixed feed, $f$ = 0.2 mm. The selection of such cutting parameters is related with the larger chip sections, comparatively to other experimentally tested configurations. The simulation of smaller chips is hindered by the very fine required meshes and associated computational costs.

Figure 30 shows the numerical final chip geometry of each simulated set of cutting parameters (for a limited cutting length of 5 mm), and the corresponding experimental chip geometry (for indefinitely long, >>5 mm, cutting length), illustrating their similar tendency to identical chip formation. This means that for minimum depth of cut ($a_p$ = 0.1 mm) a ribbon-like chip morphology is developed, while for bigger chip sections curling seems to occur, promoting helical chip formation as the one being developed in the numerical model with $a_p$ = 0.5 mm.

Regarding the principal cutting forces, the simulated results are compared with the experimental analogous conditions in Figure 31. A very satisfactory correlation between the experimental and numerical results is observed, showing the robustness of the identified material model towards the principal cutting force prediction. The good experimental-numerical correlation and successful simulation of the industrial turning process address the urgent need towards shifting from theoretical 2D models into more accurate and complex 3D simulations [4].

Despite the good performance of the numerical simulation for the cutting force estimates, the underestimation of the other vector components should be highlighted. In orthogonal cutting the experimental feed force ($F_f$) accounts for averagely 57% of the principal cutting force ($F_c$). Regardless of the accurate numerical prediction of the principal cutting force, the numerical feed force is underestimated (35% of the $F_c$). Concerning the numerical simulation of the turning process, a similar trend is observed, in which the numerical estimate of feed force is less than 35% of the principal cutting force. These results are consistent with those found in the literature [11], which are still not sufficiently understood. It is a common belief that lack of information about flow stresses and friction at the rates and temperatures experienced in practical cutting has primary responsibility for this disagreement [10]. Nevertheless, the authors of the present research, after an extensive mechanical–tribological characterization under extreme loading conditions, have the strong confidence that a lack of information about flow stresses and friction at the rates and temperatures is not the cause for the disagreement. The mechanical–tribological response of the material throughout the shear plane and over the rake surface can be adequately calibrated and modelled for the numerical simulation of the metal cutting processes. Possible reasons for mismatches between numerical estimates and experimental measurements could come from the singularities of the metal cutting mechanics located where the chip formation begins and where the chip-tool interfacial contact ends. In the first case, the size effect of the cutting-edge radius or ploughing effect [50] is pointed out as an additional contribution to the overall cutting load [51]. Some authors also claim that while the chip-rake contact interface is steady, the workpiece-clearance contact occurs under highly dynamic conditions because of inappropriate vibration (chatter) that often results in poor surface quality and feed load peaks [52]. The vibration in the direction of the cutting speed is relatively smaller, whereas in the direction of the depth of cut it is relatively higher. The vibration amplitude is promoted by the relatively low stiffness of the overall machine-tool-workpiece set and the workpiece mechanical strength that is a major obstacle, when machining difficult-to-cut materials, such as hardened steels and titanium alloys [53]. Surface free energy is also pointed out as another important contribution from the point of view of the ductile fracture mechanics [54]. Clearance surface is also of major importance since its texture scratches and rubs the machined surface masking the contribution of the primary rake face on the cutting forces amplitude. The higher the elastic recovery of the machine-tool-workpiece set, the higher the relevance of this effect.

In the second case, perhaps less known, it has been shown that pressure-welded junctions occur near the point at which the chip detaches from the cutting tool, and it has been established that there is an intimate relation between the oxide films formation and the oxygen concentration in the surrounding medium. Thus, an additional shear force parallel to the feed force should be applied to break the weld spots to allow the chip to slide over the rake surface. At these welded spots no relevant normal force to the rake surface, parallel to the cutting force, is noticed. Thus, the friction coefficient can be artificially promoted. The thinner the uncut chip thickness, the higher relevance of this effect [55].

As discussed above, the numerical underestimation of the secondary vector components of the principal cutting force seems to suggest significant limitations of the finite element codes. The effectiveness of the numerical models to predict the machining performance depends on how accurately these models can represent the actual metal cutting process, namely the severe mesh distortion around the tool cutting edge. A highly refined mesh is the first step usually taken to address the problem [56]. However, the sparse finite element mesh used in the 3D simulations of Figure 30 showed a significant computational cost of approximately 48 h, using 10 multiple processors for each numerical simulation. This high computational effort is incompatible with a practical application for the numerical simulation of metal cutting. Nevertheless, even simple 2D simulations of the orthogonal metal cutting using a highly refined mesh shown a similar underestimation of the feed force. The accuracy of the numerical methods seems not to be at stake, but rather the concept of which physico-chemical phenomena should or should not be considered in the numerical modelling of metal cutting. The availability of numerical features in the commercial codes to couple these physico-chemical phenomena is also of utmost importance to establish a realistic numerical model of metal cutting. However, despite only the cutting force can be accurately predicted, the underestimation of the secondary vector components can be minimized considering that the relative difference between the experimental measurements and the numerical estimates is about 30%. This is perhaps one of the main results of the present investigation, clarifying the influence of tribo-mechanical modelling and numerical methods on the estimates accuracy, pointing out the need to investigate the physico-chemical phenomena in the singularity zones of the chip formation mechanism.

7. Conclusions

In metal cutting modelling, the input data calibration has always relied on the uniaxial compression testing given its state-of-stress similarity and due to being the most effective way of achieving large plastic strains. As an additional benefit, uniaxial compression also allows mechanical testing in extreme mechanical conditions, resembling those in metal cutting processes. Friction models can also be calibrated by the ring uniaxial compression test over the same range of operative conditions. In this part of the study, special focus has been on identification of the individual contribution of each phenomenon involved in the tribo-mechanical mechanism. The proposed optimization-based methodology showed to be effective in subtracting the friction-dissipated energy of the experimentally determined flow stress, as well in precise determination of the friction coefficient under extreme mechanical conditions. This tribo-mechanical characterization made it possible to partly cover the deficit in the scientific literature on the material behavior over wide ranges in temperature and strain-rates for AMed 18Ni300 maraging steel.

Looking at the scientific literature, there are cases where the traditional calibration methodologies seem unable to provide accurate input data values, with negative impact on the numerical simulation results. In general, this occurs when the material plastic behavior is highly sensitive to the stress triaxiality. This sensitivity was observed in the tested AMed 18Ni300 maraging steel and is compatible with similar materials in the literature from both AMed and conventional metallurgical conditions. The input data calibrated exclusively on the basis of uniaxial compression tests provided numerical overestimates around 30% for the cutting forces. In most cases, this accuracy level is sufficient to carry out a sensitivity analysis to the process parameters, such as the study on the impact of AMed materials on the metal cutting forces and chip morphology. This research showed that where more accurate estimates are to be produced, it is helpful do have a better understanding of the plastic flow and the damage evolution associated with the manufacturing process.

An adequate constitutive model and well determined coefficients are the major key points in metal cutting modelling in order to better describe the tribo-mechanical response of the materials. The better the tribo-mechanical response is captured by the model, the better the accuracy of numerical estimates from the metal cutting simulations. However, a complete calibration of a constitutive model for general application, such as in sheet metalworking, bulk metalworking and metal cutting, is a complex an extremely time-consuming process. The proposed methodology demonstrated that the calibration procedure can be efficiently managed and simplified when the nature of the manufacturing process is considered. The almost perfectly plastic behavior of the maraging steel also exposed the inadequacy of the previously selected Johnson–Cook hardening law (first term of Equation (1)), and thus a Swift-Voce model was successfully employed even though its simplicity.

The proposed calibration methodology proved to efficiently provide accurate input data for the tribo-mechanical constitutive models by numerically reproducing all mechanical testing results successfully. Nevertheless, the simple orthogonal cutting test under controlled laboratorial conditions was also necessary for validation of the implemented numerical model for metal cutting simulation. It should be noted that the tribological condition of the ring compression test differs from the metal cutting due the existence of metallic oxides and thus a slight variation in the friction coefficient was to be expected. The friction coefficient was adjusted upwards by about 9% in order to better reproduce the experimental chip curling. Its sensitivity to strain rate and interface temperature was kept constant to that determined by the tribo-mechanical testing. Finally, the smooth cylindrical and the cylindrical-notch tests under tensile loading have been shown to be relevant for additional accuracy in the numerical prediction of the chip types and surface integrity.

The critical damage value required for chip separation is always maintained ahead of the cutting edge, but similar values are also found to occur along the rake surface of the cutting tool. This means that more damage accumulation can occurs after the material passes through out the primary shear zone. The existence of high levels of ductile damage along the rake surface of the cutting tool is not expected to promote new crack formation because this region of the chip is subjected to compressive hydrostatic stresses which inhibit crack formation. However, the chip acquires more curl as it passes through the primary deformation zone and departure from the rake surface. The material located outside the uncut chip thickness (inner side of curvature) experiences a different damage path under positive stress triaxiality. Thus, initiation and propagation of cracks from the outside the uncut chip thickness to the inside chip bulk is possible to happen and it occurs for a variable critical damage value, demanding tensile testing on easy-to-test cylindrical samples. The chip type and its curvature radius value are probably defined by an energy compromise between the plastic work, the amount of frictional work and the initiation of new surfaces/cracks. Future research at the constitutive modelling shall consider, in addition to damage mechanics, the contribution of the additional energy required to form new surfaces on metal cutting. Likewise, the establishment of new experimental methodologies to characterize the fracture toughness under similar operative conditions as those observed in machining processes.

Finally, though not less important, the double notched plane strain specimen had a central role in the inverse calibration methodology of the flow stress curve and critical damage values under plane strain conditions. This has the advantage of generating both negative and positive stress triaxiality values for the calibration of the coupled damage-plasticity constitutive model. Few double notched specimens were necessary as the previous calibrated mechanical model, based on uniaxial compression tests, served as an initial reference for the optimization-based procedure for determination of the plasticity model coefficients and damage initiation coefficients. The number of double notched specimens needed to perform the inverse calibration is of importance for industrial applications that demand a rapid effective response. The time taken in the inverse calibration procedures depends on its quantity, geometrical variants, and experimental repeatability. It is worth noting the high volume of these specimens and elevate price per kilo of the additively manufactured material to test; Furthermore, most of this material to be removed by machining. Each specimen requires a different geometry to allow different stress triaxiality values (pressure angles), thus a different manufacturing setup is required for each specimen. All this makes the double notched specimen much more expensive than the uniaxial compression cylinders. From the point of view of the authors, the double notched plane strain specimens can be improved through adoption of a simple, unique, and standard specimen geometry that allows the control of the triaxiality value by the testing machine. The adaptation to the specimen geometry should also take in account the notch geometry to enable a direct characterization of the fracture toughness values.