Fundamental Investigations in Tool Wear and Characteristics of Surface Microstructure for Ultrasonic Vibration Superimposed Machining of Heat-Treated X46Cr13 Steel Using Different Cutting Materials

Abstract

The importance of functional surfaces is continuously growing in the context of increasing demands on the sustainability of performance, resource efficiency and manufacturing costs of technical systems. For example, microstructured substrate surfaces can contribute to enhance the adhesion of layers, which in turn ensure the wear protection of a highly loaded component. Many microstructuring processes require a system change, entailing high costs. However, the ultrasonic vibration superimposed machining (UVSM) can be implemented as a finishing process. Due to its defined cutting-edge geometry and kinematics, UVSM represents a suitable method for a reliable generation of predefined surface microstructures. In order to optimize the process regarding the tool wear behavior and thus the geometrical characteristics of the surface microstructure, experimental investigations are carried out to find the most suitable combination of heat treatment condition of the martensitic stainless-steel X46Cr13 and various cutting materials. A vibration system for workpiece-side excitation is used for the experimental cutting tests. The most promising results were obtained within the combination of cemented carbide as a cutting tool and soft annealing as a heat treatment condition. They serve as a base for extensive investigations on the effects of substrate microstructuring to the adhesion of chemical vapor deposition (CVD) diamond layers to steel.

1. Introduction

1.1. Chemical Vapor Deposition (CVD) of Diamond on Steel

The martensitic stainless-steel X46Cr13 is used in many areas, for example as a cutting tool in the food industry, for surgical instruments, pump and valve components, as well as bearings. All fields of application offer the opportunity to reduce wear or increase the lifetime by applying diamond coatings. The application of CVD diamond on steel has been a field of research for many years in which only little progress has been made. However, so far, no industrially relevant system could be established. In addition to chemical diffusion, thermal expansion is still a major challenge to the adherent deposition of diamond coatings, although there were already attempts to limit this problem. For this purpose, Bareiß et al. took certain steels which undergo a phase transformation with the cooling process at temperatures between 750 and 800 °C for coating to counteract the effects of thermal expansion (during heating) and shrinkage (during cooling) [1]. This effect made it possible to partially compensate for the resulting residual stresses in the CVD diamond layer. Based on those results, Kellermann et al. used the combination of steel substrate with phase transformation (41Cr4) and chromized interlayer to vary the diamond deposition temperature from 650 up to 980 °C. They found that with deposition temperatures between 760 and 920 °C, adherent diamond coatings can be applied [2].

However, it only affected layer thicknesses of a maximum of 2 µm and not even closed in some cases. Industrially relevant layer thicknesses could not be achieved by solely utilizing the phase transformation of the steel.

In their review on CVD diamond deposition on steel using different interlayers, Damm et al. also consider the influence of a deterministic microstructure of the steel surface on the adhesion of the diamond layer [3]. They justified this by the formation of high thermally induced residual stresses within the layer, which lead to spontaneous delamination in the case of very flat substrate surfaces. For this reason, they investigated a substrate surface that was microstructured by a laser and showed as a result that spontaneous delamination can be prevented if suitable intermediate layers are used. This was mainly attributed to the mechanical interlocking, whereas no conclusions were drawn on the influence of the microstructure on the residual stresses within the diamond layer. No detailed information was provided on the design of the microstructure either. Based on this, various research papers were compared under Börner et al., which took up the surface microstructure of the substrate as a partial solution and found a positive influence of the roughness on the layer adhesion [4]. However, it was concluded that most of the substrate microstructures had a stochastic character and the few surfaces with geometrically defined microstructures were not systematically investigated. Consequently, in the research work were some instructions for both the recording and the derivation of defined properties of particle-blasted surfaces presented. Subsequently, the characteristic surface features were converted into quantitative process parameters and the manufacturing of deterministic surface microstructures, generated by ultrasonic vibration superimposed machining (UVSM), was investigated. The oscillating excitation was in the direction of the tool axis and thus orthogonal to the workpiece surface. The design of the surface microstructure was developed using both a kinematic surface simulation tool as well as a finite element analysis (FEA) for the cooling process of the compound of substrate and coating layer.

Moreover, Börner et al. have also described the generation of surface microstructures on the specimen surface by ultrasonic vibration superimposed machining of the steel X20CrMoV11 using face milling regarding manufacturing aspects [5]. The effects of recutting and displacement of the substrate microstructures in particular were investigated using a kinematic surface simulation for comparison. Based on this, under Prieske et al., similar substrate microstructures were coated with diamond using a Laser-induced plasma CVD process without a vacuum chamber. The principal suitability of such substrate microstructures with regard to diamond growth and adhesion could be shown. However, it was not possible to apply thick (up to 8 µm) and simultaneously adhesive diamond layers, especially due to the large mismatch of the thermal expansion between the diamond coating and the steel substrate [6].

Using a hot filament CVD coating process and the steel X46Cr13, Börner et al. were able to deposit adherent diamond coatings on steel specimens microstructured by UVSM with a thickness of up to 10 µm [7]. However, it was shown that surface defects lead to coating delamination. These can be caused by spontaneous or strongly progressing tool wear, for example.

From this, on the one hand, the advantages of deterministic microstructuring of the substrate surface for increasing the adhesive strength and thus the quality of the diamond layers deposited by means of the CVD process can be derived. On the other hand, the necessity of guaranteeing a high reproducibility of the microstructures becomes apparent. This is associated with a stable machining process as well as a low wear behavior of the tools used.

1.2. Machining by Cutting

As already mentioned in Section 1.1, the additional superposition of the effective motion of the cutting tool offers a proven possibility for the generation of deterministic surface microstructures. For this purpose, vibration assistance, often in the ultrasonic range, in different directions is possible, which has already been presented in numerous research papers. A current overview of this topic is given by Zheng et al. [8] and Yang et al. [9], respectively. The focus in Reference [8] is primarily on the vibration devices used. In Reference [9], on the other hand, the kinematic principles and the processed workpieces are described. However, it clearly emerges from both overviews that the aim for deterministic microstructuring accounts only for a small proportion. Furthermore, almost exclusively, materials are considered that are favorable concerning machining, such as aluminum alloys, among others, by Tao et al. [10], Xing et al. [11] and Sajjady at al. [12], copper by Liu et al. [13], or brass by Zhu et al. [14]. This allowed the use of very hard cutting materials such as single crystalline diamond (SCD) [6,7] or polycrystalline [12] diamond (PCD), which have a sharp cutting edge with a small cutting edge radius. Therefore, they are predestined for microstructuring in the micrometer range. On the other hand, in References [10,11], end mills made of cemented carbide were used for the experimental investigations, with the ultrasonic vibration excitation taking place perpendicular to the tool axis. However, tool wear was not considered in any of the research studies mentioned.

If ultrasonic vibration superimposition is used in the machining of steel, the focus is often on reducing the surface roughness or decreasing wear of diamond-based tools. For example, research on machining of austenitic stainless-steel (X5CrNi18-10) by Zou et al. is presented, which investigated a reduction in roughness during orthogonal turning with ultrasonic vibration superimposition in the direction of the cutting speed [15]. Here, industrially common tools made of cemented carbide with a multilayer coating system were used. However, a wear investigation was not addressed. Diamond-based cutting materials are also often used, since the superimposed effective movement in the cutting direction, or elliptical, enables more efficient cooling of the cutting zone through short-term lift-off effects. This enables in particular a drastic reduction of chemical wear. For example, Zhang et al. investigated the use of PCD tools as an alternative to SCD in the machining of hardened stainless-steel (typical Stavax, 49 HRC) with elliptical ultrasonic vibration superimposition [16]. The aim was to reduce the roughness to enable the production of mirror-like surfaces. This was realized by means of a suitable combination of process parameters. It was also found that the flank wear increased with an increase in the cutting speed. However, this type of ultrasonic vibration superimposition requires different demands on the tool, in particular on the sensitive cutting edge, compared to excitation in the direction of the passive force (in face milling: co-axial to the tool). Therefore, the findings obtained there are only transferable to a limited extent.

The surface structuring of steel materials with ultrasonic vibration superimposition was investigated by Maurotto and Wickramarachchi [17] and Zhang et al. [18], among others. In Reference [17], a feasibility study was carried out on ultrasonic vibration-assisted milling with axial vibration of the cutter of austenitic stainless-steel (X2CrNiMo17-12-2), where mainly a frequency variation was investigated. It was found that at 20 kHz, the tool wear, in the form of delaminated coating from the cemented carbide substrate, was the lowest compared to 40, 60 kHz and without, respectively. However, the structuring in the dimension of the roughness was not focused but resulted solely from the variation of the process parameters. It was also pointed out that the use of specially adapted tools is recommended for this type of process, since the requirements are different from those of a conventional face milling process. On the other hand, in Reference [18] elliptical vibration cutting was used specifically for surface structuring. Here, SCD tools were used for machining hardened martensitic stainless-steel (X30Cr13, 53 HRC). However, the structuring was carried out in the nanometer range, which makes it difficult to transfer the findings because of much lower mechanical stress for the tools.

When considering resulting surface microstructures or comparing them with corresponding kinematically simulated surface microstructures in conventional milling of steel, other cutting materials are again primarily used. Freiburg and Biermann, for example, used end milling tools made of cemented carbide with different cutting-edge geometries for microstructuring an ASP2023 (62 HRC). They found a high degree of conformity with the simulated surfaces, which enables machining of surfaces with tailored roughness [19]. Meijer et al. used end milling tools with solid cubic boron nitride (CBN) cutting edges in their investigations of the kinematic roughness in the end milling process on high-speed steel (X130WMoCrV 6-5-4-3). They increased the predictive ability of the model by taking into account the roughness of the cutting edge as well as the main, back and lateral overlapping cuts [20].

It can be seen that there are several research papers that consider some of the aspects addressed in this paper. However, only limited conclusions can be drawn with regard to the focused topic: UVSM in co-axial tool direction in face milling of steel for reproducible surface microstructuring.

1.3. Heat Treatment of Steel to Improve Machinability

Due to the fact that coating at the prevailing process temperatures of about 900 °C eliminates any kind of the preceding heat treatment condition (HTC) of the substrate material, there are no specific requirements concerning heat treatment. Thus, the most favorable material condition can be used for microstructuring since tool wear is the major challenge for reliable processes. Furthermore, the heat treatment condition influences the behavior of the substrate material concerning plastic deformation and burr formation. From the literature, only limited recommendations can be derived. Typical heat treatment of stainless martensitic chromium steels, especially of X46Cr13, are soft annealing (750–850 °C), quenching and tempering (hardening: 950–1050 °C and tempering: 650–700 °C) and also stress relief annealing (200 °C).

Hoseiny et al. investigated the effect of the austenitization temperature on machinability with regard to the cutting force and tool life in end milling of a modified 35CrMo7 steel in pre-hardened condition. In this steel, an originally austenite grain is split into several martensitic packets which represent effective grain boundaries according to the hypothetical approach in the martensitic structures that contribute to mechanical properties, e.g., yield strength. They concluded that the cutting force generally increases with the martensitic packet size. An exception was the largest considered packet size at the highest cutting speed. Furthermore, they found that the increase of the cutting force with the packet size is connected with an increase in the degree of work hardening in the material. Derived therefrom, for the workpieces with smaller packet size, the tool life was longer, which is correlated to both a lower absolute value as well as a smaller spread of the cutting force [21]. Furthermore, Hoseiny et al. studied the machinability of modified 35CrMo7 steel, which was heat-treated to realize three different material microstructures exhibiting the same hardness. A main conclusion was that the spheroidizing plus quenching and tempering (S-QT) treatment led to the best machinability (regarding tool life and cutting force) at a similar hardness (about 44–45 HRC), with a few decreasing total elongation, impact toughness and ultimate tensile strength in comparison to austempering and conventional quenching and tempering (QT). To explain this effect, they considered the work hardening as the most important mechanical characteristic that adversely influences the machinability of the steel. Also, the scratches caused by abrasion on the used cutting tools for the S-QT-treated workpiece were smoother due to the round morphology of the carbides rather than the dominant plate-like carbides in the austempered and QT-treated workpieces. In addition, it is suggested that the presence of some amount of un-tempered martensite in the austempered workpiece increases its abrasiveness [22].

Demir carried out experimental machining tests on micro-alloyed steel using cemented carbide tools. Different states of hardening as well as material microstructures were adjusted by the cooling conditions. It could be stated that the surface roughness varies mainly depending on the cutting speed for the different heat treatment conditions and therefore no trend can be derived. Only the statement that the cutting forces in the hardest condition are clearly higher can be taken from Demir [23].

1.4. Scientific Research Demand

It can be concluded that certain studies on the machinability of steel were carried out depending on the heat treatment condition, in which surface roughness and tool wear were the main issues. However, it was difficult to deduce clear trends. Furthermore, the results are strongly influenced by the surrounding conditions, such as the alloying elements, the process parameters, or the tool properties. In addition, no research studies are known that deal with UVSM of steel for the purpose of surface microstructuring with regard to a cutting material selection. Accordingly, ultrasonic vibration superimposed milling for predefined surface microstructuring requires an extensive series of fundamental experimental investigations to close this knowledge gap. Useful aspects can be derived from this with regard to the reproducible generation of microstructures on steel surfaces by UVSM. The machining tests were also carried out on brass (CuZn40Al2), as in comparison to steel, better machinability and lower tool wear were expected. This was intended to achieve a high degree of accuracy compared to the simulated surface microstructures and thus to create a reference for the tests in steel.

2. Materials and Methods

2.1. Test Preparation

2.1.1. Heat Treatment

In this study, the martensitic stainless chromium steel X46Cr13 was used. The chemical composition and the permitted limits are shown in

Table 1. Chemical composition of X46Cr13: mass fractions in % according to Reference [24].

	C	Si	Mn	P	S	Cr
Min	0.43	-	-	-	-	12.5
Max	0.5	1	1	0.04	0.03	14.5

.

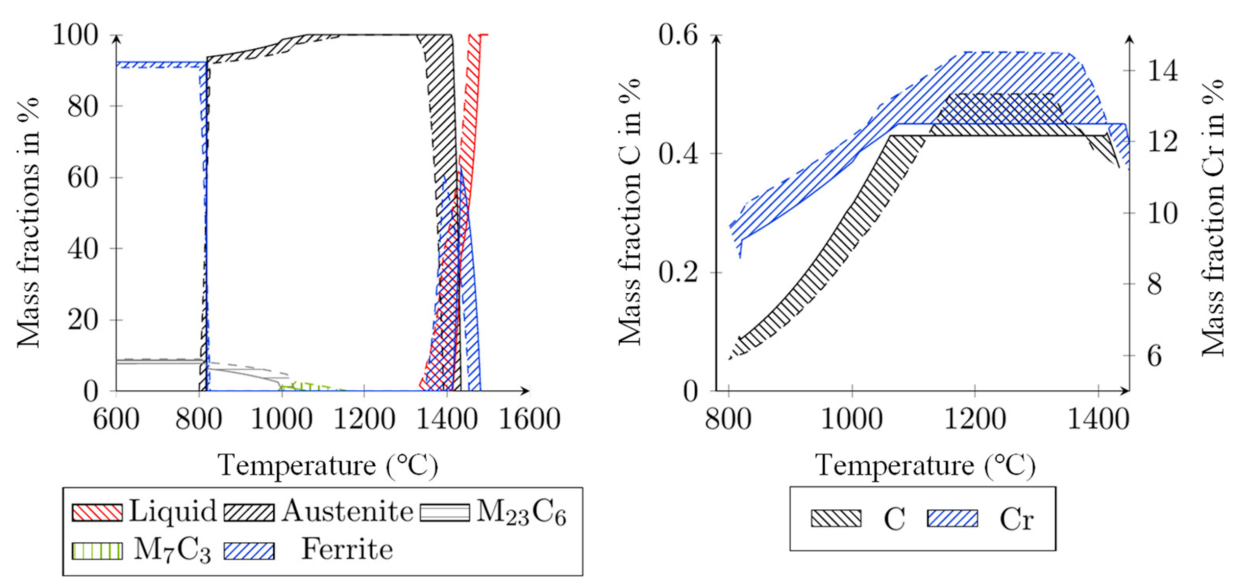
Thermodynamic calculations were performed for the minimum (solid line) and maximum (dashed line) permissible alloy content using JMatPro^® V7.0 (Sene Software Ltd., Guildford, UK), compare Table 1. This includes the calculation of the phase diagram, see Figure 1 (left), and the chemical element distribution (carbon (black line) and chromium (blue line)) in austenite in equilibrium state as a function of temperature, see Figure 1 (right). It can be observed in Figure 1 (left) that from approximately 800 °C (max) and 817 °C (min), the transformation of ferrite into austenite starts. Besides austenite, there are carbides. With increasing temperature, the mass fraction of the carbides decreases, and the austenite fraction increases. 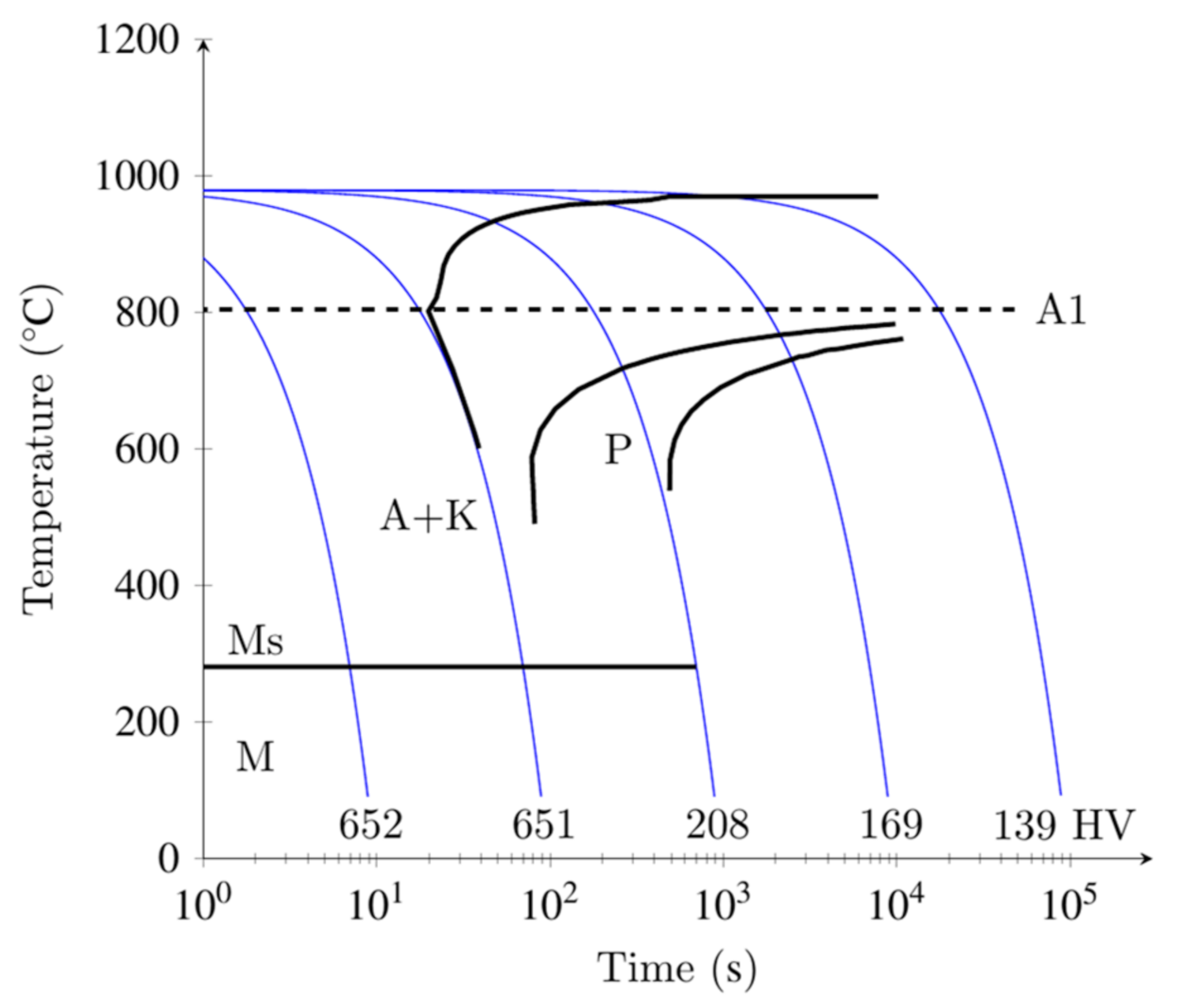In Figure 1 (right), it can be seen that with increasing temperature, the contents of carbon and chromium in austenite increase. This is due to the increasing solubility of the carbides. A maximum of the carbon and chromium content is reached at approximately 1062 °C (min) and 1160 °C (max). Continuous time-temperature diagrams (CCT) indicate the resulting phases and hardness as a function of the austenitizing temperature and the cooling rate, compare Figure 2. The phase diagram, the chemical composition of austenite and the CCT enable the possibility to design the heat treatment and to classify the heat treatment results in terms of metal physics.

Figure 2 shows the phase composition and the resulting hardness as a function of the cooling rate. It can be clearly seen that the hardness decreases as the cooling rate decreases. The hardness varies from a maximum of 652 to 139 HV. It has to be noted that the austenitizing temperature is 980 °C. If the austenitizing temperature is different, the CCT changes. In general, with increasing austenitizing temperature, the transformation lines shift to longer times, i.e., the steel transforms more slowly. This can be explained by the increase in the mass proportion of alloying elements in austenite with increasing austenitizing temperature, comparing the mass content of chromium, Figure 1 (right). With increasing carbon content, martensite start temperature and martensite finish temperature decrease, and stabilized retained austenite can be present at room temperature. At high temperatures, grain growth takes place due to the minimization of the surface energy. This means that with increasing holding time at high temperature, the grains grow. Coarser grains generally also lead to a reduction in the conversion and precipitation effort, as there are fewer germination or impurity sites, such as grain boundaries, in the lattice. The heat treatment carried out within the framework of the study is intended to exploit these effects in a targeted manner. The initial condition (soft annealed) and three heat treatment variations were realized, see

Table 2. Heat treatment conditions and materials’ properties.

Heat Treatment	Abbreviation	Aim	Parameters ϑA, tH, Cooling Medium, Cooling Rate between 800 and 500 °C
Soft-annealed	SA	Soft and ductile	As-delivered
Annealing with slow cooling	SC	Carbide precipitations	1030 °C, 0.5 h, furnace cooling, 0.25 K/S
Annealing with long holding time and slow cooling	LH	Coarse grain and carbide precipitations	1030 °C, 20 h, furnace cooling, 0.25 K/S
Hardening	H	Hard and brittle	1030 °C, 0.5 h, oil quenching, 100 K/s–20 K/s

and Figure 3.

It should be noted that the heat treatments carried out within the scope of the study are partly different from the typical heat treatment carried out in industry, such as hardening and tempering at high temperatures (quenching and tempering), in order to specifically show the individual heat treatment influences of cooling rate and holding time. In Figure 3, the recording of the temperature profile of the hardening process ends before quenching in oil. A rough estimate shows that the cooling rate between 800 and 500 °C, based on Reference [27], is among 100 K/s (high-speed oil) and 20 K/s (normal speed oil).

The differently heat-treated material microstructures are compared in Figure 4. The soft annealed condition (SA) shows distributed globular carbides. Occasional carbides can also be seen at grain boundaries. In the conditions SC and also LH, carbide accumulations (possibly pearlite) are visible at the grain boundaries. Although the holding time of 20 h is considerably longer than with SC (0.5 h), the grain sizes look similar. A grain size comparison according to ISO 643, 2020 [28], using standardized image series tables from ASTM E 112:2013 [29], showed an average grain diameter of approximately 18.5 µm for condition SC and an average grain diameter of approximately 26.5 µm for LH. The ratio of the area shares of the grain boundary carbides (dark) was quantified in a phase analysis (threshold analysis). The thermally stable carbides (according to JMatPro^®: M₂₃C₆, M₇C₃) seem to stabilize the grain boundaries and have apparently minimized grain growth. At the condition SC, the area shares of the grain boundary carbides are approximately 20.6%, slightly higher than at LH, with approximately 15.2%. This indicates a higher precipitation kinetics during cooling at condition SC due to the finer grains. For the other heat treatment conditions, it is not possible to determine the grain size, as grain boundaries cannot be traced. The image H shows the hardened condition. It should be mentioned that when comparing different images of conditions H, a difference in the number of carbides was noticed, which indicates a dissimilar distribution of the carbides in the initial condition (segregation).

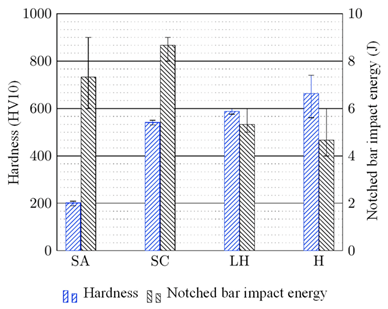
Figure 5 shows the hardness and notched bar impact energy of the specimens that have been heat-treated differently. It is noticeable that the soft-annealed condition has the lowest hardness of approximately 200 HV10 and at the same time, compared to the other heat treatment conditions (LH and H), high notched bar impact energy. The condition annealed at 1030 °C for half an hour with slow cooling (SC) can bear a higher notched bar impact energy than the soft-annealed condition (SA), at a hardness of approximately 540 HV10. Condition LH has a slightly higher hardness of about 590 HV10. This can be attributed, among other things, to the fact that during the long holding time of 20 h, the diffusion processes are close to the equilibrium state and thus more carbon is dissolved in the austenitic matrix compared to the heat treatment condition SC. According to Reference [30], the lower toughness can be attributed to pre-eutectoid carbide precipitations along the former austenitic grain boundaries and relatively coarse grains. The highest hardness of 660 HV10 and at the same time the lowest notched bar impact energy of approximately E_NBI = 4.5 J are shown in the hardened condition (H). It should be noted that the notched bar impact energy is generally at a low level.

Figure 6 shows the macroscopic surfaces of the impact test specimens. Condition SA has a shiny area, and this indicates a crystalline structure and therefore a brittle fracture. The surfaces of the conditions SC, LH and H are more matte and show hardly any differences between them. In all four conditions, there is a largely flat fracture surface, and no shear lips or similarly strongly deformed areas are visible. It can be seen that despite the different heat treatment conditions (SC, LH and H) and hardness values, the fracture surfaces look very similar and are almost fractured purely brittle.

Figure 7 displays the fracture surfaces recorded by scanning electron microscopy (SEM), determined with an acceleration voltage of 25 kV and a working distance of about 9–10 mm. The lower magnifications show back-scattered electron (BSD) images and the higher magnifications show secondary electrons (SE) images for the respective heat treatment condition of the different notched bar impact test specimens. In all conditions, transcrystalline and inter-crystalline cleavage fractures as well as inter-crystalline and transcrystalline slip fractures appear to occur in varying proportions. The differentiation between intergranular and transcrystalline fracture surfaces is mostly not clearly possible due to the heterogeneity of the fracture surfaces caused by the carbides.

In condition SA, a transcrystalline fracture is visible. The dimple structure of the different conditions indicates that the carbides trigger the more ductile areas and thus prevent further deformation. The dimple structure can therefore be interpreted as ductile deformation of a transcrystalline fracture. The visible differences are apparently determined by the carbide distribution and size. With smaller and more finely distributed carbides, the structure looks more differentiated. This can be seen, for example, when comparing the condition LH and the condition H. Condition H shows smaller and finely distributed carbides. In condition SC, isolated grain boundaries are visible. In condition LH, the grain boundaries are more clearly visible in comparison to the conditions SA, SC and H. Hence, the fracture surface appears more faceted. If the grain boundaries are embrittled by precipitation and therefore the bonds along the grain boundaries are sufficiently weak, intergranular brittle fracture occurs. The crack can spread more easily along the weakened grain boundaries. Mayer et al. showed that the increasing presence of carbide precipitates at the former austenite grain boundaries has a negative effect on toughness [31]. This was found when they investigated various hardening processes for the steel X37CrMoV5-1 regarding the resulting mechanical properties. The fracture behavior is therefore also influenced by the cooling behavior. However, despite the microstructural differences of the fracture surfaces, the overall appearance is very similar.

2.1.2. Conception and Characterization of the Vibration System

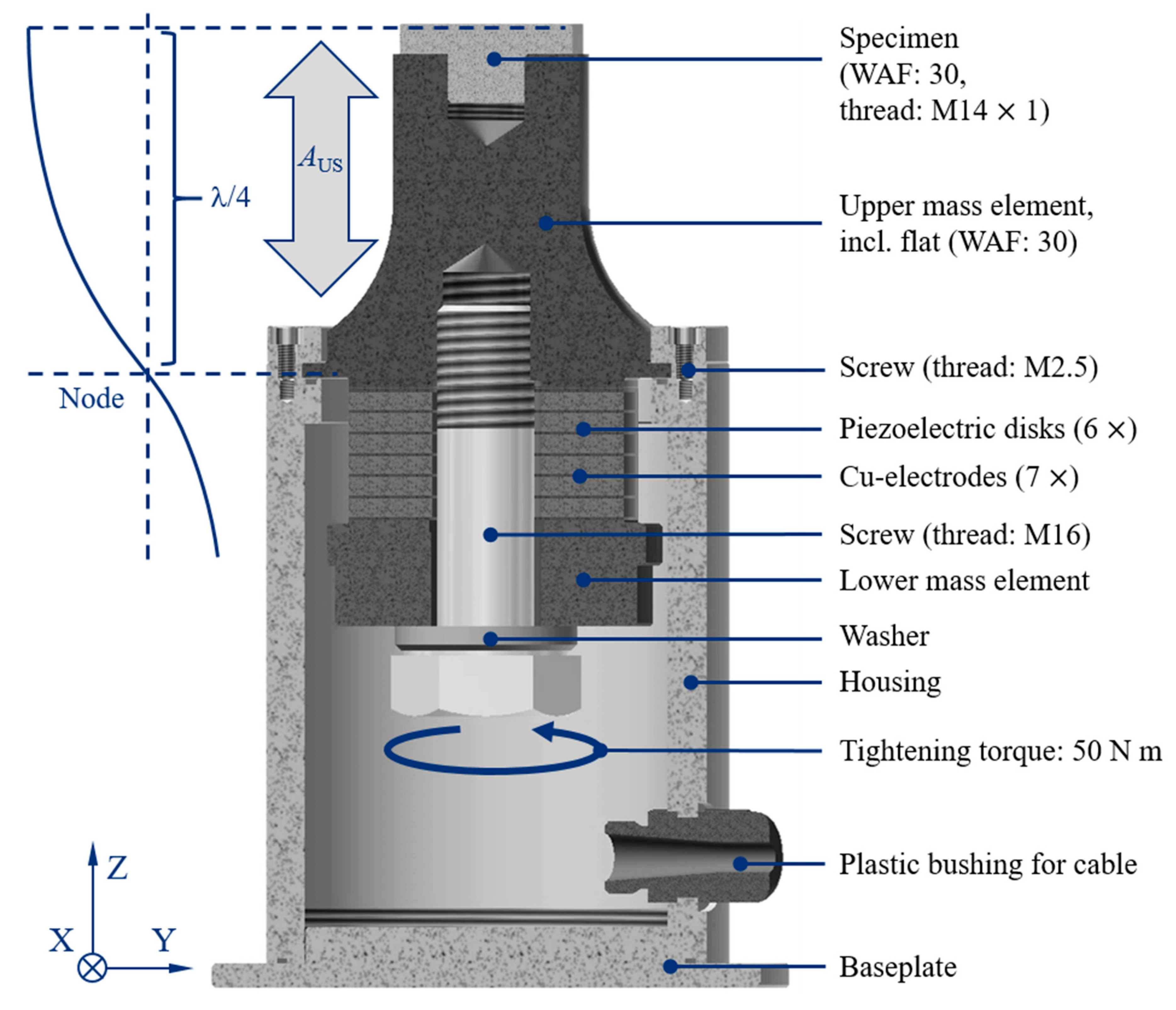
For the experimental investigations, a vibration system was developed to generate the ultrasonic vibrations. It was conceived and manufactured as a longitudinal oscillator in “λ-half design”, as described, for example, in Reference [32]. This common structure was designed with the help of a FEA to estimate the resonant frequency. The oscillator consists of upper and lower mass elements and a screw for preload, all made of Ti-6Al-4V, Figure 8. In addition, the seven copper electrodes transfer the voltage to the six piezoelectric disks. These transform the applied electric field into a linear motion due to the inverse piezoelectric effect. It becomes possible to tune the system to the desired resonant frequency using the masses. The mounting of the oscillator was realized by means of contact clamping at the node-point, as this is where the smallest strains take place, with the housing, and this was connected by a thread with the baseplate. A plastic bushing for the cable and corresponding O-rings at the connection points seal the inner against the use of lubricants. A preload of approximately 50 N m was used to tighten the screw in order to prevent the components of the oscillator from chattering and to a significant change in the resonant frequency of the system. This would result in the controller stopping due to high energy losses. To minimize the influence on the resonant frequency of the system through an additional mass, the specimens had only a small height (4 mm). The upper mass element has an internal thread (M14 × 1) and connects the specimen by a screw. The hexagonal profile with a width across flats (WAF) of 30 mm allowed for a material specific torque of up to 100 N m for the specimens with condition SA, SC and LH, 40 N m for the hardened specimens and 50 N m for the specimens made of brass. Those torques were proven to ensure a strong connection for an almost lossless oscillation.

For the generation of predefined surface microstructures, determining of the amplitude of the relative motion between the tool and the various heat-treated specimens was necessary. Therefore, a single-point laser vibrometer was used to achieve the relation between the output power of the generator and the amplitude at the specimen surface before each single experiment. The corresponding measurement setup is shown in Section 2.2. Figure 9 shows a frequency sweep to achieve the lowest needed voltage while maintaining the target amplitude for a specimen in the SA condition. The determined resonant frequency, f_US, was about 19 kHz with this testing method. This value was used for all UVSM experiments as fixed frequency.

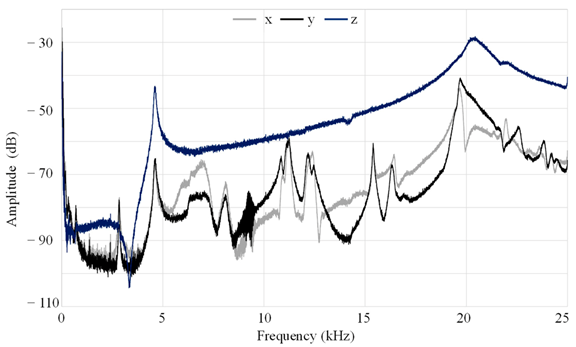
In addition, non-contact scanning measurements using a three-dimensional (3D) laser vibrometer were carried out to investigate the vibration system in more detail. The 3D laser vibrometer measurement allows simultaneous detection of the displacement in the spatial directions by evaluating the interference patterns of three laser beams reflected from the measurement object. It was excited directly by a signal from the measuring device using a so-called “periodic chirp”, i.e., from 0 to 25 kHz. Thus, both the natural frequencies and the vibration modes in all three spatial directions were determined. The results of this investigation are shown in the diagram in Figure 10, where the amplitude is given in dB.

The analysis of the plots from Figure 10 exhibits a resonance frequency in the relevant range, at approximately 20.3 kHz. There is a difference of more than 10 dB between the z-axis and the other two axes, which indicates a clear dominance of the vibration in the intended direction. The minor differences in the radial x- and y-directions can be explained by the slightly asymmetric geometry of the actuator and workpiece. The excitation frequency of 19 kHz used with the other generator is close to the measured resonance frequency, whereby the z-oscillation also dominates here.

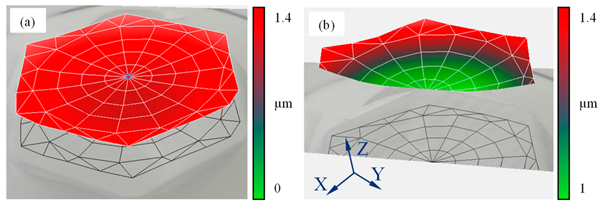
When interpreting the deflection shape, it can be determined that a quasi-homogeneous oscillation in the z-direction is present, see Figure 11a, with negligible vibration in the perpendicular directions x and y, but only in the sub-micrometer range. In addition, a slight deflection of the surface of the specimen centered towards the edges can be detected, which is evident from the sharp increase in the color scale in the range from 1.0 to 1.4 µm, see Figure 11b. However, since the field to be processed by UVSM covers an area of 1 × 1 cm, arranged centrally, these effects are negligible for surface analysis as well as the wear progress of the tools.

2.1.3. Surface Design and Simulation

To characterize the surface microstructures generated by UVSM, at first, their geometry was simulated assuming a geometrically exact tool corner with a radius of r_ε = 30 µm. For this purpose, a self-developed Matlab-based simulation tool was used, which has already been described in detail in References [4,5].

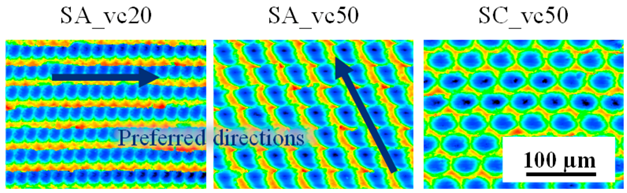
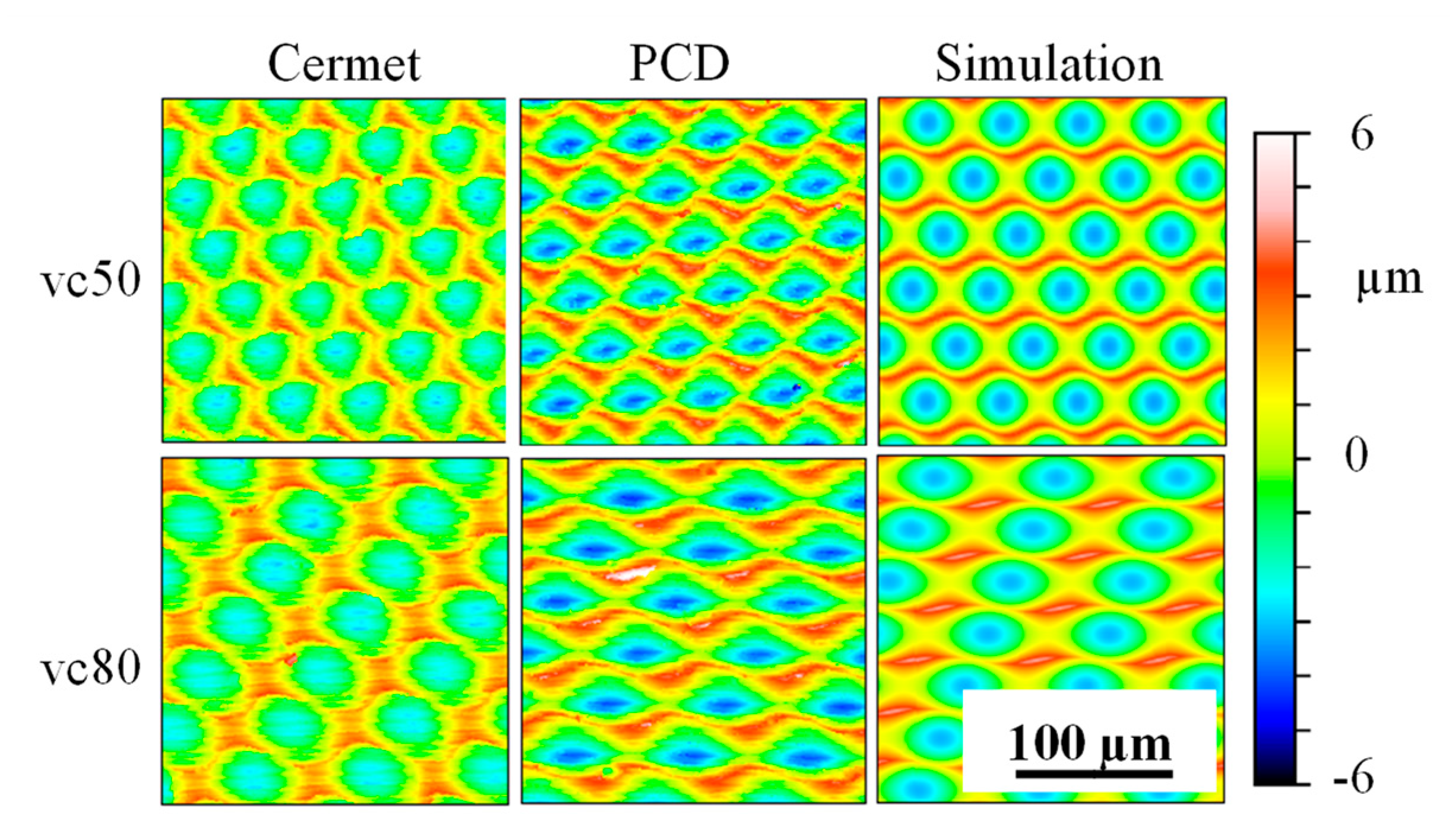
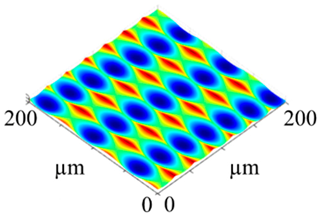
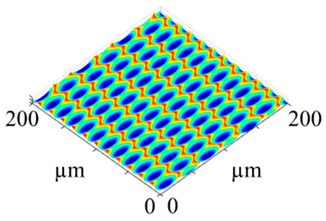
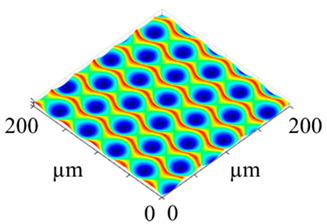
Corresponding to the two extreme cases—with (peak follows on valley) and without (peak follows on peak) structural displacement—these were simulated for the cutting speeds of v_c = 20 m/min (in the following denoted as vc20), v_c = 50 m/min (vc50) and v_c = 80 m/min (vc80), whereby the value of the feed was kept constant. The resulting surfaces are shown in

Table 3. Simulated surfaces assuming a geometrically exact tool corner (rounded, r_ε = 30 µm) and variation of cutting speed with two different structural designs (with and without structural displacement).

No structural displacement	vc = 20 m/min (ntool = 353 min−1)	vc = 50 m/min (881 min−1)	vc = 80 m/min (1404 min−1)
	Sdr = 16%/Str = 4.9%	Sdr = 6%/Str = 10.6%	Sdr = 4.8%/Str = 28.7%
With structural displacement	vc ≈ 20 m/min (ntool = 351 min−1)	vc ≈ 50 m/min (880 min−1)	vc ≈ 80 m/min (1410 min−1)
	Sdr = 16.4%/Str = 58.8%	Sdr = 7.3%/Str = 60.9%	Sdr = 6.2%/Str = 44.9%

. In addition, the respective surface parameters for the surface magnification (Sdr) and the surface texture isotropy (Str) were derived from the ISO 25178-2 [33]. Consequently, the Str values strongly depend on the structural displacement: surfaces with a structural displacement have a much more isotropic character than those without. The value of the developed interfacial area ratio increases with the number of elements per scale-limited surface, whereby the difference between the surfaces for v_c = 50 m/min and v_c = 80 m/min is almost negligible. However, the structural displacement also has an influence on the Sdr value, which shows the following example: despite the fact that they image fewer elements, the surface generated with v_c = 80 m/min results in combination with a structural displacement in a higher value of the developed interfacial ratio than those created with v_c = 50 m/min and without exhibiting any structural displacement. Subsequently, a comparison with laser-microscopically measured surfaces is possible. In addition, the influence of the steel’s material behavior, regarding plastic deformation, can be detected, since the kinematic simulation is solely based on the mathematical operation of the Boolean intersection and neglects plastic effects of material separation. Thus, quantitative values, such as the achieved structural height, and qualitative conclusions, such as for burr formation, can be derived.

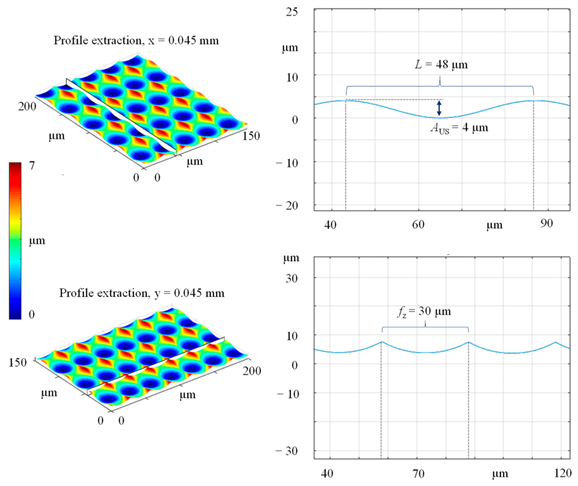
In order to characterize the simulated and the machined surface microstructures, profile extractions in the direction of primary motion (a) and feed motion (b) have been made, see Figure 12. Due to the small distance shown (right), the path curvature at (a), resulting from the tool circumference, is negligible. It shows the clearly sinusoidal curve in the direction of the cutting speed, which results from the superposition of the ultrasonic vibration. The structure height in this direction corresponds to the selected oscillation amplitude, defined here in this paper as peak-peak-value. The profile in the feed direction also shows the existing kinematic roughness. In both cases, it is irrelevant for the shape of the profile at which position (x- or y-value) the respective extraction is placed, only a height shift would occur. The symmetrical shape in the direction of feed motion becomes clear, as the corner radius is still completely engaged. In the real UVSM process, this should also be ensured by the fact that the angles of the major and minor cutting edge are identical.

2.2. Experimental Set-Up

The experimental investigations were carried out at the high precision machining center KERN Pyramid Nano. According to Figure 13, the set-up was clamped on the machine table so the direction of the vibrations coincides with the rotational tool axis z to generate the desired surface microstructures on the surface of the specimens.

In order to eliminate the influence of the curvature of the path on the surface, a single-edged insert cutter with a diameter of D_tool = 18 mm was used. Moreover, a relatively small measurement area was chosen due to the deterministic properties and therefore repeating geometry of the UVSM surface microstructures. An area of 10 × 10 mm² was previously machined for the subsequent UVSM process, to avoid the effect of re-cutting, which is described in Reference [5]. This is due to the larger diameter of the cutting tool (milling head with indexable insert of the kind SPGW 1204 according to ISO 1832 [34]) in comparison to the maximum dimension of the microstructured area. In order to avoid a smoothing of the surface microstructure with the tools flank face, like shown in Reference [5], modified inserts with an especially high clearance angle of α = 40° in the area of the corner were used. The experiments were done applying an emulsion cooling. The ultrasonic generator applied offers the possibility of using a fixed oscillation frequency, which was kept constant over all tests at 19 kHz.

It was necessary to individually evaluate the vibration behavior of the specimen before each experimental microstructuring in order to know the energy level for the desired amplitude. In addition, a single-point laser vibrometer was used, which was aligned nearly perpendicular to the specimen surface, as shown in Figure 13, right. Thus, the amplitude was measured in idle state, whereby, for example, damping effects caused by the machining process are not recorded.

Due to the process requirements and the atypical machining parameters for steel machining, which cover the entire spectrum from soft roughing, e.g., relatively low cutting speed, to hard finishing, e.g., small depth of cut, the selection of a suitable cutting material (CM) represents a major challenge. For this reason, in addition to cemented carbide (CC; grain size max. 1.5 µm, binder content: 6%) and cubic boron nitride (CBN; grain size: 4–5 µm, binder: Titanium matrix, CBN content: 55%), high-speed steel (HSS) and Cermet as a tungsten carbid-free alternative to cemented carbide were also tested. Due to the low cutting speeds, a relatively low temperature increase in the cutting zone was assumed. Therefore, the diamond-based cutting materials Polycrystalline diamond (PCD grain size max. 6 µm, binder: Cobalt, PCD content: 94%) and CVD diamond (CVD-D; higher hardness) were also considered, as the influence of diffusion wear was estimated to be low. The corner of the tools in unworn condition is shown in

Table 4. Overview about cutting tools in unworn condition.

Cutting Material	Unworn Condition of the Corner		Corner Geometry
	Flank Face	Rake Face
HSS			Nearly sharp rε < 15 µm
CC			Rounded rε ≈ 30 µm
Cermet			Rounded rε ≈ 30 µm
CBN			Nearly sharp, rε < 15 µm
PCD			Nearly sharp, rε < 15 µm
CVD-D			Chamfered (length: 30 µm)

, with a view of the rake face and the flank face. For this purpose, the indexable inserts were measured in a reproducible position using an optical 3D laser scanning microscopy of the type Keyence VK-9700 (Keyence Corporation, Osaka, Japan) with 50 × (flank face) or 20 × (rake face) magnification, respectively. It can be seen that only CC and Cermet inserts exhibit the requested corner radius of r_ε = 30 µm, whereas for CVD-D, only corners with a chamfer could be realized. The HSS, CBN and PCD tools have almost sharp corners (approximately 15 µm radius) related to the respective manufacturing process.

For a comprehensive evaluation of the suitability of the cutting material for different heat treatment conditions of the specimens, the experimental cutting tests were carried out using three different cutting speeds. The cutting speed is particularly important for the plastic material deformation in machining. In addition, a change in the effective rake angle (Figure 14, right) causes a change in the cutting force. This could have a significant influence on tool wear, whereby a different effect is expected depending on the type of cutting material. Furthermore, the cutting speed influences the surface microstructure, since the structural distance along the tool circumference is determined from its ratio to the ultrasonic speed, v_US. Although the nominal rake angle of both the insert and the tool holder is 0°, the effective rake angle, γ_eff, at the point of maximum ultrasonic speed, v_US, in perpendicular direction to the surface, which corresponds to the zero position of the vibration, reaches its minimum at −35° (position (b)), as shown in Figure 14. This results in a strong pressure on the specimen surface during machining and thus influences the surface layer surface microstructure. Positions (a) and (c), on the other hand, represent the reversal points of the oscillation motion, in which the effective rake angle is equal to the nominal rake angle (0°).

The remaining process parameters were fixed. The feed per tooth, f_z, also determines the surface microstructure and was set to 30 µm, which corresponds to the CC and Cermet tools to the corner radius, r_ε. The depth of cut a_p = 30 µm was chosen to be relatively low in order to reduce the load on the cutting corner. The value of the ultrasonic frequency, which also determines the structural distance, was set at a constant value of f_US = 19 kHz for all tests. The ultrasonic amplitude, A_US (peak-peak), was set at 4 µm, thus achieving the minimum required aspect ratio of AR = 1/4 for the lowest cutting speed of v_c = 20 m/min (structure height of A_US = 4 µm to structure width of L = 16 µm).

3. Results and Discussion

The evaluation of the suitability of the cutting materials used and the heat treatment conditions applying different cutting speeds should provide information on the optimum combination concerning various criteria. The tool wear behavior, the characteristics of the surface microstructures produced and the surface layer, mainly regarding plastic deformation and distribution of carbides, are considered. In addition, the process itself is characterized. A test designation in the form CM-HTC_vcXX was realized, whereby sometimes only selected elements are used if the context is explained in the text (e.g., same tool type).

3.1. Tool Wear Analysis

Due to the fact that a large number of the tools used showed clear signs of wear, often up to corner breakage, the scope of the tests was already reduced during the experimental investigations. For example, the number of machining tests with samples in hardened condition or with the super-hard cutting materials CBN, PCD, and CVD-D were reduced to an exemplary minimum. Based on these findings, the test matrix shown in

Table 5. Test matrix with qualitative assessment of the wear behavior of each tool used. The analyzed main test combinations CC/Cermet–SA/SC are framed.

Material		Brass			SA			SC			LH			H
vc (m/min)		20	50	80	20	50	80	20	50	80	20	50	80	20	50	80
Cutting material	HSS	∙∙∙	-	-	∙∙∙		-			-	∙∙∙	-	-	-	-	-
	CC	-	-	-	∙	∙∙	∙	∙	∙∙	∙	∙∙∙	∙∙	-	✸	-	-
	Cermet	∙	∙∙	∙	∙∙∙	∙∙∙	-	∙∙∙	∙∙∙	-	✸	-	-	-	-	-
	CBN	-	-	-	✸	✸	-	­	∙∙∙	-	✸	-	-	-	-	-
	PCD	∙			✸	∙∙	-	✸	∙∙	-	✸	-	-	-	-	-
	CVD-D	✸	-	-	✸	-	-	-	-	-	-	-	-	-	-	-
Legend		∙ Slight wear			∙∙ Moderate wear			∙∙∙ Massive wear			✸ Broken corner			- Not analyzed

resulted, whereby the tool wear behavior is subject to a qualitative assessment. These results are divided into four categories.

As can be seen from the table, the corner breakage occurs in a high number of cases, especially when using CBN, PCD or CVD-D. It can be assumed that due to the significantly higher mechanical alternating stress compared to machining without ultrasonic vibration superimposition, early failure of the super-hard cutting materials occurs. An exception to this is the test series with PCD at v_c = 50 m/min, where only low wear was recorded for brass and moderate wear for machining of the specimens in the conditions SA and SC. This reflects the comparatively higher toughness of the cutting material compared to CBN or CVD-D, respectively. Indexable inserts made of HSS behaved differently. Massive abrasive wear occurred due to the significantly lower hardness. As a result, the cutting edges were strongly worn and cannot be used for further cutting tests.

In order to illustrate the different types of failure, SEM micrographs of all cutting corners of the SA_vc20 test series are compared in Figure 15, with the exception of CC. A clear separation between abrasion (HSS and Cermet) and (brittle) fracture (CBN, PCD and CVD-D) is evident in these images.

Due to the relatively high number of tools showing such a high degree of wear that a quantitative determination of the wear characteristics did not seem to be appropriate, the analysis is focused on indexable inserts made of CC or Cermet and specimens in the SA and the SC conditions. The displacement of the major cutting edge, SV_CE, the displacement of the cutting edge in direction to the rake face, SV_γ, and the flank wear at the rounded corner, VB_C, were considered. Their determination is shown in Figure 16 by means of a schematic representation of the theoretical (dashed line), real (pointed line) and worn (black line) geometry in the tool orthogonal and reference planes, respectively. The measurement was done by using 3D laser scanning micrographs of the rake face and of the flank face respectively, with the software VK Analyzer from Keyence.

As can be seen in Figure 16, the wear on the major cutting edge dominates in comparison to the minor cutting edge. Consequently, only the wear of the major cutting edge is evaluated quantitatively. The different wear behavior results from the much higher mechanical stress on the major cutting edge because of chip formation. This effect arose for all cutting speeds.

3.1.1. Displacement of the Major Cutting Edge and the Cutting Edge in Direction to the Rake Face

Based on the wear analyses, it becomes clear that even with cutting materials resulting in wear, which is classified as comparatively moderate, the values for the displacement of the major cutting edge and the displacement of the cutting edge in direction to the rake face are in the middle two-digit micrometer range and exceed the amplitude of the surface microstructure (=structural height). Thus, a large influence of the wear behavior on the surface microstructure characteristics can be assumed. Furthermore, it stands out that the wear values for Cermet in all cases considered are above those of CC, which indicates a greater susceptibility to abrasive wear. The increases are shown as percentages in the diagrams in Figure 17.

In addition to the mentioned displacement of the major cutting edge, an enlargement of the corner radius occurs simultaneously. However, this cannot be quantified due to the change in shape of the profile of the cutting edge in the tool’s reference plane. In summary, however, the changed profile has a significant influence on the shape of the surface microstructures in the direction of feed motion. Referring to the simulated surfaces (Figure 12), there are symmetrical depressions with a symmetrical course of the unworn, geometrically exact cutting edge. The surface microstructures actually produced are characterized by a preferred direction, since the flank generated by the continuously wearing major cutting edge is significantly steeper than that generated by the minor cutting edge. In addition, the minor cutting edge exerts a sufficiently high pressure on the remaining material tips to cause plastic deformation, which contributes to an additional deviation in the shape of the surface microstructures. In the top view of the surface, a kind of drift can be seen, see Figure 18. As an example, the combination Cermet-SC_vc50 was used, since the displacement of the major cutting edge is significantly larger for Cermet and the burr formation is less for SC specimens than for SA specimens (see the following section on surface analysis).

It is also clear that, among almost all the tools considered, the measured wear is slightly higher for machining LH than for SC and that there is a general increase in wear from vc20 to vc50. This could be related to the slightly finer grain at SC.

3.1.2. Flank Wear at the Rounded Corner

The development of the flank wear land width is accompanied by a reduction of the clearance angle. This has a further influence on the characteristics of the surface microstructures, especially in the direction of the primary motion, as already explained in Section 2.2. It was expected that the effect of a reduced clearance angle is significantly higher for structures with a large aspect ratio (vc20, AR = 1:4) than for those with a smaller aspect ratio, such as vc50 (AR = 1:12), as the flank face comes into contact earlier with the preliminarily generated surface microstructure and, as a result, a smoothing effect occurs and the value of the VB_C increases, respectively. However, this only occurs for Cermet, while for CC, another trend could be found. While the values of VB_C for vc20 were still quite close for SA and SC, as can be seen in the diagram in Figure 19, they are almost identical for vc50. This, once again, reinforces the assumption that CC is more wear-resistant to abrasive stresses. Since there is hardly any contact between the surface microstructure and the flank face of the tool for all cutting speeds applied, the wear values are also more similar.

Furthermore, no clear difference in machining could be found between SA and SC with regard to the development of the flank wear at the rounded corner. In addition to the diagram, Figure 20 also shows a qualitative comparison of 3D laser micrographs of the CC and Cermet tools for the test combination SC_vc20. The flank wear can be clearly seen in the views of the flank faces. Moreover, there are damages on the rake faces characterized by chipping. In each case, the dimensions of the flank wear land width along the major cutting edge (left side next to the corner radius) are visible.

3.2. Characteristics of the Surface Microstructure

All 3D surface data are derived from laser scanning micrographs, which were generated using a magnification of 50× in the center of the microstructured surfaces. The measuring field was also aligned parallel to the direction of the feed motion. For the filtering and characterization, the software MountainsMap^® 7.4 (Digital Surf, Besançon, France) was used. At first, the surface microstructures of the brass specimens were characterized. Due to the comparatively sharper cutting edges (see Table 1), specimens microstructured with Cermet and PCD indexable inserts were selected. Furthermore, specimens machined with HSS or CVD-D tools were analyzed for vc20. It should be mentioned that all three structural variants were manufactured with the same insert when using PCD as a cutting material. This was possible because of the low tool wear. Due to the high degree of wear when using HSS inserts and the breakage of the corner of CVD-D tipped inserts, even for the relatively soft brass specimens, it is not appropriate to consider these surface microstructures. When comparing the surfaces generated with Cermet or PCD inserts, it is noticeable that, in particular, due to the slightly higher wear of the major cutting edge of the Cermet insert, an asymmetry of the valleys of the surface microstructure, visible in the cross-section in the direction of the feed motion, can be detected. The surface microstructures produced by a PCD insert appear nearly symmetrical concerning the cross-section and therefore more similar to the simulated surfaces. This is exemplified in Figure 21 for the cutting speeds v_c = 50 m/min and v_c = 80 m/min, whereby a simulated surface assuming an unworn tool is shown in each case for comparison. To increase the comparability, the simulated surfaces exhibit an almost identical structural displacement as the manufactured surface microstructures by adjusting the spindle speed. The accuracy of the process is accordingly relatively high, provided negligible tool wear.

Most of the surface microstructures manufactured with a cutting speed of v_c = 20 m/min do not show a sinusoidal shape in the cross-section in the direction of the primary motion, but rather a groove profile. For this relatively large aspect ratio of the surface microstructure (AR = 1:4), even a comparatively low flank wear or only slightly increased cutting edge rounding in the area of the corner radius has a strong influence on the characteristics of the surface microstructure, because the already produced surface microstructure is intersected or smoothed by the flank face. This also reinforces a further effect for UVSM with a cutting speed of v_c = 20 m/min: since the kinematic roughness becomes more important due to the reduction of the structure height in the direction of the primary motion, the feed grooves are less segmented, resulting in the formation of characteristic scoring marks. These provide for a stronger anisotropy of the surface, since the surface microstructures have a strong preferred direction. The values for the parameter Str shown in Figure 22 support this optical appearance quantitatively. The surfaces of the test combinations are considered analogous to the tool wear analysis.

For a cutting speed of v_c = 50 m/min, the presence of a direction-dependence results from the ultrasonic vibration superposition. The alternating arrangement of peak and valley as well as their structural displacement clearly dominate in comparison to the structural elements determined by the feed, see Figure 23. It can be seen that only for the combination CC-SC_vc50 was a rather isotropic surface generated (Str = 53.3%). In spite of almost the same structural displacement as with SA, a surface was created that does not show a preferred direction. This is possibly due to the lowest wear value of the displacement of the major cutting edge, whereby the surface microstructures in the cross-section are nearly uniformly formed in the direction of the feed motion. As a result, an equidistant structural height of the surface microstructure in the direction of the feed as well as in the direction of the primary motion occurs.

Comparing the values for the developed interfacial area ratio in the diagram in Figure 22, it can firstly be established that the trend from the simulation in Section 2.1.3 complies with the real surfaces. A higher developed interfacial area ratio was achieved by a lower cutting speed and thus by a higher number of structural elements. However, especially for CC, the Sdr values were significantly higher than predicted. This is due to the comparatively higher “real amplitudes”, A_US, in the cutting direction, which were generated by using cemented carbide tools. These were determined on the basis of three cross-sections within the measuring field in order to ensure a sufficient confidence level. The characteristic of the amplitudes is directly related to the flank wear land width, VB_c, which can be seen from a comparison of the diagrams in Figure 20 and Figure 24. It is shown that surface microstructures with a larger aspect ratio are significantly more affected by a deviation of the achieved amplitudes from the target value, since the already described effect of the reduction of the clearance angle has a significantly higher influence on them as the flank wear progresses.

Furthermore, the diagram shows that the heat treatment condition has hardly any influence on the amplitudes achieved. For an estimation of the influence of the specimen material on the amplitude of the surface microstructures, the test combinations considered in Figure 24. were extended by CC-LH and Cermet-B, each realized with v_c = 20 m/min and v_c = 50 m/min. Based on these relationships, the interdependence between the tool wear behavior and the surface microstructure is again clearly shown.

SEM can also be used to show the influence of the materials’ behavior of the specimen material on the geometry of the surface microstructures, Figure 25. Thus, an increased burr formation in the SA specimens can be perceived as compared to the SC specimens, for both using cemented carbide indexable insert and a cutting speed of v_c = 50 m/min. This results from the plastic deformation of the material, as already shown in Figure 18. However, it is not yet possible to predict whether this burr will have a positive or negative contribution to the adhesive strength of a subsequently applied CVD coating system. In the case of surface microstructures produced by UVSM at a cutting speed of v_c = 20 m/min, the burr formation can be considered less separately. This can be explained by the significantly higher influence of tool wear on the geometric characteristics, e.g., in comparison with Figure 23.

3.3. Characteristics of the Surface Layer Material Microstructure

A representative selection of differently heat-treated and machined specimens is presented in Figure 26. UVSM influences the material microstructure in the surface layer area. Despite the low notched bar impact energy and thus low toughness, see Figure 5 and Figure 6, it is evident that local deformation takes place. The distribution of the carbides at the grain boundaries indicates a local deformation due to the machining process: compare Figure 26 conditions SC and LH. The structures do not seem to have been separated directly in the area of grain boundaries and carbides, therefore a part of the martensitic/ferritic matrix (white) has been retained. Even in the soft-annealed and hardened condition, this can be seen from the distribution of the carbides. There seems to be an accumulation of carbides in the machined area. However, the effect of the carbide accumulation on the sub-roughness of the surface microstructure is negligible compared to the dimensions of the surface microstructures. Furthermore, no influence of the changed effective angle can be seen on the rising or falling flanks of the surface microstructures.

In order to characterize the hypothesis presented in Section 2.1, that heat treatment of the steel substrate influences the surface microstructure and the behavior of the tools shown in Table 5. on the basis of wear, SEM micrographs of tools used for the CC_vc20 test series were compared for the different HTCs of the specimens, Figure 27. The micrographs clearly show that the wear increases from SA or SC (moderate) respectively, to LH (massive) and H (breakage), although the hardness values for SC, LH and H are similar (diagram in Figure 5). This indicates further main influencing variables, such as the distribution and size of effective carbides in the steel substrate, for the wear behavior of the tools.

3.4. Process Characterization

The vibration system was able to fulfill the requirements regarding the amplitude, as the evaluation of the amplitudes in Figure 24 shows for the cases with A_US = 4 µm. For all other surfaces, where the required amplitudes were not reached, the reasons are already broken down and essentially not attributable to the vibration system. However, Börner et al. already showed in further investigations in UVSM on steel that the influence of cooling lubricant on the vibration performance cannot be neglected since the whole oscillating behavior of the vibration system is influenced. Thereby, it was found that the real achieved structural heights of the substrate microstructure were lower with cooling lubricant than without [7]. In addition, the surface characteristics were investigated with regard to the structural displacement. It was found that a relatively regular displacement occurred due to the fixed frequency. The speed control has a much smaller influence at a higher rotational speed (corresponds to the cutting speed), since the spindle speed variation amounts to approximately ±3 rpm for all cutting speeds. As a result, the standard deviation of the structural displacement was lowest for a cutting speed of v_c = 80 m/min and highest for v_c = 20 m/min.

4. Summary and Conclusions

The aim of the presented investigations was to find a suitable combination of the cutting material and the heat treatment condition of X46Cr13 steel for the production of surface microstructures by UVSM. The machining tests were carried out on a self-developed vibration system, which was characterized in advance using a 3D laser vibrometer. The following conclusions can be drawn, especially relevant for a subsequent CVD coating of the steel:

• Despite the different hardness values, no significant differences can be found between the UVSM of specimens in SA and SC condition with regard to tool wear or surface characteristics. Only a stronger burr formation was observed for SA specimens. Depending on whether this is desired or rather disadvantageous in the subsequent coating process, the respective HTC should be selected. The two other HTCs were more critical from the above-mentioned points of view.
• Cemented carbide was the first choice for the cutting material. In addition, only Cermet and, with a few exceptions, PCD cutting tools could be considered, while HSS, CBN and CVD-D in particular proved to be too susceptible to wear.
• However, even the wear at cemented carbide tools leads to shape deviations of the surface microstructure compared to the simulation. In particular, the displacement of the major cutting edge influences the symmetry of the surface microstructure profile in the direction of feed motion, while the wear of the flank face in connection with the displacement of the cutting edge in direction to the rake face leads to a reduction of the structural height (=amplitude A_US).
• For a reliable surface microstructuring of areas > 1 cm², further adjustments especially concerning tool wear are necessary.
• The influence of the effective rake angle on the surface layer was relatively small. Therefore, no influence on the specimen surface microstructure is to be expected in the case of a geometrical change, which requires an adjustment of the cutting speed and entails a change of the varying effective rake angle.

However, it should be noted that the selected surfaces are only representative measuring fields. With increasing wear as well as a slight drift in the structural displacement, which results from the relationship between the cutting speed and the ultrasonic vibration frequency, the parameter Str in particular is subject to greater fluctuations. Since the subsequent measurement of the achieved “amplitudes” on the basis of the profile sections is strongly dependent on other factors, such as the tool wear behavior, an in-process recording of the amplitude would also be useful for process monitoring and possibly even control to increase the process stability.