Research on Tool Wear Based on 3D FEM Simulation for Milling Process
Abstract
:1. Introduction
2. Compilation of Subprogram and Establishment of Milling Finite Element Simulation Model
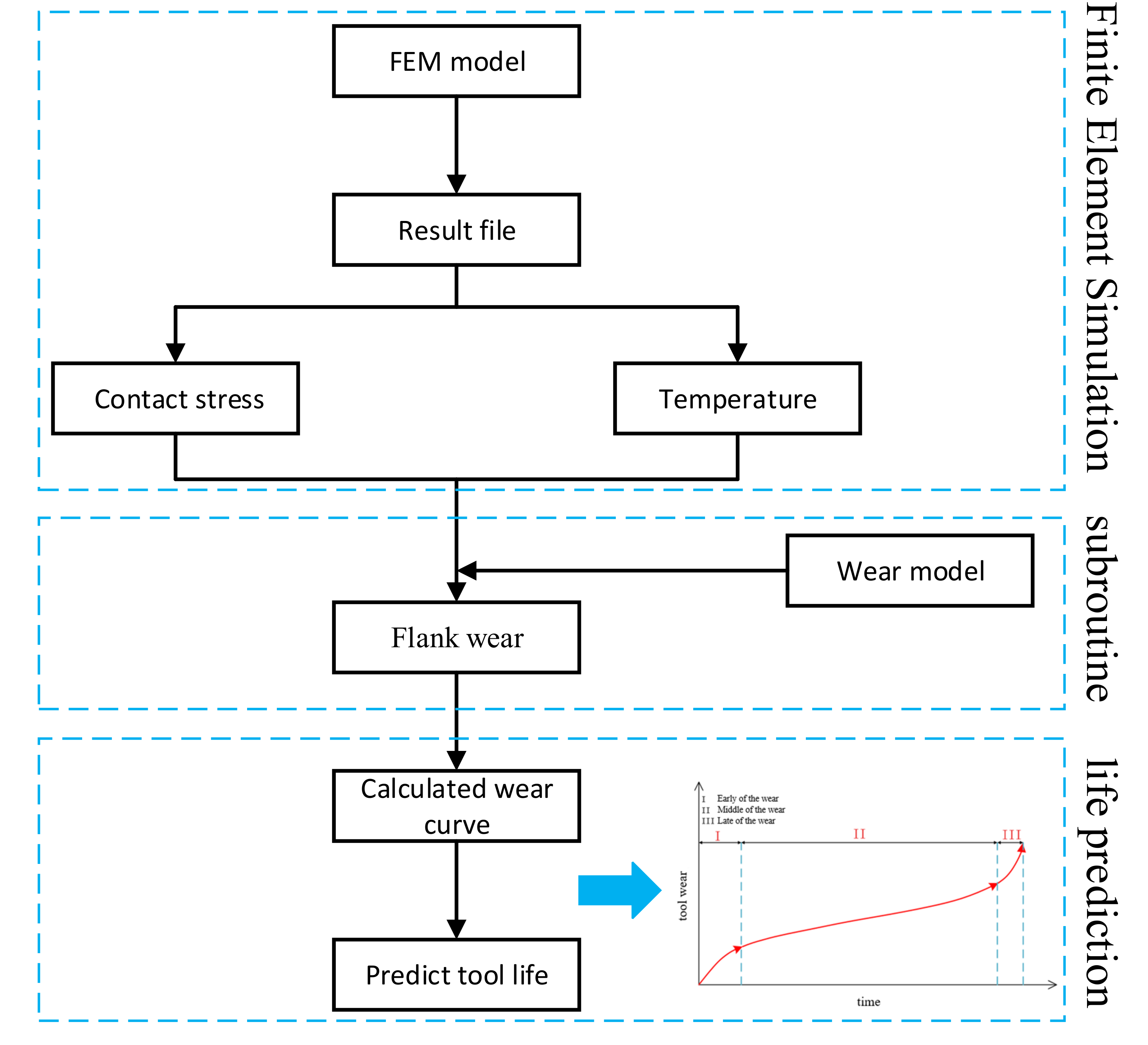
2.1. Design of Subprogram for the Tool Abrasion Prediction
2.2. Establishment of Milling Simulation Model
2.2.1. Ti6Al4V Constitutive Model
2.2.2. Friction Model
2.2.3. Damage Model
2.2.4. Cuttings Separation Criterion
2.3. Grid Partition of Finite Element Model
2.4. Prediction of Tool Abrasion Course and Tool Service
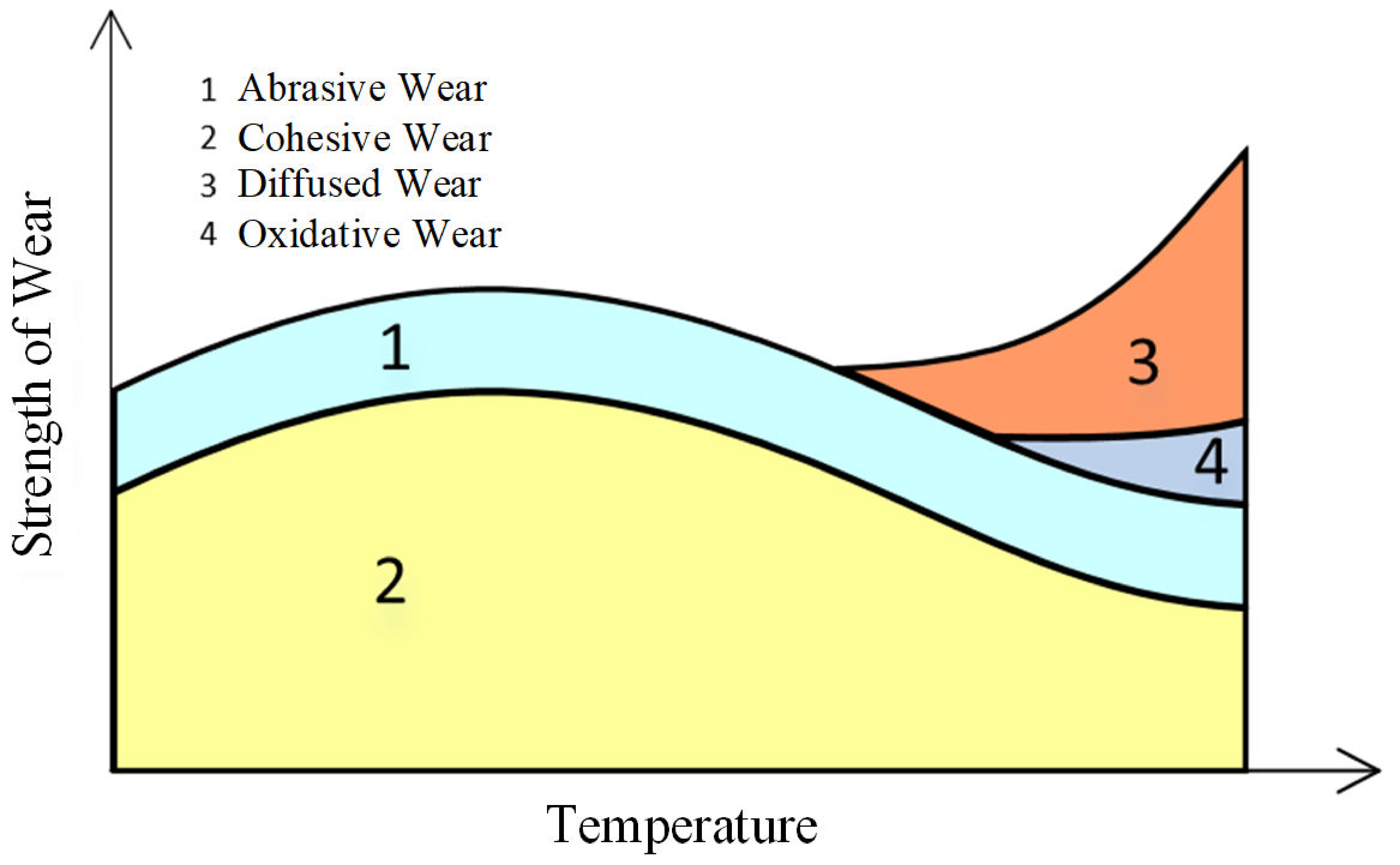
3. Expression of Different Types of Tool Abrasion Loss
3.1. Adhesion Abrasion (AD)
3.2. Grains Abrasion (GA)
3.3. Diffusion Abrasion (DA)
4. Experimental Verification and Simulation Results
4.1. Milling Experiment Design
4.2. Milling Experimental Results
4.3. Discussion of Finite Element Simulation Results
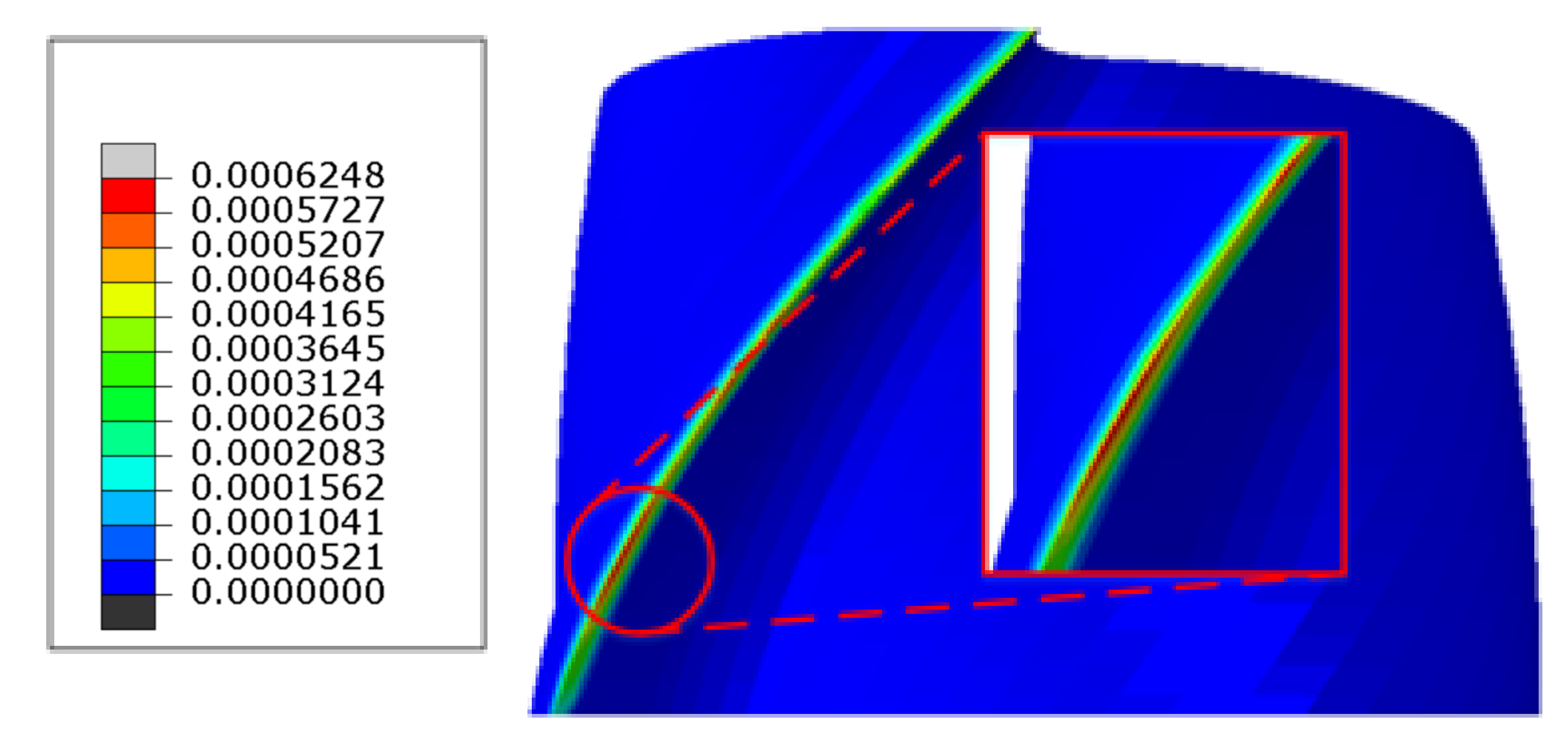
4.3.1. Analysis of Temperature Field Results of Tool
4.3.2. Analysis of Tool Abrasion Results
- (1)
- Error caused by grid dimension: The grid dimension decides the simulation precision. Oversized grid is difficult to guarantee the simulation precision and undersized grid causes an overly long simulation time. Hence, the appropriate grid dimension shall be selected after comprehensive consideration.
- (2)
- Milling vibration factors are not considered in the established simulation process of finite element simulation model.
- (3)
- The tool abrasion caused due to tipping is not considered in simulation process, and the tool Mises press is mainly observed to find tool tripping in the finite element simulation.
- (4)
- In the milling process of cemented carbide end mill, there is oxidation abrasion on its flank surface, but the oxidation abrasion is not considered in the abrasion prediction model.
5. Conclusions
- (1)
- On account of the change of tool abrasion type at different temperatures, the carbide cutter abrasion model considering temperature effect is constructed to avoid the limitation of single model and improve the prediction precision of the tool abrasion;
- (2)
- Combined the simulation results with the empirical formula, the tool abrasion course function can be calculated, which saves lots of simulation time and realizes the rapid prediction of the tool’s service life;
- (3)
- The test about on the service life of tool is carried out, and the simulation results and experiment measurement results are compared and analyzed. The simulation results can better simulate the change rules of tool abrasion in cutting process, and prediction error is within 30%, which can predict the service life of the tool to some extent.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choudhury, S.K.; Srinivas, P. Tool wear prediction in turning. J. Mater. Process. Technol. 2004, 153–154, 276–280. [Google Scholar] [CrossRef]
- Zhou, J.M.; Walter, H.; Andersson, M.; Ståhl, A.E. Effect of chamfer angle on wear of PCBN cutting tool. Int. J. Mach. Tools Manuf. 2003, 43, 301–305. [Google Scholar] [CrossRef]
- Denkena, B.; Lucas, A.; Bassett, E. Effects of the cutting edge microgeometry on tool wear and its thermo-mechanical load. CIRP Ann. Manuf. Technol. 2011, 60, 73–76. [Google Scholar] [CrossRef]
- Rathod, K.B.; Lalwani, D.I. Modeling of flank wear progression for coated cubic boron nitride tool during hard turning of AISI H11steel. Mater. Today Proc. 2018, 5, 6692–6701. [Google Scholar] [CrossRef]
- Liu, H.Z.; Zong, W. Prediction model of tool wear volume in precision turning of ceramic particle reinforced aluminum matrix composites. Int. J. Adv. Manuf. Technol. 2019, 100, 2689–2700. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, C. Modeling Flank Wear Progression Based on Cutting Force and Energy Prediction in Turning Process. Procedia Manuf. 2016, 5, 536–545. [Google Scholar] [CrossRef] [Green Version]
- Pervaiz, S.; Deiab, I.; Rashid, A.; Nicolescu, M. Minimal quantity cooling lubrication in turning of Ti6Al4V: Influence on surface roughness, cutting force and tool wear. Proc. Inst. Mech. Part B J. Eng. Manuf. 2017, 231, 1542–1558. [Google Scholar] [CrossRef]
- Wanigarathne, P.C.; Kardekar, A.D.; Dillon, O.W.; Poulachon, G.; Jawahir, I.S. Progressive tool-wear in machining with coated grooved tools and its correlation with cutting temperature. Wear 2005, 259, 1215–1224. [Google Scholar] [CrossRef]
- Attanasio, A.; Ceretti, E. 3D finite element analysis of tool wear in machining. Manuf. Technol. 2008, 57, 61–64. [Google Scholar] [CrossRef]
- Binder, M.; Klocke, F. An advanced numerical approach on tool wear simulation for tool and process design in metal cutting. Simul. Model. Pract. Theory 2017, 70, 65–82. [Google Scholar] [CrossRef]
- Lotfi, M. 3D FEM simulation of tool wear in ultrasonic assisted rotary turning. Ultrasonics 2018, 88, 106–114. [Google Scholar] [CrossRef] [PubMed]
- Attanasio, A.; Faini, F.; Outeiro, J.C. FEM Simulation of Tool Wear in Drilling. Procedia CIRP 2017, 58, 440–444. [Google Scholar] [CrossRef]
- Xie, L.J.; Schmidt, J.; Schmidt, C.; Biesinger, F. 2D FEM estimate of tool wear in turning operation. Wear 2005, 258, 1479–1490. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, J.; Li, J. Finite Element Analysis on Prediction of Tool Wear in Milling Titanium. J. Mech. Eng. 2016, 52, 199–207. [Google Scholar] [CrossRef]
- Malakizadi, A.; Gruber, H.; Sadik, I.; Nyborg, L. An FEM-based approach for tool wear estimation in machining. Wear 2016, 368, 10–24. [Google Scholar] [CrossRef]
- Giovanna, M.A.; Terrazas, G.; Ratchev, S. Tool wear classification using time series imaging and deep learning. Int. J. Adv. Manuf. Technol. 2019, 104, 3647–3662. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Zhang, B. Research on tool wear prediction based on fuzzy C-means clustering algorithm. Estat. Sci. Trib. 2011, 10, 59–61. [Google Scholar]
- Yue, C.; Liu, X.; Liu, Z. Tool optimization for stitching die milling based on finite element simulation. Chin. J. Mech. Eng. 2019, 52, 199–207. [Google Scholar]
- Wang, X. Study on Tribologieal Behaviorand Tool Life in Ti6A14V High Performance Maehining; Shandong University: Jinan, China, 2009. [Google Scholar]
- Li, K.; Song, Q. Fundamentals of Mechanical Manufacturing Technology; Shandong Science and Technology Press: Jinan, China, 2008. [Google Scholar]
- Usui, E.; Shirakashi, T.; Kitagawa, T. Analytical prediction of cutting tool wear. Wear 1984, 100, 129–151. [Google Scholar] [CrossRef]
- Rabinowicz, E.; Dunn, L.A.; Russell, P.G. A study of abrasive wear under three-bod conditions. Wear 1961, 4, 345–355. [Google Scholar] [CrossRef]
- Komanduri, R. Some clarifications on the mechanics of chip formation when machining titanium alloys. Wear 1982, 76, 15–34. [Google Scholar] [CrossRef]
- Sun, Y. Parametric Modeling of Milling Titanium Alloy and Prediction of Tool Wear State; Shandong University: Jinan, China, 2014. [Google Scholar]
- Li, Y. Chemieal Performance Match between Cemented Carbide Tools and Ti-6Al-4V Alloy; Shandong University: Jinan, China, 2010. [Google Scholar]
- Molinari, A.; Nouari, M. Modeling of tool wear by diffusion in metal cutting. Wear 2002, 252, 135–149. [Google Scholar] [CrossRef]











| Material | A/MPa | B/MPa | C | n | m |
|---|---|---|---|---|---|
| T6Al4V | 543.75 | 1363.6 | 0.127 | 0.33 | 0.303 |
| d1 | d2 | d3 | d4 | d5 |
|---|---|---|---|---|
| −0.09 | 0.25 | −0.5 | 0.014 | 3.87 |
| 0.7573 | −7.277 | 3.2676 | 9.6475 | 8.3551 | 0.9567 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Yue, C.; Li, X.; Liu, X.; Liang, S.Y.; Wang, L. Research on Tool Wear Based on 3D FEM Simulation for Milling Process. J. Manuf. Mater. Process. 2020, 4, 121. https://doi.org/10.3390/jmmp4040121
Liu Z, Yue C, Li X, Liu X, Liang SY, Wang L. Research on Tool Wear Based on 3D FEM Simulation for Milling Process. Journal of Manufacturing and Materials Processing. 2020; 4(4):121. https://doi.org/10.3390/jmmp4040121
Chicago/Turabian StyleLiu, Zhibo, Caixu Yue, Xiaochen Li, Xianli Liu, Steven Y. Liang, and Lihui Wang. 2020. "Research on Tool Wear Based on 3D FEM Simulation for Milling Process" Journal of Manufacturing and Materials Processing 4, no. 4: 121. https://doi.org/10.3390/jmmp4040121
APA StyleLiu, Z., Yue, C., Li, X., Liu, X., Liang, S. Y., & Wang, L. (2020). Research on Tool Wear Based on 3D FEM Simulation for Milling Process. Journal of Manufacturing and Materials Processing, 4(4), 121. https://doi.org/10.3390/jmmp4040121








