1. Introduction
In the milling processes, vibrations of e.g., the milling tool or workpiece caused by the regenerative effect are often limiting the process stability and thus the material removal rate and productivity [
1]. The regenerative effect is based on the excitation of dynamically compliant structures within the force flow of the machining process in their natural frequencies, whereby the generated deflections lead to a periodic modulation of the chip thickness during successive tooth engagements. These in turn lead to an excitation and self-excited oscillations of the system which are called the regenerative effect [
2,
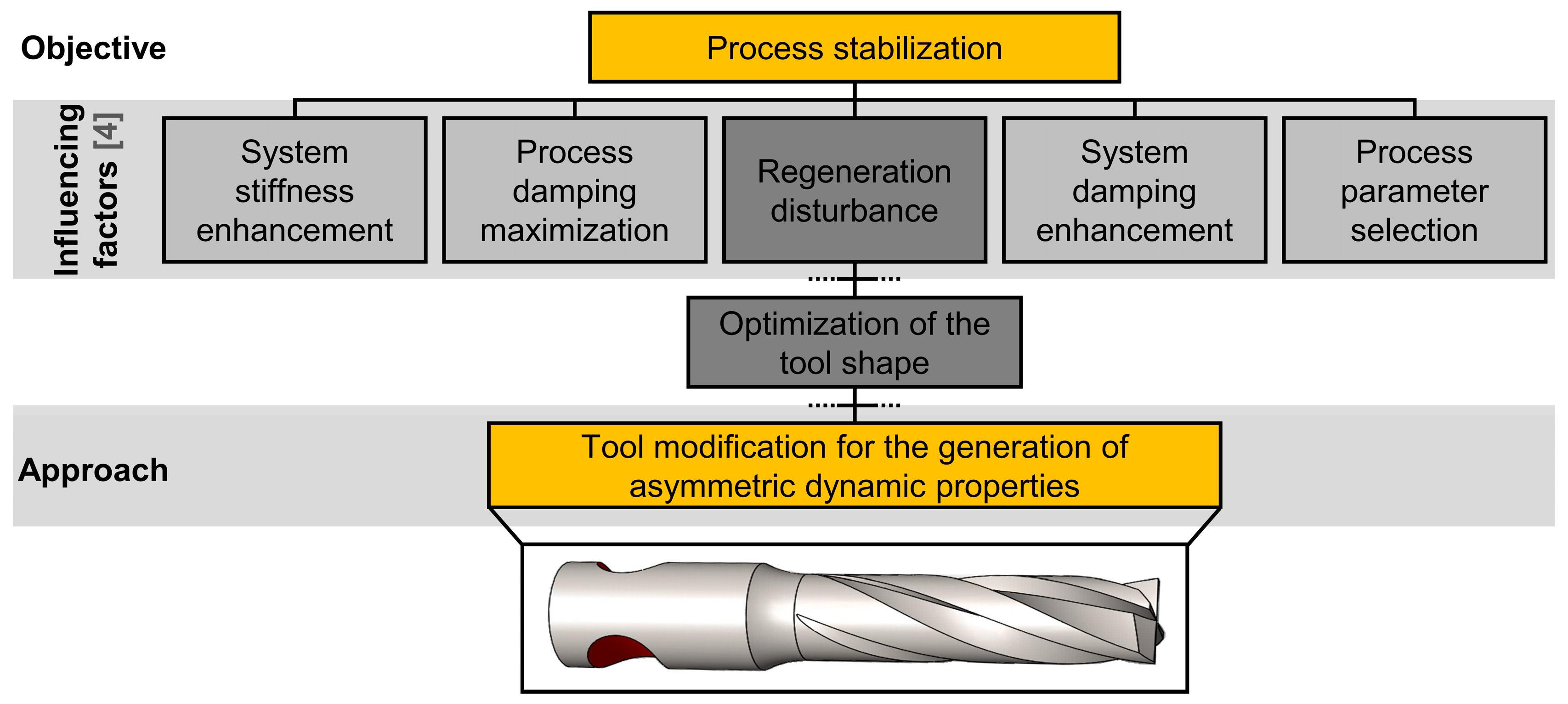
3]. In order to avoid or reduce the disturbing dynamic effects in milling processes, various strategies are available within the construction of production systems as well as in process planning, design and control, or are the subject of current research and development. These are aimed at influencing five key factors of the process and thus can be divided into the following five categories [
4,
5].
1.1. Process Parameter Selection
Generally, the spindle speed and infeed are in focus when optimizing the process parameters with regard to the dynamic effects within the process. Stability lobe diagrams [
6,
7] can be used to configure these parameters in consideration of the dynamic properties of the production system to increase infeed and productivity while maintaining process stability [
8]. Moreover, complete manufacturing processes can be analyzed and optimized using process simulations [
9,
10,
11,
12]. For this purpose, analytical [
6] or geometric physically-based simulation systems based on abstract compliance models [
13] or zeroth-order approximation (ZOA) [
14] are used, for example, to avoid elaborate experimental test series [
15].
1.2. Regeneration Disturbance
The literature described two approaches for the disturbance of the regenerative effect, which are based either on special tool geometries or spindle speed variation techniques [
4]. An optimized tool design can, for example, lead to a reduced transient excitation of a dynamic system, reduce the maximum force amplitudes and thereby disturb the occurrence of the regenerative effect [
15,
16,
17]. Typical examples are geometrical features such as the constant and variable helix angles [
18,
19,
20,
21,
22], inequalities [
23,
24,
25] or serrated [
26,
27,
28], set-back cutting edges [
29] or structured tools [
5,
30]. A variation of the spindle speed and thus of the excitation frequency modulates the engagement specific wavelength and disturbs the regenerative effect [
31,
32,
33]. This stabilizing strategy can also be combined with e.g., the use of variable pitch cutters [
34].
Other investigations target an adaptive variation of the stiffness properties of e.g., the workpiece or tool [
34]. An excitation of a dynamically critical system in a specific disturbance frequency [
35,
36,
37] or using an active mode control system [
34,
38] can suppress or reduce dynamic effects. Moreover, systems based on electrorheological fluids which actively change the eigenfrequencies, and thus suppress the regenerative effect, were analyzed [
39,
40].
1.3. Process Damping Maximization
The process damping takes effect in the direct interaction between the tool and the workpiece. Process-related damping effects can be influenced, for example, by using specially prepared milling tools [
4,
5,
10]. Additional ploughing effects generated by the actively generated elliptical vibrations of the milling tool can enhance process damping and improve the process stability [
41].
1.4. System Stiffness Enhancement
As the eigenfrequencies of a system are defined by the stiffnesses and modal masses of the compliant elements, such as the spindle and cutting tool, the components of machine tools are designed to be light and stiff [
42,
43]. In order to enhance the stiffness, e.g., the tools are clamped with a short cantilever length if no machining of deep cavities is required [
4]. To reduce the vibrations of compliant workpieces, the use of a multi-point support head following the milling cutter to locally increase the stiffness and damping was analyzed and proven to improve process stability [
44].
1.5. System Damping Enhancement
Besides the eigenfrequencies and modal masses, damping describes the modal properties of a dynamic system. Materials such as highly damping polymer concrete and bearing types such as hydrostatic plain bearings, which can be used in machine tool components, have specific properties that can increase the damping capacity of a production system [
4,
43,
45].
Recent investigations combine various strategies for process damping and the disturbance of the regenerative effect using process simulation for the configuration of stable milling processes. For example, a structuring of the functional surfaces of a milling tool led to a significantly higher process stability [
5], as well as the combination of a variation of the spindle speed and the pitch angle [
46]. Adaptions of the tool path for, e.g., maximizing the axial depth of cut in five-axis ball-end milling [
47] or minimizing the tool engagement angle in plunge milling [
48], can also be used to increase the process stability and productivity.
However, adjusting the process parameter values or the cutting edges of a tool also influences the process conditions and the characteristics of the manufactured workpiece as well. Moreover, the dynamic behavior of the machine-cutting tool system is influenced by the position of the axes of the machine tool [
49,
50], by thermal effects [
51] and by the preloading of the bearings [
52]. These time variant influences have to be taken into account in the optimization of milling processes and complicate the process parameter optimization of complete operations. Most techniques for regeneration disturbance and process damping maximization are associated with an influence on the fundamental cutting operations. Therefore, they often have a negative influence on the cutting process or limit the optimization within other degrees of the freedom of the process. An adjustment of the damping or stiffness of the system requires extensive and complex modifications in e.g., the machine structure, which are not always feasible. In this paper, a new approach for disturbing the regenerative effect is presented, which is based on an optimization of the tool shape to achieve asymmetric dynamic properties (
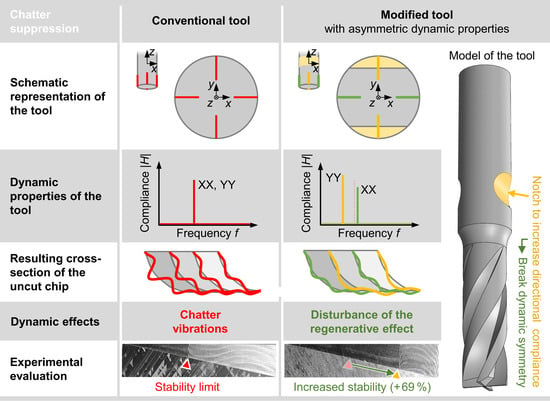
Figure 1). This new approach requires no modification of the cutting edges and thus, should not influence the fundamental cutting operation and allows for widely universal applications.
1.6. Working Hypothesis
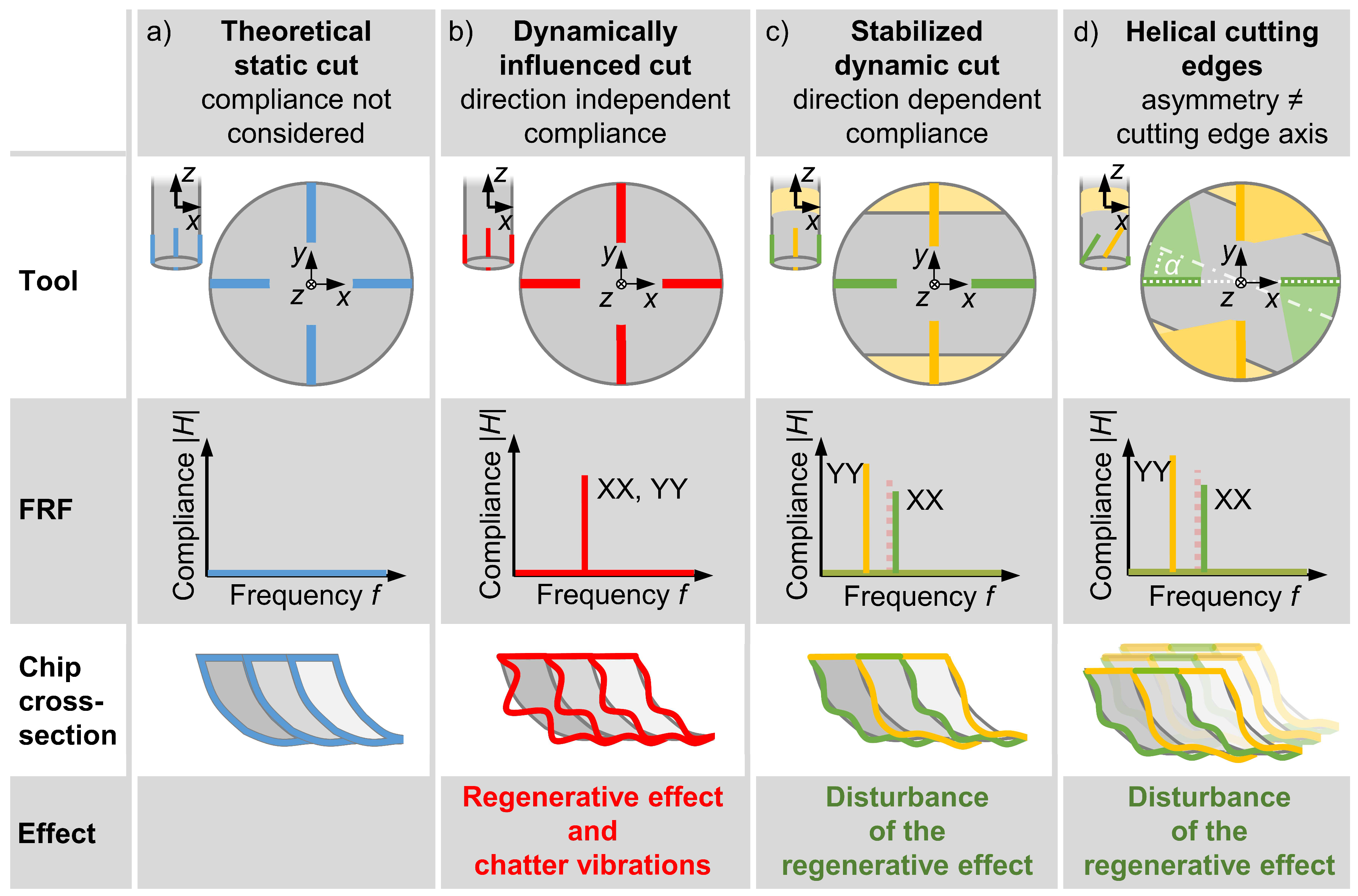
In milling processes, the production of a defined shape of a workpiece is realized by the successive removal of chips. The shape of each chip is substantially defined by the changing workpiece as a result from the previous cuts and the motion of the tool (
Figure 2a).
The regenerative effect is based on a self-excitation of a system in its eigenfrequencies. It occurs due to a modulation of the uncut chip thickness leading to periodic excitations in consecutive tooth engagements (
Figure 2b). By using four-fluted milling tools with a direction-dependent frequency response function (FRF), the modulation of the chip thickness can be systematically influenced (
Figure 2c). With successive tooth engagements, different eigenfrequencies of the tool are excited. As a result, each cut is still influenced by dynamic effects, but the resulting modulation of the uncut chip thickness no longer directly corresponds to the natural frequency of the cutting tooth. Thus, the regenerative effect can be disturbed and in the best case even completely avoided. The preparation of parallel, opposing grooves in the tool shank allows a targeted increase in the compliance in a defined direction and thus producing asymmetrical dynamic properties of the milling tool. In the case of four-fluted tools, a clear change in the dynamic properties for successive cuts can be realized. This means that the structural weakening of an element in the process-related force flow can even have a stabilizing effect on the process, as it results in a difference in the eigenfrequencies and thus, the surface generated by successively engaging teeth. In order to achieve a defined change in the eigenfrequencies of the tool during successive tooth engagements, the grooves must be inserted tangentially offset depending on the helix angle of the tool and the desired infeed depth (
Figure 2d).
In the following, finite element analyses of the influence of the groove geometry on the dynamic properties are presented and a method for the preparation of the tools is depicted (
Section 2). In
Section 3 and
Section 4, experiments on the performance of these modified tools are presented and discussed, respectively. The paper is concluded with a summary and an outlook (
Section 5).
2. Materials and Methods
2.1. Finite Element Analysis and Design of Milling Tools with Asymmetric Dynamic Properties
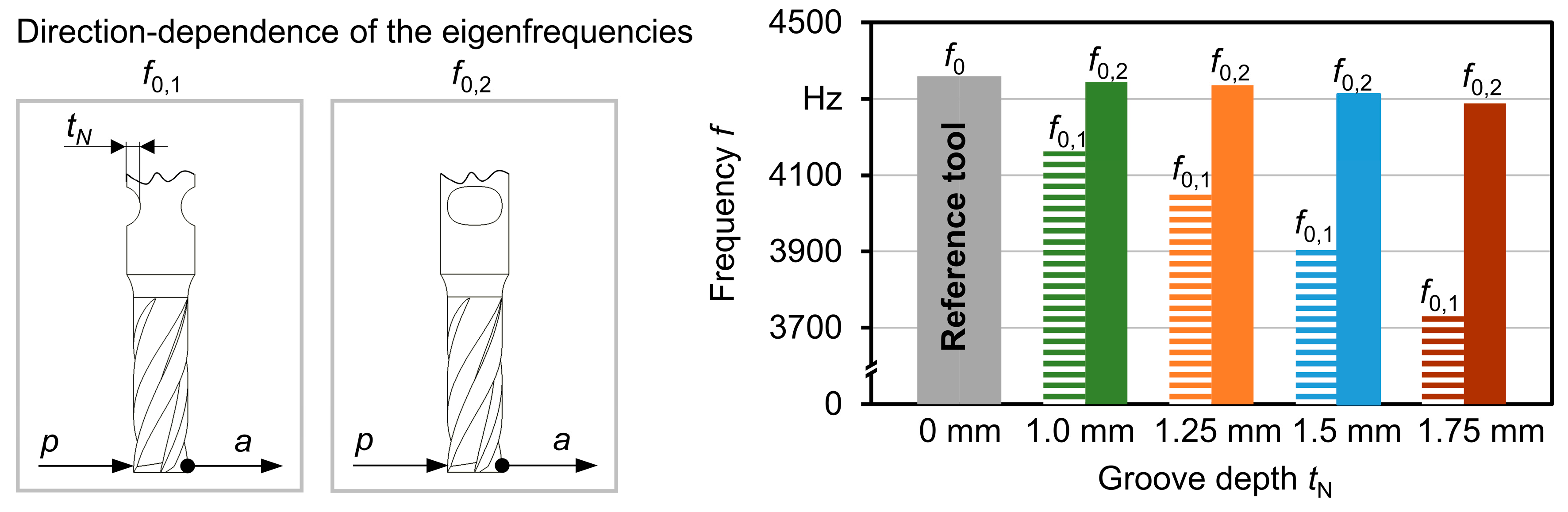
In order to create tools with asymmetrical dynamic properties and to achieve a direction-dependent shift of the eigenfrequencies, a milling tool was modified by machining parallel grooves into the tool shank. As the geometrical shape and position of these grooves influence the dynamic properties of the tool, finite element analyses (FEA) were calculated using ANSYS Workbench in order to investigate the influence of the depth of the grooves, which are shaped like segments of a circle, and to identify a suitable groove depth. A simplified model of the cutting tool, which represents the macroscopic properties of the tool such as the helical flutes and thicker tool shaft as well as the grooves in the tool shank and the material characteristics, was used to analyze its dynamic characteristics (
Figure 3). Simulations were conducted for a depth of the notches of
tN,min = 0 mm to
tN,max = 1.75 mm. In the FEA, the eigenfrequencies of the tool in the direction perpendicular to the grooves
f0,1 was lowered by up to ∆
f0,1 = 620 Hz, while the eigenfrequency in the direction parallel to the notches was slightly decreased by ∆
f0,2 = 80 Hz as shown in
Figure 3.
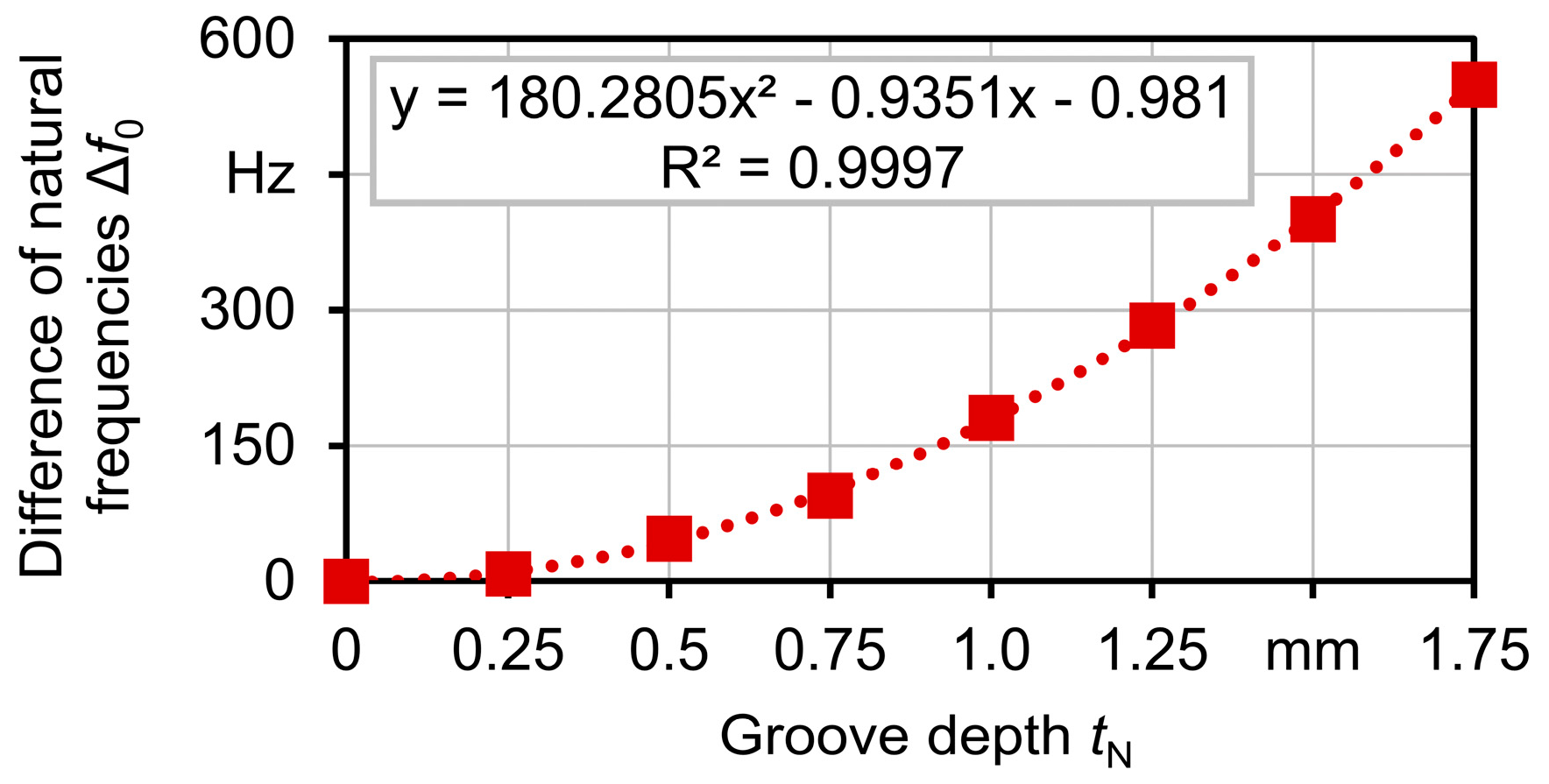
For all preparation states, the difference between the eigenfrequencies calculated for both directions can be predicted by a quadratic regression model in dependency of the depth of the grooves
tN with a high accuracy (
Figure 4). To achieve a significant directional dependency of the eigenfrequencies of about ∆
f0 =
f0,2 −
f0,1 ≈ 5% ·
f0, a minimal depth of the grooves of
tN = 1.0 mm was chosen for the preparation of a milling tool and for the experimental investigations.
2.2. Modification of the Milling Tools
This section shows the preparation of the milling tools for generating asymmetric dynamic properties, which were used in the experiments. In the experiments, four-fluted cylindrical high-speed steel (HSS) end mills with a diameter of
d = 8 mm and a shank diameter of
d = 10 mm were used. In order to reduce the impact of possible side effects, all the trials were carried out with the same cutting tool, clamped and fine-balanced in a shrink chuck, without re-shrinking the tool. The grooves were produced by five-axis milling using a spherical solid carbide end mill with a diameter of
d = 8 mm, as shown in
Figure 5.
To validate the initial groove depth of
tN,min = 1 mm chosen based on the simulations, operational trials were conducted, increased in the steps of Δ
tN = 0.25 mm up to
tN,max = 1.75 mm. The position of the grooves was chosen with a distance to the tool holder of
zN = 5 mm in order to achieve the greatest possible distance to the tool tip, respectively, to the area on which the process forces act. This way, a maximal change of the eigenfrequencies can be achieved with a minimal depth of the grooves and thus, a small increase in the related compliance amplitude. For different depths of the grooves in the tool shank, the dynamic compliance of the milling tool attached in the spindle of the machine tool Röders TEC RFM 1000 was measured in the direction of the grooves and perpendicular to it, to calculate the frequency response functions (FRFs). For this purpose, an impact hammer (Bruel & Kjær Type 8206) was used for the excitation, while the resulting response of the tool was determined by the means of acceleration measurements (PCB Piezotronics Model 352C23).
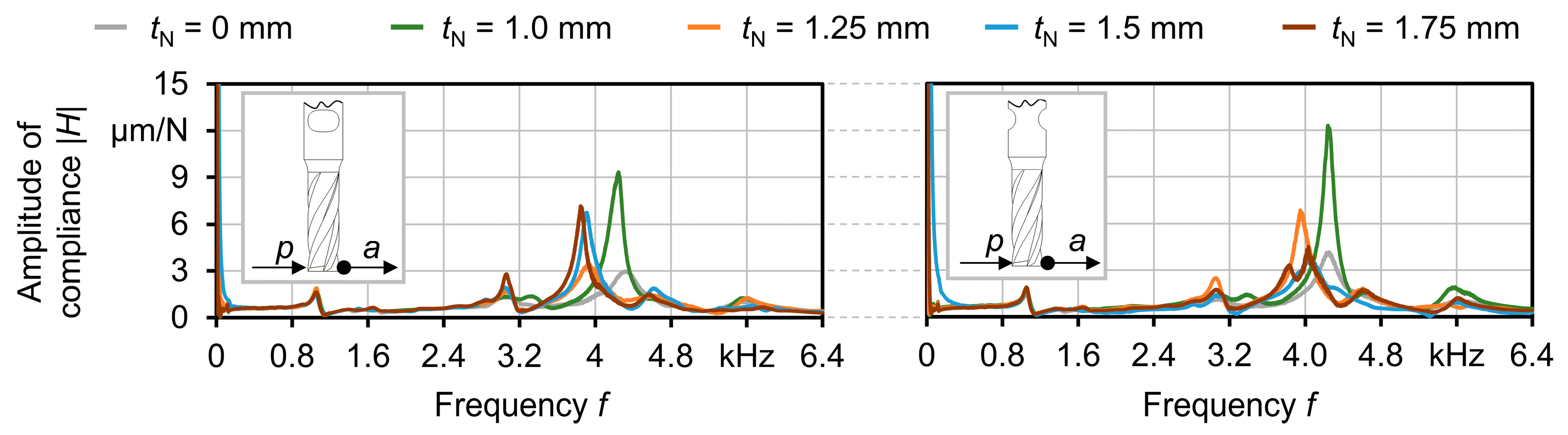
Figure 6 depicts the influence of the depth of the grooves on the FRFs of the milling tools. In both directions, the highest peak of the compliance amplitude of the cutting tools, which was located at a frequency of about
f0 = 4.2 kHz for the reference tool, was shifted towards lower frequencies, while its amplitude raised. With a depth of the grooves of
tN = 1.5 mm and
tN = 1.75 mm, a difference between the eigenfrequencies in both directions of Δ
f0 = 200 Hz and Δ
f0 = 250 Hz was measured, respectively. With a depth of the grooves of
tN = 1.75 mm, an additional eigenfrequency at
f0 = 3800 Hz was observed. As the excitation and measurement could not be conducted exactly in the directions of the grooves and perpendicular to it due to the axial slots of the cutting tool, the measurements were subject to influences of cross frequency responses. This results in deviations from the FRFs previously determined based on the FEM analyses.
3. Results
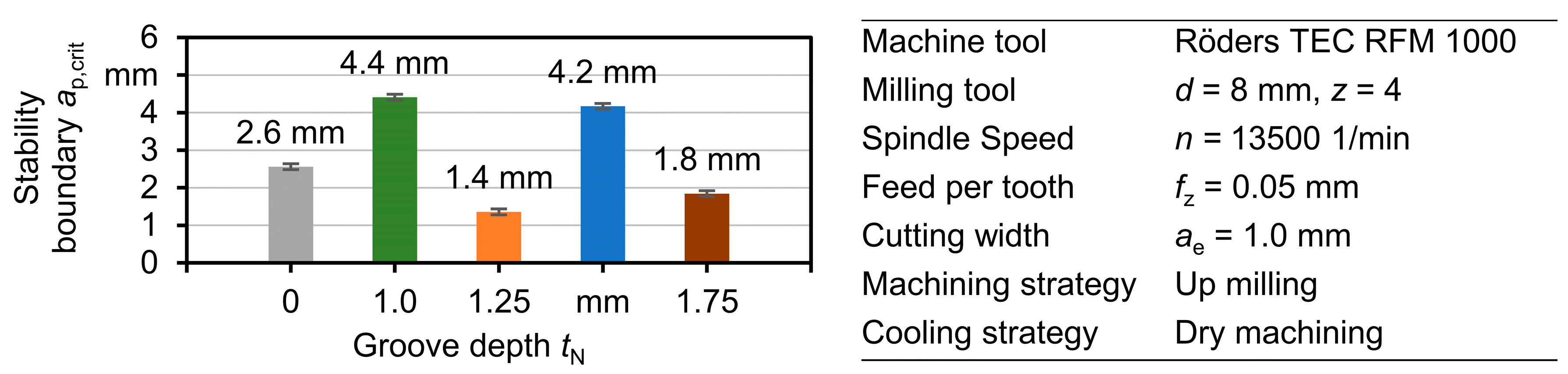
In the following, the operational behavior of milling tools with asymmetric dynamic characteristics is described. To assess the performance of the asymmetrically modified cutting tools, milling experiments were conducted with the reference tool as well as the modified tools in different stages with specific depths of the grooves. In the validation experiments, the side-milling of aluminum EN AW-7075 workpieces in the up-milling direction with a width of cut of ae = 1.0 mm and a constantly increasing depth of cut of ap,min = 0.0 mm to ap,max = 7.0 mm was conducted. To achieve a good repeatability of the trials, a sufficient running-in period of the tool used was conducted. The spindle speed was set to n = 13,500 1/min in all experiments, where a minimum of the stability limit was analytically predicted based on a calculation of the vertical asymptotes of the stability lobes. In-process measurements of the acoustic emissions were conducted using a Tascam DR 40 audio recorder to evaluate the process dynamics and determine the stability limit. Additionally, the resulting workpiece surfaces were analyzed after the trials to validate the stability limit, which was determined based on an analysis of the particular acoustic emissions. Each experiment was repeated three times using the same milling tool, for statistical validation and avoidance of additional influencing effects.
The stability limits could be determined based on the acoustic emissions with a very good agreement with the occurrence of chatter marks on the workpiece surfaces. In
Figure 7, the stability limit is shown for the reference tool and the modified tool, with depths of the grooves of
tN = 1.0 mm to
tN = 1.75 mm varied in steps of ∆
tN = 0.25 mm. For the reference tool, the stability limit was identified at
ap,crit = 2.6 mm. With the modified tools with a depth of the grooves of
tN = 1.0 mm and
tN = 1.5 mm, the stability limit could be increased to
ap,crit = 4.4 mm and
ap,crit = 4.2 mm, respectively. In contrast to these results, a reduction of the stability limit to
ap,crit = 1.4 mm and
ap,crit = 1.8 mm was observed in the experiments conducted with a depth of the grooves of
tN = 1.25 mm and
tN = 1.75 mm, respectively. For all trials, the low standard deviation of the stability limits indicated a good repeatability and validity of the test results.
According to the application trials, there is no proportional correlation between the depth of the grooves tN and the stability boundary ap,crit, showing the presence of several local optima of the depth of the grooves. This indicates complex interdependencies and a conflict of the objectives between maximizing the difference in the direction-specific eigenfrequencies and minimizing the weakening of the tool in one direction caused by the grooves.
4. Discussion
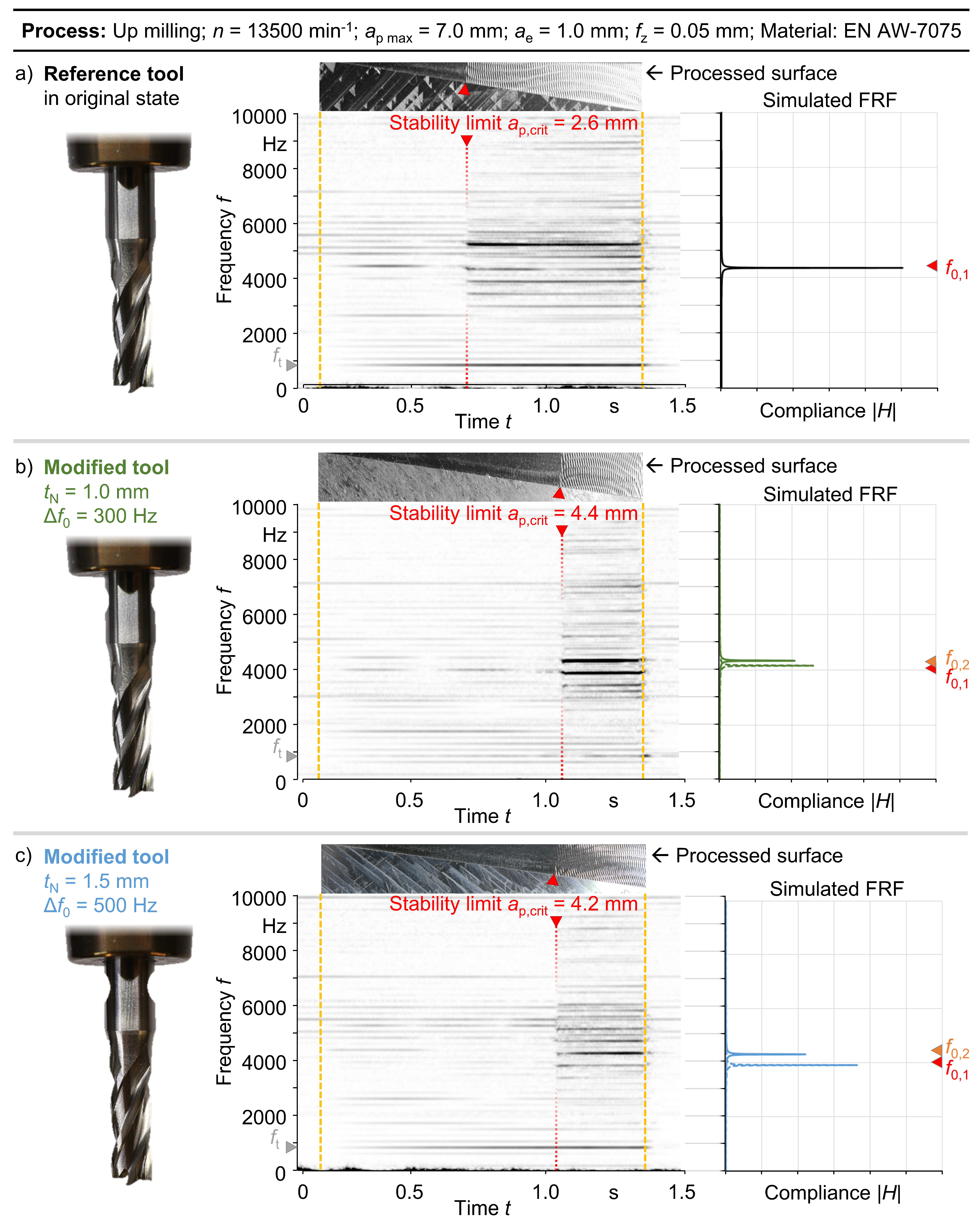
In this section, the effect mechanisms which lead to an increased stability limit were analyzed and discussed. For this, the FRFs of the modified tools and the acoustic emission measurements conducted during the operating trials are compared in
Figure 8. This in-depth analysis was supplemented by an evaluation of the novel approach in terms of the potential and requirements for process optimization, the capabilities compared to the established and recent chatter suppression techniques, as well as the applicability for industrial use.
Using the reference tool, the stability limit was identified at
ap,crit = 2.6 mm (
tcrit ≈ 0.7 s) due to an excitation of the eigenfrequency
f0,1 = 4350 Hz, which caused the appearance of increased amplitudes in the range of the surrounding harmonics of the tooth engagement frequency
fh,i = i ∙
ft with i ∈
N (
Figure 8a). The presented modification of the tool leads to asymmetric dynamic properties which in turn manifest in two directionally different eigenfrequencies,
f0,1 and
f0,2. By applying these different eigenfrequencies for consecutive tooth engagements, which can be achieved by using a four-fluted tool, the regenerative effect could be disturbed. Thus, the stability limit could be significantly increased to
ap,crit = 4.4 mm and
ap,crit = 4.2 mm for the tools with a depth of the notches of
tN = 1.0 mm and
tN = 1.5 mm, respectively (
Figure 8b,c). When the critical depth of cut
ap,crit was exceeded, the vibrations with increased amplitudes occurred within the ranges of both eigenfrequencies
f0,1 and
f0,2. In analogy to the increasing depth of cut along the tool path and the resulting increase in the cutting forces, the amplitudes of the process-related externally excited vibration within the frequency of the tooth engagement increase. In comparison to the reference process, the chatter vibrations indicate even higher amplitudes if the modified tools are applied. These are related to the significantly higher process and external excitation forces, which occur due to the increased depth of cut when the regenerative effect becomes dominant.
In contrast to these results, a reduction in the stability limit to
ap,crit = 1.4 mm and
ap,crit = 1.8 mm was observed in the experiments conducted with a depth of the grooves of
tN = 1.25 mm and
tN = 1.75 mm, respectively (
Figure 7). Especially for the depth of the grooves of
tN = 1.25 mm, an eigenfrequency of the tool was excited at
f0,2 ≈ 4050 Hz, which corresponded to a harmonic of the spindle speed
n = 13,500 1/min ≙ 225 Hz (
f0,2 ≈ 18 ·
fn). As mentioned, the presence of multiple local optima of the depth of the grooves indicates complex interdependencies and a conflict between the objectives of maximizing the difference in the direction-specific eigenfrequencies and minimizing the weakening of the tool in one direction caused by the notches (
Figure 9). It can be assumed that a maximum difference between the eigenfrequency of subsequent engaging teeth is beneficial in terms of the disturbance of the regenerative effect, since a recurring self-excitation is avoided. As in most cases a directional stiffening is at least impractical, a modification of the dynamic properties by integrating weakening elements such as notches is more flexible. A reduction of the structural stiffness of a tool directly causes higher deflections under the load conditions during a milling operation. However, these increased deflections are not critical as long as the remaining stiffness and process damping effects limit the main proportion of the amplitude of the deflections and, thus, the influence of one cut on subsequent tooth engagements. Only if the weakening of a tool leads to deflections greater than the undeformed chip thickness, the next but one cut is excited by a modulation of the undeformed chip thickness, which correlates to its actual natural frequency. In this case, the disturbance of the regenerative effect is eliminated and chatter vibrations can occur.
In contrast to the existing techniques for process stabilization, the presented approach does not require a process-specific adjustment considering the individual properties of, e.g., the tool or workpiece. The new approach does not involve a modification of the cutting edges. Therefore, the fundamental cutting operation is not influenced, which allows a widely universal application and combination with other process optimization techniques regarding the process dynamics, but also other objectives such as wear resistance, productivity and resource efficiency.
5. Conclusions and Outlook
In this paper, a new, promising approach to disturb the regenerative effect in milling processes by using tools which were purposefully modified to exhibit asymmetric dynamic properties is presented. By inducing different eigenfrequencies and compliance amplitudes for consecutive tooth engagements, the deflections of the tool and thus the modulation of the uncut chip thickness can be influenced. This changes the alteration of the process forces and prevents a recurring self-excitation of the milling tool. This way, the regenerative effect can be disturbed. The approach for disturbing regenerative chatter oscillations was validated for an exemplary milling process of an aluminum wrought alloy by preparing the shank of the tool with grooves of different depths. The modification was achieved by machining with a spherical cutter but might also be realized in e.g., grinding processes if carbide tools should be applied. Depending on the depth of the grooves, both a reduction and an increase in the stability limit could be observed. This indicates a positive influence of the direction-dependently differing eigenfrequencies of the cutting tool on the stability limit conflicting with a negative impact of the increased compliance amplitude, which results from the weakening of the tool shank due to the grooves. This conflict of objectives indicates the need for a systematic optimization of the modified tool shape.
The described method of tool preparation has great potential for disturbing the regenerative effect and thus increasing the material removal rate and the productivity of milling processes. As only the tool shaft is modified, the cutting fundamentals are not affected. Therefore, the method of tool modification has the potential to be used in a wide range of milling processes that are subjected to chatter vibrations. The stabilization mechanism of the presented technique could not be conclusively investigated in the studies presented. The influence of the different types of cutting tools, engagement conditions and materials, which change the process forces, on the effectiveness of the procedure must be explored in detail. Therefore, further technological investigations should be carried out to determine the influence of the size, shape and position of the parallel grooves in the tool shank. The use of a process simulation to investigate the influence of asymmetric dynamic properties on a milling process would allow to efficiently investigate the different variants and to support the process of designing and parameterizing the shape, size and position of the grooves.
Author Contributions
Conceptualization, J.B.; methodology, J.B.; software, J.B., A.W. and T.S.; validation, A.W. and J.B.; formal analysis, J.B., A.W. and T.S.; investigation, A.W., J.B. and T.S.; resources, D.B.; data curation, J.B., A.W. and D.B.; writing—original draft preparation, A.W.; writing—review and editing, J.B., A.W., T.S. and D.B.; visualization, A.W.; supervision, D.B.; project administration, D.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
Gefördert durch die Deutsche Forschungsgemeinschaft (DFG)—403392440. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—403392440.
Acknowledgments
We acknowledge financial support by Deutsche Forschungsgemeinschaft and Technische Universität Dortmund/TU Dortmund Technical University within the funding programme Open Access Publishing.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Weck, M.; Brecher, C. Werkzeugmaschinen 5; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-642-38748-7. [Google Scholar]
- Altintas, Y. Manufacturing Automation: Metal. Cutting Mechanics, Machine Tool Vibrations, and CNC Design; Cambridge University Press: New York, NY, USA, 2012; ISBN 978-1-107-00148-0. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stépán, G. Chatter suppression techniques in metal cutting. CIRP Ann. Manuf. Technol. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Baumann, J.; Krebs, E.; Biermann, D. Chatter avoidance in milling by using advanced cutting tools with structured functional surfaces. MM Sci. J. 2019, 04, 3019–3026. [Google Scholar] [CrossRef]
- Altintas, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Budak, E.; Altintaş, Y. Analytical prediction of chatter stability in milling—Part I: General formulation. J. Dyn. Syst. Meas. Control 1998, 120, 358–362. [Google Scholar] [CrossRef]
- Brecher, C.; Esser, M. Stability prediction: Advances and current restrictions, Bd. 21. In Proceedings of the 6th International Conference on High Speed Machining, San Sebastian, Spain, 21–22 March 2007. [Google Scholar]
- Insperger, T.; Gradisek, J.; Kalveram, M.; Stépán, G.; Weinert, K.; Govekar, E. Machine tool chatter and surface quality in milling processes. In Manufacturing Engineering and Materials Handling—2004: Presented at the 2004 ASME International Mechanical Engineering Congress, Anaheim, California, USA, 13–19 November 2004; ASME: New York, NY, USA, 2004; pp. 971–983. ISBN 0-7918-4713-6. [Google Scholar]
- Altintas, Y.; Kersting, P.; Biermann, D.; Budak, E.; Denkena, B.; Lazoglu, I. Virtual process systems for part machining operations. CIRP Ann. Manuf. Technol. 2014, 63, 585–605. [Google Scholar] [CrossRef]
- Siebrecht, T.; Kersting, P.; Biermann, D.; Odendahl, S.; Bergmann, J. Modeling of surface location errors in a multi-scale milling simulation system using a tool model based on triangle meshes. Procedia CIRP 2015, 37, 188–192. [Google Scholar] [CrossRef]
- Wiederkehr, P.; Siebrecht, T. Virtual machining: Capabilities and challenges of process simulations in the aerospace industry. Procedia Manuf. 2016, 80–87. [Google Scholar] [CrossRef]
- Wiederkehr, P.; Siebrecht, T.; Baumann, J.; Biermann, D. Point-based tool representations for modeling complex tool shapes and runout for the simulation of process forces and chatter vibrations. Adv. Manuf. 2018, 6, 301–307. [Google Scholar] [CrossRef]
- Ozkirimli, O.; Tunc, L.T.; Budak, E. Generalized model for dynamics and stability of multi-axis milling with complex tool geometries. J. Mater. Process. Technol. 2016, 238, 446–458. [Google Scholar] [CrossRef]
- Stone, B. Chatter and Machine Tools; Springer: Cham, Switzerland, 2014; ISBN 978-3-319-05236-6. [Google Scholar]
- Sellmeier, V. Über den Einfluss der Werkzeuggestalt auf die Dynamische Stabilität des Fräsprozesses. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität, Hannover, Germany, 26 June 2012. [Google Scholar] [CrossRef]
- Grabowski, R.; Denkena, B.; Köhler, J. Prediction of process forces and stability of end mills with complex geometries. Procedia CIRP 2014, 14, 119–124. [Google Scholar] [CrossRef][Green Version]
- Guo, Q.; Jiang, Y.; Zhao, B.; Ming, P. Chatter modeling and stability lobes predicting for non-uniform helix tools. Int. J. Adv. Manuf. Technol. 2016, 87, 251–266. [Google Scholar] [CrossRef]
- Comak, A.; Budak, E. Modeling dynamics and stability of variable pitch and helix milling tools for development of a design method to maximize chatter stability. Precis. Eng. 2017, 47, 459–468. [Google Scholar] [CrossRef]
- Niu, J.; Ding, Y.; Zhu, L.; Ding, H. Mechanics and multi-regenerative stability of variable pitch and variable helix milling tools considering runout. Int. J. Mach. Tools Manuf. 2017, 123, 129–145. [Google Scholar] [CrossRef]
- Otto, A.; Rauh, S.; Ihlenfeldt, S.; Radons, G. Stability of milling with non-uniform pitch and variable helix tools. Int. J. Adv. Manuf. Technol. 2017, 89, 2613–2625. [Google Scholar] [CrossRef]
- Iglesias, A.; Dombovari, Z.; Gonzalez, G.; Munoa, J.; Stepan, G. Optimum selection of variable pitch for chatter suppression in face milling operations. Materials 2019, 12, 112. [Google Scholar] [CrossRef]
- Sellmeier, V.; Denkena, B. Stable islands in the stability chart of milling processes due to unequal tooth pitch. Int. J. Mach. Tools Manuf. 2011, 51, 152–164. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, C.; Ding, Y.; Xiong, Y. Variable-step integration method for milling chatter stability prediction with multiple delays. Sci. China Technol. Sci. 2011, 54, 3137–3154. [Google Scholar] [CrossRef]
- Volokh, V.; Boulakhov, S.; Sharivker, L.; Zeidner, S.; Galipko, V. Chatter-Resistant End Mill. U.S. Patent 8,221,036, 17 July 2012. [Google Scholar]
- Merdol, S.D.; Altintas, Y. Mechanics and dynamics of serrated cylindrical and tapered end mills. J. Manuf. Sci. Eng. 2004, 126, 317–326. [Google Scholar] [CrossRef]
- Dombovari, Z.; Altintas, Y.; Stepan, G. The effect of serration on mechanics and stability of milling cutters. Int. J. Mach. Tools Manuf. 2010, 50, 511–520. [Google Scholar] [CrossRef]
- Denkena, B.; Léon, L.; Grove, T. Prozessstabilität eines kordelierten Schaftfräsers. Z. Wirtsch. Fabr. 2010, 105, 37–41. [Google Scholar] [CrossRef]
- Denkena, B.; Grabowski, R.; Krödel, A.; Ellersieh, L. Process stability of a novel roughing-finishing end mill. Prod. Eng. Res. Dev. 2010. [Google Scholar] [CrossRef]
- Suzuki, N.; Takahashi, W.; Igeta, H.; Nakanomiya, T. Flank face texture design to suppress chatter vibration in cutting. CIRP Ann. Manuf. Technol. 2020. [Google Scholar] [CrossRef]
- Seguy, S.; Insperger, T.; Arnaud, L.; Dessein, G.; Peigné, G. On the stability of high-speed milling with spindle speed variation. Int. J. Adv. Manuf. Technol. 2010, 48, 883–895. [Google Scholar] [CrossRef]
- Seguy, S.; Insperger, T.; Arnaud, L.; Dessein, G.; Peigné, G. Suppression of period doubling chatter in high-speed milling by spindle speed variation. Mach. Sci. Technol. 2011, 15, 153–171. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, J. Internal energy based analysis on mechanism of spindle speed variation for regenerative chatter control. J. Vib. Control. 2010, 16, 281–301. [Google Scholar] [CrossRef]
- Sahu, G.N.; Vashisht, S.; Wahi, P.; Law, M. Validation of a hardware-in-the-loop simulator for investigating and actively damping regenerative chatter in orthogonal cutting. CIRP J. Manuf. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Möhring, H.-C.; Wiederkehr, P.; Lerez, C.; Siebrecht, T.; Schmitz, H. Case study 1.1: Identification and active damping of critical workpiece vibrations in milling of thin walled workpieces, Bd. 53. In Intelligent Fixtures for the Manufacturing of Low Rigidity Components; Lecture Notes in Production Engineering; Möhring, H.-C., Wiederkehr, P., Gonzalo, O., Kolar, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–23. ISBN 978-3-319-45290-6. [Google Scholar]
- Abele, E.; Dohnal, F.; Feulner, M.; Sielaff, T.; Daume, C. Numerical investigation of chatter suppression via parametric anti-resonance in a motorized spindle unit during milling. Prod. Eng. 2018, 12, 309–317. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, D.; Zhang, X. Chatter stability and precision during high-speed ultrasonic vibration cutting of a thin-walled titanium cylinder. Chin. J. Aeronaut. 2020. [Google Scholar] [CrossRef]
- Wan, S.; Li, X.; Su, W.; Yuan, J.; Hong, J. Active chatter suppression for milling process with sliding mode control and electromagnetic actuator. Mech. Syst. Signal. Process. 2020, 136, 106528. [Google Scholar] [CrossRef]
- Wang, M.; Fei, R. Improvement of machining stability using a tunable-stiffness boring bar containing an electrorheological fluid. Smart Mater. Struct. 1999, 8, 511–514. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, D.; Wu, B.; Luo, M.; Liu, Y. Stability improvement and vibration suppression of the thin-walled workpiece in milling process via magnetorheological fluid flexible fixture. Int. J. Adv. Manuf. Technol. 2017, 88, 1231–1242. [Google Scholar] [CrossRef]
- Gao, J.; Altintas, Y. Chatter stability of synchronized elliptical vibration assisted milling. CIRP J. Manuf. Sci. Technol. 2020, 28, 76–86. [Google Scholar] [CrossRef]
- Hirsch, A. Werkzeugmaschinen: Grundlagen, Auslegung, Ausführungsbeispiele; Springer: Hannover, Germany, 2012; ISBN 978-3-8348-2364-9. [Google Scholar]
- Möhring, H.C.; Wiederkehr, P.; Baumann, J.; König, A.; Spieker, C.; Müller, M. Intelligent hybrid material slide component for machine tools. J. Mach. Eng. 2017, 17, 17–30. [Google Scholar]
- Xiao, J.; Zhang, Q.; Liu, H.; Huang, T.; Shan, X. Research on vibration suppression by a multi-point flexible following support head in thin-walled parts mirror milling. Int. J. Adv. Manuf. Technol. 2020, 106, 3335–3344. [Google Scholar] [CrossRef]
- Vogel, F.A.M.; Berger, S.; Özkaya, E.; Biermann, D. Vibration suppression in turning TiAl6V4 using additively manufactured tool holders with specially structured, particle filled hollow elements. Procedia Manuf. 2019, 40, 32–37. [Google Scholar] [CrossRef]
- Jin, G.; Qi, H.; Li, Z.; Han, J. Dynamic modeling and stability analysis for the combined milling system with variable pitch cutter and spindle speed variation. Commun. Nonlinear Sci. Numer. Simul. 2018, 63, 38–56. [Google Scholar] [CrossRef]
- Tunc, L.T. Smart tool path generation for 5-axis ball-end milling of sculptured surfaces using process models. Robot. Comput.-Integr. Manuf. 2019, 56, 212–221. [Google Scholar] [CrossRef]
- Huang, N.; Krebs, E.; Baumann, J.; Wirtz, A.; Jaeger, E.M.; Biermann, D. A Universal Pocket Plunge Milling Method to Decrease the Maximum Engagement Angle. J. Manuf. Sci. Eng. 2020, 142. [Google Scholar] [CrossRef]
- Baumann, J.; Siebrecht, T.; Wiederkehr, P. Modelling the dynamic behavior of a machine tool considering the tool-position-dependent change of modal parameters in a geometric-kinematic simulation system. Procedia CIRP 2017, 62, 351–356. [Google Scholar] [CrossRef]
- Semm, T.; Nierlich, M.B.; Zaeh, M.F. Substructure coupling of a machine tool in arbitrary axis positions considering local linear damping models. ASME J. Manuf. Sci. Eng. 2019, 141, 071014. [Google Scholar] [CrossRef]
- Baumann, J.; Hense, R.; Wiederkehr, P.; Nguyen, L.-T.; Möhring, H.-C.; Spieker, C.; Müller, M. Thermal effects on machine tool compliance. In Proceedings of the Thirteenth International Conference on High Speed Machining 2016, Metz, France, 4–5 October 2016. [Google Scholar]
- Hung, J.-P.; Lai, Y.-L.; Lin, C.-Y.; Lo, T.-L. Modeling the machining stability of a vertical milling machine under the influence of the preloaded linear guide. Int. J. Mach. Tools Manuf. 2011, 51, 731–739. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).