An Iterative Size Effect Model of Surface Generation in Finish Machining
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
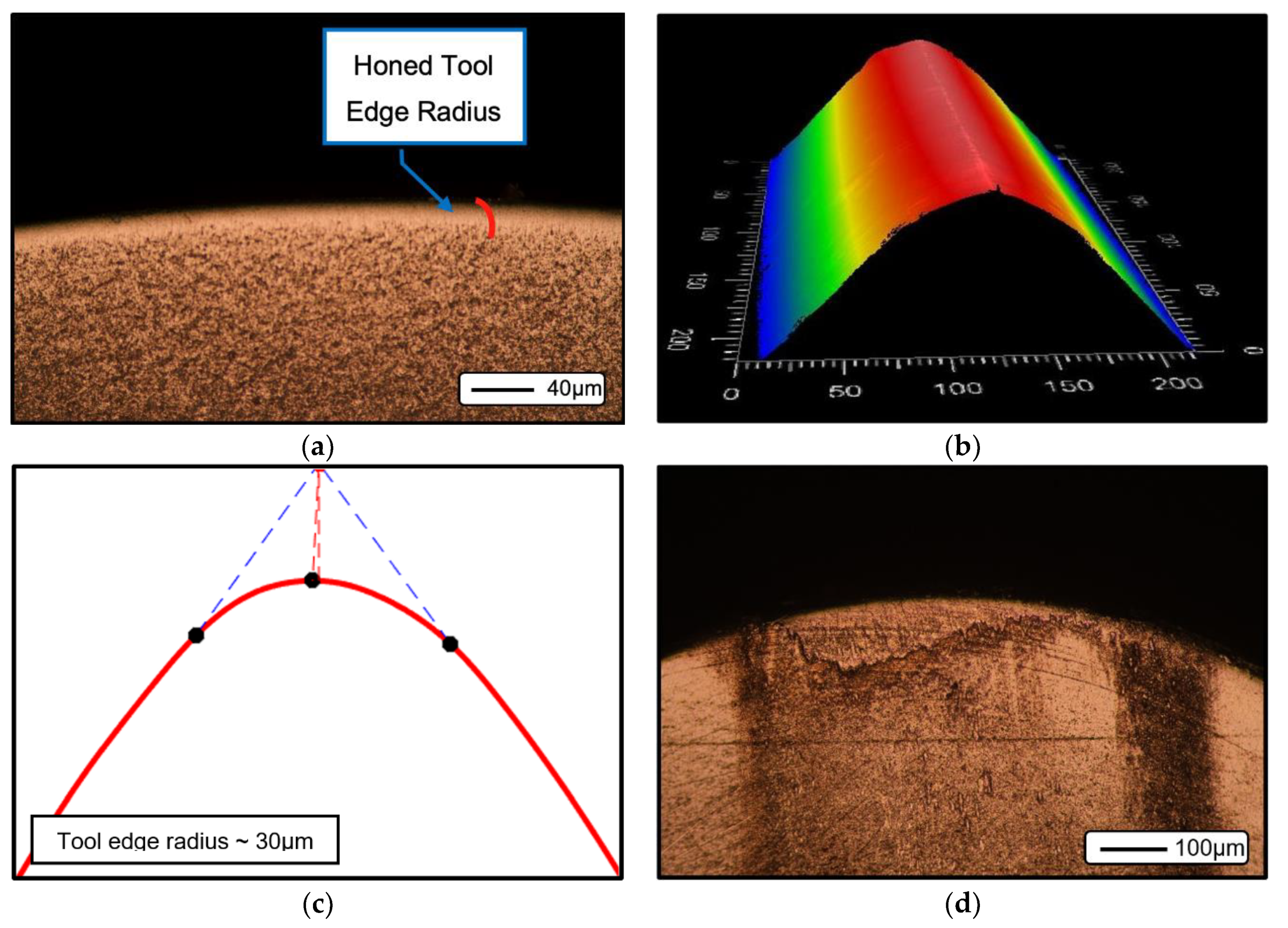
3.1. Model Assumptions
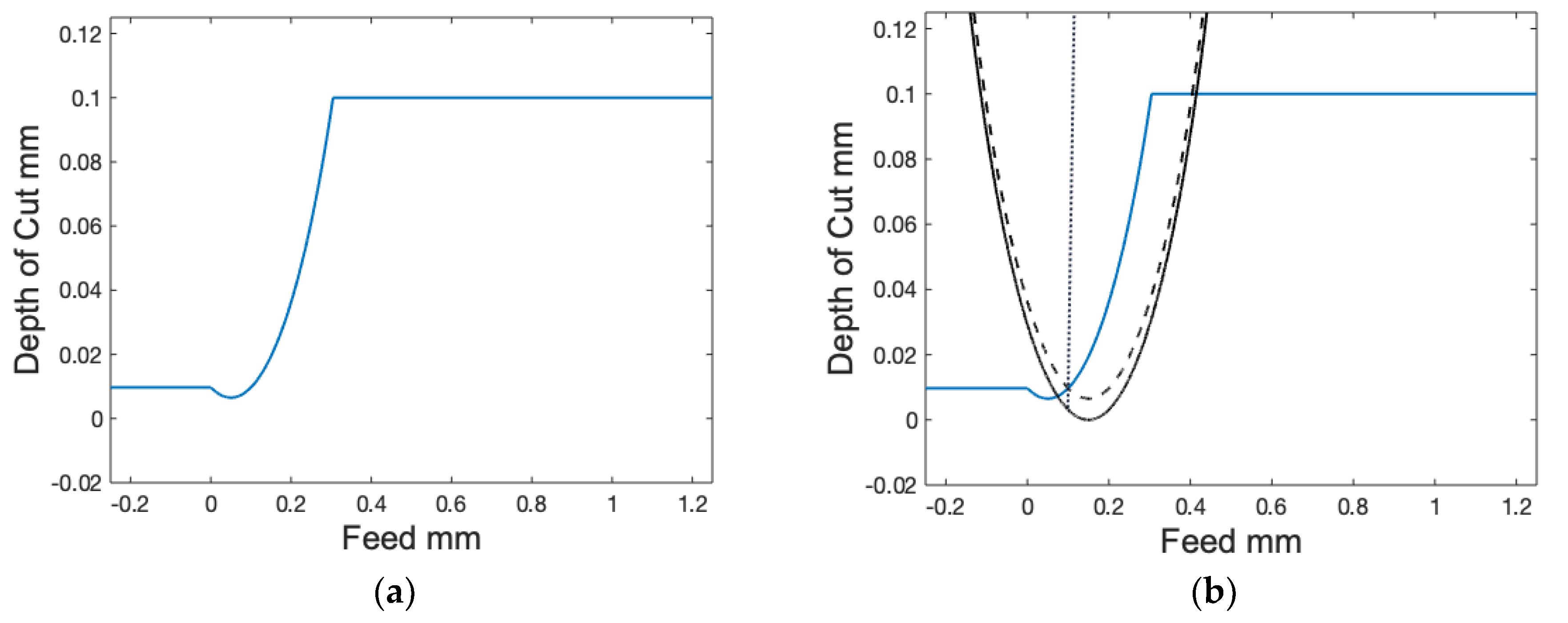
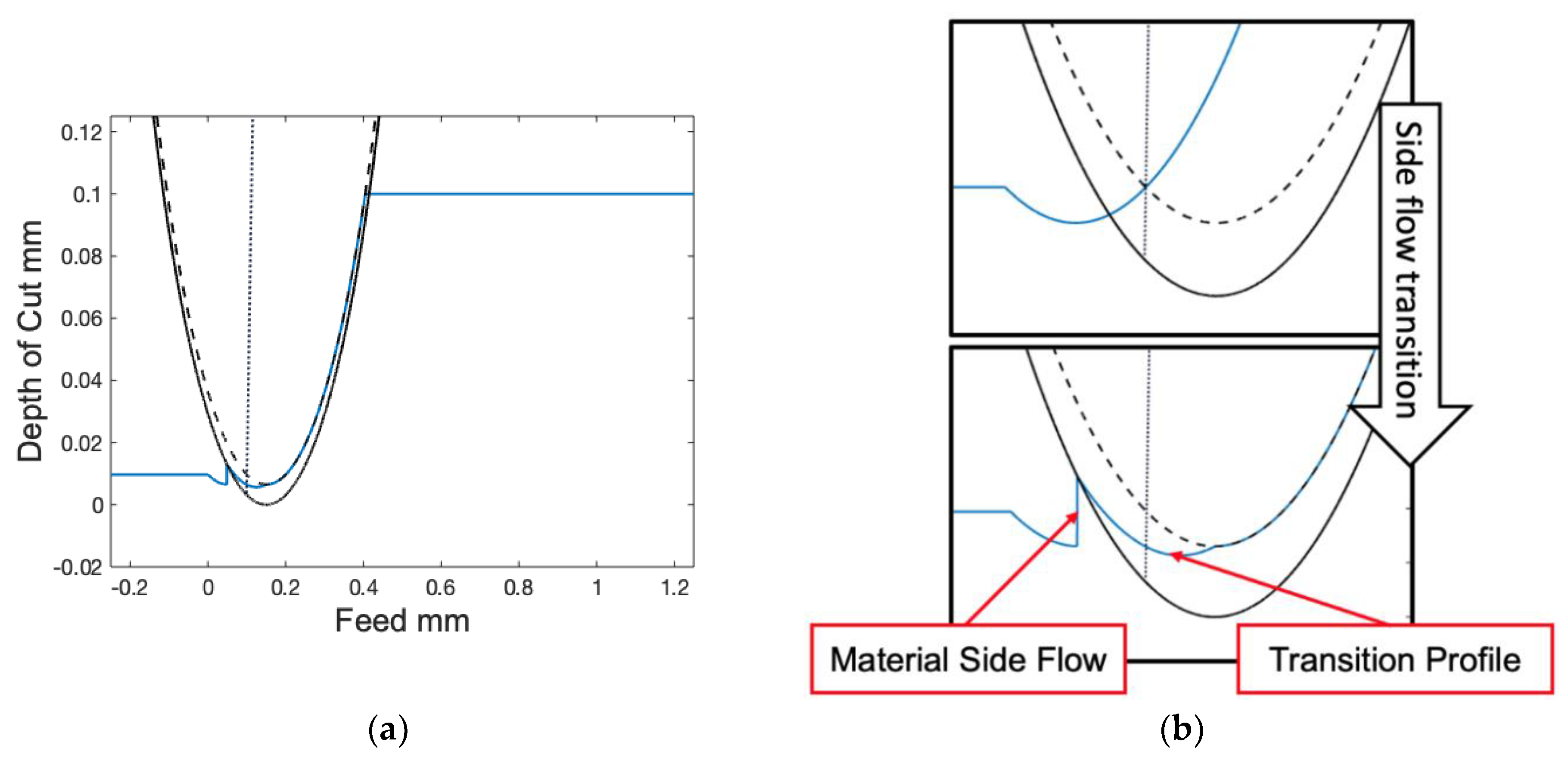
3.2. Model Development
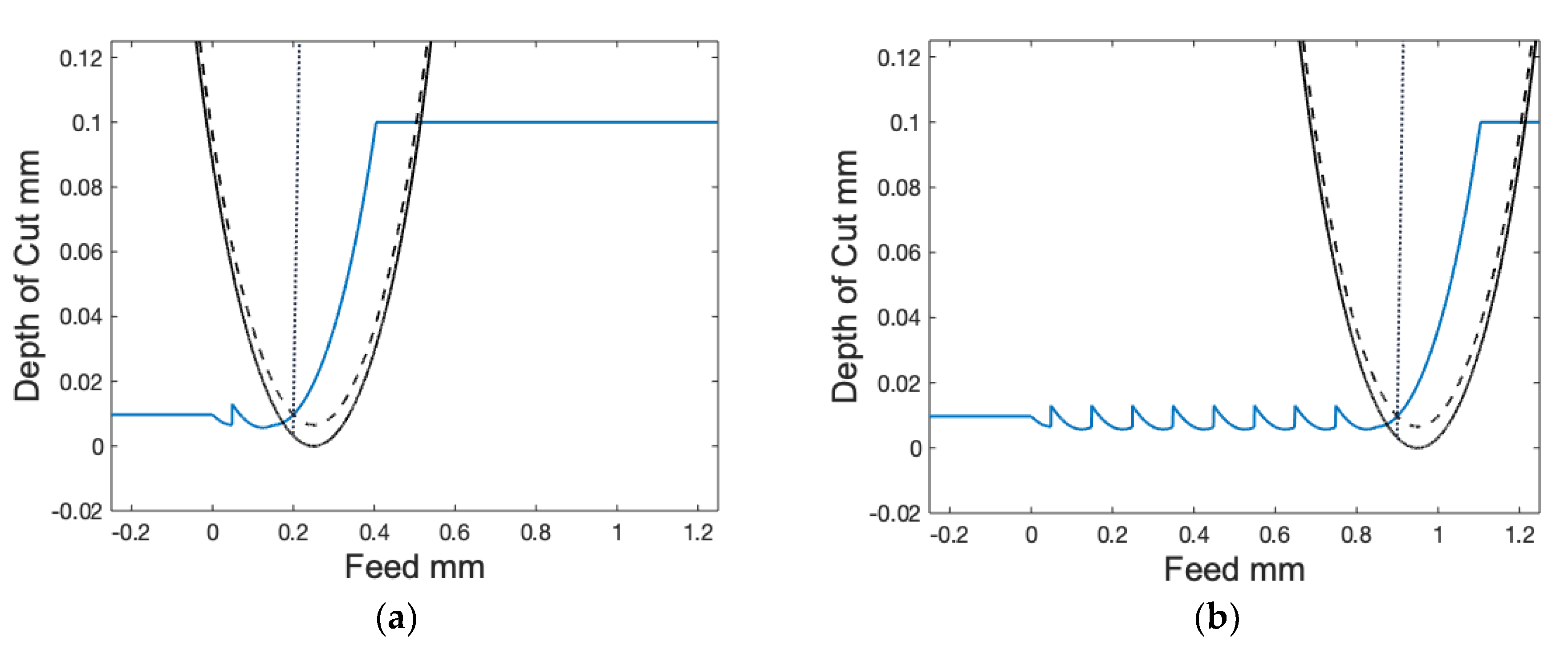
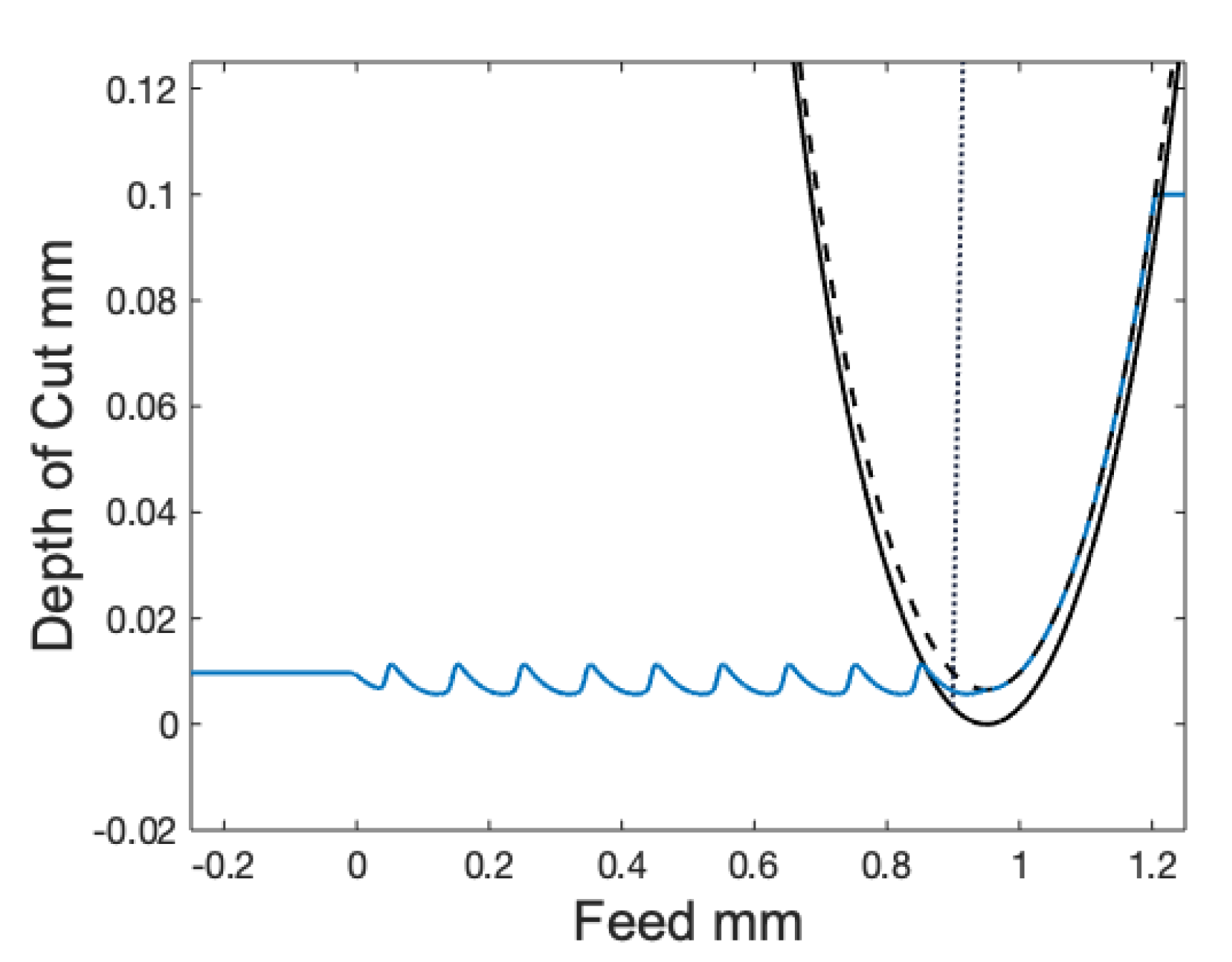
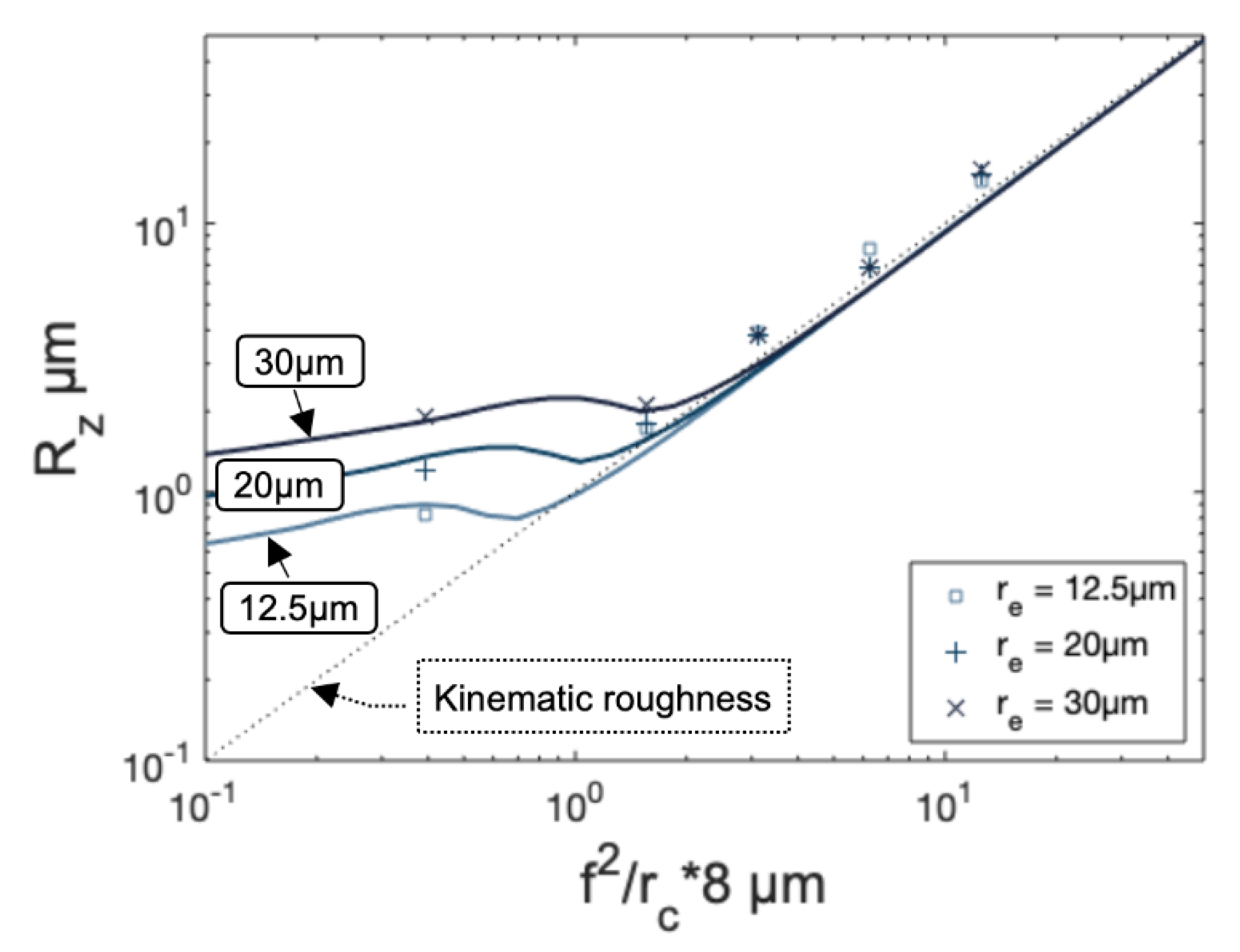
3.3. Model Validation
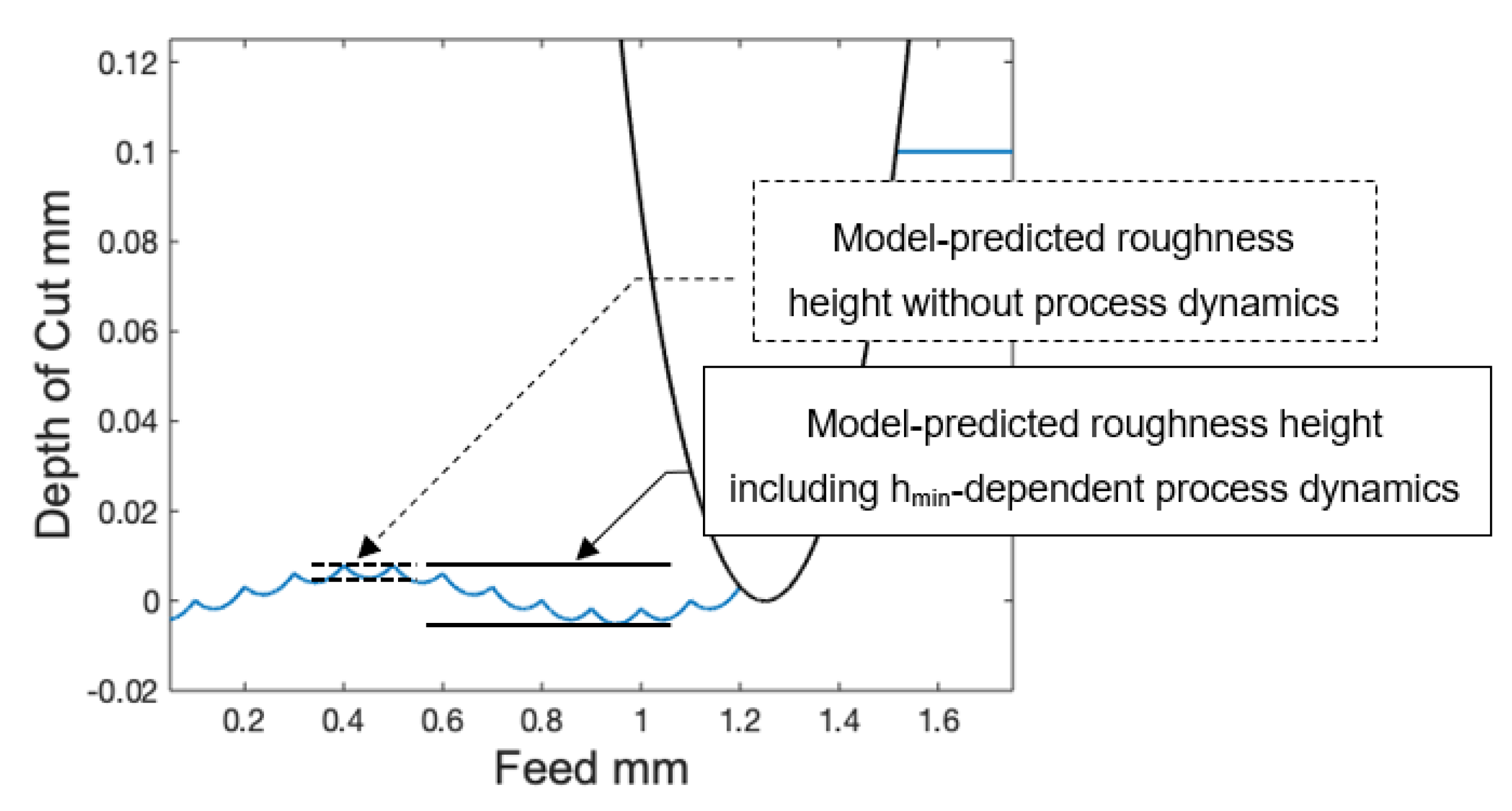
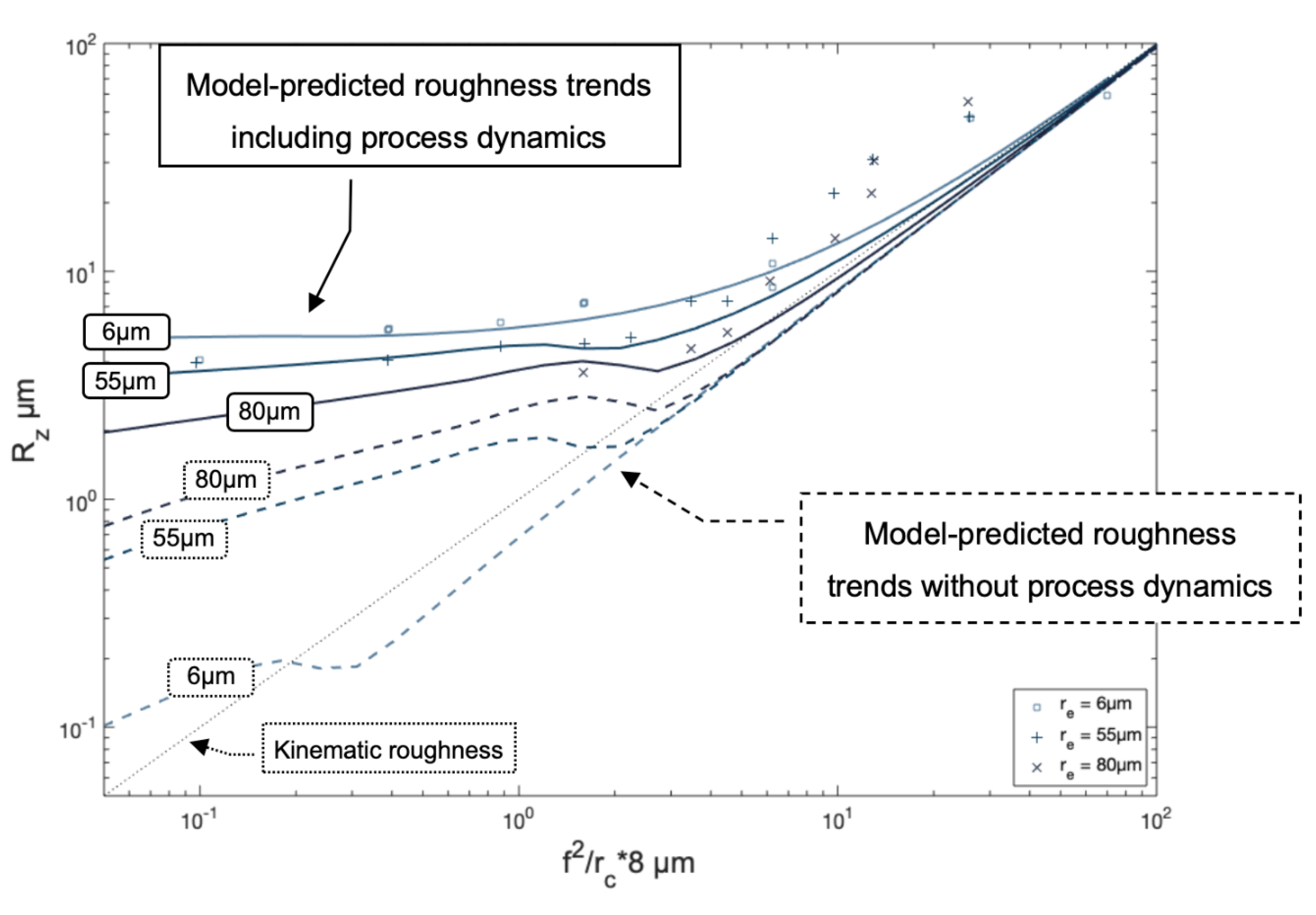
3.4. Machine Tool Error Incorporation
4. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Moll, H. Die Herstellung Hochwertiger Drehflächen: Einfluß der Schnittbedingungen auf die Oberflächengüte beim Drehen, Schlichten und Feinschlichten; VDI-Verl.: Berlin, Germany, 1940. [Google Scholar]
- Sokolowski, A. Präzision in der Metallbearbeitung; VEB-Verlag Technik: Berlin, Germany, 1955. [Google Scholar]
- Albrecht, P. New Developments in the Theory of the Metal-Cutting Process: Part I. The Ploughing Process in Metal Cutting. J. Eng. Ind. 1960, 82, 348–357. [Google Scholar] [CrossRef]
- Ikawa, N.; Shimada, S.; Tanaka, H. Minimum thickness of cut in micromachining. Nanotechnology 1992, 3, 6–9. [Google Scholar] [CrossRef]
- Brammertz, P. Die entstehung der oberflächenrauheit beim feindrehen. Ind. Anz. 1961, 2, 25–32. [Google Scholar]
- Yuan, Y.; Jing, X.; Ehmann, K.F.; Zhang, D. Surface roughness modeling in micro end-milling. Int. J. Adv. Manuf. Technol. 2017, 95, 1655–1664. [Google Scholar] [CrossRef]
- Grzesik, W. A revised model for predicting surface roughness in turning. Wear 1996, 194, 143–148. [Google Scholar] [CrossRef]
- Childs, T.H.C.; Sekiya, K.; Tezuka, R.; Yamane, Y.; Dornfeld, D.; Lee, D.-E.; Min, S.; Wright, P. Surface finishes from turning and facing with round nosed tools. CIRP Ann. 2008, 57, 89–92. [Google Scholar] [CrossRef]
- Knuefermann, M.M. Machining Surfaces of Optical Quality by Hard Turning. Ph.D. Thesis, Cranfield University, Cranfield, UK, 2003. [Google Scholar]
- Shaw, M.C.; Cookson, J. Metal Cutting Principles; Oxford university press New York: New York, NY, USA, 2005; Volume 2. [Google Scholar]
- Lambert, H. Two years of finish-turning research at the Technological University, Delft. Ann. CIRP 1961, 10, 246–255. [Google Scholar]
- Sata, T. Surface finish in metal cutting. Ann. CIRP 1964, 13, 190–197. [Google Scholar]
- Pekelharing, A.; Gieszen, C. Material side flow in finish turning. Ann. CIRP 1971, 20, 21–22. [Google Scholar]
- El-Wardany, T.; Elbestawi, M. Phenomenological analysis of material side flow in hard turning: Causes, modeling, and elimination. Mach. Sci. Technol. 1998, 2, 239–251. [Google Scholar] [CrossRef]
- Liu, K. Process Modeling of Micro-Cutting Including Strain Gradient Effects; Melkote, S.N., Ed.; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2005. [Google Scholar]
- Kishawy, H.; Haglund, A.; Balazinski, M. Modelling of Material Side Flow in Hard Turning. CIRP Ann. 2006, 55, 85–88. [Google Scholar] [CrossRef]
- Kishawy, H.; Elbestawi, M. Effects of process parameters on material side flow during hard turning. Int. J. Mach. Tools Manuf. 1999, 39, 1017–1030. [Google Scholar] [CrossRef]
- Liu, K.; Melkote, S.N. Effect of plastic side flow on surface roughness in micro-turning process. Int. J. Mach. Tools Manuf. 2006, 46, 1778–1785. [Google Scholar] [CrossRef]
- Özel, T.; Hsu, T.-K.; Zeren, E. Effects of cutting edge geometry, workpiece hardness, feed rate and cutting speed on surface roughness and forces in finish turning of hardened AISI H13 steel. Int. J. Adv. Manuf. Technol. 2004, 25, 262–269. [Google Scholar] [CrossRef]
- Özel, T.; Karpat, Y. Predictive modeling of surface roughness and tool wear in hard turning using regression and neural networks. Int. J. Mach. Tools Manuf. 2005, 45, 467–479. [Google Scholar] [CrossRef]
- Thiele, J.D.; Melkote, S.N. Effect of cutting edge geometry and workpiece hardness on surface generation in the finish hard turning of AISI 52100 steel. J. Mater. Process. Technol. 1999, 94, 216–226. [Google Scholar] [CrossRef]
- Zhao, T.; Zhou, J.M.; Bushlya, V.; Ståhl, J.E. Effect of cutting edge radius on surface roughness and tool wear in hard turning of AISI 52100 steel. Int. J. Adv. Manuf. Technol. 2017, 91, 3611–3618. [Google Scholar] [CrossRef]
- Childs, T.H.C.; Dornfeld, D.; Lee, D.-E.; Min, S.; Sekiya, K.; Tezuka, R.; Yamane, Y. The influence of cutting edge sharpness on surface finish in facing with round nosed cutting tools. CIRP J. Manuf. Sci. Technol. 2008, 1, 70–75. [Google Scholar] [CrossRef]
- Mai, Q.; Quan, Y.; Liu, P.; Ding, G. A new geometrical model of the formation of machined surface. Int. J. Adv. Manuf. Technol. 2017, 91, 3493–3502. [Google Scholar] [CrossRef]
- Schultheiss, F.; Hägglund, S.; Bushlya, V.; Zhou, J.; Ståhl, J.-E. Influence of the Minimum Chip Thickness on the Obtained Surface Roughness during Turning Operations. Procedia CIRP 2014, 13, 67–71. [Google Scholar] [CrossRef][Green Version]
- Kountanya, R. Surface finish and tool wear characterization in hard turning using a mathematical cutting tool representation. Mach. Sci. Technol. 2011, 15, 429–452. [Google Scholar] [CrossRef]
- Aouici, H.; Yallese, M.A.; Chaoui, K.; Mabrouki, T.; Rigal, J.-F. Analysis of surface roughness and cutting force components in hard turning with CBN tool: Prediction model and cutting conditions optimization. Measurement 2012, 45, 344–353. [Google Scholar] [CrossRef]
- Abbas, A.T.; Pimenov, D.Y.; Erdakov, I.N.; Taha, M.A.; El Rayes, M.M.; Soliman, M.S. Artificial Intelligence Monitoring of Hardening Methods and Cutting Conditions and Their Effects on Surface Roughness, Performance, and Finish Turning Costs of Solid-State Recycled Aluminum Alloy 6061 Сhips. Metals 2018, 8, 394. [Google Scholar] [CrossRef]
- Yang, A.; Han, Y.; Pan, Y.; Xing, H.; Li, J. Optimum surface roughness prediction for titanium alloy by adopting response surface methodology. Results Phys. 2017, 7, 1046–1050. [Google Scholar] [CrossRef]
- Zong, W.; Huang, Y.; Zhang, Y.; Sun, T. Conservation law of surface roughness in single point diamond turning. Int. J. Mach. Tools Manuf. 2014, 84, 58–63. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Q. A model for predicting surface roughness in single-point diamond turning. Measurement 2015, 69, 20–30. [Google Scholar] [CrossRef]
- He, C.; Zong, W.; Sun, T. Origins for the size effect of surface roughness in diamond turning. Int. J. Mach. Tools Manuf. 2016, 106, 22–42. [Google Scholar] [CrossRef]
- Lin, S.; Chang, M. A study on the effects of vibrations on the surface finish using a surface topography simulation model for turning. Int. J. Mach. Tools Manuf. 1998, 38, 763–782. [Google Scholar] [CrossRef]
- Zhang, S.; To, S.; Zhang, G.; Zhu, Z. A review of machine-tool vibration and its influence upon surface generation in ultra-precision machining. Int. J. Mach. Tools Manuf. 2015, 91, 34–42. [Google Scholar] [CrossRef]
- Altintas, Y.; Weck, M. Chatter Stability of Metal Cutting and Grinding. CIRP Ann. 2004, 53, 619–642. [Google Scholar] [CrossRef]
- Biermann, D.; Baschin, A. Influence of cutting edge geometry and cutting edge radius on the stability of micromilling processes. Prod. Eng. 2009, 3, 375–380. [Google Scholar] [CrossRef]
- Yusoff, A.R.; Turner, S.; Taylor, C.M.; Sims, N. The role of tool geometry in process damped milling. Int. J. Adv. Manuf. Technol. 2010, 50, 883–895. [Google Scholar] [CrossRef]
- Budak, E.; Tunc, L. Identification and modeling of process damping in turning and milling using a new approach. CIRP Ann. 2010, 59, 403–408. [Google Scholar] [CrossRef]
- Arcona, C.; Dow, T.A. An Empirical Tool Force Model for Precision Machining. J. Manuf. Sci. Eng. 1998, 120, 700–707. [Google Scholar] [CrossRef]
- Maiss, O.; Grove, T.; Denkena, B. Influence of asymmetric cutting edge roundings on surface topography. Prod. Eng. 2017, 11, 383–388. [Google Scholar] [CrossRef]
- De Oliveira, F.B.; Rodrigues, A.R.; Coelho, R.T.; De Souza, A.F. Size effect and minimum chip thickness in micromilling. Int. J. Mach. Tools Manuf. 2015, 89, 39–54. [Google Scholar] [CrossRef]
- Challen, J.; Oxley, P. Slip-line fields for explaining the mechanics of polishing and related processes. Int. J. Mech. Sci. 1984, 26, 403–418. [Google Scholar] [CrossRef]
- Malekian, M.; Mostofa, M.; Park, S.S.; Jun, M. Modeling of minimum uncut chip thickness in micro machining of aluminum. J. Mater. Process. Technol. 2012, 212, 553–559. [Google Scholar] [CrossRef]
- Outeiro, J.C. Influence of tool sharpness on the thermal and mechanical phenomena generated during machining operations. Int. J. Mach. Mach. Mater. 2007, 2, 413–432. [Google Scholar] [CrossRef]
- Ducobu, F.; Filippi, E.; Riviére-Lorphévre, E. Modélisation de l’influence de la profondeur de coupe en micro-coupe orthogonale. In Proceedings of the Congrès français de mécanique, Marseille, France, 24–28 August 2009; pp. 24–28. [Google Scholar]






| Feed f | Nose Radius rc | Theoretical/Kinematic Roughness Rt | Edge Radius re |
|---|---|---|---|
| 0.1 mm | 3.2 mm | 0.39 µm | 12.5 µm |
| 0.1 mm | 0.8 mm | 1.56 µm | 20 µm |
| 0.1 mm | 0.4 mm | 3.13 µm | 30 µm |
| 0.2 mm | 0.8 mm | 6.25 µm | |
| 0.2 mm | 0.4 mm | 12.5 µm |
| Material | yeff | hmin/re (+/−0.05) | Ultimate Tensile Strength | Young’s Modulus | Thermal Conductivity |
|---|---|---|---|---|---|
| AL 1075 | −71 | 0.06 | 90 MPa | 69 GPa | 236 W/mK |
| 51CrV4 | −68 | 0.07 | 1950 MPa | 190 GPa | 46.6 W/mK |
| Ti-6Al4V | −67 | 0.08 | 1100 MPa | 115 GPa | 7.2 W/mK |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, I.; Schoop, J. An Iterative Size Effect Model of Surface Generation in Finish Machining. J. Manuf. Mater. Process. 2020, 4, 63. https://doi.org/10.3390/jmmp4030063
Brown I, Schoop J. An Iterative Size Effect Model of Surface Generation in Finish Machining. Journal of Manufacturing and Materials Processing. 2020; 4(3):63. https://doi.org/10.3390/jmmp4030063
Chicago/Turabian StyleBrown, Ian, and Julius Schoop. 2020. "An Iterative Size Effect Model of Surface Generation in Finish Machining" Journal of Manufacturing and Materials Processing 4, no. 3: 63. https://doi.org/10.3390/jmmp4030063
APA StyleBrown, I., & Schoop, J. (2020). An Iterative Size Effect Model of Surface Generation in Finish Machining. Journal of Manufacturing and Materials Processing, 4(3), 63. https://doi.org/10.3390/jmmp4030063






