Lateral Vibrations in Deep Hole Drilling Due to Land Width Variation
Abstract
1. Introduction
2. Research Objective
3. Methodology
3.1. Experimental Setup and Process Chain
3.2. Analysis of Variance (ANOVA)
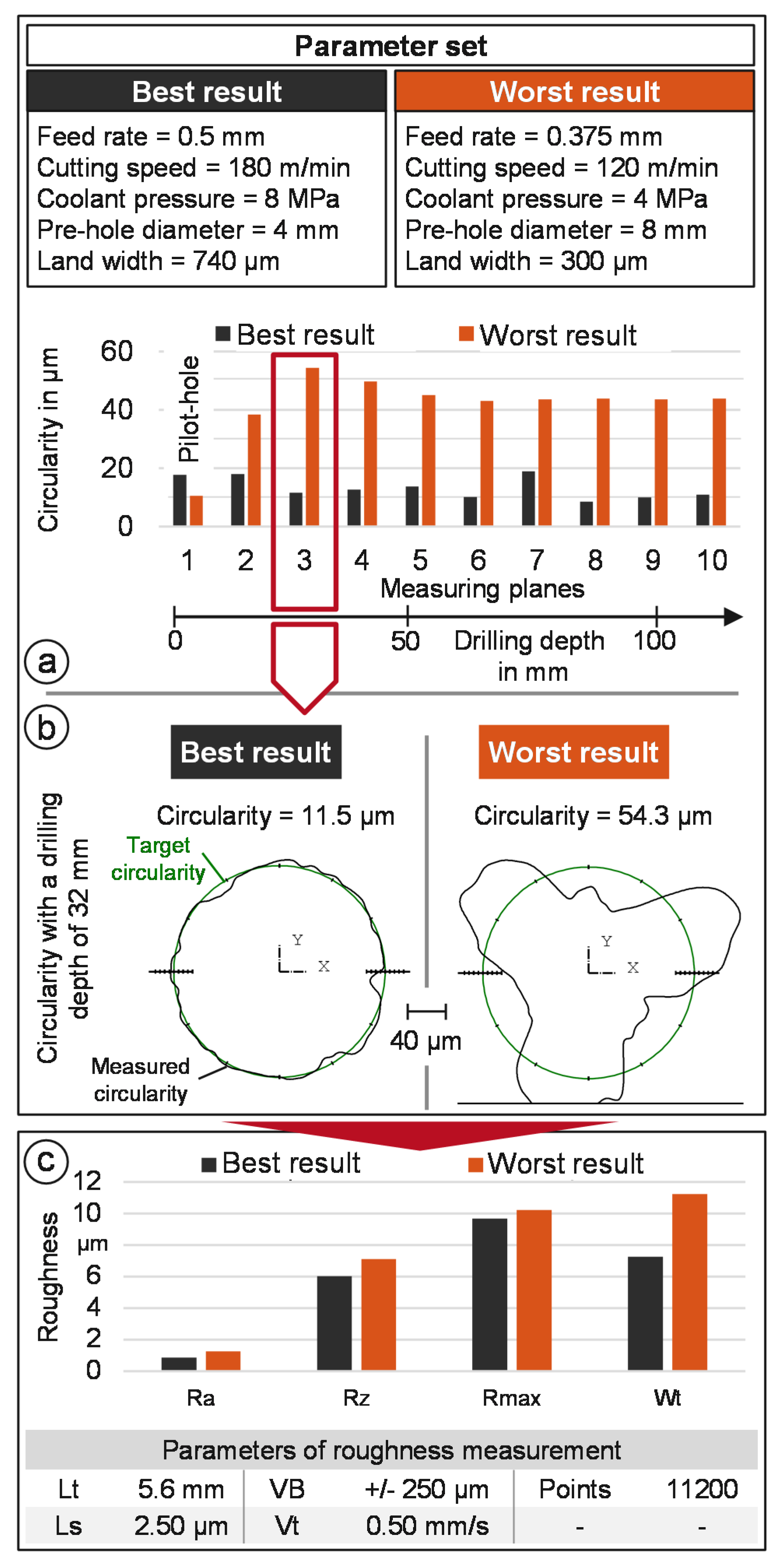
4. First Investigation: Drilling in Solid
Results and Discussion
5. Second Investigation: Drilling Out
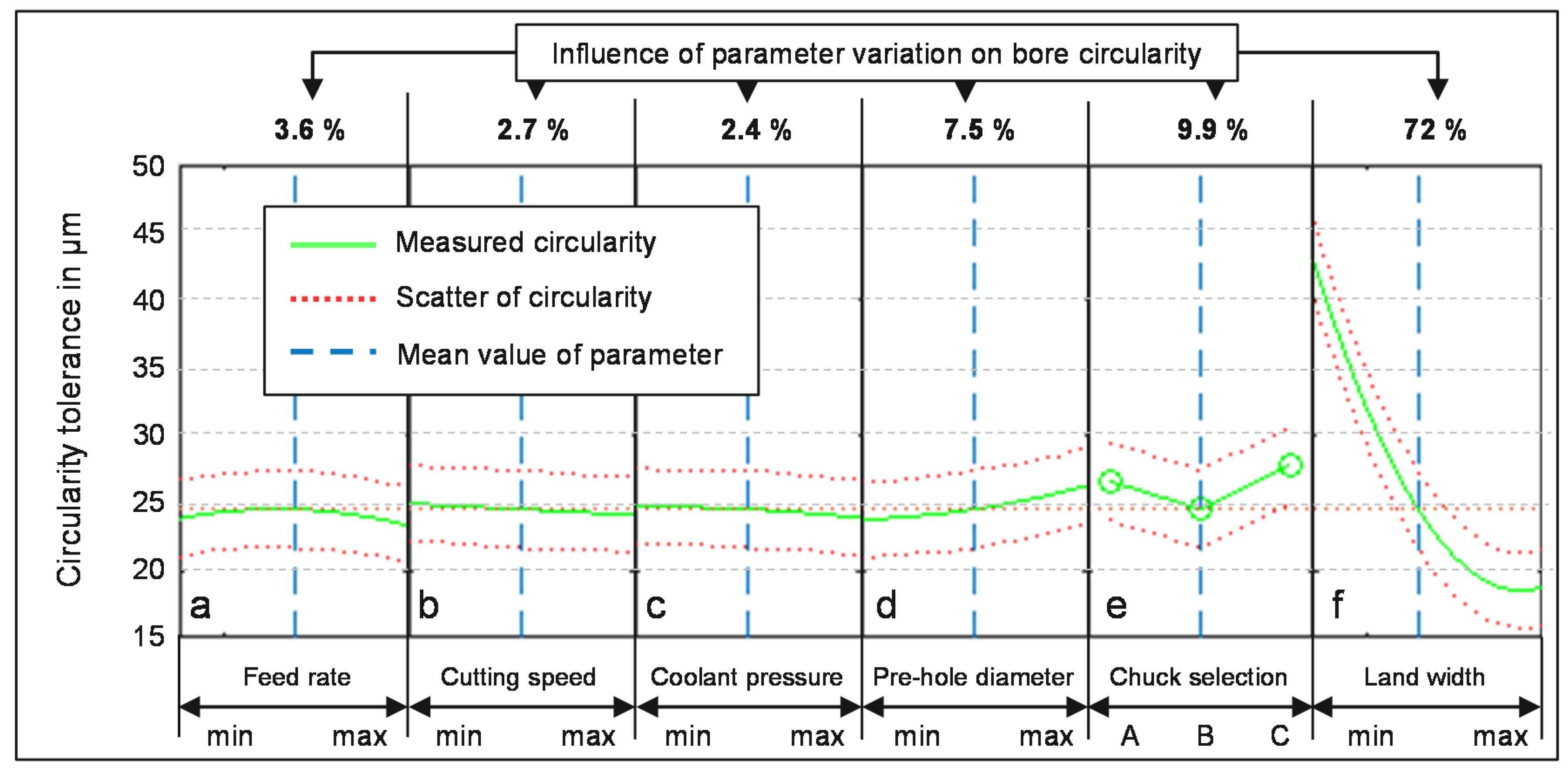
5.1. Discussion of the Influence of Parameter Variation on the Generation of Lateral Vibrations
5.1.1. Influence of Feed Rate on Circularity
5.1.2. Influence of Cutting Speed on Circularity
5.1.3. Influence of Coolant Pressure on Circularity
5.1.4. Influence of Pre-Hole Diameter on Circularity
5.1.5. Influence of Chuck Selection on Circularity
5.1.6. Influence of Land Width on Circularity
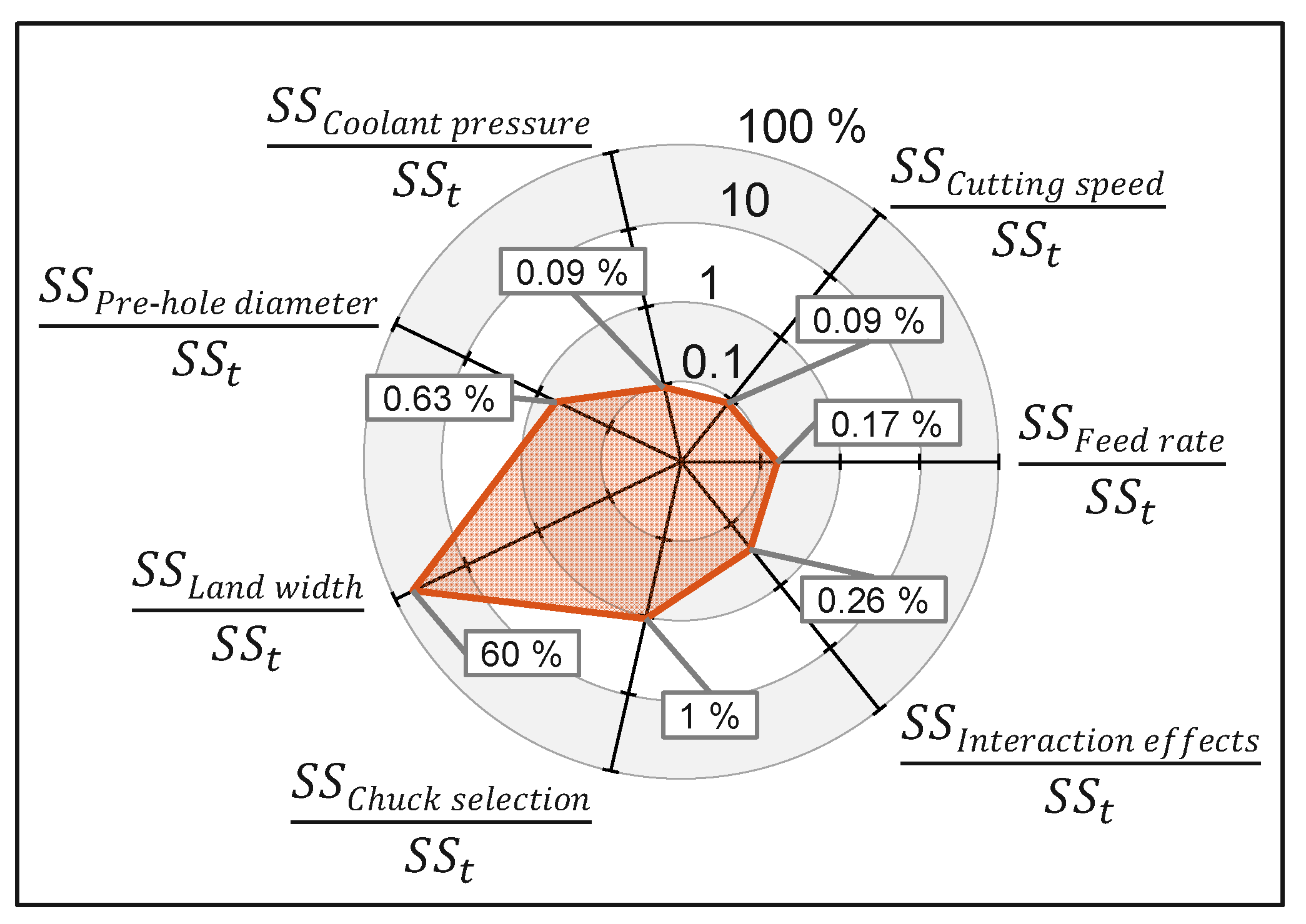
5.2. Summary of the Investigation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Astakhov, V.P. Drills: Science and Technology of Advanced Operations. Manufacturing Design and Technology; Taylor and Francis: Hoboken, NJ, USA, 2014. [Google Scholar]
- Brehl, D.E.; Dow, T.A. Review of vibration-assisted machining. Precis. Eng. 2008, 32, 153–172. [Google Scholar] [CrossRef]
- Tobias, S.A.; Fishwick, W. The Vibrations of Radial-Drilling Machines under Test and Working Conditions. Proc. Inst. Mech. Eng. 1956, 170, 232–264. [Google Scholar] [CrossRef]
- Galloway, D.F. Some Experiments on the Infuence of Various Factors on Drill Performance. Trans. ASME 1957, 79, 191–231. [Google Scholar]
- Katz, Z.; Poustie, A. On the Hole Quality and Drill Wandering Relationship. AMT 2001, 17, 233–237. [Google Scholar] [CrossRef]
- Aized, T.; Amjad, M. Quality improvement of deep-hole drilling process of AISI D2. AMT 2013, 69, 2493–2503. [Google Scholar] [CrossRef]
- Pirtini, M.; Lazoglu, I. Forces and hole quality in drilling. Int. J. Mach. Tools Manuf. 2005, 45, 1271–1281. [Google Scholar] [CrossRef]
- Bayly, P.V.; Lamar, M.T.; Calvert, S.G. Low-Frequency Regenerative Vibration and the Formation of Lobed Holes in Drilling. J. Manuf. Sci. Eng. 2002, 124, 275. [Google Scholar] [CrossRef]
- Roukema, J.C.; Altintas, Y. Generalized modeling of drilling vibrations. Part I: Time domain model of drilling kinematics, dynamics and hole formation. Int. J. Mach. Tools Manuf. 2007, 47, 1455–1473. [Google Scholar] [CrossRef]
- Roukema, J.C.; Altintas, Y. Generalized modeling of drilling vibrations. Part II: Chatter stability in frequency domain. Int. J. Mach. Tools Manuf. 2007, 47, 1474–1485. [Google Scholar] [CrossRef]
- Gupta, K.; Ozdoganlar, O.B.; Kapoor, S.G.; DeVor, R.E. Modeling and Prediction of Hole Profile in Drilling, Part 2: Modeling Hole Profile. J. Eng. Ind. 2003, 125, 14. [Google Scholar] [CrossRef]
- Ahmadi, K.; Savilov, A. Modeling the mechanics and dynamics of arbitrary edge drills. International Int. J. Mach. Tools Manuf. 2015, 89, 208–220. [Google Scholar] [CrossRef]
- Parsian, A.; Magnevall, M.; Beno, T.; Eynian, M. A Mechanistic Approach to Model Cutting Forces in Drilling with Indexable Inserts. In Proceedings of the 6th CIRP International Conference on High Performance Cutting, HPC2014, Berkeley, CA, USA, 23–25 June 2014; Volume 24, pp. 74–79. [Google Scholar]
- Parsian, A.; Magnevall, M.; Eynian, M.; Beno, T. Time domain simulation of chatter vibrations in indexable drills. Int. J. Adv. Manuf. Technol. 2017, 89, 1209–1221. [Google Scholar] [CrossRef]
- Parsian, A. Dynamics of Torsional and Axial Vibrations in Indexable Drills. Ph.D. Thesis, University West, Trollhättan, Sweden, 2015. [Google Scholar]
- Parsian, A.; Magnevall, M.; Beno, T.; Eynian, M. Sound Analysis in Drilling, Frequency and Time Domains. Procedia CIRP 2017, 58, 411–415. [Google Scholar] [CrossRef]
- Ema, S.; Fujii, H.; Marui, E. Chatter Vibration in Drilling. J. Eng. Industry 1988, 110, 309. [Google Scholar] [CrossRef]
- Ema, S.; Fujii, H.; Marui, E. Whirling Vibration in Drilling. Part 3: Vibration Analysis in Drilling Workpiece with a Pilot Hole. J. Eng. Industry 1988, 110, 315. [Google Scholar]
- Ema, S.; Marui, E. Theoretical analysis on chatter vibration in drilling and its suppression. J. Mater. Process. Technol. 2003, 138, 572–578. [Google Scholar] [CrossRef]
- Mehrabadi, I.M.; Nouri, M.; Madoliat, R. Investigating chatter vibration in deep drilling, including process damping and the gyroscopic effect. Int. J. Mach. Tools Manuf. 2009, 49, 939–946. [Google Scholar] [CrossRef]
- Tschannerl, M. Beitrag zur Qualitätssteigerung beim Bohren mit VHM-Spiralbohrern unter Berücksichtigung radialer Schwingungen und Kräfte. In Schriftenreihe des PTW: “Innovation Fertigungstechnik”; Shaker Verlag: Aachen, Germany, 2007. [Google Scholar]
- Ahmadi, K.; Altintas, Y. Stability of lateral, torsional and axial vibrations in drilling. Int. J. Mach. Tools Manuf. 2013, 68, 63–74. [Google Scholar] [CrossRef]
- Biermann, D.; Abrahams, H.; Goeke, S. Optimization of guide pads for the BTA deep hole drilling of high alloyed steels by microfinishing. Prod. Eng. Res. Devel. 2014, 8, 33–40. [Google Scholar] [CrossRef]
- Biermann, D.; Kessler, N.; Upmeier, T.; Stucky, T. Modified DLC-Coated Guide Pads for BTA Deep Hole Drilling Tools. KEM 2010, 438, 195–202. [Google Scholar] [CrossRef]
- Dilley, D.N.; Stephenson, D.A.; Bayly, P.V.; Schaut, A.J. Frequency Shift in Drilling due to Margin Engagement. J. Manuf. Sci. Eng. 2005, 127, 271. [Google Scholar] [CrossRef]
- Ostermann, F. Anwendungstechnologie Aluminium; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. Multivariate Analysemethoden: Eine Anwendungsorientierte Einführung, 14., Überarbeitete und Aktualisierte Auflage; Springer Gabler: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Riedwyl, H.; Ambühl, M. Statistische Auswertungen mit Regressionsprogrammen: Lineare Regression und Verwandtes—Multivariate Statistik—Planung und Auswertung von Versuchen. In Lehr—und Handbücher der Statistik; Reprint 2018; Oldenbourg Wissenschaftsverlag: Berlin, Gemany, 2018. [Google Scholar]
- Nebeling, P.H. Dynamisches Verhalten von Werkzeugaufnahmen: Vergleich gängiger Werkzeugaufnahmen für Schaftwerkzeuge. Werkstatt Betr. 2014, 9, 90–94. [Google Scholar]
- Volz, M.; Abele, E. Spanungsquerschnittsmodell für Bohrprozesse: Auswirkungen von Lateral—Und Torsionsschwingung auf den Spanungsquerschnitt beim Bohren. wt Werkstattstech. 2018, 108, 45–50. [Google Scholar]
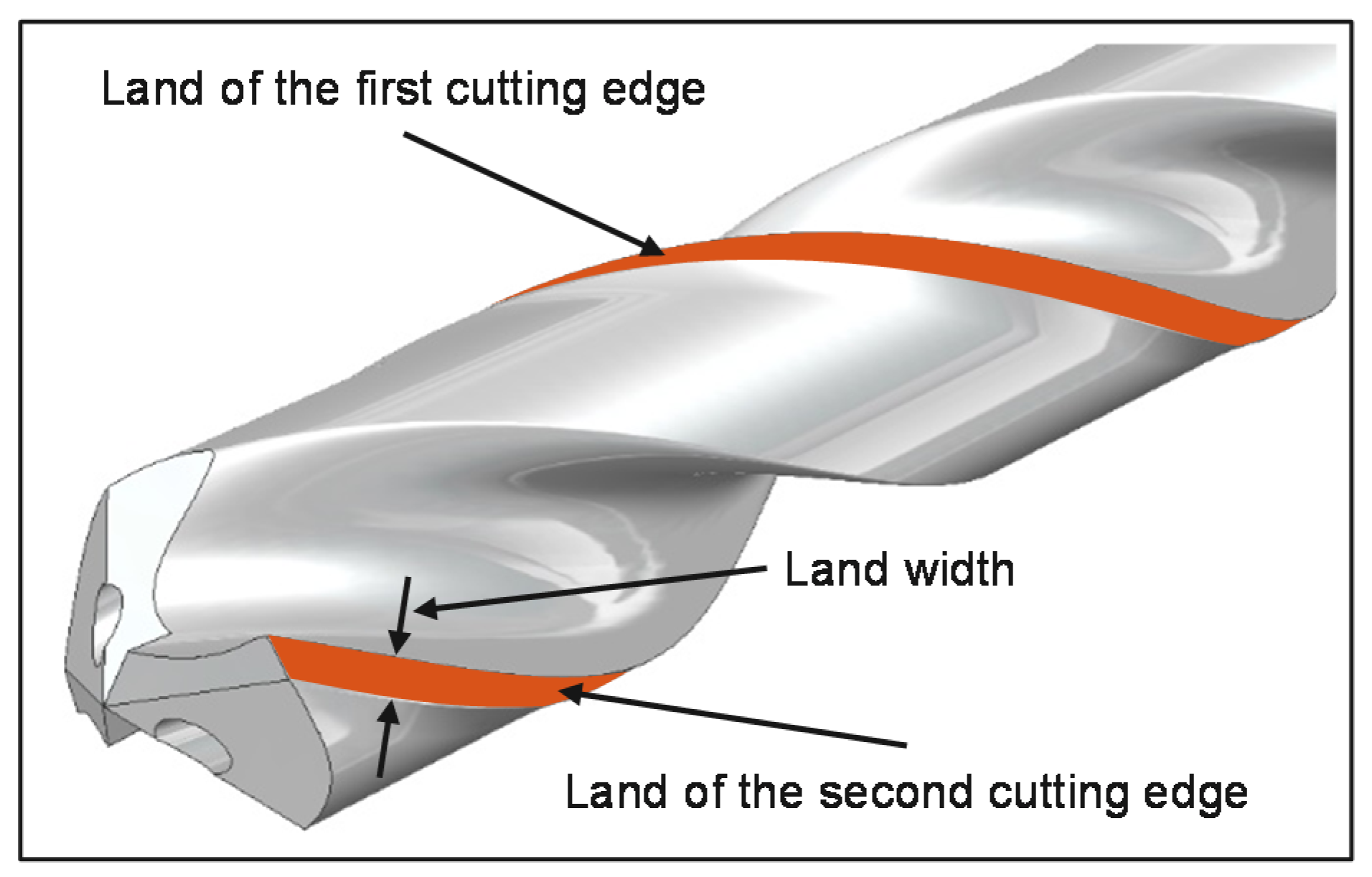
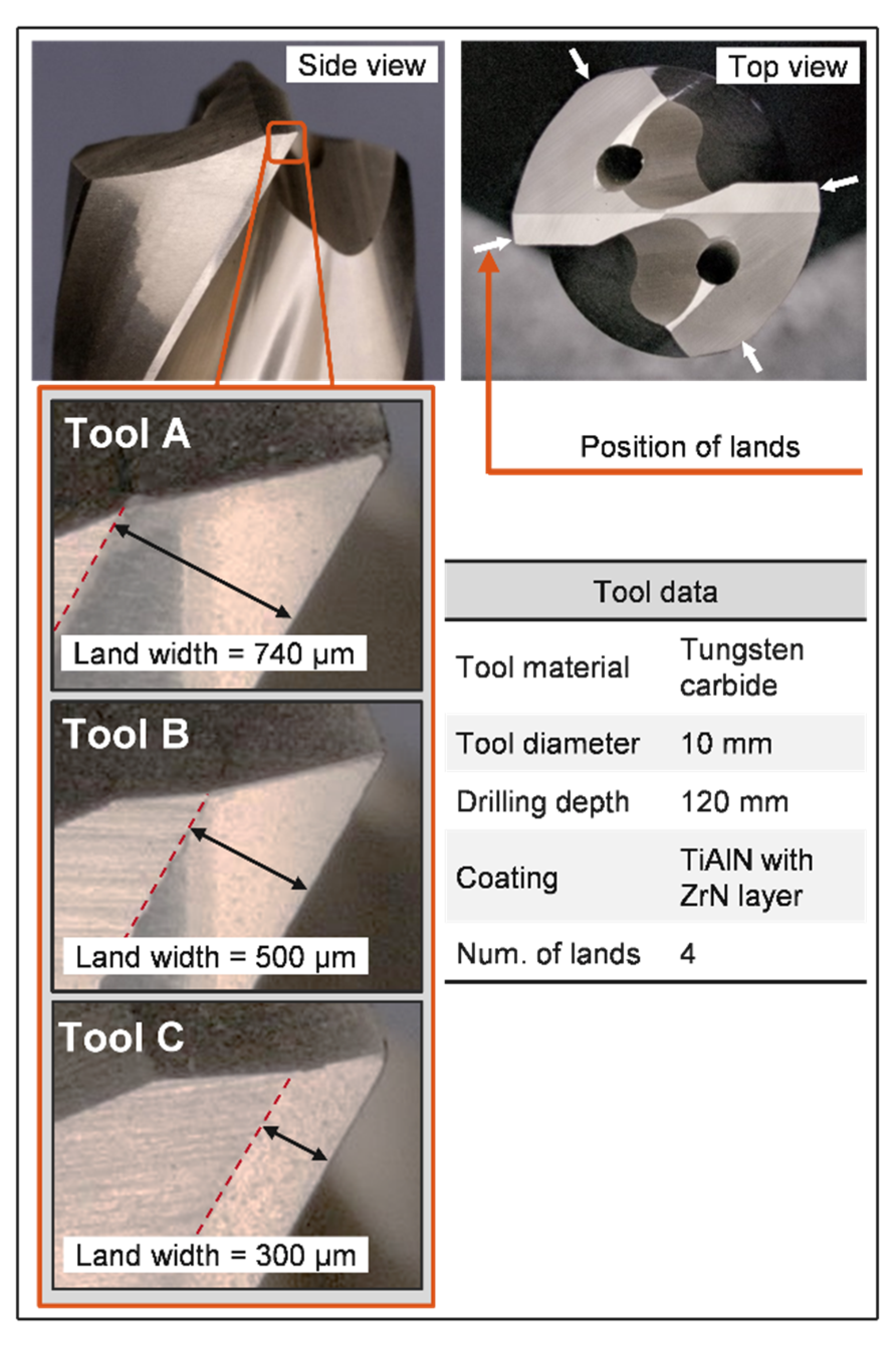
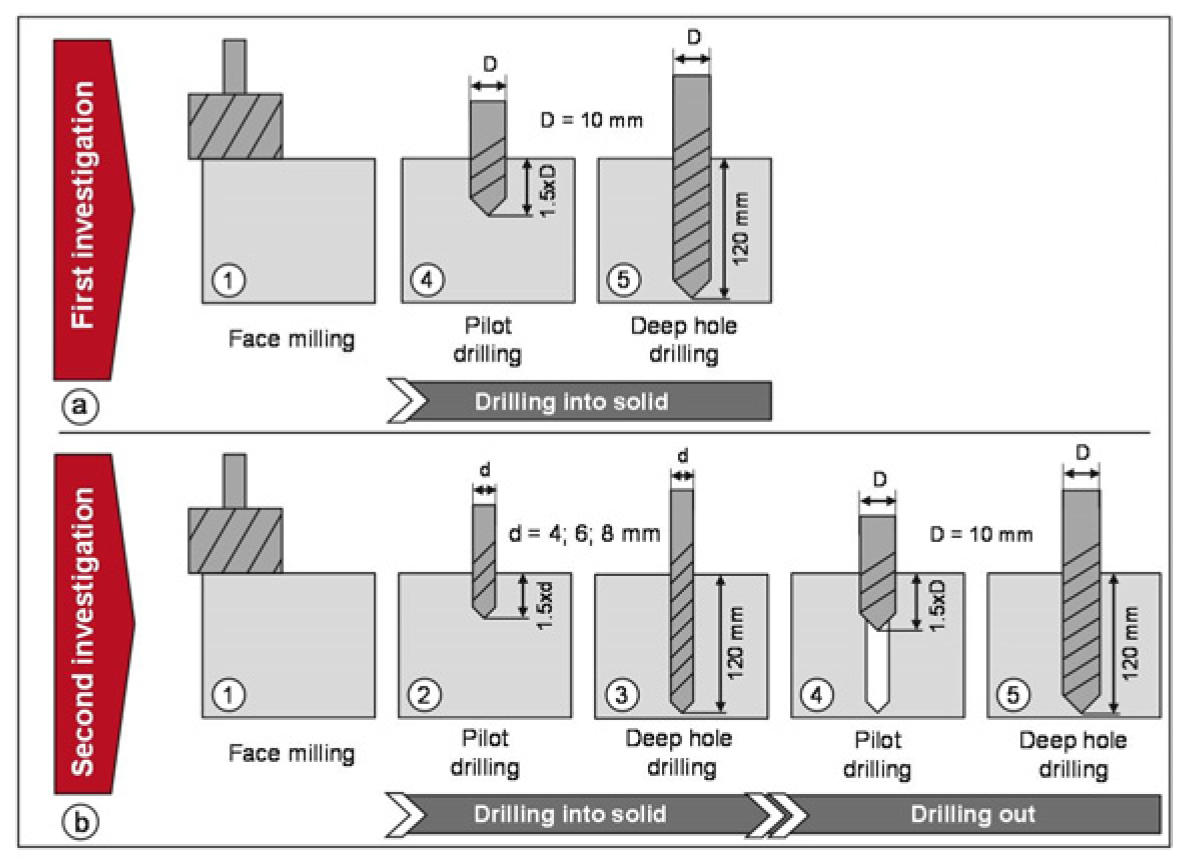
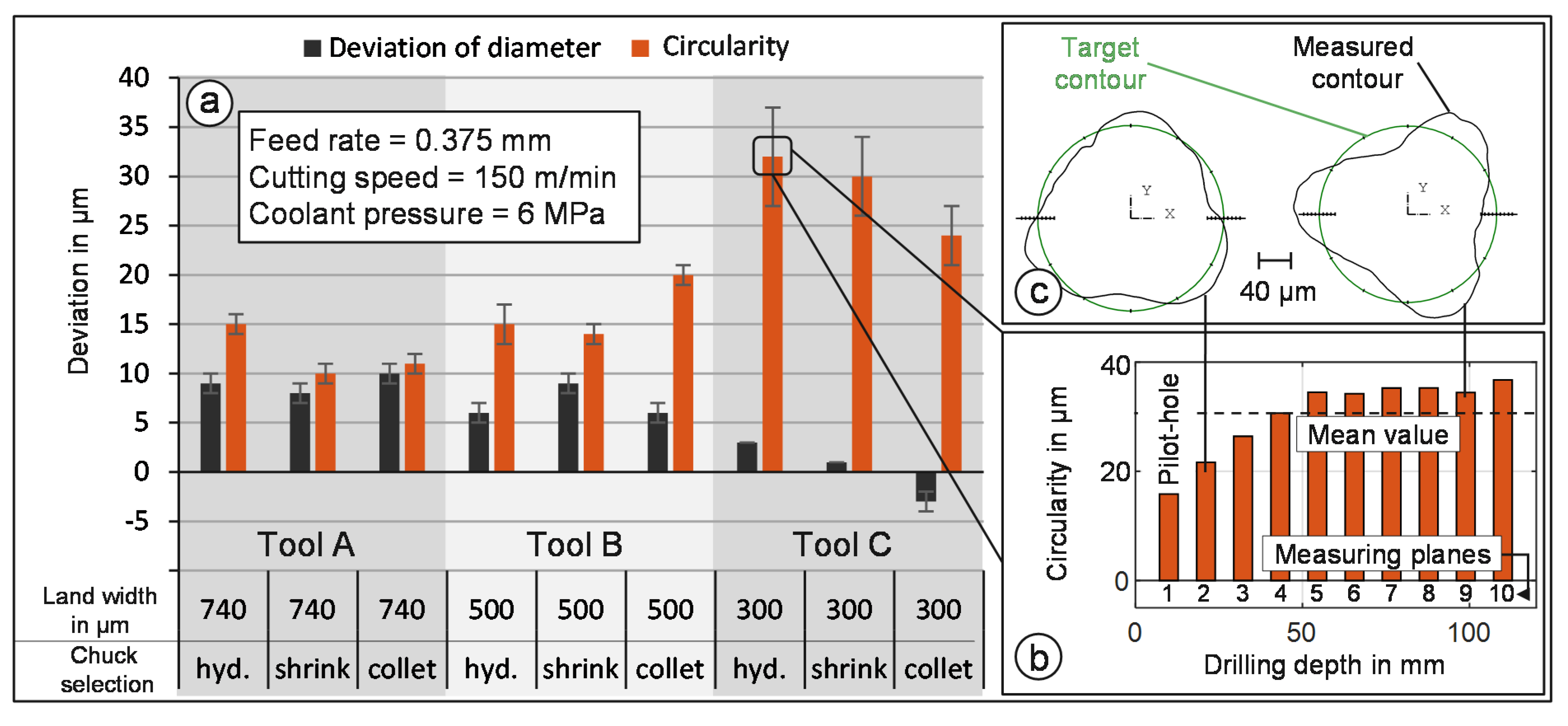
| Parameter | Value | Unit |
|---|---|---|
| Feed rate | 0.25, 0.375, 0.5 | mm/rev. |
| Cutting speed | 120, 150, 180 | m/min |
| Coolant high pressure | 4, 6, 8 | Mpa |
| Pre-hole diameter | 4, 6, 8 | mm |
| Land width | 300, 500, 740 | µm |
| Chuck selection (cantilever lengths) | Hydraulic chuck (80), Collet chuck (80), Shrink chuck (85) | - (mm) |
| SS | df | MS | Femp | p-Value | Ftab(0.95) | Eta2 | |
|---|---|---|---|---|---|---|---|
| Feed rate | 6.6 × 10-4 | 2 | 3.3 × 10-4 | 4.9 × 100 | 7.3 × 10-3 | 3.0 × 100 | |
| Cutting speed | 3.6 × 10-4 | 2 | 1.8 × 10-4 | 2.7 × 100 | 6.9 × 10-3 | 3.0 × 100 | |
| Coolant pressure | 3.4 × 10-4 | 2 | 1.7 × 10-4 | 2.5 × 100 | 7.9 × 10-3 | 3.0 × 100 | |
| Pre-hole | 2.4 × 10-3 | 2 | 1.2 × 10-3 | 1.8 × 101 | 1.5 × 10-8 | 3.0 × 100 | |
| Land width | 2.3 × 10-1 | 2 | 1.2 × 10-1 | 1.7 × 103 | < × 10-20 | 3.0 × 100 | |
| Chuck selection | 4.0 × 10-3 | 2 | 2.0 × 10-3 | 3.0 × 101 | 1.3 × 10-13 | 3.0 × 100 | |
| Interaction effects | 1.0 × 10-3 | ||||||
| Error | 1.5 × 10-1 | 2174 | 6.7 × 10-5 | 1 | |||
| Total | 3.8 × 10-1 | 2186 | 1.8 × 10-4 | 0.62 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volz, M.; Abele, E.; Weigold, M. Lateral Vibrations in Deep Hole Drilling Due to Land Width Variation. J. Manuf. Mater. Process. 2020, 4, 28. https://doi.org/10.3390/jmmp4020028
Volz M, Abele E, Weigold M. Lateral Vibrations in Deep Hole Drilling Due to Land Width Variation. Journal of Manufacturing and Materials Processing. 2020; 4(2):28. https://doi.org/10.3390/jmmp4020028
Chicago/Turabian StyleVolz, Marcel, Eberhard Abele, and Matthias Weigold. 2020. "Lateral Vibrations in Deep Hole Drilling Due to Land Width Variation" Journal of Manufacturing and Materials Processing 4, no. 2: 28. https://doi.org/10.3390/jmmp4020028
APA StyleVolz, M., Abele, E., & Weigold, M. (2020). Lateral Vibrations in Deep Hole Drilling Due to Land Width Variation. Journal of Manufacturing and Materials Processing, 4(2), 28. https://doi.org/10.3390/jmmp4020028




