Correlations between Thermal Loads during Grind-Hardening and Material Modifications Using the Concept of Process Signatures
Abstract
:1. Introduction
2. Experimental Setup and Methods
3. Results and Discussion
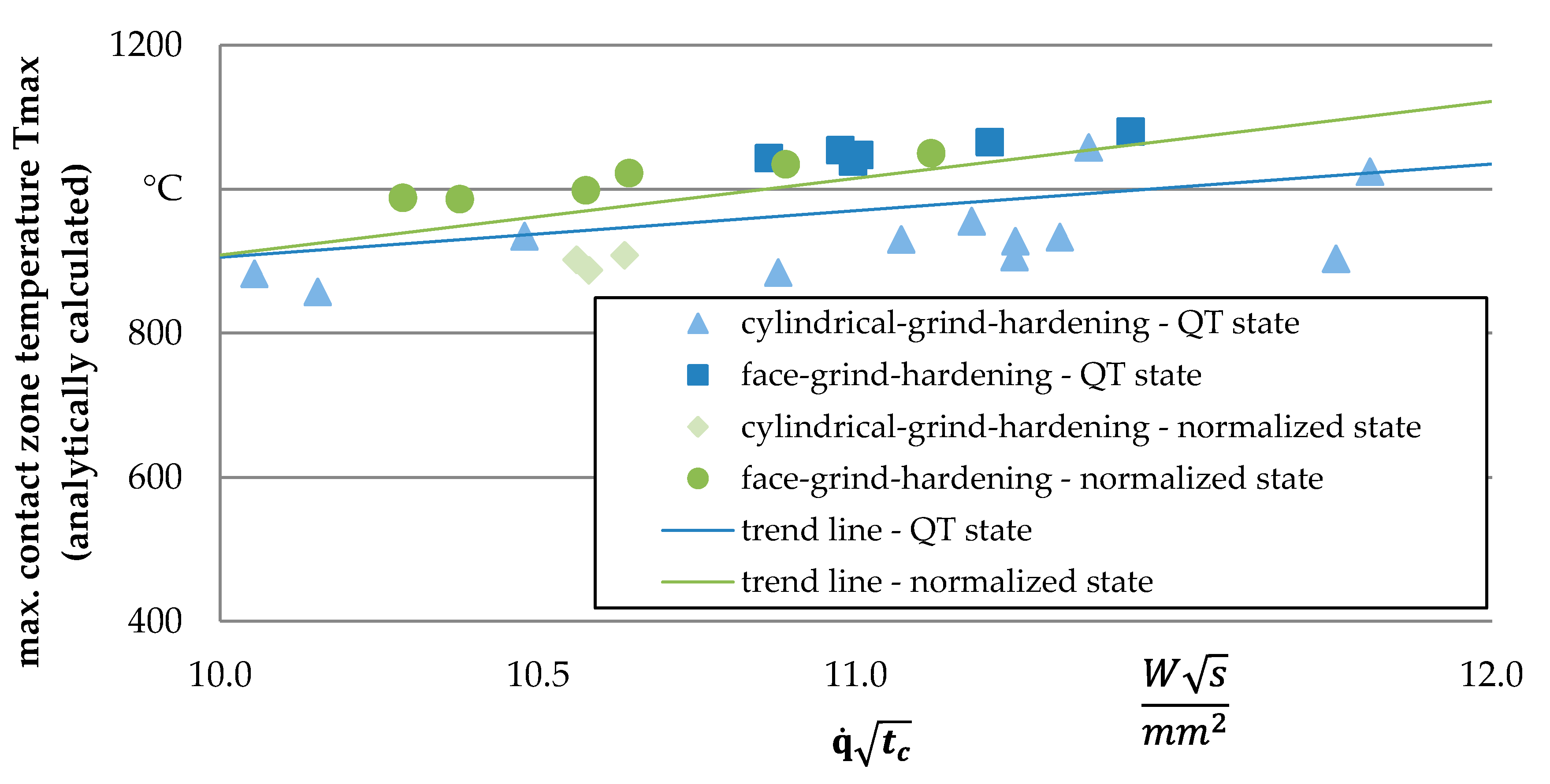
3.1. Correlation of Internal Material Loads with Process Quantities
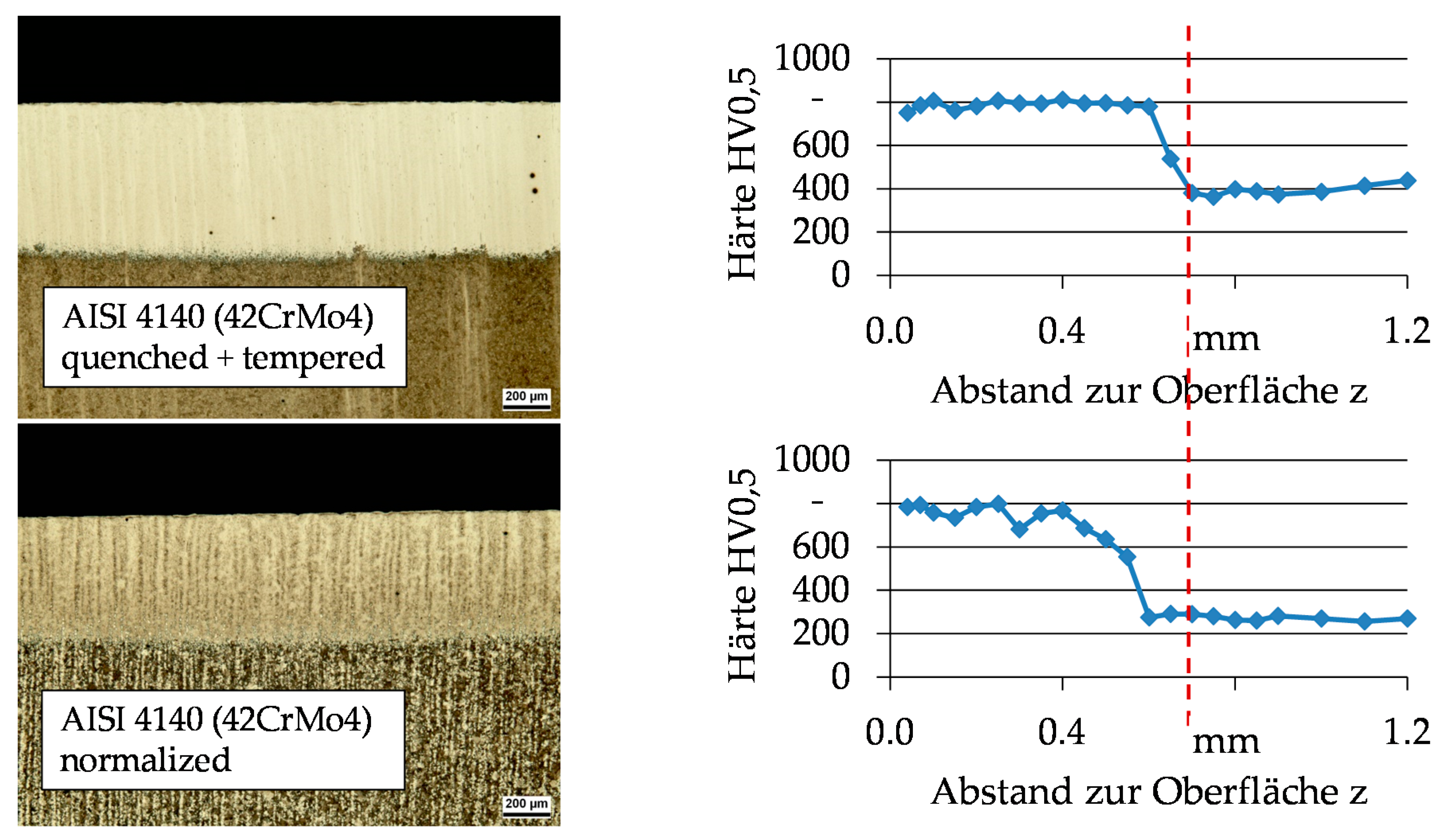
3.2. Correlation of Internal Material Loads with Material Modifications (the Concept of Process Signatures)
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
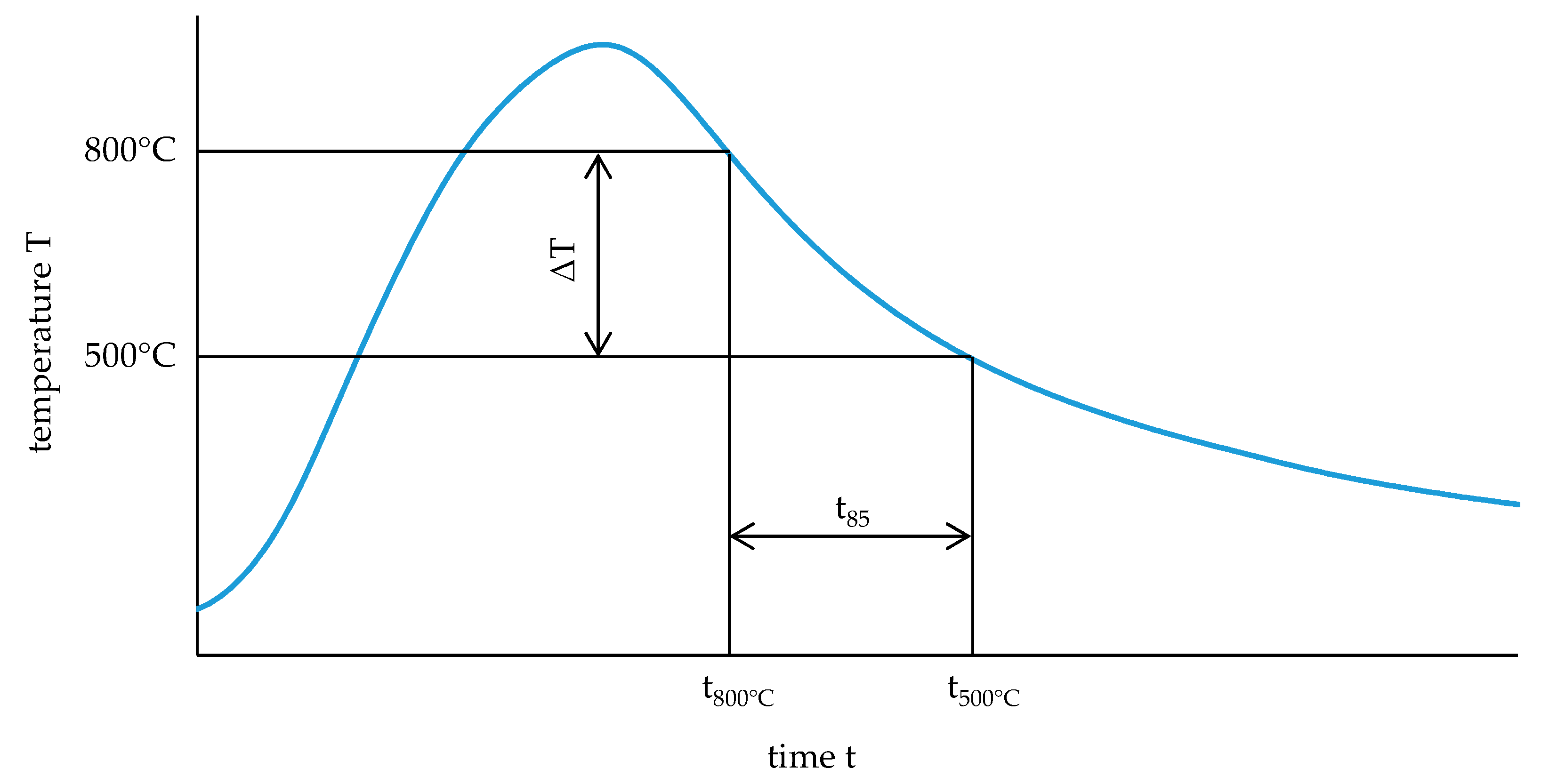
Nomenclature
| ae | depth of cut (mm) |
| aed | depth of cut during dressing (µm) |
| α | specific heat capacity (J/(kg∙K)) |
| deq | equivalent grinding wheel diameter (mm) |
| ds | grinding wheel diameter (mm) |
| dw | workpiece diameter (mm) |
| ΔHV | hardness change at the surface (N/A) |
| kw | heat partition fraction to the workpiece (N/A) |
| L | length of the heat source (mm) |
| lg | geometric contact length in grinding (mm) |
| λ | thermal conductivity (W/(m∙K)) |
| ρ | density (kg/m3) |
| Pc′′ | specific grinding power (W/mm2) |
| heat flux to the workpiece (W/mm2) | |
| specific material removal rate (mm3/(mm∙s)) | |
| SHD | surface hardening depth (mm) |
| t85 | quenching time from 800 °C–500 °C (s) |
| contact time (s) | |
| Tmax | Maximum temperature (°C) |
| (dT/dx)max | Maximum temperature gradient (K/mm) |
| Ud | overlapping ratio in dressing (N/A) |
| V | velocity of the heat source (mm/min) |
| tangential feed speed (mm/min) | |
| grinding wheel speed (m/s) |
Appendix A
References
- Jawahir, I.S.; Brinksmeier, E.; M’Saoubi, R.; Aspinwall, D.K.; Outeiro, J.C.; Meyer, D.; Umbrello, D.; Jayal, A.D. Surface integrity in material removal processes: Recent advances. CIRP Ann. Manuf. Technol. 2011, 60, 603–626. [Google Scholar] [CrossRef]
- Stenberg, N.; Proudian, J. Numerical Modelling of Turning to Find Residual Stresses. Procedia CIRP 2013, 8, 258–264. [Google Scholar] [CrossRef]
- Dehmani, H.; Salvatore, F.; Hamdi, H. Numerical Study of Residual Stresses Induced by Multi-steps Orthogonal Cutting. Procedia CIRP 2013, 8, 299–304. [Google Scholar] [CrossRef]
- Budak, E.; Ozlu, E. Analytical Modeling of Chatter Stability in Turning and Boring Operations. CIRP Ann. Manuf. Technol. 2007, 56, 401–404. [Google Scholar] [CrossRef]
- Lazoglu, I.; Ulutan, D.; Alaca, B.E.; Engin, S. An enhanced analytical model for residual stress prediction in machining. CIRP Ann. Manuf. Technol. 2008, 57, 81–84. [Google Scholar] [CrossRef]
- Brockhoff, T. Grind-Hardening: A Comprehensive View. CIRP Ann. Manuf. Technol. 1999, 48, 255–260. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Minke, E.; Wilke, T. Investigations on Surface Layer Impact and Grinding Wheel Performance for Industrial Grind-Hardening Applications. Prod. Eng. 2005, 12, 35–40. [Google Scholar]
- Chryssolouris, G.; Tsirbas, K.; Salonitis, K. An Analytical, Numerical, and Experimental Approach to Grind Hardening. SME J. Manuf. Processes 2005, 7, 1–9. [Google Scholar] [CrossRef]
- Wilke, T. Energieumsetzung und Gefügebeeinflussung beim Schleifhärten. Ph.D. Thesis, University of Bremen, Bremen, Germany, 2008. [Google Scholar]
- Zäh, M.F.; Brinksmeier, E.; Heinzel, C.; Huntemann, J.W.; Föckerer, T. Experimental and numerical identification of process parameters of grind-hardening and resulting part distortions. Prod. Eng. 2009, 3, 271–279. [Google Scholar] [CrossRef]
- Föckerer, T.; Kolkwitz, B.; Heinzel, C.; Zäh, M.F. Experimental and numerical analysis of transient behavior during grind-hardening of AISI 52100. Prod. Eng. 2012, 6, 559–568. [Google Scholar] [CrossRef]
- Salonitis, K.; Stavropoulos, P.; Stournaras, A.; Chryssolouris, G. Finite Element Modeling of Grind Hardening Process. In Proceedings of the 10th CIRP International Workshop on Modeling of Machining Operations, Reggio Calabria, Italy, 27–28 August 2007; pp. 117–123. [Google Scholar]
- Fricker, D.C.; Pearce, T.R.A.; Harrison, A.J.L. Predicting the occurrence of grind hardening in cubic boron nitride grinding of crankshaft steel. Proc. Inst. Mech. Eng. 2004, 218, 1339–1356. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Klocke, F.; Lucca, D.A.; Sölter, J.; Meyer, D. Process signatures—A new approach to solve the inverse surface integrity problem in machining processes. Procedia CIRP 2014, 13, 429–434. [Google Scholar] [CrossRef]
- Kuschel, S.; Sölter, J.; Brinksmeier, E. Analysing internal material loads in manufacturing processes. Adv. Mater. Res. 2014, 1018, 83–90. [Google Scholar] [CrossRef]
- Frerichs, F.; Sölter, J.; Lübben, T.; Brinksmeier, E.; Zoch, H.-W. A simulation based development of Process Signatures for manufacturing processes with thermal loads. Procedia CIRP 2016, 45, 327–330. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process: Part I—Temperature rise distribution due to shear plane heat source. Int. J. Mech. Sci. 2000, 42, 1715–1752. [Google Scholar] [CrossRef]
- Jaeger, J.C. Moving sources of heat and the temperature at sliding contacts. J. Proc. R. Soc. N. S. W. 1942, 76, 203–224. [Google Scholar]
- Malkin, S.; Guo, C. Thermal Analysis in Grinding. CIRP Ann. Manuf. Technol. 2007, 56, 760–782. [Google Scholar] [CrossRef]
- Kuschel, S.; Kolkwitz, B.; Sölter, J.; Brinksmeier, E.; Heinzel, C. Experimental and Numerical Analysis of Residual Stress Change Caused by Thermal Loads During Grinding. Procedia CIRP 2016, 45, 51–54. [Google Scholar] [CrossRef]
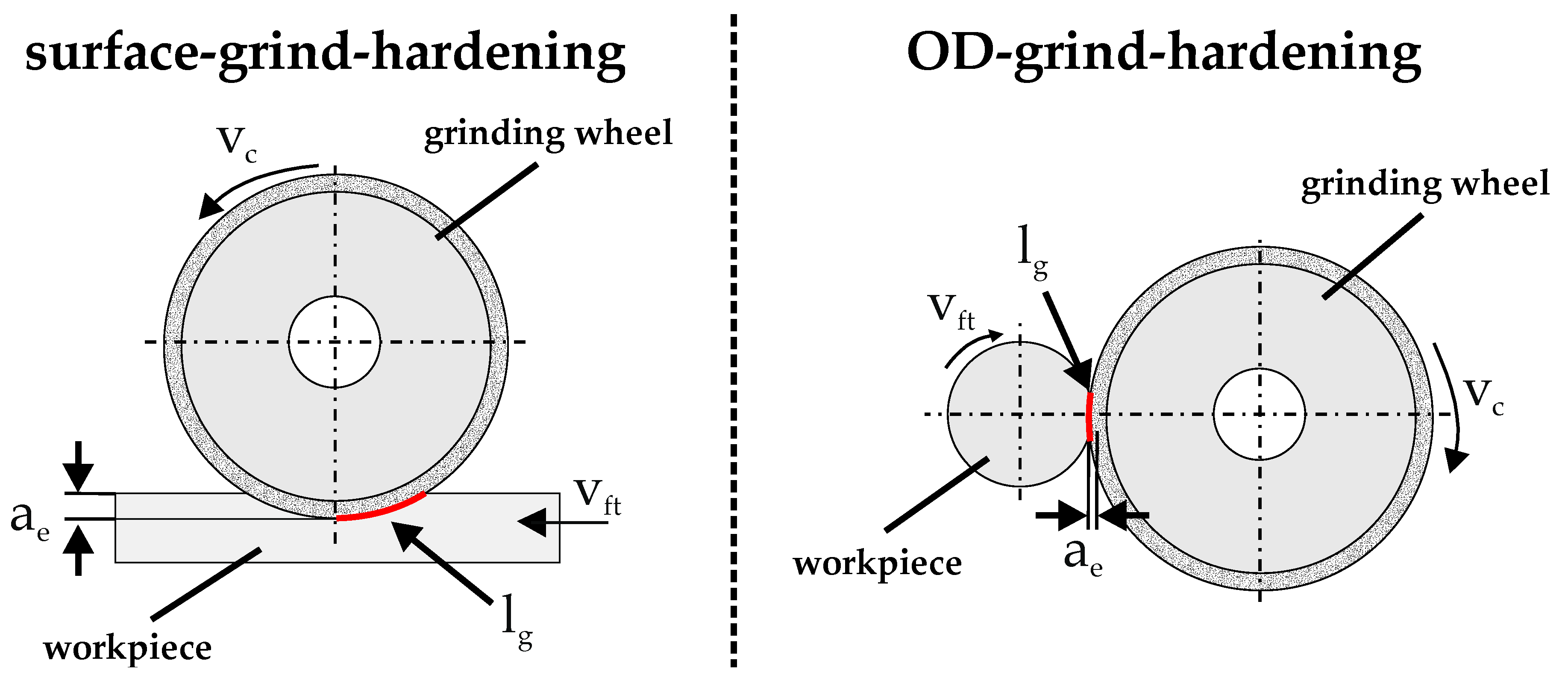
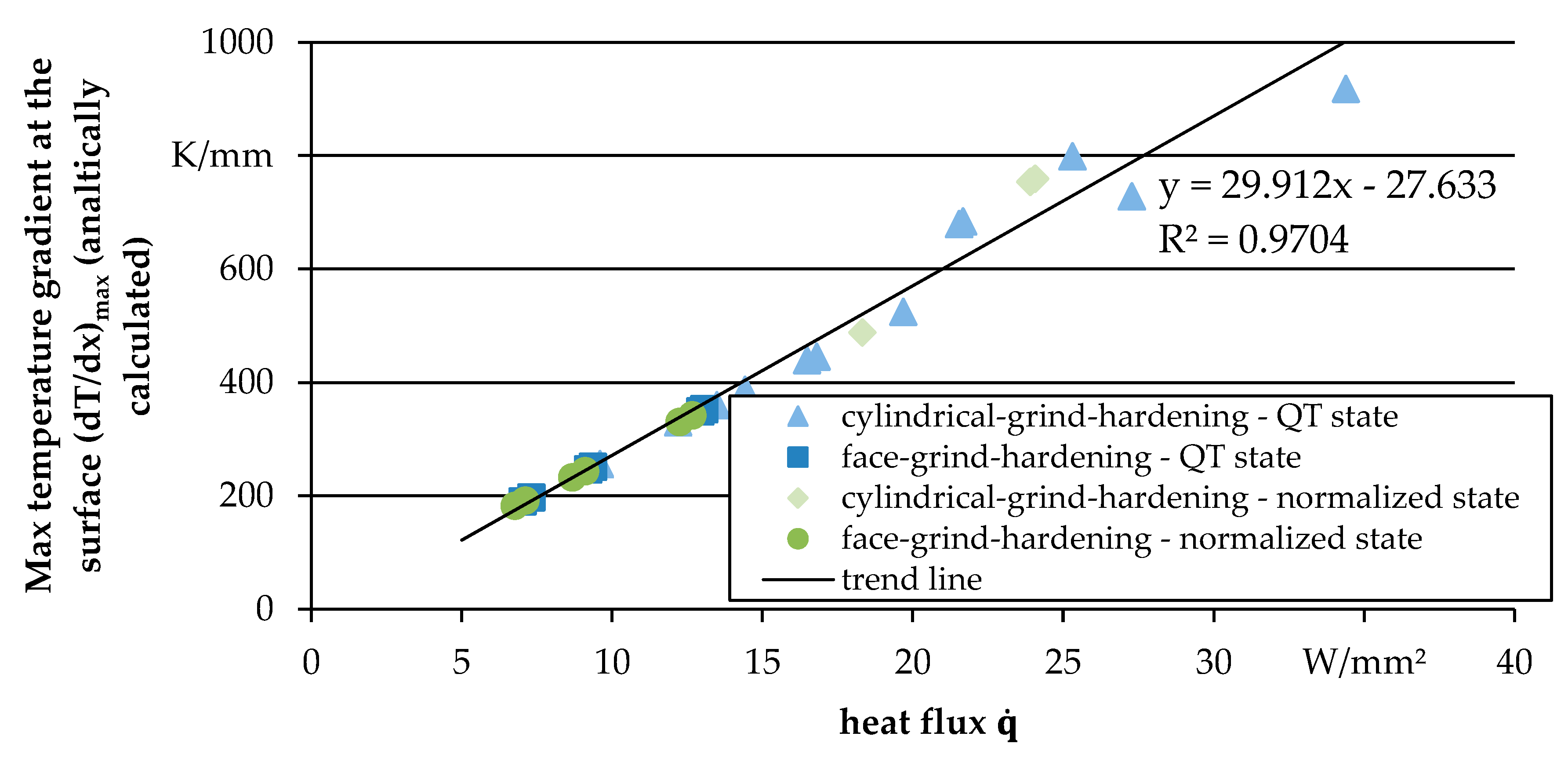
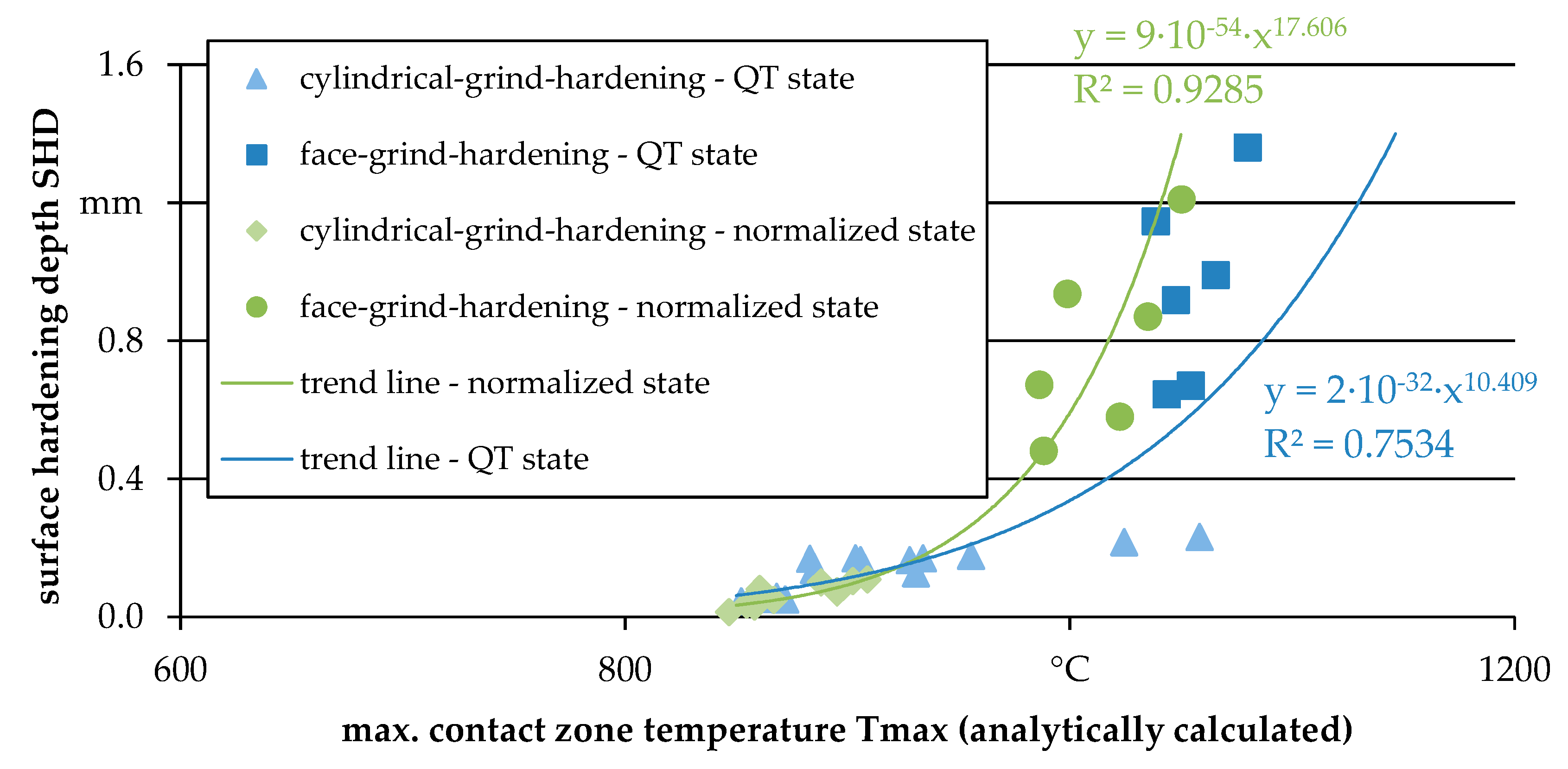
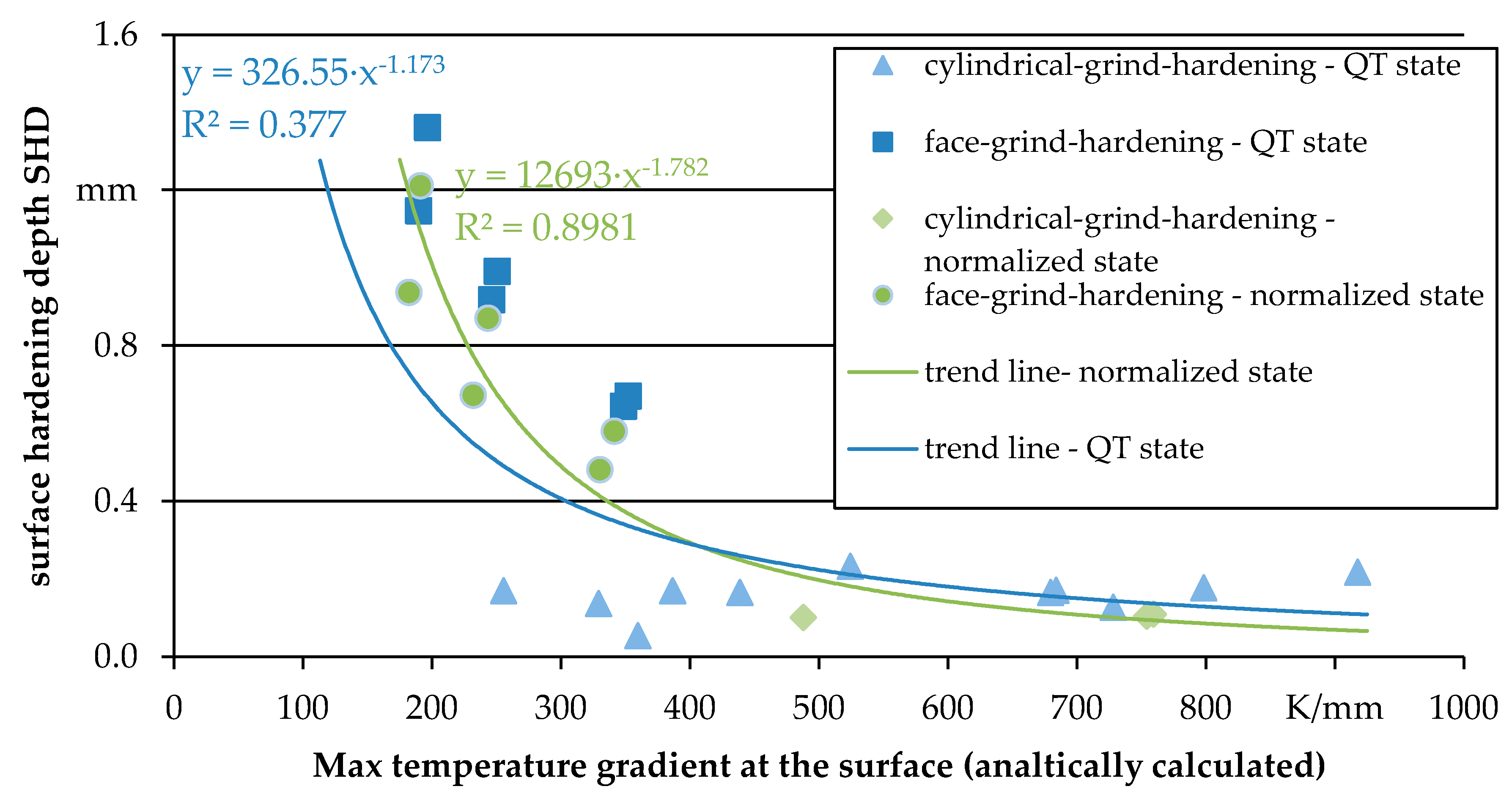
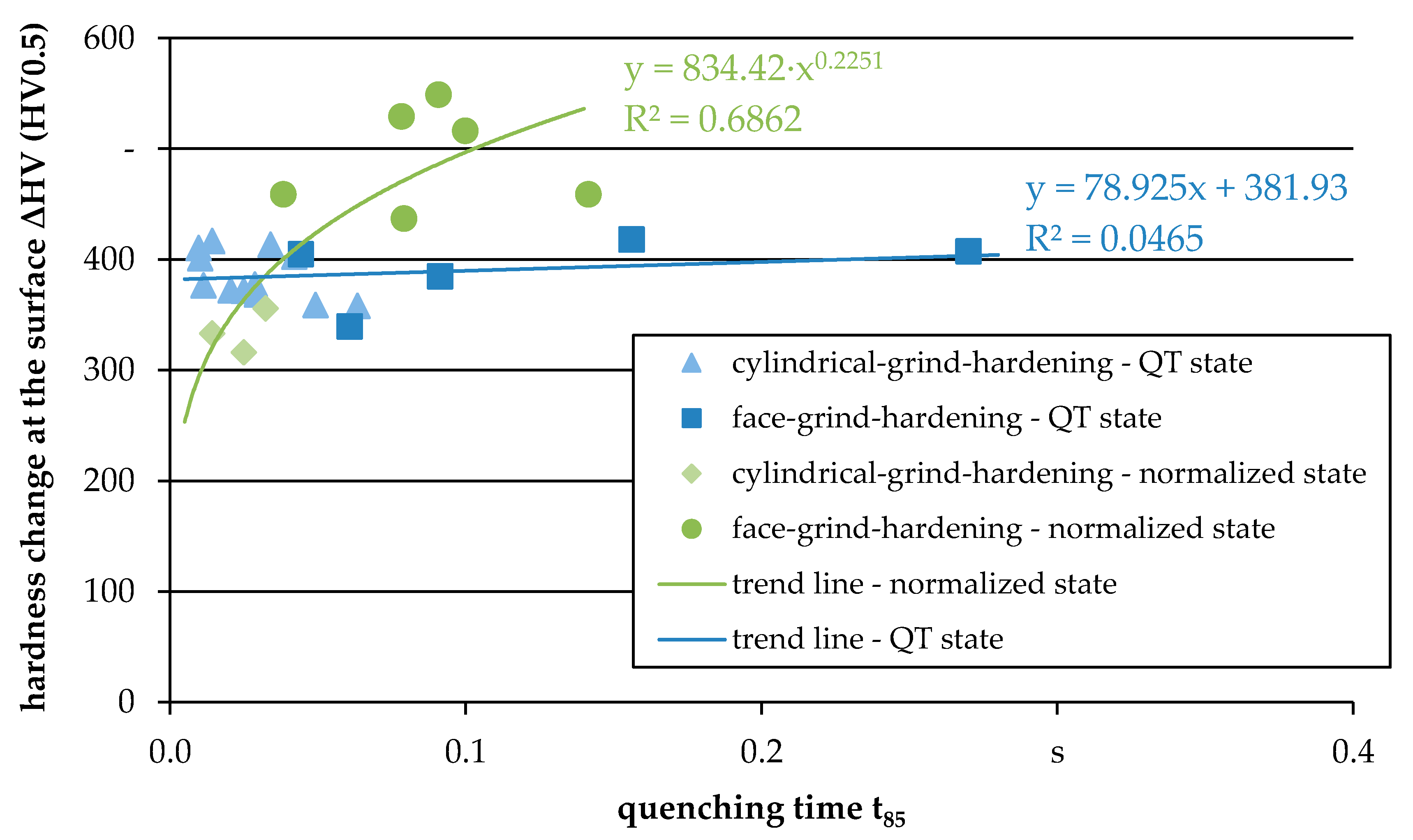
| Process | Heat Treatment | ae (mm) | vft (mm/min) | Q’w {mm³/(mm∙s)} | tc (s) | ds (mm) | deq (mm) | lg (mm) |
|---|---|---|---|---|---|---|---|---|
| surface-grind-hardening | QT/normalized | 0.5 | 1200 | 10.0 | 0.71 | 400 | 400 | 14.1 |
| QT/normalized | 0.7 | 700 | 8.2 | 1.43 | 400 | 400 | 16.7 | |
| QT/normalized | 1 | 490 | 8.2 | 2.45 | 400 | 400 | 20.0 | |
| OD-grind-hardening | QT | 0.5 | 313 | 2.6 | 0.80 | 400 | 31.8 | 4.2 |
| QT | 0.5 | 439 | 3.7 | 0.57 | 400 | 31.8 | 4.2 | |
| QT | 0.5 | 775 | 6.5 | 0.39 | 400 | 44.8 | 5.0 | |
| QT | 0.5 | 794 | 6.6 | 0.16 | 400 | 9.3 | 2.2 | |
| normalized * | 0.5 | 794 | 6.6 | 0.16 | 400 | 9.3 | 2.2 | |
| QT | 0.5 | 1110 | 9.3 | 0.12 | 400 | 9.3 | 2.2 | |
| normalized * | 0.5 | 1110 | 9.3 | 0.12 | 400 | 9.3 | 2.2 | |
| QT * | 0.7 | 277 | 3.2 | 1.29 | 400 | 44.8 | 5.0 | |
| QT * | 0.7 | 314 | 3.7 | 0.94 | 400 | 31.8 | 4.9 | |
| QT * | 0.7 | 398 | 4.6 | 0.39 | 400 | 9.3 | 2.6 | |
| QT | 0.7 | 567 | 6.6 | 0.27 | 400 | 9.3 | 2.6 | |
| normalized * | 0.7 | 567 | 6.6 | 0.27 | 400 | 9.3 | 2.6 | |
| QT/normalized | 0.7 | 793 | 9.3 | 0.20 | 400 | 9.3 | 2.6 | |
| QT * | 1 | 199 | 3.3 | 0.93 | 400 | 9.3 | 3.1 | |
| QT | 1 | 278 | 4.6 | 0.66 | 400 | 9.3 | 3.1 | |
| normalized * | 1 | 278 | 4.6 | 0.66 | 400 | 9.3 | 3.1 | |
| normalized * | 1 | 313 | 5.2 | 1.13 | 400 | 31.8 | 5.9 | |
| QT | 1 | 388 | 6.5 | 1.10 | 400 | 44.8 | 7.1 | |
| QT | 1 | 397 | 6.6 | 0.47 | 400 | 9.3 | 3.1 | |
| normalized * | 1 | 397 | 6.6 | 0.47 | 400 | 9.3 | 3.1 | |
| QT/normalized | 1 | 555 | 9.3 | 0.33 | 400 | 9.3 | 3.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolkwitz, B.; Kohls, E.; Heinzel, C.; Brinksmeier, E. Correlations between Thermal Loads during Grind-Hardening and Material Modifications Using the Concept of Process Signatures. J. Manuf. Mater. Process. 2018, 2, 20. https://doi.org/10.3390/jmmp2010020
Kolkwitz B, Kohls E, Heinzel C, Brinksmeier E. Correlations between Thermal Loads during Grind-Hardening and Material Modifications Using the Concept of Process Signatures. Journal of Manufacturing and Materials Processing. 2018; 2(1):20. https://doi.org/10.3390/jmmp2010020
Chicago/Turabian StyleKolkwitz, Benjamin, Ewald Kohls, Carsten Heinzel, and Ekkard Brinksmeier. 2018. "Correlations between Thermal Loads during Grind-Hardening and Material Modifications Using the Concept of Process Signatures" Journal of Manufacturing and Materials Processing 2, no. 1: 20. https://doi.org/10.3390/jmmp2010020
APA StyleKolkwitz, B., Kohls, E., Heinzel, C., & Brinksmeier, E. (2018). Correlations between Thermal Loads during Grind-Hardening and Material Modifications Using the Concept of Process Signatures. Journal of Manufacturing and Materials Processing, 2(1), 20. https://doi.org/10.3390/jmmp2010020






