Random and Systematic Errors Share in Total Error of Probes for CNC Machine Tools
Abstract
1. Introduction
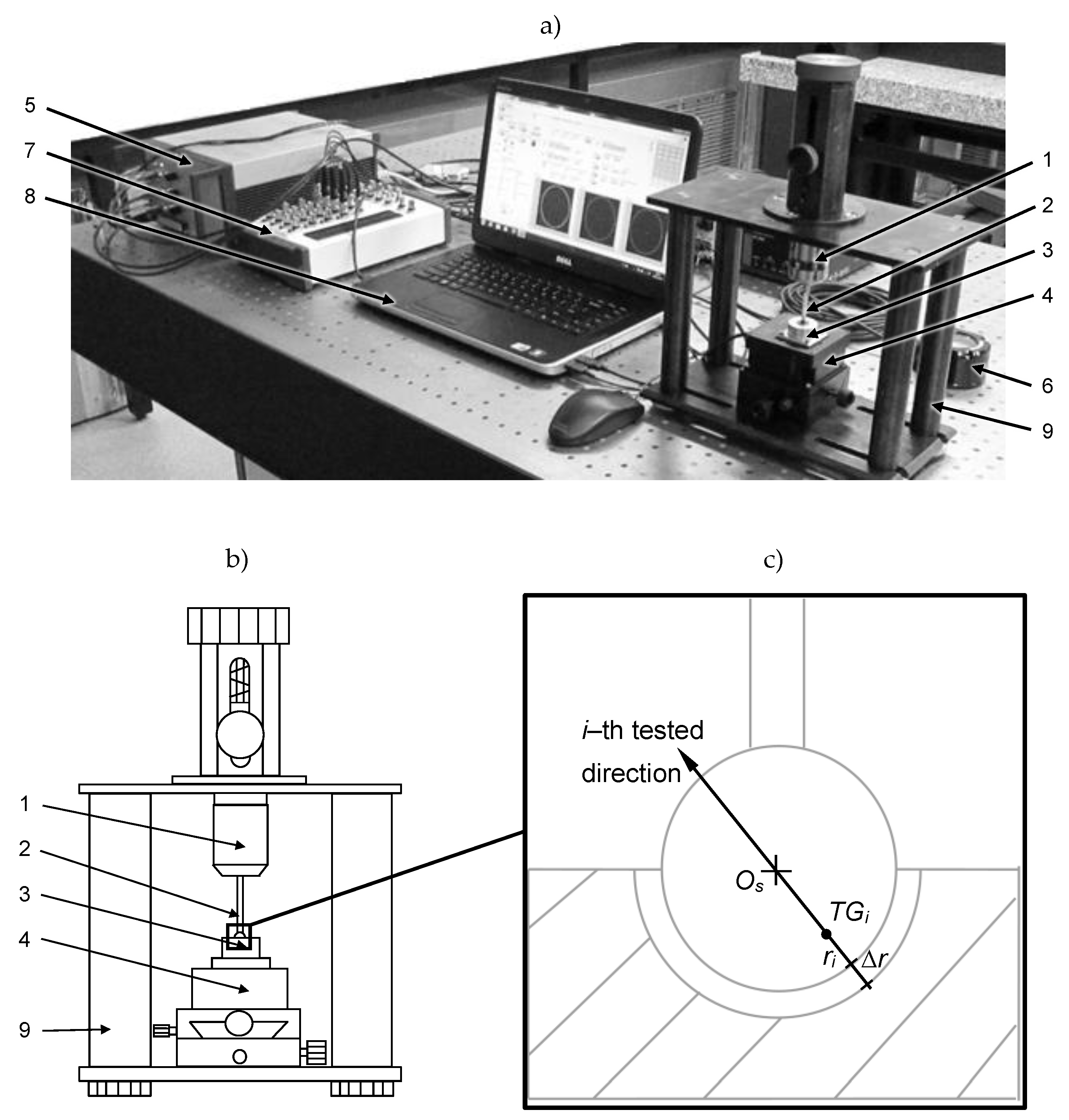
2. Materials and Methods
3. Results
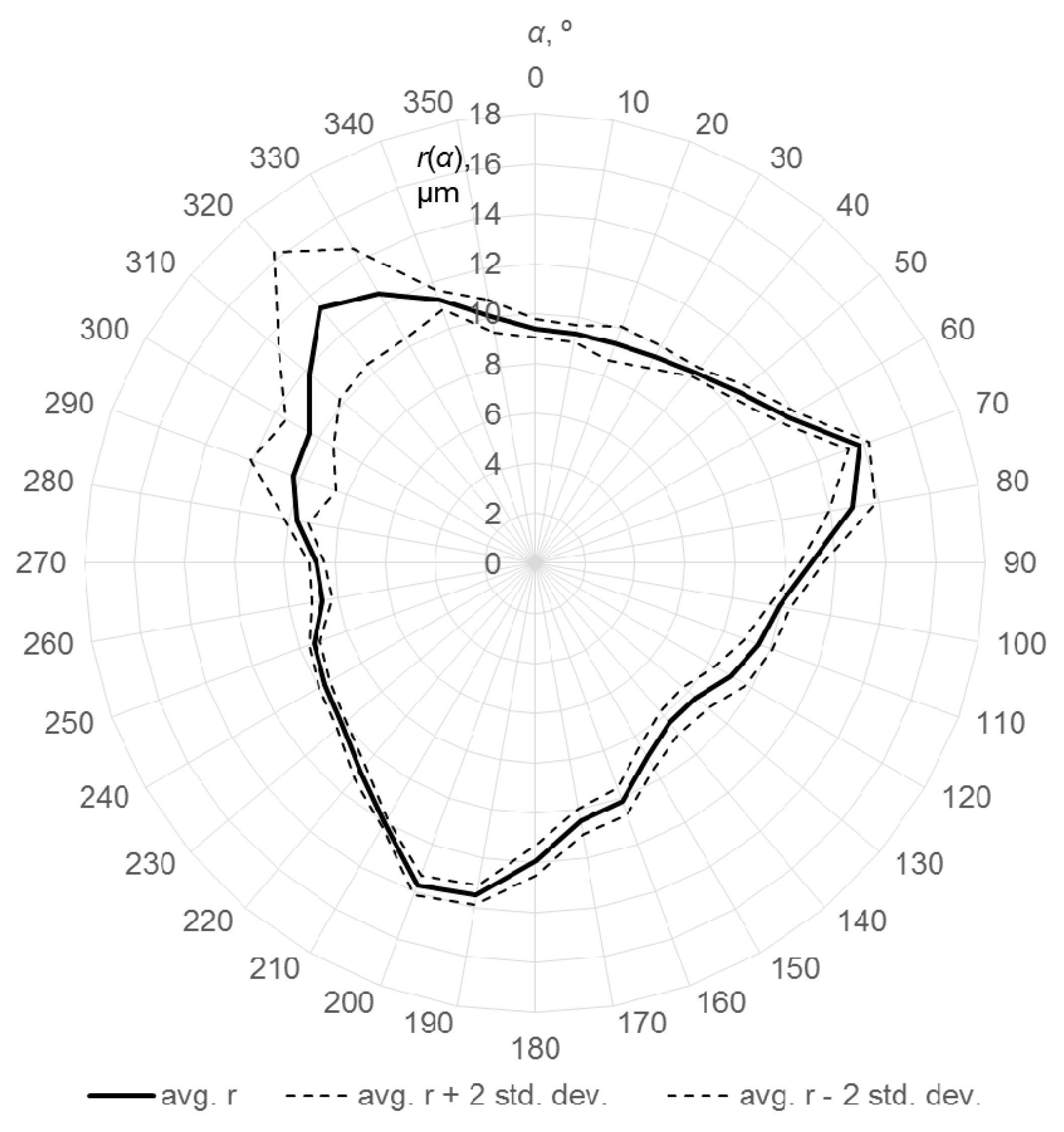
3.1. Tests in the Laboratory
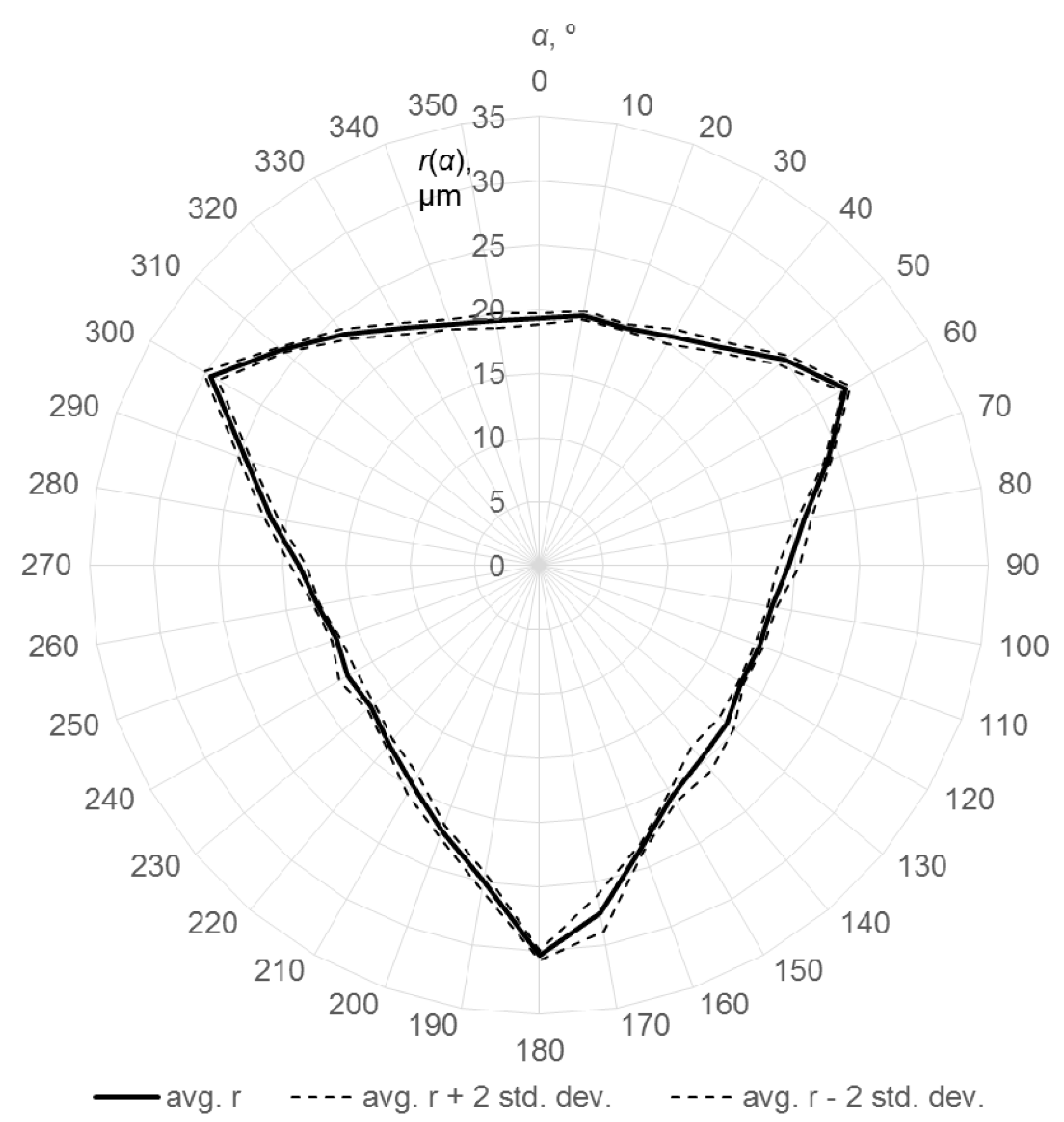
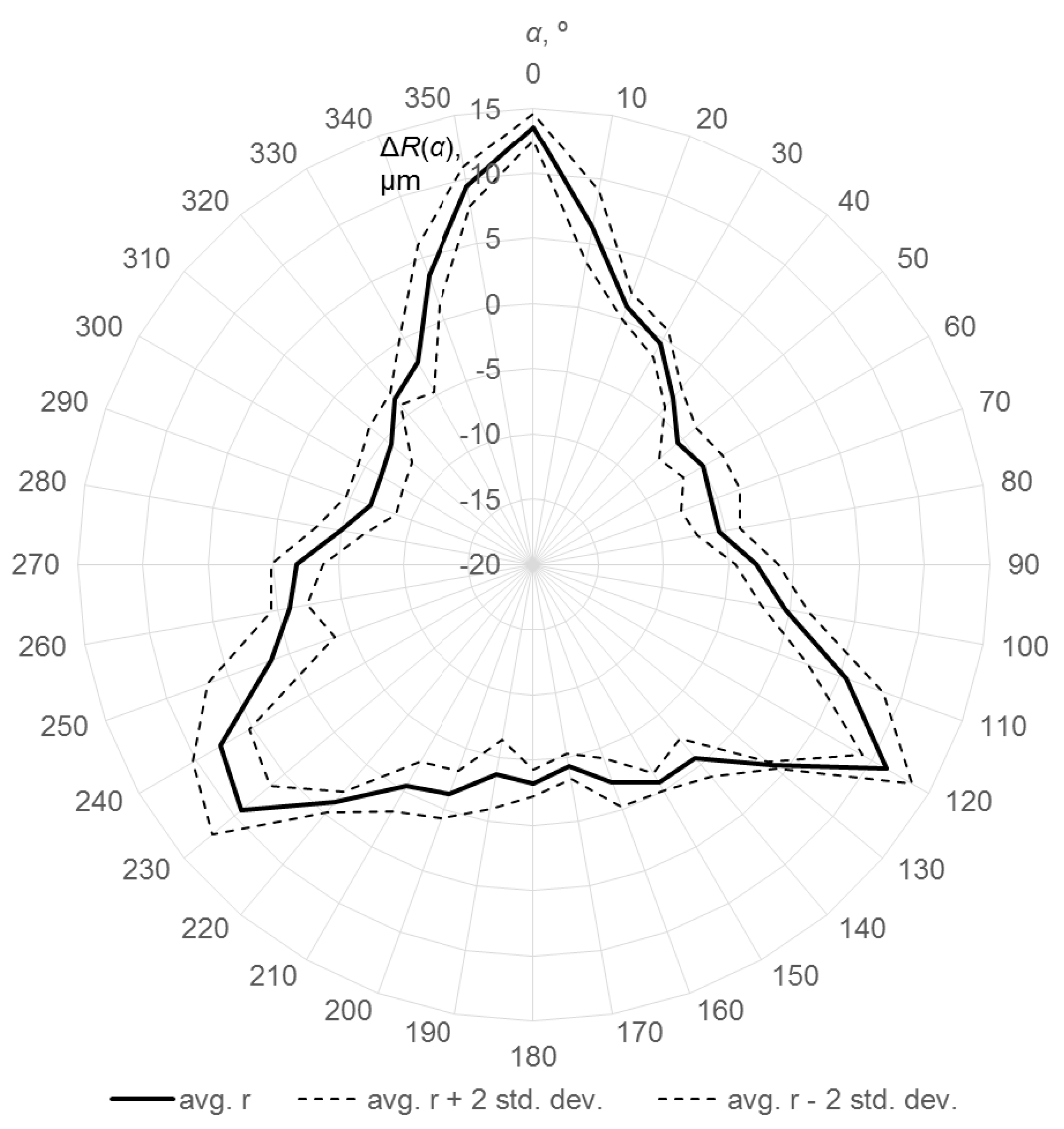
3.2. Tests on the Machine Tool
- the measured radial distance in a given point, for a given direction i; and
- the radius of the best-fitted circle
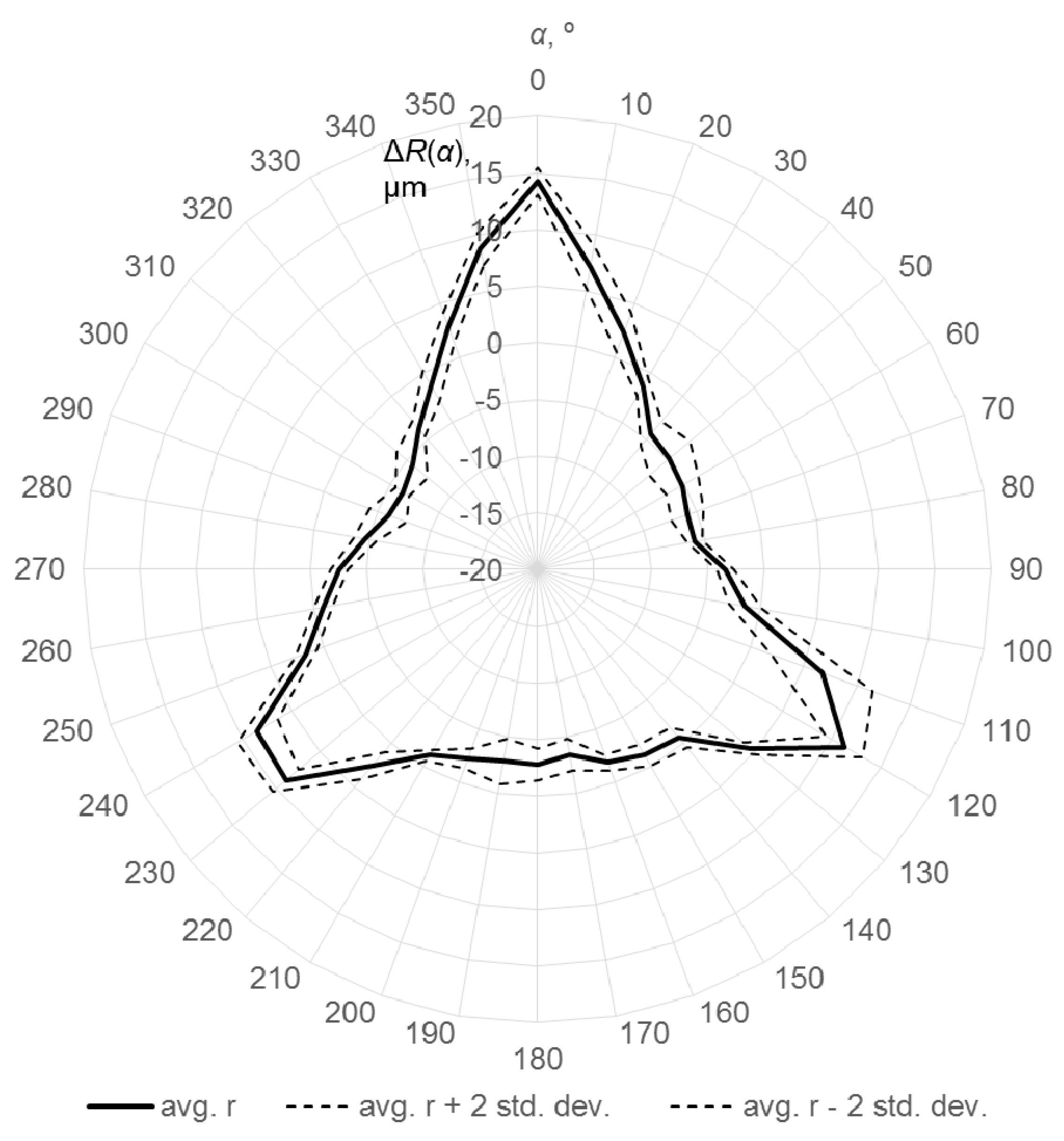
4. Discussion
5. Conclusions
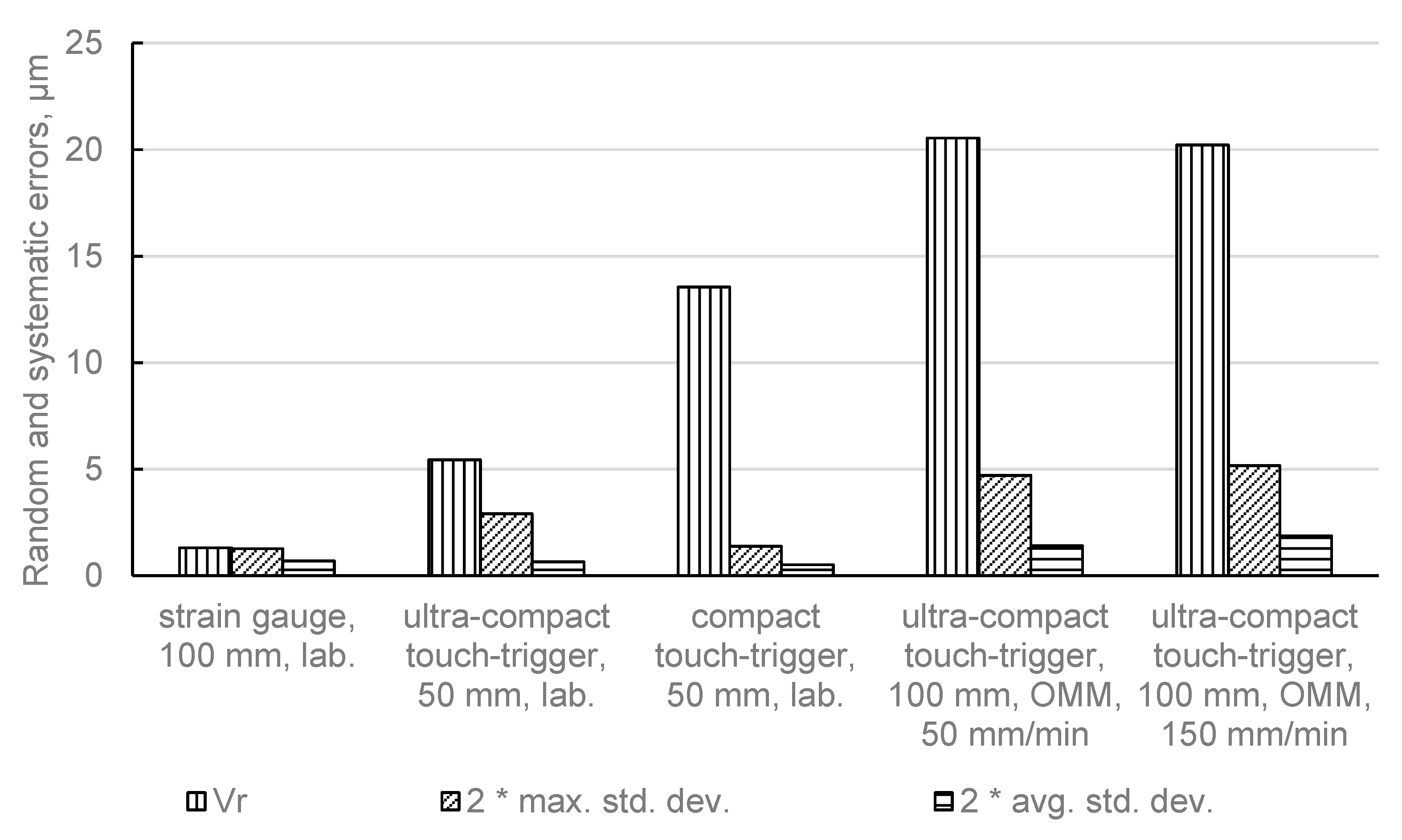
- in the case of three-point (touch-trigger) kinematic probes, systematic errors are greater than random errors. Even in the on-machine measurement, when machine tool’s errors are present, the largest part of the probing errors can be the one resulting from the probe’s systematic errors. It means that numeric correction or compensation of kinematic probes’ systematic errors can significantly reduce errors of on-machine measurements. However, to apply this solution, systematic errors of the probe have to be known—mapped or modelled.
- in the case of the precise, strain gauge probe, systematic errors are not significantly greater than random errors. Thus, probe correction or compensation of systematic errors would not give significant benefit.
- The unidirectional repeatability value, usually provided by the probes’ manufacturers, is not sufficient to estimate the accuracy of the probe. For the kinematic probes tested in the laboratory, the one with the largest random errors still has systematic errors at least twice as large.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Semotiuk, L.; Józwik, J.; Kuric, I. Measurement uncertainty analysis of different CNC machine tools measurement systems. Adv. Sci. Technol. Res. J. 2013, 7, 41–47. [Google Scholar] [CrossRef]
- Verma, M.R.; Chatzwagiannis, E.; Jones, D.; Maropoulos, P.G. Comparison of the measurement performance of high precision multi-axis metal cutting machine tools. Procedia CIRP 2014, 25, 138–145. [Google Scholar] [CrossRef][Green Version]
- Bohan, Z.; Feng, G.; Yan, L. Study on Pre-travel Behaviour of Touch Trigger Probe under Actual Measuring Conditions. Procedia CIRP 2015, 27, 53–58. [Google Scholar] [CrossRef]
- Erkan, T.; Mayer, J.R.R.; Dupont, Y. Volumetric distortion assessment of a five-axis machine by probing a 3D reconfigurable uncalibrated master ball artefact. Precis. Eng. 2011, 35, 116–125. [Google Scholar] [CrossRef]
- Mayer, J.R.R. Five-axis machine tool calibration by probing a scale enriched reconfigurable uncalibrated master balls artefact. CIRP Ann. Manuf. Technol. 2012, 61, 515–518. [Google Scholar] [CrossRef]
- Ibaraki, S.; Iritani, T.; Matsushita, T. Error map construction for rotary axes on five-axis machine tools by on-the-machine measurement using a touch-trigger probe. Int. J. Mach. Tools Manuf. 2013, 68, 21–29. [Google Scholar] [CrossRef]
- Jiang, Z.; Bao, S.; Zhou, X.; Tang, X.; Zheng, S. Identification of location errors by a touch-trigger probe on five-axis machine tools with a tilting head. Int. J. Adv. Manuf. Technol. 2015, 81, 149–158. [Google Scholar] [CrossRef]
- Mayer, J.R.R.; Rahman, M.M.; Łoś, A. An uncalibrated cylindrical indigenous artefact for measuring inter-axis errors of a five-axis machine tool. CIRP Ann. Manuf. Technol. 2015, 64, 487–490. [Google Scholar] [CrossRef]
- Rahman, M.M.; Mayer, R. Calibration performance investigation of an uncalibrated indigenous artefact probing for five-axis machine tool. J. Mach. Eng. 2016, 16, 33–42. [Google Scholar]
- Cho, M.; Seo, T.I.; Kwon, H.D. Integrated error compensation method using OMM system for profile milling operation. J. Mater. Process. Technol. 2003, 136, 88–99. [Google Scholar] [CrossRef]
- Choi, J.P.; Min, B.K.; Lee, S.J. Reduction of machining errors of a three-axis machine tool by on-machine measurement and error compensation system. J. Mater. Process. Technol. 2004, 155–156, 2056–2064. [Google Scholar] [CrossRef]
- Zeleny, J.; Janda, M. Automatic on-machine measurement of complex parts. Mod. Mach. Sci. J. 2009, 1, 92–95. [Google Scholar] [CrossRef]
- Qian, X.M.; Ye, W.H.; Chen, X.M. On-machine measurement for touch-trigger probes and its error compensation. Key Eng. Mater. 2008, 375–376, 558–563. [Google Scholar] [CrossRef]
- Sung, C.K.; Lu, C.H. Modeling/analysis of four-half axis machine tool via modified denavit-hartenberg notation. J. Mech. Sci. Technol. 2014, 28, 5135–5142. [Google Scholar] [CrossRef]
- Olvera, D.; López de Lacalle, L.N.; Compeán, F.I.; Fz-Valdivielso, A.; Lamikiz, A.; Campa, F.J. Analysis of the tool tip radial stiffness of turn-milling centers. Int. J. Adv. Manuf. Technol. 2012, 60, 883–891. [Google Scholar] [CrossRef]
- Lamikiz, A.; López de Lacalle, L.N.; Ocerin, O.; Díez, D.; Maidagan, E. The Denavit and Hartenberg approach applied to evaluate the consequences in the tool tip position of geometrical errors in five-axis milling centres. Int. J. Adv. Manuf. Technol. 2008, 37, 122–139. [Google Scholar] [CrossRef]
- Jankowski, M.; Wozniak, A.; Byszewski, M. Machine tool probes testing using a moving inner hemispherical master artifact. Precis. Eng. 2014, 38, 421–427. [Google Scholar] [CrossRef]
- Woźniak, A.; Jankowski, M. Wireless communication influence on CNC machine tool probe metrological parameters. Int. J. Adv. Manuf. Technol. 2016, 82, 535–542. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 230-10:2011: Test Code for Machine Tools—Part 10: Determination of the Measuring Performance of Probing Systems of Numerically Controlled Machine Tools; International Organization for Standardization: Geneva, Switzerland.

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wozniak, A.; Jankowski, M. Random and Systematic Errors Share in Total Error of Probes for CNC Machine Tools. J. Manuf. Mater. Process. 2018, 2, 17. https://doi.org/10.3390/jmmp2010017
Wozniak A, Jankowski M. Random and Systematic Errors Share in Total Error of Probes for CNC Machine Tools. Journal of Manufacturing and Materials Processing. 2018; 2(1):17. https://doi.org/10.3390/jmmp2010017
Chicago/Turabian StyleWozniak, Adam, and Michal Jankowski. 2018. "Random and Systematic Errors Share in Total Error of Probes for CNC Machine Tools" Journal of Manufacturing and Materials Processing 2, no. 1: 17. https://doi.org/10.3390/jmmp2010017
APA StyleWozniak, A., & Jankowski, M. (2018). Random and Systematic Errors Share in Total Error of Probes for CNC Machine Tools. Journal of Manufacturing and Materials Processing, 2(1), 17. https://doi.org/10.3390/jmmp2010017



