Discrete Element Simulation of Orthogonal Machining of Soda-Lime Glass
Abstract
:1. Introduction
2. DEM Model of Soda-Lime Glass
2.1. Fundamentals of Flat-Joint Model
2.2. Creation of the Bonded Particle Specimen
3. Calibration of the DEM Model (Mechanical Properties)
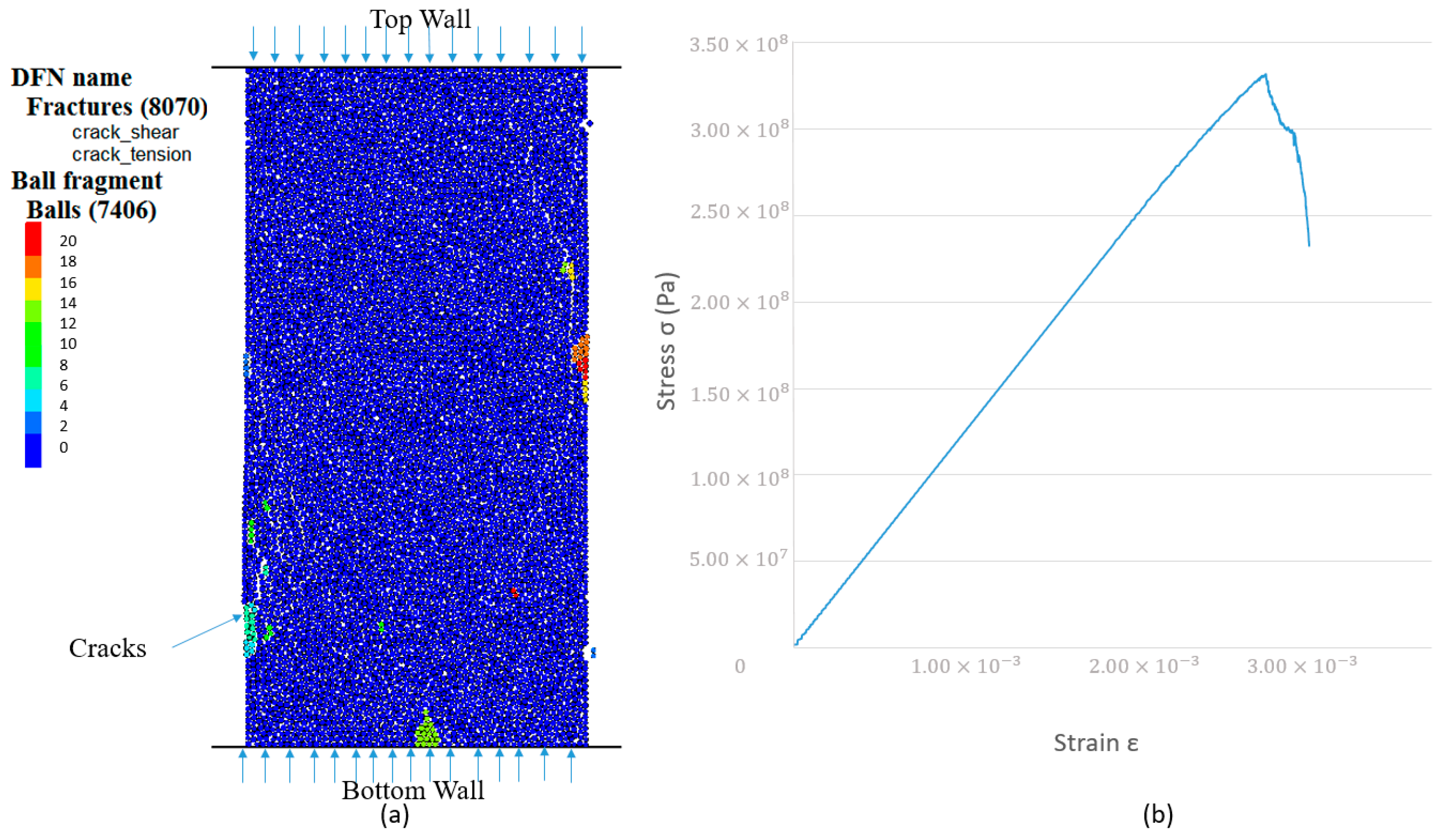
3.1. Uniaxial Tensile Test
3.2. Uniaxial Compressive Test
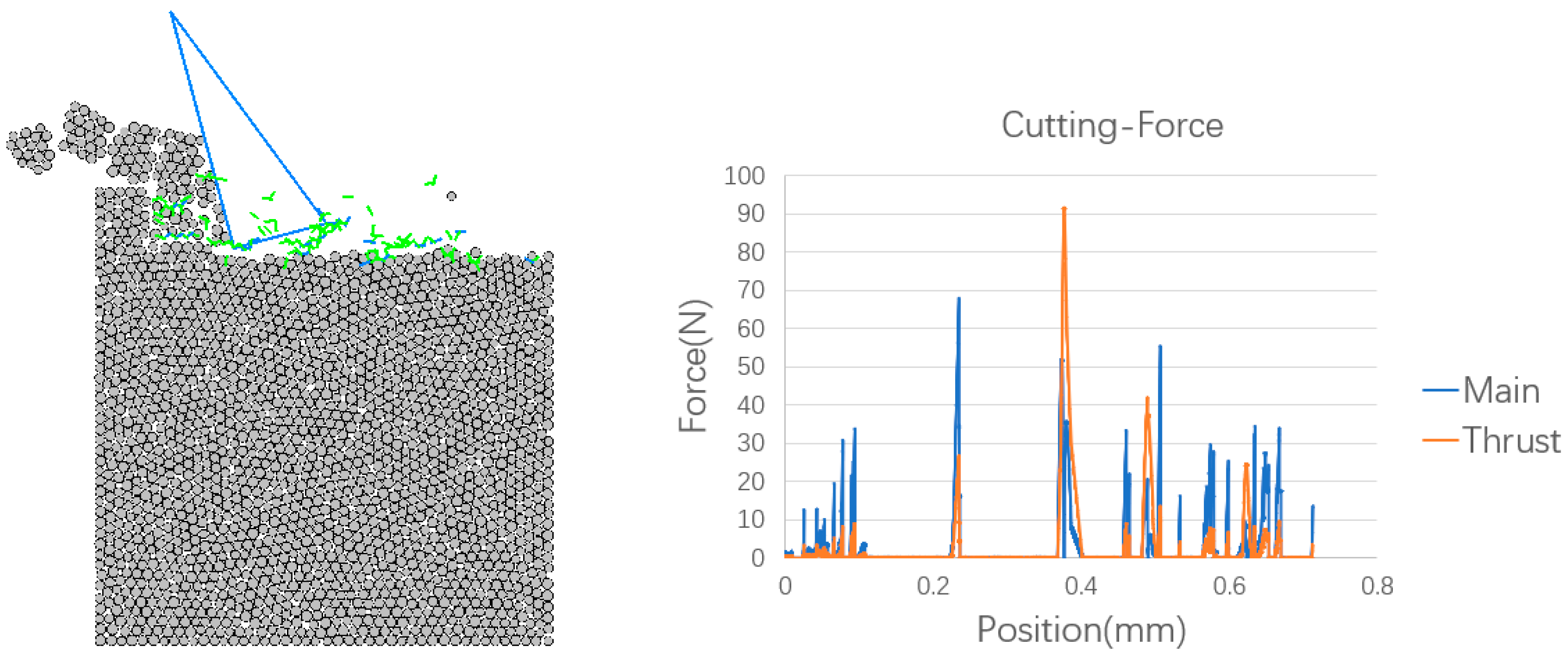
4. Cutting Simulation
- (1)
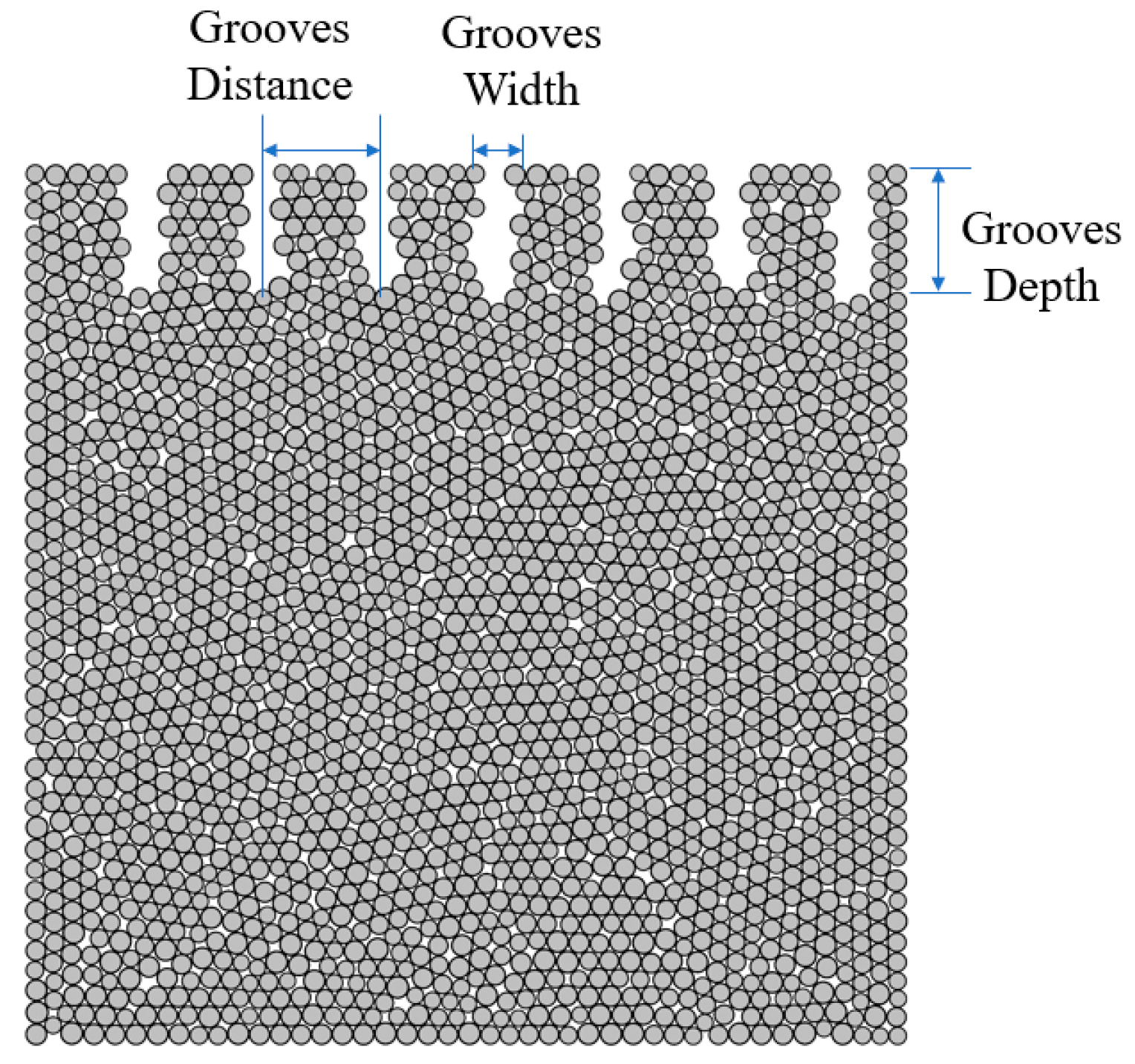
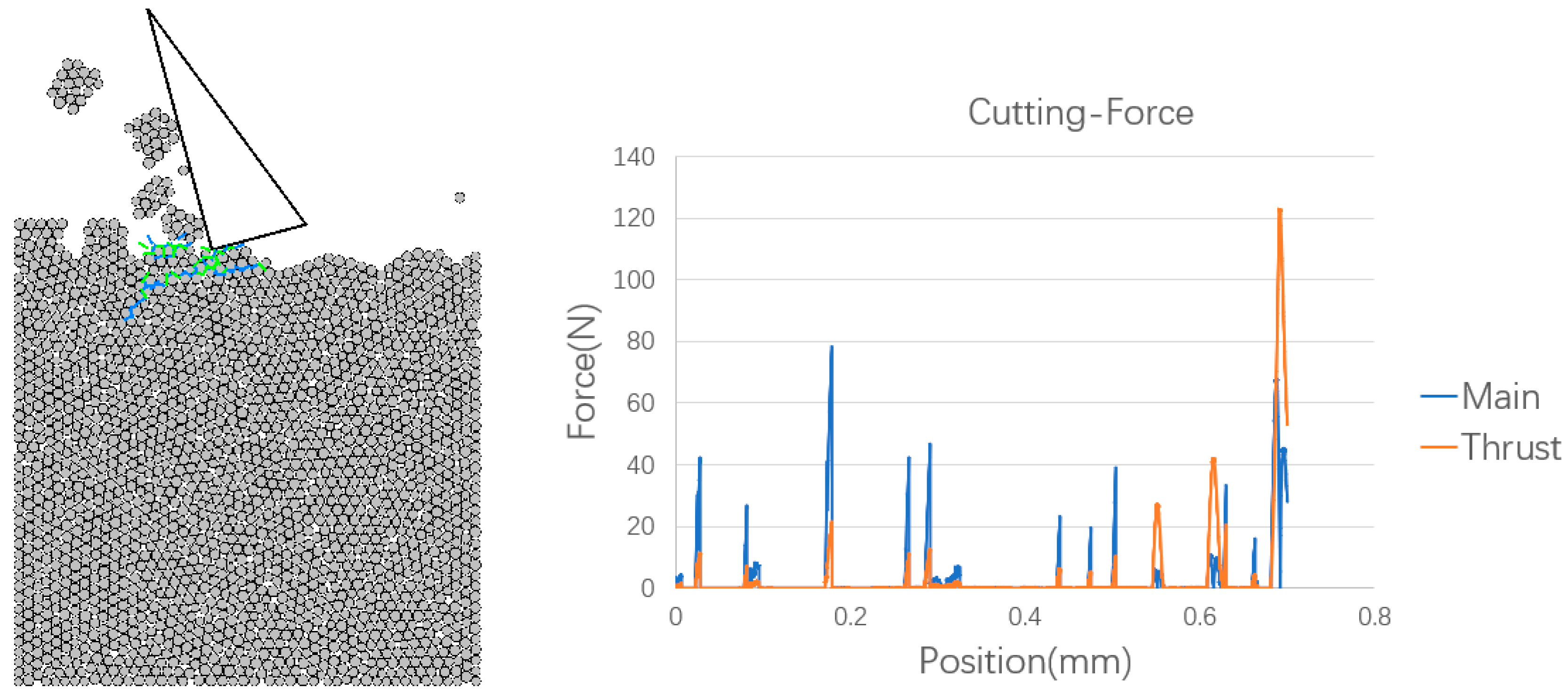
- A 0.1 mm depth of cut without microgrooves:
- (2)
- A 0.1 mm depth of cut with microgrooves:
- (3)
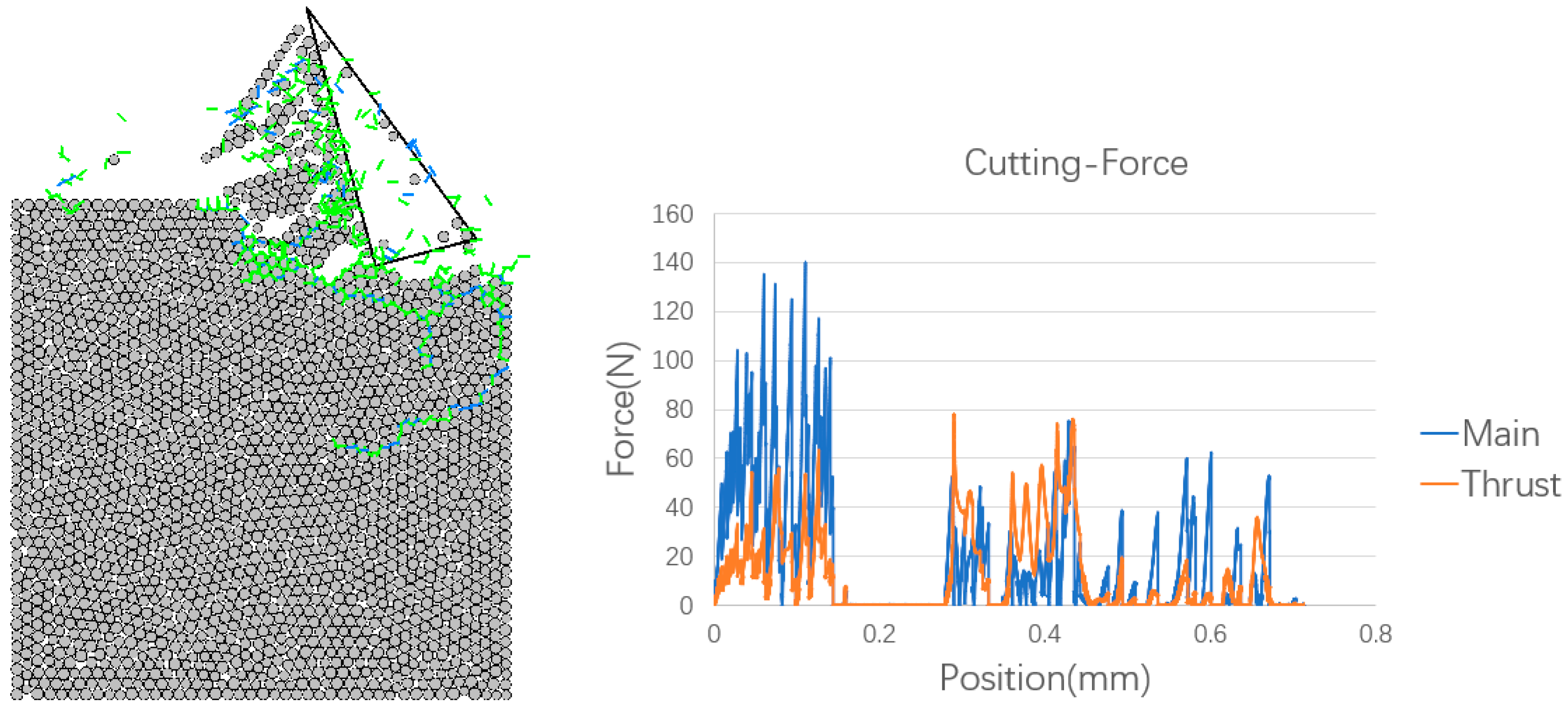
- A 0.2 mm depth of cut without microgrooves:
- (4)
- A 0.2 mm depth of cut with microgrooves:
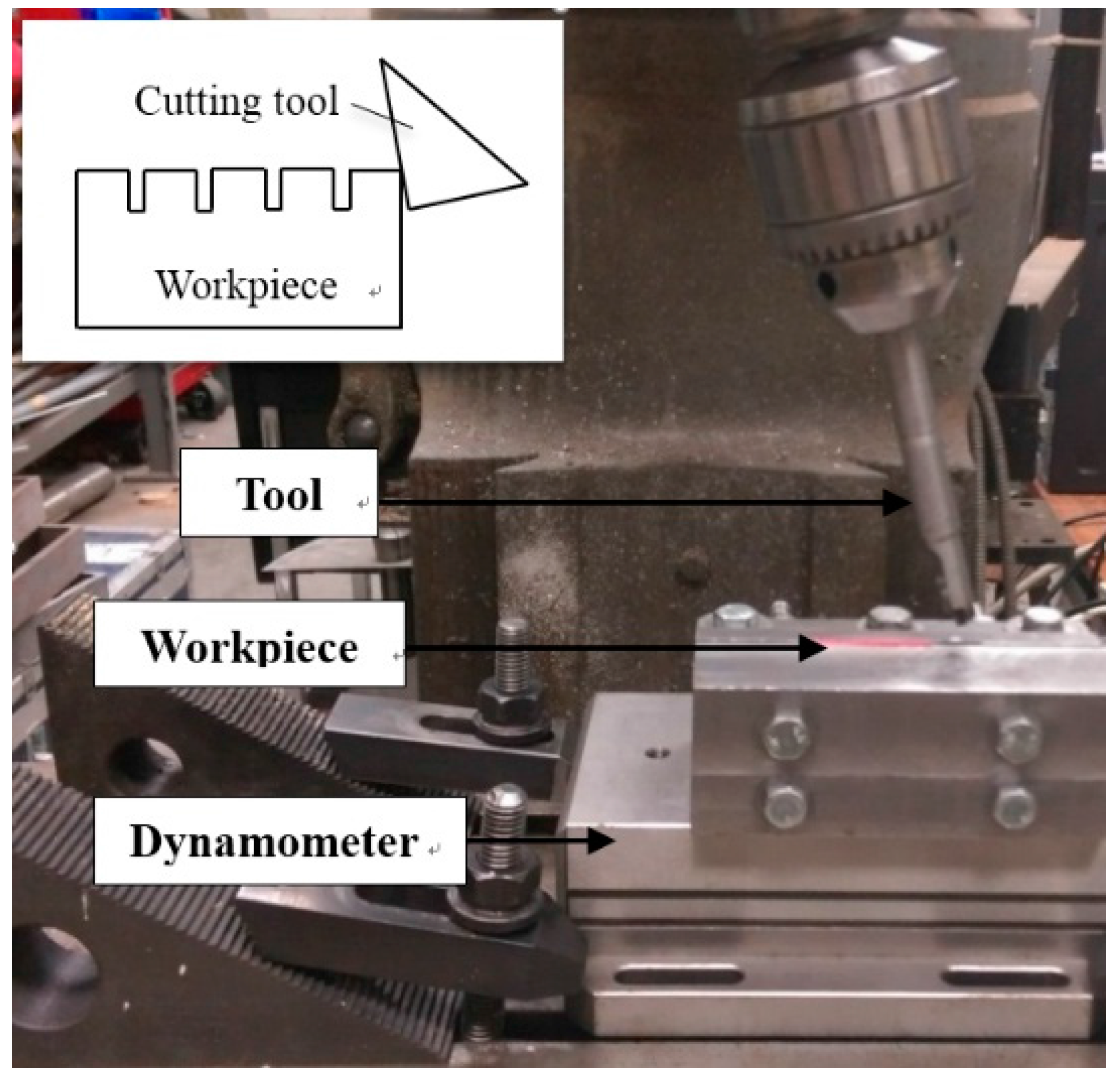
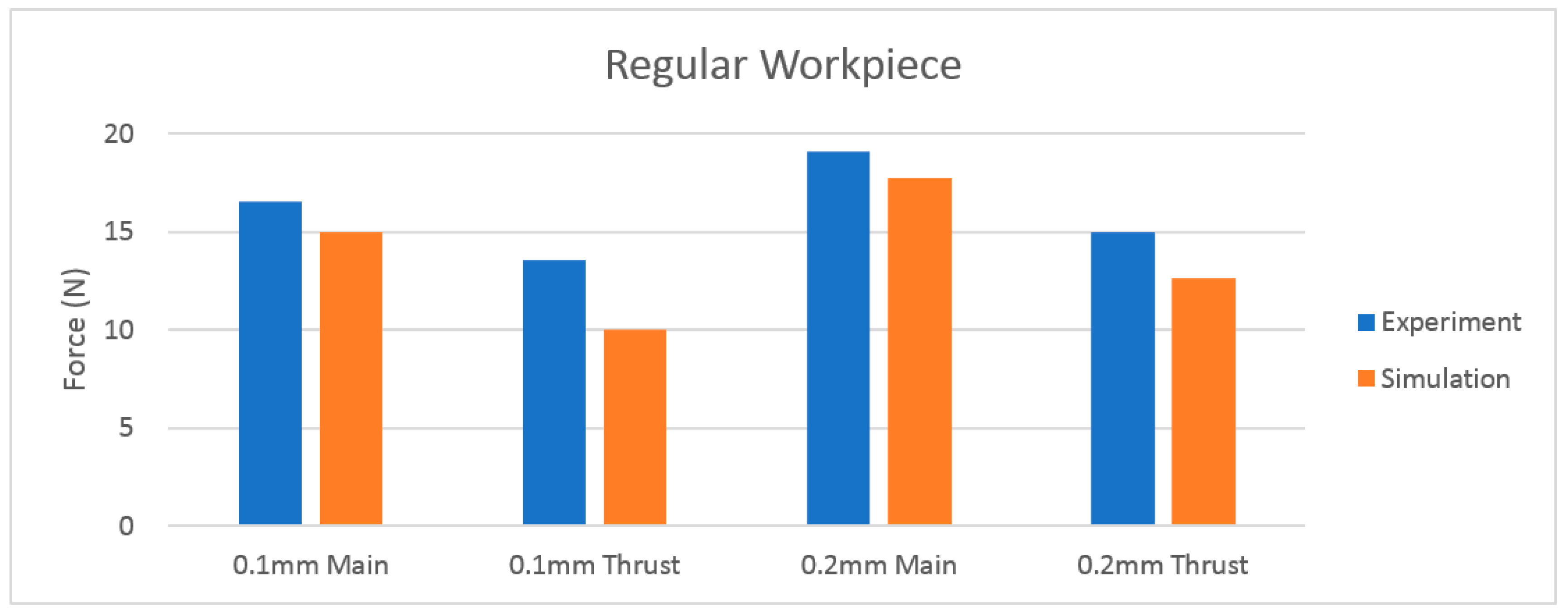
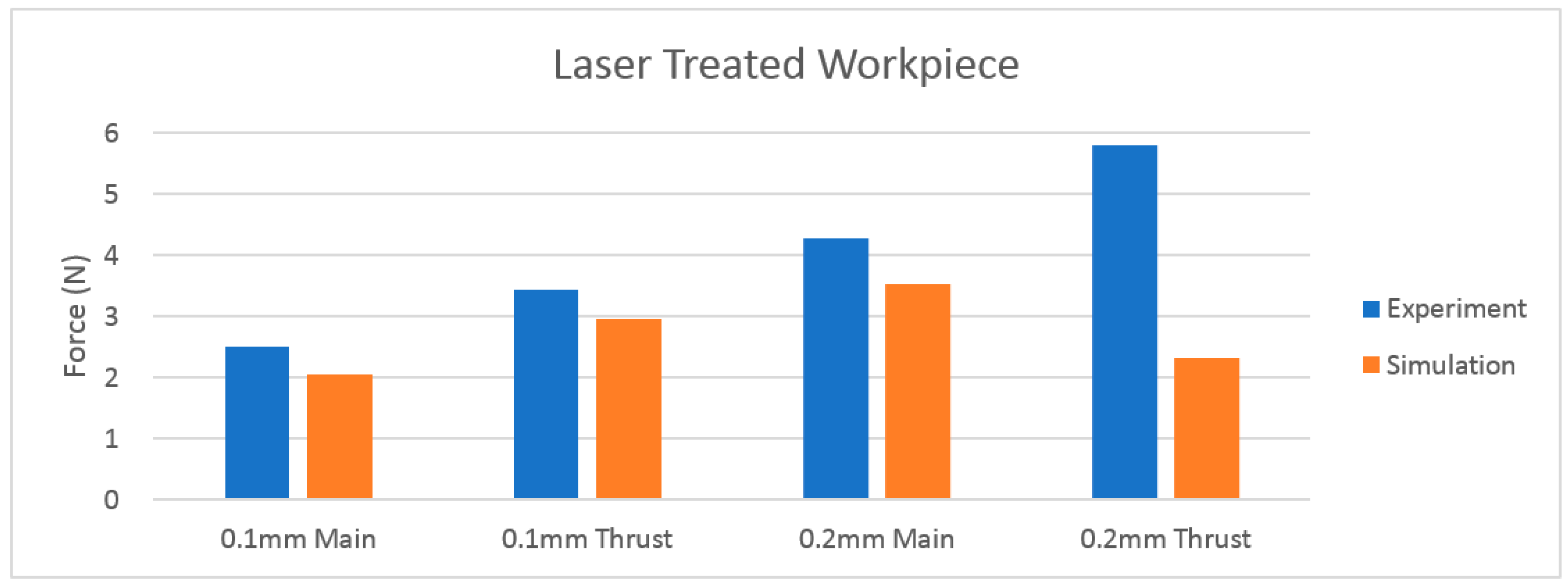
5. Model Validation
6. Conclusions
- The cause of crack initiation can be identified by the simulation model. There are two types of cracks: one is caused by shear force and the other is caused by tensile force.
- The simulations show that cutting forces can be reduced and subsurface cracks can be eliminated when cutting grooved workpieces.
- The geometries of the simulation model highly affect the result. Compared to the grooved specimen, the simulation result for the regular one is more accurate and repeatable.
- Simulation time is highly dependent on the number of particles for the model and computing capacity. Smaller particle size and larger number of particles can enhance the details of the model. More powerful computing methods are recommended, such as parallel computing and supercomputing to increase the simulation efficiency.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shanmugam, N.; Yu, X.; Alkotami, H.; Devin, G.; Lei, S. Machining of Transparent Brittle Material Assisted by Laser-Induced Seed Cracks. In Proceedings of the ASME 2016 11th International Manufacturing Science and Engineering Conference, Blacksburg, VA, USA, 27 June 27–1 July 2016; V001T02A019. American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar]
- Larcher, M.; Arrigoni, M.; Bedon, C.; Van Doormaal, J.; Haberacker, C.; Hüsken, G.; Millon, O.; Saarenheimo, A.; Solomos, G.; Thamie, L. Design of blast-loaded glazing windows and facades: A review of essential requirements towards standardization. Adv. Civ. Eng. 2016, 2016, 2604232. [Google Scholar] [CrossRef]
- Bedon, C.; Louter, C. Numerical investigation on structural glass beams with GFRP-embedded rods, including effects of pre-stress. Compos. Struct. 2018, 184, 650–661. [Google Scholar] [CrossRef]
- Pawar, P.; Ballav, R.; Kumar, A. A review on machining of glass materials. IEEE conference on emerging trends in engineering, business and disaster management. J. Emerg. Technol. Mech. Sci. Eng. 2015, 18–22. [Google Scholar] [CrossRef]
- Pawar, P.; Ballav, R.; Kumar, A. Review on Material Removal Technology of Soda-Lime Glass Material. Indian J. Sci. Technol. 2017, 10. [Google Scholar] [CrossRef]
- Jawalkar, C.; Sharma, A.K.; Kumar, P.; Variable, D. Micromachining with ECDM: Research potentials and experimental investigations. Channels 2012, 40, 46. [Google Scholar]
- Sajjadi, M.; Malekian, M.; Park, S.S.; Jun, M.B. Investigation of micro scratching and machining of glass. In Proceedings of the ASME 2009 International Manufacturing Science and Engineering Conference, West Lafayette, IN, USA, 4–7 October 2009; American Society of Mechanical Engineers: New York, NY, USA, 2009; pp. 401–408. [Google Scholar]
- Lautre, N.K.; Sharma, A.K.; Kumar, P.; Das, S. A photoelasticity approach for characterization of defects in microwave drilling of soda lime glass. J. Mater. Process. Technol. 2015, 225, 151–161. [Google Scholar] [CrossRef]
- Jia, P.; Zhou, M. Tool wear and its effect on surface roughness in diamond cutting of glass soda-lime. Chin. J. Mech. Eng. 2012, 25, 1224–1230. [Google Scholar] [CrossRef]
- El-Hofy, H. Advanced Machining Processes: Nontraditional and Hybrid Machining Processes; McGraw Hill Professional: New York, NY, USA, 2005. [Google Scholar]
- Cheng, J.; Gong, Y. Experimental study on ductile-regime micro-grinding character of soda-lime glass with diamond tool. Int. J. Adv. Manuf. Technol. 2013, 69, 147–160. [Google Scholar] [CrossRef]
- Cheng, J.; Gong, Y.; Wang, J. Modeling and evaluating of surface roughness prediction in micro-grinding on soda-lime glass considering tool characterization. Chin. J. Mech. Eng. 2013, 26, 1091–1100. [Google Scholar] [CrossRef]
- Yu, G.; Zheng, Y.; Feng, B.; Liu, B.; Meng, K.; Yang, X.; Chen, H.; Xu, J. Computation modeling of laminated crack glass windshields subjected to headform impact. Comput. Struct. 2017, 193, 139–154. [Google Scholar] [CrossRef]
- Jaśkowiec, J. Numerical modeling mechanical delamination in laminated glass by XFEM. Procedia Eng. 2015, 108, 293–300. [Google Scholar] [CrossRef]
- Shet, C.; Deng, X. Finite element analysis of the orthogonal metal cutting process. J. Mater. Process. Technol. 2000, 105, 95–109. [Google Scholar] [CrossRef]
- Strack, O.; Cundall, P.A. The Distinct Element Method as a Tool for Research in Granular Media; Department of Civil and Mineral Engineering, University of Minnesota: Minneapolis, MN, USA, 1978. [Google Scholar]
- Su, O.; Akcin, N.A. Numerical simulation of rock cutting using the discrete element method. Int. J. Rock Mech. Min. Sci. 2011, 48, 434–442. [Google Scholar] [CrossRef]
- Shen, X.; Lei, S. Distinct Element Simulation of Laser Assisted Machining of Silicon Nitride Ceramics: Surface/Subsurface Cracks and Damage. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; Volume 5, pp. 1267–1274. [Google Scholar]
- Iliescu, D.; Gehin, D.; Iordanoff, I.; Girot, F.; Gutiérrez, M. A discrete element method for the simulation of CFRP cutting. Compos. Sci. Technol. 2010, 70, 73–80. [Google Scholar] [CrossRef]
- Wang, X.-E.; Yang, J.; Liu, Q.-F.; Zhang, Y.-M.; Zhao, C. A comparative study of numerical modelling techniques for the fracture of brittle materials with specific reference to glass. Eng. Struct. 2017, 152, 493–505. [Google Scholar] [CrossRef]
- Cundall, P.; Strack, O. Particle Flow Code in 2 Dimensions; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 1999. [Google Scholar]
- Wu, S.; Xu, X. A study of three intrinsic problems of the classic discrete element method using flat-joint model. Rock Mech. Rock Eng. 2016, 49, 1813–1830. [Google Scholar] [CrossRef]
- Glass and Glass-Ceramic. Available online: https://www.makeitfrom.com/material-properties/Annealed-Soda-Lime-Glass (accessed on 15 November 2017).
- Christoffersen, J.; Mehrabadi, M.; Nemat-Nasser, S. A micromechanical description of granular material behavior. J. Appl. Mech. 1981, 48, 339–344. [Google Scholar] [CrossRef]
- Evans, K. Measurement of Poisson’s Ratio. In Mechanical Properties and Testing of Polymers; Springer: Berlin, Germany, 1999; pp. 140–142. [Google Scholar]
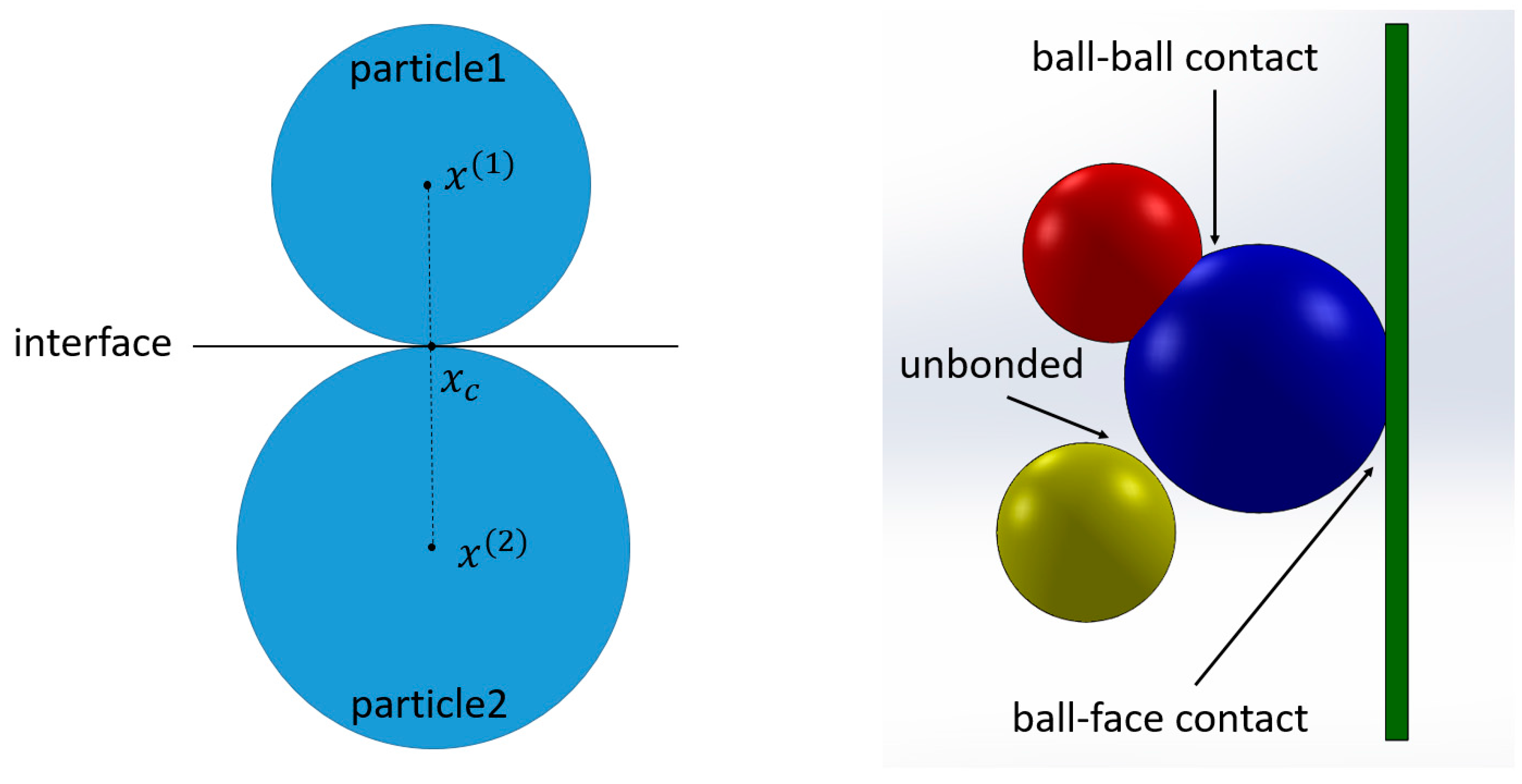

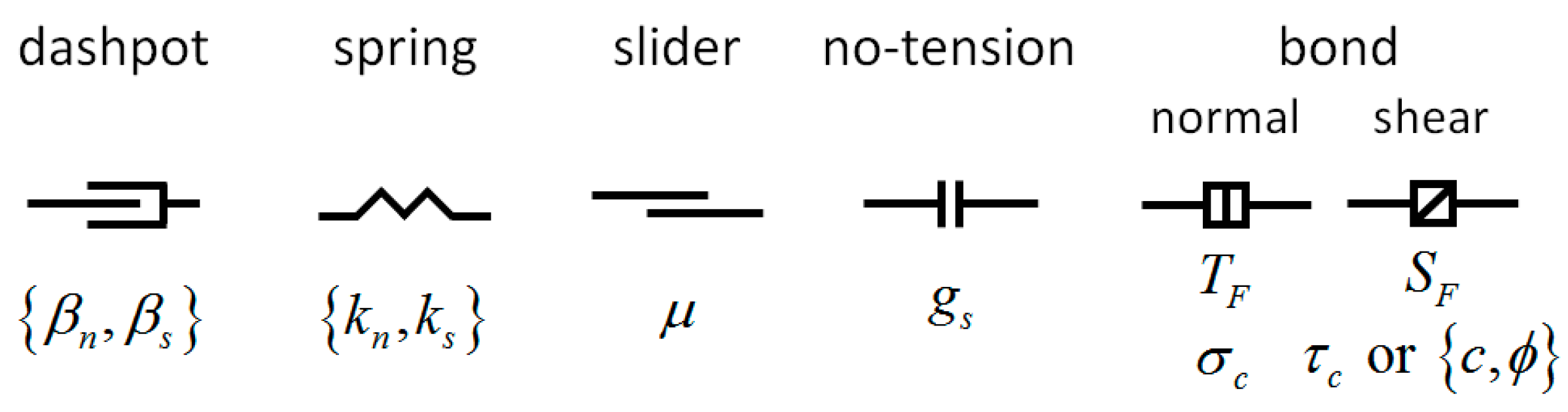
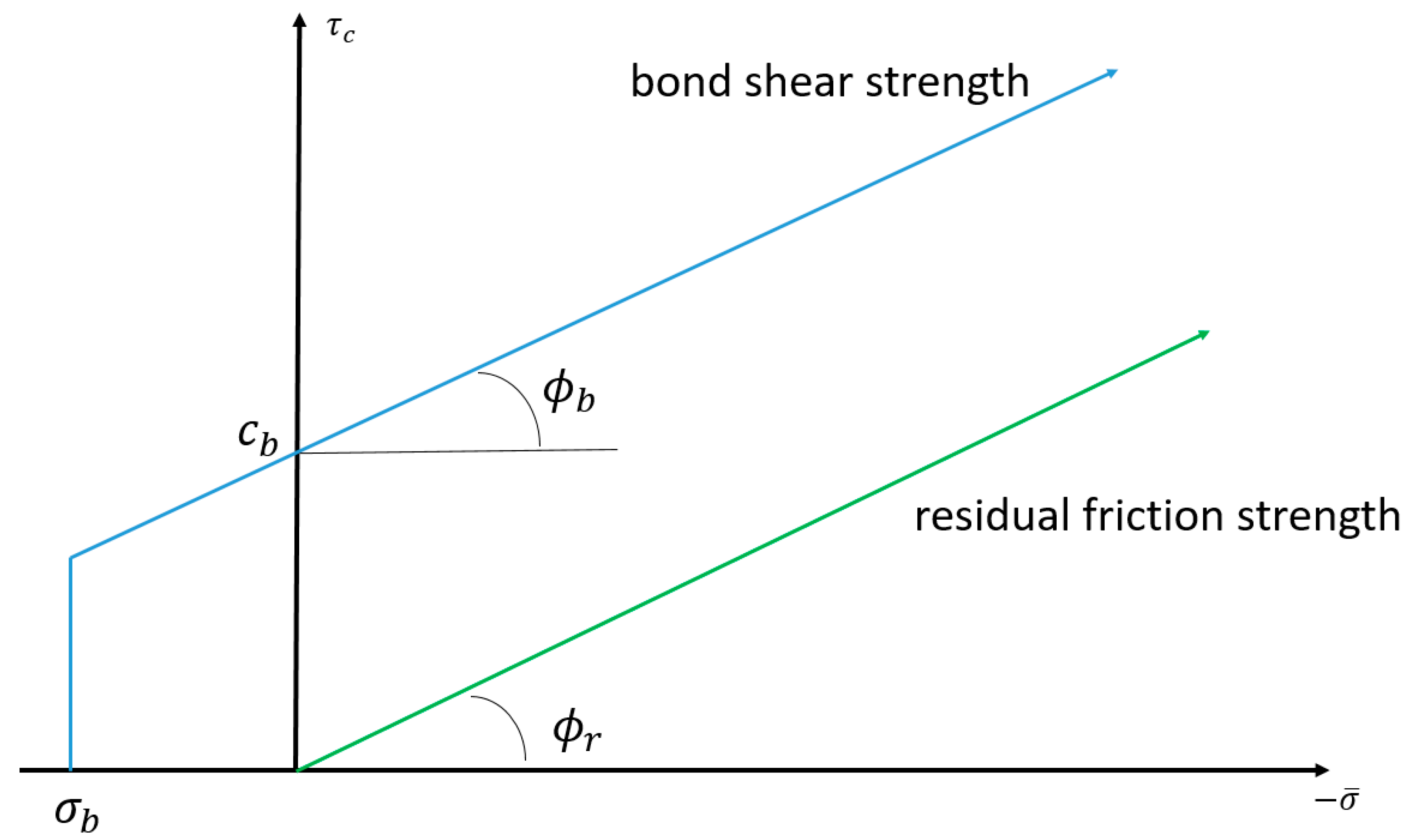


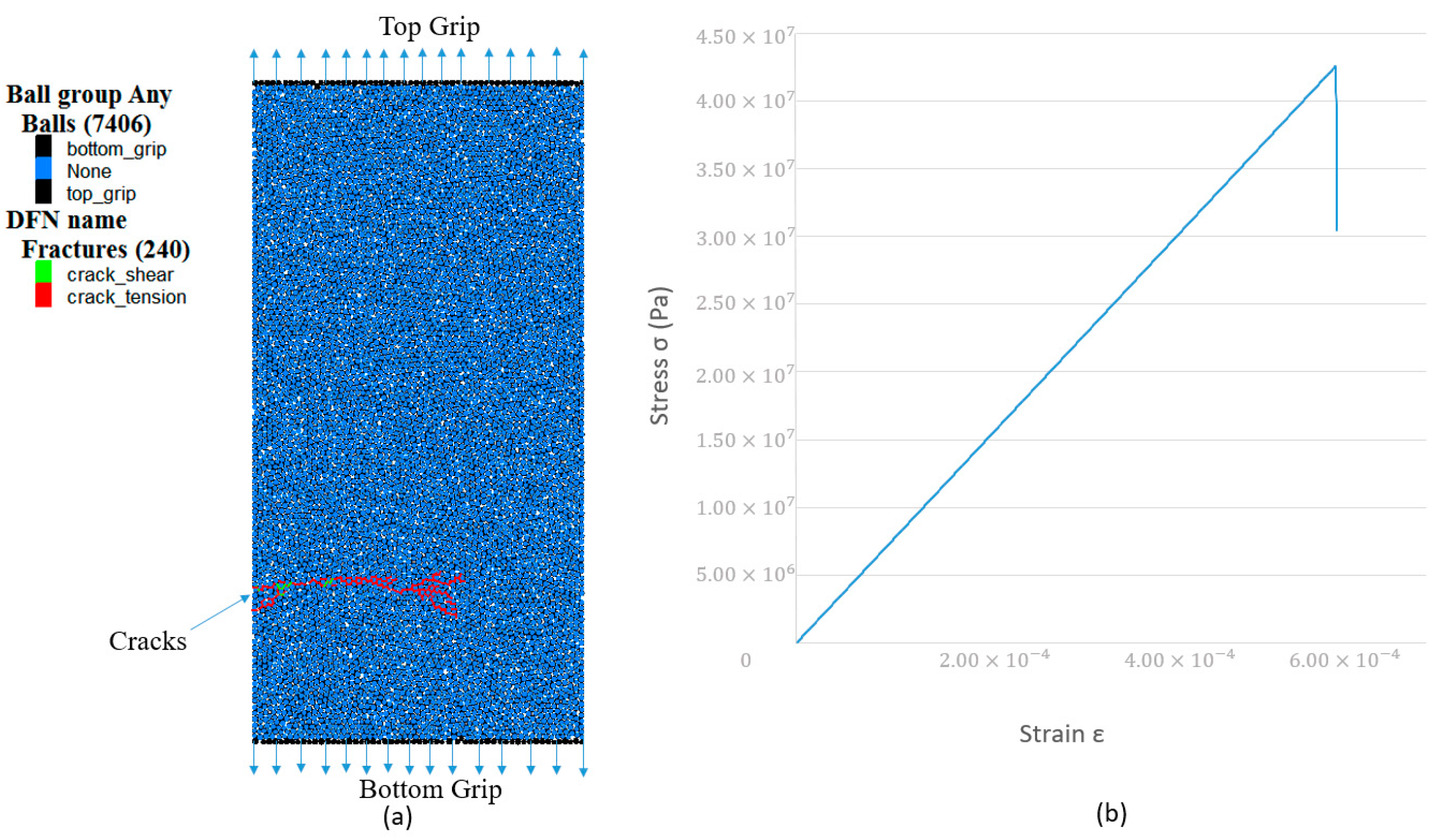



| Macro-Parameters | Description | Value | Micro-Parameters | Description | Value |
|---|---|---|---|---|---|
| ρ | Ball density (kg/m3) | 2.4 × 103 | Ball-ball contact modulus (Pa) | 107.0 × 109 | |
| H | Sample height (m) | 2.0 × 10−3 | Ball stiffness ratio | 3.1 × 10 | |
| W | Sample width (m) | 1.0 × 10−3 | Flat-joint bond modulus (Pa) | 107.0 × 109 | |
| Rmin | Minimum ball radius (m) | 1.5 × 10−5 | Flat-joint bond stiffness ratio | 3.1 × 10 | |
| Rmax | Maximum ball radius (m) | 2.0 × 10−5 | Ball friction coefficient | 0.577 | |
| Flat-joint normal strength (Pa) | 200.0 × 106 | ||||
| Flat-joint shear strength (Pa) | 113.0 × 106 | ||||
| Friction angle (degree) | 25.0 × 10 |
| Mechanical Property | Elastic Modulus E (GPa) | Tensile Strength σt (MPa) | Compressive Strength σc (MPa) | Poisson’s Ratio ν |
|---|---|---|---|---|
| Soda-lime glass | 71 | 41 | 330 | 0.23 |
| DEM Model | 71.1 | 42.6 | 332 | 0.228 |
| Parameter | Description | Value |
|---|---|---|
| V (mm/s) | Cutting speed | 4.23 |
| t (mm) | Depth of cut | 0.1, 0.2 |
| α (degree) | Rake angle | −15 |
| L (mm) | Width of cut | 1 |
| Depth of Cut (mm) | Replications | Average Cutting Force (N) | |||
|---|---|---|---|---|---|
| Regular Workpiece | Grooved Workpiece | ||||
| Main | Thrust | Main | Thrust | ||
| 0.1 | 1 | 14.15 | 10.29 | 1.72 | 2.84 |
| 2 | 15.40 | 9.27 | 2.82 | 3.13 | |
| 3 | 15.38 | 10.38 | 1.60 | 2.87 | |
| 0.2 | 1 | 17.45 | 13.54 | 3.68 | 2.98 |
| 2 | 17.24 | 12.16 | 3.14 | 2.95 | |
| 3 | 18.41 | 12.19 | 3.73 | 1.06 | |
| Parameter | Description | Value |
|---|---|---|
| V (mm/s) | Cutting speed | 4.23 |
| t (mm) | Depth of cut | 0.1, 0.2 |
| α (degree) | Rake angle | −15 |
| L (mm) | Width of cut | 25.4 |
| Depth of Cut (mm) | Replications | Average Cutting Force (N) | |||
|---|---|---|---|---|---|
| Regular Workpiece | Laser Treated Workpiece | ||||
| Main | Thrust | Main | Thrust | ||
| 0.1 | 1 | 17.8 | 14.1 | 2.0 | 3.1 |
| 2 | 15.0 | 12.5 | 2.9 | 4.0 | |
| 3 | 16.7 | 14.0 | 2.6 | 3.2 | |
| 0.2 | 1 | 19.9 | 15.5 | 4.3 | 5.6 |
| 2 | 18.1 | 14.6 | 4.6 | 6.4 | |
| 3 | 19.2 | 14.8 | 3.9 | 5.4 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Alkotami, H.; Lei, S. Discrete Element Simulation of Orthogonal Machining of Soda-Lime Glass. J. Manuf. Mater. Process. 2018, 2, 10. https://doi.org/10.3390/jmmp2010010
Yang G, Alkotami H, Lei S. Discrete Element Simulation of Orthogonal Machining of Soda-Lime Glass. Journal of Manufacturing and Materials Processing. 2018; 2(1):10. https://doi.org/10.3390/jmmp2010010
Chicago/Turabian StyleYang, Guang, Hazem Alkotami, and Shuting Lei. 2018. "Discrete Element Simulation of Orthogonal Machining of Soda-Lime Glass" Journal of Manufacturing and Materials Processing 2, no. 1: 10. https://doi.org/10.3390/jmmp2010010
APA StyleYang, G., Alkotami, H., & Lei, S. (2018). Discrete Element Simulation of Orthogonal Machining of Soda-Lime Glass. Journal of Manufacturing and Materials Processing, 2(1), 10. https://doi.org/10.3390/jmmp2010010






