Pearl-Chain Formation of Discontinuous Carbon Fiber under an Electrical Field
Abstract
1. Introduction
2. Theoretical Derivation for Calculating Required Minimum Electrical Field for Discontinuous Carbon Fiber Alignment
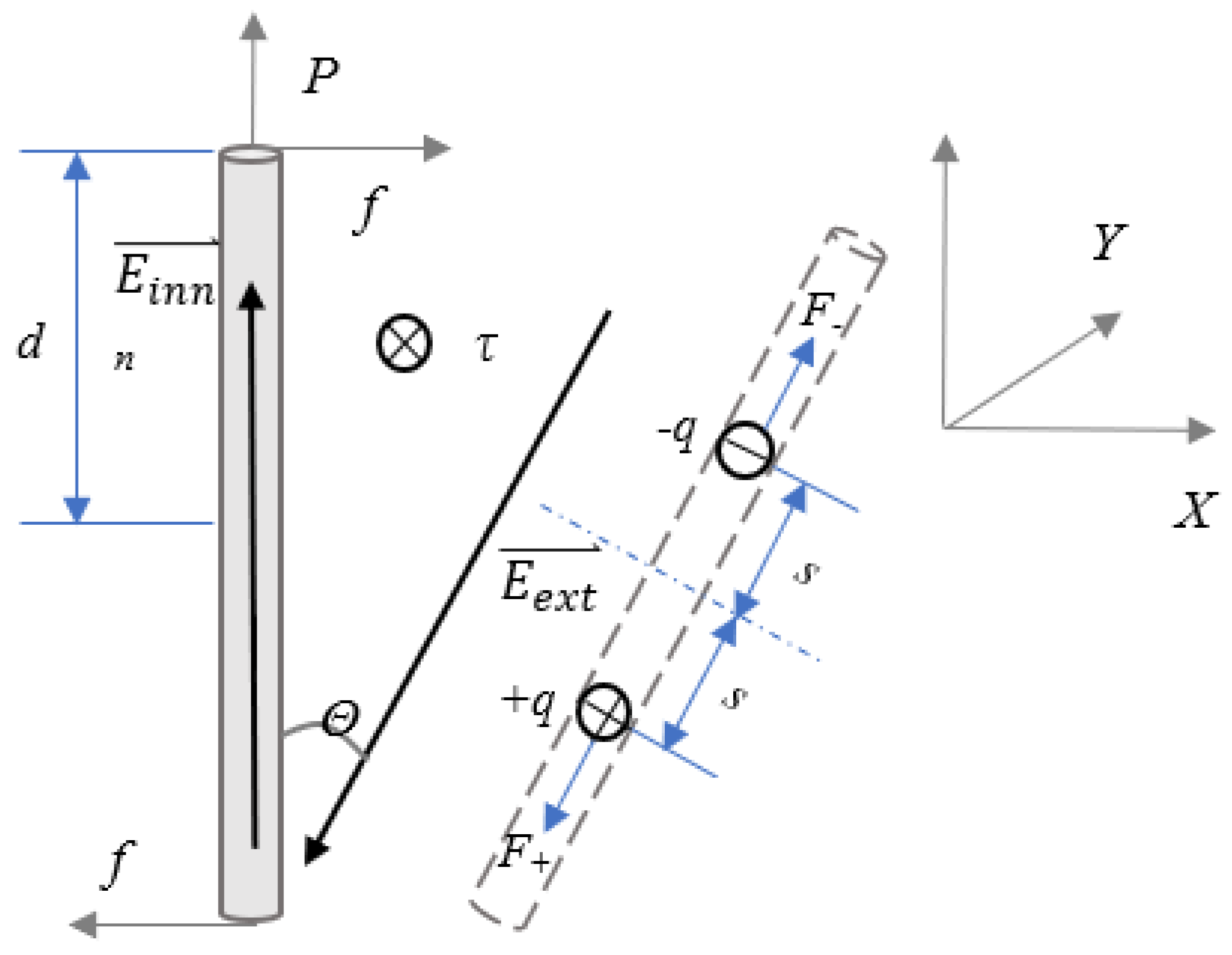
2.1. Producing Dipole along the Carbon Fiber
2.2. Aligning the Fiber along the Direction of the Electrical Field
2.3. Total Work Required for Discontinuous Carbon Fiber Alignment
2.4. Summary on Minimum Required Electrical Field for Alignment
3. Simulation Result on Required Minimum Electrical Field
- (1)
- Length of the discontinuous fibers: the longer the fiber, the smaller the required electrical field intensity (E).
- (2)
- Diameter of the discontinuous fibers: this factor usually can be ignored with a large aspect-ratio (>10). If it is considered, the smaller the diameter, the smaller the required E.
- (3)
- Combined effect-dielectric constant of the discontinuous fibers () and dielectric constant of the liquid resin (): the larger the value, the smaller the required E.
- (4)
- Fabrication temperature: the lower the temperature, the smaller the required E.
- (5)
- Viscosity of the liquid resin: Viscosity value does not affect the required E. However, the smaller the viscosity, the shorter time required to align the fiber. For a high viscous material, the time for alignment will still be within minutes.
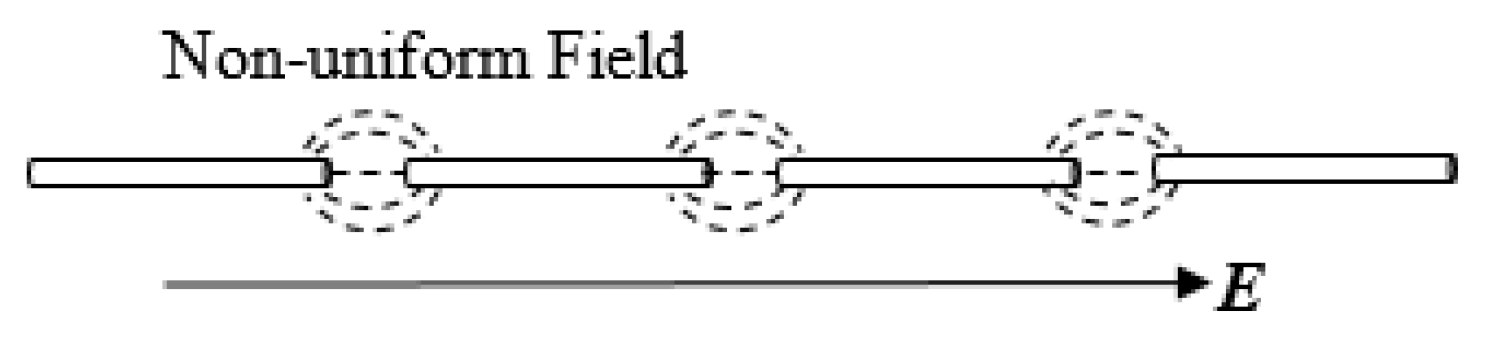
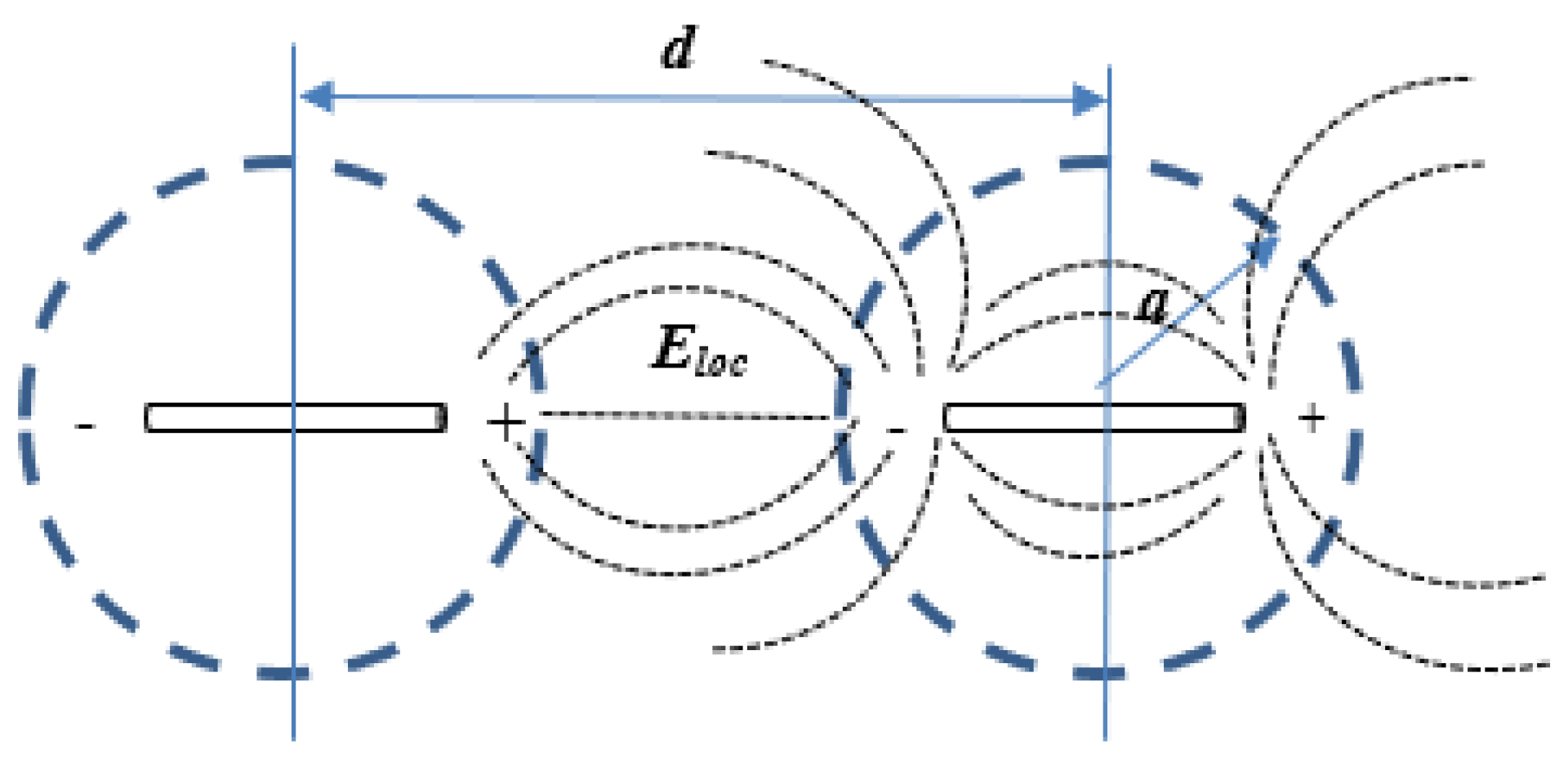
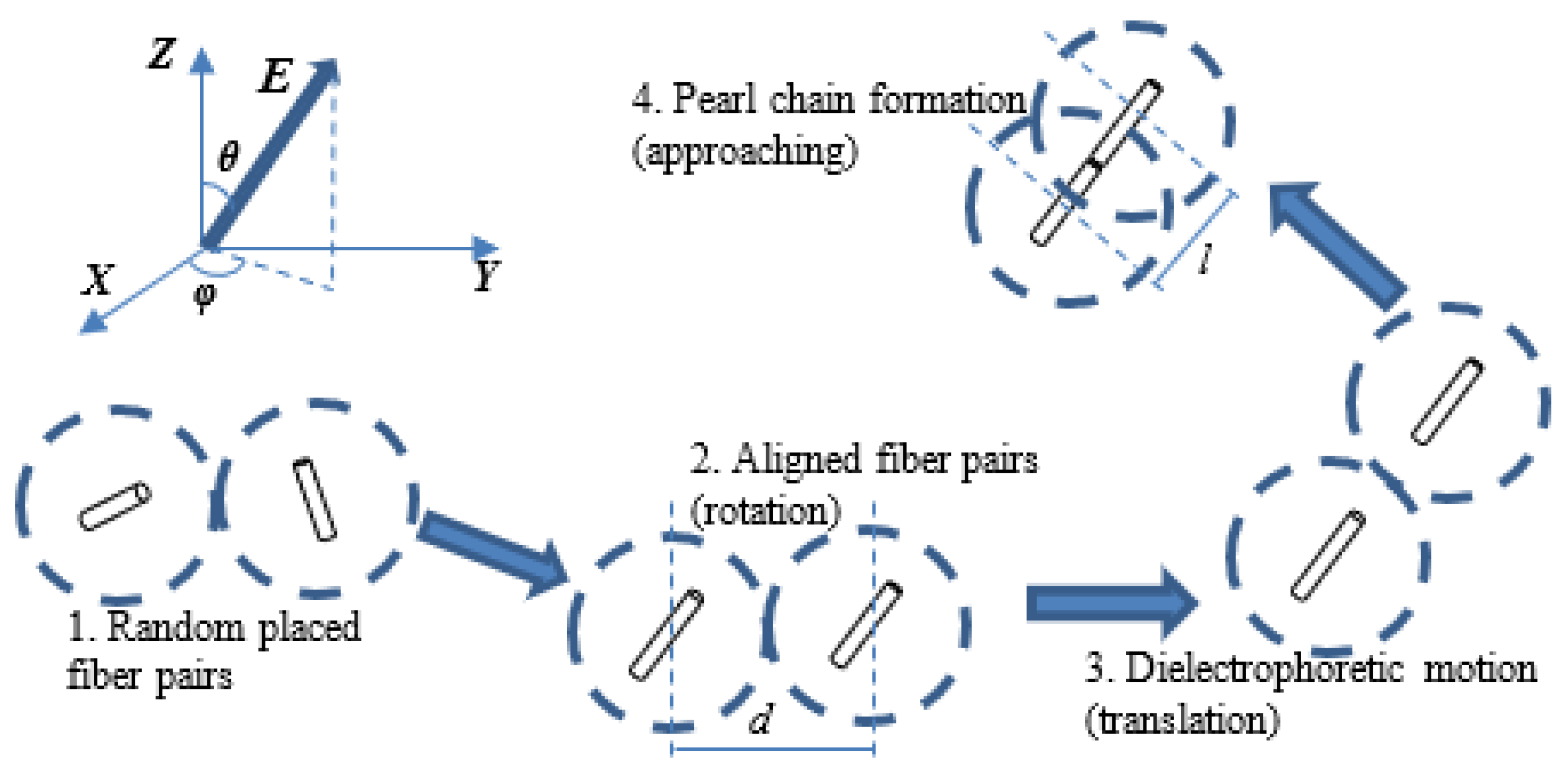
4. Pearl-Chain Formation
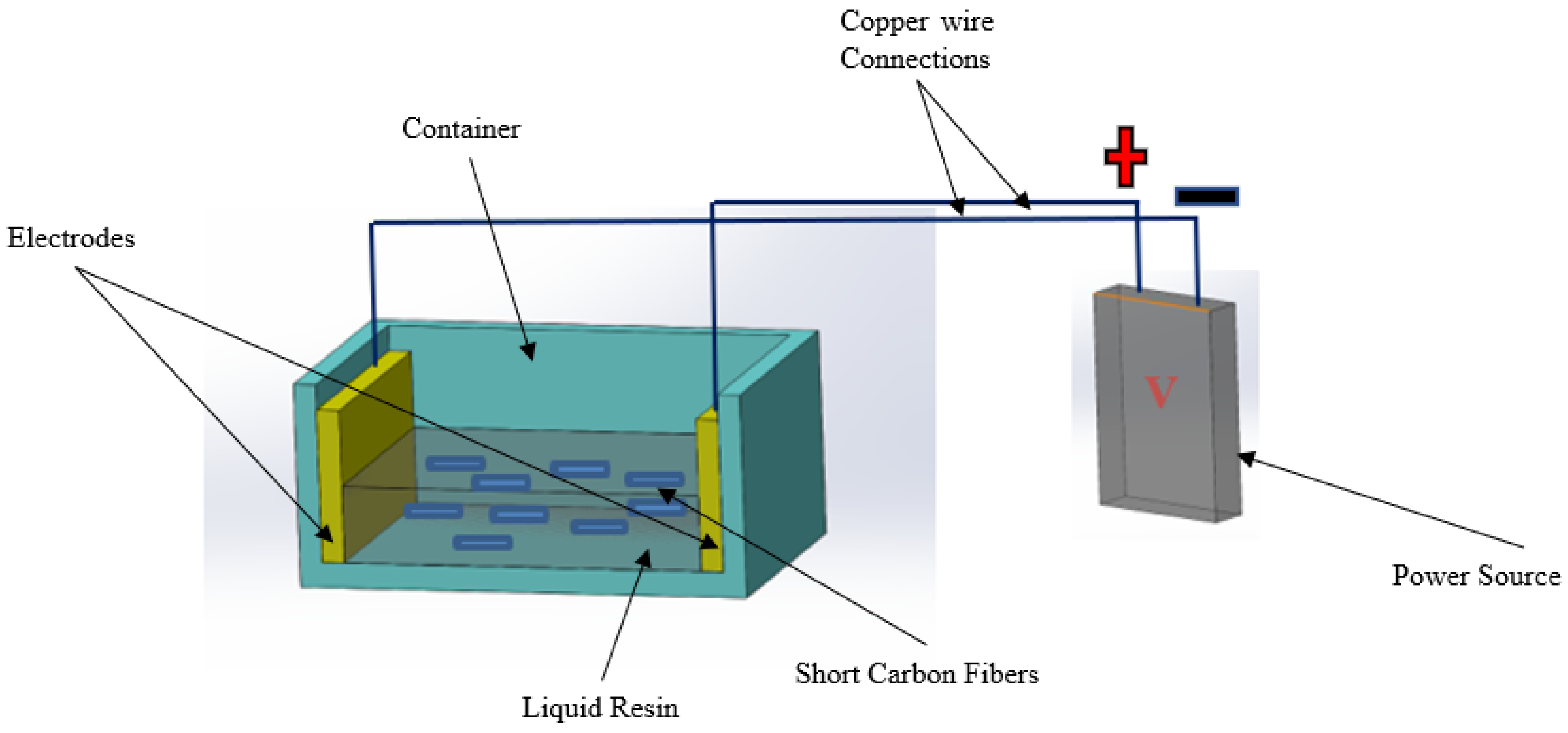
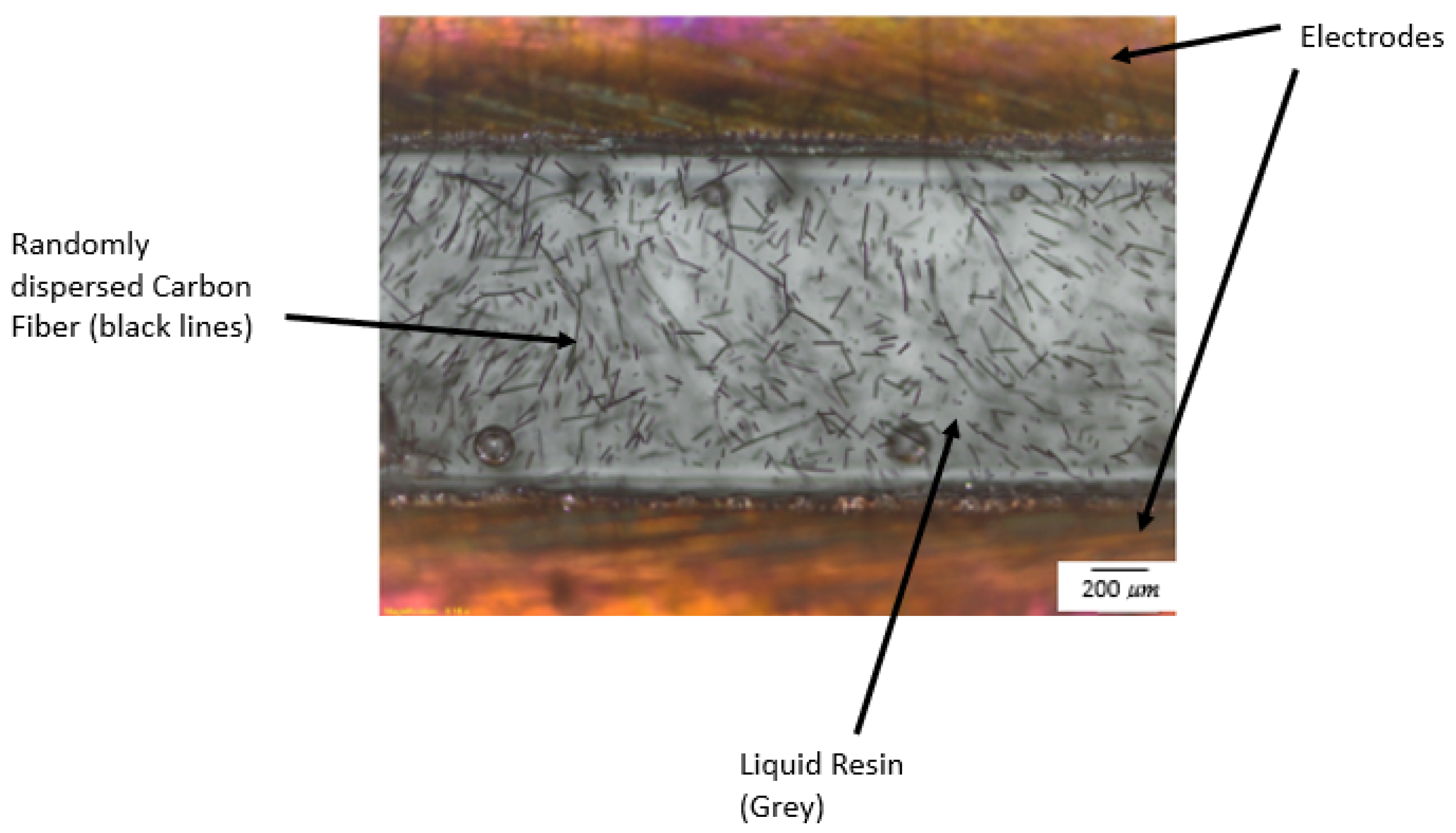
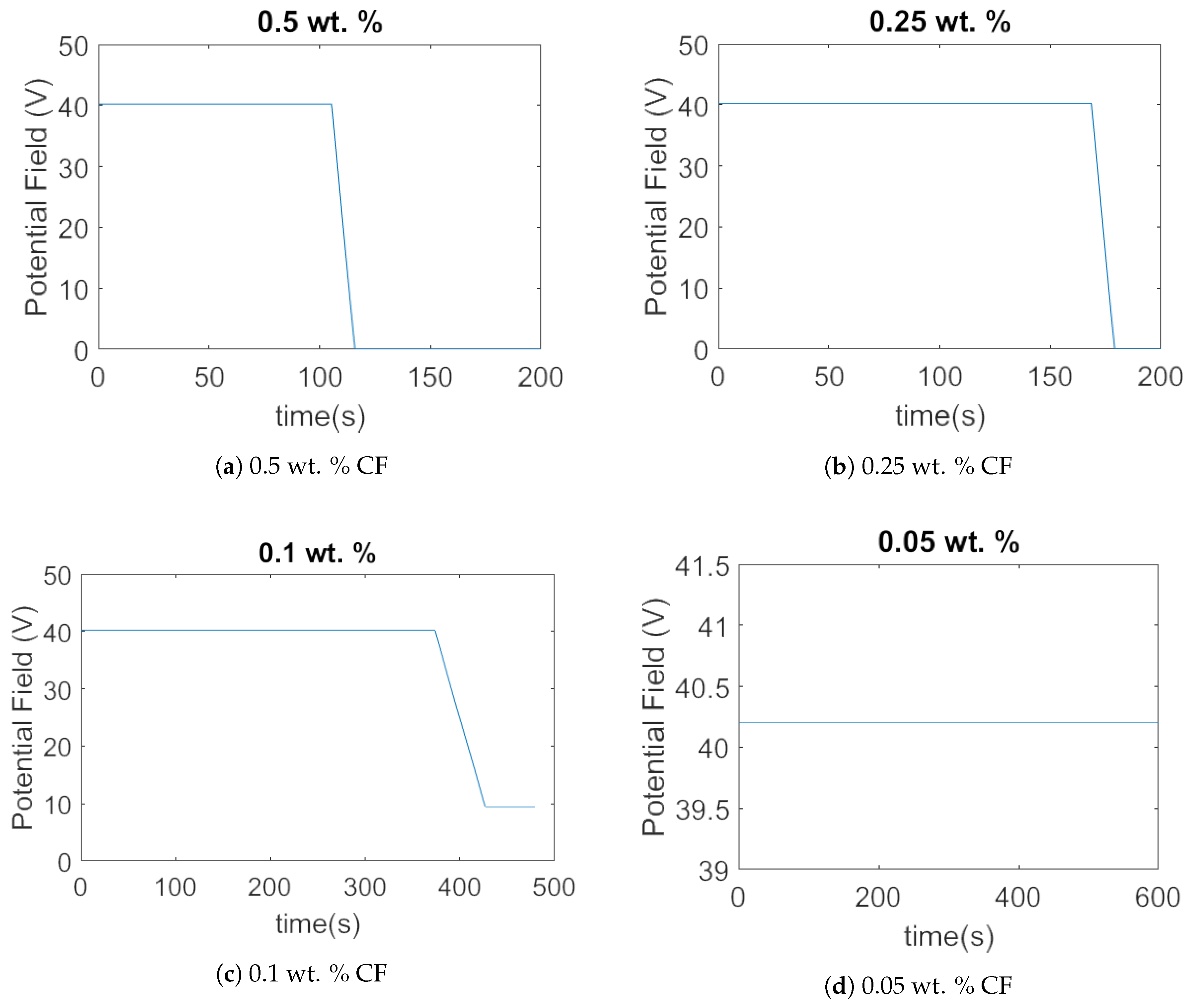
5. Experimental Setup and Result
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Chung, D. Carbon Fiber Composites; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Bradford, P.D.; Wang, X.; Zhao, H.; Maria, J.P.; Jia, Q.; Zhu, Y. A novel approach to fabricate high volume fraction nanocomposites with long aligned carbon nanotubes. Compos. Sci. Technol. 2010, 70, 1980–1985. [Google Scholar] [CrossRef]
- Yang, J.; Dong, S.; Xu, C. Mechanical response and microstructure of 2D carbon fiber reinforced ceramic matrix composites with SiC and Ti3SiC2 fillers. Ceram. Int. 2016, 42, 3019–3027. [Google Scholar] [CrossRef]
- Shirvanimoghaddam, K.; Hamim, S.U.; Akbari, M.K.; Fakhrhoseini, S.M.; Khayyam, H.; Pakseresht, A.H.; Ghasali, E.; Zabet, M.; Munir, K.S.; Jia, S.; et al. Carbon fiber reinforced metal matrix composites: Fabrication processes and properties. Compos. Part A Appl. Sci. Manuf. 2017, 92, 70–96. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Rubinstein, M. RH Colby Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Prasse, T.; Cavaille, J.Y.; Bauhofer, W. Electric anisotropy of carbon nanofibre/epoxy resin composites due to electric field induced alignment. Compos. Sci. Technol. 2003, 63, 1835–1841. [Google Scholar] [CrossRef]
- Yang, J.; Downes, R.; Schrand, A.; Park, J.G.; Liang, R.; Xu, C. High electrical conductivity and anisotropy of aligned carbon nanotube nanocomposites reinforced by silicon carbonitride. Scr. Mater. 2016, 124, 21–25. [Google Scholar] [CrossRef]
- Yang, J.; Downes, R.; Yu, Z.; Park, J.G.; Liang, R.; Xu, C. Strong and ultra-flexible polymer-derived silicon carbonitride nanocomposites by aligned carbon nanotubes. Ceram. Int. 2016, 42, 13359–13367. [Google Scholar] [CrossRef]
- Tian, Y.; Park, J.G.; Cheng, Q.; Liang, Z.; Zhang, C.; Wang, B. The fabrication of single-walled carbon nanotube polyelectrolyte multilayer composites by layer-by-layer assembly and magnetic field assisted alignment. Nanotechnology 2009, 20, 335601. [Google Scholar] [CrossRef] [PubMed]
- Steinert, B.W.; Dean, D.R. Magnetic field alignment and electrical properties of solution cast PET-carbon nanotube composite films. Polymer 2009, 50, 898–904. [Google Scholar] [CrossRef]
- Byszewski, P.; Baran, M. Magnetic susceptibility of carbon nanotubes. Europhys. Lett. 1995, 31, 363. [Google Scholar] [CrossRef]
- Camponeschi, E.; Vance, R.; Al-Haik, M.; Garmestani, H.; Tannenbaum, R. Properties of carbon nanotube-polymer composites aligned in a magnetic field. Carbon 2007, 45, 2037–2046. [Google Scholar] [CrossRef]
- Xin, H.; Woolley, A.T. Directional orientation of carbon nanotubes on surfaces using a gas flow cell. Nano Lett. 2004, 4, 1481–1484. [Google Scholar] [CrossRef]
- Hedberg, J.; Dong, L.; Jiao, J. Air flow technique for large scale dispersion and alignment of carbon nanotubes on various substrates. Appl. Phys. Lett. 2005, 86, 143111. [Google Scholar] [CrossRef]
- Sulong, A.B.; Park, J. Alignment of multi-walled carbon nanotubes in a polyethylene matrix by extrusion shear flow: Mechanical properties enhancement. J. Compos. Mater. 2011, 45, 931–941. [Google Scholar] [CrossRef]
- Dijkstra, D.J.; Cirstea, M.; Nakamura, N. The orientational behavior of multiwall carbon nanotubes in polycarbonate in simple shear flow. Rheol. Acta 2010, 49, 769–780. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.W. Aligned multi-walled carbon nanotube-reinforced composites: Processing and mechanical characterization. J. Phys. D Appl. Phys. 2002, 35, L77. [Google Scholar] [CrossRef]
- Wang, D.; Song, P.; Liu, C.; Wu, W.; Fan, S. Highly oriented carbon nanotube papers made of aligned carbon nanotubes. Nanotechnology 2008, 19, 075609. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Dong, S.; Webster, D.; Gilmore, J.; Xu, C. Characterization and Alignment of Carbon Nanofibers under Shear Force in Microchannel. J. Nanomater. 2016, 2016, 40. [Google Scholar] [CrossRef]
- Cheng, Q.; Bao, J.; Park, J.; Liang, Z.; Zhang, C.; Wang, B. High mechanical performance composite conductor: Multi-walled carbon nanotube sheet bismaleimide nanocomposites. Adv. Funct. Mater. 2009, 19, 3219–3225. [Google Scholar] [CrossRef]
- Martin, C.; Sandler, J.; Windle, A.; Schwarz, M.K.; Bauhofer, W.; Schulte, K.; Shaffer, M. Electric field-induced aligned multi-wall carbon nanotube networks in epoxy composites. Polymer 2005, 46, 877–886. [Google Scholar] [CrossRef]
- Park, C.; Wilkinson, J.; Banda, S.; Ounaies, Z.; Wise, K.E.; Sauti, G.; Lillehei, P.T.; Harrison, J.S. Aligned single-wall carbon nanotube polymer composites using an electric field. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 1751–1762. [Google Scholar] [CrossRef]
- Takahashi, T.; Murayama, T.; Higuchi, A.; Awano, H.; Yonetake, K. Aligning vapor-grown carbon fibers in polydimethylsiloxane using dc electric or magnetic field. Carbon 2006, 44, 1180–1188. [Google Scholar] [CrossRef]
- Oliva-Avilés, A.; Avilés, F.; Sosa, V.; Oliva, A.; Gamboa, F. Dynamics of carbon nanotube alignment by electric fields. Nanotechnology 2012, 23, 465710. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Saito, T.; Yamada, H.; Matsushige, K. Aligning single-wall carbon nanotubes with an alternating-current electric field. Appl. Phys. Lett. 2001, 78, 3714–3716. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Ma, C.; Zhang, W.; Zhang, R.P.; Koratkar, N.; Liang, J. Alignment of multiwalled carbon nanotubes in bulk epoxy composites via electric field. J. Appl. Phys. 2009, 105, 054319. [Google Scholar] [CrossRef]
- Zhang, Y.; Chang, A.; Cao, J.; Wang, Q.; Kim, W.; Li, Y.; Morris, N.; Yenilmez, E.; Kong, J.; Dai, H. Electric-field-directed growth of aligned single-walled carbon nanotubes. Appl. Phys. Lett. 2001, 79, 3155–3157. [Google Scholar] [CrossRef]
- Pohl, H.A.; Pohl, H. Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields; Cambridge University Press: Cambridge, UK, 1978; Volume 80. [Google Scholar]
- Hughes, M.P. AC electrokinetics: Applications for nanotechnology. Nanotechnology 2000, 11, 124. [Google Scholar] [CrossRef]
- Fu, S.Y.; Lauke, B. Effects of fiber length and fiber orientation distributions on the tensile strength of short-fiber-reinforced polymers. Compos. Sci. Technol. 1996, 56, 1179–1190. [Google Scholar] [CrossRef]
- Jones, T. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Peng, N.; Zhang, Q.; Li, J.; Liu, N. Influences of ac electric field on the spatial distribution of carbon nanotubes formed between electrodes. J. Appl. Phys. 2006, 100, 024309. [Google Scholar] [CrossRef]
- Von Hippel, A.R. Dielectrics and Waves; Artech House: Norwood, MA, USA, 1954. [Google Scholar]
- Poon, W.C.; Weeks, E.R.; Royall, C.P. On measuring colloidal volume fractions. Soft Matter 2012, 8, 21–30. [Google Scholar] [CrossRef]
- Riedel, R.; Passing, G.; Schönfelder, H.; Brook, R.J. Synthesis of dense silicon-based ceramics at low temperatures. Nature 1992, 355, 714. [Google Scholar] [CrossRef]


| Parameter | Symbol | Parameter | Symbol |
|---|---|---|---|
| Dipole Moment | Exterior Electric Field | ||
| Polarizability | Electric Field Amplitude | A | |
| Electrical Field | Final Work | W | |
| Radius of sphere | a | Boltzmann’s Constant | |
| Vacuum Permittivity | Absolute Temperature | T | |
| Dielectric Constant(Resin) | Dielectrophoretic Force | ||
| Dielectric Constant(fiber) | Conductivity of Carbon Fiber | ||
| Polarization Forces | Conductivity of liquid Resin | ||
| Charge of Carbon Fiber | q | Local Electric Field | |
| Torque | Total Dipole | ||
| Electric Potential | Distance between Carbon Fibers | d | |
| Electric Potential(initial state) | U(0) | Potential of Carbon Fiber Pairs | |
| Dipole Work | Work to bring Carbon Fibers together | ||
| Aligning Dipole Work | Density Ratio | v | |
| Radius of Fiber | R | Density of Carbon Fiber | |
| Length | l | Density of Liquid Resin | |
| Inner Electrical Field | Number of Fibers | n | |
| Radius of Spacing between Carbon Fiber Pairs |
| Parameter | Symbol | Value | Units | |
|---|---|---|---|---|
| Input | Length | l | 0.15 | mm |
| Radius of Fiber | R | 8 | µm | |
| Dielectric Constant(fiber) | 2.85 | |||
| Dielectric Constant(Resin) | 3.45 | |||
| Vacuum Permittivity | 8.85 × 10−12 | F/m | ||
| Output | Electric Field Amplitude | A | 20.12 | V/mm |
| Fiber Diameter = 16 µm | ||||
|---|---|---|---|---|
| Required Electrical Field (V) | Fabrication Temperature | Fabrication Temperature | Fabrication Temperature | |
| 25 °C | 75 °C | 100 °C | ||
| 16 µm | 16 µm | 16 µm | ||
| Fiber Length | 10 mm | 11.26 | 11.71 | 11.91 |
| 50 mm | 1.01 | 1.05 | 1.07 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daniel, J.; Ju, L.; Yang, J.; Sun, X.; Gupta, N.; Schrand, A.; Xu, C. Pearl-Chain Formation of Discontinuous Carbon Fiber under an Electrical Field. J. Manuf. Mater. Process. 2017, 1, 22. https://doi.org/10.3390/jmmp1020022
Daniel J, Ju L, Yang J, Sun X, Gupta N, Schrand A, Xu C. Pearl-Chain Formation of Discontinuous Carbon Fiber under an Electrical Field. Journal of Manufacturing and Materials Processing. 2017; 1(2):22. https://doi.org/10.3390/jmmp1020022
Chicago/Turabian StyleDaniel, Justin, Licheng Ju, Jinshan Yang, Xiangzhen Sun, Nikhil Gupta, Amanda Schrand, and Chengying Xu. 2017. "Pearl-Chain Formation of Discontinuous Carbon Fiber under an Electrical Field" Journal of Manufacturing and Materials Processing 1, no. 2: 22. https://doi.org/10.3390/jmmp1020022
APA StyleDaniel, J., Ju, L., Yang, J., Sun, X., Gupta, N., Schrand, A., & Xu, C. (2017). Pearl-Chain Formation of Discontinuous Carbon Fiber under an Electrical Field. Journal of Manufacturing and Materials Processing, 1(2), 22. https://doi.org/10.3390/jmmp1020022






