Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review
Abstract
1. Introduction
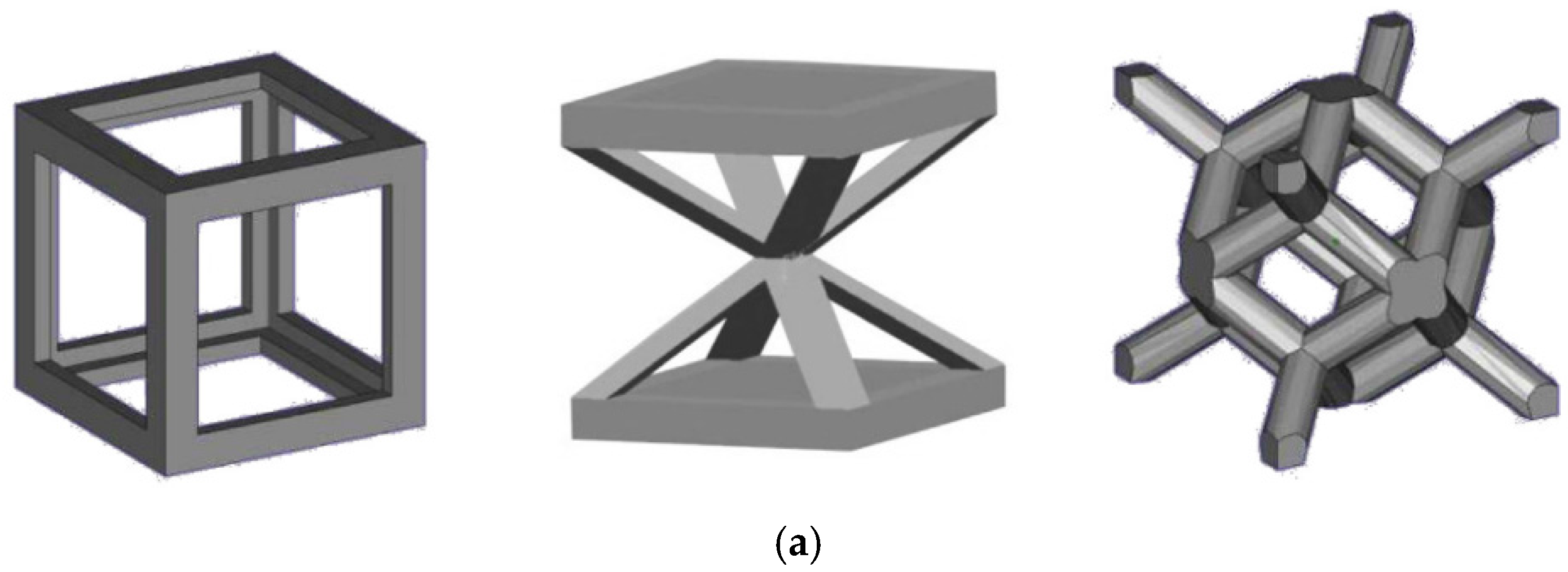
2. Lattice Structure
2.1. Classification
2.2. Manufacturing
2.3. Characterization
2.4. Modelling and Validation
3. FGM
3.1. Classification and Manufacturing
3.2. Case Studies
4. Challenges and Future Directions
- The overall characterization of lattice structures needs to be improved. A standard protocol for assessing the dimensions/microstructure/mechanical performance needs to be developed.
- There is a need to trace the defects of lattice structures manufactured by AM technology to their root causes. This can be performed by creating a process-structure-property (PSP) relationships for different lattice structures.
- A library for the different unit cells used in orthopedic implants should be established to allow for the assessment of different unit cells’ performances in different applications. Moreover, the database should contain both mechanical and biological information about the different unit cells.
- The development of new FGM designed from biomaterials using AM technologies should be studied in more depth. The combination of metallic, ceramic, and inorganic materials could result in an implant having high functionality.
- Integration between the simulation and AM of implants fabricated from FGM is needed to ensure that the gap between modelling and fabrication is eliminated.
- The long-term performance of functionally graded implants produced by additive manufacturing technologies needs to be assessed. The in vivo performance determines the benefits and limitations from a biological point of view.
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Tofail, S.A.M.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2017. [Google Scholar] [CrossRef]
- Gibson, I. Advanced Manufacturing Technology for Medical Applications; John Wiley & Sons Ltd.: London, UK, 2005; Volume 53. [Google Scholar]
- Guo, N.; Leu, M.C. Additive manufacturing: Technology, applications and research needs. Front. Mech. Eng. 2013, 8, 215–243. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing; Springer: New York, NY, USA, 2014. [Google Scholar]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.C.L.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput. Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Niinomi, M.; Narushima, T.; Nakai, M. Advances in Metallic Biomaterials, Processing and Applications; Springer: Berlin/Heidelberg, Germany, 2015; Volume 3. [Google Scholar]
- Rajpura, A.; Kendoff, D.; Board, T.N. The current state of bearing surfaces in total hip replacement. Bone Jt. J. 2014, 96-B, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Thouas, G.A. Metallic implant biomaterials. Mater. Sci. Eng. R Rep. 2015, 87, 1–57. [Google Scholar] [CrossRef]
- Huiskes, R.; Weinans, H.; van Rietbergen, B. The relationship between stress shielding and bone resorption around total hip stems and the effects of flexible materials. Clin. Orthop. Relat. Res. 1992, 274, 124–134. [Google Scholar] [CrossRef]
- Frost, H.M. Skeletal structural adaptations to mechanical usage (SATMU): 3. The hyaline cartilage modeling problem. Anat. Rec. 1990, 226, 423–432. [Google Scholar] [CrossRef] [PubMed]
- Attar, H.; Löber, L.; Funk, A.; Calin, M.; Zhang, L.C.; Prashanth, K.G.; Scudino, S.; Zhang, Y.S.; Eckert, J. Mechanical behavior of porous commercially pure Ti and Ti-TiB composite materials manufactured by selective laser melting. Mater. Sci. Eng. A 2015, 625, 350–356. [Google Scholar] [CrossRef]
- Attar, H.; Bönisch, M.; Calin, M.; Zhang, L.C.; Scudino, S.; Eckert, J. Selective laser melting of in situ titanium-titanium boride composites: Processing, microstructure and mechanical properties. Acta Mater. 2014, 76, 13–22. [Google Scholar] [CrossRef]
- Okulov, I.V.; Volegov, A.S.; Attar, H.; Bönisch, M.; Ehtemam-Haghighi, S.; Calin, M.; Eckert, J. Composition optimization of low modulus and high-strength TiNb-based alloys for biomedical applications. J. Mech. Behav. Biomed. Mater. 2017, 65, 866–871. [Google Scholar] [CrossRef] [PubMed]
- Levine, B.R.; Fabi, D.W. Porous metals in orthopedic applications—A review. Materialwiss. Werkst. 2010, 41, 1001–1010. [Google Scholar] [CrossRef]
- Van Der Stok, J.; Van Der Jagt, O.P.; Amin Yavari, S.; De Haas, M.F.P.; Waarsing, J.H.; Jahr, H.; Van Lieshout, E.M.M.; Patka, P.; Verhaar, J.A.N.; Zadpoor, A.A.; et al. Selective laser melting-produced porous titanium scaffolds regenerate bone in critical size cortical bone defects. J. Orthop. Res. 2013, 31, 792–799. [Google Scholar] [CrossRef] [PubMed]
- Bothe, R.T.; Beaton, L.E.; Davenport, H.A. Reaction of bone to multiple metallic implants. Surg. Gynecol. Obstet. 1940, 71, 598. [Google Scholar]
- Leventhal, G.S. Titanium, a Metal for Surgery. J. Bone Jt. Surg. 1951, 33A, 473–474. [Google Scholar] [CrossRef]
- Harrysson, O.L.A.; Cansizoglu, O.; Marcellin-Little, D.J.; Cormier, D.R.; West, H.A. Direct metal fabrication of titanium implants with tailored materials and mechanical properties using electron beam melting technology. Mater. Sci. Eng. C 2008, 28, 366–373. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Martinez, E.; Medina, F.; Wicker, R.B. Next generation orthopaedic implants by additive manufacturing using electron beam melting. Int. J. Biomater. 2012, 2012, 245727. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; Vahabzadeh, S.; Bandyopadhyay, A. Bone tissue engineering using 3D printing. Mater. Today 2013, 16, 496–504. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Shah, K.; Haq, I.; Khan, A.; Shah, S.A.; Khan, M.; Pinkerton, A.J. Parametric study of development of Inconel-steel functionally graded materials by laser direct metal deposition. Mater. Des. 2014, 54, 531–538. [Google Scholar] [CrossRef]
- Hao, L.; Harris, R. Customised implants for bone replacement and growth. In Bio-Materials and Prototyping Applications in Medicine; Springer: Berlin, Germany, 2008; pp. 79–108. [Google Scholar]
- Pompe, W.; Worch, H.; Epple, M.; Friess, W.; Gelinsky, M.; Greil, P.; Hempel, U.; Scharnweber, D.; Schulte, K. Functionally graded materials for biomedical applications. Mater. Sci. Eng. A 2003, 362, 40–60. [Google Scholar] [CrossRef]
- Sola, A.; Bellucci, D.; Cannillo, V. Functionally graded materials for orthopedic applications-an update on design and manufacturing. Biotechnol. Adv. 2016, 34, 504–531. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Rosen, D.W.; Duty, C.E. Comparing mechanical and geometrical properties of lattice structure fabricated using Electron Beam Melting. Solid Free. Fabr. Proc. 2015, 1, 1359–1370. [Google Scholar]
- Rashed, M.G.; Ashraf, M.; Mines, R.A.W.; Hazell, P.J. Metallic microlattice materials: A current state of the art on manufacturing, mechanical properties and applications. Mater. Des. 2016, 95, 518–533. [Google Scholar] [CrossRef]
- Tan, X.P.; Tan, Y.J.; Chow, C.S.L.; Tor, S.B.; Yeong, W.Y. Metallic powder-bed based 3D printing of cellular scaffolds for orthopaedic implants: A state-of-the-art review on manufacturing, topological design, mechanical properties and biocompatibility. Mater. Sci. Eng. C 2017, 76, 1328–1343. [Google Scholar] [CrossRef] [PubMed]
- Cansizoglu, O.; Cormier, D.; Harrysson, O.; West, H.; Mahale, T. An Evaluation of non-stochastic lattice structures fabricated via electron beam melting. In Proceedings of the 17th Solid Freeform Fabrication Symposium, Austin, TX, USA, 6–8 August 2006; pp. 209–219. [Google Scholar]
- Chu, T.G.; Halloran, J.W. An image-based approach for designing and manufacturing craniofacial scaffolds. Int. J. Oral Maxillofac. Surg. 2000, 29, 67–71. [Google Scholar]
- Giannitelli, S.M.; Accoto, D.; Trombetta, M.; Rainer, A. Current trends in the design of scaffolds for computer-aided tissue engineering. Acta Biomater. 2014, 10, 580–594. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Radman, A.; Xie, Y.M. Topological design of microstructures of cellular materials for maximum bulk or shear modulus. Comput. Mater. Sci. 2011, 50, 1861–1870. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review. Biomaterials 2016, 83, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Bobbert, F.S.L.; Lietaert, K.; Eftekhari, A.A.; Pouran, B.; Ahmadi, S.M.; Weinans, H.; Zadpoor, A.A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [PubMed]
- Hao, L.; Raymont, D.; Yan, C.; Hussein, A.; Young, P. Design and additive manufacturing of cellular lattice structures. Innov. Dev. Virtual Phys. Prototyp. 2011, 249–254. [Google Scholar] [CrossRef]
- Lin, C.; Hsiao, C.; Chen, P.; Hollister, S.J. Interbody fusion cage design using integrated global layout and local microstructure topology optimization. Spine 2004, 29, 1747–1754. [Google Scholar] [CrossRef] [PubMed]
- Li, S.J.; Xu, Q.S.; Wang, Z.; Hou, W.T.; Hao, Y.L.; Yang, R.; Murr, L.E. Influence of cell shape on mechanical properties of Ti-6Al-4V meshes fabricated by electron beam melting method. Acta Biomater. 2014, 10, 4537–4547. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Luo, Z.; Zhang, N.; Qin, Q. Topological shape optimization of multifunctional tissue engineering scaffolds with level set method. Struct. Multidiscip. Optim. 2016, 54, 333–347. [Google Scholar] [CrossRef]
- Ryan, G.; Pandit, A.; Apatsidis, D.P. Fabrication methods of porous metals for use in orthopaedic applications. Biomaterials 2006, 27, 2651–2670. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Frith, J.E.; Dehghan-Manshadi, A.; Attar, H.; Kent, D.; Soro, N.D.M.; Bermingham, M.J.; Dargusch, M.S. Mechanical properties and biocompatibility of porous titanium scaffolds for bone tissue engineering. J. Mech. Behav. Biomed. Mater. 2017, 75, 169–174. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.W.; Yong, M.S.; Tay, B.Y.; Lim, C.S. Synthesis and bioactivity of porous Ti alloy prepared by foaming with TiH2. Mater. Sci. Eng. C 2009, 29, 1515–1520. [Google Scholar] [CrossRef]
- Bram, M.; Stiller, C.; Buchkremer, H.P.; Stöver, D.; Baur, H. High-porosity titanium, stainless Steel, and superalloy parts. Adv. Eng. Mater. 2000, 2, 196–199. [Google Scholar] [CrossRef]
- Deng, X.; Wang, Y.; Yan, J.; Liu, T.; Wang, S. Topology optimization of total femur structure: Application of parameterized Level set method under geometric constraints. J. Mech. Des. 2015, 138, 11402. [Google Scholar] [CrossRef]
- Das, M.; Balla, V.K.; Kumar, T.S.S.; Manna, I. Fabrication of biomedical implants using laser engineered net shaping (LENSTM). Trans. Indian Ceram. Soc. 2013, 72, 169–174. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Ramirez, D.A.; Martinez, E.; Hernandez, J.; Amato, K.N.; Shindo, P.W.; Medina, F.R.; Wicker, R.B. Metal fabrication by additive manufacturing using laser and electron beam melting technologies. J. Mater. Sci. Technol. 2012, 28, 1–14. [Google Scholar] [CrossRef]
- Zhao, X.; Li, S.; Zhang, M.; Liu, Y.; Sercombe, T.B.; Wang, S.; Hao, Y.; Yang, R.; Murr, L.E. Comparison of the microstructures and mechanical properties of Ti–6Al–4V fabricated by selective laser melting and electron beam melting. Mater. Des. 2015, 95, 21–31. [Google Scholar] [CrossRef]
- Attar, H.; Ehtemam-Haghighi, S.; Kent, D.; Wu, X.; Dargusch, M.S. Comparative study of commercially pure titanium produced by laser engineered net shaping, selective laser melting and casting processes. Mater. Sci. Eng. A 2017, 705, 385–393. [Google Scholar] [CrossRef]
- Sallica-Leva, E.; Jardini, A.L.; Fogagnolo, J.B. Microstructure and mechanical behavior of porous Ti-6Al-4V parts obtained by selective laser melting. J. Mech. Behav. Biomed. Mater. 2013, 26, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.M.; Hedayati, R.; Ashok Kumar Jain, R.K.; Li, Y.; Leeflang, S.; Zadpoor, A.A. Effects of laser processing parameters on the mechanical properties, topology, and microstructure of additively manufactured porous metallic biomaterials: A vector-based approach. Mater. Des. 2017, 134, 234–243. [Google Scholar] [CrossRef]
- Wauthle, R.; Vrancken, B.; Beynaerts, B.; Jorissen, K.; Schrooten, J.; Kruth, J.P.; Van Humbeeck, J. Effects of build orientation and heat treatment on the microstructure and mechanical properties of selective laser melted Ti6Al4V lattice structures. Addit. Manuf. 2015, 5, 77–84. [Google Scholar] [CrossRef]
- Sing, S.L.; Yeong, W.Y.; Wiria, F.E.; Tay, B.Y. Characterization of titanium lattice structures fabricated by selective laser melting using an adapted compressive test method. Exp. Mech. 2016, 56, 735–748. [Google Scholar] [CrossRef]
- Sing, S.L.; Wiria, F.E.; Yeong, W.Y. Selective laser melting of lattice structures: A statistical approach to manufacturability and mechanical behavior. Robot. Comput. Integr. Manuf. 2018, 49, 170–180. [Google Scholar] [CrossRef]
- Sing, S.L.; Miao, Y.; Wiria, F.E.; Yeong, W.Y. Manufacturability and mechanical testing considerations of metallic scaffolds fabricated using selective laser melting: A review. Biomed. Sci. Eng. 2016, 1. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Medina, F.; Martinez, E.; Martinez, J.L.; Hernandez, D.H.; Machado, B.I.; Ramirez, D.A.; Wicker, R.B. Characterization of Ti–6Al–4V open cellular foams fabricated by additive manufacturing using electron beam melting. Mater. Sci. Eng. A 2010, 527, 1861–1868. [Google Scholar] [CrossRef]
- Karlsson, J.; Horn, T.; West, H.; Aman, R.; Snis, A.; Engqvist, H.; Lausmaa, J.; Harrysson, O. Thickness dependency of mechanical properties for thin-walled titanium parts manufactured by Electron Beam Melting (EBM). Addit. Manuf. 2016, 12, 45–50. [Google Scholar]
- Cheng, X.Y.; Li, S.J.; Murr, L.E.; Zhang, Z.B.; Hao, Y.L.; Yang, R.; Medina, F.; Wickerc, R.B. Compression deformation behavior of Ti–6A1–4V alloy with cellular structures fabricated by electron beam melting. J. Mech. Behav. Biomed. Mater. 2012, 16, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Cansizoglu, O.; Harrysson, O.; Cormier, D.; West, H.; Mahale, T. Properties of Ti–6Al–4V non-stochastic lattice structures fabricated via electron beam melting. Mater. Sci. Eng. A 2008, 492, 468–474. [Google Scholar] [CrossRef]
- Ashby, A.M.F. The Properties of Foams and Lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.M.; Yavari, S.A.; Wauthle, R.; Pouran, B.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Additively manufactured open-cell porous biomaterials made from six different space-filling unit cells: The mechanical and morphological properties. Materials 2015, 8, 1871–1896. [Google Scholar] [CrossRef] [PubMed]
- Yánez, A.; Herrera, A.; Martel, O.; Monopoli, D.; Afonso, H. Compressive behaviour of gyroid lattice structures for human cancellous bone implant applications. Mater. Sci. Eng. C 2016, 68, 445–448. [Google Scholar] [CrossRef] [PubMed]
- Amin Yavari, S.; Wauthle, R.; Van Der Stok, J.; Riemslag, A.C.; Janssen, M.; Mulier, M.; Kruth, J.P.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Fatigue behavior of porous biomaterials manufactured using selective laser melting. Mater. Sci. Eng. C 2013, 33, 4849–4858. [Google Scholar] [CrossRef] [PubMed]
- Hrabe, N.W.; Heinl, P.; Flinn, B.; Ko, C.; Bordia, R.K. Compression-compression fatigue of selective electron beam melted cellular titanium ( Ti–6Al–4V). J. Biomed. Mater. Res. B Appl. Biomater. 2011, 99, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Amin Yavari, S.; Ahmadi, S.M.; Wauthle, R.; Pouran, B.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Relationship between unit cell type and porosity and the fatigue behavior of selective laser melted meta-biomaterials. J. Mech. Behav. Biomed. Mater. 2015, 43, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Fang, G.; Zhou, J. Additively manufactured scaffolds for bone tissue engineering and the prediction of their mechanical. Materials 2017, 10, 50. [Google Scholar] [CrossRef] [PubMed]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Wauthle, R.; Ahmadi, S.M.; Amin Yavari, S.; Mulier, M.; Zadpoor, A.A.; Weinans, H.; Van Humbeeck, J.; Kruth, J.P.; Schrooten, J. Revival of pure titanium for dynamically loaded porous implants using additive manufacturing. Mater. Sci. Eng. C 2015, 54, 94–100. [Google Scholar] [CrossRef] [PubMed]
- Speirs, M.; Van Hooreweder, B.; Van Humbeeck, J.; Kruth, J.-P. Fatigue behaviour of NiTi shape memory alloy scaffolds produced by SLM, a unit cell design comparison. J. Mech. Behav. Biomed. Mater. 2017, 70, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Hao, L.; Hussein, A.; Young, P. Ti–6Al–4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J. Mech. Behav. Biomed. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef] [PubMed]
- Mines, R.A.W.; Shen, Y.; Cantwell, W.J.; Brooks, W.; Sutcliffe, C.J. The influence of processing parameters on the mechanical properties of selectively laser melted stainless steel microlattice structures. J. Manuf. Sci. Eng. 2010, 132, 1–12. [Google Scholar]
- Mines, W. Compressive behaviour of stainless steel micro-lattice structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar]
- Smith, M.; Guan, Z.; Cantwell, W.J. Finite element modelling of the compressive response of lattice structures manufactured using the selective laser melting technique. Int. J. Mech. Sci. 2013, 67, 28–41. [Google Scholar] [CrossRef]
- Quevedo González, F.J.; Nuño, N. Finite element modelling approaches for well-ordered porous metallic materials for orthopaedic applications: Cost effectiveness and geometrical considerations. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Chen, W.; Bao, H.; Zhang, H.; Peng, Q. Real-time voxelization for complex polygonal models. In Proceedings of the IEEE 12th Pacific Conference on Computer Graphics and Applications, 6–8 October 2004; pp. 43–50. [Google Scholar]
- Dumas, M.; Terriault, P.; Brailovski, V. Modelling and characterization of a porosity graded lattice structure for additively manufactured biomaterials. Mater. Des. 2017, 121, 383–392. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.; Subhash, G. Effects of cell shape and strut cross-sectional area variations on the elastic properties of three-dimensional open-cell foams. J. Mech. Phys. Solids 2006, 54, 783–806. [Google Scholar] [CrossRef]
- Herrera, A.; Yánez, A.; Martel, O.; Afonso, H.; Monopoli, D. Computational study and experimental validation of porous structures fabricated by electron beam melting: A challenge to avoid stress shielding. Mater. Sci. Eng. C 2014, 45, 89–93. [Google Scholar] [CrossRef] [PubMed]
- González, F.J.Q.; Nuño, N. Finite element modeling of manufacturing irregularities of porous materials. Biomater. Biomech. Bioeng. 2016, 3, 1–14. [Google Scholar] [CrossRef]
- Crupi, V.; Kara, E.; Epasto, G.; Guglielmino, E.; Aykul, H. Static behavior of lattice structures produced via direct metal laser sintering technology. Mater. Des. 2017. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Montazerian, H.; Darabi, A.C.; Anaraki, A.P.; Ahmadi, S.M.; Zadpoor, A.A.; Schmauder, S. Failure mechanisms of additively manufactured porous biomaterials: Effects of porosity and type of unit cell. J. Mech. Behav. Biomed. Mater. 2015, 50, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Campoli, G.; Borleffs, M.S.S.; Amin Yavari, S.; Wauthle, R.; Weinans, H.; Zadpoor, A.A.A. Mechanical properties of open-cell metallic biomaterials manufactured using additive manufacturing. Mater. Des. 2013, 49, 957–965. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Montazerian, H.; Darabi, A.C.; Zargarian, A.; Schmauder, S. The relationships between deformation mechanisms and mechanical properties of additively manufactured porous biomaterials. J. Mech. Behav. Biomed. Mater. 2017, 70, 28–42. [Google Scholar] [CrossRef] [PubMed]
- Rasheedat Modupe Mahamood, E.T.A.; Tammas-Williams, S.; Todd, I. Functionally Graded Materials; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Pei, E.; Loh, G.H.; Harrison, D.; de Amorim Almeida, H.; Monzón Verona, M.D.; Paz, R. Exploring the concept of functionally graded additive manufacturing. Assem. Autom. 2017, 37, 147–153. [Google Scholar] [CrossRef]
- Roop Kumar, R.; Wang, M. Functionally graded bioactive coatings of hydroxyapatite/titanium oxide composite system. Mater. Lett. 2002, 55, 133–137. [Google Scholar] [CrossRef]
- Mahamood, R.M.; Akinlabi, E.T.; Shukla, M.; Pityana, S. Functionally graded material: An overview. In Proceedings of the World Congress on Engineering (WCE 2012), London, UK, 4–6 July 2012; Volume III, pp. 2–6. [Google Scholar]
- Kieback, B.; Neubrand, A.; Riedel, H. Processing techniques for functionally graded materials. Mater. Sci. Eng. A 2003, 362, 81–105. [Google Scholar] [CrossRef]
- Watanabe, Y.; Inaguma, Y.; Sato, H.; Miura-Fujiwara, E. A novel fabrication method for functionally graded materials under centrifugal force: The centrifugal mixed-powder method. Material 2009, 2, 2510–2525. [Google Scholar] [CrossRef]
- Boccaccio, A.; Uva, A.E.; Fiorentino, M.; Mori, G.; Monno, G. Geometry design optimization of functionally graded scaffolds for bone tissue engineering: A mechanobiological approach. PLoS ONE 2016, 11, e0146935. [Google Scholar] [CrossRef] [PubMed]
- Sing, S.L.; An, J.; Yeong, W.Y.; Wiria, F.E. Laser and electron-beam powder-bed additive manufacturing of metallic implants: A review on processes, materials and designs. J. Orthop. Res. 2016, 34, 369–385. [Google Scholar] [CrossRef] [PubMed]
- Krishna, B.V.; Bose, S.; Bandyopadhyay, A. Low stiffness porous Ti structures for load-bearing implants. Acta Biomater. 2007, 3, 997–1006. [Google Scholar] [CrossRef] [PubMed]
- Choy, S.Y.; Sun, C.N.; Leong, K.F.; Tan, K.E.; Wei, J. Functionally graded material by additive manufacturing. In Proceedings of the 2nd International Conference on Progress in Additive Manufacturing (PRO-AM), Singapore, 16–19 May 2016; pp. 206–211. [Google Scholar]
- Popovich, V.A.; Borisov, E.V.; Popovich, A.A.; Sufiiarov, V.S.; Masaylo, D.V.; Alzine, L. Functionally graded Inconel 718 processed by additive manufacturing: Crystallographic texture, anisotropy of microstructure and mechanical properties. Mater. Des. 2016, 114, 441–449. [Google Scholar] [CrossRef]
- Popoola, P.; Farotade, G.; Fatoba, O.; Popoola, O. Laser engineering net shaping method in the area of development of functionally graded materials (FGMs) for aero engine applications—A review. In Fiber Laser; InTech: Vienna, Austria, 2016; pp. 383–399. [Google Scholar]
- Gabbrielli, R.; Turner, I.; Bowen, C.R. Development of modelling methods for materials to be used as bone substitutes. Key Eng. Mater. 2008, 361, 903–906. [Google Scholar] [CrossRef]
- Gabbrielli, R.; Turner, I.G.; Bowen, C.R.; Wang, H.; Johnston, S.; Rosen, D.; Cheng, A.; Humayun, A.; Cohen, D.J.; Boyan, B.D.; et al. Design of a graded cellular structure for an acetabular hip replacement component. Biofabrication 2006, 6, 45007. [Google Scholar]
- España, F.A.; Balla, V.K.; Bose, S.; Bandyopadhyay, A. Design and fabrication of CoCrMo alloy based novel structures for load bearing implants using laser engineered net shaping. Mater. Sci. Eng. C 2010, 30, 50–57. [Google Scholar] [CrossRef]
- Hazlehurst, K.B.; Wang, C.J.; Stanford, M. The potential application of a Cobalt Chrome Molybdenum femoral stem with functionally graded orthotropic structures manufactured using Laser Melting technologies. Med. Hypotheses 2013, 81, 1096–1099. [Google Scholar] [CrossRef] [PubMed]
- Hazlehurst, K.B.; Wang, C.J.; Stanford, M. An investigation into the flexural characteristics of functionally graded cobalt chrome femoral stems manufactured using selective laser melting. Mater. Des. 2014, 60, 177–183. [Google Scholar] [CrossRef]
- Limmahakhun, S.; Oloyede, A.; Chantarapanich, N. Alternative designs of load—Sharing cobalt chromium graded femoral stems. Mater. Today Commun. 2017, 12, 1–10. [Google Scholar] [CrossRef]
- Quevedo González, F.J. Computational Design of Functionally Graded Hip Implants by Means of Additively Manufactured Porous Materials. Ph.D. Thesis, École de Technologie Supérieure, Montreal, QC, Canada, 2016. [Google Scholar]
- Arabnejad, S.; Pasini, D. Multiscale Design and Multiobjective Optimization of Orthopedic Hip Implants with Functionally Graded Cellular Material. J. Biomech. Eng. 2012, 134, 31004. [Google Scholar] [CrossRef] [PubMed]
- Arabnejad, S.; Johnston, B.; Tanzer, M.; Pasini, D. Fully porous 3D printed titanium femoral stem to reduce stress-shielding following total hip arthroplasty. J. Orthop. Res. 2016, 23, 29–31. [Google Scholar] [CrossRef] [PubMed]
- Arabnejad, S.; Pasini, D. Fatigue design of a mechanically biocompatible lattice for a proof-of-concept femoral stem. J. Mech. Behav. Biomed. Mater. 2013, 22, 65–83. [Google Scholar] [CrossRef] [PubMed]
- Oshkour, A.; Abu Osman, N.; Yau, Y.; Tarlochan, F.; Wan Abas, W. Design of new generation femoral prostheses using functionally graded materials: A finite element analysis. Proc. Inst. Mech. Eng. H 2012, 227, 3–17. [Google Scholar] [CrossRef] [PubMed]
- Oshkour, A.; Abu Osman, N.; Davoodi, M.; Yau, Y.; Tarlochan, F.; Wan Abas, W.; Bayat, M. Finite element analysis on longitudinal and radial functionally graded femoral prosthesis. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 1412–1427. [Google Scholar] [CrossRef] [PubMed]
- Hedia, H.S.; Shabara, M.A.N.; El-Midany, T.T.; Fouda, N. A method of material optimization of cementless stem through functionally graded material. Int. J. Mech. Mater. Des. 2005, 1, 329–346. [Google Scholar] [CrossRef]
- Al-Jassir, F.F.; Fouad, H.; Alothman, O.Y. In vitro assessment of Function Graded (FG) artificial Hip joint stem in terms of bone/cement stresses: 3D Finite Element (FE) study. Biomed. Eng. Online 2013, 12, 5. [Google Scholar] [CrossRef] [PubMed]
- Bahraminasab, M.; Sahari, B.B.; Edwards, K.L.; Farahmand, F.; Hong, T.S.; Naghibi, H. Material tailoring of the femoral component in a total knee replacement to reduce the problem of aseptic loosening. Mater. Des. 2013, 52, 441–451. [Google Scholar] [CrossRef]


| Unit Cells | Material/Method | Relative Density (%) | Pore Size (µm) | Strut Size (µm) | Yield Strength (Mpa) | Normalized Fatigue Strength at 106 Cycles | Ref. | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Nominal | Measured | Nominal | Measured | Nominal | Measured | |||||
| Cube | Ti-6AL-4V/SLM | 24.2–39.1 | 29.7–49.3 | 2040–1000 | 1960–765 | 450–800 | 466–941 | 7.28–163.02 | --- | [65] |
| Ti-6AL-4V/SLM | 11–34 | 11–36 | 1452–1080 | 1413–1020 | 348–720 | 451–823 | 29.9–112.6 | 0.2 σy | [63] | |
| Diamond | Ti-6AL-4V/EBM | 17–40 | --- | 1540–570 | 430–570 | --- | 19.1–112.73 | 0.15-0.25 σy | [62] | |
| Ti-6AL-4V/SLM | 20–33 | 17–36 | 1040–807 | 1142–826 | 234–693 | 350–564 | 6.8–70.6 | 0.32 σy | [63] | |
| Dodecahedron | Ti-6AL-4V/SLM | 10–34 | 11–32 | 1250–950 | 1305–920 | 250–550 | 246–506 | ~10–120 | --- | [59] |
| Ti-6AL-4V/SLM | --- | 15.8–31.6 | 500–450 | 608–560 | 120–230 | 140–251 | 19.4–117.2 | 0.12 σy | [61] | |
| CP Ti/SLM | 19–34 | 18.3–33.7 | 500–450 | --- | 120–230 | --- | 8.6–36.9 | 0.32-0.51 σy | [66] | |
| Truncated cuboctahedron | Ti-6AL-4V/SLM | 18–36 | 19–36 | 1024–807 | 1142–862 | 324–693 | 350–564 | ~30–150 | ---- | [59] |
| Ti-6AL-4V/SLM | 11–34 | 13–37 | 1452–1080 | 1413–1020 | 348–720 | 451–823 | 41.4–110.1 | 0.35 σy | [63] | |
| Gyroid | NiTi/SLM | 21.7 | 25.2 | 850 | --- | 320 | 298 | 29 | 0.2 σy | [67] |
| Ti-6AL-4V/SLM | 5–20 | --- | 1600–560 | --- | --- | --- | 6.5–81.3 | --- | [68] | |
| Ti-6AL-4V/SLM | 31–49 | 38–52 | --- | 464–406 | 169–261 | 258–330 | ~120–240 | ~0.6 σy | [34] | |
| Unit Cell | Material/Method | Material Model | Element | Model Size | Input Model | Stiffness Prediction Deviation between Numerical/Experimental | Ref. |
|---|---|---|---|---|---|---|---|
BCC 1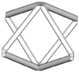 | Stainless steel/SLM | Same as bulk | 1D and 3D | Infinite | CAD | Underestimated by 10% when using 1D elements Initial prediction is acceptable in 3D elements, | [70] |
| 316 L SS/SLM | Less than bulk | 1D and 3D | Finite | CAD | Overestimated by 15% 1D and 3D mesh elements | [71] | |
| Ti-6AL-4V/SLM | Same as bulk | 3D | Finite/Infinite | CAD | Overestimated by 5% finite Overestimated by 9% infinite, | [78] | |
BCC-Z 2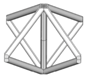 | 316 L SS/SLM | Less than bulk | 1D and 3D | Finite | CAD | Overestimated by 5% 1D mesh elements 30% by 3D mesh | [71] |
Diamond | Ti-6AL-4V/SLM | Linear isotropic | 3D | Finite | CAD | Overestimated by an average of 27.5 ± 3.1% | [76] |
| Ti-6AL-4V/SLM | Same as bulk | 3D | Finite | Voxel mesh | Overestimated by 40% | [74] | |
| Ti-6AL-4V/SLM | Elastic–plastic model | 3D | Infinite | CAD | Overestimated and underestimated by 6–21% | [79] | |
Cubic | Ti-6AL-4V/EBM | ---- | 1D | Finite | CAD | Overestimated specially in high densities | [80] |
| Ti-6AL-4V/SLM | Elastic–plastic model | 3D | Infinite | CAD | Overestimated by 21–117% | [79] | |
I-WP 3 | Ti-6AL-4V/SLM | Elastic–plastic model | 3D | Finite | Voxel mesh | Underestimated by 6.6% (30% relative density) Overestimated by 10.2% (45% relative density) | [81] |
F-RD 3 | Ti-6AL-4V/SLM | Elastic–plastic model | 3D | Finite | Voxel mesh | Overestimated by 31.6% | [81] |
| FGM Type | Proposed Design | Description | Ref. |
|---|---|---|---|
| Porosity | 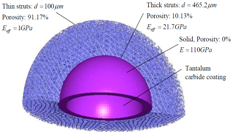 |
| [95] |
| Porosity and Composition | 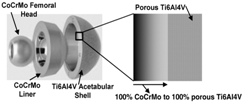 |
| [96] |
| Porosity | 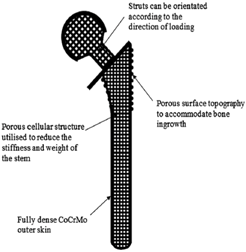 |
| [97] |
| Porosity | 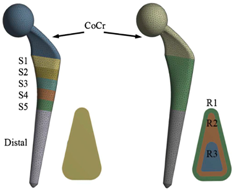 |
| [99] |
| Porosity | 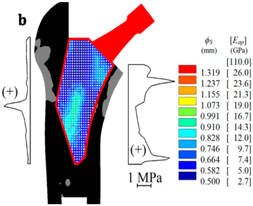 |
| [100] |
| Porosity | 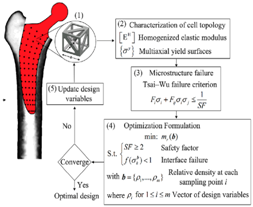 |
| [102] |
| Composition | 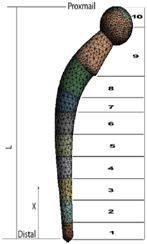 |
| [107] |
| Composition and porosity | 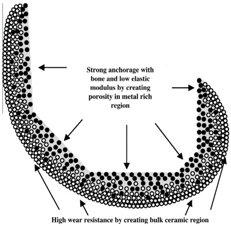 |
| [108] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, D.; Elbestawi, M.A. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review. J. Manuf. Mater. Process. 2017, 1, 13. https://doi.org/10.3390/jmmp1020013
Mahmoud D, Elbestawi MA. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review. Journal of Manufacturing and Materials Processing. 2017; 1(2):13. https://doi.org/10.3390/jmmp1020013
Chicago/Turabian StyleMahmoud, Dalia, and Mohamed A. Elbestawi. 2017. "Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review" Journal of Manufacturing and Materials Processing 1, no. 2: 13. https://doi.org/10.3390/jmmp1020013
APA StyleMahmoud, D., & Elbestawi, M. A. (2017). Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review. Journal of Manufacturing and Materials Processing, 1(2), 13. https://doi.org/10.3390/jmmp1020013





