Configuration Trade-Off and Co-Design Optimization of Hybrid-Electric VTOL Propulsion Systems

Highlights

What are the main findings?

• A novel powertrain configuration trade-off and optimization framework is proposed.
• Configuration selection principles are established for diverse mission scenarios.

What is the implication of the main finding?

• The method offers a scalable approach to accelerate early-stage decision-making.
• The trade-off results provide guidelines for advancing component technologies.

Abstract

Unmanned vertical takeoff and landing (VTOL) aircraft are increasingly deployed for logistics, surveillance, and urban air mobility (UAM) applications. However, the limitations of full-electric (FE) and internal combustion engine (ICE) systems in meeting diverse mission requirements have motivated the development of hybrid-electric (HE) propulsion systems. The design of HE powertrains remains challenging due to configuration flexibility and the lack of unified criteria for performance trade-offs among FE, ICE-powered, and HE configurations. This study proposes an integrated propulsion co-design framework coupling power allocation, energy management, and component capacity constraints through parametric system modeling. These interdependencies are represented by three key matching parameters: the power ratio (Φ), energy ratio (Ω), and maximum continuous discharge rate (rc). Through Pareto-optimal design space exploration, trade-off analysis results and optimization principles are derived for diverse mission scenarios such as UAM, remote sensing, and military surveillance. Different technological conditions are considered to guide component-level technological advancements. The method was applied to the power system retrofit of the Great White eVTOL. Subsystem steady-state tests provided accurate design inputs, and a simulation model was developed to reproduce the full flight mission. By comparing the simulation with flight-test measurements, mean absolute percentage errors of 8.91% for instantaneous fuel consumption and 0.26% for battery voltage were obtained. Based on these error magnitudes, a dynamic design margin was defined and then incorporated into a subsequent re-optimization, which achieved the 1.5 h endurance target with a 10.49% increase in cost per ton-kilometer relative to the initial design. These results demonstrate that the proposed co-design methodology offers a scalable, data-driven foundation for early-stage hybrid-electric VTOL powertrain design, enabling iterative performance correction and supporting system optimization in subsequent design stages.

1. Introduction

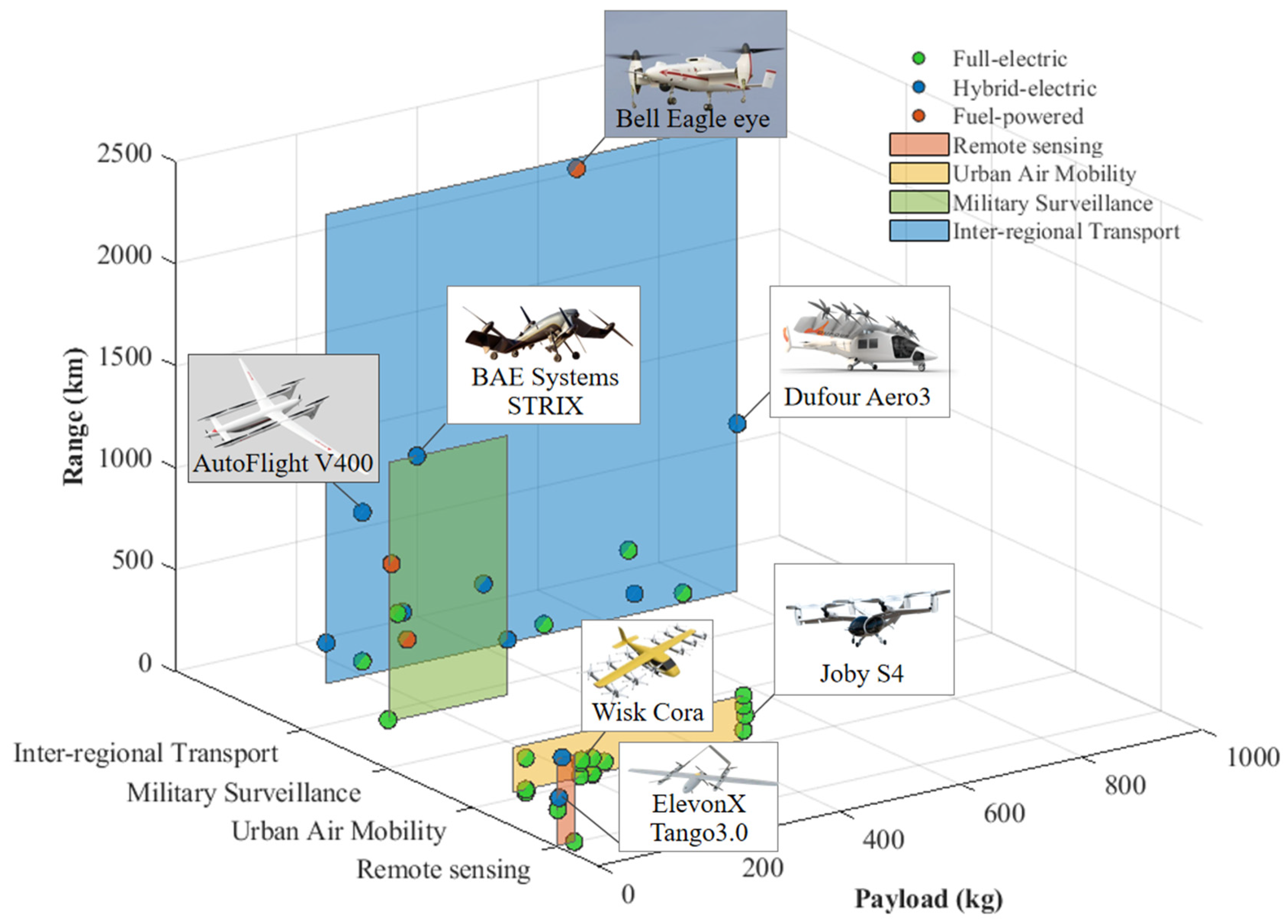
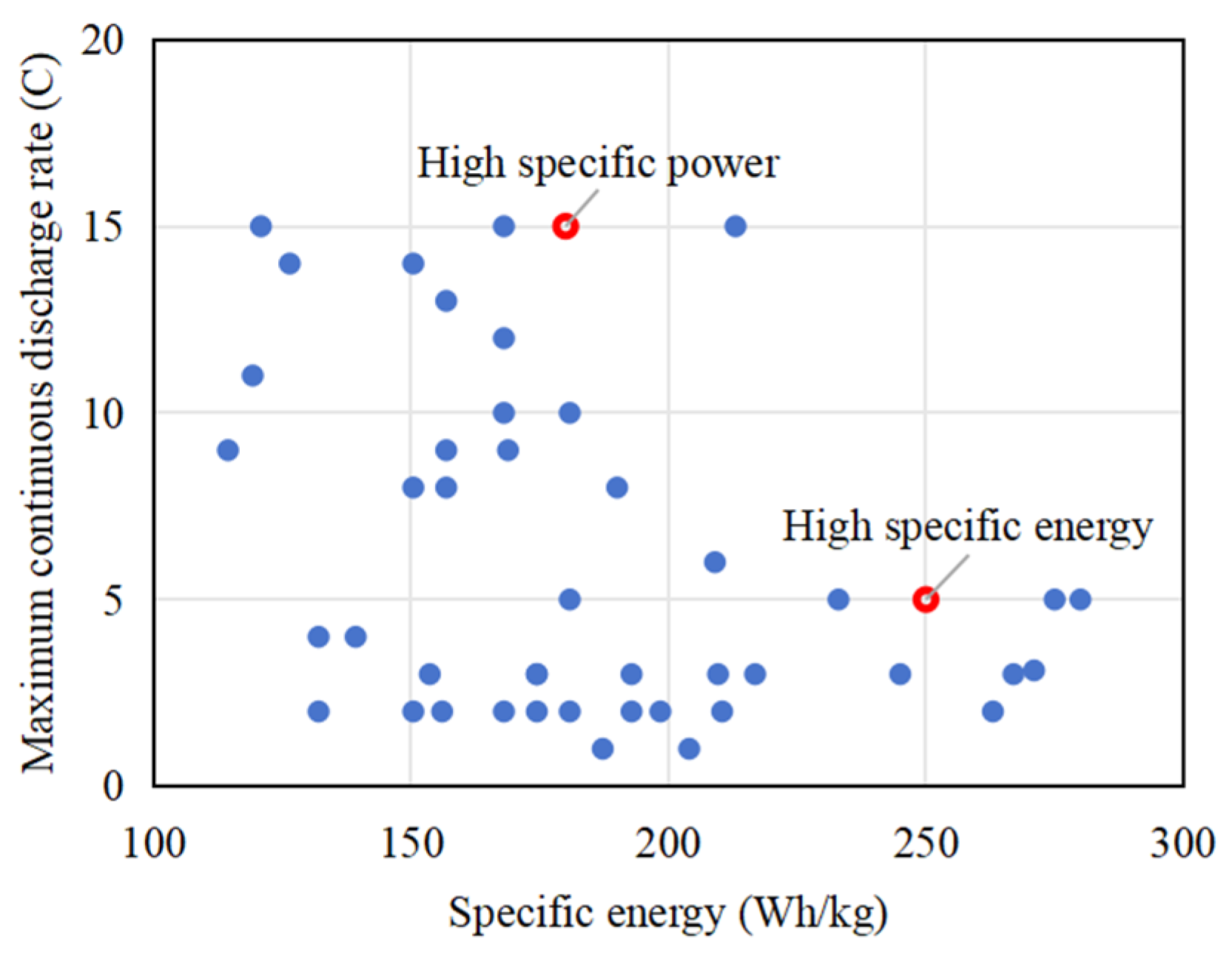
Unmanned vertical takeoff and landing (VTOL) aircraft, prized for their runway-independent operation, are increasingly applied in civilian sectors, such as remote sensing and transportation, and in military missions, including island reconnaissance and surveillance [1]. Traditional internal combustion engines (ICEs) perform inefficiently due to the large power gap between takeoff and cruise [2,3]. For instance, the Wisk Cora eVTOL operates at 20% cruise power relative to maximum takeoff power, below the 25–40% typical of conventional ICE aircraft. This disparity arises from its dual aerodynamic constraints: takeoff thrust-to-weight ratios exceeding those of fixed-wing platforms, combined with cruise lift-to-drag efficiency surpassing those of helicopters. Although full-electric (FE) propulsion can be adopted to various load conditions, its application is restricted by battery energy density, restricting long-range endurance [4]. In contrast, hybrid-electric systems offer flexibility by varying the distribution between power and energy source [5]. Nevertheless, designing VTOL power systems remains complex due to multi-condition constraints, strong nonlinear coupling among variables, and diverse optimization objectives—necessitating precise parameter matching for effective performance optimization.

Researchers have developed a range of design methodologies and modeling frameworks to develop VTOL aircraft design solutions. Early-stage sizing and integration have been supported by frameworks aided by researchers, such as Chakraborty and Finger [6,7]. Additionally, conventional aircraft design platforms have been adapted for VTOL-specific applications, such as NASA’s OpenAeroVTOL and Seoul National University’s RISPECR+ [8]. These advancements have accelerated productization, leading to the entry of several FE VTOLs into commercial service. Autoflight recently demonstrated a 250 km flight test, marking a key milestone in VTOL range capability [9,10]. To address the increasing demands for longer-range and heavier payloads, hybrid-electric (HE) VTOL platforms are being actively developed. The NASA Greased Lightning project demonstrates the viability of HE VTOL, showcasing a diesel-battery hybrid propulsion system [5,11]. Several small-scale hybrid VTOL prototypes have already completed bench and flight tests [12,13,14]. Meanwhile, hydrogen-electric VTOLs are rapidly progressing, with the Joby SHy4 achieving an 840 km flight test in 2024 [15,16].

Recent studies have increasingly focused on design optimization methodologies, focusing on multidisciplinary optimization at design points and energy management strategies under off-design conditions [17,18,19,20,21]. Advanced algorithms, including genetic algorithms [18,22,23] and AI-driven optimization [24,25], are being integrated into VTOL propulsion design [26]. However, systematic methodologies for evaluating and selecting optimal VTOL powertrain configurations remain underdeveloped. The current methods often rely on oversimplified models or fixed configurations, potentially resulting in suboptimal efficiency and performance. As the design progresses through refinement, modification costs increase exponentially, necessitating comprehensive design space exploration during initial development phases.

Previous studies have laid the groundwork for HE aircraft sizing. Nam [27] introduced a power–energy-based aircraft sizing approach, moving from traditional thrust–fuel matching to power–energy matching, and established the theoretical foundation for multi-energy power system parameter design. Vries [28] proposed the power ratio (HP) to quantify power distribution in HE aircraft systems, realizing range estimation for various power architectures despite lacking power architecture and control strategy information; however, it overlooked power demand variations across flight phases. Isikveren and Lampl later incorporated both power ratios (HP) and energy (HE) ratios to model all types of powertrain configurations and estimate propulsion system weight and size, though their approach neglected the inner relationships between HP and HE [29,30]. To address this issue, Harish developed a matrix-based framework linking energy, power, and thrust sources; preserved the connectivity characteristics between diverse sources; and achieved higher fidelity to real-world hardware implementations [31,32]. While these methods apply to the multi-condition constraints of parameter-coupled preliminary design of VTOLs, there is a critical gap between theoretical formulations and physical implementations.

Building on Harish’s matrix-based approach, this study introduces a propulsion system sizing method tailored to VTOL aircraft, offering a scalable approach to accelerate early-stage decision-making. The main contributions are summarized as follows:

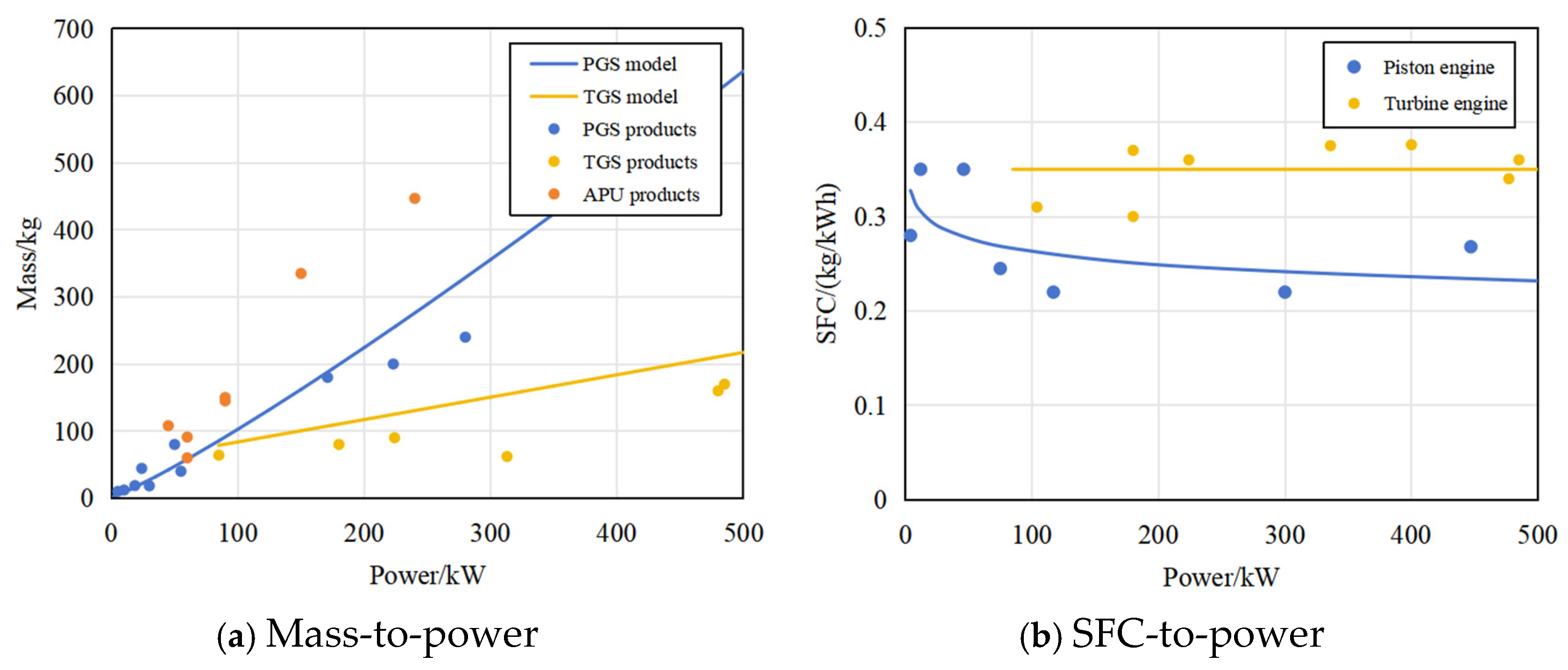
(i) By integrating real-world application scenarios and incorporating commercial Off-the-Shelf (COTS) products and data sources, this methodology bridges the gap between theoretical frameworks and physical implementations, demonstrating its viability in engineering practice.

(ii) A universal parametric configuration is defined, and corresponding range equations are derived for various powertrain configurations. Through full-factorial decomposition, key independent matching parameters are identified, simplifying the design process and enabling efficient navigation of the VTOL powertrain design space, reducing computational costs and accelerating design iterations.

(iii) Through power–energy matching parameter analysis, configuration selection and optimization principles are established for diverse mission scenarios and technological conditions, guiding component-level technology advancements.

2. Powertrain Matching Design Approach

As shown in Figure 1, the VTOL aircraft design process typically consists of four iterative components: power requirement analysis, propulsion system sizing, mission analysis, and total weight calculation [17]. Power analysis translates top-level design goals into propulsion design requirements. The propulsion system sizing and mission analysis process guarantees matching power and energy supply with demand. Finally, the design process concludes with total weight verification to validate the overall design outcomes. Due to the integration of multiple energy sources, hybrid powertrain systems exhibit greater design flexibility in power and energy matching compared to conventional powertrains. To enable rapid convergence of diverse architectural solutions, a novel power–energy matching method is introduced. Through the full-factor decomposition of the range equation, the factors influencing platform range–payload performance are thoroughly considered. The first-level decomposition yields key parameters including the overall efficiency ${\eta }_{ov}$, lift-to-drag ratio $L/D$, specific fuel energy $S{e}_{fuel}$, and platform initial-to-final mass ratio $W_{in}/W_{fin}$. This mass ratio can be further decomposed into subsystem mass fractions, specifically empty weight fraction $W_e/W_0$, payload fraction $W_{pl}/W_0$, power system weight fraction $W_p/W_0$, and residual fuel fraction $W_{fuel,re}/W_0$. Three independent key matching parameters are extracted: the power ratio (Φ), energy ratio (Ω), and maximum continuous discharge rate (rc). A sensitivity analysis of these parameters against predefined performance metrics is conducted to derive matching principles. These insights are then applied to guide the determination of power and energy matching parameters, such as optimal battery power distribution under various operating conditions.

The proposed method offers several advantages. It unifies diverse propulsion configurations within a universal power system parametric model, enabling cross-architectural comparisons among FE, ICE-powered, and HE configurations, while quantitatively delineating the operational superiority boundaries of each powertrain topology. The extracted key matching parameters uniquely characterize corresponding powertrain configurations through mutually orthogonal variables. Benefiting from low parametric dimensionality, this formulation enables cost-efficient exhaustive exploration of the entire design space, thereby propelling preliminary design iterations into neighborhoods of optimal solutions.

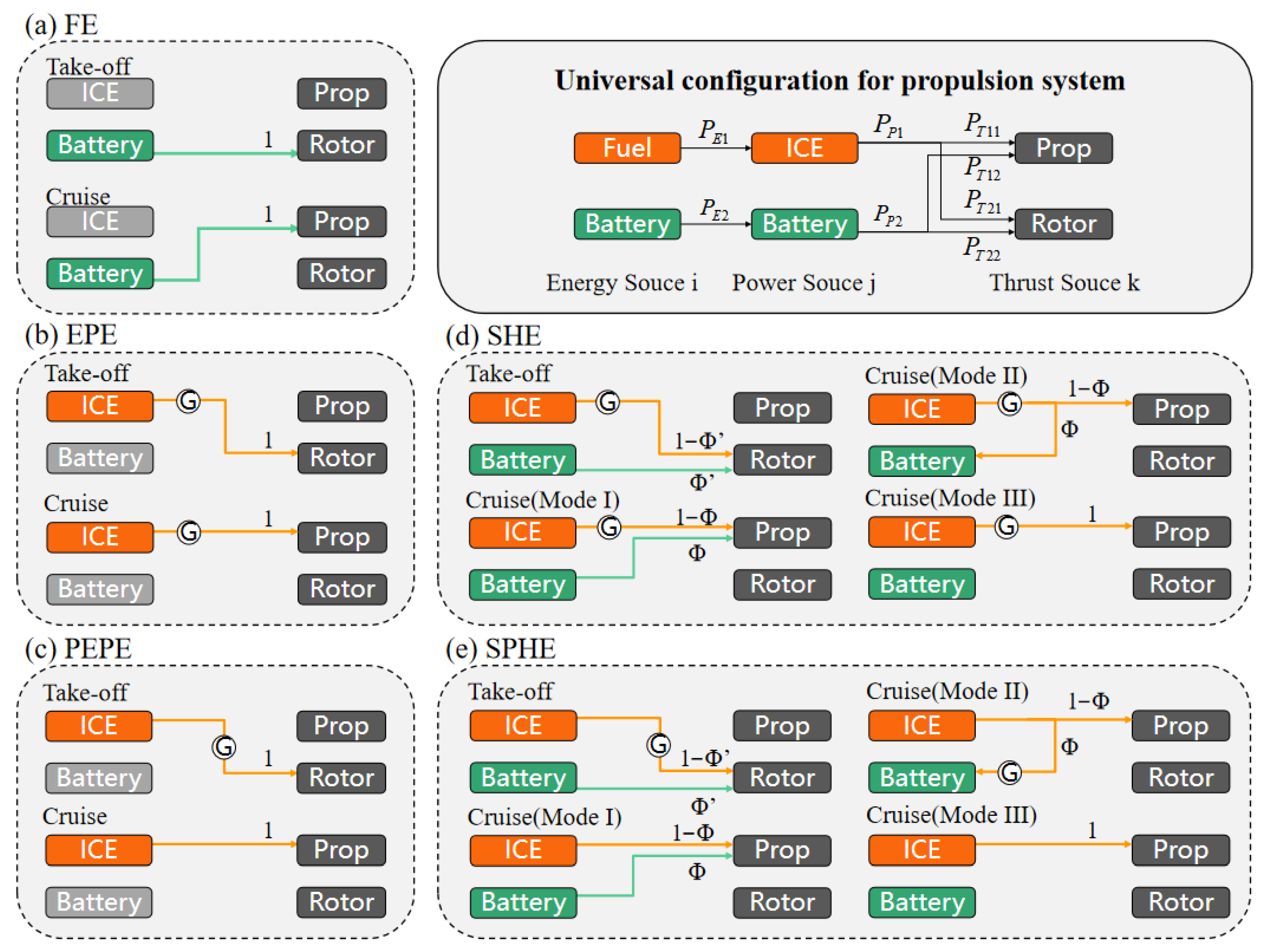
2.1. Universal Propulsion System Configuration

A universal power system configuration is introduced for propulsion system sizing, which can describe various propulsion configurations and their operating modes in a parametric framework (Figure 2) [33]. The propulsion configuration can be characterized by five matrices: $D_E$ (energy distribution matrix), $T_E$ (energy-to-power source transfer matrix), $T_p$ (power-to-thrust source transfer matrix), ${\Phi }_E$ (power allocation matrix), and $\eta$ (efficiency chain matrix for propulsion power generation).

The definitions of the five matrices are as follows:

$$D_E=\left[\begin{array}{c}d{E}_{fuel}\\ d{E}_{bat}\end{array}\right]$$

(1)

$$T_E=\left[P_{Pj}/P_{Ei}\right],i=1,2; j=1,2$$

(2)

$$T_p=\left[P_{Tjk}/P_{Pj}\right],j=1,2; k=1,2$$

(3)

$${\Phi }_E=\left[P_{Pj}/{\displaystyle \sum P_{Pj}}\right],j=1,2$$

(4)

$$\eta =\left[{\eta }_{ik}\right],i=1,2; k=1,2$$

(5)

where $P_{Ei}$ signifies power from the energy source ‘i’, $P_{Pj}$ implies power from the power source ‘j’, and $P_{Tjk}$ denotes the thrust source ‘j’. For VTOL aircraft, the distributed arrangement of propulsion systems enables multiple configurations, including FE (full-electric), EPE (engine-powered electric), PEPE (partial engine-powered electric), SHE (series hybrid-electric), and SPHE (series-parallel hybrid-electric) configurations. Figure 2 presents their corresponding topologies across different operational modes. We define the power ratio Φ of the battery in the cruise phase and the power ratio Φ’ at the takeoff point. For Φ > 0, the battery and generator jointly power the propulsor, representing Mode I in Figure 2; when Φ < 0, the generator powers the propulsor while charging the battery, denoting Mode II. Φ = 0 indicates all generator power is directed to the propulsor, representing Mode III.

The power ratio Φ is the ratio of the battery power $P_{bat}$ to the sum of the battery power and the generated power $P_{gen}$.

$$\Phi ={\displaystyle \frac{P_{P2}}{P_{P1}+P_{P2}}}={\displaystyle \frac{P_{bat}}{P_{bat}+P_{gen}}}$$

(6)

Under the assumption of constant generator power output, Φ′ at takeoff is derived as a function of Φ and is given by

$$\Phi \prime =\left\{\begin{array}{l}1-\left(1-\Phi \right)P_{cr}/P_{max} \hspace{0.17em} \mathrm{SHE} \mathrm{configuration}\hfill \\ 1-{\displaystyle \frac{{\eta }_{ele}{\eta }_{gen}}{{\eta }_{mec}}}\left(1-\Phi \right)P_{cr}/P_{max} \hspace{0.17em} \mathrm{SPHE} \mathrm{configuration}\hfill \\ 0 \mathrm{EPE} \mathrm{and} \mathrm{PEPE} \mathrm{configuration}\hfill \end{array}\right.$$

(7)

where $P_{cr}$ and $P_{max}$ refer to the cruising and maximum power requirement of the VTOL platform. ${\eta }_{ele}$, ${\eta }_{gen}$, and ${\eta }_{mec}$ refer to the efficiency of the electric system, generator, and planetary gear mechanism separately.

2.2. Range Equations of Each Configuration

As defined by Seitz [34], the total range can be derived from the integrated incremental flight distance per energy consumption, as shown in Equation (8). Following Seitz’s method, the overall system efficiency ${\eta }_{ov}$ is defined in Equation (9) [31]. $W$ is the weight of the platform.

$$R={\displaystyle \int {\eta }_{ov}\frac{L}{D}\frac{1}{W}dE}$$

(8)

$${\eta }_{ov}=\left[{(\eta \circ T_P)}^T\times T_E^T\times {\Phi }_E^T\right]\cdot \mathbf{1}$$

(9)

For FE configurations, the weight of the platform remains constant during flight, enabling its removal from the integral and resulting in Equation (10) [32], where $W_{bat,cr}/W_0$ signifies the equivalent battery weight fraction of cruise energy, as defined in Equation (11), which can be derived from empty weight fraction $W_e/W_0$, payload fraction $W_{pl}/W_0$, and residual battery weight fraction $W_{bat,re}/W_0$.

$$R={\eta }_{ov}{\displaystyle \frac{L}{D}}{\displaystyle \frac{S{e}_{bat}{W}_{bat,cr}}{W_0}}$$

(10)

$${\displaystyle \frac{W_{bat,cr}}{W_0}}={\displaystyle \frac{W_{bat}}{W_0}}-{\displaystyle \frac{W_{bat,re}}{W_0}}=1-{\displaystyle \frac{W_e}{W_0}}-{\displaystyle \frac{W_{pl}}{W_0}}-{\displaystyle \frac{W_{bat,re}}{W_0}}$$

(11)

For HE configurations, the fuel consumption leads to in-flight weight variation, necessitating the integration of weight into range calculations, with energy terms expressed by weight differentials in Equation (12) [31,32]. We consider the SHE configuration as an example. Assuming that $P_{cr}$ and Φ remain constant during cruising, the cruise-phase fuel energy ratio $d{E}_{fuel}$ can be expressed as Equation (13). The initial-to-final weight fraction of the platform $W_{in}/W_{fin}$ during the cruise phasecan be derived from $W_e/W_0$, $W_{pl}/W_0$, power system weight $W_p/W_0$, and residual fuel fraction $W_{fuel,re}/W_0$, as shown in Equation (14).

$$R={\displaystyle \int {\eta }_{ov}\frac{L}{D}\frac{1}{W}(\frac{S{e}_{fuel}}{d{E}_{fuel}}dW})={\eta }_{ov}{\displaystyle \frac{L}{D}}{\displaystyle \frac{S{e}_{fuel}}{d{E}_{fuel}}}\ln {\displaystyle \frac{W_{in}}{W_{fin}}}$$

(12)

$$d{E}_{fuel}={\displaystyle \frac{E_{fuel,cr}}{E_{tot}}}={\displaystyle \frac{\left(1-\Phi \right)P_{cr}/{\eta }_{pr}{\eta }_{ele}{\eta }_{eng}{\eta }_{gen}}{P_{cr}/{\eta }_{ov}}}={\displaystyle \frac{\left(1-\Phi \right){\eta }_{ov}}{{\eta }_{pr}{\eta }_{ele}{\eta }_{eng}{\eta }_{gen}}}$$

(13)

$${\displaystyle \frac{W_{fin}}{W_{in}}}={\displaystyle \frac{W_e}{W_0}}+{\displaystyle \frac{W_{pl}}{W_0}}+{\displaystyle \frac{W_p}{W_0}}+{\displaystyle \frac{W_{fuel}}{W_0}}-{\displaystyle \frac{W_{fuel,cr}}{W_0}}={\displaystyle \frac{W_e}{W_0}}+{\displaystyle \frac{W_{pl}}{W_0}}+{\displaystyle \frac{W_p}{W_0}}+{\displaystyle \frac{W_{fuel,re}}{W_0}}$$

(14)

Table 1. Range equations and power system weight for different configurations.

Configuration	Range Equation	Weight Decomposition
FE	$R={\eta }_{pr}{\eta }_{ele}{\eta }_{bat}{\displaystyle \frac{L}{D}}{\displaystyle \frac{S{e}_{bat}{W}_{bat,cr}}{W_0}}$	$W_p=W_{bat}$
EPE	$R={\eta }_{pr}{\eta }_{ele}{\eta }_{eng}{\eta }_{gen}{\displaystyle \frac{L}{D}}S{e}_{fuel}\ln {\displaystyle \frac{W_{in}}{W_{fin}}}$	$W_p=W_{pms}+W_{apu}$
PEPE	$R={\eta }_{pr}{\eta }_{mec}{\eta }_{eng}{\displaystyle \frac{L}{D}}S{e}_{fuel}\ln {\displaystyle \frac{W_{in}}{W_{fin}}}$	$W_p=W_{pms}+W_{mec}+W_{apu}$
SHE	$R={\eta }_{pr}{\eta }_{ele}{\displaystyle \frac{{\eta }_{eng}{\eta }_{gen}}{1-\Phi }}{\displaystyle \frac{L}{D}}S{e}_{fuel}\ln {\displaystyle \frac{W_{in}}{W_{fin}}}$	$W_p=W_{pms}+W_{bat}+W_{apu}$
SPHE	$R={\eta }_{pr}{\eta }_{mec}{\displaystyle \frac{{\eta }_{eng}}{1-\Phi }}{\displaystyle \frac{L}{D}}S{e}_{fuel}\ln {\displaystyle \frac{W_{in}}{W_{fin}}}$	$W_p=W_{pms}+W_{bat}+W_{mec}+W_{apu}$

presents the derived range equations and power system weight $W_p$ for each configuration. The symbols ${\eta }_{pr}$, ${\eta }_{bat}$, and ${\eta }_{eng}$ represent the efficiencies of the propulsive, battery, and engine, respectively, where $W_{pms}$, $W_{apu}$, and $W_{mec}$ signify the weight of the power management system, fuel-based auxiliary power generation unit, and planetary gear mechanism, respectively.

2.3. Matching Parameter Extraction

Based on the preceding series of formula derivations, the relationship between range and weight can be ascertained. However, directly exploring the design space using component-level inputs becomes computationally expensive and inefficient. To achieve global optimization, the hybrid power system model necessitates a balance between computational cost and precision, ensuring comprehensive design space coverage within finite computational resources. This challenge can be addressed through systematic coupling analysis between component parameters and range equations to identify key design freedoms, extract the independent, physically meaningful matching parameters, which can serve as effective control variables for design space exploration while maintaining physical interpretability.

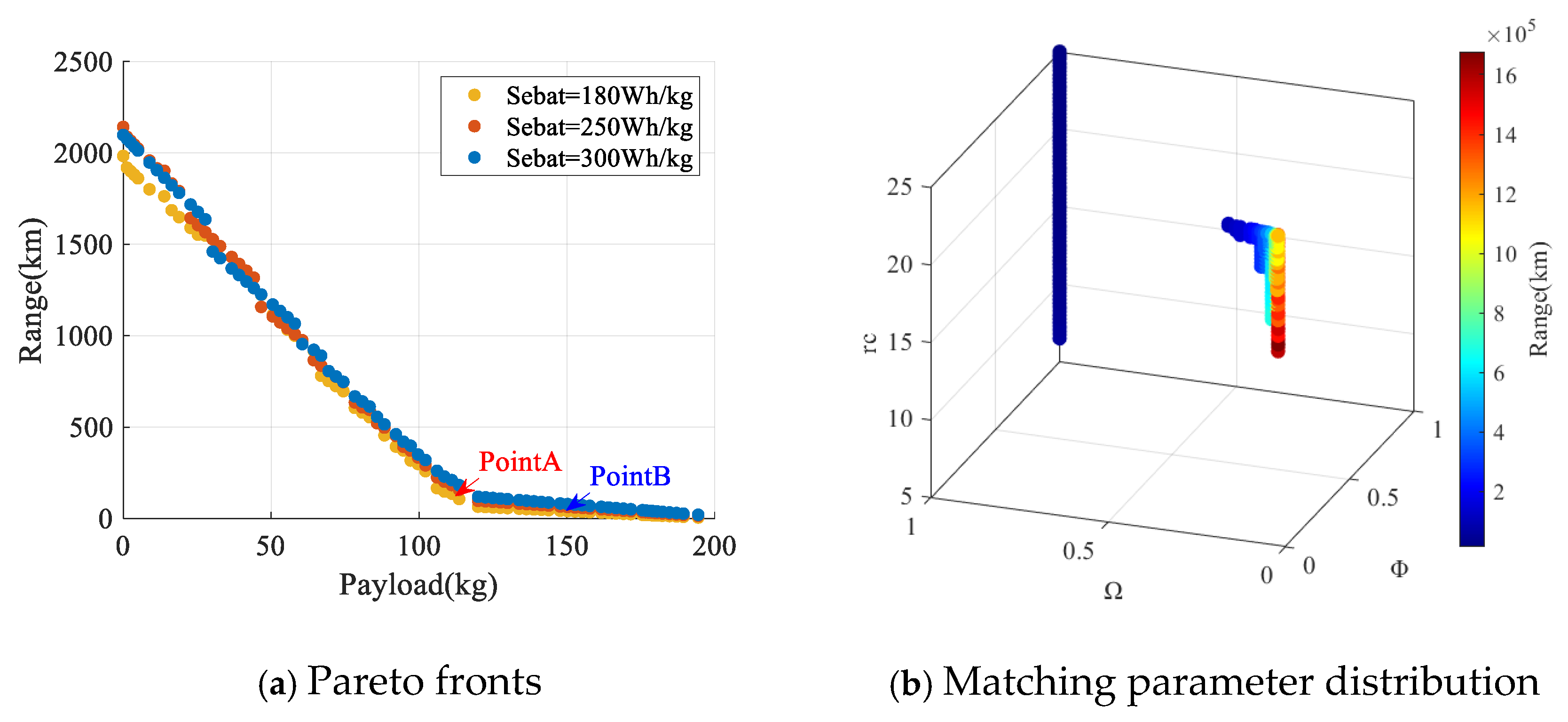
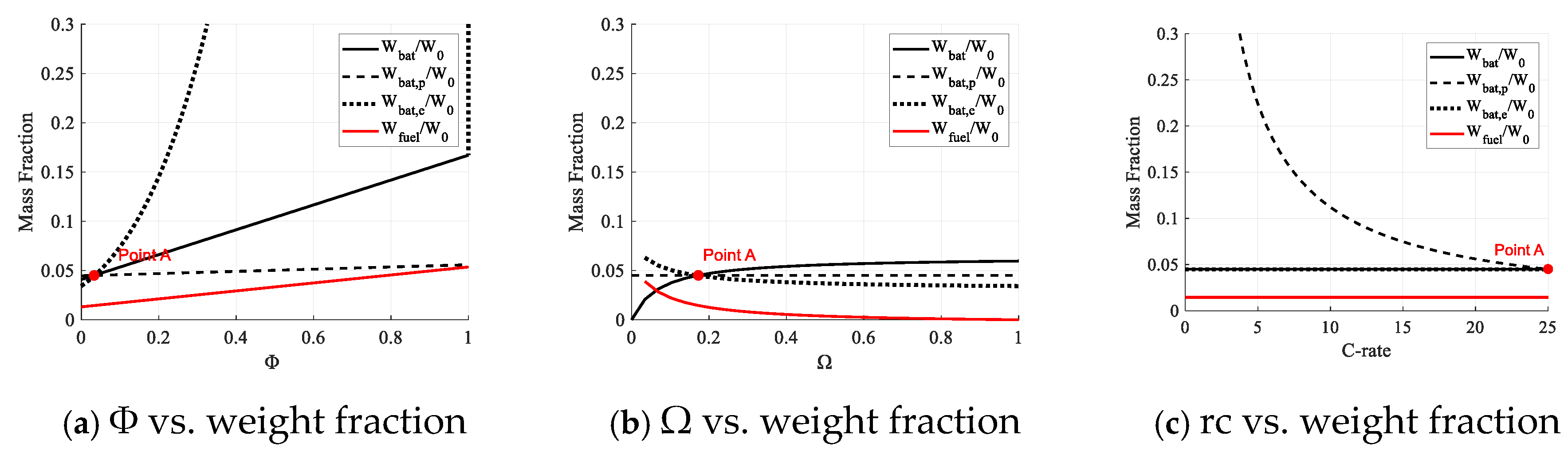
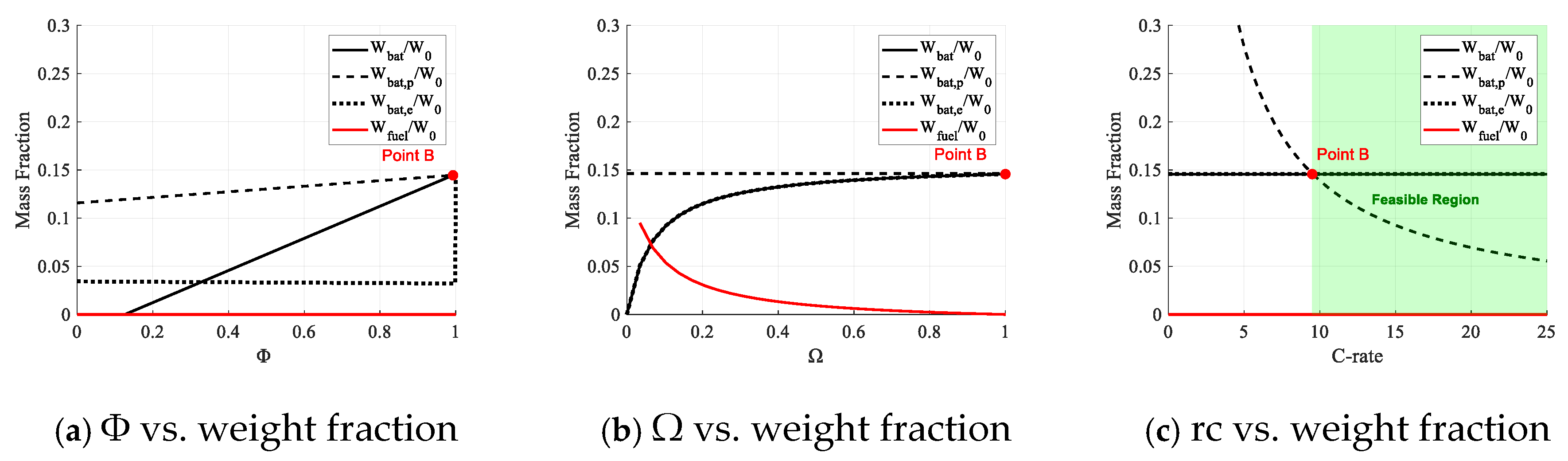
The analysis focuses on the SHE configuration. In Equation (14), the initial-to-final weight ratio enables estimation of the empty weight fraction using statistical data, while the payload, power system, and residual fuel fractions are derived analytically. According to the power–energy matching process shown in Figure 1, three fundamental matching parameters were defined to determine the component weight fraction: (1) power ratio (Φ); (2) energy ratio (Ω), representing the proportion of battery energy $E_{bat}$ in the total input energy from the battery and generator at the propulsion system input node; and (3) maximum continuous discharge rate (rc).

$$\mathrm{\Omega }={\displaystyle \frac{E_{bat}}{E_{bat}+E_{gen}}}$$

(15)

The power system can be decomposed into the power management system (PMS) and fuel-based auxiliary power generation unit (APU), which are defined by Equations (16) and (17), respectively.

$$W_{pms}/W_0={\displaystyle \frac{P_{max}/W_0}{W{g}_{pms}}}$$

(16)

$$W_{apu}/W_0={\displaystyle \frac{\left(1-\Phi \prime \right)P_{max}/W_0}{W{g}_{apu}}}$$

(17)

The weight ratio of the battery and fuel can be derived by Ω as in Equations (18) and (19).

$$W_{bat}/W_0={\displaystyle \frac{W_{bat}/W_0+W_{fuel}/W_0}{\left(1/\mathrm{\Omega }-1\right)S{e}_{bat}/{\eta }_{eng}{\eta }_{gen}S{e}_{fuel}+1}}$$

(18)

$$W_{fuel}/W_0={\displaystyle \frac{\left(1/\mathrm{\Omega }-1\right)DODS{e}_{bat}}{{\eta }_{eng}{\eta }_{gen}S{e}_{fuel}}}{W}_{bat}/W_0$$

(19)

Three constraints are applied to the energy system to ensure compliance with platform performance requirements. The battery weight ratio is restricted by takeoff capacity, which is relative to the maximum continuous discharge rate (rc) of the battery. Residual battery and fuel weight must satisfy takeoff and landing energy constraints under continuous maximum power operation during these phases.

$$W_{bat}/W_0\ge {\displaystyle \frac{{\Phi }^{\prime }{P}_{max}/W_0}{rcW{g}_{bat}}}$$

(20)

$$W_{bat,re}/W_0\ge W_{bat,tl}/W_0={\displaystyle \frac{{\Phi }^{\prime }{t}_{tl}{P}_{max}/W_0}{{\eta }_{pr}{\eta }_{ele}{\eta }_{bat}S{e}_{bat}}}$$

(21)

$$W_{fuel,re}/W_0\ge W_{fuel,tl}/W_0={\displaystyle \frac{(1-{\Phi }^{\prime })t_{tl}{P}_{max}/W_0}{{\eta }_{pr}{\eta }_{ele}{\eta }_{eng}{\eta }_{gen}S{e}_{fuel}}}$$

(22)

Once subsystem weight fractions are defined, the range can be calculated. This approach fundamentally applies to all powertrain configurations, since their architectural differences are fully characterized by linear mappings within the Φ-Ω-rc parameter space. Specifically, the FE configuration represents the singular case where Φ = Ω =1. The extracted matching parameters effectively decouple interdependencies among variables, allowing independent tuning of key design factors and improving optimization stability.

3. Multi-Configuration Performance Modeling

To enable a comprehensive trade-off study of propulsion system configuration, the performance modeling necessitates defined operational scenarios, standardized modeling methodologies, and uniform parameter constraints criteria. Through analysis of the existing product deployments, operational envelopes for trade-off study are defined. A performance model reflecting current technological capabilities is developed, from which matching parameter constraints are reverse-engineered based on range–payload optimization outcomes. The parametric matching criteria are established to accelerate design optimization through strategic constraint allocation. This design scheme provides both a theoretical framework and quantitative foundations for the configuration trade-off.

3.1. Application Scenario Analysis

VTOL aircraft, with their runway-independent operating capability, are well-suited for diverse low-altitude missions, including agriculture, air logistics, short-haul transport, urban air mobility, military, and rescue operations. As indicated in Figure 3 and Table S1, existing VTOL products reveal that HE VTOLs outperform FE VTOLs in range and altitude, while fuel-powered VTOL demonstrates superior overall performance. Most operational scenarios fall within a cruise range of ≤1000 km and payloads of ≤500 kg. Consequently, this study limits its parametric analysis to these representative operational envelopes.

3.2. Propulsion System Component Model

3.2.1. Propulsion System Power Requirement

Beyond conventional rotorcraft, VTOL propulsion systems can be categorized into three main configurations: “L + C,” “L = C,” and “L + L/C” [47,48]. As illustrated in Figure 4, “L + C” signifies independent lift (L) and cruise (C) thrust devices, “L = C” implies switchable lift and cruise thrust devices, and “L + L/C” partial lift thrust is redirected for the cruise. Propulsion system design is primarily driven by two key parameters: the maximum power, which generally corresponds to hover conditions, and cruise power, which defines steady forward flight requirements [13].

The cruise power is calculated based on the stable horizontal flight equation, resulting in the cruise power-to-weight ratio, as shown in Equation (23), where ${\eta }_{pr}$ signifies the propulsive efficiency and $V$ denotes the cruise speed. It is assumed that the platform operates at the maximum $L/D$ during the cruise, with the $L/D$ of different propulsion configurations referring to the data of a typical VTOL platform in [47].

$$P_{cr}/W={\displaystyle \frac{V}{{\eta }_{pr}\left(L/D\right)}}$$

(23)

The vertical ascent power-to-weight ratio was derived from the actuator disk theory [48], where $T$ indicates the rotor thrust, $V_C$ signifies the climb speed, $V_i$ denotes the induced speed, and $FM$ refers to the hovering efficiency.

$$P_{max}/W={\displaystyle \frac{T/W}{FM}}\left(V_C+V_i\right)$$

(24)

Given the variation in parameter choices and differences across VTOL configurations and mission requirements, this study adopts statistical analysis methods to extract representative power-to-weight ratios from the existing platforms. Compared to strict theoretical calculations, statistical methods more accurately capture the real-world distribution patterns of actual VTOL propulsion systems, and they are more applicable for conceptual design across various configurations.

Figure 5 illustrates the correlation between maximum and cruise power-to-weight ratios for VTOL and conventional takeoff and landing (CTOL) aircraft. According to existing data [49,50], VTOL aircraft generally exhibit a higher maximum power-to-weight ratio, typically between 0.15 and 0.35 kW/kg, compared to CTOL aircraft, while their cruise power ratios fall within 0.02 to 0.15 kW/kg. As noted in [51], a proportional relationship exists between the maximum and cruise power ratios.

Table 2. Typical $L/D$ and power-to-weight ratio values.

Propulsion Configurations	$\mathit{L}/\mathit{D}$	${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}/\mathit{W}$	${\mathit{P}}_{\mathit{c}\mathit{r}}/\mathit{W}$
L + L/C	13.5	0.3	0.08
L = C	17	0.25	0.05
L + C	10.4	0.20	0.05

summarizes representative statistical values, providing a practical reference for selecting suitable power-to-weight ratio ranges and supporting a more generalized propulsion system matching analysis.

3.2.2. Battery

A comprehensive analysis was conducted on the maximum continuous discharge rate (rc) and energy density of commercial 18,650 cylindrical battery cells [52,53]. As shown in Figure 6, a clear trade-off is observed: increasing the energy density from 150 to 280 Wh/kg leads to a reduction in the rc from 15 C to approximately 5 C. To accommodate the varying power demands of the VTOL aircraft, two representative battery configurations were selected. The first is a high-discharge-rate battery (10 C, 180 Wh/kg), optimized for the high-power demands during takeoff and hover. The second is a high-energy-density battery (5 C, 250 Wh/kg), better suited for sustaining the energy needs during a cruise. According to Yang et al. [54], the battery of the FE VTOL must provide a power density of 150 to 350 W/kg during cruise and 500 to 900 W/kg during hover. These two configurations effectively meet the power density requirements of both flight phases.

The mass of PMS is obtained by multiplying the total mass of the power conversion and distribution port components by an integration coefficient λ, which is specified as 1.3 in [2]. The power-to-weight ratio of each port component $W{g}_{cvt}$ is specified as 20 kW/kg, referring to [8]. As shown in Equation (25), the PMS of the SHE configuration includes a generator power input port, a battery power input port, and a motor power output port. For other architectures, the formula should be adjusted according to the actual port configuration.

$$W_{pms}/W_0=\lambda (P_{ge}+P_{bat}+P_{req})/W{g}_{cvt}{W}_0$$

(25)

3.2.3. Fuel-Based Power Generation System

Both piston and turboshaft engines were analyzed in this study. To evaluate their suitability for VTOL power requirements, product data within the 0 to 500 kW power range was collected to establish the power-to-weight fitting relationships for piston engines [2], turboshaft engines, and generators [55].

$$W_{piston}=0.375\cdot {P_{max}}^{1.170},(R^2=0.967,0<P_{max}<500 \mathrm{kW})$$

(26)

$$W_{turboshaft}=0.139\cdot P_{max}+49.145,(R^2=0.680,85 \mathrm{kW}<P_{max}<500 \mathrm{kW})$$

(27)

$$W_{generator}=0.195\cdot P_{max}+1.130,(R^2=0.926,0<P_{max}<500 \mathrm{kW})$$

(28)

Based on these established component relationships, the power-to-weight performance characteristics of a piston-generated system (PGS) and a turboshaft-generated system (TGS) were evaluated. As shown in Figure 7, piston power systems are capable of covering the entire 0 to 500 kW range, while turboshaft systems are suitable for applications within the 85 to 500 kW range. The fuel consumption rates (SFC) for piston engines are defined by Equation (29), while the SFC of turboshaft engines is assumed to be 0.35 kg/kWh based on available product data. The power decay of piston and turboshaft engines with increasing altitude is considered using Equations (30) and (31), respectively [56], where P and ρ are the shaft power output and density, respectively, at a given altitude. P_max and ρ₀ are the corresponding values at sea level.

$$SF{C}_{piston}=-0.02\cdot \ln (P_{max})+0.355,(R^2=0.428,0<P_{max}<500 \mathrm{kW})$$

(29)

$${\displaystyle \frac{P}{P_{max}}}=1.132{\displaystyle \frac{\rho }{{\rho }_0}}-0.132$$

(30)

$${\displaystyle \frac{P}{P_{max}}}={\left({\displaystyle \frac{\rho }{{\rho }_0}}\right)}^n, n=0.7$$

(31)

A comparative analysis of the existing power generation system products indicates that the PGS model closely aligns with the available product data. In contrast, the TGS model yields a lower mass than aerospace auxiliary point units (APUs) but a higher mass than dedicated TGS at equivalent power levels. This discrepancy primarily arises from differing design requirements: onboard APUs for conventional aircraft are engineered with substantial power extraction margins to support high-altitude operations, which reduces their power-to-weight ratios. In contrast, TGS units optimized for low-altitude VTOL applications can achieve superior power-to-weight performance due to less stringent altitude-related constraints.

Among various VTOL platform types, the “L + C” configuration has been identified as the most broadly optimal configuration [47], offering superior cruise while maintaining relatively low technical complexity. Therefore, the “L + C” configuration was selected as the primary research subject for subsequent analysis. System parameters were selected based on current technological capabilities to construct the performance model as listed in

Table 3. Performance model parameters.

Parameters	Value	Parameters	Value
$W_e/W_0$	0.50	${\eta }_{pr}$	0.70
$P_{max}/W$(kW/kg)	0.20	${\eta }_{ele}$	0.88
$P_{cr}/W$(kW/kg)	0.05	${\eta }_{gen}$	0.90
$W{g}_{mec}$(kW/kg)	0.6	${\eta }_{eng}$	0.25
$L/D$	10.4	${\eta }_{mec}$	0.97
DOD	0.8	${\eta }_{bat}$	0.90

. Parameter settings for representative hybrid-electric VTOL Configurations were concluded in Table S2.

3.3. Matching Parameter Sensitivity

The previous section demonstrated that Φ, Ω, and rc are critical matching parameters for the propulsion system. To establish guidelines for selecting these parameters, an optimization was conducted with the objective of maximizing range and payload. The traversal method was employed to generate the Pareto front for the range–payload trade-off from which the corresponding matching parameters were obtained. As illustrated in Figure 8, the Pareto fronts for three battery energy densities, 180, 250, and 300, were compared. The Pareto frontier exhibits a distinct linear knee point, with the optimal configurations on either side corresponding to the SHE and FE configurations, respectively. As the battery energy density increases, this knee point shifts upward, indicating an expanding dominance for the FE configuration. Figure 8b illustrates that the matching parameters are distributed at opposite ends of the parameter space. Notably, HE configurations impose more stringent requirements on rc, while FE configurations exhibit lower rc demands.

To analyze the sensitivity of the matching parameters and derive the underlying design principle, points A and B in the Pareto frontier in Figure 8a, corresponding to the SHE and FE configurations, were selected for detailed analysis. At these points, the trends in weight decomposition were evaluated by varying the cruise Φ, Ω, and rc at these points.

As quantified in Figure 9a, the weight fractions exhibit distinct growth gradients with increasing power ratios, revealing a sensitivity hierarchy of $W_{bat}/W_0$ > $W_{bat,e}/W_0$ > $W_{bat,p}/W_0$. As the power ratio increases, the three weight fraction curves converge at a critical point where the battery weight fraction simultaneously meets the requirements of both power and energy constraints. Once the critical ratio is exceeded, the battery weight fraction shifts from breaching the power constraint to violating the energy constraint, mathematically confirming this intersection as the unique mathematically valid solution for optimizing the power ratio. The coordinates of this point precisely match the parametric configuration of Point A in the design space.

In contrast to the HE configuration, the FE setup exhibits a wider feasible rc range, as shown in Figure 10c. The minimum rc, represented by Point B, defines the performance threshold. Design analysis indicates that optimal platform performance is achieved when the battery weight meets both power and energy constraints, requiring at least the minimum rc requirement.

4. Configuration Trade-Off and Optimization

4.1. Minimum Total Weight Configuration Distribution

Using the modeling approach outlined in Section 3, all the propulsion system configurations shown in Figure 2, including the FB configuration, were evaluated under identical range and payload missions. Given the trade-offs between battery-specific energy and maximum continuous discharge rate, and between the engine power-to-weight ratio and SFC, a detailed component selection analysis was performed. The assessment also accounts for how technological advancements influence the distribution and performance of each configuration.

Figure 11 illustrates the distribution of minimum MTOM configurations across various battery selection strategies. Figure 11a indicates that under the high discharge rate battery selection preference, the SPHE configurations dominate 69% of the mission space, particularly effective for the medium–long-range (200–1000 km) missions. In contrast, the SHE and EPE configurations are optimal for short-range operations (0–200 km), with the EPE systems favoring the high-payload domains. The FB configuration performs best under light payload conditions (0–15 kg), whereas FE is suited for ultra-short-range scenarios (0–40 km). Configuration preferences stem from two fundamental relationships: payload capacity is more influenced by the propulsion system power density, while range endurance is dictated by energy density. These performance variations arise from how the battery and FB power systems are integrated, shaping distinct power and energy density profiles through their unique integration approaches.

Figure 11b illustrates that using high-specific-energy batteries expands the FE configuration’s advantage area down to the 100 km range. However, the associated drop in power density reduces its effectiveness at shorter ranges. As a result, the advantage zones for battery-equipped configurations (SHE and SPHE) shrink, enabling battery-free configurations (FB, EPE, and PEPE) to outperform them in both low- (0–35 kg) and high (200–500 kg)-payload missions. These outcomes highlight two critical battery selection guidelines: FE configurations benefit from high-specific-energy batteries for extended range, whereas battery-based systems favor high-discharge-rate batteries to minimize mass and enhance short-range performance.

To investigate the influence of platform type on configuration selection, a minimum MTOM configuration distribution map was generated based on the platform parameters listed in Table 2, as shown in Figure 12a, which presents the results for the L = C platform. Compared with the L + C platform, the advantages of the SHE, EPE, and FB configurations become more pronounced. These configurations are characterized by relatively low efficiency but a high power-to-weight ratio, indicating that the L = C platform is more sensitive to the power-to-weight characteristics of the propulsion system.

On the L + L/C platform shown in Figure 12b, this effect is further amplified. The EPE configuration exhibits a distinct corner region in the 200–250 kg range, resulting from the trade-off between power-to-weight ratio and cruise efficiency. On the left side of this region, when the payload reaches about 200 kg, the required total power exceeds a threshold, and the optimal power source shifts from a more efficient piston engine to a higher power-to-weight turboshaft engine. After this transition, the simpler and lighter EPE configuration becomes advantageous.

As the range extends, the inferior cruise efficiency of EPE progressively increases the fuel demand, while the heavier but more efficient SPHE configuration becomes preferable as its fuel savings offset its structural mass. At approximately 600 km, a consistent EPE–SPHE boundary appears, where the fuel saving of SPHE exactly compensates for its additional weight. As the payload increases, both the weight penalty and the fuel-saving benefit scale proportionally, keeping this boundary stable around 600 km.

At the powertrain system level, three major technological breakthroughs are anticipated by 2035, as summarized in

Table 4. Technology levels of power system components.

Technology Level	$\mathit{S}{\mathit{e}}_{\mathit{b}\mathit{a}\mathit{t}}$ (Wh/kg)	$\mathit{W}{\mathit{g}}_{\mathit{a}\mathit{p}\mathit{u}}$ (kW/kg)	$\mathit{S}\mathit{F}{\mathit{C}}_{\mathit{t}\mathit{u}\mathit{r}\mathit{b}\mathit{o}\mathit{s}\mathit{h}\mathit{a}\mathit{f}\mathit{t}}$ (kg/kWh)
2025	180 ($r{c}_{\max }=15$)	Equations (26)–(29)	0.35
2035	300 ($r{c}_{\max }=15$)	+20%	0.30

. First, battery energy density is projected to reach 300 Wh/kg through integration and optimization efforts [52]. Second, the integration of the APU system is expected to yield a 20% improvement in power-to-weight ratio, enabled by advancements in coupled electromagnetic–thermal design innovations. Third, the modernization of turboshaft engines is anticipated to reduce the SFC to 0.30 kg/kWh by implementing adaptive thermodynamic cycle control and optimized operational parameters [57].

Figure 13a shows that improvements in $S{e}_{bat}$ significantly expand the dominance of the FE configuration while diminishing the EPE’s advantages, highlighting the growing role of battery-integrated systems in future deployments. Battery integration in HE systems proves essential for minimizing optimal weight. Figure 13b,c demonstrate that increasing generator power-to-weight ratios and lowering turboshaft SFC can extend EPE mission capability to 500 km. Overall, electrifying long-range, heavy-duty missions demands parallel advancements in battery and combustion technologies, supporting a dual-path optimization strategy.

4.2. Configuration Optimization Under Various Application Scenarios

To enhance the generalizability of the configuration selection results, two contrasting scenarios, transportation and military surveillance, were analyzed. The evaluation metrics were established to determine the optimal configuration for each case, with specific parameter settings provided in

Table 5. Evaluation metrics and task parameters across different scenarios.

Task	UAM	Remote Sensing	Military Surveillance
Metrics	$F{C}_{tkm}$, $C_{tkm}$	W0	W0
Payloads	200 kg	5 kg + 70 W	90 kg + 600 W
Range/endurance	50 km–500 km	1–5 h	1–5 h
Flight altitude	300 m	150 m	3000 m

.

For the transportation applications, three payload categories, small parcels, large cargo, and passenger transport, were analyzed across various ranges, including intra-city, inter-city, county, and provincial ranges. Minimum fuel consumption per ton-kilometer $F{C}_{tkm}$ (kg/(t·km)) and cost per ton-kilometer $C_{tkm}$ (CNY/(t·km)) served as the optimization targets. Assuming comparable maintenance costs between the FE and SHE systems, total operating costs included only energy and manufacturing components [58], as expressed in Equations (32) and (33). Manufacturing costs, linearly dependent on gross weight, were amortized over a 10-year lifespan, assuming 500 flights annually [59].

$$C_{Manufacture}=(65.3\cdot W_0+3795.7)/500$$

(32)

$$C_{Energy}=W_{bat}\cdot S{e}_{bat}\cdot 0.5+W_{fuel}\cdot 10.44$$

(33)

To ensure near-term realizability, the analysis focused solely on the FE and SHE configurations. The optimization outcomes of the $F{C}_{tkm}$ and $C_{tkm}$ under varying ranges are shown in Figure 14. The configuration archetypes are determined through parametric decoding, where $\Phi =1$ represents FE configuration, other values ($0\le \Phi <1$) imply the SHE configuration, and $\Phi =0$ signifies full generation power supply throughout cruise operations. When optimizing for $F{C}_{tkm}$, the FE configuration retains a clear advantage up to 100 km range—an edge that is more prominent than in weight-optimized scenarios. When optimizing for $C_{tkm}$, the FE configuration remains advantageous only within a 50 km range. Beyond this range, the battery weight grows more rapidly than that of HE systems, necessitating heavier platforms to sustain payload capacity, resulting in steeper cost escalation with increased range.

Remote sensing missions were benchmarked against the DJI Phantom 4 RTK aerial survey platform. Military surveillance missions inspired by the Bell Eagle Eye and KARI smart UAVs [41] were examined under 1–5 h surveillance missions with a high-power optical sensor payload (Wpl = 90 kg, P = 600 W, H = 3000 m, 50 s takeoff, 900 s climb). Figure 15a shows the minimum W₀ optimization result of remote sensing missions. During the 3–3.5 h mission phase, the power ratio Φ transitioned from positive to negative, indicating that the hybrid-electric architecture from combined power supply (generator-battery collaborative loading) to generation-dominant operation with simultaneous battery charging. As shown in Figure 15b, the Φ remained negative, which indicates the significant influence of the high-power generation requirement for military surveillance missions on the architectural configuration.

Based on the above analysis, the following configuration guidelines are yielded: For transportation missions, 100 km represents the threshold between the FE and SHE systems. FE configurations are more cost-effective and efficient for ranges under 100 km, while the SHE configurations are better suited for longer distances. For military surveillance missions, high-altitude operations with substantial power demands during climb and cruise require engine power levels that slightly exceed cruise requirements to facilitate in-flight battery charging.

4.3. Case Study

4.3.1. Hybrid-Electric Propulsion System Design

The method was applied to the retrofit process of an eVTOL aircraft (Great White VTOL, HUI XING HAI, Tianjin, China) propulsion system, which aims at 1.5 h remote sensing missions with a 5 kg payload, by converting the power system from all-electric to hybrid-electric to meet the endurance requirement (Figure 16). The technical specifications of the platform are summarized in

Table 6. Aircraft technical parameters.

Parameters	Value
AR	11.35
MTOM	24 kg
Cruising altitude	150 m
Cruising speed	23 m/s

.

The publicly available technical data for the Great White has been experimentally validated [60,61]. As shown in Figure 17, propeller (PER3_20x12, APC, Los Angeles, CA, USA) thrust-to-power ratio (TPR) vs. advance ratio (J) data from manufacturers allows for thrust calculation from shaft power and free-stream velocity during cruise, facilitating $L/D$ estimation.

Based on the experimental data from the FE platform, the lift-to-drag ratio, propulsion efficiency, and power-to-weight ratio were obtained. These parameters were used to construct the minimum gross weight distribution among different configurations. As shown in Figure 18a, for a 5 kg payload, the optimal configuration shifts from FE to SHE and finally to SPHE as endurance increases. Since the target endurance is 1.5 h, where the performances of SPHE and SHE are comparable, the SHE configuration was selected for its easier implementation.

Figure 18b compares the total weight trends of SHE and FE under the minimum-weight objective. The FE configuration consistently exhibits a higher total weight, and feasible solutions exist only up to about 1 h, consistent with Figure 18a. The corresponding optimal matching parameters for different endurance missions are shown below. To achieve a lower total weight, Φ is generally less than zero, indicating that the generator output slightly exceeds the cruise power demand.

Figure 18c shows the results under the minimum-cost objective. Although FE offers a lower cost, no feasible solution exists at 1.5 h. In contrast, the optimized parameters for SHE show Φ mostly greater than zero, reflecting a trade-off between fuel consumption and weight. Therefore, the optimal parameters derived from the minimum-cost objective were adopted for the hybrid system prototype, as listed in

Table 7. Design and optimized result of the demonstrator.

Parameters	Design Parameter	Physical Parameter	Optimized Parameter
$\Phi$	0.350	0.319	0.319
$\Omega$	0.500	0.309	0.468
$rc$	4.09	5.95	4.20
$P_{gen}$(W)	735	770	770
$W_{apu}/W_0$	0.068	0.084	0.084
$SFC$ (g/kWh)	361	549	549
$W_{fuel}/W_0$	0.0190	0.0373	0.0259
$S{e}_{bat}$ (Wh/kg)	180	173	173
$W_{bat}/W_0$	0.262	0.171	0.240
$W_{pl}/W_0$	0.210	0.210	0.210
$R$	130,551	86,691	124,590
$C_{tkm}$	25.84	36.03	28.55
$\Delta C_{tkm}$	/	39.43%	10.49%

.

4.3.2. Subsystem Calibration

During the physical implementation of the hybrid system, the rated output power of the generation system was first determined based on the Φ value. The engine and generator were then selected accordingly, and component-level tests were conducted to characterize the power output, specific fuel consumption (SFC), and fuel mass ratio, from which the fuel consumption was estimated. Based on the total weight constraint, the battery capacity ratio was subsequently determined.

The calibrated subsystem parameters and the estimated range derived from the prototype tests are listed in Table 7. The total weight of the generation system agrees well with the estimated value, whereas a significant deviation is observed in SFC. Figure 19 presents the cooperative operating MAP of the generator (HXT-QF-100-15-00, LingYiFeiHang, Tianjin,China) and ICE (GF40, O.S.ENGINES, Osaka, Japan). Limited by the generator output capability, the ICE operates predominantly in the low-load, high-consumption region, resulting in a much higher actual fuel consumption than predicted. This necessitates recalibration of the power and fuel-efficiency parameters according to the engine–generator matching characteristics.

Due to the elevated fuel consumption, the battery capacity had to be reduced to satisfy the total weight constraint, leading to a prototype range insufficient to meet the 1.5 h endurance target (124 km).

4.3.3. Integrated System Validation

The parameter correction described above was based on the steady-state operating points of the subsystems. To evaluate the influence of the dynamic characteristics of the generation and battery subsystems on the actual flight range, a simulation model (Matlab/Simulink R2019b Softwawre) was established using subsystem experimental data and validated against flight test results. This comparison was used to determine the required design margin when dynamic effects are considered. The detailed modeling process is described in [60]

Figure 20 illustrates the variations in instantaneous fuel consumption and battery voltage Ub during a 900 s flight mission. The mean absolute percentage errors (MAPEs) between the simulation and experimental results were 8.91% and 0.26%, respectively, indicating a relatively large prediction error in fuel consumption but a high accuracy in battery voltage prediction (error below 5% is considered accurate).

The reasons for the fuel consumption deviation can be inferred from the trend shown in Figure 20a. After engine start-up, both the experimental and simulated instantaneous fuel consumptions exhibit fluctuations until approximately t = 100 s, when they stabilize and show good agreement, suggesting that the engine model predicts steady-state fuel consumption with reasonable accuracy. As the mission continues, the battery voltage decreases, leading to a reduction in generation power. Consequently, the simulated fuel consumption gradually decreases, while the experimental value continues to increase, implying that accumulated thermal effects during prolonged operation may reduce the overall efficiency of the power system. In the final stage of the mission (t = 800–900 s), the load decreases sharply. The experimental fuel consumption drops, whereas the simulated result rises due to the low efficiency of the model under low-load and low-speed conditions.

These observations indicate that a static efficiency model cannot capture the dynamic behaviors of the engine during different phases, such as cold start, thermal degradation, and shutdown. Therefore, an additional design margin must be reserved. Based on the MAPE of instantaneous fuel consumption, a 10% fuel allowance is recommended for the platform design.

4.3.4. Maching Parameter Optimization

After calibrating the input parameters using prototype test data and determining the design margin required to account for system dynamics, the configuration was re-optimized. The fuel and battery allocations were adjusted to meet the initial endurance requirement. The detailed parameter results are presented in Table 7. The optimized configuration achieved the target range, with the cost per kilometer (Ctkm) increased by 10.49% compared with the original design.

These results demonstrate that the proposed design methodology can provide a valuable baseline configuration at the early design stage. Moreover, the framework is capable of progressively integrating experimental data from subsystems and full-system tests, thereby enabling iterative correction of performance predictions. This feature indicates the potential of the proposed method for application across future design and validation phases.

5. Conclusions and Outlook

This study presents a novel configuration trade-off and optimization framework for VTOL aircraft. The configuration selection guidelines and optimization outcomes are derived for a range of mission scenarios. Finally, the proposed method was validated using VTOL platforms representing different aircraft classes. The key findings are summarized as follows:

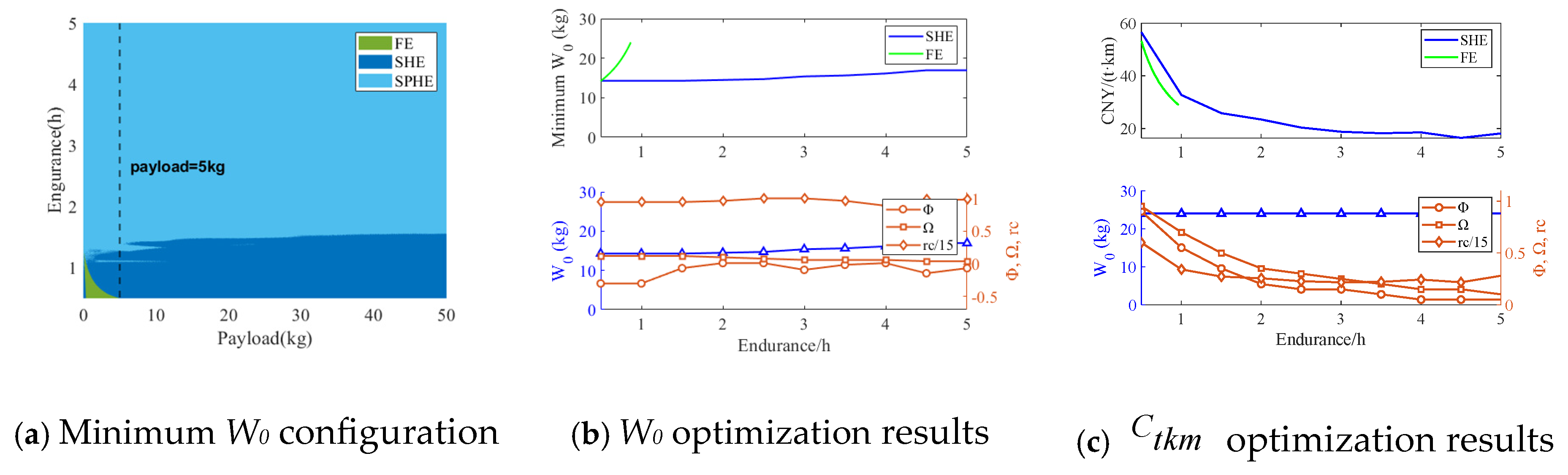
(1) The minimum MTOM configuration distributions derived for a 1000 km range and 500 kg payload indicate distinct applicability zones. The SPHE configurations are well-suited for medium–long-range missions (200–1000 km), while the SHE and EPE configurations dominate short-range operations (0–200 km). FE configurations are optimal for ultra-short-range scenarios (0–40 km). To enable the electrification of long-range, heavy-duty missions, coordinated advancements in both battery and combustion technologies are essential, supporting a dual-path optimization strategy.

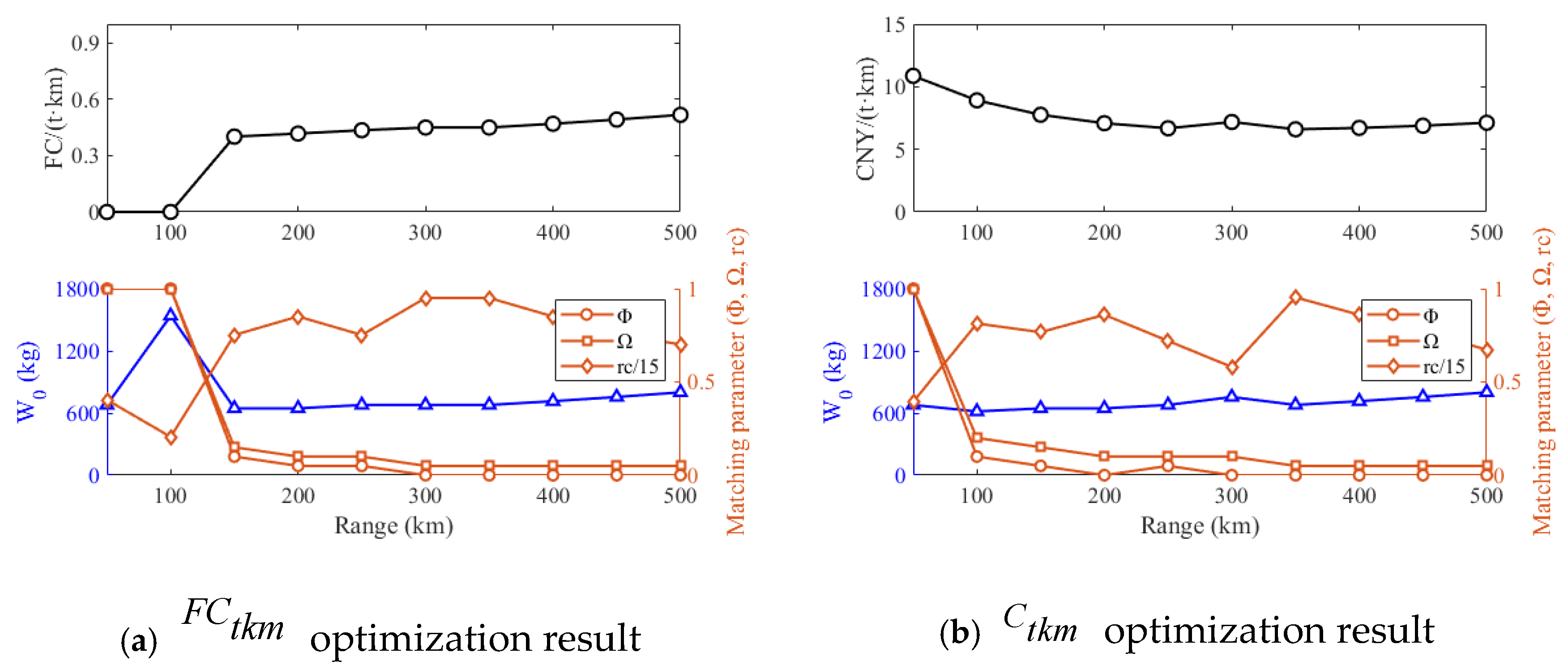
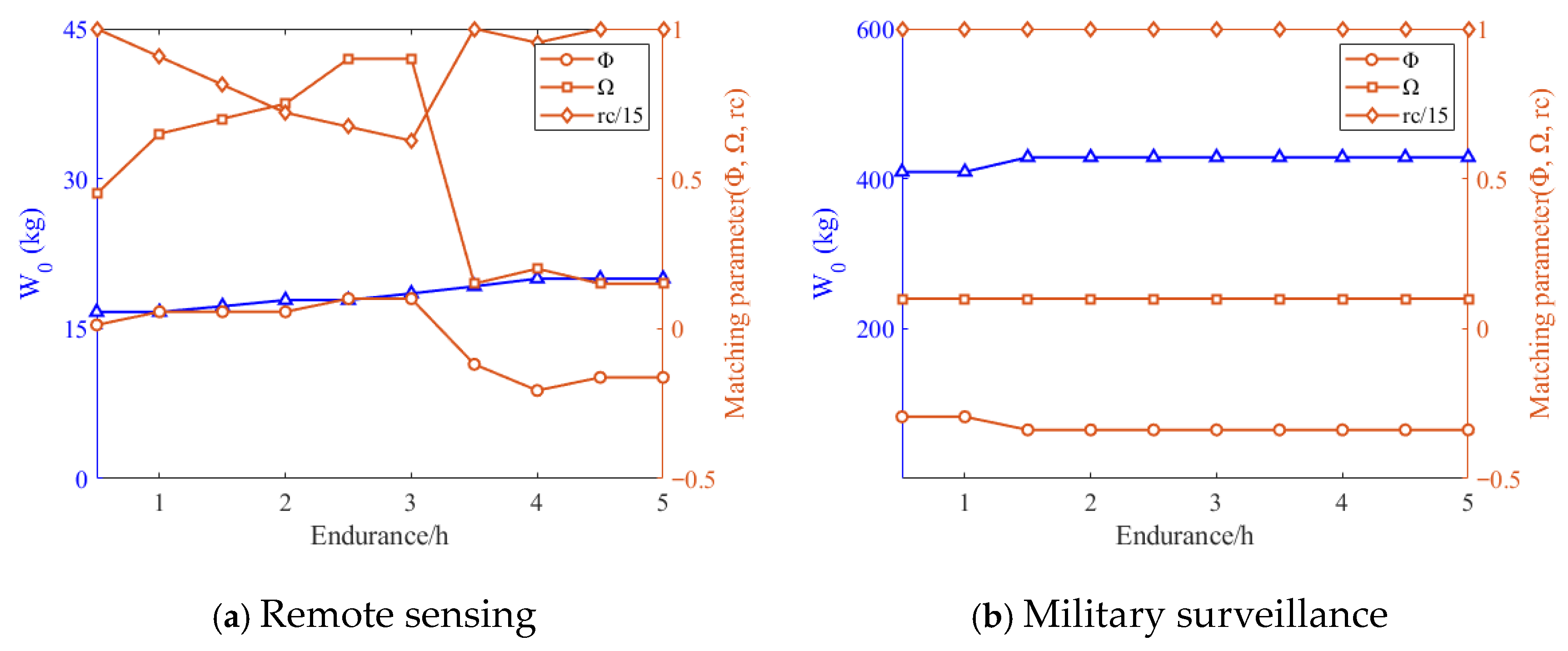
(2) Configuration optimizations were conducted across two distinct operational scenarios using tailored evaluation metrics. In transportation applications, 100 km serves as the current threshold between the FE and SHE configurations. For missions below 100 km, FE configurations provide superior cost and efficiency. Beyond this threshold, the SHE configurations become more favorable due to their improved energy management capabilities. In military surveillance missions, where high-altitude operations impose substantial power demands during climb and cruise, the engine must provide power slightly exceeding cruise requirements to enable in-flight battery charging.

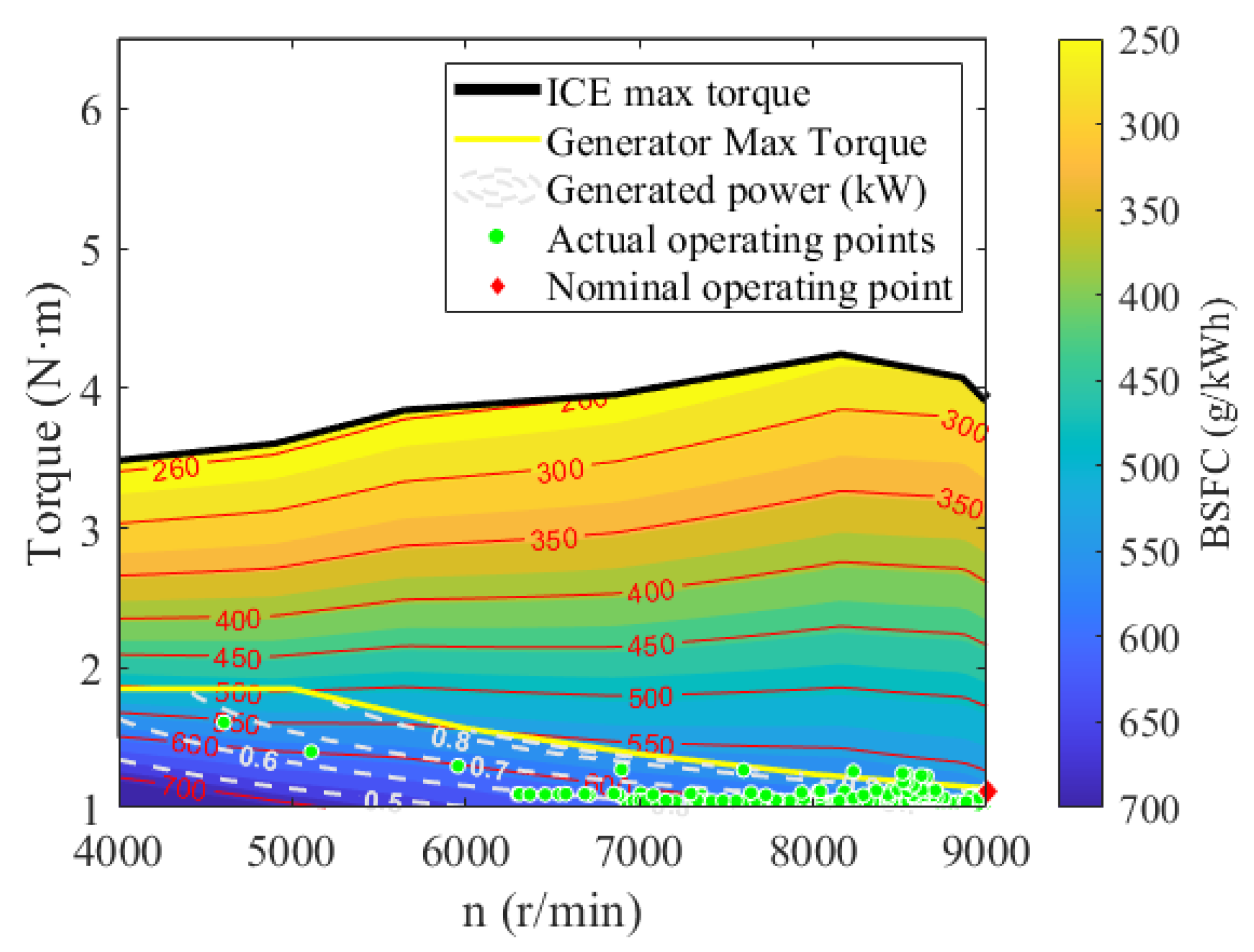
(3) The retrofit process of the Great White eVTOL power system demonstrated the practical engineering value of the proposed method. Based on the subsystem steady-state characteristics and the overall dynamic behavior of the platform, the design scheme was progressively refined. Following the preceding corrections, the configuration was iteratively optimized, resulting in a 10.49% increase in cost per ton-kilometer compared with the initial design. These results confirm that the proposed co-design methodology provides a scalable, data-driven foundation for early-stage hybrid-electric VTOL powertrain design, enabling iterative performance correction and supporting system optimization across future design and validation phases.

While the current model includes necessary simplifications of physical realities, it serves as a robust foundation for architectural assessment and optimization. Three primary extension pathways emerge: (1) Model refinement through the integration of off-design effects, such as power–energy density coupling in batteries and thermo-mechanical coupling in hybrid powerplants. (2) Incorporation of environmental coupling factors, including altitude-dependent performance degradation and the influence of atmospheric condition effects. (3) Expansion of applicability to a broader range of VTOL application scenarios and next-generation propulsion systems, including fuel cell-electric and hydrogen-combustion systems. These enhancements would bridge the gap between conceptual design optimization and real-world operational performance.