Off-Policy Deep Reinforcement Learning for Path Planning of Stratospheric Airship
Abstract
1. Introduction
- The high-reward prioritized experience replay (HR-PER) mechanism innovatively adopts an episode-based sequential storage structure that preserves the complete temporal trajectory of agent–environment interactions. The cumulative reward of each episode is used as a novel metric for assessing its learning value.
- We propose an adaptive decay scaling mechanism that addresses the issue of premature convergence to suboptimal policies in traditional PER. This mechanism weakens prioritization during early training to encourage exploration and gradually intensifies it later to accelerate convergence.
- This work also innovatively integrates a LSTM network into the Actor–Critic framework of TD3. This design enables the airship to capture the dynamic evolution patterns of wind fields and their sustained effects on its motion state, thereby significantly enhancing the model’s perception of environmental dynamics and its adaptability.
2. Task Model for Path Planning
2.1. Problem Description and Basic Assumptions
- It is assumed that the wind characteristics remain constant within a fixed time interval and a minimum spatial grid, i.e., a spatiotemporal grid cell with a minimum resolution.
- The planning time step is set to 15 min. Within each step, closed-loop control of the airship’s speed and attitude is assumed to be achievable. Therefore, action execution is considered instantaneous in this problem.
- Since stratospheric airship predominantly operates in the horizontal (isobaric) plane due to their limited altitude-adjustment capability, this study considers only two-dimensional motion.
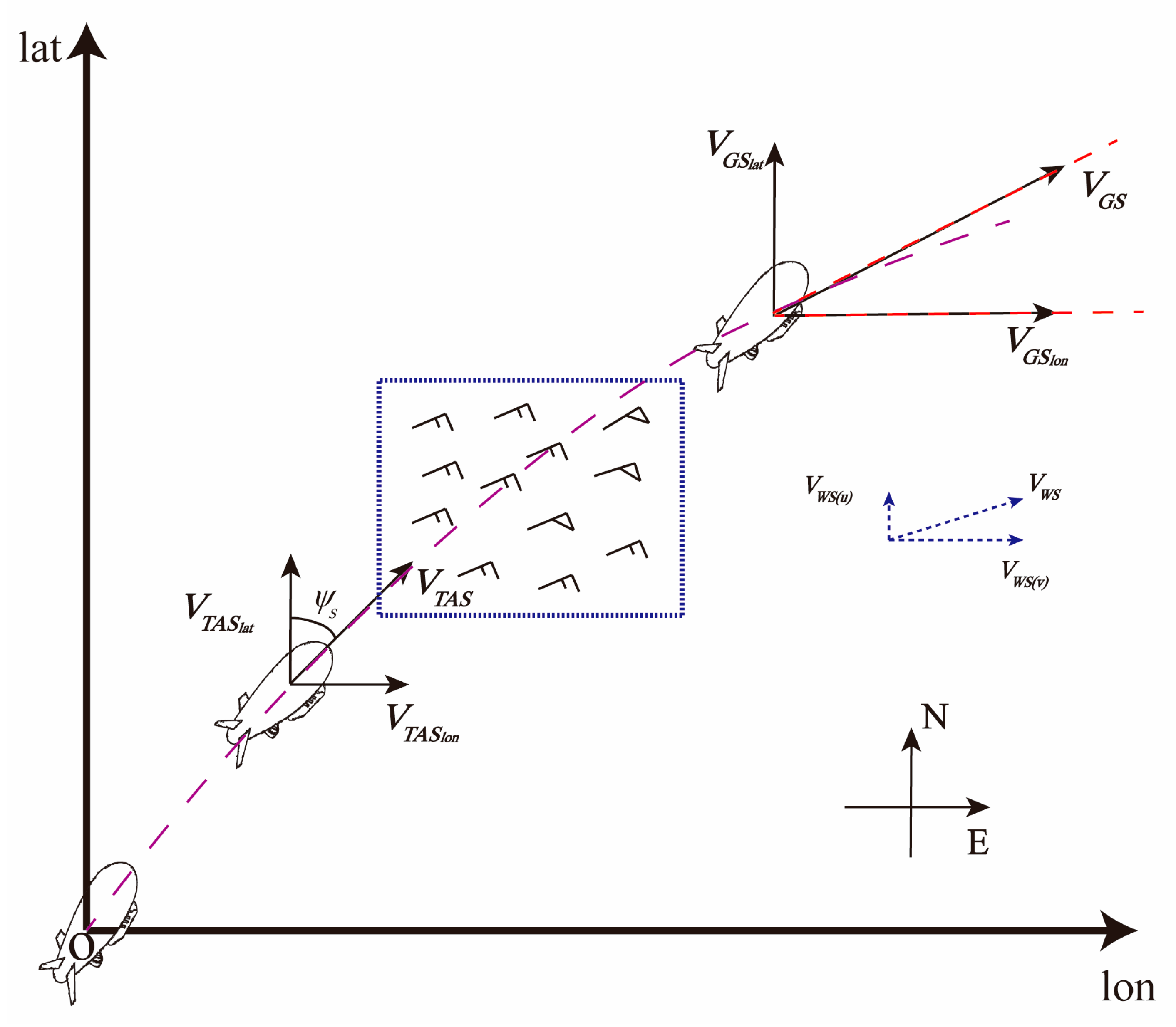
2.2. Time-Sequential Uncertainty Wind Field Model
2.3. Stratospheric Airship Agent Model
2.3.1. Kinematic Model
2.3.2. Energy Model
2.4. MDP Model
2.4.1. Markov Decision Process
2.4.2. States and Actions
2.4.3. Reward Function
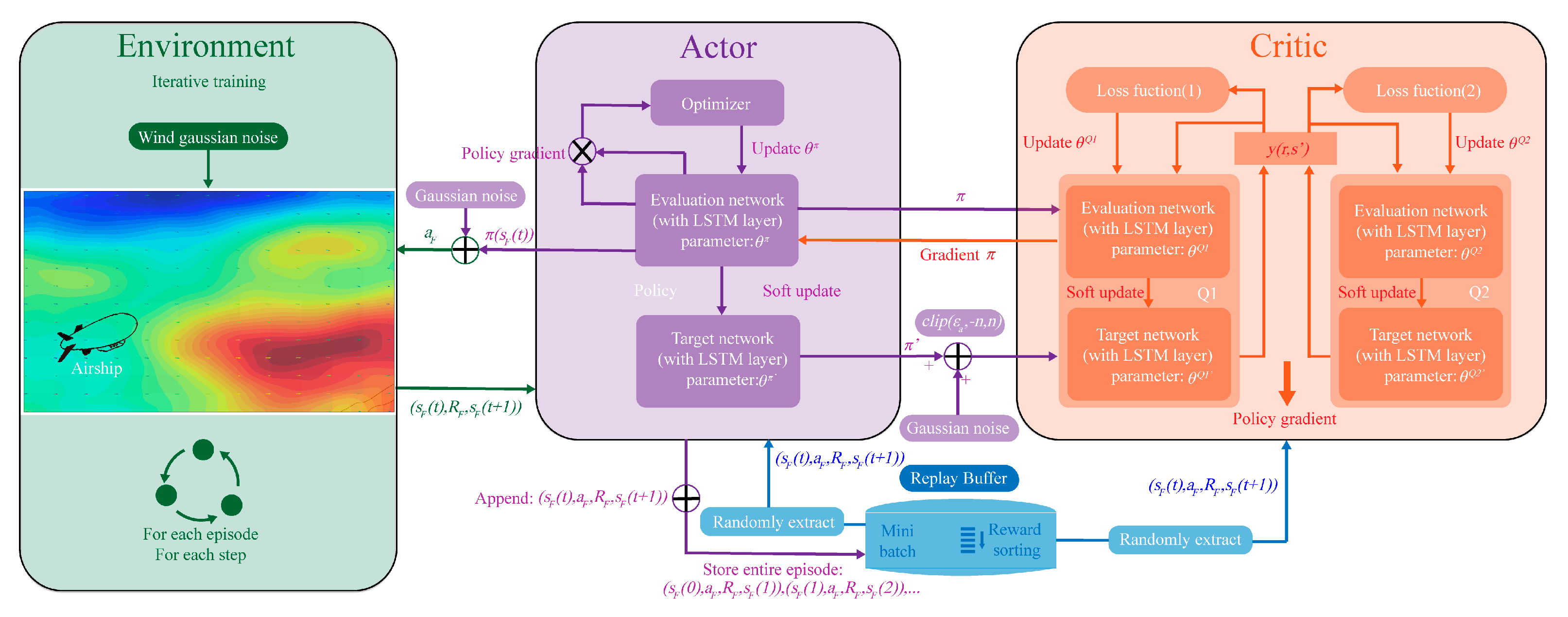
3. Method
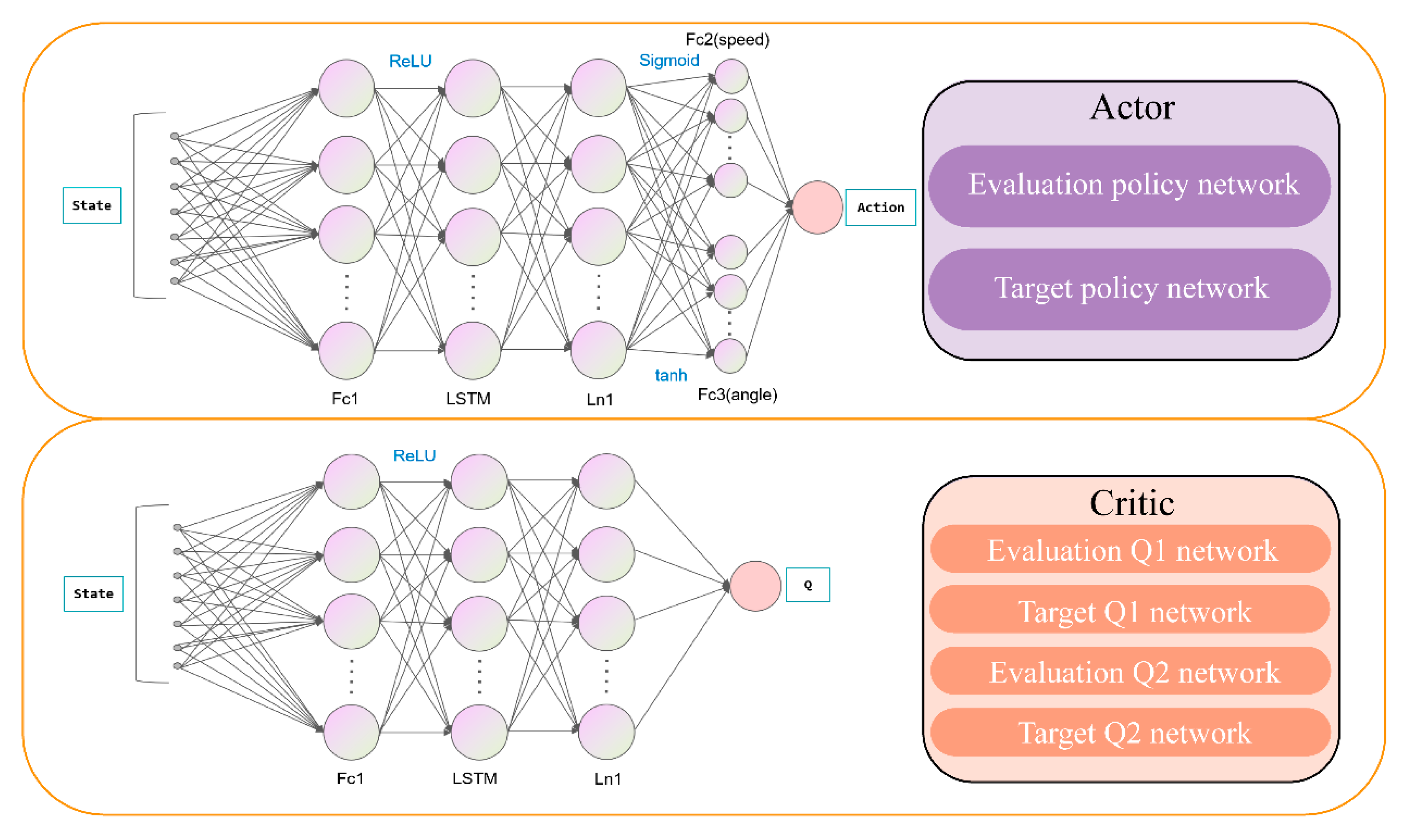
3.1. Twin Delayed Deep Deterministic Policy Gradient
3.2. Algorithm Improvements
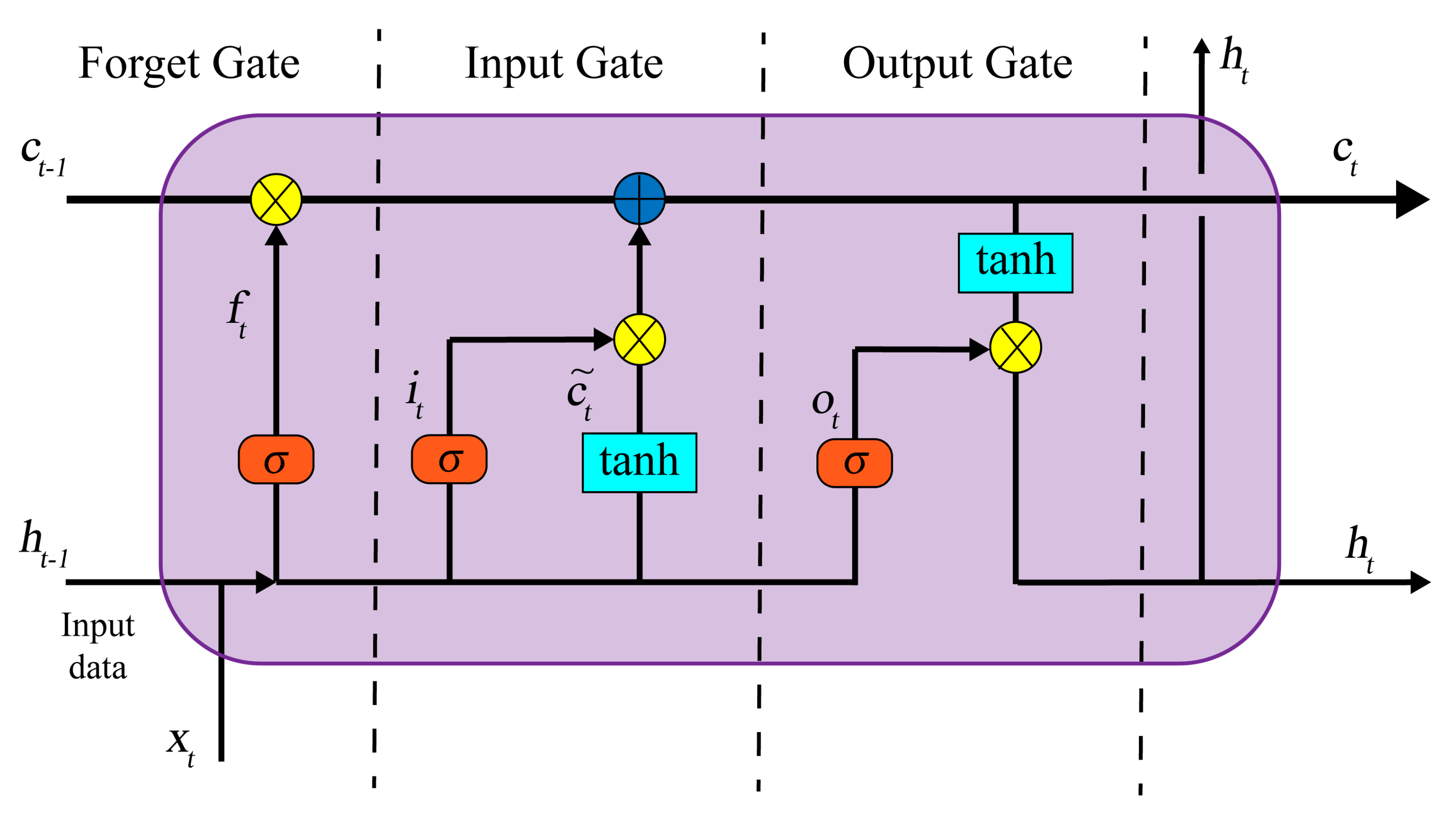
3.2.1. LSTM Network Architecture
3.2.2. High-Reward Prioritized Experience Replay Mechanism (HR-PER)
| Algorithm 1: HR-PER Algorithm |
 |
3.3. RPL-TD3 Algorithm Procedure
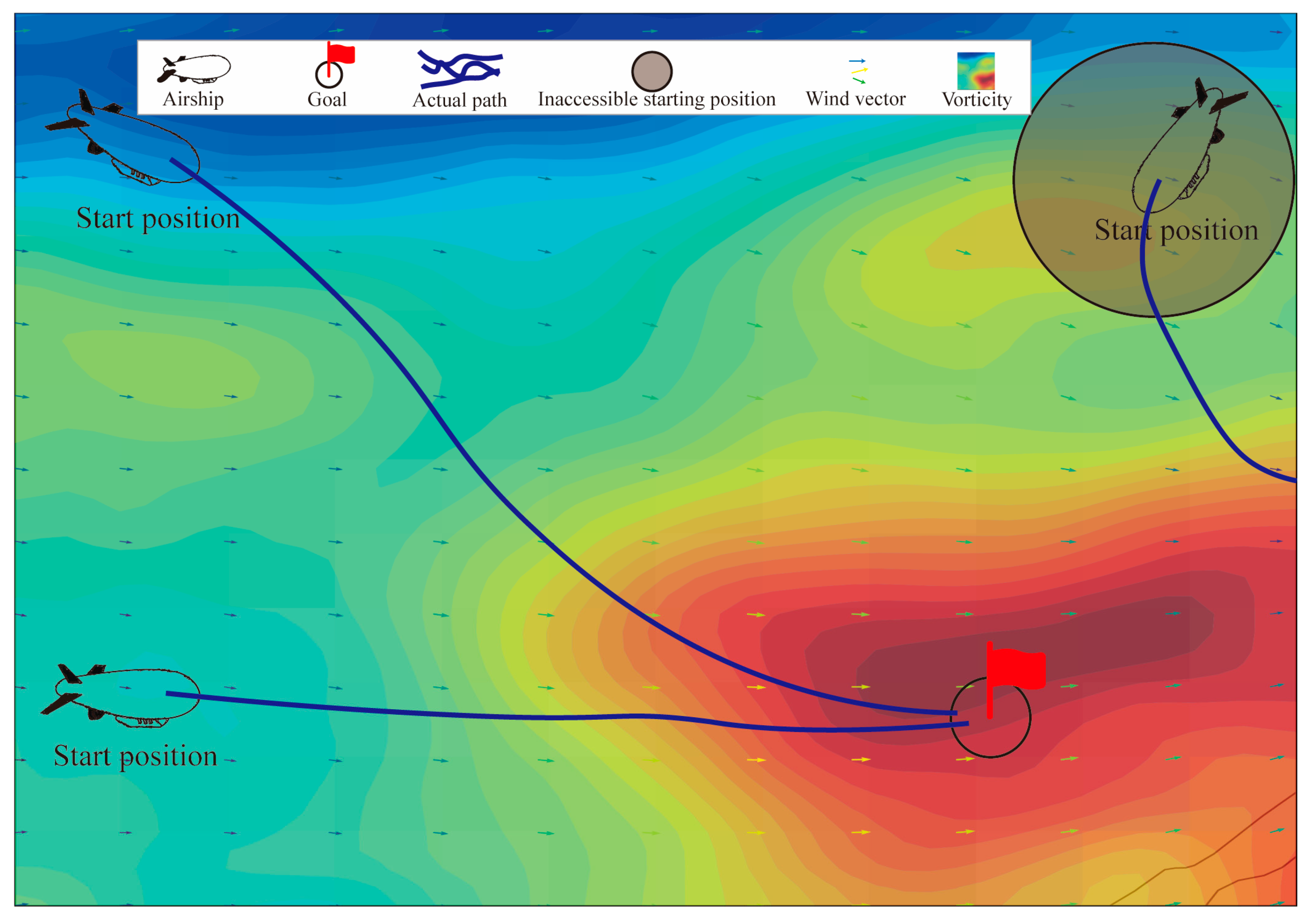
4. Experiments
4.1. Experiment Setup
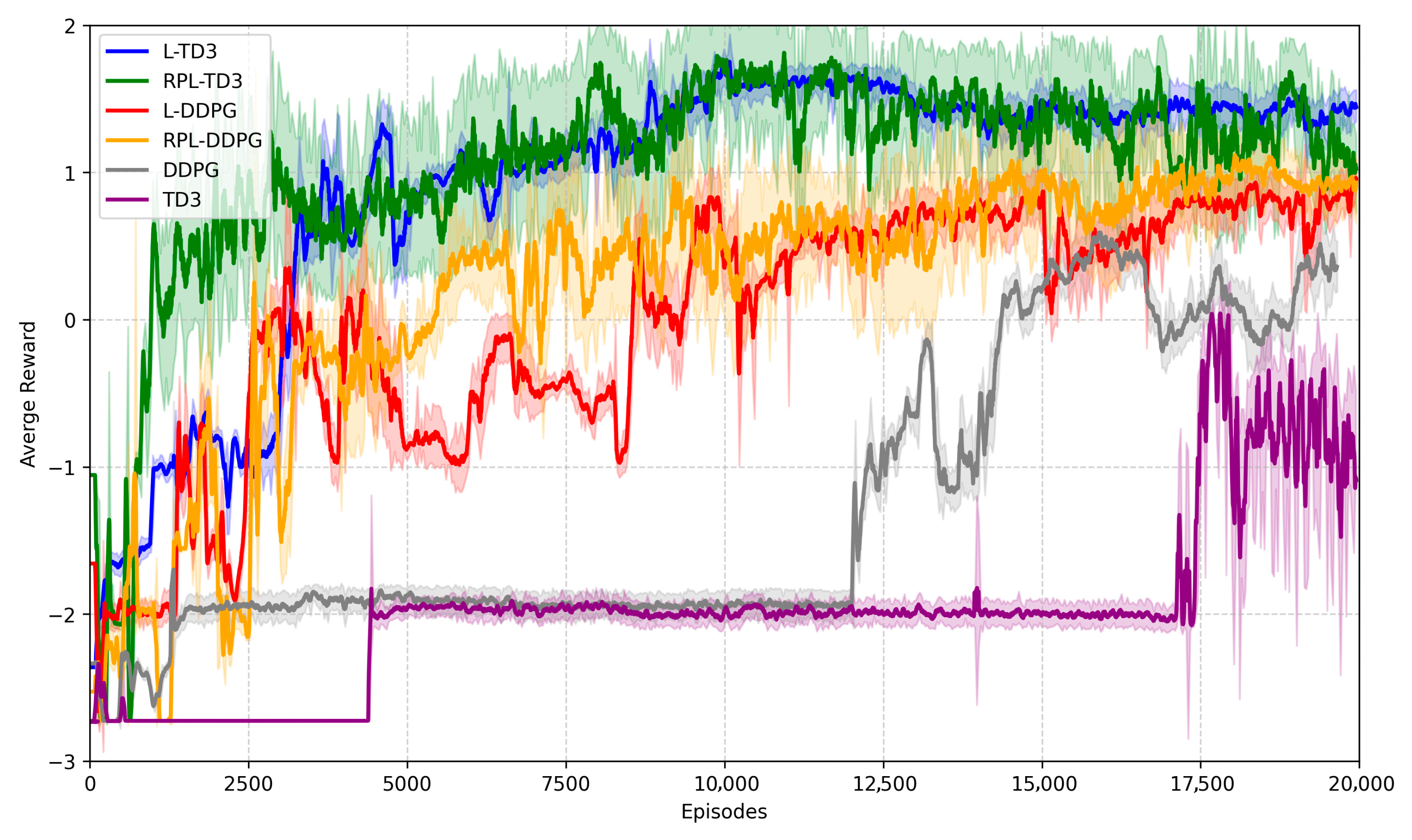
4.2. Training of the Stratospheric Airship Path Planning Model
4.3. Simulation Results of RPL-TD3
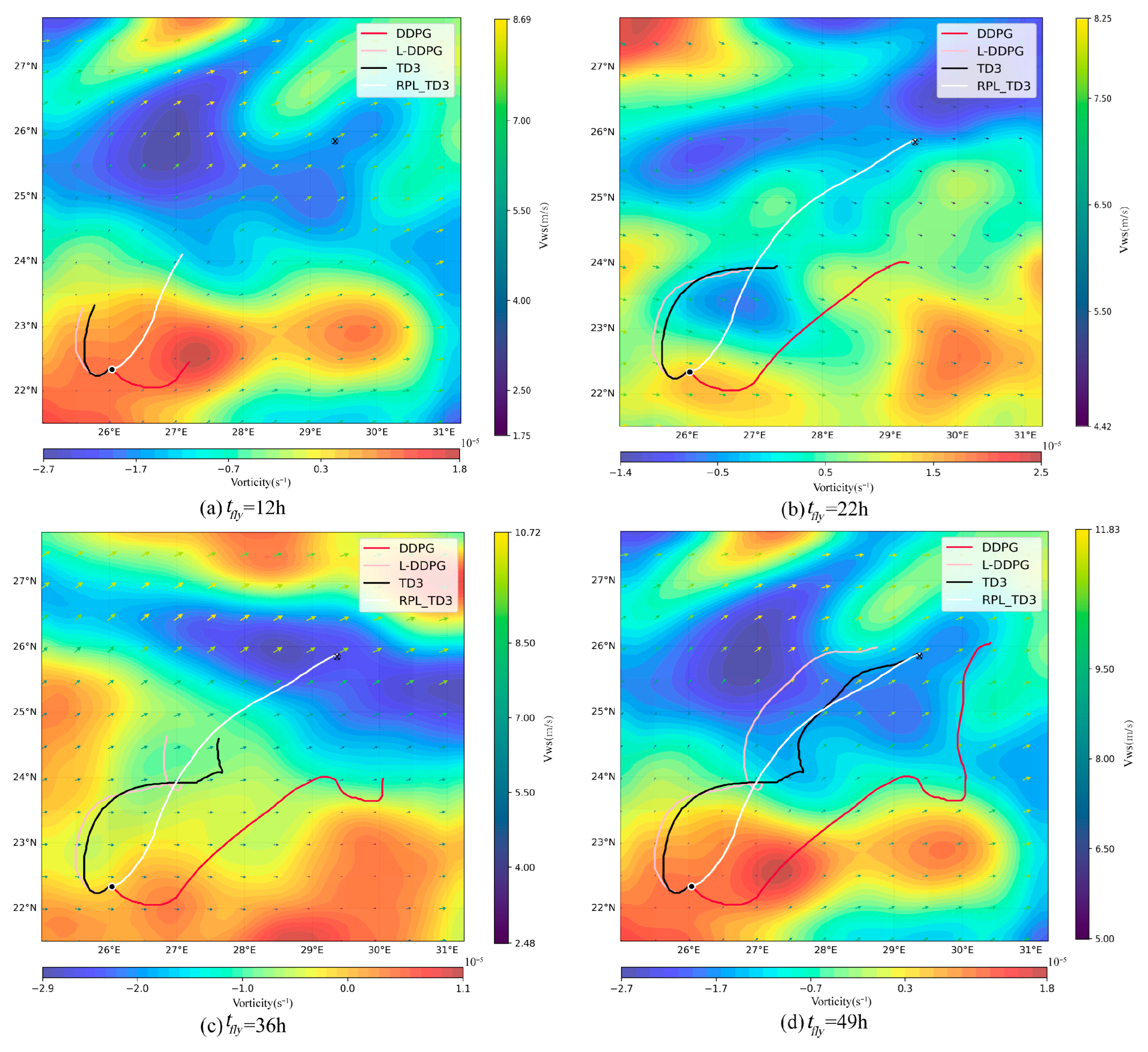
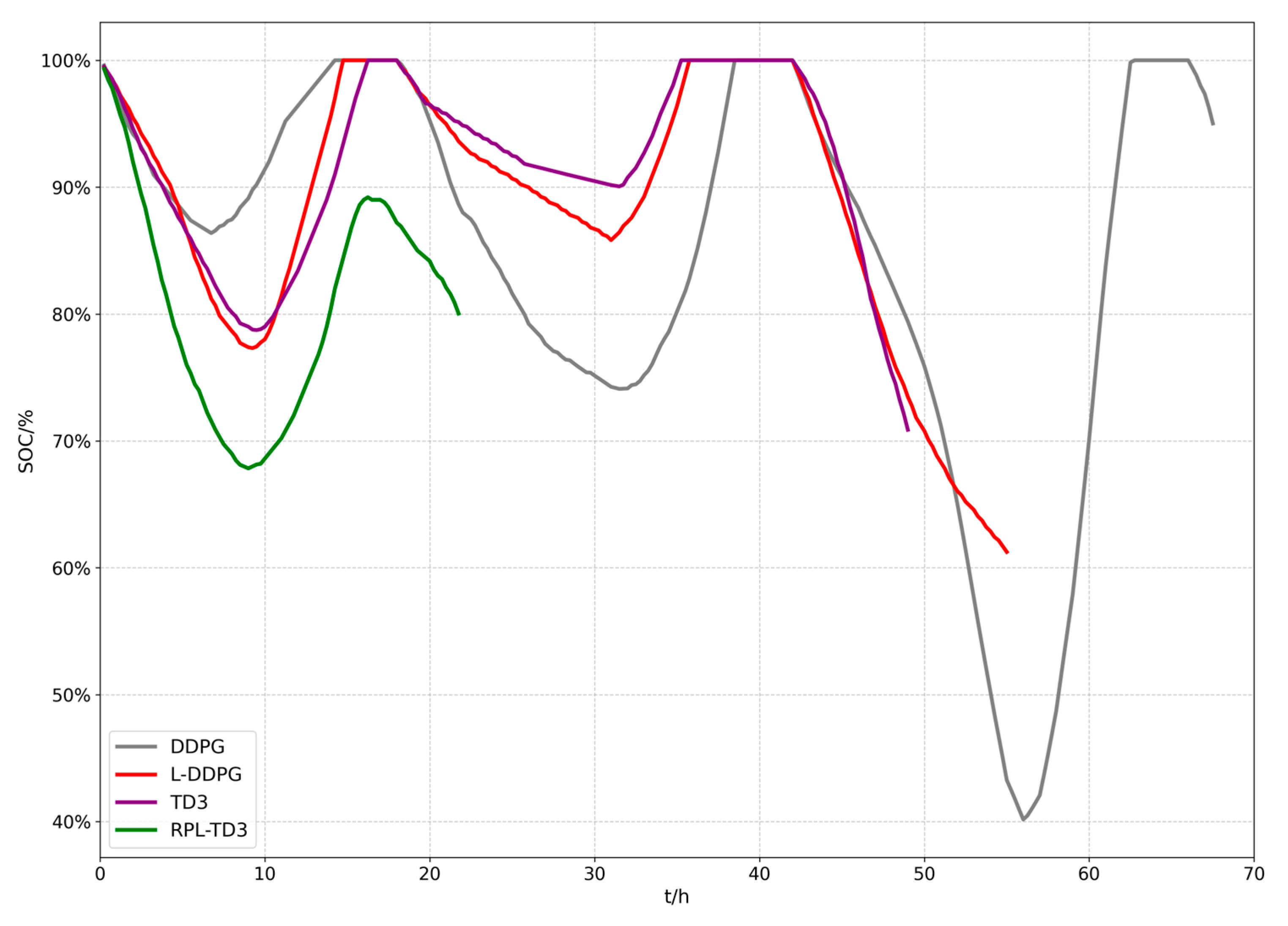
4.3.1. Comparative Simulation Experiments of RPL-TD3
4.3.2. Generalization Experiments
5. Discussion and Conclusions
- Based on the mathematical model of stratospheric airship path planning, this study uses the airship’s state and environmental information as observation data, with true airspeed and heading angle combined as action outputs. A time–energy composite reward model is designed to guide the agent’s learning. By interacting with the environment to train the deep neural network, a suitable and stable planning policy eventually converged.
- The proposed RPL-TD3 algorithm enhances planning capability by integrating an LSTM network, aiming to improve performance in strongly time-dependent path planning tasks. Additionally, to address the slow and difficult convergence of off-policy algorithms, a reward-prioritized experience replay mechanism is introduced, prioritizing high-value experiences to accelerate convergence. Comparative experiments show that RPL-TD3 exhibits strong convergence, with a 62.5% improvement in convergence speed compared to versions without reward-prioritized replay.
- Simulation results demonstrate that the proposed method is capable of generating feasible paths under kinematic and energy constraints. Compared with other baseline algorithms, it achieves the shortest flight time while maintaining a relatively high level of average residual energy. Furthermore, in multi-scenario generalization experiments, the RPL-TD3 algorithm attained a 93.3% success rate and significantly reduced path redundancy while satisfying model constraints.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Belmont, A.D.; Dartt, D.G.; Nastrom, G.D. Variations of stratospheric zonal winds, 20–65 km, 1961–1971. J. Appl. Meteorol. Climatol. 2010, 14, 585–594. [Google Scholar] [CrossRef]
- Hong, Y.J. Aircraft Technology of Near Space; National University of Defense Technology Press: Beijing, China, 2012; pp. 9–12. [Google Scholar]
- Schaefer, I.; Kueke, R.; Lindstrand, P. Airships as unmanned platforms: Challenge and chance. In Proceedings of the 1st UAV Conference, Portsmouth, VA, USA, 20–23 May 2002; p. 3423. [Google Scholar]
- d’Oliveira, F.A.; Melo, F.C.L.D.; Devezas, T.C. High-altitude platforms—Present situation technology trends. J. Aerosp. Technol. Manag. 2016, 8, 249–262. [Google Scholar] [CrossRef]
- Manikandan, M.; Pant, R.S. Research and advancements in hybrid airships—A review. Prog. Aerosp. Sci. 2021, 127, 100741. [Google Scholar] [CrossRef]
- Shaw, J.A.; Nugent, P.W.; Kaufman, N.A.; Pust, N.J.; Mikes, D.; Knierim, C.; Faulconer, N.; Larimer, R.M.; DesJardins, A.C.; Knighton, W.B. Multispectral imaging systems on tethered balloons for optical remote sensing education and research. J. Appl. Remote Sens. 2012, 6, 063613. [Google Scholar] [CrossRef]
- Golkar, A. Experiential systems engineering education concept using stratospheric balloon missions. IEEE Syst. J. 2019, 14, 1558–1567. [Google Scholar] [CrossRef]
- Jones, W.V. Evolution of scientific ballooning and its impact on astrophysics research. Adv. Space Res. 2014, 53, 1405–1414. [Google Scholar] [CrossRef]
- Azinheira, J.; Carvalho, R.; Paiva, E.; Cordeiro, R. Hexa-Propeller Airship for Environmental Surveillance and Monitoring in Amazon Rainforest. Aerospace 2024, 11, 249. [Google Scholar] [CrossRef]
- S. INC. Sceye Airships. 2021. Available online: https://www.sceye.com/ (accessed on 10 March 2025).
- Alam, M.I.; Pasha, A.A.; Jameel, A.G.A.; Ahmed, U. High Altitude Airship: A Review of Thermal Analyses and Design Approaches. Arch. Comput. Methods Eng. 2023, 30, 2289–2339. [Google Scholar] [CrossRef]
- Chen, P.; Huang, Y.; Papadimitriou, E.; Mou, J.; van Gelder, P. Global path planning for autonomous ship: A hybrid approach of fast marching square and velocity obstacles methods. Ocean Eng. 2020, 214, 107793. [Google Scholar] [CrossRef]
- Sands, T. Virtual sensoring of motion using Pontryagin’s treatment of Hamiltonian systems. Sensors 2021, 21, 4603. [Google Scholar] [CrossRef] [PubMed]
- Vashisth, A.; Rückin, J.; Magistri, F.; Stachniss, C.; Popović, M. Deep reinforcement learning with dynamic graphs for adaptive informative path planning. IEEE Robot. Autom. Lett. 2024, 9, 7747–7754. [Google Scholar] [CrossRef]
- Yang, Y.; Fu, Y.; Xin, R.; Feng, W.; Xu, K. Multi-UAV Trajectory Planning Based on a Two-Layer Algorithm Under Four-Dimensional Constraints. Drones 2025, 9, 471. [Google Scholar] [CrossRef]
- MTipaldi, R.; Iervolino, P.R. Massenio, Reinforcement learning in spacecraft control applications: Advances, prospects, and challenges. Annu. Rev. Control 2022, 54, 1–23. [Google Scholar] [CrossRef]
- Xie, G.; Fang, L.; Su, X.; Guo, D.; Qi, Z.; Li, Y.; Che, J. Research on Risk Avoidance Path Planning for Unmanned Vehicle Based on Genetic Algorithm and Bezier Curve. Drones 2025, 9, 126. [Google Scholar] [CrossRef]
- Cândido, B.; Rodrigues, C.; Moutinho, A.; Azinheira, J.R. Modeling, Altitude Control, and Trajectory Planning of a Weather Balloon Subject to Wind Disturbances. Aerospace 2025, 12, 392. [Google Scholar] [CrossRef]
- Luo, Q.; Sun, K.; Chen, T.; Zhang, Y.-F.; Zheng, Z.-W. Trajectory planning of stratospheric airship for station-keeping mission based on improved rapidly exploring random tree. Adv. Space Res. 2024, 73, 992–1005. [Google Scholar] [CrossRef]
- Hu, Z.D.; Xia, Q.; Cai, H. Various Stochastic Search Algorithms for High-Altitude Airship Trajectory Planning. Comput. Simul. 2007, 7, 55–58. [Google Scholar]
- Sun, H.; Zhang, W.; Yu, R.; Zhang, Y. Motion planning for mobile robots—Focusing on deep reinforcement learning: A systematic review. IEEE Access 2021, 9, 69061–69081. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, R.; Zhong, L.; Hou, Z. Multi-UAV Path Planning and Following Based on Multi-Agent Reinforcement Learning. Drones 2024, 8, 18. [Google Scholar] [CrossRef]
- Panov, A.I.; Yakovlev, K.S.; Suvorov, R. Grid path planning with deep reinforcement learning: Preliminary results. Procedia Comput. Sci. 2018, 123, 347–353. [Google Scholar] [CrossRef]
- Bellemare, M.G.; Candido, S.; Castro, P.S.; Gong, J.; Machado, M.C.; Moitra, S.; Ponda, S.S.; Wang, Z. Autonomous navigation of stratospheric balloons using reinforcement learning. Nature 2020, 588, 77–82. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Y.; Du, H.; Lv, M. Station-keeping for high-altitude balloon with reinforcement learning. Adv. Space Res. 2022, 70, 733–751. [Google Scholar] [CrossRef]
- Bai, F.; Yang, X.; Deng, X.; Ma, Z.; Long, Y. Station keeping control method based on deep reinforcement learning for stratospheric aerostat in dynamic wind field. Adv. Space Res. 2024, 75, 752–766. [Google Scholar] [CrossRef]
- Luo, Q.; Sun, K.; Chen, T.; Zhu, M.; Zheng, Z. Stratospheric airship fixed-time trajectory planning based on reinforcement learning. Electron. Res. Arch. 2025, 33, 1946–1967. [Google Scholar] [CrossRef]
- Zheng, B.; Zhu, M.; Guo, X.; Ou, J.; Yuan, J. Path planning of stratospheric airship in dynamic wind field based on deep reinforcement learning. Aerosp. Sci. Technol. 2024, 150, 109173. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, S.; Miao, J.; Shang, H.; Cui, Y.; Lu, Y. Autonomous Trajectory Planning Method for Stratospheric Airship Regional Station-Keeping Based on Deep Reinforcement Learning. Aerospace 2024, 11, 753. [Google Scholar] [CrossRef]
- Hausknecht, M.; Stone, P.; Mc, O. On-policy vs. off-policy updates for deep reinforcement learning. In Deep Reinforcement Learning: Frontiers and Challenges, IJCAI 2016 Workshop; AAAI Press: New York, NY, USA, 2016. [Google Scholar]
- Qi, L.; Yang, X.; Bai, F.; Deng, X.; Pan, Y. Stratospheric airship trajectory planning in wind field using deep reinforcement learning. Adv. Space Res. 2025, 75, 620–634. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, B.; Lou, W.; Sun, L.; Lv, C. Trajectory planning of stratosphere airship in wind-cloud environment based on soft actor-critic. In Proceedings of the 2024 IEEE International Conference on Artificial Intelligence in Engineering and Technology (IICAIET), Kota Kinabalu, Malaysia, 26–28 August 2024; pp. 401–406. [Google Scholar]
- Hou, J.; Zhu, M.; Zheng, B.; Guo, X.; Ou, J. Trajectory Planning Based On Continuous Decision Deep Reinforcement Learning for Stratospheric Airship. In Proceedings of the 2023 China Automation Congress (CAC), Chongqing, China, 17–19 November 2023; pp. 1508–1513. [Google Scholar]
- He, Y.; Guo, K.; Wang, C.; Fu, K.; Zheng, J. Path Planning for Autonomous Balloon Navigation with Reinforcement Learning. Electronics 2025, 14, 204. [Google Scholar] [CrossRef]
- Lv, C.; Zhu, M.; Guo, X.; Ou, J.; Lou, W. Hierarchical reinforcement learning method for long-horizon path planning of stratospheric airship. Aerosp. Sci. Technol. 2025, 160, 110075. [Google Scholar] [CrossRef]
- Neves, D.E.; Ishitani, L.; do Patrocinio Junior, Z.K.G. Advances and challenges in learning from experience replay. Artif. Intell. Rev. 2024, 58, 54. [Google Scholar] [CrossRef]
- Özalp, R.; Varol, N.K.; Taşci, B.; Uçar, A. A review of deep reinforcement learning algorithms and comparative results on inverted pendulum system. Mach. Learn. Paradig. Adv. Deep. Learn.-Based Technol. Appl. 2020, 18, 237–256. [Google Scholar]
- Hou, Y.; Liu, L.; Wei, Q.; Xu, X.; Chen, C. A novel DDPG method with prioritized experience replay. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 316–321. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2016, arXiv:1511.05952. [Google Scholar] [CrossRef]
- Hassani, H.; Nikan, S.; Shami, A. Traffic navigation via reinforcement learning with episodic-guided prioritized experience replay. Eng. Appl. Artif. Intell. 2024, 137, 109147. [Google Scholar] [CrossRef]
- Smierzchała, Ł.; Kozłowski, N.; Unold, O. Anticipatory Classifier System With Episode-Based Experience Replay. IEEE Access 2023, 11, 41190–41204. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present. Copernic. Clim. Change Serv. (C3s) Clim. Data Store (Cds) 2018, 10. [Google Scholar]
- Wolf, M.T.; Blackmore, L.; Kuwata, Y.; Fathpour, N.; Elfes, A.; Newman, C. Probabilistic motion planning of balloons in strong, uncertain wind fields. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Piscataway, NJ, USA, 3–7 May 2010; pp. 1123–1129. [Google Scholar]
- Li, J.; Liao, J.; Liao, Y.; Du, H.; Luo, S.; Zhu, W.; Lv, M. An approach for estimating perpetual endurance of the stratospheric solar-powered platform. Aerosp. Sci. Technol. 2018, 79, 118–130. [Google Scholar] [CrossRef]
- Shani, G.; Heckerman, D.; Brafman, R.I. An MDP-based recommender system. J. Mach. Learn. Res. 2005, 6, 1265–1295. [Google Scholar]
- Andrychowicz, M.; Raichuk, A.; Stańczyk, P.; Orsini, M.; Girgin, S.; Marinier, R.; Hussenot, L.; Geist, M.; Pietquin, O.; Michalski, M.; et al. What matters in on-policy reinforcement learning? a large-scale empirical study. arXiv 2020, arXiv:2006.05990. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 3 July 2018; pp. 1587–1596. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]

| Symbol | Description |
|---|---|
| Probability distribution function of meridional and zonal wind speed (average wind speed and standard deviation) | |
| the average wind speed of all states in the local region and the Gaussian distribution coefficient | |
| Meridional wind, zonal wind, and wind direction angle | |
| Airship ground speed, true airspeed, wind speed at its location, and heading angle | |
| Solar cells generate energy, the remaining energy of storage batteries, the rated capacity of batteries, and the minimum energy threshold for normal system operation | |
| The total energy consumption of the airship, propulsion system energy consumption, payload energy consumption, and measurement, avionics control system energy consumption | |
| The total power of the airship propulsion system and the power consumption of other parts | |
| Solar cell photovoltaic conversion efficiency, airship propulsion system propeller efficiency, and motor efficiency | |
| The total area of solar cells on the stratospheric airship and the reference area of the stratospheric airship | |
| The power generation of solar cells per unit area and the direct solar irradiance per unit area per unit time | |
| Solar elevation angle, solar declination angle, and hourly angle | |
| Atmospheric density and drag coefficient at the flight altitude of the stratospheric airship | |
| The number of experimental days and the total number of days selected within one year | |
| Total flight time and the state of charge for storage battery | |
| The agent’s state and action taken by the agent at time | |
| MDP five-tuple (state space, action space, state transition probability, reward function, discount factor) | |
| Agent rewards upon goal reward, distance penalty, boundary penalty, time reward, and energy reward | |
| The distance function between the current position and the goal position of the stratospheric airship agent | |
| Reward function weight parameters | |
| Critic network target value, Critic network estimate value and Actor network policy | |
| Exploration rate of the agent’s decision-making | |
| Actor network parameters and Critic network parameters | |
| Target policy for smoothing noise, noise distribution, and clipping limit | |
| The information of the input gate, forget gate and output gate of the LSTM neuron | |
| LSTM neuron cell state (combination of long- and short-term information) and hidden state (short-term memory) | |
| Current input and current state of LSTM neuron | |
| Sigmoid layer (in LSTM), weight matrix, and bias vector | |
| Individual experience, experience sequence length, reward of individual experience, self-sampling probability of individual experience, and sampling probability | |
| Adaptive decay scaling factor and decay coefficient | |
| Current training step and total training steps | |
| Current episode and delayed update episode |
| Parameters | Value |
|---|---|
| Wind field spatial resolution | 0.25° |
| Wind field time resolution | 1 h |
| Maximum true speed of airship | 15 m/s |
| Minimum energy of airship | 20% |
| Wing field size | 21.5° N–22.75° N, 25° E–31.25° E |
| Parameters | Value |
|---|---|
| Batch size | 128 |
| Hidden layer dimension | 128 |
| Discount rate | 0.99 |
| Replay buffer | 3 × 106 |
| Optimizer | Adam |
| Actor learning rate | 3 × 10−4 |
| Critic learning rate | 3 × 10−4 |
| Experience sequence length | 1 × 103 |
| Delayed policy update frequency | 2 |
| Target policy smoothing regularization | 1 × 10−2 |
| Time-step interval | 15 min |
| Algorithm | DDPG | L-DDPG | TD3 | RPL-TD3 |
|---|---|---|---|---|
| Flight time | 67.5 h | 55 h | 49 h | 21.75 h |
| Average energy | 84.70% | 88.54% | 91.77% | 89.63% |
| Min energy | 40.15% | 61.25% | 70.87% | 67.83% |
| Scenario | Start | Goal | Flight Time | Average Energy |
|---|---|---|---|---|
| 1 | (25.50° E, 23.55° N) | (28.37° E, 26.85° N) | 21.25 h | 92.23% |
| 2 | (28.99° E, 24.03° N) | (26.98° E, 23.16° N) | 8.75 h | 69.78% |
| 3 | (28.46° E, 25.56° N) | (30.88° E, 25.30° N) | 28.25 h | 89.55% |
| 4 | (31.11° E, 24.55° N) | (29.33° E, 26.57° N) | 9.50 h | 76.34% |
| 5 | (26.47° E, 22.30° N) | (28.56° E, 25.62° N) | 18.00 h | 93.23% |
| 6 | (26.02° E, 22.58° N) | (30.23° E, 24.44° N) | 30.50 h | 85.78% |
| 7 | (27.36° E, 24.85° N) | (30.91° E, 23.10° N) | 22.50 h | 90.30% |
| 8 | (26.12° E, 23.84° N) | (29.67° E, 21.84° N) | 48.75 h | 80.26% |
| 9 | (31.12° E, 25.86° N) | (28.12° E, 22.22° N) | 33.00 h | 74.35% |
| 10 | (29.04° E, 24.36° N) | (30.25° E, 26.13° N) | 11.25 h | 78.85% |
| 11 | (27.09° E, 25.84° N) | (25.11° E, 25.85° N) | 4.50 h | 83.24% |
| 12 | (25.54° E, 26.60° N) | (30.85° E, 26.30° N) | 27.75 h | 90.18% |
| 13 | (25.91° E, 25.56° N) | (27.90° E, 27.12° N) | 12.75 h | 81.66% |
| 14 | (26.19° E, 22.26° N) | (29.59° E, 22.95° N) | 22.50 h | 88.49% |
| 15 | (29.77° E, 24.49° N) | (26.87° E, 24.75° N) | 7.00 h | 71.28% |
| 16 | (29.85° E, 25.78° N) | (30.72° E, 24.03° N) | 4.50 h | 80.49% |
| 17 | (26.91° E, 25.93° N) | (30.36° E, 26.29° N) | 13.50 h | 87.54% |
| 18 | (26.47° E, 22.30° N) | (28.56° E, 25.62° N) | 13.00 h | 84.88% |
| 19 | (26.22° E, 22.91° N) | (26.69° E, 27.01° N) | 24.50 h | 84.83% |
| 20 | (26.00° E, 22.98° N) | (30.02° E, 24.33° N) | 15.25 h | 76.45% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Huang, W.; Miao, J.; Li, J.; Cao, S. Off-Policy Deep Reinforcement Learning for Path Planning of Stratospheric Airship. Drones 2025, 9, 650. https://doi.org/10.3390/drones9090650
Xie J, Huang W, Miao J, Li J, Cao S. Off-Policy Deep Reinforcement Learning for Path Planning of Stratospheric Airship. Drones. 2025; 9(9):650. https://doi.org/10.3390/drones9090650
Chicago/Turabian StyleXie, Jiawen, Wanning Huang, Jinggang Miao, Jialong Li, and Shenghong Cao. 2025. "Off-Policy Deep Reinforcement Learning for Path Planning of Stratospheric Airship" Drones 9, no. 9: 650. https://doi.org/10.3390/drones9090650
APA StyleXie, J., Huang, W., Miao, J., Li, J., & Cao, S. (2025). Off-Policy Deep Reinforcement Learning for Path Planning of Stratospheric Airship. Drones, 9(9), 650. https://doi.org/10.3390/drones9090650






