Error-Constrained Fixed-Time Synchronized Trajectory Tracking Control for Unmanned Airships with Disturbances
Abstract
1. Introduction
- For accurate trajectory tracking, the error should be confined to a specified range, ensuring compliance with practical performance criteria. Through the implementation of the error transformation function (ETF), the tracking errors are systematically transformed, enforcing tracking errors strictly confined in prescribed time-varying error boundaries throughout the tracking process.
- Distinct from conventional nonlinear control approaches that are irrespective of synchronization of each state convergence, built upon the Norm-Normalized sign (NNS) function, this work establishes a control algorithm, effectively ensuring simultaneous stabilization of all tracking error and estimation error components.
- In contrast to DOs that solely ensure fixed-time disturbance estimation, this work proposes a fixed-time synchronized disturbance observer (FTSDO) to achieve the exact reconstruction of uncertain disturbances while guaranteeing the synchronous fixed-time convergence of all estimation errors.
2. Preliminaries
- 1.
- The same constants , and in Lemma 1 satisfy the inequality in (3).
- 2.
- The system state maintains ratio persistence:where denotes the direction of ratio persistence.
3. Problem Statement
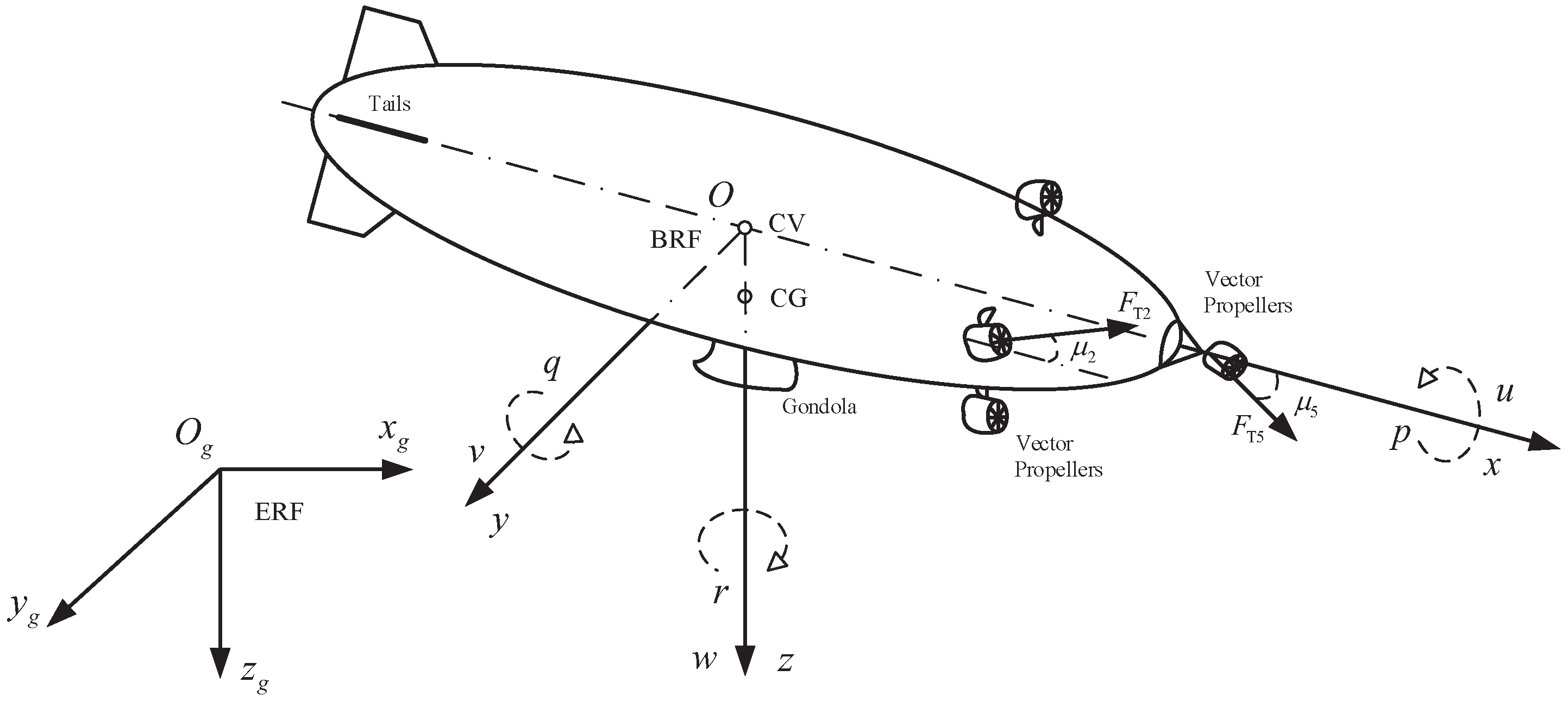
3.1. Airship Model
3.2. Model Transformation
3.3. Control Objective
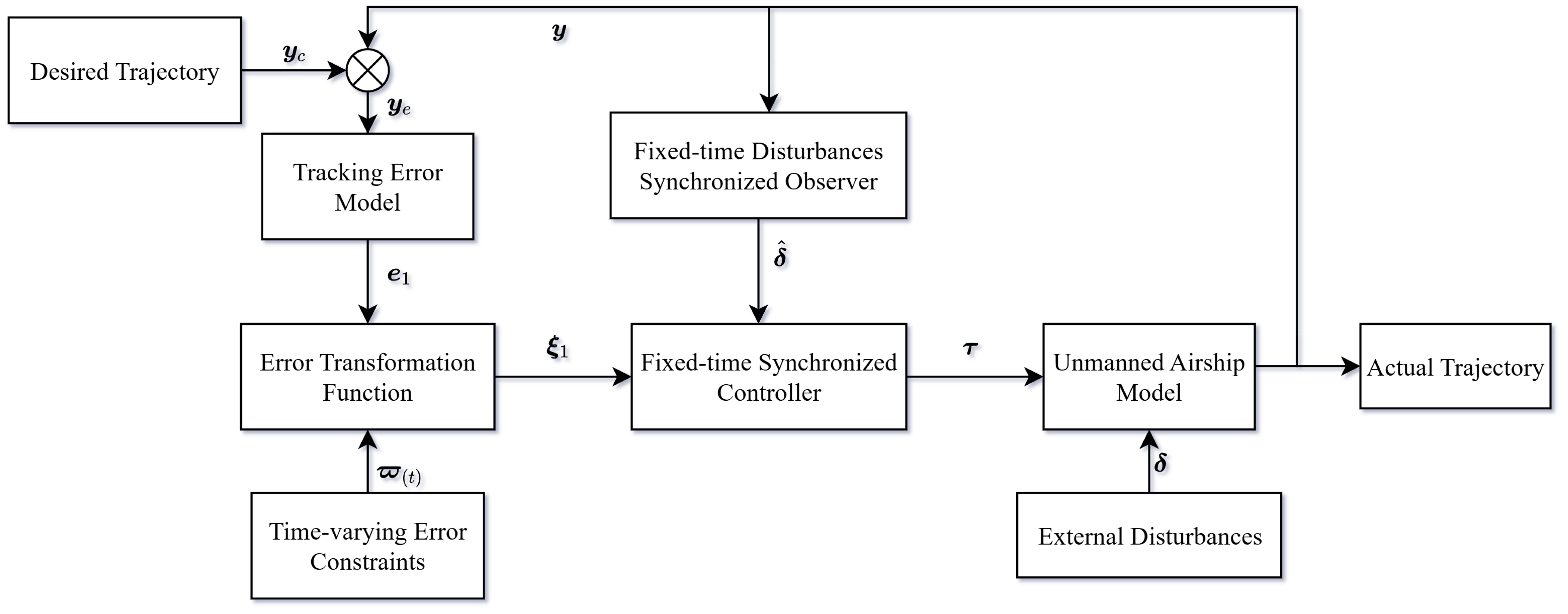
4. Main Results
4.1. Fixed-Time Synchronized Observer Design
4.2. Fixed-Time Synchronized Controller Design
- 1.
- Smooth, monotonically increasing;
- 2.
- ;
- 3.
- , ;
4.3. Stability Analysis
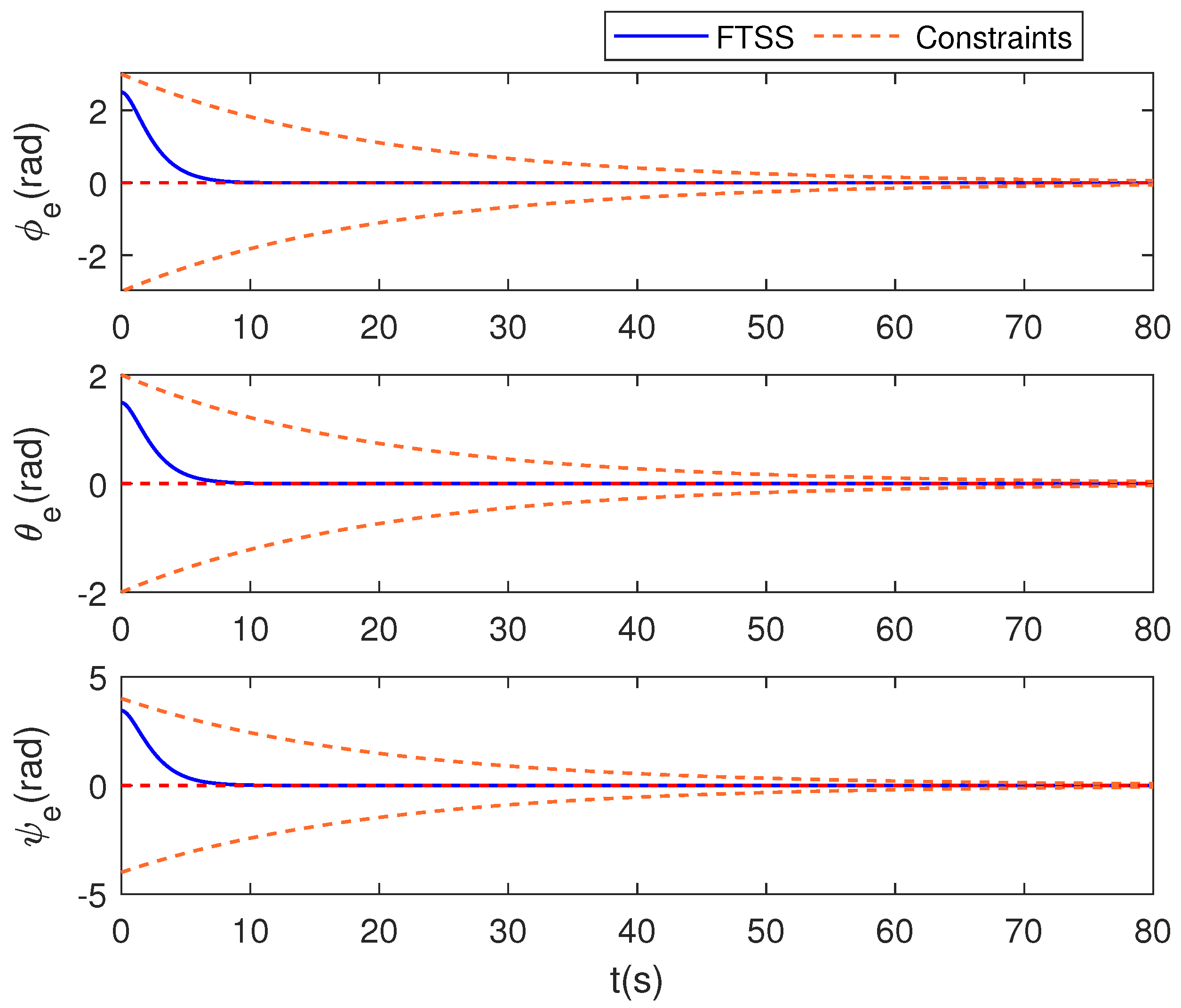
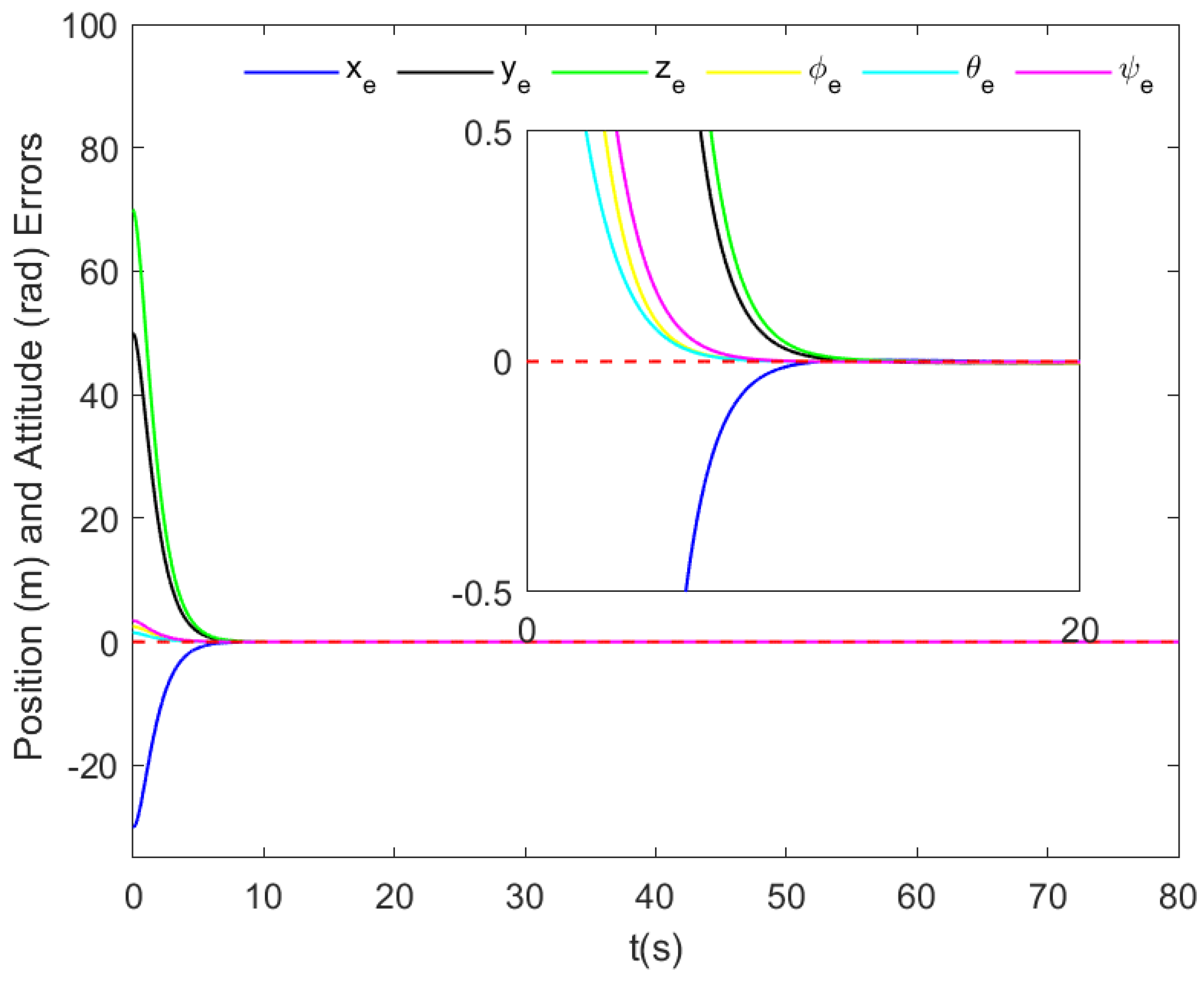
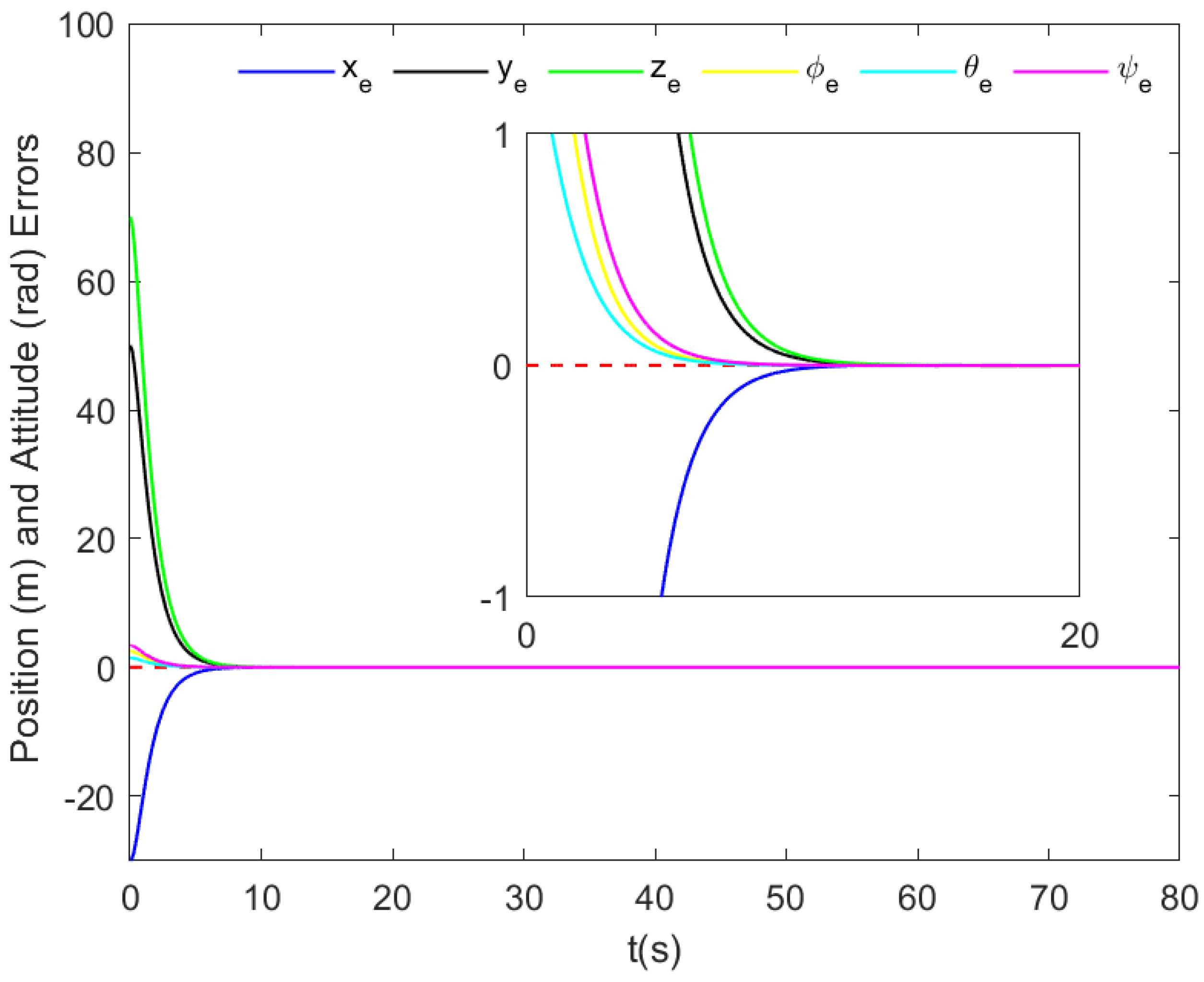
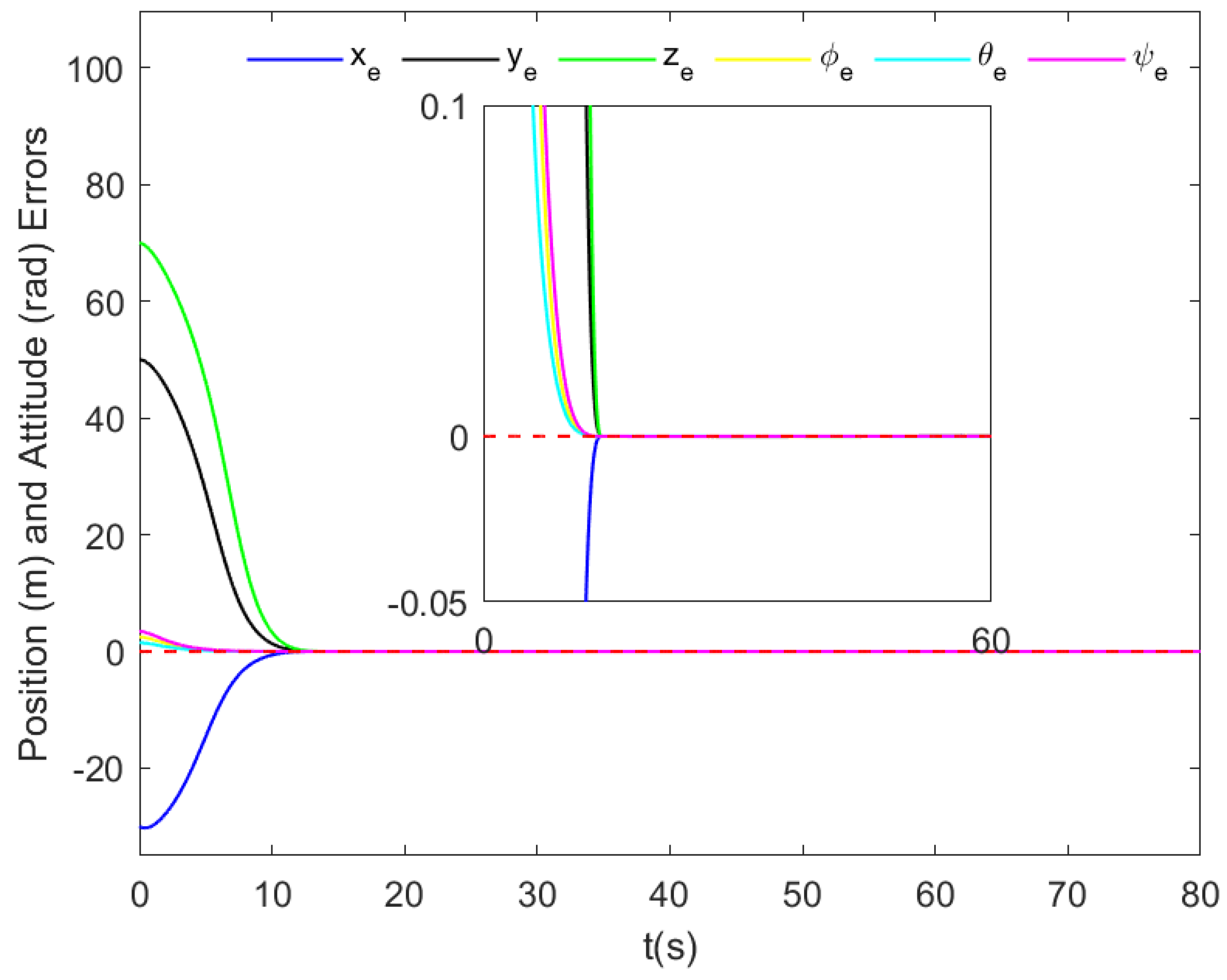
- Based on Theorem 1, , for all , and is arbitrarily small. Therefore, all tracking errors are fixed-time stable according to Lemma 1. Combining (50) with Lemma 3, exhibits FTSS with the convergence time . Then, from (38), we have , and and achieve synchronized stability with the convergence time . Consequently, , all tracking errors exhibit FTSS.
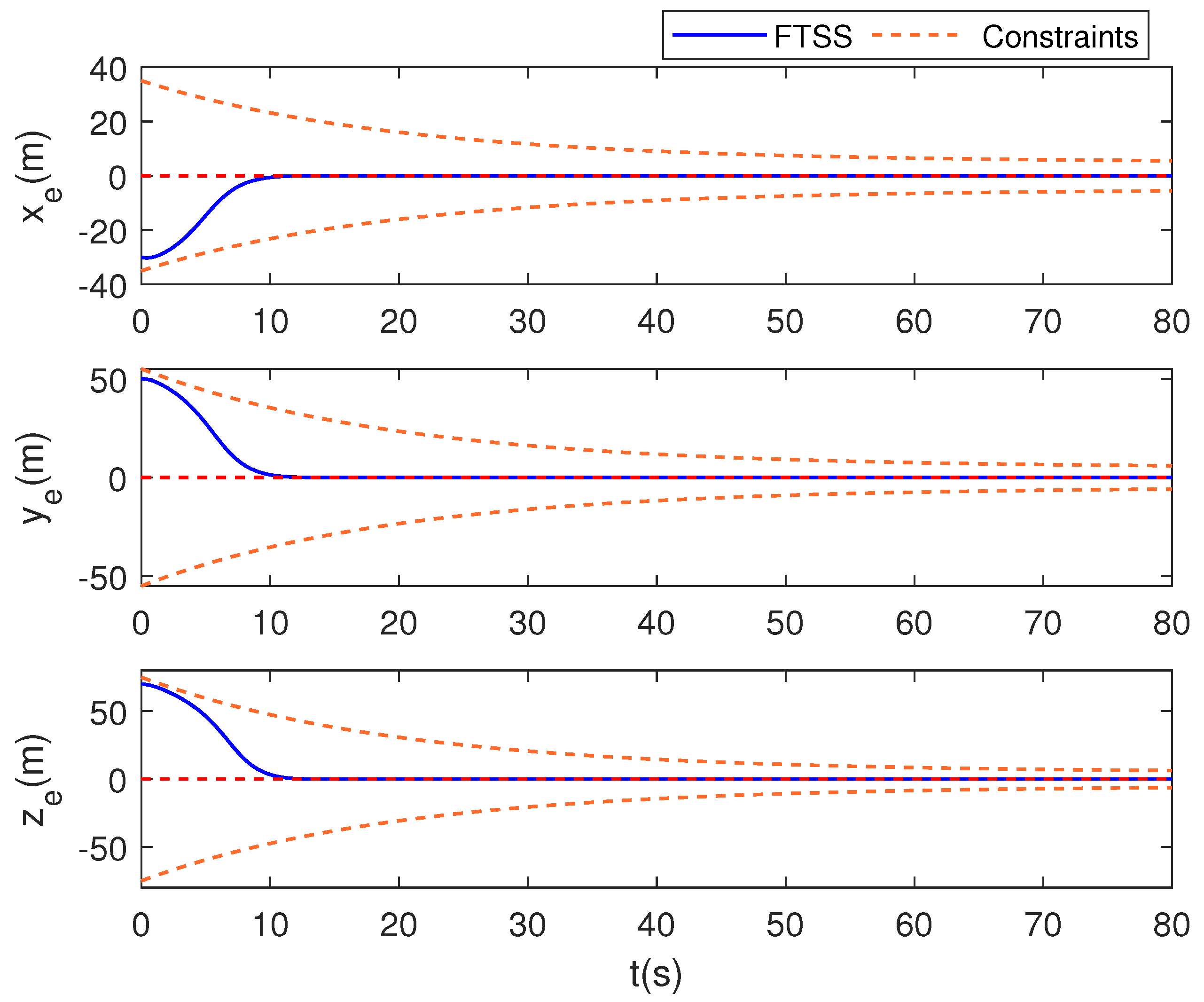
- Furthermore, considering inequality (60), since if and only if , and given the initial condition , we can rigorously establish that the error constraint remains strictly satisfied throughout the convergence process.
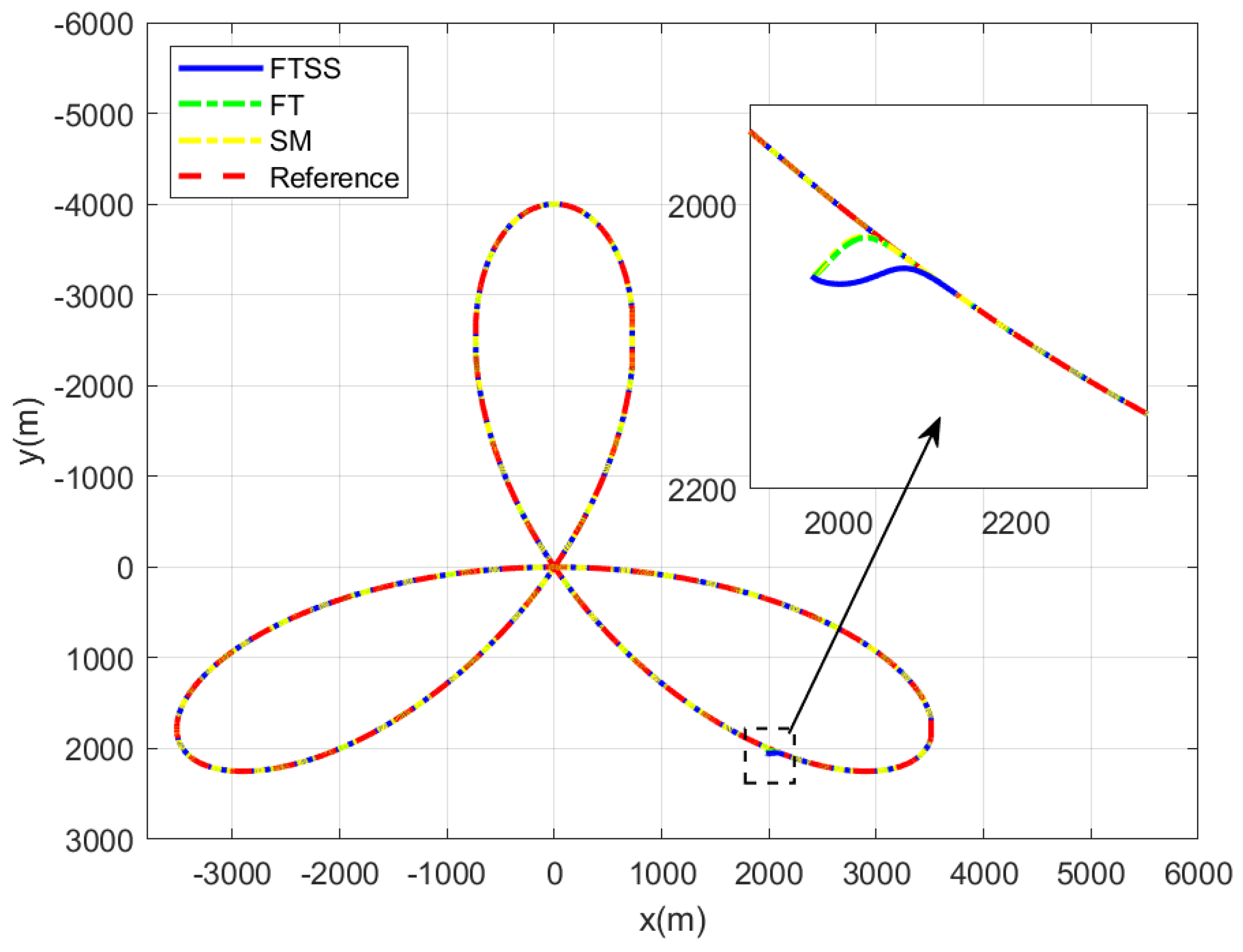
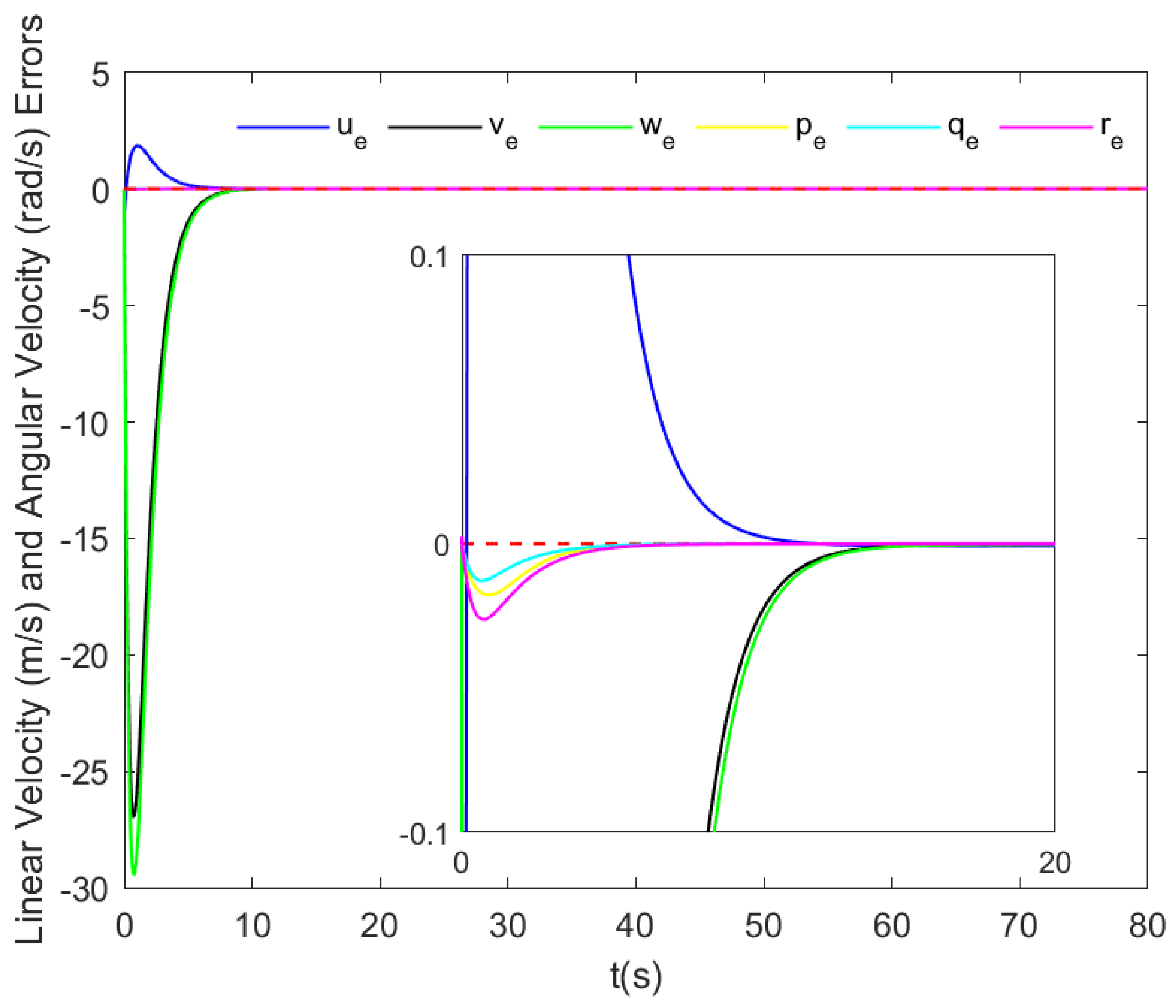
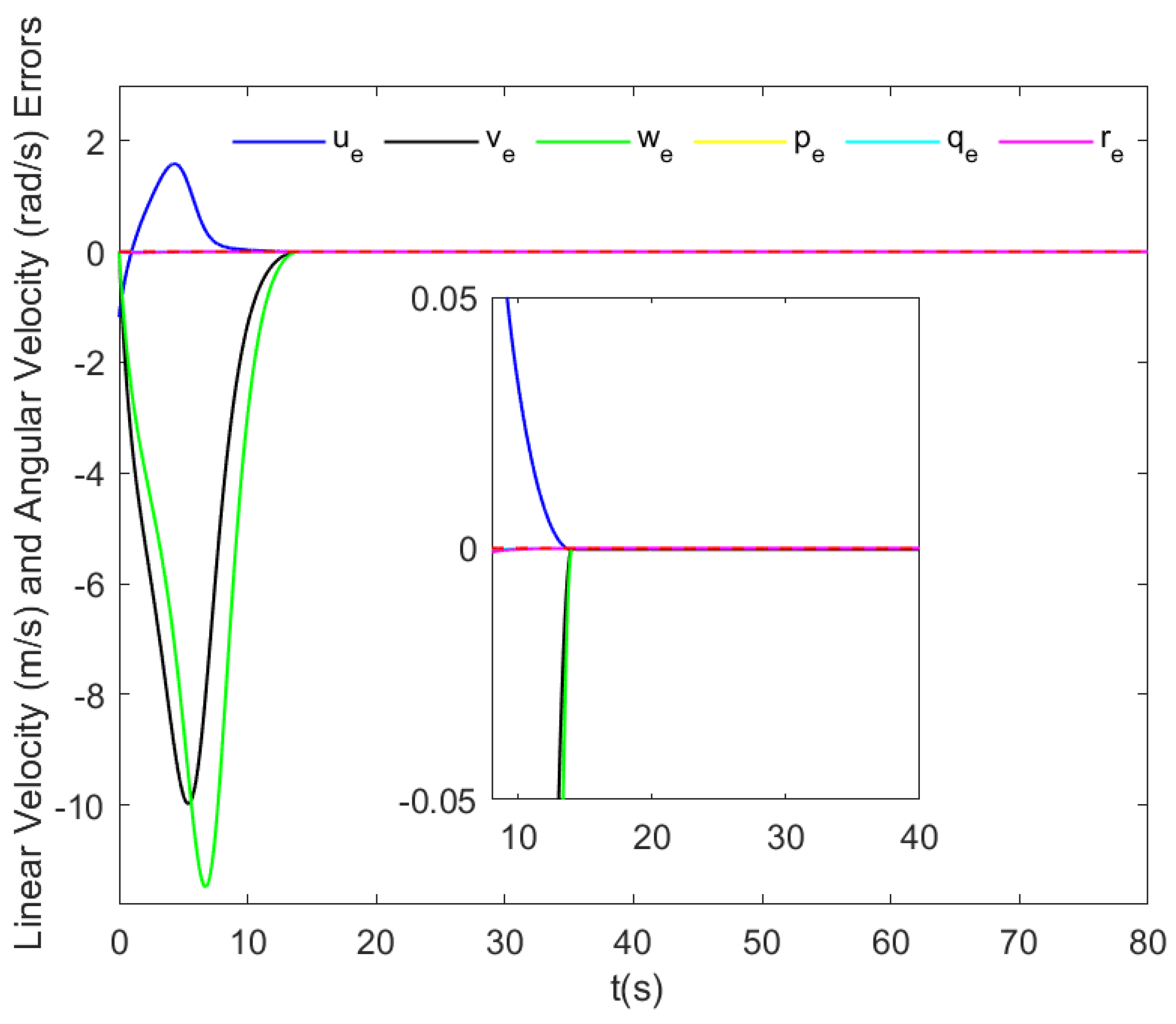
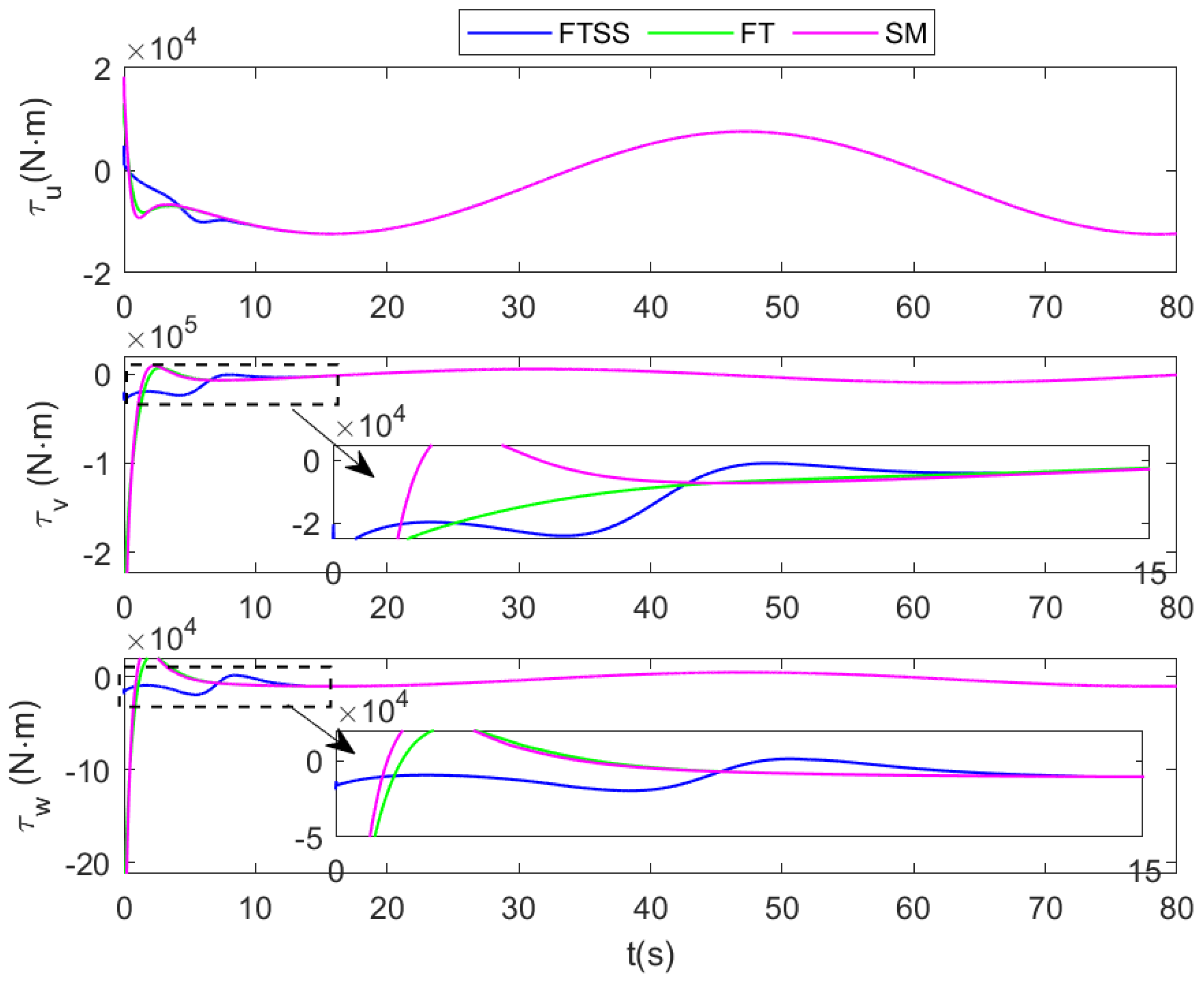
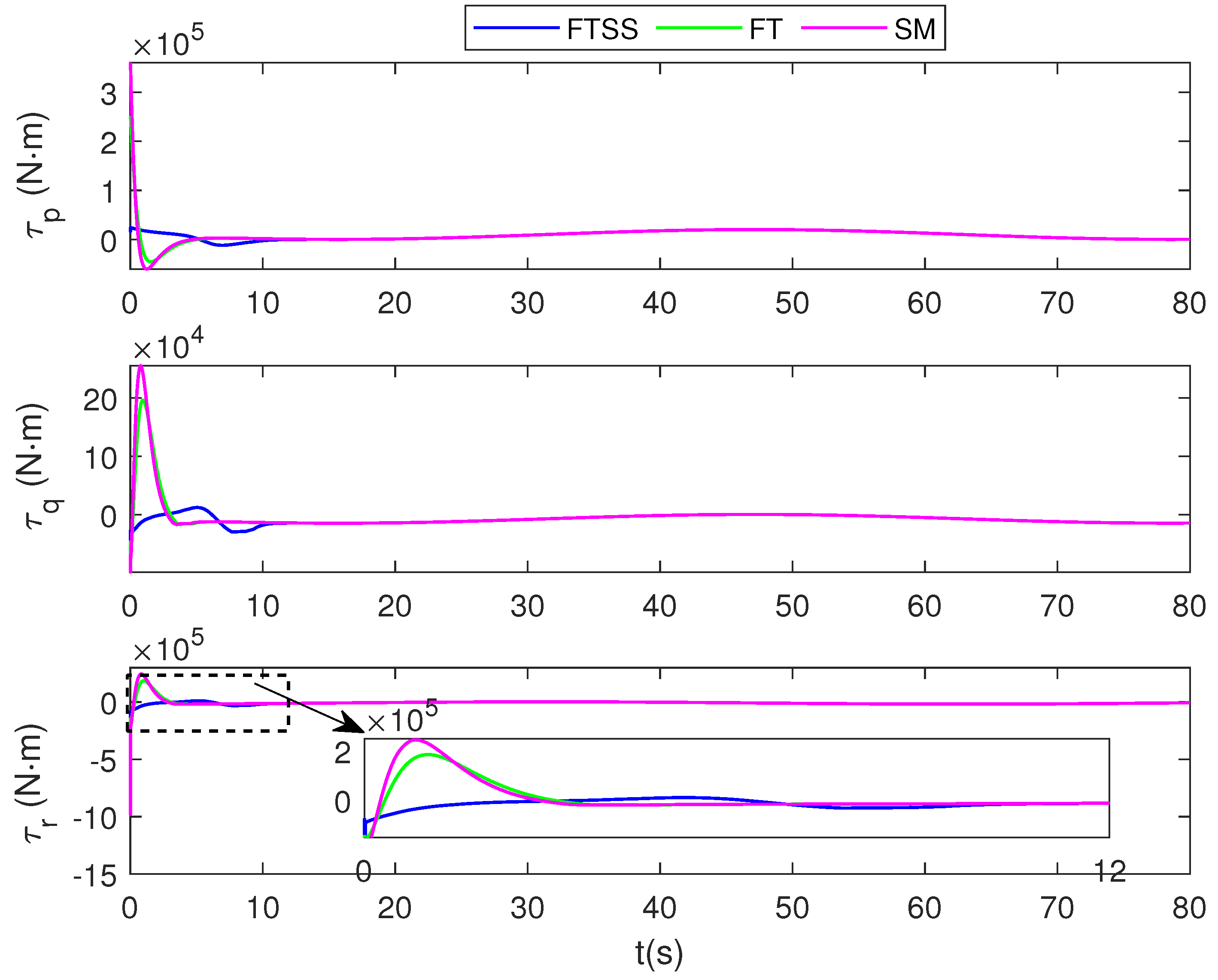
5. Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Durán-Delfín, J.; García-Beltrán, C.D.; Guerrero-Sánchez, M.E.; Valencia-Palomo, G.; Hernández-González, O. Modeling and Passivity-Based Control for a convertible fixed-wing VTOL. Appl. Math. Comput. 2024, 461, 128298. [Google Scholar] [CrossRef]
- Zheng, B.; Zhu, M.; Guo, X.; Ou, J.; Yuan, J. Path planning of stratospheric airship in dynamic wind field based on deep reinforcement learning. Aerosp. Sci. Technol. 2024, 150, 109173. [Google Scholar] [CrossRef]
- Sun, R.; Ahn, C.K.; Liu, D.; Wang, W.; Zhang, C. Near-asteroid spacecraft formation control with prescribed-performance: A dynamic event-triggered reinforcement learning control approach. Aerosp. Sci. Technol. 2025, 161, 110138. [Google Scholar] [CrossRef]
- Ye, Z.; Cai, G.; Xu, H.; Shang, Y.; Hu, C. Prescribed Performance Sliding Mode Fault-Tolerant Tracking Control for Unmanned Morphing Flight Vehicles with Actuator Faults. Drones 2025, 9, 292. [Google Scholar] [CrossRef]
- Mechali, O.; Xu, L. Distributed fixed-time sliding mode control of time-delayed quadrotors aircraft for cooperative aerial payload transportation: Theory and practice. Adv. Space Res. 2023, 71, 3897–3916. [Google Scholar] [CrossRef]
- Airaldi, F.; De Schutter, B.; Dabiri, A. Reinforcement Learning with Model Predictive Control for Highway Ramp Metering. IEEE Trans. Intell. Transp. Syst. 2025, 26, 5988–6004. [Google Scholar] [CrossRef]
- Taheri, S.; Amiri, A.J.; Razban, A. Real-world implementation of a cloud-based MPC for HVAC control in educational buildings. Energy Convers. Manag. 2024, 305, 118270. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S. Adaptive backstepping control for uncertain nonlinear strict-feedback systems with full state triggering. Automatica 2024, 163, 111574. [Google Scholar] [CrossRef]
- Li, Y.; Fan, Y.; Li, K.; Liu, W.; Tong, S. Adaptive optimized backstepping control-based RL algorithm for stochastic nonlinear systems with state constraints and its application. IEEE Trans. Cybern. 2021, 52, 10542–10555. [Google Scholar] [CrossRef]
- Montoya-Morales, J.; Guerrero-Sánchez, M.; Valencia-Palomo, G.; Hernández-González, O.; López-Estrada, F.; Hoyo-Montaño, J. Real-time robust tracking control for a quadrotor using monocular vision. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2729–2741. [Google Scholar] [CrossRef]
- Wang, Y.; Zong, G.; Yang, D.; Shi, K. Finite-time adaptive tracking control for a class of nonstrict feedback nonlinear systems with full state constraints. Int. J. Robust Nonlinear Control 2022, 32, 2551–2569. [Google Scholar] [CrossRef]
- Zhou, B.; Michiels, W.; Chen, J. Fixed-time stabilization of linear delay systems by smooth periodic delayed feedback. IEEE Trans. Autom. Control 2021, 67, 557–573. [Google Scholar] [CrossRef]
- Yu, L.; He, G.; Wang, X.; Zhao, S. Robust fixed-time sliding mode attitude control of tilt trirotor UAV in helicopter mode. IEEE Trans. Ind. Electron. 2021, 69, 10322–10332. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, M.; Chen, T.; Zheng, Z. Distributed event-triggered fixed-time formation and trajectory tracking control for multiple stratospheric airships. ISA Trans. 2022, 130, 63–78. [Google Scholar] [CrossRef]
- Xie, X.; Sheng, T.; Chen, X. Dynamic event-triggered and self-triggered fault-tolerant attitude control for multiple spacecraft systems with uncertainties and input saturation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2922–2933. [Google Scholar] [CrossRef]
- Sun, H.; Zong, G.; Cui, J.; Shi, K. Fixed-time sliding mode output feedback tracking control for autonomous underwater vehicle with prescribed performance constraint. Ocean Eng. 2022, 247, 110673. [Google Scholar] [CrossRef]
- Song, X.; Sun, P.; Song, S.; Stojanovic, V. Event-driven NN adaptive fixed-time control for nonlinear systems with guaranteed performance. J. Frankl. Inst. 2022, 359, 4138–4159. [Google Scholar] [CrossRef]
- Li, X.; Qin, H.; Li, L.; Xue, Y. Adaptive fixed-time fuzzy formation control for multiple AUV systems considering time-varying tracking error constraints and asymmetric actuator saturation. Ocean. Eng. 2024, 297, 116936. [Google Scholar] [CrossRef]
- Hu, X.; Wei, X.; Gong, Q.; Gu, J. Adaptive synchronization of marine surface ships using disturbance rejection without leader velocity. ISA Trans. 2021, 114, 72–81. [Google Scholar] [CrossRef]
- Gao, Y.; Li, D.; Ge, S.S. Time-synchronized tracking control for 6-DOF spacecraft in rendezvous and docking. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1676–1691. [Google Scholar] [CrossRef]
- Zhai, A.; Wang, J.; Zhang, H.; Lu, G.; Li, H. Adaptive robust synchronized control for cooperative robotic manipulators with uncertain base coordinate system. ISA Trans. 2022, 126, 134–143. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Ge, S.S.; Lee, T.H. Time-Synchronized Control: Analysis and Design; Springer: New York, NY, USA, 2022. [Google Scholar]
- Jang, S.G.; Yoo, S.J. Predefined-time-synchronized backstepping control of strict-feedback nonlinear systems. Int. J. Robust Nonlinear Control 2023, 33, 7563–7582. [Google Scholar] [CrossRef]
- Wang, D.; Ge, S.S.; Liang, X.; Li, D. Time-synchronized formation control of unmanned surface vehicles. IEEE Trans. Intell. Veh. 2024. early access. [Google Scholar] [CrossRef]
- Guan, H.; Sui, S.; Sui, Y.; Chen, C.P. NN-based adaptive event-triggered predefined time control of flexible joint robot with full-state error constraints. Neurocomputing 2025, 631, 129658. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, Y.; Liang, H. Event-triggered predefined-time control for full-state constrained nonlinear systems: A novel command filtering error compensation method. Sci. China Technol. Sci. 2024, 67, 2867–2880. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, H.; Sun, Y.; Qin, H. Adaptive prescribed performance second-order sliding mode tracking control of autonomous underwater vehicle using neural network-based disturbance observer. Ocean Eng. 2022, 260, 111939. [Google Scholar] [CrossRef]
- Wang, Y.; Zong, G.; Zhao, X.; Yi, Y. Adaptive practical fixed-time synchronized tracking control of ASV with prescribed performance. Automatica 2024, 166, 111716. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, P.; Qian, C.; Hua, C. Adaptive Trajectory Tracking Error Constraint Control of Unmanned Underwater Vehicle Based on a Fully Actuated System Approach. J. Syst. Sci. Complex. 2024, 37, 2633–2653. [Google Scholar] [CrossRef]
- He, H.; Wang, N.; Huang, D.; Han, B. Active vision-based finite-time trajectory-tracking control of an unmanned surface vehicle without direct position measurements. IEEE Trans. Intell. Transp. Syst. 2024, 25, 12151–12162. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, M.; Zheng, Z.; Feroskhan, M. Fixed-time autonomous shipboard landing control of a helicopter with external disturbances. Aerosp. Sci. Technol. 2019, 84, 18–30. [Google Scholar] [CrossRef]
- Sun, L.; Sun, K.; Guo, X.; Yuan, J.; Zhu, M. Prescribed-time error-constrained moving path following control for a stratospheric airship with disturbances. Acta Astronaut. 2023, 212, 307–315. [Google Scholar] [CrossRef]
- Hernández-González, O.; Targui, B.; Valencia-Palomo, G.; Guerrero-Sánchez, M.E. Robust cascade observer for a disturbance unmanned aerial vehicle carrying a load under multiple time-varying delays and uncertainties. Int. J. Syst. Sci. 2024, 55, 1056–1072. [Google Scholar] [CrossRef]
- An, S.; Wang, L.; He, Y. Robust fixed-time tracking control for underactuated AUVs based on fixed-time disturbance observer. Ocean Eng. 2022, 266, 112567. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Li, D.; Ge, S.S.; Lee, T.H. Fixed-time-synchronized consensus control of multiagent systems. IEEE Trans. Control. Netw. Syst. 2020, 8, 89–98. [Google Scholar] [CrossRef]
- Li, D.; Yu, H.; Tee, K.P.; Wu, Y.; Ge, S.S.; Lee, T.H. On time-synchronized stability and control. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 52, 2450–2463. [Google Scholar] [CrossRef]
- Luo, X.; Zhu, M.; Zhang, Y.; Zheng, Z.; Chen, T. Self-triggered fuzzy trajectory tracking control for the stratospheric airship. Adv. Space Res. 2024, 74, 5874–5889. [Google Scholar] [CrossRef]




| FTSS | FT | SM | FTSDO | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
| 0.3 | 0.8 | 0.8 | 2 | ||||
| 0.6 | 0.8 | 0.4 | 2 | ||||
| 0.3 | 0.5 | 2 | 0.65 | ||||
| 0.6 | 0.5 | ð | 2 | 1.1 | |||
| 0.65 | – | – | – | – | 0.05 | ||
| 0.65 | – | – | – | – | 3 | ||
| 1.1 | – | – | – | – | – | – | |
| 1.1 | – | – | – | – | – | – | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yuan, J.; Li, R. Error-Constrained Fixed-Time Synchronized Trajectory Tracking Control for Unmanned Airships with Disturbances. Drones 2025, 9, 403. https://doi.org/10.3390/drones9060403
Chen J, Yuan J, Li R. Error-Constrained Fixed-Time Synchronized Trajectory Tracking Control for Unmanned Airships with Disturbances. Drones. 2025; 9(6):403. https://doi.org/10.3390/drones9060403
Chicago/Turabian StyleChen, Jie, Jiace Yuan, and Ruohan Li. 2025. "Error-Constrained Fixed-Time Synchronized Trajectory Tracking Control for Unmanned Airships with Disturbances" Drones 9, no. 6: 403. https://doi.org/10.3390/drones9060403
APA StyleChen, J., Yuan, J., & Li, R. (2025). Error-Constrained Fixed-Time Synchronized Trajectory Tracking Control for Unmanned Airships with Disturbances. Drones, 9(6), 403. https://doi.org/10.3390/drones9060403






