An Aircraft Skin Defect Detection Method with UAV Based on GB-CPP and INN-YOLO
Abstract
Highlights
- In the task of using drones for aircraft skin inspection, a coverage path planning method based on greedy algorithm and breadth-first search (GB-CPP) was proposed.
- The proposed INN-YOLO algorithm, based on YOLOv11, demonstrated superior performance in comparative experiments on three public datasets.
- Proposes a collaborative framework integrating geometry-guided coverage path planning with a lightweight detection network to optimize UAV inspection routes and enable real-time defect identification, thereby enhancing operational efficiency and intelligence levels.
- The INN-YOLO detection model meets the onboard low-latency requirements, supporting immediate decision-making and feedback during the inspection process.
- The proposed collaborative framework promotes a closed-loop system of “precise path planning—efficient image acquisition—onboard real-time recognition,” providing a replicable industrial solution for automated inspection of large-scale infrastructure such as aviation facilities.
Abstract
1. Introduction
2. Methodology
2.1. UAV Coverage Path Planning
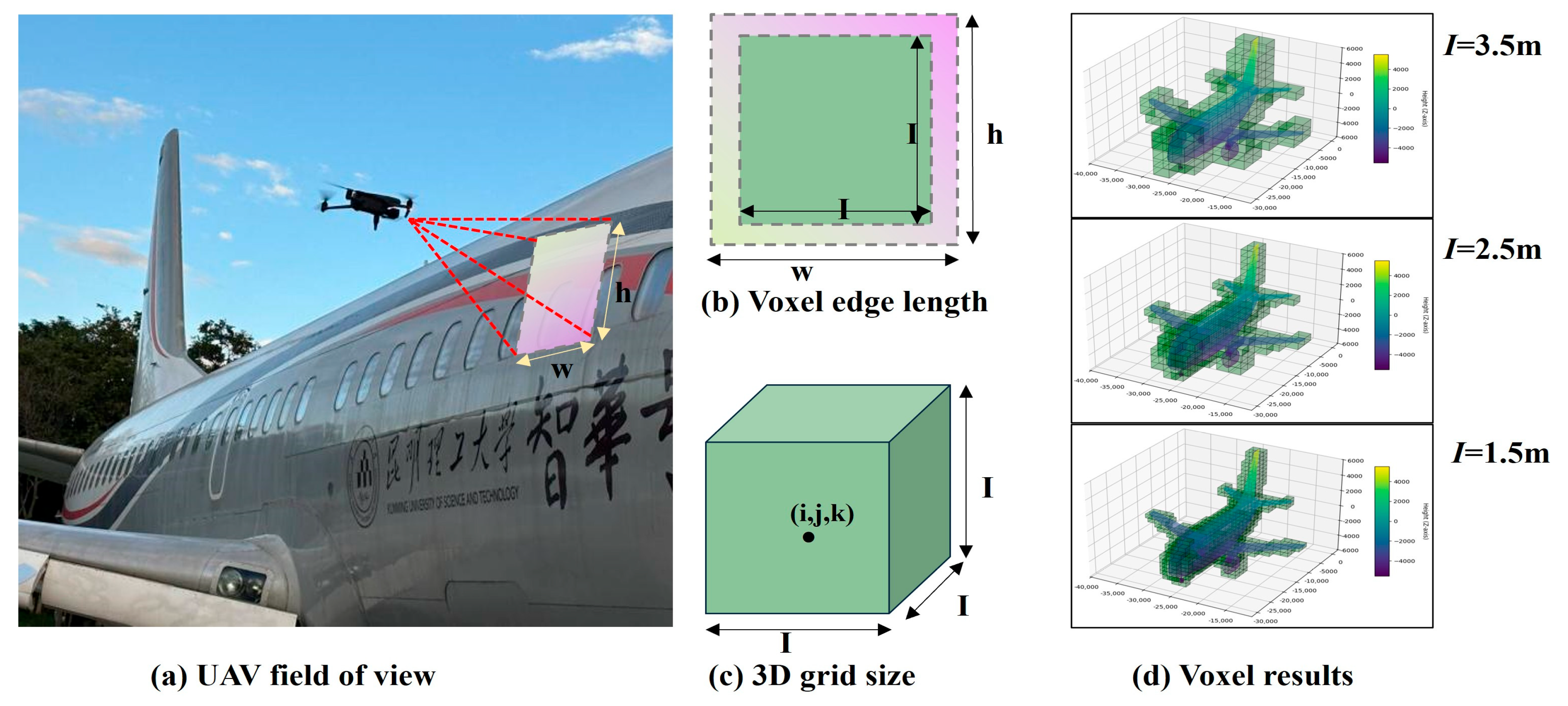
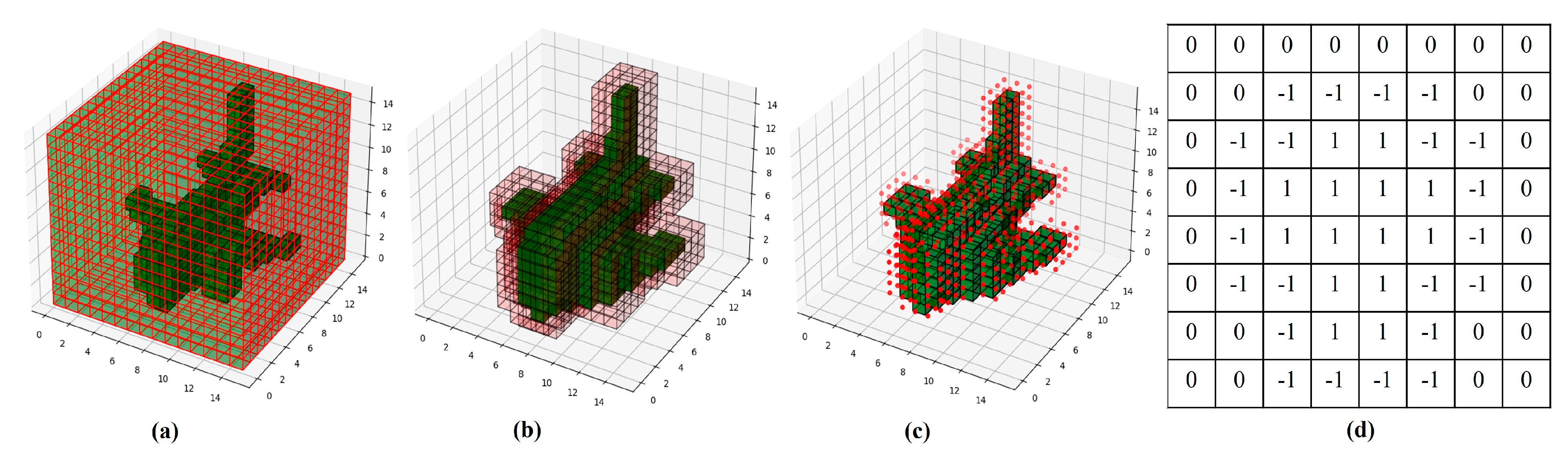
2.1.1. Model Voxelization
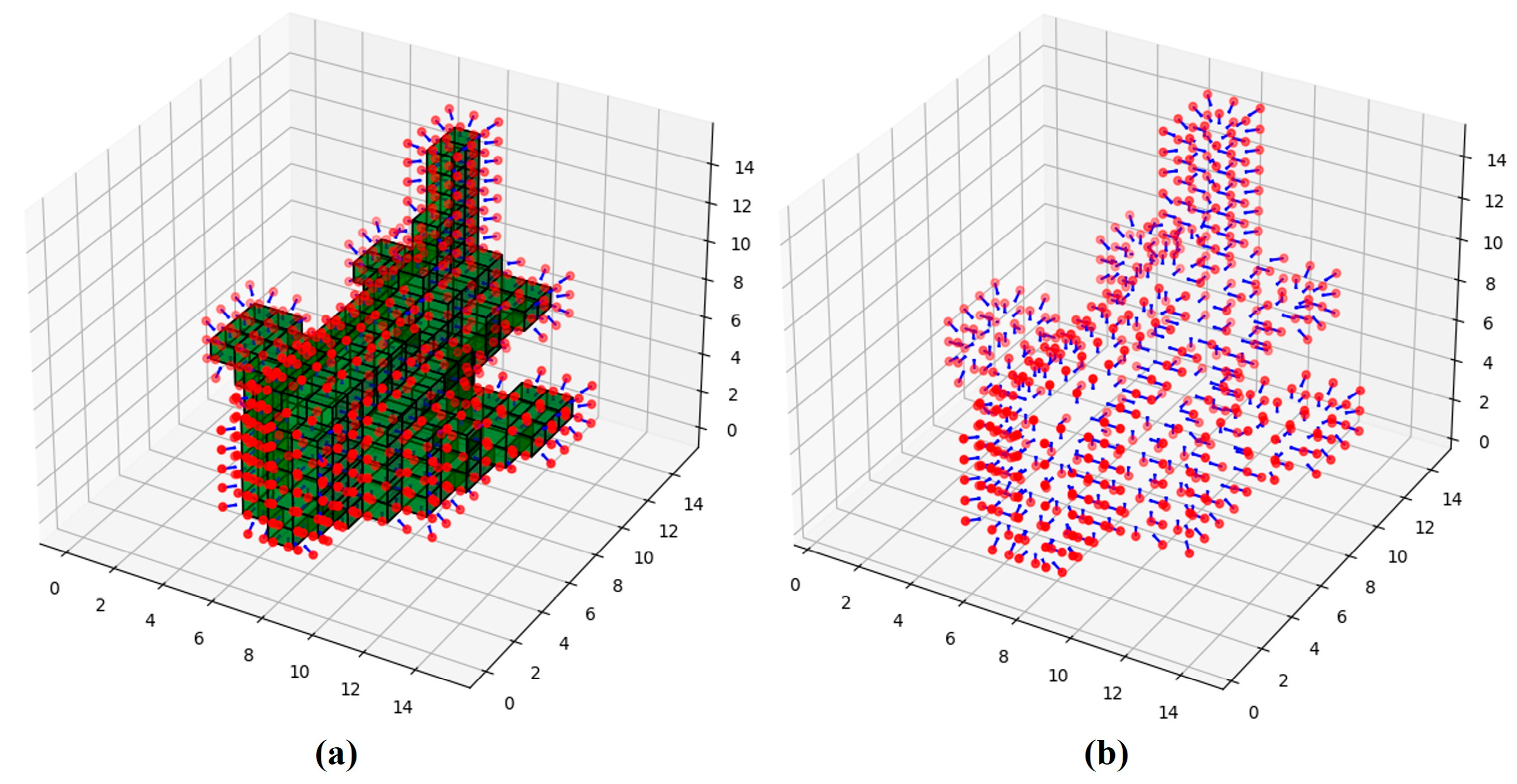
2.1.2. Viewpoint Labeling
2.1.3. Generation of Viewing Direction
2.1.4. Path Planning
2.1.5. GB-CPP Experimental Evaluation Metrics
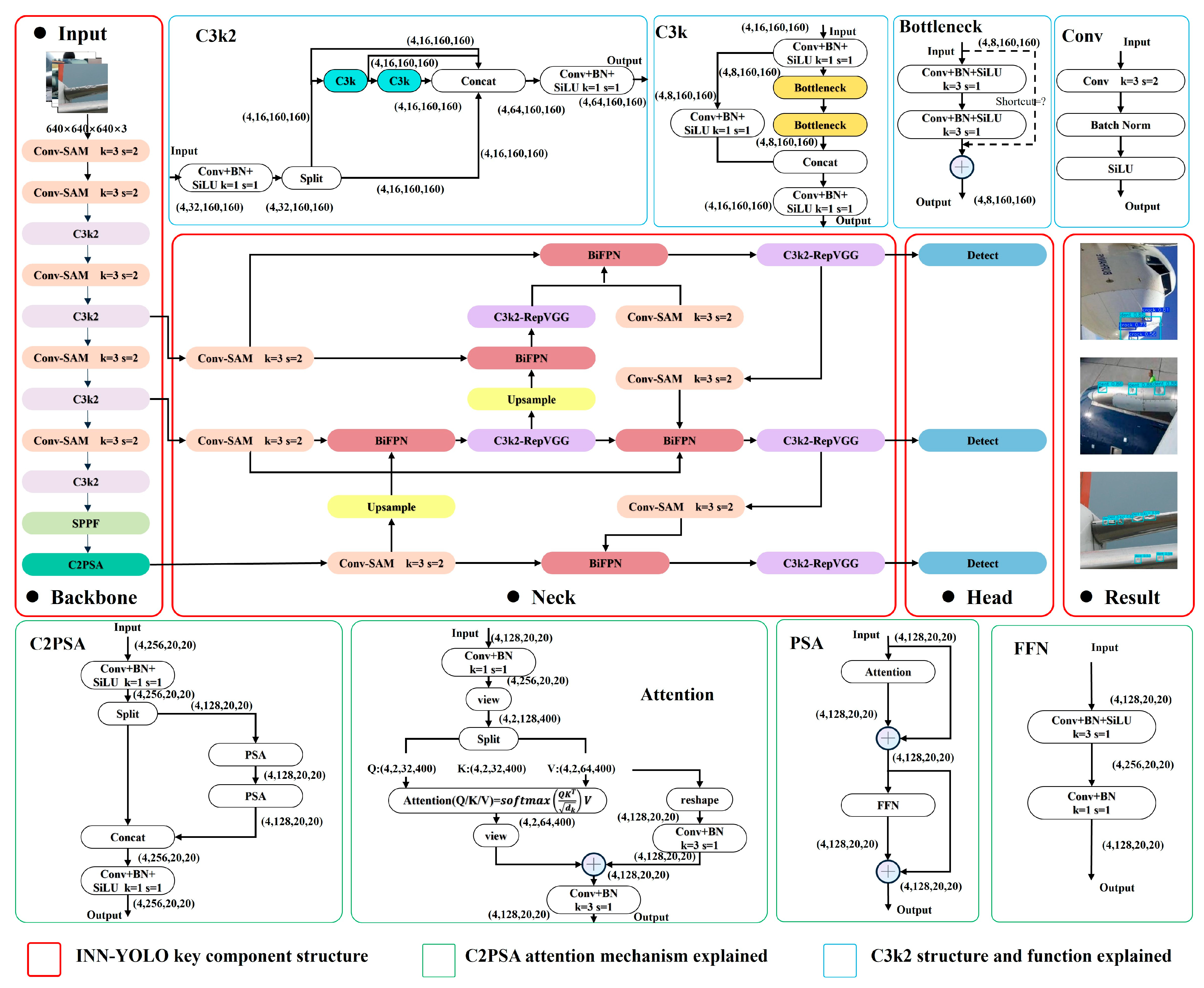
2.2. Improved YOLOv11 Algorithm
2.2.1. YOLOv11 Overview
2.2.2. INN-YOLO Algorithm
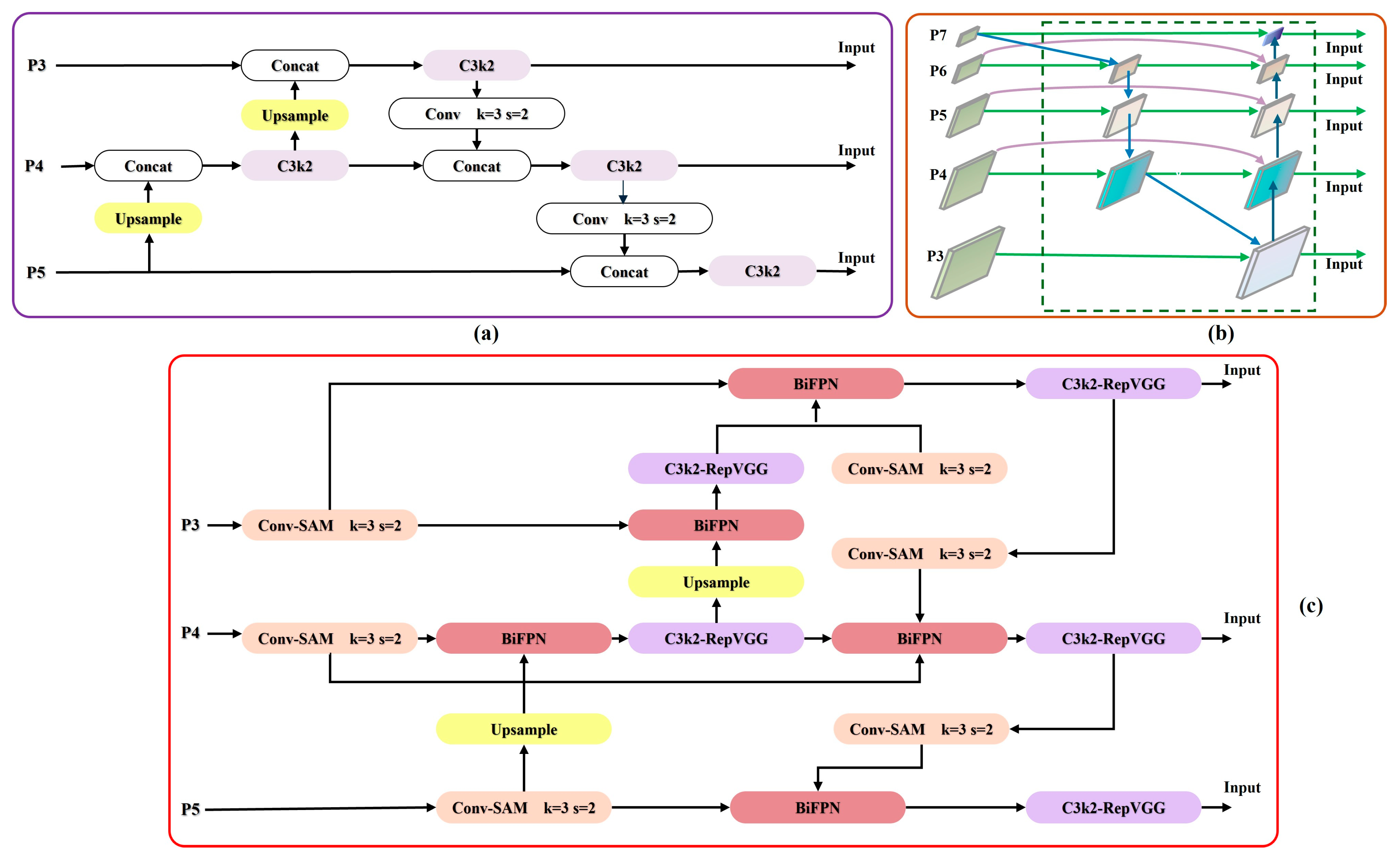
2.2.3. Multi-Scale Fusion of the Neck
2.2.4. Conv-SAM Module
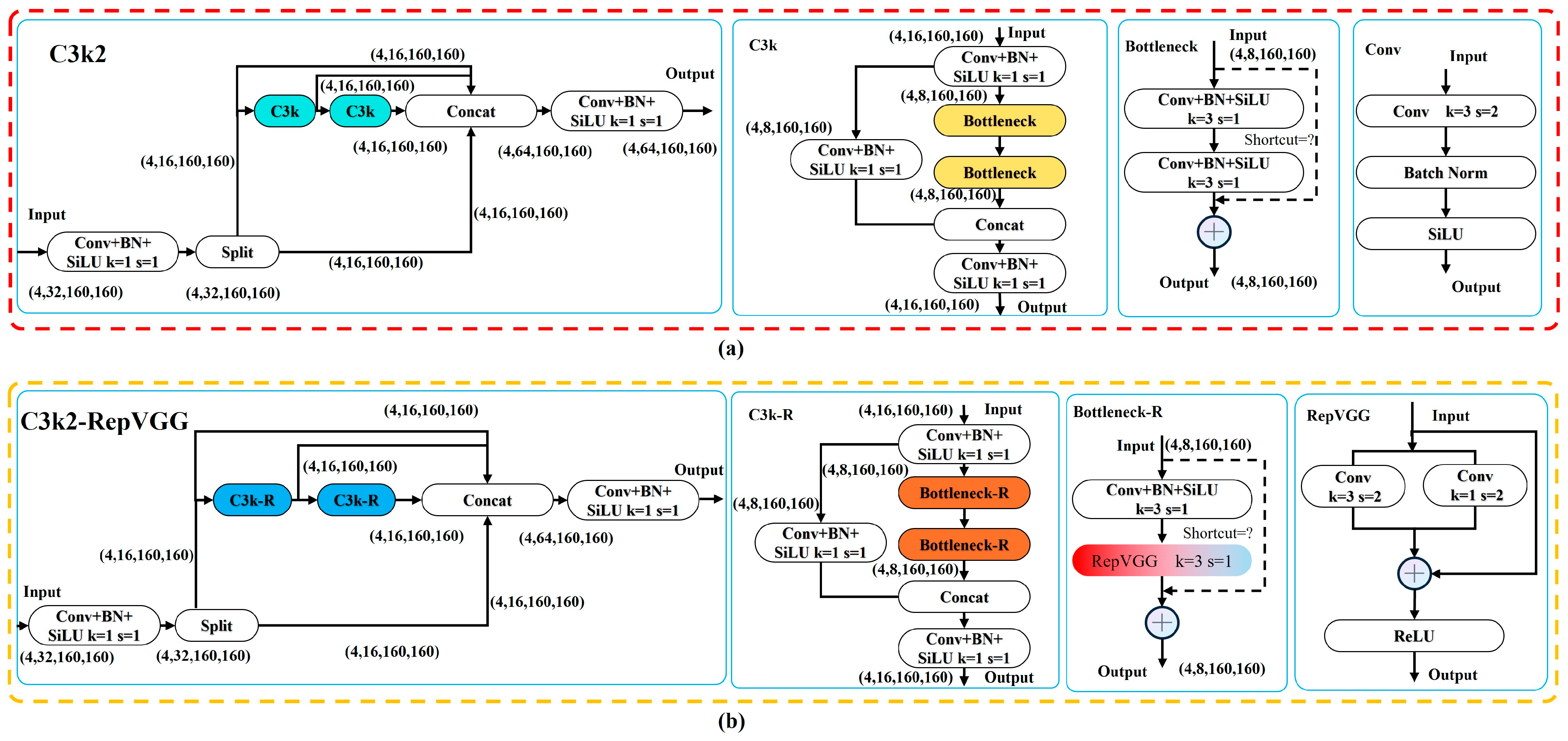
2.2.5. Lightweight C2f-RepVGG Block
2.2.6. Indicators for Model Evaluation
2.3. Datasets
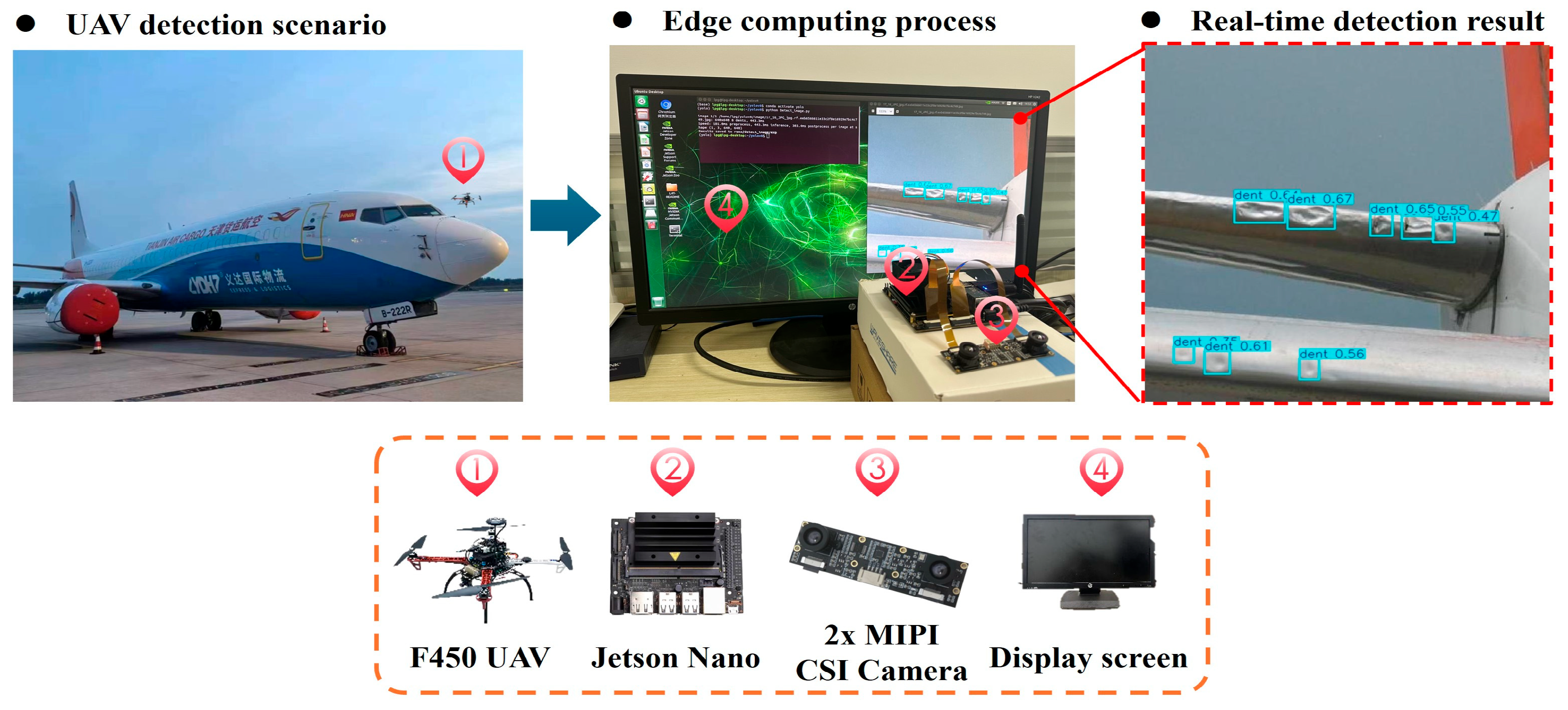
2.4. Experimental Environment and Deployment for INN-YOLO
3. Results
3.1. Experimental Validation and Analysis of UAV Coverage Path Planning
3.2. Analysis of INN-YOLO Experimental Results
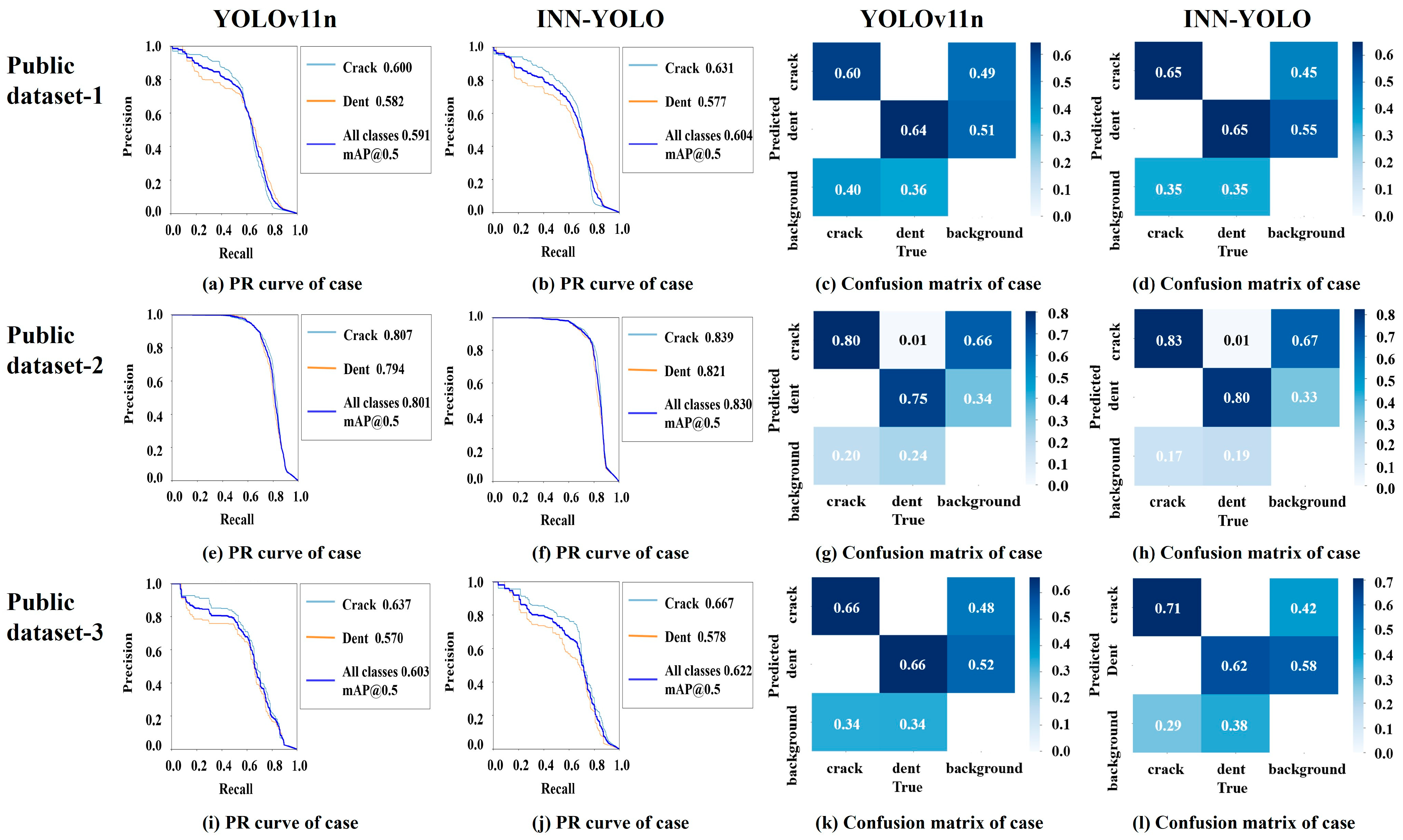
3.2.1. Comparison Experiment
3.2.2. Ablation Experiment
3.2.3. Visualization Analysis of Detection Results
3.2.4. Model Generalization Validation
4. Discussion
4.1. Discussion of the Coverage Path Planning Results
4.2. Discussion of Target Detection Results of Aircraft Skin Defects
4.3. Feasibility Analysis
4.4. Limitations Analysis
5. Conclusions
- (a)
- The proposed detection method achieves efficient and comprehensive aircraft skin defect detection without missions. Based on a voxel model of the aircraft and leveraging the relationship between voxel space and grid maps, viewpoints on the aircraft surface are generated. GB-CPP are used to generate coverage paths, ensuring the UAV flight path fully covers the aircraft surface.
- (b)
- The proposed INN-YOLO network model demonstrates superior precision in detecting aircraft skin defects. Comparative experiments on three public datasets show that the proposed model outperforms others in Precision, Recall, mAP@0.5, and mAP@0.5–0.95 metrics, exhibiting the best overall performance.
- (c)
- Ablation experiments reveal that training the dataset using only YOLOv11n or individually modifying the baseline network yields unsatisfactory recognition results. Only by effectively combining all the improved modules on the baseline model to enhance the capability of target feature extraction could the model’s detection performance be effectively improved.
- (d)
- Generalization validation of INN-YOLO on a self-built dataset achieved Precision, Recall, mAP@0.5, and mAP@0.5–0.95 values of 90.20%, 74.70%, 80.30%, and 55.10%, respectively, representing improvements of 6.50%, 4.60%, 6.70%, and 11.70% over the baseline model. These results demonstrate the strong generalization capability of the model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| The camera’s field of view is projected onto the target surface, forming a rectangular coverage area. | |
| The voxel edge length. | |
| Each leaf node corresponds to the index of a cubic cell (voxel) with side length . | |
| The 3D model point set. | |
| The set of all voxels | |
| The side length of the cubic box that contains the 3D model. | |
| A unit vector representing the line of sight, describing the direction of the line of sight. | |
| A constant used to adjust the calculation of attraction, whose value needs to be set according to the specific application scenario. | |
| The location where the UAV takes photos. | |
| The center position of the voxel; only voxels within the sensor’s visible range are considered in the calculation of the average viewing direction of the viewpoint. | |
| The minimum values of attraction. | |
| The maximum values of attraction. | |
| Adjacency matrix | |
| Distance cost between viewpoints | |
| Incomplete graph | |
| Set of feasible paths | |
| Distance between two viewpoints in 3D space | |
| Middle features of the sixth layer from top to bottom. | |
| Output features of the sixth layer from bottom to top. | |
| A weight parameter between 0 and 1. | |
| A constant used to avoid numerical instability. | |
| Linear transformation weight of the target neuron | |
| Linear transformation bias of the target neuron | |
| Ideal output labels of target neuron t and other neurons | |
| A regularization coefficient used to regularize weights in the energy function, preventing overfitting and enhancing the model’s generalization capability. | |
| The variance of neurons other than the target neuron . | |
| The mean of neurons other than the target neuron . | |
| The mean of all neurons on the channel (including the target neuron ). | |
| The variance of all neurons on the channel (including the target neuron ). | |
| AP | Average Precision. |
| mAP | mean Average Precision. |
| The number of positive samples correctly detected. | |
| The number of positive samples that were missed. | |
| The number of negative samples incorrectly classified as positive. | |
| The average precision for the target category. |
References
- Huang, B.; Ding, Y.; Liu, G. ASD-YOLO: An aircraft surface defects detection method using deformable convolution and attention mechanism. Measurement 2024, 238, 115300. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, J.; Li, Y.; Gong, X.; Wang, J. A UAV-based aircraft surface defect inspection system via external constraints and deep learning. IEEE Trans. Instrum. Meas. 2022, 71, 5019315. [Google Scholar] [CrossRef]
- Deane, S.; Avdelidis, N.P.; Ibarra-Castanedo, C. Development of a thermal excitation source used in an active thermographic UAV platform. Quant. InfraRed Thermogr. J. 2022, 20, 198–229. [Google Scholar] [CrossRef]
- Saha, A.; Kumar, L.; Sortee, S.; Dhara, B.C. An Autonomous Aircraft Inspection System using Collaborative Unmanned Aerial Vehicles. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Fevgas, G.; Lagkas, T.; Argyriou, V.; Sarigiannidis, P. Coverage Path Planning Methods Focusing on Energy Efficient and Cooperative Strategies for Unmanned Aerial Vehicles. Sensors 2022, 22, 1235. [Google Scholar] [CrossRef]
- Dogru, S.; Marques, L. ECO-CPP: Energy constrained online coverage path planning. Robot. Auton. Syst. 2022, 157, 104242. [Google Scholar] [CrossRef]
- Abou-Bakr, E.; Alnajim, A.M.; Alashwal, M.; Elmanfaloty, R.A. Chaotic sequence-driven path planning for autonomous robot terrain coverage. Comput. Electr. Eng. 2025, 123, 110032. [Google Scholar] [CrossRef]
- Kyriakakis, N.A.; Marinaki, M.; Matsatsinis, N.; Marinakis, Y. A cumulative unmanned aerial vehicle routing problem approach for humanitarian coverage path planning. Eur. J. Oper. Res. 2022, 300, 992–1004. [Google Scholar] [CrossRef]
- Jing, W.; Polden, J.; Lin, W.; Shimada, K. Sampling-based view planning for 3D visual coverage task with Unmanned Aerial Vehicle. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 1808–1815. [Google Scholar] [CrossRef]
- Bircher, A. Structural inspection path planning via iterative viewpoint resampling with application to aerial robotics. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6423–6430. [Google Scholar] [CrossRef]
- Abdi, A.; Ranjbar, M.H.; Park, J.H. Computer Vision-Based Path Planning for Robot Arms in Three-Dimensional Workspaces Using Q-Learning and Neural Networks. Sensors 2022, 22, 1697. [Google Scholar] [CrossRef]
- Jung, S.; Song, S.; Youn, P.; Myung, H. Multi-Layer Coverage Path Planner for Autonomous Structural Inspection of High-Rise Structures. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Tong, H.W.; Li, B.; Huang, H.; Wen, C. UAV Path Planning for Complete Structural Inspection using Mixed Viewpoint Generation. In Proceedings of the International Conference on Control, Singapore, 11–13 December 2022; pp. 727–732. [Google Scholar] [CrossRef]
- Almadhoun, R.; Taha, T.; Dias, J. Coverage path planning for complex structures inspection using unmanned aerial vehicle (UAV). In Intelligent Robotics and Applications; Springer: Cham, Switzerland, 2019; pp. 243–266. [Google Scholar] [CrossRef]
- Almadhoun, R.; Taha, T.; Gan, D.; Dias, J.; Zweiri, Y.; Seneviratne, L. Coverage Path Planning with Adaptive Viewpoint Sampling to Construct 3D Models of Complex Structures for the Purpose of Inspection. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7047–7054. [Google Scholar] [CrossRef]
- Papaioannou, S.; Kolios, P.; Theocharides, T.; Panayiotou, C.G.; Polycarpou, M.M. UAV-based Receding Horizon Control for 3D Inspection Planning. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 1121–1130. [Google Scholar] [CrossRef]
- Jing, W.; Deng, D.; Xiao, Z.; Liu, Y.; Shimada, K. Coverage Path Planning using Path Primitive Sampling and Primitive Coverage Graph for Visual Inspection. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1472–1479. [Google Scholar] [CrossRef]
- Panigati, T.; Zini, M.; Striccoli, D.; Giordano, P.F.; Tonelli, D.; Limongelli, M.P.; Zonta, D. Drone-based bridge inspections: Current practices and future directions. Autom. Constr. 2025, 173, 106101. [Google Scholar] [CrossRef]
- Liu, Y.; Moghaddas, S.A.; Shi, S.; Huang, Y.; Kong, J.; Bao, Y. Review on applications of computer vision techniques for pipeline inspection. Measurement 2025, 252, 117370. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Li, Y.; Cheng, Z.; Li, R. High efficiency and high precision measurement method for the volume of weights using computer vision. Measurement 2025, 252, 117353. [Google Scholar] [CrossRef]
- Cheng, Y.; Tian, Z.; Ning, D.; Feng, K.; Li, Z.; Chauhan, S.; Vashishtha, G. Computer vision-based non-contact structural vibration measurement: Methods, challenges and opportunities. Measurement 2025, 243, 116426. [Google Scholar] [CrossRef]
- Niu, Y.; Li, Z.; Li, J.; Sun, B. Accelerometer-assisted computer vision data fusion framework for structural dynamic displacement reconstruction. Measurement 2025, 242, 116021. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, realtime object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, J.; Yan, Z. FC-YOLO: An Aircraft Skin Defect Detection Algorithm Based on Multi-Scale Collaborative Feature Fusion; IOP Publishing Ltd.: Bristol, UK, 2024. [Google Scholar] [CrossRef]
- Malekzadeh, T.; Abdollahzadeh, M.; Nejati, H. Aircraft Fuselage Defect Detection using Deep Neural Networks. arXiv 2017, arXiv:1712.09213. [Google Scholar] [CrossRef]
- Ramalingam, B.; Manuel, V.H.; Elara, M.R. Visual inspection of the aircraft surface using a teleoperated reconfigurable climbing robot and enhanced deep learning technique. Int. J. Aerosp. Eng. 2019, 2019, 5137139. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Liu, Y. Yolo-fdd: Efficient defect detection network of aircraft skin fastener. Image Video Process. 2024, 18, 3197–3211. [Google Scholar] [CrossRef]
- Wang, H.; Fu, L.; Wang, L. Detection algorithm of aircraft skin defects based on improved YOLOv8n. Signal Image Video Process. 2024, 18, 3877–3891. [Google Scholar] [CrossRef]
- Bouarfa, S.; Doğru, A.; Arizar, R. Towards Automated Aircraft Maintenance Inspection. A use case of detecting aircraft dents using Mask R-CNN. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0389, Information and Command and Control Systems. [Google Scholar] [CrossRef]
- Doğru, A.; Bouarfa, S.; Arizar, R.; Aydoğan, R. Using Convolutional Neural Networks to Automate Aircraft Maintenance Visual Inspection. Aerospace 2020, 7, 171. [Google Scholar] [CrossRef]
- Ding, M.; Wu, B.; Xu, J.; Kasule, A.N.; Zuo, H. Visual inspection of aircraft skin: Automated pixel-level defect detection by instance segmentation. Chin. J. Aeronaut. 2022, 35, 254–264. [Google Scholar] [CrossRef]
- Ameri, R.; Hsu, C.-C.; Band, S.S. A systematic review of deep learning approaches for surface defect detection in industrial applications. Eng. Appl. Artif. Intell. 2024, 130, 107717. [Google Scholar] [CrossRef]
- Pan, H.; Guan, S.; Zhao, X. LVD-YOLO: An efficient lightweight vehicle detection model for intelligent transportation systems. Image Vis. Comput. 2024, 151, 105276. [Google Scholar] [CrossRef]
- Modi, T.M.; Venkateswararao, K.; Swain, P. Integration of SDN into UAV, edge computing, & Blockchain: A review, challenges, & future directions. Comput. Sci. Rev. 2025, 58, 100790. [Google Scholar] [CrossRef]
- Aishwarya, N.; Kannaa, G.S.Y.; Seemakurthy, K. YOLOSkin: A fusion framework for improved skin cancer diagnosis using YOLO detectors on Nvidia Jetson Nano. Biomed. Signal Process. Control 2025, 100, 1746–8094. [Google Scholar] [CrossRef]
- Dai, J.; Gong, X.; Wang, J. Unmanned Aerial Vehicle Coverage Path Planning Method for Aircraft External Surface Inspection Tasks. J. Mech. Eng. 2023, 59, 243–253. [Google Scholar]
- Meagher, D. Geometric modeling using octree encoding. Comput. Graph. Image Process. 1982, 19, 129–147. [Google Scholar] [CrossRef]
- Melo, A.G.; Pinto, M.F.; Marcato, A.L.M.; Honório, L.M.; Coelho, F.O. Dynamic Optimization and Heuristics Based Online Coverage Path Planning in 3D Environment for UAVs. Sensors 2021, 21, 1108. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A Comprehensive Review of Coverage Path Planning in Robotics Using Classical and Heuristic Algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Khanam, R.; Hussain, M. Yolov11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar] [CrossRef]
- Tan, M.; Pang, R.; Le, Q.V. EfficientDet: Scalable and Efficient Object Detection. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10778–10787. [Google Scholar] [CrossRef]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path Aggregation Network for Instance Segmentation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, R.Y.; Li, L. SimAM: A Simple, Parameter-Free Attention Module for Convolutional Neural Networks. Int. Conf. Mach. Learn. 2021, 139, 11863–11874. Available online: https://api.semanticscholar.org/CorpusID:235825945 (accessed on 6 June 2025).
- Ding, X.; Zhang, X.; Ma, N.; Han, J.; Ding, G.; Sun, J. RepVGG: Making VGG-style ConvNets Great Again. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13728–13737. [Google Scholar] [CrossRef]
- Russell, B.C.; Torralba, A.; Murphy, K.P. LabelMe: A Database and Web-Based Tool for Image Annotation. Int. J. Comput. Vis. 2008, 77, 157–173. [Google Scholar] [CrossRef]




| Dataset | Quantity | Defects (Number) | Image Size (Pixels) | Sample Images |
|---|---|---|---|---|
| Public dataset-1 a | training set: 3659 validation set: 416 test set: 94 | crack: 5970 dent: 3787 | 640 × 640 |  |
| Public dataset-2 b | training set: 2530 validation set: 712 test set: 352 | crack: 8141 dent: 3477 | 416 × 416 640 × 640 |  |
| Public dataset-3 c | training set: 2948 validation set: 168 test set: 58 | crack: 3800 dent: 3309 | 640 × 640 416 × 416 |  |
| Self-built datasets d | training set: 1338 validation set: 192 test set: 29 | crack: 3833 dent: 3271 | 320 × 320 2098 × 2796 |  |
| Algorithm: Deploy INN-YOLO on Jetson Nano | Jetson Nano Physical Image |
|---|---|
| Input: ModelPath, ImagePath Output: DetectionResults ① Initialize INN-YOLO model with TensorRT: network = Initialize_INN-YOLO(ModelPath) ② Load input image: img = LoadImage(ImagePath) ③ Perform object detection: DetectionResults = net.Detect(img) ④ For each detection in DetectionResults: Extract class ID, confidence score, and bounding box. |  |
| Path Planning Schematic | Path Evaluation Indicators | Path Evaluation Values |
|---|---|---|
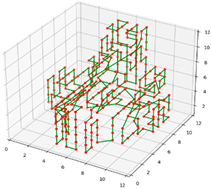 (a) I = 3.5 m | Resolution | 3.5 |
| Number of viewpoints (number) | 326 | |
| Total number of paths covered (number) | 344 | |
| Duplicate coverage areas (number) | 18 | |
| Repeat coverage (%) | 5.23 | |
| Time consumption/s | 3.00 | |
 (b) I = 2.5 m | Resolution | 2.5 |
| Number of viewpoints (number) | 443 | |
| Total number of paths covered (number) | 475 | |
| Duplicate coverage areas (number) | 32 | |
| Repeat coverage (%) | 6.74 | |
| Time consumption/s | 4.00 | |
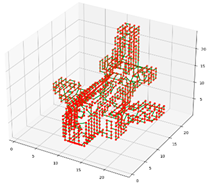 (c) I = 1.5 m | Resolution | 1.5 |
| Number of viewpoints (number) | 1042 | |
| Total number of paths covered (number) | 1098 | |
| Duplicate coverage areas (number) | 56 | |
| Repeat coverage (%) | 5.1 | |
| Time consumption/s | 11.69 |
| Dataset | Metrics | YOLOv5n | YOLOv6n | YOLOv8n | YOLOv9t | YOLOv10n | YOLOv11n | INN-YOLO | p | 95%CI |
|---|---|---|---|---|---|---|---|---|---|---|
| Public dataset-1 | Precision (%) | 58.80 | 51.30 | 65.80 | 65.00 | 55.60 | 64.50 | 67.00 | 2.23 × 10−3 | (1.68, 3.88) |
| Recall (%) | 33.30 | 24.70 | 32.50 | 24.80 | 29.60 | 30.30 | 41.00 | 5.84 × 10−8 | (9.48, 11.38) | |
| mAP@0.5 (%) | 33.10 | 23.20 | 32.70 | 24.90 | 29.80 | 31.60 | 42.30 | 3.18 × 10−7 | (9.10, 11.40) | |
| mAP@0.5–0.95 (%) | 15.30 | 10.30 | 15.60 | 11.20 | 13.90 | 14.90 | 21.50 | 4.01 × 10−6 | (5.02, 6.88) | |
| parameters | 2,182,054 | 4,155,222 | 2,684,758 | 1,730,214 | 2,695,196 | 2,582,542 | 2,634,330 | - | - | |
| GFLOPs | 5.8 | 11.5 | 6.8 | 6.4 | 8.2 | 6.3 | 7.1 | - | - | |
| Public dataset-2 | Precision (%) | 87.40 | 84.90 | 88.00 | 82.90 | 81.90 | 87.10 | 90.90 | 3.00 × 10−4 | (2.40, 4.56) |
| Recall (%) | 69.00 | 54.60 | 69.10 | 65.70 | 70.20 | 74.10 | 76.60 | 5.79 × 10−6 | (2.34, 3.26) | |
| mAP@0.5 (%) | 78.10 | 65.40 | 79.70 | 73.60 | 77.60 | 81.60 | 84.10 | 6.48 × 10−5 | (2.62, 4.18) | |
| mAP@0.5–0.95 (%) | 51.80 | 43.40 | 54.50 | 48.30 | 52.20 | 55.00 | 57.30 | 1.75 × 10−5 | (2.06, 3.00) | |
| parameters | 2,182,054 | 4,155,222 | 2,684,758 | 1,730,214 | 2,695,196 | 2,582,542 | 2,634,330 | - | - | |
| GFLOPs | 5.8 | 11.5 | 6.8 | 6.4 | 8.2 | 6.3 | 7.1 | - | - | |
| Public dataset-3 | Precision (%) | 60.10 | 65.50 | 60.70 | 64.30 | 58.20 | 58.70 | 64.80 | 5.96 × 10−8 | (6.10, 7.36) |
| Recall (%) | 52.90 | 49.00 | 59.30 | 52.00 | 49.00 | 52.70 | 59.70 | 8.54 × 10−7 | (5.92, 7.70) | |
| mAP@0.5 (%) | 53.30 | 48.00 | 52.30 | 51.00 | 47.00 | 53.20 | 56.40 | 3.36 × 10−5 | (2.74, 4.14) | |
| mAP@0.5–0.95 (%) | 27.40 | 21.90 | 25.00 | 24.90 | 23.70 | 25.30 | 27.90 | 4.72 × 10−5 | (2.16, 3.42) | |
| parameters | 2,182,054 | 4,155,222 | 2,684,758 | 1,730,214 | 2,695,196 | 2,582,542 | 2,634,330 | - | - | |
| GFLOPs | 5.8 | 11.5 | 6.8 | 6.4 | 8.2 | 6.3 | 7.1 | - | - |
| Dataset | Method | Metrics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | YOLOv11n | Conv-SAM | BiFPN | C3k2-RepVGG | Precision (%) | Recall (%) | mAP@0.5 (%) | mAP@0.5–0.95 (%) | Parameters | GFLOPs | |
| Public dataset-1 | (a) | √ | 64.50 | 30.30 | 31.60 | 14.90 | 2,582,542 | 6.3 | |||
| (b) | √ | √ | 62.40 | 33.10 | 33.20 | 15.80 | 2,583,230 | 6.3 | |||
| (c) | √ | √ | 64.20 | 35.30 | 37.70 | 16.00 | 2,670,538 | 7.0 | |||
| (d) | √ | √ | 63.30 | 32.60 | 33.50 | 14.50 | 2,598,078 | 6.4 | |||
| (e) | √ | √ | √ | 54.00 | 32.30 | 29.80 | 13.10 | 2,671,418 | 7.0 | ||
| (f) | √ | √ | √ | 59.70 | 30.40 | 30.60 | 13.90 | 2,697,034 | 7.0 | ||
| (g) | √ | √ | √ | 61.70 | 32.40 | 35.40 | 15.80 | 2,598,766 | 6.4 | ||
| (h) | √ | √ | √ | √ | 67.00 | 41.00 | 42.30 | 21.50 | 2,634,330 | 7.1 | |
| Public dataset-2 | (a) | √ | 87.10 | 74.10 | 81.60 | 55.00 | 2,582,542 | 6.3 | |||
| (b) | √ | √ | 89.20 | 71.50 | 81.00 | 53.70 | 2,583,230 | 6.3 | |||
| (c) | √ | √ | 83.00 | 70.20 | 76.30 | 53.40 | 2,670,538 | 7.0 | |||
| (d) | √ | √ | 87.30 | 72.90 | 79.00 | 55.10 | 2,598,078 | 6.4 | |||
| (e) | √ | √ | √ | 86.30 | 64.50 | 74.30 | 50.60 | 2,671,418 | 7.0 | ||
| (f) | √ | √ | √ | 85.70 | 64.20 | 73.80 | 49.80 | 2,697,034 | 7.0 | ||
| (g) | √ | √ | √ | 88.50 | 70.20 | 77.50 | 52.00 | 2,598,766 | 6.4 | ||
| (h) | √ | √ | √ | √ | 90.90 | 76.60 | 84.10 | 57.30 | 2,634,330 | 7.1 | |
| Public dataset-3 | (a) | √ | 58.70 | 52.70 | 53.20 | 25.30 | 2,582,542 | 6.3 | |||
| (b) | √ | √ | 61.70 | 55.10 | 55.50 | 26.40 | 2,583,230 | 6.3 | |||
| (c) | √ | √ | 68.30 | 50.40 | 51.80 | 26.00 | 2,670,538 | 7.0 | |||
| (d) | √ | √ | 61.70 | 55.80 | 53.60 | 26.40 | 2,598,078 | 6.4 | |||
| (e) | √ | √ | √ | 58.80 | 58.70 | 55.70 | 25.10 | 2,671,418 | 7.0 | ||
| (f) | √ | √ | √ | 65.70 | 50.40 | 50.70 | 25.00 | 2,697,034 | 7.0 | ||
| (g) | √ | √ | √ | 60.80 | 54.80 | 51.70 | 25.80 | 2,598,766 | 6.4 | ||
| (h) | √ | √ | √ | √ | 64.80 | 59.70 | 56.40 | 27.90 | 2,634,330 | 7.1 | |
| Method | Metrics | |||
|---|---|---|---|---|
| Precision (%) | Recall (%) | mAP@0.5 (%) | mAP5@0.5–0.95 (%) | |
| YOLOv5n | 80.70 | 72.20 | 74.30 | 44.10 |
| YOLOv6n | 72.80 | 65.40 | 65.90 | 37.00 |
| YOLOv8n | 84.30 | 70.60 | 72.80 | 42.80 |
| YOLOv9t | 87.10 | 71.10 | 75.10 | 45.80 |
| YOLOv10n | 83.20 | 67.30 | 71.80 | 42.70 |
| YOLOv11n | 83.70 | 70.10 | 73.60 | 43.40 |
| INN-YOLO | 90.20 | 74.70 | 80.30 | 55.10 |
| Method | Metrics | |||||||
|---|---|---|---|---|---|---|---|---|
| Case | YOLOv11n | Conv-SAM | BiFPN | C3k2-RepVGG | Precision (%) | Recall (%) | mAP@0.5 (%) | mAP@0.5–0.95 (%) |
| (a) | √ | 83.70 | 70.10 | 73.60 | 43.40 | |||
| (b) | √ | √ | 83.50 | 69.90 | 73.80 | 44.70 | ||
| (c) | √ | √ | 83.80 | 73.20 | 76.50 | 44.50 | ||
| (d) | √ | √ | 84.20 | 72.40 | 74.10 | 45.00 | ||
| (e) | √ | √ | √ | 87.20 | 71.40 | 75.40 | 43.00 | |
| (f) | √ | √ | √ | 83.40 | 68.90 | 70.50 | 42.30 | |
| (g) | √ | √ | √ | 82.40 | 72.20 | 74.40 | 45.10 | |
| (h) | √ | √ | √ | √ | 90.20 | 74.70 | 80.30 | 55.10 |
| Dataset | Metrics | Defect Type | YOLOv5n | YOLOv6n | YOLOv8n | YOLOv9t | YOLOv10n | YOLOv11n | INN-YOLO |
|---|---|---|---|---|---|---|---|---|---|
| Public dataset-1 | Precision (%) | crack | 56.80 | 46.60 | 59.40 | 61.10 | 47.00 | 58.10 | 67.30 |
| dent | 59.60 | 56.10 | 72.10 | 68.90 | 64.20 | 70.90 | 66.70 | ||
| Recall (%) | crack | 40.70 | 29.30 | 40.00 | 32.00 | 36.00 | 38.00 | 46.30 | |
| dent | 25.90 | 20.10 | 25.00 | 17.60 | 23.10 | 22.60 | 35.60 | ||
| mAP@0.5 (%) | crack | 40.20 | 26.60 | 39.80 | 32.10 | 35.10 | 37.90 | 48.90 | |
| dent | 25.90 | 19.90 | 25.60 | 17.70 | 24.50 | 25.20 | 35.80 | ||
| mAP@0.5–0.95 (%) | crack | 17.30 | 11.50 | 17.80 | 13.30 | 15.30 | 17.80 | 22.80 | |
| dent | 13.20 | 9.16 | 13.40 | 9.04 | 12.60 | 11.90 | 20.20 | ||
| Public dataset-2 | Precision (%) | crack | 86.10 | 84.30 | 89.20 | 82.30 | 79.40 | 85.70 | 89.60 |
| dent | 88.60 | 85.40 | 86.80 | 83.50 | 84.40 | 88.50 | 92.10 | ||
| Recall (%) | crack | 65.90 | 51.20 | 65.70 | 63.90 | 69.30 | 71.90 | 74.00 | |
| dent | 72.10 | 57.90 | 72.40 | 67.50 | 71.00 | 76.20 | 79.20 | ||
| mAP@0.5 (%) | crack | 76.30 | 62.50 | 78.20 | 70.80 | 77.10 | 80.10 | 83.00 | |
| dent | 79.90 | 68.20 | 81.10 | 76.40 | 78.20 | 83.10 | 85.10 | ||
| mAP@0.5–0.95 (%) | crack | 49.00 | 41.50 | 51.50 | 46.00 | 49.60 | 51.80 | 54.50 | |
| dent | 54.60 | 45.20 | 57.50 | 50.60 | 54.80 | 58.20 | 60.10 | ||
| Public dataset-3 | Precision (%) | crack | 61.00 | 65.50 | 61.30 | 64.00 | 58.70 | 62.30 | 64.30 |
| dent | 59.20 | 65.50 | 60.10 | 64.60 | 57.80 | 55.00 | 65.30 | ||
| Recall (%) | crack | 58.10 | 54.80 | 67.70 | 54.80 | 56.50 | 50.00 | 61.00 | |
| dent | 47.70 | 43.10 | 50.90 | 49.20 | 41.50 | 55.40 | 58.50 | ||
| mAP@0.5 (%) | crack | 56.50 | 56.40 | 54.90 | 51.20 | 51.50 | 52.50 | 57.70 | |
| dent | 50.10 | 39.60 | 49.80 | 50.80 | 42.40 | 53.90 | 55.10 | ||
| mAP@0.5–0.95 (%) | crack | 27.50 | 24.80 | 24.70 | 25.00 | 25.20 | 23.60 | 26.20 | |
| dent | 27.20 | 19.10 | 25.40 | 24.70 | 22.20 | 27.10 | 29.60 | ||
| Self-built dataset | Precision (%) | crack | 84.60 | 77.60 | 83.80 | 87.50 | 87.70 | 88.70 | 89.90 |
| dent | 76.90 | 68.00 | 84.70 | 86.90 | 78.60 | 78.80 | 90.60 | ||
| Recall (%) | crack | 70.70 | 68.30 | 72.30 | 73.30 | 68.30 | 69.70 | 71.40 | |
| dent | 73.80 | 62.60 | 68.90 | 68.90 | 66.30 | 70.50 | 77.90 | ||
| mAP@0.5 (%) | crack | 78.90 | 72.40 | 74.70 | 77.20 | 78.30 | 79.50 | 81.70 | |
| dent | 69.70 | 59.30 | 70.90 | 72.90 | 65.30 | 67.60 | 78.90 | ||
| mAP@0.5–0.95 (%) | crack | 52.10 | 46.30 | 50.30 | 54.00 | 51.30 | 52.90 | 60.60 | |
| dent | 36.10 | 27.80 | 35.30 | 37.70 | 34.10 | 34.00 | 49.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, J.; Li, P.; Sun, Y.; Xiang, J.; Xia, H. An Aircraft Skin Defect Detection Method with UAV Based on GB-CPP and INN-YOLO. Drones 2025, 9, 594. https://doi.org/10.3390/drones9090594
Xiong J, Li P, Sun Y, Xiang J, Xia H. An Aircraft Skin Defect Detection Method with UAV Based on GB-CPP and INN-YOLO. Drones. 2025; 9(9):594. https://doi.org/10.3390/drones9090594
Chicago/Turabian StyleXiong, Jinhong, Peigen Li, Yi Sun, Jinwu Xiang, and Haiting Xia. 2025. "An Aircraft Skin Defect Detection Method with UAV Based on GB-CPP and INN-YOLO" Drones 9, no. 9: 594. https://doi.org/10.3390/drones9090594
APA StyleXiong, J., Li, P., Sun, Y., Xiang, J., & Xia, H. (2025). An Aircraft Skin Defect Detection Method with UAV Based on GB-CPP and INN-YOLO. Drones, 9(9), 594. https://doi.org/10.3390/drones9090594






