UAV Path Planning via Semantic Segmentation of 3D Reality Mesh Models

Abstract

Traditional unmanned aerial vehicle (UAV) path planning methods for image-based 3D reconstruction often rely solely on geometric information from initial models, resulting in redundant data acquisition in non-architectural areas. This paper proposes a UAV path planning method via semantic segmentation of 3D reality mesh models to enhance efficiency and accuracy in complex scenarios. The scene is segmented into buildings, vegetation, ground, and water bodies. Lightweight polygonal surfaces are extracted for buildings, while planar segments in non-building regions are fitted and projected into simplified polygonal patches. These photography targets are further decomposed into point, line, and surface primitives. A multi-resolution image acquisition strategy is adopted, featuring high-resolution coverage for buildings and rapid scanning for non-building areas. To ensure flight safety, a Digital Surface Model (DSM)-based shell model is utilized for obstacle avoidance, and sky-view-based Real-Time Kinematic (RTK) signal evaluation is applied to guide viewpoint optimization. Finally, a complete weighted graph is constructed, and ant colony optimization is employed to generate a low-energy-cost flight path. Experimental results demonstrate that, compared with traditional oblique photogrammetry, the proposed method achieves higher reconstruction quality. Compared with the commercial software Metashape, it reduces the number of images by 30.5% and energy consumption by 37.7%, while significantly improving reconstruction results in both architectural and non-architectural areas.

1. Introduction

In application scenarios such as smart cities [1], digital twins [2], cultural heritage preservation [3], and disaster emergency [4], the demand for high-quality 3D reality models continues to grow. Compared with LiDAR-based 3D reconstruction, image-based 3D reconstruction is more cost-effective and capable of capturing rich texture details [5]. Image-based 3D reconstruction technologies have become relatively mature with many open-source software solutions available, such as Colmap, OpenMVG combined with OpenMVS, AliceVision’s Meshroom, and MVE. The fundamental principle of image-based 3D reconstruction involves recovering 3D structures from 2D images taken from different camera viewpoints, typically comprising two main stages: Structure from Motion (SfM) [6] and Multi-view Stereo (MVS) [7]. SfM estimates camera poses and reconstructs a sparse 3D point cloud from overlapping images, while MVS computes per-pixel depth based on these poses to generate dense point clouds or mesh models. This method requires only a monocular camera to achieve satisfactory results and has been widely adopted in current high-resolution 3D reality modeling tasks [6].

Benefiting from the continuous advancement of unmanned aerial vehicle (UAV) technology, flexible and cost-effective multi-rotor UAVs have been widely used for image acquisition, providing essential data for real-world 3D reconstruction [8]. For example, the DJI Phantom 4 RTK [9] is capable of achieving millimeter-level positioning accuracy. Equipped with a gimbal camera, it can flexibly capture high-resolution, multi-angle images even in complex environments. To obtain high-quality 3D mesh models, the UAV must ensure fine and complete coverage of the real-world scene during image acquisition. Therefore, it is of great significance to study how to plan UAV paths to enable comprehensive and efficient image collection.

However, UAV path planning for fine-grained 3D reconstruction encounters numerous challenges. On the one hand, in practical operations, most existing methods rely on manually delineating target areas before generating flight paths, which is time-consuming and inefficient. On the other hand, some researchers have proposed automated flight path generation methods based on coarse initial 3D meshes (referred to as proxy models) which help reduce manual intervention [10,11,12]. These methods are mostly focused on architectural objects and typically adopt very close-range photography to acquire high-resolution images. In the planning process, they rely solely on the geometric information of the proxy model while neglecting semantic information [13]. As a result, when applied to complex scenes, they tend to collect large amounts of redundant image data in non-architectural areas.

To address the above issues, this paper proposes a UAV path planning method that leverages semantic segmentation of 3D reality mesh models, enabling efficient image acquisition while ensuring flight safety and providing a reliable solution for large-scale, high-quality 3D reconstruction. The main contributions of this paper are as follows:

(1)

An automatic method is implemented to extract simplified photography targets from the proxy model. By performing semantic segmentation on the proxy model, the scene is divided into object categories such as buildings, vegetation, ground, and water bodies. For buildings, which are of primary interest, a lightweight polygonal surface model [14] is reconstructed to produce simplified photography targets. For non-building objects, surface and line targets are extracted, and those with areas below a certain threshold are simplified into point targets.

(2)

A multi-resolution UAV path planning strategy that considers object categories is proposed. Based on the characteristics of different object types and their corresponding observation accuracy requirements, different image capture strategies are designed at multiple resolutions, enabling high-resolution coverage of key areas while allowing for rapid scanning of general regions.

(3)

A Real-Time Kinematic (RTK) signal evaluation method for UAV photography points based on sky-view constraints is proposed. Utilizing the proxy model and the positions of candidate photography points, the sky view at each point is simulated [15]. By calculating the proportion of visible sky area in the simulated sky view, the RTK signal quality at each point is assessed. Points with potential RTK signal occlusion are then adjusted accordingly, improving both flight safety and the continuity of the planned flight path.

2. Related Works

2.1. Semantic Segmentation Methods for 3D Models

Three-dimensional data is commonly represented as point clouds, voxels, or meshes. Semantic segmentation assigns labels (e.g., building, road, vegetation) to basic units (points, voxels, or mesh faces) depending on the data type. Methods can be grouped into point-based, mesh-based, voxel-based, and multi-view projection-based approaches.

Point-based methods process raw, irregular point clouds (e.g., PointNet [16], PointNet++ [17], Point Transformer [18], Spiking Point Transformer [19]), but suffer from high computational costs and lack of topological structure, limiting geometric understanding. Mesh-based methods segment directly on mesh models, leveraging topology and normals for accurate feature extraction. For example, MeshNet [20] extracts features from adjacent triangles; Singh et al. [21] introduced multi-ring neighborhoods; and classical methods like RF-MRF [22] and SUM-RF [23] employ random forests for large-scale scenes. Deep learning-based approaches include PSSNet [24] which is based on a graph convolutional network (GCN), Yang et al.’s [25] texture convolution module, Zhang et al.’s [26] integration of DGCNN with texture fusion, and METNet [27] which leverages convolutional neural networks (CNNs) to effectively process the structure of mesh exploring tensor (MET). These methods enable accurate, efficient segmentation while preserving structural detail. Voxel-based methods convert 3D data into regular voxels for 3D CNNs (e.g., VoxNet [28], MinkowskiNet [29]), enabling efficient processing but often smoothing fine details and edges due to quantization. Multi-view projection methods generate 2D views of 3D data, segment these images, then map results back to 3D (e.g., MVCNN [30], SnapNet [31]). While effective, they require multiple renderings and struggle with occlusions and label fusion inconsistencies.

Considering the prevalence of mesh models in UAV and 3D applications and the trade-offs among the methods, this paper adopts a mesh-based segmentation strategy for the proxy model.

2.2. UAV Path Planning Methods for 3D Reconstruction

UAV path planning significantly influences the efficiency and quality of 3D reconstruction. An optimal path ensures collision-free navigation, minimal energy consumption and travel time, and adherence to mission-specific constraints like target coverage or dynamic obstacle avoidance [32]. Methods can be classified as model-free or model-based, depending on whether a proxy model is used [8].

2.2.1. Model-Free Approaches

Model-free approaches enable UAVs to simultaneously build maps and plan views in unknown environments to improve reconstruction completeness [33,34,35,36,37,38]. A typical strategy is the Next Best View (NBV) method, which iteratively selects viewpoints to maximize information gain without a proxy model [39]. Variants include using curvature prediction [40], Poisson surface estimation [37], geometric primitives [41], and volume analysis based on Truncated Signed Distance Field (TSDF) [42] to guide NBV selection. Despite their adaptability, NBV methods often suffer from incomplete reconstructions and substantial computational overhead, failing to achieve complete global coverage [12].

2.2.2. Model-Based Approaches

Model-based approaches use a proxy model as prior information to guide viewpoint generation and route connection, following a two-stage “coarse-to-fine” strategy.

The proxy model is typically reconstructed from a small number of nadir images acquired via a regular lawnmower or grid flight pattern. Though low in detail, the proxy model captures the overall structure and extent of the scene. Smith et al. [43] denoised the proxy model and filled sidewall gaps using a height map, then generated no-fly zones by expanding outward based on a safety margin; Koch et al. [44] performed semantic segmentation using a fully convolutional network (FCN) on 2D images to assign semantic labels to 3D model points via a voting scheme, which is among the few that incorporate scene semantics, mainly to define no-fly zones for later flight planning; Yan et al. [12] generated point clouds as a proxy model from only a subset of images to accelerate 3D reconstruction process. Other studies [45,46] have estimated building heights from shadows in satellite images and used maps to generate simplified 2.5D models.

After obtaining the proxy model, candidate viewpoints are generated. Strategies fall into two categories: one generates a one-to-one mapping between sampled surface points and viewpoints [45,47]; the other randomly or regularly distributes viewpoints in the surrounding free space, then selects a minimal subset that maximizes model coverage based on visibility and reconstructability metrics [12,44,48]. Redundant viewpoints are then pruned, and remaining ones are refined in position and orientation to improve image overlap and parallax. Furukawa et al. [7] suggest that a parallax angle around 90° is optimal; many methods incorporate this constraint explicitly or implicitly [43,48,49,50]. Moreover, to mitigate matching difficulties and diminishing returns resulting from an excessive number of viewpoints, many approaches set an upper bound on viewpoint count or employ submodular optimization strategies [43,48,50].

Finally, the selected viewpoints are connected into a 3D flight path that satisfies UAV kinematic and safety constraints. This is typically modeled as a Traveling Salesman Problem (TSP) or its variants. Common solutions include ant colony optimization (ACO) [12], 2-opt combined with B-spline smoothing [43], and RRT* for obstacle-aware planning [49].

In this paper, a UAV path planning method based on a proxy model is employed. To ensure the regularity of the flight path, a one-to-one correspondence strategy between viewpoints and sampling points is adopted. Considering both computational complexity and theoretical completeness, an energy cost function is constructed under UAV flight dynamic constraints. The final route is obtained by solving the TSP using the ACO algorithm.

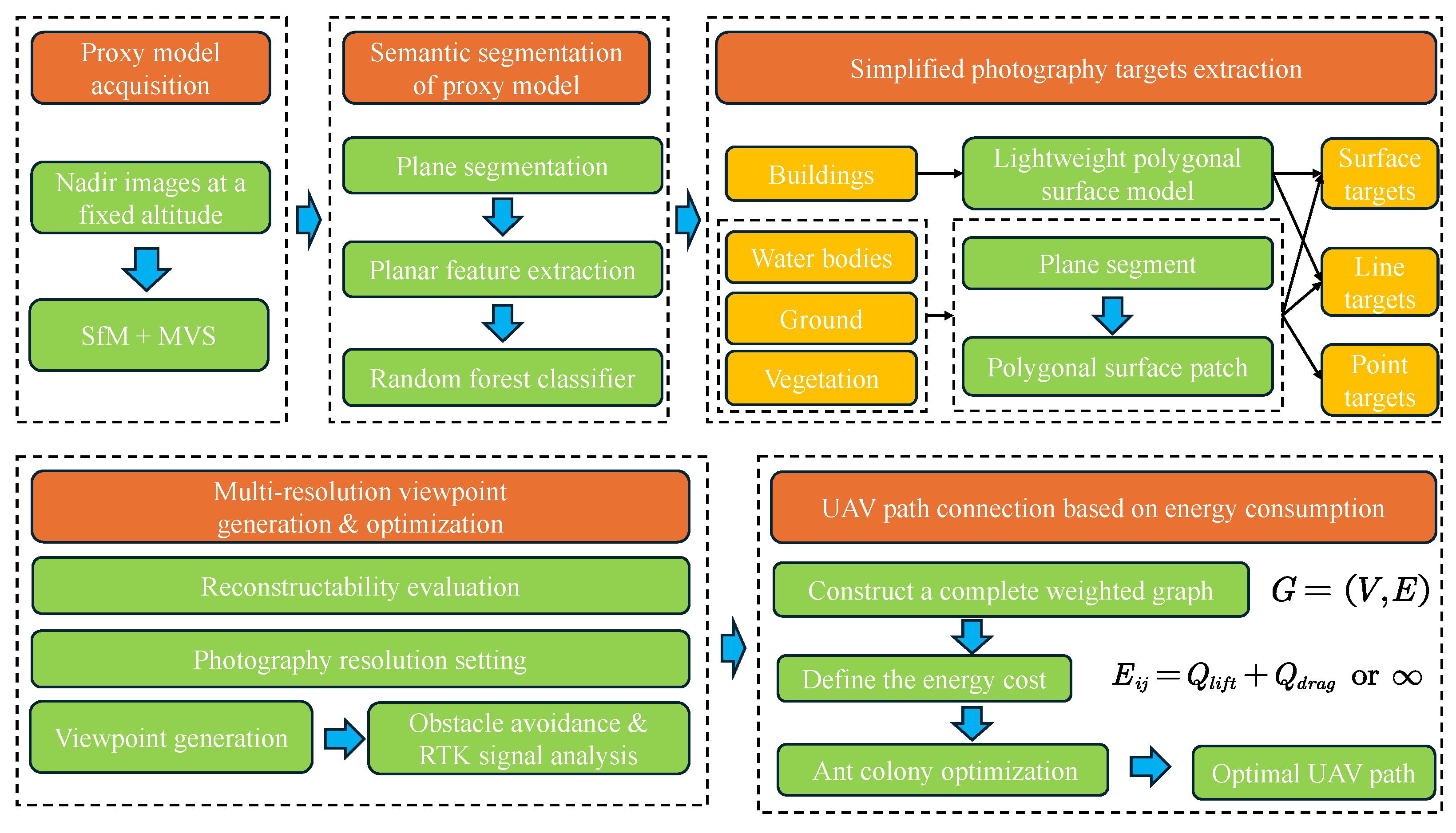
3. Proposed Method

3.1. Overview

This section provides a detailed overview of the proposed method for UAV path planning, as illustrated in Figure 1. First, a coarse proxy model of the scene is constructed (Section 3.2), which serves as the basis for subsequent semantic segmentation (Section 3.3). Based on the segmentation results, simplified photography targets—namely point, line, and surface targets—are extracted (Section 3.4.1). Then, multi-resolution viewpoints are generated (Section 3.4.2) and optimized from two perspectives: obstacle avoidance and RTK signal analysis (Section 3.5). Finally, UAV flight routes are connected based on energy cost, resulting in a collision-free, energy-efficient path capable of achieving high-quality 3D reconstruction (Section 3.6). Figure 2 provides a visual summary of the UAV flight planning workflow proposed in this paper.

3.2. Proxy Model Acquisition

When planning UAV flight paths, a coarse initial 3D model of the scene—referred to as a proxy model—is required as prior information to support subsequent semantic analysis, target extraction, viewpoint generation, and viewpoint optimization. In this paper, a small number of nadir or oblique images are captured at a fixed altitude, and a 3D mesh model with coarse geometric detail but sufficient positional accuracy is reconstructed using an SfM and MVS pipeline.

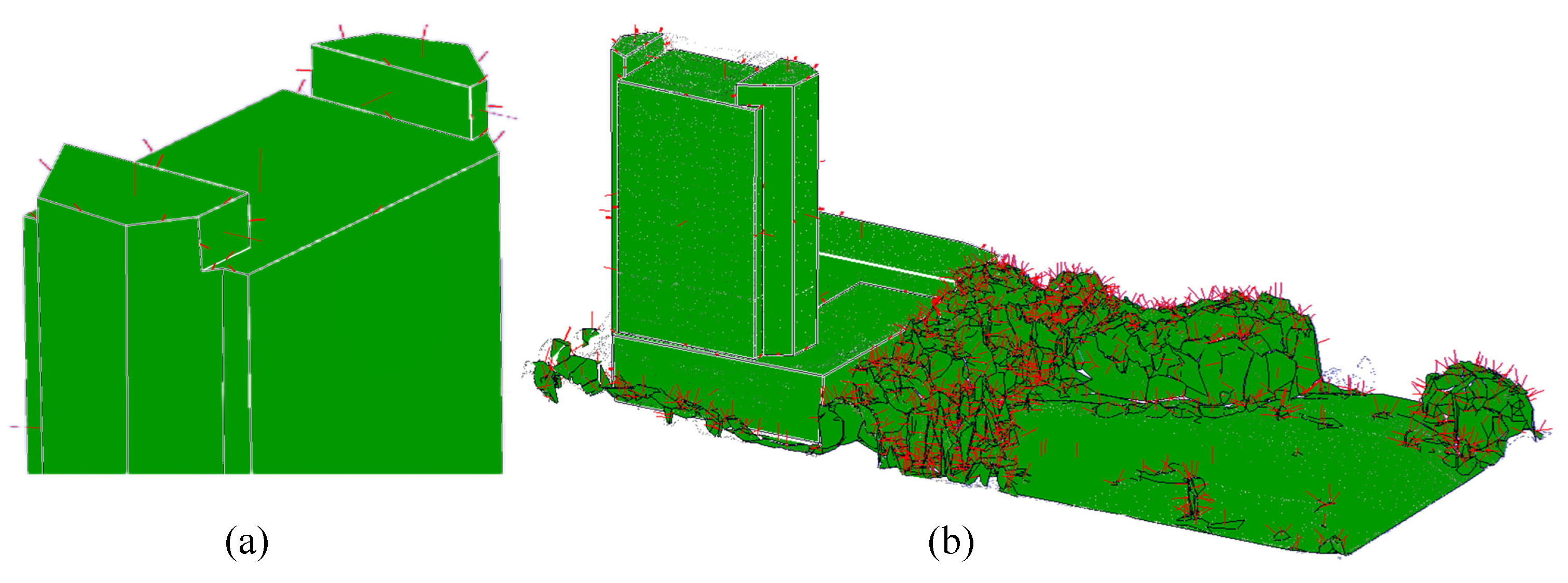
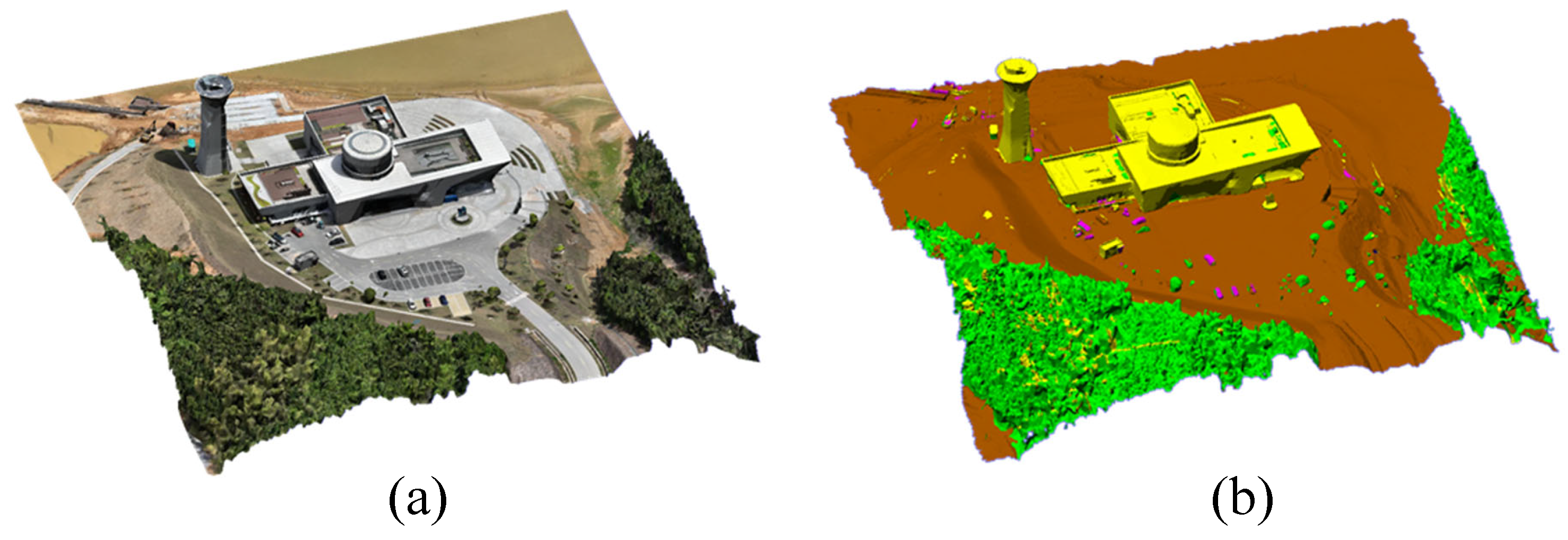
3.3. Semantic Segmentation of Proxy Model

To enable different path planning strategies for various categories of land features, this paper first performs semantic segmentation on the proxy model after its acquisition, dividing it into distinct land feature categories.

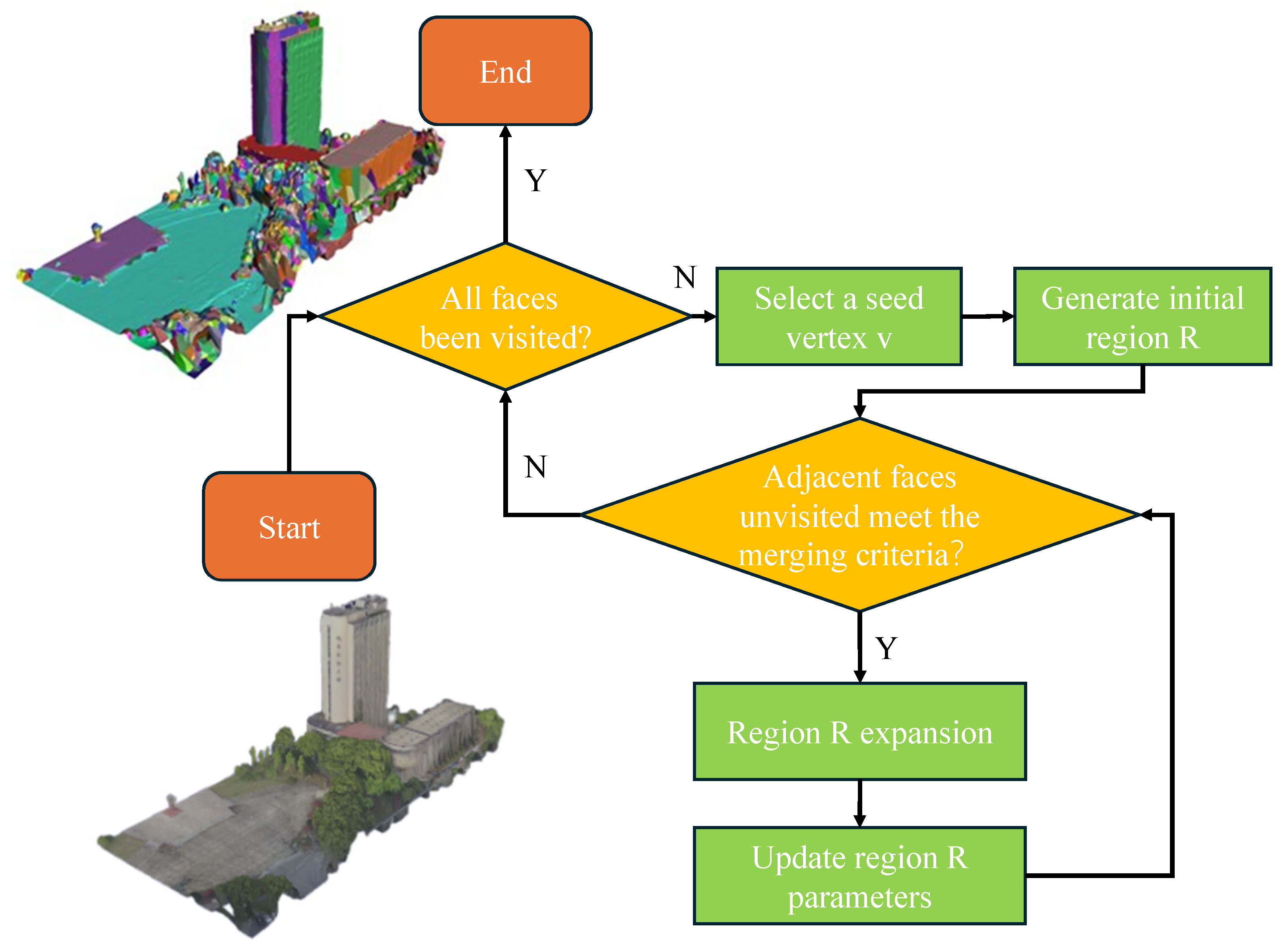
3.3.1. Plane Segmentation Based on Least Squares Plane Fitting

To ensure local consistency in subsequent planar feature extraction and classification, and to avoid redundant computations on numerous triangular faces, this paper first performs plane segmentation on the input proxy model. The main steps include seed vertex selection and initial region construction, followed by region growth and iteration. The detailed procedure and segmentation results are shown in Figure 3:

• Seed Vertex Selection and Initial Region Construction

First, the planarity of vertices in the proxy model is sorted, and vertices with relatively high local planarity are selected as seed vertices for region growing. For each seed vertex v, the faces within its one-ring neighborhood are regarded as the initial region. Let the seed vertex be v, and all faces in its neighborhood constitute the region R. For each face f in the region R, the following steps are carried out:

(1)

Mark the face f as visited;

(2)

Calculate the area of the region $A_R$ and the cumulative color value of the region $C_R$, then compute the average color $C_{avg}=C_R/\left|R\right|$, where the color is represented in the RGB color space;

(3)

Perform least squares plane fitting on all faces in region R to obtain the unit normal vector of the plane ${\mathit{n}}_R$ and the distance from the coordinate system origin to the plane d.

• Region Growing and Merging Criteria

All triangular faces adjacent to region R are traversed, and unvisited faces are considered as candidate faces. A candidate face f can be merged into R only if it satisfies the following conditions:

Distance criterion. The non-shared vertex p of face f satisfies the condition that its distance to the current region’s fitting plane is less than a threshold, namely $\left|{\mathit{n}}_R·\mathit{p}+d\right|<{\tau }_d$. Here, ${\tau }_d$ is the distance threshold, which is set to 0.5 m in this paper.

Angle criterion. Compute the angle $\theta$ between the unit normal vector of the current region ${\mathit{n}}_R$ and that of the candidate face ${\mathit{n}}_f$, namely $\theta ={cos}^{-1}\left({\mathit{n}}_R·{\mathit{n}}_f\right)$. The face is accepted only if $\theta <{\tau }_{\theta }$. Here, ${\tau }_{\theta }$ is the angle threshold set to 90° in this paper to handle cases of strong local noise, where faces are spatially close with large angular deviations.

Color similarity criterion. The L1 distance between the average color of the current region $C_{avg}$ and the color of the candidate face $C_f$ must be less than a specified threshold, namely ${\parallel C_{avg}-C_f\parallel }_1<{\tau }_{color}$. Here, ${\tau }_{color}$ is the color distance threshold, which is set to 30/255 in this paper.

Once the candidate face f is merged into region R, the following operations are performed:

(1)

Mark the face f as visited;

(2)

Update the area of the region $A_R$ and cumulative color $C_R$, and recalculate the average color $C_{avg}$;

(3)

Refit the plane parameters using the least squares method, and update the unit normal vector ${\mathit{n}}_R$ and the distance to the origin d.

3.3.2. Planar Feature Extraction and Random Forest Classifier

This paper adopts the 3D mesh semantic segmentation method based on random forest (RF) proposed by Gao et al. [23], using the Semantic Urban Meshes (SUM) dataset as the training set. For each plane segment, a total of 44 handcrafted features are extracted, including geometric features, elevation-related features, and color features. These multi-category features are then concatenated in a predefined order to form a high-dimensional feature vector representing each plane segment. The SUM dataset includes object categories such as ground, buildings, vegetation, water bodies, vehicles, boats, and unclassified objects. In this paper, vehicles and ground are merged into a single category, and boats and water bodies are also merged, resulting in five semantic labels: ground, buildings, vegetation, water bodies, and unclassified.

Based on the trained RF classifier, semantic segmentation can then be performed on the input proxy model. In addition, small misclassified regions in the proxy model can be filtered out by applying a threshold-based post-processing step.

3.4. Semantic Segmentation-Based Viewpoint Generation

After performing semantic segmentation on the proxy model, corresponding photography targets for different types of terrain can be extracted based on the segmentation results, with different resolution parameters set to generate multi-resolution viewpoints. However, the surface of the proxy model is often uneven and contains a large number of noise points. Directly generating sample points on such a surface may lead to irregular flight paths. Therefore, this paper first extracts simplified photography targets before generating sample points and viewpoints.

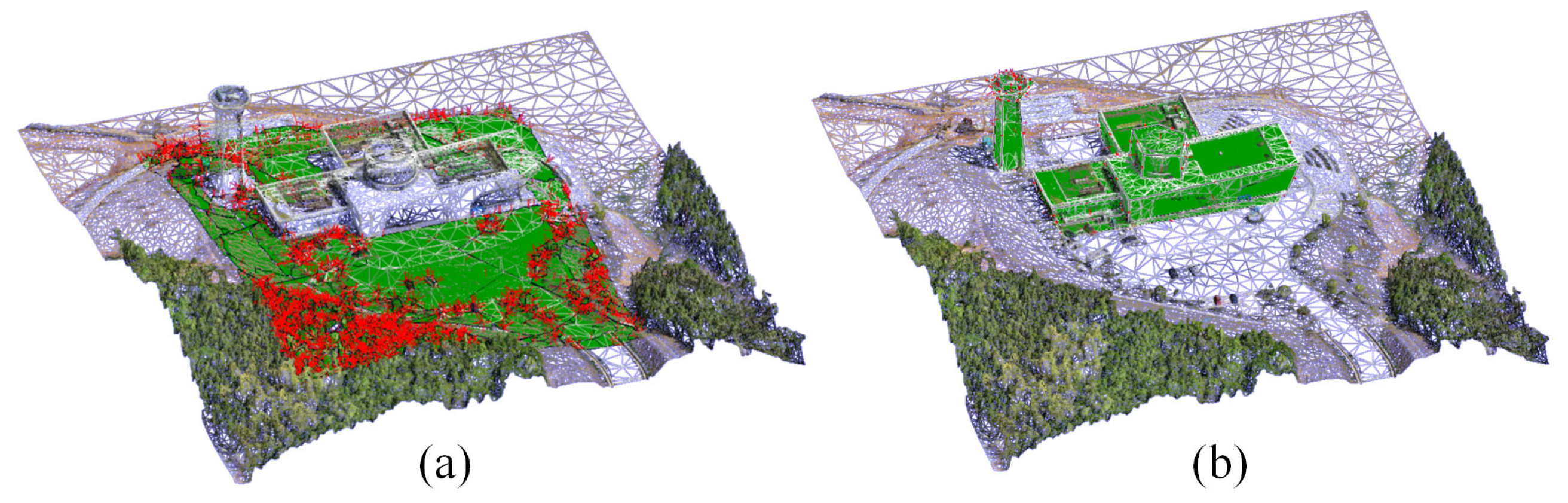
3.4.1. Simplified Photography Targets Extraction

Manual flight path planning typically relies on four basic photographic geometric targets: points, lines, surfaces, and volumes. Point targets are used to cover scattered details, line targets connect different surfaces, surface targets represent large continuous areas, and volume targets describe complete architectural structures. This paper draws on the concept of manual flight path planning, combining semantic segmentation results to extract simplified geometric models for building and non-building areas, which are then decomposed into point targets, line targets, and surface targets.

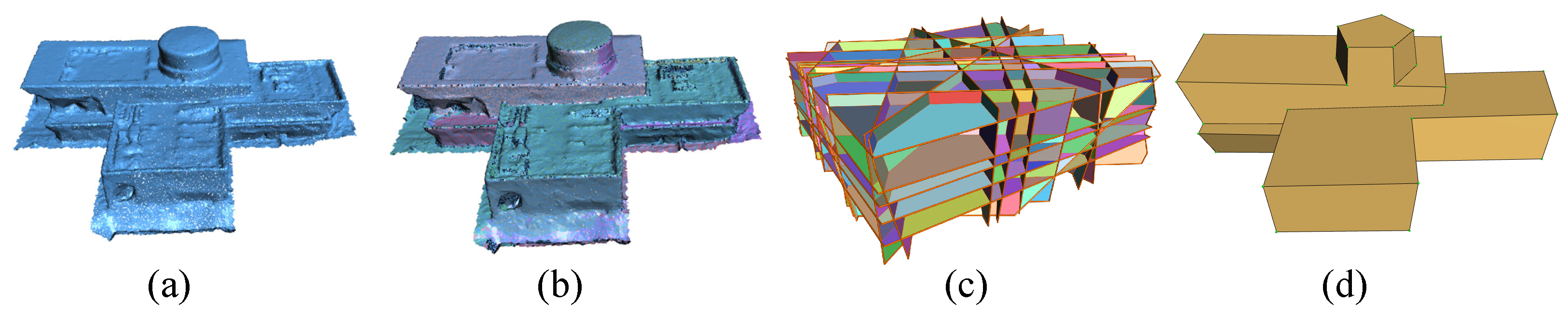
• Lightweight Polygonal Surface Model Reconstruction of Buildings

This paper reconstructs the lightweight polygonal surface model of the building area based on Polyfit proposed by Nan et al. [14]. The process can be divided into five main steps shown in Figure 4: preprocessing, plane segment extraction based on plane segmentation, spatial slicing and candidate surface generation, candidate surface indicator construction, and global optimization selection.

Preprocessing. Based on the results of semantic segmentation, the building area is extracted by calculating the area of the triangular face connected regions classified as buildings and the elevation difference within the region. Two corresponding thresholds are then set to filter out small misclassified areas as buildings. After extracting the building area, the paper samples it as a point cloud.

Plane Segmentation. First, this paper performs plane segmentation based on the Random Sample Consensus (RANSAC) [51] on the point cloud P obtained from the survey. By randomly selecting points to fit the planes and calculating the planes that best fit these points, such as the building walls and roof planes, the points are segmented into regions corresponding to each plane. Each detected plane

$$a_{i}x+b_{i}y+c_{i}z+d_i=0$$

(1)

forms a set of points $S_i\subseteq P$ as the support points. To eliminate errors due to cloud data noise and measurement errors, further optimization of the initial segmentation result is necessary. The optimization method mainly involves calculating the angles ${\theta }_{ij}$ between two planes ${\pi }_i$ and ${\pi }_j$, and then starting from the smallest angle, calculating the support points $N_{ij}$ of the planes. When ${\theta }_{ij}$ is smaller than a threshold ${\theta }_t$ and $N_{ij}$ is greater than a threshold $N_t$, the two planes are combined. For the newly formed plane segment, the support points are merged into a new support set, and Principal Component Analysis (PCA) is used to calculate the new plane parameters. In this paper, ${\theta }_t$ is set to ${10}^{\circ }$ and $N_t$ is set to $1/5$ of the minimum number of support points in the two planes.

Spatial Slicing and Candidate Surface Generation. Consider the set of intersection lines between all planes and subdivide each plane into polygonal regions. These regions represent the candidate polygonal patches, which potentially belong to the object surface. To obtain the actual surface patches of the object, this paper selectively retains the candidate polygonal patches based on information such as the number of support points.

Selection of Surface Indicators and Global Optimization. To select the appropriate polygonal surface, this paper uses the data-fitting $E_f$, model complexity $E_m$, and point coverage $E_c$ proposed by Nan et al. as surface indicators. This paper formulates the candidate polygon patch subset selection problem as a binary optimization problem. The objective is to select a subset of polygon patches that minimizes the weighted sum of three indicators.

$$arg\underset{x}{min}{\lambda }_f·E_f+{\lambda }_m·E_m+{\lambda }_c·E_c,$$

(2)

where ${\lambda }_f,{\lambda }_m,{\lambda }_c$ are used to control the weight of the three indicators, which are set to 0.43, 0.3 and 0.27 respectively; x represents the binary decision vector indicating whether to retain each candidate patch. Additionally, the following constraints must be satisfied for each edge $e_i$ of selected polygonal patches: the number of connected planes should be either 0 or 2 to ensure that the selected polygonal surface is closed. By solving the above optimization function, a subset of candidate polygonal patches can be selected from all the candidates, ensuring that the selected patches cover the surface of the entire point cloud and form a closed shell.

• Non-Building Area Photography Target Extraction

This paper extracts surface targets as the photography targets for non-building areas based on the plane segmentation results from semantic segmentation. Specifically, all triangular faces belonging to the same plane segment are first fitted to the corresponding plane equation. Then, the triangular faces are projected onto the plane, and the boundaries of the triangles are extracted in the 2D space to obtain a polygonal surface patch. This patch is treated as the surface target for the plane segment, whose semantic information is recorded as the category for the patch.

To accurately reconstruct the surface boundaries of these regions, this paper first preprocesses the projected point set S using the Delaunay triangulation algorithm [52], then employs the alpha-shape algorithm [53] for boundary extraction. The alpha-shape is a generalization of the convex hull and can more precisely extract the boundary of the input point set based on a control parameter $\alpha$. The basic principles and steps are as follows:

(1)

For a given input point set S, evaluate any two points $p,q$;

(2)

If there exists a circle with radius $r=1/\alpha$ passing through p and q, and the circle contains no other points from S, then retain the edge $S_{pq}$ as a boundary edge;

(3)

If the distance between p and q exceeds twice the radius r, skip this pair;

(4)

For each pair of points, there are typically two circles symmetric about the edge. If either circle satisfies the above condition, the edge is considered a boundary edge.

To eliminate the jagged contours of the extracted polygonal boundaries and facilitate the subsequent generation of regular sample points, this paper employs the Douglas–Peucker algorithm [54] to simplify the extracted polygonal boundaries.

Through the above method shown in Figure 5, the concave polygonal boundaries of non-building areas fitted to the plane can be effectively extracted, providing a foundation for subsequent viewpoint generation.

• Photography Target Decomposition and Processing

Before generating viewpoints, the extracted photography targets are decomposed and processed to obtain the basic target entities for path planning. For the lightweight polygonal surface model of building areas, this paper decomposes it into surface targets and line targets. The surface targets refer to the polygonal surfaces, while the shared edges between polygonal surfaces are treated as line targets. The normal vector of a line target is computed from the normals of its two adjacent surface targets. Introducing line targets can effectively prevent feature matching failures and improve the quality of 3D reconstruction.

For non-building areas, polygonal surfaces with an area smaller than a certain threshold (1 ${\mathrm{m}}^2$) are degraded into point targets, using the centroid of the polygon as the target location. For polygons with sufficient area, they are treated as surface targets, and their boundaries are simultaneously extracted as line targets. Unlike those in building areas, polygons in non-building areas may not share edges. Therefore, the normal vector of each line target is directly determined by the normal of its associated plane. These line targets mainly serve to mitigate matching failures that may occur when images of different resolution are captured for different types of targets.

As a result, the entire scene to be reconstructed is represented by a combination of surface targets, line targets, and point targets. Figure 6a illustrates the building area, where the normal vectors of line targets are calculated by summing the unit normal vectors of adjacent surfaces. Figure 6b shows the entire 3D scene. Regions with dense normal vectors correspond to point targets in non-building areas, while sparser normal vectors on the ground represent surface and line targets in non-building areas.

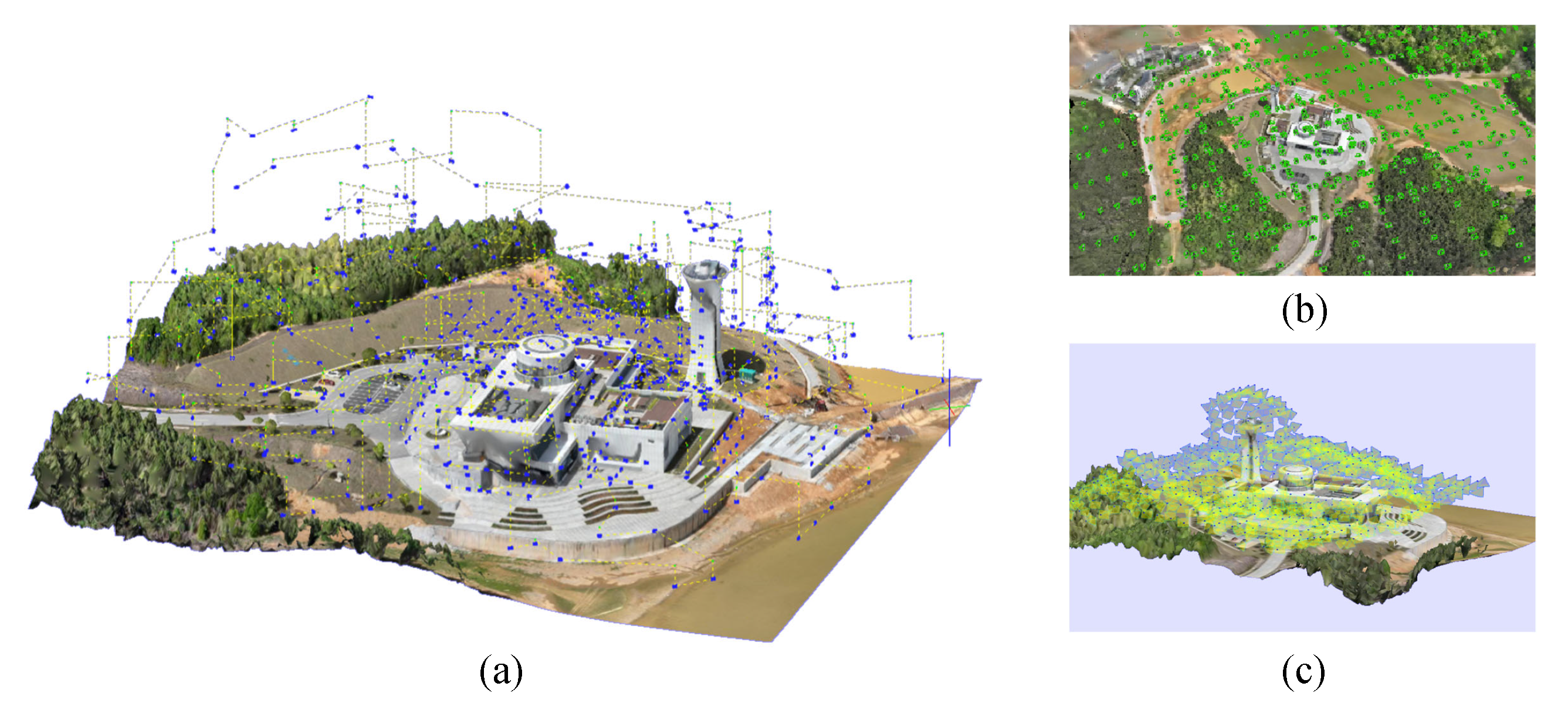
3.4.2. Multi-Resolution Viewpoint Generation and Optimization

• Reconstructability Evaluation of Viewpoints

In UAV image acquisition, the reconstructability measure can be used to evaluate the contribution of a specific viewpoint to the overall reconstruction accuracy and completeness, thus guiding the generation and optimization of viewpoints. Considering computational complexity and theoretical completeness, this paper adopts the reconstructability measure proposed by Smith et al. [43]

In the set of photography points V, the contribution of a pair of photography points $(V_i,V_j)$ to the reconstructability of a sampling point s is defined as follows:

$$c\left(s,V_i,V_j\right)={\displaystyle \frac{exp\left(-k_3\left(\alpha -{\alpha }_3\right)\right)·\left(1-min\left(d/d_{max},1\right)\right)cos\theta }{\left(1+exp\left(-k_1\left(\alpha -{\alpha }_1\right)\right)\right)·\left(1+exp\left(-k_3\left(\alpha -{\alpha }_3\right)\right)\right)}}$$

(3)

As shown in Figure 7, $\alpha$ represents the parallax angle between the two connecting lines $s{V}_1$ and $s{V}_2$; $\theta$ is the larger of the two observation angles formed by the sample point’s normal vector $\mathit{n}$ and the two connecting lines. The distance d represents the larger distance of the two connecting lines, namely $max(\parallel s{V}_1\parallel ,\parallel s{V}_2\parallel )$. Additionally, $k_1$ and $k_3$ are two constants, typically set to 32 and 8; constants ${\alpha }_1$ and ${\alpha }_3$, which are set to $\pi /16$ and $\pi /4$, are approximately used for the lower and upper limits of the parallax angle to reduce the error of aerial triangulation. The distance $d_{max}$ is used to limit the maximum photography distance. In this paper, it is set to twice the photography distance corresponding to the required ground sampling distance (GSD).

Finally, the definition of the reconstructability for a sample point s in the viewpoints set V is as follows:

$$H(s,V)=\sum _{1\le i<j\le \left|V\right|}v(s,V_i)v(s,V_j)c(s,V_i,V_j),$$

(4)

where $v(s,V_i)$ and $v(s,V_j)$ are indicator functions used to quantify the visibility between the viewpoints $V_i,V_j$ and the sample point s. When the viewpoint and sample point are in the line of sight, the value is 1; otherwise, it is 0. Based on the research by Zhou et al. [47], when the reconstructability is in the range of $(1.3,5.0)$, the reconstruction requirement can be considered satisfied.

• Photography Resolution Setting Based on Object Categories

UAV path planning in this paper focuses primarily on four object categories: buildings, ground, vegetation, and water bodies. Based on the characteristics of these four object categories, different image acquisition resolution parameters are set. This approach effectively reduces the number of images while ensuring the 3D reconstruction quality of key targets, thus saving both data acquisition time and 3D reconstruction processing time.

For buildings, they generally have relatively clear geometric features (such as facades, edges, etc.) and rich textures, making them a key focus for high-quality 3D reconstruction. In this paper, the GSD of the building area and the photography distance d are used as the baseline to describe the resolution and photography distance parameters for other three object categories.

For the ground, most areas are large, flat regions, and the difficulty of reconstruction mainly depends on the texture features. The resolution and accuracy requirements are not as high as those for buildings. In UAV path planning, the change in number of images is roughly proportional to the square of the change in resolution. In Figure 8, the details and textures are better at a photography distance of 15 m than 50 m, but the difference is not significant. However, the number of images captured at a 50 m photography distance is approximately one-tenth of that at a 15 m photography distance. Considering both reconstruction accuracy and the number of images, this paper sets the resolution for ground areas to 2 GSD and the photography distance to $2d$. As a result, the number of images can be reduced to approximately one-quarter of the number of images taken at a distance of d.

Vegetation, especially dense trees, has always been one of the challenges in image-based 3D reconstruction. For image acquisition in vegetation areas, this paper adopts a larger photography distance, allowing the image matching algorithm to focus more on the macroscopic features of the tree canopy rather than the microscopic leaves. This approach results in better matching and reconstruction outcomes at the cost of some resolution. The 3D reconstruction of vegetation at different photography distances is shown in Figure 9. The reconstruction result at 15 m contains a large number of matching errors in terms of model details and textures. However, the models at 50 m and 70 m show little overall difference. Specifically, this paper sets the resolution for vegetation areas to 3 GSD and the photography distance to $3d$. As a result, the number of images can be reduced to approximately one-ninth of the number of images taken at a photography distance of d.

For water bodies, surface reconstruction is one of the most challenging tasks in image-based 3D reconstruction. In water body reconstruction, the usual approach is to increase the photography distance in order to increase the proportion of non-water areas in the image, thereby alleviating the matching issues. Figure 10 shows the issues in water body 3D reconstruction. In terms of model details and textures, the 50 m reconstruction results show large holes, while the 70 m reconstruction results exhibit depressions, indicating height noise. Considering the reconstructability requirements for photography distance and to prevent matching failures in transition areas between different types of terrain, this paper sets the resolution for water body areas to 3 GSD and the photography distance to $3d$, the same as for vegetation areas.

• Viewpoint Generation Based on Reconstructability

For the previously extracted point targets, line targets, and surface targets, since the line targets and surface targets are relatively regular and each target has a consistent normal vector, this paper introduces the concept of flight strip units from aerial photogrammetry to generate viewpoints on the line targets and surface targets.

For surface targets, the viewpoint generation method based on flight strip units is shown in Figure 11. First, structural lines $\left(l_1,l_2,\dots ,l_n\right)$ are generated at equal intervals on the surface target, with the normal vectors of the structural lines aligned with the normal vector of the surface target. For each structural line $l_i$, sample points are generated at equal intervals along it, namely $s_i=\left(s_{i1},s_{i2},\dots ,s_{im}\right)$. The spacing between the structural lines and sample points is determined by the forward overlap $h_{overlap}$ and the lateral overlap $w_{overlap}$:

$$\begin{array}{cc}\hfill dis\left(s_{ij},s_{ij+1}\right)& =\left(1-h_{overlap}\right)·GSD·{\mathrm{pixels}}_h\hfill \\ \hfill dis\left(l_i,l_{i+1}\right)& =\left(1-w_{overlap}\right)·GSD·{\mathrm{pixels}}_w\hfill \end{array}$$

(5)

where GSD is the ground sample distance; ${\mathrm{pixels}}_h,{\mathrm{pixels}}_w$ are the height and width of the image, measured in pixels. The viewpoint $V_i=\left(x_i,y_i,z_i,{\mathrm{pitch}}_i,{\mathrm{yaw}}_i\right)$ generated from the sample point $s_i$ ensures that the principal optical axis of the camera is parallel to the normal vector of the surface target $\mathit{n}=(n_X,n_Y,n_Z)$. The coordinate calculation method is given as follows:

$$\left(x_i,y_i,z_i\right)=s_i+d_i\mathit{n},{\mathrm{pitch}}_i={cos}^{-1}{n}_Z,{\mathrm{yaw}}_i=-{tan}^{-1}\left({\displaystyle \frac{n_Y}{n_X}}\right)$$

(6)

where the parameter $d_i$ is derived from the GSD of the photography target. Given the focal length f, the calculation follows: $d=f·GSD/\mathrm{pixelsize}$.

For line targets, the same method is employed to generate flight strips, with the difference that only a single flight strip is required. According to Zhou et al. [47], for both surface and line targets, a 50% overlap ratio in both the flight direction and lateral direction ensures sufficient reconstructability for satisfactory results. However, when the overlap exceeds 66%, image acquisition becomes redundant. Thus, the recommended overlap range is typically (50%, 66%). In this paper, a forward overlap of 65% and a lateral overlap of 50% are adopted.

For point targets, a submodular function optimization-based approach is employed to generate viewpoints. Specifically, each point target is treated as a sample point, and the corresponding viewpoint is calculated using Equation (6), forming a viewpoint set $V_p$. Through submodular optimization, the viewpoint that provides the maximum incremental reconstructability is iteratively selected, ensuring sufficient reconstruction quality while avoiding redundancy of viewpoints. The submodular function is defined in Equation (7).

$$\begin{array}{cc}\hfill v_i& =arg\underset{v_i\in V_p}{max}EH\hfill \\ \hfill EH& =\sum _{s\in S_{v_i}}\left[exp\left(H_T-H\left(s,V\right)\right)-1\right]·A_s\hfill \end{array}$$

(7)

Here, $A_s$ denotes the neighborhood area represented by a sample point and serves as a weighting parameter. $S_{v_i}$ refers to the set of sample points corresponding to point targets visible from viewpoint $v_i$. The reconstructability threshold $H_T$ is set to 1.3, while $H(s,V)$ represents the reconstructability of sample point s given the current set of optimized viewpoints V. The set V comprises viewpoints generated for surface/line targets and those previously selected for point targets.

For each candidate viewpoint $v_i$, this paper calculates the sum of reconstructability gains $EH$ across all visible sample points $S_{v_i}$. The viewpoint with the maximal $EH$ is iteratively selected from the candidate set $V_p$. The formula of $EH$ satisfies the submodularity condition: as the reconstructability H of all sampling points increases, the $EH$ value monotonically decreases. After selecting a new viewpoint, the reconstructability of its covered sample points is updated, and the selection process repeats until $EH$ falls below 0.

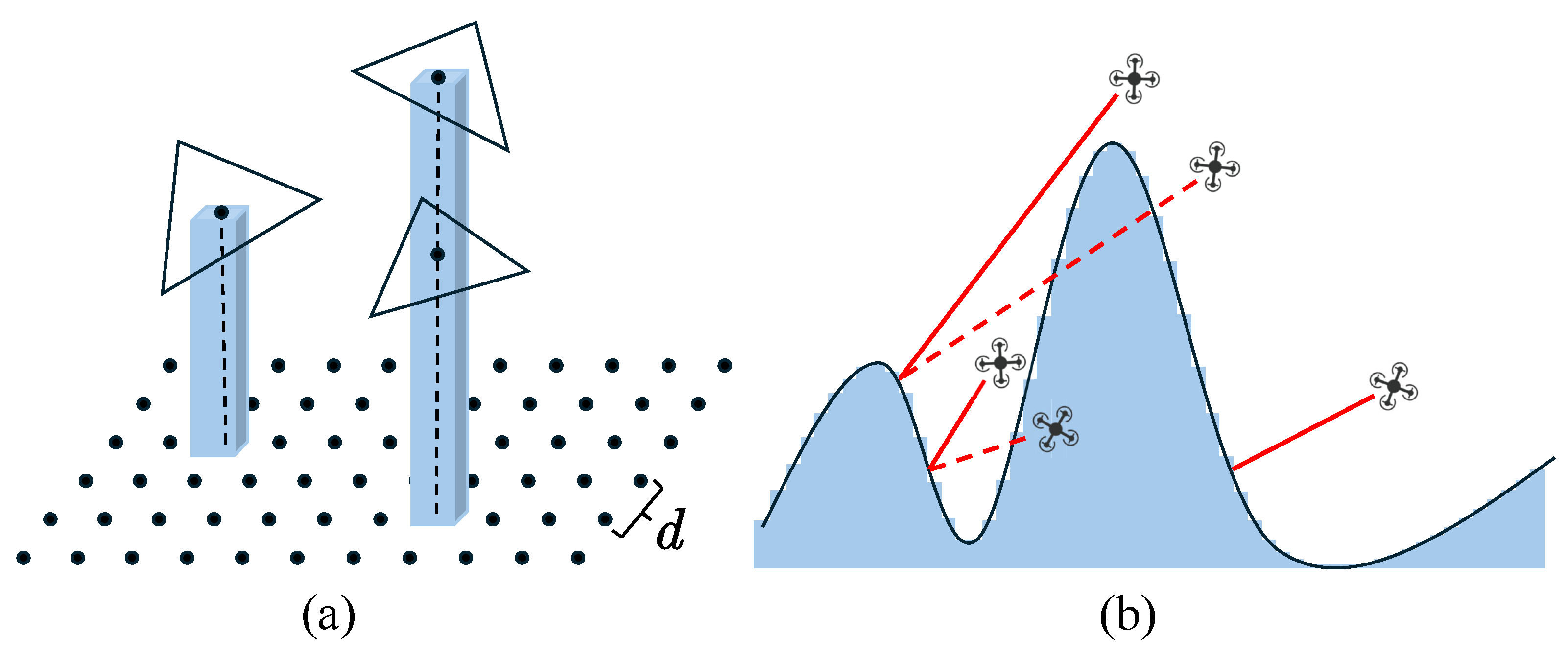
3.5. Obstacle-Aware and RTK Signal-Based Viewpoint Optimization

After planning the UAV viewpoints, it is also necessary to consider flight safety during the execution of the flight mission. In this paper, a gridded Digital Surface Model (DSM)-based safety shell is constructed from the proxy model to perform collision detection in different scenarios, enabling efficient and reliable obstacle avoidance along the planned route. In addition, a sky-view analysis method is introduced to evaluate the RTK signal strength at each viewpoint, helping to prevent risks or mission interruptions caused by RTK signal loss.

3.5.1. Obstacle Avoidance Analysis Based on DSM Safety Shell

The proxy model consists of a large number of triangular meshes, making direct collision detection computationally intensive and time-consuming. Moreover, due to the coarse nature of the proxy model, the reconstruction may be incomplete, leading to reduced accuracy in collision detection. Therefore, this paper samples the proxy model to generate a DSM safety shell, which is then used for collision detection. This approach improves detection efficiency and introduces a certain level of redundancy to enhance flight safety.

The generation method of the gridded DSM safety shell is similar to that of a standard DSM. First, $m\times n$ grid points are created on the $XOY$ plane at the lowest elevation of the proxy model, with a sampling interval d. The values of m and n are determined by the projection range of the proxy model onto the $XOY$ plane and the chosen interval d. After generating the grid points, a ray is cast upward along the positive Z-axis from each grid point. The intersection points between the rays and the triangular faces of the proxy model are computed, and the highest intersection point is taken as the elevation value for that grid point. Based on this elevation, an axis-aligned bounding box (AABB) is constructed for each grid point, with a base of $d\times d$. A schematic illustration is shown in Figure 12. It should be noted that an appropriate sampling interval must be selected. In practical applications, the sampling interval is typically set between 0.5 m and 1 m.

After obtaining the viewpoints and the DSM safety shell of the scene, this paper performs obstacle avoidance checks and adjustments for the generated viewpoints. As illustrated in Figure 12, two main cases are considered: (1) the viewpoint is too close to or located inside the safety shell, and (2) there is an occlusion between the viewpoint and the corresponding sample point. To address these cases, a bounding box with a side length of $2d_{safe}$ (where $d_{safe}$ is the avoidance distance, set to 5 m) is generated for each viewpoint. Collision detection is then performed between this bounding box and the safety shell. If an intersection is detected, the photography point is rotated around the sample point within the vertical plane until the bounding box no longer intersects with the safety shell or until the rotation angle exceeds a predefined threshold, typically set to 60°. If the required angle exceeds this threshold, the photography point is considered to contribute too little to the reconstruction and is thus removed. Subsequently, line-of-sight occlusion is evaluated by checking whether the line segment connecting the viewpoint and its corresponding sample point intersects the safety shell. If occlusion is present, the same rotation-based adjustment strategy is applied.

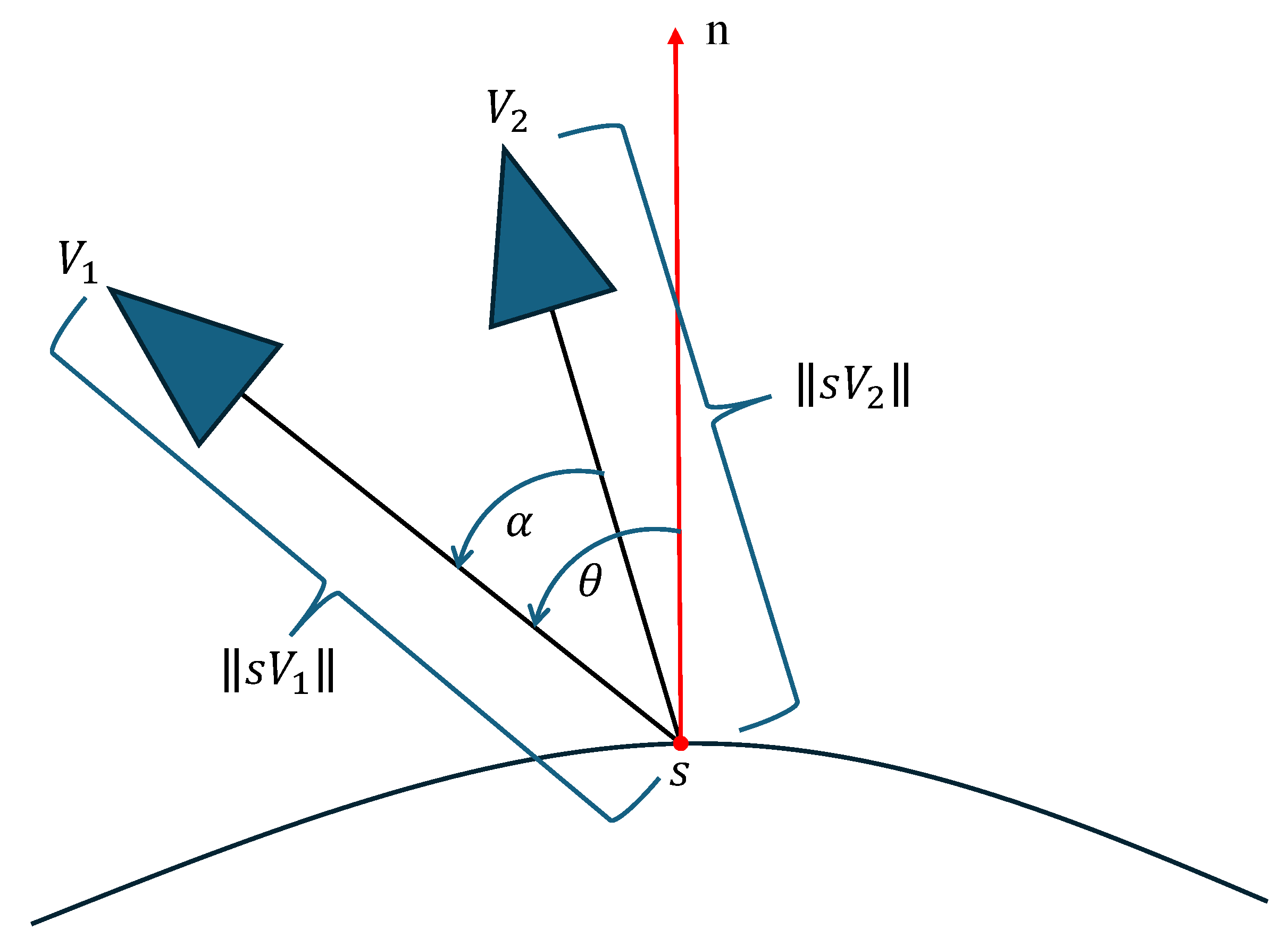
3.5.2. RTK Signal Analysis and Optimization Based on Sky-View Maps

In actual flights, UAV RTK signal degradation often occurs when the UAV is flying close to the base of buildings. Obstructions such as buildings and trees can reduce the number of GNSS satellite signals received, thereby affecting RTK positioning accuracy. To address this issue, this paper proposes a sky-view-based method for evaluating RTK signal quality. Based on the evaluation results, viewpoints are adjusted to reduce the likelihood of weak RTK signals during flight.

In the field of Global Navigation Satellite System (GNSS) positioning accuracy research, sky-view analysis from the perspective of the rover station is commonly used to assess satellite signal obstruction. In such methods, studies [15] have shown that when the visible sky area in the sky-view map exceeds 50%, GNSS signals can typically be received reliably, resulting in higher positioning accuracy. Following this idea, this paper simulates sky-view maps at designated viewpoints on the proxy model and calculates the proportion of visible sky area. For viewpoints with a sky-view ratio below 50%, an elevation adjustment is applied. The specific steps are as follows:

(1)

Among the viewpoints generated for buildings, identify those whose heights are less than half the height of the corresponding building.

(2)

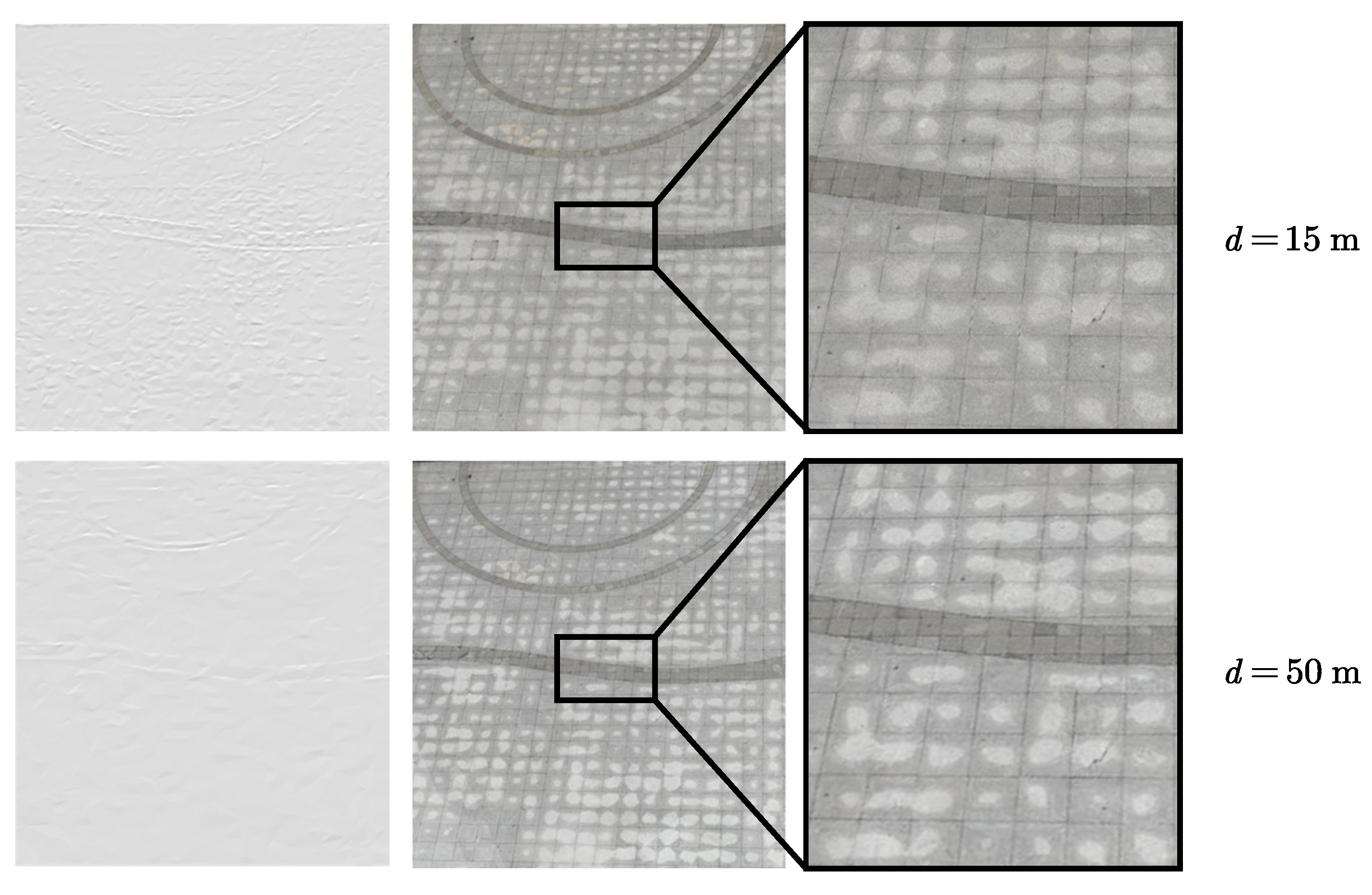
For these viewpoints, use an OpenGL renderer to generate upward-facing virtual images of the proxy model, then convert them into fisheye images. Based on a sky mask, extract the non-sky area and calculate the sky-view ratio.

(3)

For viewpoints with a sky-view ratio below 50%, incrementally raise their height in 2 m steps. During elevation, maintain the camera orientation toward the original sample point.

(4)

After each elevation step, recalculate the sky-view ratio at the new position. Continue this process until the ratio exceeds 50% or the elevation causes the viewing angle to surpass a predefined threshold (60°).

Figure 13 illustrates the RTK signal evaluation based on sky-view analysis. In Figure 13a, the proxy model is shown with three red points representing viewpoints positioned 6.67 m away from a building facade at heights of 10 m, 15 m, and 20 m above ground level. In Figure 13b–d, the corresponding sky-view maps are shown, with calculated sky-view ratios of 52.41%, 56.58%, and 65.84%, respectively. For each viewpoint, the top row displays the original sky-view image, while the bottom row shows the extracted non-sky region obtained via a sky mask.

3.6. UAV Path Connection Based on Energy Consumption

After obstacle avoidance adjustments and RTK signal analysis are made to the viewpoints, connecting them sequentially yields the final flight route. For UAVs, energy consumption is a key factor affecting the efficiency of flight missions. Therefore, this paper proposes a route connection method that incorporates energy cost considerations to improve the overall efficiency of UAV mission execution.

Given a set of viewpoints $V=\left\{v_1,v_2,\dots ,v_n\right\}$, where each viewpoint represents the 3D position of the UAV and the camera orientation, a complete weighted graph $G=(V,E)$ is constructed. In this graph, each edge represents a potential flight path between two viewpoints, and the edge weight corresponds to the energy cost for the UAV to fly from $v_i$ to $v_j$, denoted as $E_{ij}$. Assuming the UAV flies at a constant speed v and does not hover during the entire image acquisition process, the energy consumption for any flight segment $(v_i,v_j)$ is defined as the sum of the work done against gravity $Q_{lift}$ and the work done against air resistance $Q_{drag}$ [55]. The energy cost for a given flight path segment $(v_i,v_j)$ is calculated as follows:

$$E_{ij}=Q_{lift}+Q_{drag}={\displaystyle \frac{d_{ij}·{\left(mg\right)}^{\frac{3}{2}}}{v\sqrt{2\rho A}}}+{\displaystyle \frac{1}{2}}{C}_D\rho S{v}^2{d}_{ij}$$

(8)

where $d_{ij}$ is the distance between $v_i$ and $v_j$, m is the mass of the UAV, g is the gravitational acceleration, $\rho$ is the air density, A is the total rotor swept area, $C_D$ is the drag coefficient, and S is the frontal area of the UAV. Since the UAVs in this paper operate mostly at low altitudes (below 100 m), the air density $\rho$ is assumed to be constant across all altitudes.

In the following two cases, the energy cost $E_{ij}$ should be set to infinity:

(1)

The flight path intersects an obstacle, i.e., for any pair of photography points $(v_i,v_j)$, the line segment connecting them intersects the safety shell, as determined through collision detection.

(2)

When a viewpoint lies on a flight strip unit, only the energy costs between adjacent points on the same strip are retained; the energy costs between non-adjacent points are set to infinity. In this way, each flight strip unit is treated as an indivisible segment during route connection.

To find the route with minimal energy consumption that visits all viewpoints, the ACO algorithm [56] is employed to search for the optimal path on the complete weighted graph G. The algorithm terminates when either the maximum number of iterations (set to 500 in this paper) is reached, or when the total energy consumption of the optimal solution remains unchanged over several consecutive iterations. Upon termination, the path with the minimum energy consumption is selected as the UAV’s final flight route.

4. Experimental Results

To validate the effectiveness of the proposed method, experiments are conducted on real-world scenes containing various categories of land features. Flight routes are generated and aerial images are collected accordingly. The planned path and the resulting refined 3D mesh are compared against those obtained using two baseline methods: oblique photogrammetry and the flight planning approach provided by Metashape software (referred to as the MS method).

4.1. Experimental Setup

The software platforms include Nap3D, DJI Terra, and Agisoft Metashape. Nap3D is a flight planning tool designed for close-range photogrammetry. It supports functions such as initial model import and visualization, UAV parameter configuration, safety shell generation, and virtual image simulation. In this paper, the proposed path planning method is integrated into Nap3D. By inputting the results of semantic segmentation and simplified photography target extraction, Nap3D is used to generate the final multi-resolution flight paths. DJI Terra is primarily employed for 3D reconstruction of both the initial and refined models in the experiments. Agisoft Metashape is a commercial software that supports both 3D reconstruction and automatic flight route generation. In this paper, its automatic UAV path planning function is used as a baseline for comparison with the proposed method.

The primary hardware platform is the DJI Mavic 3E UAV. This drone is widely used in surveying and mapping applications due to its compact and lightweight design, high-resolution camera (image resolution of $5280\times 3956$ with up to 20 megapixels), wide gimbal pitch control range (from −90° to 35°), and integrated high-precision RTK module, which enables centimeter-level positioning accuracy.

The experimental site for this study is the Chinese UAV Test Valley, located in Chibi City, Hubei Province. This facility is primarily used for the integrated testing and evaluation of various unmanned systems. The site features a central command and control building aligned along the central axis, an astronomical observation tower to its northwest, and is surrounded by open fields and large areas of forest vegetation. These diverse and challenging environmental conditions provide a suitable setting for validating the proposed method. An overview of the test site is shown in Figure 14.

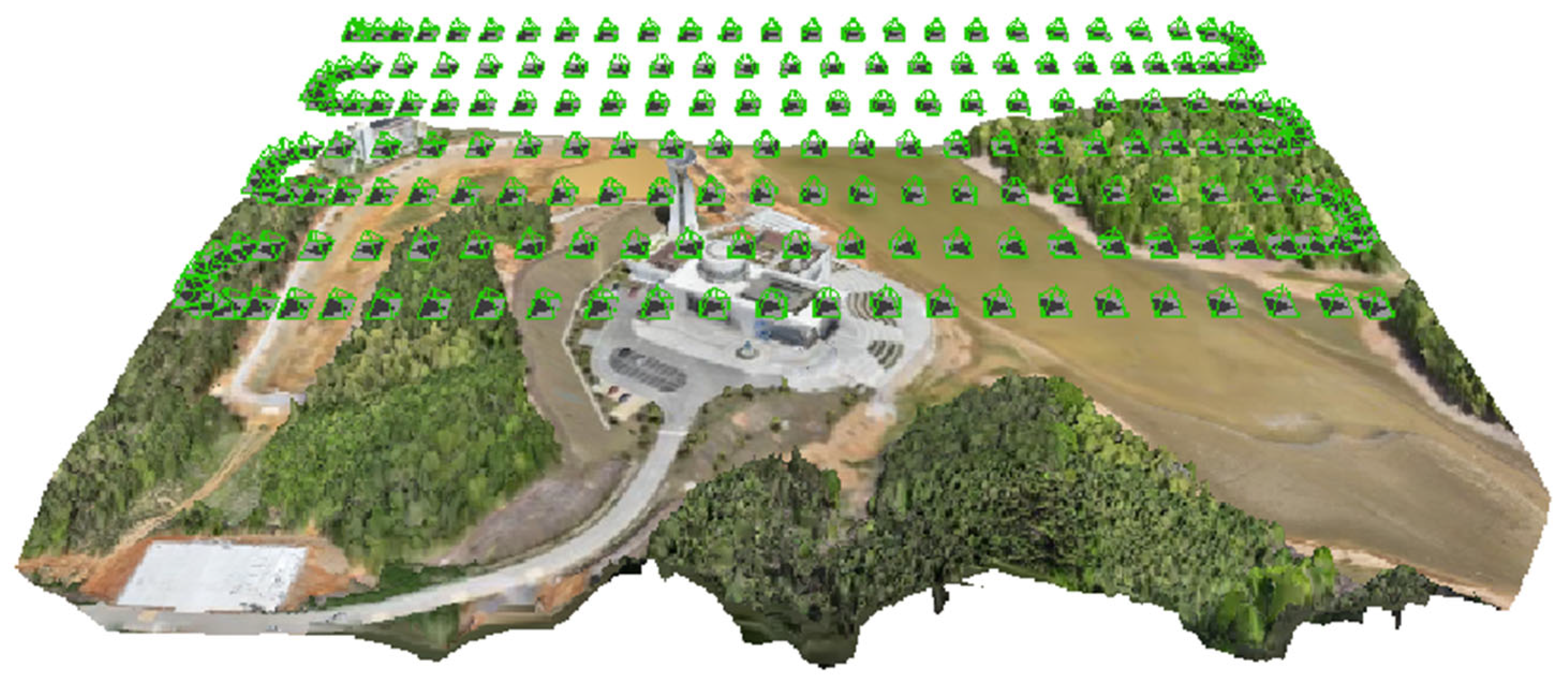
4.2. Experimental Procedure

4.2.1. Proposed Method

The experimental procedure of the proposed method mainly includes the acquisition of the proxy model, semantic segmentation and photography target extraction on the proxy model, flight path generation, high-resolution image acquisition, and refined 3D reconstruction of the real scene.

For acquiring the proxy model, a zigzag flight path at an altitude of 70 m with vertically downward-facing camera angles was employed, as shown in Figure 15. The collected images were processed using DJI Terra for reconstruction, which quickly generates a relatively coarse proxy model of the target area.

After obtaining the proxy model, a trained random forest classifier is applied to perform semantic segmentation on the proxy model, yielding the results shown in Figure 16. The scene is primarily divided into vegetation (green), buildings (yellow), ground (brown), and vehicles (pink), which are later reclassified as ground. For safety considerations, a DSM-based safety shell is generated from the proxy model for obstacle avoidance during path planning. Therefore, the reconstruction area must be smaller than the proxy model to ensure the safety of viewpoints located near the boundaries of the reconstruction area. Based on the semantic segmentation results and the defined reconstruction area, different target extraction strategies are applied to non-building and building areas to obtain simplified photography targets, as shown in Figure 17.

A baseline imaging distance of 15 m was set, corresponding to a ground sampling distance (GSD) of 0.412 cm/pixel, with 65% forward overlap and 50% lateral overlap. A total of 617 viewpoints were generated, forming a multi-resolution flight path as shown in Figure 18a. Based on the baseline distance, the resulting flight plan includes an imaging distance of 30 m for ground surfaces and 45 m for vegetation areas. As illustrated in Figure 18a, the proposed method produces flight paths with regular linear segments, which helps reduce energy consumption during UAV operation.

4.2.2. Oblique Photogrammetry

In this paper, oblique photogrammetry is achieved by planning a 2D grid-shaped flight path at a fixed altitude, while the UAV gimbal sweeps during flight to capture multi-angle images of the real-world scene. The oblique photogrammetry flight route used in this section is shown in Figure 18b and was planned using DJI’s Pilot2 software on the Mavic 3E platform. Considering the presence of tall buildings in the scene, such as the astronomical observation tower, the photography distance is set to 50 m, corresponding to a GSD of 1.375 cm/pixel. This photography distance is also close to the 45 m used in the proposed method for the lowest resolution level (3 GSD).

4.2.3. Metashape (MS) Method

In the same scene, UAV path planning was also performed using Metashape (version 2.2.0, build 19630). The proxy model used in this method is the same as that used in the proposed method. However, unlike the proposed method, Metashape does not consider semantic information of the scene; instead, it generates sample points directly on the surface of the proxy model based solely on its geometric features. In the MS method, a 2D area of interest is first delineated on the proxy model, and flight routes are then generated using the Mission Plan function by specifying the photography parameters. For a fair comparison, the flight parameters such as photography distance and overlaps were set to be consistent with those used in the proposed method. Specifically, the photography distance was set to 15 m, corresponding to a GSD of 0.412 cm/pixel. The resulting flight path, as shown in Figure 18c, contains a total of 888 viewpoints.

Finally, the images collected by the three methods were used for 3D reconstruction in DJI Terra, and the resulting 3D mesh models will be comparatively analyzed in the following section.

4.3. UAV Path Planning Method Comparison

4.3.1. Quality Evaluation Metrics

The proposed method is evaluated from two main aspects: the quality of the flight path and the quality of the refined 3D model. For flight path quality, both the number of viewpoints and the percentage of energy consumption are considered. For model quality, the evaluation focuses on two criteria: completeness and visual quality. Completeness is assessed based on the presence of holes in the model and whether object structures are fully reconstructed. Visual quality is evaluated in terms of texture clarity, edge sharpness, and planar smoothness of the reconstructed surfaces.

4.3.2. Comparison with Oblique Photogrammetry

For oblique photogrammetry, due to its generally longer photography distance and lower resolution, the comparison is focused solely on model completeness and visual quality. Figure 19 shows a comparison of local reconstruction results between the proposed method and the oblique photogrammetry method. The refined 3D mesh generated by the proposed method demonstrates better reconstruction of architectural details, such as building edges (see Figure 19a,e) and eaves (see Figure 19b,f), owing to its ability to capture images closer to the surface of buildings. In contrast, reconstruction differences in ground areas (see Figure 19b,f) and vegetation regions (see Figure 19d,h) are less significant, as the proposed method also adopts longer photography distances in these areas.

4.3.3. Comparison with Metashape (MS) Method

To further evaluate the contribution of semantic segmentation, the proposed method is compared with the MS method, which does not incorporate semantic information during flight path planning. As the MS method is widely used in commercial photogrammetry workflows, this comparison highlights the added value of incorporating semantic cues into path planning.

Regarding the completeness and visual quality of the 3D models, Figure 20 presents a comparison between the results obtained by the proposed method and the MS method. In Figure 20a–c, excluding the glass surfaces that are inherently difficult to reconstruct, the refined 3D mesh generated by the proposed method shows better preservation of architectural geometry. In contrast, in Figure 20d,e, the model produced by the MS method contains numerous holes on building surfaces, particularly evident in Figure 20e, indicating that the viewpoints generated by Metashape were suboptimal for such structures, leading to image matching failures. In Figure 20f, the reconstruction result of the observatory roof obtained by the proposed method is less accurate. This may be due to an insufficient number of extracted photography targets representing the geometric features of the structure, resulting in a sparse distribution of viewpoints. In Figure 20g, although the proposed method uses a doubled photography distance (30 m) for ground targets compared to the 15 m used in the MS method, the reconstruction quality remains comparable. In Figure 20h, for vegetation areas, the proposed method uses a tripled photography distance (45 m), significantly reducing the number of viewpoints. Nevertheless, it achieves even better reconstruction quality, suggesting that appropriately increasing the photography distance for vegetation can enhance feature extraction and lead to improved reconstruction results.

Figure 21 presents a comparison of untextured (white) models generated by the proposed method and the MS method. The absence of texture allows for a clearer observation of differences in geometric structure and model accuracy, particularly in building outlines and vegetation regions. In the vegetation areas, it is evident that although the MS method uses a shorter photography distance, it results in poorer reconstruction quality. This highlights the importance and effectiveness of adopting different image acquisition strategies for different types of objects. For buildings, both methods use the same imaging distance and overlap settings. However, the reconstruction quality achieved by the proposed method is significantly better. This demonstrates the effectiveness of the proposed method in extracting lightweight polygonal surface models of buildings to guide the generation of viewpoints.

In terms of flight path quality, the proposed method and the MS method captured 617 and 888 images, respectively, during the experiment, with corresponding battery consumption rates of 245% and 393%. The proposed method reduces the number of viewpoints by approximately one-third compared to the MS method. Moreover, in building regions, the reconstruction results obtained by the proposed method are significantly better than those of the MS method. Unlike the MS method, which samples viewpoints directly on the surface of the proxy model, the proposed approach first extracts regular geometric photography targets to guide viewpoint generation. It also introduces the concept of flight strip units, leading to more structured and regular flight segments within the planned path. This contributes to lower energy consumption during UAV operations. On average, each image captured by the proposed method consumes approximately 0.3971% of the battery, while the MS method consumes about 0.4426% per image. Therefore, under the same battery conditions, the proposed method enables the UAV to capture more images, improving overall efficiency.

The results demonstrate that the proposed method achieves better coverage of semantically important regions and improved adaptability to the underlying terrain. This confirms that semantic segmentation enhances the efficiency and task-specific focus of the planned flight paths, thereby contributing significantly to the overall performance of the proposed system.

5. Discussion

The proposed UAV path planning method based on semantic segmentation of 3D reality models has significantly improved the efficiency and accuracy of high-quality real-world 3D model reconstruction. By incorporating semantic information to differentiate land cover types and setting distinct photography targets and image acquisition resolutions for each class, the method effectively reduces redundant data while enhancing reconstruction quality in key regions. However, certain limitations remain in the practical implementation.

Firstly, the current multi-resolution setting uses fixed image acquisition resolutions for different object categories, which lacks flexibility. This is especially problematic for weakly textured areas such as water bodies, where fixed resolutions may fail to balance matching accuracy and data efficiency.

Secondly, although the lightweight polygonal reconstruction approach for buildings based on planar features performs well in most cases, it may not represent curved or circular structures adequately, leading to potential loss of geometric completeness.

Furthermore, due to the difficulty in obtaining a ground truth for large-scale real-world scenarios, the evaluation in this study mainly relies on visual inspection of model completeness and detail quality. A lack of quantitative accuracy assessment highlights the need to construct synthetic datasets with realistic textures and diverse semantic categories to support more comprehensive and robust performance validation in future work.

Lastly, while semantic segmentation accuracy may influence photography target extraction, particularly at category boundaries, the overall reconstruction performance is not highly sensitive to such errors. This is because the proxy model used for semantic segmentation is inherently coarse, and the viewpoint generation process allows for sufficient tolerance. Prior studies have demonstrated that effective reconstruction can still be achieved using simplified proxy models such as DSMs [43], sparse point clouds [12], or 2.5D approximations [46]. Therefore, the proposed method maintains robustness in reconstruction quality even in the presence of moderate segmentation inaccuracies.

6. Conclusions

With the growing demand for high-quality 3D reconstruction, this paper addresses the limitations of existing UAV path planning methods in terms of data redundancy and resolution mismatch. A semantic-guided reconstruction task planning method is proposed, which systematically integrates key components including proxy model construction, semantic classification of scene elements, differentiated viewpoint generation, obstacle avoidance, RTK signal analysis, and energy-efficient flight path optimization.

Experimental results demonstrate that, under the same image resolution, the proposed method yields higher-quality 3D reconstructions in building areas and achieves better completeness in vegetation areas even with greater photography distances. Compared with commercial software such as Metashape, the proposed method reduces the number of collected images by approximately 30.5%, validating the effectiveness of multi-resolution flight planning in enhancing modeling efficiency without compromising reconstruction quality. Additionally, safety-aware mechanisms—such as shell-based obstacle avoidance and sky-view-based RTK signal analysis—are introduced to minimize flight risks and ensure mission reliability.

In conclusion, the proposed method demonstrates significant advantages in improving reconstruction accuracy, reducing data redundancy, and enhancing system robustness. It provides a feasible and efficient solution for high-quality UAV-based 3D modeling in complex real-world environments.