Combined Robust Control for Quadrotor UAV Using Model Predictive Control and Super-Twisting Algorithm
Abstract
1. Introduction
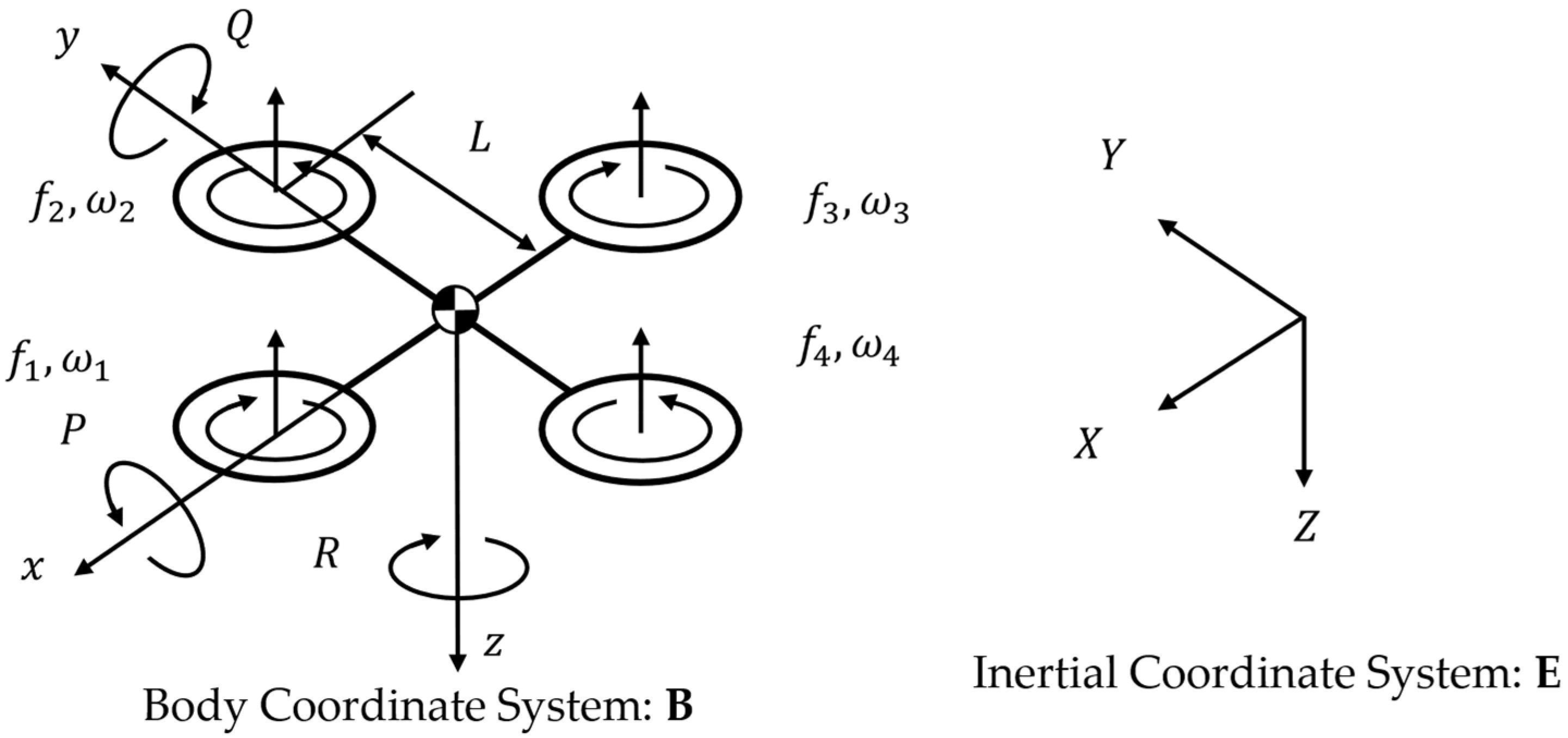
2. Dynamics of Quadrotor UAV
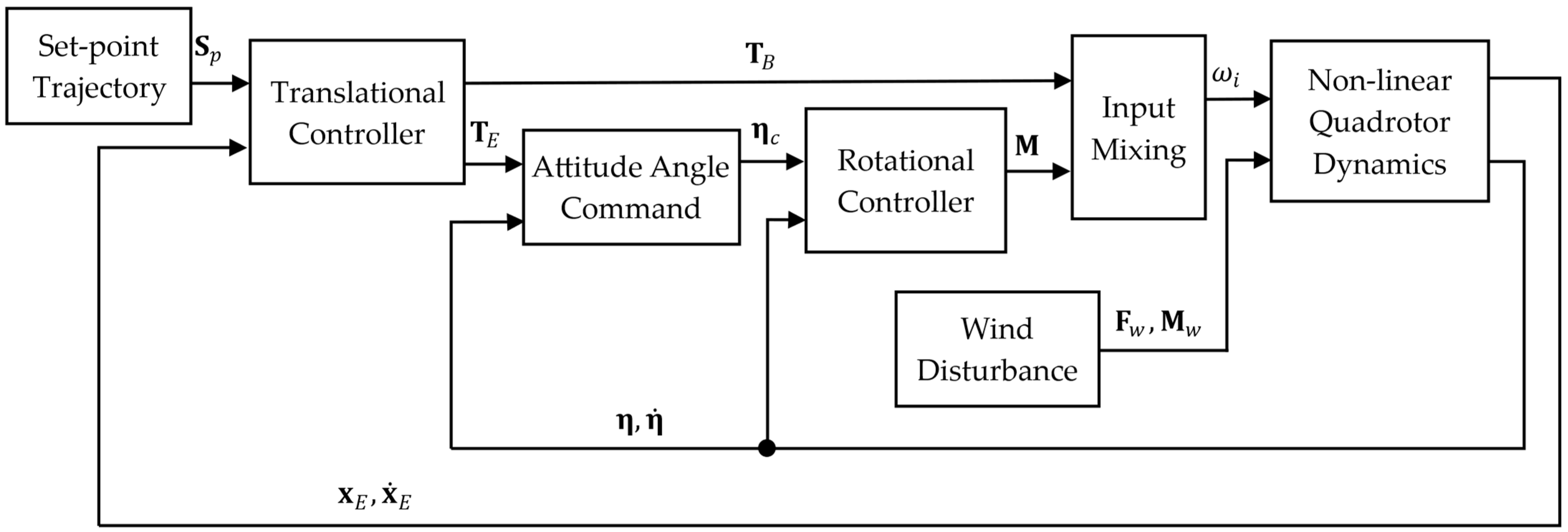
3. Controller Design
3.1. Dynamic Inversion Method
3.2. Model Predictive Control
3.3. Adaptive Super-Twisting Sliding Mode Disturbance Observer
| Algorithm 1. Proposed control method. |
| . |
| . |
| . |
| . |
| . |
| . using the Dynamic Inversion method |
| to the quadrotor. |
| 10: Proceed to the next step. |
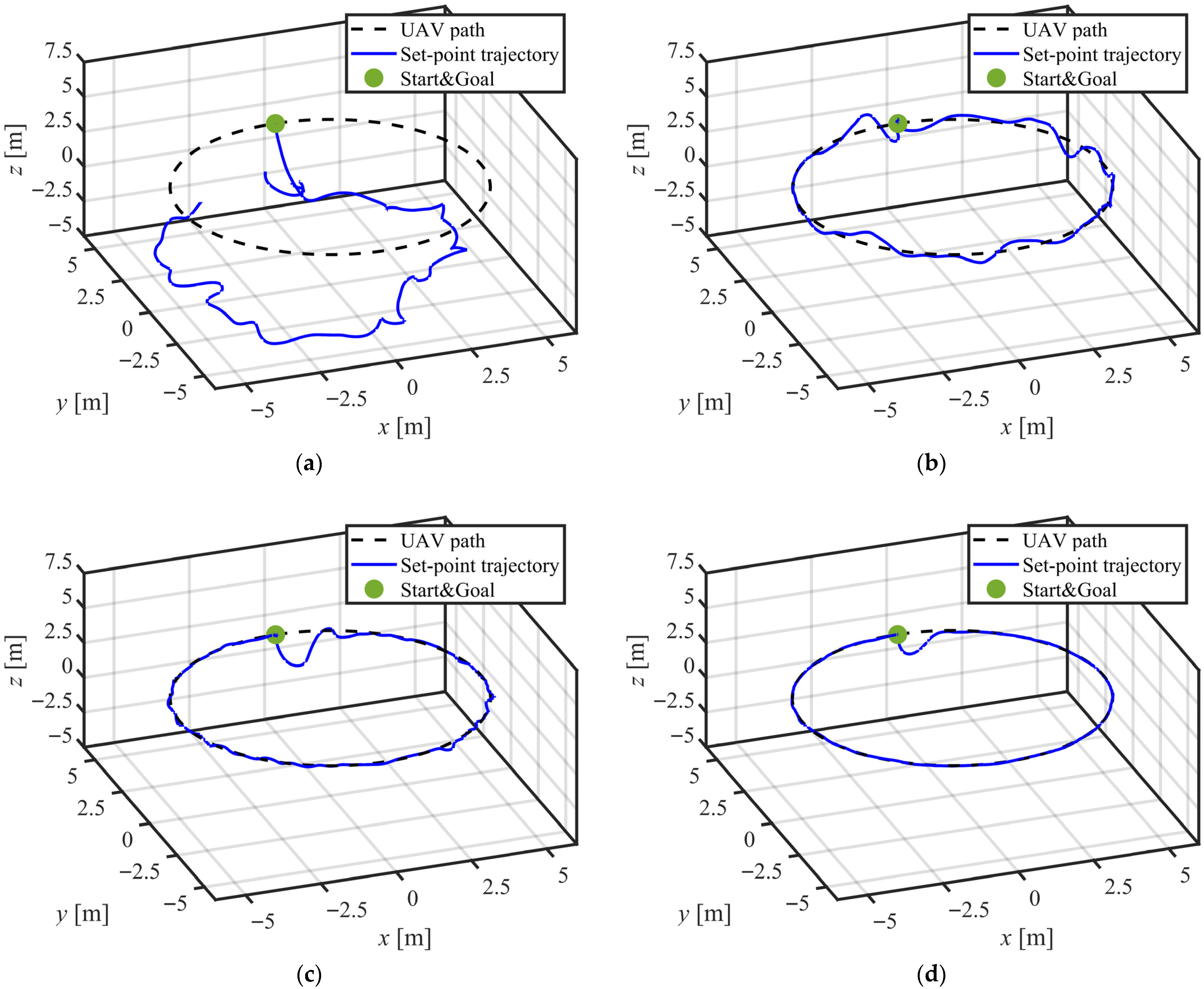
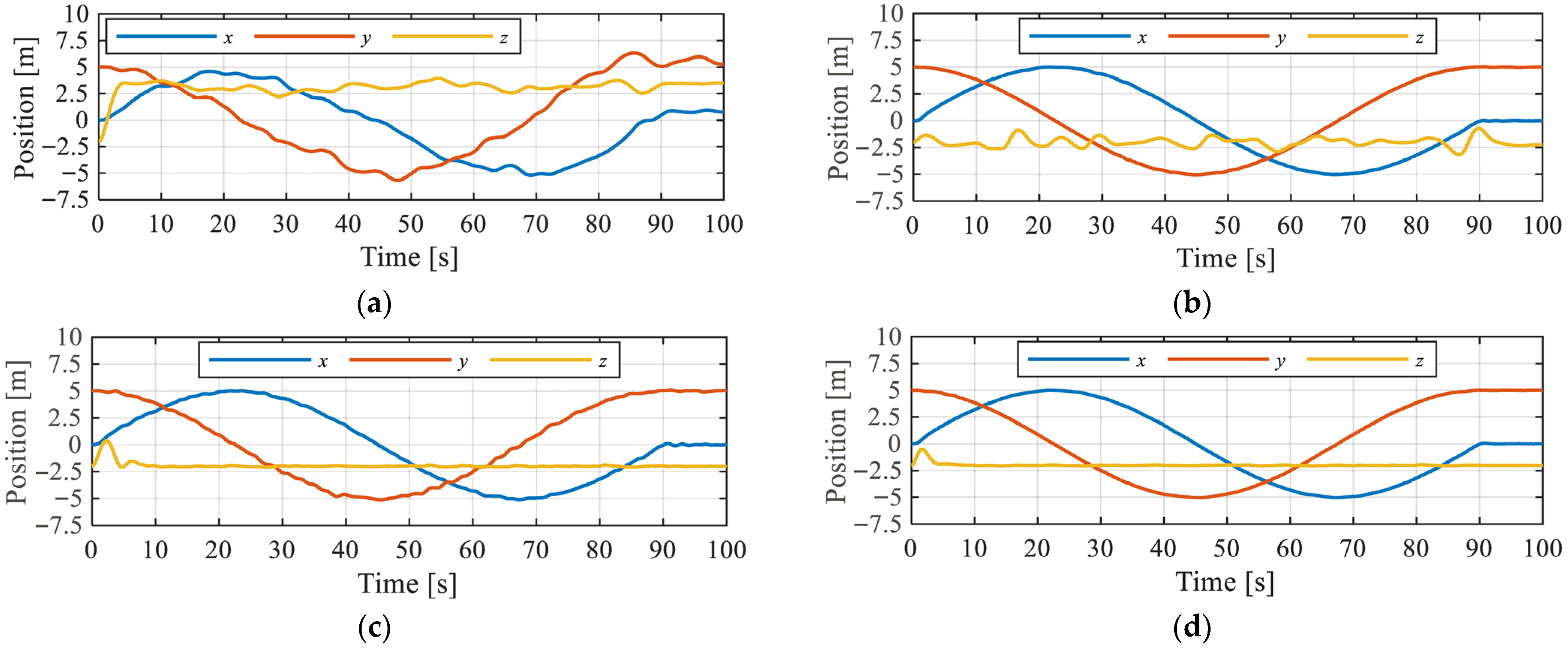
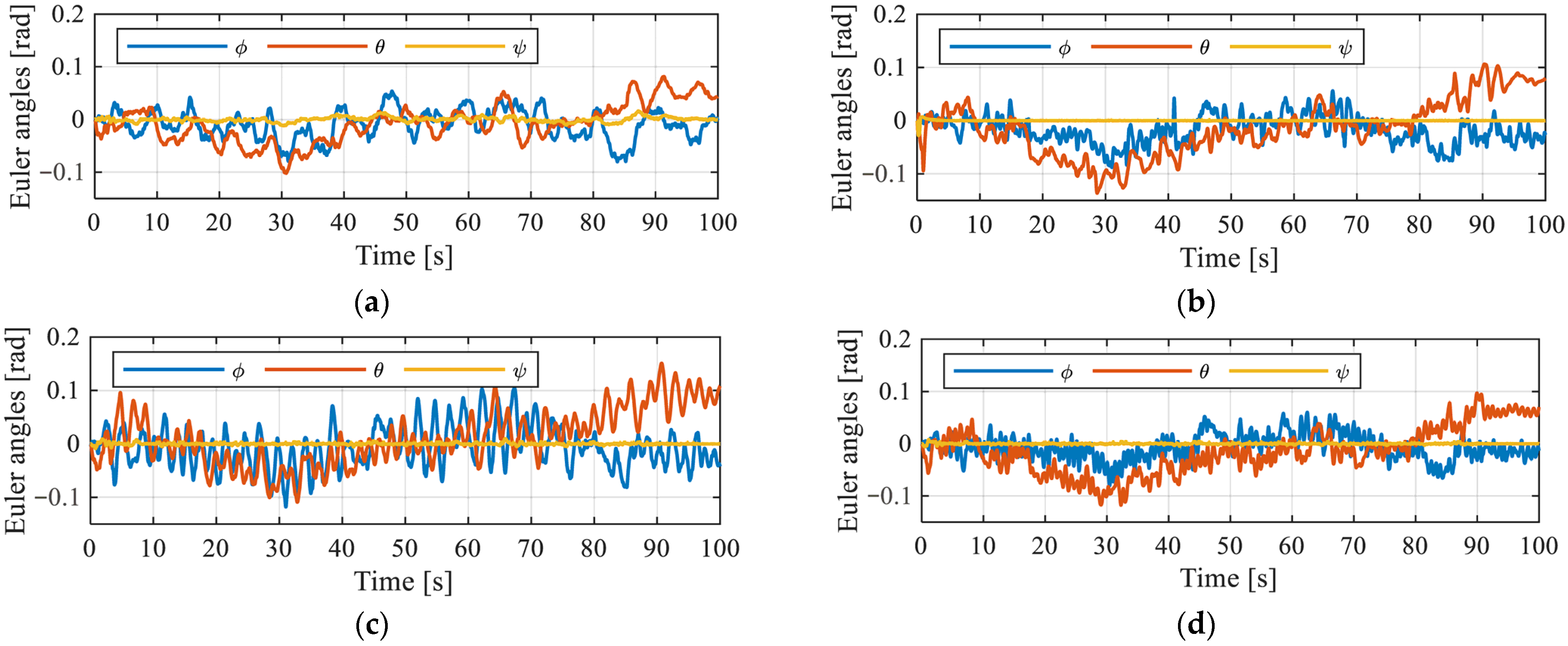
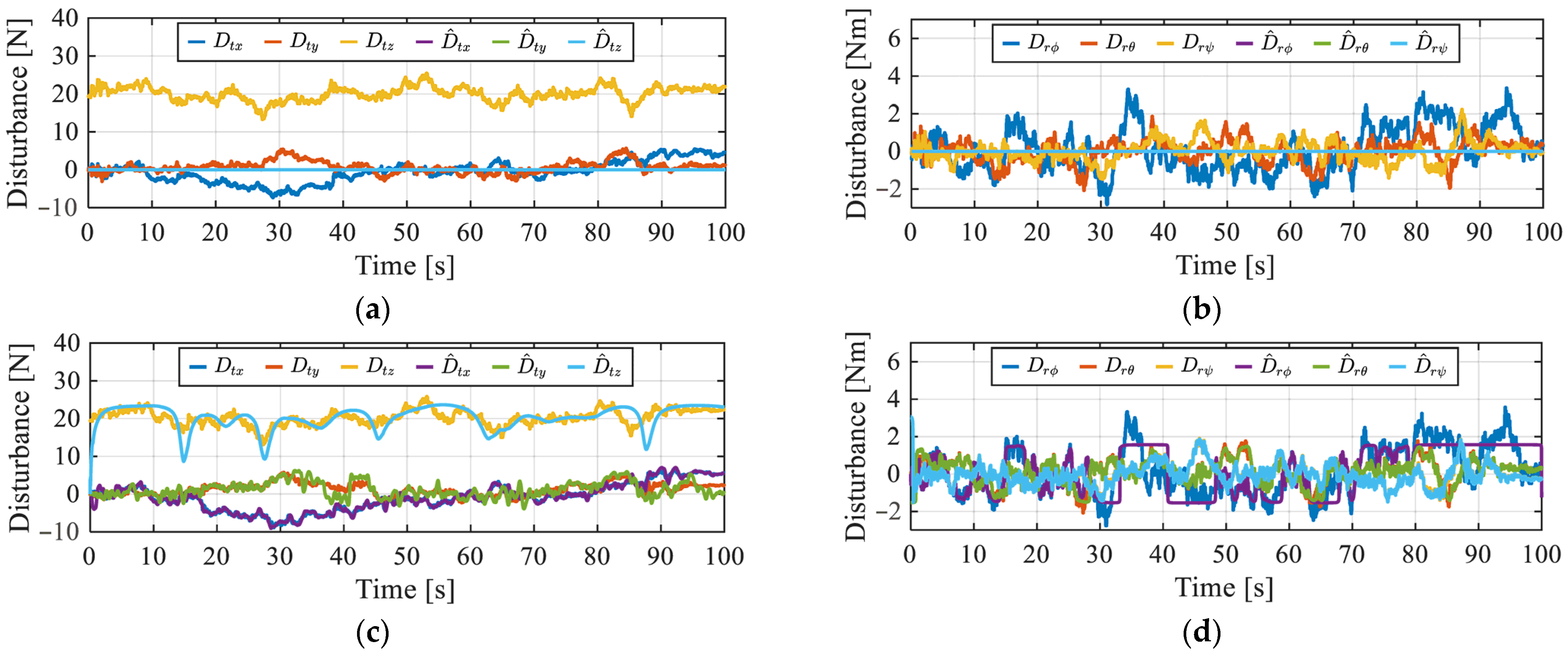
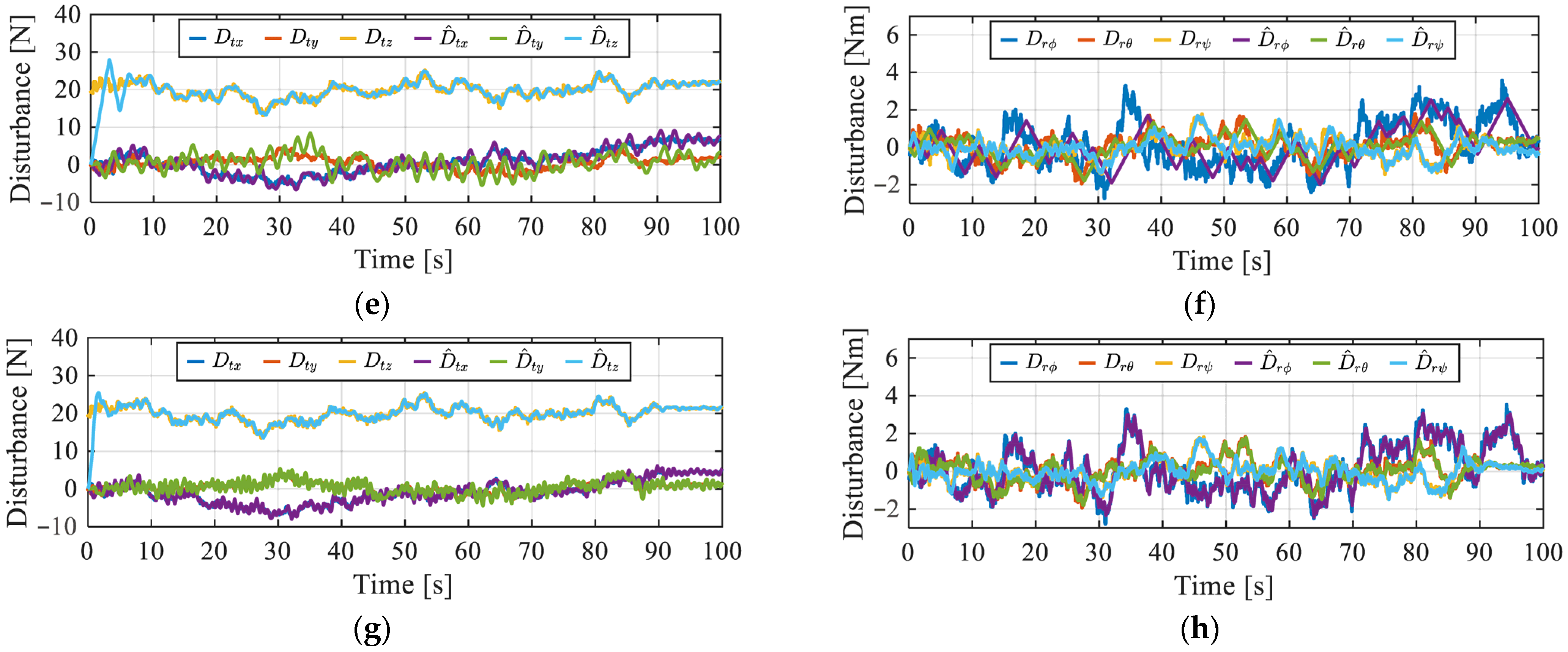
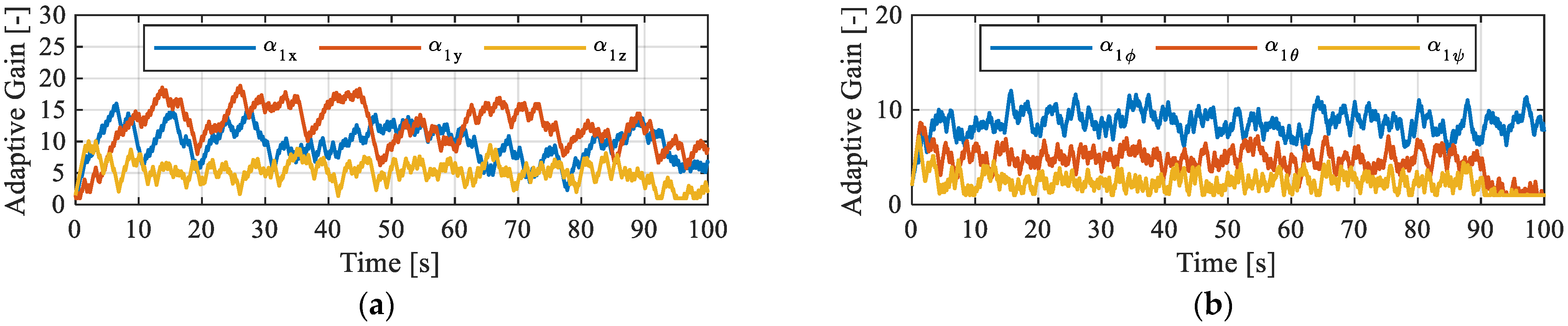
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shakhatreh, H.; Sawalmeh, A.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Elbasueny, B.; El-Sebah, M.I.A.; Shaaban, S. Dynamic Modelling and Control of Quadrotor’s Attitude around Its Hover Position. In Proceedings of the 2019 6th International Conference on Advanced Control Circuits and Systems (ACCS) & 2019 5th International Conference on New Paradigms in Electronics & Information Technology (PEIT), Hurgada, Egypt, 25–28 October 2019; pp. 247–252. [Google Scholar] [CrossRef]
- Qiu, X.; Liao, S.; Yang, D.; Li, Y.; Wang, S. Visual geo-localization and attitude estimation using satellite imagery and topographical elevation for unmanned aerial vehicles. Eng. Appl. Artif. Intell. 2025, 153, 110759. [Google Scholar] [CrossRef]
- Zhou, S.; He, Z.; Chen, X.; Chang, W. An Anomaly Detection Method for UAV Based on Wavelet Decomposition and Stacked Denoising Autoencoder. Aerospace 2024, 11, 393. [Google Scholar] [CrossRef]
- Bolandi, H.; Rezaei, M.; Mohsenipour, R.; Nemati, H.; Smailzadeh, S. Attitude Control of a Quadrotor with Optimized PID Controller. Intell. Control Autom. 2013, 4, 335–342. [Google Scholar] [CrossRef]
- Liu, C.; Pan, J.; Chang, Y. PID and LQR Trajectory Tracking Control for an Unmanned Quadrotor Helicopter: Experimental Studies. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 10845–10850. [Google Scholar] [CrossRef]
- Saibi, A.; Boushaki, R.; Belaidi, H. Backstepping Control of Drone. Eng. Proc. 2022, 14, 4. [Google Scholar] [CrossRef]
- Roy, R.; Islam, M.; Sadman, N.; Mahmud, M.A.P.; Gupta, K.D.; Ahsan, M.M. A Review on Comparative Remarks, Performance Evaluation and Improvement Strategies of Quadrotor Controllers. Technologies 2021, 9, 37. [Google Scholar] [CrossRef]
- Heng, X.; Cabecinhas, D.; Cunha, R.; Silvestre, C.; Qingsong, X. A Trajectory Tracking LQR Controller for a Quadrotor: Design and Experimental Evaluation. In Proceedings of the IEEE Region 10 Conference (TENCON 2015), Macao, China, 1–4 November 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M.; Buscarino, A. Optimal and Robust Control: Advanced Topics with MATLAB®; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Ganga, G.; Dharmana, M.M. MPC Controller for Trajectory Tracking Control of Quadcopter. In Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, Y. Model Predictive Control and PID for Path Following of an Unmanned Quadrotor Helicopter. In Proceedings of the 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 768–773. [Google Scholar] [CrossRef]
- Islam, M.; Idres, M.M. Dynamics and Control of Quadcopter Using Linear Model Predictive Control Approach. IOP Conf. Ser. Mater. Sci. Eng. 2017, 184, 012007. [Google Scholar] [CrossRef]
- Maciejowski, J.M. Predictive Control: With Constraints; Prentice Hall: London, UK, 2020. [Google Scholar]
- Campo, P.J.; Morari, M. Robust Model Predictive Control. In Proceedings of the 1987 American Control Conference (ACC), Minneapolis, MN, USA, 10–12 June 1987; pp. 1021–1026. [Google Scholar]
- Zhou, Z.; Wang, M.; Liang, T. H-Infinity Model Predictive Control of Discrete-Time Constrained Singular Piecewise-Affine Systems with Time Delay. In Proceedings of the 2014 Fourth International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 18–20 September 2014; pp. 447–461. [Google Scholar] [CrossRef]
- Thakur, M.B.; Schmid, M. Efficient Uncertainty Mitigation in Automated Vehicles: Combining MPC with Model Reference Adaptive Control. IFAC-PapersOnLine 2023, 56, 259–264. [Google Scholar] [CrossRef]
- Bhattacharjee, D.; Subbarao, K. Robust Control Strategy for Quadcopters Using Sliding Mode Control and Model Predictive Control. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. AIAA 2020–2071. [Google Scholar] [CrossRef]
- Incremona, G.P.; Ferrara, A.; Magni, L. MPC for Robot Manipulators with Integral Sliding Modes Generation. IEEE/ASME Trans. Mechatron. 2017, 22, 1299–1307. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Mode Control Design Principles and Applications to Electric Drives. IEEE Trans. Ind. Electron. 1993, 40, 23–36. [Google Scholar] [CrossRef]
- Levant, A. Sliding Order and Sliding Accuracy in Sliding Mode Control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Rajappa, S.; Masone, C.; Bülthoff, H.H.; Stegagno, P. Adaptive Super Twisting Controller for a Quadrotor UAV. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 2971–2977. [Google Scholar] [CrossRef]
- El Atwi, H.; Daher, N. A Composite Model Predictive and Super Twisting Sliding Mode Controller for Stable and Robust Trajectory Tracking of Autonomous Ground Vehicles. In Proceedings of the 2021 IEEE 3rd International Multidisciplinary Conference on Engineering Technology, Beirut, Lebanon, 2–3 December 2021; pp. 107–112. [Google Scholar] [CrossRef]
- Alazki, H.; Escobar, A.G.; Valenzuela, J.E.; Garcia, O. Embedded Super Twisting Control for the Attitude of a Quadrotor. IEEE Lat. Am. Trans. 2016, 14, 3974–3979. [Google Scholar] [CrossRef]
- Shtessel, Y.B.; Moreno, J.A.; Plestan, F.; Fridman, L.M.; Poznyak, A.S. Super-Twisting Adaptive Sliding Mode Control: A Lyapunov Design. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5109–5113. [Google Scholar] [CrossRef]
- Nurettin, A.; İnanç, N. High-Performance Induction Motor Speed Control Using a Robust Hybrid Controller with a Super twisting Sliding Mode Load Disturbance Observer. IEEE Trans. Ind. Electron. 2023, 70, 7743–7752. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-Observer-Based Complementary Sliding-Mode Speed Control for PMSM Drives: A Super-Twisting Sliding-Mode Observer-Based Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Anwar, J.; Malik, F.M.; Abdullah, M.; Abbas, A. High Gain and Super-Twisting Sliding Mode Observers for the Adaptive Control of Quadrotor UAV. In Proceedings of the 13th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 12–16 January 2016; pp. 145–153. [Google Scholar] [CrossRef]
- Yin, S.; Yang, H.; Kaynak, O. Sliding Mode Observer-Based FTC for Markovian Jump Systems with Actuator and Sensor Faults. IEEE Trans. Autom. Control 2017, 62, 3551–3558. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiao, J.; Guo, L. Adaptive Sliding Mode Disturbance Observer-Based Composite Control with Prescribed Performance of Space Manipulators for Target Capturing. IEEE Trans. Ind. Electron. 2019, 66, 1973–1983. [Google Scholar] [CrossRef]
- Guo, Z.; Xue, S.; Tan, J.; Li, H.; Yan, D.; Cao, H. Neural Observer-Based Fixed-Time Formation Control of Multiagent Systems. Neurocomputing 2025, 620, 129263. [Google Scholar] [CrossRef]
- Al-Hiddabi, S.A. Quadrotor Control Using Feedback Linearization with Dynamic Extension. In Proceedings of the 6th International Symposium on Mechatronics and Its Applications (ISMA), Sharjah, United Arab Emirates, 23–26 March 2009; pp. 1–3. [Google Scholar] [CrossRef]
- Hu, Q.; Fei, Q.; Wu, Q.; Geng, Q. Flight Control Design for UAV Using Hierarchical Dynamic Inversion. In Proceedings of the International Conference on Automatic Control and Artificial Intelligence, (ACAI 2012), Xiamen, China, 10–12 March 2012; pp. 1069–1072. [Google Scholar] [CrossRef]
- Komiyama, S.; Uchiyama, K.; Masuda, K. Robust Controller Design for Quadrotor Using Model Predictive Control and Adaptive Super Twisting Sliding Mode Control. In Proceedings of the 2024 10th International Conference on Control, Decision and Information Technologies (CoDIT), Valletta, Malta, 22–25 April 2024; pp. 1607–1612. [Google Scholar] [CrossRef]
- U.S. Department of Defense. Flying Qualities of Piloted Airplanes; U.S. Military Specification MIL-F-8785C; U.S. Department of Defense: Washington, DC, USA, 1980. [Google Scholar]


| Mass | ||
| Variation in mass | ||
| Rotor and axis distance | ||
| Inertia tensor | ||
| Air drag coefficient | ||
| Lift coefficient of rotor | ||
| Drag coefficient of rotor | ||
| Time constant |
| Translation | Rotation | ||
|---|---|---|---|
| Time constant | |||
| Predictive horizon | |||
| Control horizon | |||
| Window parameter | |||
| Weighting matrix | |||
| Weighting matrix | |||
| ASTSMO parameter | |||
| STSMO parameter | |||
| SMO parameter | |||
| ISE | IAE | |
|---|---|---|
| MPC+ASTSMO | 3.542 | 5.502 |
| MPC+STSMO | 10.98 | 11.88 |
| MPC+SMO | 17.77 | 33.03 |
| MPC | 2701 | 515.2 |
| MPC+ASTSMO | 1742 | 1708 | 1733 | 1730 | 6913 |
| MPC+STSMO | 1751 | 1700 | 1742 | 1724 | 6917 |
| MPC+SMO | 1784 | 1689 | 1762 | 1712 | 6947 |
| MPC | 1727 | 1723 | 1729 | 1746 | 6925 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komiyama, S.; Uchiyama, K.; Masuda, K. Combined Robust Control for Quadrotor UAV Using Model Predictive Control and Super-Twisting Algorithm. Drones 2025, 9, 576. https://doi.org/10.3390/drones9080576
Komiyama S, Uchiyama K, Masuda K. Combined Robust Control for Quadrotor UAV Using Model Predictive Control and Super-Twisting Algorithm. Drones. 2025; 9(8):576. https://doi.org/10.3390/drones9080576
Chicago/Turabian StyleKomiyama, Shunsuke, Kenji Uchiyama, and Kai Masuda. 2025. "Combined Robust Control for Quadrotor UAV Using Model Predictive Control and Super-Twisting Algorithm" Drones 9, no. 8: 576. https://doi.org/10.3390/drones9080576
APA StyleKomiyama, S., Uchiyama, K., & Masuda, K. (2025). Combined Robust Control for Quadrotor UAV Using Model Predictive Control and Super-Twisting Algorithm. Drones, 9(8), 576. https://doi.org/10.3390/drones9080576






