Network Design and Content Deployment Optimization for Cache-Enabled Multi-UAV Socially Aware Networks

Highlights

What are the main findings?

• Proposes a socially aware multi-UAV network where UAVs with “selfish/selfless” attributes dynamically control cooperation levels to reduce aggregate system delay for edge users while enhancing stability under UAV disconnections and resource allocation under uneven demand.
• Demonstrates that tuning social parameters $N_{\mathrm{s}}$ (selfishness level) and $N_{\mathrm{QoS}}$ (QoS strictness) directly balances fairness and efficiency of the socially aware network.

What is the implication of the main finding?

• Proposes a novel socially aware network architecture which enables seamless transition between ad hoc networks and traditional UAV networks, offering a more adaptable resource allocation solution for real-world deployments with heterogeneous user demands.
• Identifies a critical trade-off between content diversity and request probability, establishing an efficient method for transforming multi-objective optimization into single-objective optimization and facilitating deeper investigation of the proposed network.

Abstract

Unmanned aerial vehicles (UAVs) with high mobility and self-organization capabilities can establish highly connected networks to cache popular content for edge users, which improves network stability and significantly reduces access time. However, an uneven distribution of demand and storage capacity may reduce the utilization of the storage capacity of UAVs without a proper UAV coordination mechanism. This work proposes a multi-UAV-enabled caching socially aware network (SAN) where UAVs can switch roles by adjusting the social attributes, effectively enhancing data interaction within the UAVs. The proposed network breaks down communication barriers at the UAV layer and integrates the collective storage resources by incorporating social awareness mechanisms to mitigate these imbalances. Furthermore, we formulate a multi-objective optimization problem (MOOP) with the objectives of maximizing both the diversity of cached content and the total request probability (RP) of the network, while employing a multi-objective particle swarm optimization (MOPSO) algorithm with a mutation strategy to approximate the Pareto front. Finally, the impact of key parameters on the Pareto front is analyzed under various scenarios. Simulation results validate the benefits of leveraging social attributes for resource allocation and demonstrate the effectiveness and convergence of the proposed algorithm for the multi-UAV caching strategy.

1. Introduction

In recent years, the rapid development of mobile communication technology and the widespread adoption of smart mobile devices have led to explosive growth in data traffic [1]. To ensure the quality of communication services, future networks urgently need to meet performance demands such as ultra-low latency, ultra-high reliability, ultra-high density, and ultra-high security [2,3]. However, deploying more ground base stations (BSs) is not an ideal solution from a cost perspective. Therefore, caching is considered a technology with the potential to reduce transmission latency in cellular networks [4,5].

In caching networks, small BS caching architectures significantly reduce system latency and increase the number of serviceable users compared to conventional macro BS caching networks [6,7,8,9,10,11]. In [6], a proactive, cooperative caching strategy for a multi-cell network is proposed to meet the demand of the user, effectively reducing the latency of the network. In [7], the authors deploy micro BSs within the traditional BS network to expand its storage space, and utilize macro BSs to control the caching strategies of micro BSs, addressing user requests during different time periods. The work in [8] proposed a two-tier heterogeneous Internet of Things (IoTs) network which simultaneously operates with edge micro BSs and cache-enabled IoT devices to improve the cache hit rate. In [9], the authors consider a two-tier heterogeneous caching network, where the most popular content is cached in the macro BS, and the remaining content is cached randomly in the small BS. To address the randomness of user trajectories, a three-tier network consisting of Macro-BSs, micro-BSs, and pico-BSs is established to maximize the amount of cached content [10]. In [11], the authors focus on a cache-enabled heterogeneous network, where MUs can flexibly schedule their traffic between traditional sub-6 GHz macro cells and dense millimeter-wave small cells. Unfortunately, the fixed location of BSs has some drawbacks. Firstly, serving users with trajectory randomness by deploying more micro BSs will lead to severe resource wastage. Additionally, frequent user handovers between networks must also be considered.

Due to the flexible mobility, cache-enabled unmanned aerial vehicles (UAVs) can dynamically adjust their positions based on the caching needs of specific ground users and intelligently store content according to specific requests [12]. Some recent works focused on the applications of the cache-enabled UAVs [13,14,15,16,17]. The authors in [13] investigated a cache-enabled UAV emergency communication network, where the UAVs are regarded as aerial BSs to assist damaged cellular networks. In [14], an adjustable cache distribution model was developed to support caching in UAV networks. Moreover, the average service success probability of cache placement was studied to evaluate the performance of heterogeneous UAV networks [15]. The work in [16] proposed a layered caching scheme using scalable video coding for cache-enabled multi-UAV networks to balance video content quality and diversity. The aforementioned studies still regarded a single UAV and multiple users within the same jurisdiction as the benchmark unit. This paper refers to it as a traditional UAV caching network. When UAVs could not meet user requirements, they were connected to the BS via direct wireless links. Compared to the BS, nearby available UAVs can provide faster access services. The absence of UAV cooperation may lead to increased latency for uncached content. Therefore, a user-centric cooperation approach for cache-enabled UAV networks was proposed, where a user-centric UAV group is formed for each user to increase cache hit probability, thus reducing latency [17]. However, such a cooperation mechanism did not consider the interaction among UAVs. When the number of UAVs is small, collaborating with dynamically flying UAVs to serve one user might reduce the cache hit probability for others. As a result, it is impossible to guarantee the quality of service (QoS) for users in the jurisdiction of those UAVs. Additionally, a large UAV group could lead to resource dissipation, and uneven distribution of demand and storage capacity might further exacerbate this issue. In a multi-UAV network, considering collaboration to allocate resources reasonably to ensure resource utilization while guaranteeing the QoS for users in the jurisdiction needs to be addressed urgently.

Recently, integrating individual social attributes with device-to-device (D2D) communications has also shown significant application potential for collaboration mechanisms in terrestrial networks [18,19,20]. A network that combines social selfishness with D2D link quality optimization was proposed to enable effective collaboration [18]. However, D2D communication for user caching devices, such as a smartphone, often involves user privacy policies, posing certain risks to overall resource planning in the user layer. Fortunately, UAVs with social attributes are considered public resources. The cached content of UAV does not require the permission of the users in the jurisdiction and is not subject to the privacy agreement. Thus, they possess tremendous potential and should be studied in depth. To the best of our knowledge, developing a multi-UAV network that considers the interaction among UAVs to enhance resource utilization and introduces social attributes to guarantee QoS for users has yet to be investigated in prior research.

To tackle the aforementioned issue, this paper bridges this gap by proposing a cache-enabled multi-UAV socially aware network (SAN), which considers resource utilization and user QoS. In the network, UAVs prioritize connecting to nearby available UAVs to enhance interaction at the UAV layer. Meanwhile, UAVs possess social attributes that enable them to decide whether to assist other UAVs with task offloading. Specifically, UAVs reserve storage space of different sizes according to different social attributes. These storage spaces are integrated into a huge resource pool to optimize and allocate resources uniformly. Among them, “selfish” UAVs with less storage space can only provide less help to other UAVs, while “selfless” UAVs with more storage space can provide more help. The proposed network can be transitioned into an ad hoc network or a traditional cache-enabled UAV network by adjusting the proportion of assistant UAVs, which demonstrates the extremely strong universality of the proposed network. The key contributions of this work are as follows:

• Novel Socially Aware UAV Network Model: We propose a cache-enabled multi-UAV SAN, where UAVs possess inherent social attributes, providing a novel architecture for controlling cooperation and resource allocation.
• Comprehensive Multi-Objective Formulation: We formulate the caching deployment as a multi-objective optimization problem (MOOP) that captures the fundamental trade-off between the cached content diversity (a proxy for fairness) and the aggregation of the request probability (RP) (a proxy for efficiency).
• Advanced Algorithmic Solution: To address this MOOP, we transform it into a form that is easily solvable by the multi-objective particle swarm optimization (MOPSO) algorithm. The Pareto optimal solution set is approximated by establishing the MOPSO algorithm with a mutation strategy for the proposed MOOP.
• In-depth simulation Evaluation: The simulation demonstrates the substantial advantages of social attributes on the caching resource allocation when demand and storage capacity are not evenly distributed. The gain of constraints imposed by social attributes can promote the diversity of cached content. Furthermore, two approaches—the establishment of a constructor and the adjustment of constraints—are thoroughly examined to balance the objective functions.

The remainder of this paper is organized as follows. Section 2 details the system model of the proposed cache-enabled multi-UAV SAN framework. Section 3 presents the MOPSO with a mutation strategy-based proposed MOOP. Section 4 provides and discusses the simulation results. Finally, Section 5 concludes the paper.

2. System Model

2.1. Cache-Enabled UAV Model

As illustrated in Figure 1, we consider a cache-enabled multi-UAV SAN serving multiple users, where each UAV serves a group of ground users. The number of the UAVs is denoted by M. The number of users served by UAV m is $K_m$, with the set defined as ${\mathcal{K}}_m=\left\{1,2,\dots ,K_m\right\}$. Different from the traditional cache-enabled UAV model, the target UAV is linked to available UAVs nearby prior to the BS when it is unable to fulfill user requests in the proposed network. Each UAV possesses either a “selfish” or “selfless” attribute. The role of each UAV depends on whether the storage resources of the target UAV are sufficient. “Selfish” UAVs must prioritize their own needs, resulting in limited available space. Therefore, it can only provide a small amount of resources to other UAVs. In contrast, “selfless” UAVs prioritize the needs of other UAVs, enabling them to provide more resources. A network comprised entirely of “selfish” UAVs degenerates into the traditional cache-enabled UAV network. Conversely, the network with all “selfless” UAVs is transformed into an ad hoc network. To better discuss the impact of the social attributes of UAVs on networks, this paper assumes that multiple UAVs are flying in a relatively small area, within which they remain within communication range of each other.

All content requests can only be predicted in probabilistic terms [13], and generated through the recommendation algorithm that integrates user preferences [21]. Assuming that the number of content requests of all users connected to UAV m is $N_m$, and its set is represented as ${\mathcal{N}}_m=\left\{1,2,\dots ,N_m\right\}$. The total number of the predicted content is N; its set is $\mathcal{N}=\left\{1,2,\dots ,N\right\}$. To simplify the design and facilitate understanding, suppose ${\displaystyle \bigcup _{m=1}^{m=M}}{\mathcal{N}}_m=\mathcal{N}$, ${\displaystyle \bigcap _{m=1}^{m=M}}{\mathcal{N}}_m=Ø$. For all users connected to UAVs, content requests follow Zipf’s law [13]. Thus, the request probability $a_m^j$ and the normalized request probability ${\widehat{a}}_m^j$ of the content j for the UAV m are expressed as

$$a_m^j={\displaystyle \frac{1/\phantom{1j^{\kappa }}{j}^{\kappa }}{{\sum }_{j=1}^{N_m}1/\phantom{1j^{\kappa }}{j}^{\kappa }}},j\in {\mathcal{N}}_m,\forall m,$$

(1)

$${\widehat{a}}_m^n={\displaystyle \frac{a_m^{j^{\prime }}}{{\displaystyle \sum _{m=1}^M}{\displaystyle \sum _{j=1}^{N_m}}{a}_m^j}}={\displaystyle \frac{a_m^{j^{\prime }}}{M}},\forall m,$$

(2)

The request matrix ${\mathbf{r}}_m^{\mathrm{UAV}}=\left(r_{m,1}^{\mathrm{UAV}},r_{m,2}^{\mathrm{UAV}},\dots ,r_{m,N}^{\mathrm{UAV}}\right)\in {\mathbb{Z}}^{1\times N}$ of the UAV m is expressed as

$$r_{m,n}^{\mathrm{UAV}}=\left\{\begin{array}{c}1,{\widehat{a}}_m^n>0,\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

where content $j^{\prime }$ of the set ${\mathcal{N}}_m$ is content n in the set $\mathcal{N}$.

In practice, the size of cached content is different. Therefore, it is necessary to establish a baseline content size. This can be achieved by dividing each cached content into several baseline segments with the same size for storage. In fact, the current data transmission is also conducted by segmenting the content into multiple data packets. Therefore, we assume that the size of each content item is the same. Because of the limited storage capacity of UAVs, the storage capacity can be converted into the quantity of the stored contents, that is $L_m^{\mathrm{UAV}}$. Define a caching policy ${\mathbf{e}}_m=\left\{e_m^1,e_m^2,\dots ,e_m^N\right\}\in {\mathbb{Z}}^{1\times N}$, where $e_m^n=1$ means that the UAV m will cache the content n. Therefore, the constraints on the local caching capacity of UAV m can be obtained

$$\sum _{n=1}^N{e}_m^n⩽L_m^{\mathrm{UAV}},\forall m.$$

(4)

Table 1. Explanation of symbols in the system model.

Symbol	Meaning
$M,K,K_m$	The number of UAVs, users, and users served by the m-th UAV
$L_m^{\mathrm{UAV}}$	The storage capacity limit of UAV m
${\widehat{a}}_m^j$,	The RP of the content j for the UAV m
${\mathbf{r}}_m^{\mathrm{UAV}}$	The demand matrices of UAV m
${\mathbf{e}}_m$	The caching strategy of UAV m
$N_s$	Local content affinity of UAV
${\mathbf{s}}^{\mathrm{UAV}}$	The social awareness coefficient matrices of UAV
${\mathbf{c}}^{\mathrm{UAV}}$	The connectivity matrices of UAV-UAV
$N_{QoS}$	Quality of Service coefficient
V	The diversity of the content
I	The total RP of the system

summarizes the key symbols and their meanings as used in the system model. It defines the notation for the main components, including UAVs, users, and their associated parameters like storage capacity and demand matrices. The table also explains important coefficients that govern network behavior, such as local affinity and QoS.

2.2. Socially Aware Model

The matching quantity of local cached contents and local requests is introduced, reflecting the degree of satisfaction of user requests. The constraint is as

$${\mathbf{r}}_m^{\mathrm{UAV}}·{\mathbf{e}}_m⩾\min \left(\sum _{n=1}^N{N}_s{r}_{m,n}^{\mathrm{UAV}},L_m^{\mathrm{UAV}}\right),\forall m,$$

(5)

where ${\mathbf{r}}_m^{\mathrm{UAV}}·{\mathbf{e}}_m$ represents the dot product of two matrices. When $N_s=1$, it means that the UAV must prioritize ensuring its users requests, embodying a “selfish” attribute; when $N_s\to 0$, it implies that the UAV can allocate more and more resources to assist other UAVs, having a “selfless” attribute. In practice, when UAVs have a small amount of requested content or a lot of idle storage space, they can be converted into “selfless” UAVs. In different time periods, “selfless” UAVs and “selfish” UAVs can be transformed into each other according to their own idle space. This makes the network extremely risk-resistant. In the SAN, the socially aware coefficient is a pivotal metric to determine whether the data can be exchanged among individuals. According to [19], the socially aware coefficient $s_{m,m^{\prime }}^{\mathrm{UAV}}$ and connectivity variable $c_{m,m^{\prime }}^{\mathrm{UAV}}$ between UAV m and UAV $m^{\prime }$ are defined as

$${\mu }_{m,m^{\prime }}^n=\left\{\begin{array}{c}0,e_m^n=e_{m^{\prime }}^n=0,\hfill \\ 1,\mathrm{otherwise}.\hfill \end{array}\right.$$

(6)

$$s_{m,m^{\prime }}^{\mathrm{UAV}}\stackrel{\Delta }{=}\sum _{n=1}^N{r}_{m,n}^{\mathrm{UAV}}{\mu }_{m,m^{\prime }}^n,$$

(7)

$$c_{m,m^{\prime }}^{\mathrm{UAV}}=\left\{\begin{array}{c}1\left(s_{m,m^{\prime }}^{\mathrm{UAV}}⩾\overline{s}\mathrm{or}{s}_{m^{\prime },m}^{\mathrm{UAV}}⩾\overline{s}\right)\mathrm{and}m\ne m^{\prime },\hfill \\ 0\mathrm{otherwise}.\hfill \end{array}\right.$$

(8)

The threshold $\overline{s}$ can control the strict degree of connectivity among UAVs. In this paper, $\overline{s}={\mathbf{r}}_m^{\mathrm{UAV}}·{\mathbf{e}}_m+1$. Define $c_{m,m^{\prime }}^{\mathrm{UAV}}=c_{m^{\prime },m}^{\mathrm{UAV}}$. Such loose conditions foster the generation of large-scale connectivity. According to (8), the constraints on fulfilling the QoS of the user are delineated as

$$p_m^n=\left\{\begin{array}{c}1,\mathrm{if}{e}_m^n+{\displaystyle \sum _{m^{\prime }=1,m^{\prime }\ne m}^M}{c}_{m,m^{\prime }}^{\mathrm{UAV}}{e}_{m^{\prime }}^n>0\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.,\forall m,n,$$

(9)

$$\sum _{m=1}^M\sum _{n=1}^N{p}_m^n{r}_{m,n}^{\mathrm{UAV}}⩾\min \left(\sum _{m=1}^M\sum _{n=1}^N{N}_{QoS}{r}_{m,n}^{\mathrm{UAV}},\sum _{m=1}^M{L}_m^{\mathrm{UAV}}\right).$$

(10)

where $N_{QoS}$ represents the proportion of fulfillment of all system requests.

2.3. Problem Statement

Let $v_n$ denote the caching policy for content n, such as (11). Consequently, the objective function $f_1:V={\sum }_{n=1}^N{v}_n$ represents the total amount of distinct contents within the network, where

$$v_n=\left\{\begin{array}{c}1,{\displaystyle \sum _{m=1}^M}{e}_m^n⩾1,\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(11)

Maximizing $f_1$ guarantees the requests of more users. When $f_1\to N$, the diversity of the cache content is maximized, and all requests can be met in the cache network. Simultaneously, maximizing the overall RP of the network (the quantity of contents with the highest RP) is an inevitable outcome of the evolution driven by interests. Imagine a caching network where UAVs are independent of each other and will only evolve in the direction of maximizing profits. Suppose two UAVs with the same requests $\left\{a_1,a_2\right\}$ can only cache one file; will they cache both $a_1$ to maximize their benefits or will they cache $a_1$ and $a_2$, respectively? However, the latter can benefit more from the collaborative mechanism. An intuitive example of the above situation is the prisoner’s dilemma game. The two UAVs stand for two prisoners, each making the seemingly optimal choice from their own perspective. However, this approach fails to achieve the maximum overall gain. Paradoxically, when the two prisoners cooperate by making decisions that appear suboptimal for their individual interests, they collectively maximize the total gain. Therefore, the objective function $f_2$ is expressed as

$$f_2:I=\sum _{m=1}^M\sum _{n=1}^N{\widehat{a}}_m^n\left(e_m^n+\sum _{m^{\prime }=1,m^{\prime }\ne m}^M{c}_{m,m^{\prime }}^{\mathrm{UAV}}{e}_{m^{\prime }}^n\right)$$

(12)

It is worth noting that $f_1$ and $f_2$ can be regarded as the cost function and benefit function of the network, respectively. $f_1$ and $f_2$ are mutually conflicting objectives. Increasing content diversity will inevitably crowd out cache space for high-RP content, thereby reducing the overall system gain. Assuming that the RPs of users are known, this paper aims to maximize simultaneously $f_1$ and $f_2$ by optimizing the multi-UAV caching strategy $\mathbf{e}$. The MOOP is as follows:

$$\begin{array}{cc}\hfill & \mathrm{P}1:\underset{\mathbf{e}}{max}\left(f_1:V,f_2:I\right)\hfill \end{array}$$

(13a)

$$\begin{array}{c}\hfill s.t.e_m^n\in \left\{0,1\right\},\forall m,n,\end{array}$$

(13b)

$$\begin{array}{cc}\hfill & \sum _{i=1}^n{e}_m^n⩽L_m^{\mathrm{UAV}},\forall m,\hfill \end{array}$$

(13c)

$$\begin{array}{cc}\hfill & {\mathbf{r}}_m^{\mathrm{UAV}}·{\mathbf{e}}_m⩾\min \left(\sum _{n=1}^N{N}_s{r}_{m,n}^{\mathrm{UAV}},L_m^{\mathrm{UAV}}\right),\forall m,\hfill \end{array}$$

(13d)

$$\begin{array}{cc}\hfill & \sum _{m=1}^M\sum _{n=1}^N{p}_m^n{r}_{m,n}^{\mathrm{UAV}}⩾\min \left(\sum _{m=1}^M\sum _{n=1}^N{N}_{QoS}{r}_{m,n}^{\mathrm{UAV}},\sum _{m=1}^M{L}_m^{\mathrm{UAV}}\right).\hfill \end{array}$$

(13e)

where (13b) specifies the binary nature of the variables. (13c) indicates that the number of cached items for each UAV cannot exceed its capacity limit. (13d) requires that the cached content on each UAV must satisfy a certain proportion of local demand. (13e) mandates that the total cached content in the system must meet the QoS minimum threshold. This problem enables multiple UAVs to identify the equilibrium point between content diversity and overall system gain under multiple constraints, delivering the optimal UAV deployment as a trade-off solution.

3. Solution Approach

In this section, the caching strategy optimization for multi-UAV SAN is examined. It is intrinsically tough because P1 is a discrete MOOP and an NP-hard problem [19]. Thus, we re-encode the variables and transform P1 into a solvable form that applies to the MOPSO algorithm. A MOPSO algorithm with a mutation strategy based on the Pareto model is proposed to solve P1.

3.1. Problem Transformation

The objective functions and the bivariate variables $\mathbf{e}$ are discrete, which results in the non-convexity of P1. To adapt to the MOPSO algorithm, the variables $\mathbf{e}$ are transformed into the variables ${\mathbf{e}}^{\mathrm{index}}$, which are a set of ${\mathbf{e}}_m^{\mathrm{index}}$. ${\mathbf{e}}_m^{\mathrm{index}}$ represent the index set of cached contents in UAV m, and their sizes are no greater than $L_m^{\mathrm{UAV}}$, assuming that UAV m caches the 1st, 3rd, 5th, and 7th content items in $\mathcal{N}$, ${\mathbf{e}}_m^{\mathrm{index}}=\left\{1,3,5,7\right\}$.

Theorem 1.

In P1, the constraint (13c) is a sufficient condition for the constraint $u\left({\mathbf{e}}_m^{\mathrm{index}}\right)=L_m^{\mathrm{UAV}},\forall m$. Here, $u\left(\mathbf{e}\right)$ denotes the quantity of elements for vector $\mathbf{e}$.

Proof. 

We assume that $u\left({\mathbf{e}}_m^{\mathrm{index}}\right)<L_m^{\mathrm{UAV}}$. Because $V\left(\mathbf{x}\right)$ and $I\left(\mathbf{x}\right)$ are incremented within $\mathbf{x}\in {\mathbf{e}}_m^{\mathrm{index}}$. Then an uncached content $n^{\prime }$ always exists that makes $V\left({\mathbf{e}}_m^{\mathrm{index}}\right)⩽V\left({\mathbf{e}}_m^{\mathrm{index}}\cup \left\{n^{\prime }\right\}\right)$ and $I\left({\mathbf{e}}_m^{\mathrm{index}}\right)⩽I\left({\mathbf{e}}_m^{\mathrm{index}}\cup \left\{n^{\prime }\right\}\right)$. So the solution set ${\mathbf{e}}_m^{\mathrm{index}}\cup \left\{n^{\prime }\right\}$ is not inferior to ${\mathbf{e}}_m^{\mathrm{index}}$, let ${\mathbf{e}}_m^{\mathrm{index}}\leftarrow {\mathbf{e}}_m^{\mathrm{index}}\cup \left\{n^{\prime }\right\}$ up to $u\left({\mathbf{e}}_m^{\mathrm{index}}\right)=L_m^{\mathrm{UAV}}$.    □

Theorem 1 states that UAV m can always fetch $L_m^{\mathrm{UAV}}$ contents, which means that UAV m has $C_N^{L_m^{\mathrm{UAV}}}$ schemes, so we define the mapping $\Theta :{\mathbf{e}}_m^{index}\to z$,

$$\Theta \left({\mathbf{e}}_m^{\mathrm{index}}\right)\triangleq z_m^{\mathrm{UAV}},z_m^{\mathrm{UAV}}\in {\mathcal{N}}_m^{\mathrm{UAV}}=\left\{1,2,\dots ,C_N^{L_m^{\mathrm{UAV}}}\right\},\forall m.$$

(14)

Table 2. New notation description of Section 3.

Notation	Description
${\mathbf{e}}_m^{\mathrm{index}}$	The index set of cached contents in UAV m
$u\left(\mathbf{e}\right)$	The quantity of elements for vector $\mathbf{e}$
$c_m$	Local demand constraint for UAV m
d	QoS guarantee constraint for the system
g	The penalty function

summarizes the key symbols and their meanings as used in Section 3. The MOOP P1 can be rewritten as follows:

$$\begin{array}{cc}\hfill & \mathrm{P}2:\underset{{\mathbf{e}}^{\mathrm{index}}}{max}\left(f_1:V,f_2:I\right)\hfill \end{array}$$

(15a)

$$\begin{array}{c}\hfill s.t.\Theta \left({\mathbf{e}}_m^{\mathrm{index}}\right)\in \left\{1,2,\dots ,C_N^{L_m^{\mathrm{UAV}}}\right\},\forall m,\end{array}$$

(15b)

$$\begin{array}{cc}\hfill & u\left({\mathbf{e}}_m^{\mathrm{index}}\right)=L_m^{\mathrm{UAV}},\forall m,\hfill \end{array}$$

(15c)

$$\begin{array}{cc}\hfill & u\left({\mathcal{N}}_m\bigcap {\mathbf{e}}_m^{\mathrm{index}}\right)⩾c_m,\forall m,\hfill \end{array}$$

(15d)

$$\begin{array}{cc}\hfill & u\left(\left({\bigcup }_{m=1}^M{\mathbf{e}}_m^{\mathrm{index}}\right)\bigcap \mathcal{N}\right)⩾d,\hfill \end{array}$$

(15e)

where $d=\min \left(N_{QoS}u\left(\mathcal{N}\right)\right.$$\left.,{\sum }_{m=1}^M{L}_m^{\mathrm{UAV}}\right)$ and $c_m=\min \left(L_m^{\mathrm{UAV}}\right.$$,N_s·u\left.\left({\mathcal{N}}_m\right)\right)$ in (15e) and (15d), respectively. (15b) specifies that each UAV selects one caching strategy from $C_N^{L_m^{\mathrm{UAV}}}$ alternative strategies. (15c) mandates that the number of cached items per UAV is strictly equal to its capacity limit. (15d) requires that the intersection between cached content and local demand on each UAV must exceed a threshold ratio. (15e) ensures that the intersection between cached content and the total demand of the system satisfies the QoS requirement.

3.2. MOPSO Algorithm with Mutation Strategy

The MOPSO algorithm with a mutation strategy exhibits capabilities in rapid convergence and global optimization. The critical steps of the algorithm are illustrated, including mutation strategy, density estimation, and setting of step size and direction. The detailed process is shown in Algorithm 1.

Algorithm 1: A MOPSO Algorithm with Mutation Strategy for Multi-UAV Caching Strategy.

Phase 1: Initialization   1. Set population size $N_{\mathrm{p}}$, max iterations $l_{\max }$, learning factors ${\beta }_1,{\beta }_2$, inertia weight bounds ${\omega }_{\max },{\omega }_{\min }$, and mutation coefficient ${\rho }_{\mathrm{mu}}$. Initialize positions ${\mathbf{z}}^0$, velocities ${\mathbf{Y}}^0$ and the external archive ${\mathcal{A}}^0$. Phase 2: Iterative Optimization   2. Set iteration counter $l\leftarrow 0$.   3. repeat   4.     for each particle $i=1,\dots ,N_{\mathrm{p}}$ do   5.       Update velocity ${\mathbf{Y}}_i^{l+1}$ based on its inertia, cognitive component (distance to ${\mathbf{zbest}}_i^l$), and social component (distance to ${\mathbf{gbest}}^l$) via (18).   6.       Update position ${\mathbf{znew}}_i^{l+1}$ by applying the new velocity to the old position via (21).   7.     end $O\left(N_{\mathrm{p}}M\right)$   8.     Apply mutation strategy to ${\mathbf{znew}}^{l+1}$ to generate ${\mathbf{zmu}}^{l+1}$ for population diversity, then select the next generation population ${\mathbf{z}}^{l+1}$. $O\left(N_{\mathrm{p}}\right)$   9.     Evaluate the new population ${\mathbf{z}}^{l+1}$ by calculating fitness and penalty values. $O\left((N_m^{\mathrm{req}}+L)L{N}_{\mathrm{p}}{M}^2\right)$ 10.     Update the historical best ${\mathbf{zbest}}^{l+1}$ for each particle by comparing its new solution with its previous best. $O({(N_{\mathrm{p}})}^2)$ 11.     Update the external archive ${\mathcal{A}}^{l+1}$: combine ${\mathcal{A}}^l$ with the current population ${\mathbf{z}}^{l+1}$, remove all dominated solutions, and if necessary, use density estimation to prune the archive to its maximum size. Then, select a new ${\mathbf{gbest}}^{l+1}$ from ${\mathcal{A}}^{l+1}$. $O({(N_{\mathrm{p}})}^2)$ 12.     $l\leftarrow l+1$. 13. until $l\ge l_{\max }$ or the stopping criterion (e.g., convergence) is met. Phase 3: Output

14. return The final set of non-dominated solutions stored in the archive ${\mathcal{A}}^l$.

Calculation of penalty function: The penalty function $g=g_1+g_2$ guides the population for the constraints in P2. During the execution of the algorithm, the precedence of the penalty function value supersedes that of the fitness function.

$$g_1={\sum }_{m=1}^M\max \left(0,c_m-u\left({\mathcal{N}}_m\bigcap {\mathbf{e}}_m^{\mathrm{index}}\right)\right),$$

(16)

$$g_2=\max \left(0,d-u\left(\left({\bigcup }_{m=1}^M{\mathbf{e}}_m^{\mathrm{index}}\right)\bigcap \mathcal{N}\right)\right).$$

(17)

Density estimation: In the process of identifying optimal solutions $\mathbf{gbes}{\mathbf{t}}^l$ within a population, the random selection process may inadvertently lead to individuals who have identical fitness function values predominantly occupying the elite population. Consequently, despite these individuals having a high frequency of occurrence, they may not contribute to the diversity required for effective evolutionary progress. To augment the population diversity, density estimation is employed to select the individuals with the least frequency of fitness function values in the elite population. Thus, the population can constantly explore minorities, thereby avoiding falling into the local optimal solution.

Setting of step size and direction: The selection of step size and direction profoundly affects the convergence speed of the MOPSO algorithm. If the step size is excessively large, it becomes too easy to surpass the optimal solution and results in a solution explosion. Conversely, it will lead to a slow convergence rate and increase the likelihood of falling into the local optimal solution. The velocity $\mathbf{Y}$ and position $\mathbf{z}$ of the particles are updated as

$$Y_m^{l+1}:={\omega }^l{Y}_m^l+{\beta }_1{\lambda }_1^l\left(zbes{t}_m^l-z_m^l\right)+{\beta }_2{\lambda }_2^l\left(gbes{t}_m^l-z_m^l\right),$$

(18)

$${\chi }^l={\sum }_{m=1}^M\left|gbes{t}_m^l-z_m^l\right|/\phantom{{\sum }_{m=1}^M\left|gbes{t}_m^l-z_m^l\right|\left(M\left(C_N^{L_m^{\mathrm{UAV}}}-1\right)\right)}\left(M\left(C_N^{L_m^{\mathrm{UAV}}}-1\right)\right),$$

(19)

$${\omega }^l={\omega }_{\max }-\left({\omega }_{\max }-{\omega }_{\min }\right)·{\left({\chi }^l-1\right)}^2,$$

(20)

$$z_m^{l+1}=\left(z_m^l+Y_m^{l+1}+C_N^{L_m^{\mathrm{UAV}}}\right)mod{C}_N^{L_m^{\mathrm{UAV}}},$$

(21)

where mod denotes the modular operator. The notation description is detailed in

Table 3. Notation description of the MOPSO algorithm.

Notation	Description (The mth Dimension in the lth Iteration)
$Y_m^l$,$z_m^l$,${\omega }^l$	Velocity, position, and inertia weight of particles
${\beta }_1$,${\beta }_2$	Individual learning factors, social learning factors
${\lambda }_1^l$,${\lambda }_2^l$	Random numbers with normal distribution
$zbes{t}_m^l$	Historical optimal solution
$gbes{t}_m^l$	Population optimal solution
${\omega }_{\max }$, ${\omega }_{\min }$	Maximum inertia weight, minimum inertia weight
${\rho }_{\mathrm{mu}}$	Coefficient of mutation
$N_{\mathrm{p}}$	Population size
$l_{\max }$	Max iterations

. Equation (21) illustrates that when the step size exceeds the boundaries of the feasible domain, it is recalibrated through the remainder operation. This mechanism is also a means to prevent the solution from exploding.

Mutation strategy: A mutation strategy is employed to enhance the diversity within the population. During the mutation process, the mutation probability $p_{\mathrm{mu}}$ is calculated by the mutation coefficient ${\rho }_{\mathrm{mu}}$,

$$p_{\mathrm{mu}}=1-{\displaystyle \frac{\left(l-1\right)}{{\left(l_{\max }-1\right)}^{1/\phantom{1{\rho }_{\mathrm{mu}}}{\rho }_{\mathrm{mu}}}}}.$$

(22)

This calculation yields the upper and lower bounds of the mutation range. In the mutation process, the mutation operation randomly selects one dimension of a particle and randomly generates a new value for it within the predefined mutation range, while the remaining dimensions of the particle remain unaltered.

Complexity and convergence of Algorithm 1: $N_m^{\mathrm{req}}$ is defined as the total amount of user requests for UAV m. The population size is $N_{\mathrm{p}}$. The computational complexity of each step is shown in Algorithm 1. In general, the number of the particles is larger than UAVs, so $O\left({\left(N_{\mathrm{p}}\right)}^2\right)>O\left(N_{\mathrm{p}}M\right)$. Meanwhile, $O\left(\left(N_m^{\mathrm{req}}+L\right)L{N}_{\mathrm{p}}{M}^2\right)\gg O\left({\left(N_{\mathrm{p}}\right)}^2\right)$. Thus, the computational complexity of Algorithm 1 is $O\left(\left(N_m^{\mathrm{req}}+L\right)L{N}_{\mathrm{p}}{M}^2{l}_{\max }\right)$. Refs. [22,23] concluded that the MOPSO algorithm could converge globally to the Pareto optimal solution set by introducing a mutation strategy. The measure ${\rho }_{\mathrm{A}}$ defined the convergence of the algorithm, i.e., $\underset{l\to \infty }{lim}D\left({\mathrm{A}}^l\right)=\underset{l\to \infty }{lim}\left|{\rho }_{{\mathrm{A}}^l}-{\rho }_{\Lambda }\right|\to 0$. Different from the continuous function in [22], the non-dominated solution set $\left({\mathbf{f}}_1^l,{\mathbf{f}}_2^l\right)$ is sequentially connected in the lth iteration. Next, the edge points $\left(\min \left({\mathbf{f}}_1^l\right),\max \left({\mathbf{f}}_2^l\right)\right)$ and $\left(\max \left({\mathbf{f}}_1^l\right),\min \left({\mathbf{f}}_2^l\right)\right)$ are obtained. Finally, two line segments that start from $\left(\min \left({\mathbf{f}}_1^l\right),\max \left({\mathbf{f}}_2^l\right)\right)$ and $\left(\max \left({\mathbf{f}}_1^l\right),\min \left({\mathbf{f}}_2^l\right)\right)$ are perpendicular to the Y-axis and X-axis, respectively. The closed area mentioned above is ${\rho }_{A^l}$. The generation method for this closed region is also suitable for cases where the non-dominated solution set is a single point.

4. Simulation Results

In this section, numerical results are provided to elaborate the advantages of cache-enabled multi-UAV SAN. We consider a multi-UAV scenario with $M=4$, where user requests ${\mathbf{N}}^{\mathrm{req}}$ and storage capacity $\mathbf{L}$ are set in different schemes, which is detailed in

Table 4. Different schemes of user requests and storage capacity.

Scheme	Description
Scheme 1 (S1)	$L_m^{\mathrm{UAV}}=N_m^{\mathrm{req}}=n,\forall m$, and n is 3, 4, and 5 respectively
Scheme 2 (S2)	$L_m^{\mathrm{UAV}}=4,N_m^{\mathrm{req}}=n,\forall m$, and n is 3, 4, and 5 respectively
Scheme 3 (S3)	$L_m^{\mathrm{UAV}}=4,\forall m$,$N_m^{\mathrm{req}}=[5,3,6,2]$
Scheme 4 (S4)	S3 without social mechanism
Scheme 5 (S5)	$L_m^{\mathrm{UAV}}=4,\forall m$,$N_m^{\mathrm{req}}=[7,1,7,1]$

. In S1, $\left(N_s,N_{QoS}\right)$ is set as $\left(0,0\right)$, $\left(0.3,0.5\right)$, and $\left(0.3,1\right)$, respectively. We set Algorithm 1 with parameters $N_{\mathrm{p}}=200$, ${\beta }_1=0.8$, ${\beta }_2=1.2$, ${\omega }_{\max }=1.7$, ${\omega }_{\min }=0.1$, ${\rho }_{\mathrm{mu}}=0.8$, and $l_{\max }=20,000$.

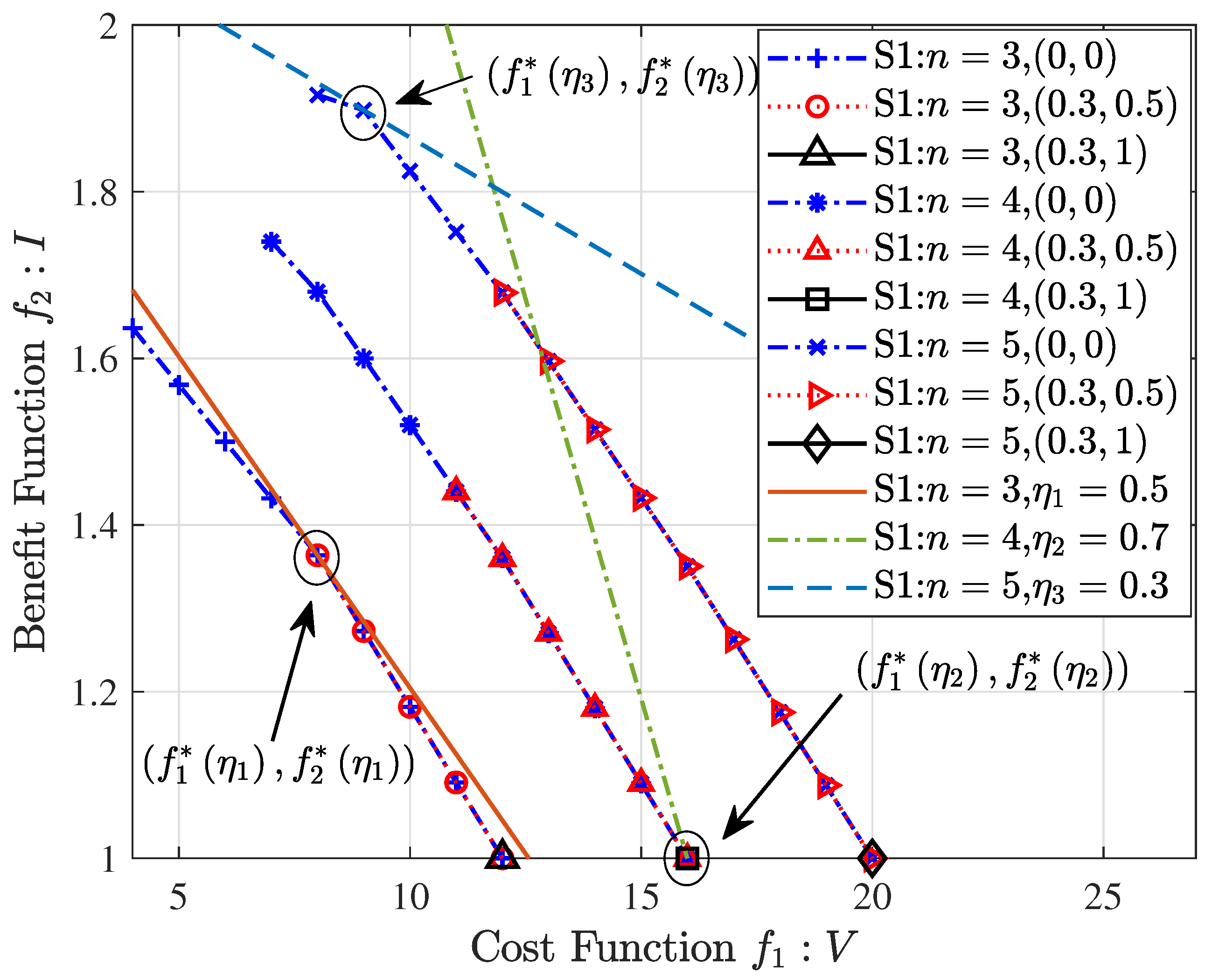
Figure 2 shows the Pareto front approximation of S1. An inverse relationship is observed between $f_1$ and $f_2$. The observation that low RP contents replace the higher leads to an augmentation of diversity, and vice versa. A conventional approach to the compromise between $f_1$ and $f_2$ is to establish a constructor

$$f=\eta {\displaystyle \frac{f_1^{\max }-f_1}{f_1^{\max }-f_1^{\min }}}+\left(1-\eta \right){\displaystyle \frac{f_2^{\max }-f_2}{f_2^{\max }-f_2^{\min }}},$$

(23)

where $\eta$ represents the weight coefficient of $f_1$ and can control whether the system tends towards $f_1$ or $f_2$.

As depicted in Figure 2, the optimal point $\left(f_1^{*},f_2^{*}\right)$ can be calculated by the linear function $f\left(f_1,f_2\right)$ and the Pareto optimal solution set. Subsequently, the optimal configuration scheme ${\mathbf{e}}^{*}$ can be obtained. In S1, the Pareto front approximation continues to expand towards higher values as n increases. When the diversity of cached contents remains constant, an increase in cache capacity causes multi-UAV to sequentially cache existing contents from high RP to low RP until the cache limit is reached. This not only augments the total RP but also enhances the connectivity of the network. On the contrary, an increase in cache capacity ensures the storage of more contents when the total RP remains unchanged. It elucidates that enhancements in storage capacity can significantly elevate the gain of the diversity and total RP for the network.

Figure 2 displays that the solution set that satisfies (13d) and (13e) is a subset of the unconstrained solution set in each Pareto front approximation. Relaxing constraint (13d) results in an increase in network connectivity. Conversely, enforcing this constraint leads to a decrease in connectivity. By manipulating the parameter $N_s$, we can effectively balance the risks associated with latency and network stability. The connectivity can serve as a quantifiable metric for assessing these risks. When constraint (13e) is relaxed, the diversity of cached contents will decrease; otherwise, it will increase. In scenarios involving a lower $N_{QoS}$, the system can utilize the additional available space to cache existing high RP content, thereby ensuring profitability after satisfying a smaller portion of the content restrictions. This strategy helps to enhance content diversity and profitability while ensuring network performance. In summary, adjusting $N_s$ and $N_{QoS}$ has a significant impact on the connectivity, latency, content diversity, and profitability of the network. The gain of $N_s$ and $N_{QoS}$ jointly promotes the diversity of cached content. Therefore, the method on balancing $f_1$ and $f_2$ can also be obtained by adjusting $N_{QoS}$ and $N_s$. Concurrently, more efficient and reliable solutions can be designed for UAV network systems by optimizing these parameters and constraints.

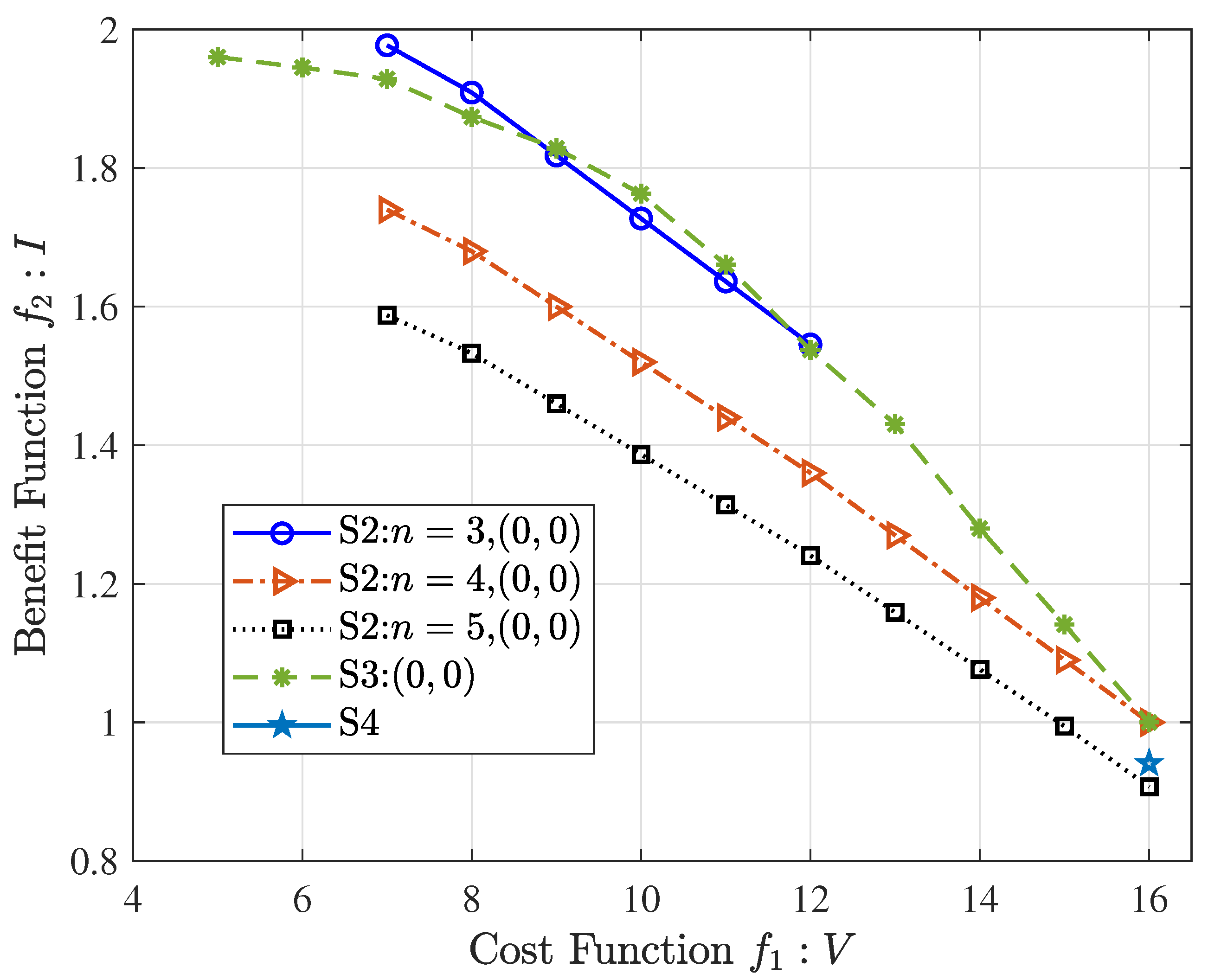
Figure 3 displays the Pareto front approximation of S2, S3, and S4. In S2, ${\mathbf{N}}^{\mathrm{req}}$ completely exceeds $\mathbf{L}$ as n increases, resulting in a continual contraction of the Pareto front toward smaller values. When ${\mathbf{N}}^{\mathrm{req}}<\mathbf{L}$, the UAVs have the idle space after fulfilling diversity requirements. The idle space will cache contents with higher RP until the space is fully occupied. As ${\mathbf{N}}^{\mathrm{req}}$ exceeds $\mathbf{L}$, the UAVs must abandon some low RP contents to prioritize the total RPs. This leads to the contraction of the Pareto front. It is worth noting that the social attributes make the storage space of multi-UAV a cohesive entity, which transforms the relationship between ${\mathbf{N}}^{\mathrm{req}}$ and $\mathbf{L}$ into the relationship between the aggregate quantity of request contents ${\sum }_m^M{N}^{\mathrm{req}}\left(m\right)$ and total storage space ${\sum }_m^{M}L\left(m\right)$. In fact, the various relationships between $N^{\mathrm{req}}\left(m\right)$ and its corresponding $L\left(m\right)$ simultaneously exist in a network, as in S3. The UAV social network can adjust the overall storage space to mitigate resource scarcity among other UAVs. Comparing S3 with S4, the benefits of networks devoid of social attributes diminish significantly. Since the UAVs only rely on local content to serve the users within their jurisdiction, it reduces the total profit of the network.

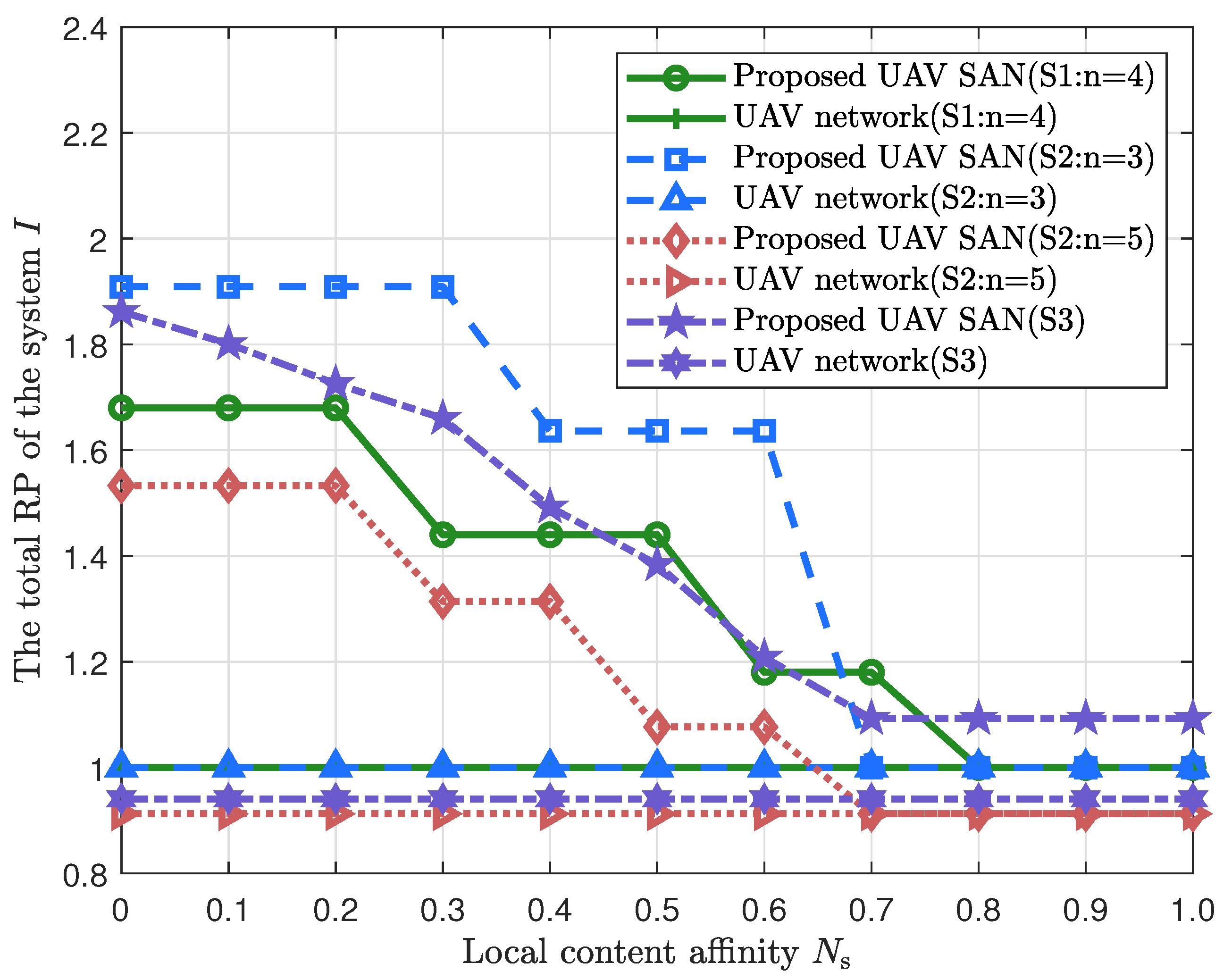
Figure 4 illustrates the impact of parameter $N_{QoS}$ on overall network performance. To demonstrate the advantages of social attributes, we compare the proposed UAV SAN with conventional UAV networks in [13,15]. In the SAN, the total system RP decreases as $N_{QoS}$ increases, consistent with trends in Figure 2. The system must maintain a minimum cached content number to preserve network connectivity for RP maximization, resulting in stable RP during low $N_{QoS}$ phases. As n increases, RP gradually declines—aligning with Figure 2. Critically, SAN consistently achieves higher RP than conventional networks due to the latter’s isolated UAV layers that cannot cooperatively cache high-RP content. Increasing $N_{QoS}$ reduces unconstrained storage space, forcing systems to deprioritize high-RP content for low-RP items. Notably, in both S2 and S3 schemes, SAN’s RP strictly dominates conventional networks.

Figure 5 characterizes the impact of $N_s$ on network performance. Increasing $N_s$ compresses unconstrained storage space, weakening network connectivity and driving a decline in total system RP. At maximum $N_s$, RP of SAN converges with conventional networks under demand-uniform scenarios, indicating that SAN degenerates to conventional networks when devices operate in absolute selfishness states. As n rises, resource scarcity forces systems to prioritize high-RP content over low-RP items, further reducing RP. Crucially, in S3 (demand-maldistributed scenarios), UAV storage limitations prevent full selfishness, resulting in total RP of SAN superiority over conventional networks.“Selfish” UAVs prioritize their own demands at the expense of overall system gain. An increase in such “selfish” UAVs diminishes the collective resource pool and causes severe network degradation. Ultimately, all nodes lose interaction capability, resulting in catastrophic resource wastage.

Figure 6 presents the total system RP under UAV disconnection scenarios. To demonstrate the stability advantages of SAN, we simulate scenarios with exactly one UAV disconnecting at a probability $P_{\mathrm{uav}}$. $P_{\mathrm{uav}}$ is defined as probability of disconnection. Results show that greater UAV storage capacity reduces disconnection impact—i.e., storage sufficiency directly enhances network robustness. Crucially, UAV SAN maintains significantly higher RP than conventional UAV networks after post-disconnection, confirming its superior stability.

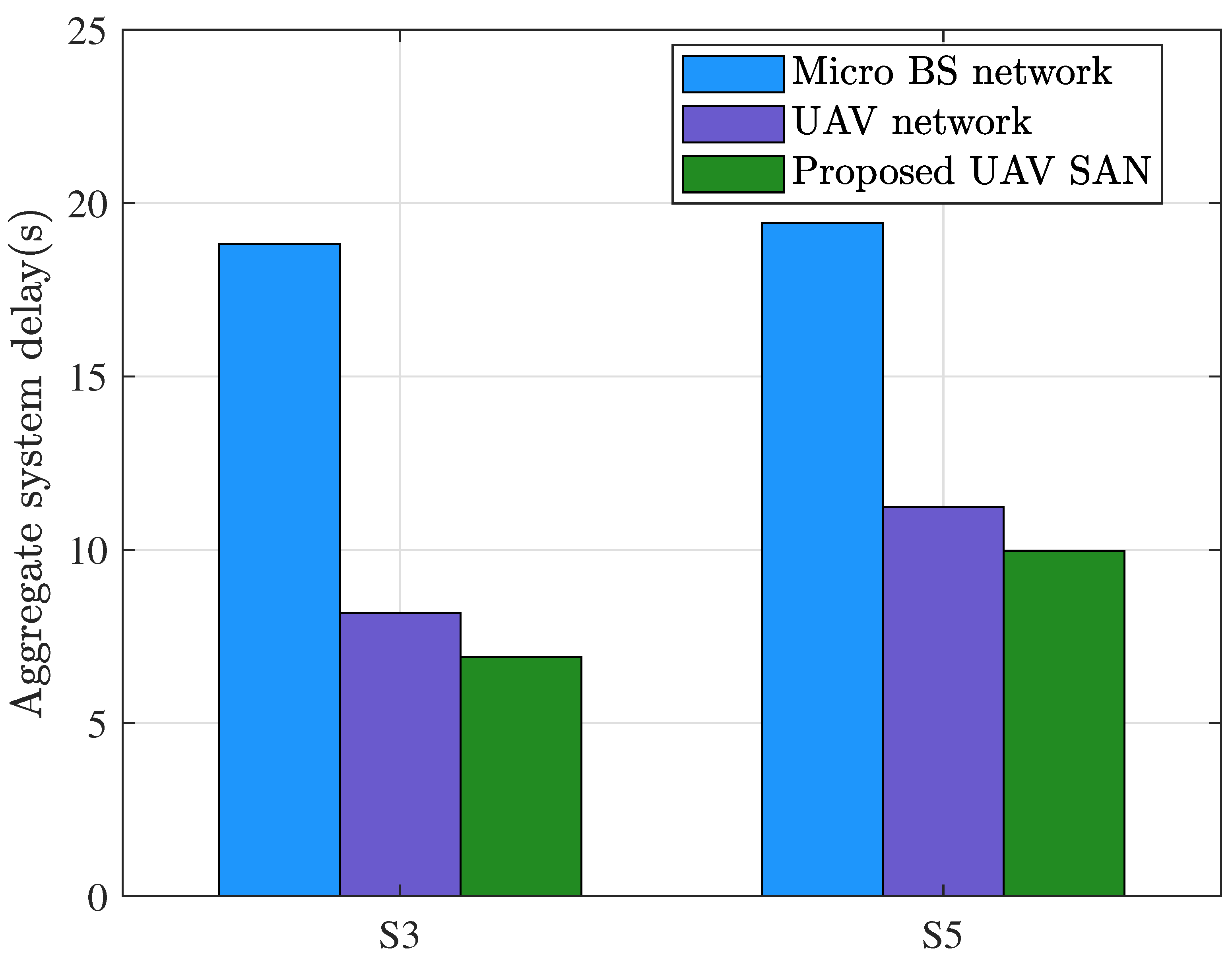
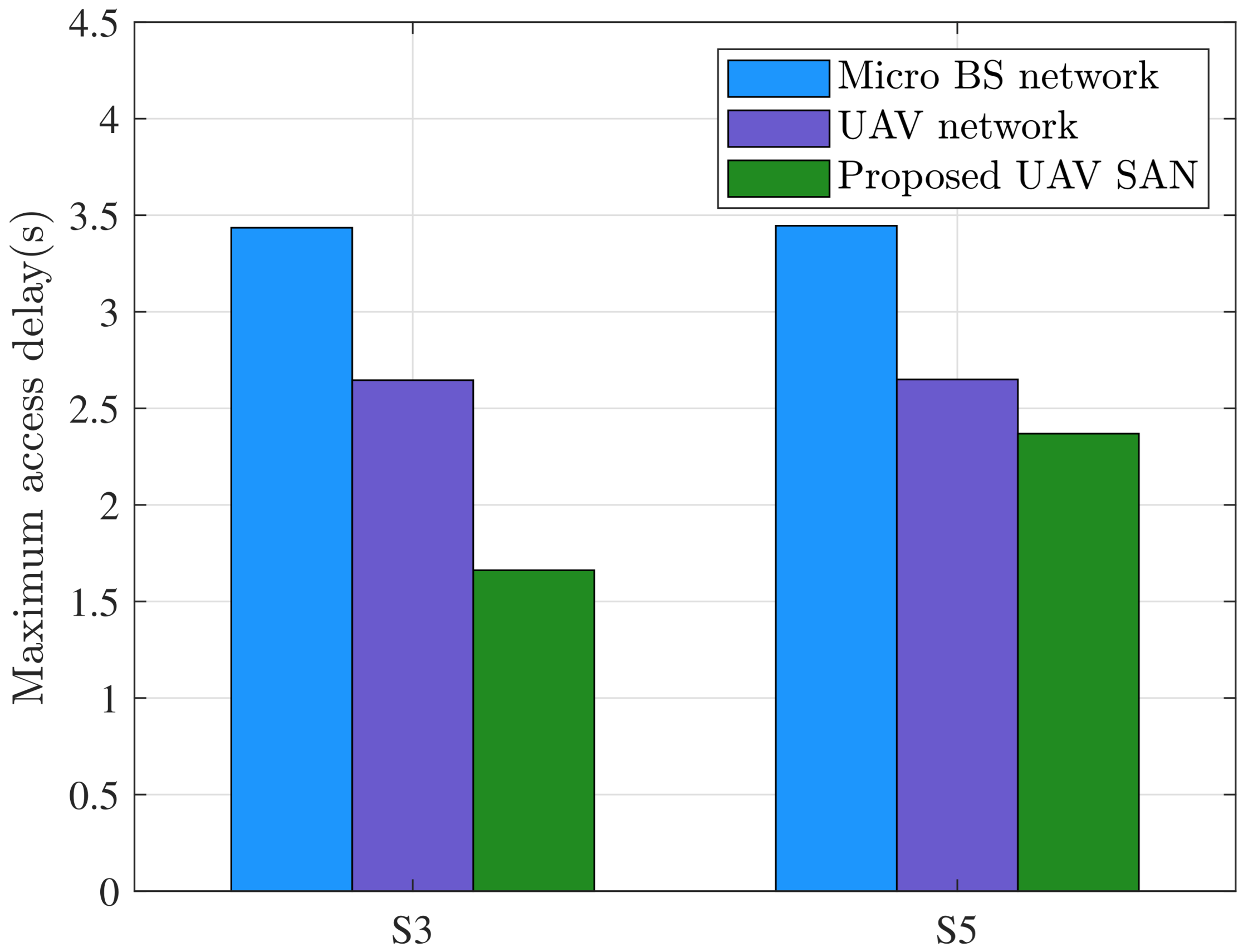
Figure 7 and Figure 8 compare delay performance across micro BS networks [6,7], UAV networks [13,15], and the proposed UAV SAN. Simulation parameters are specified in

Table 5. Parameters configuration for delay calculation.

Parameter	Value	Parameter	Value
Transmit power of UAV	1 W	Transmit power of Micro BS	1 W
Content size	500 MB	Bandwidth	100 MHz
Noise power	−110 dBm	Rice factor	0.7

. Comparing S3 and S5, the severely maldistributed demand (S5) increases system delay because high-demand content must be fetched from distant micro BSs and neighboring UAVs, extending communication paths and amplifying delay. In both S3 and S5, UAV networks significantly outperform micro BSs in maximum access delay and aggregate system delay. Crucially, UAV SAN further reduces both delay metrics through its integrated social architecture.

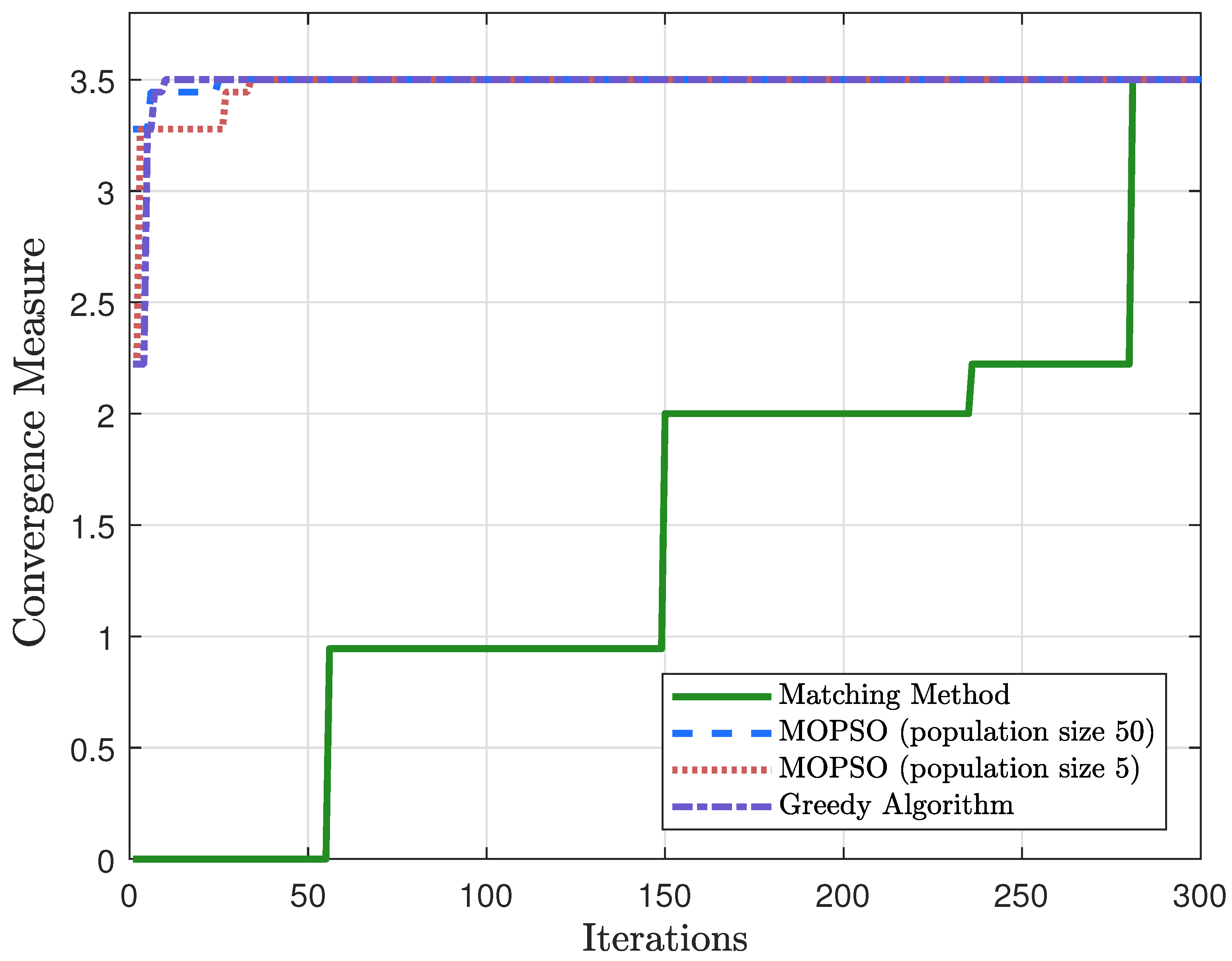
Figure 9 reveals the convergence of S1. The convergence curves of $n=3,4$ converge before 2000 iterations, while the curve of $n=5$ converges around 7000 iterations. The increase in n significantly broadens the feasible range, which leads to a decrease in convergence speed. Figure 10 demonstrates that the MOPSO algorithm exhibits significantly stronger convergence than the matching method. While the greedy algorithm achieves rapid convergence, its substantial computational overhead per iteration leads to a notable increase in overall runtime. Moreover, increasing the population size accelerates the convergence of the MOPSO algorithm.

5. Conclusions

In this paper, we addressed the pressing challenge of optimizing resource allocation in cache-enabled multi-UAV networks, where imbalances in user demand and storage capacity can degrade performance. We introduced a novel cache-enabled multi-UAV socially aware network (SAN) that incorporates “selfish” and “selfless” social attributes to intelligently control the degree of cooperation among UAVs. To balance the competing goals of network-wide efficiency and fairness to user groups, we formulated the caching deployment strategy as a multi-objective optimization problem (MOOP), aiming to simultaneously maximize the aggregated request probability (a proxy for QoS) and the diversity of cached content (a proxy for fairness). The MOPSO algorithm demonstrates superior convergence speed and enhanced exploration capability in 10-objective problems compared to other metaheuristics (e.g., NSGA-II). Furthermore, through the problem transformation proposed in this paper, it effectively reduces the feasible region relative to conventional binary encoding schemes, thereby substantially lowering computational complexity. Confronting the NP-hard nature of this discrete MOOP, we designed an effective solution based on a Multi-Objective Particle Swarm Optimization (MOPSO) algorithm, enhanced with a mutation strategy to ensure population diversity and prevent premature convergence to local optima. The algorithm efficiently approximates the Pareto optimal front, offering network operators a valuable set of optimal trade-off solutions rather than a single, rigid operating point.

The simulation results validated the efficacy of our approach and yielded several key insights. Firstly, the introduction of the social awareness mechanism provides a significant performance gain over traditional, non-cooperative caching schemes, particularly in realistic scenarios with uneven distributions of user requests and storage resources. By enabling collaboration, the framework allows the collective storage of all UAVs to be utilized as a cohesive whole, effectively mitigating localized resource shortages. Secondly, our results confirmed the fundamental trade-off between maximizing content diversity and total request probability, demonstrating the validity of the MOOP formulation. Finally, we demonstrated that the social constraint parameters, $N_s$ and $N_{QoS}$, serve as effective tools for tuning network behavior, allowing for a deliberate balance between fairness and efficiency to meet diverse operational requirements. $N_s$ determines the priority level of UAV cells, while $N_{QoS}$ governs the priority of the entire macro zone. Thus, the configuration of $N_s$ and $N_{QoS}$ is traffic-dependent. In high-traffic venues (e.g., stadiums), both $N_s=1$ and $N_{QoS}=1$ can be set to prioritize user demands in cells and macro zones. During low-traffic periods, $N_s$ and $N_{QoS}$ can be reduced to release resources for neighboring cells and macro zones. The convergence of the proposed algorithm was also verified, confirming its robustness and suitability for this complex optimization task.