4.1. Dueling DQN-ALNS Algorithm Framework
To solve the scheduling problem of multi-base station collaborative multi-UAV return guidance communication tasks in disaster environments, we propose a two-stage collaborative optimization framework (DRL-ALNS) based on deep reinforcement learning and adaptive large neighborhood search. Using the Dueling Deep Q-Network algorithm as the reinforcement learning component, we design an improved joint algorithm (Dueling DQN-ALNS), combining Dueling Deep Q-Network and an adaptive large neighborhood algorithm specifically for this guidance task scheduling problem. This framework adopts a combination of offline pre-training and online real-time optimization, fully leveraging the capabilities of deep reinforcement learning in strategy learning and the advantages of adaptive large neighborhood search (ALNS) in local search. In the offline phase, we train the Dueling DQN algorithm using historical alternating scenario data. These data cover multiple attributes of UAVs and communication base stations, such as initial positions, speeds, communication ranges, and time windows. Through these data, the network can learn optimal destruction–repair strategy combinations in different environments, and these strategy parameters are subsequently stored in the experience replay buffer. The Dueling DQN algorithm can more accurately estimate Q-values by separating the value stream and advantage stream, thereby improving the accuracy of destruction–repair strategy selection.
Specifically, the Dueling DQN network includes a feature extraction layer, value stream, advantage stream, and output layer. The training process aims to minimize the mean squared error between predicted Q-values and actual calculated Q-values. In the online phase, the pre-trained Dueling DQN parameter model is loaded, and network weights are frozen to ensure the stability of learned parameters. At this point, the state encoder perceives the environmental state of the current scheduling solution in real time, including base station load characteristics and the global optimization state, forming a high-dimensional state vector of the scheduling solution as input to the DQN network. The Dueling DQN Agent generates adaptive destruction and repair strategy combinations based on the current state, which are used to guide the destruction and repair operations of the ALNS algorithm. Within each appropriate rolling optimization window, the Dueling DQN-ALNS algorithm framework transfers the strategy knowledge learned offline to the online decision engine, thereby generating a globally optimal guidance communication scheduling solution that satisfies energy constraints and avoids time window conflicts. The structure of the Dueling DQN-ALNS algorithm framework is shown in
Figure 3 below.
The specific algorithms are detailed in Algorithms 1 and 2:
| Algorithm 1 Offline training |
|
| Algorithm 2 Online optimization |
|
In these two algorithms, the ALNS algorithm is used during the offline training phase to generate diverse experience samples, helping the Dueling DQN network learn the effects of different strategy combinations; during the online optimization phase, it is used to adjust and optimize scheduling solutions in real time, ensuring the real-time performance and adaptability of the algorithm. By combining ALNS and Dueling DQN, the algorithm can effectively handle complex task scheduling for UAV return guidance communication in rescue environments, generating high-quality communication scheduling solutions.
4.2. Improved ALNS Main Search Algorithm
The adaptive large neighborhood search (ALNS) algorithm is a heuristic method that enhances neighborhood search by incorporating measures for evaluating the effectiveness of operators such as destruction and repair. This enables the algorithm to adaptively select effective operators to destroy and repair solutions, thereby increasing the probability of obtaining better solutions. Building upon LNS, ALN allows the use of multiple destroy and repair methods within the same search process to construct the neighborhood of the current solution. ALNS assigns a weight to each destroy and repair method, controlling their usage frequency during the search. Throughout the search process, ALNS dynamically adjusts the weights of various destroy and repair methods to build better neighborhoods and obtain improved solutions. This paper designs an improved Adaptive Large Neighborhood Search (ALNS) algorithm for UAV swarm return guidance communication scheduling, implemented through a four-phase optimization framework: First, construct a high-quality initial solution based on time urgency, task weights, and potential utility. Second, employ an intelligent strategy selection mechanism to dynamically match the optimal destruction–repair strategy combination for the current solution, precisely removing critical tasks during the targeted destruction phase and reconstructing scheduling solutions during the intelligent repair phase. Then, balance exploration and exploitation through hybrid solution acceptance criteria. Finally, dynamically adjust search weights based on the performance of selected strategies. This algorithm innovatively integrates multi-factor utility models with complex constraint handling mechanisms, enabling collaborative optimization of communication utility, energy costs, failure risks, and network congestion while significantly enhancing solution efficiency, scheduling solution quality, and real-time decision-making capabilities.
4.2.1. Encoding Method
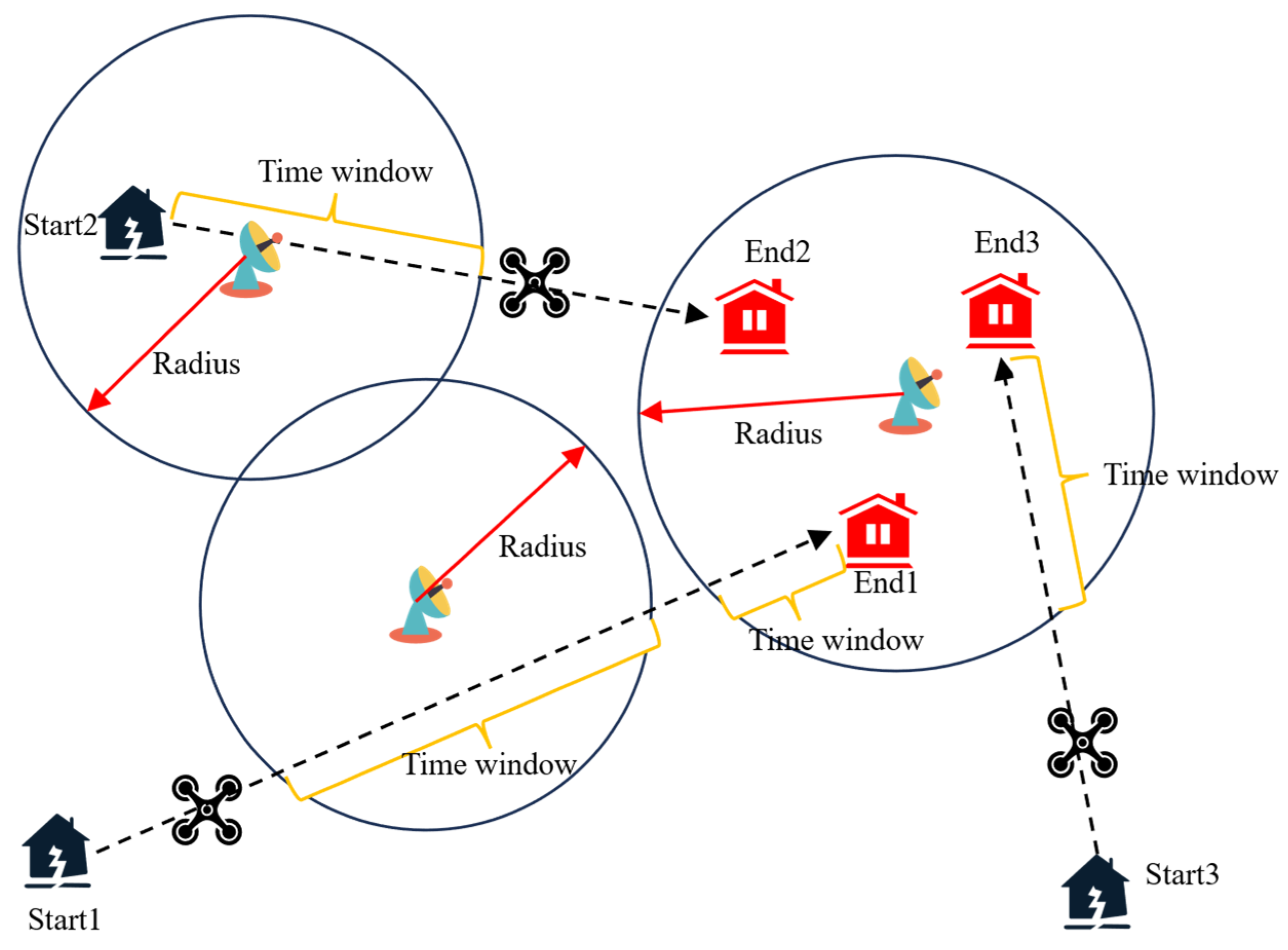
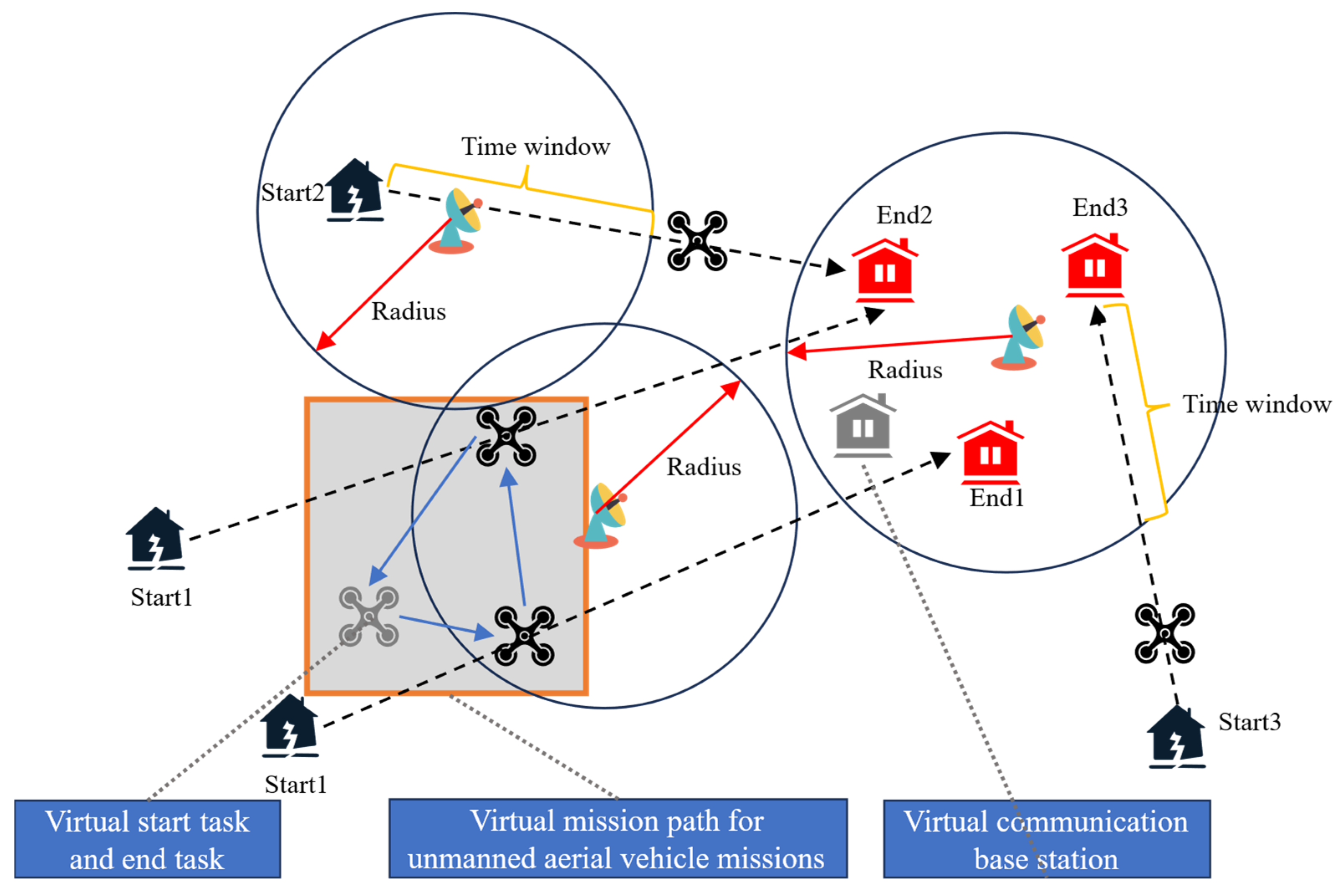
To better reflect local and global characteristics in scheduling solutions, the current communication task scheduling solution is converted into a state vector
. The state vector at the current stage is
, providing comprehensive state information for the deep reinforcement learning model. The overall state space is
. The state vector contains base station features and global scheduling solution features:
The information represented by the constructed coding structure is shown in
Figure 4 below:
Here, denotes the number of tasks at base station , represents energy consumption utilization rate, indicates time window utilization rate, is the current objective function value, is the iteration progress ratio, and is the current temperature parameter. By designing a state vector incorporating both base station features and global features, comprehensive state information is provided for the Dueling DQN model. Base station features reflect the current load and resource usage of each base station, while global features provide macroscopic information about the entire scheduling solution. This encoding method not only preserves the core elements of the problem but also provides rich contextual information for the Dueling DQN model, enabling more accurate assessment of the current solution state and thereby facilitating better strategy selection.
4.2.2. Initial Solution Construction
The quality of the initial solution in the ALNS algorithm has a direct impact on subsequent search processes and optimal results. A good initial solution can significantly accelerate the search optimization process. Given that UAV return guidance communication tasks in disaster environments possess multiple attributes, the initial solution construction adopts a greedy heuristic method. This method comprehensively considers factors such as time windows, task weights, and potential utility to assign appropriate communication base stations to each UAV, constructing a feasible and high-quality initial scheduling solution.
For each UAV
, a comprehensive score is calculated, reflecting its urgency and importance:
where
,
, and
are weighting coefficients. The time factor weighting coefficient
reflects the importance of time urgency in the comprehensive score. The weight factor weighting coefficient
reflects the importance of task weight in the comprehensive score. The utility factor weighting coefficient
reflects the importance of potential utility in the comprehensive score.
represents the time urgency of the UAV, where
denotes the time window span.
represents the task weight.
represents potential utility. By appropriately setting the weighting coefficients, the initial solution construction can better reflect the urgency and task priorities of the problem, providing a good starting point for subsequent optimization.
Sort UAVs in descending order based on their scores, prioritizing tasks of UAVs with higher scores. For each UAV in the sorted list, assign it to the base station that can provide the maximum utility while satisfying constraints, including time windows and energy limitations. After assigning each task, update the task list and energy consumption status of the corresponding base station, ensuring no time overlap between tasks, to obtain the final initial solution.
By comprehensively considering time windows, task weights, and potential utility, the initial solution’s construction can generate a high-quality starting point. This method considers not only the urgency of tasks (time windows) but also their importance and utility, ensuring the rationality of the initial solution under multi-factor tradeoffs. Compared to traditional random initialization or simple heuristic initialization, this multi-factor comprehensive evaluation-based initialization method can significantly improve the algorithm’s convergence speed and solution quality.
4.2.3. Destruction Strategies
In the adaptive large neighborhood search (ALNS) algorithm, the design of destruction strategies is crucial. Its core function is to selectively remove some tasks from the current solution, breaking the limitations of local optima and creating opportunities for reoptimizing task allocation during the repair phase. Reasonable destruction strategies can effectively reduce the quality of the current solution without affecting its feasibility, thereby improving solution quality through task reinsertion during the repair phase. This process of destruction and reconstruction helps the algorithm explore extensively in the solution space, avoiding entrapment in local optima. The five destruction strategies designed in this paper damage the current solution from different perspectives, comprehensively exploring the potential of the solution space and enhancing the algorithm’s global search capability and solution quality.
This strategy randomly selects a subset of base stations and removes a portion of tasks from them. Let
be the set of mobile communication base stations and
be the set of UAVs. Given a removal ratio
, a random subset
is selected, with
.
is the set of tasks for base station
. Randomly remove
tasks.
is the set of tasks after the destruction:
- B.
Task-Based Random Removal
This strategy removes a random selection of tasks from the entire set, irrespective of their associated base station. Let
be the complete task set. Given a removal ratio
, the number of tasks to remove is
.
tasks are then randomly selected and removed. The resulting task set
is as follows:
- C.
Low-Benefit Removal
This strategy prioritizes removing tasks contributing least to the objective function, freeing resources for potentially higher-benefit tasks. Let
be the complete task set. Each task
has a benefit value
calculated as
Given a removal ratio
, all tasks are sorted in ascending order of
. The number of tasks to remove is
. The
tasks with the smallest
values are removed. The resulting task set
is
where
selects the
tasks with the smallest
values.
- D.
Time-Critical Removal
This strategy prioritizes removing tasks with tight time windows, facilitating the reallocation of time resources and resolving scheduling conflicts. Let
be the complete task set. The time criticality
of task
is defined as its time window length:
. Given a removal ratio
, the number of tasks to remove is
. The
tasks with the smallest
values (i.e., tightest time windows) are removed. The resulting task set
is
where
selects the
tasks with the smallest
values.
- E.
High-Weight Removal
This strategy prioritizes removing high-weight tasks to trigger their rescheduling, aiming to discover more optimal resource allocations. Let
be the complete task set. The weigh
of task
is calculated as
. Given a removal ratio
, the number of tasks to remove is
. The
tasks with the largest
values are removed. The resulting task set
is
where
selects the
tasks with the largest
values.
These five destruction strategies remove tasks from the current solution in distinct ways, creating modified solutions that serve as starting points for the repair phase to rebuild and optimize task assignments. The diversity and specificity of these strategies enable the enhanced ALNS algorithm to efficiently explore the solution space, improve solution quality, and strengthen algorithmic robustness. By intelligently selecting and combining these destruction strategies, the ALNS algorithm becomes highly effective for addressing the UAV return communication mission scheduling problem in disaster relief environments.
4.2.4. Repair Strategies
This strategy assigns removed tasks to feasible base stations starting with the earliest available time window. Let
be the set of mobile base stations and
be the UAV swarm. The complete task set is
, with removed tasks
. For each task
, calculate its earliest feasible start time at base station
:
where
is the current task set at base station
. Tasks are then reinserted into base stations in ascending order of
.
- B.
Random Repair
This strategy randomly reinserts removed tasks by first selecting a task uniformly at random and then assigning it to a randomly chosen base station . The stochastic nature of this approach promotes solution space exploration during the repair phase.
- C.
Maximum-Benefit Repair
Tasks are reinserted to maximize benefit by calculating the value for each removed task and assigning it to the base station that yields the highest value. This greedy selection prioritizes high-impact task allocations.
- D.
Weight-Priority Repair
This approach prioritizes high-weight tasks by computing the weight for each removed task and assigning it to the optimal base station . The strategy focuses resources on tasks with elevated operational significance.
- E.
Greedy Repair
Net value optimization is achieved through the evaluation metric , representing benefit minus cost. Each removed task is assigned to the base station maximizing , ensuring locally optimal resource utilization during reinsertion.
These five repair strategies implement distinct mathematical methodologies for task reallocation, collectively enhancing the algorithm’s adaptability and flexibility. Their synergistic operation enables effective optimization of UAV return communication scheduling in disaster relief scenarios through systematic reconstruction of solutions.
4.2.5. SA and RRT Acceptance Criteria
The ALNS algorithm requires a critical decision mechanism: whether to accept newly generated solutions to replace the current solution. This decision significantly impacts the algorithm’s exploration (searching broadly for new feasible solutions) and exploitation (intensively improving solutions in promising regions). An effective acceptance criterion balances these capabilities, preventing premature convergence to local optima while guiding the algorithm toward global optima. Traditional criteria (e.g., solely objective-based improvement) show limitations in complex scheduling environments. Thus, we designed a hybrid criterion integrating simulated annealing (SA) and Rapid Restoration Threshold (RRT).
The SA criterion, inspired by metallurgical annealing, probabilistically accepts inferior solutions. We implement geometric cooling:
, where
is a fixed cooling factor. The acceptance probability is calculated as
Here, denotes the objective value difference, and represents the temperature parameter that decreases iteratively. Solutions with (superior/equal quality) are always accepted. Solutions with (inferior quality) are accepted with probability , which decreases as temperature cools.
The RRT criterion prevents premature convergence by establishing a dynamic acceptance threshold. This permits solutions with marginal quality deterioration, balancing exploration and exploitation. The dynamic threshold is defined as follows:
where
controls threshold strictness (
). Solutions satisfying requests are candidate solutions. The combined SA-RRT acceptance condition is
where
is a uniform random number. The SA and RRT criteria complement each other effectively in the hybrid mechanism. The SA criterion’s stochastic nature allows the algorithm to explore new regions of the solution space, helping it escape local optima and ensuring a diverse search. Meanwhile, the RRT criterion’s conservative approach, with its dynamic acceptance threshold, prevents the algorithm from deviating too far from promising solutions, thus maintaining a degree of exploitation to refine and improve upon better-than-average solutions. This balance between exploration and exploitation makes the combined criterion particularly effective for complex scheduling tasks like UAV return communication task scheduling.
4.2.6. Strategy Weight Update
The strategy weight update mechanism is a core innovation in Dueling DQN-ALNS, serving as the foundation for action selection in Dueling Deep Q-Networks. By dynamically adjusting destruction and repair strategy weights based on historical performance, this mechanism enables automatic selection of optimal strategy combinations. This adaptive capability significantly enhances search efficiency and solution quality in complex optimization environments.
The hybrid Dueling DQN-ALNS framework enables dynamic weight updates for strategy pairs. Each combined strategy
consists of a destruction strategy
and repair strategy
, forming 25 unique combinations. The cooperative evaluation principle assesses strategy pairs while updating weights independently. The composite score is calculated as
Here, denotes objective function improvement, quantifies total energy constraint violation, and indicates time window compliance. The weight coefficients are , , and .
The weight coefficients , , and were chosen based on extensive experimental validation. These values reflect the relative importance of solution quality, energy constraint adherence, and time window compliance in our scheduling problem. The higher weight for emphasizes the importance of improving the objective function value, which directly impacts the overall efficiency of UAV return communication task scheduling. The weight ensures that energy constraints are closely monitored to prevent battery depletion in UAVs, while reinforces the critical nature of time window compliance to maintain the feasibility of schedules. This multi-objective scoring approach evaluates solution quality, energy constraints, and temporal feasibility, with normalized energy violation to mitigate scale bias. The binary term reinforces time sensitivity.
- B.
Scoring Mechanism for Strategies
The destruction strategy weights are updated as follows:
where
Here, = weight of tactic , = learning rate, and = average reward over sliding window (size = 100).
The repair strategy weights follow symmetrically:
- C.
Dynamic Learning Rate Adjustment
While repair strategy updates mirror destruction updates, they use a separate sliding window
. To adapt to task phases, learning rates
and
are dynamically adjusted:
where
(normalized mission time). A constraint-sensitive modifier further adjusts rates during energy violations:
- D.
Strategy Diversity and Urgency Response
Diversity maintenance prevents strategy space collapse. When strategy weight ranges narrow (), the following occurs:
Top performing strategies: Weights increased by 10% ();
Others: Weights reduced by 5% ().
Symmetric rules apply for repair strategies.
Time window urgency response prioritizes time-critical tasks by boosting faster strategies as communication windows close:
where
= time urgency of destruction tactic
,
= execution speed of repair tactic
, and
.
This decoupled weight update mechanism enables independent optimization of destruction/repair strategies while maintaining dynamic balance, significantly enhancing robustness and adaptability for disaster relief UAV scheduling.
4.3. Deep Reinforcement Learning
Reinforcement learning (RL) has gained significant attention in both academic research and industrial applications. While traditional RL algorithms demonstrate strong performance for certain complex problems, they often struggle with relevance in specific practical scenarios. Meanwhile, deep learning has achieved notable success across domains due to its powerful feature extraction and pattern recognition capabilities. RL offers unique advantages for task scheduling through its dynamic policy adjustments based on state–action relationships. However, the high-dimensional and uncertain state spaces in UAV task scheduling pose challenges for traditional RL methods like Q-learning, which rely on tabular Q-value storage. This approach becomes computationally inefficient and memory-intensive for large state spaces, leading to poor sample efficiency during training.
Deep reinforcement learning (DRL) addresses these limitations by integrating deep neural networks. DRL replaces tabular Q-functions with function approximators and incorporates experience replay, effectively mitigating sample sparsity issues. Combining RL’s policy optimization strengths with deep learning’s feature extraction capabilities, DRL excels in decision-making and scheduling within complex, high-dimensional environments. Among DRL algorithms, Deep Q-Networks (DQNs) and its variants like Dueling DQN are widely adopted. The key innovation of Dueling DQN is its decomposition of the Q-value function into separate value and advantage streams, respectively estimating state value and action advantages. This architecture improves Q-value estimation accuracy. The network takes environmental states as inputs and outputs Q-value estimates for each action, providing robustness in continuous and uncertain state spaces. The Dueling DQN architecture used in this study is shown in
Figure 5.
4.3.1. State Design
To effectively integrate Dueling DQN with ALNS, the state representation aligns with ALNS encoding. The state space is defined as vector , comprising base station features and global mission characteristics: .
4.3.2. Loss Function
We employ a modified Huber loss function as the optimization objective, designed for the complexities of UAV return communication tasks and training stability requirements in disaster relief scenarios. This loss combines benefits of the mean squared error (MSE) and mean absolute error (MAE): it uses quadratic behavior for small errors to stabilize gradients and linear behavior for large errors to prevent gradient explosion. The DQN loss function is defined as follows:
where
denotes the target Q-value, calculated as
where
represents parameters of the online Q-network (including feature extraction layers, value stream, and advantage stream weights).
denotes the training batch size.
is the immediate reward after taking the action
in state
.
is the discount factor balancing immediate and future rewards.
denotes parameters of the target Q-network, which stabilizes training.
estimates the maximum future Q-value.
is the current network’s Q-value prediction for state–action pair
, representing expected cumulative reward.
is a threshold parameter controlling quadratic–linear transitions.
When the predicted and target values are close, use the MSE term for stable gradient updates. For large differences, switch to the linear term to avoid gradient explosion. This enhances the loss function’s robustness and improves training stability and convergence speed.
In Dueling DQN, the Q-value is decomposed into a value function
and an advantage function
, combined as
4.3.3. Action Space Design
Action space consists of all possible combinations of destruction and repair strategies. Specifically, the destruction strategies include time urgency-based destruction and minimum profit destruction, among others, while the repair strategies include maximum profit repair and priority based repair, among others. Each action corresponds to selecting one destruction strategy (such as base station-based random destruction or weight-based destruction) and one repair strategy (such as time-window-awareness repair or greedy repair). The combination forms action , creating a discrete decision-making action space of 25 strategy combinations, where .
4.3.4. Reward Function Design
The reward function is designed to balance exploration and exploitation, encouraging the agent to select high-quality strategies. It is defined as
where
. This function motivates the agent to pursue higher goals by offering tiered rewards: high rewards when the new solution’s objective value exceeds historical bests, medium rewards when it surpasses the current solution, and low rewards when it does not exceed the current solution but is still acceptable. This tiered reward mechanism effectively guides the agent to balance exploration and exploitation.
4.3.5. Action Selection Policy
The agent uses a
-greedy strategy to balance exploration and exploitation. The action selection rule is
Here, is the probability of choosing action in state , and (the exploration rate) starts at 1.0 and decays to 0.01 over iterations. represents the expected cumulative reward for choosing action in state , determined by the Q-network parameter . This strategy ensures thorough exploration early in learning and focuses on exploitation later, effectively balancing exploration and exploitation.
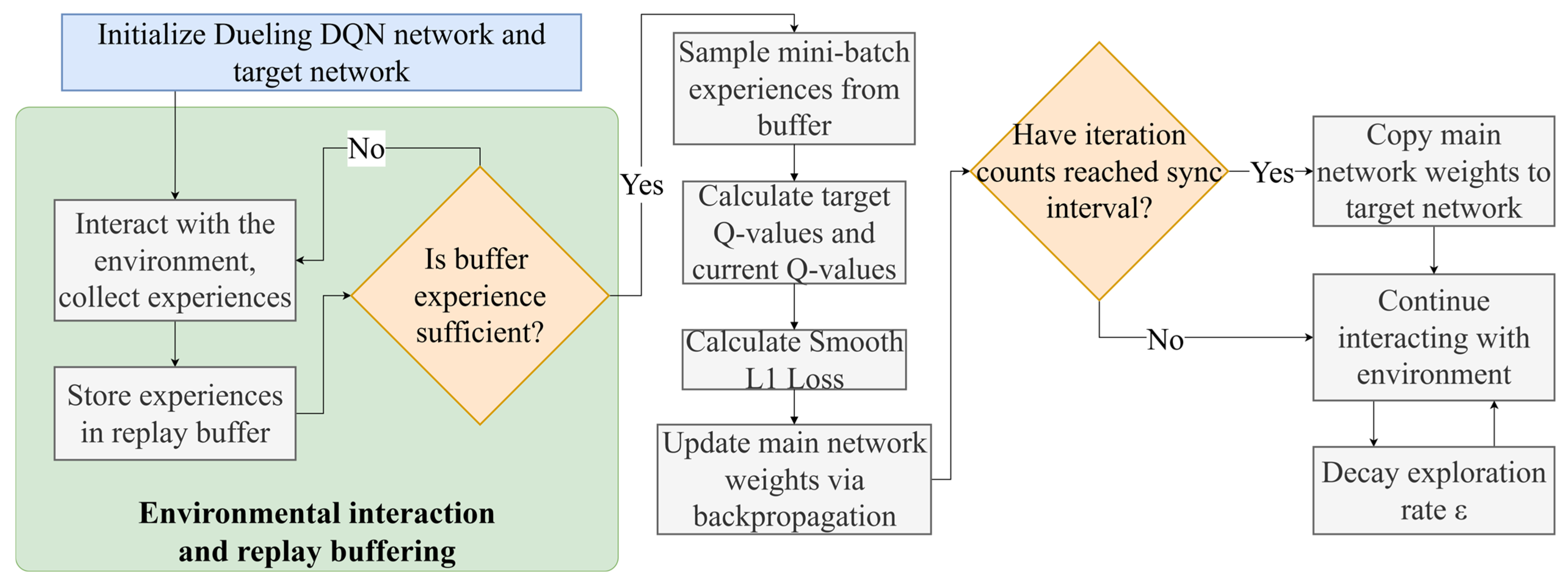
4.3.6. DQN Agent Optimization Process
The DQN Agent continuously learns and optimizes strategies through interaction with the environment, utilizing a Dueling DQN network to enhance the accuracy of Q-value estimation. Initially, the Dueling DQN network and its target network are randomly initialized. During interaction with the environment, the DQN Agent gathers experiences, including states, actions, rewards, and new states, and stores them in a replay buffer. Periodically, it samples small batches of experiences from the buffer to compute the loss function and updates the network weights via backpropagation. Every certain number of steps, the weights of the primary network are copied to the target network to maintain its stability. Q-values are calculated by the Dueling DQN network, which outputs Q-values for each action. The specific process is shown in
Figure 6.