Model-Free UAV Navigation in Unknown Complex Environments Using Vision-Based Reinforcement Learning
Abstract
1. Introduction
1.1. Background
1.2. Review of Related Works
- Mapping difficulty and low robustness: Conventional SLAM or mapping-based navigation methods suffer from significant challenges related to real-time operation and robustness because of the dense and irregular distribution of obstacles. First, building high-quality maps under conditions such as dynamic lighting is difficult. Second, the map update process requires high computing resources, which affects navigation efficiency [48,49].
- Single-objective optimization and low flexibility: Conventional navigation algorithms optimize a single goal, and although the local planner combines obstacle avoidance functions, these algorithms rely on manually adjusted fixed weights to implement multicriteria cost functions. This rigidity results in the trade-off between path efficiency, energy consumption, and safety in unknown complex environments [52,53].
1.3. Proposed Method and Contribution
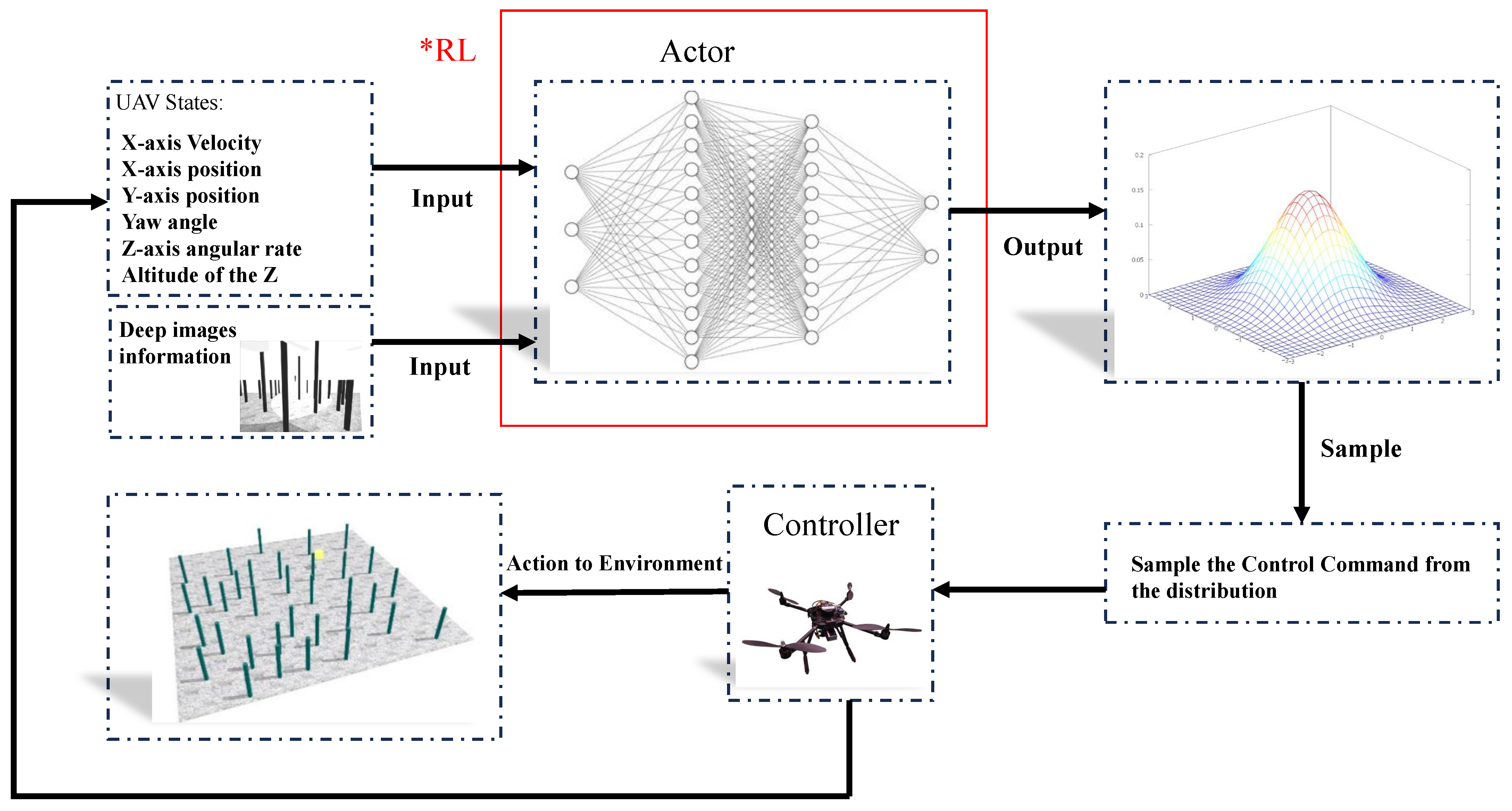
- A UAV navigation architecture based on vision-driven reinforcement learning is proposed. Unlike conventional methods, the proposed architecture operates without map construction. Furthermore, it integrates a convolutional network with a policy network and considers the real-time status information of UAV and depth images as input, thereby enabling it to replace conventional path planning algorithms and position controllers. Moreover, it effectively mitigates response delays by avoiding the separation and coordination issues commonly found in modular systems. Additionally, the proposed architecture enables UAVs to autonomously adapt their flight paths and navigation strategies in unknown complex environments with low computational complexity, enhancing real-time responsiveness and maneuverability.
- We design a multifactor reward function that simultaneously considers target distance, energy consumption, and safety to address the limitations of single-objective optimization employed in conventional navigation algorithms. This multifactor reward formulation enables the UAV to learn more flexible and balanced navigation strategies, enhancing overall performance while reducing the risk of collisions in unknown complex environments.
- The proposed policy is trained and optimized by constructing multiple simulation environments with different obstacle distributions and lighting conditions. The trained policy does not require prior map generation, and its output can be directly applied to UAV navigation, thereby achieving successful flight in simulated and real environments, which demonstrates the practical feasibility and robustness of the proposed method. The experimental process is detailed in [54], and the corresponding code is available in [55].
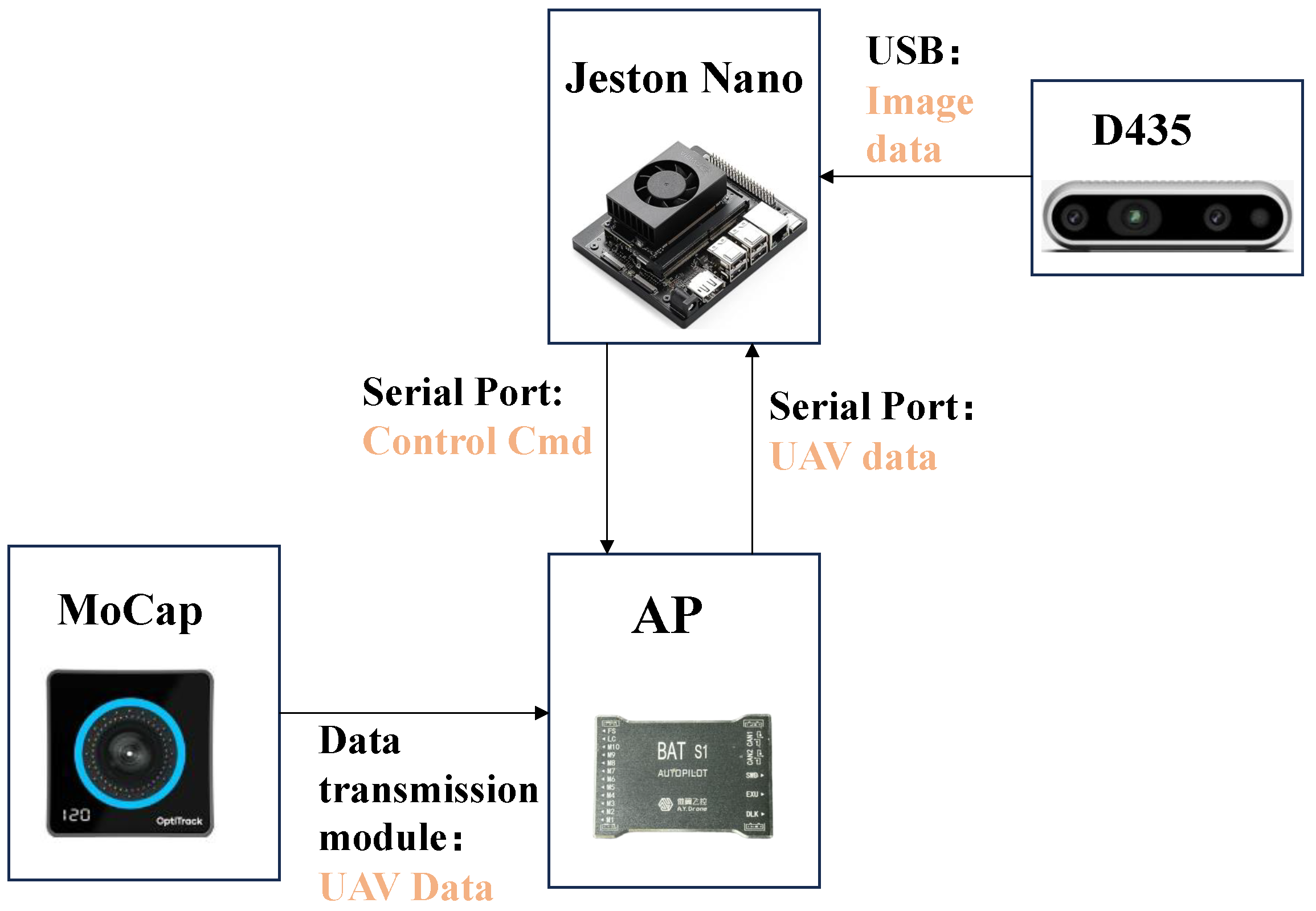
2. System Architecture
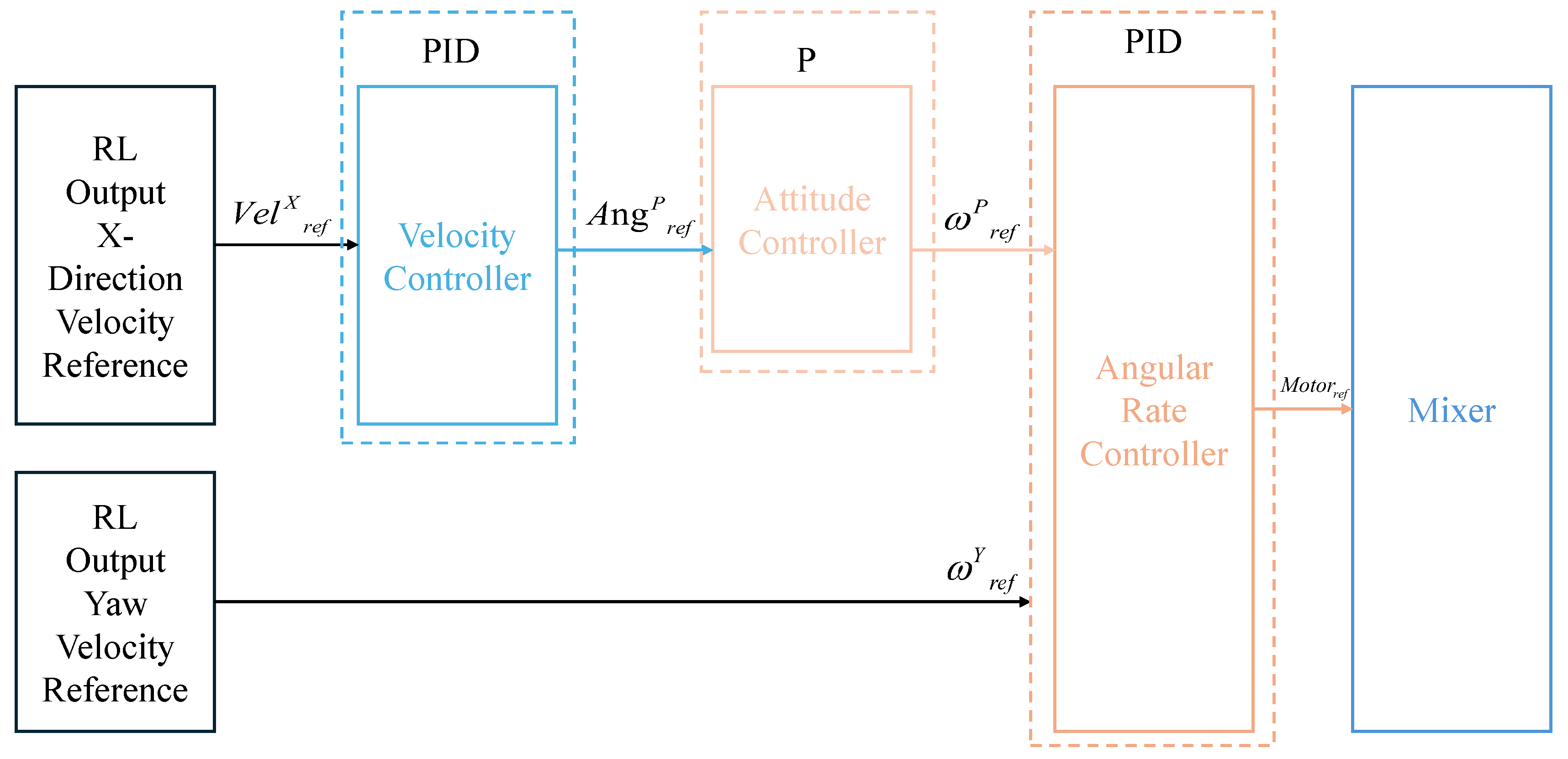
3. Navigation Method
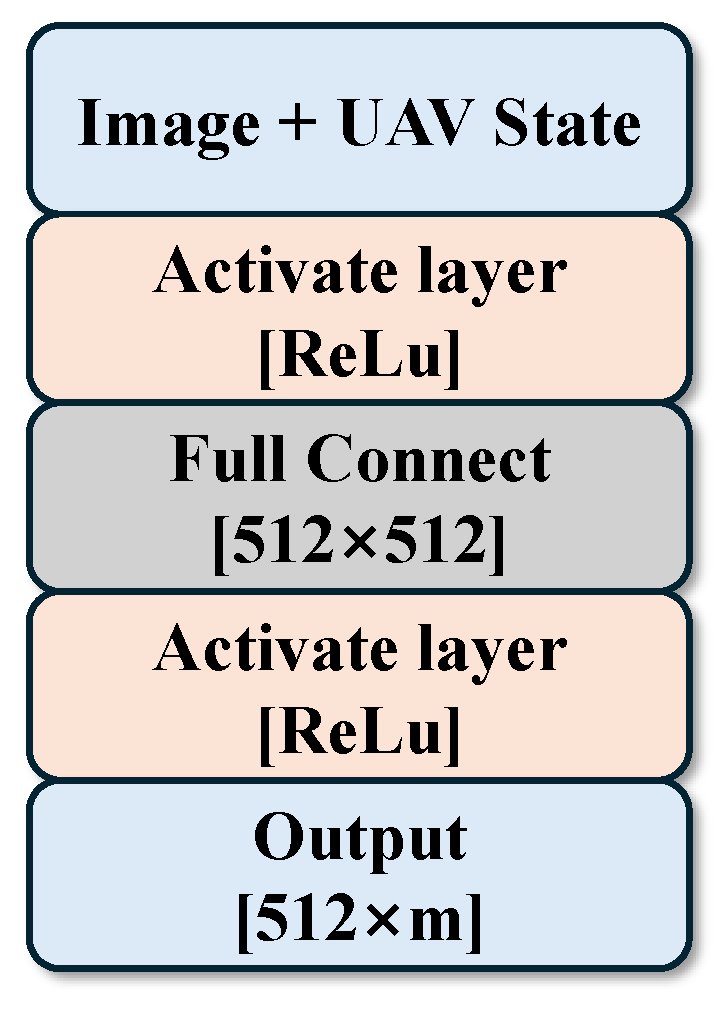
3.1. Navigation Policy Structure
3.2. Design of State and Action Spaces
3.3. Design of the Reward Function
4. Experiment
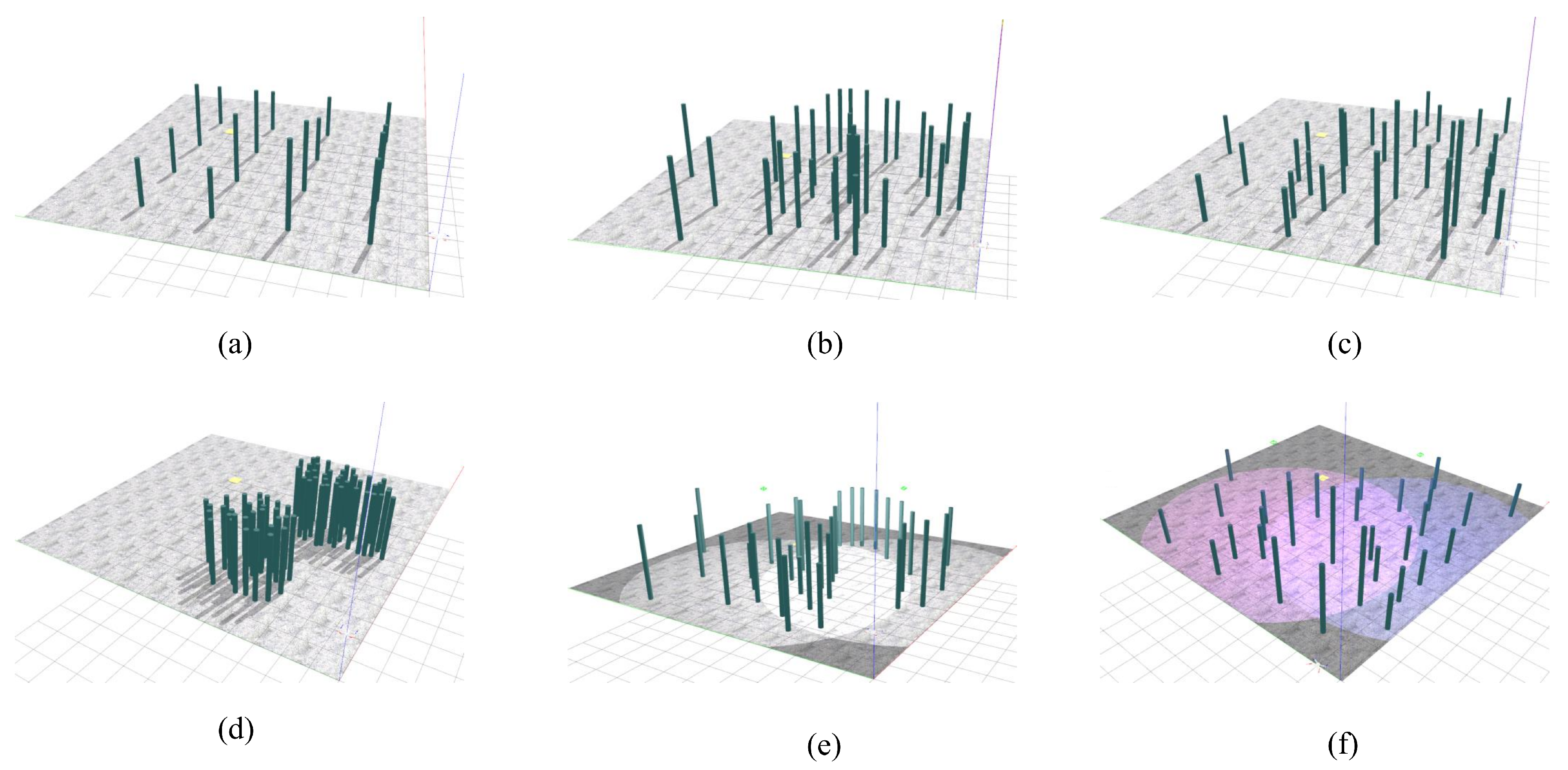
4.1. Simulation Experiment
4.1.1. Simulation Training Design
| Algorithm 1 PPO (Proximal Policy Optimization) optimization algorithm with clipped advantage |
|
4.1.2. Simulation Training Process
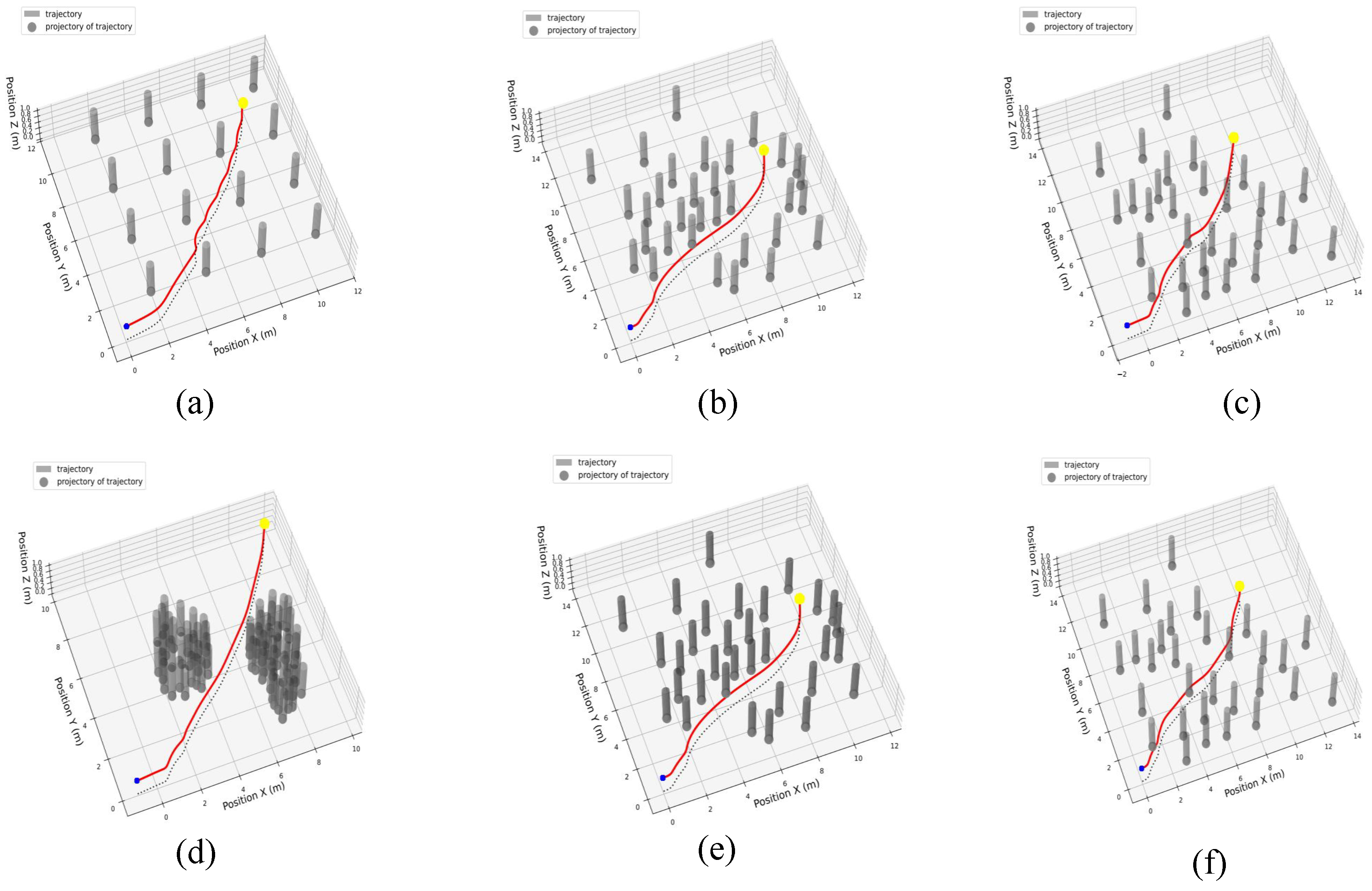
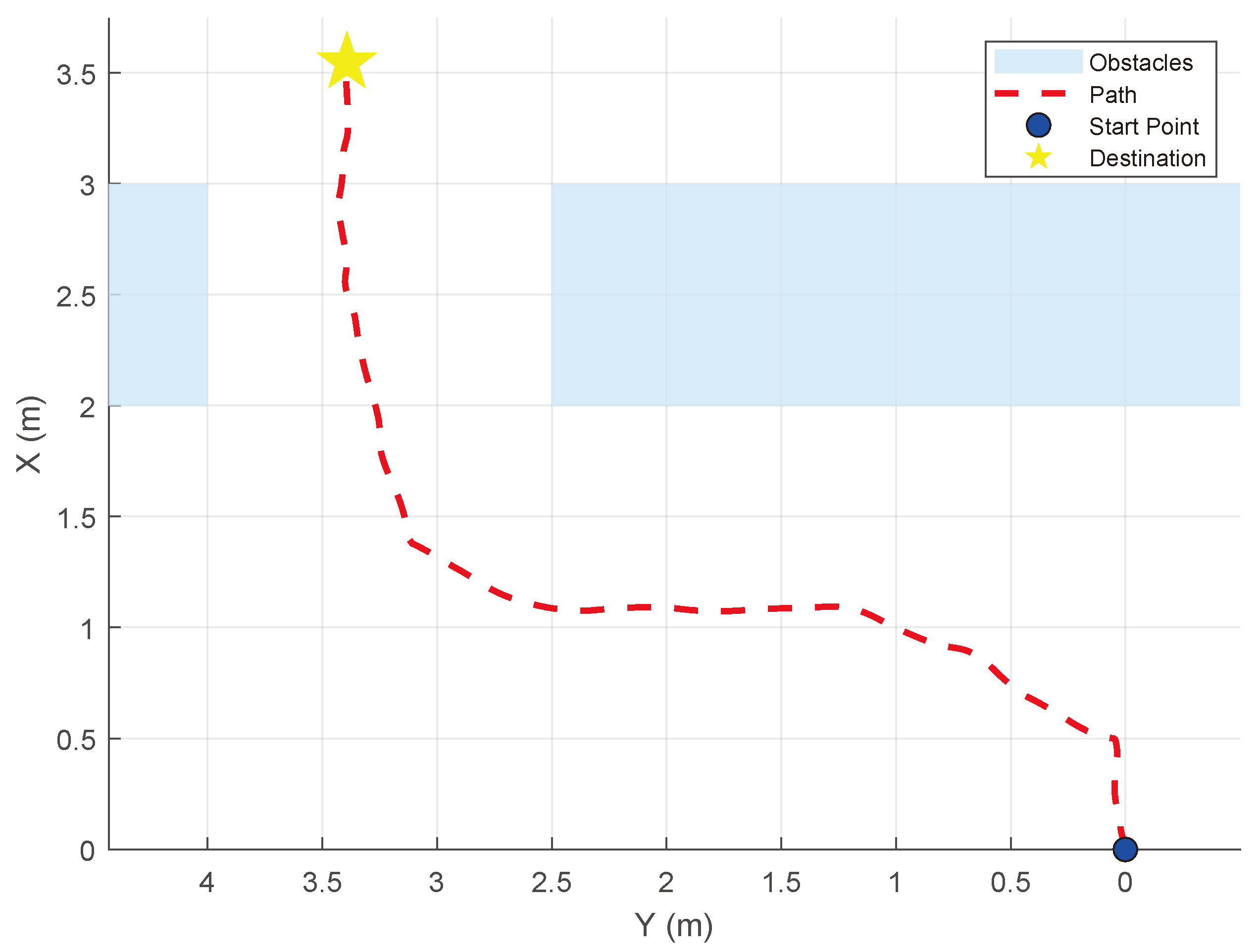
4.1.3. Simulation Training Result
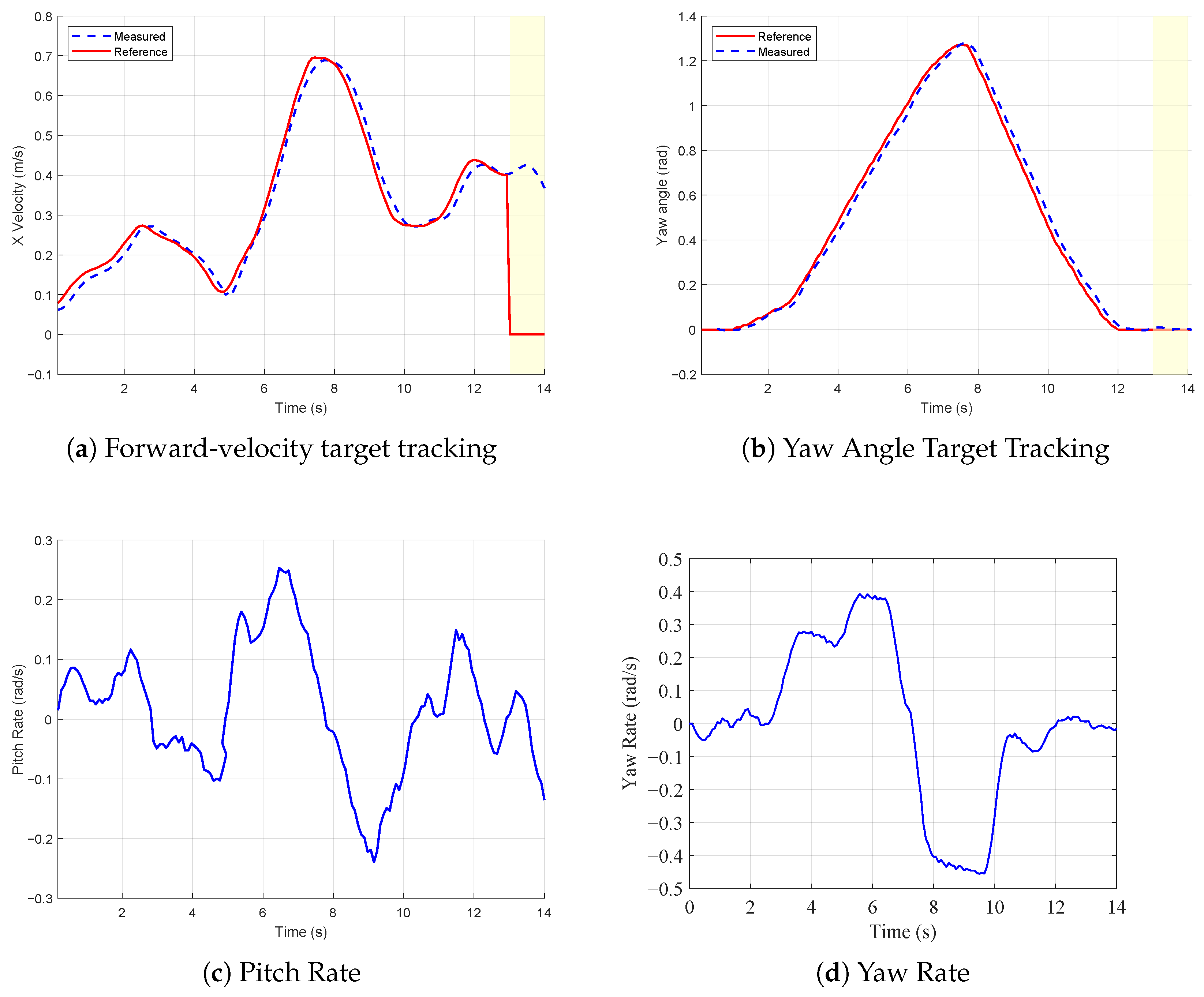
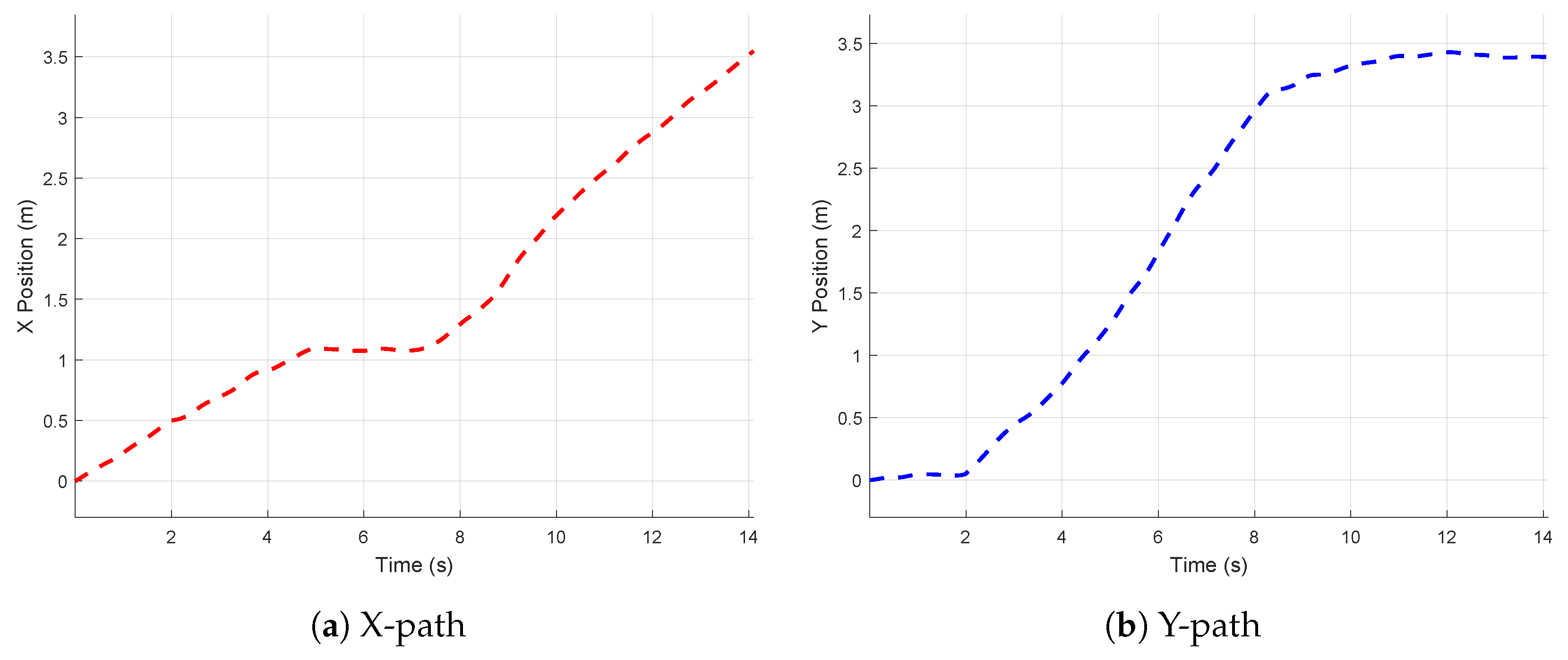
4.2. Real-World Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rezwan, S.; Choi, W. Artificial intelligence approaches for UAV navigation: Recent advances and future challenges. IEEE Access 2022, 10, 26320–26339. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Wang, G.; Chen, Y.; An, P.; Hong, H.; Hu, J.; Huang, T. UAV-YOLOv8: A small-object-detection model based on improved YOLOv8 for UAV aerial photography scenarios. Sensors 2023, 23, 7190. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, T.; Huang, S.; Li, K. A hybrid optimization framework for UAV reconnaissance mission planning. Comput. Ind. Eng. 2022, 173, 108653. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, Y.; Huang, C.; Huang, H. Unmanned aerial vehicles for search and rescue: A survey. Remote Sens. 2023, 15, 3266. [Google Scholar] [CrossRef]
- Srivastava, A.; Prakash, J. Techniques, answers, and real-world UAV implementations for precision farming. Wirel. Pers. Commun. 2023, 131, 2715–2746. [Google Scholar] [CrossRef]
- Ghambari, S.; Golabi, M.; Jourdan, L.; Lepagnot, J.; Idoumghar, L. UAV path planning techniques: A survey. RAIRO-Oper. Res. 2024, 58, 2951–2989. [Google Scholar] [CrossRef]
- Wooden, D.; Malchano, M.; Blankespoor, K.; Howardy, A.; Rizzi, A.A.; Raibert, M. Autonomous navigation for BigDog. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4736–4741. [Google Scholar]
- Hening, S.; Ippolito, C.A.; Krishnakumar, K.S.; Stepanyan, V.; Teodorescu, M. 3D LiDAR SLAM integration with GPS/INS for UAVs in urban GPS-degraded environments. In Proceedings of the AIAA Information Systems-AIAA Infotech@ Aerospace, Kissimmee, FL, USA, 8–12 January 2017; p. 0448. [Google Scholar]
- Kumar, G.A.; Patil, A.K.; Patil, R.; Park, S.S.; Chai, Y.H. A LiDAR and IMU integrated indoor navigation system for UAVs and its application in real-time pipeline classification. Sensors 2017, 17, 1268. [Google Scholar] [CrossRef]
- Qin, H.; Meng, Z.; Meng, W.; Chen, X.; Sun, H.; Lin, F.; Ang, M.H. Autonomous exploration and mapping system using heterogeneous UAVs and UGVs in GPS-denied environments. IEEE Trans. Veh. Technol. 2019, 68, 1339–1350. [Google Scholar] [CrossRef]
- Gomez-Ojeda, R.; Moreno, F.A.; Zuniga-Noël, D.; Scaramuzza, D.; Gonzalez-Jimenez, J. PL-SLAM: A stereo SLAM system through the combination of points and line segments. IEEE Trans. Robot. 2019, 35, 734–746. [Google Scholar] [CrossRef]
- Zhou, H.; Zou, D.; Pei, L.; Ying, R.; Liu, P.; Yu, W. StructSLAM: Visual SLAM with building structure lines. IEEE Trans. Veh. Technol. 2015, 64, 1364–1375. [Google Scholar] [CrossRef]
- Low, D.G. Distinctive image features from scale-invariant keypoints. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Cho, G.; Kim, J.; Oh, H. Vision-based obstacle avoidance strategies for MAVs using optical flows in 3-D textured environments. Sensors 2019, 19, 2523. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, W.G.; Álvarez, L.; Grijalva, S.; Rojas, I. Monocular vision-based dynamic moving obstacles detection and avoidance. In Proceedings of the Intelligent Robotics and Applications: 12th International Conference, ICIRA 2019, Shenyang, China, 8–11 August 2019; Proceedings, Part V 12. pp. 386–398. [Google Scholar]
- Mahjri, I.; Dhraief, A.; Belghith, A.; AlMogren, A.S. SLIDE: A straight line conflict detection and alerting algorithm for multiple unmanned aerial vehicles. IEEE Trans. Mob. Comput. 2017, 17, 1190–1203. [Google Scholar] [CrossRef]
- Miller, A.; Miller, B. Stochastic control of light UAV at landing with the aid of bearing-only observations. In Proceedings of the Eighth International Conference on Machine Vision (ICMV 2015), Barcelona, Spain, 19–21 November 2015; Volume 9875, pp. 474–483. [Google Scholar]
- Expert, F.; Ruffier, F. Flying over uneven moving terrain based on optic-flow cues without any need for reference frames or accelerometers. Bioinspiration Biomimetics 2015, 10, 026003. [Google Scholar] [CrossRef]
- Goh, S.T.; Abdelkhalik, O.; Zekavat, S.A.R. A weighted measurement fusion Kalman filter implementation for UAV navigation. Aerosp. Sci. Technol. 2013, 28, 315–323. [Google Scholar] [CrossRef]
- Mnih, V. Playing atari with deep reinforcement learning. arXiv 2013. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep reinforcement learning framework for autonomous driving. arXiv 2017, arXiv:1704.02532. [Google Scholar] [CrossRef]
- Faust, A.; Oslund, K.; Ramirez, O.; Francis, A.; Tapia, L.; Fiser, M.; Davidson, J. Prm-rl: Long-range robotic navigation tasks by combining reinforcement learning and sampling-based planning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5113–5120. [Google Scholar]
- Pham, H.X.; La, H.M.; Feil-Seifer, D.; Nguyen, L.V. Autonomous uav navigation using reinforcement learning. arXiv 2018. [Google Scholar] [CrossRef]
- Loquercio, A.; Maqueda, A.I.; Del-Blanco, C.R.; Scaramuzza, D. Dronet: Learning to fly by driving. IEEE Robot. Autom. Lett. 2018, 3, 1088–1095. [Google Scholar] [CrossRef]
- Lu, Y.; Xue, Z.; Xia, G.S.; Zhang, L. A survey on vision-based UAV navigation. Geo-Spat. Inf. Sci. 2018, 21, 21–32. [Google Scholar] [CrossRef]
- Chen, T.; Gupta, S.; Gupta, A. Learning exploration policies for navigation. arXiv 2019. [Google Scholar] [CrossRef]
- Polvara, R.; Patacchiola, M.; Sharma, S.; Wan, J.; Manning, A.; Sutton, R.; Cangelosi, A. Autonomous quadrotor landing using deep reinforcement learning. arXiv 2017, arXiv:1709.03339. [Google Scholar]
- Kalidas, A.P.; Joshua, C.J.; Md, A.Q.; Basheer, S.; Mohan, S.; Sakri, S. Deep reinforcement learning for vision-based navigation of UAVs in avoiding stationary and mobile obstacles. Drones 2023, 7, 245. [Google Scholar] [CrossRef]
- AlMahamid, F.; Grolinger, K. VizNav: A Modular Off-Policy Deep Reinforcement Learning Framework for Vision-Based Autonomous UAV Navigation in 3D Dynamic Environments. Drones 2024, 8, 173. [Google Scholar] [CrossRef]
- Xu, G.; Jiang, W.; Wang, Z.; Wang, Y. Autonomous obstacle avoidance and target tracking of UAV based on deep reinforcement learning. J. Intell. Robot. Syst. 2022, 104, 60. [Google Scholar] [CrossRef]
- Yang, J.; Lu, S.; Han, M.; Li, Y.; Ma, Y.; Lin, Z.; Li, H. Mapless navigation for UAVs via reinforcement learning from demonstrations. Sci. China Technol. Sci. 2023, 66, 1263–1270. [Google Scholar] [CrossRef]
- Zhao, H.; Fu, H.; Yang, F.; Qu, C.; Zhou, Y. Data-driven offline reinforcement learning approach for quadrotor’s motion and path planning. Chin. J. Aeronaut. 2024, 37, 386–397. [Google Scholar] [CrossRef]
- Sun, T.; Gu, J.; Mou, J. UAV autonomous obstacle avoidance via causal reinforcement learning. Displays 2025, 87, 102966. [Google Scholar] [CrossRef]
- Sonny, A.; Yeduri, S.R.; Cenkeramaddi, L.R. Q-learning-based unmanned aerial vehicle path planning with dynamic obstacle avoidance. Appl. Soft Comput. 2023, 147, 110773. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Z.; Zhou, D.; Shi, J.; Deng, R. Vision-Based Deep Reinforcement Learning of UAV Autonomous Navigation Using Privileged Information. arXiv 2024. [Google Scholar] [CrossRef]
- Samma, H.; El-Ferik, S. Autonomous UAV Visual Navigation Using an Improved Deep Reinforcement Learning. IEEE Access 2024, 12, 79967–79977. [Google Scholar] [CrossRef]
- Shao, X.; Zhang, F.; Liu, J.; Zhang, Q. Finite-Time Learning-Based Optimal Elliptical Encircling Control for UAVs With Prescribed Constraints. IEEE Trans. Intell. Transp. Syst. 2025, 26, 7065–7080. [Google Scholar] [CrossRef]
- Li, X.; Cheng, Y.; Shao, X.; Liu, J.; Zhang, Q. Safety-Certified Optimal Formation Control for Nonline-ar Multi-Agents via High-Order Control Barrier Function. IEEE Internet Things J. 2025, 12, 24586–24598. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Moreno-Valenzuela, J. PID control of quadrotor UAVs: A survey. Annu. Rev. Control 2023, 56, 100900. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Suzuki, S.; Namiki, A.; Liu, H.; Li, Z. Design and implementation of UAV velocity controller based on reference model sliding mode control. Drones 2023, 7, 130. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Suzuki, S. UAV trajectory tracking under wind disturbance based on novel antidisturbance sliding mode control. Aerosp. Sci. Technol. 2024, 149, 109138. [Google Scholar] [CrossRef]
- Zeghlache, S.; Rahali, H.; Djerioui, A.; Benyettou, L.; Benkhoris, M.F. Robust adaptive backstepping neural networks fault tolerant control for mobile manipulator UAV with multiple uncertainties. Math. Comput. Simul. 2024, 218, 556–585. [Google Scholar] [CrossRef]
- Ramezani, M.; Habibi, H.; Sanchez-Lopez, J.L.; Voos, H. UAV path planning employing MPC-reinforcement learning method considering collision avoidance. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; pp. 507–514. [Google Scholar]
- Li, S.; Shao, X.; Wang, H.; Liu, J.; Zhang, Q. Adaptive Critic Attitude Learning Control for Hypersonic Morphing Vehicles without Backstepping. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 8787–8803. [Google Scholar] [CrossRef]
- Zhang, Q.; Dong, J. Disturbance-observer-based adaptive fuzzy control for nonlinear state constrained systems with input saturation and input delay. Fuzzy Sets Syst. 2020, 392, 77–92. [Google Scholar] [CrossRef]
- Tian, Y.; Chang, Y.; Arias, F.H.; Nieto-Granda, C.; How, J.P.; Carlone, L. Kimera-multi: Robust, distributed, dense metric-semantic slam for multi-robot systems. IEEE Trans. Robot. 2022, 38, 2022–2038. [Google Scholar] [CrossRef]
- Yang, M.; Yao, M.R.; Cao, K. Overview on issues and solutions of SLAM for mobile robot. Comput. Syst. Appl. 2018, 27, 1–10. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, X.; Zhang, Z.; Wang, K.; Wang, Y.; Xiong, R.; Liao, Y. Ngel-slam: Neural implicit representation-based global consistent low-latency slam system. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; Volume 2024, pp. 6952–6958. [Google Scholar]
- Pendleton, S.D.; Andersen, H.; Du, X.; Shen, X.; Meghjani, M.; Eng, Y.H.; Rus, D.; Ang, M.H. Perception, planning, control, and coordination for autonomous vehicles. Machines 2017, 5, 6. [Google Scholar] [CrossRef]
- Airlangga, G.; Sukwadi, R.; Basuki, W.W.; Sugianto, L.F.; Nugroho, O.I.A.; Kristian, Y.; Rahmananta, R. Adaptive Path Planning for Multi-UAV Systems in Dynamic 3D Environments: A Multi-Objective Framework. Designs 2024, 8, 136. [Google Scholar] [CrossRef]
- Airlangga, G.; Sukwadi, R.; Basuki, W.W.; Sugianto, L.F.; Nugroho, O.I.A.; Kristian, Y.; Rahmananta, R. Multi-objective path planning of an autonomous mobile robot using hybrid PSO-MFB optimization algorithm. Appl. Soft Comput. 2020, 89, 106076. [Google Scholar]
- Wu, H. Model-Free UAV Navigation in Unknown Complex Environments Using Vision-Based Reinforcement Learning. Figshare, 6 May 2025. Video, 37 Seconds. Available online: https://figshare.com/articles/media/Model-Free_UAV_Navigation_in_Unknown_Complex_Environments_Using_Vision-Based_Reinforcement_Learning/28934846/1?file=54234020 (accessed on 26 July 2025).
- Wu, H. Model-Free UAV Navigation in Unknown Complex Environments Using Vision-Based Reinforcement Learning. 26 July 2025. Available online: https://github.com/ORI-coderH/Vision-Based-RL-Navigation.git (accessed on 26 July 2025).
- Furrer, F.; Burri, M.; Achtelik, M.; Siegwart, R. Robot Operating System (Ros): The Complete Reference (Volume 1); Springer International Publishing: Cham, Switzerland, 2016; Volume 1, pp. 595–625. [Google Scholar]
- López, E.; García, S.; Barea, R.; Bergasa, L.M.; Molinos, E.J.; Arroyo, R.; Romera, E.; Pardo, S. A Multi-Sensorial Simultaneous Localization and Mapping (SLAM) System for Low-Cost Micro Aerial Vehicles in GPS-Denied Environments. Sensors 2017, 17, 802. [Google Scholar] [CrossRef]
- Norbelt, M.; Luo, X.; Sun, J.; Claude, U. UAV Localization in Urban Area Mobility Environment Based on Monocular VSLAM with Deep Learning. Drones 2025, 9, 171. [Google Scholar] [CrossRef]
- Elamin, A.; El-Rabbany, A.; Jacob, S. Event-Based Visual/Inertial Odometry for UAV Indoor Navigation. Sensors 2025, 25, 61. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Z.; Zhou, D.; Shi, J.; Deng, R. Vision-Based Deep Reinforcement Learning of Unmanned Aerial Vehicle (UAV) Autonomous Navigation Using Privileged Information. Drones 2024, 8, 782. [Google Scholar] [CrossRef]
- Tezerjani, M.D.; Khoshnazar, M.; Tangestanizadeh, M.; Kiani, A.; Yang, Q. A survey on reinforcement learning applications in slam. arXiv 2024. [Google Scholar] [CrossRef]
- Kolagar, S.A.A.; Shahna, M.H.; Mattila, J. Combining Deep Reinforcement Learning with a Jerk-Bounded Trajectory Generator for Kinematically Constrained Motion Planning. arXiv 2024. [CrossRef]










| Study | Approach | Advantages | Limitations |
|---|---|---|---|
| [9] | SLAM + LiDAR + EKF | High local positioning accuracy | Performance degrades in unknown complex environments |
| [10] | LiDAR–IMU scan-matching + Kalman filter | Good indoor SLAM performance | Limited LiDAR stability; high computational load |
| [15,16,17] | Vision-/sensor-based obstacle avoidance | No global map required | Vulnerable to recognition errors and delays |
| [18,19,20] | EKF/UKF filtering | Reduces noise | Sensitive to environment and noise |
| [24] | PRM + RL | Better indoor navigation | Depends on pre-generated maps; poor real-time adaptability |
| [25] | PID + Q-learning | Demonstrates RL potential | Input limited to position; discrete action space |
| [28] | Q-learning (RGB) | Basic avoidance | Struggles under poor lighting/occlusion |
| [29] | DQN + Camera | Simplified landing control | Ignores dynamic obstacles; discrete actions |
| [32] | MPTD3 | Faster convergence | Single-objective; limited generalization |
| [33] | SACfD | Mapless navigation | Highly dependent on expert data; no multi-objective |
| [34] | Offline RL + Q-value estimation | Improved robustness | Weak real-time adaptability |
| [35] | Causal RL | Faster reaction | Only optimizes safety; ignores efficiency |
| [36] | Classic Q-learning | Reduced path length | Low resolution; ignores energy and robustness |
| Parameters | Values | Units |
|---|---|---|
| Total mass | 2.1 | kg |
| Rotational inertia along the x-axis | 0.0358 | kg·m2 |
| Rotational inertia along the y-axis | 0.0559 | kg·m2 |
| Rotational inertia along the z-axis | 0.0988 | kg·m2 |
| Rotor arm length | 0.511 | m |
| Fuselage width | 0.472 | m |
| Fuselage height | 0.120 | m |
| Individual rotor mass | 0.0053 | kg |
| Rotor diameter | 0.230 | m |
| Maximum rotor angular velocity | 858 | rad/s |
| Parameter | Value | Unit |
|---|---|---|
| Field of View (FOV) | 87° × 58° | degrees |
| Minimum depth range (Min-Z) | 0.2 | m |
| Maximum depth range (Max-Z) | 10 | m |
| Resolution | 640 × 480 | pixels |
| Frame rate | 30 | FPS |
| Sensor technology | Time-of-Flight | – |
| Depth accuracy | of distance | |
| Camera dimensions | 100 × 50 × 30 | mm |
| Hyperparameter | Value |
|---|---|
| Update Interval (s) | s |
| Total Step Count | |
| Steps per Episode | 800 |
| State Space Dimensions | 128 |
| Action Space Dimensions | 2 |
| Batch Timesteps | 2048 |
| Reward Discount Factor | 0.99 |
| Updates per Iteration | 10 |
| Learning Rate | |
| Clip Function Threshold | 0.25 |
| Covariance Matrix Value | 0.5 |
| Method | Value (ms) | Our (ms) | Improvement (%) |
|---|---|---|---|
| [57] | 130 | 28 | 78.46 |
| [58] | 41–45 | 28 | 34.88 |
| [59] | 38 | 28 | 26.32 |
| Method | Success Rate (%) | Task Time (s) |
|---|---|---|
| Proposed Method | ∼100 | 5–12 |
| [60] | 95–97 | 8–18 |
| [61] | 94.8 | 13–23 |
| Method | Task Time (s) | Energy Consumption |
|---|---|---|
| With energy-related | 6.23 | 1.1022 |
| Without energy-related | 6.63 | 1.2132 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Wang, W.; Wang, T.; Suzuki, S. Model-Free UAV Navigation in Unknown Complex Environments Using Vision-Based Reinforcement Learning. Drones 2025, 9, 566. https://doi.org/10.3390/drones9080566
Wu H, Wang W, Wang T, Suzuki S. Model-Free UAV Navigation in Unknown Complex Environments Using Vision-Based Reinforcement Learning. Drones. 2025; 9(8):566. https://doi.org/10.3390/drones9080566
Chicago/Turabian StyleWu, Hao, Wei Wang, Tong Wang, and Satoshi Suzuki. 2025. "Model-Free UAV Navigation in Unknown Complex Environments Using Vision-Based Reinforcement Learning" Drones 9, no. 8: 566. https://doi.org/10.3390/drones9080566
APA StyleWu, H., Wang, W., Wang, T., & Suzuki, S. (2025). Model-Free UAV Navigation in Unknown Complex Environments Using Vision-Based Reinforcement Learning. Drones, 9(8), 566. https://doi.org/10.3390/drones9080566






